1 Introduction

Blood donation is an essential component of the Blood Supply Chain Network (BSCN); today, almost every blood supply center relies on blood donations daily. According to the World Health Organization, 118.5 million people donate blood each year, with 40% of those donations coming from high-income countries, which account for 16% of the global population. In the United States, about 10 million units of blood are required each year (World Health Organization, 2020).

Blood consists of various components, including Plasma, Platelets, Red Blood Cells (RBCs), and Cryoprecipitate. Blood may be stored as whole blood or fractionated in a central blood facility center due to blood fractionation. They have a different shelf life, cross-matching, and require different storage conditions. Table 1 represents blood groups that can be donated to other blood groups. Each blood group is separated into two subgroups. For instance, blood group A is divided by A- and A + subgroups. Also, substituting these two subgroups must adhere to both ABO-Rh(D) compatible alternatives and preferential ABO-Rh(D) rules to ensure safety during transfusion (Dehdari Ebrahimi et al., 2022; Dillon et al., 2017).

Table 1 RBCs Cross-matching (American Red Cross, 2020b)
Full size table

This paper studied a Closed-Loop Blood Supply Chain Network (CLBSCN), consisting of several stages, including RBC collection, screening, processing, storage, distribution, transportation, and medical procedure. Multiple processes are needed at each stage to ensure the safety of the blood transshipment. Also, the blood facility center determines a blood donor’s eligibility for donating blood. The blood examination, called Screening Processing (SP), begins once the blood is collected at the blood center to differentiate healthy from unhealthy blood to prevent infectious diseases. When the SP is completed, the blood bags are either deployed for clinical use or discarded and shipped to the disposal center (World Health Organization, 2009). The blood being deployed for clinical use is then processed and stored before being transferred to the national blood bank to meet a hospital’s demand. The blood bank is in charge of distributing and using healthy blood at the hospital level. Finally, the outdated units must be retrieved from blood banks and hospitals to be transferred and discarded at the disposal center.

A growing concern regarding an efficient CLBSCN is two-fold; first, the total costs of every supply chain should be minimized (Billal et al., 2022; Dehghani et al., 2021; Ebrahimi et al., 2022; Ghahremani-Nahr et al., 2022; Khalilpourazari & Hashemi Doulabi, 2022; Zhou et al., 2021). Second, the service level of the patients should be maximized. When these two goals are met, it can be said that the designed CLBSCN is efficient and has considered patients’ needs. Also, to meet the service level of each patient, blood substitution plays an important role, which has been addressed in this study as lateral resupply (Arani et al., 2020). In this way, patients need to receive the same blood groups if they exist. In emergencies, if the requested blood group is unavailable, a cross-matching must be done to find a blood group that matches the patient’s need (see Table 1). Also, blood substitution can reduce the possibility of shortages at hospitals and national blood banks, which have some benefits for the decision-makers to decide properly (Arani et al., 2020; Dehghani & Abbasi, 2018; Eren & Chan, 2015; Momenitabar et al., 2022).

According to the explanations mentioned above, this study, for the first time, considers the newly objective functions that aim to maximize the minimum service level of patients at the hospitals besides the cost minimization that exists in published studies to avoid patient death and provide more alternative to the patient’s health with unmatched blood groups (Fahimnia et al., 2017; Zahiri et al., 2018). Furthermore, due to some fluctuations in blood supplies and demand, which have a major impact on the network’s performance and increases the complexity of designing the CLBSCN, this study includes some uncertainty elements to simulate the real condition of blood banks. Therefore, the issue of uncertainty should be carefully addressed to efficiently design the CLBSCN.

Based on what was discussed, this study aims to design an efficient CLBSCN by proposing a fuzzy Mixed-Integer Non-Linear Programming (MINLP) model. Also, demand and supply are considered fuzzy numbers for better approximating reality, and they are included in temporary and permanent blood facility centers and hospitals. The proposed fuzzy mathematical model in Sect. 3 is converted to a crisp mathematical model and then solved by two different approaches, including Torabi-Hasini (TH) method proposed by Torabi and Hassini (2008) and Gholamian-Mahdavi-Mahdavi Amiri-TavakkoliMoghaddam (GMMT) method proposed by Gholamian et al. (2021). These two approaches are compared together to find the best one for the proposed model of this study. Then, the result of the model is provided in detail, and sensitivity analysis is conducted on some crucial parameters to measure the scalability of the proposed model.

By conducting this study, we are looking for the answer to the following questions as follows:

  • What effect does the lateral resupply system have on the two proposed objective functions?

  • What methods, including TH and GMMT, could efficiently reach the solution more robustly?

  • What would be the effects of demand, supply, and capacity on the two proposed objective functions?

The rest of the paper is organized as follows: Sect. 2 identifies the published studies in the past and finds the research gap in this study. Section 3 describes the problem definition and the mathematical model of this study. Section 4 presents the solution methodologies of the proposed model. In Sect. 5, the case study is considered to validate the proposed model, and the result of the model has been discussed. Also, sensitivity analysis of critical parameters of the model has been brought to show how much they affect the two objective functions. Finally, the conclusion and future research directions are provided in Sect. 6.

2 Literature review

This section aims to review the past studies related to CLBSCN. Table 2 organized a more comprehensive list of published studies in different terms, including objective functions, solution methodologies, and the case studies applied by researchers to easily find the research gaps in this study. Also, the current state of the CLBSCN is reviewed by three papers that applied diverse viewpoints to the components of the CLBSCN (Beliën & Forcé, 2012; Osorio et al., 2015; Pirabán et al., 2019).

Table 2 List of previous studies
Full size table

Many studies have addressed the CLBSCN, which is in line with this approach (Attari & Jami, 2018; Eskandari-Khanghahi et al., 2018; Heidari-Fathian & Pasandideh, 2018; Hosseini-Motlagh et al., 2020a, 2020b; Masoumi et al., 2017; Nagurney & Dutta, 2019; Samani & Hosseini-Motlagh, 2019). For instance, an integrated supply chain network for a blood platelet bank, including donor groups, blood collection facilities, distribution centers, and hospitals as the demand points is proposed by Eskandari-Khanghahi et al. (2018). Heidari-Fathian and Pasandideh (2018) designed a BSCN by proposing a mixed-integer mathematical programming model to minimize the total environmental adverse effects. Arani et al. (2020) proposed robust possibilistic programming models by including outdated units and cross-matching to design a BSCN incorporating an integrated inventory system. They applied the concept of lateral resupply to avoid hospital shortages in the other hospitals’ inventories. In another study, Masoumi et al. (2017) presented an optimization model to design the BSCN for pre-and post-merger and acquisition models within blood bank systems to produce the optimal route and connection flow based on operating and disposal costs over time. Nagurney and Dutta (2019) proposed a generalized Nash equilibrium BSCN model of competition among blood service organizations. Also, they applied a variant equilibrium concept and used a Lagrange analysis to produce economic insights. Hosseini-Motlagh et al., (2020a, 2020b) presented a bi-objective model to design the CLBSCN under uncertainty to optimize two objective functions, including network costs and blood substitution, by considering blood demand and facility disruptions as uncertain parameters. Eskandari-Khanghahi et al. (2018) developed a mixed-integer linear programming model to construct and optimize the CLBSCN connected to blood products with three objective functions. Also, they utilized the ε-constraint method to convert the multi-objective model to a single-objective one.

In real-world instances, supply and demand are uncertain parameters. When designing a CLBSCN, the degree of uncertainty has a major impact on the CLBSCN. Some studies considered supply and demand parameters as deterministic (Duan et al., 2018; Maeng et al., 2018; Sawadogo et al., 2019; Vermeulen et al., 2019); others treated them as stochastic (Ayer et al., 2018; Dehghani & Abbasi, 2018; Lowalekar & Ravichandran, 2017). Also, a few studies considered them a fuzzy number (Eskandari-Khanghahi et al., 2018; Rabbani et al., 2017; Samani & Hosseini-Motlagh, 2019; Zahiri & Pishvaee, 2017). Considering the volatility in demand, Zahiri and Pishvaee (2017) considered the blood group compatibility to design a BSCN by proposing a bi-objective mathematical model to minimize unsatisfied demand and the total cost of the network. A stochastic bi-objective optimization model for the BSCN in a disaster situation is proposed by Fahimnia et al. (2017) to minimize the total cost of the network and delivery time. They solved the model by combining ε-constraint and Lagrangian relaxation methods to obtain the result. Yaghoubi et al. (2020) designed an efficient BSCN of multiple platelet-derived to consider trade-offs between the network’s costs and platelet’s freshness. Ensafian et al. (2017) applied a robust optimization approach to face uncertainty and objective multiplicity. Indeed, they applied two credibility-based robust possibilistic approaches to cope with imprecise input parameters like a demand. Similarly, Rabbani et al. (2017) proposed a multi-objective possibilistic integer linear programming model. The proposed model is divided into two phases; first, the original model is converted to an auxiliary crisp multi-objective integer linear model, and second, the model is solved by applying a fuzzy programming solution. Laslty, Attari and Jami (2018) proposed a two-stage stochastic bi-objective model to minimize the total costs and the time for blood transfusion. To solve the model, they considered three methods simultaneously considering two types of uncertainties.

Blood substitution is among the critical decisions that need to be paid attention to avoid shortage in the BSCN. Arani et al. (2020) proposed an optimization model to design a CLBSCN considering lateral resupply, which allows hospitals to satisfy the demand by the other hospitals’ inventories in the absence of the required product at the blood center and its excess in any hospital. Zahiri and Pishvaee (2017) addressed the design of BSCN considering blood group compatibility and substitution in their model. Similar to Zahiri and Pishvaee (2017), Hosseini-Motlagh et al., (2020a, 2020b) designed a CLBSCN considering blood group compatibility, blood substitution, location, and capacity decisions. Some other studies considered blood substitution when one type of blood is unavailable. For instance, Salehi et al. (2019) presented a robust stochastic model to design a BSCN during a possible earthquake in Tehran. Also, they included the possibility of transfusion of one blood type to other types based on the medical requirements in their model. In a similar study, Zhou et al. (2021) proposed a dynamic decision-making frame for designing a BSCN using the Estimated Withdrawal & Aging strategy. A recent study by Dehghani et al. (2021) considered the proactive transshipment policy to avoid future shortages. Also, they formulated the problem as a two-stage stochastic programming model, and the Quasi-Monte Carlo sampling approach is employed to determine the optimal number of scenarios by conducting stability tests. Also, they found that considering the transshipment policy reduced the total costs of the BSCN.

Based on the published studies reviewed in this section, a few studies considered the maximization of minimum service level to the patients as a separate objective. Also, the concept of lateral resupply is rarely studied by researchers, and its effect has not been investigated on the CLBSCN. Also, a few studies included an outdated blood unit in their CLBSCN to collect the returned blood from BFCs, BMs, NBBs, and hospitals. Paying attention to these research gaps as mentioned, this study, for the first time, considers the concept of maximization of minimum service level at the Hospital, finding an appropriate location of disposal centers, and concept of lateral resupply simultaneously to design an efficient CLBSCN by avoiding shortage happening at the hospitals. Therefore, the main contributions of this study can be summarized as follows:

  • Designing an efficient CLBSCN, considering the concept of lateral resupply to avoid shortage at hospitals by maximizing the minimum service Laval to each patient.

  • Coping with uncertainty by utilizing an interactive fuzzy possibilistic programming approach, including TH and GMMT methods, and comparing them to find the best one for the proposed model of this study.

3 Problem definition

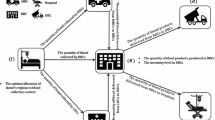
This paper addresses the design of RBC multi-echelon CLBSCN, which includes donors in the first level, blood facility centers (BFCs), bloodmobiles (BMs) at the second level (for more difference between BMs and BFCs), national blood banks (NBBs) in the third level, hospitals as demand points at the fourth level, and blood disposal centers (BDCs) located at the last level of CLBSCN for outdated blood returned from hospitals, NBBs, BFCs, and BMs (Momenitabar et al., 2020; Zahiri et al., 2018). The proposed network is schematically represented in Fig. 1. Initially, the network deals with donors who arrive at the facility to donate blood. The donated blood is collected by either permanent blood facilities centers (BFCs) or temporary bloodmobiles (BMs). When the donors arrive at the BFCs or BMs, they must be registered and screened to prevent transmitting diseases such as HIV, HCV, HBV, and Syphilis caused by blood transfusion. In BFCs, collected blood must be processed and stored. Some collected blood is directed to the BFCs from BMs for more examination. After that, the collected blood is tested for any blood diseases. During the third phase, hospitals place orders with the assigned NBBs and are allowed to keep inventories of substitute RBCs that can be administered following medical guidelines.

Fig. 1
figure 1

Structure of multi-echelon CLBSCN

Full size image

Moreover, blood can be collected and stored at the hospitals to be used for the patients. Hospitals also link together to prevent any supply shortage that NBBs may not fulfill. The outdated blood in hospitals, NBB, BFC, and BM are also sent to the disposal centers.

In this study, the main reason for establishing the BDC is to gather the returned outdated blood units from the BM, BFC, NBB, and Hospitals. Also, lateral resupply is utilized to govern the interconnections of hospitals’ excess blood units and permit a hospital to cater to its demand by the other hospitals’ inventories in the absence of the required product at the Hospital (Arani et al., 2020). More interestingly, demand and supply are considered uncertain parameters due to the nature of these parameters worldwide. Additionally, RBCs units are categorized based on the two significant medical preferences, including blood types and Rh(D) factors. There are eight blood groups for RBC, and the compatibility matrix of ABO-Rh(D) is considered in blood assignment to the patients. As illustrated in Table 1, the medical preferences are categorized in a compatibility matrix. Table 3 displays the ABO-Rh(D) priority orders for substituting blood groups. Based on this, the penalty factor for any replaced blood unit is considered for this study.

Table 3 RBC ABO-Rh(D) Priority (Hosseini-Motlagh et al., 2020a, 2020b)
Full size table

Also, some assumptions have been considered to build the model, which are listed as follows:

  • The blood units are transferred between hospitals to alleviate shortages (Arani et al., 2020; Dehghani & Abbasi, 2018).

  • Each period is one day (Arani et al., 2020).

  • Capacity is limited at each BFC, NBB, Hospital, and BDC level (Khalilpourazari & Hashemi Doulabi, 2022; Shirazi et al., 2021).

  • The blood demand and supply are considered fuzzy numbers (Attari & Jami, 2018; Babaee Tirkolaee & Aydın, 2021).

  • The shelf life of RBC units is integrated into the formulation along with cross-matching and the FIFO policy (Arani et al., 2020; Hosseini-Motlagh et al., 2020a, 2020b; Samani & Hosseini-Motlagh, 2019).

  • The locations of blood donors and hospitals are predetermined (Arani et al., 2020).

  • Hospitals may encounter shortages anytime, and backorders are neglected (Zahiri & Pishvaee, 2017; Zahiri et al., 2018).

  • The ABO-Rh(D) compatibility matrix priority rule is regarded (Ghatreh Samani et al., 2018; Hosseini-Motlagh et al., 2020a, 2020b).

Furthermore, this study aims to ascertain the various decision variables by solving the fuzzy multi-objective MINLP model, including the number of blood units substituted between the hospitals in each period, the inventory level of blood units, and the number of outdated types of blood in NBBs and hospitals in each period, and the blood shortage units at each Hospital in each period.

Figure 2 shows the conceptual outline of the model of this study, including various fuzzy parameters such as supply, demand, wastage costs, transportation costs, and many other parameters as main inputs to the mathematical model, in which two objective functions display minimization and maximization goals, and constraints constructing a feasible solution, and main outputs are the number of decisions variables in a deterministic space. By proposing a fuzzy multi-objective MINLP model, the allocation of different levels of the network, inventory blood units, blood inventory levels, inventory assignment, blood substitution units, and service levels have been defined. Also, the framework of this study is shown in Fig. 3. In the upcoming paragraphs, we define the notations of the proposed model of this study in detail.

Fig. 2
figure 2

A conceptual outline of the proposed model

Full size image
Fig. 3
figure 3

A framework of this study

Full size image

4 Notations of the model

The indices, parameters, and variables are defined in Tables 4, 5, 6, 7 and 8.

Table 4 Indices
Full size table

Parameters:

Table 5 Fuzzy parameters
Full size table
Table 6 Certain parameters
Full size table
Table 7 Continuous variables
Full size table
Table 8 Binary variables
Full size table

4.1 Mathematical formulation

The mathematical model of this study has been formulated as follows:

$$ \begin{aligned} \widetilde{TTC} & = \sum\limits_{p}^{P} {\sum\limits_{l}^{L} {\sum\limits_{j}^{J} {\sum\limits_{t}^{T} {\tilde{T}^{1}_{pljt} \times N_{pljt}^{3} + } } } } \sum\limits_{p}^{P} {\sum\limits_{j}^{J} {\sum\limits_{n}^{N} {\sum\limits_{t}^{T} {\tilde{T}^{2}_{pjnt} \times N_{pjnt}^{4} } } } } \\ & \quad + \sum\limits_{p}^{P} {\sum\limits_{n}^{N} {\sum\limits_{h}^{H} {\sum\limits_{t}^{T} {\tilde{T}^{3}_{pnht} \times N_{pnht}^{5} } } } } \\ \end{aligned} $$
(1)
$$ \begin{aligned} \widetilde{HC} & = \sum\limits_{p}^{P} {\sum\limits_{j}^{J} {\sum\limits_{t}^{T} {\tilde{H}^{1}_{pjt} \times I^{1}_{pjt} } } } \sum\limits_{p}^{P} {\sum\limits_{n}^{N} {\sum\limits_{t}^{T} {\tilde{H}^{2}_{pnt} \times I^{2}_{pnt} } } } \\ & \quad + \sum\limits_{p}^{P} {\sum\limits_{h}^{H} {\sum\limits_{t}^{T} {\tilde{H}^{3}_{pht} \times I^{3}_{pht} } } } \\ \end{aligned} $$
(2)
$$ \begin{aligned} \widetilde{WA} & = \sum\limits_{p}^{P} {\sum\limits_{j}^{J} {\sum\limits_{t}^{T} {\widetilde{W}^{1}_{pjt} \times WA^{1}_{pjt} } } } \sum\limits_{p}^{P} {\sum\limits_{n}^{N} {\sum\limits_{t}^{T} {\widetilde{W}^{2}_{pnt} \times WA^{2}_{pnt} } } } \\ & \quad + \sum\limits_{p}^{P} {\sum\limits_{h}^{H} {\sum\limits_{t}^{T} {\widetilde{W}^{3}_{pht} \times WA^{3}_{pht} } } } \\ \end{aligned} $$
(3)
$$ \begin{aligned} \widetilde{OC} & = \sum\limits_{p}^{P} {\sum\limits_{d}^{D} {\sum\limits_{l}^{L} {\sum\limits_{t}^{T} {\tilde{O}_{t}^{1} \times N_{pdlt}^{1} } } } } + \sum\limits_{p}^{P} {\sum\limits_{l}^{L} {\sum\limits_{j}^{J} {\sum\limits_{t}^{T} {\tilde{O}_{jt}^{2} \times N_{pljt}^{3} } } } } \\ & \quad + \sum\limits_{p}^{P} {\sum\limits_{d}^{D} {\sum\limits_{j}^{J} {\sum\limits_{t}^{T} {\tilde{O}_{jt}^{2} \times N_{pdjt}^{2} } } } } + \sum\limits_{p}^{P} {\sum\limits_{j}^{N} {\sum\limits_{n}^{J} {\sum\limits_{t}^{T} {\tilde{O}_{nt}^{3} \times N_{pjnt}^{4} } } } } \\ & \quad + \sum\limits_{p}^{P} {\sum\limits_{n}^{N} {\sum\limits_{h}^{H} {\sum\limits_{t}^{T} {\tilde{O}_{ht}^{4} \times N_{pnht}^{5} } } } } + \sum\limits_{p}^{P} {\sum\limits_{l}^{L} {\sum\limits_{w}^{W} {\sum\limits_{t}^{T} {\tilde{O}_{wt}^{5} \times N_{plwt}^{7} } } } } \\ & \quad + \sum\limits_{p}^{P} {\sum\limits_{j}^{J} {\sum\limits_{w}^{W} {\sum\limits_{t}^{T} {\tilde{O}_{wt}^{5} \times N_{pjwt}^{8} } } } } + \sum\limits_{p}^{P} {\sum\limits_{n}^{N} {\sum\limits_{w}^{W} {\sum\limits_{t}^{T} {\tilde{O}_{wt}^{5} \times N_{pnwt}^{9} } } } } \\ & \quad + \sum\limits_{p}^{P} {\sum\limits_{h}^{H} {\sum\limits_{w}^{W} {\sum\limits_{t}^{T} {\tilde{O}_{wt}^{5} \times N_{phwt}^{10} } } } } \\ \end{aligned} $$
(4)
$$ \widetilde{FC} = \sum\limits_{d}^{D} {\sum\limits_{l}^{L} {\sum\limits_{t}^{T} {\tilde{F} \times Y_{dlt}^{1} } } } $$
(5)
$$ \widetilde{SUB} = \sum\limits_{p} {\sum\limits_{p^{\prime}} {\sum\limits_{h} {\sum\limits_{h^{\prime}} {\sum\limits_{t} {CSUB_{hh^{\prime}t} \times PI_{pp^{\prime}} \times PSUB_{pp^{\prime}} \times N_{phh^{\prime}t}^{6} } } } } } $$
(6)
$$ \begin{aligned} \widetilde{DC} & = \sum\limits_{p}^{P} {\sum\limits_{l}^{L} {\sum\limits_{w}^{W} {\sum\limits_{t}^{T} {\tilde{D}_{pwt}^{1} \times N_{plwt}^{7} } } } } + \sum\limits_{p}^{P} {\sum\limits_{j}^{J} {\sum\limits_{w}^{W} {\sum\limits_{t}^{T} {\tilde{D}_{pwt}^{1} \times N_{pjwt}^{8} } } } } \\ & \quad + \sum\limits_{p}^{P} {\sum\limits_{n}^{N} {\sum\limits_{w}^{W} {\sum\limits_{t}^{T} {\tilde{D}_{pwt}^{1} \times N_{pnwt}^{9} } } } } + \sum\limits_{p}^{P} {\sum\limits_{h}^{H} {\sum\limits_{w}^{W} {\sum\limits_{t}^{T} {\tilde{D}_{pwt}^{1} \times N_{phwt}^{10} } } } } \\ \end{aligned} $$
(7)
$$ MinZ_{1} = \widetilde{TC} = \widetilde{TTC} + \widetilde{HC} + \widetilde{WA} + \widetilde{OC} + \widetilde{FC} + \widetilde{SUB} + \widetilde{DC} $$
(8)
$$ MaxZ_{2} = \widetilde{SL} = \mathop {\min }\limits_{h,t} \left[ {1 - \sum\limits_{p}^{P} {\left( {\frac{{SO_{pht} }}{{\tilde{D}_{pht}^{2} }}} \right)} } \right] $$
(9)

The first objective function, Eq. (8), plans to minimize the total cost, including transportation costs in different levels of the network, including BM, BFC, NBB, and Hospitals [Eq. (1)], holding costs at BFC, NBB, and Hospitals [Eq. (2)], wastage costs at BFC, NBB, and Hospitals [Eq. (3)], operating costs at BM, BFC, NBB, Hospitals, and BDC [Eq. (4)], facility costs at BM [Eq. (5)], substitute costs of facility center by considering the penalty factor for each blood substitution and ABO-Rh(D) preference rules from the NBB to hospitals and substitution between hospitals [Eq. (6)], and blood disposal costs at BM, BFC, NBB, and Hospitals [Eq. (7)]. The second objective function shown by Eq. (9) tries to maximize the minimum level of service among the current hospitals in each period. This function maximizes the percentage of demand satisfied in each Hospital for a given period.

Subject to:

$$ \sum\limits_{p} {N_{pljt}^{3} } \le \tilde{C}_{jt}^{1} \times Y_{ljt}^{3} ,\quad \forall l,j,t $$
(10)
$$ \sum\limits_{p} {N_{pjnt}^{4} } \le \tilde{C}_{nt}^{2} \times Y_{jnt}^{4} ,\quad \forall j,n,t $$
(11)
$$ \sum\limits_{p} {N_{pnht}^{5} } \le \tilde{C}_{ht}^{3} \times Y_{nht}^{5} ,\quad \forall n,h,t $$
(12)
$$ \sum\limits_{p} {N_{plwt}^{7} } \le \tilde{C}_{wt}^{4} \times Y_{lwt}^{7} ,\quad \forall l,w,t $$
(13)
$$ \sum\limits_{p} {N_{pjwt}^{8} } \le \tilde{C}_{wt}^{4} \times Y_{jwt}^{8} ,\quad \forall j,w,t $$
(14)
$$ \sum\limits_{p} {N_{pnwt}^{9} } \le \tilde{C}_{wt}^{4} \times Y_{nwt}^{9} ,\quad \forall n,w,t $$
(15)
$$ \sum\limits_{p} {N_{phwt}^{10} } \le \tilde{C}_{wt}^{4} \times Y_{hwt}^{10} ,\quad \forall h,w,t $$
(16)

Constraints (10)–(16) relate to the capacities of each BFC, NBB, Hospital, and BDC. These equations are controlled the number of transferred amounts of different types of blood in the designed network that should be less than the capacities of each BFC, NBB, Hospital, and BDC center. In comparison, constraints (17) and (18) are designed to show the limitations of donor regions at the first stages.

$$ N_{pdlt}^{1} \le \tilde{S}_{pdt} \times Y_{dlt}^{1} ,\quad \forall p,d,l,t $$
(17)
$$ N_{pdjt}^{2} \le \tilde{S}_{pdt} \times Y_{djt}^{2} ,\quad \forall p,d,j,t $$
(18)

Equations (19)–(30) are designed to balance the flow of the designed CLBSCN. These constraints are fundamental equations for reaching the feasible solution space.

$$ \sum\limits_{j} {N_{pljt}^{3} \le } \sum\limits_{d} {N_{pdlt}^{1} } ,\quad \forall p,l,t $$
(19)
$$ \sum\limits_{j} {N_{pljt}^{3} } = R_{plt}^{1} ,\quad \forall p,l,t $$
(20)
$$ (1 - \eta_{l}^{1} ) \times \sum\limits_{d} {N_{pdlt}^{1} } = R_{plt}^{1} ,\quad \forall p,l,t $$
(21)
$$ \sum\limits_{l} {N_{pljt}^{3} } + (1 - \eta_{j}^{2} ) \times \sum\limits_{d} {N_{pdjt}^{2} } = R_{pjt}^{2} ,\quad \forall p,j,t $$
(22)
$$ \sum\limits_{n} {N_{pjnt}^{4} } \le R_{pjt}^{2} ,\quad \forall p,j,t $$
(23)
$$ (1 - \eta_{n}^{3} ) \times \sum\limits_{j} {N_{pjnt}^{4} } = R_{pnt}^{3} ,\quad \forall p,n,t $$
(24)
$$ \sum\limits_{h} {N_{pnht}^{5} } = R_{pnt}^{3} ,\quad \forall p,n,t $$
(25)
$$ \sum\limits_{w} {N_{plwt}^{7} } \le \sum\limits_{d} {N_{pdlt}^{1} } ,\quad \forall p,l,t $$
(26)
$$ \sum\limits_{w} {N_{pjwt}^{8} } \le R_{pjt}^{2} ,\quad \forall p,j,t $$
(27)
$$ \sum\limits_{w} {N_{pnwt}^{9} } \le \sum\limits_{j} {N_{pjnt}^{4} } ,\quad \forall p,n,t $$
(28)
$$ \sum\limits_{w} {N_{phwt}^{10} } \le \sum\limits_{n} {N_{pnht}^{5} } ,\quad \forall p,h,t $$
(29)
$$ R_{pwt}^{4} = \sum\limits_{l} {N_{plwt}^{7} } + \sum\limits_{j} {N_{pjwt}^{8} } + \sum\limits_{n} {N_{pnwt}^{9} } + \sum\limits_{h} {N_{phwt}^{10} } ,\quad \forall p,w,t $$
(30)

Equations (19)–(30) are designed to balance the flow of the designed CLBSCN. These constraints are fundamental equations for reaching the feasible solution space. For instance, Eq. (23) indicates that transferred amounts of blood between BFC and NBB could not exceed the processed units of blood in BFC. The same thing can be interpreted for the remaining equations as well.

$$ I_{pjt}^{1} = I_{pj(t - 1)}^{1} + \sum\limits_{l} {N_{pljt}^{3} } + \sum\limits_{d} {N_{pdjt}^{2} } - \sum\limits_{n} {N_{pjnt}^{4} } - WA_{pjt}^{1} - \sum\limits_{w} {N_{pjwt}^{8} } ,\quad \forall p,j,t $$
(31)
$$ I_{pnt}^{2} = I_{pn(t - 1)}^{2} + \sum\limits_{j} {N_{pjnt}^{4} } - \sum\limits_{h} {N_{pnht}^{5} - \sum\limits_{w} {N_{pnwt}^{9} } - } WA_{pnt}^{2} ,\quad \forall p,n,t $$
(32)
$$ \begin{aligned} & I_{pht}^{3} + \tilde{D}_{pht}^{2} - SO_{pht} = I_{ph(t - 1)}^{3} + \sum\limits_{n} {N_{pnht}^{5} } - \sum\limits_{h^{\prime}} {CM_{pp^{\prime}} \times N_{phh^{\prime}t}^{6} } \\ & \quad + \sum\limits_{h^{\prime}} {CM_{p^{\prime}p} \times N_{ph^{\prime}ht}^{6} } - WA_{pht}^{3} ,\quad \forall p,h,t \\ \end{aligned} $$
(33)
$$ I_{pht}^{3} \times SO_{pht} = 0,\quad \forall p,h,t $$
(34)
$$ \sum\limits_{p} {I_{pjt}^{1} } \le \tilde{C}_{jt}^{1} ,\quad \forall j,t $$
(35)
$$ \sum\limits_{p} {I_{pnt}^{2} } \le \tilde{C}_{nt}^{2} ,\quad \forall n,t $$
(36)
$$ \sum\limits_{p} {I_{pht}^{3} } \le \tilde{C}_{ht}^{3} ,\quad \forall h,t $$
(37)

Constraints (31)–(37) represent the inventory level in the whole designed network. Indeed, Eq. (31) through Eq. (34) is intended to show the amount of stock in each BFC, NBB, Hospital, and BDC. More importantly, these equations guarantee that the FIFO approach used in blood unit inventory management, which includes shelf life and RBC unit substitutes, is compelling. Also, three Eq. (35) through Eq. (37) assure that the level of inventories in each BFC, NBB, Hospital, and BDC should not exceed the capacity of each defined center.

$$ \sum\limits_{l} {Y_{dlt}^{1} } + \sum\limits_{j} {Y_{djt}^{2} } \le 1,\quad \forall d,t $$
(38)
$$ \sum\limits_{d} {\sum\limits_{l} {Y_{dlt}^{1} } \le N^{m} ,\quad \forall } t $$
(39)
$$ \sum\limits_{d} {Y_{dlt}^{1} \le 1,} \quad \forall l,t $$
(40)
$$ \sum\limits_{j} {Y_{ljt}^{3} \le 1,} \quad \forall l,t $$
(41)
$$ \sum\limits_{n} {Y_{jnt}^{4} \le 1,} \quad \forall j,t $$
(42)
$$ \sum\limits_{n} {Y_{nht}^{5} \le 1,} \quad \forall h,t $$
(43)
$$ \sum\limits_{w} {Y_{lwt}^{7} } \le 1,\quad \forall l,t $$
(44)
$$ \sum\limits_{w} {Y_{jwt}^{8} } \le 1,\quad \forall j,t $$
(45)
$$ \sum\limits_{w} {Y_{nwt}^{9} } \le 1,\quad \forall n,t $$
(46)
$$ \sum\limits_{w} {Y_{hwt}^{10} } \le 1,\quad \forall h,t $$
(47)

Equation (38) through Eq. (47) are allocation constraints that show which BFC, NBB, Hospitals, and BDC should be assigned together. In other words, which BFC should be given to NBB in each period. Also, Eq. (38) emphasizes that only donors can go to either BFC or BM.

$$ \sum\limits_{p} {N_{pdlt}^{1} } \le N \times Y_{dlt}^{1} ,\quad \forall d,l,t $$
(48)
$$ \sum\limits_{p} {N_{pdjt}^{2} } \le N \times Y_{djt}^{2} ,\quad \forall d,j,t $$
(49)
$$ \sum\limits_{p} {N_{pljt}^{3} } \le N \times Y_{ljt}^{3} ,\quad \forall l,j,t $$
(50)
$$ \sum\limits_{p} {N_{pjnt}^{4} } \le N \times Y_{jnt}^{4} ,\quad \forall j,n,t $$
(51)
$$ \sum\limits_{p} {N_{pnht}^{5} } \le N \times Y_{nht}^{5} ,\quad \forall n,h,t $$
(52)
$$ \sum\limits_{p} {N_{phh\prime t}^{6} } \le N \times Y_{hh\prime t}^{6} ,\quad \forall h,h^{\prime},t $$
(53)
$$ \sum\limits_{p} {N_{plwt}^{7} } \le N \times Y_{lwt}^{7} ,\quad \forall l,w,t $$
(54)
$$ \sum\limits_{p} {N_{pjwt}^{8} } \le N \times Y_{jwt}^{8} ,\quad \forall j,w,t $$
(55)
$$ \sum\limits_{p} {N_{pnwt}^{9} } \le N \times Y_{nwt}^{9} ,\quad \forall n,w,t $$
(56)
$$ \sum\limits_{p} {N_{phwt}^{10} } \le N \times Y_{hwt}^{10} ,\quad \forall h,w,t $$
(57)

Moreover, constraints (48) through (57) guarantee that the transferred number of various types of blood between various centers should be less than a large amount if they are assigned to the centers like BFC, NBB, Hospitals, and BDC. These constraints, like Constraints (10)–(16), control the transferred amounts of different blood types in the network.

$$ WA_{pjt}^{1} = \max \left\{ {\left( {I_{{pj(t - \Delta_{RBC} )}}^{1} - \sum\limits_{n} {N_{pjnt}^{4} - } WA_{{pj(t - \Delta_{RBC} )}}^{1} } \right),0} \right\},\quad \forall p,j,t \ge \Delta_{RBC} + 1 $$
(58)
$$ WA_{pnt}^{2} = \max \left\{ {\left( {I_{{pn(t - \Delta_{RBC} )}}^{2} - \sum\limits_{h} {N_{pnht}^{5} - } WA_{{pn(t - \Delta_{RBC} )}}^{2} } \right),0} \right\},\quad \forall p,n,t \ge \Delta_{RBC} + 1 $$
(59)
$$ WA_{pht}^{2} = \max \left\{ {\left( {I_{{ph(t - \Delta_{RBC} )}}^{2} - \sum\limits_{h^{\prime}} {N_{phh^{\prime}t}^{6} - } WA_{{ph(t - \Delta_{RBC} )}}^{2} } \right),0} \right\},\quad \forall p,h,t \ge \Delta_{RBC} + 1 $$
(60)
$$ \begin{aligned} & N_{pdlt}^{1} ,N_{pdjt}^{2} ,N_{pljt}^{3} ,N_{pjnt}^{4} ,N_{pnht}^{5} ,N_{phh^{\prime}t}^{6} ,N_{plwt}^{7} , \\ & N_{pjwt}^{8} ,N_{pnwt}^{9} ,N_{phwt}^{10} ,I_{pjt}^{1} ,I_{pnt}^{2} ,I_{pht}^{3} , \\ & WA_{pjt}^{1} ,WA_{pnt}^{2} ,WA_{pht}^{3} ,SO_{pht} ,R_{plt}^{1} ,R_{pjt}^{2} , \\ & R_{pnt}^{3} ,R_{pwt}^{4} \in Z,\quad \forall p,p^{\prime},d,l,j,n,h,h^{\prime},w,t \\ \end{aligned} $$
(61)
$$ Y_{dlt}^{1} ,Y_{djt}^{2} ,Y_{ljt}^{3} ,Y_{jnt}^{4} ,Y_{nht}^{5} ,Y_{hh^{\prime}t}^{6} ,Y_{lwt}^{7} ,Y_{jwt}^{8} ,Y_{nwt}^{9} ,Y_{hwt}^{10} \in \left\{ {0,1} \right\},\quad \forall d,l,j,n,h,h\prime ,p,w,t $$
(62)

Constraints (58) through (60) indicate the outdated units in each BFC, NBB, and Hospital. Indeed, defining these three equations ensures that the amounts of wastage cannot be a negative value. Finally, Eqs. (61) and (62) denote the domains of decision variables, including binary variables and continuous variables, as applied in this study.

4.2 Linearization

The proposed mathematical model in the previous section has non-linear equations that need to be converted to linear equations (Momenitabar et al., 2022; Safaei et al., 2022). First, the second objective function shown by Eq. (9) is non-linear and has been converted to a linear function as follows:

$$ \begin{aligned} & MaxZ_{2} = S\tilde{L} = \lambda \\ & s.t.\quad \lambda \le \left[ {1 - \sum\limits_{p}^{P} {\left( {\frac{{SO_{pht} }}{{\tilde{D}_{pht}^{2} }}} \right)} } \right],\quad \forall h,t \\ & \quad \lambda \ge 0 \\ \end{aligned} $$
(63)

Equation (34) is a non-linear function and is constituted by two integer variables. A large number of M has been applied to convert the non-linear constraint to the linear one. Therefore, we have:

$$ \begin{aligned} & I_{pht}^{2} \le M \times \varphi_{pht} ,\quad \forall p,h,t \\ & SO_{pht} \le M \times \tau_{pht} ,\quad \forall p,h,t \\ & \varphi_{pht} + \tau_{pht} \le 1,\quad \forall p,h,t \\ \end{aligned} $$
(64)

Constraints (58), (59), and (60) are non-linear constraints. Three \(\delta ,\psi ,\xi \) have been applied to convert these three equations to a linear one, which has been formulated as follows:

$$ \delta \ge \left( {I_{{pj(t - \Delta_{RBC} )}}^{1} - \sum\limits_{n} {N_{pjnt}^{4} } - WA_{{pj(t - \Delta_{RBC} )}}^{1} } \right),\delta \ge 0,\quad \forall p,j,t \ge \Delta_{RBC} + 1 $$
(65)
$$ \psi \ge \left( {I_{{pn(t - \Delta_{RBC} )}}^{2} - \sum\limits_{h} {N_{pnht}^{5} - } WA_{{pn(t - \Delta_{RBC} )}}^{2} } \right),\psi \ge 0,\quad \forall p,n,t \ge \Delta_{RBC} + 1 $$
(66)
$$ \xi \ge \left( {I_{{ph(t - \Delta_{RBC} )}}^{3} - \sum\limits_{h^{\prime}} {N_{phh^{\prime}t}^{6} - } WA_{{ph(t - \Delta_{RBC} )}}^{3} } \right),\xi \ge 0,\quad \forall p,h,t \ge \Delta_{RBC} + 1 $$
(67)

5 Solution methodology

This section is dedicated to the solution methodology of the proposed model. First, the equivalent auxiliary crips model has been utilized to transform the fuzzy multi-objective MINLP into crisp multi-objective MINLP (Gholamian et al., 2021; Vahdani et al., 2013). Second, the two methods proposed by Torabi and Hassini (2008) called the TH and proposed by Gholamian et al. (2021) called GMMT have been utilized to solve the model of this study. Finally, the result of two methods in terms of satisfaction degree, objective functions, and two performance measures of distance and dispersion has been applied to find the best one.

5.1 The equivalent auxiliary crisp model

An equivalent auxiliary crisp model has been applied to convert the fuzzy MINLP model to crisp MINLP. Also, the fuzzy number considered in this study is a triangular fuzzy number, which is constituted by three numbers, which are the pessimistic, most likely, and optimistic values (Ahmed et al., 2021; Pouraliakbari-Mamaghani et al., 2022). Geometrically, the first objective function is shown by three numbers, including \((T{C}^{p},0)\), \((T{C}^{m},1)\), and \((T{C}^{o},0)\). To minimize the first objective function, \(T{C}^{p},T{C}^{m}, and T{C}^{o}\) have been solved simultaneously. By using the method, we should minimize \(T{C}^{m}\), maximize \(T{C}^{m}-T{C}^{p}\), and minimize \(T{C}^{o}-T{C}^{m}\) separately. Thus, we have:

$$ \min Z_{1a} = TC^{m} = TTC^{m} + HC^{m} + WA^{m} + OC^{m} + FC^{m} + SUB^{m} + DC^{m} $$
(68)
$$ \begin{aligned} \max Z_{1b} & = (TC^{m} - TC^{p} ) = (TTC^{m} - TTC^{p} ) + (HC^{m} - HC^{p} ) + (WA^{m} - WA^{p} ) \\ & \quad + (OC^{m} - OC^{p} ) + (FC^{m} - FC^{p} ) + (SUB^{m} - SUB^{p} ) + (DC^{m} - DC^{p} ) \\ \end{aligned} $$
(69)
$$ \begin{aligned} \min Z_{1c} & = (TC^{o} - TC^{m} ) = (TTC^{o} - TTC^{m} ) + (HC^{o} - HC^{m} ) + (WA^{o} - WA^{m} ) \\ & \quad + (OC^{o} - OC^{m} ) + (FC^{o} - FC^{m} ) + (SUB^{o} - SUB^{m} ) + (DC^{o} - DC^{m} ) \\ \end{aligned} $$
(70)

Similarly, for the second objective function, we have:

$$ \max Z_{2a} = SL^{m} = \mathop {\min }\limits_{h,t} \left[ {1 - \sum\limits_{p}^{P} {\left( {\frac{{SO_{pht} }}{{D_{pht}^{2,m} }}} \right)} } \right] $$
(71)
$$ \min Z_{2b} = (SL^{m} - SL^{p} ) = \mathop {\min }\limits_{h,t} \left[ {1 - \sum\limits_{p}^{P} {\left( {\frac{{SO_{pht} }}{{(D_{pht}^{2,m} - D_{pht}^{2,p} )}}} \right)} } \right] $$
(72)
$$ \max Z_{2c} = (SL^{o} - SL^{m} ) = \mathop {\min }\limits_{h,t} \left[ {1 - \sum\limits_{p}^{P} {\left( {\frac{{SO_{pht} }}{{(D_{pht}^{2,o} - D_{pht}^{2,m} )}}} \right)} } \right] $$
(73)

The weighted average method is applied to de-fuzzify the fuzzy constraints (10)–(18), (33), and (35)–(37) by converting the fuzzy constraints to crisp.

$$ \sum\limits_{p} {N_{pljt}^{3} } \le (\omega_{1} \times C_{jt,\beta }^{1,p} + \omega_{2} \times C_{jt,\beta }^{1,m} + \omega_{3} \times C_{jt,\beta }^{1,o} ) \times Y_{ljt}^{3} ,\quad \forall l,j,t $$
(74)
$$ \sum\limits_{p} {N_{pnht}^{5} } \le (\omega_{1} \times C_{ht,\beta }^{3,p} + \omega_{2} \times C_{ht,\beta }^{3,m} + \omega_{3} \times C_{ht,\beta }^{3,o} ) \times Y_{nht}^{5} ,\quad \forall n,h,t $$
(75)
$$ \sum\limits_{p} {N_{plwt}^{7} } \le (\omega_{1} \times C_{wt,\beta }^{4,p} + \omega_{2} \times C_{wt,\beta }^{4,m} + \omega_{3} \times C_{wt,\beta }^{4,o} ) \times Y_{lwt}^{7} ,\quad \forall l,w,t $$
(76)
$$ \sum\limits_{p} {N_{pjwt}^{8} } \le (\omega_{1} \times C_{wt,\beta }^{4,p} + \omega_{2} \times C_{wt,\beta }^{4,m} + \omega_{3} \times C_{wt,\beta }^{4,o} ) \times Y_{jwt}^{8} ,\quad \forall j,w,t $$
(77)
$$ \sum\limits_{p} {N_{pnwt}^{9} } \le (\omega_{1} \times C_{wt,\beta }^{4,p} + \omega_{2} \times C_{wt,\beta }^{4,m} + \omega_{3} \times C_{wt,\beta }^{4,o} ) \times Y_{nwt}^{9} ,\quad \forall n,w,t $$
(78)
$$ \sum\limits_{p} {N_{phwt}^{10} } \le (\omega_{1} \times C_{wt,\beta }^{4,p} + \omega_{2} \times C_{wt,\beta }^{4,m} + \omega_{3} \times C_{wt,\beta }^{4,o} ) \times Y_{hwt}^{10} ,\quad \forall h,w,t $$
(79)
$$ N_{pdlt}^{1} \le (\omega_{1} \times S_{pdt,\beta }^{p} + \omega_{2} \times S_{pdt,\beta }^{m} + \omega_{3} \times S_{pdt,\beta }^{o} ) \times Y_{dlt}^{1} ,\quad \forall p,d,l,t $$
(80)
$$ N_{pdjt}^{2} \le (\omega_{1} \times S_{pdt,\beta }^{p} + \omega_{2} \times S_{pdt,\beta }^{m} + \omega_{3} \times S_{pdt,\beta }^{o} ) \times Y_{djt}^{2} ,\quad \forall p,d,j,t $$
(81)
$$ \begin{aligned} & I_{pht}^{3} + (\omega_{1} \times D_{pht,\beta }^{2,p} + \omega_{2} \times D_{pht,\beta }^{2,m} + \omega_{3} \times D_{pht,\beta }^{2,o} ) - SO_{pht} = I_{ph(t - 1)}^{3} \\ & \quad + \sum\limits_{n} {N_{pnht}^{5} } - \sum\limits_{h^{\prime}} {CM_{pp\prime } \times N_{phh\prime t}^{6} } + \sum\limits_{h^{\prime}} {CM_{pp\prime } \times N_{ph\prime ht}^{6} } \\ & \quad - WA_{pht}^{3} ,\quad \forall p,h,t \\ \end{aligned} $$
(82)
$$ \sum\limits_{p} {I_{pjt}^{1} } \le (\omega_{1} \times C_{jt,\beta }^{1,p} + \omega_{2} \times C_{jt,\beta }^{1,m} + \omega_{3} \times C_{jt,\beta }^{1,o} ),\quad \forall j,t $$
(83)
$$ \sum\limits_{p} {I_{pnt}^{2} } \le (\omega_{1} \times C_{nt,\beta }^{2,p} + \omega_{2} \times C_{nt,\beta }^{2,m} + \omega_{3} \times C_{nt,\beta }^{2,o} ),\quad \forall n,t $$
(84)
$$ \sum\limits_{p} {I_{pht}^{3} } \le (\omega_{1} \times C_{ht,\beta }^{3,p} + \omega_{2} \times C_{ht,\beta }^{3,m} + \omega_{3} \times C_{ht,\beta }^{3,o} ),\quad \forall h,t $$
(85)

where \({\omega }_{1}+{\omega }_{2}+{\omega }_{3}=1,\) and each of them is defined as a weight of each most pessimistic, the most possible, and the most optimistic value. Moreover, the value \(\beta \) is the minimum acceptable possibility, which is between zero and one, determined by DMs. Also, the values of \({\omega }_{1},{\omega }_{3}=1/6\) and \({\omega }_{2}=4/6\), and \(\beta =0.5\) are set as follows. Therefore, a crisp multi-objective MINLP model can be shown below.

$$ \begin{aligned} & Min\quad Z_{Total} = [Z_{1a} , - Z_{1b} ,Z_{1c} , - Z_{2a} ,Z_{2b} , - Z_{2c} ] \\ & Z_{1a} = TC^{m} ,\quad Z_{1b} = (TC^{m} - TC^{p} ),\quad Z_{1c} = (TC^{o} - TC^{m} ) \\ & Z_{2a} = SL^{m} ,\quad Z_{2b} = (SL^{m} - SL^{p} ),\quad Z_{2c} = (SL^{o} - SL^{m} ), \\ & s.t.\quad x \in F(x) \\ \end{aligned} $$
(86)

where x shows a vector of the feasible solution, including all the variables previously defined, moreover, F(x) displays the feasible region that includes the crisp constraints (19)–(32), (34), and (38)–(62).

5.2 Interactive fuzzy programming approach

After applying the equivalent auxiliary crisp model, the two proposed approaches discussed previously, including TH and GMMT, have been utilized to solve the model of this study (Goudarzi et al., 2022; Khalilpourazari & Hashemi Doulabi, 2022). First, the steps of the TH method are as follows:

  • Step 1: Determine the distribution of each fuzzy parameter with the most pessimistic, the most possible, and the most optimistic values.

  • Step 2: Converting the fuzzy multi-objective MINLP model to the crisp multi-objective MINLP model.

  • Step 3: Dedicating the minimum acceptable membership level to each fuzzy parameter, \(\alpha \), and converting the fuzzy constraint to the crisp constraints.

  • Step 4: Determining the positive ideal solution (PIS) and negative ideal solution (NIS) for each objective function through solving the crisp multi-objective MINLP model that has been converted as follows:

    $$ Z_{1a}^{PIS} = \min TC^{m} ,\quad Z_{1a}^{NIS} = \max TC^{m} $$
    (87)
    $$ Z_{1b}^{PIS} = \max (TC^{m} - TC^{p} ),\quad Z_{1b}^{NIS} = \min (TC^{m} - TC^{p} ) $$
    (88)
    $$ Z_{1c}^{PIS} = \min (TC^{o} - TC^{m} ),\quad Z_{1c}^{NIS} = \max (TC^{o} - TC^{m} ) $$
    (89)
    $$ Z_{2a}^{PIS} = \max SL^{m} ,\quad Z_{2a}^{NIS} = \min SL^{m} $$
    (90)
    $$ Z_{2b}^{PIS} = \min (SL^{m} - SL^{p} ),\quad Z_{2b}^{NIS} = \max (SL^{m} - SL^{p} ) $$
    (91)
    $$ Z_{2c}^{PIS} = \max (SL^{o} - SL^{m} ),\quad Z_{2c}^{NIS} = \min (SL^{o} - SL^{m} ) $$
    (92)
    $$ s.t.\quad x \in F(x) $$
    (93)

    Torabi and Hassini (2008) proposed heuristic rules to alleviate the computational complexity by estimating the NIS using the PIS instead of solving the 12 objective functions.

    $$ \begin{aligned} Z_{i}^{NIS} & = \mathop {\max }\limits_{j = 1a,\ldots,2c} \left\{ {Z_{i} (x_{j}^{*} )} \right\};\quad i = 1a,1c,2b \\ Z_{i}^{NIS} & = \mathop {\min }\limits_{j = 1a,\ldots,2c} \left\{ {Z_{i} (x_{j}^{*} )} \right\};\quad i = 1b,2a,2c \\ \end{aligned} $$
    (94)

  • Step 5: Defining a linear membership function for each objective function as follows:

    $$ \mu_{1a} (x) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad if\,\,Z_{1a} < Z_{1a}^{PIS} ,} \hfill \\ {\frac{{Z_{1a}^{NIS} - Z_{1a} }}{{Z_{1a}^{NIS} - Z_{1a}^{PIS} }}} \hfill & {\quad if\,\,Z_{1a}^{PIS} \le Z_{1a} \le Z_{1a}^{NIS} ,} \hfill \\ 0 \hfill & {\quad if\,\,Z_{1a} > Z_{1a}^{NIS} ,} \hfill \\ \end{array} } \right. $$
    (95)
    $$ \mu_{1b} (x) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad if\,\,Z_{1b} > Z_{1b}^{PIS} ,} \hfill \\ {\frac{{Z_{1b} - Z_{1b}^{NIS} }}{{Z_{1b}^{PIS} - Z_{1b}^{NIS} }}} \hfill & {\quad if\,\,Z_{1b}^{NIS} \le Z_{1b} \le Z_{1b}^{PIS} ,} \hfill \\ 0 \hfill & {\quad if\,\,Z_{1b} < Z_{1b}^{NIS} ,} \hfill \\ \end{array} } \right. $$
    (96)
    $$ \mu_{1c} (x) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad if\,\,Z_{1c} < Z_{1c}^{PIS} ,} \hfill \\ {\frac{{Z_{1c}^{NIS} - Z_{1c} }}{{Z_{1c}^{NIS} - Z_{1c}^{PIS} }}} \hfill & {\quad if\,\,Z_{1c}^{PIS} \le Z_{1c} \le Z_{1c}^{NIS} ,} \hfill \\ 0 \hfill & {\quad if\,\,Z_{1c} > Z_{1c}^{NIS} ,} \hfill \\ \end{array} } \right. $$
    (97)
    $$ \mu_{2a} (x) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\quad if\,\,Z_{2a} > Z_{2a}^{PIS} ,} \hfill \\ {\frac{{Z_{2a} - Z_{2a}^{NIS} }}{{Z_{2a}^{PIS} - Z_{2a}^{NIS} }}} \hfill & {\quad if\,\,Z_{2a}^{NIS} \le Z_{2a} \le Z_{2a}^{PIS} ,} \hfill \\ 0 \hfill & {\quad if\,\,Z_{2a} < Z_{2a}^{NIS} ,} \hfill \\ \end{array} } \right. $$
    (98)
    $$ \mu_{2b} (x) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad if\,\,Z_{2b} < Z_{2b}^{PIS} ,} \hfill \\ {\frac{{Z_{2b}^{NIS} - Z_{2b} }}{{Z_{2b}^{NIS} - Z_{2b}^{PIS} }}} \hfill & {\quad if\,\,Z_{2b}^{PIS} \le Z_{2b} \le Z_{2b}^{NIS} ,} \hfill \\ 0 \hfill & {\quad if\,\,Z_{2b} > Z_{2b}^{NIS} ,} \hfill \\ \end{array} } \right. $$
    (99)
    $$ \mu_{2c} (x) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad if\,\,Z_{2c} > Z_{2c}^{PIS} ,} \hfill \\ {\frac{{Z_{2c} - Z_{2c}^{NIS} }}{{Z_{2c}^{PIS} - Z_{2c}^{NIS} }}} \hfill & {\quad if\,\,Z_{2c}^{NIS} \le Z_{2c} \le Z_{2c}^{PIS} ,} \hfill \\ 0 \hfill & {\quad if\,\,Z_{2c} < Z_{2c}^{NIS} ,} \hfill \\ \end{array} } \right. $$
    (100)

    \(\mu_{i} (x)\) represents the satisfaction degree of the ith objective function for the vector x.

  • Step 6: Converting the auxiliary crisp multi-objective MINLP model to a single-objective MINLP model by using the below formulation.

    $$ \begin{aligned} & \max \quad \lambda (x) = \gamma \times \lambda_{0} + (1 - \gamma ) \times \sum\limits_{i} {\theta_{i} \mu_{i} (x)} \\ & s.t.\quad \lambda_{0} \le \mu_{i} (x),\quad i = 1a, \ldots ,2c \\ & \quad \,\,\,\,\,\,\,x \in F(x),\lambda_{0} ,\quad \gamma \in [0,1], \\ \end{aligned} $$
    (101)

    where \({\uplambda }_{0}={\mathrm{min}}_{\mathrm{i}}\{{\upmu }_{\mathrm{i}}(\mathrm{x})\}\) denotes the minimum satisfaction degree of total objective functions in this study. While \({\uptheta }_{\mathrm{i}}\) and \(\upgamma \) display the relative importance of ith objective function and compensation coefficient. \(\mathrm{x}\in \mathrm{F}(\mathrm{x})\) is the original problem converted into a crisp model (Hosseini Dehshiri et al., 2022; Khalilpourazari & Hashemi Doulabi, 2022). Also, \({\uptheta }_{\mathrm{i}}>0\) is determined by DMs based on their preferences given to each objective function. Moreover, the sum of these parameters should be equal to 1.

  • Step 7: Assigning numbers to two parameters \({\theta }_{i},\gamma \) as defined in step 6 to solve the proposed equivalent auxiliary crisp model. If the DMs are unsatisfied with the solution obtained, the two parameters should be changed to give a better solution by running the proposed equivalent crisp model.

Also, the steps of the GMMT method are as follows:

  • Step 1: Determine the linear membership function considering the soft constraints.

    $$ \mu_{i}(a_{i}^{T} \times x) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\quad if\,\,a_{i}^{T} \times x \ge b_{i} + d_{i} } \hfill \\ {1 - \frac{{(a_{i}^{T} \times x - b_{i} )}}{{d_{i} }}} \hfill & {\quad if\,\,b_{i} < a_{i}^{T} \times x < b_{i} + d_{i} } \hfill \\ {1,} \hfill & {\quad if\,\,a_{i}^{T} \times x \le b_{i} } \hfill \\ \end{array} } \right. $$
    (102)

    where i is the index of constraints, and di is the admissible violation of fuzzy resource b of the ith constraints.

  • Step 2 and Step 3: Same as step 4 (TH method).

  • Step 4: Same as step 5 (TH method).

  • Step 5: Construct the min–max operator with membership function as defined in steps 1 through 4.

    $$ \mu_{1a} (x) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad if\,\,Z_{1a} < Z_{1a}^{PIS} ,} \hfill \\ {\frac{{Z_{1a}^{NIS} - Z_{1a} }}{{Z_{1a}^{NIS} - Z_{1a}^{PIS} }}} \hfill & {\quad if\,\,Z_{1a}^{PIS} \le Z_{1a} \le Z_{1a}^{NIS} ,} \hfill \\ 0 \hfill & {\quad if\,\,Z_{1a} > Z_{1a}^{NIS} ,} \hfill \\ \end{array} } \right. $$
    (103)

  • Step 6: Obtain an optimal solution by solving the top equation. After that, put the optimal solution to the membership functions of each objective function and soft constraints to calculate \({\mu }_{k}(x),k=1a,\ldots,2c\) \({\mu }_{i}(x),\) [constraints (10) through (18) and (35) through (37)].

  • Step 7: Solve the below equation.

    $$ \begin{aligned} & \max \quad \lambda (x) = \gamma \times \lambda_{0} + (1 - \gamma ) \times \left( {\pi \times \sum\limits_{k} {\theta_{k} \times \lambda_{k} ) + (1 - \pi ) \times \left( {\sum {\theta_{i} \times \mu_{i} (x)} } \right)} } \right) \\ & s.t.\quad \mu_{k} (x^{0} ) \le \lambda_{0} + \lambda_{k} \le \mu_{k} (x),\quad k = 1a, \ldots ,2c \\ & \quad \mu_{i} (x^{0} ) \le \lambda_{0} + \lambda_{i} \le \mu_{i} (x),\quad \forall i \\ & \quad x \in F(x),\lambda_{0} ,\lambda_{i} ,\lambda_{k} ,\pi ,\gamma \in [0,1],\quad \forall k,h \\ \end{aligned} $$
    (104)

    where k shows the number of the objective function and i refers to the number of soft constraints; \({\lambda }_{0},{\theta }_{i},{\theta }_{k},\gamma ,\pi ,{\mu }_{k}(x),{\mu }_{i}(x)\) display minimum satisfaction degree of objective functions, the relative importance of ith objective functions, the compensation coefficient that controls the minimum satisfaction level of the objectives concerning the soft constraints, as well as the compromised degree among the objectives through the existing interaction between them and flexible constraints implicitly, the measure of interaction between the objective functions and soft constraints, membership functions of each objective functions, and soft constraints respectively. More interestingly, \({\theta }_{i},{\theta }_{k}\) are determined by DMs and are equal to \({\sum }_{i}{\theta }_{i}=1\) and \({\sum }_{k}{\theta }_{k}=1\).

  • Step 8: Solve the equation in step 7. If the DMs accept the solution, we go to step 9; otherwise, we go to step 3.

  • Step 9: Put the optimal number computed in the previous step into the original model.

6 Implementation and results

This section aims to provide the result of the model. First, the case study was implemented, and then the result of the proposed model in different sub-sections was discussed.

6.1 Case study

In this sub-section, the real case study has been applied to validate the proposed mathematical model of this study. This study considered the Mazandaran province as a case study located in the north of Iran and is constituted of 21 cities and 60 counties with more than 3 million residents (Shirazi et al., 2021). For more information, readers are referred to Shirazi et al. (2021). Figure 4 displays the aerial map of Mazandaran province and all facilities of the CLBSCN, including BM, BFC, NBB, and BDC.

Fig. 4
figure 4

The aerial map of Mazandaran province in the CLBSCN

Full size image

6.2 Result

This sub-section shows the result of the proposed mathematical model. First, the result of the model has been reported by solving two proposed TH and GMMT methods discussed in Sect. 4 and then compared to find the best one in terms of some criteria such as satisfaction degree, objective functions, and two performance measures of distance and dispersion. Second, the result of strategic and planning decisions defined in the proposed model is provided. Finally, the variability of some crucial parameters has been investigated to show how the two proposed objective functions may alter. The proposed model runs on a laptop with an Intel Core i7 CPU, 8 GB RAM coded on the GAMS software, and solved by BARON solver.

6.2.1 Result of the TH method

According to step 4 of the TH method, the PIS and NIS are computed using \(\alpha =0.1\). The result of this step is computed and brought in Table 9. As shown in Table 9, the maximum level of service to the customer is 100%, which is equal to the minimum cost of the supply chain of $554,608.

Table 9 PIS and NIS of each objective function by TH method through solving Eqs. (87)–(94)
Full size table

In step 5, the membership function of six objective functions by Eq. (95)–(100) has been computed, which are reported in Table 10. In the next step, Eq. (101) is solved by determining \(\gamma ,{\theta }_{i}\). The process is repeated as many times as necessary until the decision-maker is completely satisfied with the optimal solution found. To obtain the value of the first objective function, 38 iterations, including 49,501 variables and 36,602 constraints, have been carried out to achieve the solution. We could solve all the models by utilizing the BARON solver. Then, some stop criteria have been considered to solve each iteration of the model, including CPU time limitation of 300 s, optimality gap of 0.05, \(\alpha =0.1\), and some controllable parameters which are determined by decision-makers like \(\gamma ,{\theta }_{i}\).

Table 10 The membership function value of each objective functions
Full size table

Equation (101) in step 6 has some input parameters such as \(\gamma \) and \({\theta }_{i}\). We consider these parameters \(\gamma =0.4\) and \({\theta }_{1}=0.10,{\theta }_{2}=0.19,{\theta }_{3}=0.16,{\theta }_{4}=0.22,{\theta }_{5}=0.08,{\theta }_{6}=0.25\). It is noteworthy to mention that the reason for selecting \(\gamma =0.4\) is that the first objective function substantially affects other objective functions while optimizing the proposed model. Although the problem cases are large and acceptable in real-world terms, CPU time was not an issue in our tests. All the above approaches result in an “excellent” practicable solution in a matter of seconds.

6.2.2 Result of the GMMT method

This sub-section describes results obtained from the GMMT method. First, the number of parameters presented for the GMMT method is more than the number of parameters for the TH method. Because of the comparison plans to conduct in the following sub-section, an equal number for the same parameters of these two methods have been considered. Then, we have: \(\gamma =0.4\) and \({\theta }_{1}=0.10,{\theta }_{2}=0.19,{\theta }_{3}=0.16,{\theta }_{4}=0.22,{\theta }_{5}=0.08,{\theta }_{6}=0.25\).

The weighted least squares method has been applied to give the appropriate weight to each objective function. Also, we have weighted all the fuzzy constraints (original model), including (10)–(18), (33), and (35)–(37), equally at 0.076.

Table 11 displays the membership function value for every objective function and its constraints in the GMMT method. As can be seen, the membership function values of constraints reach more than objective functions due to considering the constraints and objective functions simultaneously.

Table 11 The membership function value of each objective functions
Full size table

6.2.3 Comparing the TH and GMMT methods

The comparison is accomplished based on two viewpoints: satisfaction degree and value of objective functions. Table 12 shows the comparison based on the satisfaction degree obtained by two methods of TH and GMMT. As is evident in Table 12, the satisfaction degree resulting for all values of \(\alpha \) by the GMMT method was more stable and better than the TH method. On the other hand, Fig. 5 shows this result geometrically, similar to the result obtained by Gholamian et al. (2021).

Table 12 Satisfaction degree of TH and GMMT methods
Full size table
Fig. 5
figure 5

Satisfaction degree comparison obtained by two GMTM and TH methods

Full size image

Lastly, Table 13 shows objective function values obtained by substituting the optimal variables into the objective functions. It is clear from Table 13 that the GMMT method performed better than the TH method (4 out of 6). Noteworthy, the GMMT method could generate a better result for maximizing customer service level (2 out of 3).

Table 13 Objective functions values obtained by two TH and GMMT methods
Full size table

6.2.4 Evaluations

Besides two performance measures of satisfaction degree comparison and objective function values that have been discussed in the previous sub-section, this sub-section aims to consider two other performance measures of distance and dispersion suggested by Torabi and Hassini (2008). The distance measure aims to determine how close each solution is to the corresponding ideal solution. Therefore, the family of distance functions proposed by Abd El-Wahed and Lee (2006) is as follows:

$$ D_{p} (\gamma ,k) = \left[ {\sum\limits_{k = 1}^{K} {\gamma_{k}^{p} \times (1 - l_{k} )^{p} } } \right]^{1/p} $$
(105)

The degree of closeness regarding compromised solution concerning the kth objective function is shown by \({l}_{k}\). Moreover, power p shows the parameter of distance, and it is usually displayed with 1 (Manhattan distance), 2 (Euclidean distance), and \(\infty \) (Tchebycheff distance). When the power p increases, the distance \({D}_{p}(\gamma ,k)\) decreases. Generally, the fuzzy approach with the minimum \(p=1\) is superior to other methods (Torabi & Hassini, 2008).

The second performance measure is dispersion, which measures the range of satisfaction degree of objective functions. Equation (106) show how the dispersion is computed.

$$ RSD(x) = \mathop {\max }\limits_{k} (\mu_{k} (x)) - \mathop {\min }\limits_{k} (\mu_{k} (x)) $$
(106)

The RSD refers to the measure of balancing several compromised solutions by computing the difference between the minimum and maximum satisfaction degree of objective functions. Table 14 compares two performance measures, including distance and dispersion, by GMMT and TH methods. The points obtained from Table 14 is that the distance measure of the TH method \(p=2,\infty \) outperformed the GMMT method. But, based on Torabi and Hassini (2008), the appropriate power of p would be \(p=1\) for comparison. As the values of \({D}_{1}(\gamma ,k)\) for two methods are close to each other, it is not appropriate to compare both methods with the distance measurement alone. In this way, the dispersion parameter is crucial in determining which methods perform better than others. The RSD is greater when the TH method’s distance values are smaller than the GMMT methods. Based on this observation, it is safe to conclude that the GMMT approach produces less balanced results than the TH method.

Table 14 Performance measure of distance by TH and GMMT methods
Full size table

Therefore, based on the discussion, it can be said that by changing the value of \(\gamma \) and \(\pi \) at the same time, the GMMT method can generate compromised balanced and unbalanced solutions. Also, the sensitivity analysis for the value of \(\pi \) has been shown in Table 15. Based on the DM’s preference, the GMMT method can produce both compromised balanced and unbalanced solutions.

Table 15 Generating unbalanced solutions by variation in \(\pi \)
Full size table

6.3 The strategic and planning decisions

The binary variables describe the strategic decisions of the proposed mathematical model, and its results are presented in Table 16. As stated earlier, one donor can simultaneously be assigned to BM or BFC. Therefore, donors, 5 and 6 are assigned to BM of 1, donors 2 and 4 are assigned to BM of 2, and donors 1 and 3 are given to BFC of 1. It is necessary to mention that because binary variables depend on time index and change in different periods, Table 16 shows the results for only period t = 49.

Table 16 Result of strategic decisions (t = 49)
Full size table

The planning decisions of the designed CLBSCN are explained in Fig. 2. As it can be shown, these variables are the inventory level of blood at BFC, NBB, and hospitals, the number of outdated blood units at BFC, NBB, and hospitals, the number of blood shortage at hospitals, the number of blood units which is substituted by another type of blood group between hospitals, the transferred number of blood units between different levels of the blood network, and the processed unit of blood type in varying levels of the network. Results for shortages, outdated blood units, and inventory in BMs, BFC, NBB, and hospitals are shown in Tables 17, 18, 19 and 20. Moreover, because of our aim to show the shortage and outdated units, we started the period from 48 to 50 (the shelf-life of RBC is about 42 days) in the below tables. Based on Tables 17 and 19, in periods 48 and 50, the level of inventories in NBB is in the highest amount compared to another period, so there would be no shortages in hospitals in these periods. Also, Table 18 reports the number of outdated blood units for type 3 in BFC, NBB, and hospitals. As can be seen, an outdated blood unit in BFC of 1 and 2 does not exist, while in periods 48 through 50, NBB has experienced outdated blood units in their own center 1.

Table 17 Result of planning decisions for inventory
Full size table
Table 18 Result of planning decisions for the outdated unit
Full size table
Table 19 Result of planning decisions for shortage
Full size table
Table 20 Result of planning decisions for the substituted unit between hospitals
Full size table

It is essential to mention that one of the critical variables defined previously is the number of shortages that may happen in hospitals. This variable is considered in the second objective function [see Eq. (9)]. This function aims to maximize the level of service in hospitals. In other words, we aim to minimize the number of shortages by substituting a different type of RBCs blood in hospitals. In this way, how much demand could not be satisfied is considered a shortage. Table 19 shows the number of shortages that may occur while transmitting various RBC blood types. What is clear from Table 19 is that the number of shortages in a period is different. For instance, in period 48, there were no shortages in any of the three hospitals, while in period 49, all the hospitals experienced shortages. The reason for the shortage in these two periods is related to the level of zero inventories.

Another vital thing considered in this study is the concept of lateral resupply, which helps hospitals avoid shortages that may occur that will be analyzed later. Defining the substitution variable could help hospitals avoid becoming out-of-stock. Table 20 reports the number of various types of RBCs substituted between hospitals. As shown in Table 20, in periods 48 through 50, hospitals 1 and 3 did not need to replace any blood type by obtaining it together. In contrast, this substitution happened for hospitals 1 to 2 and 3 to 2 in period 49 (Arani et al., 2020).

Figure 6 displays the Pareto frontier of this study for the two proposed objective functions. As evident in the Pareto optimal solution, when the value of the first objective function increases, the value of the second objective function decreases. Similarly, Table 21 indicates that none of the Pareto optimal solutions is superior to the other solutions, and all the solutions obtained are non-dominated.

Fig. 6
figure 6

The Pareto fronts of the first and second objective functions

Full size image
Table 21 Set of the Pareto optimal solution obtained
Full size table

6.4 Computational time

The proposed model has been tested in 10 different small and medium test-size problems to show the computational time of the proposed model, which is shown in Table 22 (Shirazi et al., 2021). Also, Tables 23 and 24 display the values of fuzzy and certain parameters of the model. The CPU time of all problem numbers solved by two utilized TH and GMMT methods is depicted in Fig. 7. What is visible from Fig. 7 is that with increasing the size of the problem, the CPU time of both two applied methods has changed slightly. Although the proposed model of this study has many constraints, the solution time of the model is still reasonable. Also, the finding shows that the GMMT outperforms the TH method for the model of this study, and also, the proposed model has the capability to solve the large size problem in a reasonable and fastest time. The model could reach the feasible solution in the fastest time because of utilizing the linearization technique as discussed in Sect. 3.2, which helped the model, including both the second objective function and some non-linear constraints.

Table 22 Defining the different sets of test-size problem
Full size table
Table 23 Values of certain parameters
Full size table
Table 24 Values of triangular fuzzy parameters
Full size table
Fig. 7
figure 7

The CPU time of all test-size problems solved by two TH and GMMT methods

Full size image

6.5 Sensitivity analysis

This sub-section is aimed at conducting sensitivity analysis on various parameters of the model, including capacity, supply, and demand to see how changing these parameters affects the two proposed objective functions.

6.5.1 Demand variations

The first analysis is related to the proposed model’s various demands, which are based on variations from −%20 to +%20 (Arani et al., 2020; Momenitabar et al., 2022). As shown in Fig. 8, when the supply value is assumed to be constant, the first objective function value increases by increasing demand. In contrast, the second objective function value decreases. Arguably, it is shown that by increasing the demand, the value of the first objective function increases due to the costs that demand imposes on the designed CLBSCN. Conversely, the second objective function value has decreased by increasing the demand due to the increasing number of shortages. In other words, when demand increases, the shortage increases too, which leads to the second objective function decreasing.

Fig. 8
figure 8

Demand variation with the first and second objective function

Full size image

6.5.2 Supply variations

The second important parameter is donors’ variation of supply in CLBSCN. The supply is analyzed when the number of donors increases or decreases during the time, based on variations from −%20 to +%20. The American Red Cross, for example, has reported a severe blood shortage due to the cancellation of blood drives in response to the coronavirus outbreak (American Red Cross, 2020a). In this situation, the number of supplies decreased. Figure 9 shows the first and second objective function values when supply is altered. It is clear from Fig. 9b that the shortage decreases with increasing the number of supplies, and the second objective function reaches a higher value. Similarly, the same thing happened for the first objective function shown in Fig. 9a.

Fig. 9
figure 9

Supply variation with the first and second objective function

Full size image

6.5.3 Capacity variations

The third thing is the capacities changes in various centers in the designed CLBSCN (Safaei et al., 2022). The result of capacity variation in different centers like BFC, NBB, Hospitals, and BDC are shown in Fig. 10. According to Fig. 10, increasing in capacities from −%20 to +%20 resulted in an increase in the first objective function from $1,490,000 to $1,610,000. What Fig. 10 indicates is that a 40 percent increase in capacities of various opening centers like BFC for receiving more blood from donors can increase the total cost of CLBSCN by a value of $120,000 approximately.

Fig. 10
figure 10

Capacity variation with the first and second objective function

Full size image

6.6 Lateral resupply

Also, the effect of lateral resupply on the total costs of the CLBSCN in terms of positive or adverse effects has been investigated (Arani et al., 2020; Momenitabar et al., 2022). By considering two situations, the total costs of the designed CLBSCN have been examined. Figure 11 displays the impact of lateral resupply on the designed network.

Fig. 11
figure 11

Analyzing lateral resupply based on demand variations for two objective functions

Full size image

According to Fig. 11, when the concept of lateral resupply is applied, a considerable decrease in the total value of the objective function has seen compared to when this concept has not been applied. Also, this concept has been included by defining the substitute variable as shown in Eqs. (33) and (60). These two equations are related to inventory and outdated blood unit equations. Defining this variable aimed to avoid shortages in hospitals and reduce the total cost of the designed network.

It is clear from Fig. 11 that by considering the lateral resupply, the value of the first objective function decreases considerably. As can be seen, considering this concept could significantly save the costs of the designed network by a total of $343,000. Similarly, taking this concept could increase hospitals’ service levels from 58 to 68%. Therefore, we can conclude that the concept of lateral resupply had positive effects on the designed CLBSCN.

7 Conclusion

This paper studied the design of multi-echelon CLBSCN, which includes donors, BFCs, BMs, NBBs, Hospitals as demand points, and BDCs for outdated blood, which collects the returned blood from hospitals, NBB, BFC, and BM. Due to the nature of demand and supply, these two parameters are considered uncertain. RBCs are also gathered because of two primary medical preferences: blood types and Rh(D) factors. To define the allocation of different levels of the network, we proposed a fuzzy multi-objective MINLP model, in which the first objective function is aimed at minimizing the total cost of the CLBSCN. In contrast, the second objective function is aimed at maximizing the minimum level of service to the patients at hospitals in each period.

First, the equivalent auxiliary crisp model is utilized to convert the fuzzy multi-objective MINLP model to the crisp multi-objective MINLP model. Second, two interactive fuzzy programming approaches, including the TH and the GMMT applied to solve the crisp multi-objective MINLP model to find solution. Also, by comparing these two methods based on various criteria such as satisfaction degree comparison, the value of objective functions, and two performance measures of distance and dispersion, the GMMT method outperformed the TH.

Also, the proposed model of this study has been applied to the case study of IRAN to be validated. Solving the proposed model could reach the optimal value of critical decision variables defined in Sect. 3. The results showed that considering service level maximization increased the level of service to the patients at hospitals from 58 to 68%. More importantly, the cross-matching and the ABO-Rh(D) priority orders for substituting blood groups could substantially reduce the number of substituted blood types in each Hospital in the designed CLBSCN. By conducting sensitivity analysis on three critical parameters of the model, increasing in demand resulted in incrementing the total costs of the first objective function and decreasing the service level to the patients from 96 to 87%. Also, the increase in supply led to an increase in both the first and second objective functions. Incrementing in supply could improve the service level to the patients by avoiding shortages. Lastly, an increase in capacity could lead to an increase in total costs of the first objective function and the service level to the hospital patients.

By conducting this study, some managerial insights have been proposed as follows:

  • Considering lateral resupply improved the values of two proposed objective functions and reduced the required inventory in hospitals despite its fuzziness (see Fig. 11 and Table 17).

  • Since the proposed network reflects the reality that mismatched blood or substituted blood type can be administered to patients, a much more accurate analysis could be obtained for the network’s management.

  • The compatibility matrix’s real practice reveals that the percentage of a specific blood product could be used interchangeably. This provides valuable guidance to practitioners.

  • By applying a classic well-known solution methodology, the model’s capability to solve real-world instances increases, particularly the success in linearizing the non-linear problem. The linearization techniques permit us to search for a convex feasible solution and considerably reduce the complexity of the model, guiding us to optimum solutions in most cases.

The findings of this study are significant due to the following reasons. First, it allows national blood banks and hospitals to reduce waste and enhance their quality of service to their patients. Second, designing a current BSCN assists the national/international institutions in effectively managing and transferring irreplaceable blood products. Indeed, several organizations benefit from a CLBSCN, including the American Red Cross, American Blood Resources Association, and Community Blood Banks. Lastly, the proposed model of this study has the applicability to be implemented in different parts of the world.

Several research directions can be pursued based on the current work. The first thing is to consider disruption probabilities and/or backorder shortage in coping with hospital demands. Second, in terms of solution methodology, introducing other uncertainty programming methods such as mixed fuzzy stochastic programming and comparing the efficiency of the results with the current approach is recommended. Additionally, applying other meta-heuristic solution techniques may also elevate the accuracy of the results. Interestingly, the multi-choice goal programming approach, the Lagrangian approach, and the L-shaped method are appropriate strategies for large-scale problems to find an optimal solution. Lastly, the usefulness of developing a decentralized system can be an alternative for future research.