1 Introduction

The main goal of competitive sports is to yield a higher ranking sporting performance getting promotions or winning relevant competitions. Data concerning athletes’ performance and their behavior are the essential core for competitive sports (Du & Yuan, 2021). Technological enhancements concerning remote sensor technology or motion capture systems have been developed together with advanced statistical approaches to model, infer or predict performance outcomes in sport [e.g. (Albert et al., 2016; Nevill et al., 2008)]. An analysis of sports statistics can effectively identify athletes’ behavioral patterns (Legg et al., 2012; Losada et al., 2016), including their individual contribution and degree of activity. However, sports data contain multiple dimensions, and relying purely on numbers cannot fully represent the data analysis results. Apart from the value of the performance indicators used to categorise athletes’ and teams’ achievements, there is still a lack of understanding regarding why and how some behaviours emerge in performance contexts (McGarry, 2009). It provides a basis for the study of the law of athletes’ life and the habits of athletes’ beings (Du & Yuan, 2021).

Recently, an increasing interest has been devoted to understanding the psychological behaviour of some athletes and how personality traits influence their performance [see (Aidman & Schofield, 2004; Laborde et al., 2020), among others], also by means of complex statistical models (Fabbricatore et al., 2021; Fabbricatore & Iannario, 2022). This data analysis work would be helpful for professional analytics, allowing effective behavior-based decision-making during games, improving the effects of teams’ training and performance in competitions (Janetzko et al., 2014; Legg et al., 2012, 2013; Rusu et al., 2010). Some contributions focused on interpersonal relationships in athlete-athlete and coach-athlete dyads studying their interdependence to improve results (Bell, 2007; Jowett & Nezlek, 2012; Rhind & Jowett, 2011). Others collect Likert-type responses as psychometric item scoring schemes for attempting to quantify athletes’ opinions, interests, or perceived efficacy of an intervention relaying on multi-block data. The statistical techniques that can be used to analyse them are called multi-block methods (Smilde et al., 2000). The essential requirement is that these blocks have one dimension or mode in common, i.e. different groups of variables are observed on the same statistical units, or the same set of variables is observed on different groups of statistical units. Our contribution fits these areas aiming to understand the feeling between coach and athlete, their possible (dis)agreement and the psychological factors/reasons that motivate/influence their relationship. The coach-athlete dyad is probably one of the most relevant within athletic communities because it is a relationship whereby the athlete expresses needs (e.g., autonomy, competence) and goals (e.g., skill development, performance success) (Côté & Gilbert, 2009; Lyle, 2002). The analysis concerns several observed variables collected on the dyads, which are grouped into homogeneous blocks measuring partial aspects of the phenomenon under investigation. Data come from a survey collected in 2019 for the Statistical Modelling and Data Analytics for Sports project, which involved the University of Naples Federico II and the Italian Swimmer Federation (Campania Regional Committee). They gather information about psychosocial aspects influencing swimmers’ performance. Data concern 100 elite swimmers and their coaches; the latter were sampled by the Italian Swimmer Federation (Campania Regional Committee) picking among their lists with a random selection. Each coach randomly selected one of her/his athlete and asked her/him to fill out a questionnaire. Interviewed people answered several questions concerning their mental strategies and skills based on one of the main theoretical framework for analysing personality and coping behaviour in sport: the five-factor model (McCrae & Costa, 2008), also named Big Five (BigF5). The complex structure of data derives both from the dyads and the large number of observed and corresponding latent variables with respect to the sample size. The degree of complexity is also related to the mixed-type data, categorical and quantitative ones. This enhances practical and theoretical challenges requiring a specific treatment and a “statistical learning” from data (Hastie et al., 2013).

The approach pursued in our proposal exploits quantile regression (Koenker & Bassett, 1978), in line with a previous proposal (Davino et al., 2020) where such method has been used as kernel of a strategy to assess heterogeneity in a different multi-block type data structure. The study models the actor/partner interdependence in the case of dyadic data by presenting an alternative approach with respect to the current used methods (Kenny et al., 2006). After a preliminary analysis of the athletes/coaches matrix of responses, aiming to evaluate the consistency of perceived assessments on some topics related to the performance, a quantile regression has been implemented to disclose how disagreement is connected to athletes’ psychological aspects. The remainder of the paper is structured as follows. Section 2 provides a detailed description of the survey, the complex data and the latent variables considered in the research. Section 3 illustrates the statistical method used for the analysis and the main results. Conclusions and discussion of further research developments to be explored are included in Sect. 4.

2 Survey description

In the last few years, it has been common practice to collect complex data sets composed of different groups of variables observed on the same units. Such costume has been largely adopted in the contexts of sports analytics (Lebed, 2017), where surveys and in-depth interviews are collected for both description, and prediction aims (Davenport & Harris, 2007). In this study, the complexity is threefold. On the one hand, there are dyads, consisting of scores/evaluations provided by coaches and athletes on the athletes’ performance. On the other hand, there are the variables on athletes: the athletic profile, personal data, habits and demographics. Finally, psychometric scales are used to measure elite swimmers’ latent traits, i.e. groups of items that aim to measure the corresponding latent constructs. Analyzing such complex datasets requires a multi-step strategy investigating the relationships between different groups of variables using supervised and unsupervised methods. In some cases, the groups of variables are synthesized through dimensionality reduction techniques (Hastie et al., 2013), specifically principal component analysis (Jolliffe, 1986). At other times, as in the case of psychometric scales, an appropriate synthesis can be the sum or the average of the items of each block (McNeish & Wolf, 2020).

A sample of 100 elite swimmers (from now on, simply swimmers) enrolled in professional-level registers was examined. They were randomly selected by coaches who, in turn, were sampled by the Italian Swimming Federation (Campania unit) list. Leading details on the sample are reported in Table 1.

Table 1 Summary statistics concerning the characteristics of the 100 athletes of the survey
Full size table
Fig. 1
figure 1

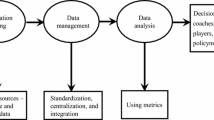
Scheme of the data analysis strategy: (1.a) the dyad (\({{\mathbf {Z}}}{{\mathbf {1}}}-{{\mathbf {Z}}}{{\mathbf {2}}}\)) is studied using the deviation of the respective values (\({\mathbf {Y}}\)), (1.b) from which a small number of relevant dimensions (\({\mathbf {T}}\)) are extracted; (2.) the BigF5 psychometric scale is summarized in block \({\mathbf {B}}\), including the syntheses of the 5 dimensions (\(\mathbf {E, A, C, S, O}\)); (3.) the synthesis of the BigF5 scale and personal data on the athletes (\({\mathbf {G}}\)) are regressed on the dimensions of the disagreement (\({\mathbf {T}}\))

Full size image

Personality was assessed by using a list of 25 adjectives representative of the five-factor model (Big Five–BigF5) in the Italian lexical context (Barbaranelli et al., 2007; Caprara & Perugini, 1994). The list consists of 5 adjectives for each of the five personality dimensions: Extraversion, Emotional stability, Openness, Agreeableness, and Conscientiousness. Swimmers were required to fill out the questionnaire indicating how appropriate each adjective was for describing themselves on a 5-point scale. Furthermore, athletes and coaches answered nine questions assessed by visual analogue scales about their perceived assessments on some topics related to the performance.

The strategy proposed in this study, graphically outlined in Fig. 1 and detailed in the next section, consists of the following steps, each requiring specific statistical learning techniques:

  1. 1.

    Analysis of the dyads (see step 1. in Fig. 1):

    1. a.

      Analysis of the disagreement between the two groups of variables on the athletes’ sport performance: here the disagreement matrix \({\mathbf {Y}}\) was derived resorting to absolute values of the differences in scores of coaches (\({{\mathbf {Z}}}{{\mathbf {1}}}\)) and athletes (\({{\mathbf {Z}}}{{\mathbf {2}}}\)) (see step 1.a in Fig. 1).

    2. b.

      Synthesis of the disagreement through a reduced number of dimensions embedded in the \({\mathbf {T}}\) matrix: here we exploited principal component analysis (PCA) (Jolliffe, 1986; Mardia et al., 1979) on the disagreement matrix \({\mathbf {Y}}\) (see step 1.b in Fig. 1).

  2. 2.

    Summary of the psychometric scale: different options could be exploited for this step, among them: sum/average/weighted average/principal components by dimension. Regardless of the specific method used to synthesise the five dimensions of the BigF5 scale (\(\mathbf {B1-B5}\)), the final result will be the new block of variables denoted \({\mathbf {B}}\), which contains the five syntheses (\(\mathbf {E, A, C, S, O}\)) (see step 2 in Fig. 1).

  3. 3.

    Analysis of the influence of psychological factors and athletes’ personal data on the dimensions of the disagreement: we exploited quantile regression (QR) (Koenker & Bassett, 1978) both for its distribution-free nature and for modelling the dependence structure at different locations of the response. Specifically, the dependence relationship between the block of predictors \({\mathbf {X}}\), composed of the variables in \({\mathbf {B}}\) (obtained in step 2) and \({\mathbf {G}}\) (personal data on the athletes), and the block of dependent variables \({\mathbf {T}}\), including the disagreement dimensions obtained in step 1.a, is analyzed through QR (see step 3 in Fig. 1).

3 Data analytics

The following subsections details the steps of the strategy outlined in Fig. 1, briefly recalling the involved statistical methods.

3.1 Analysis of the dyads through dimension reduction methods

In this study, available data follow the dyad structure (Kenny et al., 2006), where each dyad corresponds to a statistical unit on which two levels of each variable are observed. The two levels correspond to athletes and coaches, and the variables are nine measures of the athletes’ sports performance (see Fig. 1 for details). Formally, data are organised into two datasets, each consisting of J variables measured on I objects/dyads. The two datasets, of orders (\(I \times J\)), are denoted here by \({{\mathbf {Z}}}{{\mathbf {1}}}\) and \({{\mathbf {Z}}}{{\mathbf {2}}}\): \({{\mathbf {Z}}}{{\mathbf {1}}}\) contains coaches’ scores, \({{\mathbf {Z}}}{{\mathbf {2}}}\) athletes’ scores. Coaches’ and athletes’ variables are shown in Fig. 2 where divergent stacked bar charts are reported. Each panel refers to a given variable related to coaches and athletes. The bars in each panel are located with reference to the neutral point scale expressed on a discretized version of a 7-point scale of a visual analogue scale [see (Cox, 1980), for the discretization]. Therefore, if the bar for a given item tends to lie in the right part of the plot, this denotes a percentage of respondents with points in the upper part of the correspondent scale. Inversely, in case the major part of the bar is located in the left part of the plot. Segments of the same level in the same color are comparable across items and panels.

Figure 2 shows that the expressed values for coaches are lower than those of athletes for the variables anxiety, recovery and get nervous, while being higher for talent, work out, pressure and sacrifice. The visual inspection indicates the variables with the most outstanding disagreement between coach and athletes. Here, disagreement stands for under(over) evaluation of the athlete with respect to the coach (and vice versa), that is both a level of feeling and compliance from one side and a different perception of ability/skill from the other side.

Fig. 2
figure 2

Divergent stacked bar chart for the nine measures of the athletes’ sport performance

Full size image

Different types of multivariate analysis techniques can be used to analyse the relationships between two datasets depending on the relationship hypothesised between the two sets of variables. For example asymmetric methods try to predict one dataset from another, thus treating the two datasets differently. Principal Component Regression (Martens & Næs, 1992), Partial Least Squares Regression (Abdi, 2010; Geladi & Kowalski, 1986), Redundancy Analysis (Van Den Wollenberg, 1977) are among these methods. Symmetric methods treat the two datasets similarly. Here, the goal is to study relationships between the two sets rather than predict one from the other. Examples of these methods are Canonical Correlations (Hotelling, 1936) and Procrustes Analysis (Schönemann, 1966). The relationship analysed in dyadic data analysis is usually of symmetrical type. Specifically, the main interest in this research is to study the disagreement between coaches’ and athletes’ scores. Therefore, examining the deviation between the two matrices seems more appropriate. To this end, the strategy of analysis proposed here consists of calculating the matrix of absolute deviations \({\mathbf {Y}} = |{{\mathbf {Z}}}{{\mathbf {1}}}-{{\mathbf {Z}}}{{\mathbf {2}}}|\) and applying a PCA to identify the dimensions of maximum disagreement.

PCA is a well-established, and long-standing multivariate statistical technique (Hotelling, 1933; Pearson, 1901) that has made a comeback as an unsupervised machine learning technique (Hastie et al., 2013) due to its information synthesis capabilities. Let us consider a matrix \({\mathbf {Y}}\) with I rows (\(i=1, \ldots , I\), usually samples/objects) and J columns (\(j=1, \ldots , J\), usually variables). Formally, PCA aims to obtain a small number of new variables, called principal components, which are linear combinations of the variables in \({\mathbf {Y}}\) and contain as much as possible variation present in \({\mathbf {Y}}\). Given the first linear combination \({\mathbf {t}}={{\mathbf {Y}}}{{\mathbf {w}}}\) and the corresponding variance \(var({\mathbf {t}})\), the problem turns into maximizing this variance, choosing the optimal \({\mathbf {w}}\) of length one

$$\begin{aligned} \mathop {{\mathrm {argmax}}}\limits _{{\left\| {\mathbf {w}} \right\| }} var({\mathbf {t}}), \end{aligned}$$
(1)

where the matrix \({\mathbf {Y}}\) is mean-centered. The restriction on the length of \({\mathbf {w}}\) is needed to obtain a unique solution. The problem in equation (1) is a standard problem in linear algebra and the selected \({\mathbf {w}}\) is the first eigenvector of the covariance matrix \({\mathbf {Y}}^{T}{\mathbf {Y}}/(I-1)\).

The following components are obtained in the same way, but with the additional constraint that each is uncorrelated to the component that precedes it. The maximum number A of possible components equals the minimum of \(I-1\) and J. The eigenvalue \(\lambda \) corresponding to each eigenvector provides a measure of the variability conveyed by the component. Therefore, it is possible to calculate the percentage of explained variation of \({\mathbf {t}}_{a}\) as

$$\begin{aligned} \frac{\lambda _{a}}{\sum _{a=1}^{A}\lambda _{a}}100\%. \end{aligned}$$
(2)

Figure 3 reports the scree plot of the explained variability (left-hand side), and the biplot (right-hand side) resulting from the PCA on the \({\mathbf {Y}}\) matrix. The scree plot highlights two relevant dimensions of disagreement. The biplot suggests interpreting the first dimension as a disagreement concerning attitudinal and psychological factors that influence the athletes’ performance (psycho-attitudinal disagreement). In contrast, the second dimension describes a disagreement with the athletes’ commitment to the discipline (commitment disagreement).

Fig. 3
figure 3

Percentage of explained variance (left-hand side) and corresponding biplot (right-hand side) carried out by PCA on the disagreement matrix

Full size image

A question of relevant importance for interpreting the results of a PCA concerns the selection of the statistically significant principal components. Several procedures have been proposed for this purpose: resampling methods (Peres-Neto et al., 2005), cross-validation methods (Bro et al., 2008; Josse & Husson, 2012), statistical tests (Choi et al., 2017), and parallel analysis (Horn, 1965). The present work applies the recent bootstrap approach proposed by Forkman et al. (2019). The null hypotheses are \(H_{0}{:}~m=K\), where m is the unknown true number of principal components. Tests at significance level \(\alpha =0.05\) are carried out sequentially, for \(k=0, 1, 2, \ldots ,\) up to \(K=M-2\), where \(M=min(I-1, J)\), or a non-significant (\(p>0.05\)) result is obtained. The corresponding alternative hypotheses are \(H_{1}{:}~m>K\), where K is the candidate order of the model. For the disagreement block, only the first principal component was highly significant (\(p=0.000\)), while the second component was not significant (\(p=0.095\)).

3.2 Extraction of the latent dimensions of the psychometric scale

Frequently psychologists need to measure abstract concepts (constructs) that are not directly measurable. One way to obtain a more reliable measure of the concept is to use a series of highly correlated items (scale) corresponding to different measurements of the same phenomenon. The construct is defined as one-dimensional if correlations between items emerge from a single underlying dimension. On the other hand, a multidimensional construct has two or more underlying dimensions that appear from groups of variables with high intra-group correlations and less relevant inter-group correlations. A detailed description of the psychometric scale employed in this study and the analysed traits/constructs is reported in Table 2. The five-factor model (Big Five–BigF5) is multidimensional and includes five dimensions, each measured by five items corresponding to adjectives, each measuring one of the five personality dimensions.

Table 2 Description of the scales and related constructs used in the analysis
Full size table

Two are the two main methods of combining the different items of a one-dimensional or a multidimensional construct into a single measurement: a) the sum of the scores of the individual items (Gleser & Dubois, 1951); b) the factor analysis (Fabrigar et al., 1999). The latter, in particular, is used when the aim is to propose a new scale or to validate a scale on a specific sample. Since the BigF5 is a widely known and utilised scale, and the paper’s objective is not to validate it, the sum of the items is adopted to obtain the score of each of the five dimensions. These, as also shown graphically in the Fig. 1, are used in the next section as predictors of the disagreement.

3.3 Analysis of the relations between disagreement and psychosocial factors

This section deals with quantile regression, introducing it in Sect. 3.3.1, then using it on the analyzed data in Sect. 3.3.2 to relate the dimensions of disagreement and the psychosocial variables. The analysis concerns only the first dimension as the second dimension is resulted to be not significant, as described in Sect. 3.1.

3.3.1 A short briefing on quantile regression

Quantile regression (QR) extends classical regression to a set of quantile functions of a response variable \({\mathbf {y}}\), conditional on a set of covariates \({\mathbf {X}}\). Initially proposed by Koenker and Basset (Koenker & Bassett, 1978), QR is a regression approach completely distribution-free, since it does not pose any parametric assumption on the error (and hence response) distribution. It aims to estimate the effects of a set of regressors on the quantiles of a response variable. In particular, QR estimates separate models for different asymmetries \(\tau \in (0, 1)\), where \(\tau \) denotes the particular conditional quantile of interest. Unlike the classical regression model, where the conditional mean of the error \(E(\epsilon _{i\tau }) = 0\), in QR the \(\tau \)-quantile of the error term is 0, namely \(P(\epsilon _{i\tau } \le 0) = \tau \). The separate models provided by QR, one for each quantile of interest, are interpretable in terms of regression models for the associated conditional quantiles of the response. A dense set of quantiles completely characterizes the conditional distribution of the response: the use of “enough” quantiles makes it possible to virtually analyze any property of the response distribution (Davino et al., 2013). Although it is theoretically possible to extract infinite quantiles, a finite number is numerically distinct in practice, which is known as the quantile process (Furno & Vistocco, 2018). A good tension between the wealth of information and interpretation issues leads to using a selected set of quantiles, typically the three quartiles, along with two extreme quantiles, to model the tails.

As stated above, the effect of covariates acts not only on the conditional mean but on the complete conditional distribution of the response given the covariates. Moreover, not including the classical restrictive assumptions of the mean regression model, QR is well suited to deal with heteroscedasticity, but even more important, to model the higher-order characteristics of the response in terms of covariates. One should also bear in mind that in many studies, as the assessment reported in our analysis, there is a genuine interest in conditional quantiles, and hence the QR ability to describe extreme observations in terms of covariates provides an incomparable added value. This can be attractive in sports applications, since the focus on the distribution’s tails helps inspect dependence models for athletes with low/high performance, low/high level of stress, low/high motivation, and in our case, with low/high disagreement with coaches judgment.

The QR model, linking the response of each single unit to the regressors, is estimated for different quantiles

$$\begin{aligned} {\mathbf {y}} = {\mathbf {X}} {\beta }(\tau ) + {\epsilon }. \end{aligned}$$

The conditional quantile estimator (Koenker, 2005) is

$$\begin{aligned} {\hat{{\beta }}}(\tau ) = \underset{{\beta }(\tau )}{\mathrm {argmin}} \, \rho _{\tau } \left( {\mathbf {y}} - {\mathbf {X}} {\beta }(\tau )\right) {,} \end{aligned}$$
(3)

where \(\rho _{\tau } (.) \) is the check function which asymmetrically weights positive and negative residuals

$$\begin{aligned} \rho _{\tau } ( u ) = {\left\{ \begin{array}{ll} \tau \, u, &{} \text{ if } u > 0 \\ (\tau - 1) \, u, &{} \text{ if } u \le 0. \end{array}\right. } \end{aligned}$$

Equation (3) provides a quantile regression line for each conditional quantile \(\tau \) of interest.

The bootstrap procedure is typically used for inference to avoid the assumptions required by finite sample or asymptotic theory. Bootstrap offers the flexibility to obtain the standard error and confidence interval for any estimates and combinations of estimates, whilst also keeping the distribution-free nature of QR. Finally, it is worth recalling that QR estimates are not sensitive to outliers in \({\mathbf {y}}\). Specifically, any change in the value of the response variable for a data point lying above (or below) the fitted QR lines does not affect the estimates when the data point does not change its previous position concerning the specific line. Instead, QR estimator can be very sensitive to outliers in the explanatory variables, even if several proposals in the literature attempt to attain more robust estimators (Furno & Vistocco, 2018).

The machinery for solving the quantile regression problem initially exploited linear programming, and in particular, the simplex algorithm (Furno & Vistocco, 2018). However, the least absolute deviation criterion is even more ancient than the most popular least squares counterpart (Stigler, 1986). Wagner (1959) presented the linear programming techniques in the mainstream statistical literature. A few years later, the least absolute deviations were approached using linear programming and later adopted for quantile regression. Indeed, the original algorithm for solving the quantile regression problem (Koenker & D’Orey, 1987) extended the Barrodale and Roberts algorithm (Barrodale & Roberts, 1973) to conditional quantiles. The Barrodale and Roberts algorithm was initially introduced for solving the median regression problem. Koenker and Bassett (1978) slightly modified the original \(L_1\) problem placing asymmetric weights on positive and negative residuals, introducing quantile regression. The simplex approach is not the only available approach for quantile regression. Indeed, while the simplex approach exploits the movement along the corner of the feasible region (exterior-point methods), barrier methods (interior-point methods) start from an initial point inside the feasible region and, at each iteration, move to a better feasible solution. A detailed treatment of interior-point methods is available in Koenker (2000).

See the literature mentioned in Furno and Vistocco (2018) for recent alternative QR estimators. In our analysis, even if analyzed data have a complex structure, their dimension is not huge. Therefore there is no relevant difference in the solutions provided by the different algorithms.

3.3.2 Quantile regression results

As outlined in Sect. 2, QR has been exploited to analyse the influence of psychosocial factors on the first dimension of disagreement. In particular, the five personality dimensions (Extraversion, Emotional stability, Openness, Agreeableness, and Conscientiousness) representative of the BigF5 scale were used as regressors in a QR model: the first dimension of the disagreement obtained using PCA is the response variable. Figure 4 depicts the QR coefficients for the regressors. In particular, the horizontal axis displays the different quantiles, while the effect of each feature holding the others constant (QR estimate) is represented on the vertical axis. The shaded area depicts the confidence intervals, the horizontal solid lines placed at 0 helping to reveal significant effects. Each panel refers to a different personality dimension. The aim is to graphically catch the coefficient trends moving from lower to upper quantiles. Coefficients have been estimated for a sequence of quantiles from 0.1 to 0.9 with a step of 0.05.

Fig. 4
figure 4

QR coefficients for significant regressors. Each panel refers to a personality dimension, the horizontal axis depicts the different quantiles, and the vertical axis the QR coefficients. A solid horizontal line is placed at 0. The shaded area in each panel shows the 95% confidence intervals for the QR coefficients

Full size image

Figure 4 shows a significant positive effect of Agreeableness for high levels of disagreement (\(\tau = 0.75\)). Emotional stability has a significant negative impact on low levels of disagreement (\(\tau = 0.25\)) and shows a slight upward trend. Extraversion shows a positive and significant effect for almost all levels of disagreement, except the extremes. Finally, Openness always has a negative impact, significant in some extreme parts of the distribution.

Some additional information has been tested in the analysis. Among these, the age of the athlete, the gender, and some measures related to the objective performance, because they may influence the personality and the possible dis(agreement). However they are not significant from a statistical point of view signaling a sort of homogeneity in the sample of respondents.

4 Conclusions and discussion

The study of personality in sports psychology is focused on assessing the associations between personality, participation and athletic achievement (Aidman & Schofield, 2004; Allen et al., 2013; Allen & Laborde, 2014). When the BigF5 scale is considered, the main findings concerning organized sports suggest higher athletes’ score on Extraversion (Egloff & Gruhn, 1996), Conscientiousness (Kajtna et al., 2004), Emotional stability (Kajtna et al., 2004; Mckelvie et al., 2003), and Openness (Kajtna et al., 2004) when compared with non-athletes. Individual sport athletes, instead, demonstrated higher Conscientiousness, Openness and Emotional stability, as well as lower levels of Extraversion than team-sport athletes (Allen et al., 2011; Eagleton et al., 2007). The analysis we reported opens a new perspective. It shows the relationship in the coach/athlete dyad. The disagreement explained as the score distance between the subjective evaluation of the couple, is a measure of understanding and synergy. Higher levels of disagreement point out an under(over) evaluation of the athlete with respect to the coach (and vice versa), which is both a low level of feeling and compliance from one side and a different perception of ability/skill from the other side. The study on elite swimmers underlines high levels of disagreement for agreeable athletes, that is, polite, trusting, and cooperative, over competitive subjects. These athletes, evaluated as straightforward, altruistic, compliant and modest, may underestimate their value with respect to coaches’ perception. Emotionally stable swimmers, a characteristic trait of high-level athletes (e.g., athletes competing at a national or international level) (Allen et al., 2011; Kirkcaldy, 1982) reduce the distance of their evaluation concerning their coaches (Allen et al., 2011; Kirkcaldy, 1982). This result is marked for the highest level of compliance, possibly related to swimmers with high levels of self-confidence. Openness athletes, more aware of their feelings and more likely to engage in risky behaviour, reveal a high distance from their coache’s assessment.

A multi-step data analysis strategy gave these results, making it possible to extract information from multiple sources. Despite the remarkable development of statistical methods for multi-block data, when blocks are linked together in a complex structure of relationships, there is no simultaneous analysis method. Therefore, a strategy that sequentially combines information sources (blocks) is needed. In the approach adopted in this study, we used some well-founded methods such as PCA and others more recently introduced, such as QR. We faced the dyadic structure starting with an analysis of the differences in the scores of the athletes and their coaches. Then, relevant dimensions were derived from these differences. Such dimensions can be interpreted as dimensions of disagreement. Next, we summarized the blocks relating to the different dimensions of the psychological scale into a single block by adding the scores of the individual items. Finally, we connected the two previous syntheses through a linear quantile regression model. The use of quantile regression was crucial to highlight the impact of psychological variables on the whole distribution of disagreement. For example, it was possible to highlight a significant effect of agreeableness on high levels of disagreement (\(\tau = 0.75\)), effect not detectable using the classical linear regression model. The innovative contribution of this paper is, therefore, twofold. On the one hand, the dataset’s structure combines the dyad with the psychometric scale and other demographic variables of the athletes. On the other hand, the proposed data analysis strategy combines dimensionality reduction techniques with a quantile regression model. The study signals the personality traits on which the dyadic relationship needs a more efficient dialogue to eliminate possible gaps. It also deals with a homogeneous sample in which young athletes’ age stands for a limitation, especially for assessing the questions related to their personality. It remains unclear whether the results are cyclically related and caused by such factors as sociocultural variables and other factors related to the coaches’ relationship. Further investigations on these topics represent a possible future subject of research analysis.