Scale characteristics of variable returns-to-scale production technologies with ratio inputs and outputs

Abstract

Applications of data envelopment analysis (DEA) often include inputs and outputs represented as percentages, ratios and averages, collectively referred to as ratio measures. It is known that conventional DEA models cannot correctly incorporate such measures. To address this gap, the authors have previously developed new variable and constant returns-to-scale models and computational procedures suitable for the treatment of ratio measures. The focus of this new paper is on the scale characteristics of the variable returns-to-scale production frontiers with ratio inputs and outputs. This includes the notions of the most productive scale size (MPSS), scale and overall efficiency as measures of divergence from MPSS. Additional development concerns alternative notions of returns to scale arising in models with ratio measures. To keep the exposition as general as possible and suitable in different contexts, we allow all scale characteristics to be evaluated with respect to any selected subsets of volume and ratio inputs and outputs, while keeping the remaining measures constant. Overall, this new paper aims at expanding the range of techniques available in applications with ratio measures.

1 Introduction

Applications of data envelopment analysis (DEA) often involve inputs and outputs represented by ratio data. Such data may reflect the environment in which the decision making units (DMUs) operate or describe the quality of inputs and outputs involved in the production process. For example, in the context of assessment of school performance, ratio measures may include the average income per capita in the catchment area of a school, proportion of pupils with special needs and the percentage of students achieving a certain high level in exams.

The two standard DEA models are based on the assumptions of constant and variable returns-to-scale (CRS and VRS). These models were introduced in DEA by Charnes et al. (1978) and Banker et al. (1984) and can be seen as continuing the earlier developments in the economics literature by Afriat (1972), Shephard (1974), Färe and Lovell (1978) and Färe et al. (1983a). It has long been realised that the standard CRS and VRS DEA models are generally not suitable if some data are given in the form of ratios—see, e.g., Dyson et al. (2001), Cooper et al. (2007), and Emrouznejad and Amin (2009). The main reason for this is that production technologies with ratio data do not generally satisfy the assumption of convexity which is incorporated in the VRS and CRS technologies. In the case of CRS, a further problem arises because ratio measures are generally not scalable in the same way as conventional volume inputs and outputs such as costs, labor and physical levels of production or services. As also noted by Pastor et al. (2013), the input and output projections of inefficient DMUs obtained in the CRS model may result in the target values located outside the range of values observed in the empirical data set. This becomes a particular problem in the case of ratio measures, such as percentages, which may have a natural upper bound such as unity or 100%.¹

In order to overcome the highlighted problems with the use of ratio data in DEA, Olesen et al. (2015) introduced new ratio-VRS (R-VRS) and ratio-CRS (R-CRS) production technologies that incorporate both volume and ratio inputs and outputs as native types of data, i.e., without any modification. Both technologies are formally derived from the explicitly stated sets of production axioms. In particular, to allow a different treatment of ratio measures compared to volume measures, Olesen et al. (2015) utilize the axiom of selective convexity of Podinovski (2005), instead of the conventional convexity assumption. In the case of R-CRS, the standard axiom of full proportionality (scalability) is replaced by the axiom of selective proportionality, which also distinguishes between the volume and ratio inputs and outputs.

The R-VRS and R-CRS models with ratio data are further explored by Olesen et al. (2017). The latter paper discusses efficiency concepts in models with ratio data, including the new notion of potential ratio efficiency, and computational approaches for their testing. In the most recent paper on this subject, Olesen et al. (2022) explore the geometric structure of the R-VRS technology and the R-CRS technology with fixed ratio inputs and outputs. In particular, they prove that the R-VRS technology is the union of a finite number of specially constructed standard VRS technologies.

In the current paper we consider scale characteristics of the production frontier of the R-VRS technology that have not yet been explored. This includes the notions of the most productive scale size (MPSS), scale and overall efficiency, and the related notions of returns to scale (RTS). All these notions have conceptually been defined and discussed in the literature—see, e.g., Frisch (1965) and Färe et al. (1983b, 1985). Methods of their evaluation in the standard VRS technology (see, e.g., Banker 1984; Banker and Thrall 1992; Førsund and Hjalmarsson 2004; Chambers and Färe 2008) and in the whole large classes of polyhedral and convex technologies (Podinovski et al. 2016; Podinovski 2017) have also been developed. However, these methods do not generally apply to the R-VRS technology (because it is not a convex technology), and even the known conceptual characteristics such as scale efficiency may not appear to be uniquely defined. In our paper we address these issues.

Several contributions of our paper are worth highlighting. First, following the approach of Banker (1984), we define and interpret scale efficiency in the R-VRS technology as a measure of divergence from MPSS. A challenging problem here is that the cone and CRS extensions of the R-VRS technology do not coincide. What appears to be a straightforward extension of the traditional approach to the evaluation of scale efficiency turns out to be a conceptual dilemma.

Second, to make the exposition as general as possible, we give the definition of MPSS and scale efficiency with respect to any selected subsets of volume and ratio inputs and outputs, while keeping the remaining measures constant. Conceptually, this is a generalization of the approach of Banker and Morey (1986) who consider technical and scale efficiency with respect to discretionary inputs and outputs only. However, because the R-VRS technology has a more complex structure than the standard VRS technology, the actual extension of the approach of Banker and Morey (1986) to the R-VRS technology is not straightforward.

In the additional development, we explore the notion of RTS. We differentiate between the cases in which the types of RTS are evaluated with respect to volume inputs and outputs only and the general case involving ratio measures. In the former case, we explore the local characterization of RTS with respect to the selected inputs and outputs. In the latter case, we show that the conventional local RTS characterization becomes trivial and uninformative. Instead, we employ the global RTS characterization of production frontiers developed by Podinovski (2004a, 2004b) whose types are indicative of the direction to MPSS.

The methodology developed in our paper extends the well-known approaches to the evaluation of scale efficiency and RTS to the technologies with ratio inputs and outputs. Furthermore, because our approach allows for a selection of inputs and outputs with respect to which we measure scale characteristics, it now becomes possible to explore the relationship between the volume inputs and outputs, while keeping the socio-economic and quality characteristics of the production process (represented by percentages) constant. Alternatively, it is also possible to explore the relationship between the socio-economic factors and quality characteristics of the production process, for the given levels of volume inputs and outputs. We illustrate the usefulness of such approach in an application to secondary schools in England.

We proceed as follows. In Sect. 2, we introduce basic definitions and notation. In Sect. 3, we briefly outline the R-VRS technology and give a clarifying illustrative example.

Section 4 contains the main theoretical results of our paper. We first define the partial cone extension of the R-VRS technology, which is subsequently used to define MPSS and overall and scale efficiency of DMUs with regard to arbitrary subsets of volume and ratio inputs and outputs. We also show that the cone and CRS extensions of the R-VRS technologies are generally different sets and discuss implications of this result.

In Sect. 5, we operationalize the models developed for the assessment of scale characteristics in the R-VRS technology. In Sect. 6, we show that several known technologies and methods of evaluation of scale characteristics are special cases of our newly developed approach. In Sect. 7, we consider local and global RTS characterizations in the R-VRS technology. In Sect. 8, we consider an application in the context of secondary education which illustrates the evaluation of scale characteristics in the R-VRS technology. Section 9 contains concluding remarks.

All mathematical proofs are given in Appendix A. An additional example clarifying the discussion in Sect. 4 is considered in Appendix B. The full data set used in the application is given in Appendix C. The GAMS code used for computations in the application is available online.

2 Preliminaries

Following the notation introduced by Olesen et al. (2015), let $T \subset {\mathbb {R}}^m_+ \times {\mathbb {R}}^s_+$ be a production technology with the sets $\mathrm{I} = \{ 1,...,m\}$ and $\mathrm{O} = \{ 1,...,s\}$ of nonnegative inputs and outputs, respectively. We denote ${\mathrm{I}^V} \subseteq \mathrm{I}$ and ${\mathrm{O}^V} \subseteq \mathrm{O}$ the subsets of volume inputs and outputs. The complementary subsets ${\mathrm{I}^R} = \mathrm{I}\backslash {\mathrm{I}^V}$ and ${\mathrm{O}^R} = \mathrm{O}\backslash {\mathrm{O}^V}$ include ratio inputs and outputs. We assume that both sets ${\mathrm{I}} = \mathrm{I}^V \cup {\mathrm{I}^R}$ and ${\mathrm{O}} = \mathrm{O}^V \cup {\mathrm{O}^R}$ are not empty, although any of their subsets $\mathrm{I}^V$, $\mathrm{I}^R$, $\mathrm{O}^V$ and $\mathrm{O}^R$ may be empty.

DMUs are elements of technology T and are stated in the form

$$\begin{aligned} (X,Y) = ({X^V},{X^R},{Y^V},{Y^R}), \end{aligned}$$

where $X \in {\mathbb {R}}_+^m$ and $Y \in {\mathbb {R}}_+^s$ are the vectors of inputs and outputs, and their subvectors $X^V$, $X^R$, $Y^V$ and $Y^R$ correspond to the sets of volume and ratio measures $\mathrm{I}^V$, $\mathrm{I}^R$, $\mathrm{O}^V$ and $\mathrm{O}^R$, respectively.

Let $({X_j},{Y_j})$ be observed DMUs, where $j \in J = \{ 1,...,n\}$. We assume that each observed DMU has at least one strictly positive input and at least one strictly positive output, i.e., $X_j \ne \mathbf{0}$ and $Y_j \ne \mathbf{0}$, for all $j \in J$. (We use bold symbols $\mathbf{0}$ and $\mathbf{1}$ to denote the vectors of zeros and ones whose dimensions are clear from the context.)

Denote DMU $(X_o,Y_o)$ the particular DMU whose efficiency or scale efficiency is being considered. This may be any DMU from technology T, including one of the observed DMUs.

Often, ratio inputs and outputs have certain upper bounds, typically either unity or 100%. Following Olesen et al. (2015), we state these bounds in the form

$$\begin{aligned} {X^R} \le {{\bar{X}}^R} \ \text { and } \ {Y^R} \le {{\bar{Y}}^R}, \end{aligned}$$

(1)

where each component of vectors ${{\bar{X}}^R}$ and ${{\bar{Y}}^R}$ can be either finite or $+ \infty$. (Vector inequalities mean that the specified inequality is true for each component, e.g., ${X^R} \le {{\bar{X}}^R}$ means that $X_i^R \le {\bar{X}}_i^R$, for all $i \in {\mathrm{I}^R}$.) We naturally assume that the vectors of ratio inputs and outputs $X^R_j$ and $Y^R_j$ of all observed DMUs $j \in J$ satisfy the inequalities (1).

3 The R-VRS technology

Olesen et al. (2015) note that the conventional VRS technology of Banker et al. (1984) should generally not be used if some inputs and outputs are ratio measures. The main reason for this is that ratio measures cannot be assumed to satisfy the axiom of convexity which is explicitly required by the definition of the VRS technology. Instead, Olesen et al. (2015) demonstrate that one should exclude the ratio inputs and outputs from the convexity assumption, while keeping the convexity property only for the volume measures.

For a formal definition of the R-VRS technology, Olesen et al. (2015) assume the following three axioms, the last of which is a special case of the axiom of selective convexity introduced by Podinovski (2005).

Axiom 1

(Feasibility of observed data) For any $j \in J$, $({X_j},{Y_j}) \in T$.

Axiom 2

(Free disposability) Let $(X,Y) \in T$. Consider any $({{\tilde{X}}},{{\tilde{Y}}}) = ({{\tilde{X}}}^V, {{\tilde{X}}}^R,{{\tilde{Y}}}^V, {{\tilde{Y}}}^R) \in {\mathbb {R}}_ + ^m \times {\mathbb {R}}_ + ^s$ whose subvectors ${{\tilde{X}}}^R$ and ${{\tilde{Y}}}^R$ satisfy inequalities (1). Let ${{\tilde{X}}} \ge X$ and ${{\tilde{Y}}} \le Y$. Then $({{\tilde{X}}},{{\tilde{Y}}}) \in T$.

Axiom 3

(Selective convexity) Let $({{\tilde{X}}},{{\tilde{Y}}}) \in T$ and $({\hat{X}},{\hat{Y}}) \in T$. Assume that ${{{\tilde{X}}}^R} = {{\hat{X}}^R}$ and ${{{\tilde{Y}}}^R} = {{\hat{Y}}^R}$. Then $\gamma ({{\tilde{X}}},{{\tilde{Y}}}) + (1 - \gamma )({\hat{X}},{\hat{Y}}) \in T$, for any $\gamma \in [0,1]$.

Axiom 3 reflects the fact that, although we cannot generally assume that convex combinations of DMUs in the presence of ratio data remain in technology T, we can nevertheless do so provided the combined DMUs have identical ratio inputs and outputs.²

Importantly, a combination of Axioms 2 and 3 also allows us to form convex combinations of DMUs that have different ratio inputs and outputs. This is illustrated by the following example.

Example 1

Consider DMUs A and B shown in Table 1, which are in some technology T with two inputs and two outputs. Input 1 and Output 1 are volume measures, Input 2 is a ratio measure (proportion), and Output 2 is a ratio measure (percentage). We assume that technology T satisfies Axioms 1–3.

Table 1 An illustration to the notion of R-convex combination

Suppose we wish to form a convex combination of DMUs A and B taken with the weights 1/3 and 2/3, respectively. Note that we cannot use Axiom 3 directly, because the ratio input and output of DMUs A and B are not identical. Instead, we first employ Axiom 2 and reduce the ratio output of DMU A from 90 to 70%, to match the ratio output of DMU B. Similarly, we use Axiom 2 to raise the ratio input of DMU B from 0.3 to 0.5, to make it equal to the ratio input of DMU A.

The resulting DMUs can be stated as $A^*=(6,0.5,4,70\%)$ and $B^*=(3,0.5,1,70\%)$. By Axiom 2, both DMUs $A^*$ and $B^*$ are in technology T. Because the ratio input and output of DMUs $A^*$ and $B^*$ are identical, by Axiom 3, any convex combination of these DMUs is in technology T. In particular, using the weights 1/3 and 2/3 for DMUs $A^*$ and $B^*$, respectively, we obtain DMU C shown in Table 1.

The above example shows that, although we cannot form convex combinations of DMUs with different ratio inputs and outputs, we can still form their ratio-convex (R-convex) combinations as defined by Olesen et al. (2017). Namely, in a R-convex combination of DMUs, the volume inputs and outputs form conventional convex combinations, while the ratio inputs are taken at their maximum levels across all combined DMUs, and the ratio outputs are taken at their minimum levels. In other words, the weighted average used for volume measures is replaced by the operations of maximum for the ratio inputs and minimum for the ratio outputs.

In line with the minimum extrapolation principle used by Banker et al. (1984) and Olesen et al. (2015) give the following definition:

Definition 1

The R-VRS technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ is the intersection of all technologies (sets) $T \subset {\mathbb {R}}_ + ^m \times {\mathbb {R}}_ + ^s$ that satisfy Axioms 1–3.

Following Olesen et al. (2015), technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ can equivalently be stated as follows.

Theorem 1

Technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ is the set of all DMUs $(X,Y) = ({X^V},{X^R},{Y^V},{Y^R}) \in {\mathbb {R}}_ + ^m \times {\mathbb {R}}_ + ^s$ for which there exists a vector $\lambda \in {{\mathbb {R}}^n}$ such that

$$\begin{aligned}&\sum \limits _{j \in J} {{\lambda _j}Y_j^V} \ge {Y^V}, \end{aligned}$$

(2a)

$$\begin{aligned}&\sum \limits _{j \in J} {{\lambda _j}X_j^V} \le {X^V}, \end{aligned}$$

(2b)

$$\begin{aligned}&{\lambda _j}\left( {Y_j^R - {Y^R}} \right) \ge \mathbf{{0}}, \qquad \forall j \in J, \end{aligned}$$

(2c)

$$\begin{aligned}&{\lambda _j}\left( {X_j^R - {X^R}} \right) \le \mathbf{{0}}, \qquad \forall j \in J, \end{aligned}$$

(2d)

$$\begin{aligned}&\mathbf{{1}}^{\top } \lambda = 1, \end{aligned}$$

(2e)

$$\begin{aligned}&{X^R} \le {{\bar{X}}^R}, \end{aligned}$$

(2f)

$$\begin{aligned}&{Y^R} \le {{\bar{Y}}^R}, \end{aligned}$$

(2g)

$$\begin{aligned}&\lambda \ge \mathbf{{0}}. \end{aligned}$$

(2h)

In this statement of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$, the first two vector inequalities (2a) and (2b) describe conventional convex combinations of volume inputs and outputs of the observed DMUs taken with the weights $\lambda _j \ge 0$, $j \in J$, that add up to 1 as in equality (2e).

To see the role of inequalities (2c) and (2d), restate them as follows:

$$\begin{aligned} \text {if } \lambda _j > 0 \text { then } Y^R_j \ge Y^R \text { and } X^R_j \le X^R, \ \forall j \in J. \end{aligned}$$

(3)

Conditions (3) imply that an observed DMU $(X_j,Y_j)$, $j \in J$, may be used in the convex combination of volume inputs and outputs in constraints (2a) and (2b) with a positive $\lambda _j$ only if DMU $(X_j,Y_j)$ is not worse than the DMU (X, Y) on all ratio inputs and outputs.

It is clear that technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ stated by conditions (2) consists of all R-convex combinations of observed DMUs and all DMUs outperformed (dominated) by them, subject to the upper bounds (1) on the ratio measures. This is similar to the conventional VRS technology which includes all convex combinations of observed DMUs and all DMUs outperformed by them.

It is worth noting that $T_{\mathrm{VRS}}^{\mathrm{R}}$ is generally not a convex set, but is a closed set (Olesen et al. 2015).

Example 2

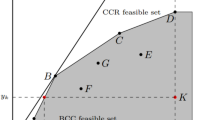
Consider DMUs A and B with one volume input, one volume output and one ratio output as shown in Table 2. Fig. 1 shows technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ generated by these two DMUs. Observe that this technology does not include convex combinations of DMUs A and B because they have different levels of the ratio output. (The line AB is not included in the technology.) Instead, the technology includes the line AD which represents all R-convex combinations of DMUs A and B. On this line, the ratio output is taken at the minimum level 0.25 of the ratio outputs of DMUs A and B, while the volume inputs and outputs of DMUs A and B form standard convex combinations.

Table 2 DMUs A and B in Example 2

Fig. 1

The R-VRS technology generated by DMUs A and B in Example 2

Also note that the technology in Fig. 1 satisfies Axioms 1–3. In particular, Axiom 3 of selective convexity is satisfied because, for each level of ratio output, the corresponding section of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ is a convex set. For example, the section corresponding to the output level 0.25 of DMU A is the convex polyhedron KCADE. The section corresponding to the output level 1.5 of DMU B is the polyhedron HFBG. However, the whole technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ is not a convex set.

Remark 1

Technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ may be seen as a generalization of several technologies. Suppose that there are no ratio inputs and outputs. In this case the inequalities (2c), (2d), (2f) and (2g) are omitted and $T_{\mathrm{VRS}}^{\mathrm{R}}$ is the conventional VRS technology of Banker et al. (1984). If there are no volume inputs and outputs then $T_{\mathrm{VRS}}^{\mathrm{R}}$ is free disposal hull (FDH) of Deprins et al. (1984), with the additional upper bounds (1) on the ratio measures. If we have only volume and ratio inputs and volume outputs, i.e., there are no ratio outputs, technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ is similar to model (7) stated by Ruggiero (1996) in which the ratio factor Z characterizes the quality of the environment.

A subtle difference between our approach and the approach of Ruggiero (1996) is that we consider any ratio input and output (including those of environmental nature) as yet another dimension of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$. In contrast, Ruggiero (1996) does not formally include the environmental factor Z as an input of the technology but instead defines the conventional VRS technology $T_{\mathrm{VRS}}(Z)$, for every value of Z treated as a parameter. It is clear that the parametric family of technologies $T_{\mathrm{VRS}}(Z)$ of Ruggiero is the collection of the sections of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ defined in the volume input and output dimensions for each fixed value of parameter Z.

The treatment of environmental factors (and any other ratio measures) as inputs and outputs of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ allows us, if required, to account for such factors in the evaluation of efficiency and various scale characteristics. For example, we may explore the question of optimal scale of production and returns to scale with regard to several inputs and outputs, including environmental factors. These possibilities are considered in the general setting in the subsequent sections.

4 Scale efficiency in the R-VRS technology

In this section we follow the approach of Banker (1984) and show how the simultaneous development of the notions of MPSS and scale efficiency in the standard VRS technology could be extended to technology $T_{\mathrm{VRS}}^{\mathrm{R}}$.

4.1 The general setting

To keep the exposition as general as possible, we consider scale properties of the production frontier with respect to some selected nonempty subsets of inputs $\mathrm{I}'$ and outputs $\mathrm{O}'$:

$$\begin{aligned} {\mathrm{I}'} \subseteq \mathrm{I} = {\mathrm{I}^V} \cup {\mathrm{I}^R}, \quad {\mathrm{O}'} \subseteq \mathrm{O} = {\mathrm{O}^V} \cup {\mathrm{O}^R}. \end{aligned}$$

In different applications, the sets $\mathrm{I}'$ and $\mathrm{O}'$ may represent discretionary inputs and outputs in the sense explored by Banker and Morey (1986) and Golany and Roll (1993). These sets may also include measures that are not discretionary, such as certain exogenous factors.³

For example, consider a scenario in which the policy maker uses a DEA model with several volume and ratio inputs and outputs for the assessment of school efficiency. Suppose that this model uses the percentage of families from the higher socio-economic background as an exogenously fixed non-discretionary ratio input $x'$ and the percentage of school graduates going to university $y'$ as a discretionary ratio output representing quality of education. Suppose that the policy maker is interested in the relationship between these two factors on the production frontier (i.e., among the efficient schools only) while keeping all the other inputs and outputs constant. This leads to the question of optimal scale and returns to scale defined in the selective (partial) sense, for which $\mathrm{I}'=\{ x' \}$ and $\mathrm{O}'=\{ y' \}$, even though the input $x'$ is not discretionary.

For a DMU $({X_o},{Y_o}) \in T_{\mathrm{VRS}}^{\mathrm{R}}$, define vectors ${X_o}(\varphi )$ and ${Y_o}(\psi )$, where $\varphi , \psi \ge 0$ are scaling factors, as follows:

$$\begin{aligned} {X_{oi}}(\varphi ) = {\left\{ \begin{array}{ll} \varphi {X_{oi}}, &{}\text {if } \ i \in {\mathrm{I}'},\\ {X_{oi}}, &{}\text {if } \ i \in \mathrm{I}\backslash {\mathrm{I}'}, \end{array}\right. } \quad {Y_{or}}(\psi ) = {\left\{ \begin{array}{ll} \psi {Y_{or}}, &{}\text {if } \ r \in {\mathrm{O}'},\\ {Y_{or}}, &{}\text {if } \ r \in \mathrm{O}\backslash {\mathrm{O}'}. \end{array}\right. } \end{aligned}$$

(4)

The output radial efficiency (technical efficiency) of DMU $({X_o},{Y_o})$ measured with respect to the selected subset of outputs ${\mathrm{O}'}$ is defined as the inverse of the optimal value of the following program (in its statement, for consistency of notation maintained throughout this paper, we change variable $\psi$ to $\eta$):

$$\begin{aligned} \begin{aligned}&{\tilde{\eta }} = \max \ \eta \\&\text {subject to } \left( {{X_o},{Y_o}(\eta )} \right) \in T_{\mathrm{VRS}}^{\mathrm{R}}, \ \eta \ge 0. \end{aligned} \end{aligned}$$

(5)

Assessing the efficiency of DMU $(X_o,Y_o)$ by program (5) is straightforward. This requires replacing the DMU (X, Y) in conditions (2) by DMU $\left( {{X_o},{Y_o}(\eta )} \right)$, and maximizing $\eta$ subject to the resulting conditions (Olesen et al. 2015, 2017).

4.2 The partial cone extension of the R-VRS technology

In this section we consider the partial cone extension of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ defined with respect to the selected input and output sets ${\mathrm{I}'}$ and ${\mathrm{O}'}$. This cone extension is useful in exploring the notions of MPSS and scale efficiency in $T_{\mathrm{VRS}}^{\mathrm{R}}$ undertaken in subsequent sections.

Define the partial cone extension ${C}(\mathrm{I}',\mathrm{O}')$ of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ as follows:

$$\begin{aligned} {C}(\mathrm{I}',\mathrm{O}') = \left\{ (X,Y) \in {\mathbb {R}}^{m+s} \mid \exists ({{\tilde{X}}}, {{\tilde{Y}}}) \in T_{\mathrm{VRS}}^{\mathrm{R}}, \alpha \ge 0: (X,Y)= ({{\tilde{X}}} (\alpha ), {{\tilde{Y}}} (\alpha )) \right\} , \end{aligned}$$

(6)

where the DMU $({{\tilde{X}}} (\alpha ), {{\tilde{Y}}} (\alpha ))$ is as defined by (4) with $\varphi =\psi =\alpha$. The cone ${C}(\mathrm{I}',\mathrm{O}')$ includes all partially scaled DMUs $( X(\alpha ), Y(\alpha ))$ obtained from all DMUs $(X,Y) \in T_{\mathrm{VRS}}^{\mathrm{R}}$, for all $\alpha \ge 0$. If $\mathrm{I}'= \mathrm{I}$ and $\mathrm{O}'= \mathrm{O}$, the cone ${C}(\mathrm{I}',\mathrm{O}') = {C}(\mathrm{I},\mathrm{O})$ is the full cone extension of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$.

It is straightforward to show that the cone ${C}(\mathrm{I}',\mathrm{O}')$ is generally not a closed set.⁴ Define its closure as

$$\begin{aligned} {{\bar{C}}}(\mathrm{I}',\mathrm{O}') = \mathrm{cl} \ {C}(\mathrm{I}',\mathrm{O}'). \end{aligned}$$

(7)

The next result provides an explicit statement of the closed cone ${{\bar{C}}}(\mathrm{I}',\mathrm{O}')$. It is proved under the following mild assumption about all observed DMUs.

Assumption 1

For each $j \in J$, there exists an $i \in {\mathrm{I}'}$ (generally different for different j) such that $X_{j i} > 0$.

Theorem 2

Let Assumption 1 be true. Then the closed partial cone extension ${{\bar{C}}}(\mathrm{I}',\mathrm{O}')$ of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ is the set of all DMUs $(X,Y) = ({X^V},{X^R},{Y^V},{Y^R}) \in {\mathbb {R}}_ + ^m \times {\mathbb {R}}_ + ^s$ for which there exist a vector $\lambda \in {{\mathbb {R}}^n}$ and a scalar $\sigma$ such that

$$\begin{aligned}&\sum \limits _{j \in J} {{\lambda _j} \sigma Y_{jr}^V} \ge Y_{r}^V, \qquad \forall r \in {\mathrm{O}^V} \cap {\mathrm{O}'}, \end{aligned}$$

(8a)

$$\begin{aligned}&\sum \limits _{j \in J} {{\lambda _j}Y_{jr}^V} \ge Y_{r}^V, \qquad \forall r \in {\mathrm{O}^V}\backslash {\mathrm{O}'}, \end{aligned}$$

(8b)

$$\begin{aligned}&\sum \limits _{j \in J} {{\lambda _j} \sigma X_{ji}^V} \le X_{i}^V, \qquad \forall i \in {\mathrm{I}^V} \cap {\mathrm{I}'}, \end{aligned}$$

(8c)

$$\begin{aligned}&\sum \limits _{j \in J} {{\lambda _j}X_{ji}^V} \le X_{i}^V, \qquad \forall i \in {\mathrm{I}^V}\backslash {\mathrm{I}'}, \end{aligned}$$

(8d)

$$\begin{aligned}&{\lambda _j}(\sigma Y_{jr}^R - Y_{r}^R) \ge 0, \qquad \forall j \in J,\quad \forall r \in {\mathrm{O}^R} \cap {\mathrm{O}'}, \end{aligned}$$

(8e)

$$\begin{aligned}&{\lambda _j}(Y_{jr}^R - Y_{r}^R) \ge 0, \qquad \forall j \in J,\qquad \forall r \in {\mathrm{O}^R} \backslash {\mathrm{O}'}, \end{aligned}$$

(8f)

$$\begin{aligned}&{\lambda _j}(\sigma X_{ji}^R - X_{i}^R) \le 0, \qquad \forall j \in J,\qquad \forall i \in {\mathrm{I}^R} \cap {\mathrm{I}'}, \end{aligned}$$

(8g)

$$\begin{aligned}&{\lambda _j}(X_{ji}^R - X_{i}^R) \le 0, \qquad \forall j \in J,\qquad \forall i \in {\mathrm{I}^R}\backslash {\mathrm{I}'}, \end{aligned}$$

(8h)

$$\begin{aligned}&\mathbf{{1}}^{\top } \lambda = 1, \end{aligned}$$

(8i)

$$\begin{aligned}&{Y^R_{r}} \le \sigma {{\bar{Y}}^R_r}, \qquad \forall r \in {\mathrm{O}^R} \cap {\mathrm{O}'}, \end{aligned}$$

(8j)

$$\begin{aligned}&{Y^R_{r}} \le {{\bar{Y}}^R_r}, \qquad \forall r \in {\mathrm{O}^R} \backslash {\mathrm{O}'}, \end{aligned}$$

(8k)

$$\begin{aligned}&{X^R_{i}} \le \sigma {{\bar{X}}^R_i}, \qquad \forall i \in {\mathrm{I}^R} \cap {\mathrm{I}'}, \end{aligned}$$

(8l)

$$\begin{aligned}&{X^R_{i}} \le {{\bar{X}}^R_i}, \qquad \forall i \in {\mathrm{I}^R} \backslash {\mathrm{I}'}, \end{aligned}$$

(8m)

$$\begin{aligned}&\lambda \ge \mathbf{{0}}, \sigma \ge 0. \end{aligned}$$

(8n)

It is clear that conditions (8) are closely related to conditions (2). The difference is that, in (8), the scaling factor $\sigma$ is attached to all volume and ratio inputs $i\in \mathrm{I}'$ and outputs $r\in \mathrm{O}'$ with respect to which we define the cone extension, and the remaining inputs and outputs in the sets $\mathrm{I} \setminus \mathrm{I}'$ and $\mathrm{O} \setminus \mathrm{O}'$ are kept fixed. As a result, the closed partial cone extension $\bar{C}(\mathrm{I}',\mathrm{O}')$ of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ includes all partially scaled R-convex combinations of the observed DMUs, where only the inputs and outputs in the sets $\mathrm{I}'$ and $\mathrm{O}'$ are scaled by $\sigma \ge 0$, and the remaining inputs $i\in \mathrm{I} \setminus \mathrm{I}'$ and $r\in \mathrm{O} \setminus \mathrm{O}'$ are not scaled.

4.3 The most productive scale size in the R-VRS technology

Recall that Banker (1984) introduces the notion of MPSS evaluated with respect to the entire vectors of inputs and outputs in the VRS technology $T_{\mathrm{VRS}}$ (which, according to Remark 1, can be viewed as a special case of the R-VRS technology $T_{\mathrm{VRS}}^{\mathrm{R}}$). Namely, let DMU $(X_o,Y_o) \in T_{\mathrm{VRS}}$, and let $\varphi >0$ and $\psi >0$ be the scaling factors for the input and output vectors, respectively. Consider the parametric set of all DMUs $(\varphi X_o,\psi Y_o) \in T_{\mathrm{VRS}}$. All such DMUs have the same structure of the input and output vectors as the original DMU $(X_o,Y_o)$. Then DMU $(X_o,Y_o)$ is at MPSS if, for any $\varphi$ and $\psi$ such that $(\varphi X_o,\psi Y_o) \in T_{\mathrm{VRS}}$, we have $\psi / \varphi \le 1$. In other words, DMU $(X_o,Y_o)$ is at MPSS if it maximizes the average productivity $\psi / \varphi$ among all DMUs $(\varphi X_o,\psi Y_o) \in T_{\mathrm{VRS}}$.

Below we follow the same approach and introduce the notion of MPSS in technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ evaluated with respect to the subsets ${\mathrm{I}'}$ and ${\mathrm{O}'}$. Consider the program

$$\begin{aligned} \begin{aligned}&\theta ^* = \sup \ (\psi / \varphi )\\&\text {subject to } \left( {{X_o}(\varphi ),{Y_o}(\psi )} \right) \in T_{\mathrm{VRS}}^{\mathrm{R}}, \ \varphi > 0, \ \psi \ge 0, \end{aligned} \end{aligned}$$

(9)

where the vectors ${X_o}(\varphi )$ and ${Y_o}(\psi )$ are defined as in (4).

If the sets ${\mathrm{I}'}$ and ${\mathrm{O}'}$ include all inputs and outputs (i.e., if ${\mathrm{I}'}=\mathrm{I}$ and ${\mathrm{O}'}=\mathrm{O}$), the condition $\left( {{X_o}(\varphi ),{Y_o}(\psi )} \right) \in T_{\mathrm{VRS}}^{\mathrm{R}}$ of program (9) is restated as $\left( \varphi {X_o}, \psi {Y_o} \right) \in T_{\mathrm{VRS}}^{\mathrm{R}}$. In this case, similar to the standard definition of Banker (1984), program (9) maximizes the average productivity $\psi / \varphi$ among all DMUs stated in the form $(\varphi X_o,\psi Y_o) \in T_{\mathrm{VRS}}^{\mathrm{R}}$, i.e., preserving the input and output structures of the DMU $(X_o,Y_o)$ under the consideration.

In the general case, program (9) maximizes the ratio $\psi / \varphi$ which is interpretable as the ratio of the quantity $\psi$ of the subvector of selected outputs $Y_{or}$, $r \in {\mathrm{O}'}$, to the quantity $\varphi$ of the subvector of selected inputs $X_{oi}$, $i \in {\mathrm{I}'}$, while keeping the remaining inputs and outputs constant.

Because $\varphi =\psi =1$ is a feasible solution of program (9), we always have $\theta ^* \ge 1$.

Definition 2

DMU $(X_o,Y_o) \in T_{\mathrm{VRS}}^{\mathrm{R}}$ is at MPSS evaluated with respect to the subsets ${\mathrm{I}'}$ and ${\mathrm{O}'}$ if $\theta ^* = 1$.

Let us show that solving program (9) can be replaced by assessment of the partial output radial efficiency of DMU $(X_o,Y_o)$ (with respect to the outputs in the set ${\mathrm{O}'}$ only) in the closed partial cone extension ${{\bar{C}}}(\mathrm{I}',\mathrm{O}')$ of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ whose statement is obtained by Theorem 2. This result is formally stated and proved as Theorem 3 below. Let us first provide its intuitive explanation.

Consider program (9). Note that we can substitute technology $T^\mathrm{R}_{\mathrm{VRS}}$ in its constraints by its cone extension ${C}(\mathrm{I}',\mathrm{O}')$. Indeed, for any feasible solution $\langle \varphi , \psi \rangle$ of program (9), changing $T^\mathrm{R}_{\mathrm{VRS}}$ to ${C}(\mathrm{I}',\mathrm{O}')$ adds the full ray $\langle \alpha \varphi , \alpha \psi \rangle$, $\alpha > 0$, to its feasible region. However, because $\alpha \psi / \alpha \varphi = \psi / \varphi$, this change does not affect the supremum of the objective function.

Furthermore, because the value of the objective function $\psi / \varphi$ of the resulting program (9) with $T^\mathrm{R}_{\mathrm{VRS}}$ replaced by ${C}(\mathrm{I}',\mathrm{O}')$ is constant along any ray of feasible solutions $\langle \alpha \varphi , \alpha \psi \rangle$, $\alpha > 0$, we can restrict the feasible set to only one point on each ray, by requiring that $\varphi = 1$. After this normalization of variable $\varphi$ and renaming variable $\psi$ to $\eta$, we obtain the following program:

$$\begin{aligned} \begin{aligned}&\eta ' = \sup \ \eta \\&\text {subject to } \left( {{X_o},{Y_o}(\eta )} \right) \in C(\mathrm{I}',\mathrm{O}'), \ \eta \ge 0. \end{aligned} \end{aligned}$$

(10)

Taking into account that the cone ${C}(\mathrm{I}',\mathrm{O}')$ is generally not a closed set, we replace it in the constraints of program (10) by the closed cone ${{\bar{C}}}(\mathrm{I}',\mathrm{O}')$. This results in a linear program in which we conventionally change the supremum of the objective function to its maximum:

$$\begin{aligned} \begin{aligned}&\eta ^* = \max \ \eta \\&\text {subject to } \left( {{X_o},{Y_o}(\eta )} \right) \in {\bar{C}}(\mathrm{I}',\mathrm{O}'), \ \eta \ge 0. \end{aligned} \end{aligned}$$

(11)

The next result requires an additional assumption about DMU $(X_o,Y_o)$ which should be true in any meaningful application:

Assumption 2

There exists an $r \in {\mathrm{O}'}$ such that $Y_{or} > 0$.

Theorem 3

Let both Assumptions 1 and 2 be true. Then the supremum $\theta ^*$ of program (9) is equal to the maximum $\eta ^*$ of program (11), and both are attained.

Corollary 1

The DMU $\left( {{X_o},{Y_o}(\eta ^*)} \right) \in {{\bar{C}}}(\mathrm{I}',\mathrm{O}')$ at which the maximum in program (11) is attained is also in the cone ${C}(\mathrm{I}',\mathrm{O}')$.

It is clear that program (11) which uses the statement (8) of the cone ${{\bar{C}}}(\mathrm{I}',\mathrm{O}')$ is nonlinear and would be problematic in practical computations. Therefore, Theorem 3 should primarily be of theoretical interest. It shows that the evaluation of MPSS for DMU $(X_o,Y_o)$ in technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ (with respect to the subsets $\mathrm{I}'$ and $\mathrm{O}'$) is equivalent to the evaluation of its partial output radial efficiency (with respect to the subset $\mathrm{O}'$) in the closed partial cone extension ${{\bar{C}}}(\mathrm{I}',\mathrm{O}')$ of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$. In particular, DMU $(X_o,Y_o)$ is at MPSS with respect to $\mathrm{I}'$ and $\mathrm{O}'$ in $T_{\mathrm{VRS}}^{\mathrm{R}}$ if and only if its partial output radial efficiency in ${{\bar{C}}}(\mathrm{I}',\mathrm{O}')$ evaluated with respect to the subset $\mathrm{O}'$ is equal to 1.

Consider the special case in which technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ is the standard VRS technology $T_\mathrm{VRS}$ of Banker et al. (1984) and the sets $\mathrm{I}'$ and $\mathrm{O}'$ include all inputs and outputs. Then the closed cone ${{\bar{C}}}(\mathrm{I}',\mathrm{O}')$ is the standard CRS technology $T_\mathrm{CRS}$ of Charnes et al. (1978). In this case, Theorem 3 becomes a well-known result that DMU$_o \in T_\mathrm{VRS}$ is at MPSS if and only if its output radial efficiency $\eta ^*$ in the benchmark CRS technology $T_\mathrm{CRS}$ is equal to 1.

In Sect. 5, we consider computational approaches to solving program (9). We transform this program to an equivalent form that, depending on the sets $\mathrm{I}$, $\mathrm{O}$, $\mathrm{I}'$ and $\mathrm{O}'$, either becomes a linear program or can be solved as a mixed integer linear program.

4.4 Overall and scale efficiency in the R-VRS technology

Following the approach of Banker (1984), we interpret the inverse optimal value $1 / \theta ^*$ of program (9) [or, equivalently, the inverse value $1 / \eta ^*$ of program (11)] as the overall efficiency $OE(X_o,Y_o)$ of DMU $(X_o,Y_o)$ assessed with respect to the subsets ${\mathrm{I}'}$ and ${\mathrm{O}'}$.

By Definition 2, DMU $(X_o,Y_o)$ is at MPSS if and only if $OE(X_o,Y_o)=1$. Otherwise we can decompose the overall efficiency into the product of its technical and scale efficiency components $TE(X_o,Y_o)$ and $SE(X_o,Y_o)$:

$$\begin{aligned} OE(X_o,Y_o) = TE(X_o,Y_o) \times SE(X_o,Y_o), \end{aligned}$$

where $TE(X_o,Y_o)=1/{\tilde{\eta }}$ is evaluated by solving program (5). Then $SE(X_o,Y_o) = {\tilde{\eta }} / \eta ^*$ is the scale efficiency of DMU $({X_o},{Y_o})$ evaluated with respect to the subsets ${\mathrm{I}'}$ and ${\mathrm{O}'}$. Because $T_{\mathrm{VRS}}^{\mathrm{R}} \subset {{\bar{C}}}(\mathrm{I}',\mathrm{O}')$, we have ${\tilde{\eta }} \le \eta ^*$ and $SE(X_o,Y_o) \le 1$.

Following Banker (1984), the scale efficiency $SE(X_o,Y_o)$ is interpretable as a measure of divergence from MPSS with respect to the sets ${\mathrm{I}'}$ and ${\mathrm{O}'}$. Indeed, let for simplicity DMU $(X_o,Y_o)$ be technically efficient but scale inefficient. Then DMU $(X_o,Y_o)$ is not at MPSS (for the selected sets ${\mathrm{I}'}$ and ${\mathrm{O}'}$) and, in program (9), we have $\theta ^* > 1$. By Theorem 3, the supremum $\theta ^*$ is attained at some feasible solution $\langle \varphi ^*, \psi ^* \rangle$ of program (9), and we have $\theta ^* = \psi ^* / \varphi ^* > 1$.

The DMU $(X_o(\varphi ^* ), Y_o(\psi ^* ))$ defined by (4) represents MPSS for DMU $(X_o,Y_o)$. If DMU $(X_o,Y_o)$ scales its inputs in the set ${\mathrm{I}'}$ by the factor $\varphi ^*$ and outputs in the set ${\mathrm{O}'}$ by the factor $\psi ^*$, while keeping the remaining inputs and outputs fixed, its average productivity (measured only with respect to the selected inputs and outputs) will increase by $\psi ^* / \varphi ^* > 1$. Therefore, the ratio $\psi ^* / \varphi ^* =1 / SE(X_o,Y_o)$ shows by how much the average productivity of this DMU, measured with respect to the selected inputs and outputs in the sets ${\mathrm{I}'}$ and ${\mathrm{O}'}$, could increase if it were to change these inputs and outputs by the factors $\varphi ^*$ and $\psi ^*$, respectively, to match those of its MPSS. This is similar to the standard notion of MPSS in the VRS technology. Following Banker (1984), the optimal ratio $\psi ^* / \varphi ^*$ is interpretable as a measure of divergence of the technically efficient DMU $(X_o,Y_o)$ from its MPSS, if we restrict the scaling of the inputs and outputs to the sets ${\mathrm{I}'}$ and ${\mathrm{O}'}$ only, while keeping the remaining inputs and outputs constant.

This interpretation is illustrated by the following example.

Example 3

Let us refer to technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ in Example 2. Consider the following three scenarios in which the set ${\mathrm{I}'}$ includes the single input but the sets ${\mathrm{O}'}$ are defined differently. Note that both DMUs A and B are technically efficient in all three scenarios.

• (i) Let the set ${\mathrm{O}'}$ include both the volume and ratio outputs. Consider assessing the scale efficiency of DMU A by program (9). Its unique optimal solution is $\varphi ^*=2$ and $\psi ^*=3$, which corresponds to DMU P (see Table 3 and Fig. 2).⁵ DMU P uses twice the amount of volume input of DMU A but produces three times its vector of outputs. The optimal value of the objective function of program (9) is equal to 3/2, and the scale efficiency of DMU A is 2/3. Note that, in the given scenario, DMU P represents MPSS for DMU A. Similarly, in the case of DMU B, the unique optimal solution to program (9) is $\varphi ^*=\psi ^*=1$. Therefore, DMU B is at MPSS.⁶

• (ii) Let the set ${\mathrm{O}'}$ include only the volume output but not the ratio output. In this case, program (9) assesses the scale efficiency of DMU A by keeping its ratio output constant, i.e., by restricting the evaluation to the section of technology KCADE. In this case the optimal solution is $\varphi ^*=2$ and $\psi ^*=3$. This means that the scale efficiency of DMU A is equal to 2/3 and its MPSS is DMU D. Similarly, the scale efficiency of DMU B is assessed on the section HFBG, and DMU B is at MPSS.

• (iii) Let the set ${\mathrm{O}'}$ include only the ratio output but not the volume output. To evaluate the scale efficiency of DMU A, we search among all DMUs on the broken line ALVW. The highest ratio of the ratio output to the volume input is achieved at DMU V, which corresponds to $\varphi ^* = 2$ and $\psi ^*=6$ in program (9). Therefore, in this scenario, the scale efficiency of DMU A is $\varphi ^*/\psi ^*=1/3$, and DMU V represents MPSS for DMU A. A similar investigation shows that DMU B is at MPSS.

Table 3 DMUs representing MPSS in Example 3

Fig. 2

MPSS in the R-VRS technology evaluated with respect to different sets of outputs $O'$

4.5 The cone extension and the CRS extension of the R-VRS technology

The cone and CRS extensions of the standard VRS technology are the same sets, and both can be used as the reference technologies in the evaluation of MPSS and scale efficiency of the DMUs. The purpose of this section is to demonstrate that the same identity does not hold for the R-VRS technology. Namely, its CRS extension is generally different from its cone extension, and it is the latter that we employ in the evaluation of MPSS and other scale characteristics.

In order to demonstrate this difference and avoid excessive technicalities, for the discussion in this section, we assume that $\mathrm{I' = I}$ and $\mathrm{O' = O}$. We also assume that the bounds (1) are not specified.

As noted in Remark 1, if all inputs and outputs are volume measures, technology $T^{\mathrm{R}}_{\mathrm{VRS}}$ is the standard VRS technology $T_{\mathrm{VRS}}$ of Banker et al. (1984). In this case, program (9) represents the standard approach of Banker (1984) for the assessment of MPSS in the VRS technology. Further, the closed cone extension of technology $T_{\mathrm{VRS}}$ coincides with its CRS extension $T_{\mathrm{CRS}}$, which is the CRS technology of Charnes et al. (1978). This implies that the evaluation of MPSS for DMU $(X_o, Y_o)$ by solving program (9) (in the case in which all inputs and outputs are volume measures) is equivalent to the assessment of output radial efficiency of this DMU in the CRS technology $T_{\mathrm{CRS}}$.

Below we show that the same equivalence does not hold in the case of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$. To demonstrate this, we use the CRS extension of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ introduced by Olesen et al. (2015) in which the ratio inputs and outputs are of the proportional type with no bounds. Such inputs and outputs are assumed to be scalable in the same proportion as the volume measures. Following Olesen et al. (2015), we denote such technology $T_{\mathrm{VRS}}^{\mathrm{P}}$. This technology is defined (in the sense of the minimum extrapolation principle) by Axioms 1–3 and the following additional axiom:

Axiom 4

(Proportionality) Let $(X^V,X^R,Y^V,Y^R) \in T$. Then, for all scaling factors $\alpha \ge 0$, $( \alpha X^V, \alpha X^R, \alpha Y^V, \alpha Y^R ) \in T$.

By Theorem 2 in Olesen et al. (2015), technology $T_{\mathrm{CRS}}^{\mathrm{P}}$ is the set of all DMUs $(X,Y) = (X^V,X^R,Y^V,Y^R) \in {\mathbb {R}}_ + ^m \times {\mathbb {R}}_ + ^s$ for which there exist vectors $\lambda , \sigma \in {{\mathbb {R}}^n}$ such that

$$\begin{aligned} \begin{aligned}&\sum \limits _{j \in J} {{{\lambda }_j}{\sigma _j} Y_j^V} \ge Y^V, \\&\sum \limits _{j \in J} {{{\lambda }_j}{\sigma _j} X_j^V} \le X^V,\\&\lambda _j ( {\sigma _j} Y_{j}^R - Y^R) \ge \mathbf{{0}}, \qquad \forall j \in J, \\&\lambda _j( {\sigma _j} X_{j}^R - X^R) \le \mathbf{{0}}, \qquad \forall j \in J, \\&\mathbf{{1}}^{\top } {\lambda } = 1, \\&\lambda , \sigma \ge \mathbf{{0}}. \end{aligned} \end{aligned}$$

(12)

The full closed cone extension ${{\bar{C}}}(\mathrm{I},\mathrm{O})$ of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ and its R-CRS extension $T_{\mathrm{CRS}}^{\mathrm{P}}$ are in general different sets. Indeed, the former is stated by conditions (8) in which $\mathrm{I' = I}$ and $\mathrm{O' = O}$. In these conditions, all observed DMUs $(X_j,Y_j)$, $j \in J$, are scaled by the same single factor $\sigma$. In contrast, in (12), all observed DMUs are scaled independently by generally different factors $\sigma _j$, $j \in J$. Therefore, we have ${{\bar{C}}}(\mathrm{I},\mathrm{O}) \subseteq T_{\mathrm{CRS}}^{\mathrm{P}}$. Example 4 considered below and a further example in Appendix B show that, generally, this embedding is not an equality.

To facilitate the graphical illustration in the next example, we first establish the following useful result which is true if the specification of technology $T_{\mathrm{CRS}}^{\mathrm{P}}$ includes only a single ratio measure. This measure can be a ratio input or a ratio output, but not both. This result is not valid if the technology incorporates more than one ratio measure.

Theorem 4

Let technology $T_{\mathrm{CRS}}^{\mathrm{P}}$ include a single ratio measure, i.e., let the union of the sets $\mathrm{I}^R \cup \mathrm{O}^R$ be a singleton. Also, let this ratio measure be strictly positive for every observed DMU. (E.g., in the case of single ratio input $X^R$, we assume that $X^R_j >0$, for all $j=1,\dots ,n$.) Then technology $T_{\mathrm{CRS}}^{\mathrm{P}}$ is the standard CRS technology $T_{\mathrm{CRS}}$ generated by the same set of observed DMUs.

As established in Sect. 4.3, the maximum average productivity that DMU $(X_o,Y_o)$ achieves at its MPSS in technology $T_{\mathrm{VRS}}^{\mathrm{R}}$, as represented by the maximum of the objective function $\psi / \varphi$ of program (9), is equal to the average productivity of its output radial projection in the closed cone extension ${{\bar{C}}}(\mathrm{I},\mathrm{O})$. The following example illustrates the case in which the maximum average productivity for DMU $(X_o,Y_o)$ with $T_{\mathrm{VRS}}^{\mathrm{R}}$ (or ${{\bar{C}}}(\mathrm{I},\mathrm{O})$) as the benchmark technology falls below the average productivity in technology $T_{\mathrm{CRS}}^{\mathrm{P}}$.

Example 4

The example involves four DMUs A, B, C and D with one volume input $x^V$, one proportional ratio input $x^R$ and one volume output $y^V$, as shown in Table 4.

Table 4 DMUs in Example 4

Fig. 3

Technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ in Example 4

Technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ generated by DMUs A, B and C is shown in Fig. 3. It is not convex and consists of the two shaded parts. Note that the ratio input $x^R$ of the DMUs B and C is equal. By Axiom 3 of selective convexity, the line segment BC is included in technology $T_{\mathrm{VRS}}^{\mathrm{R}}$. Because the ratio input $x^R$ of the DMUs A and B is different, the line segment AB is not included in this technology.

Let us evaluate the scale efficiency of DMU D. This requires that we consider all DMUs in $T_{\mathrm{VRS}}^{\mathrm{R}}$ stated as $(2 \alpha , 2 \alpha , y^V)$ and identify the largest ratio $y^V /\alpha$ among all such DMUs.

Consider the two-dimensional piecewise linear section of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ with the input mix described parametrically as $(2 \alpha , 2 \alpha )$. In other words, we measure input by $\alpha \ge 0$. The mix $(\alpha , y^V)=(1,1.75)$ is feasible and corresponds to DMU D. This is illustrated in Fig. 4 in which the red piecewise linear line corresponds to the line $\bar{D}DLM$ in Fig. 3. The closed cone ${{\bar{C}}}(\mathrm{I},\mathrm{O})= \bar{C}\left( \left\{ 1,2\right\} ,\left\{ 1\right\} \right)$ generated by technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ according to (6) is represented by the ray OK.

Fig. 4

The $(\alpha ,y^V)$-diagram of the two-dimensional sections of technologies $T_{\mathrm{VRS}}^{\mathrm{R}}$, $T_{\mathrm{CRS}}^{\mathrm{P}}$ and the closed cone ${{\bar{C}}}(\mathrm{I},\mathrm{O})$

It is clear that DMU D is scale efficient. It achieves the maximum average productivity equal to $y/\alpha =1.75/1$ among all DMUs stated in the form $(2 \alpha , 2 \alpha , y^V)$ and plotted on the red line in Fig. 4. Expressed differently, DMU D is also located on the ray OK. This ray represents the upper boundary of the closed cone extension ${{\bar{C}}}(\mathrm{I},\mathrm{O})$ of $T_\mathrm{VRS}^\mathrm{R}$.

The R-CRS technology $T_{\mathrm{CRS}}^{\mathrm{P}}$ is shown as the shaded area in Fig. 5. In this example, by Theorem 4, it coincides with the standard CRS technology $T_{\mathrm{CRS}}$ generated by the observed DMUs A, B and C. The cone spanned by DMUs A and B of dimension 2 is a facet in $T_{\mathrm{CRS}}^{\mathrm{P}}$.⁷ DMU D is located below this facet and is an interior point of technology $T_{\mathrm{CRS}}^{\mathrm{P}}$.

Fig. 5

Technology $T_{\mathrm{CRS}}^{\mathrm{P}}$ in Example 4

Consider the two-dimensional piecewise linear section of $T_\mathrm{CRS}^\mathrm{P}$ with the input mix fixed to (2, 2) of DMU D. The possible increase in the observed average product for D (equal to 1.75) to be obtained with $T_\mathrm{CRS}^\mathrm{P}$ as benchmark can now be estimated by the maximal expansion of the current output (equal to 1.75) with inputs fixed at the level (2, 2).

Straightforward calculations show that the output projection of DMU D on the boundary of technology $T_{\mathrm{CRS}}^{\mathrm{P}}$ is DMU $D'$ with the input mix equal to (2, 2) and $y^V=2$. Using the result of Theorem 4, we identify DMU $D'$ as the radial projection of DMU D in the standard output-oriented CRS model with DMUs A, B and C as the three observed DMUs.

The maximal output expansion is shown by the movement of D to $D'$ in Fig. 5. DMU $D'$ is located on the facet spanned by A and B. Point D is MPSS and $SE(D)=1$ with $T_\mathrm{VRS}^\mathrm{R}$ as the benchmark technology, while D is not at MPSS with $T_\mathrm{CRS}^\mathrm{P}$ as the benchmark technology. The output radial improvement factor for DMU D is now $\theta ={2}/{1.75}\approx 1.143$ with $T_\mathrm{CRS}^\mathrm{P}$ as benchmark, because the maximal average product for DMU D increases from 1.75 with $T_\mathrm{VRS}^\mathrm{R}$ as benchmark to 2 with $T_\mathrm{CRS}^\mathrm{P}$ as benchmark.

5 Computation of scale efficiency

As highlighted in Sect. 4, the evaluation of MPSS and overall and scale efficiency by nonlinear programs (9) or (11) is generally problematic. In this section we obtain an equivalent statement of these programs whose use in practical computations is straightforward.

Below, when referring to program (9), we assume that its constraint $\left( {{X_o}(\varphi ),{Y_o}(\psi )} \right) \in T_{\mathrm{VRS}}^{\mathrm{R}}$ is replaced by conditions (2) in which the DMU (X, Y) is changed to $\left( {{X_o}(\varphi ),{Y_o}(\psi )} \right)$. This program is stated in terms of the variable vector $\lambda$ and scalars $\varphi$ and $\psi$. Similarly, we restate program (11) using the statement of the closed partial cone ${{\bar{C}}}(\mathrm{I}',\mathrm{O}')$ by Theorem 2. (The full statement of the resulting program (11) is shown as program (28) in the proof of Theorem 5.) We now use the substitution $\lambda '=\lambda \sigma$. Suppressing the prime symbol, we state the resulting program as

$$\begin{aligned}&{\hat{\eta }} = \max \ \eta \end{aligned}$$

(13a)

$$\begin{aligned}&{\text {subject to}} \nonumber \\&\sum \limits _{j \in J} {{\lambda _j}Y_{jr}^V} \ge \eta Y_{or}^V, \qquad \forall r \in {\mathrm{O}^V} \cap {\mathrm{O}'}, \end{aligned}$$

(13b)

$$\begin{aligned}&\sum \limits _{j \in J} {{\lambda _j}Y_{jr}^V} \ge \sigma Y_{or}^V, \qquad \forall r \in {\mathrm{O}^V}\backslash {\mathrm{O}'}, \end{aligned}$$

(13c)

$$\begin{aligned}&\sum \limits _{j \in J} {{\lambda _j}X_{ji}^V} \le X_{oi}^V, \qquad \forall i \in {\mathrm{I}^V} \cap {\mathrm{I}'}, \end{aligned}$$

(13d)

$$\begin{aligned}&\sum \limits _{j \in J} {{\lambda _j}X_{ji}^V} \le \sigma X_{oi}^V, \qquad \forall i \in {\mathrm{I}^V}\backslash {\mathrm{I}'}, \end{aligned}$$

(13e)

$$\begin{aligned}&{\lambda _j}(\sigma Y_{jr}^R - \eta Y_{or}^R) \ge 0, \qquad \forall j \in J,\quad \forall r \in {\mathrm{O}^R} \cap {\mathrm{O}'}, \end{aligned}$$

(13f)

$$\begin{aligned}&{\lambda _j}(Y_{jr}^R - Y_{or}^R) \ge 0, \qquad \forall j \in J,\quad \forall r \in {\mathrm{O}^R} \backslash {\mathrm{O}'}, \end{aligned}$$

(13g)

$$\begin{aligned}&{\lambda _j}(\sigma X_{ji}^R - X_{oi}^R) \le 0, \qquad \forall j \in J,\quad \forall i \in {\mathrm{I}^R} \cap {\mathrm{I}'}, \end{aligned}$$

(13h)

$$\begin{aligned}&{\lambda _j}(X_{ji}^R - X_{oi}^R) \le 0, \qquad \forall j \in J,\quad \forall i \in {\mathrm{I}^R}\backslash {\mathrm{I}'}, \end{aligned}$$

(13i)

$$\begin{aligned}&\mathbf{{1}}^{\top } \lambda = \sigma , \end{aligned}$$

(13j)

$$\begin{aligned}&\eta {Y^R_{or}} \le \sigma {{\bar{Y}}^R_r} \qquad \forall r \in {\mathrm{O}^R} \cap {\mathrm{O}'}, \end{aligned}$$

(13k)

$$\begin{aligned}&{Y^R_{or}} \le {{\bar{Y}}^R_r}, \qquad \forall r \in {\mathrm{O}^R} \backslash {\mathrm{O}'}, \end{aligned}$$

(13l)

$$\begin{aligned}&{X^R_{oi}} \le \sigma {{\bar{X}}^R_i}, \qquad \forall i \in {\mathrm{I}^R} \cap {\mathrm{I}'}, \end{aligned}$$

(13m)

$$\begin{aligned}&{X^R_{oi}} \le {{\bar{X}}^R_i},\qquad \forall i \in {\mathrm{I}^R} \backslash {\mathrm{I}'}, \end{aligned}$$

(13n)

$$\begin{aligned}&\lambda \ge \mathbf{{0}}, \ \sigma , \eta \ge 0. \end{aligned}$$

(13o)

In program (13), the bounds (13l) and (13n) do not restrict decision variables. They are included only to show the relationship of program (13) with the statement (8) of the closed cone ${{\bar{C}}}(\mathrm{I}',\mathrm{O}')$ and can be omitted as redundant in actual computations.

The next result establishes a one-to-one correspondence between the optimal solutions of programs (9) and (13). We prove it under the following stronger variant of Assumption 2:

Assumption 3

Either there exists an $r' \in {\mathrm{O}^V} \cap {\mathrm{O}'}$ such that $Y_{or'} > 0$, or there exists an $r'' \in {\mathrm{O}^R} \cap {\mathrm{O}'}$ such that both $Y_{or''} > 0$ and the upper bound ${{\bar{Y}}}^R_{r''}$ in the corresponding constraint (13k) is finite. (Such constraint needs to be specified and should not be omitted.⁸)

Clearly, a simple sufficient, but not necessary, condition that guarantees that Assumption 3 is satisfied, is that all outputs of DMU $(X_o,Y_o)$ are strictly positive and, additionally, all ratio outputs have a specified finite upper bound (1).

Theorem 5

Let Assumptions 1 and 3 be true. Then the following statements are true:

• (i) The maximum value ${\hat{\eta }}$ of program (13) is attained and equal to the supremum $\theta ^*$ of program (9).

• (ii) In any optimal solution $\langle \lambda , \sigma , \eta \rangle$ to program (13), we have $\sigma >0$.

• (iii) Solution $\langle {\hat{\lambda }}, {\hat{\eta }}, {\hat{\sigma }} \rangle$ is optimal in program (13) if and only if the solution $\langle \lambda ', \varphi ', \psi ' \rangle$, where $\lambda ' = {\hat{\lambda }}/{\hat{\sigma }}$, $\varphi '=1/ {\hat{\sigma }}$ and $\psi ' = {\hat{\eta }} /{\hat{\sigma }}$, is optimal in program (9).

To see the importance of Theorem 5, recall that the evaluation of MPSS and the overall efficiency of DMU $(X_o,Y_o)$ rely on our ability to solve program (9). Any of its optimal solutions $\langle \varphi ', \psi ' \rangle$ would correspond to the MPSS $(X_o(\varphi '), Y_o(\psi '))$ of DMU $(X_o,Y_o)$ in technology $T_{\mathrm{VRS}}^{\mathrm{R}}$, defined with respect to the selected input and output sets $\mathrm{I}'$ and $\mathrm{O}'$. The inverse of the optimal value $1 / \theta ^*$ is the overall efficiency of the DMU $(X_o,Y_o)$. Because program (9) is nonlinear, we face obvious computational challenges in its practical use.

Theorem 3 stated in Sect. 4.3 appears to suggest a conventional way to overcome this computational difficulty. Namely, instead of evaluating the maximum average productivity $\psi / \varphi$ by solving the nonlinear program (9), we may equivalently solve program (11) which evaluates the partial (with respect to the set $\mathrm{O}'$) output radial efficiency of DMU $(X_o,Y_o)$ in the closed partial cone extension ${{\bar{C}}}(\mathrm{I}',\mathrm{O}')$ of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$.

Unfortunately, the described conventional approach based on solving program (11) instead of (9) does not resolve all computational problems. First, if we state program (11) in the full extended form (shown in the proof of Theorem 5), we obtain a nonlinear program. Second, even if we solve this program and identify its optimal solution $\langle \lambda ^*, \eta ^*, \sigma ^* \rangle$, Theorem 3 does not tell us how to convert this solution to an optimal solution of program (9) and identify the MPSS of DMU $(X_o,Y_o)$.

The new Theorem 5 resolves the above problems. It shows that the nonlinear program (11) can be equivalently restated as program (13). As discussed in Remark 2 below, the latter program is easy to solve. Furthermore, Theorem 5 establishes a one-to-one correspondence between the optimal solutions of programs (9) and (13), and provides simple formulae that transform an optimal solution of either program to an optimal solution of the other program. This means that, in practice, we can solve only program (13) and subsequently convert its optimal solution to an optimal solution of program (9), thus identifying the MPSS of DMU $(X_o,Y_o)$.

Remark 2

In practical applications, solving program (13) should be unproblematic. Indeed, if the sets $\mathrm{I}'$ and $\mathrm{O}'$ do not include ratio inputs and outputs, then the sets ${\mathrm{I}^R} \cap {\mathrm{I}'}$ and ${\mathrm{O}^R} \cap {\mathrm{O}'}$ are empty, the constraints (13f), (13h), (13k) and (13m) are omitted and program (13) becomes a linear program. If at least one ratio input or output is included in the sets $\mathrm{I}'$ and $\mathrm{O}'$, then program (13) is nonlinear. In this case, the constraints (13f) and (13h) can be restated as “either-or” conditions and further linearized using the “big M” method as discussed in Olesen et al. (2017). This transforms program (13) to a mixed integer linear program.

6 Special cases

Below we consider several special cases of program (13). Recall that, as discussed in Sect. 5, solving this program is equivalent to the identification of MPSS by program (9).

6.1 The model of Banker and Morey (1986)

Suppose that there are no ratio measures, i.e., $\mathrm{I} =\mathrm{I}^V$ and $\mathrm{O} =\mathrm{O}^V$. In this case, the inequalities (13f)–(13i) and (13k)–(13n) are omitted from program (13). If the set ${\mathrm{O}'}$ includes all volume outputs but ${\mathrm{I}'}$ does not include all volume inputs, the resulting program (13) is the model of Banker and Morey (1986) in which the inputs in the complementary subset $\mathrm{I}^V \setminus {\mathrm{I}'}$ are regarded as non-discretionary. If additionally some (non-discretionary) outputs are permitted and are not included in the set ${\mathrm{O}'}$, program (13) is a generalization of the model of Banker and Morey (1986) provided by Golany and Roll (1993). In both models, the inequalities (13c) and (13e) disallow proportional scaling of the volume measures that are not included in the sets $\mathrm{I}'$ and $\mathrm{O}'$.

6.2 The partial cone extension of the model of Ruggiero (1996)

Let ${\mathrm{I}'} = {\mathrm{I}^V}$ and ${\mathrm{O}'} = {\mathrm{O}^V}$. This corresponds to an important practical situation in which the ratio inputs and outputs, often representing environmental and quality characteristics, are assumed constant in the evaluation of the technical and scale efficiency (Ruggiero 1996). In the described scenario, conditions (13c), (13e), (13f), (13h) and (13k)–(13n) are omitted, and equality (13j) and variable $\sigma$ become redundant. Then program (13) is stated as follows:

$$\begin{aligned} \begin{aligned}&{\hat{\eta }} = \max \ \eta \\&\text{ subject } \text{ to } \\&\sum \limits _{j \in J} {{\lambda _j}Y_j^V} \ge \eta {Y^V_o}, \\&\sum \limits _{j \in J} {{\lambda _j}X_j^V} \le {X^V_o}, \\&{\lambda _j}\left( {Y_j^R - {Y^R_o}} \right) \ge \mathbf{{0}}, \qquad \forall j \in J, \\&{\lambda _j}\left( {X_j^R - {X^R_o}} \right) \le \mathbf{{0}}, \qquad \forall j \in J, \\&\lambda \ge \mathbf{{0}}, \eta \ge 0. \end{aligned} \end{aligned}$$

(14)

The technology employed by model (14) allows proportional scaling of the volume inputs and outputs while keeping the ratio measures constant. This corresponds to the special case of the R-CRS technology, denoted $T_{\mathrm{CRS}}^{\mathrm{F}}$, in which all ratio inputs and outputs are of the fixed type (Olesen et al. 2015).⁹ Technology $T_{\mathrm{CRS}}^{\mathrm{F}}$ can be viewed as the partial cone extension (with respect to the volume inputs and outputs only) of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ stated by Theorem 1. It can also be seen as the CRS extension of the model of Ruggiero (1996) which allows proportional scaling of the volume measures, while keeping the exogenous ratio measures fixed.

6.3 The full scale efficiency

Let the sets $\mathrm{I}'$ and $\mathrm{O}'$ include all volume and ratio measures, i.e., let ${\mathrm{I}'} = \mathrm{I}$ and ${\mathrm{O}'} = \mathrm{O}$. This case was illustrated by scenario (i) of Example 3. As a practical example, in an application to schools, volume measures may represent the teaching hours, expenditure and the number of pupils. The ratio inputs and outputs may represent the percentage of pupils with good grades on entry and exit, and also the percentage of pupils from the higher socio-economic background. The policy maker may be interested in the full scale characterization of the production frontier, in which case the sets $\mathrm{I}'$ and $\mathrm{O}'$ include all, volume and ratio, inputs and outputs. Note that, regardless of whether some inputs or outputs are discretionary or non-discretionary, it may still be useful to consider the full scale characterization that takes into account all such measures—see Sect. 4.1.

In the described scenario, program (13) takes on the following simplified form:

$$\begin{aligned}&\eta ^* = \max \ \eta \end{aligned}$$

(15a)

$$\begin{aligned}&\text {subject to} \nonumber \\&\sum \limits _{j \in J} {{{\lambda }_j} Y_j^V} \ge \eta Y_o^V, \end{aligned}$$

(15b)

$$\begin{aligned}&\sum \limits _{j \in J} {{{\lambda }_j} X_j^V} \le X_o^V, \end{aligned}$$

(15c)

$$\begin{aligned}&{\lambda _j}( \sigma Y_{j}^R - \eta Y_{o}^R) \ge \mathbf{{0}}, \qquad \forall j \in J, \end{aligned}$$

(15d)

$$\begin{aligned}&{\lambda _j}( \sigma X_{j}^R - X_{o}^R) \le \mathbf{{0}}, \qquad \forall j \in J, \end{aligned}$$

(15e)

$$\begin{aligned}&\mathbf{{1}}^{\top } {\lambda } = \sigma , \end{aligned}$$

(15f)

$$\begin{aligned}&\eta {Y^R_o} \le \sigma {{\bar{Y}}^R}, \end{aligned}$$

(15g)

$$\begin{aligned}&{X^R_{o}} \le \sigma {{\bar{X}}^R}, \end{aligned}$$

(15h)

$$\begin{aligned}&\lambda \ge \mathbf{{0}}, \ \sigma , \eta \ge 0. \end{aligned}$$

(15i)

All observed DMUs $(X_j,Y_j)$, $j \in J$, and the bounds on the ratio measures (1) in program (15) are fully scaled by the scaling factor $\sigma$. Note that the factor $\sigma$ is not explicitly present in constraints (15b) and (15c). However, taking into account (15f), the conical combinations of the volume inputs and outputs of the observed DMUs in (15b) and (15c) can also be viewed as the convex combinations of the scaled vectors $\sigma Y^V_j$ and $\sigma X^V_j$ taken with the weights $\lambda _j/ \sigma$ that add up to 1.

7 Returns to scale in the R-VRS technology

If a DMU is scale inefficient, a further question arises: is it too small or too large compared to its MPSS? Answering this question leads to the RTS characterization of the production frontier. For the conventional VRS technology, such characterization is based on the underlying notion of (one-sided) scale elasticity. It was originally developed by Banker (1984) and Banker and Thrall (1992) and further explored in the literature—see, e.g., Førsund and Hjalmarsson (2004), Hadjicostas and Soteriou (2006), Chambers and Färe (2008), Zelenyuk (2013) and Sahoo and Tone (2015).

In this section, we show that the notion of RTS can also be extended to the R-VRS technology. Because the R-VRS technology is generally nonconvex, such extension is not straightforward. In particular, the scale elasticity as a marginal scale characteristic and the RTS characterization based on it are not generally suitable indicators of a direction to MPSS.

In order to extend the notion of RTS to the R-VRS technology, we employ two approaches, depending on the selected sets $\mathrm{I}'$ and $\mathrm{O}'$ of inputs and outputs with respect to which we measure the scale efficiency. Namely, if the selected inputs and outputs are volume measures, we employ a variant of the standard notion of local RTS (Banker and Thrall 1992). If at least one of the selected inputs or outputs is a ratio measure, we identify a direction to MPSS by exploring the range of optimal values of variable $\sigma$ in program (13). This approach is conceptually related to the approach of Färe et al. (1983b, 1985) and leads to the notion of global RTS (Podinovski 2004a, b).

The returns-to-scale characterization applies to DMUs located on the production frontier.¹⁰ We therefore require that DMU $(X_o,Y_o)$ satisfies the following assumption:

Assumption 4

DMU $({X_o},{Y_o})$ is output radial efficient with respect to the subset of outputs ${\mathrm{O}'}$, i.e., in program (5), we have ${\tilde{\eta }} = 1$.

7.1 Local RTS in the R-VRS technology

Below we define the local RTS characterization of the production frontier of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ with respect to the volume inputs and outputs only, while keeping the ratio inputs and outputs fixed.

Let the sets $\mathrm{I}'$ and $\mathrm{O}'$ include all volume measures and exclude all ratio measures: ${\mathrm{I}'} = {\mathrm{I}^V}$, ${\mathrm{O}'} = {\mathrm{O}^V}$. Also, let DMU $(X_o,Y_o)$ satisfy Assumption 4. The conventional RTS characterization of the VRS production frontier is determined by the one-sided (left-hand and right-hand) scale elasticities evaluated at DMU $(X_o,Y_o)$. This RTS characterization is local in nature as it depends on the production frontier in a marginal neighborhood of the DMU $(X_o,Y_o)$.

In the case of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$, we can similarly define local RTS (with respect to volume inputs and outputs only) by evaluating the one-sided scale elasticities at the DMU $(X_o, Y_o)$ in the section $\Delta T$ of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ obtained for the fixed vectors $X^R_o$ and $Y^R_o$. The section $\Delta T$ can be regarded as a technology which represents all volume input and output combinations $(X^V, Y^V)$ possible for the fixed vectors $X^R_o$ and $Y^R_o$ of the ratio inputs and outputs.

Taking into account Theorem 1, technology $\Delta T$ is the set of all nonnegative DMUs $(X^V, Y^V)$ for which there exists a vector $\lambda \in {\mathbb {R}}^n$ such that the following conditions are true (note that the vectors $X^R_o$ and $Y^R_o$ are fixed, and there is no need to specify bounds (1) on the ratio measures):

$$\begin{aligned} \begin{aligned}&\sum \limits _{j \in J} {{\lambda _j}Y_j^V} \ge {Y^V}, \\&\sum \limits _{j \in J} {{\lambda _j}X_j^V} \le {X^V}, \\&{\lambda _j}\left( {Y_j^R - {Y^R_o}} \right) \ge \mathbf{{0}}, \qquad \forall j \in J, \\&{\lambda _j}\left( {X_j^R - {X^R_o}} \right) \le \mathbf{{0}}, \qquad \forall j \in J, \\&\mathbf{{1}}^{\top } \lambda = 1, \\&\lambda \ge \mathbf{{0}}. \end{aligned} \end{aligned}$$

Technology $\Delta T$ can be viewed as the standard VRS technology generated by the subset $J'$ of observed DMUs $(X_j,Y_j)$ such that both vector inequalities $Y_j^R \ge Y^R_o$ and $X_j^R \le {X^R_o}$ are true. If an observed DMU $(X_j,Y_j)$ does not satisfy these inequalities, we have $\lambda _j = 0$, which excludes this DMU from the subset $J'$.

By Assumption 4, DMU $(X_o, Y_o)$ is output radial efficient in technology $\Delta T$. Denote $\varepsilon ^+ (X^V_o,Y^V_o)$ and $\varepsilon ^- (X^V_o,Y^V_o)$ the partial right-hand and left-hand scale elasticities evaluated at the DMU $(X^V_o,Y^V_o)$ on the boundary of $\Delta T$. Because $\Delta T$ is a VRS technology, their computation is straightforward. Indeed, let $\omega ^{\min }$ and $\omega ^{\max }$ be the minimum and maximum optimal values of the dual variable $\omega$ to the normalizing equality $\mathbf{{1}}^{\top } \lambda = 1$ of the output-oriented linear program stated for DMU $(X_o,Y_o)$. (Identifying $\omega ^{\min }$ and $\omega ^{\max }$ requires solving two linear programs.) Then

$$\begin{aligned} \varepsilon ^+ (X^V_o,Y^V_o)= 1 - \omega ^{\mathrm{max}}, \quad \varepsilon ^- (X^V_o,Y^V_o)= 1 - \omega ^{\mathrm{min}}. \end{aligned}$$

(16)

In line with Banker and Thrall (1992), we have the following definition.

Definition 3

DMU $(X_o,Y_o) \in T_{\mathrm{VRS}}^{\mathrm{R}}$ exhibits the following types of partial RTS evaluated with respect to the volume inputs and outputs only:

• (i) IRS if $1 < \varepsilon ^+(X_o,Y_o) \le \varepsilon ^-(X_o,Y_o)$;

• (ii) DRS if $\varepsilon ^+(X_o,Y_o) \le \varepsilon ^-(X_o,Y_o) < 1$;

• (iii) CRS if $\varepsilon ^+(X_o,Y_o) \le 1 \le \varepsilon ^-(X_o,Y_o)$.

Remark 3

The one-sided scale elasticities $\varepsilon ^+ (X^V_o,Y^V_o)$ and $\varepsilon ^- (X^V_o,Y^V_o)$ can also be calculated using the linear program that evaluates the input radial efficiency of the DMU $(X^V_o,Y^V_o)$ in the VRS technology $\Delta T$ (Førsund and Hjalmarsson 2004; Hadjicostas and Soteriou 2006; Sahoo and Tone 2015; Zelenyuk 2013). Furthermore, in some applications, only a subset of volume inputs and outputs may be of interest and included in these sets, i.e., we may have ${\mathrm{I}'} \subseteq {\mathrm{I}^V}$, ${\mathrm{O}'} \subseteq {\mathrm{O}^V}$. The partial one-sided scale elasticities with respect to the selected subsets ${\mathrm{I}'}$ and ${\mathrm{O}'}$ can be evaluated in technology $\Delta T$ using the linear programming approach of Podinovski et al. (2016) of which formulae (16) are a special case.

7.2 Global RTS in the R-VRS technology

The global RTS (GRS) characterization of production frontiers was introduced by Podinovski (2004a, 2004b). The types of GRS are indicative of the direction in which DMU $(X_o,Y_o)$ should resize to achieve MPSS. For example, DMU $(X_o,Y_o)$ exhibits global increasing RTS if it is smaller than its MPSS and, therefore, needs to increase the scale of its operations to achieve its MPSS.¹¹

In any convex technology, including the VRS technology, the local and global RTS characterizations are identical (Podinovski 2017). However, in a nonconvex technology such as the R-VRS technology, the local types of RTS are no longer indicative of the direction to MPSS (see the example in Sect. 7.3), and the global characterization needs to be used instead.

In this section, we consider arbitrary nonempty subsets of volume and ratio inputs and outputs ${\mathrm{I}'} \subseteq \mathrm{I}$ and ${\mathrm{O}'} \subseteq \mathrm{O}$. Let DMU $(X_o,Y_o)$ satisfy Assumption 4. In order to evaluate its scale efficiency with respect to the selected sets ${\mathrm{I}'}$ and ${\mathrm{O}'}$, we solve program (9) or equivalent program (13).

Any optimal solution $\langle \varphi ^*, \psi ^* \rangle$ of program (9) defines the MPSS of DMU $(X_o,Y_o)$ evaluated with respect to the inputs and outputs from the sets ${\mathrm{I}'}$ and ${\mathrm{O}'}$ and stated as

$$\begin{aligned} (X_o(\varphi ^*),Y_o(\psi ^*)) \in T_{\mathrm{VRS}}^{\mathrm{R}}. \end{aligned}$$

(17)

Assume that DMU $(X_o,Y_o)$ is scale inefficient, i.e., that $\psi ^* / \varphi ^* > 1$. Then either $\varphi ^* < 1$ or ${\varphi ^* > 1}$.¹² If $\varphi ^* < 1$, the corresponding MPSS (17) is smaller than DMU $(X_o,Y_o)$. If $\varphi ^* > 1$, the MPSS (17) is larger than DMU $(X_o,Y_o)$. It is theoretically possible that program (9) has alternative optimal solutions $\langle \varphi ^*,\psi ^* \rangle$, each identifying a different MPSS (17).

By statement (iii) of Theorem 5, the case $\varphi ^* < 1$ corresponds to ${\hat{\sigma }} >1$ in an optimal solution of program (13), and the case $\varphi ^* > 1$ corresponds to ${\hat{\sigma }} <1$. We can now extend the characterization of GRS defined in Podinovski (2004a) in the case ${\mathrm{I}'} = {\mathrm{I}}$ and ${\mathrm{O}'} = {\mathrm{O}}$ to the case of partial GRS evaluated only with respect to the sets of inputs and outputs ${\mathrm{I}'}$ and ${\mathrm{O}'}$.

Let DMU $(X_o,Y_o) \in T_{\mathrm{VRS}}^{\mathrm{R}}$ satisfy Assumption 4. In order to determine if DMU $(X_o,Y_o)$ is at MPSS and, if not, whether there exists an MPSS that is smaller or larger than DMU $(X_o,Y_o)$, we solve two additional programs derived from program (13). The first can be viewed as the non-increasing returns-to-scale (NIRS) analogue of program (13), and the second as its non-decreasing returns-to-scale (NDRS) analogue.

$$\begin{aligned} \begin{aligned}&{\hat{\eta }}_1 = \max \ \eta \\&\text{ subject } \text{ to } (13\mathrm{b}) - (13\mathrm{o}) \text { and } \sigma \le 1, \end{aligned} \end{aligned}$$

(18)

and

$$\begin{aligned} \begin{aligned}&{\hat{\eta }}_2 = \max \ \eta \\&\text{ subject } \text{ to } (13\mathrm{b}) - (13\mathrm{o}) \text { and } \sigma \ge 1. \end{aligned} \end{aligned}$$

(19)

It is clear that ${\hat{\eta }}_1 \ge 1$ and ${\hat{\eta }}_2 \ge 1$. We also have ${\hat{\eta }} = \min \{{\hat{\eta }}_1, {\hat{\eta }}_2 \}$, where ${\hat{\eta }}$ is the optimal value of program (13). The following four mutually exclusive cases are now possible.

If ${\hat{\eta }}_1 = {\hat{\eta }}_2 =1$, the optimal value ${\hat{\eta }}$ of program (13) is equal to 1 and DMU $(X_o,Y_o)$ is at MPSS with respect to the sets ${\mathrm{I}'}$ and ${\mathrm{O}'}$. In this case, we class DMU $(X_o,Y_o)$ as exhibiting global CRS (G-CRS).

Let $1 \le {\hat{\eta }}_2 < {\hat{\eta }}_1$. Then ${\hat{\eta }} = {\hat{\eta }}_1 >1$ and, for any optimal solution $\langle {\hat{\lambda }}, {\hat{\sigma }}, {\hat{\eta }} \rangle$ to (13), we have ${\hat{\sigma }}<1$. By statement (iii) of Theorem 5, for any optimal solution $\langle \psi ^*, \varphi ^* \rangle$ of program (9), we have $\varphi ^* =1/ {\hat{\sigma }} >1$. The MPSS of DMU $(X_o,Y_o)$ calculated by formula (17) is larger than DMU $(X_o,Y_o)$, for any optimal solution of (13), and we class DMU $(X_o,Y_o)$ as exhibiting global IRS (G-IRS).

Similarly, if $1 \le {\hat{\eta }}_1 < {\hat{\eta }}_2$, then for any optimal solution $\langle {\hat{\lambda }}, {\hat{\sigma }}, {\hat{\eta }} \rangle$ to (13) we have ${\hat{\sigma }}>1$ and, in program (9), $\varphi ^* =1/ {\hat{\sigma }} <1$. Therefore, any MPSS of DMU $(X_o,Y_o)$ is smaller than this DMU and the latter exhibits global DRS (G-DRS).

The final logical possibility is the case in which $1 < {\hat{\eta }}_1 = {\hat{\eta }}_2$. In this case, DMU $(X_o,Y_o)$ is scale inefficient and has at least two different directions to MPSS, one of which is larger, and the other smaller, than the DMU $(X_o,Y_o)$. We class DMU $(X_o,Y_o)$ as exhibiting global sub-constant RTS (G-SCRS).

Remark 4

Assume that DMU $(X_o,Y_o)$ does not satisfy Assumption 4, i.e., it is not efficient with respect to the vector of outputs included in the set $\mathrm {O}'$. It is straightforward to show that, in this case, the described approach will characterize GRS at the projection of DMU $(X_o,Y_o)$ on the boundary of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$. Indeed, let the efficiency of DMU $(X_o,Y_o)$ in technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ evaluated with respect to the outputs in the set $\mathrm {O}'$ by program (5) be equal to $1/ {\tilde{\eta }} <1$. Denote $(X^*,Y^*) = (X_o,Y_o({\tilde{\eta }}))$ the projection of DMU $(X_o,Y_o)$ on the boundary of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$. Then the projected DMU $(X^*,Y^*)$ satisfies Assumption 4 and we can characterize its type of GRS by solving programs (18) and (19). Let the corresponding optimal values of these two programs be ${\hat{\eta }}^*_1$ and ${\hat{\eta }}^*_2$, respectively. It is clear that ${\hat{\eta }}^*_1 = {\hat{\eta }}_1 / {\tilde{\eta }}$ and ${\hat{\eta }}^*_2 = {\hat{\eta }}_2 / {\tilde{\eta }}$, where ${\hat{\eta }}_1$ and ${\hat{\eta }}_2$ are the optimal values of programs  (18) and (19) stated for the evaluation of DMU $(X_o,Y_o)$. Then ${\hat{\eta }}^*_1 \le {\hat{\eta }}^*_2$ if and only if ${\hat{\eta }}_1 \le {\hat{\eta }}_2$. This implies that the procedure for the characterization of GRS based on the optimal values ${\hat{\eta }}_1$ and ${\hat{\eta }}_2$ of programs (18) and (19) stated for DMU $(X_o,Y_o)$ (at which the notion of GRS is undefined) in fact characterizes GRS at the projection $(X^*,Y^*)$.

7.3 Example of evaluation of RTS

Let $T_{\mathrm{VRS}}^{\mathrm{R}}$ be the R-VRS technology considered in Examples 2 and 3. We first illustrate the notion of local RTS, by referring to scenario (ii) in which we define ${\mathrm{I}'}=\mathrm{I}$ and ${\mathrm{O}'}=\mathrm{O}$. In this case, technology $\Delta T$ is the section KCADE shown in Fig. 1 and, separately, in Fig. 6.

Fig. 6

Section $\Delta T$ of the R-VRS technology for DMU A

Consider DMU A and note that it satisfies Assumption 4. The left-hand scale elasticity at DMU A is undefined because it is not possible to reduce its input in technology $\Delta T$, and we can conventionally take $\varepsilon ^- (A) = +\infty$. The right-hand scale elasticity $\varepsilon ^+ (A) = 2$. It corresponds to the movement along the side AD away from A and can be calculated as the ratio of the marginal productivity (equal to the slope 2 of the line AD) to the average productivity at A (equal to $1/1=1$). By Definition 3, DMU A exhibits IRS with respect to the volume input and output.

Because the section $\Delta T$ is convex, the local type of RTS of DMU A coincides with its global (G-IRS) type, and both are indicative of the direction to its MPSS at DMU D.

Now consider scenario (i) in which the set ${\mathrm{I}'}$ includes the single volume input and the set ${\mathrm{O}'}$ includes both volume and ratio outputs. As shown in Example 3, DMU A is scale inefficient and its MPSS is DMU P. Because DMU P is larger than A, the latter exhibits G-IRS with respect to all inputs and outputs. Note that, in this scenario, the right-hand scale elasticity $\varepsilon ^- (A) = 0$ and corresponds to the movement along the line AL (see Footnote 5). Therefore, locally, DMU A exhibits DRS to the right, although in the global sense, it should increase the scale of its operations to achieve its MPSS at DMU P.

Finally, consider scenario (iii) in which the set ${\mathrm{O}'}$ includes only the ratio output. As shown in Example 3, DMU A is scale inefficient and its MPSS is at DMU V, which is larger than A. Therefore, DMU A exhibits G-IRS in this scenario as well. As in scenario (i), the right-hand scale elasticity at A in the section of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ defined by its boundary ALVW is equal to zero and corresponds to the marginal movement along the line AL away from A. Therefore, DMU A exhibits DRS, and this local characterization is not indicative of the direction to MPSS.

8 Illustrative application

In this section, we illustrate the application of the developed methodology using a sample of 39 secondary schools in the West Midlands region of England. The data was collected in 2020-21 and is publicly available from the official website of Department for Education.

Table 5 Descriptive statistics for the application

Table 5 shows summary statistics of the measures used in the application. (The full data set used in this application is given in Appendix C.) The volume inputs 1 and 2 represent the number of teachers and expenses in thousands of British pounds (excluding teacher salaries) at each school. The ratio input 3 measures the percentage of pupils who are not eligible for free school meals (NFSM). This input is a socio-economic characteristic of the catchment area which is assumed to have a positive effect on the performance of the school. The volume output 1 is the number of all pupils at the school. The ratio output 2 is the proportion of the final year (sixth form) pupils proceeding to higher education (HE) and is included in the model as a measure of quality of education. (In Sect. 8.4, we discuss potential computational issues arising from the use of small ratios in DEA models.¹³)

We consider three scenarios of evaluation of scale characteristics, by choosing the sets $\mathrm {I}'$ and $\mathrm {O}'$ in different ways: first, as the sets of all (volume and ratio) measures; second, as the sets of all volume inputs and outputs; and third, as the sets of all ratio inputs and outputs, respectively.

Preliminary calculations show that 23 schools in the current sample are strongly (Pareto) efficient and, therefore, satisfy Assumption 4. It also turns out that, in each scenario, no additional observed DMUs satisfy this assumption, i.e., the set of observed DMUs that are efficient with respect to the outputs in the set $\mathrm {O}'$ is the set of strongly efficient DMUs of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$.¹⁴

8.1 Evaluation with respect to both volume and ratio measures

Consider the evaluation of scale efficiency and RTS characterization of the schools with respect to all, volume and ratio, inputs and outputs. In this scenario, we define the sets ${\mathrm{I}'} = \mathrm{I}$ and ${\mathrm{O}'} = \mathrm{O}$.

Table 6 Efficiency and scale characteristics evaluated with respect to both volume and ratio measures (for inefficient schools, see Remark 5)

Table 6 shows the results of computations. Its second column shows the output radial efficiency of each school in the R-VRS technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ evaluated with respect to the vector of two outputs. The next three columns show the output radial efficiency of the schools in models (13), (18) and (19) which are based on the closed full cone extension ${{\bar{C}}}(\mathrm{I},\mathrm{O})$ of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ and its NIRS and NDRS analogues. Note that the efficiencies shown in Table 6 are inverse to the optimal values ${\hat{\eta }}$, ${\hat{\eta }}_1$ and ${\hat{\eta }}_2$ of these programs.¹⁵

Following the discussion of Sect. 6.3, instead of solving program (13), we solve the simpler, but equivalent, program (15). We also solve this program with the additional constraints $\sigma \le 1$ and $\sigma \ge 1$, instead of the NIRS and NDRS programs (18) and (19).

According to Sect. 4.4, the overall scale efficiency of each school is equal to its efficiency in model (13), as shown in the third column of Table 6. The scale efficiency of each school is shown in the second last column of this table. It is obtained as the ratio of its output efficiency in model (13) to its efficiency in technology $T_{\mathrm{VRS}}^{\mathrm{R}}$.

Let us now consider the RTS characterization of schools located on the frontier of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$. As highlighted in Sect. 7, because this technology is not convex, the standard RTS characterization of its frontier is generally not well-defined and is not indicative of the direction to MPSS. Instead, we use the global RTS characterization to identify the direction to MPSS for each school.

As already established, 23 schools from the sample are output radial efficient and are located on the frontier of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$. (The efficiency of these schools in the R-VRS model is equal to 1, as shown in the second column of Table 6.) As discussed in Sect. 7.2, the characterization of GRS for these schools can be obtained by comparing their efficiency in the NIRS and NDRS programs (18) and (19).

The last column of Table 6 shows the resulting GRS characterization. For example, School 2 is at MPSS (or, equivalently, exhibits G-CRS). School 11 exhibits G-IRS and is, therefore, smaller than its MPSS. (Note that, in this case, for the optimal values of programs (18) and (19), we have ${\hat{\eta }}_1=1/0.9463 > 1/1 = {\hat{\eta }}_2$). School 24 exhibits G-DRS and is, therefore, larger than its MPSS.

Remark 5

For the inefficient schools, the last column of Table 6 shows the GRS characterization of their radial projections on the boundary of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ (see Remark 4 for the discussion of GRS evaluated at the projections of inefficient DMUs). For example, School 1 is inefficient. Improving its efficiency by proportional increase of both outputs (by the factor $1/0.9337=1.071$) would result in the school that exhibits G-IRS. Such projection would be smaller than its MPSS.

8.2 Evaluation with respect to volume measures only

Consider the evaluation of scale efficiency and RTS with respect to volume measures only, by keeping the ratio input and output fixed. Define $\mathrm {I}'=\{ {\text {input~1, input~2}} \}$ and $\mathrm {O}'=\{ {\text {output~1}} \}$. In this scenario, we investigate the relationship between the volume parameters of the schools (teachers, expenses and pupils) by assuming that the socio-economic characteristic of the school catchment area (ratio input 3) and quality of education (ratio output 2) remain unchanged.

In this case, model (13) becomes program (14). Models (18) and (19) are obtained from the latter program by the reinstatement of constraint (13j) and the incorporation of additional constraints $\sigma \le 1$ and $\sigma \ge 1$, respectively.

Table 7 shows the results of computations in a format similar to Table 6. The difference with the previous scenario is that the efficiencies of all schools are now evaluated with respect to the volume output 1 only.¹⁶ Also, as discussed in Sect. 7.1, in this scenario, the local and global characterizations of RTS are identical.

Consider for example, School 3. As shown in Table 7, this school exhibits DRS (or G-DRS in the equivalent terminology of GRS). This means that a marginal proportional increase of the number of teachers and expenses of this school would result in a smaller rate of increase of the number of pupils, assuming that the ratio measures (input 3 and output 2) remain constant. From a policy-maker’s perspective, School 3 is scale inefficient and moving to MPSS means making the school smaller, without any change to the socio-economic environment and without affecting the quality of education.

Table 7 Efficiency and scale characteristics evaluated with respect to volume measures only

8.3 Evaluation with respect to ratio measures only

Suppose that we are interested in the impact of the socio-economic environment on the proportion of pupils going to university, while keeping the volume measures fixed. Define $\mathrm {I}'=\{ {\text {input~3}} \}$ and $\mathrm {O}'=\{ {\text {output~2}} \}$.

Table 8 shows the results of computations using appropriately specified programs (13), (18) and (19).

For example, consider School 11. Because it exhibits G-IRS, it is smaller than its MPSS evaluated with respect to the ratio input and output. This implies that, if we keep the size of the school unchanged (represented by the number of teachers, expenses and pupils), then the socio-economic characteristic of the pupil intake (percentage of pupils not eligible for free school meals) has a more than proportional impact on the quality of education (proportion of pupils going to university).

Table 8 Efficiency and scale characteristics evaluated with respect to ratio measures only

8.4 Notes on computations with small ratios

As mentioned in Footnote 13, in the discussed application, output 2 represents the proportion of final-year pupils proceeding to higher education. We could, of course, convert these proportions to percentages, by rescaling the proportions by a factor of 100. However, we preferred to keep this output unchanged, in line with the way the data was reported by Department for Education.

Using proportions and any other very small numerical values (compared, for example, with the numerical values for school expenditure all of which are in excess of 1000) in DEA models may present well-known computational problems, and rescaling the data prior to calculations may be required in order to obtain correct results. (In the reported application, we were aware of potential problems and repeated our computations with the rescaled ratios, but did not detect any discrepancy between the results.)

The scaling of linear optimization problems is a technique utilized in linear optimization solvers with the aim to improve the conditioning of the constraint matrix and decrease the computational effort for solution—see, e.g., Bixby (2002). As observed by Elble and Sahinidis (2012), scaling provides a relative point of reference for absolute tolerances. This is especially important when solving the linearized counterparts of models (13), (18) and (19), because the linearization of constraints (13f) and (13h) involves one binary variable used with one “Big M” for each DMU in the sample. (The value of “Big M” should of course be chosen sufficiently large but not much larger than necessary. To avoid too large “Big M” values, it is of course valid to use two different “Big M” values, one for constraints (13f) and the other for (13h).)

Absolute tolerances are applied to every node of the branch-and bound tree used in the simplex method to determine when a binary variable in a relaxed solution is considered to be integer or a reduced cost coefficient is considered to be nonnegative. The use of absolute tolerances is challenging when, for example, rows in the constraint matrix are of different numerical magnitude as in the constraint matrix for the data set in Table 10. For example, in the discussed application, the numerical values for school expenditure are up to five orders of magnitude larger than the corresponding proportions of pupils proceeding to higher education. A further computational challenge may arise with the use of the “Big M” approach to the linearization of optimization programs with an unbalanced constraint matrix.

In the reported application, we could balance the constraint matrix by restating expenditures in £100,000, pupils in hundreds and their proportion going to higher education as percentages. This would result in all data being in the range [0; 100]. It has been decided to maintain data as is rather than to rescale it. This proved not to be a problem for industry-leading solvers, e.g., CPLEX or Gurobi, because their presolvers include sophisticated rescaling of the constraint matrix by default.

9 Conclusion

The notions of the most productive scale size, scale and overall efficiency play an important role in efficiency and productivity analysis based on the conventional VRS model. This paper develops an extension of such scale characteristics to the R-VRS technology of Olesen et al. (2015). The latter technology is defined axiomatically and allows both volume and ratio inputs and outputs to be incorporated in the model.

Following the approach of Banker (1984), we start by defining the notion of MPSS in the R-VRS technology. Continuing with the same approach, we define and interpret scale efficiency as a measure of divergence from MPSS and decompose the overall efficiency of a DMU into its technical and scale components.

Similar to the case of conventional VRS technology, the evaluation of MPSS and scale efficiency of a DMU in the R-VRS technology turns out to be equivalent to the assessment of its output radial efficiency in the closed cone extension of the R-VRS technology. Obtaining an explicit statement of such cone extension suitable for optimization is a nontrivial task accomplished in our paper.

Despite the conceptual similarities between the cases of VRS and R-VRS technologies, there is an important distinction to be noted. In the former case, the closed cone extension of the VRS technology is the CRS technology. This allows the scale efficiency in the VRS technology to be alternatively interpreted as the technical efficiency in the benchmark CRS technology. However, as shown in this paper, the closed cone extension of the R-VRS technology is generally different from the R-CRS technology axiomatically defined by Olesen et al. (2015). As demonstrated by examples in this paper, the MPSS and scale efficiency in the R-VRS technology defined according to the approach of Banker (1984) cannot generally be evaluated using the R-CRS technology.

In order to keep the exposition more general and suitable for different applications, we allow the evaluation of MPSS and scale efficiency with respect to any selected subsets of inputs and outputs, while keeping the remaining measures constant. This corresponds to the scenario in which we want to test the response of a selected subset of outputs to changes of a selected subset of inputs while treating the other inputs and outputs as fixed exogenous measures.

We also consider returns-to-scale characterizations of the production frontier of the R-VRS technology. Depending on the choice of inputs and outputs with respect to which we evaluate the MPSS and scale efficiency of a DMU, we employ the local and global variants of the notion of returns to scale. For a scale inefficient DMU, the type of returns to scale (increasing or decreasing) is indicative of the direction to its MPSS, when the resizing is allowed only with respect to the selected inputs and outputs.

To outline further potential research avenues, it is worth noting that the use of ratio data presents similar difficulties in many alternative convex DEA models, for example the models based on assumptions of weak disposability, models incorporating value judgements in the form of weight restrictions and models with complex network structures. It is clear that ratio inputs and outputs are inconsistent with the assumption of convexity and the additional assumption of scalability often made in such models. Exploring the ways to incorporate ratio data and developing approaches to the efficiency and RTS evaluation in such models is a challenging task for future research.

Appendices

Appendix A: Proofs

Lemma 1

Define W as the set of all DMUs $(X,Y) \in {{\mathbb {R}}}^{m+s}_+$ that satisfy conditions (8) with some $\lambda$ and $\sigma$. Then W is a closed set.

Proof of Lemma 1

Let a sequence of DMUs $\{({X^k},{Y^k}) \} \subset W$ converge to $({X^*},{Y^*}) \in {{\mathbb {R}}^{m+s}}$ as $k \rightarrow + \infty$. We need to prove that $({X^*},{Y^*}) \in W$.

For each $k=1,2,\dots$, $({X^k},{Y^k})$ satisfies (8) with some vector ${\lambda ^k}$ and scalar $\sigma ^k$. Because the sequence $\{ \lambda ^k \}$ is contained in the compact set $[0,1]^n$, where n is the number of observed DMUs, there exists some (not necessarily unique) convergent subsequence $\{ \lambda ^{k_t} \}$, $t=1,2,...$, of the sequence $\{ \lambda ^k \}$. Let the limit point of $\{ \lambda ^{k_t} \}$ be $\lambda ^*$. Because $[0,1]^n$ is a closed set, $\lambda ^* \in [0,1]^n$. Therefore, $\{ \lambda ^{k_t} \} \rightarrow \lambda ^*$ as $t \rightarrow + \infty$. To simplify the proof, and without loss of generality, let us assume that the sequence $\{ \lambda ^k \}$ itself is converging, i.e., that $\{ \lambda ^k \} \rightarrow \lambda ^*$ as $k \rightarrow + \infty$.

Let us prove that the sequence $\{ \sigma ^k \}$ is contained in a compact set. Because $\{ X^k \}$ converges to $X^*$, it is bounded and there exists an $M >0$ such that $X^k_i < M$, for all $i \in \mathrm{I}$ and $k=1,2,...$ Because $\lambda ^*$ satisfies (8i), there exists a $j' \in J$ such that $\lambda ^*_{j'} >0$. Because $\{ \lambda ^k_{j'} \} \rightarrow \lambda ^*_{j'}$ as $k \rightarrow + \infty$, there exists an $\varepsilon >0$ and ${\bar{k}} \ge 1$ such that $\lambda ^k_{j'} \ge \varepsilon >0$, $\forall k > {\bar{k}}$.

The inequalities (8c) and (8g) stated for all DMUs $({X^k},{Y^k})$, $k > {\bar{k}}$, imply

$$\begin{aligned}&\lambda ^k_{j'} \sigma ^k X_{j'i}^V \le (X^k_{i})^V, \qquad \forall i \in {\mathrm{I}^V} \cap {\mathrm{I}'}, \nonumber \\&\lambda ^k_{j'}(\sigma ^k X_{j'i}^R - (X^k_{i})^R) \le 0, \qquad \forall i \in {\mathrm{I}^R} \cap {\mathrm{I}'}. \end{aligned}$$

(20)

By definition, we have $0 < \varepsilon \le \lambda ^k_{j'}$ and $M > X^k_i$, $\forall k > {\bar{k}}$ and $\forall i \in \mathrm{I}$. Then, from the inequalities (20), for all $k > {\bar{k}}$, we have

$$\begin{aligned}&\varepsilon \sigma ^k X_{j'i}^V \le \lambda ^k_{j'} \sigma ^k X_{j'i}^V \le (X^k_{i})^V \le M, \qquad \forall i \in {\mathrm{I}^V} \cap {\mathrm{I}'}, \end{aligned}$$

(21a)

$$\begin{aligned}&\sigma ^k X_{j'i}^R \le (X^k_{i})^R \le M, \qquad \forall i \in {\mathrm{I}^R} \cap {\mathrm{I}'}. \end{aligned}$$

(21b)

By Assumption 1, there exists an $i' \in {\mathrm{I}'}$ such that $X_{j' i'} > 0$. If $i' \in \mathrm{I}^V$, then $X_{j'i'}^V >0$ and (21a) implies that $\sigma ^k \le \sigma _1$, for all $k > {\bar{k}}$, where $\sigma _1 = M / (\varepsilon X_{j'i'}^V) >0$. If $i' \in \mathrm{I}^R$, then $X_{j'i'}^R >0$ and (21b) implies that $\sigma ^k \le \sigma _2$, for all $k > {\bar{k}}$, where $\sigma _2 = M / X_{j'i'}^R >0$. Denote ${\bar{\sigma }} = \min \{\sigma _1, \sigma _2 \}$. We have proved that the sequence $\{ \sigma ^k \}$, $k \ge {\bar{k}}$, is contained in the compact set $[0, {\bar{\sigma }}]$. Then there exists its subsequence that converges to some $\sigma ^* \in [0, {\bar{\sigma }}]$. Without loss of generality, assume that the sequence $\{ \sigma ^k \}$ itself is converging, i.e., that $\{ \sigma ^k \} \rightarrow \sigma ^* \in [0, {\bar{\sigma }}]$ as $k \rightarrow + \infty$.

By assumption, conditions (8) are true for each DMU $(X^k, Y^k)$ with the corresponding $\lambda ^k$ and $\sigma ^k$, $k=1,2,...$. We also have $({X^k},{Y^k}) \rightarrow ({X^*},{Y^*})$, as $k \rightarrow +\infty$. Furthermore, as proved, without loss of generality, we can assume that $\lambda ^k \rightarrow \lambda ^*$ and $\sigma ^k \rightarrow \sigma ^*$ as $k \rightarrow +\infty$. This implies that conditions (8) are also true at the limit, i.e., for $(X^*,Y^*)$, $\lambda ^*$ and $\sigma ^*$. Therefore, $(X^*,Y^*) \in W$. $\square$

Proof of Theorem 2

Define W as in Lemma 1. We need to prove that ${{\bar{C}}}(\mathrm{I}',\mathrm{O}') = W$. First, consider any DMU $(X,Y) = ({{\tilde{X}}} (\alpha ), {{\tilde{Y}}} (\alpha )) \in {C}(\mathrm{I}',\mathrm{O}')$, where $({{\tilde{X}}}, {{\tilde{Y}}}) \in T_{\mathrm{VRS}}^{\mathrm{R}}$ and $\alpha \ge 0$. DMU $({{\tilde{X}}},{{\tilde{Y}}})$ satisfies (2) with some vector $\lambda$. Then (X, Y) satisfies (8) with the same vector $\lambda$ and $\sigma = \alpha$. Therefore, $(X,Y) \in W$ and ${C}(\mathrm{I}',\mathrm{O}') \subseteq W$. Taking the closure of both sides and noting equality (7) and Lemma 1, we have ${{\bar{C}}}(\mathrm{I}',\mathrm{O}') \subseteq W$.

It remains to be proved that $W \subseteq {{\bar{C}}}(\mathrm{I}',\mathrm{O}')$. Consider any DMU $({\hat{X}}, {\hat{Y}}) \in W$. Then $({\hat{X}}, {\hat{Y}})$ satisfies (8) with some ${\hat{\lambda }}$ and ${\hat{\sigma }}$. We need to prove that $({\hat{X}}, {\hat{Y}}) \in {{\bar{C}}}(\mathrm{I}',\mathrm{O}')$.

The idea of the proof is to consider two possibilities: ${\hat{\sigma }} > 0$ and ${\hat{\sigma }} = 0$. In the former case, the proof is straightforward. In the latter case, we first define a sequence of DMUs $\{(X_{(k)}, Y_{(k)})\}$, $k=1,2,...$, such that $(X_{(k)}, Y_{(k)}) \in T_{\mathrm{VRS}}^{\mathrm{R}} \subset C(\mathrm{I}',\mathrm{O}')$. In other words, $(X_{(k)}, Y_{(k)})$ satisfies conditions (2), $\forall k$. In addition, the sequence $\{(X_{(k)}, Y_{(k)})\}$ is constructed in such a way that the DMU $({\hat{X}}, {\hat{Y}})$ is its limit point. Therefore, $({\hat{X}}, {\hat{Y}}) \in {\bar{C}}(\mathrm{I}',\mathrm{O}')$, which completes the proof.

(i) Let ${\hat{\sigma }} > 0$. Using notation (4), where $\varphi =\psi =1/{{\hat{\sigma }}}$, define $(X',Y') = ( {\hat{X}} (1 / {{\hat{\sigma }}}), {\hat{Y}} (1 / {{\hat{\sigma }}}) )$. Dividing both sides of inequalities (8a), (8c), (8e), (8g), (8j) and (8l) by ${\hat{\sigma }}$, observe that $(X',Y')$ satisfies (2) with ${\hat{\lambda }}$ and is therefore in $T_{\mathrm{VRS}}^{\mathrm{R}}$. Because $({\hat{X}},{\hat{Y}}) = (X' ({\hat{\sigma }}), Y' ({\hat{\sigma }}))$, we have $({\hat{X}},{\hat{Y}}) \in C(\mathrm{I}',\mathrm{O}') \subseteq {{\bar{C}}}(\mathrm{I}',\mathrm{O}')$.

(ii) Let ${\hat{\sigma }}=0$. We now use the following extended notation for any DMU (X, Y):

$$\begin{aligned} (X, Y) = (X^{V'}, X^{V''}, X^{R'_1}, X^{R'_2}, X^{R''}, Y^{V'}, Y^{V''}, Y^{R'}, Y^{R''}). \end{aligned}$$

(22)

In (22), we use the single prime symbol for the measures in the sets $\mathrm{I}'$ and $\mathrm{O}'$, and the double prime for the measures in $\mathrm{I} \setminus \mathrm{I}'$ and $\mathrm{O} \setminus \mathrm{O}'$. For example, the subvector $X^{V'}$ includes inputs $i \in {\mathrm{I}^V} \cap {\mathrm{I}'}$, and $Y^{R''}$ includes outputs $r \in {\mathrm{O}^R} \setminus {\mathrm{O}'}$. The subvector $X^{R'_1}$ includes the inputs from the set ${\mathrm{I}^R} \cap {\mathrm{I}'}$ for which we have a finite bound in (1). The subvector $X^{R'_2}$ includes the inputs from ${\mathrm{I}^R} \cap {\mathrm{I}'}$ for which the bound in (1) is either not specified or is infinite.

Because ${\hat{\sigma }}=0$, inequalities (8a) and (8l) imply that ${{\hat{Y}}}^{V'}$ and ${{\hat{X}}}^{R'_1}$ are zero vectors. By (8i), there exists a $j' \in J$ such that ${\hat{\lambda }}_{j'} >0$. Then the inequality (8e) for $j=j'$ implies that ${{\hat{Y}}}^{R'}$ is also a zero vector. Using notation as in (22) and replacing the three zero subvectors by $\mathbf{0}$, state DMU $({\hat{X}}, {\hat{Y}})$ as follows:

$$\begin{aligned} ({\hat{X}}, {\hat{Y}}) = ({\hat{X}}^{V'}, {\hat{X}}^{V''}, \mathbf{0}, {\hat{X}}^{R'_2}, {\hat{X}}^{R''}, \mathbf{0}, {\hat{Y}}^{V''}, \mathbf{0}, {\hat{Y}}^{R''}). \end{aligned}$$

(23)

Define the sequence of DMUs $\{(X_{(k)}, Y_{(k)})\}$, $k=1,2,...$, as follows. Denote $J' = \{j \in J: {\hat{\lambda }}_j > 0 \}$. For each k, define

$$\begin{aligned} \begin{aligned}&X^{V'}_{(k)} = \sum \limits _{j \in J'} {{{\hat{\lambda }} _j} X_{j}^{V'}} + k {\hat{X}}^{V'}, \\&X^{R'_1}_{(k)} = \overline{\max }_{j \in J'} \{ X^{R'_1}_j \}, \quad X^{R'_2}_{(k)} = \overline{\max }_{j \in J'} \{ X^{R'_2}_j \} + k {\hat{X}}^{R'_2}, \end{aligned} \end{aligned}$$

where $\overline{\max }$ is the operator of component-wise maximum. For example, each component $X^{R'_1}_{(k),i}$ is defined as the maximum of the corresponding components $X^{R'_1}_{j,i}$, where $j \in J'$.

Let the other components of $(X_{(k)}, Y_{(k)})$ be the same as in $({\hat{X}}, {\hat{Y}})$. Note that component $X^{R'_1}_{(k)}$ satisfies (1). It is straightforward to verify that each DMU $(X_{(k)}, Y_{(k)})$ satisfies (2) with the same $\lambda ={\hat{\lambda }}$ and is therefore in $T_{\mathrm{VRS}}^{\mathrm{R}}$. Using notation (4), where $\varphi =\psi =1/k$, define $({\hat{X}}_{(k)}, {\hat{Y}}_{(k)}) =( X_{(k)}(1/k), Y_{(k)}(1/k))$, for any $k=1, 2, \dots$ We have:

$$\begin{aligned} \begin{aligned} \left( \begin{array}{l} {\hat{X}}_{(k)} \\ {\hat{Y}}_{(k)} \end{array} \right) = \left( \begin{array}{c} (1/k) \Bigl (\sum _{j \in J'} {{{\hat{\lambda }} _j} X_{j}^{V'}} \Bigr ) + {\hat{X}}^{V'}, {\hat{X}}^{V''}, \\ (1/k) \Bigl (\overline{\max }_{j \in J'} \{X^{R'_1}_j \}\Bigr ), \\ (1/k) \Bigl (\overline{\max }_{j \in J'} \{X^{R'_2}_j \}\Bigr ) + {\hat{X}}^{R'_2}, {\hat{X}}^{R''} \\ (1/k) {\hat{Y}}^{V'}, {\hat{Y}}^{V''}, (1/k) {\hat{Y}}^{R'}, {\hat{Y}}^{R''} \end{array} \right) . \end{aligned} \end{aligned}$$

By definition, $({\hat{X}}_{(k)}, {\hat{Y}}_{(k)}) \in {C}(\mathrm{I}',\mathrm{O}')$. DMU $({\hat{X}}, {\hat{Y}})$ stated in (23) is the limit point of $\{ ({\hat{X}}_{(k)}, {\hat{Y}}_{(k)}) \}$. Therefore, $({\hat{X}},{\hat{Y}}) \in {{\bar{C}}}(\mathrm{I}',\mathrm{O}')$. Cases (i) and (ii) imply that $W \subseteq {{\bar{C}}}(\mathrm{I}',\mathrm{O}')$. $\square$

Lemma 2

If Assumptions 1 and 2 are true, the supremum of program (11) is attained.

Proof of Lemma 2

By Theorem 2, the feasible region $\Pi$ of program (11) includes all triplets $\langle \lambda , \sigma , \eta \rangle$ that satisfy conditions (8) in which DMU (X, Y) is substituted by $\left( {{X_o},{Y_o}(\eta )} \right)$. It suffices to prove that the set $\Pi$ is closed and bounded. Conditions (8i) and (8n) imply $\lambda \in [0,1]^n$. As proved in Lemma 1, Assumption 1 implies that there exists a ${\bar{\sigma }} >0$ such that $\sigma \in [0,{\bar{\sigma }}]$. Then condition (8a) stated as $\sum _{j \in J} {{\lambda _j} \sigma Y_{jr}^V} \ge \eta Y_{or}^V$, for all $r \in {\mathrm{O}^V} \cap {\mathrm{O}'}$, and Assumption 2 imply that there exists an upper bound $M>0$ on $\eta$. Therefore, $\Pi$ is a bounded set. Furthermore, $\Pi$ is a closed set because it is defined by nonstrict inequalities and an equality with continuous functions on both sides. Because the objective function $\eta$ is continuous on $\Pi$, its supremum is attained at some $\langle \lambda ^*, \sigma ^*, \eta ^* \rangle \in \Pi$. $\square$

Proof of Theorem 3 and Corollary 1

Replace $T_{\mathrm{VRS}}^{\mathrm{R}}$ in program (9) by ${C}(\mathrm{I}',\mathrm{O}')$. For any feasible solution $\langle \varphi , \psi \rangle$ of program (9), we now have the ray of feasible solutions $\langle \alpha \varphi , \alpha \psi \rangle$, $\alpha > 0$, in the modified program. Because $\alpha \psi / \alpha \varphi = \psi / \varphi$, the supremum of $\psi / \varphi$ is not affected. The ratio $\psi / \varphi$ is constant along each ray $\langle \alpha \varphi , \alpha \psi \rangle$, $\alpha > 0$, and remains unchanged if we require $\varphi = 1$ and rename $\psi$ as $\eta$. Program (9) is now restated as (10).

We have proved that $\theta ^* = \eta '$. Let us prove that $\eta ' = \eta ^*$. Because ${C}(\mathrm{I}',\mathrm{O}') \subseteq {{\bar{C}}}(\mathrm{I}',\mathrm{O}')$, we have $\eta ' \le \eta ^*$. By Lemma 2, $\eta ^*$ in program (11) is attained. It now suffices to prove that $\left( {{X_o}, {Y_o}(\eta ^*)} \right) \in {C}(\mathrm{I}',\mathrm{O}')$, as stated in Corollary 1.

We first note that $\eta ^* \ge 1$. Because $\left( {X_o}, {Y_o}(\eta ^*) \right) \in {{\bar{C}}}(\mathrm{I}',\mathrm{O}')$, by Theorem 2, it satisfies conditions (8) in which we take $(X,Y) = \left( {X_o}, {Y_o}(\eta ^*) \right)$, with some ${\hat{\lambda }}$ and ${\hat{\sigma }}$. If we assume that ${\hat{\sigma }}=0$, conditions (8a) imply that $Y^V_{or} =0$, $\forall r \in {\mathrm{O}^V} \cap {\mathrm{O}'}$, and (8e) and (8i) imply that $Y^R_{or} =0$, $\forall r \in {\mathrm{O}^R} \cap {\mathrm{O}'}$, which contradicts Assumption 2. Therefore, ${\hat{\sigma }} >0$. Following (4), define DMU $({{\tilde{X}}}, {{\tilde{Y}}}) = \left( {{X_o} (1/{\hat{\sigma }}), {Y_o}(\eta ^*/{\hat{\sigma }})} \right)$. Then $({{\tilde{X}}}, {{\tilde{Y}}})$ satisfies (2) with ${\hat{\lambda }}$ and is in $T_{\mathrm{VRS}}^{\mathrm{R}}$. Because $(X_o, Y_o(\eta ^*)) = ({{\tilde{X}}} ({\hat{\sigma }}), {{\tilde{Y}}} ({\hat{\sigma }}))$, we have $\left( {{X_o}, {Y_o} (\eta ^*)} \right) \in {C}(\mathrm{I}',\mathrm{O}')$. $\square$

Proof of Theorem 4

By definition (Olesen et al. 2015), technology $T_{\mathrm{CRS}}^{\mathrm{P}}$ is the intersection of all sets in ${\mathbb {R}}_+^m \times {\mathbb {R}}_+^s$ that satisfy Axioms 1–4. Similarly, technology $T_{\mathrm{CRS}}$ is the intersection of all sets in ${\mathbb {R}}_+^m \times {\mathbb {R}}_+^s$ that satisfy Axioms 1, 2, 4 and the standard axiom of convexity (Banker et al. 1984). It suffices to prove that, under the assumptions of Theorem 4, Axiom 3 of selective convexity implies the standard axiom of convexity. (The opposite is always true). To be specific, let the single ratio measure be a ratio input. (The case of ratio output is similar and is not considered.) Consider any two DMUs $({{\tilde{X}}}^V,{{\tilde{X}}}^R,{{\tilde{Y}}}^V) \in T_{\mathrm{CRS}}^{\mathrm{P}}$ and $({\hat{X}}^V,{\hat{X}}^R,{\hat{Y}}^V) \in T_{\mathrm{CRS}}^{\mathrm{P}}$, and any scalar $\gamma \in [0,1]$. Define

$$\begin{aligned} (X^V_{\gamma },X^R_{\gamma },Y^V_{\gamma }) = \gamma ({{\tilde{X}}}^V,{{\tilde{X}}}^R,{{\tilde{Y}}}^V) + (1-\gamma ) ({\hat{X}}^V,{\hat{X}}^R,{\hat{Y}}^V). \end{aligned}$$

(24)

We need to prove that $(X^V_{\gamma },X^R_{\gamma },Y^V_{\gamma }) \in T_{\mathrm{CRS}}^{\mathrm{P}}$. As assumed, ${{\tilde{X}}}^R >0$ and ${\hat{X}}^R >0$. Then $X^R_{\gamma } >0$, and we can also define the two strictly positive scaling factors

$$\begin{aligned} {\tilde{\alpha }} = X^R_{\gamma } / {{\tilde{X}}}^R, \quad {\hat{\alpha }} = X^R_{\gamma } / {\hat{X}}^R. \end{aligned}$$

(25)

From (24), we have $\gamma {{\tilde{X}}}^R + (1-\gamma ) {\hat{X}}^R = X^R_{\gamma }$. Dividing both sides of this equality by $X^R_{\gamma } > 0$, noting (25) and rearranging, we have

$$\begin{aligned} \frac{\gamma }{{\tilde{\alpha }}} + \frac{(1-\gamma )}{{\hat{\alpha }}} = 1. \end{aligned}$$

(26)

Restate (24) as follows:

$$\begin{aligned} (X^V_{\gamma },X^R_{\gamma },Y^V_{\gamma }) = \frac{\gamma }{{\tilde{\alpha }}} ({{\tilde{\alpha }}} {{\tilde{X}}}^V,{{\tilde{\alpha }}} {{\tilde{X}}}^R, {{\tilde{\alpha }}} {{\tilde{Y}}}^V) + \frac{(1-\gamma )}{{\hat{\alpha }}} ({{\hat{\alpha }}} {\hat{X}}^V,{{\hat{\alpha }}} {\hat{X}}^R,{{\hat{\alpha }}} {\hat{Y}}^V). \end{aligned}$$

(27)

By Axiom 4, the scaled DMUs $({{\tilde{\alpha }}} {{\tilde{X}}}^V,{{\tilde{\alpha }}} {{\tilde{X}}}^R, {{\tilde{\alpha }}} {{\tilde{Y}}}^V)$ and $({{\hat{\alpha }}} {\hat{X}}^V,{{\hat{\alpha }}} {\hat{X}}^R,{{\hat{\alpha }}} {\hat{Y}}^V)$ are in $T_{\mathrm{CRS}}^{\mathrm{P}}$. Note that the scaling is defined in such away that the resulting ratio inputs are now equal. Indeed, from (25), ${{\tilde{\alpha }}} {{\tilde{X}}}^R = {{\hat{\alpha }}} {\hat{X}}^R = X^R_{\gamma }$. Taking into account (26) and (27), DMU $(X^V_{\gamma },X^R_{\gamma },Y^V_{\gamma })$ is a convex combination of these two scaled DMUs. By Axiom 3, $(X^V_{\gamma },X^R_{\gamma },Y^V_{\gamma }) \in T_{\mathrm{CRS}}^{\mathrm{P}}$. $\square$

Lemma 3

The incorporation of the additional inequality $\eta \ge 1$ in the constraints of programs (13) and (28) (as defined in the proof of Theorem 5) does not affect the value and attainability of their suprema ${\hat{\eta }}$ and $\eta ^*$, and does not affect any of their optimal solutions. If Assumption 3 is satisfied, in any of the feasible solutions $\langle \lambda , \sigma , \eta \rangle$ of the resulting programs, we have $\sigma >0$.

Proof of Lemma 3

The first statement follows from the fact that the solution $\langle \lambda ', \sigma ', \eta ' \rangle$, where $\lambda '$ is any vector with which DMU $(X_o,Y_o) \in T_{\mathrm{VRS}}^{\mathrm{R}}$ satisfies (2) and $\sigma '=\eta '=1$, is feasible in (13). Further, assume that in program (13) with the constraint $\eta \ge 1$, we have $\sigma =0$. Then (13j) and (13o) imply $\lambda = \mathbf{0}$. Then (13b) and (13k) contradict Assumption 3 and the inequality $\eta \ge 1$. Therefore, $\sigma > 0$. The proof for program (28) is similar. $\square$

Proof of Theorem 5

Using Theorem 2, we can restate program (11) as follows:

$$\begin{aligned} \begin{aligned}&\eta ^* = \max \ \eta \\&\text {subject to} \\&\sum \limits _{j \in J} {{\lambda _j} \sigma Y_{jr}^V} \ge \eta Y_{or}^V, \qquad \forall r \in {\mathrm{O}^V} \cap {\mathrm{O}'}, \\&\sum \limits _{j \in J} {{\lambda _j}Y_{jr}^V} \ge Y_{or}^V, \qquad \forall r \in {\mathrm{O}^V}\backslash {\mathrm{O}'}, \\&\sum \limits _{j \in J} {{\lambda _j} \sigma X_{ji}^V} \le X_{oi}^V, \qquad \forall i \in {\mathrm{I}^V} \cap {\mathrm{I}'}, \\&\sum \limits _{j \in J} {{\lambda _j}X_{ji}^V} \le X_{oi}^V, \qquad \forall i \in {\mathrm{I}^V}\backslash {\mathrm{I}'}, \\&{\lambda _j}(\sigma Y_{jr}^R - \eta Y_{or}^R) \ge 0, \qquad \forall j \in J,\quad \forall r \in {\mathrm{O}^R} \cap {\mathrm{O}'}, \\&{\lambda _j}(Y_{jr}^R - Y_{or}^R) \ge 0, \qquad \forall j \in J,\qquad \forall r \in {\mathrm{O}^R} \backslash {\mathrm{O}'}, \\&{\lambda _j}(\sigma X_{ji}^R - X_{oi}^R) \le 0, \qquad \forall j \in J,\qquad \forall i \in {\mathrm{I}^R} \cap {\mathrm{I}'}, \\&{\lambda _j}(X_{ji}^R - X_{oi}^R) \le 0, \qquad \forall j \in J,\qquad \forall i \in {\mathrm{I}^R}\backslash {\mathrm{I}'}, \\&\mathbf{{1}}^{\top } \lambda = 1, \\&\eta {Y^R_{or}} \le \sigma {{\bar{Y}}^R_r}, \qquad \forall r \in {\mathrm{O}^R} \cap {\mathrm{O}'}, \\&{Y^R_{or}} \le {{\bar{Y}}^R_r}, \qquad \forall r \in {\mathrm{O}^R} \backslash {\mathrm{O}'}, \\&{X^R_{oi}} \le \sigma {{\bar{X}}^R_i}, \qquad \forall i \in {\mathrm{I}^R} \cap {\mathrm{I}'}, \\&{X^R_{oi}} \le {{\bar{X}}^R_i}, \qquad \forall i \in {\mathrm{I}^R} \backslash {\mathrm{I}'}, \\&\lambda \ge \mathbf{{0}}, \sigma , \eta \ge 0. \end{aligned} \end{aligned}$$

(28)

By Theorem 3, the optimal value $\eta ^*$ of program (28) is attained. Incorporate the inequality $\eta \ge 1$ as a constraint in programs (13) and (28). Statement (ii) now follows from Lemma 3. Note that, with the constraint $\eta \ge 1$ incorporated (which guarantees $\sigma > 0$), any feasible solution $\langle \lambda ^*, \sigma ^*, \eta ^* \rangle$ of program (28) becomes a feasible solution $\langle {\hat{\lambda }}, \sigma ^*, \eta ^* \rangle$ of program (13), where ${\hat{\lambda }}= \lambda ^* \sigma ^*$, and vice versa. As noted, $\eta ^*$ is attained. Therefore, ${\hat{\eta }} = \eta ^*$ is also attained in program (13), which proves statement (i). To prove (iii), note that $\langle {\hat{\lambda }}, {\hat{\eta }}, {\hat{\sigma }} \rangle$ is feasible in (13) if and only if $\langle \lambda ', \varphi ', \psi ' \rangle$, where $\lambda ' = {\hat{\lambda }}/{\hat{\sigma }}$, $\varphi '=1/ {\hat{\sigma }}$ and $\psi ' = {\hat{\eta }} /{\hat{\sigma }}$, is feasible in (9). Because $\psi ' / \varphi ' = {\hat{\eta }}$ and, by statement (i), ${\hat{\eta }} = \theta ^*$, solution $\langle \lambda ', \varphi ', \psi ' \rangle$ is optimal in (9) if and only if $\langle {\hat{\lambda }}, {\hat{\eta }}, {\hat{\sigma }} \rangle$ is optimal in (13). $\square$

Appendix B: Comparison of cone ${{\bar{C}}}(\mathrm{I}, \mathrm{O})$ and technology $T_{\mathrm{CRS}}^{\mathrm{P}}$

The following example clarifies the difference between the full closed cone extension ${{\bar{C}}}(\mathrm{I}, \mathrm{O})$ of technology $T_{\mathrm{VRS}}^{\mathrm{R}}$ and technology $T_{\mathrm{CRS}}^{\mathrm{P}}$ of Olesen et al. (2015). It shows that (i) ${{\bar{C}}}(\mathrm{I}, \mathrm{O})$ does not satisfy Axiom 3 of selective convexity and (ii) ${{\bar{C}}}(\mathrm{I}, \mathrm{O}) \ne T_{\mathrm{CRS}}^{\mathrm{P}}$. For simplicity, we assume that there are no upper bounds (1) on the ratio input and output.

Let DMUs A and B in Table 9 be observed. DMU F is not observed and is obtained by scaling DMU A with $\alpha =2$. All three DMUs A, B and F belong to ${{\bar{C}}}(\mathrm{I}, \mathrm{O})$ and to $T_{\mathrm{CRS}}^{\mathrm{P}}$.

Table 9 DMUs in the example

By definition, technology $T_{\mathrm{CRS}}^{\mathrm{P}}$ satisfies Axiom 3 of selective convexity. Because both ratio input and output of DMUs B and F are equal, by Axiom 3, DMU G, constructed as the average of DMUs B and F, belongs to technology $T_{\mathrm{CRS}}^{\mathrm{P}}$. Let us show that $G \notin {{\bar{C}}}(\mathrm{I}, \mathrm{O})$ and, therefore, the closed cone ${{\bar{C}}}(\mathrm{I}, \mathrm{O})$ does not satisfy Axiom 3 of selective convexity.

We need to prove that conditions (8) in which $\mathrm{I'} = \mathrm{I}$ and $\mathrm{O'} = \mathrm{O}$ and DMU (X, Y) is G cannot be satisfied. Changing notation from $\lambda _1$ and $\lambda _2$ to $\lambda _A$ and $\lambda _B$, we have:

$$\begin{aligned}&1 \sigma \lambda _A + 4 \sigma \lambda _B \ge 3, \end{aligned}$$

(29a)

$$\begin{aligned}&1 \sigma \lambda _A + 4 \sigma \lambda _B \le 3,\end{aligned}$$

(29b)

$$\begin{aligned}&\lambda _A ( 1\sigma - 2) \ge 0, \end{aligned}$$

(29c)

$$\begin{aligned}&\lambda _A ( 1\sigma - 2) \le 0, \end{aligned}$$

(29d)

$$\begin{aligned}&\lambda _B ( 2\sigma - 2) \ge 0, \end{aligned}$$

(29e)

$$\begin{aligned}&\lambda _B ( 2\sigma - 2) \le 0, \end{aligned}$$

(29f)

$$\begin{aligned}&\lambda _A + \lambda _B = 1, \end{aligned}$$

(29g)

$$\begin{aligned}&\lambda _A, \lambda _B, \sigma \ge 0. \end{aligned}$$

(29h)

Let $\lambda _A =1$ and $\lambda _B=0$. Then (29a) and (29b) imply $\sigma = 3$. However, (29c) and (29d) imply $\sigma = 2$. Therefore, this case is impossible. Similarly, if $\lambda _A =0$ and $\lambda _B=1$, then (29a) and (29b) imply $\sigma = 3/4$, while (29e) and (29f) imply $\sigma = 1$. Therefore, this case is also impossible. Finally, assume that $\lambda _A > 0$ and $\lambda _B >0$. Then (29c) and (29d) imply $\sigma = 2$. This is inconsistent with conditions (29e) and (29f) which imply $\sigma = 1$.

We have shown that DMU $G \notin {{\bar{C}}}(\mathrm{I}, \mathrm{O})$. Therefore, the cone ${{\bar{C}}}(\mathrm{I}, \mathrm{O})$ does not satisfy Axiom 3 of selective convexity. In contrast, technology $T_{\mathrm{CRS}}^{\mathrm{P}}$ satisfies Axiom 3 by definition (Olesen et al. 2015). In particular, DMU G satisfies (12) with $\lambda _A = \lambda _B = 1/2$, $\sigma _A = 2$ and $\sigma _B = 1$. Therefore, $G \in T_{\mathrm{CRS}}^{\mathrm{P}}$. This also implies that ${{\bar{C}}}(\mathrm{I}, \mathrm{O}) \ne T_{\mathrm{CRS}}^{\mathrm{P}}$.

Appendix C: The data set used in the application is Sect. 8

Table 10 shows the inputs and outputs of all schools used in the application in Sect. 8. The latter section includes description of the inputs and outputs. Summary statistics for these data were given in Table 5.

Table 10 The data set used in the application