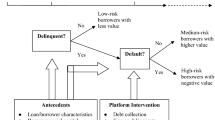
Abstract
Over the past years, studies shed light on how social norms and perceptions potentially affect loan repayments, with overtones for strategic default. Motivated by this strand of the literature, we incorporate collective social traits in predictive frameworks on credit card delinquencies. We propose the use of a two-stage framework. This allows us to segment a market into homogeneous sub-populations at the regional level in terms of social traits, which may proxy for perceptions and potentially unravelled behaviours. On these formed sub-populations, delinquency prediction models are fitted at a second stage. We apply this framework to a big dataset of 3.3 million credit card holders spread in 12 UK NUTS1 regions during the period 2015–2019. We find that segmentation based on social traits yields efficiency gains in terms of both computational and predictive performance compared to prediction in the overall population. This finding holds and is sustained in the long run for different sub-samples, lag counts, class imbalance correction or alternative clustering solutions based on individual and socio-economic attributes.
Graphical abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Over the last decades, and in particular after the global financial crisis, there has been a noteworthy rise in personal bankruptcy filings. This increase has alarmed politicians and economists alike, signifying the understanding of the potential explanatory factors of this phenomenon. However, most of the literature focuses on residential mortgages (among others, see Jackson & Kaserman, 1980; Campbell & Dietrich, 1983; Bernanke, 2008; Pinheiro & Igan, 2009; Elul et al., 2010; Guiso et al., 2013), with consumer debt being a “significantly under-studied asset class” (Gross & Souleles, 2002a). An early study by Jackson and Kaserman (1980) posited two alternative theories on why individuals may default on their mortgages. The first concerns whether they are able to make payments, focusing on macro or micro factors affecting the flow of individuals’ income. The second concerns whether they are willing to make payments. Following a cost–benefit analysis, this results in a decision as to whether individuals should discontinue the periodic payments, despite their ability to repay. This is of paramount importance, as strategic default is a de facto unobservable event; that is, an individual may have incentives to disguise himself as one that is seemingly unable to pay, making it very difficult to identify in the data (Guiso et al., 2013).
The role of moral and social determinants of strategic default has received increased attention in the literature in recent times. Using survey data from American households, Guiso et al. (2009) find that, when faced with negative equity concerns, about a quarter of mortgage defaults are estimated to be strategic. Gerardi et al. (2018) identify strategic motives to be present in about 38% of the households. Additionally, Guiso et al. (2009) find that: (1) people who consider it immoral to default, are 77% less likely to declare their intention to do so, and (2) people who know someone who defaulted, are 82% more likely to declare their intention to do so. This reflects a “neighbourhood” effect, a phenomenon that has been empirically and experimentally documented in numerous studies (Bradley et al., 2015; Chomsisengphet et al., 2018; Rabanal, 2014; Towe & Lawley, 2013). According to Guiso et al. (2009), this could relate to diminishing social stigma concerns as more and more people start filling for bankruptcy in one’s broader area, which could potentially turn into a contagious downward spiral of strategic defaults (Seiler et al., 2013). The latter authors note (p. 446) that “as social animals, people knowingly or otherwise look to their peers before reaching financially life-altering choices. As such, we recognize the need to factor into our understanding the social aspects of this critical decision”. Indeed, there may be social norms built into societies that accelerate or impede waves of such actions at large, and these could be inherently linked to perceptions about how individuals might be perceived by their surroundings. “[…] People who choose to continue paying their mortgages do so because of the negative emotional attributes, such as fear, shame and guilt that arise when they default […].” (Seiler et al., 2012, p. 200). On the same note, Brown et al. (2017) argue that “when a large part of the population considers strategic default to be immoral, even debtors without personal moral constraints may refrain from defaulting to avoid the social costs and stigma associated with defying the norm that debts should be paid”. So, strategic default, or lack thereof, could have overtones related to behavioural attributes and/or social norms that may be (un)consciously affecting one’s actions through endogenous social effects (Manski, 1993) that need to be modelled.
Indeed, studies present arguments in support of strategic default being driven by emotional considerations, social stigma, or lack of social capital (see Fay et al., 2002; Gross & Souleles, 2002a; Guiso et al., 2009, 2013; Li et al., 2020; Clark et al, 2021). According to White (2010), frustration, anger, and lack of trust to different parties–ranging from the government to financial institutions alike—could be a reason why one chooses to default strategically. Moreover, people may be more likely to inflict a loss on others when they suffer a loss themselves, particularly if they perceive this to be unfair (Fowler et al., 2005). This is also confirmed by Guiso et al. (2013) in the context of mortgage defaults. They show that people who trust banks less are more willing to walk away from their loan payments. Reasonably, counterparty trust in a borrower-lender relationship is of paramount importance, particularly in the aftermath of the global financial crisis. “[…] the nature of the lender-borrower relationship is changing and mortgage lenders are increasingly perceived as remote, profit-obsessed entities undeserving of moral concern” (Ryan, 2011, p. 1546). This argument may easily extend to the broader social environment through aspects of social trust and social capital, given the potential negative externality inflicted not only to the lender of distrust, but to the society at large. For example, Clark et al. (2021) find that, in communities with higher social capital, individuals may choose not to strategically default on their mortgage, in order not to pass on their negative externalities to the society at large.
Apart from considerations on emotions and social capital, social traits related to national culture have also been found to correlate with mortgage defaults (Tajaddini & Gholipour, 2017). These types of traits have been recently embodied in the finance literature (see Karolyi, 2016, for a recent review), following seminal studies from the field of psychology (see Hofstede, 2011, for a discussion).
From a theoretical point of view, individualism may be seen as the difference between a construal of the self as independent and a construal of the self as interdependent (Markus & Kitayama, 1991). Individualistic people tend to “enhance or protect their self‐esteem by taking credit for success and denying responsibility for failure” (Zuckerman, 1979, p. 245). In the context of externalities and inflicting loss to society at large, arguably, individualistic borrowers may face lower social stigma concerns and show higher tendency to default strategically (Seiler et al., 2012). Tajaddini and Gholipour (2017) show that borrowers from countries with high individualism may default more on their mortgages during both normal and turbulent periods. At the same time, individualism is linked to overconfidence in one’s ability (Heine et al., 1999) and overestimation of their predictions (Van den Steen, 2004). In the context of credit card utilisation, this could be crucial to consider when it comes to accumulating debt and repayment thereof in situations where one is unemployed yet believes that this situation will change. Turning to uncertainty avoidance -the degree to which the members of a society feel uncomfortable with uncertainty and ambiguity around them (Hofstede, 2011)-, societies characterised by high uncertainty avoidance are prone to being more risk averse (Riddle, 1992). This potentially suggests that more conservative and risk averse attitudes could regard the use of debt to finance different activities riskier and thus being avoided or moderated. In fact, uncertainty avoidance has been negatively associated with firm debt financing (Chui et al., 2002) and outstanding residential loans to GDP (Gaganis et al., 2020).
Most of the literature on social traits or perceptions and their effects on loan defaults focuses on residential mortgages. Reasonably, that is due to the inherent financial shortfall that is at stake and the potential of negative equity, thus presenting an opportunity where behaviour could develop towards a said externality. However, other consumer credit products, such as credit card loans -which are significantly under-studied- would be equally interesting to investigate. This is because credit cards are equally as sharp in terms of rates (Gross & Souleles, 2002a) and are forms of unsecured loans for institutions. Additionally, credit card utilisation may be seen as a proxy for (il)liquidity (Gross & Souleles, 2002b), which could potentially be a gateway into a first default, preceding the one of a mortgage (Clark et al., 2021). In addition, by benchmarking Federal Reserve data versus surveys on credit card account ownership and use, Gross and Souleles (2002a) find that households seem to underreport their credit card borrowing, which they attribute to households avoiding perceived stigma, this being an aspect that has been also associated to credit card default rates (Lopes, 2008).
Interestingly, modelling consumer credit risk has received increased attention due to the challenges it presents, with sophisticated mathematical and statistical models being used to assess the scoring of consumers and predict default events (see Hand, 2001; Thomas et al., 2001; Crook & Bellotti, 2010; Bellotti & Crook, 2013, for some interesting studies). From a modelling viewpoint, behaviour has been proxied through the use of factors such as, among others, the credit bureau score, outstanding account balance and repayments (Gross & Souleles, 2002a), payment amounts, annual percentage rate (APR), credit limit and number of transactions (Belotti & Crook, 2013).
However, to the best of our knowledge, no previous study has considered collective social traits in prediction frameworks to model consumer credit risk. As discussed earlier, these collective traits could explain why groups of people may behave or perceive situations differently, and thus lead to an (un)intentional default, which could later overspill into other loan products. What is more, these social traits may explain other behaviours that are being modelled in heterogeneously behavioural societies but may be best modelled in more homogeneous groups. This is because behaviours may be similarly expressed within those groups and reduce noise stemming from such heterogeneity.
In this study, we propose the use of a two-stage framework to improve credit card delinquency prediction. During the first stage, we use information stemming from social surveys to proxy for potentially unfolding behaviours through informal institutions, by segmenting customers into more homogeneous samples in terms of their social norms and perceptions. In particular, we use the answers to survey questions from the European Social Survey (ESS) at the NUTS-1 level,Footnote 1 and replicate social dimensions of behaviours and perceptions. This allows us to partition the market into NUTS-level homogeneous groups of customers. This is in line with approaches segmenting a population into subpopulations due to potentially different behaviours of the accountholders (see Thomas et al., 2001, for an abridged discussion in the context of consumer credit), hence developing segments of similar perceptions. Under the assumption that collective social norms and traits explain, interact or correlate with factors that explain values and thus potentially enveloped behaviours at a later stage, we then use—at a second stage—predictive modelling techniques to assess the probability of a credit card holder to default within each homogeneous cluster.
We illustrate the use of the proposed framework on a large dataset from the European Data Warehouse. This dataset is sourced from a British bank, covers the period 2015–2019, and contains more than 3.3 million unique credit card holders across different regions in the UK. We find a significant improvement in predictive accuracy compared to a standard model that does not incorporate this kind of information. This finding holds for different time horizons, alternative sub-samples, and correction for class imbalance.
2 Data and methodology
2.1 Data
2.1.1 Consumer credit defaults and control features
The primary source of our data is the European Data Warehouse (EDW), which is a repository of the universe of loan and bond level data under the European Central Bank’s loan level initiative.Footnote 2 EDW has recently started gaining traction, used in studies that examine various issues like the impact of collateral eligibility on credit supply (Van Bekkum et al., 2018), the association between asset transparency and credit supply (Balakrishnan & Ertan, 2019), the riskiness of securitised loans granted to small and medium enterprises (Bedin et al., 2019), the impact of lending standards on the default rates of residential loans (Gaudêncio et al., 2019), the determinants of mortgage default (Linn & Lyons, 2020), and the association between the energy efficiency of buildings and mortgage defaults (Billio et al., 2021). When it comes to credit card default data, there is only one case study by Licari et al. (2021) that uses the Markov decision process model to generate a dynamic credit limit policy.
For the purpose of this paper, we collect loan-level data of credit card asset-backed securities (ABS) transactions of 3.3 million UK credit card holders, during the period January 2015 to December 2019 from a British bank. To model delinquency, the dependent variable is of a dummy format and denotes whether an account holder has defaulted or not. We focus on default, which is one of the most important stages of credit card delinquency. In more detail, initially an account is said to be in arrears if it does not make the minimum payment. Subsequently, a default is said to occur when an account goes 3 months in arrears. For the late payment to be reported to the credit bureaus, the customer must normally be at least 30 days past the due date. Therefore, this might have implications for the credit report of the customer. Most importantly, should the customer default, this will appear in the customer’s credit file for a few years. Apparently, one could model earlier stages of delinquency (e.g. 30 days, 60 days) and look at the transition between states arrears in the preceding months. Alternatively, one could use information about past credit delinquency while modelling the probability of default. Unfortunately, historical information about either the payment behaviour of the customers or earlier stages of credit delinquency is not available in our case. Therefore, we focus on the 90 days default event, which is consistent with the definition of credit cards’ default used in past UK studies (Bellotti & Crook, 2012, 2013; Leow & Crook, 2016). Our approach not to consider the transition between states arrears in the preceding months is consistent with earlier studies (e.g. Leow & Crook, 2016).
The choice of independent features is relatively large according to the literature. Following Clark et al. (2021), we control for the natural logarithm of the outstanding balance and its squared term (in addition to the level, and as in Bellotti & Crook, 2013), the utilisation rate (%), and a dummy variable capturing whether the account holder has been unemployed over the last 12-month period. Similar to Belotti and Crook (2013), we also include the time (in months) the individual is with the credit card provider, as well as dummies on whether the individual is part-time employed, a student or retired, and whether one has been in arrears. Unfortunately, we do not have data on APR, credit bureau scores or income data as in their study, but we use the NUTS-1 region’s gross income figures from the ONS to capture the regional averages, as well as house prices (natural logarithm), and unemployment rates at the NUTS-1 level, both of which found to be great predictors of credit card delinquency (Gross & Souleles, 2002a, b). For an overview of the coverage and summary statistics of the key features, we refer the interested reader to the online supplementary appendix.
2.1.2 Features of interest: social traits
All the data that we use and describe below are from the European Social Survey (ESS). This is an academically-driven cross-national survey that has been conducted across Europe, with the intention to measure the attitudes, beliefs and behavioural patterns of population in this continent.Footnote 3 The surveys run on a biannual basis (rounds) starting from 2002 and are currently updated up to 2018. As our data span the period 2015–2019, we use rounds 7–9, which correspond to the years ending in 2014, 2016 and 2018. Although such traits have been argued to be slowly changing over time, or to be “sluggish” (Papadimitri et al., 2020), we use linear interpolation to estimate the social trait proxies (to be discussed below) for the years 2015 and 2017, and a naïve extrapolation from 2018 for the year 2019. We should, however, note that by using other means of interpolation (e.g. naïve interpolation over the entire period or a simple average of the three waves as a typical time-constant proxy), the main findings that we present in the following section remain the same. The answers to these surveys are available for several layers, i.e. at the country, or regional (different NUTS levels). As regards the United Kingdom, the ESS surveys delve up to the NUTS 1 level, corresponding to the following 12 major socio-economic UK regions: East Midlands, East of England, London, North East, North West, Northern Ireland, Scotland, South East, South West, Wales, West Midlands and Yorkshire and the Humber.
In what follows, we describe the proxies for the social traits that we use in this study. We should note at this point that we focus on these particular social traits for two reasons. First and foremost, we believe that they are of paramount importance for behavioural reasons that could be associated with credit card defaults as outlined in the literature and discussed in an earlier section of our manuscript. Second, cultural attributes like uncertainty avoidance and individualism are usually being measured at the country level with the use of the Hofstede's (1980) original scores. However, these scores have been estimated with data collected in the late 1960s and early 1970s. Therefore, the ESS data have allowed the re-construction of such indices in the European context for more recent years (Beilmann et al., 2018; Minkov & Hofstede, 2014). Most importantly, in the present study, instead of the country-level we delve down to the regional level in the spirit of Kaasa et al., (2013, 2014, 2016).
Social capital
Social capital is a wide term that has received extensive work in sociology, starting from seminal studies, such as that of Coleman (1988). The literature on how social capital facilitates economic decision making is extensive (see, e.g., Coleman, 1988; Fukuyama, 1996; Putnam et al., 1994). On the note of default, social capital has been inversely correlated to consumer bankruptcy (Agarwal et al., 2011; Clark et al., 2021), whilst empirical studies of microfinance, such as that of Karlan (2007) find delinquency to be lower in groups with greater social capital. An interesting discussion on the channels through which social capital affects default is presented in the recent study of Clark et al. (2021).
As in past studies we proxy for social capital with the use of social trust (e.g. Boulila et al., 2008; Kelly et al, 2009; Van Bastelaer & Leathers, 2006; Whiteley, 2000) as the latter is considered one of the key elements of social capital (Beilmann and Lilleoja (2015); Whiteley, 2000; and references therein). Additionally, the literature suggests that “Virtually every commercial transaction has within itself an element of trust” (Arrow, 1972, p. 357), and therefore trust can affect people’s economic decisions in several ways (Guiso et al., 2006). Financial contracts, in particular, have been characterized as the “ultimate trust-intensive contracts” (Guiso et al., 2004, p. 527), and trust has been associated positively with repayment performance in joint-liability seed loans (Van Bastelaer & Leathers, 2006), and negatively with the probability of default in peer-to-peer lending (Duarte et al., 2012). Following, among others, von dem Knesebeck et al. (2005) Poortinga (2006), Kelly et al. (2009), Beilmann and Lilleoja (2015), and Beilmann et al. (2018), we construct a generalized social trust index that takes into account: (1) generalized trust, (2) fairness, and (3) helpfulness. In particular, we develop an index (unweighted average) based on sub-indicators composed of the following dimensions: (1) an indicator of interpersonal trust that is based on the following question: “Generally speaking, would you say that most people can be trusted, or that you can’t be too careful in dealing with people?”; (2) an indicator of fairness that is based on the following question “Do you think that most people would try to take advantage of you if they got the chance, or would they try to be fair?”Footnote 4 and (3) an indicator of helpfulness that is based on the following question: “Would you say that most of the time people try to be helpful or that they are mostly looking out for themselves?”. For all three questions, answers range on a 0–10 scale, where 0 corresponds to a negatively associated outcome (e.g. “you can’t be too careful”, “most people would try to take advantage of me”, or “people mostly look out for themselves”) and 10 to a positive one (e.g. “most people can be trusted”, “most people would try to be fair”, or “people mostly try to be helpful”). Data are consolidated from ESS as the % of people in each NUTS 1 region that declared a particular option in this ordinal scale for each of these questions. So, for each NUTS 1 region, l, we aggregate this information to a typical answer expressed for that region as \({p}_{lr}\times {o}_{r}\), where \({o}_{r}\) is simply a vector of integers in the [0,10] space indexed by r, and \({p}_{lr}\) is a vector of the percentages of respondents declaring option r in that ordinal scale for region l.
Uncertainty avoidance
Uncertainty avoidance expresses the extent to which the members of a group feel threatened by the presence of uncertain or unknown situations and the degree of aversion to risk they may experience. Societies characterised by high uncertainty avoidance avoid unpredictable situations and are prone to being more risk averse (Riddle, 1992). This potentially suggests that more conservative and risk averse attitudes could regard the use of debt to finance different activities riskier and thus being avoided or moderated. This dimension has been negatively associated with firm debt financing (Chui et al., 2015), corporate risk-taking (Li et al., 2013), outstanding residential loans to GDP (Gaganis et al., 2020), as well as lower levels of firm debt (Arosa et al., 2014).
To develop a proxy for this dimension, we follow the study by Minkov and Hofstede (2014). They replicate the original and well-known uncertainty avoidance index of Hofstede (Hofstede, 1980) with the use of the following three ESS items: (1) how often the participants felt calm and relaxed in the past 2 weeks, (2) whether the participants think all laws should be obeyed strictly, and (3) how important it is to the participants to have a secure job. We develop the indicator using an approach similar to the case of the social capital abridged above, with the only exception being the length of the ordinal scale. In this case, the responses were expressed on a scale from 1 (e.g. “none or almost none of the time” or “a little like me”—depending on the question) to 5 (e.g. “all or almost all of the time”, or “very much like me”), with larger values expressing experience or preference towards higher calmness, law abeyance and a secure job.
Individualism
As discussed earlier, individualism can be associated with lower stigma concerns, higher overconfidence and overestimation of own predictions, (Seiler et al., 2012; Heine et al., 1999; Van den Steen, 2004; At the same time, the literature suggests that optimism and overconfidence are related to attitudes toward risk (Puri & Robinson, 2007; Pan & Statman, 2012) and debt growth (Lim & Bone, 2022). Most importantly, recent studies document that a culture of individualism is associated with risk-taking in household finance (Breuer et al., 2014), higher tendency to mortgage default (Tajaddini & Gholipour, 2017) and higher corporate risk-taking (Frijns et al., 2022).
Following Beilmann et al. (2018), we use the Schwartz's (2003) Openness to Change-Conservation framework to proxy for the individualism-collectivism dimension (Hofstede, 1980). As the authors suggest, we consider the following categories from Schwartz (2003): (1) Self-direction (proxied by questions related to the importance to “think up new ideas and be creative” and “to make own decisions and be free”), (2) Stimulation (proxied by questions related to the importance to “try new and different things in life” and “to seek adventures and have an exciting life”); (3) Security (proxied by questions related to the importance to “live in secure and safe surroundings”, and “that government is strong and ensures safety”); (4) Tradition (proxied by questions related to the importance to “be humble and modest, not draw attention” and “to follow traditions and customs”), (5) Benevolence (proxied by questions related to “helping people and caring for others’ well-being” and “to be loyal to friends and devoted to people close”); (6) Universalism (proxied by questions related to “people being treated equally and have equal opportunities”, “to understand different people”, and “to care for nature and environment”); (7) Achievement (proxied by questions related to “showing abilities and be admired” and “to be successful and that people recognize achievements”); (8) and, finally, Power (proxied by questions related to “being rich, have money and expensive things” and “to get respect from others”). For the calculation of Individualism, we follow the exact same approach to social trust. The answers to the questions from these categories are coded in such a way that higher values correspond to higher individualism and vice versa.Footnote 5
2.2 Methodology
The proposed framework is based on a two-stage procedure that potentially yields a twofold gain. First, it could yield gains in terms of the model’s predictive accuracy. Second, it could yield gains in terms of processing power in the presence of a big dataset since it is partitioned into smaller sub-samples. This framework consists of a customer segmentation procedure as a first step, followed by the development of predictive models within each segment. Customer segmentation can be very beneficial in improving the prediction accuracy in credit default models. In the words of Wu and Wang (2018, p. 198): “Directly using the whole raw data to build models could not only hurt the accuracy but also limit the explanation power of the models”. By separating a firm’s customer database into homogeneous clusters, permits a model to fit the data better and thus improve the overall model accuracy. This is in line with approaches segmenting a population into subpopulations due to potentially different behaviours of the accountholders (see Thomas et al., 2001, for an abridged discussion in the context of consumer credit), hence developing segments of similar perceptions. Lim and Sohn (2007, p. 427) mention that: “[…] presently available models apply single classification rule to every customer monotonously. This kind of classification model can be ineffective because a single classification rule cannot catch the fine nuance of various individual borrowers”.
Understandably, banking institutions have shown strong interest over the past years in exploring clustering techniques to strengthen their credit decisions (Bakoben et al., 2020; Doumpos et al., 2019; Lim & Sohn, 2007; Wu & Wang, 2018). Previous studies have used attributes at the individual level as model features to predict default. These include, among others, the gender, marriage, education and age, or information on past transactions, utilisation and default counts (Bakoben et al., 2020; Doumpos et al., 2019; Lim & Sohn, 2007; Wu & Wang, 2018) and how these change overtime—otherwise ‘behavioural scoring’ (Thomas et al., 2001).
In contrast, the proposal that we put forward in this study relies on a vast literature of collective attributes and perceptions that are shared across groups of a wider population and how using this information may potentially explain behaviours that could either be common across those groups, or commonly affect how these groups may act upon different situations presented to them. In a nutshell, the conjecture we make is that social traits can be quantified and forthwith be used as information on otherwise unobserved factors that segment a population into smaller segments. This may allow us to explain the unravelled behaviours better, compared to a non-segmented overall model applied to the whole population. As this approach relies on very few data points, it makes it computationally more efficient in the presence of a big dataset. Additionally, it has an edge in the presence of lack of information about individuals’ features, as it is the case here. At the same time, we should note that it could be combined with all previous proposals on clustering using individual attributes, potentially yielding even more significant benefits through a twofold segmentation—i.e. first segmenting the population into subpopulations based on collective social traits, and then segmenting each subpopulation into more clusters based on individual attributes.
2.2.1 Customer segmentation based on social traits
As far as segmentation is concerned, from a conceptual viewpoint, clustering is a straightforward procedure designed to create homogeneous segments based on (dis)similarity (Kaufman & Rousseeuw, 2009). From a methodological viewpoint, there are several alternative approaches one could follow depending on the data at hand and the assumptions about the proxy to be used to measure (dis)similarity (see Saxena et al., 2017, for a recent review on clustering techniques). Two of the most frequently used approaches in this strand of literature are the k-means and the k-medoids, the former being the most popular partitioning algorithm (Doumpos et al., 2019). Although computationally more demanding in big datasets in its originally proposed form (a faster algorithm has been proposed by Park & Jun, 2009), k-medoids has a distinct advantage, boasting lower sensitivity to outliers and reduced noise compared to the k-means (Arora et al., 2016). Furthermore, it uses an exemplar alternative -an actual region in this particular case study- as a typical example, compared to an otherwise non-existent average used as a cluster centre in the case of k-means, allowing for greater interpretability.
In this study, we use the k-medoids algorithm to group the 12 NUTS-1 regions of the UK -on the basis of the 3 social traits discussed in Sect. 2.1- into k clusters, using the Euclidean distance as the metric of dissimilarity. We originally apply the k-medoids to the average of the standardised social traits proxies, essentially treating the regions’ values as a cross-section instead of a panel. This helps us simplify the analysis in terms of training/validation at a later stage. However, by applying the clustering algorithm independently in every wave of responses in our sample, we find that the clustering solutions do not change across this period, which is potentially due to such traits evolving very slowly over time (Papadimitri et al., 2020). We also use 100 random starting solutions to find a better clustering result and address the dependence on the initial clustering of the regions (Doumpos et al., 2019). To find the “optimal” k value, we use the elbow method and the gap statistic (Tibshirani et al., 2001). Whilst these methods are arguably acceptable in industry practice, we also use the NbClust R package (Charrad et al., 2014) for robustness purposes. This provides 30 different indices to help determine the number of clusters in a data set, ultimately offering the best scheme overall.
It is important to note at this stage that, whilst we apply this customer segmentation procedure on UK NUTS 1 data, we postulate that this could be applicable to other samples accordingly, whether these concern other UK banks or time periods, or other countries for which social traits proxies can be estimated in a similar manner. We base our reasoning on prior literature supporting our conjecture that these social traits are important to consider and thus model from a behavioural point of view when it comes to delinquency, as discussed in Sect. 2.1.2. Elaborating on this from a modelling perspective, creating homogeneous clusters in terms of beliefs and norms may capture non-linearities in how individual control features may be affecting delinquency, as well as potentially capturing omitted information that correlates with social norms in a non-linear manner. However, a limitation at this stage remains the fact that we cannot test this conjecture unless more data become available to us.
2.2.2 Model fitting
Once the entire population is segmented into homogeneous clusters of UK regions, we fit a binary classification model of the general form: \({D}_{itc}={f}_{c}({{\varvec{X}}}_{it-l})\), where \({D}_{itc}\) is a binary response variable denoting whether customer i in cluster c in time \(t-l (l\) annotating the lag count in monthly frequency), is in default. This is being modelled as a cluster-specific function (for each cluster \(c=1,\dots ,k\)) of the individual or region-level features collected in the vector of covariates \({{\varvec{X}}}_{it-l}\), as these were discussed in Sect. 2.1, and NUTS 1 fixed effects. There is a variety of modelling options to choose for \(f\). The domain of Multicriteria Decision Analysis (MCDA) contains families that have been used in validating credit models, such as Value Function and Outranking Models (see Doumpos et al., 2019), with the former being the most commonly used. Indeed, MCDA approaches such as UTADIS (Zopounidis & Doumpos, 1999) have been widely used to forecast binary outcomes pertaining to default, mainly owed to its capacity to predict well, but also its transparency in enabling the credit analyst to calibrate them based on his/her expert domain knowledge, allowing for justification of the obtained results. In this paper, we use statistical and machine learning models that are widely used in failure prediction for two reasons. Firstly, they do not require assumptions that need the input of a decision-maker (e.g. a credit analyst), the presence of whom is absent on this occasion. Secondly, we do not have to assume restrictive rules such as monotonicity and linearity for some of these models, and thus allow for a more general setting. In this study, we use the Logistic Regression (LR) model to serve as a baseline estimation due to its popularity, and complement it with the Linear Discriminant Analysis (LDA), Support Vector Machines (SVM; Schölkopf et al., 2002; Vapnik, 1998) and AdaBoost algorithm (Freund & Schapire, 1997).
When one applies classification algorithms in a set of data that present a significant disproportion in one of the two categories (hereby the ‘default’ class), one is inherently faced with several types of issues (see Sun et al., 2009 and He & Garcia, 2009, for two detailed reviews). A handful of solutions have been proposed to this effect, depending on the computational or sample cost at stake. One solution that is particularly desirable in our case, given the nature of the size of the dataset we deal with, is a data-level sub-sampling approach. In more detail, class imbalance can be alleviated through either (conditionally or unconditionally) under-sampling the dominant class or over-sampling the rare one. Reasonably, under-sampling would be the ideal solution here. A similar solution is followed by Manthoulis et al. (2020), although in a multi-class setting. The authors use the random under-sampling boosting algorithm (RUSBOOST; Seiffert et al., 2009), which combines a data sampling scheme with the popular AdaBoost algorithm (Freund & Schapire, 1997) to deal with the class imbalance problem following an uninformative (random) under-sampling procedure, based on which weak learners are employed and combined.
As we would also like to yield comparable results with the other estimation approaches of the fitting function we employ, and to gain computational efficiency by reducing the big sample into more manageable and computationally less-demanding sub-samples, we under-sample the population to create balanced class (50–50) samples by uniformly under-sampling the dominant class in each cluster and use the new under-sampled cluster-populations to fit all four models (LR, LDA, SVM, BOOST). To ensure that there is no rare occurrence we under-sample 1000 times and present the average classification metrics (to be discussed below). In addition, and for robustness purposes, we also use a targeted under-sampling procedure using the ROSE (Lunardon et al., 2014; Menardi & Torelli, 2014) algorithm. In this case, under-sampling is not entirely random but uses a kernel density estimate of \({f}_{c}({{\varvec{X}}}_{it-l}|{D}_{itc})\) with an asymptotically optimal smoothing matrix H under the assumption of multivariate normality (see Menardi & Torelli, 2014, for a more detailed discussion). Whilst the classification results (to be presented in the following Section) are actually improved in the under-sampled space, we also tested whether they hold without delving into data-level sub-sampling solutions -due to issues with under-sampling in potentially removing important information (McCarthy et al., 2005). We obtain qualitatively similar results even if we do not under-sample, which are not reported or discussed here to conserve space.
2.2.3 Performance metrics and modelling options
To test whether there are significant gains from the proposed clustering approach, we fit the four different models for each sub-sample (cluster) and compare it to the responding fit in the entire population. We do so for different lag periods \(l\) up to a year (12 months), and apply a range of statistical metrics widely used in classification studies (Manthoulis et al., 2020; Tsagkarakis et al., 2021). These are:
-
$$\begin{aligned} &\mathrm{Sensitivity }\left(\mathrm{True\, Positive\, Rate}\right): SENS\\&\quad=\frac{No.\, of \,correctly \,classified \,defaulted \,individuals}{Total \,no. \,of \,defaulted \,individuals},\end{aligned}$$
-
$$\begin{aligned} &\mathrm{Specificity }\left(\mathrm{True \,Negative\,Rate}\right):SPEC\\&\quad=\frac{No.\, of\, correctly\, classified \,non-defaulted\, individuals}{Total \,no.\, of\, non-defaulted \,individuals},\end{aligned}$$
-
$$\mathrm{Average\, Classification\, Accuracy}:ACA=\frac{SENS+SPEC}{2},$$
-
$$\begin{aligned} &\mathrm{Overall \,Classification \,Accuracy}:OCA\\&\quad=\frac{No.\, of\, correctly\, classified \,defaulted\, individuals}{Total\, no.\, of \,defaulted\, \&\, non-defaulted \,individuals},\end{aligned}$$
-
$$\mathrm{Area \,Under \,the \,Curve}:AUROC=\frac{1}{{m}_{D}{m}_{ND}}{\sum }_{i\in D}{\sum }_{i\in ND}I\left[f\left({{\varvec{X}}}_{it-l}\right)>f\left({{\varvec{X}}}_{jt-l}\right)\right],$$
-
$$\mathrm{Kolmogorov}-\mathrm{Smirnov \,distance}:KS=\underset{0\le f\le 1}{\mathrm{max}}\left|{F}_{D}\left(f\right)-{F}_{ND}\left(f\right)\right|,$$
where \({m}_{D}{, m}_{ND}\) are the numbers of defaulted and non-defaulted individuals respectively, \(f\left({{\varvec{X}}}_{it-l}\right)\) is the output of the default prediction model in question for individual i in time t − l, and \(I[\cdot ]\) is a mapping function that takes the value ‘1’ if the classifier ranks the chosen defaulting instance higher than another non-defaulting one j and ‘0’ otherwise, and \({F}_{D}\) and \({F}_{ND}\) are the cumulative distribution functions of the scores for individuals that defaulted (D) or did not default (ND).
We use different lag counts, l, of the features X to test the predictive power of the model up to a year in advance (12 months).Footnote 6 Once we have obtained the under-sampled version (50–50 defaulted and non-defaulted individuals) of each cluster’s population, we split it using the 70–30 rule for training and testing, accordingly. Due to the panel structure of our data, we carefully construct bootstrapped samples by sampling with replacement from the set of unique individuals in the full dataset, similar to Tsagkarakis et al. (2021).
3 Results
Starting with the segmentation process and the implementation of the k-medoids algorithm, we chose the solution of k = 5, based on both the elbow method and the gap statistic (see Fig. 1). This is also the solution we would choose with the use of the NbClust algorithm, based on a variety of indices and clustering solutions. We provide an abridged figure of the average performance benefits for different values of k in the online supplementary appendix to conserve space in the manuscript. The regional clusters for k = 5 are formed as follows: North East, East Midlands, East of England and the South East form Cluster 1; Northern Ireland forms Cluster 2 on its own; West Midlands, Yorkshire and the Humber, North West and Wales form Cluster 3; South West and Scotland form Cluster 4, and the English Capital, London, forms Cluster 5.
Deciding on the optimal k value. The above figure shows the total within sum of squares (left) and the gap statistic (right) according to the different clustering solutions on the basis of social traits. Clustering algorithm is k-medoids, with Euclidean distance metric and 100 random starting solutions, applied to the standardised three social traits proxies (average of waves in the period 2014–2018) of the 12 NUTS 1 UK regions. Chosen solution is k = 5
The solution is graphically illustrated in Fig. 2 as projections in the space of social traits (two principal components of the social traits in the left part of the graph) and the map of the UK (right part). In addition, Table 1 shows the chosen clustering solution and the social traits’ values for each medoid representing the cluster. Among the medoids, the cluster characterised by the South West appears to have the dominant social capital and collectivistic value, but also the lowest uncertainty avoidance value. Northern Ireland presented the highest value in terms of uncertainty avoidance, whilst the UK capital holds the highest value in the individualism dimension.
Turning to the second stage of the framework, we employ the four models mentioned in Sect. 2.2.2. According to the results, the performance metrics are always consistently better in the clusters compared to the overall model with NUTS-1 fixed effects.Footnote 7 The BOOST algorithm tends to yield superior results under all settings, compared to the other three models. Therefore, to conserve space, we only report the BOOST findings for a variety of modelling options (l = 1, 4, 8, 12) and performance metrics. The results are reported in Table 2. To render the results comparable, we keep accountholders with at least 12 months’ data. These are the average metrics from the 1000 replications conducted to alleviate potential sampling issues due to the under-sampling of the major category. It appears that the sub-populations, based on the social traits, present increasingly superior results as the lag-count increases to 12 months, particularly evident in the KS performance metric. In particular, for all but the KS performance metric, the average difference in performance jumps from just under a marginal 4% gain, when l = 1, to roughly under 13% for l = 12. In the case of the KS metric, the results present an 8.8% gain for l = 1 that reaches a high of 34.82% average gain when l = 12. These average gains are delineated in Fig. 3. To ensure that the results are not driven by homogeneity that could be simplified even more –from a behavioural or other viewpoint– if we run those models for each NUTS 1 region independently, we perform the following test. We compare the results of Clusters 1 (North East, East Midlands, East of England and the South East), 3 (West Midlands, Yorkshire and the Humber, North West and Wales) and 4 (South West and Scotland) versus the individual regions that they contain. With the exception of the South East, all other regions perform worse on their own than the results obtained as clusters. The average difference is 4.9% (South East excluded, it performs better on its own than when it is part of a cluster by 1.4%), ranging between 0.6% and 6.1%. One potential explanation for this is that the South East would form its own cluster in the next best k-medoids solution, i.e. should we had chosen k = 6 instead of 5 as a clustering solution (see Fig. 2).
Average performance benefits. This figure summarises the results of Table 2, showing the average increase (taking into account all clusters) in classification accuracy versus the full sample classification metrics, as a function of the metrics and lag count (l). Metrics shown are the Kolmogorov–Smirnov distance (KS), Area Under the Curve (AUROC), Overall Classification Accuracy (OC), Average Classification Accuracy (ACA), Specificity (SPEC) and Sensitivity (SENS). For more details on the performance metrics, see Sect. 2.2.3. Results concern the best-performing, BOOST algorithm
In addition, we compare the improvement from clustering the population based on the NUTS 1 social traits to the improvement from clustering the population based on the features included in the model, \({{\varvec{X}}}_{it-l}\), as in a regular two-stage framework. We attempt to cluster individuals based on the reduced sub-sample (50–50 split between defaulted and non-defaulted individuals) due to computational constraints,Footnote 8 but to avoid sampling issues, we calculate the average total within sum of square (WSS) in 1000 under-sampling random scenarios and construct the scree plot presented in Fig. 4. It appears that k = 5 happens to be again the preferred solution when taking the average WSS metric into account. Since we have an identical k value, we examine the similarities in the clustering solution between the use of social traits at the NUTS 1 level and the use of both the individual and NUTS 1 socio-economic data. In particular, we look at what percentage of the observations belonging to k = 1, 2,…,5 based on our clustering solution are bundled together in just one but the main cluster in the alternative clustering solution.Footnote 9 We find that 68.70% of the observations in Cluster 1, 61.23% of the observations in Cluster 2, 99.11% of the observations in Cluster 3, 39.81% of observations in Cluster 4 and 99.91% of observations in Cluster 4 are grouped together in the alternative clustering solution.
Deciding on the optimal k value. This figure shows the average total within sum of squares (WSS) in 1000 random under-sampling scenarios as a function of different values of k when k-medoids is applied on the set of individual and regional features, \({{\varvec{X}}}_{it-l}.,\) as an alternative clustering solution to the social traits
We now replicate the analysis for the clustering solution that is based on the features \({{\varvec{X}}}_{it-l}\), and we compare the average performance gains to the ones we presented in Fig. 3. The results appear in Table 3. In the short term (l = 1), clustering on the basis of individual and socio-economic features instead of social traits at the NUTS 1 level yields more significant improvements compared to the overall model. However, this is reversed for all other lag values (l = 4, 8, 12), and is particularly improved for l = 12. It appears that clustering on the basis of social traits continues yielding sustained improvements, even for l = 12, whilst clustering on the basis of individual and other regional features yields significant improvements for up to l = 8 and diminishes afterwards (always compared to the overall model). We should hereby note that, a potential drawback of the alternative clustering solution is the lack of better quality data at the individual level (e.g. the interest the account carries, the credit score, the gender, education, personal income etc.), which could potentially make up for this lost performance. Furthermore, we only observe results from data stemming from a single bank in the time period 2015–2019. It would be of interest to see whether these also hold for either a different bank in the UK, a different time period, or perhaps a different country.
4 Conclusions
Over the past years, a strand of literature has attempted to shed light on how behavioural factors and social norms and perceptions may potentially affect loan repayments, with overtones for strategic default. Within this context, several studies link social stigma, shame, guilt, trust and other social considerations with the possibility to deter or ease individuals’ decisions to default. However, these studies are of an explanatory nature and no prior study has attempted to use this information in predictive frameworks.
To close this gap, we propose a two-stage predictive framework to predict credit card delinquencies. In more detail, considering seminal studies on the quantification of informal institutions, and recent studies replicating these proxies at a regional level in Europe, we compute proxies for three social traits that potentially affect behaviours leading to and perceptions affecting consumer credit default. These are, namely, social capital, individualism and uncertainty avoidance at the NUTS 1 level. Using this information at a first stage permits the segmentation of a market into sub-populations that are homogeneous in terms of their beliefs and social norms. Then alternative predictive models are fitted in each of the homogeneous clusters.
We apply the proposed framework to an illustrative case study using monthly data on 3.3 million credit card holders from a UK bank during the period 2015–2019. We find a significant improvement in predictive accuracy in the homogeneous clusters compared to the overall population that holds for different modelling options as to the lags, alternative sub-samples, and correction for class imbalance. According to the results, predictive capacity increases and is sustained for predictions up to 12 months in advance of the default event. Additionally, we compare our results with those of traditional two-stage frameworks, which rely on clustering solutions based on individual and socio-economic data. We find that, in the short term (l = 1), clustering solution based on individual traits yields better results compared to the overall population yet, in the longer run (l = 4, 8 and 12), clustering based on social traits yields better and more sustained results compared to the population prediction model.
As any empirical study, our work is not without its limitations, and we suggest here some avenues for future research. For example, we do not have qualitative information about the risk management framework of the lender or its local loan officers. Perhaps that could further improve the clustering solution. In addition, our study is constrained to a single country and bank, which implies that there is potentially selection bias in our sample, or that this may not necessarily be generalisable in others. Therefore, future research could also investigate alternative country case studies (or a cross-country setting), alternative time periods and samples, or cardinal criteria, such as the loss given default. Additionally, in the presence of more data, such as interest rates charged, credit bureau scores, or other customer-related attributes, it would be interesting to see if more meaningful sub-clusters could be formed within the homogeneous groups on the basis of social traits, enhancing the two-step into a three-step framework. On the same note, it would be interesting to observe if and how these relationships change by controlling for other loan products the customers may have with the bank, as well as if they have pledged for collateral, or whether loss given default is chosen as a cardinal measure to predict instead of the binary default variable.
Furthermore, one could claim that assessing creditworthiness with region-based social traits (as opposed to individual characteristics) can raise ethical concerns. While this might not necessarily be the case, future research may consider issues raised in the literature on discrimination in the credit market (Beck et al., 2018; Cozarenco & Szafarz, 2018; Delis & Papadopoulos, 2019) and the consequences of automatic creditworthiness assessment, in the context of the risk of algorithmic discrimination (Williams et al., 2018). Such an attempt could bring together the quantitative modelling literature with the business ethics literature. Last, but not least, whilst we have hereby resorted to the use of machine learning algorithms in line with industry practices on delinquency prediction, other MCDA methods could be used in the presence of a decision-maker, both for classification and clustering. For instance, the use of rough sets theory (Greco et al., 2001) or value function models such as UTADIS (Zopounidis & Doumpos, 1999), in combination with MCDA clustering algorithms (Meyer and Olteanu, 2013) -even accounting for stochastic preferences (Ishizaka et al., 2021)- could be chosen to replace the existing two-stage framework with the aid of a decision-maker.
Notes
ESS provides data that, in some cases, delve down to the NUTS-3 level. In our case, we construct these indicators at the NUTS-1 level, as this is the lower level of data we could find for the United Kingdom.
Following the outburst of the 2007 financial crisis, the need for transparency and a centralised reporting system of the European Securitisation was essential. In order to fulfil this need the European Central Bank established the loan-level initiative in 2010, which mandates the disclosure of information about the quality of the underlying assets of ABS eligible loans. Hence, market participants are since able to assess the content and quality of a pool of loans prior to the investment process. The EDW was launched in 2011 in order to enable the collection and validation of loan-level information for asset-backed securities (ABS). Data coverage commences from 2012 onwards and covers transactions from originators situated across ten different countries. The loans included in the database are used for collateral and are eligible for securitised loans for a variety of asset classes, namely RMBS, Auto Asset Backed securities, SME, Consumer, leasing, credit card, and CMBS. A detailed discussion of the loan-level initiative can be found in the following link: https://www.ecb.europa.eu/paym/coll/loanlevel/shared/files/ABS_loan_level_initiative_letter.pdf?5b9d73f93d1635573d1408591c02624d. For a detailed overview of loan-level data templates, including the variable description of each asset class provided by EDW is provided by the ECB and accessed by the following link: https://www.ecb.europa.eu/paym/coll/loanlevel/transmission/html/index.en.html.
For a fully detailed documentation on the conducted surveys, we refer the interested reader to their official website: https://www.europeansocialsurvey.org/data/.
For more information on the calculation process, see Beilmann et al. (2018).
In additional analyses, we tested the results with lag counts of up to 24 months, finding qualitatively similar results that, although decline in accuracy overall, improvement in classification is still present. To conserve space, we do not report all the specifications, but these are available from the authors upon request.
In alternative specifications, we employ NUTS 2 or 3 fixed effects, or replace the NUTS 1 fixed effects with cluster fixed effects according to the solution employed in this study (k = 5).
Indeed, in trying to achieve a clustering solution in the whole population, we encountered a few issues with the ‘cluster’ package implementing the PAM algorithm in R and noticed a significant slowdown due to the required memory.
That is equivalent to creating a 5 × 5 confusion matrix, columns being the social traits clustering and rows the alternative one, normalised by the column sum and selecting the max value per column.
References
Agarwal, S., Chomsisengphet, S., & Liu, C. (2011). Consumer bankruptcy and default: The role of individual social capital. Journal of Economic Psychology, 32(4), 632–650.
Arora, P., & Varshney, S. (2016). Analysis of k-means and k-medoids algorithm for big data. Procedia Computer Science, 78, 507–512.
Arosa, C. M. V., Richie, N., & Schuhmann, P. W. (2014). The impact of culture on market timing in capital structure choices. Research in International Business and Finance, 31, 178–192.
Arrow, K. J. (1972). Gifts and exchanges. Philosophy & Public Affairs, 1, 343–362.
Bakoben, M., Bellotti, T., & Adams, N. (2020). Identification of credit risk based on cluster analysis of account behaviours. Journal of the Operational Research Society, 71(5), 775–783.
Balakrishnan, K., & Ertan, A. (2019). Bank asset transparency and credit supply. Review of Accounting Studies, 24(4), 1359–1391.
Beck, T., Behr, P., & Madestam, A. (2018). Sex and credit: Do gender interactions matter for credit market outcomes? Journal of Banking & Finance, 87, 380–396.
Bedin, A., Billio, M., Costola, M., & Pelizzon, L. (2019). Credit scoring in SME asset-backed securities: An Italian case study. Journal of Risk and Financial Management, 12(2), 89.
Beilmann, M., Kööts-Ausmees, L., & Realo, A. (2018). The relationship between social capital and individualism–collectivism in Europe. Social Indicators Research, 137(2), 641–664.
Beilmann, M., & Lilleoja, L. (2015). Social trust and value similarity: The relationship between social trust and human values in Europe. Studies of Transition States and Societies, 7, 19–30.
Bellotti, T., & Crook, J. (2012). Loss given default models incorporating macroeconomic variables for credit cards. International Journal of Forecasting, 28, 171–182.
Bellotti, T., & Crook, J. (2013). Forecasting and stress testing credit card default using dynamic models. International Journal of Forecasting, 29(4), 563–574.
Bernanke, B. S. (2008). Mortgage delinquencies and foreclosures, speech at the Columbia Business School, 32nd annual dinner.
Billio, M., Costola, M., Pelizzon, L., & Riedel, M. (2021). Buildings’ energy efficiency and the probability of mortgage default: The Dutch case. The Journal of Real Estate Finance and Economics. https://doi.org/10.1007/s11146-021-09838-0
Boulila, G., Bousrih, L., & Trabelsi, M. (2008). Social capital and economic growth: Empirical investigations on the transmission channels. International Economic Journal, 22, 399–417.
Bradley, M. G., Cutts, A. C., & Liu, W. (2015). Strategic mortgage default: The effect of neighborhood factors. Real Estate Economics, 43, 271–299.
Breuer, W., Riesener, M., & Salzmann, A. J. (2014). Risk aversion vs. individualism: What drives risk taking in household finance? European Journal of Finance, 20, 446–462.
Brown, M., Schmitz, J., & Zehnder, C. (2017). Social norms and strategic default. University of St. Gallen, School of Finance Research Paper (2016/08).
Campbell, T. S., & Dietrich, J. K. (1983). The determinants of default on insured conventional residential mortgage loans. The Journal of Finance, 38(5), 1569–1581.
Chomsisengphet, S., Kiefer, H., & Liu, X. (2018). Spillover effects in home mortgage defaults: Identifying the power neighbor. Regional Science and Urban Economics, 73, 68–82.
Chui, A. C., Lloyd, A. E., & Kwok, C. C. (2002). The determination of capital structure: Is national culture a missing piece to the puzzle? Journal of International Business Studies, 33(1), 99–127.
Clark, B., Hasan, I., Lai, H., Li, F., & Siddique, A. (2021). Consumer defaults and social capital. Journal of Financial Stability, 53, 100821.
Coleman, J. S. (1988). Social capital in the creation of human capital. American Journal of Sociology, 94, S95–S120.
Cozarenco, A., & Szafarz, A. (2018). Gender biases in bank lending: Lessons from microcredit in France. Journal of Business Ethics, 147(3), 631–650.
Crook, J., & Bellotti, T. (2010). Time varying and dynamic models for default risk in consumer loans. Journal of the Royal Statistical Society: Series A (statistics in Society), 173(2), 283–305.
Delis, M., & Papadopoulos, P. (2019). Mortgage lending discrimination across the US: New methodology and new evidence. Journal of Financial Services Research, 56, 341–368.
Doumpos, M., Lemonakis, C., Niklis, D., & Zopounidis, C. (2019). Applications to corporate default prediction and consumer credit. In Analytical techniques in the assessment of credit risk (pp. 77–98). Springer.
Duarte, J., Siegel, S., & Young, L. (2012). Trust and credit: The role of appearance in peer-to-peer lending. Review of Financial Studies, 25, 2455–2484.
Elul, R., Souleles, N. S., Chomsisengphet, S., Glennon, D., & Hunt, R. (2010). What" triggers" mortgage default? American Economic Review, 100(2), 490–494.
Fay, S., Hurst, E., & White, M. J. (2002). The household bankruptcy decision. American Economic Review, 92(3), 706–718.
Fowler, J. H., Johnson, T., & Smirnov, O. (2005). Egalitarian motive and altruistic punishment. Nature, 433(7021), E1–E1.
Frijns, B., Hubers, F., Kim, D., Roh, T-.Y., & Xu, Y., (2022), National culture and corporate risk-taking around the world. Global Finance Journal, 52, Article 100710.
Fukuyama, F. (1996). Trust: The social virtues and the creation of prosperity. Simon and Schuster.
Gaganis, C., Hasan, I., & Pasiouras, F. (2020). National culture and housing credit. Journal of Empirical Finance, 56, 19–41.
Gaudêncio, J., Mazany, A., & Schwarz, C. (2019). The impact of lending standards on default rates of residential real-estate loans. ECB occasional paper (220).
Gerardi, K., Herkenhoff, K. F., Ohanian, L. E., & Willen, P. S. (2018). Can’t pay or won’t pay? Unemployment, negative equity, and strategic default. The Review of Financial Studies, 31(3), 1098–1131.
Greco, S., Matarazzo, B., & Slowinski, R. (2001). Rough sets theory for multicriteria decision analysis. European Journal of Operational Research, 129(1), 1–47.
Gross, D. B., & Souleles, N. S. (2002a). An empirical analysis of personal bankruptcy and delinquency. The Review of Financial Studies, 15(1), 319–347.
Gross, D. B., & Souleles, N. S. (2002b). Do liquidity constraints and interest rates matter for consumer behavior? Evidence from credit card data. The Quarterly Journal of Economics, 117(1), 149–185.
Guiso, L., Sapienza, P., & Zingales, L. (2009). Moral and social constraints to strategic default on mortgages (No. w15145). National Bureau of Economic Research.
Guiso, L., Sapienza, P., & Zingales, L. (2004). The role of social capital in financial development. American Economic Review, 94(3), 526–556.
Guiso, L., Sapienza, P., & Zingales, L. (2006). Does culture affect economic outcomes? Journal of Economic Perspectives, 20, 23–48.
Guiso, L., Sapienza, P., & Zingales, L. (2013). The determinants of attitudes toward strategic default on mortgages. The Journal of Finance, 68(4), 1473–1515.
Hand, D. J. (2001). Modelling consumer credit risk. IMA Journal of Management Mathematics, 12(2), 139–155.
He, H., & Garcia, E. A. (2009). Learning from imbalanced data. IEEE Transactions on Knowledge and Data Engineering, 21(9), 1263–1284.
Heine, S. J., Lehman, D. R., Markus, H. R., & Kitayama, S. (1999). Is there a universal need for positive self-regard? Psychological Review, 106(4), 766.
Hofstede, G. (1980). Culture’s consequences: International differences in work-related values. Sage Publications.
Hofstede, G. (2011). Dimensionalizing cultures: The Hofstede model in context. Online Readings in Psychology and Culture, 2(1), 2307–919.
Ishizaka, A., Lokman, B., & Tasiou, M. (2021). A stochastic multi-criteria divisive hierarchical clustering algorithm. Omega, 103, 102370.
Jackson, J. R., & Kaserman, D. L. (1980). Default risk on home mortgage loans: A test of competing hypotheses. Journal of Risk and Insurance, 47, 678–690.
Kaasa, A., Vadi, M., & Varblane, U. (2013). European Social Survey as a source of new cultural dimensions estimates for regions. International Journal of Cross Cultural Management, 13, 137–157.
Kaasa, A., Vadi, M., & Varblane, U. (2014). Regional cultural differences within European countries: Evidence from multi-country surveys. Management International Review, 54, 825–852.
Kaasa, A., Vadi, M., & Varblane, U. (2016). A new dataset of cultural distances for European countries and regions. Research in International Business and Finance, 37, 231–241.
Karlan, D. S. (2007). Social connections and group banking. The Economic Journal, 117(517), F52–F84.
Kaufman, L., & Rousseeuw, P. J. (2009). Finding groups in data: An introduction to cluster analysis (Vol. 344). Wiley.
Kelly, B. D., Davoren, M., Mhaolain, A. N., Green, E. G., & Casey, P. (2009). Social capital and suicide in 11 European countries: An ecological analysis. Social Psychiatry and Epidemiology, 44, 971–977.
Leow, M., & Crook, J. (2016). The stability of survival model parameter estimates for predicting the probability of default: Empirical evidence over the credit crisis. European Journal of Operational Research, 249, 457–464.
Li, K., Griffin, D., Yue, H., & Zhao, L. (2013). How does culture influence corporate risk-taking? Journal of Corporate Finance, 23, 1–22.
Li, L., Ucar, E., & Yavas, A. (2020). Social capital and mortgage delinquency. The Journal of Real Estate Finance and Economics. https://doi.org/10.1007/s11146-020-09775-4
Licari, J., Loiseau-Aslanidi, O, Tolstova, V., & Sadat, M. (2021). Determining the optimal credit card limit. Case Study, February 2021. Moody’s Analytics. Available at: https://www.moodysanalytics.com/-/media/article/2021/Determining-the-Optimal-Dynamic-Credit-Card-Limit.pdf
Lim, S. S. & Bone, M. (2022). Optimism, debt accumulation, and business growth. Journal of Behavioral and Experimental Economics, 97, Article 101828.
Lim, M. K., & Sohn, S. Y. (2007). Cluster-based dynamic scoring model. Expert Systems with Applications, 32(2), 427–431.
Linn, A., & Lyons, R. C. (2020). Three triggers? Negative equity, income shocks and institutions as determinants of mortgage default. The Journal of Real Estate Finance and Economics, 61(4), 549–575.
Lunardon, N., Menardi, G., & Torelli, N. (2014). ROSE: A package for binary imbalanced learning. R Journal, 6(1), 79.
Malika, C., Ghazzali, N., Boiteau, V., & Niknafs, A. (2014). NbClust: An R package for determining the relevant number of clusters in a data set. Journal of Statistical Software, 61, 1–36.
Manski, C. F. (1993). Identification of endogenous social effects: The reflection problem. The Review of Economic Studies, 60(3), 531–542.
Manthoulis, G., Doumpos, M., Zopounidis, C., & Galariotis, E. (2020). An ordinal classification framework for bank failure prediction: Methodology and empirical evidence for US banks. European Journal of Operational Research, 282(2), 786–801.
Markus, H. R., & Kitayama, S. (1991). Culture and the self: Implications for cognition, emotion, and motivation. Psychological Review, 98(2), 224.
Menardi, G., & Torelli, N. (2014). Training and assessing classification rules with imbalanced data. Data Mining and Knowledge Discovery, 28(1), 92–122.
Minkov, M., & Hofstede, G. (2014). A replication of Hofstede’s uncertainty avoidance dimension across nationally representative samples from Europe. International Journal of Cross Cultural Management, 14(2), 161–171.
Pan, C. H., & Statman, M. (2012). Questionnaires of risk tolerance, regret, overconfidence, and other investor propensities. Journal of Investment Consulting, 13, 54–63.
Papadimitri, P., Pasiouras, F., & Tasiou, M. (2020). Do national differences in social capital and corporate ethical behaviour perceptions influence the use of collateral? Cross-country evidence. Journal of Business Ethics, 172, 1–20.
Park, H. S., & Jun, C. H. (2009). A simple and fast algorithm for K-medoids clustering. Expert Systems with Applications, 36(2), 3336–3341.
Pinheiro, M., & Igan, D. O. (2009). Exposure to real estate losses; Evidence from the US Banks (No. 2009/079). International Monetary Fund.
Poortinga, W. (2006). Social capital: An individual or collective resource for health? Social Science & Medicine, 62, 292–302.
Puri, M., & Robinson, D. T. (2007). Optimism and economic choice. Journal of Financial Economics, 86, 71–99.
Putnam, R. D., Leonardi, R., & Nanetti, R. Y. (1994). Making democracy work. Princeton University Press.
Rabanal, J. P. (2014). Strategic default with social interactions: A laboratory experiment. In Experiments in financial economics. Emerald Group Publishing Limited.
Riddle, D. (1992). Leveraging cultural factors in international service delivery. Advances in Services Marketing and Management, 1(1), 297–322.
Saxena, A., Prasad, M., Gupta, A., Bharill, N., Patel, O. P., Tiwari, A., & Lin, C. T. (2017). A review of clustering techniques and developments. Neurocomputing, 267, 664–681.
Schölkopf, B., Smola, A. J., & Bach, F. (2002). Learning with kernels: Support vector machines, regularization, optimization, and beyond. MIT press.
Schwartz, S. (2003). A proposal for measuring value orientations across nations. Chapter 7 in the questionnaire development package of the European Social Survey. Available at: https://www.europeansocialsurvey.org/methodology/ess_methodology/source_questionnaire/source_questionnaire_development.html
Seiffert, C., Khoshgoftaar, T. M., Van Hulse, J., & Napolitano, A. (2009). RUSBoost: A hybrid approach to alleviating class imbalance. IEEE Transactions on Systems, Man, and Cybernetics-Part a: Systems and Humans, 40(1), 185–197.
Seiler, M., Collins, A., & Fefferman, N. (2013). Strategic mortgage default in the context of a social network: An epidemiological approach. Journal of Real Estate Research, 35(4), 445–476.
Seiler, M. J., Seiler, V. L., Lane, M. A., & Harrison, D. M. (2012). Fear, shame and guilt: Economic and behavioral motivations for strategic default. Real Estate Economics, 40, S199–S233.
Tajaddini, R., & Gholipour, H. F. (2017). National culture and default on mortgages. International Review of Finance, 17(1), 107–133.
Thomas, L. C., Ho, J., & Scherer, W. T. (2001). Time will tell: Behavioural scoring and the dynamics of consumer credit assessment. IMA Journal of Management Mathematics, 12(1), 89–103.
Tibshirani, R., Walther, G., & Hastie, T. (2001). Estimating the number of clusters in a data set via the gap statistic. Journal of the Royal Statistical Society: Series B (statistical Methodology), 63(2), 411–423.
Towe, C., & Lawley, C. (2013). The contagion effect of neighboring foreclosures. American Economic Journal: Economy Policy, 5, 313–335.
Tsagkarakis, M. P., Doumpos, M., & Pasiouras, F. (2021). Capital shortfall: A multicriteria decision support system for the identification of weak banks. Decision Support Systems, 145, 113526.
Van Bastelaer, T., & Leathers, H. (2006). Trust in lending: Social capital and joint liability seed loans in Southern Zambia. World Development, 34, 1788–1807.
Van Bekkum, S., Gabarro, M., & Irani, R. M. (2018). Does a larger menu increase appetite? Collateral eligibility and credit supply. The Review of Financial Studies, 31(3), 943–979.
Van den Steen, E. (2004). Rational overoptimism (and other biases). American Economic Review, 94(4), 1141–1151.
Vapnik, V. (1998). The support vector method of function estimation. In Nonlinear modeling (pp. 55–85). Springer.
Vapnik, V. (2013). The nature of statistical learning theory. Springer.
von dem Knesebeck, O., Dragano, N., & Siegrist, J. (2005). Social capital and self-rated health in 21 European countries. GMS Psycho-Social-Medicine, 2, 1–9.
White, B. T. (2010). Take this house and shove it: The emotional drivers of strategic default. SMUL Rev., 63, 1279.
Whiteley, P. F. (2000). Economic growth and social capital. Political Studies, 48, 443–466.
Wu, H., & Wang, C. C. (2018). Customer segmentation of credit card default by self organizing map. American Journal of Computational Mathematics, 8(03), 197.
Zopounidis, C., & Doumpos, M. (1999). A multicriteria decision aid methodology for sorting decision problems: The case of financial distress. Computational Economics, 14(3), 197–218.
Zuckerman, M. (1979). Attribution of success and failure revisited, or: The motivational bias is alive and well in attribution theory. Journal of Personality, 47(2), 245–287.
Acknowledgements
The authors would like to thank two anonymous reviewers and the participants of the research seminar at the Centre for Responsible Banking and Finance (CRBF), for their comments in improving this manuscript.
Funding
The authors have no funding.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
No ethics approval and/or other consents to declare.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gaganis, C., Papadimitri, P., Pasiouras, F. et al. Social traits and credit card default: a two-stage prediction framework. Ann Oper Res 325, 1231–1253 (2023). https://doi.org/10.1007/s10479-022-04859-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-022-04859-1