Simultaneous scheduling of replacement and repair of common components in operating systems

Abstract

In order for a system to stay operational, its components need maintenance. We consider two stakeholders—a system operator and a maintenance workshop—and a contract governing their joint activities. Components in the operating systems that are to be maintained are sent to the maintenance workshop, which should perform all maintenance activities on time in order to satisfy the contract. The maintained components are then sent back to be used in the operating systems. Our modeling of this system-of-systems includes stocks of damaged and repaired components, the workshop scheduling, and the planning of preventive maintenance for the operating systems. Our modeling is based on a mixed-binary linear optimization (MBLP) model of a preventive maintenance scheduling problem with so-called interval costs over a finite and discretized time horizon. We generalize and extend this model with the flow of components through the workshop, including the stocks of spare components. The resulting scheduling model—a mixed-integer optimization (MILP) model—is then utilized to optimize the main contract in a bi-objective setting: maximizing the availability of repaired (or new) components and minimizing the costs of maintaining the operating systems over the time horizon. We analyze the main contract and briefly discuss a turn-around time contract. Our results concern the effect of our modeling on the levels of the stocks of components over time, in particular minimizing the risk for lack of spare components.

1 Introduction

While a system operates its components deteriorate and in order for the system to stay operational, the components have to be maintained regularly in relation to their usage in the system. When planning the maintenance for the system, the decisions to be made concern when each of its components should be maintained (i.e., repaired or serviced) and what kind of maintenance should then be performed, with respect to the operational schedule of the system. So-called preventive maintenance (PM) can often be planned well in advance, while corrective maintenance (CM) is done after a failure has occurred, which may come on very short notice. On the other hand, an unexpected but necessary CM action may provide an opportunity for PM actions to be be rescheduled, starting from the system’s current state. While both PM and CM are aimed at restoring the components in order to put the system back in an operational state, CM is often much more costly than PM, due to a longer system down-time and also due to possible damages to other components caused by the failure. In this research, we consider PM scheduling, while CM is implicitly included by an additional cost which increases with the time between PM occasions. The increasing cost reflects the increased risk of having to perform CM. See Yu and Strömberg (2021) for a model that uses failure time distributions to model such additional costs.

We consider a setting with one system operator and one maintenance workshop, which are typically two separate stake-holders, and a contract governing their joint activities. Components that are to be maintained are sent to a maintenance workshop that should schedule and perform all maintenance activities while satisfying the contract, which may define conditions on delivery dates for and/or requirements on the availability of components for the system operator. The workshop’s ability to fulfill the contract is dependent on its capacity, in terms of the number of parallel repair lines; the investment costs for additional repair lines should thus be weighed against the cost of not being able to fulfill the contract at hand.

The original goal of the research leading to the results presented in this paper was to investigate how different contracting forms affect the efficiency of maintenance activities, the flow of components through the system-of-systems, as well as the availability of the systems over time. The first contract modeled resembles one commonly used contract in the aviation maintenance industry, i.e., a component repair turn-around time based contract. Since the resulting mathematical model appeared to be computationally intractable we chose to challenge and compare this contract’s performance with a contract aimed at regulating the availability of repaired components. The corresponding mathematical model appeared to be substantially more tractable, and also the solutions—in terms of resulting numbers of repaired components on the stock—seem to be more robust in terms of ability to keep the systems running.

We formulate a multi-objective optimization model of the following system-of-systems: (i) scheduling the PM occasions for the components of the system(s) and (ii) scheduling the repair activities in the maintenance workshop. The contract types analysed are (iii) a contract aimed at regulating the availability of components and (iv) a component repair turn-around time based contract. The objectives considered are (v) minimizing the preventive maintenance costs for the system operator (i.e., set-up costs for the maintenance occasions as well as component replacement costs which depend on the maintenance intervals), (vi) maximizing the availability (to the system operator) of components repaired by the maintenance workshop, and (vii) minimizing the penalty costs (paid by the maintenance workshop) for late or early deliveries of repaired components.

The main contributions of this work are a mathematical model of the integration and simultaneous scheduling of replacement and repair of components used in multiple systems, mathematical modeling of contracting forms between stakeholders, and an analysis of these contracts via a bi-objective optimization problem corresponding to each given contract.

The motivation behind this research lies in real-world applications. Any system that performs some sort of operations and undergoes maintenance can be applied to our modeling; some of numerous examples are railway and air traffic, and manufacturing machines in industry (see, e.g., Robert et al., 2018; Verhoeff et al., 2015; Boliang et al., 2019; Papakostas et al., 2010). The outcome of our modeling and computations—for a specific application and instance—is a maintenance schedule, which takes into account the operational requirements on and schedules for the systems, the maintenance requirements for the components of the systems, and the capacity of the maintenance workshop.

The incentive for considering the tight integration of the maintenance planning for the systems and the scheduling of the maintenance workshop is threefold. In the first place, it provides a useful planning tool for the case when the workshop is actually integrated with the operating systems (i.e., when there is only one stakeholder). However, also when the workshop is controlled by another stakeholder, our tightly integrated model will provide optimistic estimates of achievable results which can be used as benchmarks for assessing current results. Lastly, our integration enables an investigation of schedules resulting from different types of contracts between the stakeholders as well as from different capacity levels of the workshop. We also study the load level of the workshop for different capacity levels. Results from this type of analysis can be used as decision support for the stakeholders/operations management when setting up a contract as well as when making investment decisions.

Part of the model presented in this article (i.e., scheduling of PM activities) is based on the preventive maintenance scheduling problem with interval costs (PMSPIC) model presented in Gustavsson et al. (2014). The PMSPIC considers a system with multiple component types and for which the costs for replacement/repair of components take into account the interval between any two consecutive replacements/maintenance occasions; in Obradović (2021) we generalize the PMSPIC to considering multiple individuals of each component type and such that each individual may be placed in any of the systems. In this paper—in order to improve the computational efficiency for our integrated scheduling problem—we utilize an extension to multiple systems of the PMSPIC.

In order to reduce the probability of unexpected failures, which will reduce the need for CM, we enforce the PM activities to be scheduled before the end of the respective component’s expected life. We also take into account the operational schedules for the systems which yield time windows in which the different maintenance activities may or must be performed.

An efficient way of generating the operational schedules (e.g., timetables) for the systems considered is presented in Gavranis and Kozanidis (2015), where the availability of a fleet of aircraft is maximized subject to requirements on the transport missions and on the maintenance of the aircraft and their components. The results obtained include a tool for deciding which aircraft to fly when and for how long, and at what times the aircraft may and/or must undergo maintenance. The goal is to maximize the fleet availability over the planning horizon while ensuring that the operational and maintenance requirements are met. We use methods from that article to generate timetables used as input to our model.

The remainder of this article is organized as follows. In Sect. 2, we define the multi-system PMSPIC (MS-PMSPIC), the structure of the maintenance workshop, the stock dynamics modeling, and their integration with the operational demand on the systems. We define the objectives associated with the two stake-holders, one on the system maintenance side and one on the workshop side. In Sect. 3, we present our multi-objective modeling. Tests and results are presented in Sect. 4, and in Sect. 5 we draw conclusions and present ideas for future research and continuation of the work presented.

2 Definition of the maintenance scheduling problem

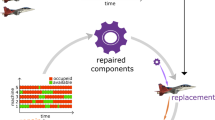
The problem studied in this article is described as follows. A number of systems are operating to fulfill a common production demand; their operating schedules are assumed to be predefined, resulting in certain time-windows during which maintenance of the systems’ components may be performed. While the systems operate their components degrade, which lead to a requirement for maintenance (i.e., service, replacement, or repair of the components of the systems). At a maintenance occasion, one or several components are taken out of the system, sent to the maintenance workshop for repair, and returned back to the stock of repaired components, ready to be used again (by any of the systems). The components that are sent for repair are instantly replaced by components that are currently on the the stock of repaired components. Hence, there is a circulating flow of individual components, being used and degraded, replaced, repaired or serviced, and then put back in a system to be used again. This structure of the system-of-systems is illustrated in Fig. 1. We model this system-of-systems such that (i) the operating systems (if possible) should be preserved operational and (ii) the capacity of the maintenance workshop should be respected. Unlike in Obradović (2021), we do not keep track of individual components, the reason being that the flow of individual components leads to a computational intractability of the model for larger instance sizes (see Sect. 4.2.1). To enable a so-called time-indexed modeling (e.g., van den Akker et al., 2000) time is discretized. Depending on the length of the planning horizon, components will undergo repair different many times.

Fig. 1

The operating systems and the maintenance workshop, with operational demand as input and scheduling of component replacement and repair as output

We begin by making a formal definition of the MS-PMSPIC—which models the replacement scheduling for the components of the systems considered—along with a mixed-binary linear optimization (MBLP) formulation. Then, the scheduling of the maintenance workshop is modeled using mixed-integer linear optimization (MILP). These systems are then integrated through the dynamics of the stocks of components waiting to be maintained and those that have finished maintenance and are available to be used again by the systems. The section is concluded with a summary of the combined MILP model.

2.1 The multi-system preventive maintenance scheduling problem with interval costs

The multi-system preventive maintenance scheduling problem with interval costs (MS-PMSPIC) is defined as follows; cf. (Gustavsson et al., 2014, Sec. 5).

Definition 1

(MS-PMSPIC) Consider K systems $k \in \mathcal {K} := \{ 1, \ldots , K \}$ with component types $i \in \mathcal {I} := \{ 1, \ldots , I \}$ with $J_i$ as the total number of individual components of type i, and a set $\mathcal {T} := \{ 1, \ldots , T \}$ of time steps at which maintenance of the systems can be performed, where T represents the planning horizon. A PM schedule consists of a set of scheduled replacement times in $\mathcal {T}$ for each system k and component type i. A maintenance occasion for system k at time t generates the maintenance occasion cost $d_t^k$. If PM of a component of type i in system k is scheduled at the times $s \in \mathcal {T} \cup \{0\}$ and $t \in \{s+1,\ldots ,T+1\}$, but not in the (possibly empty) time interval $\{s+1,\ldots ,t-1\}$, then the maintenance interval, denoted (s, t), generates the interval cost $c_{st}^{i}$. For each component type $i \in \mathcal {I}$ no maintenance interval should be longer than $\bar{t}_i$. Find a PM schedule that minimizes the sum of maintenance occasion and interval costs. $\square$

The special case of the MS-PMSPIC with $K = 1$ coincides with the PMSPIC, which according to Gustavsson et al. (2014) (see also Arkin et al., 1989; Boctor et al., 2004) is NP-hard,¹ implying that the MS-PMSPIC is NP-hard. This means that the optimal scheduling of the PM occasions for the components of the systems is a computationally demanding problem.

We next model the MS-PMSPIC as a linear optimization problem. With the decision variables being defined as

$$\begin{aligned} x_{st}^{ik}&= {\left\{ \begin{array}{ll} 1, &{} \text {if a component of type } i \text { in system } k \text { recieves} \\ &{} \text {PM at times } s \text { and } t, \text { but not in-between,} \\ 0, &{} \text {otherwise,} \end{array}\right. } \quad \begin{array}{l} i \in \mathcal {I}, \; k \in \mathcal {K}, \\ 0 \le s < t \le T+1, \end{array} \\ z_{t}^{k}&= {\left\{ \begin{array}{ll} 1, &{} \text {if maintenance of system } k \text { occurs at time } t, \\ 0, &{} \text {otherwise,} \end{array}\right. } \quad k \in \mathcal {K}, \; t \in \mathcal {T}, \end{aligned}$$

the feasible set of the MS-PMSPIC is modeled by the constraints

$$\begin{aligned} \sum _{r=1}^{T+1} x_{0r}^{ik}&= 1,&i \in \mathcal {I}, \; k \in \mathcal {K}, \end{aligned}$$

(1a)

$$\begin{aligned} \sum _{s=0}^{t-1}{x_{st}^{ik}}&= \sum _{r=t+1}^{T+1} x_{tr}^{ik},&i \in \mathcal {I}, \; t \in \mathcal {T}, \; k \in \mathcal {K}, \end{aligned}$$

(1b)

$$\begin{aligned} \sum _{s=0}^{t-1} {x_{st}^{ik}}&\le z_t^{k},&i \in \mathcal {I}, \; t \in \mathcal {T}, \; k \in \mathcal {K}, \end{aligned}$$

(1c)

$$\begin{aligned} x_{st}^{ik}&= 0,&\bar{t}_i \le s + \bar{t}_i < t \le T+1, \; i \in \mathcal {I}, \; k \in \mathcal {K}. \end{aligned}$$

(1d)

For each system k and component type i, a maintenance interval starts at time 0, which is modeled by (1a), while the constraints (1b) ensure that the same number (i.e., 0 or 1) of maintenance intervals ends and starts at time t. The constraints (1c) model that if a maintenance interval of component type i in system k ends at time t, then maintenance of system k must occur at time t. The constraints (1d) prevent any maintenance interval for component type $i \in \mathcal {I}$ from being longer than $\bar{t}_i \le T$, which prevents from having to perform corrective maintenance.

2.2 The maintenance workshop scheduling problem

Components that should be maintained are sent to the maintenance workshop, which contains a number of (identical) repair lines for component repair, each of which has a repair capacity of one unit while each component repair requires one unit of this capacity per time step during a prespecified and consecutive number of time steps. Even though the repair of a component is done in consecutive time steps, it is possible that the resulting schedule from our model is such that the repair is done on more than one repair line. Therefore, we do not guarantee non-preemption. When a component arrives at the workshop it is available for repair. Once repaired, the component is returned back to the system operator. This problem is identified as an identical parallel machines scheduling problem (IPMSP; commonly denoted $P \Vert \sum C_j$); see Brucker and Knust (2012, Ch. 1.2.2). A solution to the maintenance workshop scheduling problem specifies at which time each component arriving at the workshop should start maintenance.

Definition 2

(IPMSP) Consider a set $\mathcal {L} := \{ 1, \ldots , L \}$ of identical component repair machines and the (individual) components $j \in \mathcal {J}_i$ of types $i \in \mathcal {I}$ that arrive at the workshop. Each component has a repair time $p^i > 0$. At most $L \ge 1$ machines can operate simultaneously. Find a schedule for the maintenance workshop such that a given objective is optimized. $\square$

The IPMSP with a (weighted) sum objective is polynomially solvable (Lawler et al., 1993, Ch. 8.0), whereas its version with a minimax, i.e., makespan, objective is NP-hard (Brucker & Knust, 2012, Ch. 2.1).

To model the IPMSP as a MILP, define for each $i \in \mathcal {I}$ and $t\in \mathcal {T}$ the variables:

$$\begin{aligned} u_t^{i} \in \mathbb {Z}_+&\,: \text { the number of components of type } i \text { starting maintenance at time } t; \\ \ell _t \in \mathbb {Z}_+&\, : \text { the number of active parallel machines at time } t. \end{aligned}$$

The number $\ell _t$ of active parallel machines at time t should fulfill the inequalities

$$\begin{aligned} 0 \le \ell _t&= \ell _{t-1} + \sum _{i \in \mathcal {I}} \left( u_t^{i} - u_{t-p^i}^{i} \right) \le L,&\, t \in \mathcal {T}, \end{aligned}$$

(2)

where $\ell _0$ and $u_t^{i}$, $t \le 0$, are initial (fixed) values that constitute input to the model; see (6) for details. The constraints (2) state that the number of active parallel machines at time t equals the number of active machines in the previous time step (i.e., $t-1$) plus the difference between the numbers of components starting and finishing repair (i.e., the number of parallel machines being activated and deactivated, respectively) at time step t; they also state that the number of activated machines at any time step must be in the interval [0, L]. In our study, we also vary the number, L, of parallel machines, to enable decision support for capacity investments in the maintenance workshop.

To connect the mathematical models of the IPMSP and the MS-PMSPIC we next introduce the stock dynamics modeling.

2.3 The stock dynamics

When a component of type i is taken out of system k it is sent—with no time delay—to the stock of damaged components, where it stays until its scheduled repair. The transport time between the stock of damaged components and the maintenance workshop is denoted $\delta _a^i$. Upon being repaired, it goes to the stock of repaired (i.e., as good as new) components—with a transport time denoted $\delta _b^i$—where it is kept until its scheduled time for placement in a(nother) system $k \in \mathcal {K}$. All transport times are represented by non-negative integers.

The integration of the models of the MS-PMSPIC and the IPMSP requires the modeling of the two stocks of damaged and repaired components, respectively. We introduce the following variables for all $i \in \mathcal {I}$:

$$\begin{aligned} a_t^{i} \; (b_t^{i})&\; : \text {the number of individuals of component type } i \text { on the stock of damaged }\\&\quad \text {(repaired) components at time}~ t \in \mathcal {T} \cup \{0\}; \\ \alpha _t^{i} \; (\beta _t^{i})&\; : \text { the number of individuals of component of type } i \text { taken out of (placed in) any}\\&\text { of the systems } k \in \mathcal {K} \text { at time } t \in \mathcal {T}. \end{aligned}$$

The stock of damaged components is then modeled by the constraints

$$\begin{aligned} \alpha ^{i}_t&= \sum _{k \in \mathcal {K}} \sum _{s=0}^{t-1} x^{ik}_{st},&\, i \in \mathcal {I}, \, t \in \mathcal {T}, \end{aligned}$$

(3a)

$$\begin{aligned} a_{t}^{i}&= a_{t-1}^{i} + \alpha ^{i}_t - u^{i}_{t+\delta _a^i} \ge 0,&i \in \mathcal {I}, \, t \in \{ 1 - \delta _a^i, \ldots , T+1 \}. \end{aligned}$$

(3b)

The constraints (3a) connect the variables from the MS-PMSPIC with the stock: taking out a component of type i from one (or, $n \ge 0$) of the systems $k \in \mathcal {K}$ at time t yields the value of $\alpha ^{i}_t = 1$ (or, $\alpha ^{i}_t = n$). The constraints (3b) provide the (non-negative) number of components of type i at time t on the stock of damaged components. The stock level at time t depends on the level in the previous time step $t-1$, whether components are taken out of any system k and placed on the stock at time step t, and whether they are starting maintenance at time step $t + \delta _a^i$. The variables $a_0^{i}$ and $\alpha _t^{i}$, $t \in \{ 1-\delta _a^i, \ldots , 0 \}$, comprise (fixed) input data, which must fulfill the initialization constraints (6), below.

The stock of repaired components is modeled analogously, as

$$\begin{aligned} \beta ^{i}_t&=\sum _{k \in \mathcal {K}} \sum _{r=t+1}^{T+1} x^{ik}_{tr},&i \in \mathcal {I}, \, t \in \mathcal {T}, \end{aligned}$$

(4a)

$$\begin{aligned} b_{t}^{i}&= b_{t-1}^{i} - \beta _t^{i} + u^{i}_{t-\delta _b^i-p^i} \ge \underline{b}^i,&i \in \mathcal {I}, \, t \in \mathcal {T} \cup \{T+1\} , \end{aligned}$$

(4b)

The constraints (4a) connect the stock of repaired components with the MS-PMSPIC. Placing a component of type i in one (or, in $n \ge 0$) of the systems $k \in \mathcal {K}$ at time t, yields the value $\beta ^{i}_t = 1$ (or, $\beta ^{i}_t = n$). The constraints (4b) keep track of the stock levels at time t which depend on the level in the previous time step $t-1$, the components taken out of the stock of repaired components and placed in one of the systems k at time t, and the components arriving at the stock of repaired components at time t (i.e., the number $u_{t-\delta _b^i-p^i}^{i}$ of components of type i starting maintenance at time $t-\delta _b^i-p^i$). They also express that the stock level of repaired components of type i may not go below the lower stock limit $\underline{b}^i \ge 0$ at any point in time. The variables $b_0^{i}$, $\beta _0^{i}$, and $u^{i}_t$, $t \in \{ 1-\delta _b^i-p^i, \ldots , 0 \}$ comprise (fixed) input data, which must fulfill the initialization constraints (6), below.

The constraints (3)–(4) enable the control of the levels of the stocks/inventory of damaged and repaired components, respectively, subject to relevant constraints.

2.4 Integration with the operational demand of the systems

What drives the need for maintenance of components, and constitutes the input to our modeling, is the operational demand: We assume that operational schedules are given for the systems $k \in \mathcal {K}$ such that the demand for operations can be fulfilled. For our maintenance planning problem, these schedules are represented in terms of time intervals when the system is either operating—at which times maintenance cannot be performed—or accessible for maintenance. In other words, PM may not be scheduled while a system is operating. In the case of railway systems; e.g., Lidén (2020), each train is assigned time slots when it should operate (i.e., transport goods or passengers); hence, PM may be scheduled only in-between these time slots. In the case of offshore wind turbine maintenance (e.g., Shaee et al., 2013), the operational demand is fulfilled by wind energy production, while maintenance work can be done only during time periods of not too harsh weather conditions. When planning any PM occasion the (predicted or planned) operational schedules for the systems provide time windows during which maintenance may be performed. As input to the integrated MS-PMSPIC and IPMSP model, for all $t \in \mathcal {T}$ and all $k \in \mathcal {K}$ we thus let the parameters

$$\begin{aligned} \overline{z}_t^{k}&=\left\{ \begin{array}{ll} 1 ,&{} \text {if PM is allowed to be scheduled for system } k \text { at time } t ,\\ 0, &{}\text {otherwise,} \end{array}\right. \end{aligned}$$

and define upper limits on the variables representing maintenance occasions as

$$\begin{aligned} z_t^{k} \le \overline{z}_t^{k},&t \in \mathcal {T}, \, k \in \mathcal {K}, \end{aligned}$$

(5)

the fulfilment of which implies that the time windows for PM are respected.

2.5 Boundary conditions

We next ensure that our system is properly initialized at $t=0$ and that its state at the end of the planning horizon is close enough to that at the beginning.

2.5.1 Initialization

As an initialization of the model (1)–(5) at $t=0$ for each component type $i \in \mathcal {I}$, the $J_i$ individual components are distributed over the K systems, the stocks of damaged and repaired components, and the workshop; the distribution should further fulfill the workshop capacity as well as the requirements on the stock of repaired components. Hence, we set fixed values (randomized, or according to the systems’ states at the respective time points) to the variables $a_0^i := \bar{a}_0^i$, $b_0^i := \bar{b}_0^i \ge \underline{b}^i$, $\alpha _r^i := \bar{\alpha }_r^i$, $r \in \{ - \delta _a^i + 1, \ldots , 0 \}$, and $u_r^i := \bar{u}_r^i$, $r \in \{ -\delta _b^i-p^i+1, \ldots , \max \{ p^i; \delta _a^i \} \}$, $i \in \mathcal {I}$, such that the equalities

$$\begin{aligned}&J_i = K + \bar{a}_0^i + \bar{b}_0^i + \sum _{r=-\delta _b^i-p^i+1}^0 \bar{u}_r^i,&i \in \mathcal {I},&&\end{aligned}$$

(6)

and the constraints (2)–(4), for the respective relevant indices, are fulfilled.

2.5.2 End of the planning period

Since our model is meant to be used as a planning and decision making tool, the model (constraints and objectives) should ensure that the system-of-systems is in a controlled and desired state at the end of the planning period. This means that the systems’ states should then possess similar properties as in the beginning, such that when a new planning period starts at the end of the previous one, the starting point is desirable. To ensure this, and to eliminate possible boundary effects (such as, e.g., too high levels of damaged components), we require that the levels of the stocks of repaired components are not (much) lower than in the beginning of the planning period. We model this by the constraints

$$\begin{aligned} b_{t}^i \ge b_0^i - \mu ^i,&i \in \mathcal {I}, \; t \in \{T+2-\bar{s},\dots ,T+1\}, \end{aligned}$$

(7)

where $\bar{s} \ge 1$ is the number of time steps at the end of the planning period during which the tolerance levels²$\mu ^i \ge 0$ are applied to component types $i \in \mathcal {I}$.

2.6 The complete feasibility model of the system-of-systems

In summary, the set of feasible solutions to our maintenance scheduling problem is modeled by (1)–(7) with binary requirements on the variables $x_{st}^{ik}$ and $z_{t}^{k}$ and non-negative and integer requirements on the variables $u_{t}^{i}$, $a_{t}^{i}$, $b_{t}^{i}$, $\alpha _{t}^{i}$, $\beta _{t}^{i}$, and $\ell _t$, for all relevant values of the indices.

3 Contracts and optimization objectives

The turn-around time contract requires a measurement of the lateness/earliness of each individual component, which calls for a modeling of individual components (for details, see Obradović, 2021). Since our preliminary tests (see Sect. 4.2.1) indicated an increased model complexity, which yields a computational intractability for larger instances, we choose to adopt an availability contract.

3.1 Contract between the stakeholders

To model an turn-around time contract between the stakeholders, and its dependence on the capacity level in the maintenance workshop, we define the objectives to (i) minimize the maintenance cost for the system operator and (ii) minimize the penalty for late and early deliveries of repaired components, which is paid by the maintenance workshop to the system operator.

To model an availability contract between the stakeholders, we define the objectives (i) (as defined above) and (iii) to maximize the availability of components on the stock of repaired components (which can be interpreted as minimizing the risk for lack of repaired components).

3.2 Optimization objectives

Below follows our detailed modeling of the three objectives defined in Sect. 3.1.

Minimizing costs for maintenance set-up and intervals Each maintenance occasion yields a set-up/maintenance cost for the system operator. Besides this, there is a so-called interval cost for each component type which is determined based on the length of the interval between any two consecutive maintenance occasions. We assume that the interval cost is non-decreasing with the length of the interval. The rationale behind this assumption that (i) the longer time the component has been used for operations, the more costly will the maintenance be, and (ii) it enables the enforcement of scheduling the maintenance at the latest at the end of each individual component’s life (cf. (1d)). From the system operators’ point of view, the objective is to minimize the total costs for maintenance during a pre-specified time period. We formulate mathematically this objective as to

$$\begin{aligned}&\mathop {\text {minimize}}&\sum _{k \in \mathcal {K}} \sum _{t \in \mathcal {T}} d_t z_t^k&+ \sum _{k \in \mathcal {K}} \sum _{i \in \mathcal {I}} \sum _{t=1}^{T+1} \sum _{s=0}^{t-1} c_{st}^i x_{st}^{ik},&\end{aligned}$$

(8)

where the first sum represents the maintenance set-up costs and the second the interval costs. Every maintenance occasion for the system k (i.e., when $z_t^k = 1$) generates a cost $d_t > 0$ while every maintenance interval (s, t) for a component of type i in system k (i.e., when $x_{st}^{ik} = 1$) yields an interval cost $c_{st}^{i} > 0$, which is such that $c_{st}^{i} \ge c_{sr}^{i}$ for all $r \ge t$.

Minimizing the risk of exceeding the contracted turn-around times for component repair When a component individual arrives at the workshop it is available for repair and assigned a due date, at which the repair should be finished and the component be returned to the system operator. Whenever a component is delivered before³ or after its due date, the maintenance workshop has to pay a fee to the system operator. Modeling the ’turn-around time’ contract requires variables defined corresponding to an individual component flow according to the following. The variable $x_{st}^{ijk} = 1$ if individual $j \in \mathcal {J}_i$ of component type $i \in \mathcal {I}$ in system $k \in \mathcal {K}$ receives PM at times s and $t>s$, but not in-between; otherwise $x_{st}^{ijk} = 0$. The variable $u_t^{ij} = 1$ if individual j of component type i starts repair at time t; otherwise $u_t^{ij} = 0$. The variable $\alpha _t^{ij} = 1$ if individual component j of type i is taken out of one of the systems k at time t; otherwise $\alpha _t^{ij} = 0$. For details of the constraints corresponding to (1)–(7) for the case of individual components, see Obradović (2021).

The turn-around time of an individual component (i, j) is defined as the time from when it is taken out of one of the systems in $\mathcal {K}$ (i.e., a time t such that $\alpha _t^{ij} = 1$) until it has been repaired and is available for usage again in one of the systems (i.e., a time t such that $u_{t - \delta _b^i - p^i}^{ij} = 1$). The total turn-around time, $v_{\text {tat}}^{ij}$, for component individual (i, j), $j \in \mathcal {J}_i$, $i \in \mathcal {I}$, over the planning period $\mathcal {T}$, is thus computed as

$$\begin{aligned} v_{\text {tat}}^{ij}&= \left( p^i + \delta _b^i \right) u^{ij}_0 + \sum _{t=1}^{T+1} \left( \left( t + \delta _b^i + p^i \right) u^{ij}_t - t \alpha ^{ij}_{t} \right) , \end{aligned}$$

(9a)

where the term $(\delta _b^i + p^i) u^{ij}_0$ is positive if component (i, j) is initially on the stock of damaged components, and the equalities $u^{ij}_{T+1} = a^{ij}_0 - u^{ij}_0 + \sum _{t \in \mathcal {T}} (\alpha ^{ij}_t - u^{ij}_t)$ and $\alpha _{T+1}^{ij} = 0$ hold.

Letting $c^{ij}_\text {delay} >0$ and $c^{ij}_\text {early} \in (0, c^{ij}_\text {delay}]$ denote the penalties for late and early, respectively, delivery of a repaired component, this objective is expressed as to

$$\begin{aligned}&\mathop {\text {minimize}}&\sum _{i \in \mathcal {I}} \sum _{j \in \mathcal {J}_i} \left( c_{\text {delay}}^{ij} v_{\text {delay}}^{ij} - c_{\text {early}}^{ij} v_{\text {early}}^{ij} \right) ,&\end{aligned}$$

(9b)

where $v_{\text {delay}}^{ij}$ ($v_{\text {early}}^{ij}$) denotes the total delay (earliness) for component (i, j) over the planning period. These variables are due to the constraints

$$\begin{aligned} v_{\text {early}}^{ij}&\le v_{\text {tat}}^{ij} - q_\mathrm{due}^{ij} \left( a^{ij}_0 + \sum _{t=1}^{T+1} \alpha ^{ij}_t \right) \le v_{\text {delay}}^{ij}, \end{aligned}$$

(9c)

$$\begin{aligned} v_{\text {early}}^{ij}&\le 0 \le v_{\text {delay}}^{ij}, \end{aligned}$$

(9d)

where $q_{\text {due}}^{ij} > 0$ denotes the contracted due date for component (i, j), $j \in \mathcal {J}_i$, $i \in \mathcal {I}$.

Minimizing the risk for lack of spare parts To ensure that the operational schedule is undisturbed, or at least that the disturbance is minimal, it is crucial that enough many spare components are available. Then, whenever an unexpected failure occurs, the damaged component can be replaced by a new one without the planned operations of the system at hand having to be stopped. A way of minimizing the risk for lack of spare components is to maximize a weighted sum of the lowest resulting stock levels over the planning period, i.e., $e^i$, $i \in \mathcal {I}$, subject to a lower limit for the availability of each component type. Letting $w^i > 0$, $i \in \mathcal {I}$, denote the assigned weights this is modeled as to

$$\begin{aligned}&&\mathop {\text {maximize}}&\sum _{i \in \mathcal {I}} w^i e^i&, \end{aligned}$$

(10a)

$$\begin{aligned}&&\text {subject to}&\underline{b}^i \le e^i&\le b_t^{i},&i \in \mathcal {I}, \, t \in \mathcal {T}.&&\end{aligned}$$

(10b)

If a certain component type i has a larger spread in repair times $p^i$, or if there is a need to prioritize a certain component type for repair (e.g., due to weak stock levels), we can set a higher value of the corresponding weight $w^i$, such that the lowest stock level $e^i$ will most likely get a higher level than for the other types. This means that this type will be prioritized (to start earlier) in the workshop, thus reducing the risk for lack of this specific component type. An alternative way to reducing this risk could be to set a higher lower limit, $\underline{b}^i$. We will refer to the value of the objective in (10) as availability.

4 Application: implementation, tests, and results

We present an application from the aerospace industry, from a collaboration with the Swedish aerospace and defence company Saab AB. For contract assessment purposes, he instance sizes are considered reasonable from a practical application point of view and the data sets used are based on knowledge mediated from the industrial partner; all numbers are normalized. Our implementation is made using Julia (2012) and JuMP (see Dunning et al., 2017), and the computations are performed by Gurobi (2020) on a laptop computer with a 2.4 GHz Intel Core i5 processor and 8 GB of RAM memory. The computer used has eight available processors. Gurobi usually uses all cores available, but can choose to use less. We investigated the thread count: for all the results reported, Gurobi used all eight threads, which also performs faster as compared to using single thread operations.

4.1 The main test instances and multi-objective settings

As main test cases, we consider $K \in \{5,10\}$ systems, each having $I \in \{3,5\}$ component types and $J_i \in \{10,15\}$ (individual) components of each type $i \in \mathcal {I}$. The operational and maintenance related differences of the component types are reflected by their respective repair times in the maintenance workshop, as well as their respective due dates, which are chosen randomly within the same order of magnitude. The different component types are also assigned differently structured interval costs, all increasing with the time between maintenance occasions, reflecting the increasing risk of having to perform CM. The planning horizon is $T \in \{ 20,40\}$ time steps and the workshop capacity is either $L \in \{3,10\}$ parallel machines. We have investigated two main cases of our planning problem: (i) with no lower limits on the stocks of repaired components, i.e., with $\underline{b}^i=0$, $i \in \mathcal {I}$, and (ii) with the lower limits $\underline{b}^i=1$, $i \in \mathcal {I}$. The weights in (10) are set to $w^i=1$, $i \in \mathcal {I}$. The timetable for the systems’ operations is generated by applying the model in Gavranis and Kozanidis (2015) to the set $\mathcal {K}$ of systems over the planning period $\mathcal {T}$.

When solving a multi-objective optimization problem, one is usually interested in finding Pareto optimal, or efficient solutions; see e.g., (Ehrgott, 2005, Ch. 2.1). A solution is called Pareto optimal if none of the objective functions can be improved in value without degrading at least one of the other objectives’ values. To find points on the Pareto front—the set of all Pareto optimal points—we employ the $\epsilon$-constraint method (see Mavrotas, 2009), which—in the bi-objective case—optimizes iteratively one objective function, while the other is being constrained.

4.2 Computational tests and results

In Sect. 4.2.1 we study the turn-around time contract. The preliminary results then obtained motivate the continuation with an availability contracting form, which is studied in Sect. 4.2.2.

4.2.1 The turn-around time contract and comparison with an availability contract

The turn-around time contract is modeled as a bi-objective optimization problem. The system operator’s objective is modeled as to minimize the total costs for maintenance, i.e., the objective (8), while the minimization of the penalty for late and early deliveries is achieved by the objective defined in (9). The set of feasible schedules is defined by constraints similar to (1)–(7), but involving also individual components (see Obradović, 2021 for details). The size of the resulting MBLP model for the turn-around time contract is shown in Table 1, which also reveals that obtaining a feasible solution with a verified duality gap of 1% requires around 10 h of computing time, while reducing the gap below 0.5% takes around 124 h. While the smaller instances are solved to optimality in a reasonable computing time, the larger ones require significantly longer time to reach a duality gap of 0.45%; for details, see Table 1. Presolve times are around 0.45 s for the first and around 12 s for the second instance; hence, the solver quickly eliminates redundant variables and/or constraints.⁴ From these preliminary tests we conclude that the model becomes intractable for larger instance sizes.

4.2.2 Investigation of the availability contract

In Table 2, solution times required to solve instances of different sizes with our model are listed. Computing times grow with the instance sizes. It is noticeable that the problem size grows significantly with an increasing length of the planning horizon. However, since re-planning is often needed (e.g., at unexpected failures, leading to necessary CM), any schedule will be subject to changes in due time. Therefore, it is not a big priority to solve our model to optimality over long time horizons, which may also yield approximate schedules and costs.

In our scheduling problem, increasing the total number of components of type i is equivalent to decreasing the lower limit, $\underline{b}^i$ on the stock of available/repaired components. While adding components comes with a higher cost, decreasing the lower limit $\underline{b}^i$ comes with a higher risk. It is the decision maker who chooses the trade-off between cost and risk. For example, if there is no available component on the stock, it may lead to disruptions in the operations until a component arrives, which is a risk and most likely leads to a cost as well. In our test, we use $\underline{b}^i=1, i \in \mathcal {I}$, but results could naturally be different for different values of $\underline{b}^i$.

Figure 2 shows the computed points on the Pareto front for the objectives (8) and (10), and the workshop capacity $L=10$ and $L=3$, respectively. The availability, defined in (10) as the weighted sum of the lowest resulting stock levels over the planning period, is in the interval⁵ [5, 10] while the total maintenance cost is in the interval [5542, 5828] for $L=10$ and in the interval [5631, 5856] for $L=3$. We observe that for every increase by one in the availability, the increase in the maintenance cost becomes higher. To receive a higher availability, there has to be a loss on the maintenance scheduling side, which could be, for example, that maintenance intervals are longer which lead to higher maintenance costs, or to a higher risk for unforeseen failures. Another observation is that the difference between maintenance costs, for both $L=3$ and $L=10$, decreases with an increasing availability. This means that the high cost of obtaining a high availability is (almost) regardless of the capacity in the maintenance workshop.

Table 1 Instance sizes and computing times for the turn-around time contract

Table 2 Computing times and optimality gaps for different instance sizes

Fig. 2

Pareto front for the availability objective (10) versus the maintenance cost objective (8); here, $(I,J_i,K,T,\underline{b}^i,w^i)=(5,15,10,40,1,1)$ and $L \in \{3,10\}$; $\epsilon =1$ in the $\epsilon$-constraint method

Fig. 3

Stock levels for $(I,J_i,K,T,L,\underline{b}^i)=(5,15,10,40,10,1)$. Point on the Pareto front for the objectives (10) and (8): availability = 5; maintenance cost = 5542; no constraints on the stock levels at the end of the planning horizon

Figure 3 shows the stock levels for the capacity $L=10$ in the maintenance workshop. Comparing with Fig. 4, where constraints on the levels of the stocks of repaired components at the end of the planning horizon (Sect. 2.5.2) are included, we observe that the effect of piling up of components to be repaired by the end is reduced, if not eliminated. In both figures, $\underline{b}^i=1$ and availability equals five, which means that at each time step there is one component of each type available. It is noticeable that the levels of repaired components are higher in the first half of the planning period, which is partly due to the initialization of the systems and the levels of the stocks of repaired components (i.e., $b_0^i, i \in \mathcal {I}$).

A reduction of the workshop capacity from $L=10$ (Fig. 4) to $L=3$ repair lines (Fig. 5) yields slightly higher stock levels of components (total average of repaired (damaged) components over the planning period: 10.8 (2.55) for $L=10$ and 12.45 (3.525) for $L=3$). The higher stock levels resulting from a lower workshop capacity is likely due to fewer repairs then being performed at the expense of longer maintenance intervals, resulting in a higher maintenance cost (cf. Fig. 2).

Fig. 4

Stock levels for $(I,J_i,K,T,L,\underline{b}^i)=(5,15,10,40,10,1)$. Point on the Pareto front for objectives (10) and (8): availability = 5; maintenance cost = 5563; with constraints (7) on the stock levels at the planning horizon: $\bar{s} = 1$, $\mu ^i=0$, $i \in \mathcal {I}$

Fig. 5

Stock levels for $(I,J_i,K,T,L,\underline{b}^i)=(5,15,10,40,3,1)$. Point on the Pareto front for objectives (10) and (8): availability = 6, maintenance cost = 5655; with constraints (7) on the stock levels at the planning horizon: $\bar{s} = 1$, $\mu ^i=0$, $i \in \mathcal {I}$

Figure 6 shows the load of the maintenance workshop over time, for the capacities $L \in \{ 3, 5, 10 \}$. We observe that for $L=10$ the number of active repair lines does not exceed seven, which implies that no capacity limit $L \ge 7$ restricts the number of active repair lines at any time in an optimal solution. When reducing the capacity to $L=5$, the workshop is, however, working at full capacity in many time steps, which is even more expressed for $L=3$. If some unexpected failure occur, or if some components possess longer repair times, a full capacity utilization of the workshop at multiple consecutive time steps can lead to postponed deliveries. This may, in turn, lead to lower levels on the stock of repaired components and even to not satisfying the lower limit on availability. A further consequence could be that maintenance intervals have to be extended (incurring higher maintenance costs), or that some systems simply become unable to operate. Hence, modeling some excess workshop capacity will yield a more robust system-of-systems.

Fig. 6

Maintenance workshop load over time for $(I,J_i,K,T,\underline{b}^i)=(5,15,10,40,1)$ and $L \in \{ 10, 5, 3 \}$. Points on the Pareto front for objectives (10) and (8): availability = 5; maintenance cost $\in \{ 5542, 5546, 5631 \}$; no constraints on the stock levels at the end of the planning horizon

In terms of the specific application to maintenance of military aircraft, a real instance size could differ from the ones we present. For example, the number, I, of component types may be larger (typically in the range of 20–50), while the number, $J_i$, of individual components may be smaller than the considered value of 15 (due to the components considered being usually quite expensive). The capacity, L, of the maintenance workshop may vary as well but most of the time it is not very high. The fleet size, K, would be in the range of 5–30 aircraft. The length of the planning horizon depends heavily on the length of each time step (e.g., 1 h/half-day/day/week). The use of our model in different applications will thus result in varying instance sizes. For example, rail traffic or commercial airlines instances would have a larger number of systems (i.e., train sets/aircraft).

5 Conclusions and future research

We start from an NP-hard maintenance scheduling problem, generalize it to consider multiple systems and incorporate modeling for a maintenance workshop, stock dynamics and an availability objective. The resulting solutions can be used to find a lower limit for an optimal performance of a collaboration between stakeholders governing a common system-of-systems. Our modeling also enables an investigation of contracting forms between stakeholders and provides a planning tool when the maintenance workshop and the system operator are integrated. We conclude that a turn-around time contract with modeling of the individual components is inferior to an availability contract due to its computational intractability.

Our intended application typically comprises several maintenance workshops/companies who may enter into the cooperation by means of different contracting forms. Such generalizations of our problem is a topic for further research.

We define and analyze one form of each of the two contract types studied (i.e., availability and turn-around time). As a future research topic, we will investigate alternative ways to define and benchmark the two contract types.

An important extension of this work for the intended application is to include corrective maintenance (CM) in terms of the risk of having to perform CM due to unexpected failures. At the current stage, the means to handle and reduce this risk are to not allow too large maintenance intervals (cf. the constraints (1d)).

We intend to integrate the scheduling of the systems’ operations (currently used as input data to our model) with our maintenance scheduling for the components.