Abstract
We show that deciding the feasibility of a booking (FB) in the European entry-exit gas market is coNP-hard if a nonlinear potential-based flow model is used. The feasibility of a booking can be characterized by polynomially many load flow scenarios with maximum potential-difference, which are computed by solving nonlinear potential-based flow models. We use this existing characterization of the literature to prove that FB is coNP-hard by reducing Partition to the infeasibility of a booking. We further prove that computing a potential-difference maximizing load flow scenario is \({\textsc {NP}}\)-hard even if we can determine the flow direction a priori. From the literature, it is known that FB can be decided in polynomial time on trees and a single cycle. Thus, our hardness result draws the first line that separates the easy from the hard variants of FB and finally answers that FB is hard in general.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The entry-exit market system has been introduced for the European gas market as the outcome of the European gas market liberalization (Directive , 1998; Directive , 2003; Directive , 2009). One of the main goals of the entry-exit system is to decouple the trade and transport of gas. To this end, the current market system is split into different stages, which are formally described in Grimm et al. (2019) by a multilevel model of the European entry-exit gas market. In these stages, the transmission system operator (TSO) and the gas traders interact with each other via so-called bookings and nominations. A booking is a mid- to long-term capacity-right contract between the gas traders and the TSO in which the gas traders buy capacity rights for the maximum injection or withdrawal quantity of gas at entry and exit nodes of the network. On a day-ahead basis, the traders nominate the quantity of gas for an injection, respectively withdrawal, on the next day such that the nominated quantity of gas stays within the booked capacities and the total injection and withdrawal quantities are balanced. By signing the booking contracts, the TSO is obliged to guarantee the feasibility of transport of the nominated amounts of gas through the network. Since the gas traders can nominate any booking-compliant nomination, i.e., any balanced quantities of injections and withdrawals up to the booked-capacities, the TSO has to guarantee the feasibility of transport for every booking-compliant nomination. Hence, the TSO has to generally verify the feasibility of infinitely many booking-compliant nominations before the TSO signs a booking. On the one hand, this property of the entry-exit market system decouples trade and transport. On the other hand, it leads to many new challenges, e.g., deciding the feasibility of a booking or the computation of bookable capacities, so-called technical capacities; see Fügenschuh et al. (2013), Labbé et al. (2019), Martin et al. (2011), Schewe et al. (2020).
In this work, we focus on deciding the feasibility of a booking in general graphs. To this end, we consider passive networks without active elements, i.e., no controllable elements such as valves or compressors are present in the network. We further focus on stationary models of gas transport with nonlinear potential-based flows; see, e.g., Gross et al. (2019), Labbé et al. (2019), Schewe et al. (2019). Here, nonlinear potential-based flows means that the potential function is nonlinear. We note that potential-based flows significantly differ from the frequently used linear network flows with arc capacities. The latter flows consist of flow conservation and capacities on the flow through an arc. However, linear flows with arc capacities neglect pressure levels. Thus, the corresponding flows are not pressure-driven. In the following, we refer to linear flows with arc capacities as capacitated linear flows.
One of the main differences between the physically more accurate potential-based flows and the capacitated linear flows is that in a passive potential-based flow model, no cyclic flows are possible, which is not necessarily the case for capacitated linear flows. This structural property of potential-based flows can be algorithmically exploited; see e.g., Habeck and Pfetsch (2021). However, the link between node potentials and arc flows is usually given by nonlinear constraints. Consequently, potential-based flows generally lead to a harder class of optimization problems compared to capacitated linear flows. We note that potential-based flows are also used to model hydrogen, water, or power distribution networks; see Gross et al. (2019), Robinius et al. (2019).
Many optimization methods for the transport of gas in pipeline networks have been researched in the recent years, e.g., see the book Koch et al. (2015) and the survey article Ríos-Mercado and Borraz-Sánchez (2015) for a comprehensive overview. In doing so, the research mainly focuses on cost-optimal transport, respectively feasible transport, of a single nomination, respectively load flow scenario. The gas flow in pipelines follows physical laws, which lead to challenging mathematical optimization models. Thus, in the literature, approximations considering different classes of optimization models are used. Based on the descriptions in Labbé et al. (2019), Schewe et al. (2020), Labbé et al. (2021), we now state some examples for these approximations. In De Wolf and Smeers (2000), the gas physics are approximated by piecewise linear functions and the authors analyze the cost-optimal transport in the Belgian network before the European market liberalization. In Bakhouya and De Wolf (2007), the cost-optimal transport in the Belgian network is again analyzed considering the different market situation due to the progressed market liberalization. A combination of piecewise linearizations together with sequential quadratic programming is applied in Domschke et al. (2011). Furthermore, in many works piecewise linear relaxations are considered for approximating the gas transport, e.g., see Geißler (2011), Geißler et al. (2013, 2015, 2018). Approaches based on continuous nonlinear optimization methods, respectively complementarity-constraint modeling, are used in, e.g., Rose et al. (2016), Baumrucker and Biegler (2010), Schmidt et al. (2015a, 2015b, 2015c), Schmidt et al. (2016). Even more sophisticated and challenging nonlinear mixed-integer models are studied, e.g., in Geißler et al. (2015, 2018), Humpola (2017). For details on optimization w.r.t. partial differential equations and optimal control of gas networks, we refer to the survey Hante et al. (2017) and the references therein.
Regarding the complexity, deciding the feasibility of a nomination for capacitated linear flows as well as for potential-based flows with linear potential functions is in P since both problems can be decided by solving linear programs; see e.g., Labbé et al. (2019), Schewe et al. (2019). In the following, we refer to potential-based flows with linear potential functions as linear potential-based flows. If active elements such as valves are present in the network, then deciding the feasibility of a nomination is \({\textsc {NP}}\)-hard for the potential-based flow model; see Szabó (2012).
The literature on bookings, especially on deciding the feasibility of a booking, is rather small in comparison with the research on nominations. Following the literature review in Schewe et al. (2020), we now briefly summarize the literature on bookings. We note that deciding the feasibility of a booking can be seen as a specific two-stage or adjustable robust feasibility problem, see e.g., Ben-Tal and El Ghaoui (2009), Gorissen et al. (2015), since a feasible booking requires the feasibility of all, generally infinitely many, nominations within the given booking bounds. One of the first results about the mathematical properties of bookings are given within the PhD theses Hayn (2016), Willert (2014). Further structural properties such as (non-)convexity of the set of feasible nominations and bookings are shown in Schewe et al. (2019). We note that the reservation-allocation problem considered in Fügenschuh et al. (2014) is similar to the feasibility of a booking. Moreover, the authors of Aßmann et al. (2018) develop approaches to decide robust feasibility and infeasibility of specific two-stage robust optimization problems using techniques of polynomial optimization. These approaches can also be used to decide the feasibility of a booking in pipe-only networks. In case of capacitated linear flows, deciding the feasibility of a booking is coNP-complete in general networks, but can be decided in polynomial time in tree-shaped networks; see Hayn (2016). For the more accurate potential-based flows in pipe-only networks, the feasibility of a booking can be characterized by polynomially many nominations with maximum potential-difference; see Labbé et al. (2019). Using this characterization, the authors of Labbé et al. (2019) show that for linear potential-based flows deciding the feasibility of a booking is in P for general graphs. Additionally, they also prove that this holds for nonlinear potential-based flows in tree-shaped networks; see Labbé et al. (2019). We note that the latter also follows from Robinius et al. (2019) under additional assumptions on the potential bounds. Moreover, the authors of Labbé et al. (2021) extend these results by proving that deciding the feasibility of a booking in a single cycle is in P. In doing so, again special structures of the nominations with maximum potential-difference are exploited. In this paper, we finally answer that deciding the feasibility of a booking is coNP-hard in general graphs. Thus, we draw the first line that separates the easy from the hard variants of deciding the feasibility of a booking.
We finally refer to the topic of computing maximal feasible bookings, which are called technical capacities. These technical capacities are introduced in Martin et al. (2011) and first results are obtained in Hayn (2016), Willert (2014). They can also be seen as a more sophisticated application of the radius of robust feasibility, e.g., see Goberna et al. (2014), Chuong and Jeyakumar (2017), Liers et al. (2021). Regarding the complexity exponential upper bounds for computing technical capacities w.r.t. capacitated linear flows are given in Hayn (2016). An extensive complexity analysis is provided in the recent work Schewe et al. (2020). The authors prove that computing technical capacities, i.e., maximizing over the set of feasible bookings, is \({\textsc {NP}}\)-hard for capacitated linear, linear-, and nonlinear-potential based flows even on trees.
Our contribution is the following. We prove that deciding the feasibility of a booking considering a nonlinear potential-based flow model is coNP-hard in general graphs. The proof is obtained by reducing Partition to the infeasibility of a booking. It is the first hardness result for deciding the feasibility of a booking w.r.t. potential-based flows since the latter is in P for linear potential-based flows in general graphs and for nonlinear potential-based flows in trees and a single-cycle network. We further prove that computing a nomination with maximum potential-difference is \({\textsc {NP}}\)-hard even if we can determine the flow direction a priori. We summarize our contribution w.r.t. bookings together with a review of the results from the literature in Fig. 1, which is an adapted and extended version of Fig. 3 in Sect. 6 of Labbé et al. (2019).
Overview of known complexity results for deciding the feasibility of a booking. The figure is an adapted and extended version of the one in Sect. 6 of Labbé et al. (2019). We note that for the case of no flow bounds, respectively no potential bounds, it is not hard to observe that every booking is feasible. Thus, we do not explicitly cite this result
The remainder of this paper is structured as follows. In Sect. 2, we formally introduce the problem of deciding the feasibility of a booking. Notations and first results, which are necessary for the hardness proof, are stated in Sect. 3. Afterward, in Sect. 4 the coNP-hardness of deciding the feasibility of a booking considering a nonlinear potential-based flow model is shown. Finally, we close with a conclusion in Sect. 5.
2 Problem description
The problem description closely follows the one in Labbé et al. (2021). We represent a gas network by a weakly connected and directed graph \(G = (V, A)\) with node set \(V \) and arc set \(A \). The set of nodes is partitioned into the set \(V_+ \) of entry nodes, at which gas is injected, the set \(V_- \) of exit nodes, where gas is withdrawn, and the set \(V_0 \) of the remaining inner nodes. These node types are equipped with a vector \(\sigma {\in \mathbb {R} ^{V}}\) given by
In this paper, only passive networks, i.e., without active elements such as control valves or compressors, are considered. In the following, we introduce notations and definitions which are taken from Schewe et al. (2019), Labbé et al. (2021) and follow the corresponding descriptions therein.
Definition 2.1
A load flow is a vector \(\ell \in \mathbb {R} _{\ge 0}^{V}\), with \(\ell _u =0\) for all \(u \in V_0 \). The set of load flow vectors is denoted by \(L\).
A load flow represents an actual situation of the demand in the network at a single point in time by specifying the amount of gas \(\ell _u \) that is injected at \(u \in V_+ \) or withdrawn at \(u \in V_- \). Since we only consider stationary flows, we need to impose that the total injection and withdrawal quantities are balanced, which leads to the definition of a nomination.
Definition 2.2
A nomination is a balanced load flow \(\ell \), i.e., \(\sigma ^\top \ell = 0\). The set of nominations is given by
Definition 2.3
A booking is a vector \(b\in \mathbb {R} _{\ge 0}^{V}\), with \(b_u =0\) for all \(u \in V_0 \).
From a mathematical perspective, load flows and bookings are the same. Further, nominations and bookings are linked as described in the following definition.
Definition 2.4
A nomination \(\ell \) is called booking-compliant w.r.t. the booking \(b\) if \(\ell \le b\) holds, where “\(\le \)” is meant component-wise. The set of booking-compliant (or \(b\)-compliant) nominations is given by
As in Labbé et al. (2021), we now introduce the notion of feasible nominations and bookings. To do so, we model stationary gas flows by an abstract physics model that is based on the Weymouth pressure drop equation and potential-based flows; see, e.g., Gross et al. (2019) or Labbé et al. (2019). It consists of arc flow variables \(q \in \mathbb {R} ^A \) and nodal potentials \(\pi \in \mathbb {R} _{\ge 0}^V \). These arc flows couple the potentials, which leads to the nonlinear potential-based flow model (2.5) below. We note that in gas networks with horizontal pipes the potentials \(\pi \in \mathbb {R} ^{V}_{\ge 0}\) are closely linked to the gas pressures \(p \in \mathbb {R} ^{V}_{\ge 0}\) at the nodes of the pipeline networks by \(\pi _u = p _u ^2\) for \(u \in V \). In case of non-horizontal pipes, we refer to Koch et al. (2015).
Definition 2.5
A nomination \(\ell \in N\) is feasible if a point \((q,\pi )\) exists that satisfies
where  and
and  represent the set of arcs leaving and entering node \(u \in V \), \(\Lambda _a >0\) is an arc-specific constant for any \(a \in A \), and \(0 < {\pi }^-_u \le {\pi }^+_u \) are potential bounds for any \(u \in V \).
represent the set of arcs leaving and entering node \(u \in V \), \(\Lambda _a >0\) is an arc-specific constant for any \(a \in A \), and \(0 < {\pi }^-_u \le {\pi }^+_u \) are potential bounds for any \(u \in V \).
Constraints (1a) ensure mass flow conservation at every node of the network. The flows \(q \) couple the potentials for every arc of the network in Constraint (1b). Since we model a gas network as a directed graph, we can interpret the direction of flow. Thus, for an arc \((u, v) \in A \), the arc flow can be negative if it flows in the opposite direction of the orientation of the arc, i.e., if it flows from \(v\) to \(u \). Moreover, technical restrictions of the network impose that the potentials are bounded (1c). For other models of gas transport such as capacitated linear and linear potential-based flows, we refer to Schewe et al. (2019), Labbé et al. (2019).
For a given nomination \(\ell \in N\) and a weakly connected pipe-only network, the corresponding flows \(q = q (\ell )\), i.e., they satisfy Constraints (1a) and (1b), are unique because they are the optimal solution of a strictly convex minimization problem; see Maugis (1977). Moreover, the corresponding potentials \(\pi = \pi (\ell )\) are unique up to constant shifts; see Ríos-Mercado et al. (2002). Consequently, the potential-differences \(\pi _{u} - \pi _{v}\) for \(u, v\in V \) are unique for a given nomination \(\ell \). We further note that the feasibility of a nomination can be verified by different approaches; see e.g., Koch et al. (2015), Gotzes et al. (2016). We now turn to the feasibility of a booking, which is less studied in the literature and very challenging.
Definition 2.6
We say that a booking \(b\) is feasible if all booking-compliant nominations \(\ell \in N(b)\) are feasible.
For deciding the feasibility of a booking, an infinite number of nominations has to be checked for feasibility, in general. As in Labbé et al. (2021), we make the following non-restrictive assumption on the potential bounds.
Assumption 2.7
The potential bound intervals have a non-empty intersection, i.e.,
This assumption is a necessary condition for the feasibility of a booking, since it ensures that the zero nomination, which is always booking-compliant, with corresponding zero flows is feasible in the network. Consequently, if this assumption is not satisfied, it directly follows that all bookings are infeasible. Moreover, we can check this assumption in polynomial time a priori.
It is shown in Labbé et al. (2019), that the feasibility of a booking \(b\) can be characterized by polynomially many nominations with maximum potential-difference between all pairs of nodes. To this end, the authors introduce, for every pair of nodes \(({w_1},{w_2}) \in V ^2\), the following problem
where \(\varphi _{{w_1}{w_2}}\) is the corresponding optimal value function that depends on the booking b. We note that the zero vector is feasible for Problem (2) due to Assumption 2.7. Consequently, an optimal solution always exists since the variables \(\ell \) and \(q \) are bounded, and thus, we can bound the potentials \(\pi \) by a finite positive constant due to Theorem 7.1 of Chapter 7 in Koch et al. (2015).
Problem (2) computes the maximum potential-difference between the given nodes \({w_1}\) and \({w_2}\) within the booking \(b\). Thus, we do not consider any potential bounds that possibly restrict the maximum potential-difference. From Theorem 10 in Labbé et al. (2019) it then follows that these maximum potential-differences satisfy certain potential bounds if and only if booking \(b\) is feasible. More precisely, booking \(b\) is feasible if and only if
holds for every pair of nodes \(({w_1}, {w_2})\in V ^2\). Exploiting this approach, we can decide the feasibility of a booking by solving the nonlinear and nonconvex optimization problems (2) for every pair of nodes. For trees and single-cycle networks, this can be done in polynomial time; see Labbé et al. (2019), Robinius et al. (2019), Labbé et al. (2021). In this paper, we show that deciding the feasibility of a booking w.r.t. nonlinear potential-based flow model (2.5) is coNP-hard. We further prove that the decision variant of (2) is \({\textsc {NP}}\)-hard. To this end, we formally define the problem of deciding the feasibility of a booking w.r.t. nonlinear gas flow model (2.5) and the decision problem corresponding to (2).
Deciding the feasibility of a booking (FB).
- Input: :
-
Graph \(G =(V,A)\) with entries \(V_+ \), exits \(V_- \), inner nodes \(V _0\), potential drop coefficients \(\Lambda _a \in \mathbb {Q} _{> 0}\) for \(a \in A \), potential bounds \({\pi }^-_u \le {\pi }^+_u, {\pi }^-_u, {\pi }^+_u \in \mathbb {Q} _{> 0}\) for all \(u \in V \), and a booking \(b\in \mathbb {Q} _{\ge 0}^{V}\).
- Question: :
-
Is booking \(b\) feasible, i.e., does for every booking-compliant nomination \(\ell \in N(b)\) a feasible point \((q, \pi )\) for (2.5) exist?
Computing a maximum potential-difference nomination (MPD).
- Input: :
-
Graph \(G =(V,A)\) with entries \(V_+ \), exits \(V_- \), inner nodes \(V _0\), potential drop coefficients \(\Lambda _a \in \mathbb {Q} _{> 0}\) for \(a \in A \), a booking \(b\in \mathbb {Q} _{\ge 0}^{V}\), two nodes \({w_1},{w_2}\in V \), and a threshold \(T\in \mathbb {Q} \).
- Question: :
-
Does a solution of (2) with objective \( \varphi _{{w_1}{w_2}}(b) \ge T\) exist?
3 Notations and basic observations
We now introduce notations and basic observations, which are taken from Labbé et al. (2021). Using these results, we prove that FB w.r.t. our nonlinear potential-based flow model (2.5) is coNP-hard in Sect. 4. In the following, we consider the directed and weakly connected graph \(G = (V, A)\) that models the considered gas network. For a nomination \(\ell \in N\), entry and exit nodes \(v\in V_+ \cup V_- \) are called active if \(\ell _v>0\) holds. We denote the set of active entries by \(V_+ ^{>}\mathrel {{\mathop :}{=}}\left\{ {v\in V_+ :\ell _v>0} \right\} \) and the set of active exits by \(V_- ^{>}\mathrel {{\mathop :}{=}}\left\{ {v\in V_- :\ell _v>0} \right\} \). Furthermore, the set of non-zero nominations is given by \(N^0\mathrel {{\mathop :}{=}}N\setminus \left\{ {0} \right\} \).
Modeling gas networks by directed graphs enables us to interpret the direction of arc flows. However, the physical flow in a potential-based network is independent from the direction of the arcs. As described in Ahuja et al. (1993), we introduce a path in a directed graph \(G =(V, A)\) as a sequence of nodes and arcs without any repetition of nodes. For two nodes \(v_{1}, v_{r} \in V \), a path  between nodes \(v_{1}\) and \(v_{r}\) is a sequence \(v_{1} - a_{1} - v_{2} - a_{2} - \ldots - a_{r-1} - v_{r}\) such that for each \(1 \le k \le r-1\) either \(a_{k} = (v_{k}, v_{k+1}) \in A \) or \(a_{k} = (v_{k+1}, v_{k}) \in A \) holds. As in Ahuja et al. (1993), we partition the arcs of a path into forward and backward arcs. An arc (i, j) of the considered path is called a forward arc if the path visits node i before node j and otherwise it is called a backward arc. Further, path
between nodes \(v_{1}\) and \(v_{r}\) is a sequence \(v_{1} - a_{1} - v_{2} - a_{2} - \ldots - a_{r-1} - v_{r}\) such that for each \(1 \le k \le r-1\) either \(a_{k} = (v_{k}, v_{k+1}) \in A \) or \(a_{k} = (v_{k+1}, v_{k}) \in A \) holds. As in Ahuja et al. (1993), we partition the arcs of a path into forward and backward arcs. An arc (i, j) of the considered path is called a forward arc if the path visits node i before node j and otherwise it is called a backward arc. Further, path  is a directed path from \(v_{1}\) to \(v_{r}\) if it does not contain any backward arcs.
is a directed path from \(v_{1}\) to \(v_{r}\) if it does not contain any backward arcs.
To provide a more compact representation of paths, we denote a path  by the corresponding set of arcs, i.e.,
by the corresponding set of arcs, i.e.,  , in the following. If it is clear from the context, we may omit the start and end node and simply use
, in the following. If it is clear from the context, we may omit the start and end node and simply use  to express that arc \(a \) is part of the considered path. We further note that the considered paths do not contain any cycles in the graph underlying \(G \). This is in line with the considered physics of gas transport, since in every solution \((q, \pi )\) of (2.5) no cyclic flow exists due to (1b).
to express that arc \(a \) is part of the considered path. We further note that the considered paths do not contain any cycles in the graph underlying \(G \). This is in line with the considered physics of gas transport, since in every solution \((q, \pi )\) of (2.5) no cyclic flow exists due to (1b).
For an arc \(a =(u,v)\in A \), we now introduce the following characteristic function

where  is an arbitrary path. The following lemma of Labbé et al. (2021) uses a classical result from linear flow models to construct a flow decomposition without cyclic flows.
is an arbitrary path. The following lemma of Labbé et al. (2021) uses a classical result from linear flow models to construct a flow decomposition without cyclic flows.
Lemma 3.1
(Lemma 2 and Corollary 3 in Labbé et al. (2021)) For \(\ell \in N^0\), let  be the set of paths in \(G \) with an active entry as start node and an active exit as end node. Then, a decomposition of the given arc flows \(q = q (\ell )\), satisfying (1a) and (1b), into path flows exists, such that
be the set of paths in \(G \) with an active entry as start node and an active exit as end node. Then, a decomposition of the given arc flows \(q = q (\ell )\), satisfying (1a) and (1b), into path flows exists, such that

where  is the nonnegative flow along the path
is the nonnegative flow along the path  . Furthermore, the flows \(q \) can be chosen such that if \(q _{a} > 0\) for \(a \in A \) and
. Furthermore, the flows \(q \) can be chosen such that if \(q _{a} > 0\) for \(a \in A \) and  for
for  , then
, then  for \(a \in A \) and
for \(a \in A \) and  for
for  , then
, then  holds. Moreover, the flows satisfy
holds. Moreover, the flows satisfy

Similar to Labbé et al. (2021), we express the potential-difference function along a given path.
Definition 3.2
Let a path  be given. Then, the potential-difference function along
be given. Then, the potential-difference function along  is given by
is given by

As described in Labbé et al. (2021), from Constraints (1b) it follows that for any node pair \(u,v\in V \) and for any path  , the equation
, the equation  is satisfied, where \(\pi (\ell )\) and \(q (\ell )\) correspond to the potentials and flows of a given nomination \(\ell \in N\). If \( from \)\(u \) to \(v\), then the potential-difference function simplifies to
is satisfied, where \(\pi (\ell )\) and \(q (\ell )\) correspond to the potentials and flows of a given nomination \(\ell \in N\). If \( from \)\(u \) to \(v\), then the potential-difference function simplifies to

As last basic observation, we explicitly state some properties for directed paths and the potential-difference function proven in Labbé et al. (2021).
Lemma 3.3
For \(u,v\in V \), let  be a directed path from \(u \) to \(v\). Then, the following holds:
be a directed path from \(u \) to \(v\). Then, the following holds:
-
(a)
 is continuous.
is continuous. -
(b)
 is strictly increasing w.r.t. every component. That means, for \(q \) fixed except for one value \(q _{a}\),
is strictly increasing w.r.t. every component. That means, for \(q \) fixed except for one value \(q _{a}\),  ,
, 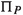 is increasing in \(q _a \).
is increasing in \(q _a \). -
(c)
 is unbounded w.r.t. every component, i.e., for
is unbounded w.r.t. every component, i.e., for  ,
, 
-
(d)
 is additive w.r.t. the path, i.e., for every node \(v'\) of the path
is additive w.r.t. the path, i.e., for every node \(v'\) of the path  ,
, 
with
 .
. -
(e)
If \((\ell , q, \pi )\) satisfies Constraints (1a) and (1b), then
 holds if and only if \(\pi _u \ge \pi _v\) holds.
holds if and only if \(\pi _u \ge \pi _v\) holds.
4 Hardness
In this section, we prove that deciding the feasibility of a booking (FB) w.r.t. nonlinear potential-based flow model (2.5) is coNP-hard. To this end, we reduce Partition to the infeasibility of a booking. We consider Partition as it is defined in Garey and Johnson (1990).
Partition (Part).
- Input: :
-
\(S_1,\dotsc ,S_n \in \mathbb {N} \) with \(n \in \mathbb {N} \), \(I= \left\{ {1, \dotsc , n} \right\} \).
- Question: :
-
Does \( I_1 \subseteq I\) with \( \sum _{i \in I_1}S_i = \sum _{I\setminus I_1} S_i\) exist?
In the following, we denote a Partition instance by \(\mathcal {S}\). The value \(K= \sum _{i \in I} S_i\) further represents the sum of all numbers of Partition instance \(\mathcal {S}\) and we assume without loss of generality that \(n \ge 3\) holds.
For a given Partition instance \(\mathcal {S}\), we now construct a corresponding booking instance with its graph \(G (\textsf {Part})= (V, A)\). To this end, we introduce for every number \(S_i\) of the Partition instance \(\mathcal {S}\) an entry node \(z^+_i\) and an exit node \(z^-_i\), which are connected by an arc. Furthermore, we add a main entry node \(s\) and a main exit node \(t\). Each of these two nodes is connected to every entry node \(z^+_i\) for \(i \in I\). The booking and potential bounds are chosen such that we only have to consider (2) w.r.t. \((s, t)\) for deciding the feasibility of the considered booking. We then prove that the corresponding objective value, i.e., the potential-difference between \(s\) and \(t\), exceeds a certain threshold value if and only if the Partition instance \(\mathcal {S}\) is feasible. In detail, graph \(G (\textsf {Part})= (V, A)\) is constructed as
A visualization of the graph \(G (\textsf {Part})\) is given in Fig. 2. We consider for \(G (\textsf {Part})\) the booking \(b\)
and potential drop coefficients \(\Lambda _a > 0\) for \(a \in A \) given by
We finally set the potential bounds for this booking instance. To this end, we first introduce some parameters depending on the input \(K\) that are required throughout this section.
We note that \({0<} \ T(K)< 1\) holds due to \(K\ge 1\). Further, we do not explicitly simplify these parameters by computing the maxima, because each of these parameters is separately used in the following proofs. Thus, the extensive form of (3a) and (3b) is useful for the remainder of this section.
The lower \({\pi }^-\) and upper \({\pi }^+\) potential bounds for \(G (\textsf {Part})\) are given by
We note that for a given instance of Partition, we can build the corresponding booking instance \(G (\textsf {Part})\) in polynomial time and its coding length is polynomially bounded from above by the coding length of the given Partition instance. We now consider \(G (\textsf {Part})\) and its booking \(b\) throughout this section. From Sect. 2, it follows that the booking \(b\) is feasible if and only if
holds for every pair of nodes \(({w_1}, {w_2})\in V ^2\), where \(\varphi _{{w_1}{w_2}}(b)\) is the optimal value function of (2) that denotes the maximum potential-difference between \({w_1}\) and \({w_2}\) within booking \(b\).
We first show that Inequality (4) is directly satisfied for \(({w_1}, {w_2}) \in V ^2 \setminus \left\{ {(s, t)} \right\} \), due to the choice of the lower and upper potential bounds.
Lemma 4.1
For any node pair \(({w_1}, {w_2}) \in V ^2 \setminus \left\{ {(s, t)} \right\} \) of \(G (\textsf {Part})=(V,A)\), Inequality (4) is satisfied.
Proof
Let \((q, \pi )\) be an optimal solution of \(\varphi _{{w_1}{w_2}}(b)\). We note that for the case \({w_1}={w_2}\), the equation \(\varphi _{{w_1}{w_2}}(b)=0\) holds and, thus, Condition (4) is satisfied in this case due to \({\pi }^-_{u} \le {\pi }^+_{u}\) for all \(u \in V \). Consequently, we assume \({w_1}\ne {w_2}\in V \) in the following. From (1a), (1b), and \(\sum _{u \in V_+} b_u = ({3}/{2}) K\), it follows \(\left| q _a \right| \le ({3}/{2}) K\) for every arc \(a \in A \). For an arbitrary path  , it holds
, it holds

Since the path  with minimal number of arcs consists of at most 4 arcs, this leads to
with minimal number of arcs consists of at most 4 arcs, this leads to
\(\square \)
Consequently, deciding the feasibility of booking \(b\) for \(G (\textsf {Part})\) reduces to the following.
Corollary 4.2
Booking \(b\) is feasible for \(G (\textsf {Part})\) if and only if \(\varphi _{st}(b) \le T(K)\).
Proof
Booking \(b\) is feasible if and only if for every pair of nodes Inequalities (4) hold. From Lemma 4.1 it follows that for each pair of nodes except \((s, t) \in V ^{2}\) Inequalities (4) are satisfied. Consequently, booking \(b\) is feasible if and only if
which proves the claim. \(\square \)
In the remainder of this section, we prove that \(\varphi _{st}(b) > T(K)\) is satisfied if and only if the given Partition instance \(\mathcal {S}\) is feasible. We first prove that if Partition instance \(\mathcal {S}\) is feasible, then \(\varphi _{st}(b)\) exceeds the threshold \(T(K)\).
Lemma 4.3
If Partition instance \(\mathcal {S}\) is feasible, then \(\varphi _{st}(b) \ge 1 > T(K)\) holds.
Proof
Since Partition instance \(\mathcal {S}\) is feasible, \(M_1\subset I\) and \(M_2\subset I\) with \(M_1\cap M_2= \emptyset \) and \(M_1\cup M_2= I\) exist such that \(\sum _{i \in M_1} S_i = \sum _{i \in M_2} S_i = {K}/{2}\) holds. We now construct a feasible point \((\ell , q, \pi )\) of (2) w.r.t. \((s, t)\) that has an objective value of 1.
We note that the constructed point \((\ell , q, \pi )\) satisfies Constraints (1a) as well as (1b) and \(\ell \) respects the booking bounds. Consequently, \((\ell , q, \pi )\) is a feasible point for (2) w.r.t. \((s, t)\). Moreover, the corresponding objective value equals 1. Thus, the optimal solution of \(\varphi _{st}(b)\) has an objective value of at least \(1 > T(K)\). \(\square \)
We next prove that if we require nonnegative flow in (2) and Partition instance \(\mathcal {S}\) is infeasible, then an optimal solution does not exceed the threshold value \(T(K)\), i.e., \(\varphi _{st}(b) < T(K)\) holds. To this end, we introduce the nonnegative flow variant of (2) for node pair \((s, t)\):
With the help of Lemmas 4.5–4.13, we prove that \(\varphi ^+_{st}(b) < T(K)\) is satisfied if Partition instance \(\mathcal {S}\) is infeasible. Afterward, we use these results to show the general case \(\varphi _{st}(b)\!\!< \!\!T(K)\). The main idea is that if the considered Partition instance is infeasible, then for at least one \(i \in I\) the flows satisfy \({q _{(s, z^+_i)} > 0}\) and \({q _{(z^+_i, t)} > 0}\); see Lemma 4.6. This together with the considered nonlinear potential-based flow (1b) plays an important role in the remaining section which is based on the following observation.
Observation 4.4
Let be \(a > 0\) and \(b > 0\) with \(a^2 + b^2 = c\). Then, \(a + b > \sqrt{c}\) holds.
To provide an intuition for the main idea, we give the following explanation. For every \(i \in I\) and solution \((\ell , q, \pi )\) of (5), the equality
holds, which we will show in Lemma 4.7. From Observation 4.4, it follows that we need strictly more flow in terms of \(q _{(s, z^+_i)} + q _{(z^+_i, t)}\) to obtain a potential-difference of \(\pi _s- \pi _t\) if \(q _{(s, z^+_i)} >0 \) and \( q _{(z^+_i, t)} > 0\) hold in comparison to the case if one of these flows is zero. We prove in Lemma 4.6 that if Partition instance \(\mathcal {S}\) is infeasible, \(q _{(s, z^+_i)} >0 \) and \( q _{(z^+_i, t)} > 0\) for at least one \(i \in I\) in an optimal solution of (5) is satisfied. The latter is not necessarily the case if \(\mathcal {S}\) is feasible; see Lemma 4.3. Consequently, we need strictly more flow to obtain a certain potential-difference \(\pi _s- \pi _t\) if \(\mathcal {S}\) is infeasible in contrast to the case if \(\mathcal {S}\) is feasible. This is one of the main reasons why the optimal value of (5) cannot exceed the threshold \(T(K)\) if Partition instance \(\mathcal {S}\) is infeasible due to the monotonicity of the potential drop  w.r.t. the flow \(q \); see Lemma 3.3 (b).
w.r.t. the flow \(q \); see Lemma 3.3 (b).
We start the proof of \(\varphi ^+_{st}(b) < T(K)\) by characterizing optimal solutions of (5) in the next two lemmas.
Lemma 4.5
Let \((\ell , q, \pi )\) be an optimal solution of (5). Then,
holds.
Proof
We consider a flow decomposition of Lemma 3.1 for given \((\ell ,q)\) and prove the claim by the distinction of three different cases.
If \(\ell _{s} < {K}/{2}\) and \(\ell _{t} < {K}/{2}\) hold, then from Lemma 3.3 it follows that \(\varepsilon _i > 0\) for all \(i \in I\) exist such that
and we can increase the flow  by \(\varepsilon _i\) for \(i \in I\), such that the potential drop
by \(\varepsilon _i\) for \(i \in I\), such that the potential drop  is the same for \(i \in I\). Here, \(P_{i} {(s, t)}\) is the directed path from \(s\) to \(t\) via \(z^+_i\), i.e., \(P_{i} {(s, t)} = {\left\{ {(s, z^+_i), (z^+_i, t)} \right\} }\). The modification increases the potential drop \(\pi _{s} - \pi _{t}\) due to Lemma 3.3 (b). This is a contradiction to the optimality of \((\ell , q, \pi )\) for (5).
is the same for \(i \in I\). Here, \(P_{i} {(s, t)}\) is the directed path from \(s\) to \(t\) via \(z^+_i\), i.e., \(P_{i} {(s, t)} = {\left\{ {(s, z^+_i), (z^+_i, t)} \right\} }\). The modification increases the potential drop \(\pi _{s} - \pi _{t}\) due to Lemma 3.3 (b). This is a contradiction to the optimality of \((\ell , q, \pi )\) for (5).
If \(\ell _{s} = {K}/{2}\) and \(\ell _{t} < {K}/{2}\) hold, then from (1a) it follows that the total flow leaving node \(s\) is \({K}/{2}\) and the total flow entering node \(t\) is strictly less than \({K}/{2}\). Moreover, no negative flow is entering \(s\) or leaving node \(t\) due to (5c). Thus, there is \(i \in I\) such that  for
for  holds. We additionally consider the path \(P_{i} {(s, t)}\) as in the previous case. Due to Lemma 3.3 and the graph structure of \(G (\textsf {Part})\), \(\varepsilon > 0\) and \(0< \tilde{\varepsilon } < \varepsilon \) exist such that decreasing
holds. We additionally consider the path \(P_{i} {(s, t)}\) as in the previous case. Due to Lemma 3.3 and the graph structure of \(G (\textsf {Part})\), \(\varepsilon > 0\) and \(0< \tilde{\varepsilon } < \varepsilon \) exist such that decreasing  by \(\varepsilon \) and increasing
by \(\varepsilon \) and increasing  by \(\tilde{\varepsilon }\) does not change the potential drop
by \(\tilde{\varepsilon }\) does not change the potential drop  and \(\ell _t< {K}/{2}\) as well as (5c) still holds. Consequently, \(\ell _{s} < {K}/{2}\) and \(\ell _{t} < {K}/{2}\) is satisfied and analogously to the above this is a contradiction to the optimality of the considered solution.
and \(\ell _t< {K}/{2}\) as well as (5c) still holds. Consequently, \(\ell _{s} < {K}/{2}\) and \(\ell _{t} < {K}/{2}\) is satisfied and analogously to the above this is a contradiction to the optimality of the considered solution.
If \(\ell _{t} = {K}/{2}\) and \(\ell _{s} < {K}/{2}\) are satisfied, then, analogously to the previous case, from (1a) and (5c) it follows that \(i \in I\) exist such that  for
for  holds. We again consider the path \(P_{i} {(s, t)}\) as before. Due to Lemma 3.3 and the graph structure of \(G (\textsf {Part})\), \(\varepsilon > 0\) and \(0< \tilde{\varepsilon } < \varepsilon \) exist such that decreasing
holds. We again consider the path \(P_{i} {(s, t)}\) as before. Due to Lemma 3.3 and the graph structure of \(G (\textsf {Part})\), \(\varepsilon > 0\) and \(0< \tilde{\varepsilon } < \varepsilon \) exist such that decreasing  by \(\varepsilon \) and increasing
by \(\varepsilon \) and increasing  by \(\tilde{\varepsilon }\) does not change the potential drop
by \(\tilde{\varepsilon }\) does not change the potential drop  and \(\ell _{s} < {K}/{2}\) as well as (5c) still holds. Consequently, \(\ell _{s} < {K}/{2}\) and \(\ell _{t} < {K}/{2}\) is satisfied and analogously to the above this is a contradiction to the optimality of the considered solution. \(\square \)
and \(\ell _{s} < {K}/{2}\) as well as (5c) still holds. Consequently, \(\ell _{s} < {K}/{2}\) and \(\ell _{t} < {K}/{2}\) is satisfied and analogously to the above this is a contradiction to the optimality of the considered solution. \(\square \)
We now show that if Partition instance \(\mathcal {S}\) is infeasible, then every optimal solution of (5) satisfies that at least one path \(P_{i} {(s, t)} = {\left\{ {(s, z^+_i), (z^+_i, t)} \right\} }\) with \(i \in I\) and \(q _a > 0\) for \(a \in P_{i} {(s, t)}\) exists.
Lemma 4.6
If Partition instance \(\mathcal {S}\) is infeasible, then for any optimal solution \((\ell , q, \pi )\) of (5), there exists an index \(i \in I\) such that \(q _{(s, z^+_i)} > 0\) and \(q _{(z^+_i, t)} > 0\) hold.
Proof
We prove the contraposition. To this end, let \((\ell , q, \pi )\) be an optimal solution of (5) that satisfies \(q _{(s, z^+_i)} = 0\) or \(q _{(z^+_i, t)} = 0\) for each \(i \in I\). Due to Lemma 4.5 and (5c), \(q _{(s, z^+_i)} = q _{(z^+_i, t)} = 0\) is not satisfied for any \(i \in I\) in an optimal solution of (5). Thus, the index sets
satisfy \(M_1\cap M_2= \emptyset \) and \(M_1\cup M_2= I\). Consequently, if \(i \in M_1\), then \(q _{(s, z^+_{i})} >0\) and \(q _{(z^+_{i},t)} = 0\) hold. Thus, the structure of graph \(G (\textsf {Part})\) implies \(q _{(s, z^+_{i})} \le S_{i}\) since positive flow via arc \((s, z^+_{i})\) can only be sent to exit \(z^-_{i}\), which demand is bounded from above by \(S_{i}\). Analogously it follows the case for \(i \in M_2\) and we obtain the flow bounds
Furthermore, from Lemma 4.5 it follows \(\ell _{s} = \ell _{t} = {K}/{2}\). The latter together with flow conservation (1a) and (6), leads to
From this and \(\sum _{i \in M_1\cup M_2} S_i = \sum _{i \in I} S_i = K\), we obtain
and thus, Partition instance \(\mathcal {S}\) is feasible. \(\square \)
In the next lemma, we express a relation between certain flows and the objective value of Problem (5), which we exploit multiple times in the following proofs.
Lemma 4.7
Let \((\ell , q, \pi )\) be a feasible point of Problem (5) with objective value \(\varphi \). Then, for each \(i \in I\) the following equality
holds.
Proof
For every \(i \in I\), it follows from Constraints (1b) that
In addition, the flows \(q \) are nonnegative since they satisfy Constraints (5c), which in combination with the previous equality proves the claim. \(\square \)
With the help of the previous three lemmas, we now prove that if Partition instance \(\mathcal {S}\) is infeasible, then the optimal value of (5) is strictly smaller than 1.
Lemma 4.8
If Partition instance \(\mathcal {S}\) is infeasible, then \(\varphi ^+_{st}(b) < 1\) holds.
Proof
Let \((\ell ,q, \pi )\) be an optimal solution of (5) with objective value \(\phi \). Due to Lemma 4.5 and flow conservation (1a), the equalities
are satisfied. From Lemma 4.6, it follows that an index \(l \in I\) with \(q _{(s,z^+_l)} > 0\) and \(q _{(z^+_l, t)} > 0\) exists. Further, Lemma 4.7 implies that for every \(i \in I\) Equality (7) is satisfied. Applying Observation 4.4 then leads to
From this and (8), we obtain
which implies \(\phi < 1\). \(\square \)
Up to now, we have shown that if Partition instance \(\mathcal {S}\) is feasible, then \(\varphi _{st}(b) \ge 1\) holds; see Lemma 4.3. Furthermore, if \(\mathcal {S}\) is infeasible, then \(\varphi ^+_{st}(b) < 1\) is satisfied. In general, it now suffices to show that there is a small \(\varepsilon >0\) such that for infeasible \(\mathcal {S}\) the inequality \(\varphi _{st}(b) \le 1- \varepsilon \) holds. Then, we can set \({\pi }^-_{t} = {\pi }^+_{{t}} -1 + \varepsilon \) and analogously to Corollary 4.2 it follows that the considered booking \(b\) is feasible if and only if \(\varphi _{st}(b) \le 1 - \varepsilon \). In doing so, the coding length of \(\varepsilon >0\) has to be polynomially bounded from above by the coding length of \(\mathcal {S}\) since \(\varepsilon > 0\) is part of the booking instance. In the following Lemmas 4.9–4.13, we now show that if \(\mathcal {S}\) is infeasible, then \(\varphi ^+_{st}(b)< T(K)< 1\) holds. Afterward, we use this result for nonnegative flows to prove that for infeasible \(\mathcal {S}\) also the general case \(\varphi _{st}(b)< T(K)< 1\) is satisfied. Consequently, booking \(b\) is feasible if and only if \(\mathcal {S}\) is infeasible due to Corollary 4.2.
For a feasible point \((\ell , q, \pi )\) of (5) with positive objective value, we introduce the following partition of the indices \(I\)
We note that \(q _{(s, z^+_i)} = q _{(z^+_i, t)} = 0\) does not hold for any \(i \in I\) due to the positive objective value of the considered feasible point \((\ell , q, \pi )\). Moreover, the parameters \(\varepsilon (K)\) and \(M(K)\) of (3a) come now into play.
Lemma 4.9
Let Partition instance \(\mathcal {S}\) be infeasible. If \((\ell , q, \pi )\) is an optimal solution of (5) such that \(q _{(s, z^+_l)} > 0\) and \(q _{(z^+_l, t)} > 0\) hold for exactly one index \(l \in I\), then the corresponding objective value \(\phi \) satisfies
Proof
We assume for a contradiction that an optimal solution \((\ell , q, \pi )\) of (5) exists such that the requirements are satisfied and the objective value \(\phi \) satisfies \(\phi \ge 1-\varepsilon (K)> 0\). From Lemma 4.8, it follows \(\phi < 1\). We partition the index set \(I\) according to (9).
Due to the requirements, \(M_1\cap M_2= \emptyset \), \(M_3= \left\{ {l} \right\} \), and \(M_1\cup M_2\cup \left\{ {l} \right\} = I\) hold. Consequently, Lemma 4.5 and flow conservation (1a) lead to
Additionally, we can apply Lemma 4.7 and thus, from Equalities (7) it follows
Combining Eqs. (10) and (11) leads to
We now distinguish different cases for the value of \(\sum _{i \in M_1} S_i\), respectively \(\sum _{i \in M_2} S_i\).
If \(\sum _{i \in M_1} S_i = {K}/{2}\) holds, then \(\sum _{i \in I\setminus M_1} S_i = {K}/{2}\) holds due to \(\sum _{i \in I} S_i = K\). This is a contradiction to the infeasibility of Partition instance \(\mathcal {S}\). Analogously it follows that \(\sum _{i \in M_2} S_i = {K}/{2}\) cannot hold.
If \(\sum _{i \in M_1} S_i > {K}/{2}\) holds, then \(\sum _{i \in M_1} S_i \ge {K}/{2} + {1}/{2}\) holds due to the integrality of \(S_i\) for \(i \in I\). This together with (12), and
leads to
which is a contradiction to \(q _{(s, z^+_l)} \ge 0\). Analogously it follows that \(\sum _{i \in M_2} S_i > {K}/{2}\) cannot hold.
Consequently, \(\sum _{i \in M_1} S_i < {K}/{2}\) and \(\sum _{i \in M_2} S_i < {K}/{2}\) hold. Due to the integrality of \(S_i\) for \(i \in I\), \(\sum _{i \in M_1} S_i \le {K}/{2} - {1}/{2}\) and \(\sum _{i \in M_2} S_i \le {K}/{2} -{1}/{2}\) are satisfied. From this, (12), and \(\phi < 1\), which holds due to Lemma 4.8, it follows
Combining the latter inequalities, Equality (7), and the strict inequalities \(2 \frac{1}{8K} \sqrt{\phi } S_l < 1/4\) as well as \(\left( \frac{1}{8 K} \right) ^2 < 1/4\), that follow from \(\phi < 1\) and \(S_l \le K\), leads to
and consequently, we obtain
From (10), (11), (13), and \(\sum _{i \in I} S_i = K\) we obtain
and consequently,
holds. This is a contradiction to the assumption
\(\square \)
We have proven that the optimal value of (5) does not exceed the threshold \(1 - \varepsilon (K)\) if exactly one index \(i \in I\) with \(q _{(s, z^+_i)} > 0\) and \(q _{(z^+_i, t)} > 0\) exists and Partition instance \(\mathcal {S}\) is infeasible. We now use this result to show that if arbitrarily many indices satisfy the latter property, the optimal objective value of (5) is bounded above by a threshold value smaller than 1. To this end, we consider two cases. In Lemma 4.12 at most one index \(i \in I\) satisfies the stricter property \(q _{(s, z^+_i)} \ge \varepsilon (K)> 0\) and \(q _{(z^+_i, t)} \ge \varepsilon (K)> 0\) where \(\varepsilon (K)\), defined in (3a), is a positive lower arc flow bound. Afterward, we consider that at least two indices satisfy this lower arc flow bound; see Lemma 4.13. To this end, we first prove two technical lemmas that we use in the following.
In the next lemma, we show that a feasible point for (1a), (5b), and (5c) with a minimum potential-difference between \(s\) and \(t\) can be modified to a feasible point of (5) while preserving the potential-difference between \(s\) and \(t\).
Lemma 4.10
Let \(M \ge 0\) and \((\ell , q)\) be a feasible point for (1a), (5b), (5c), and for all \(i \in I\)
holds. Then, a point \((\tilde{\ell }, {\tilde{q}}, \pi )\) satisfying (1a), (5b), (5c), and additionally (1b) with
for all \(i \in I\) exists. Moreover, \((\tilde{\ell }, {\tilde{q}}, \pi )\) is a feasible point for (5) with objective value of M.
Proof
Let \((\ell , q)\) be a point that satisfies the requirements. Since \((\ell , q)\) satisfies (1a) and (5c) for graph \(G (\textsf {Part})\), the flow \(q \) cannot contain any cycle flow. Thus, we obtain a flow decomposition as in Lemma 3.1 for \((\ell , q)\) by applying Theorem 3.5 of Ahuja et al. (1993). Due to \(q _a \ge 0\) for \(a \in A \) and the graph structure of \(G (\textsf {Part})\), this flow decomposition satisfies that a positive flow \(q _{(s, z^+_i)} > 0\), respectively \(q _{(z^+_i, t)} > 0\) for any \(i \in I\) can only be the result of a positive flow  with
with  being one of the following paths
being one of the following paths



For every \(i \in I\) with
we decrease positive flows  with
with  of (14) until
of (14) until
holds. This is possible since the left-hand side of the Equality (15), respectively the previous strict inequality, is continuous and strictly increasing w.r.t. \(q _{(s, z^+_i)}\) and \(q _{(z^+_i, t)}\); see Lemma 3.3. Thus, we can decrease positive flows  with
with  of (14) such that Equality (15) is satisfied. Furthermore, (1a), (5b), (5c) are still satisfied.
of (14) such that Equality (15) is satisfied. Furthermore, (1a), (5b), (5c) are still satisfied.
We now can define the following potentials
which satisfy (1b) due to (15) and (5c). Moreover, for every \(i \in I\) the potentials satisfy
where the last equation follows from (15). Thus, \(\pi _s- \pi _{t} = M\) is satisfied. \(\square \)
In the next lemma, we prove that for every optimal solution of (5) an optimal solution with a specific flow decomposition exists. Moreover, the flows on arcs of the paths  for all \(i \in I\) do not differ between the two considered optimal solutions.
for all \(i \in I\) do not differ between the two considered optimal solutions.
Lemma 4.11
Let Partition instance \(\mathcal {S}\) be infeasible. Let \((\ell , q,\pi )\) be an optimal solution of (5). Then an optimal solution \((\tilde{\ell }, {\tilde{q}}, \tilde{\pi })\) of (5) with a flow decomposition of Lemma 3.1 for \((\tilde{\ell },\tilde{q})\) exists such that if  , then
, then  is defined by either (14a) or (14b). Additionally, \(q _{(s, z^+_i)} = {\tilde{q}}_{(s, z^+_i)}\) and \(q _{(z^+_i, t)} = {\tilde{q}}_{(z^+_i, t)}\) for \(i \in I\) is satisfied.
is defined by either (14a) or (14b). Additionally, \(q _{(s, z^+_i)} = {\tilde{q}}_{(s, z^+_i)}\) and \(q _{(z^+_i, t)} = {\tilde{q}}_{(z^+_i, t)}\) for \(i \in I\) is satisfied.
Proof
Let \((\ell , q, \pi )\) be an optimal solution of (5) with objective value \(\phi \). Consequently, for each \(i \in I\) the equation \(q _{(s, z^+_i)}^2 + q _{(z^+_i, t)}^2 = \phi S^2_i\) is satisfied due Lemma 4.7. Further, from Lemma 4.8, it follows \(\phi < 1\) and thus, flows \(q \) satisfy \(q _{(s, z^+_i)} < S_i\) as well as \(q _{(z^+_i, t)} < S_i\) for \(i \in I\). We now consider a flow decomposition of Lemma 3.1 corresponding to solution \((\ell , q, \pi )\). Since \(q _a \ge 0\) for \(a \in A \) holds and the graph structure of \(G (\textsf {Part})\), this flow decomposition can be chosen such that  can only be positive for a path
can only be positive for a path  of (14) or
of (14) or  consisting of arc \((z^+_i, z^-_i)\) for an \(i \in I\), which follows from Theorem 3.5 in Ahuja et al. (1993).
consisting of arc \((z^+_i, z^-_i)\) for an \(i \in I\), which follows from Theorem 3.5 in Ahuja et al. (1993).
If  for an index \(i \in I\) holds, then we delete this flow. We note that this does not modify flow on arcs \((s, z^+_i)\), respectively \((z^+_i, t)\), for \(i \in I\). Thus, the modified nomination and flows \((\tilde{\ell }, {\tilde{q}})\) can be extended to a solution \((\tilde{\ell }, {\tilde{q}}, \tilde{\pi })\) of (5) with objective value \(\phi \), where the potentials \(\tilde{\pi }\) are given by (16). Consequently, we can assume w.l.o.g.
for an index \(i \in I\) holds, then we delete this flow. We note that this does not modify flow on arcs \((s, z^+_i)\), respectively \((z^+_i, t)\), for \(i \in I\). Thus, the modified nomination and flows \((\tilde{\ell }, {\tilde{q}})\) can be extended to a solution \((\tilde{\ell }, {\tilde{q}}, \tilde{\pi })\) of (5) with objective value \(\phi \), where the potentials \(\tilde{\pi }\) are given by (16). Consequently, we can assume w.l.o.g.  for \(i \in I\) in the remaining proof.
for \(i \in I\) in the remaining proof.
We now consider \(i \in I\) with  . Due to \(q _{(s, z^+_i)} < S_i\) and \(q _{(z^+_i, t)} < S_i\) for \(i \in I\), booking \(b\), and (5c), we can set
. Due to \(q _{(s, z^+_i)} < S_i\) and \(q _{(z^+_i, t)} < S_i\) for \(i \in I\), booking \(b\), and (5c), we can set  to zero and increase
to zero and increase  and
and  by \(\varepsilon \) such that the corresponding solution \((\tilde{\ell }, {\tilde{q}})\) satisfies (5b), (5c), and (1a). We note that
by \(\varepsilon \) such that the corresponding solution \((\tilde{\ell }, {\tilde{q}})\) satisfies (5b), (5c), and (1a). We note that
holds since before the modification  and, thus,
and, thus,

were satisfied. Analogously it follows \(\tilde{\ell }_{z^+_i} = \ell _{z^+_i} + \varepsilon \le b_{z^+_i} = S_i\). Additionally, we note that the flow on arc \((s, z^+_i)\), respectively \((z^+_i, t)\), for \(i \in I\) is not modified. We now repeat the above procedure for every \(i \in I\) with  . Afterward, we can extend the modified nomination and flows \((\tilde{\ell }, {\tilde{q}})\) to a solution \((\tilde{\ell }, {\tilde{q}}, \tilde{\pi })\) of (5) with objective value \(\phi \), where the potentials \(\tilde{\pi }\) are given by (16). Due to the modification, \(q _{(s, z^+_i)} = {\tilde{q}}_{(s, z^+_i)}\) and \(q _{(z^+_i, t)} = {\tilde{q}}_{(z^+_i, t)}\) for \(i \in I\) hold and the required flow decomposition is constructed. \(\square \)
. Afterward, we can extend the modified nomination and flows \((\tilde{\ell }, {\tilde{q}})\) to a solution \((\tilde{\ell }, {\tilde{q}}, \tilde{\pi })\) of (5) with objective value \(\phi \), where the potentials \(\tilde{\pi }\) are given by (16). Due to the modification, \(q _{(s, z^+_i)} = {\tilde{q}}_{(s, z^+_i)}\) and \(q _{(z^+_i, t)} = {\tilde{q}}_{(z^+_i, t)}\) for \(i \in I\) hold and the required flow decomposition is constructed. \(\square \)
For the case that Partition instance \(\mathcal {S}\) is infeasible, we now prove that if in an optimal solution of (5) for at most one \(i \in I\) the flow on the arcs \((s, z^+_i)\) and \((z^+_i, t)\) exceeds \(\varepsilon (K)\), then the corresponding objective value is below the threshold \(1 - \varepsilon (K)+ \varepsilon (K)^2\).
Lemma 4.12
Let Partition instance \(\mathcal {S}\) be infeasible. Let
and \((\ell , q, \pi )\) be an optimal solution of (5) that satisfies
Then, the objective value \(\phi \) corresponding to solution \((\ell , q, \pi )\) satisfies
Proof
We assume for a contradiction that \((\ell , q, \pi )\) is an optimal solution of (5) that satisfies the requirements and its objective value is \(\phi \ge 1 - \varepsilon (K)+ \varepsilon (K)^2\). We further assume w.l.o.g. that the corresponding flow decomposition of Lemma 3.1 for \((\ell , q)\) satisfies Lemma 4.11. From Lemma 4.8, it follows that \(\phi < 1\). In the following, we consider the paths (14) and partition the index set \(I\) as in (9).
Due to \(\phi \ge 1 - \varepsilon (K)+ \varepsilon (K)^2\) and Lemmas 4.6 and 4.9, \(\left| M_3\right| \ge 2\) holds. Further, the inequality \(q _{(s, z^+_i)} > \varepsilon (K)\) or \(q _{(z^+_i, t)} > \varepsilon (K)\) holds due to
where the first equality follows from Lemma 4.7 and the last inequality holds due to
We now set \(q _a = 0\) for each \(a =(u, v) \in \left\{ {(s, z^+_i):i \in I} \right\} \cup \left\{ {(z^+_i, t):i \in I} \right\} \) that satisfies \(q _a \le \varepsilon (K)\). This can be done in the considered flow decomposition by decreasing flows  , respectively
, respectively  for \(i \in I\). We denote the modified flows by \({\tilde{q}}\) and its corresponding nomination by \(\tilde{\ell }\), which satisfy (1a), (5b), and (5c). We further note that now \(\left| M_3\right| \le 1\) holds, due to (17).
for \(i \in I\). We denote the modified flows by \({\tilde{q}}\) and its corresponding nomination by \(\tilde{\ell }\), which satisfy (1a), (5b), and (5c). We further note that now \(\left| M_3\right| \le 1\) holds, due to (17).
For an arbitrary index \(i \in I\), we assume that \(q _{(z^+_i, t)}\) has been modified, i.e., \({\tilde{q}}_{(z^+_i, t)} = 0 < q _{(z^+_i, t)}\). Consequently, \({\tilde{q}}_{(s, z^+_i)} = q _{(s, z^+_i)}\) holds. This together with Lemma 4.7, \(\phi \ge 1 - \varepsilon (K)+ \varepsilon (K)^2\), and \(S_i \ge 1\) leads to
Analogously we can handle the case that \(q _{(s, z^+_i)}\) has been modified.
Due to this and \(\Lambda _{(s, z^+_i)} = \Lambda _{(z^+_i, t)} = 1/S_i^{2}\), we can apply Lemma 4.10 and obtain a solution \((\tilde{\ell }, {\tilde{q}}, \tilde{\pi })\) for (5) with objective value \( \tilde{\phi } \ge 1 - \varepsilon (K)> 0\). This solution satisfies \(\left| M_3\right| \le 1\) due to the modification, (17), and the fact that we only possibly decrease flows in Lemma 4.10 to obtain \((\tilde{\ell }, {\tilde{q}}, \tilde{\pi })\).
If \(\left| M_3\right| = 1\) holds, then this is a direct contradiction to Lemma 4.9.
We now assume \(\left| M_3\right| = 0\). Due to \(\left| M_3\right| \ge 2\) before the modification and the requirements, at least one arc flow was decreased by the above. Consequently, \(\tilde{\ell }_{s} < {K}/{2}\) or \(\tilde{\ell }_{t} < {K}/{2}\) holds. Furthermore, \(\left| M_1\right| \ge 1\) or \(\left| M_2\right| \ge 1\) is satisfied after the modification. We now modify the solution such that its objective stays the same but \(\left| M_3\right| = 1\) holds which is a contradiction to Lemma 4.9.
If \(\tilde{\ell }_{s} < {K}/{2}\) and \(\tilde{\ell }_{t} < {K}/{2}\) hold, then we assume w.l.o.g. that \(q _{(s, z^+_i)} > 0\) holds for some \(i \in I\). Due to the considered flow decomposition and Lemma 3.3, we now can decrease  and increase
and increase  by \(\tilde{\varepsilon } > 0\) such that both arc flows \({\tilde{q}}_{(s, z^+_i)}\) and \({\tilde{q}}_{(z^+_i, t)}\) are positive, the potential drop
by \(\tilde{\varepsilon } > 0\) such that both arc flows \({\tilde{q}}_{(s, z^+_i)}\) and \({\tilde{q}}_{(z^+_i, t)}\) are positive, the potential drop  stays the same, and \(\tilde{\ell } \le b\) holds. Consequently, \(\left| M_3\right| = 1\) is satisfied for the modified solution \((\tilde{\ell }, {\tilde{q}}, \tilde{\pi })\) and its objective value \(\tilde{\phi }\) satisfies \(\tilde{\phi } \ge 1 - \varepsilon (K)\), which is a contradiction to Lemma 4.9.
stays the same, and \(\tilde{\ell } \le b\) holds. Consequently, \(\left| M_3\right| = 1\) is satisfied for the modified solution \((\tilde{\ell }, {\tilde{q}}, \tilde{\pi })\) and its objective value \(\tilde{\phi }\) satisfies \(\tilde{\phi } \ge 1 - \varepsilon (K)\), which is a contradiction to Lemma 4.9.
If \(\tilde{\ell }_{s} < {K}/{2}\) and \(\tilde{\ell }_{t} = {K}/{2}\) hold, then this and (1a) imply that \(q _{(z^+_i, t)} > 0\) exists. Due to the considered flow decomposition and Lemma 3.3, we can decrease  by \(\varepsilon > 0\) and increase
by \(\varepsilon > 0\) and increase  by \(\tilde{\varepsilon }\) with \(\varepsilon \ge \tilde{\varepsilon } > 0\) such that the potential drop
by \(\tilde{\varepsilon }\) with \(\varepsilon \ge \tilde{\varepsilon } > 0\) such that the potential drop  stays the same, \(\tilde{\ell } \le b\), and \({\tilde{q}}_{(s, z^+_i)}\) and \({\tilde{q}}_{(z^-_i, t)}\) are positive. Consequently, \(\left| M_3\right| = 1\) is satisfied for the modified solution \((\tilde{\ell }, {\tilde{q}}, \tilde{\pi })\) and its objective value \(\tilde{\phi }\) satisfies \(\tilde{\phi } \ge 1 - \varepsilon (K)\), which is a contradiction to Lemma 4.9. Analogously we handle the case \(\tilde{\ell }_{s} = {K}/{2}\) and \(\tilde{\ell }_{t} < {K}/{2}\). \(\square \)
stays the same, \(\tilde{\ell } \le b\), and \({\tilde{q}}_{(s, z^+_i)}\) and \({\tilde{q}}_{(z^-_i, t)}\) are positive. Consequently, \(\left| M_3\right| = 1\) is satisfied for the modified solution \((\tilde{\ell }, {\tilde{q}}, \tilde{\pi })\) and its objective value \(\tilde{\phi }\) satisfies \(\tilde{\phi } \ge 1 - \varepsilon (K)\), which is a contradiction to Lemma 4.9. Analogously we handle the case \(\tilde{\ell }_{s} = {K}/{2}\) and \(\tilde{\ell }_{t} < {K}/{2}\). \(\square \)
We now consider the counterpart of Lemma 4.12, i.e.,
Lemma 4.13
Let Partition instance \(\mathcal {S}\) be infeasible. Let
and \((\ell , q, \pi )\) be a solution of (5) that satisfies (18). Then, the corresponding objective value \(\phi \) satisfies
Proof
We assume for a contradiction that a solution \((\ell , q, \pi )\) of (5) satisfying (18) with an objective value \(\phi \ge 1 - {\varepsilon (K)^2}/{K^2}\) exists. From Lemma 4.8, it follows \(\phi < 1\). Further, Condition (18), which is satisfied by \((\ell , q, \pi )\), implies that two indices \(l\ne r\in I\) exist such that
hold. This and
lead, analogously to (13), to the inequalities
We now consider the partition \(M_1, M_2,\) and \(M_3\) of \(I\) according to (9). Consequently, (11) is satisfied. From this, flow conservation (1a), and booking \(b\), it follows
Combining the previous inequalities, \(\sum _{i \in I} S_i = K\), Observation 4.4, (19), and \(\phi \ge 1 - {\varepsilon (K)^2}/{K^2}\) lead to
This leads to the contradiction
because \(1> \phi \ge 1 - {\varepsilon (K)^2}/{K^2} > 0\) holds. \(\square \)
Lemmas 4.12 and 4.13 prove that if Partition instance \(\mathcal {S}\) is infeasible, then \(\varphi ^+_{st}(b)\) can be bounded above by \(M(K)\) given as
where the coding length of \(M(K)\) is polynomially bounded above by the coding length of the given Partition instance. In the following two lemmas, we prove an analogue statement for the case that the flow is not necessarily nonnegative, i.e., we consider the general maximum potential-difference problem (2) w.r.t. \((s, t)\). To this end, \(M(K)\) and \(\tilde{\varepsilon }(K)= {(1-M(K))}/{5}\) come into play; see (3). Moreover, we need the following auxiliary Lemma.
Lemma 4.14
Let Partition instance \(\mathcal {S}\) be infeasible. Let \((\ell , q, \pi )\) be an optimal solution of (2) w.r.t. \((s, t)\) with objective value \(\phi \) > 0. Further, there is at least one arc \(a \in A \) with negative arc flow \(q _{a} < 0\). Then, for all \(i \in I\), the inequalities
hold.
Proof
Let \((\ell , q, \pi )\) be an optimal solution of (2) w.r.t. \((s, t)\) that satisfies the requirements. For all \(i \in I\), the inequality \(q _{(z^+_{i}, z^-_{i})} \ge 0\) holds due to the structure of graph \(G (\textsf {Part})\). Moreover, for all \(i \in I\), at least one of the arc flows \(q _{(s, z^+_{i})}\) and \(q _{(z^+_{i}, t)}\) is positive due to \(\phi >0\).
For every \(i \in I\) for which either \(q _{(s, z^+_{i})}<0\) or \(q _{(z^+_{i}, t)}<0\) holds, the flow bounds (20) follow from the graph structure of \(G (\textsf {Part})\), (1a), and the considered booking \(b\). From the requirements, it further follows that there is at least one index \(l \in I\) for which either \(q _{(s, z^+_{l})}\!\!<0\) or \(q _{(z^+_{l}, t)}<0\) holds and thus, flow bounds (20) are satisfied for this index l. Consequently,
is satisfied, where the second equality follows from (1b). Furthermore, the last inequality is satisfied since at least one of the summands is negative and the flow bounds (20) are satisfied for l. Thus, \(\phi < 1\) holds.
Moreover, for every \(i \in I\) with \(q _{(s, z^+_{i})}\ge 0\) and \(q _{(z^+_{i}, t)}\ge 0\), Conditions (1b) and \(\phi < 1\) lead to
which implies that the flow bounds (20) are satisfied for the considered index i. \(\square \)
Lemma 4.15
Let Partition instance \(\mathcal {S}\) be infeasible and \(n \ge 3\) denotes the number of elements of \(\mathcal {S}\). Let \(M(K)\) and \(\tilde{\varepsilon }(K)\) be given as in (3) and \((\ell , q, \pi )\) be an optimal solution of (2) w.r.t. \((s, t)\) with objective value \(\phi \). If this solution satisfies \(\left| q _a \right| \le {\tilde{\varepsilon }(K)}/{n}\) for each \(a \in A \) with \(q _a < 0\), then
holds.
Proof
We assume for a contradiction that an optimal solution \((\ell , q, \pi )\) for (2) w.r.t. \((s, t)\) with objective value \(\phi \) that satisfies the requirements, explicitly \(\left| q _{a}\right| \le {\tilde{\varepsilon }(K)}/{n}\) for \(a \in A \) with \(q _a < 0\), exists and \(\phi \ge M(K)+ 4 \tilde{\varepsilon }(K)\) holds.
If \(q _a \ge 0\) holds for all \(a \in A \), then this is a contradiction to Lemma 4.12 or 4.13 due to the objective value \(\phi \ge M(K)+ 4 \tilde{\varepsilon }(K)\).
Now at least one arc \(a \in A \) satisfies \(q _a < 0\). From the graph structure of \(G (\textsf {Part})\) and booking \(b\), it follows \(q _{(z^+_i, z^-_i)} \ge 0\) for all \(i \in I\). Since \(\phi >0\) and (1b), for every \(i \in I\) at least one arc flow \(q _{(s, z^+_i)}\) or \(q _{(z^+_i, t)}\) is positive. Consequently, at most n arcs with negative flow exist. Moreover, from Lemma 4.14, it follows that the flow bounds (20) are satisfied for \(i \in I\). Additionally, \(q _{(s,z^+_i)} > \tilde{\varepsilon }(K)\) or \(q _{(z^+_i,t)} > \tilde{\varepsilon }(K)\) holds for every \(i \in I\) because of
We now consider a flow decomposition of Lemma 3.1 for \((\ell , q)\). For every arc \(a \in A \) with \(q _{a} < 0\), we delete every positive flow  where the path
where the path  satisfies
satisfies  . Consequently, we obtain \({\tilde{q}}_a \ge 0\) for \(a \in A \) with corresponding nomination \(\tilde{\ell }\). Due to the chosen flow decomposition and maximally n arcs \(a \) with negative arc flow, satisfying \(\left| q _a \right| \le {\tilde{\varepsilon }(K)}/{n}\), exist, this modification decreases an arbitrary arc flow by at most \(n ({\tilde{\varepsilon }(K)}/{n}) = \tilde{\varepsilon }(K)\). Further, the flow bounds (20) still hold for \(i \in I\).
. Consequently, we obtain \({\tilde{q}}_a \ge 0\) for \(a \in A \) with corresponding nomination \(\tilde{\ell }\). Due to the chosen flow decomposition and maximally n arcs \(a \) with negative arc flow, satisfying \(\left| q _a \right| \le {\tilde{\varepsilon }(K)}/{n}\), exist, this modification decreases an arbitrary arc flow by at most \(n ({\tilde{\varepsilon }(K)}/{n}) = \tilde{\varepsilon }(K)\). Further, the flow bounds (20) still hold for \(i \in I\).
If either \(q _{(s,z^+_i)} > \tilde{\varepsilon }(K)\) or \( q _{(z^+_i,t)} > \tilde{\varepsilon }(K)\) holds, then we assume w.l.o.g. that \(q _{(s,z^+_i)}\!\!>\!\!\tilde{\varepsilon }(K)\) is satisfied. This leads to
If \(q _{(s, z^+_i)} > \tilde{\varepsilon }(K)\) and \(q _{(z^+_i, t)} > \tilde{\varepsilon }(K)\) hold, then this leads to
Thus, the modification decreases the potential drop  , but it is at least \(M(K)\). Furthermore, \({\tilde{q}}\ge 0\) holds and we only decreased flows of \(q \) to obtain \({\tilde{q}}\). Consequently, \((\tilde{\ell }, {\tilde{q}})\) satisfy (1a), (5b), and (5c). Due to this and \(\Lambda _{(s, z^+_i)} = \Lambda _{(z^+_i, t)} = 1/S_i^{2}\), we can apply Lemma 4.10 and obtain a feasible point of (2) w.r.t. \((s, t)\) with \(q _a \ge 0\) and objective value of at least \(M(K)\). But this is a contradiction to Lemma 4.12 or 4.13. \(\square \)
, but it is at least \(M(K)\). Furthermore, \({\tilde{q}}\ge 0\) holds and we only decreased flows of \(q \) to obtain \({\tilde{q}}\). Consequently, \((\tilde{\ell }, {\tilde{q}})\) satisfy (1a), (5b), and (5c). Due to this and \(\Lambda _{(s, z^+_i)} = \Lambda _{(z^+_i, t)} = 1/S_i^{2}\), we can apply Lemma 4.10 and obtain a feasible point of (2) w.r.t. \((s, t)\) with \(q _a \ge 0\) and objective value of at least \(M(K)\). But this is a contradiction to Lemma 4.12 or 4.13. \(\square \)
We now prove that if Partition instance \(\mathcal {S}\) is infeasible and in an optimal solution of (2) w.r.t. \((s, t)\) at least one negative arc flow has an absolute flow of at least \({\tilde{\varepsilon }(K)}/{n}\), then we can bound the objective of (2) as follows.
Lemma 4.16
Let Partition instance \(\mathcal {S}\) be infeasible. Further, let \(\varepsilon (K), M(K)\), and \( \tilde{\varepsilon }(K)\) be given as in (3). Moreover, let \((\ell , q, \pi )\) be a feasible point of (2) w.r.t. \((s, t)\) such that at least one arc \(a \in A \) satisfies \(q _a < 0\) and \(\left| q _a \right| \ge {\tilde{\varepsilon }(K)}/{n}\). Then, the corresponding objective value \(\phi \) satisfies
Proof
We assume for a contradiction that a solution \((\ell , q,\pi )\) of (2) w.r.t. \((s, t)\) with objective value
satisfies the requirements. Consequently, an arc \(a \in A \) with \(q _a < 0\) and \(\left| q _a \right| \ge {\tilde{\varepsilon }(K)}/{n}\) exists. We now consider the case that \(a = (s, z^+_i)\) for some \(i \in I\) holds.
Due to Lemma 4.14 and the value of \(\phi {\ > 0}\), the flow bounds \(0 \le q _{(z^+_i, t)} \le S_i\) are satisfied. This,
and \(S_i < K\), lead to the contradiction
Analogously to the above, it follows the case of \(a = (z^+_i, t)\) for some \(i \in I\). \(\square \)
Combining now the results of Lemmas 4.12–4.16, we can bound the objective of (2) w.r.t. \((s, t)\) by the polynomial \(T(K)\) given by (3b).
Lemma 4.17
Let Partition instance \(\mathcal {S}\) be infeasible. Let \(M(K)\) and \(\tilde{\varepsilon }(K)\) be given as in (3). Then,
holds.
Proof
Let \((\ell , q, \pi )\) be an optimal solution of (2) w.r.t. \((s, t)\). If \(q _a \ge 0\) for \(a \in A \) holds, then the claim follows from Lemmas 4.12 and 4.13. If an arc \(a \in A \) with \(q _a < 0\) exists, then the claim follows from Lemmas 4.15 and 4.16. \(\square \)
Since the feasibility of a booking can be characterized by the nominations with maximum potential-difference, see (4), the previous lemma connects the feasibility of Partition instance \(\mathcal {S}\) to (2) w.r.t. \((s, t)\).
Lemma 4.18
Partition instance \(\mathcal {S}\) is feasible if and only if \(\varphi _{st}(b) > T(K)\) is satisfied. Further, the booking \(b\) is infeasible if and only if \(\mathcal {S}\) is feasible.
Proof
If Partition instance \(\mathcal {S}\) is infeasible, then from Lemma 4.17 it follows \(\varphi _{st}(b)< T(K)< 1\). If \(\mathcal {S}\) is feasible, then Lemma 4.3 implies \(\varphi _{st}(b) \ge 1 > T(K)\), since \(T(K)< 1\).
Consequently, from Corollary 4.2 it follows that booking \(b\) is infeasible if and only if \(\mathcal {S}\) is feasible. \(\square \)
Finally, we prove our main result that deciding the feasibility of a booking (FB) is coNP-hard.
Theorem 4.19
Deciding the feasibility of a booking (FB) is coNP-hard.
Proof
Deciding the feasibility of a booking is coNP-hard due to Lemma 4.18. \(\square \)
We further note that deciding whether there exists a nomination with maximum potential-difference (MPD), see (2), of at least \(T(K)\) is \({\textsc {NP}}\)-hard. Moreover, \(\textsf {MPD} \) is still \({\textsc {NP}}\)-hard with the additional restriction of nonnegative flow; see (5).
Lemma 4.20
Computing a maximum potential-difference nomination (MPD) is \({\textsc {NP}}\)-hard. Further, MPD with the additional restriction of nonnegative flow (5c) is also \({\textsc {NP}}\)-hard.
Proof
The NP-hardness of MPD follows from \(T(K)< 1\) and Lemmas 4.18 and 4.3.
Moreover, MPD with the additional restriction of nonnegative flow is \({\textsc {NP}}\)-hard, which follows from the combination of Lemma 4.3, its proof, Lemmas 4.12 and 4.13, and \(T(K)< 1\). \(\square \)
We close this section with a brief remark why the reduction of this section is not applicable to linear potential-based flows, i.e., considering \(q _a \) instead of \(q _a \left| q _a \right| \) in (1b). For the latter, we know that FB is in P; see Labbé et al. (2019).
The hardness proof of FB w.r.t. nonlinear potential-based flow model (2.5) is based on Observation 4.4. It implies that if \(q _{(s, z^+_i)} > 0 \) and \(q _{(z^+_i, t)} > 0\) hold, then we need strictly more flow in terms of \(q _{(s, z^+_i)} + q _{(z^+_i, t)}\) to obtain a pressure drop of \(\phi \), i.e., \(\Lambda _{(s, z^+_i)} q ^2_{(s, z^+_i)} + \Lambda _{(z^+_i, t)} q ^2_{(z^+_i, t)} = \phi \), in contrast to the case if one of the latter flows is zero. This does not apply if we consider a linear potential-based flow model. Thus, the previous reduction from Partition to the infeasibility of a booking is not applicable for a linear potential-based flow model.
5 Conclusion
In this paper, we prove that deciding the feasibility of a booking (FB) in the European entry-exit gas market considering a nonlinear potential-based flow model is coNP-hard in general graphs. To this end, we reduced Partition to the infeasibility of a booking. This is the first hardness result for FB w.r.t. potential-based flows, since the latter is in P for linear potential-based flows in general graphs; see Labbé et al. (2019). It is also in P for trees and a single-cycle network considering a nonlinear potential-based flow model; see Labbé et al. (2019, 2021), Robinius et al. (2019). Thus, it is finally shown that FB is hard and a first border separating the easy from the hard variants of the problem is given. Hence, main parts of the complexity regarding the considered problem are now understood; see Fig. 1 for an overview. Moreover, we prove that computing a nomination with the maximum potential-difference is \({\textsc {NP}}\)-hard even if we can determine the flow direction a priori. However, an open question is if we can sharpen the line that separates the easy from the hard cases of FB. The proof of our complexity results is strongly based on graphs with multiple cycles that share common arcs. Consequently, a reasonable next case could be the class of cactus graphs since for trees and a single cycle the considered problem is in P and for general graphs it is coNP-hard.
Furthermore, it remains open if FB is in coNP, i.e., it is open if there is an infeasibility certificate which coding length is polynomial in the coding length of the input and that can be checked in polynomial time. Since we consider a nonlinear potential-based flow model, this task seems to be challenging. This is stressed by Example 4.3 in the recent PhD thesis Plein (2021), which shows that even for a rational nomination the corresponding flows can be irrational in our nonlinear potential-based flow model. This result does neither show that FB is in coNP nor that it is not in coNP. However, as discussed in Plein (2021), it implies that any infeasibility certificate of polynomial size does not include possibly irrational flows corresponding to a nomination within our nonlinear potential-based flow model. Thus, we cannot directly use the potential-difference maximizing nominations and flows of (2), which are used to characterize the feasibility of a booking, as an infeasibility certificate. Consequently, it may be necessary to develop new characterizations for feasible bookings to address if FB is in coNP, which is out of scope of this paper. However, for capacitated linear flows deciding the feasibility of a booking is in coNP, see Hayn (2016), which is based on the fact that for a rational nomination the corresponding flows are always rational for capacitated linear flows.
Moreover, it remains an open question if FB is strongly NP-hard since we reduced the weakly NP-hard Partition problem to the infeasibility of a booking. An answer to this question also may reveal whether there is an pseudo-polynomial algorithm that decides the feasibility of a booking.
Our complexity analysis shows that FB is indeed a challenging problem for the transmission system operator (TSO) in the European entry-exit gas market system. Moreover, FB has to be solved by the TSO whenever a booking contract is signed.
Thus, the development of effective methods for FB offers new possibilities for future research. As a consequence of our complexity analyses, it might be a smart choice to consider approximation algorithms for deciding the feasibility of a booking in general graphs. Especially, the development of approximation algorithms to compute a maximum potential-difference nomination (MPD) directly allows to decide the feasibility of a booking up to a certain tolerance.
References
Ahuja, R. K., Magnanti, T. L., & Orlin, J. B. (1993). Network flows: Theory, algorithms, and applications. Prentice-Hall Inc.
Aßmann, D., Liers, F., Stingl, M., & Vera, J. C. (2018). Deciding robust feasibility and infeasibility using a set containment approach: An application to stationary passive gas network operations. SIAM Journal on Optimization, 28(3), 2489–2517. https://doi.org/10.1137/17M112470X.
Bakhouya, B., & De Wolf, D. (2007). The gas transmission problem when the merchant and the transport functions are disconnected. Technical Report. Université catholique de Lille, Jan. 2007. url: https://www.researchgate.net/publication/253816284_The_gas_transmission_problem_when_the_merchant_and_the_transport_functions_are_disconnected.
Baumrucker, B. T., & Biegler, L. T. (2010). MPEC strategies for cost optimization of pipeline operations. Computers & Chemical Engineering, 34(6), 900–913. https://doi.org/10.1016/j.compchemeng.2009.07.012.
Ben-Tal, A., El Ghaoui, L., & Nemirovski, A. (2009). Robust optimization. Princeton University Press.
Chuong, T. D., & Jeyakumar, V. (2017). An exact formula for radius of robust feasibility of uncertain linear programs. Journal of Optimization Theory and Applications, 173(1), 203–226. https://doi.org/10.1007/s10957-017-1067-6.
De Wolf, D., & Smeers, Y. (2000). The gas transmission problem solved by an extension of the simplex algorithm. Management Science, 46(11), 1454–1465. https://doi.org/10.1287/mnsc.46.11.1454.12087.
Directive 2003/55/EC of the European Parliament and of the Council of 26 June 2003 concerning common rules for the internal market in natural gas and repealing Directive 98/30/EC (OJ L 176 pp. 57–78).
Directive 2009/73/EC of the European Parliament and of the Council concerning common rules for the internal market in natural gas and repealing Directive 2003/55/EC (OJ L 211 pp. 36–54).
Directive 98/30/EC of the European Parliament and of the Council of 22 June 1998 concerning common rules for the internal market in natural gas (OJ L 204 pp. 1–12).
Domschke, P., Geißler, B., Kolb, O., Lang, J., Martin, A., & Morsi, A. (2011). Combination of nonlinear and linear optimization of transient gas networks. INFORMS Journal on Computing, 23(4), 605–617. https://doi.org/10.1287/ijoc.1100.0429.
Fügenschuh, A., Junosza-Szaniawski, K., & Kwasiborski, S. (2014). The reservation- allocation network flow problem. Tech. rep. Aug. 2014. https://www.researchgate.net/publication/265126185_The_Reservation-Allocation_Network_Flow_Problem.
Fügenschuh, A., Geißler, B., Gollmer, R., Hayn, C., Henrion, R., Hiller, B., et al. (2013). Mathematical optimization for challenging network planning problems in unbundled liberalized gas markets. Energy Systems, 5(3), 449–473. https://doi.org/10.1007/s12667-013-0099-8.
Garey, M. R., & Johnson, D. S. (1990). Computers and Intractability; A Guide to the Theory of NP-Completeness. W. H. Freeman & Co.
Geißler, B. (2011). Towards globally optimal solutions for MINLPs by discretization techniques with applications in gas network optimization. PhD thesis. Friedrich-Alexander Universität Erlangen-Nürnberg.
Geißler, B., Morsi, A., & Schewe, L. (2013). A new algorithm for MINLP applied to gas transport energy cost minimization. Facets of combinatorial optimization (pp. 321–353). Springer. https://doi.org/10.1007/978-3-642-38189-8_14
Geißler, B., Morsi, A., Schewe, L., & Schmidt, M. (2015). Solving power-constrained gas transportation problems using an MIP-based alternating direction method. Computers & Chemical Engineering, 82, 303–317. https://doi.org/10.1016/j.compchemeng.2015.07.005.
Geißler, B., Morsi, A., Schewe, L., & Schmidt, M. (2018). Solving highly detailed gas transport MINLPs: Block separability and penalty alternating direction methods. INFORMS Journal on Computing, 30(2), 309–323. https://doi.org/10.1287/ijoc.2017.0780.
Goberna, M. A., Jeyakumar, V., Li, G., & Vicente-Pérez, J. (2014). Robust solutions of multiobjective linear semi-infinite programs under constraint data uncertainty. SIAM Journal on Optimization, 24(3), 1402–1419. https://doi.org/10.1137/130939596.
Gorissen, B. L., Yanýkoglu, I., & den Hertog, D. (2015). A practical guide to robust optimization. Omega, 53, 124–137. https://doi.org/10.1016/j.omega.2014.12.006.
Gotzes, C., Heitsch, H., Henrion, R., & Schultz, R. (2016). On the quantification of nomination feasibility in stationary gas networks with random load. Mathematical Methods of Operations Research, 84(2), 427–457. https://doi.org/10.1007/s00186-016-0564-y.
Grimm, V., Schewe, L., Schmidt, M., & Zöttl, G. (2019). A multilevel model of the European entry-exit gas market. Mathematical Methods of Operations Research, 89(2), 223–255. https://doi.org/10.1007/s00186-018-0647-z.
Gross, M., Pfetsch, M. E., Schewe, L., Schmidt, M., & Skutella, M. (2019). Algorithmic results for potential-based flows: Easy and hard cases. Networks, 73(3), 306–324. https://doi.org/10.1002/net.21865.
Habeck, O., & Pfetsch, M. E. (2021). Combinatorial acyclicity models for potential-based flows. Networks. https://doi.org/10.1002/net.22038.
Hante, F. M., Leugering, G., Martin, A., Schewe, L., & Schmidt, M. (2017). Challenges in optimal control problems for gas and fluid flow in networks of pipes and canals: From modeling to industrial applications. In P. Manchanda, R. Lozi, & A. H. Siddiqi (Eds.), Industrial mathematics and complex systems: Emerging mathematical models, methods and algorithms. Industrial and applied mathematics (pp. 77–122). Springer Singapore. https://doi.org/10.1007/978-981-15-0928-5_4
Hayn, C. (2016). Computing maximal entry and exit capacities of transportation networks. PhD thesis. Friedrich-Alexander Universität Erlangen-Nürnberg.
Humpola, J. (2017). Gas network optimization by MINLP. PhD thesis. Technische Universität Berlin.
Koch, T., Hiller, B., Pfetsch, M., & Schewe, L. (2015). Evaluating gas network capacities. Society for Industrial and Applied Mathematics. https://doi.org/10.1137/1.9781611973693.ch5
Labbé, M., Plein, F., & Schmidt, M. (2019). Bookings in the European gas market: Characterisation of feasibility and computational complexity results. Optimization and Engineering. https://doi.org/10.1007/s11081-019-09447-0.
Labbé, M., Plein, F., Schmidt, M., & Thürauf, J. (2021). Deciding feasibility of a booking in the European gas market on a cycle is in P for the case of passive networks. Networks. https://doi.org/10.1002/net.22003.
Liers, F., Schewe, L., & Thürauf, J. (2021). Radius of robust feasibility for mixed- integer problems. INFORMS Journal on Computing. https://doi.org/10.1287/ijoc.2020.1030.
Martin, A., Geißler, B., Hayn, C., Morsi, A., Schewe, L., Hiller, B., Humpola, J., Koch, T., Lehmann, T., Schwarz, R., Schweiger, J., Pfetsch, M., Schmidt, M., Steinbach, M., Willert, B., & Schultz, R. (2011). Optimierung technischer Kapazitäten in Gasnetzen. In Optimierung in der Energiewirtschaft. VDI-Berichte 2157. pp. 105–114. https://opus4.kobv.de/opus4-zib/frontdoor/ index/index/docId/1512.
Maugis, J. J. (1977). Étude de réseaux de transport et de distribution de fluide. RAIRO - Operations Research, 11(2), 243–248. https://doi.org/10.1051/ro/1977110202431.
Plein, F. (2021). When Bilevel optimization meets gas networks: Feasibility of bookings in the european entry-exit gas market. Computational Complexity Results and Bilevel Optimization Approaches. PhD thesis. Université libre de Bruxelles and Trier University. https://opus4.kobv.de/opus4- trr154/frontdoor/index/index/year/2021/docId/393.
Ríos-Mercado, R. Z., & Borraz-Sánchez, C. (2015). Optimization problems in natural gas transportation systems: A state-of-the-art review. Applied Energy, 147, 536–555. https://doi.org/10.1016/j.apenergy.2015.03.017.
Ríos-Mercado, R. Z., Wu, S., Scott, L. R., & Boyd, E. A. (2002). A reduction technique for natural gas transmission network optimization problems. Annals of Operations Research, 117(1), 217–234. https://doi.org/10.1023/A:1021529709006.
Robinius, M., Schewe, L., Schmidt, M., Stolten, D., Thürauf, J., & Welder, L. (2019). Robust optimal discrete arc sizing for tree-shaped potential networks. Computational Optimization and Applications, 73(3), 791–819. https://doi.org/10.1007/s10589-019-00085-x.
Rose, D., Schmidt, M., Steinbach, M. C., & Willert, B. M. (2016). Computational optimization of gas compressor stations: MINLP models versus continuous reformulations. Mathematical Methods of Operations Research, 83(3), 409–444. https://doi.org/10.1007/s00186-016-0533-5.
Schewe, L., Schmidt, M., & Thürauf, J. (2019). Structural properties of feasible bookings in the European entry-exit gas market system. 4OR. https://doi.org/10.1007/s10288-019-00411-3.
Schewe, L., Schmidt, M., & Thürauf, J. (2020). Computing technical capacities in the European entry-exit gas market is NP-hard. Annals of Operations Research, 295(1), 337–362. https://doi.org/10.1007/s10479-020-03725-2.
Schmidt, M., Steinbach, M. C., & Willert, B. M. (2015a). An MPEC based heuristic. In T. Koch, B. Hiller, M. E. Pfetsch, & L. Schewe (Eds.), Evaluating gas network capacities (pp. 163–180). SIAM. https://doi.org/10.1137/1.9781611973693
Schmidt, M., Steinbach, M. C., & Willert, B. M. (2015b). Chapter 10: The precise NLP model. In T. Koch, B. Hiller, M. E. Pfetsch, & L. Schewe (Eds.), Evaluating gas network capacities (pp. 181–220). Society for Industrial and Applied Mathematics. https://doi.org/10.1137/1.9781611973693.ch10
Schmidt, M., Steinbach, M. C., & Willert, B. M. (2015c). High detail stationary optimization models for gas networks. Optimization and Engineering, 16(1), 131–164. https://doi.org/10.1007/s11081-014-9246-x.
Schmidt, M., Steinbach, M. C., & Willert, B. M. (2016). High detail stationary optimization models for gas networks: Validation and results. Optimization and Engineering, 17(2), 437–472. https://doi.org/10.1007/s11081-015-9300-3.
Szabó, J. (2012). The set of solutions to nomination validation in passive gas transportation networks with a generalized flow formula. Tech. rep. 11-44. ZIB, URN:urn:nbn:de:0297-zib-15151.
Willert, B. (2014). Validation of nominations in gas networks and properties of technical capacities. PhD thesis. Gottfried Wilhelm Leibniz Universität Hannover.
Acknowledgements
This research has been performed as part of the Energie Campus Nürnberg and is supported by funding of the Bavarian State Government. The author also thanks the DFG for their support within project B07 in CRC TRR 154. Furthermore, I would like to explicitly thank Fränk Plein and Martin Schmidt, who paved the way for this paper by many fruitful discussions and by our joint work Labbé et al. (2021) on the single cycle case. Moreover, I would like to thank them as well as Lars Schewe and Patrick Gemander for reading a former version of this manuscript and their comments that helped to improve the paper.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Thürauf, J. Deciding the feasibility of a booking in the European gas market is coNP-hard. Ann Oper Res 318, 591–618 (2022). https://doi.org/10.1007/s10479-022-04732-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-022-04732-1


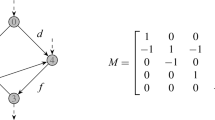

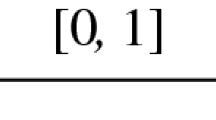

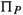 is continuous.
is continuous. is strictly increasing w.r.t. every component. That means, for
is strictly increasing w.r.t. every component. That means, for  ,
,  is increasing in
is increasing in  is unbounded w.r.t. every component, i.e., for
is unbounded w.r.t. every component, i.e., for  ,
, 
 is additive w.r.t. the path, i.e., for every node
is additive w.r.t. the path, i.e., for every node  ,
, 
 .
. holds if and only if
holds if and only if 