1  Introduction

In early 1980s, the supply chain management (SCM) was introduced to respond to companies’ intense competitions (Oliver & Webber, 1982). Over time, a growing number of companies found it important to unite/integrate their activities with the key supply chain (SC) processes rather than their separate management; thus, was formed the SCM revolution (Londe, 1997). As Handfield & Nichols (2002) have defined, the SCM is a comprehensive management approach to integrate and coordinate the flow of materials, information, and finance along the SC. Considering a forward SC, Simchi-Levi et al. (2004) and Melo et al. (2009), and the council of SCM professionals have defined the SCM to be “the process of planning, implementing, and controlling the SC operations in an effective manner”. On the other hand, among issues discussed in the SC logistics/management today are the “reverse logistics” and “waste management”. Over the past two decades, many companies and industries in the developed countries have started studying them and considered the reverse logistics as one of the important processes in their SCs.

With the definition of ISO 14000 for environmental sustainability and ISO 26000 for the social responsibility, the companies need to revise their SCs. To address the sustainable development goals, the concept of Sustainable SCM (SSCM) is defined. The simultaneous consideration of economic, environmental and social factors leads a multi-objective SC model. Generally, the supply chain network design (SCND) is an extension to the facility location problems (Santoso et al. 2005).

It is important to address the environmental sustainability in SCND models. The logistics consumes more than half of the liquid fossil fuels and is, thus, responsible for about 25% of the CO2 emitted into the air (Özkır & Başlıgil, 2013). In addition, more than 80% of the urban air pollution and about 1.3 million annual traffic accident-caused fatalities are other direct results of the activities of the transportation industry. These negative effects reflect the “environmental costs” imposed by ignorant societies and advanced economies (Sherafati et al., 2019). For example, Ahi & Searcy (2015) have analyzed some social impact indices; those that can show the social impacts quantitatively and enter the SC models include the indices of the CO2 emission, energy consumption, solid waste, water consumption, and water wastages. These reasons motivate the implementation of an environmental SCND to maximize the value created over the life of a product and create a green SC implementation (Govindan et al., 2015) that presses different organizations to reduce their negative social impacts and thereby enhance their social/economic benefits (Zailani et al., 2012).

The social sustainability focuses on the human life quality. In the literature of SCND, researchers mostly try to formulate the created job opportunities and improve the responsiveness to customers for SCND models (Nayeri et al., 2020). It is evident that the employment of more workers and managers, leads to more total cost for the company. However, a sustainable SCND should maximize the number of employed jobs to improve the human life quality. Another significant factor is to be responsiveness to satisfy the customers’ demand. Without a doubt, a responsiveness SCND creates more cost for the companies. This makes a tradeoff between the total cost and the social sustainability impact in companies for their SCs.

Since the facility location models are classified as NP-hard, the SCND models are NP-hard, too (Soleimani & Kannan, 2015). The literature of SCND is very rich in using exact, heuristic and metaheuristic algorithms. One demerit of exact methods is not able to solve the large-scale SCND in a logical time (Govindan et al., 2015). However, metaheuristics cannot guarantee the global solution (the best solution) as they use a random search mechanism. One way to reduce the high complexity of SCND models is to reformulate the original model in an efficient way to find the global solution in a logical time. This motivates our attempt to propose a set of Lagrangian relaxation reformulations for the proposed model. One difficulty for implementation the Lagrangian relaxation, is to estimate both upper and lower bounds for the initial solution. This study uses two fast heuristics with a greedy search mechanism to find the initial upper bound. The lower bound is generated by our Lagrangian relaxation reformulation. Using our generated reformulations and heuristics, we are able to solve a large-scale SCND to keep both feasibility and optimality for our proposed model.

All in all, this study proposes a sustainable SCND with energy efficiency. Our proposed model as a multi-objective mixed integer linear programming, considers the energy consumption and job opportunities. The proposed model supports both open- and closed-loop SC modes and includes all three activities of remanufacturing, recycling, and disposal of the parts; products have different parts that can be used in products’ recycling. One contribution in comparison with the state of the art, is to cover both products and components simultaneously, and since parts are sent to manufacturers for reproduction, to suppliers for recycling, and to relevant centers for disposal according to their quality rating, this approach increases the problem complexity. This motivates us to employ a set of Lagrangian relaxation reformulations and efficient heuristics for solving our complex optimization model. The model solution with real data of a closed-loop SC ensures its justifiability and functionality. In conclusion, this study makes the following highlights to the literature:

  • A sustainable closed-loop supply chain model to optimize the total profit, energy consumption and the number of created job opportunities, is developed.

  • Efficient Lagrangian relaxation reformulations and strong heuristics are proposed.

  • A real large-scale numerical example in Iran was provided to approve the applicability of this research.

Other sections are organized as follows: Sect. 2 aims to review the literature and identifies the research gaps in comparison with our contributions. Section 3 establishes our proposed optimization model to formulate a sustainable SCND with the energy efficiency. Section 4 reformulates the proposed model and applies a Lagrangian relaxation theory with two fast problem-specific heuristics. Section 5 provides a real large-size numerical example with an extensive computational test. Section 6 talks about our findings, contributions and managerial insights. Finally, Sect. 7 presents the conclusions and suggests issues for future studies.

2 Literature review

Although the literature of SCND is quite extensive and its review is very difficult, this separation can lead to convincing results. One of the earliest studies to integrate the forward and reverse SC networks, is Fleischmann et al. (2001) who have designed the closed-loop supply chain (CLSC) network with the ability of the product disposal or recovery. This paper aims at locating facilities that manage forward and reverse flows and managing the inter-facility flows. Lee et al. (2010) stated that this integration will reduce costs by up to 20% compared to the ordinal method. However, the possibility of recycling for industrial products was contributed earlier. Spengler et al. (1997) developed a model that enables products to be disposed or recycled at the end of their lifetime. They successfully applied it to the steel industry in a German–French region. Jayaraman et al. (1999) presented a model that solves facility location, transportation, production, and inventory holding problems, simultaneously. They discussed the model management applications for logistic decision-making and presented an optimization model for the forward and reverse flows without considering capacity constraints. Shih (2001) used a mixed integer programming model to optimize the infrastructure and reverse flow network design for computers and home appliances in Taiwan. Salema et al. (2007) developed the Fleischmann et al.'s (2001) model and presented a multi-product SCND with capacity constraint in a CLSC. Lieckens & Vandaele (2007) presented a mixed integer nonlinear programming model for the design of a single-product single-level reverse logistic network.

During the last decades, there are many studies on the development of CLSC with different real-life constraints. Cruz-Rivera & Ertel (2009) designed a closed-loop SC to collect the end-of-life vehicles (ELVs) in Mexico aiming at maximizing the EVL arrangement raised by the reverse logistics within the framework of the capacitated hub location problem. Pishvaee et al. (2010) presented a linear bi-objective optimization model that simultaneously maximizes the closed-loop SC network response and minimizes the total costs. They solved it using the modified version of the memetic algorithm. To minimize the transport costs and launching fixed costs in a multi-level reverse logistics network, Pishvaee et al. (2011) presented a robust linear programming model using simulation algorithms. To integrate decision levels in SCND problems, Keyvanshokooh et al. (2013) presented a mixed integer model minimizing the total costs in a multi-level, multi-period, multi-product logistics network design. Özceylan & Paksoy (2014) proposed a novel mixed-integer nonlinear programming model that optimizes the main strategic and tactical decisions of the CLSC, simultaneously.

The concept of green and sustainable CLSC is highly active nowadays, and many review papers are done (Wang et al., 2011; Ameknassi et al., 2016; Lin et al., 2014; Ahi & Searcy, 2015; Su, 2014; Khan et al., 2021; Sherafati et al., 2019) applied the cable industry to a sustainable SCND to optimize the total cost, carbon emissions and job opportunities. Chalmardi & Camacho-Vallejo (2019) developed a bi-level programming approach for a sustainable SCND considering cleaner technologies. They considered the consumer responsiveness and carbon emissions as the constraints of their bi-level model.

Nayeri et al., (2020) contributed to the uncertainty for the sustainable closed-loop SCND. They developed a multi-objective fuzzy-robust optimization approach to handle the total cost, carbon emissions and job opportunities. Fathollahi-Fard and Ahmadi (2020) proposed a sustainable SCND for the application of water supply and wastewater collection network. They proposed an enhanced social engineering optimizer as a novel metaheuristic for solving their model. Gholizadeh & Fazlollahtabar (2020) proposed a robust optimization approach for the SCND in the melting industry in Iran. To solve their model, a modified genetic algorithm is used. In another work, they (Gholizadeh et al., 2020) developed another CLSC network design using a scenario-based robust optimization approach. Gao & Cao (2020) proposed a multi-objective scenario-based optimization model to formulate a sustainable CLSC considering the reconstruction of facilities. They solved it by the epsilon constraint method.

More recently, Hasani et al. (2021) combined the concept of resiliency with the green SCM to model a CLSC network design problem. Their objectives minimize the total cost and the carbon emissions in their SCND. Soleimani et al. (2021) developed a bi-objective optimization model to analyze both carbon emissions and energy consumption in addition to the total profit in a CLSC network design. Nili et al. (2021) applied a sustainable CLSC network design for the solar photovoltaic application. They analyzed the total cost, environmental pollution and customer service levels through their multi-objective optimization model. Fathollahi-Fard et al. (2021) proposed a dual-channel CLSC network design problem in a fuzzy environment. They applied their optimization model to the tire industry in Iran. Two hybrid metaheuristics based on the advantages of traditional and recent optimization algorithms, were developed to address their model. Shabbir et al. (2021) proposed a CLSC network design with sustainability and resiliency criteria. They considered the total cost, energy consumption and job opportunities in their model and applied a Lagrangian relaxation algorithm to solve it. Fragoso & Figueira (2021) applied a sustainable SCND for the wine industry in Southern Portugal. They applied the LP-metric method to solve their multi-objective optimization model. Rajak et al. (2021) in a same way, applied a sustainable CLSC for steering column industry in India. Pazhani et al. (2021) proposed a multi-product and multi-period SCND considering the total cost and applied a Lagrangian relaxation reformulation to solve their model. Govindan & Gholizadeh (2021) for the first time integrated the concept of sustainability and resiliency with big data optimization. They considered the case of ELVs to study all economic, environmental and social criteria using a robust optimization model.

Akbari-Kasgari et al. (2022) developed a multi-objective sustainable CLSC for a copper network in which the backup suppliers are used as a resilience strategy to reduce the effects of earthquakes on mining operations. The objectives aimed to maximize the supply chain profit; minimize water consumption and air pollutants; and maximize social desirability by considering security and unemployment rates. Govindan & Gholizadeh (2021) proposed a comprehensive sustainable CLSC network containing cross-docking, location-inventory-routing, and pickup and delivery. To solve their model, a fuzzy goal programming technique is applied. Xu et al. (2022) proposed a two-stage stochastic model to design the CLSC under a carbon trading scheme in the multi-period planning context by considering the uncertain demands and carbon prices. They also provide a four-step solution procedure with scenario reduction that enables their proposed model to be solved using commercial solvers efficiently. Finally, Golpîra & Javanmardan (2022) developed an optimal sustainable CLSC by considering Carbon Emission Schemes (CESs) such as carbon cap, carbon cap-and-trade, and carbon tax, in the context of the circular economy. They formulated a risk-based robust mixed-integer linear programming using a scenario-based Conditional Value-at-Risk (CVaR) to deal with demand uncertainty. They concluded that the model performance is affected by both the Decision-Maker’s (DM’s) risk-aversion and the CESs.

To analyze aforementioned studies, Table 1 creates a survey based on different criteria to identify the research gaps. Our criteria include the option of reverse logistics, number of levels in their SCND, direct flows to customers, multi-product, multi-part, multi-period, job opportunities, energy consumption, methodology and real-life case study. Based on our findings from Table 1, the following research gaps are identified:

  • Most of recent studies mainly considered the option of reverse logistics for their optimization models.

  • Recent studies added more facility levels to consider all parts of reverse logistics.

  • In addition to the multi-product, multi-period and multi-part, the possibility of a direct flow to customers, is highly contributed to the literature among studies.

  • Customer service levels, job opportunities and energy consumption are recently contributed to the literature. However, there is no study to consider these factors, simultaneously.

  • Most of studies applied different types of metaheuristics as their methodology. However, the Lagrangian relaxation is rarely contributed to the literature.

  • Most of recent studies proposed a real-life case study to show the applicability of their model.

To fill these research gaps, the model presented in this paper is a sustainable CLSC that considers the energy consumption, customer service levels and job opportunities, simultaneously. Most notably, the customer service level is considered by this paper for the disassembling of the products into different smaller parts. Our model has five SCND levels including suppliers, manufacturers, distribution centers, customer zones, and disposal centers considering the consumption of energy. In addition, the distribution centers play the roles of warehouse and collection centers. The last contribution of this research is to develop a set of efficient Lagrangian relaxation reformulations and fast heuristics for solving a real-world numerical example.

Table 1 Summary of the literature review
Full size table

3 Proposed problem

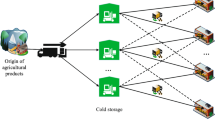
Here, we firstly explain our proposed SCND. Our proposed network includes five levels including suppliers, manufacturers, distribution centers, customers, and disposal centers. In addition, the distribution centers play the roles of warehouse and collection centers. Although our model is single-product, it is multi-part as each product is assumed to be disassembled into different parts. Our model aims to make the locational decisions for distribution centers. The proposed model also identified the right allocation and their inventory status. This model has three objectives. First, it maximizes the total profit. Second, it minimizes the energy consumption and finally, our model maximizes the number of created job opportunities. Our main constraints are the service levels determined for the customer demand as well as capacity constraints for allocation, inventory and locational decisions. The product distribution is carried out from the final producers/distribution centers to customer zones, the recycling rate has been considered in distribution centers. Finally, a graphical presentation of the proposed CLSC framework is shown in Fig. 1.

Fig. 1
figure 1

Proposed CLSC framework

Full size image

The developed CLSC is a multi-part, multi-period and multi-level SCND. However, there is one type of products. This type is supplied by different suppliers. Then, the initial materials for this type of product are sent to different manufacturers who carry out the production processes and send the final products to distribution centers or directly to customer. This creates a dual-channel CLSC to satisfy the demand of customers. One channel is traditionally determined by the distribution centers and another channel is the online purchasing from manufacturers to customers.

Distribution centers not only play the role of warehouses, but also the role of collection centers. After collecting these used or retuned parts. A quality control is done and based on the quality, they are divided into three grades A, B, and C (Soleimani et al., 2021).

  • Quality grade A: These are sent to manufacturing centers to be reproduced and sent back to distribution centers. The reproduced parts are sent to the second market and sold at lower prices.

  • Quality grade B: Parts lacking acceptable quality grades for reproduction are returned to the suppliers. These returned parts are recycled and then used as the raw materials.

  • Quality grade C: Parts lacking the reproduction/recycling potential are sent to third party disposal centers to be disposed. The goal of disposal is to clean our environment from retuned parts.

Based on the above definition of the proposed problem, our model generally covers all sustainability aspects for our CLSC framework as follows:

  • Economic sustainability: Our model maximizes the total profit and considers the secondary markets to consider all factors of economic sustainability. The first goal of our model is to maximize the total profit to optimize the revenues (products/parts sales) in comparison with the total costs including the establishment costs, processing, shipping, and inventory costs. Our model also considers the properties of a CLSC network to create the added-value for our SCND. In this regard, the role of secondary markets is very important. The proposed model considers the service level of customers whose demands are related to the remanufactured components. Similar to the customer service level mentioned above, the amount of parts supplied to customers should not be less than the customer’s actual demand and specified service level for customers. It should be mentioned that the service level is defined here as a portion of the demand rate that can be fulfilled by the CLSC. Since the demand fluctuations are not assumed as a source of uncertainty, the reason why the system may prefer not to fulfill the demand should be clarified. The fact behind the unfulfilled demand is not always the demand uncertainty, but it may occur due to the different cost components which lead the system to make a trade-off between the different cost components and profit at the lower levels of demand fulfillment rate. So, in this study, the service level constraints are embedded to push the model to make a trade-off at higher desirable points of the service level.

  • Environmental sustainability: Although most of environmental SCND models only consider the created carbon emissions for the transportation, our second objective function aims to minimize the energy consumption. Since most of the machines for manufacturing and the vehicles for the transportation, consume non-renewable energies, it is very important to minimize the energy consumption through our proposed CLSC network.

  • Social sustainability: our social factors are the number of job opportunities and customers’ satisfaction. Our third objective is to maximize the number of created job opportunities. This factor includes a set of fixed positions such as managers and variable positions such as workers with regards to the number of transferred products. Our model also considers the service levels for achieving the social sustainability. This study considers the service level (order fill rate, stock out rate, backorder level, and probability of on-time delivery) Here, the index is the order fill rate which is a fraction of the customer demand supplied from the stock and there is no need to consider the supplier/manufacturer lead time for it. In fact, the number of products supplied to customers should not be less than the customer’s actual demand and specified service level.

3.1 Assumptions

The proposed model has the following assumptions from the literature:

  • The proposed problem uses a multi-objective optimization model and all parameters are deterministic.

  • The location of all facilities is predetermined. Our model aims to find the suitable locations for all distribution networks among a set of predefined points (Edalatpour et al., 2018).

  • There is a capacity limitation for all facilities and distribution centers (Govindan et al., 2015).

  • The proposed model is a single-product, multi-part and multi-period SCND.

  • The proposed model considers the energy consumption for manufacturing and transportation activities.

  • The proposed model considers the number of job opportunities. This factor includes both fixed and variable positions.

  • Our model does the possibility of dual-channel network. Customers are able to purchase the products directly from manufacturers or traditionally from distribution centers.

  • Holding cost is considered for all products and parts in all facilities (Soleimani et al., 2021).

We have also considered some new suppositions to the literature of CLSC as follows:

  • Our distribution centers do the following activities:

    1. I.

      Delivering main products to customers as the role of warehouse centers.

    2. II.

      Collecting ELV from customers as the role of collection centers.

    3. III.

      Evaluating the quality of returned products based on the quality grades A, B, and C as the role of collection centers.

    4. IV.

      Distributing the reproduced parts to secondary markets as the role of collection centers.

    5. V.

      Storing products and parts as the role of warehouses.

  • The quality/price of a reproduced part is lower than that of an original product.

  • The customer service level should be considered for main products and parts. Hence, the shortage is not allowed.

3.2 Notations

To establish our optimization model, following indices, parameters and decision variables are defined:

Index

a

Index associated with components or parts (a = {1, 2, …, A})

g

Index associated with quality grades (g = {1, 2, …, G})

t

Index associated with periods ( t= {1, 2,…, T})

m

Index of manufacturers (m = {1, 2, …, M})

u

Index of suppliers (u = {1, 2, …, U})

r

Index of distribution centers (r = {1, 2, …, R})

d

Index of disposal centers (d = {1, 2, …, D})

c

Index of customers (c = {1, 2, …, C})

o

Index of secondary markets (o = {1, 2, …, O})

i and j

Index of all nodes including m, r, d, c, u and o

Parameter

\({F}_{r}\)

Fixed cost for establishing distributor r

\({T}_{ij}\)

Transportation costs per unit of products from facility i to j

\({T}_{ija}^{}\)

Transportation costs per unit of part a from facility i to j

\({P}_{i}^{}\)

Processing costs of products in facility i

\({P}_{ai}^{}\)

Processing costs of part a in facility i

\({FJ}_{r}\)

Fixed jobs as the managers for distributor r

\({VJ}_{it}\)

Variable jobs as the workers in facility i during period t (i.e., it is the number of products to need at least one worker).

\(HP\)

Holding costs of products

\({H}_{a}^{}\)

Holding costs of part a

\({E}_{i}\)

Energy consumption for manufacturing in facility i per unit of product.

\(ET\)

Energy consumption for the transportation be influenced by locations of source and destination

\({C}_{j}^{}\)

Capacity of facility j for manufacturing of products.

\({C}_{ja}^{}\)

Capacity of facility j for processing part a

\(SQ\)

Considered service level for products

\({S}_{a}\)

Considered service level for part a

\({RD}_{a}\)

Rate of disposal for part a

\({RR}_{a}\)

Rate of recycling for part a

\({RM}_{a}\)

Rate of manufacturing for part a

\({I}_{g}\)

Selling price of products in the quality grade g.

\({I}_{a}\)

Selling price of part a.

B

Purchasing price per unit of retuned products from customers

\({\text{D}}_{cgt}\)

Demand of customer c for the product in quality grade g during period t

\({\text{D}}_{\text{o}\text{a}\text{t}}\)

Demand of secondary market o for part a in period t

\({R}_{crt}^{}\)

Returned products from customer c to distributor r in period t

\({MAX}_{t}\)

Maximum number of distribution centers which are active during period t

Decision variable

\({y}_{rt}\)

It gets 1 if the distributor r would be open in period t, otherwise, 0

\({f}_{ijgt}\)

Flow of products for quality grade g from facility i to j during period t

\({f}_{ijat}\)

Flow of part a from facility i to j during period t.

\({h}_{igt}\)

Inventory status for the product in the quality grade g stocked in facility i at the end of period t.

3.3 Proposed model

Here, we want to establish our multi-objective optimization model to formulate a sustainable CLSC with the possibility of energy efficiency. The proposed model includes three objective functions given in Eqs. (1) to (3) and a set of constraints given in Eqs. (4) to (14).

$$\begin{aligned}{Z}_{1}&=\text{max}\left(\left(\sum _{i\in m,r;g, c,t}{f}_{icgt}\times {I}_{g}\right)+\left(\sum _{i\in r,m; o,t,a}{f}_{ioat}\times {I}_{a}\right)-\left(\sum _{r,t}{y}_{rt}\times {F}_{r}\right)\right.\\ &\left.\quad-\left(\sum _{\begin{array}{c}i\in u, m,r,c;i\ne j;\\ j\in m,r,c; g,t\end{array}}{f}_{ijgt}\times \left({{P}_{i}^{}+T}_{ij}\right)+\sum _{\begin{array}{c}i\in m,r;i\ne j;\\ j\in o,m,u,d\end{array}}{f}_{ijat}\times {({P}_{ai}^{}+T}_{ija}^{}\right)\right)\\ &\left.\quad-\left(\sum _{r,g,t}{h}_{rgt}\times HP+\sum _{r,a,t}{h}_{rat}\times {H}_{a}^{}\right)\right)\end{aligned}$$
(1)

Our first objective function given in Eq. (1) aims to maximize the total profit. The first and second terms in this objective are the income from selling products and parts or components. The third term is the cost of establishment of distributors. The fourth and fifth terms are the cost of production and transportation. Finally, the sixth and seventh terms are the cost of inventory.

$${Z}_{2}=\text{m}\text{i}\text{n}\left(\left(\sum _{\begin{array}{c}i\in p, m,r,c;i\ne j;\\ j\in m,r,c;g, t\end{array}}{f}_{ijgt}\times \left(E+{E}_{i}\right)\right)+\left(\sum _{\begin{array}{c}i\in m,r;i\ne j;\\ j\in o,m,p,d,a, t\end{array}}{f}_{ijat}\times \left(ET+{E}_{i}\right)\right)\right)$$
(2)

Our second objective function given in Eq. (2) is to minimize the energy consumption in our system. The first term is the amount of energy consumption of products from manufacturing and transportation activities. The second term is the amount of energy consumption for components or parts from manufacturing and transportation activities.

$${Z}_{3}=\text{max}\left(\sum _{r,t}{y}_{rt}\times {FJ}_{r}+\sum _{\begin{array}{c}i\in u, m,r,c;i\ne j;\\ j\in m,r,c; g,t\end{array}}{(f}_{ijgt}/{VJ}_{it})+\sum _{\begin{array}{c}i\in m,r;i\ne j;\\ j\in o,m,u,d;a,t\end{array}}{(f}_{ijat}/{VJ}_{it})\right)$$
(3)

The third objective function given in Eq. (3) aims to maximize the number of job opportunities in our CLSC network. The first term is the fixed job opportunities like the managers of distribution centers in each period. The second and third terms are the number of variable job opportunities which are related to the flow of products and components through our CLSC network.

Our constraints include service level (i.e., constraint sets (4) and (5)), capacity (i.e., constraint sets (6) to (10)), location (i.e., constraint set (11)), inventory with the flow of network constraints (i.e., constraint sets (12) and (13)), and feasibility of variables (i.e., constraint set (14)).

$$\sum _{i\in m,r;j\in c;g}{f}_{ijgt}=SQ\times \sum _{c}^{}{D}_{cgt} \forall t,g$$
(4)
$$\sum _{i\in m,r;j\in o}{f}_{ijat}={{S}_{a}}^{}\times \sum _{o}^{}{\text{D}}_{\text{o}\text{a}\text{t}} \forall t,a$$
(5)
$$\sum _{m,g}{f}_{mrgt}+\sum _{c,g}{f}_{crgt}\le {C}_{r}^{}\times {y}_{rt} \forall r,t$$
(6)
$$\sum _{m,a}{f}_{mrat}\le {C}_{ra}^{}\times {y}_{rt} \forall r,t$$
(7)
$$\sum _{u,t}{f}_{umat}+\sum _{r,t}{f}_{rmat}\le {C}_{ma}^{} \forall m,a$$
(8)
$$\sum _{r,t}{f}_{ruat}\le {C}_{ua}^{} \forall u,a$$
(9)
$$\sum _{m,t}{f}_{moat}+\sum _{r,t}{f}_{roat}\le {C}_{oa}^{} \forall o,a$$
(10)
$$\sum _{}{y}_{rt}={MAX}_{t} \forall t$$
(11)
$$\sum _{u,m.a,t}{f}_{umgt}+ \sum _{m,t}{h}_{mg\left(t-1\right)}= \sum _{mc,a,t}{f}_{mcgt}+ \sum _{mr,a,t}{f}_{mrat}+ \sum _{m,t}{h}_{mgt} \forall m,g, t$$
(12)
$$\sum _{i\in u, c,m;i\ne j;j\in r, t}{f}_{ijat}+ \sum _{r,t}{h}_{ra\left(t-1\right)}= \sum _{j\in d,o,c;r,a,t}{f}_{rjat}+ \sum _{d,t}{h}_{rat} \forall r, t,a$$
(13)
$${y}_{rt}=\left\{\text{0,1}\right\}\, and\, {f}_{ijgt}, {f}_{ijat}, {h}_{igt}, {h}_{iat}\ge 0\,and\, integer$$
(14)

Constraint sets (4) and (5) are service level requirements for both customers and secondary markets. Constraint sets (6) and (7) are the capacity constraint in distribution centers for products and components, respectively. Constraint set (8) is the capacity constraint for manufacturers. Constraint set (9) is the capacity constraint for suppliers. Constraint set (10) shows the capacity limitation for the secondary markets.

Constraint set (11) specifies the number of open distributer centers in each period. Constraint sets (12) and (13) shows the flow between facilities and the inventory status in each period. Finally, the decision variables must be feasible as given in the constraint set (14).

4 Lagrangian relaxation reformulations and heuristics

Here, we apply the theory of Lagrangian relaxation using heuristic rules for solving the proposed model. First of all, we need to transform the proposed multi-objective optimization model to a single objective model. Then, the Lagrangian relaxation theory is explained and our reformulations are proposed. Heuristic rules are developed to find initial solutions. Finally, the main structure of the proposed algorithm, is explained.

We applied the LP-metric method (Ringuest, 1997) to transform our multi-objective model into a single objective model (Asghari et al., 2022). Our main objective function is rewritten as follows:

$$Z=\frac{{Z}_{1}^{*}-{Z}_{1}}{{Z}_{1}^{*}}+\frac{{Z}_{2}-{Z}_{2}^{*}}{{Z}_{2}^{*}}+\frac{{Z}_{3}^{*}-{Z}_{3}}{{Z}_{3}^{*}}$$
(15)

where \({Z}_{1}^{*}\), \({Z}_{2}^{*}\) and are \({Z}_{3}^{*}\) the optimal solutions for our objective functions, i.e., the total profit, energy consumption and job opportunities, respectively. To reach these values, the model is solved for only one objective function and this optimal value is noted.

Our revised objective function given in Eq. (15) is to minimize the deviation from the optimal values. Here, we apply the Lagrangian relaxation theory for solving this model. Our method is in line with version applied by Bertsimas & Tsitsiklis (1997) and Fisher (1985). The first step is to generate an efficient Lagrangian relaxation reformulation for the main model given in Sect. 3. In this regard, the most difficult constraints are selected and removed from the main model. Then, they are added to the revised objective function given in Eq. (15). The solution from this reformulation is a lower bound which may not be feasible but optimal for the main model. In the original version of Lagrangian relaxation algorithm as a sub-gradient method, a feasible upper bound is generated randomly and it would be updated random per iteration. Here, in this study, two problem-specific and fast heuristics are proposed to find an upper bound which is a near-optimal solution.

4.1 Reformulations

The most important part to find an efficient Lagrangian relaxation reformulation is to relax which set of constraints. If the constraints (12) and (13) are considered to be relaxed from the original model, the Lagrangian relaxation reformulation is as follow s:

$$\begin{aligned}LB&=\text{min}\left(Z+\sum _{m,g,t}{\pi }_{mgt}\left(\sum _{u,m.a,t}{f}_{umgt}+ \sum _{m,t}{h}_{mg\left(t-1\right)}- \sum _{mc,a,t}{f}_{mcgt}- \sum _{mr,a,t}{f}_{mrat}- \sum _{m,t}{h}_{mgt}\right)\right.\\ &\quad\left.+ \sum _{r,t,a}{\phi }_{rta}\left(\sum _{i\in u, c,m;i\ne j;j\in r, t}{f}_{ijat}+ \sum _{r,t}{h}_{ra\left(t-1\right)}- \sum _{j\in d,o,c;r,a,t}{f}_{rjat}- \sum _{d,t}{h}_{rat}\right)\right)\\&\quad s.t.\, Constraints\,(4)\,to\,(11)\,and\,(14)\end{aligned}$$
(16)

where \({\pi }_{mgt}\) and \({\phi }_{rta}\) are the Lagrangian multipliers. We call this reformulation as LG1. In addition to this reformulation, other reformulations are defined in Table 2.

Table 2 Lagrangian relaxation reformulations
Full size table
Table 3 Comparison of reformulations (OG: optimality gap; CPU time is based on seconds)
Full size table

As given in Table 3, our reformulation LG1 is highly efficient in comparison with other reformulations. It is not only faster than other reformulations, but also its solution is the most near-optimal in comparison with other solutions.

4.2 Heuristics

The lower bound for the proposed problem was found by the reformulation LG1. Here, the upper bound is estimated by two problem-specific heuristics. We call the first heuristic as H1 and the second heuristic as H2. These heuristics aim to find feasible values for decision variables and then compute the objective function.

H1 establishes the distribution centers per period based on the minimum establishment cost (\({F}_{r}\)) with regards to the maximum number of open distributers per period (\({MAX}_{t}\)). However, H2 first computes a new matrix for each distributer per period and then establishes the distribution centers. This matrix is based on the average for the establishment cost as well as the transportation cost (\({T}_{rj}\) and \({T}_{rja}\)). Finally, the lowest values in this matrix for each distributor is considered to be open with regards to the maximum number of open distributers per period.

For allocation decisions, H1 assigns each facility to another facility based on the lowest cost of transportation. It means that each manufacture is assigned to a distributor which has the lowest transportation cost. This allocation is continued once the capacity of distributor is filled and a new assignment is not possible. H2 does the allocation decisions in a same way. However, the initial matrix is generated by the average of transportation cost and the production cost. In conclusion, these problem-specific heuristics are a greedy search to find an initial solution quickly.

4.3 Main loop of the proposed algorithm

After generating an initial lower bound (LB) from the Lagrangian relaxation LG1 and finding the best optimal upper bound (UB) among the solutions of our two problem-specific heuristics, the pseudo-code of the proposed algorithm is structured as follows:

Step 0: Initialize the Lagrange multipliers, \({\pi }_{mgt}^{0}\) and \({\phi }_{rta}^{0}\)with setting it = 0;

Step 1: Let \({\pi }_{mgt}^{it}={\pi }_{mgt}^{0}\), \({\phi }_{rta}^{it}={\phi }_{rta}^{0}\)and solve the reformulation LG1. Then, consider the obtained decision variables with the optimal solution from Eq. (16) to update the LBit+1 as follows:

$$L{B}^{it+1}={max}(L{B}^{it},L{B}^{it-1})$$
(17)

Step 2: Got the best solution as UB from our H1 and H2. Then, the Lagrange multipliers are updated as follows:

$$\begin{aligned}\pi _{mgt}^{it + 1} &= \max \left (\pi _{mgt}^{it} + {\mu ^{it}}\right.\\ &\quad \left.\times \left( {\mathop \sum \limits_{u,m.a,t} {f_{umgt}} + ~\mathop \sum \limits_{m,t} {h_{mg\left( {t - 1} \right)}} - ~\mathop \sum \limits_{mc,a,t} {f_{mcgt}} - ~\mathop \sum \limits_{mr,a,t} {f_{mrat}} - ~\mathop \sum \limits_{m,t} {h_{mgt}}} \right),0\right)\end{aligned}$$
(18)
$$\begin{aligned} \varphi _{rta}^{it + 1} &= \max \left(\varphi _{rta}^{it} + {\mu ^{it}} \right. \\ & \quad \left. \times \left( {\mathop \sum \limits_{i \in u,~c,m;i \ne j;j \in r,~t} {f_{ijat}} + ~\mathop \sum \limits_{r,t} {h_{ra\left( {t - 1} \right)}} - ~\mathop \sum \limits_{j \in d,o,c;r,a,t} {f_{rjat}} - ~\mathop \sum \limits_{d,t} {h_{rat}}} \right),0\right) \end{aligned} $$
(19)

where \({\mu }^{it}={f}^{it}\times \left|\frac{L{B}^{it + 1}-L{B}^{it}}{(UB-L{B}^{t+1}{)}^{2}}\right|\) and being f a number distributed by \(U(0,2)\) in the first iteration and it is decreased during the number of iterations by \({f}^{it+1}={f}^{it}\times (1-\frac{1}{Maxit})\) without any improvement. Note that Maxit is the maximum number of iterations.

Step 3: it = it + 1;

Step 4: If a feasible LB reaches or it satisfies the maximum number of iteration (\(Maxit\)) then, stop and display LB. Otherwise, go to Step 1;

5 Computational results

Here, to analyze the efficiency of the proposed model and the performance of the proposed algorithm, a real-life case study in Iran is considered. As mentioned earlier, the proposed model and algorithm are implemented on a laptop with processor Intel(R) Core (TM) i7-10850 H CPU @ 2.70 GHz 2.71 GHz. From our data in the tire industry in Iran, several test problems with different dimensions are generated. It is assumed that our CLSC network includes 1 to 5 suppliers, 2 to 5 manufacturers, 2 to 4 distributers, 1 to 5 disposal centers, 2 to 5 customers, and 2 to 5 secondary markets. For small tests, 3 to 6 periods are considered. For more details, the size of our small tests, is given in Table 4. The considered industry has 10 main customers from Tehran, Tabriz, Isfahan, Mashad, Kerman, Shiraz, Sary, Rasht and Urmia and Ahvaz. The data for the customer demand in 12 periods, are provided in Table 5.

Table 4 Details for small-sized instances
Full size table
Table 5 Customers demand
Full size table

Results of our algorithm for small test problems are given in Table 6. It is evident that the optimality gap in comparison with the CPLEX software is very low and in most of test problems, our Lagrangian relaxation algorithm finds the optimal solution. It should be noted that the gap between the lower and upper bounds of the proposed algorithm is also low and this shows that our heuristics are also successful to find an efficient solution in small-scale instances.

Fig. 2
figure 2

Comparison of CPU time for both CPLEX and Lagrangian algorithm

Full size image
Table 6 Results for small test problems
Full size table
Table 7 Size of large-scale instances
Full size table
Table 8 Results for large-scale tests (OM: Out of memory)
Full size table

From our results given in Table 8, the proposed algorithm could solve the model optimally with limited number of iterations. This statement can be concluded when we discover that the maximum deviation between the optimal and near optimal solutions in worse case is 22% in small-scale instances and 42% in large-scale instances.

6 Managerial insights

Academically, the reverse logistics and CLSC network traditionally optimizes the facility location and their right allocation based on the total cost or the total profit. However, with regards to sustainable development goals and guidelines from ISO 14000 and ISO 26000, traditional SCND models are not able to cover the triple bottom lines of sustainability. This makes the role of a multi-objective optimization important. In addition, an efficient design of a CLSC network should address the energy consumption due to the use of non-renewable energies for manufacturing and transportation activities. To increase the customers’ satisfaction, it is important to consider different service levels. To improve the human life quality, an efficient design of SCND must able to generate more job opportunities for both managers and operators in facilities. To address these issues, this study deploys a multi-objective optimization model for an efficient sustainable SCND with the energy efficiency.

As far as we know, there is no similar study to develop our multi-objective optimization model considering service levels, job opportunities and energy consumption. Although adding more factors make the problem realistic, it increases the model complexity. The exact solver like CPLEX is not able to solve real-scale instances for our realistic model. Although heuristics and metaheuristics are able to solve them, their solution cannot guarantee optimality due to random search mechanism. The best way to reduce the complexity of our model is to reformulate it with Lagrangian relaxation or Benders decomposition. This study proposes a set of efficient Lagrangian relaxation reformulations and two problem-specific heuristics for solving our model optimally and efficiently.

The viability of a sustainable CLSC in a real-life case study in Iran was demonstrated by the results. The constraints of the proposed CLSC network support the inventory statuses, the flows of materials, components and products, capacity limitations and the location of facilities. To handle these constraints, the most difficult ones were relaxed and our Lagrangian algorithm outperforms the CPLEX software (Tables 6 and 8; Fig. 2). The proposed algorithm is able to achieve the feasible optimal solution in small instances and its optimality gap is low even in large-scale instances.

7 Conclusions and future studies

This paper contributed to an active topic in the area of SCND by proposing an efficient and sustainable CLSC considering service levels, energy consumption and job opportunities. The main new assumption of our model was to consider five activities for distribution centers for the role of warehouses and collection centers. Our CLSC network include suppliers, manufacturers, distribution centers, customer zones, and disposal centers. The proposed model also addressed the customer demand with no shortage option. The proposed CLSC model made location, allocation and inventory decisions to optimize the total profit, energy consumption and job opportunities, simultaneously. Another novelty of this research was to develop a set of efficient Lagrangian relaxation reformulations and two problem-specific heuristics for solving a real-world numerical example. The results have revealed that the obtained solution is feasible and the developed solution algorithm is highly efficient for solving supply chain models. To validate our solutions, we have used the exact solver using CPLEX software. Finally, a comprehensive discussion was provided to highlight our findings and managerial insights from our results. One main finding confirms that simultaneous consideration of service levels, job opportunities and energy consumption make our sustainable CLSC more realistic and our Lagrangian algorithm can be applied to other complex SCND models.

Although this study was more complex and realistic than majority of studies in the area of sustainable CLSC, it faces with some limitations which can be considered for our future works. First of all, our model ignores the uncertainty and therefore, the development of a robust, stochastic or fuzzy programming approaches, is highly recommended for our model. As such, our model only considers the energy consumption. Hence, it is also possible to consider such other environmental factors as the CO2 emission and waste management or chemical factors to achieve the environmental sustainability. At last but not least, the proposed reformulation can be compared with the Benders decomposition reformulation and other heuristic techniques for future studies.