1 Introduction

Data Envelopment Analysis (DEA) method has been widely implemented in the literature to the performance appraisal of mutual funds (MFs) (Basso & Funari, 2016; Kaffash & Marra, 2017). DEA is a non-parametric mathematical programming approach for performance assessment, ranking and benchmarking of the homogeneous decision-making units (DMUs) in the presence of multiple inputs and outputs (De Leone, 2008; Emrouznejad, 2014; Emrouznejad & Banker, 2010). From beginning DEA technique, this approach has been widely used in many real-world problems and applications (Emrouznejad & Yang, 2018; Liu et al., 2013; Peykani, Farzipoor Saen, et al., 2021).

MF invests the money collected from investors on a specific investment plan. Accordingly, the structure of their activities can be considered as a two-stage process that the manager seeks to attract funds from investors in the first stage, and constructs the portfolio in the second stage. In other words, the MF management’s structure can be decomposed into serially linked two components including operational management and portfolio management (Premachandra et al., 2012, 2016).

Therefore, in applying DEA technique for performance appraisal of mutual funds, an internal structure of MFs should be considered. Because, ignoring the internal structure of the MFs and the intra-organizational relationships leads to the invalidity of efficiency scores and ranking of MFs. Since the conventional DEA models cannot be employed for performance measurement of DMUs with network structure, the network data envelopment analysis (NDEA) approach must be used (Castelli et al., 2010; Cook & Zhu, 2014). NDEA is an applicable and effective approach that can be applied to assess the performance of DMUs with network structure such as two-stage, series, parallel, mixed, etc. (Kao, 2014, 2017).

Another important point that should be considered in performance evaluation of MFs is the uncertainty of financial data. Because, one of the most important features of financial markets is their uncertainty. In addition, the results of classic DEA models are so sensitive to bias or deviation in data. As a result, a little variation in the values of data can cause significant differences in efficiency scores and ranking of DMUs (Peykani et al., 2018, 2019; Sadjadi & Omrani, 2008; Toloo & Mensah, 2019).

Robust optimization (RO) approach, is one of the powerful and popular methods that can be applied to deal with uncertainty of data (Keith & Ahner, 2019; Kim et al., 2018). The RO approach based on uncertainty sets does not need significant historical data and therefore it can be employed in almost all of the real-life DEA problems. So, recently, some studies about DEA have applied robust optimization to deal with data uncertainty that called robust data envelopment analysis (RDEA) (Wu et al., 2017; Lu et al., 2019; Tavana et al., 2021). According to the comprehensive and structured literature review of RDEA presented by Peykani et al., (2020a), proposing and applying RDEA models under continuous and discrete uncertainty in different studies have increased dramatically.

Thus, in this study, a novel robust network data envelopment analysis (RNDEA) approach is presented based on leader–follower (Stackelberg game or non-cooperative game) method for performance assessment, ranking, and classification of mutual funds with respect to internal structure and uncertainty of data. Additionally, the applicability and efficacy of the presented approach is demonstrated by measuring the performance of 15 active mutual funds in Iran's capital market. The rest of this paper is organized as follows. Literature review classification and literature gaps are introduced in Sect. 2. Theoretical background involving the structure of MFs and NDEA modeling based on non-cooperative game method are presented in Sect. 3. The robust network DEA approach for performance assessment of MFs under uncertainty is proposed in Sect. 4. Then, in Sect. 5, the applicability of the proposed approach is illustrated by a real-life case study. Finally, the conclusions and some directions for future researches are given in Sect. 6.

2 Literature review

In this section, the literature review from two aspects including performance measurement of MFs by network DEA, and robust network DEA are presented. Also, the literature gaps, which this study addresses are introduced.

2.1 Performance measurement of mutual funds using network DEA

Premachandra et al. (2012) were the pioneer researchers that applied network DEA model for performance evaluation of US mutual fund families. They assumed that the structure of MFs can be considered as a two-stage process including operational management and portfolio management. In a similar study, Premachandra et al. (2016) employed network DEA approach for performance appraisal of mutual fund industry. Galagedera et al. (2016) extended the proposed two-stage structure of Premachandra et al. (2012) for efficiency measurement of MFs. They considered total cash flow of investors as a leakage variable in operational management process.

Sánchez-González et al. (2017) applied network slack-based measure (NSBM) model for efficiency measurement of mutual fund companies. Galagedera et al. (2018) introduced new structure and network DEA model for performance assessment of MFs. They decomposed the overall efficiency of MFs into the efficiency of operational management, resource management, and portfolio management. Galagedera (2019) proposed a two-stage DEA model with non-discretionary output in first stage for modelling social responsibility in performance evaluation of MFs.

Galagedera et al. (2020) developed a network DEA model to evaluate the performance of MF from disbursement management viewpoint in the presence of non-discretionary input. Hsieh et al. (2020) presented a two-stage network DEA model for performance assessment of MFs, which decision quality and capital magnet are considered as a two-stage process of MFs. Last but not the least, Tsolas (2020) applied two-stage DEA approach to appraisal the performance of precious metal mutual funds.

A more detail classification of the performance assessment of mutual funds by network DEA is illustrated in Table 1 by considering three characteristics: type of NDEA modeling, network structure, and uncertainty. The characteristics of this study have also been introduced in the last row of Table 1. As summarized in Table 1, all of the existing researches in literature are neglected the uncertain nature of financial data. Also, most of studies employed additive approach that presented by Chen et al. (2009) for NDEA modeling.

Table 1 Classification of Mutual Funds Performance Measurement with Network DEA
Full size table

2.2 Robust network DEA

Ardekani et al. (2016) initially proposed robust two-stage DEA model using robust optimization approach of Bertsimas and Sim (2004) for efficiency measurement of electricity power production and distribution companies in Iran. They applied multiplicative approach of Kao and Hwang (2008) for modeling of RNDEA. Bayati and Sadjadi (2017) presented RNDEA models based on RO approaches of Ben-Tal and Nemirovski (2000) and Bertsimas and Sim (2004) for performance assessment of Iranian regional electricity power networks. They decomposed the overall efficiency of three-stage according to additive approach of Chen et al. (2009).

Esfandiari et al. (2017) introduced robust network DEA models by applying scenario based robust optimization approach of Mulvey et al. (1995) for performance measurement of DMUs with two-stage structure under discrete uncertain data. They used game theory approaches of Liang et al. (2008) including centralized (cooperative game) and leader–follower (non-cooperative game) methods for efficiency decomposition. Shakouri et al (2019) presented robust two-stage DEA models based on p-robust approach of Snyder and Daskin (2006) to deal with discrete uncertain data.

Table 2 summarizes the main characteristics of the RNDEA researches and compares them with the RNDEA model developed in this study. According to the literature review and Table 2, it is surprising that only four researches have been done in robust network DEA area and this field have potential future directions and research pristine opportunities. As it can be seen in the last row of Tables 1 and 2, the new robust network DEA model of this study is based on leader–follower approach and used for performance evaluation of mutual funds under continuous uncertainty. Also, the proposed approach is linear program and capable to be used under variable retunes to scale (VRS) assumption. Moreover, the efficiency decomposition of presented RNDEA method is unique.

Table 2 Classification of Robust Network DEA
Full size table

3 Theoretical background

In this section, theoretical background including the structure of mutual funds and non-cooperative game method for modeling of NDEA under extended two-stage structure are presented.

3.1 Mutual funds structure

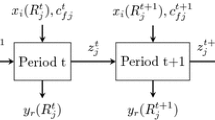
In this study, the structure of mutual funds activities is viewed as a two-stage process that the manager of MFs seeks to attract funds from investors in the first step, and in the second step, focus on the optimal portfolio construction (Premachandra et al., 2012, 2016). The graphically illustration of MFs process is depicted in Fig. 1.

Fig. 1
figure 1

Structure of mutual funds

Full size image

As can be seen in Fig. 2, marketing and distribution costs accompany with management costs are the input variables at first stage. Net asset value (NAV) is the intermediate variable that links the two stages. In other words, NAV is output and input variable at stages 1 and 2, respectively. Accordingly, a MF that can produce the highest NAV with the least amount of mentioned expenses will be more efficient than the other MFs from operational management aspect.

Fig. 2
figure 2

Extended two-stage structure

Full size image

It should be noted that fund size, standard deviation of average return, turnover ratio, and net expense ratio are another part of inputs to the stage 2 and average return is the output variable at second stage. Thus, a MF that can produce the highest average return of portfolio with the least amount of NAV, fund size, risk (standard deviation of average return), turnover ratio and net expense ratio will be more efficient than the other MFs from portfolio management aspect.

3.2 Network DEA modeling based on leader–follower approach

Let \(x_{ik} (i = 1,...,I)\) denote the input variables at first stage, \(z_{gk} (g = 1,...,G)\) denote the intermediate variables that links the two stages, \(w_{hk} (h = 1,...,H)\) denote the additional input variables at second stage, and \(y_{rk} (r = 1,...,R)\) denote the output variables at second stage of \({\text{DMU}}_{k} (k = 1,...,K)\). As illustrated in FIg.  2, the extended two stage structure of this study includes I1, IM, I2, and O2.

Note that the non-negative weights \(\alpha_{i} (i = 1,...,I)\), \({\varphi_{g}} (g = 1,...,G)\), \(\mu_{h} (h = 1,...,H)\), and \(\beta_{r} (r = 1,...,R)\) are assigned to the I1, IM, I2, and O2, respectively. Also, \(\Psi_{1}\) and \(\Psi_{2}\) are the free variables associated with returns to scale (RTS) in DEA for stages 1 and 2, respectively.

As mentioned before, the leader–follower (non-cooperative game) approach that presented by Liang et al. (2008) is one of the applicable and popular approaches for modeling of network DEA. In this method, it is assumed that one of the stages is more important and is considered to be the leader. Thus, the efficiency of the leader's stage is calculated at first, and then the efficiency of the other stages (follower's stage) is calculated according to the optimal solution of the leader's stage.

If assumed that stage 1 is more important (first stage as the leader and second stage as the follower), the efficiency of stage 1 for a specific \({\text{DMU}}_{0}\) under variable returns to scale assumption is calculated as Model (1):

$$ \begin{aligned} & \dag_{0}^{1} \, = Max\frac{{\sum\nolimits_{g = 1}^{G} {z_{g0} {\varphi_{g}} } + \Psi_{1} }}{{\sum\nolimits_{i = 1}^{I} {x_{i0} \alpha_{i} } }} \hfill \\ & \begin{array}{ll} {S.t.\frac{{\sum\nolimits_{g = 1}^{G} {z_{gk} {\varphi_{g}} } + \Psi_{1} }}{{\sum\nolimits_{i = 1}^{I} {x_{ik} \alpha_{i} } }} \le 1,} & {\forall k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\alpha_{i} {\varphi_{g}} \ge 0,} & {\forall i,g} \\ \end{array} \hfill \\ \end{aligned} $$
(1)

Model (1) is a linear fractional program which can be transformed via the transformation of Charnes and Cooper (1962) as follows:

$$ \begin{aligned} & \dag_{0}^{1} = Max \, \sum\nolimits_{g = 1}^{G} {z_{g0} {\varphi_{g}} } + \Psi_{1} \hfill \\ & S.t. \, \sum\nolimits_{i = 1}^{I} {x_{i0} \alpha_{i} } = 1 \hfill \\ & \begin{array}{ll} {\sum\nolimits_{g = 1}^{G} {z_{gk} {\varphi_{g}} } - \sum\nolimits_{i = 1}^{I} {x_{ik} \alpha_{i} } + \Psi_{1} \le 0,} & {\forall k} \\ \end{array} \hfill \\ & \alpha_{i} ,{\varphi_{g}} \ge 0, \hfill \\ \end{aligned} $$
(2)

Now, the efficiency of second stage as the objective function is maximized while the efficiency of first stage is fixed. Accordingly, Model (3) under VRS assumption is presented as follows:

$$ \begin{aligned} & \dag_{0}^{2/1} = Max\frac{{\sum\nolimits_{r = 1}^{R} {y_{r0} \beta_{r} } + \Psi_{2} }}{{\sum\nolimits_{g = 1}^{G} {z_{g0} {\varphi_{g}} } + \sum\nolimits_{h = 1}^{H} {w_{h0} \mu_{h} } }} \hfill \\ & \begin{array}{ll} {S.t. \, \frac{{\sum\nolimits_{r = 1}^{R} {y_{rk} \beta_{r} } + \Psi_{2} }}{{\sum\nolimits_{g = 1}^{G} {z_{gk} {\varphi_{g}} } + \sum\nolimits_{h = 1}^{H} {w_{hk} \mu_{h} } }} \le 1,} & {\forall k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\frac{{\sum\nolimits_{g = 1}^{G} {z_{gk} {\varphi_{g}} } + \Psi_{1} }}{{\sum\nolimits_{i = 1}^{I} {x_{ik} \alpha_{i} } }} \le 1,} & {\forall k} \\ \end{array} \hfill \\ & \frac{{\sum\nolimits_{g = 1}^{G} {z_{g0} {\varphi_{g}} } + \Psi_{1} }}{{\sum\nolimits_{i = 1}^{I} {x_{i0} \alpha_{i} } }} = \dag_{0}^{{1*}} \hfill \\ & \begin{array}{ll} {\alpha_{i},{\varphi_{g}} ,\mu_{h} ,\beta_{r} \ge 0,} & {\forall i,g,h,r} \\ \end{array} \hfill \\ \end{aligned} $$
(3)

Using the transformation of Charnes and Cooper (1962), Model (3) can be transformed into the following linear program:

$$ \begin{aligned} & \dag_{0}^{\frac{2}{1}} = \, Max \, \sum\nolimits_{r = 1}^{R} {y_{r0} \beta_{r} } + \Psi_{2} \hfill \\ & S.t. \, \sum\nolimits_{g = 1}^{G} {z_{g0} {\varphi_{g}} } + \sum\nolimits_{h = 1}^{H} {w_{h0} \mu_{h} } = 1 \hfill \\ & \begin{array}{ll} {\sum\nolimits_{r = 1}^{R} {y_{rk} \beta_{r} } - \sum\nolimits_{g = 1}^{G} {z_{gk} {\varphi_{g}} } - \sum\nolimits_{h = 1}^{H} {w_{hk} \mu_{h} } + \Psi_{2} \le 0,} & {\forall k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\sum\nolimits_{g = 1}^{G} {z_{gk} {\varphi_{g}} } - \sum\nolimits_{i = 1}^{I} {x_{ik} \alpha_{i} } + \Psi_{1} \le 0,} & {\forall k} \\ \end{array} \hfill \\ & \left( {\sum\nolimits_{g = 1}^{G} {z_{g0} {\varphi_{g}} } + \Psi_{1} } \right) - \dag_{0}^{{1*}} \left( {\sum\nolimits_{i = 1}^{I} {x_{i0} \alpha_{i} } } \right) = 0 \hfill \\ & \begin{array}{ll} {\alpha_{i} ,{\varphi_{g}} ,\mu_{h} ,\beta_{r} \ge 0,} & {\forall i,g,h,r} \\ \end{array} \hfill \\ \end{aligned} $$
(4)

Finally, the overall efficiency is calculated according to Eq. (5) as follows:

$$ \dag_{0}^{{\text{T}}} = \dag_{0}^{1} * \dag_{0}^{{\frac{2}{1}}} $$
(5)

Note that in leader–follower approach, the efficiency decomposition is unique (Li et al., 2012; Liang et al., 2008).

Alternatively, if assumed that the stage 2 is more important (second stage as the leader and first stage as the follower), the efficiency of the second stage, the first stage and the entire two-stage system will be measured in a similar manner that is presented in Appendix A.

4 The robust network data envelopment analysis (RNDEA) approach

In this section in 3 steps, the robust NDEA method using robust optimization approach is proposed for performance appraisal of two-stage DMUs in the presence of uncertain data. Note that in proposing RNDEA model, stage 1 is assumed as the leader and stage 2 as the follower.

Step 1. Preparing NDEA models

In order to consider the uncertainty in all parameters of NDEA models including \(x_{ik} (i = 1,...,I)\),\(z_{gk} (g = 1,...,G)\),\(w_{hk} (h = 1,...,H)\), and \(y_{rk} (r = 1,...,R)\), Models (2) and (4) are converted into Models (6) and (7), respectively.

$$ \begin{aligned} & \dag_{0}^{1} = Max\sum\nolimits_{g = 1}^{G} {z_{g0} {\varphi_{g}} } + \Psi_{1} \hfill \\ & S.t. \, \sum\nolimits_{i = 1}^{I} {x_{i0} \alpha_{i} } \le 1 \hfill \\ & \begin{array}{ll} {\sum\nolimits_{g = 1}^{G} {z_{gk} {\varphi_{g}} } - \sum\nolimits_{i = 1}^{I} {x_{ik} \alpha_{i} } + \Psi_{1} \le 0,} & {\forall k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\alpha_{i},{\varphi_{g}} \ge 0,} & {\forall i,g} \\ \end{array} \hfill \\ \end{aligned} $$
(6)

Proposition 1

The optimal solution of Model (6) is equal to Model (2).

Proof

Assume that the optimal solution of Model (6) is \(\left( {\bar{\alpha },\bar{\varphi },\bar{\Psi }_{1} } \right)\). By contradiction, suppose that \(\sum\nolimits_{i = 1}^{I} {x_{i0} \bar{\alpha }_{i} } < 1\) (it should be noted that \(\sum\nolimits_{i = 1}^{I} {x_{i0} \bar{\alpha }_{i} } = \Omega \& \Omega > 0\)). \( \left( {\bar{\alpha },\quad \bar{\varphi },\quad \bar{\Psi }_{1} } \right) \) are considered as \( \bar{\alpha } = \frac{{\bar{\alpha }}}{\Omega } \), \( \bar{\varphi } = \frac{{\bar{\varphi }}}{\Omega } \) and \( \bar{\Psi }_{1} = \frac{{\bar{\Psi }_{1} }}{\Omega } \). Because of \( \sum\nolimits_{{g = 1}}^{G} {z_{{gk}} \bar{\varphi }_{g} } - \sum\nolimits_{{i = 1}}^{I} {x_{{ik}} } \bar{\alpha }_{i} + \bar{\Psi }_{1} = \left( {\frac{1}{\Omega }\left( {\sum\nolimits_{{g = 1}}^{G} {z_{{gk}} \bar{\varphi }_{g} } - \sum\nolimits_{{i = 1}}^{I} {x_{{ik}} \bar{\alpha }_{i} } + \bar{\Psi }_{1} } \right)} \right) \le 0 \) (with respect to \(\left( {\frac{1}{\Omega }} \right) > 0\) and \(\sum\nolimits_{g = 1}^{G} {z_{gk} \bar{\varphi }_{g} } { - }\sum\nolimits_{i = 1}^{I} {x_{ik} \bar{\alpha }_{i} } + \bar{\Psi }_{1} \le 0\)),\( \sum\nolimits_{{i = 1}}^{I} {x_{{i0}} \bar{\alpha }} = \left( {\frac{1}{\Omega }\left( {\sum\nolimits_{{i = 1}}^{I} {x_{{i0}} \bar{\alpha }_{i} } } \right)} \right) = 1 \), \( \bar{\alpha } \ge 0 \), and \( \bar{\varphi } \ge 0 \),\( \left( {\bar{\alpha },\bar{\varphi },\bar{\Psi }_{1} } \right) \) is the feasible solution of Model (6). Also, in the objective function \( \sum\nolimits_{{g = 1}}^{G} {z_{{g0}} \bar{\varphi }_{g} } + \bar{\Psi }_{1} = \left( {\frac{1}{\Omega }\left( {\sum\nolimits_{{g = 1}}^{G} {z_{{g0}} \bar{\varphi }_{g} } + \bar{\Psi }_{1} } \right)} \right) \), with respect to suppose that \(\sum\nolimits_{i = 1}^{I} {x_{i0} \bar{\alpha }_{i} } < 1\), thus \(\left( {\frac{1}{{\sum\nolimits_{i = 1}^{I} {x_{i0} \bar{\alpha }_{i} } }}} \right) > 1\) and finally \( \sum\nolimits_{{g = 1}}^{G} {z_{{g0}} \bar{\varphi }_{g} } + \bar{\Psi }_{1} {\text{ > }}\sum\nolimits_{{g = 1}}^{G} {z_{{g0}} \bar{\varphi }_{g} } + \bar{\Psi }_{1} \) that this is contradicts with optimality of \(\left( {\bar{\alpha },\bar{\varphi },\bar{\Psi }_{1} } \right)\). So, at any optimal solution of Model (6), always \(\sum\nolimits_{i = 1}^{I} {x_{i0} \bar{\alpha }_{i} } = 1\).

$$ \begin{aligned} & \dag_{0}^{\frac{2}{1}} = Max\sum\nolimits_{r = 1}^{R} {y_{r0} \beta_{r} } + \Psi_{2} \hfill \\ & S.t. \, \sum\nolimits_{g = 1}^{G} {z_{g0} {\varphi_{g}} } + \sum\nolimits_{h = 1}^{H} {w_{h0} \mu_{h} } \le 1 \hfill \\ & \begin{array}{ll} {\sum\nolimits_{r = 1}^{R} {y_{rk} \beta_{r} } - \sum\nolimits_{g = 1}^{G} {z_{gk} {\varphi_{g}} } - \sum\nolimits_{h = 1}^{H} {w_{hk} \mu_{h} } + \Psi_{2} \le 0,} & {\forall k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\sum\nolimits_{g = 1}^{G} {z_{gk} {\varphi_{g}} } - \sum\nolimits_{i = 1}^{I} {x_{ik} \alpha_{i} } + \Psi_{1} \le 0,} & {\forall k} \\ \end{array} \hfill \\ & \left( {\sum\nolimits_{g = 1}^{G} {z_{g0} {\varphi_{g}} } + \Psi_{1} } \right) - \dag_{0}^{{1*}} \left( {\sum\nolimits_{i = 1}^{I} {x_{i0} \alpha_{i} } } \right) = 0 \hfill \\ & \begin{array}{ll} {\alpha_{i} ,{\varphi_{g}} ,\mu_{h} ,\beta_{r} \ge 0,} & {\forall i,g,h,r} \\ \end{array} \hfill \\ \end{aligned} $$
(7)

Proposition 2

The optimal solution of Model (7) is equal to Model (4).

Proof

Assume that the optimal solution of Model (7) is \(\left( {\bar{\alpha },\bar{\varphi },\bar{\mu },\bar{\beta },\bar{\Psi }_{1} ,\bar{\Psi }_{2} } \right)\). By contradiction, suppose that \(\sum\nolimits_{g = 1}^{G} {z_{g0} \bar{\varphi }_{g} } + \sum\nolimits_{h = 1}^{H} {w_{h0} \bar{\mu }_{h} } < 1\) (it should be noted that \(\sum\nolimits_{g = 1}^{G} {z_{g0} \bar{\varphi }_{g} } + \sum\nolimits_{h = 1}^{H} {w_{h0} \bar{\mu }_{h} } = \mho \& \mho > 0\)). \( \left( {\bar{\alpha },\bar{\varphi },\bar{\mu },\bar{\beta },\bar{\Psi }_{1} ,\bar{\Psi }_{2} } \right) \) are considered as \(\bar{\alpha } = \frac{{\bar{\alpha }}}{\mho }\), \(\bar{\varphi } = \frac{{\bar{\varphi }}}{\mho }\), \(\bar{\mu } = \frac{{\bar{\mu }}}{\mho }\), \(\bar{\beta } = \frac{{\bar{\beta }}}{\mho }\), \(\bar{\Psi }_{1} = \frac{{\bar{\Psi }_{1} }}{\mho }\) and \(\bar{\Psi }_{2} = \frac{{\bar{\Psi }_{2} }}{\mho }\). Because of \(\sum\nolimits_{r = 1}^{R} {y_{rk} \bar{\beta }_{r} } { - }\sum\nolimits_{g = 1}^{G} {z_{gk} \bar{\varphi }_{g} } - \sum\nolimits_{h = 1}^{H} {w_{hk} \bar{\mu }_{h} } + \bar{\Psi }_{2} = \left( {\frac{1}{\mho }\left( {\sum\nolimits_{r = 1}^{R} {y_{rk} \bar{\beta }_{r} } { - }\sum\nolimits_{g = 1}^{G} {z_{gk} \bar{\varphi }_{g} } - \sum\nolimits_{h = 1}^{H} {w_{hk} \bar{\mu }_{h} } + \bar{\Psi }_{2} } \right)} \right) \le 0\) (with respect to \(\left( {\frac{1}{\mho }} \right) > 0\) and \(\sum\nolimits_{r = 1}^{R} {y_{rk} \bar{\beta }_{r} } { - }\sum\nolimits_{g = 1}^{G} {z_{gk} \bar{\varphi }_{g} } - \sum\nolimits_{h = 1}^{H} {w_{hk} \bar{\mu }_{h} } + \bar{\Psi }_{2} \le 0\)), \(\sum\nolimits_{g = 1}^{G} {z_{g0} \bar{\varphi }_{g} } + \sum\nolimits_{h = 1}^{H} {w_{h0} \bar{\mu }_{h} } = \left( {\frac{1}{\mho }\left( {\sum\nolimits_{g = 1}^{G} {z_{g0} \bar{\varphi }_{g} } + \sum\nolimits_{h = 1}^{H} {w_{h0} \bar{\mu }_{h} } } \right)} \right) = 1\), \(\sum\nolimits_{g = 1}^{G} {z_{gk} \bar{\varphi }_{g} } { - }\sum\nolimits_{i = 1}^{I} {x_{ik} \bar{\alpha }_{i} } + \bar{\Psi }_{1} = \left( {\frac{1}{\mho }\left( {\sum\nolimits_{g = 1}^{G} {z_{gk} \bar{\varphi }_{g} } { - }\sum\nolimits_{i = 1}^{I} {x_{ik} \bar{\alpha }_{i} } + \bar{\Psi }_{1} } \right)} \right) \le 0\), \(\bar{\alpha } \ge 0\), \(\bar{\varphi } \ge 0\), \(\bar{\mu } \ge 0\), \(\bar{\beta } \ge 0\), and \(\left( {\left( {\sum\nolimits_{g = 1}^{G} {z_{g0} \bar{\varphi }_{g} } + \bar{\Psi }_{1} } \right) - \dag_{0}^{{1*}} \left( {\sum\nolimits_{i = 1}^{I} {x_{i0} \bar{\alpha }_{i} } } \right)} \right) = \left( {\frac{1}{\mho }\left( {\left( {\sum\nolimits_{g = 1}^{G} {z_{g0} \bar{\varphi }_{g} } + \bar{\Psi }_{1} } \right) - \dag_{0}^{{1*}} \left( {\sum\nolimits_{i = 1}^{I} {x_{i0} \bar{\alpha }_{i} } } \right)} \right)} \right) = \rm{0}\), \(\left( {\bar{\alpha } ,\bar{\varphi } ,\bar{\mu } ,\bar{\beta } ,\bar{\Psi }_{1} ,\bar{\Psi }_{2} } \right)\) is the feasible solution of Model (7). Also, in the objective function \(\sum\nolimits_{r = 1}^{R} {y_{r0} \bar{\beta }_{r} } + \bar{\Psi }_{2} = \left( {\frac{1}{\mho }\left( {\sum\nolimits_{r = 1}^{R} {y_{r0} \bar{\beta }_{r} } + \bar{\Psi }_{2} } \right)} \right)\), with respect to suppose that \(\sum\nolimits_{g = 1}^{G} {z_{g0} \bar{\varphi }_{g} } + \sum\nolimits_{h = 1}^{H} {w_{h0} \bar{\mu }_{h} } < 1\), thus \(\left( {\frac{1}{{\sum\nolimits_{g = 1}^{G} {z_{g0} \bar{\varphi }_{g} } + \sum\nolimits_{h = 1}^{H} {w_{h0} \bar{\mu }_{h} } }}} \right) > 1\) and finally \(\sum\nolimits_{r = 1}^{R} {y_{r0} \bar{\beta }_{r} } + \bar{\Psi }_{2} > \sum\nolimits_{r = 1}^{R} {y_{r0} \bar{\beta }_{r} } + \bar{\Psi }_{2}\) that this is contradicts with optimality of \(\left( {\bar{\alpha },\bar{\varphi },\bar{\mu },\bar{\beta },\bar{\Psi }_{1} ,\bar{\Psi }_{2} } \right)\). So, at any optimal solution of Model (7), always \(\sum\nolimits_{g = 1}^{G} {z_{g0} \bar{\varphi }_{g} } + \sum\nolimits_{h = 1}^{H} {w_{h0} \bar{\mu }_{h} } = 1\).


Step 2: Choosing robust optimization approach.


Robust optimization is one of the applicable and popular approaches that can be used to deal with uncertainty in optimization problems (Bertsimas et al., 2011; Gabrel et al., 2014; Peykani et al., 2020b; Xidonas et al., 2020). The first robust optimization approach for dealing with continuous uncertainty is presented by Soyster (1973) that is based on “box” uncertainty set. Although the RO approach of Soyster (1973) is linear programing (LP), however, by taking the worst-case value of each uncertain parameter, the RO approach becomes too conservative. Ben-Tal and Nemirovski (2000) proposed a robust formulation based on “box + ellipsoidal” uncertainty set that decision maker (DM) can adjust the conservatism level of model by setting parameter, but their robust counterpart is nonlinear programming (NLP) which can be problematic in the real-world problems. Then, Bertsimas and Sim (2004) presented a novel robust optimization approach based on “box + polyhedral” uncertainty set that has the ability to adjust the degree of model conservatism level by setting parameter remaining the robust counterpart in LP. In order to propose the robust approach presented by Bertsimas and Sim (2004), consider the following LP problem:

$$ \begin{aligned} & {\text{Max }}\sum\nolimits_{\phi } {\eta_{\phi } Z{}_{\phi }} \hfill \\ & \begin{array}{ll} {{\text{S.t.}}\sum\nolimits_{b} {\tilde{\pi }_{ab} } \lambda_{b} \le \ell_{a} ,} & {\forall a} \\ \end{array} \hfill \\ & \lambda \in \Re \hfill \\ \end{aligned} $$
(8)

Consider, \(\tilde{\pi }_{ab}\) as the uncertain parameter in the constraint \(a\), and \(\Lambda_{a}\) as the set of coefficients in constraint \(a\) that are subject to uncertainty. Note that each entry \(\tilde{\pi }_{ab} ,b \in \Lambda_{a}\) is modeled as a symmetric and bounded random variable which takes the values in \(\left[ {\pi_{ab} - \hat{\pi }_{ab} ,\pi_{ab} + \hat{\pi }_{ab} } \right]\). The central of this interval at the point \(\pi_{ab}\) is a nominal value and \(\hat{\pi }_{ab}\) is perturbation of uncertain parameters \(\tilde{\pi }_{ab} ,b \in \Lambda_{a}\). Also, it should be noted that \(\hat{\pi }_{ab}\) can be considered as \(\hat{\pi }_{ab} = \tau \, \pi_{ab}\) which \(\tau\) is the percentage of deviation from nominal value. Finally, robust formulation of Model (8) based on RO approach of Bertsimas and Sim (2004) is presented as Model (9):

$$ \begin{aligned} & Max\sum\nolimits_{\phi } {\eta_{\phi } \lambda {}_{\phi }} \hfill \\ & \begin{array}{ll} {S.t. \, \sum\nolimits_{b} {\pi_{ab} } \lambda_{b} + P_{a} \Gamma_{a} + \sum\nolimits_{{b \in \Lambda_{a} }} {Q_{ab} } \le \ell_{a} ,} & {\forall a} \\ \end{array} \hfill \\ & \begin{array}{ll} {P_{a} + Q_{ab} \ge \tau \pi_{ab} \gamma_{b} ,} & {\forall a,b \in \Lambda_{a} } \\ \end{array} \hfill \\ & \begin{array}{ll} { - \gamma_{b} \le \lambda_{b} \le \gamma_{b} ,} & {\forall b \in \Lambda_{a} } \\ \end{array} \hfill \\ & P,Q,\gamma \ge 0 \hfill \\ & \lambda \in \Re \hfill \\ \end{aligned} $$
(9)

It should be mentioned that parameter \(\Gamma\) is the budget of robustness that adjusts the robustness of Model (9) in response to solve conservatism level. Due to the linearity of robust counterpart and the ability to adjust the degree of conservatism level in RO approach of Bertsimas and Sim (2004), this method will be used in this paper for dealing with uncertainty in NDEA models.

Step 3: Proposing Robust NDEA Models.

As previously mentioned, all parameters of network DEA models including \(\tilde{x}_{ik} (i = 1,...,I)\),\(\tilde{z}_{gk} (g = 1,...,G)\), \(\tilde{w}_{hk} (h = 1,...,H)\), and \(\tilde{y}_{rk} (r = 1,...,R)\) are uncertain. Note that all uncertain parameters are considered as \(\tilde{x}_{ik} \in [x_{ik} - \hat{x}_{ik} ,x_{ik} + \hat{x}_{ik} ]\), \(\tilde{z}_{gk} \in [z_{gk} - \hat{z}_{gk} ,z_{gk} + \hat{z}_{gk} ]\), \(\tilde{w}_{hk} \in [w_{hk} - \hat{w}_{hk} ,w_{hk} + \hat{w}_{hk} ]\), and \(\tilde{y}_{rk} \in [y_{rk} - \hat{y}_{rk} ,y_{rk} + \hat{y}_{rk} ]\). Now, according to the robust optimization approach of Bertsimas and Sim (2004), the robust network DEA model for performance measurement of first stage of specific \({\text{DMU}}_{0}\) under deep uncertainty is proposed as Model (10):

$$ \begin{aligned} & \Delta_{0}^{1} \left( {\Gamma ,\tau } \right) = \, Max \, \sum\nolimits_{g = 1}^{G} {z_{g0} {\varphi_{g}} } + \Psi_{1} - \Theta_{0}^{z} \Gamma_{0}^{z} - \sum\nolimits_{g = 1}^{G} {\zeta_{g0}^{z} } \hfill \\ & \begin{array}{ll} {S.t.\Theta_{0}^{z} + \zeta_{g0}^{z} \ge \tau z_{g0} {\varphi_{g}} ,} & {\forall g} \\ \end{array} \hfill \\ & \sum\nolimits_{i = 1}^{I} {x_{i0} \alpha_{i} } + \Theta_{0}^{x} \Gamma_{0}^{x} + \sum\nolimits_{i = 1}^{I} {\zeta_{i0}^{x} } \le 1 \hfill \\ & \begin{array}{ll} {\Theta_{0}^{x} + \zeta_{i0}^{x} \ge \tau x_{i0} \alpha_{i} ,} & {\forall i} \\ \end{array} \hfill \\ & \begin{array}{ll} {\sum\nolimits_{g = 1}^{G} {z_{gk} {\varphi_{g}} } - \sum\nolimits_{i = 1}^{I} {x_{ik} \alpha_{i} } + \Psi_{1} + \Theta_{k} \Gamma_{k} + \sum\nolimits_{g = 1}^{G} {\zeta_{gk}^{z} } + \sum\nolimits_{i = 1}^{I} {\zeta_{ik}^{x} } \le 0,} & {\forall k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\Theta_{k} + \zeta_{gk}^{z} \ge \tau z_{gk} {\varphi_{g}} ,} & {\forall g,k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\Theta_{k} + \zeta_{ik}^{x} \ge \tau x_{ik} \alpha_{i} ,} & {\forall i,k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\alpha_{i} ,{\varphi_{g}} \ge 0,} & {\forall i,g} \\ \end{array} \hfill \\ & \begin{array}{ll} {\Theta_{0}^{x} ,\Theta_{0}^{z} ,\Theta_{k} \ge 0,} & {\forall k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\zeta_{i0}^{x} ,\zeta_{ik}^{x} ,\zeta_{g0}^{z} ,\zeta_{gk}^{z} \ge 0,} & {\forall i,g,k} \\ \end{array} \hfill \\ \end{aligned} $$
(10)

Also, according to the RO approach of Bertsimas and Sim (2004), the RNDEA model for performance measurement of second stage of specific \({\text{DMU}}_{0}\) under uncertainty is proposed as Model (11):

$$ \begin{aligned} & \Delta _{0}^{{\frac{2}{1}}} \left( {\Gamma ,{ }\tau } \right) = {\text{Max }}\sum\nolimits_{{r = 1}}^{R} {y_{{r0}} \beta _{r} } + \Psi _{2} - \Phi _{0}^{y} \Gamma _{0}^{{'y}} - \sum\nolimits_{{r = 1}}^{R} {\xi _{{r0}}^{y} } \hfill \\ & \begin{array}{ll} {S.t.{\text{ }}\Phi _{r}^{y} + \xi _{{r0}}^{y} \ge \tau y_{{r0}} \beta _{r} { },} & {\forall r} \\ \end{array} \hfill \\ & \sum\nolimits_{{g = 1}}^{G} {z_{{g0}} \varphi _{g} } + \sum\nolimits_{{h = 1}}^{H} {w_{{h0}} \mu _{h} } + \Phi _{0}^{{zw}} \Gamma _{0}^{{'zw}} + \sum\nolimits_{{g = 1}}^{G} {\xi _{{g0}}^{z} } + \sum\nolimits_{{h = 1}}^{H} {\xi _{{h0}}^{w} } \le 1 \hfill \\ & \begin{array}{ll} {\Phi _{0}^{{zw}} + \xi _{{g0}}^{z} \ge \tau z_{{g0}} \varphi _{g} { },} & {\forall g} \\ \end{array} \hfill \\ & \begin{array}{ll} {\Phi _{0}^{{zw}} + \xi _{{h0}}^{w} \ge \tau w_{{h0}} \mu _{h} { },} & {\forall h} \\ \end{array} \hfill \\ & \begin{array}{ll} \sum\nolimits_{{r = 1}}^{R} {y_{{rk}} \beta _{r} } - \sum\nolimits_{{g = 1}}^{G} {z_{{gk}} \varphi _{g} } - \sum\nolimits_{{h = 1}}^{H} {w_{{hk}} \mu _{h} } + \Psi _{2} + \Phi _{k} \Gamma '_{k} + \sum\nolimits_{{r = 1}}^{R} {\xi _{{rk}}^{y} } + \sum\nolimits_{{g = 1}}^{G} {\xi _{{gk}}^{z} } \\ \quad + \sum\nolimits_{{h = 1}}^{H} {\xi _{{hk}}^{w} } \le 0{ }, {\forall k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\Phi _{k} + \xi _{{rk}}^{y} \ge \tau y_{{rk}} \beta _{r} { },} & {\forall r,k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\Phi _{k} + \xi _{{gk}}^{z} \ge \tau z_{{gk}} \varphi _{g} { },} & {\forall g,k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\Phi _{k} + \xi _{{hk}}^{w} \ge \tau w_{{hk}} \mu _{h} { },} & {\forall h,k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\sum\nolimits_{{g = 1}}^{G} {z_{{gk}} \varphi _{g} } - \sum\nolimits_{{i = 1}}^{I} {x_{{ik}} \alpha _{i} } + \Psi _{1} + \Theta _{k} \Gamma _{k} + \sum\nolimits_{{g = 1}}^{G} {\zeta _{{gk}}^{z} } + \sum\nolimits_{{i = 1}}^{I} {\zeta _{{ik}}^{x} } \le 0{ },} & {\forall k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\Theta _{k} + \zeta _{{gk}}^{z} \ge \tau z_{{gk}} \varphi _{g} { },} & {\forall g,k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\Theta _{k} + \zeta _{{ik}}^{x} \ge \tau x_{{ik}} \alpha _{i} { },} & {\forall i,k} \\ \end{array} \hfill \\ & \left( {\sum\nolimits_{{g = 1}}^{G} {z_{{g0}} \varphi _{g} } \!+\! \Psi _{1} \!-\! \Theta _{0}^{z} \Gamma _{0}^{z} \!-\! \sum\nolimits_{{g = 1}}^{G} {\zeta _{{g0}}^{z} } } \right) \!-\! \Delta _{0}^{{1{ }*}} \left( {\sum\nolimits_{{i = 1}}^{I} {x_{{i0}} \alpha _{i} } + \Theta _{0}^{x} \Gamma _{0}^{x} + \sum\nolimits_{{i = 1}}^{I} {\zeta _{{i0}}^{x} } } \right) = 0 \hfill \\ & \begin{array}{ll} {\Theta _{0}^{z} + \zeta _{{g0}}^{z} \ge \tau z_{{g0}} \varphi _{g} { },} & {\forall g} \\ \end{array} \hfill \\ & \begin{array}{ll} {\Theta _{0}^{x} + \zeta _{{i0}}^{x} \ge \tau x_{{i0}} \alpha _{i} { },} & {\forall i} \\ \end{array} \hfill \\ & \begin{array}{ll} {\Phi _{0}^{y} { },{ }\Phi _{0}^{{zw}} { },{ }\Phi _{k} { } \ge 0{ },} & {\forall k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\Theta _{0}^{x} { },{ }\Theta _{0}^{z} { },{ }\Theta _{k} { } \ge 0{ },} & {\forall k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\zeta _{{i0}}^{x} { },{ }\zeta _{{ik}}^{x} { },{ }\zeta _{{g0}}^{z} { },{ }\zeta _{{gk}}^{z} { } \ge 0{ },} & {\forall i,g,k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\xi _{{g0}}^{z} { },{ }\xi _{{gk}}^{z} { },{ }\xi _{{h0}}^{w} { },{ }\xi _{{hk}}^{w} { },{ }\xi _{{r0}}^{y} { },{ }\xi _{{rk}}^{y} { } \ge 0{ },} & {\forall g,h,r,k} \\ \end{array} \hfill \\ & \begin{array}{ll} {\alpha _{i} { },{ }\varphi _{g} { },{ }\mu _{h} { },{ }\beta _{r} { } \ge 0{ },} & {\forall i,g,h,r} \\ \end{array} \hfill \\ \end{aligned} $$
(11)

Note that in measuring the efficiency of stages 1 and 2, Models (10) and (11) should be solved at the same values of \(\Gamma\) and \(\tau\). Finally, the overall efficiency of \({\text{DMU}}_{0}\) under uncertainty for specific \(\Gamma\) and \(\tau\), is calculated according to Eq. (12) as follows:

$$ \Delta_{0}^{{\text{T}}} \left( {\Gamma ,\tau } \right) = \Delta_{0}^{1} \left( {\Gamma ,\tau } \right)*\Delta_{0}^{\frac{2}{1}} \left( {\Gamma ,\tau } \right) $$
(12)

Alternatively, assuming stage 2 as the leader and stage 1 as the follower, measuring the efficiency of the second, the first and the entire two-stage system in the presence of uncertainty will be in a similar manner that presented in Appendix B.

5 A real application and experimental results

In this section, the implementation of the proposed approach of this paper for performance assessment of mutual funds, is presented for a real word case study from Iranian financial market. With respect to the advantages of MFs such as professional management, diversification, economies of scale, easy access, transparency, variety and freedom of choice, the popularity of MFs for investors has increased in recent years in Iran. Currently, there are more than 190 MFs in the Iranian financial market with a lifetime of less than a month to nearly 12 years. Notably, the return of MFs can be calculated daily, weekly, monthly, yearly and also from the beginning of activity. In this paper, average return and standard deviation are calculated for annual return.

Note that the convexity axiom of traditional DEA models can be violated in the presence of ratio variables (Emrouznejad & Amin, 2009). Hanafizadeh et al. (2014) suggested that if the DMUs are about the same size, the convexity issue can be eliminated. As results in the current study, this important point is considered in the selection of 15 MFs among 196 mutual funds in the Iran. Then, to illustrate the applicability of RNDEA approach, all required data for 15 Iranian MFs are extracted. Finally, after collecting data, the first stage, second stage and overall efficiencies of MFs are calculated for different budget of robustness \(\Gamma\) including 0, 25, 50, and 100%. Also, the percentage of deviation \(\tau\) is set equal to 1 and 10% for considering the perturbations in data.

Accordingly, Table 3 presents the results of robust network DEA approach when the stage 1 is more important.

Table 3 The Results of RNDEA Approach When First Stage Is Assumed to Be the Leader
Full size table

As seen in Tables 3 and 4, the results indicate that, as the budget of robustness \(\Gamma\) increases from 0 to 100% for uncertain parameters, the values of efficiency gets worse. Also, as the perturbations \(\tau\) increases from 1 to 10%, the values of efficiency get worse than a nominal problem.

Table 4 The Results of RNDEA Approach When Second Stage Is Assumed to Be the Leader
Full size table

Finally, for ranking all MFs, the average of all efficiency scores for each MF under all condition of uncertainty are measured. It should be noted that the average efficiency is calculated for both cases of leadership in stages 1 and 2. Also, the average efficiency that is calculated under these two assumptions is used as the final ranking criterion. The ranking of all mutual funds based on proposed RNDEA approach and conventional NDEA approach are given in Tables 5 and 6, respectively:

Table 5 The Ranking of Mutual Funds Based on Proposed RNDEA Approach (Uncertain Data)
Full size table
Table 6 The Ranking of Mutual Funds Based on Conventional NDEA Approach (Crisp Data)
Full size table

As it can be seen in Table 5, MF 14 and MF 15 have the best performance in operational management and portfolio management functions, respectively. Also, MF 14 has the best overall performance in comparison with other MFs. Accordingly, MF 14 and MF 15 are robust against the data uncertainty in comparison with other MFs. In other words, the mangers of these MFs have acceptable stability in MF management. Therefore, the performance and planning of these MFs mangers can be analyzed to be benchmark for other MF managements.

Noteworthy, in terms of the average performance, MF 07 has acceptable performance in the first stage and overall, but the standard deviation (SD) of its efficiency scores is very high for different uncertainty situations. In other words, MF 07 has the most sensitivity to uncertainty of data in comparison with other MFs. As a result, with respect to the above points, all MFs can be categorized to the four groups including:

  1. I.

    MF has desirable performance with low risk (average is high, SD is low)

  2. II.

    MF has desirable performance with high risk (average is high, SD is high)

  3. III.

    MF has undesirable performance with low risk (average is low, SD is low)

  4. IV.

    MF has undesirable performance with high risk (average is low, SD is high)

It is obvious that the MFs of first and fourth groups have the best and the worst performance, respectively. It should be noted that the scope of this categorization depends on the decision maker (DM) opinion. For example, according to the above classification, MF 07 is in second group. Notably, from Tables 5 and 6, it can be clearly observed that the discriminatory power of proposed robust NDEA approach is more than conventional NDEA method.

Finally, it is also possible to predict the dataset for future periods using forecasting methods. Then, due to the nature of uncertainty in future data, the proposed RNDEA method can be utilized for predicting the MFs' efficiency and their trends over future periods. Consequently, the proposed RNDEA approach aids managers to make better and appropriate decisions.

6 Conclusions and directions for future research

In this research, the novel robust two-stage data envelopment analysis approach is proposed for performance appraisal of mutual funds by considering the internal structure and processes. The presented approach is capable to be used in the presence of deep uncertainty, when the data are not known exactly, and the uncertain data just lie within the upper and lower bounds represented by the intervals. As it can be seen in experimental results, if uncertainty of financial data is not considered, the ranking of MFs can be invalid, especially when the efficiency scores of MFs are close to each other. The main advantages of proposed RNDEA approach for performance evaluation of MFs can be listed as follows:

  • Identifying MFs that are stable against data uncertainty

  • Identifying MFs that are very sensitive to data uncertainty

  • Ranking of MFs under data uncertainty

  • Ability to implement in the presence of financial data with deep uncertainty

  • The linearity of the proposed robust network DEA approach

  • The discriminatory power of the RNDEA method is more than classical NDEA method

  • The unique efficiency decomposition under uncertain situation

  • Comprehensive assessment of MFs for different scenarios, which stage is more important

It should be noted that the applicability of the presented robust network DEA approach is demonstrated by assessing the relative performance of 15 Iranian mutual funds. The results indicate that the proposed approach is effective for performance evaluation of mutual funds and internal activities under data uncertainty. For future studies, the uncertain programming approaches such as chance-constrained programming (CCP), interval method, and fuzzy mathematical programming (FMP) can be applied in order to dealing with data uncertainty (For more details see Izadikhah & Saen, 2018; Tavana et al., 2018; Li et al., 2019; Sarah & Khalili-Damghani, 2019; Zhou et al., 2019; Mehdizadeh et al., 2020; Shi et al., 2020; Peykani, Mohammadi, et al., 2021; Peykani et al., 2021).