1 Introduction

Over the last decade, the new product development (NPD) ecosystem witnessed a major shift in the tendency of governments and consumers toward environmental sustainability, which resulted in substantial changes in manufacturing and supply chain (SC) strategies. The “design-for-environment” was emerged as a revolutionary concept in manufacturing SCs, aiming to integrate and embed the environmental aspects into the product design at an early stage (Chen, 2001). In some sectors, such as automotive and fashion, environmental considerations (e.g., emission reduction) have had a significant influence on the NPD strategies with a desire for achieving low-emission (sometimes zero) production systems (Fung et al., 2021; Pujari et al., 2003; Zhu & He, 2017). Due to the urgency of preserving environmental resources, progressive governments are paying more attention to the UN’s sustainable development goals by playing a major role in greening critical SCs (Tseng et al., 2019). Thus, green entrepreneurship is emerged as a new strategy to address the existing conflicts between economic development goals and environmental sustainability (Wang et al., 2020).

In 2019, the green new product development (GNPD) penetration rate in the U.S. rose to 37% (from 7% in 2011) and the end consumers were found to spend 5% more on eco-friendly products.Footnote 1 It has been predicted that, by the end of 2021, the sustainable products sales in the U.S. alone will have a value among US$142.3 billion and US$150.1 billion.Footnote 2 Among different sectors, transportation is recognized as one of the most polluting industries due to its substantial greenhouse gas emissions.Footnote 3 Thanks to the effective intervention policies in the transportation sector,Footnote 4 some leading car manufacturing companies have positively responded to the environmental protection programs and committed to reduce their CO2 emissions and control fossil fuel combustion.Footnote 5

Driven by the growing intensity of market competition and to address the rising public awareness, some SME entrepreneurs have recently begun to diversify their product portfolio by offering both green and non-green products (Tseng et al., 2019; Wang et al., 2020). However, establishing a solid presence in parallel markets is extremely challenging for SME entrepreneurs due to the unique problems they face (e.g., market volatility and funding shortages) in initiating and sustaining their SC activities (Chen, 2001; Zhu & He, 2017). In the automotive industry, for example, developing a portfolio of new green and non-green products demands a huge initial capital investment not only to develop the manufacturing capabilities but also to fund the required R&D (Zhu & He, 2017). To address these issues, several supply chain finance (SCF) schemes, such as bank credit financing (BCF), trade credit financing (TCF), and partial credit guarantee (PCG), have been developed by financial institutes (Asian et al., 2020). However, due to their inherent complexities (e.g., excessively high interest rates and difficulty in securing required collaterals), these conventional methods are commonly disfavored by the SMEs (Wagner, 2021; Xu & Fang, 2020; Reza-Gharehbagh et al., 2020b).

With the growth of information technology and the emergence of innovative SCF solutions (Choi, 2020; Gao et al., 2018; Reza-Gharehbagh et al., 2021; Yu et al., 2020), some governments decided to partner with digital platforms and offer the capital-constrained SCs access to platform financing solutions to fund their GNPD activities. As a result, multi-sided Fintech platforms (MSPs) have rapidly replaced the conventional SCF schemes and gained substantial traction among the capital constrained SCs engaged in the green entrepreneurship. The MSP financing is now recognized as a viable means that not only addresses the budget shortfall of capital-constrained SCs but also enables risk-averse investors and SME entrepreneurs to hedge against the uncertainties of the GNPD market. For example, the “Green Finance Framework” is a transparent technology-enabled platform developed by a Norwegian company, MIRIS.Footnote 6 The platform helps users in choosing, tracking, and analyzing the flow of funds in different projects. The platform’s design and structural components are inspired by the Green Bond Principles, which were established by the International Capital Market Association. CarbonChainFootnote 7 is another example that assists businesses in applying and receiving green finance. Founded in 2019 in the U.K., this online platform provides quantitative and practical solutions for reducing carbon emissions in the SCs of the worlds’ largest polluting industries such as metals, oil and gas, minerals, and agriculture; hence, tracks the carbon footprints of SMEs’ SCs to determine which operations are most vulnerable to rising payable costs of the carbon tax.

Offering a diverse range of regulated entrepreneurial financing facilities, such as debt financing (DF) and equity financing (EF), the MSPs connect the SME entrepreneurs to a crowd of investors and facilitate their access to a portfolio of SCF solutions (Reza-Gharehbagh et al., 2021; Yang et al., 2017; Zheng et al., 2020). The platform financing has three key features that motivate the SME entrepreneurs to participate in the regulated GNPD programs: (i) needless of conventional intermediaries and associated challenges, the MSPs play a match-making role and enable SME entrepreneurs and investors to directly connect via a regulated digital platform; (ii) while decreasing the funding and investment costs, the MSPs enable the SME entrepreneurs and investors to reduce their fundraising and investment risks by channeling the accumulated capital into different streams (e.g., DF and EF); (iii) unlike the conventional DF mechanisms, the platform-based EF schemes are gaining significant popularity among the green entrepreneurs.Footnote 8 By promoting EF, the MSPs can incentivize the investors and SME entrepreneurs to take part in GNPD and cooperate with host governments in attaining their green entrepreneurship goals while achieving higher profits and improved competitiveness.

Besides the above-mentioned advantages, the governments face several challenges in supporting green entrepreneurship through platform SC financing. The first challenge relates to the possibility of inadequate investment by small public investors given the high degree of NPD market uncertainty, the players’ risk aversion, and competition between non-green and green products (An et al, 2020; Li & Wang, 2020). The second obstacle is unaffordability of greening and R&D costs of GNPD for the capital constrained SME entrepreneurs. To achieve their environmental and social welfare objectives, the governments may have to partially bear these costs (through greening costs sharing programs) and support the greening efforts of SME entrepreneurs (Xia et al., 2020). The third challenge relates to making a balance between the government’s economic influence and social welfare objectives when devising an intervention policy (Reza-Gharehbagh et al., 2021).

Despite the SME entrepreneurs’ GNPD challenges and the urgency of developing platform-based solutions, the idea of using MSP-driven sustainable supply chain finance (SSCF) to support green entrepreneurship is rather underexplored in the SCF literature. To bridge the gap, this paper studies the GNPD problem of a risk-averse capital constrained SC that jointly produces new green and non-green products under a hybrid environmental-green entrepreneurship policy. In particular, this study addresses the following research questions:

  • Sustainable supply chain finance: How does the proposed SSCF model facilitate GNPD and impact the performance of the individual participants (the capital-constrained SC, the MSP, and the government)? What are the optimal decisions of the players under the deregulated and regulated scenarios?

  • Government intervention: How does the government’s policy making approach (economic influence vs. social welfare) impact the success of the proposed SSCF mechanism? What is the joint impact of the government’s environmental policy and the platform’s risk attitude on the members’ participation in platform financing?

  • Green entrepreneurship: How does the proposed SSCF mechanism affect the overall success of the government’s green entrepreneurship plan?

To address the above questions, we propose a greening cost sharing mechanism between the government and the capital constrained SC. The proposed policy aims to incentivize the risk-averse SME entrepreneur and enhance green entrepreneurship, simultaneously. Considering two different government policymaking approaches (i.e., economic influence and social welfare) and using a multi-level game theoretical framework, we study and characterize the equilibrium strategies of the key players. To capture the risk attitude of the platform and the SC, we use a mean–variance (MV) approach and firstly characterize the SC’s production and the MSP’s financing decisions under a deregulated scenario. Focusing on an alternative case with government intervention (i.e., hybrid environmental-green entrepreneurship policy), we next characterize the decision-making behavior of government, MSP, and SC. The outcomes of different scenarios are compared by considering the policy approach (i.e., economic influence vs. social welfare) and the platform’s risk attitude.

The remainder of this paper is structured as follows: The related literature is reviewed in Sect. 2. Section 3 proposes the problem description and introduces a benchmark model. In Sect. 4, the optimal strategies of key players under deregulated and regulated platform financing scenarios are discussed. A computational study is presented in Sect. 5. Conclusion and some directions for future work are provided in Sect. 6. All mathematical proofs are provided in Appendix.

2 Literature review

This study is closely related to three research areas in the literature, including government environmental intervention, green entrepreneurship and GNPD, and platform-based SCF. Table 4 (see Appendix A) presents a summary of the most relevant articles by listing their key features and highlighting the position of this study.

2.1 Government environmental intervention

With the growing importance of environmental issues, some progressive governments began to promote sustainable development goals by encouraging the local and global SCs to enhance their environmental performance (Murali et al., 2019). Following this development, several studies have been conducted. Some examples include the impact of eco-labels and government intervention in GNPD (Murali et al., 2019), government subsidy for the eco-friendly product (Li et al., 2018), government regulation impact in GNPD (Hafezi & Zolfagharinia, 2018), subsidy and tax policies in green SCs (Hafezalkotob, 2018; Javadi et al., 2019; Rahimi et al., 2021), emission cap and the UN’s sustainable development goals (Asian et al., 2019; Xu & Fang, 2020).

Some recent studies focused on social welfare and investigated how the regulated GNPD programs support sustainable development goals and environmental protection activities (Huang et al., 2020; Tang & Yang, 2020). Yang et al. (2019) studied the impacts of green credit and subsidy on the decision making of enterprises that actively promote renewable energies. They found that the green credit policy positively affects the performance of capital-constrained clean energy firms. Cao and Yu (2018) investigated the operational and financial decisions of a SC under the cap-and-trade mechanism and proposed different coordinating contracts. They found that employing a revenue sharing contract could benefit the capital-constrained retailer. They also suggest that to reduce the environmental footprint of industries and promote sustainable development through green products, the governments must financially intervene and support the GNPD operations of capital-constrained SCs. The present study differs from Cao and Yu (2018) in two ways: (i) we introduce the platform financing as the main means of addressing the risk-averse SC’s budget shortfall and consider the effect of government hybrid environmental intervention policy on GNPD outcome under two policy making approaches, namely economic influence and social welfare; (ii) considering the risk-aversion of investors and the capital-constrained SC, we investigate the GNPD performance and decision making of each participant (the capital-constrained SC, the MSP, and government) in the proposed SCF mechanism under different scenarios.

2.2 Green new product development (GNPD)

A majority of existing SC sustainability studies are mainly focused on the operational problems associated with developing green products without considering the SCF challenges of the SME entrepreneurs engaged in GNPD (Albino et al., 2009; Chen, 2001; Driessen et al., 2013; Zhu & He, 2017).

Pujari et al. (2003) are among the first who developed an integrative structure for GNPD. They presented a framework that integrates different environmental aspects of NPD and discussed the firms’ greening potential under competition. They found that there exists a significant synergy between conventional NPD and new GNPD approaches. Albino et al. (2009) studied different tactical environmental approaches that can support GNPD. They found that the adoption to these tactics is one of the key strategic aspects that need further attention in GNPD. Driessen et al. (2013) focused on three research streams, including conventional NPD prospects, marketing perspective in GNPD, and greenness degree. They found that greenness plays an essential role in tying different elements in the developed integrative structure. Hafezi and Zolfagharinia (2018) investigated the relationship between the success of GNPD and associated costs. They found that the environmental decisions and performance of enterprises engaged in GNPD are highly correlated with the consumer inclination to pay extra for the environmental aspects of the new green products.

Some studies in the literature considered contractual mechanisms as a viable approach in promoting green entrepreneurship. For example, Ghosh and Shah (2015) investigated how cost sharing contracts affect the decisions making of SCs involved in green production initiatives. They found that the cost sharing agreements with bargaining result in increased greening degree and profitability. Zhu and He (2017) studied the GNPD issues under SC competition and cost sharing as well as wholesale price contracts. They investigated how the greening decision of SCs is affected by the SC structure, competition, and product type. It has been found that the price competition and decentralized SC structure could significantly affect the greening degree of SCs. Raj et al. (2018) investigated the greening and social responsibility issues in a SC under different contract settings in a decentralized SC, including greening cost sharing, wholesale pricing, linear two-part tariff, and revenue sharing. They explained how different contract types impact the ideal greening level, social responsibility, retail pricing, and profitability of SC agents. Yang and Chen (2018) studied the impact of cost sharing and revenue sharing contracts on the manufacturer’s attempt in reducing carbon emissions and the profitability of the SC members. They found that both contracts can boost system efficiency and the manufacturer’s incentive to reduce emissions.

Although the above studies address some of the key challenges of using cost sharing contracts in the development of sustainable products, the interface between green entrepreneurship, SC mechanism design, and platform-enabled SCF is rather underexplored.

2.3 Platform-based SCF

As shown in Table 4 (see Appendix A), most of the previous studies focused on traditional SCF channels, such as loan-based financing offered by conventional financing methods. Owing to the technological developments, internet enabled FinTech platforms have gained remarkable attention among the public investors and SME entrepreneurs as an innovative means of investment and funding. There exists only a limited number of studies that considered the use of platform financing in the SC context (Reza-Gharehbagh et al., 2021; Yu et al., 2020; Fatehi & Wagner, 2019; Gao et al., 2018; Yan et al., 2020; Reza-Gharehbagh et al., 2020a).

Fatehi and Wagner (2019) investigated the role of a crowdfunding platform and revenue sharing contract in maximizing the net present value of a firm, considering the investors’ participation constraints and the platform’s service fee. Reza-Gharehbagh et al. (2020a) studied the role of peer-to-peer (P2P) online platforms in assisting entrepreneurs to cope with their budget shortfall. Focusing on an alternative SCF system and considering the government’s direct and indirect intervention, they studied the equilibrium strategies of the P2P platform, government, and competing SCs under the EF and DF schemes. They found that the popularity of P2P platforms is correlated to the government’s support, the platform’s financial attributes (e.g., the interest rate under DF and equity exchange ratio under EF), and the competition degree of SCs. Reza-Gharehbagh et al. (2021) are among the first who investigated the role of hybrid government regulation in promoting crowdfunding MSPs and indigenous innovation strategies in an era of reglobalization. They found that a regulated platform financing mechanism could reduce the power disparity among small investors and local SC while enabling the host government to achieve its reglobalization goals. Yu et al. (2020) investigated an MSP-based SCF system designed to assist capital-constrained clients in managing their transportation transaction projects. The efficiency of the SCF system is considered under two scenarios, including a SCF system with the platform guarantee and a unique self-guarantee SCF approach. Although the self-guaranteed system is shown to have superior efficiency in managing risk and costs of opportunity, the platform may use an alternative prepayment method to reduce the credit risk of the low-credit consumers.

Our literature shows that while most of the previous studies in the SCF domain focused on the DF scheme (Gao et al., 2018), the regulated platform financing of GNPD with joint DF and EF offering is underexplored. Although the NPD problems have been previously studied from the lens of SCF (Tseng et al., 2019), analyzing the key features of platform financing as an alternative SSCF solution in supporting the regulated green entrepreneurship programs is rather understudied. To bridge these gaps, the current study investigates the product portfolio optimization problem of a capital-constrained SC under the government hybrid environmental intervention policy (i.e., imposing a non-green production environmental tax and offering a greening cost sharing incentive). Following a multi-level game theoretical approach, we present an integrative SSCF framework that enables the policymakers to predict and incorporate the decision-making behavior of the MSP and the capital-constrained SC into their environmental intervention policies.

3 Problem description

This study considers a centralized capital-constrained SC consists of an upstream supplier and a downstream risk-averse SME entrepreneur who suffers from the lack of initial and working capital. The supplier provides raw materials to the risk-averse SME entrepreneur who develops a portfolio of new products, including non-green (labeled with subscript 1) and green (labeled with subscript 2) and sells them to an existing market. All mathematical notations used in this paper are listed in Table 1.

Table 1 Mathematical notations
Full size table

To ensure mathematical tractability and avoid trivial cases, the following assumptions are made:

  1. (1)

    To enhance the analytical tractability and following the existing literature, we use the following normalized inverse demand functions under full substitutability as follows (Banker et al., 1998; Ghosh et al., 2018):

    $$ \begin{gathered} p_{1} = a_{1} - q_{1} - q_{2} - \alpha \theta \hfill \\ \tilde{p}_{2} = \tilde{a}_{2} - q_{2} - q_{1} + \alpha \theta \hfill \\ \end{gathered} $$
    (1)

    It is assumed that, unlike the new non-green product, the new green product has an uncertain demand (Wang et al., 2020). We also assume that \({a}_{1}>\) \({\tilde{a }}_{2}\) holds throughout the paper. These assumptions can be justified by the fact that, compared to the non-green products with predictable demand and established market share, new green products may see a less-stronger market potential while experiencing a higher demand uncertainty (Arli et al., 2018). A recent study by White et al. (2019) also showed that only about 26% of respondents who support the idea of sustainable production actually buy green products.

    As can be seen in Eq. (1), unlike the new non-green product, the new green product’s production quantity \({q}_{2}\) and retail price \({\tilde{p }}_{2}\) are affected by its uncertain market potential \({\tilde{a }}_{2}\) with mean value and variance \(\left(\overline{a },{\sigma }^{2}\right)\)(Xiao & Yang, 2008). Demand for both products is a linear function of the greening degree of new product, \(\theta \), with a negative or positive consumer sensitivity coefficient (\(+\alpha \) or \(-\alpha \)) (Ghosh et al., 2018; Zhu & He, 2017).

  1. (2)

    Given the volatility of financial markets and the uncertain nature of GNPD operations, the SC and MSPs are commonly concerned not only with the expected return on their investment, but also its variability (Li & Wang, 2020). To capture the sensitivity of the SC and MSP to risk, we follow the MV approach and formulate the utility functions of these players as follows (Xiao & Yang, 2008):

    $$ U = E\left[ {\tilde{\prod }} \right] - \lambda \cdot Var\left[ {\tilde{\prod }} \right], $$
    (2)

    where \(\lambda \) shows the risk-aversion degree of each player. This assumption is essential to model the players’ risk-aversion behavior when involved in the platform financing mechanisms.

  1. (3)

    To focus on our main contributions and reduce technical complexities, the non-green and green products are assumed to have identical unit supply and production costs \((c)\) (Wei et al., 2018; Xiao & Chen, 2009). In line with the literature, the new green product’s greening cost is represented by \(I{\theta }^{2}\), which is an increasing and convex function of the greening degree \(\theta \). \(I\) refers to the investment needed for making greening improvements in the new product (Banker et al., 1998; Ghosh & Shah, 2015; Ghosh et al., 2018).

  1. (4)

    The capital-constrained SC is assumed to have zero initial budget (Xu & Fang, 2020). Hence, the SC’s budget deficit is equal to \(c({q}_{1}+{q}_{2})\). This assumption can be justified by the fact that the SME entrepreneurs often lack the initial and working capital and need to raise capital to establish and execute their innovative ideas (Fu et al., 2021; Zheng et al., 2020).

3.1 Benchmark model

To construct a benchmark model, we first formulate a basic financing problem of a risk-averse SC. In the absence of government support (i.e., deregulation), the SC is controlled by a capital-constrained SME entrepreneur who has access to a conventional DF facility. The SME entrepreneur borrows the total amount \(c\left({q}_{1}+{q}_{2}\right)\) from bank with the interest rate \(r\). Using a two-level Stackelberg game model, we analyze the optimal strategies of the SC (the game follower) and a bank (the game leader). By receiving the required capital from the bank, the risk-averse SC maximizes its utility by determining optimal production quantities anticipating the optimal strategy of the bank. Given the SC’s decision, the bank maximizes its net profit by determining its optimal interest rate.

The profit function of SC is derived as follows:

$$ \tilde{\prod }_{SC} = \left( {p_{1} - c} \right)q_{1} + \left( {\tilde{p}_{2} - c} \right)q_{2} - I\theta^{2} - c\left( {q_{1} + q_{2} } \right)r. $$
(3)

Equation (3) comprises of three terms. The first and second terms refer to the SC’s revenue gained from selling the new non-green and green products. The third term refers to the greening costs of the new product \(I{\theta }^{2}\). The last term refers to the loan interest borrowed from the bank’s lending facility to cover the SC’s budget shortfall (to be paid at the end of the selling season).

Using the demand functions (Eq. (1)) and Eq. (3), the expected value and variance of the SC’s profit can be derived as follows:

$$ E\left[ {\tilde{\prod }_{SC} } \right] = \left( {a_{1} - q_{1} - q_{2} - \alpha \theta - c} \right)q_{1} + \left( {\overline{a}_{2} - q_{2} - q_{1} + \alpha \theta - c} \right)q_{2} - I\theta^{2} - c\left( {q_{1} + q_{2} } \right)r. $$
(4)
$$ Var\left[ {\tilde{\prod }_{SC} } \right] = \sigma^{2} q_{2}^{2} . $$
(5)

Substituting Eqs. (4) and (5) into Eq. (2), the utility function of risk-averse SC can be obtained as follows:

$$ U_{SC} = \left( {a_{1} - q_{1} - q_{2} - \alpha \theta - c} \right)q_{1} + \left( {\overline{a}_{2} - q_{2} - q_{1} + \alpha \theta - c} \right)q_{2} - c\left( {q_{1} + q_{2} } \right)r - \lambda_{sc} \sigma^{2} q_{2}^{2} - I\theta^{2} , $$
(6)

where \({\lambda }_{sc}\) refers to the degree of SC’s risk-aversion.

Proposition 1 characterizes the equilibrium production quantities of products 1 and 2.

Proposition 1

The utility function of SC is jointly concave on \({q}_{1}\) and \({q}_{2}\). Hence, the optimal production quantities under the benchmark model can be obtained as follows:

$$ q_{1} = \frac{{\left( {\Upsilon - rc} \right)\sigma^{2} \lambda_{sc} - \Lambda }}{{2\sigma^{2} \lambda_{sc} }}, $$
(7)
$$ q_{2} = \frac{\Lambda }{{2\sigma^{2} \lambda_{sc} }}, $$
(8)

where \(\Upsilon=a_{1}- \alpha \theta -c \, and \,\Lambda=2 \alpha \theta+ {\overline{a}}_{2}-a_{1}.\)

All proofs are provided in the Appendix B.

As shown in Eq. (3), the bank provides the SC’s required capital \(c\left({q}_{1}+{q}_{2}\right)\) through the DF scheme with a fixed-rate loan and receives interest (at rate \(r\)) at the end of selling season. The bank’s net profit function can be formulated as follows:

$$ {\prod}_B = c\left( {q_{1} + q_{2} } \right)r. $$
(9)

The optimal interest rate determined by bank is characterized in Proposition 2.

Proposition 2

The bank’s profit function is always concave on \(r\). Hence, the optimal interest rate under the benchmark model can be obtained as follows:

$$ r^{b} = \frac{\Upsilon }{2c}, $$
(10)

where \(\Upsilon = a_{1} - \alpha \theta - c.\)

Substituting Eq. (10) into Eqs. (7)-(8), the optimal production quantities of SC can be easily recalculated.

4 NPD financing via MSP

With the growing importance of environmental aspects of products and the rising public awareness about the necessity for pursuing green entrepreneurship, the MSPs’ involvement in backing green SME entrepreneurs is increasing. In this section, we investigate the platform financing of NPD and study the decision making of players under deregulated and regulated scenarios.

As an innovative SCF solution provider, the MSP offers a combination of DF and EF facilities (Yang et al., 2017; Zheng et al., 2020). This enables the risk-averse SC access to cover its budget deficit and afford the production and greening costs of the new non-green and green products. Given its structural power and dominance, the MSP announces \(\varphi \) first and specifies the distribution of funds to be raised by a crowd of small investors and transferred to the SC under each SCF scheme. Under the DF, the SC will receive a loan with total amount \(\varphi c\left({q}_{1}+{q}_{2}\right)\) and the interest rate \(r\). On the other hand, the SC receives \(\left(1-\varphi \right)c\left({q}_{1}+{q}_{2}\right)\) from the MSP under the EF scheme and commits to share its profits with the investors (proportional to their investment) at the end of the selling season. To avoid trivial cases, two additional assumptions are made:

i) a commission/service fee is set by MSPs, which is commonly a fixed percentage (2%-5%) of the raised capital (Fatehi & Wagner, 2019; Reza-Gharehbagh et al., 2021). Some fundraising platforms, such as GoFundMe,Footnote 9 do not apply this fee and consider no platform charge. Given its negligibility and predictability, the commission rate in our models is assumed to be zero.

ii) as part of the platform onboarding and registration process, the platform (on behalf of the prospective investors interested in EF) negotiates the share exchange ratio (i.e., X% for $Y) and other terms with the SME entrepreneur. Such information (when decided) will be made available to all parties before they commit to any form of investment/fund raising (Douglas et al., 2014). Hence, given its predictability and to reduce the complexity of our models, we assumed that the equity/share exchange ratio under the EF scheme is equal to 1.Footnote 10

Considering the above assumptions, we next formulate the problem setting in details and study the equilibrium strategies of GNPD players under two settings. Section 4.1 studies the interaction of MSP and SC in the absence of government intervention (i.e., deregulated GNPD scenario). In Sect. 4.2, we consider a regulated scenario where the government employs a hybrid policy (i.e., environmental tax and greening cost sharing incentive) and intervenes in the GNPD process. Section 4.2.1 considers an extension to the model where the government aims to maximize SW instead of EI.

4.1 Deregulated platform financing scenario

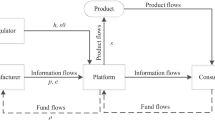
In this section, we consider the interactions between the SC and the MSP under the deregulated platform financing scenario. Using a two-level Stackelberg game model, we aim to obtain the optimal strategies of the SC (the game follower) and the MSP (the game leader). Figure 1 demonstrates the players’ interactions under the deregulated platform financing scenario.

Fig. 1
figure 1

Model schematic of the deregulated platform financing scenario

Full size image

As the game leader, the MSP first announces \(\varphi \) and determines its interest rate to be applied under the DF scheme. Participating in the platform financing, the risk-averse SC (follower) determines its production quantities of new non-green and green products, anticipating the MSP’s strategy. Following backward induction, we first study the profit function and optimal strategy of the SC (Asian & Nie, 2014).

Considering the DF and EF ratios (\(\varphi \) and \(1-\varphi \)) set by the MSP, the SC’s total net profit can be formulated as follows:

$$ \tilde{\prod }_{SC} = \varphi \left( {\left( {p_{1} - c} \right)q_{1} + \left( {\tilde{p}_{2} - c} \right)q_{2} - I\theta^{2} - \varphi c\left( {q_{1} + q_{2} } \right)r} \right). $$
(11)

Equation (11) includes four terms. The first and second terms refer to the revenue obtained from selling products 1 and 2 to the market. The third term refers to the new green product’s greening cost. The last term refers to the DF loan facility’s interest payable to the MSP.

Using Eqs. (1) and (11), the expected value and variance for the SC’s profit can be derived as follows:

$$ E\left[ {\tilde{\prod }_{SC} } \right] = \varphi \left( {\left( {a_{1} - q_{1} - q_{2} - \alpha \theta - c} \right)q_{1} + \left( {\overline{a}_{2} - q_{2} - q_{1} + \alpha \theta - c} \right)q_{2} - I\theta^{2} - \varphi c\left( {q_{1} + q_{2} } \right)r} \right). $$
(12)
$$ Var\left[ {\tilde{\prod }_{SC} } \right] = \sigma^{2} \varphi^{2} q_{2}^{2} . $$
(13)

Substituting Eqs. (12) and (13) into Eq. (2), the utility function of risk-averse SC can be obtained as follows:

$$ \begin{aligned} U_{SC}& = \varphi \left( {\left( {a_{1} - \alpha \theta } \right)q_{1} + \left( {\overline{a}_{2} + \alpha \theta } \right)q_{2} - (q_{1} + q_{2} + c)(q_{1} + q_{2} ) - I\theta^{2} } \right) \\ &\quad - \varphi^{2} \left( {c\left( {q_{1} + q_{2} } \right)r + \lambda_{sc} \sigma^{2} q_{2}^{2} } \right). \end{aligned} $$
(14)

Proposition 3 characterizes the equilibrium production quantities of products 1 and 2.

Proposition 3

The utility function of SC is jointly concave on \({q}_{1}\) and \({q}_{2}\). Hence, the optimal production quantities under the deregulated platform financing scenario can be obtained as follows:

$$ q_{1} = \frac{{\varphi \sigma^{2} \lambda_{sc} \left( {\Upsilon - \varphi cr} \right) - \Lambda }}{{2\varphi \sigma^{2} \lambda_{sc} }}, $$
(15)
$$ q_{2} = \frac{\Lambda }{{2\varphi \sigma^{2} \lambda_{sc} }}, $$
(16)

where \(\Upsilon = a_{1} - \alpha \theta - c\) and \(\Lambda = 2\alpha \theta + \overline{a}_{2} - a_{1}\).

The risk-averse MSP supports GNPD process by facilitating investment and fundraising through EF and DF facilities. The MSP’s net profit function can be expressed as follows:

$$ \tilde{\prod }_{msp} = \left( {1 - \varphi } \right)\left( {\left( {p_{1} - c} \right)q_{1} + \left( {\tilde{p}_{2} - c} \right)q_{2} - I\theta^{2} - \varphi c\left( {q_{1} + q_{2} } \right)r} \right) + \varphi c\left( {q_{1} + q_{2} } \right)r. $$
(17)

Using Eq. (1), the expected value and variance of the MSP’s profit function can be derived as follows:

$$ \begin{aligned} E\left[ {\tilde{\prod }_{msp} } \right]& = \left( {1 - \varphi } \right)\left( {\left( {a_{1} - q_{1} - q_{2} - \alpha \theta - c} \right)q_{1} + \left( {\overline{a}_{2} - q_{2} - q_{1} + \alpha \theta - c} \right)q_{2} - I\theta^{2} } \right) \\ & \quad + \varphi^{2} c\left( {q_{1} + q_{2} } \right)r. \end{aligned} $$
(18)
$$ Var\left[ {\tilde{\prod }_{msp} } \right] = \sigma^{2} \left( {1 - \varphi } \right)^{2} q_{2}^{2} . $$
(19)

Substituting Eqs. (18) and (19) into Eq. (2), the utility function of MSP can be obtained as follows:

$$ \begin{aligned} U_{msp} &= \left( {1 - \varphi } \right)\left( {\left( {a_{1} - \alpha \theta } \right)q_{1} + \left( {\overline{a}_{2} + \alpha \theta } \right)q_{2} - (q_{1} + q_{2} + c)(q_{1} + q_{2} ) - I\theta^{2} } \right) \\ &\quad + \varphi^{2} c\left( {q_{1} + q_{2} } \right)r - \lambda_{msp} \sigma^{2} \left( {1 - \varphi } \right)^{2} q_{2}^{2} . \\ \end{aligned} $$
(20)

Given its risk-aversion degree \({\lambda }_{msp}\) and the SC’s product portfolio decision, the MSP decides on its DF loan facility’s interest rate. This decision is characterized in Proposition 4.

Proposition 4

The MSP’s utility function is concave on \(\mathrm{r}\). Hence, the optimal interest rate of DF loan facility under the deregulated platform financing scenario can be obtained as follows:

$$ r^{d} = \frac{\Upsilon }{{\left( {1 + \varphi } \right)c}}, $$
(21)

where \(\Upsilon = a_{1} - \alpha \theta - c.\)

Substituting Eq. (21) into Eqs. (15) and (16), the actual optimal production quantities of SC can be obtained.

4.2 Government-backed (regulated) platform financing scenario

In this section, we extend the deregulated platform financing scenario and study the interactions between the risk-averse SC (the game follower), the risk-averse MSP (the game sub-leader), and the government. Unlike the benchmark and deregulated GNPD models, here the government is supposed to pursue its green entrepreneurship goals through a hybrid environmental intervention policy, which includes an environmental tax and a greening cost sharing incentive. Hence, using a three-level Stackelberg game model, we examine the players’ optimal strategies under the government’s hybrid intervention policy.

Figure 2 demonstrates the players’ interactions via the MSP under the regulated platform financing scenario. Figure 3 depicts the sequence of events we consider in developing the players’ models under the regulated GNPD scenario.

Fig. 2
figure 2

Model schematic of the regulated platform financing scenario

Full size image
Fig. 3
figure 3

Sequence of events under the regulated platform financing scenario

Full size image

As can be seen, to motivate the risk-averse investors and the capital-constrained SC to put more effort into GNPD, the government offers a cost sharing incentive and subsidizes the greening costs of the new product. The following decisions must be made in the new game structure:

  1. 1.

    As part of its green entrepreneurship strategy, the government agrees to pay \((1- \eta )\%\) of the SC’s total greening costs for the new green product and decides on its environmental tax to be imposed on the non-green product.

  2. 2.

    Considering the government’s strategies, the MSP first announces \(\varphi \) and specifies the distribution of funds to be raised by investors under EF and DF. The MSP must decide on the DF loan facility’s interest rate.

  3. 3.

    Given the decisions of government and MSP, the risk-averse SC decides on production quantities of new non-green and green products to optimize its product portfolio.

  4. 4.

    The SC next receives funds from the MSP’s DF and EF facilities and manufactures the committed quantities, \({q}_{1}\) and \({q}_{2}\).

  5. 5.

    The SC sells the products to the market and obtains a total revenue of \({(p}_{1}{{q}_{1}+p}_{2}{q}_{2}\)).

  6. 6.

    The SC repays the committed interest (under DF) and transfers profit share (proportional to their equity shares under EF) to the MSP at the end of the selling season.

  7. 7.

    The government collects the environmental tax \(t{q}_{1}\) and the game ends.

The profit function of SC can be derived as follows:

$$ \tilde{\prod }_{SC} = \varphi \left( {\left( {p_{1} - c - t} \right)q_{1} + \left( {\tilde{p}_{2} - c} \right)q_{2} - \eta I\theta^{2} - \varphi c\left( {q_{1} + q_{2} } \right)r} \right). $$
(22)

Equation (22) includes four terms: (i) the first term refers to the revenue obtained from selling product 1 after deducting the government’s imposed environmental tax on non-green product; (ii) the second term refers to the green product’s revenue; (iii) the third term refers to the proportion of greening costs to be paid by the SC; (iv) the last term is related to the loan interest borrowed from the MSP’s DF facility to partially cover the SC’s budget shortfall.

Using Eqs. (1) and (22), the expected value and variance of the SC’s profit function can be derived as follows:

$$ \begin{aligned} E\left[ {\tilde{\prod }_{SC} } \right] &= \varphi \left( {\left( {a_{1} - q_{1} - q_{2} - \alpha \theta - c - t} \right)q_{1} + \left( {\overline{a}_{2} - q_{2} - q_{1} + \alpha \theta - c} \right)q_{2} - \eta I\theta^{2} } \right) \\ &\quad - \varphi^{2} c\left( {q_{1} + q_{2} } \right)r. \end{aligned} $$
(23)
$$ Var\left[ {\tilde{\prod }_{SC} } \right] = \varphi^{2} \sigma^{2} q_{2}^{2} . $$
(24)

Substituting Eqs. (23) and (24) into Eq. (2), the utility function of SC is obtained as follows:

$$ \begin{aligned} U_{SC}& = \varphi \left( {\left( {a_{1} - \alpha \theta - t} \right)q_{1} + \left( {\overline{a}_{2} + \alpha \theta } \right)q_{2} - \left( {q_{1} + q_{2} + c} \right)\left( {q_{1} + q_{2} } \right) - \eta I\theta^{2} } \right) \\ &\quad - \varphi^{2} \left( {c\left( {q_{1} + q_{2} } \right)r - \lambda_{sc} \sigma^{2} q_{2}^{2} } \right). \end{aligned} $$
(25)

Proposition 5 characterizes the SC’s optimal production strategy.

Proposition 5

The utility of SC is jointly concave on \({{q}}_{1}\) and \({{q}}_{2}\). Hence, the optimal production quantities under the regulated GNPD scenario can be obtained as follows:

$$ q_{1} = \frac{{\varphi \sigma^{2} \lambda_{sc} \left( {\Upsilon - \varphi cr - t} \right) - \Lambda - t}}{{2\varphi \sigma^{2} \lambda_{sc} }}, $$
(26)
$$ q_{2} = \frac{\Lambda + t}{{2\varphi \sigma^{2} \lambda_{sc} }}, $$
(27)

where \(\Upsilon = a_{1} - \alpha \theta - c\) and \(\Lambda = 2\alpha \theta + \overline{a}_{2} - a_{1}\).

After characterizing the SC’s production portfolio decision, we next focus on the financing decision of the MSP (the game subleader). The MSP’s net profit function can be derived as follows:

$$ \tilde{\prod }_{msp} = \left( {1 - \varphi } \right)\left( {\left( {p_{1} - c - t} \right)q_{1} + \left( {\tilde{p}_{2} - c} \right)q_{2} - \eta I\theta^{2} - \varphi c\left( {q_{1} + q_{2} } \right)r} \right) + \varphi c\left( {q_{1} + q_{2} } \right)r. $$
(28)

Using Eq. (1), the expected value and variance of the risk-averse MSP’s profit can be derived as follows:

$$ \begin{aligned} E\left[ {\tilde{\prod }_{msp} } \right]& = \left( {1 - \varphi } \right)\left( {\left( {a_{1} - q_{1} - q_{2} - \alpha \theta - c - t} \right)q_{1} + \left( {\overline{a}_{2} - q_{2} - q_{1} + \alpha \theta - c} \right)q_{2} - \eta I\theta^{2} } \right) \\ &\quad + \varphi^{2} c\left( {q_{1} + q_{2} } \right)r. \\ \end{aligned} $$
(29)
$$ Var\left[ {\tilde{\prod }_{msp} } \right] = \sigma^{2} \left( {1 - \varphi } \right)^{2} q_{2}^{2} . $$
(30)

Substituting Eqs. (29) and (30) into Eq. (2), the utility function of the risk-averse MSP can be obtained as follows:

$$ \begin{aligned} U_{msp}& = \left( {1 - \varphi } \right)\left( {\left( {a_{1} - \alpha \theta - t} \right)q_{1} + \left( {\overline{a}_{2} + \alpha \theta } \right)q_{2} - \left( {q_{1} + q_{2} + c} \right)\left( {q_{1} + q_{2} } \right) - \eta I\theta^{2} } \right)\, \\ &\quad + \varphi^{2} c\left( {q_{1} + q_{2} } \right)r - \lambda_{msp} \sigma^{2} \left( {1 - \varphi } \right)^{2} q_{2}^{2} . \\ \end{aligned} $$
(31)

The optimal interest rate of MSP is characterized in Proposition 6.

Proposition 6

The MSP’s utility function is concave on \({r}\). Hence, the optimal interest rate under the regulated GNPD scenario can be obtained as follows:

$$ r = \frac{\Upsilon - t}{{\left( {1 + \varphi } \right)c}}, $$
(32)

where \(\Upsilon = a_{1} - \alpha \theta - c\).

After characterizing the SC’s and MSP’s problems, we next focus on the government’s environmental policy making problem. As the game leader, the government aims to enhance the participation of the other players (i.e., SC and MSP) in GNPD, while focusing on its economic influence (EI). Adapting a hybrid intervention policy, the government’s EI function can be obtained as follows:

$$ EI = tq_{1} - \left( {1 - \eta } \right)I\theta^{2} . $$
(33)

Proposition 7 provides the optimal environmental tax imposed by the government.

Proposition 7

The government’s EI function is always concave on \({t}\). Hence, the optimal environmental tax under the regulated GNPD scenario can be obtained as follows:

$$ t^{gb} = \frac{{\varphi \sigma^{2} \lambda_{sc} \Upsilon - \left( {1 + \varphi } \right)\Lambda }}{{2\left( {\varphi \sigma^{2} \lambda_{sc} + \varphi + 1} \right)}}, $$
(34)

where \(\Upsilon = a_{1} - \alpha \theta - c\) and \(\Lambda = 2\alpha \theta + \overline{a}_{2} - a_{1}\).

Substituting Eq. (34) into Eqs. (26), (27), and (32), the optimal production quantities of SC and interest rate of MSP can be recalculated.

Table 2 summarizes the optimal decisions of the players (i.e., SC, MSP, and government) under different scenarios.

Table 2 Equilibrium decisions under different scenarios
Full size table

Corollary 1

Regardless of the financing scenarios, the optimal production quantity of new green product is higher than that of the new non-green product, that is \({q}_{2}^{b}\ge {q}_{1}^{b}\), \({{q}}_{2}^{{d}}\ge {{q}}_{1}^{{d}}\), and \({{q}}_{2}^{{gb}}\ge {{q}}_{1}^{{gb}}\), if the following condition holds:

$$ \theta \ge \frac{{a_{1} }}{2\alpha }. $$
(35)

This finding shows that when the greening degree of products reaches a certain threshold, producing the new green product becomes more favorable than the non-green product, regardless of the financing scenarios.

Corollary 2

Under the hybrid environmental intervention policy (i.e., the regulated GNPD scenario), the SC’s optimal production quantities and the MSP’s optimal interest rate are higher than that of the deregulated scenario, that is \({q}_{1}^{gb}\ge {q}_{1}^{d}, {q}_{2}^{gb}\ge {q}_{2}^{d}, and {r}^{gb}\ge {r}^{d}\), if the following condition holds:

$$ \varphi \le \frac{\Lambda }{{\Upsilon \sigma^{2} \lambda_{sc} - \Lambda }}, $$
(36)

where \(\Upsilon = a_{1} - \alpha \theta - c\) and \(\Lambda = 2\alpha \theta + \overline{a}_{2} - a_{1}\).

Corollary 2 states that the government’s hybrid intervention approach could incentivize the SC and MSP to cooperatively work towards the environmental objectives and achieve a better environmental outcome (\({q}_{2}^{gb}\ge {q}_{2}^{d}\)) if a certain threshold for financing distribution ratio between DF and EF is met (Eq. (36)). In other words, when the right balance between DF and EF is set by the MSP, the regulated GNPD scenario enables the government to achieve a better outcome in line with its green entrepreneurship agenda.

Corollary 3

Under the regulated GNPD scenario, \({{q}}_{1}^{{gb}}\), \({{q}}_{2}^{{gb}}\), \({{r}}^{{gb}}\), and \({{t}}^{{gb}}\) have certain properties that are summarized in Table 3.

Table 3 Summary of decision variables’ properties under the regulated GNPD scenario
Full size table

Corollary 3 suggests the following insights:

  1. (a)

    As the greening degree of new green product \((\theta )\) and consumer’s sensitivity to the greening degree \((\alpha )\) of new product increase, the government reduces its environmental tax on non-green items, \(\frac{\partial {t}^{gb}}{\partial \theta }\le 0\) and \(\frac{\partial {t}^{gb}}{\partial \alpha }\le 0\). In response, the MSP decreases its DF interest rate, \(\frac{\partial {r}^{gb}}{\partial \theta }\le 0\) and \(\frac{\partial {r}^{gb}}{\partial \alpha }\le 0\). This leads the SC to prioritize green production as part of its product portfolio optimization, that is, \(\frac{\partial {q}_{1}^{gb}}{\partial \theta }\le 0\), \(\frac{\partial {q}_{1}^{gb}}{\partial \alpha }\le 0\) and \(\frac{\partial {q}_{2}^{gb}}{\partial \theta }\ge 0\), \(\frac{\partial {q}_{2}^{gb}}{\partial \alpha }\ge 0\).

  2. (b)

    As the green product’s market uncertainty \((\sigma )\) and the SC’s risk-aversion \({(\lambda }_{sc})\) increase, the government rationally imposes a higher environmental tax on the non-green product, mainly to increase its net income (EI), that is, \(\frac{\partial {t}^{gb}}{\partial \sigma }\ge 0\) and \(\frac{\partial {t}^{gb}}{\partial {\lambda }_{sc}}\ge 0\). In response, the MSP decreases its interest rate to encourage the SC to boost production,\(\frac{\partial {r}^{gb}}{\partial \sigma }\le 0\) and \(\frac{\partial {r}^{gb}}{\partial {\lambda }_{sc}}\le 0\). However, driven by its risk-aversion behavior, the SC decides to allocate fewer resources to its green production (the riskier option),\(\frac{\partial {q}_{2}^{gb}}{\partial \sigma }\le 0\) and \(\frac{\partial {q}_{2}^{gb}}{\partial {\lambda }_{sc}}\le 0\), and instead produces more non-green items,\(\frac{\partial {q}_{1}^{gb}}{\partial \sigma }\ge 0\) and \(\frac{\partial {q}_{1}^{gb}}{\partial {\lambda }_{sc}}\ge 0\).

  3. (c)

    The government imposes a higher environmental tax on non-green product, when the DF ratio \((\varphi )\) increases, that is \(\frac{\partial {t}^{gb}}{\partial \varphi }\ge 0\). To motivate the SC, the MSP reduces its DF loan facility’s interest rate, \(\frac{\partial {r}^{gb}}{\partial \varphi }\le 0\). In response, the SC decides to reduce the share of green product in its product portfolio, \(\frac{\partial {q}_{1}^{gb}}{\partial \varphi }\ge 0\) and \(\frac{\partial {q}_{2}^{gb}}{\partial \varphi }\le 0\). This is mainly because, at a lower DF loan interest rate \({r}^{gb}\), the SC is inclined to produce more non-green items to reduce the market uncertainties associated with the green product.

The counterintuitive properties discussed in Corollary 3 suggest that, given the existing uncertainty in the GNPD process and the risk-aversion behavior of the SC, the regulated GNPD system cannot achieve its full potential in supporting the green entrepreneurship goals. This might be because the government mainly focuses on net income maximization (EI) and overlooks other important factors, such as consumer surplus and environmental aspects of producing green and non-green products. To validate this hypothesis, we extend our analysis in Sect. 4.2.1 and conduct a detailed computational study in Sect. 5.

4.2.1 Social welfare approach: an extension

Improving social welfare (SW) is known as one of the key responsibilities of progressive governments. In this subsection, we extend the regulated GNPD model and consider a scenario where the government focuses on SW (instead of EI). Adapting the hybrid environmental intervention concept, the government’s SW function can be formulated as follows:

$$ SW = EI + CS + EB - EC $$
(37)

To expand the above function, the following definitions are proposed:

  1. (i).

    Focusing on the new green product and after some algebra, the consumer surplus (CS) can be derived as follows (Sheu & Chen, 2012):

    $$ CS = \frac{1}{2}q_{2}^{2} + q_{1} q_{2} - \alpha \theta q_{2} . $$
    (38)
  2. (ii).

    The environmental benefit (EB) and cost (EC) induced by producing green and non-green products can be shown by \(EB={\omega }_{2}{q}_{2}\) and \(EC={\omega }_{1}{q}_{1}\). Note \({\omega }_{1}\) and \({\omega }_{2}\) represent incremental environmental benefit and cost caused by manufacturing and supplying green and non-green products to the market.

Using Eqs. (33) and (38), the SW model of government can be rewritten as follows:

$$ SW = \left( {tq_{1} - \left( {1 - \eta } \right)I\theta^{2} } \right) + \left( {\frac{1}{2}q_{2}^{2} + q_{1} q_{2} - \alpha \theta q_{2} } \right) + \omega_{2} q_{2} - \omega_{1} q_{1} . $$
(39)

Proposition 8 provides the optimal environmental tax imposed by the government under SW objective function.

Proposition 8

The government’s SW is always a concave function of \({t}\). Hence, the optimal environmental tax under the regulated GNPD scenario can be obtained as follows:

$$ t^{gb} = \frac{{\sigma^{2} \lambda_{sc} \varphi \left( {2\sigma^{2} \lambda_{sc} \varphi \left( {\Upsilon + \omega_{1} } \right) + \Upsilon - \left( {3 + 2\varphi } \right)\Lambda - 2\left( {1 + \varphi } \right)\Gamma } \right) - \left( {1 + \varphi } \right)\Lambda }}{{1 + 2\sigma^{2} \lambda_{sc} \varphi \left( {3 + 2\varphi \left( {1 + \sigma^{2} \lambda_{sc} } \right)} \right) + \varphi }}, $$
(40)

where \(\Gamma = \alpha \theta - \omega_{1} - \omega_{2}\), \(\Upsilon = a_{1} - \alpha \theta - c\), and \(\Lambda = 2\alpha \theta + \overline{a}_{2} - a_{1}\).

Note that the presented results in Propositions 5, 6, 7 and Corollaries 2, 3 are obtained based on the EI maximization problem of the government. Using Proposition 8, one can easily regenerate the previous results and obtain the optimal solutions of the key players under the SW setting. For the sake of brevity, we omitted those results and conducted a comprehensive computational study in the following section.

5 Computational study

In this section, we run a detailed computational study and investigate the regulated GNPD scenario to validate our theoretical findings. The input values used in the numerical analysis are \({a}_{1}=35\), \({\overline{a} }_{2}=30\), \(c=9\), \(I=8\), \(\theta =20\).

We first study how the SC’s utility and the green product’s share in SC’s product portfolio are affected by other key parameters. Figure 4 depicts how the SC’s utility is influenced by the green product’s market uncertainty \(\sigma \) and coefficient of consumer sensitivity to greening degree \(\alpha \). In this experiment, we use \(\varphi =50\%\) and \(\eta =0.7\), change \(\sigma \) within the range of [0, 5], and let \(\alpha \) takes three different values 5, 10, and 15.

Fig. 4
figure 4

Impacts of \(\sigma \) and \(\alpha \) on the utility of SC (\({\lambda }_{msp}=0.6\) and \({\lambda }_{sc}=0.4\))

Full size image

As expected, our experiment confirms that increasing the green product’s market uncertainty \(\sigma \) negatively impacts the utility function of SC. It is also found that the SC achieves a higher utility as \(\alpha \) increases. This is mainly because a higher sensitivity of consumers towards environmental aspects of products intensifies the market competition between the non-green and green products which ultimately improves the performance of the SC.

We next examine the impacts of the new product’s greening degree and SC’s risk-aversion on the SC’s product portfolio. Using the same input values as before (except \(\alpha =4\) and \(\sigma =2\)), we change \({\lambda }_{sc}\) within the range of [0.2, 0.6] and evaluate the share of green product in SC’s product portfolio, \({q}_{2}/{(q}_{1}+{q}_{2})\).

Consistent with Corollaries 1 and 3, Fig. 5 shows that as the greening degree of new product \((\theta )\) increases, the SC prioritizes the green product over the non-green product in its product portfolio. It is also found that when \(\theta \) is lower than a certain threshold (here, \(\theta <15\)), the share of green product in the product portfolio of a risk-taker SC is higher than that of the risk-averse SC (region (a)). When \(\theta \) is higher than that threshold value (here, \(\theta >15\)), however, the SC should adjust its risk attitude and take a lower risk to achieve the green entrepreneurship objectives (region (b)). This is an important finding and suggests that to achieve the regulated GNPD program’s objectives, capital constrained SCs must regularly consider the required greening efforts of new products and adjust their risk attitude.

Fig. 5
figure 5

Effects of \(\theta \) and \({\lambda }_{sc}\) on GNPD

Full size image

We next investigate how key players’ preference towards the government intervention approach (EI vs. SW) is impacted by the MSP’s risk attitude and other key parameters. Using the theoretical results presented in Sect. 4, we evaluate and compare the optimal utility of players under EI and SW. We use the same input parameter values as before (except \({\omega }_{1}=30\), \({\omega }_{2}=100\), \({\lambda }_{sc}=0.4\)) and change \({\lambda }_{msp}\) between 0 and 0.6. Figure 6 demonstrates the effects of \(\varphi \) and \(\eta \) under different scenarios (when the MSP is risk-averse (Fig. 6a); when the MSP is risk-neutral (Fig. 6b)).

Fig. 6
figure 6

Joint effects of \(\varphi \), \(\eta \), and MSP’s risk attitude on players’ preference towards SW vs. EI

Full size image

As Fig. 6a, b illustrate, there exists a substantial conflict between the GNPD players about the government’s policy making approach (EI vs. SW). More importantly, the players’ preference and existing conflicts are highly impacted by the risk-attitude of the MSP as the major fund provider. For better presentation, different identified regions in Fig. 6a, b are described as follows:

  1. (i).

    Win-win EI region: all players benefit from the government’s EI maximization objective.

  2. (ii).

    Win-win SW region: all players benefit from the government’s SW maximization objective.

  3. (iii).

    Conflict region: unlike the SC, the MSP and government benefit from the government’s SW maximization objective.

  4. (iv).

    Conflict region: unlike the government, the SC and MSP benefit from the government’s EI maximization objective.

  5. (v).

    Conflict region: unlike the MSP, the SC and government benefit from the government’s EI maximization objective.

As shown in Fig. 6a, there is a high degree of conflict among the players when the MSP takes a risk-averse approach (regions III, IV, and V). All players may benefit from the government’s SW approach (region II) only when the MSP’s DF ratio is quite high (here, \(\varphi >70\%\)). However, when the MSP takes a risk-neutral approach (see Fig. 6b), the players can overcome their conflicts when the DF ratio is set either low (region I; \(\varphi <20\%\)) or high (region II; \(\varphi >70\%\)). In other words, by reducing its sensitivity to risk and adjusting the DF-EF distribution ratio according to the government’s intervention approach, the MSP enables the players to always come to a win–win agreement and further contribute to the green entrepreneurship goals (regions I and II).

6 Conclusion

Multi-sided FinTech platforms (MSPs) have recently gained significant traction among green entrepreneurs as an innovative means to support their green new product development (GNPD) plans. To simultaneously support green entrepreneurship and enhance social welfare, some governments are promoting the use of MSPs and offering a variety of sustainable supply chain finance (SSCF) schemes.

This study investigates the product portfolio optimization problem of a capital-constrained supply chain (SC) that jointly produces new green and non-green products under a hybrid government intervention policy (i.e., environmental tax on non-green product and new product greening cost sharing incentive). The risk-averse SC is given access to a combination of equity financing (EF) and debt financing (DF) facilities offered by an MSP. According to the hybrid policy of the government and considering the potential strategies of the SC, the MSP determines its interest rate that maximizes its utility function.

After constructing benchmark models, we proposed a greening cost sharing mechanism between the government and the SC and examined the equilibrium strategies of the key players under two government policy making approaches (i.e., economic influence and social welfare). Our theoretical findings revealed that, when the right balance between DF and EF is set by the MSP, the regulated scenario can effectively motivate the SC to prioritize GNPD, enabling the government to achieve better overall performance. Also, when the new product’s greening degree reaches a certain threshold, developing a new green product becomes more appealing to the risk-averse SC than producing a non-green product, independent of the financing scenario. Moreover, our computational study showed that the sensitivity of consumers towards products greening positively impact the share of new green product in SC’s product portfolio, whereas the market uncertainty of green product has an adverse effect on GNPD. Hence, to achieve the green entrepreneurship goals, capital constrained SCs must consider the required greening efforts of new products and regularly adjust their risk attitude. Our numerical results suggest that there is a high degree of conflict of objectives among the players when the MSP takes a risk-averse approach. However, taking a risk-neutral approach and setting an appropriate DF-EF distribution ratio, the MSP can moderate the conflict situation and help players further contribute to the government’s green entrepreneurship goals.

In summary, this study has four key managerial implications: (1) To achieve their green entrepreneurship goals, the policymakers are urged to consider all stakeholders’ potential strategies and adjust their environmental intervention policy, accordingly. (2) To moderate the conflict situation, the MSPs are urged to consider the limitations of the capital constrained SCs involved in GNPD and reduce their sensitivity to risk. (3) Using the right balance between the EF and DF, the MSP enables the governments to achieve their green entrepreneurship goals by enhancing the share of green product in the SC’s new products portfolio. (4) To successfully promote sustainable supply chain finance (SSCF) through digital platforms, policy makers are urged to leverage their legislative power and prioritize green entrepreneurship and social welfare over their financial maximization agenda.

We suggest some extensions that may serve as future research avenues. First, we considered a regulated GNPD program, where all investors participating in the MSP are homogenous and identical. Considering heterogenous investors with different investment and risk profiles (Reza-Gharehbagh et al., 2021) can be a challenging yet interesting future direction. Second, other government intervention policies, such as energy-saving (Javadi et al., 2019), can be combined with the proposed hybrid strategy to broaden the scope of the present study. Third, we assumed that parameter values are common knowledge. Considering information asymmetry is another interesting area for future research.