Abstract
Approximately sixty years ago two seminal findings, the cutting plane and the subgradient methods, radically changed the landscape of mathematical programming. They provided, for the first time, the practical chance to optimize real functions of several variables characterized by kinks, namely by discontinuities in their derivatives. Convex functions, for which a superb body of theoretical research was growing in parallel, naturally became the main application field of choice. The aim of the paper is to give a concise survey of the key ideas underlying successive development of the area, which took the name of numerical nonsmooth optimization. The focus will be, in particular, on the research mainstreams generated under the impulse of the two initial discoveries.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Nonsmooth optimization (NSO), sometimes referred to as Nondifferentiable optimization (NDO), deals with problems where the objective function exhibits kinks. Even though smoothness, that is the continuity of the derivatives, is present in most of the functions describing real world decision making processes, an increasing number of modern and sophisticated applications of optimization are inherently nonsmooth. The most common source of nonsmoothness is in the choice of the worst-case analysis as a modeling paradigm. It results in choosing objective functions of the max or, alternatively, of the min type, thus in stating minmax or maxmin problems, respectively. Nonsmoothness typically occurs whenever solution of the inner maximization (or minimization) is not unique. Although such phenomenon is apparently rare, nevertheless its occurrence might cause failure of the traditional differentiable optimization methods when applied to nonsmooth problems. Among other areas where nonsmooth optimization problems arise we mention here:
-
Minmaxmin models, coming from worst–case–oriented formulations of problems where two types of decision variables are considered, “here and now” and “wait and see”, respectively, with in the middle the realization of a scenario taken from a set of possible ones.
-
Right-hand-side decomposition of large scale problems (e.g., multicommodity flow optimization) where the decomposition into subproblems is controlled by a master problem which assigns resources to each of them. In such framework, the objective function of the master is typically nonsmooth.
-
Lagrangian relaxation of Integer or Mixed-Integer programs, where the Lagrangian dual problem, tackled both for achieving good quality bounds and for constructing efficient Lagrangian heuristics, consists in the optimization of a piecewise affine (hence nonsmooth) function of the multipliers.
-
Variational inequalities and nonlinear complementarity problems, which benefit from availability of effective methods to deal with systems of nonsmooth equations.
-
Bilevel problems, based on the existence, as in Stackelberg’s games, of a hierarchy of two autonomous decision makers. The related optimization problems are non-differentiable.
Although the history of nonsmooth optimization dates back to Chebyshëv and his contribution to function approximation (Chebyshëv 1961), it was in the sixties of last century when mathematicians, mainly from former Soviet Union, started to tackle the design of algorithms able to numerically locate the minima of functions of several variables, under no differentiability assumption. The subgradient was the fundamental mathematical tool adopted in such context. We recall here the contributions by Shor (1985), Demyanov and Malozemov (1974), Polyak (1987), and Ermoliev (1966).
Based on quite a different philosophy, as it will be apparent in the following, a general method able to cope with nondifferentiability was devised, independently, by Kelley (1960) and by Cheney and Goldstein (1959). Instead of trusting on a unique subgradient, the approach consisted in the simultaneous use of the information provided by many subgradients. The parallel development of convex analysis, thanks to contributions by Fenchel, Moreau and Rockafellar, was providing, at that time, the necessary theoretical support.
A real breakthrough took place approximately in the mid seventies, when the idea of an iterative process based on information accumulation did materialize in the methods independently proposed by Lemaréchal (1974) and Wolfe (1975). From those seminal papers an incredibly large number of variants flourished, under the common label of bundle type methods. This family of methods, originally conceived for treatment of the convex case, was appropriately enriched by features able to cope with non convexity.
In more recent years, motivated by the interest in solving problems where exact calculation of the objective function is either impossible or computationally costly, several methods based on its approximate computation were devised. At this time the derivative free philosophy is successfully stepping in the nonsmooth optimization world.
Establishing a taxonomy of methods in such a rich area is a difficult and somehow arbitrary task. We will adopt the following, imperfect scheme, defining a classification in terms of methods based on single-point information and those grounded on multi-point models. All subgradient-related methods, ranging from classic fixed step one to recent accelerated versions, belong to the first group, while in the second group we will comprise the cutting-plane related approaches, including bundle methods and their variants. We will see, however, that even in the multi-point approaches, to paraphrase Orwell in his Animal farm, all points are equal, but some points are more equal than others.
The methods grounded on inexact function and/or subgradient evaluation will be also cast in the above framework. Some other methods, that can hardly fit the proposed scheme, will be treated separately.
We confine ourselves to the treatment of convex unconstrained optimization problems. When appropriate, we will also focus on the extension of some algorithms to nonconvex Lipschitz functions, or to special classes of nonconvex functions, such as the Difference-of-Convex (DC) ones.
The paper is organized as follows. After stating the main NSO problem, the relevant notation, and some basic theoretical background in Sect. 2, we introduce the NSO mainstreams in Sect. 3. In Sects. 4 and 5 we discuss, respectively, about the methods based on single-point and multi-point models. Some classes of algorithms hard to classify into the two mainstreams are surveyed in Sect. 6. Motivations and issues related to the use of inexact calculations are discussed in Sect. 7, while in Sect. 8 some possible extensions of convex methods to the nonconvex case are reported. We give only the strictly necessary references in the main body of this survey, postponing to the final Sect. 9 more detailed bibliographic notes and complementary information, along with few relevant reading suggestions.
The paper is a slightly revised version of Gaudioso et al. (2020c).
2 Preliminaries
We consider the following unconstrained minimization problem
where the real-valued function \(f:{\mathbb {R}}^n \rightarrow {\mathbb {R}}\) is assumed to be convex and not necessarily differentiable (nonsmooth), unless otherwise stated. We assume that f is finite over \({\mathbb {R}}^n\), hence it is proper. Besides, in order to simplify the treatment, we assume that f has finite minimum \(f^*\) which is attained at a nonempty convex compact set \(M^* \subset {\mathbb {R}}^n\). An unconstrained minimizer of f, namely any point in \(M^*\), will be denoted by \(\mathbf {x}^*\). For a given \(\epsilon >0\), an \(\epsilon \)-approximate solution of (1) is any point \(\mathbf {x} \in {\mathbb {R}}^n\) such that \(f(\mathbf {x}) < f^* + \epsilon \). Throughout the paper, the symbol \(\Vert \cdot \Vert \) will indicate the \(\ell _2\) norm, while for any given two vectors \(\mathbf {a},\mathbf {b}\), their inner product will be denoted by \(\mathbf {a}^\top \mathbf {b}\).
Next, the fundamental tools of nonsmooth optimization are briefly summarized. Further definitions and relevant findings will be recalled at later stages as they will be necessary.
Given any point \(\mathbf {x} \in {\mathbb {R}}^n\), a subgradient of f at \(\mathbf {x}\) is any vector \(\mathbf {g} \in {\mathbb {R}}^n\) satisfying the following (subgradient-)inequality
The subdifferential of f at \(\mathbf {x} \in {\mathbb {R}}^n\), denoted by \(\partial f(\mathbf {x})\), is the set of all the subgradients of f at \(\mathbf {x}\), i.e.,
At any point \(\mathbf {x}\) where f is differentiable, the subdifferential reduces to a singleton, its unique element being the ordinary gradient \(\nabla f(\mathbf {x})\).
Previous definitions are next generalized for any nonnegative scalar \(\epsilon \). An \(\epsilon \)-subgradient of f at \(\mathbf {x}\), is any vector \(\mathbf {g} \in {\mathbb {R}}^n\) fulfilling
and the \(\epsilon \)-subdifferential of f at \(\mathbf {x}\), denoted by \(\partial f_\epsilon (\mathbf {x})\), is the set of all the \(\epsilon \)-subgradients of f at \(\mathbf {x}\), i.e.,
In case \(\epsilon = 0\) it obviously holds that \(\partial _0 f(\mathbf {x})=\partial f(\mathbf {x})\).
Since f is convex and finite over \({\mathbb {R}}^n\), the subdifferential \( \partial f(\cdot )\) is a convex, bounded and closed set; hence, for the directional derivative \(f'(\mathbf {x},\mathbf {d})\) at any \(\mathbf {x}\), along the direction \(\mathbf {d} \in {\mathbb {R}}^n\), it holds that
In particular, at a point \(\mathbf {x}\) where f is differentiable, the formula of classic calculus
easily follows from (6) and recalling that \(\partial f(\mathbf {x})= \{\nabla f(\mathbf {x})\}\).
Any direction \(\mathbf {d} \in {\mathbb {R}}^n\) is defined as a descent direction at \(\mathbf {x}\) if there exists a positive threshold \(\bar{t}\) such that
Furthermore, we remark that for convex functions the following equivalence holds true
At a later stage we will sometimes relax the convexity assumption on f, only requiring that f be locally Lipschitz, i.e., Lipschitz on every bounded set. Under such assumption, f is still differentiable almost everywhere, and it is defined at each point \(\mathbf {x}\) the generalized gradient (Clarke 1983) (or Clarke’s gradient, or subdifferential)
\(\varOmega _f\) being the set (of zero measure) where f is not differentiable. Any point \(\mathbf {x}\) with \(0 \in \partial _C f(\mathbf {x}) \) will be referred to as a Clarke stationary point.
In the rest of the article, it will be referred to as an oracle any black-box algorithm capable to provide, given any point \(\mathbf {x}\), the objective function value \(f(\mathbf {x})\) and, in addition, a subgradient in \(\partial f(\mathbf {x})\) or in \(\partial _C f(\mathbf {x})\), depending on whether f is convex or just locally Lipschitz.
3 Nonsmooth optimization mainstreams
In order to understand the main difference between smooth (i.e., differentiable) and nonsmooth functions, in an algorithmic perspective, we focus on comparing equations (6) and (7). On one hand, for smooth functions, at any point \(\mathbf {x}\) the gradient \(\nabla f(\mathbf {x})\) provides complete information about the directional derivative, along every possible direction, through the formula \(f'(\mathbf {x},\mathbf {d})=\nabla f(\mathbf {x})^\top \mathbf {d}\), see (7). On the other hand, for nonsmooth functions, at a point \(\mathbf {x}\) where f is not differentiable, the directional derivative, along any given direction, can only be calculated via a maximization process over the entire subdifferential, see (6), thus making any single subgradient unable to provide complete information about \(f'(\mathbf {x},\cdot )\). From an algorithmic viewpoint, such a difference has relevant implications that make not particularly appealing the idea of extending classic descent methods to NSO (although some elegant results for classes of nonsmooth nonconvex functions can be found in Demyanov and Rubinov (1995)). In the following remark, we highlight why most of the available NSO methods do not follow a steepest descent philosophy.
Remark 1
Let \(\mathbf {x} \in {\mathbb {R}}^n\) be given, and assume there exists a descent direction at \(\mathbf {x}\). The steepest descent direction \(\mathbf {d}^*\) at \(\mathbf {x}\) is the one where the directional derivative is minimized over the unit ball, i.e.,
We observe that \(\mathbf {d}^*\) is well defined both in the smooth and in the nonsmooth case. As for the former, it simply holds that \(\mathbf {d}^*= - \nabla f(\mathbf {x})/\Vert \nabla f(\mathbf {x})\Vert \). As for the latter, it holds that \(\mathbf {d}^*\) is the solution of the following minmax optimization problem
By applying the minmax-maxmin theorem it easily follows that
Hence, in the nonsmooth case, the steepest descent direction can only be determined, if the complete knowledge of the subdifferential is available, by finding the minimum norm point in a compact convex set.
As already mentioned, our review of the main classes of iterative algorithms for NSO is based on the distinction between single-point and multi-point models. In the rest of the article, we will denote by \(\mathbf {x}_k\) the estimate of a minimizer of f at the (current) iteration k. Methods based on single-point models look for the new iterate \(\mathbf {x}_{k+1}\) by only exploiting the available information on the differential properties of the function at \(\mathbf {x}_k\). Such information consist either of a single subgradient or of a larger subset of the subdifferential, possibly coinciding with the entire subdifferential. Sometimes, an appropriate metric is also associated to \(\mathbf {x}_k\). The aim is to define a local approximation of f around \(\mathbf {x}_k\) to suggest a move towards \(\mathbf {x}_{k+1}\), possibly obtained via a univariate minimization (line search).
Methods based on multi-point models exploit similar local information about \(\mathbf {x}_k\), which are enriched by data coming from several other points (typically the iterates \(\mathbf {x}_1, \ldots , \mathbf {x}_{k-1}\)), no matter how far from \(\mathbf {x}_k\) they are. Here the aim is no longer to obtain a local approximation of f, but to construct an (outer) approximation of the entire level set of f at \(\mathbf {x}_k\), that is, of the set
In the next two sections we will survey the two classes of methods. We wish, however, to remark that the intrinsic difficulty in calculating a descent direction for a nonsmooth function, suggests to look for iterative methods that do not require at each iteration decrease of the objective function. In other words, monotonicity is not necessarily a “pole star” for designing NSO algorithms (note, in passing, that also in smooth optimization the monotonicity of objective function values is not a must (Barzilai and Borwein 1988; Grippo et al. 1991)).
4 Methods based on single-point models
The focus of this section in on the celebrated subgradient method, introduced by N. Z. Shor in the early 60s of the last century, see (Shor 1962). In particular, we aim to review the convergence properties of the classic versions of the method, next giving some hints on recent improvements. In its simplest configuration the subgradient method works according to the following iteration scheme
where \(\mathbf {g}_k \in \partial f(\mathbf {x}_k)\) and \(t > 0\) is a constant stepsize. In order to develop a convergence theory it is crucial to introduce the concept of minimum approaching direction at any point \(\mathbf {x}\), as a direction along which there exist points which are closer to a minimizer than \(\mathbf {x}\). More specifically, a direction \(\mathbf {d}\) is defined as a minimum approaching direction at \(\mathbf {x}\), if there exists a positive threshold \(\bar{t}\) such that
As previously pointed out, see (6)–(8), taking an anti–subgradient direction \(\mathbf {d}=-\mathbf {g}\), for any \(\mathbf {g} \in \partial f(\mathbf {x})\), thus satisfying the condition \(\mathbf {g}^\top \mathbf {d} < 0\), does not guarantee that \(\mathbf {d}\) is a descent direction at \(\mathbf {x}\). On the other hand, it can be easily proved that such \(\mathbf {d}\) is a minimum approaching direction at \(\mathbf {x}\). In fact, for any \(\mathbf {x} \notin M^*\), the convexity of f implies that
As a consequence, by letting
from inequality (11) it follows that
for every \(t \in (0,\bar{t})\), namely, that \(\mathbf {d}=-\mathbf {g}\) is a minimum approaching direction at \(\mathbf {x}\).
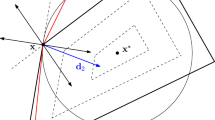
Different types of directions are depicted in Fig. 1, where the contour lines of a convex, piecewise affine function with minimum at \(\mathbf {x}^*\) are represented. Note in fact that, at point \(\mathbf {x}\), direction \(\mathbf {d}_2\) is both a descent and a minimum approaching one, since it points inside both the contour at \(\mathbf {x}\) and the sphere of radius \(\Vert \mathbf {x}-\mathbf {x}^*\Vert \) centered at \(\mathbf {x}^*\). Note also that \(\mathbf {d}_1\) is minimum approaching but not descent, while \(\mathbf {d}_3\) is descent but not minimum approaching.
In the following, taking any subgradient \(\mathbf {g} \in \partial f(\mathbf {x})\), we will indicate by \(\mathbf {d}=-\mathbf {g}\) an anti–subgradient direction, possibly normalized by setting \(\mathbf {d}=- \frac{\mathbf {g}}{\Vert \mathbf {g}\Vert }\).
The property of the anti–subgradient directions of being minimum approaching ones is crucial for ensuring convergence of the constant stepsize method based on the iteration scheme (10), as we show in the following theorem (Shor 1985).
Theorem 1
Let f be convex and assume that \(M^*\), the set of minima of f, is nonempty. Then, for every \(\epsilon >0\) and \(\mathbf {x}^* \in M^*\) there exist a point \(\bar{\mathbf {x}}\) and an index \(\bar{k}\) such that
and
Proof
Let \(U_k = \{\mathbf {x}\mid f(\mathbf {x})=f(\mathbf {x}_k)\}\) and \(L_k = \{\mathbf {x}\mid \mathbf {g}_k^\top (\mathbf {x}-\mathbf {x}_k)=0\}\) be, respectively, the contour line passing through \(\mathbf {x}_k\) and the supporting hyperplane at \(\mathbf {x}_k\) to the level set \(S_k = \{\mathbf {x} \mid f(\mathbf {x})\le f(\mathbf {x}_k)\}\), with normal \(\mathbf {g}_k\).
Consider now, see Fig. 2, \(a_k(\mathbf {x}^*)=\Vert \mathbf {x}^*-\mathbf {x}_P^*\Vert \), the distance of any point \(\mathbf {x}^* \in M\) from its projection \(\mathbf {x}_P^*\) onto \(L_k\), and observe that \(a_k(\mathbf {x}^*) \ge b_k(\mathbf {x}^*)=\Vert \mathbf {x}^*-\mathbf {x}^*_L\Vert \). Note also that \(b_k(\mathbf {x}^*)\) is an upper bound on \(dist(\mathbf {x}^*,U_k)\), the distance of \(\mathbf {x}^*\) from contour line \(U_k\). It is easy to verify that
and, as a consequence, that
Now, observe that from (10) and (13) it follows that
Next, suppose for a contradiction that \(b_k(\mathbf {x}^*) \ge \displaystyle t(1+\epsilon )/2\) for every k. Denoting by \(\mathbf {x}_1\) the starting point of the algorithm, and repeatedly applying the inequality (14), we have that for every k it holds
which contradicts \(\Vert \mathbf {x}_{k+1}-\mathbf {x}^*\Vert ^2 \ge 0\) for all k. \(\square \)
Remark 2
Note that the above theorem does not ensure that the method generates a point arbitrarily close to a minimum. In fact, it only allows to guarantee that a contour line is reached whose distance from any minimizer is arbitrarily small.
The constant stepsize subgradient method is interesting from the historical point of view but its numerical performance is strongly affected by the choice of t. Classic subgradient method (SM in the following), instead, is based on adjustable stepsize and works according to the iterative scheme
where \(\mathbf {g}_k \in \partial f(\mathbf {x}_k)\) and \(t_k > 0\). The following theorem guarantees standard convergence of SM under appropriate conditions on the stepsize \(t_k\) (Shor 1985).
Theorem 2
Let f be convex and assume that \(M^*\) is bounded and nonempty, with \(f^*=f(\mathbf {x}^*)\). If the stepsize sequence \(\{t_k\}\) in (15) satisfies the conditions
then either there exists an index \(k^*\) such that \(\mathbf {x}_{k^*} \in M^*\) or \(\lim _{k\rightarrow \infty }f(\mathbf {x}_k)=f^*\).
Remark 3
A possible choice of \(t_k\) satisfying (16) is \(t_k =\displaystyle c/k\), where c is any positive constant. The choice
known as Polyak stepsize (see Polyak 1987 for an alternative proof of convergence) is particularly popular in the area of application of nonsmooth convex optimization to solution of Integer Linear Programming (ILP) problems via Lagrangian relaxation (Gaudioso 2020). In the fairly common case when \(f^*\) is unknown, it is usually replaced in (17) by any lower bound on the optimal objective function value.
The following proposition provides an evaluation of the convergence speed of the subgradient method and an estimate of the number of iterations, under some simplifying assumptions. Detailed discussions can be found in Goffin (1977), Shor (1985).
Proposition 1
Assume that
-
(i)
f admits a sharp minimum, i.e., there exists \(\mu >0\) such that \(f(\mathbf {x}) \ge f^* + \mu \Vert \mathbf {x}-\mathbf {x}^*\Vert \), for every \(\mathbf {x} \in {\mathbb {R}}^n\), and
-
(ii)
the minimum value \(f^*\) is known, so that the Polyak stepsize (17) can be calculated.
Then, the subgradient method has linear convergence rate \(q=\sqrt{ 1- \frac{\mu ^2}{c^2}}\), where c is any upper bound on the norm of \(\mathbf {g}_k\). Moreover an \(\epsilon \)-approximate solution is achieved in \( O(\frac{1}{\epsilon ^2})\) iterations.
Proof
Note first that convexity of f implies
From (15), by adopting the Polyak stepsize (17) and taking into account (18), it follows that
hence that
The latter inequality implies boundedness of the sequence \(\{\mathbf {x}_k\}\), which in turn implies boundedness of the corresponding sequence of subgradients \(\{\mathbf {g}_k\}\), say \(\Vert \mathbf {g}_k\Vert \le c\), for every k, for some positive constant c. Taking into account assumption i) we rewrite (19) as
which proves first part of the Proposition. Next, let \( f^*_k=\min _{1 \le i \le k} f(\mathbf {x}_i)\), the best objective function value obtained up to iteration k, let \(R=\Vert \mathbf {x}_1-\mathbf {x}^*\Vert \), and observe that
From iterated application of inequality (19), for \(i=1,\ldots ,k\), since \(\Vert \mathbf {x}_{k+1}-\mathbf {x}^*\Vert \ge 0\) and \(\Vert \mathbf {g}_i\Vert \le c\), we obtain that
hence that
The latter inequality implies that an \(\epsilon \)-optimal solution is obtained in a number of iterations \(k \ge \frac{R^2c^2 }{\epsilon ^2}\) and the proof is complete. \(\square \)
Remark 4
We observe that monotonicity of the sequence \(\{f(\mathbf {x}_k)\}\) is not ensured, while the minimum approaching nature of the anti-subgradient direction is apparent from (19). On the other hand, we note that the convergence rate q can be arbitrarily close to 1.
Slow convergence of the subgradient method has stimulated several improvement attempts in more recent years. Starting from observation that the method is a black box one, as no problem structure is exploited, the newly introduced approaches have been designed for classes of weakly structured problems, still covering most of convex nonsmooth optimization programs of practical interest.
Here, we recall Nesterov’s smoothing method (Nesterov 2005), where the bound on the number of iterations improves from \( O(\frac{1}{\epsilon ^2})\) to \( O(\frac{1}{\epsilon })\). Denoting by \(S_1\) and \(S_2\) two convex and compact subsets of \(\mathbb {R}^n\) and \(\mathbb {R}^m\), respectively, the problem addressed in Nesterov (2005) is of type
with
where A is a matrix of appropriate dimension, and \(\phi : \mathbb {R}^m \rightarrow {\mathbb {R}}\) is a convex function. Note that f is convex, being the pointwise maximum of (an infinite number of) convex functions, and nonsmoothness of f occurs at those point \(\mathbf {x}\) where the maximum is not unique. In fact, smoothing of f is pursued in Nesterov (2005) by forcing such maximum to be unique. In particular, the following perturbation \(f_{\mu }\) of f is introduced
where \(\mu >0\) is the perturbation parameter, and \(\omega :\mathbb {R}^m \rightarrow \mathbb {R}\) is a strongly convex continuously differentiable function, i.e., for every \(\mathbf {v} \in {\mathbb {R}}^m\) it satisfies the condition
for some \(\sigma >0\). Minimization of the smooth function \(f_{\mu }(\mathbf {x})\) is then pursued via a gradient-type method (see also Frangioni et al. 2018 for a discussion on tuning of the smoothing parameter \(\mu \).)
The Mirror Descent Algorithm (MDA) Nemirovski and Yudin (1983) is yet another method inspired by SM. We give here its basic elements, following the presentation of Beck and Teboulle (2003), and confine ourselves to treatment of the unconstrained problem (1). Consider the following iteration scheme for passing from \(\mathbf {x}_k\) to \(\mathbf {x}_{k+1}\), once an oracle has provided both \(f(\mathbf {x}_k)\) and \(\mathbf {g}_k \in \partial f(\mathbf {x}_k)\),
where \(\gamma _k>0\). Simple calculation provides
which coincides with (15) when \( \gamma _k=\frac{t_k}{\Vert \mathbf {g}_k\Vert }\). Note that \(\mathbf {x}_{k+1}\) is obtained as the minimizer of the linearization of f rooted at \(\mathbf {x}_k\), augmented by a proximity term which penalizes long steps away from \(\mathbf {x}_k\), on the basis of the proximity parameter \(\gamma _k\). Now consider, as in previous Nesterov’s method, any strongly convex continuously differentiable function \(\omega :\mathbb {R}^n \rightarrow \mathbb {R}\) and let
Function \(\alpha _{k}(\mathbf {x})\) measures the error at \(\mathbf {x}\) associated to the linearization of \(\omega \) rooted at \(\mathbf {x}_k\), and resumes information about the curvature of \(\omega \) along the direction \((\mathbf {x}-\mathbf {x}_k)\). Moreover \(\alpha _{k}\) can be considered as a distance-like function, since strong convexity of \(\omega \) implies \(\alpha _{k}(\mathbf {x})>0\) for \(\mathbf {x} \ne \mathbf {x}_k\). On the basis of the definition of \(\alpha _{k}\) the iterative scheme (22) is generalized by setting:
Note that, letting \(\omega (\mathbf {x})=\frac{1}{2 }\Vert \mathbf {x}\Vert ^2\), it is easy to verify that
and the two iterative schemes (22) and (24) coincide. Hence, we conclude that the SM iteration scheme (22) is a special case of (24) which is, in fact, MDA (see Beck and Teboulle 2003). The function \(\alpha _k\) is usually referred to as a Bregman-like distance generated by function \(\omega \).
5 Methods based on multi-point models
As previously mentioned, here we deal with those iterative methods for NSO where the next iterate \(\mathbf {x}_{k+1}\) is calculated on the basis of information related to both the current iterate \(\mathbf {x}_k\) and to several other points (e.g., previous estimates of an optimal solution).
The fundamental leverage in constructing such class of methods is that a convex function is the pointwise supremum of affine ones, namely, for any convex function \(f: {\mathbb {R}}^n \rightarrow {\mathbb {R}}\) and every \(\mathbf {x} \in {\mathbb {R}}^n\) it holds that
where \(\mathbf {g}(\mathbf {y}) \in \partial f(\mathbf {y})\), see (Hiriart-Urruty and Lemaréchal (1993), Th. 1.3.8). The latter formula has some relevant consequences. In fact, taking any finite set of points \(\mathbf {x}_1,\mathbf {x}_2, \ldots , \mathbf {x}_k \in {\mathbb {R}}^n\), letting
for every \(i \in \{1,\ldots ,k\}\), with \(\mathbf {g}_i \in \partial f(\mathbf {x}_i)\), and defining
it holds that
Thus, function \(f_k\) is a global approximation of f, as it minorizes f everywhere, while interpolating it at points \(\mathbf {x}_1, \ldots , \mathbf {x}_k\). Note, in addition, that \(f_k\) is convex and piecewise affine, being the pointwise maximum of the affine functions \(\ell _i(\mathbf {x})\), the linearizations of f rooted at \(\mathbf {x}_1, \ldots , \mathbf {x}_k\). We observe in passing that, even for the same set of points \(\mathbf {x}_1, \ldots , \mathbf {x}_k\), the model function \(f_k\) can be not unique, since the subdifferential \(\partial f(\cdot )\) is a multifunction. In the following, we will refer to \(f_k\) as to the cutting plane function, a term which deserves some explanation.
Consider the epigraph of f, namely, the subset of \({\mathbb {R}}^{n+1}\) defined as
and define the set of halfspaces \(H_i \subset {\mathbb {R}}^{n+1}\), for every \(i \in \{1,\ldots ,k\}\):
Observing that for every \(\mathbf {x} \in {\mathbb {R}}^n\) there holds
and that
it is easy to see that \(\big (\mathbf {x}, f(\mathbf {x})\big ) \in \bigcap _{i=1}^k H_i\) and, consequently, that
Now take any point \(\mathbf {x}_{k+1}\) such that \(f(\mathbf {x}_{k+1})>f_k(\mathbf {x}_{k+1})\), define the corresponding halfspace
and the new approximation
Observe that, while \(\big (\mathbf {x}_{k+1},f_k(\mathbf {x}_{k+1})\big ) \in epi f_k\), we have \(\big (\mathbf {x}_{k+1},f_k(\mathbf {x}_{k+1})\big ) \notin epi f_{k+1}\) and
In other words, the hyperplane
separates point \(\big (\mathbf {x}_{k+1},f_k(\mathbf {x}_{k+1})\big )\) from \(epi f_{k+1}\), thus it represents a cut for \(epi f_{k}\). Note that the bigger is the difference \(f(\mathbf {x}_{k+1}) -f_k(\mathbf {x}_{k+1})\), the deeper is the cut defined by \(L_{k+1}\), see Fig. 3. The definition of the cutting plane function \(f_k\) provides a natural way to select the next trial point by setting
which is exactly the iteration scheme of the classic cutting plane method, see (Cheney and Goldstein 1959; Kelley 1960). Problem (30) is still nondifferentiable, but it is equivalent to the following linear program, defined in \({\mathbb {R}}^{n+1}\), thanks to the introduction of the additional scalar variable w
whose optimal solution is denoted by \((\mathbf {x}_{k+1}, w_k)\), with \(w_k=f_k(\mathbf {x}_{k+1}\)). Note that, since the feasible region is the nonempty set \(epi f_k\), boundedness of (31) requires feasibility of its dual which, denoting by \(\varvec{\lambda } \in {\mathbb {R}}^k\) the vector of dual variables, can be formulated as the following program
We observe that feasibility of (32) is equivalent to the condition
Hence, the boundedness of problem (31), which allows to calculate \(\mathbf {x}_{k+1}\), requires a kind of hard-to-test qualification of points \(\mathbf {x}_1, \ldots ,\mathbf {x}_k\), expressed in terms of the corresponding subgradients. We show in Fig. 4 an example where the cutting plane function is unbounded since the derivatives \(f'(\mathbf {x}_1)\) and \(f'(\mathbf {x}_2)\) are both negative, thus \(0 \notin [f'(\mathbf {x}_1),f'(\mathbf {x}_2) ]\)).
To avoid the difficulties related to possible unboundedness of the cutting plane function, we put the original problem (1) in an (artificial) constrained optimization setting. In fact, we consider the problem
where Q is a nonempty compact convex subset of \({\mathbb {R}}^{n}\). One would think of Q as a set defined by simple constraints (e.g., box constraints) and sufficiently large to contain \(M^*\). We further assume that for each \(\mathbf {x} \in Q\) both the objective function value \(f(\mathbf {x})\) and a subgradient \(g\in \partial f(\mathbf {x})\) can be computed. We also let \(L_Q\) denote the Lipschitz constant of f on Q. Thus, the cutting-plane iteration becomes
whose well-posedness is guaranteed by the continuity of \(f_k\), together with compactness of Q. Moreover, we note that, since by convexity \(f_k(\mathbf {x}) \le f(\mathbf {x})\) for every \(\mathbf {x} \in Q\), the optimal value \(f_{k}^{*}\) of \(f_k(\mathbf {x})\) provides a lower bound on \(f^*\), the optimal value of f. In addition, since
the sequence \( \{f_{k}^{*} \}\) is monotonically nondecreasing and thus the lower bound becomes increasingly better.
We state now the convergence of a slightly more general cutting plane-like method, presented in Algorithm 1, which comprises the classic version where the iteration scheme (35) is adopted, see (Polyak 1987).

We note that \(f_k(\mathbf {x}) \le f(\mathbf {x})\), for every \(\mathbf {x} \in {\mathbb {R}}^n\), ensures that selection of \(\mathbf {x}_{k+1}\) as in (35) perfectly fits with the condition \(\mathbf {x}_{k+1} \in S_k^*\) at Step 2 of GCPM. The rationale of the definition of \(S_k^*\) is to take \(\mathbf {x}_{k+1}\) well inside into the level set of \(f_k\). This allows to accommodate, at least in principle, possible inexact solution of the program
which is still linear provided Q has a polyhedral structure. GCPM with \(\mathbf {x}_{k+1}\) selected as in (35) will be simply referred in the following as Cutting Plane Method (CPM).
Remark 5
GCPM is an intrinsically nonmonotone method as no objective function decrease is guaranteed at each iteration
The proof of the convergence of Algorithm 1 is rather simple and relies on convexity of f and on compactness of Q.
Theorem 3
GCPM terminates at an \(\epsilon \)-optimal point.
Proof
We observe first that, since \(f_k(\mathbf {x}_{k+1)} \le f^*\), satisfaction of the stopping condition at Step 3 of GCPM implies that
i.e., that the point \(\mathbf {x}_{k+1}\) is \(\epsilon \)-optimal. Now, assume for a contradiction that the stopping condition is not satisfied for infinitely many iterations and, consequently, that
holds for every k. Convexity of f, along with (37) and (25), ensure that the following inequalities hold for every \( i \in \{1,\dots ,k\}\)
which imply
A consequence of (38) is that the sequence of points generated by the algorithm does not have an accumulation point, which contradicts compactness of Q. \(\square \)
While cutting plane method represents an elegant way to handle convex optimization, it exhibits some major drawbacks. We observe first that the convergence proof is based on the hypothesis of infinite storage capacity. In fact, the size of the linear program to be solved increases at each iteration as consequence of the introduction of a new constraint. A second drawback of the method is related to its numerical instability. In fact, not only monotonicity of the sequence \(\{f(\mathbf {x}_k)\}\) is not ensured (this being a fairly acceptable feature of the method, though) but it may happen that after the iterate sequence gets to points very close to the minimizer, some successive iterate points might roll very far away from it, as we show in the following simple example.
Example 1
Consider the one-dimensional quadratic program \(\min \{\frac{1}{2} x^2: x \in {\mathbb {R}}\}\), whose minimizer is \(x^* = 0\). Assume that \(k=2\), let \(x_1=-1\) and \(x_2=0.01\), with point \(x_2\) being rather close to the minimizer. It is easy to verify that \(x_3= \arg \min \{f_2(x): x \in {\mathbb {R}}\}=-0.495\), with the algorithm jumping to a point whose distance from the minimizer is much bigger than 0.01. Illustrative examples of such poor behavior of the method can be found in (Hiriart-Urruty and Lemaréchal (1993), Chapter XV.1).
5.1 Bundle methods (BM)
Bundle methods are a family of algorithms originating from the pioneering work by Lemaréchal (1975). They can be considered as a natural evolution of CPM which provides an effective answer to the previously mentioned drawbacks. The term bundle is meant to recall that, similarly to CPM, at each iteration a certain amount of cumulated information about points scattered throughout the function domain is necessary to create a model-function, whose minimization delivers the new iterate. In particular, we denote by \(B_k\) the bundle of the cumulative information available at iteration k, where \(B_k\) is the following set of point/function/subgradient triplets
In bundle methods, however, one among points \(\mathbf {x}_i\) is assigned the special role of stability center. One may think of such point as the best in terms of objective function value, but this is not strictly necessary. In the following, we will denote by \(\overline{\mathbf {x}}_k\) the current stability center, singled out from the set of iterates \(\{\mathbf {x}_1\ldots \mathbf {x}_k\}\). Adopting a term commonly used in discrete optimization, it will be referred to as the incumbent, \(f(\overline{\mathbf {x}}_k)\) being the incumbent value.
Once the stability center \(\overline{\mathbf {x}}_k\) has been fixed, the change of variables \(\mathbf {x}=\overline{\mathbf {x}}_k+\mathbf {d}\) is introduced. It expresses every point of function domain in terms of its displacement \(\mathbf {d} \in {\mathbb {R}}^n\) with respect to the stability center, and allows to rewrite the cutting plane function \(f_k(\mathbf {x})\) in the form of difference function as
where \(\alpha _i\), for every \(i \in \{1,\ldots ,k\}\), is the linearization error, see (23), associated to the affine expansion \(\ell _i(\mathbf {x})\) at \(\overline{\mathbf {x}}_k\), and is defined as
Note that convexity of f guarantees nonnegativity of the linearization error. Moreover, for every \(\mathbf {x} \in {\mathbb {R}}^n\) and \(i \in \{1,\ldots ,k\}\), since \(\mathbf {g}_i \in \partial f(\mathbf {x}_i)\), it holds that
i.e.,
The latter property, often referred to as subgradient transport, is both conceptually and practically important; it indicates that even points which are far from the stability center provide approximate information on its differential properties.
Note also that points \(\mathbf {x}_i\) do not play any role in the difference function (39), thus the bundle \(B_k\), instead of triplets, can be considered as made up of couples as follows
Note that the definition of the linearization errors is related to the current stability center. In case a new one is selected, say \(\overline{\mathbf {x}}_{k+1}\), the \(\alpha _i\) need to be updated. In fact, denoting by \(\alpha _i^+\), for each \(i \in \{1,\ldots ,k\}\), the new linearization errors updated with respect to \(\overline{\mathbf {x}}_{k+1}\), it is easy to obtain the following update formula
which is independent of the explicit knowledge of points \(\mathbf {x}_i\).
Under the transformation of variables introduced above, problem (31) becomes
whose optimal solution \((\mathbf {d}_k,v_k)\) is related to the optimal solution \((\mathbf {x}_{k+1},w_k)\) of (31) by the relations:
Note that from nonnegativity of the linearization errors it follows that the point \((\mathbf {d},v)=(\mathbf {0},0)\) is feasible in (44), hence \(v_k \le 0\) represents the predicted reduction returned by the model at point \(\mathbf {x}_{k+1}=\overline{\mathbf {x}}_k+\mathbf {d}_k\).
Bundle methods elaborate on CPM as they ensure:
-
(i)
Well-posedness of the optimization subproblem to be solved at each iteration;
-
(ii)
Stabilization of the next iterate.
A conceptual and very general scheme of a bundle method is now given, aiming at highlighting the main differences with CPM.

The schema of Algorithm 2 provides just the backbone of most bundle methods, as it leaves open a number of algorithmic decisions that can lead to fairly different methods. In fact, the body of literature devoted to BM is huge, as a vast number of variants have been proposed over time by many scientists, in order to implement such decisions. We postpone to Sect. 9 some bibliographic notes.
We give in the following a general classification of bundle methods, mainly based on the different variants of the subproblem (44) to be solved at Step 3, in order to satisfactorily deal with the aforementioned issues of well-posedness and stabilization. The approaches are substantially three:
-
Proximal BM;
-
Trust region BM;
-
Level BM.
They share the same rationale of inducing some limitation on the distance between two successive iterates \(\mathbf {x}_{k+1}\) and \(\mathbf {x}_k\) gathering, at the same time, well-posedness and stability with respect to CPM. As it will be clarified in the following, the actual magnitude of such limitation is controlled by an approach-specific parameter (to be possibly updated at each iteration). Its appropriate tuning is the real crucial point affecting numerical performance of all BM variants.
For a better understanding of the impact on the performance of the stabilization strategies, we report the results of an instructive experiment described in Frangioni (2020). For a given nonsmooth optimization problem, the Lagrangian dual of a Linear Program, the minimizer \(\mathbf {x}^*\) has been first calculated by standard CPM. Then, such an optimal point has been given as the starting point both to standard CPM and to a variant of CPM equipped with a constraint of the type \(\Vert \overline{\mathbf {x}}_{k} + \mathbf {d}-\mathbf {x}^*\Vert _{\infty } \le \varDelta \), for different values of \(\varDelta \). In Table 1, for decreasing values of \(\varDelta \), the ratio between the number of iterations upon termination of the modified CPM, \(N_{it}^{\varDelta }\), and that of the standard CPM, \(N_{it}\), is reported. The impressive effect of making more and more stringent the constraint on distance of two successive iterates is apparent.
5.1.1 Proximal BM (PBM)
The proximal point variant of BM is probably the one that attracted most of the research efforts. It has solid theoretical roots in both the properties of the Moreau-Yosida Regularization (Hiriart-Urruty and Lemaréchal 1993) and Rockafellar’s Proximal Point Algorithm (Rockafellar 1976). In such class of methods the variant of subproblem (44), to be solved at Step 3 of Algorithm 2, is
where \(\gamma _k>0\) is the adjustable proximity parameter. The latter problem can be rewritten, taking into account (39), in an equivalent unconstrained form as
hence it has a unique minimizer as a consequence of strict convexity of the objective function.
It is worth observing that in PBM the subproblem (45) is a quadratic program (QP), whose solution can be found either by applying any QP algorithm in \({\mathbb {R}}^n\), or by working in the dual space \({\mathbb {R}}^k\). In fact, the standard definition of Wolfe’s dual for problem (45) is
where \(\varvec{\lambda } = (\lambda _1,\ldots ,\lambda _k)^\top \) is the vector of dual variables (or multipliers), and \(\mathbf {e}\) is a vector of ones of appropriate size. Taking into account that
it is possible to eliminate \(\mathbf {d}\) and to restate the dual of problem (45) as follows:
Letting \((\mathbf {d}_k,v_k)\) and \(\varvec{\lambda }^{(k)}\) be, respectively, optimal solutions to (45) and (48), the following relations hold:
and
which allow to equivalently solve either problem (45) or problem (48) at Step 3 of the Conceptual BM. Note that \(\mathbf {d}_k\) is the opposite of a (scaled) convex combination of the \(\mathbf {g}_i\)s, and it reduces to the anti-subgradient with stepsize \(\frac{1}{\gamma _k}\) in case the bundle is the singleton \(\{ (\mathbf {g}_k,0)\}\), where \(\mathbf {g}_k \in \partial f(\overline{\mathbf {x}}_k)\).
Working in the dual space is, in general, preferred for both practical and theoretical reasons. In fact, problem (48) has a nice structure, being the minimization of a convex quadratic function over the unit simplex, for which powerful ad hoc algorithms are available in the literature (e.g., Kiwiel 1986; Monaco 1987; Frangioni 1996). On the other hand, relations (49)-(50) provide the theoretical basis for possibly certifying (approximate) optimality of the current stability center at Step 4 of Conceptual BM. Let \(\mathbf {g}(\varvec{\lambda })= \sum _{i=1}^k \lambda _i^{(k)} \mathbf {g}_{i}\) and suppose the following holds
for some small \(\epsilon >0\). Thus, from (49)–(50) it follows that
and
Moreover, condition (52), taking into account (42), implies that
i.e., \(\mathbf {g}(\varvec{\lambda })\) is in the \(\epsilon \)-subdifferential of f at \(\overline{\mathbf {x}}_k\). On the other hand, condition (51) provides an upper bound on the norm of \(\mathbf {g}(\varvec{\lambda })\) and hence, taking into account the inequality (4) and letting \(\delta =\sqrt{\gamma _k \epsilon }\) we obtain
which can be interpreted as an approximate optimality condition at point \(\overline{\mathbf {x}}_k\), provided that \(\delta \) is not too big. Note, however, that the magnitude of \(\delta \), once \(\epsilon \) has been fixed, depends on the adjustable proximity parameter \(\gamma _k\) and, consequently, (53) is a sound approximate optimality condition only if the sequence \(\{\gamma _k\}\) is bounded from above. Such condition is intuitively aimed at avoiding shrinking of the model around \(\overline{\mathbf {x}}_k\), which would lead to both a very small \(\mathbf {d}_k\) and to an artificial satisfaction of the condition \(v_k \ge - \epsilon \). A complementary reasoning suggests to keep the sequence \(\{\gamma _k\}\) bounded away from zero, in order for the algorithm to avoid behaving in a way very similar to standard CPM.
We have described, so far, the two possible outcomes from solving at Step 3 of Algorithm 2 problem (45) or, better, problem (48). In fact, in the PBM approach a significant displacement \(\mathbf {d}_k\) is obtained if \(v_k < - \epsilon \), while termination occurs in the opposite case when \(v_k \ge - \epsilon \).
Now suppose that Step 6 has been reached, the point \( \overline{\mathbf {x}}_k+\mathbf {d}_k\) being available as a possible candidate to become the new stability center. The predicted reduction at such point is \(v_k\), which is to be compared with the actual reduction \(f(\overline{\mathbf {x}}_k+\mathbf {d}_k)-f(\overline{\mathbf {x}}_k)\). Reasonable agreement between the two values indicates that the current cutting plane model is of good quality. Since at this stage \(v_k < -\epsilon \), the agreement test at Step 8 is generally aimed at verifying that the actual reduction is just a fixed fraction of the predicted one, as shown in the following inequality
where \(m \in (0,1)\) is the sufficient decrease parameter. Hence, (54) also plays the role of the sufficient decrease condition to be checked at Step 9. In fact, if condition (54) is fulfilled, the algorithm can proceed through Steps 10 to 13, where the stability center is updated by setting \(\overline{\mathbf {x}}_{k+1}=\overline{\mathbf {x}}_k+\mathbf {d}_k\) and a new iteration starts after updating the bundle. Such an exit is usually referred to as Serious Step. If, instead, there is poor agreement between actual and predicted reduction (i.e., a sufficient decrease has not been attained), it holds
and two possible implementations of the Conceptual BM are available, depending on whether or not a line search strategy is adopted.
In case no line-search approach is embedded in the algorithm, Conceptual BM proceeds to Steps 15 to 18, as the attempt to find a better stability center failed, and the stability center remains unchanged (i.e., a Null Step has occurred). Letting \(\mathbf {x}_{k+1}=\overline{\mathbf {x}}_k+\mathbf {d}_k\), the new couple \((\mathbf {g}_{k+1}, \alpha _{k+1})\) is joined to the bundle, where \(\mathbf {g}_{k+1}\in \partial f(\mathbf {x}_{k+1})\), and \(\alpha _{k+1}= f(\overline{\mathbf {x}}_k)-f(\mathbf {x}_{k+1})+\mathbf {g}_{k+1}^\top \mathbf {d}_k\).
In case a line-search strategy is adopted, the algorithm remains at Step 8, \(\mathbf {d}_k\) is taken as a search direction and a line search (LS) is executed by checking at points \(\overline{\mathbf {x}}_k+t\mathbf {d}_k\), with \(t \in (0,1]\), the objective function sufficient decrease condition
skipping to Step 15 as soon as t falls below a given threshold \(\eta \in (0,1)\). Checks are performed for decreasing values of t, starting from \(t=1\), according to classic Armijo’s rule (Armijo 1966).
Detailed presentation of nonsmooth LS algorithms (that is, the minimization of a nonsmooth function of one variable) is beyond the scope for this paper. We wish, however, to point out the fundamental difference between the smooth and the nonsmooth case. In the former case, once at any point \(\mathbf {x}\) a search direction \(\mathbf {d}\) is given within a descent algorithm, a trusted model, constituted by the negative directional derivative along \(\mathbf {d}\) is available. It ensures that there exists a positive threshold \(\bar{t}\) such that \(f(\mathbf {x}+t\mathbf {d}) < f(\mathbf {x})\), for every \(t \in (0,\bar{t})\). In the nonsmooth framework, instead, the cutting plane model is “untrusted”, to recall the evocative term used in Frangioni (2020). In fact, in the Conceptual BM the directional derivative at \(\overline{\mathbf {x}}_k\) along \(\mathbf {d}_k\) is not necessarily known, since \(v_k\) is just an approximation. Thus, the possibility that \(\mathbf {d}_k\) is not a descent direction has to be accommodated by the algorithm.
We have now completed the discussion on the two possible implementations of Step 8 within the proximal version of Conceptual BM. We observe that null step is a result which can occur in both cases. It corresponds to the fact that the cutting plane has revealed a poor approximation of the objective function. Consequently, whenever a null step occurs, the stability center remains unchanged, and a new couple subgradient/linearization-error is added to the bundle, with the aim of improving the model. As for the latter, some explanations are in order. Consider, for an example, the null-step occurring when
with no line search performed. In such a case, after generating the new iterate \(\mathbf {x}_{k+1}=\overline{\mathbf {x}}_{k}+\mathbf {d}_k\), the couple \(\big (\mathbf {g}_{k+1}, \alpha _{k+1}\big )\) is appended to the bundle, where \(\mathbf {g}_{k+1} \in \partial f(\mathbf {x}_{k+1})\) and \(\alpha _{k+1} = f(\overline{\mathbf {x}}_{k})-f(\mathbf {x}_{k+1})+\mathbf {g}_{k+1}^\top \mathbf {d}_{k}\). The updated model in terms of difference function, see (39), becomes
Observe that, for \(\mathbf {d}=\mathbf {d}_k\) there hold
and
which combined means that the updated model provides a more accurate estimate of the objective function f, at least around point \(\mathbf {x}_{k+1}\). Perfectly analogous considerations can be made in case a line search scheme is adopted at Step 8.
We have presented, so far, some general ideas on how the Conceptual BM works in case the proximal approach is adopted. We do not enter into the details of convergence proofs, which depend on the different strategies adopted at various steps. We only wish to sketch how a typical convergence proof works, under the assumptions that f has a finite minimum, that the proximity parameter \(\gamma _k\) stays within a range \(0 < \gamma _{min} \le \gamma _k \le \gamma _{max}\), possibly being adjusted upon modification of the stability center only. As already mentioned, such tuning is a crucial issue in view of granting numerical efficiency to the method.
The proof is based on the following three facts:
-
(a)
The objective function reduction, every time the stability center is updated, is bounded away from zero. This is a consequence of \(v_k < -\epsilon \) and of the sufficient decrease condition (54), in case no line search strategy is adopted. Whenever, instead, a line search is performed, objective function reduction is still bounded away from zero as a consequence, again, of \(v_k < -\epsilon \), of condition (55), and of the lower bound \(\eta \) on the stepsize length t.
-
(b)
Since it has been assumed that the function has finite minimum, from a) it follows that only a finite number of stability center updates may take place.
-
(c)
The Conceptual BM cannot loop infinitely many times through Step 18, that is an infinite sequence of null steps cannot occur. To prove this fact it is necessary to observe that, being the proximity parameter constant by assumption, the sequence \(\{v_k\}\) is monotonically increasing, see (58), and bounded from above by zero, hence it is convergent. The core of the proof consists in showing that \(\{v_k\} \rightarrow 0\) and, consequently, the stopping test \(v_k \ge -\epsilon \) is satisfied after a finite number of null steps.
5.1.2 Trust region BM (TBM)
The approach consists in solving at Step 3 of the Conceptual BM the following variant of problem (44), obtained through the addition of a trust region constraint
where \(\varDelta _k > 0\). Well-posedness is a consequence of continuity of the objective function, problem (60) being in fact a finite min-max, and compactness of the feasible region.
A first issue about the statement of problem (60) is the choice of the norm in the trust region constraint. It is in general preferred to adopt the \(\ell _1\) or the \(\ell _{\infty }\) norm, so that (60) is still a Linear Program. A second relevant point is the setting of the trust region parameter. Intuitively, \(\varDelta _k\) must not be too small, which would result in slow convergence due to shrinking of the next iterate close to the stability center. On the other hand, a too large \(\varDelta _k\) would kill the stabilizing effect of the trust region. A simple approach is to provide two thresholds \(\varDelta _{min}\) and \(\varDelta _{max}\), letting \(\varDelta _k \in [\varDelta _{min}, \varDelta _{max}]\). Such choice is necessary to guarantee convergence of the algorithm, but the type of heuristics adopted for tuning \(\varDelta _k\) within the prescribed interval strongly affects both convergence and the overall performance of the algorithm (see the discussion about the effect of the proximity parameter \(\gamma _k\) in PBM).
Also for the trust region approach the two classes of variants, with or without line search, can be devised. Moreover, the interplay serious-step/null-step is still embedded into the conceptual scheme.
5.1.3 Proximal level BM (PLBM)
The level set approach to BM stems from the general setting of CPM we gave earlier in this section, where point \(\mathbf {x}_{k+1}\) calculated at Step 2 of GCPM was not necessarily a minimizer of \(f_k\), convergence being ensured provided it was sufficiently inside the level set of function \(f_k\) at point \(\mathbf {x}_k\).
The approach consists in finding the closest point to the current stability center \(\overline{\mathbf {x}}_k\) where the difference function (39) takes a sufficiently negative value. In fact, problem (44) is modified as follows
where the adjustable parameter \(\theta _k >0\) indicates the desired reduction in the cutting plane function. In fact, letting, as usual, the stability center \(\overline{\mathbf {x}}_k\) be the incumbent, and denoting by \(\mathbf {d}_k\) the optimal solution of (61), the point \(\mathbf {x}_{k+1}=\overline{\mathbf {x}}_k+\mathbf {d}_k\) belongs to the following level set
of the cutting plane function \(f_k\). Note that an appropriate choice of \(\theta _k\) provides the required stabilization effect, as a small value of \(\theta _k\) results in small \(\Vert \mathbf {d}_k\Vert \).
The approach is known as Proximal Level Bundle Method (PLBM) and indeed the setting of \(\theta _k\) is the key issue to address. To this aim, the optimal value of the model function \(f_k\), say \(f_k^*\), is required. Consequently, we stay in the same constrained context (34) adopted in stating CPM, so that problem
is well posed, being the convex set Q nonempty and compact. Since the incumbent value \(f_k(\overline{\mathbf {x}}_k)\) and \(f^*_k\) are, respectively, an upper and a lower bound on \(f^*\), it is quite natural to set \(\theta _k\) on the basis of the gap
which is a nonincreasing function of the bundle size k. A possible choice is to set \(\theta _k=\mu \varGamma (k)\), for some \(\mu \in (0,1)\), but modifications of such criterion are to be accommodated on the basis of comparison with the previous value of the gap. Note that \(\varGamma (k) \le \epsilon \) provides an obvious stopping criterion for PLBM, since from \(f_k(\overline{\mathbf {x}}_k)=f(\overline{\mathbf {x}}_k)\) it follows that \(f(\overline{\mathbf {x}}_k)-f^* \le \varGamma (k)\). In terms of the Conceptual BM, Step 8 is neglected, and the test at Step 9, for possibly updating the stability center, is based on the simple reduction of the incumbent value. As for method implementation, further observations are in order.
-
Compared to PBM and TBM, setting of \(\theta _k\) appears definitely more amenable than choosing \(\gamma _k\) and \(\varDelta _k\), respectively, as it simply refers to function values, while \(\gamma _k\) and \(\varDelta _k\) are meant to capture some kind of second order behavior of f, an ambitious and fairly hard objective.
-
Unlike PBM and TBM, two distinct optimization subproblems are to be solved at each iteration: the quadratic problem (61), which consists in projecting \(\overline{\mathbf {x}}_k\) onto \(S_k(\theta _k)\), and (62), which is a linear program, in case Q has a simple structure (e.g., it is a hyper-interval).
The following theoretical result, see (Lemaréchal et al. (1995), Th. 2.2.2), provides a bound on the number of iterations needed to get an \(\epsilon \)-approximate solution.
Theorem 4
Let \(L_Q\) be the Lipschitz constant of f on Q, denote by D the diameter of Q, and by c a constant depending on parameter \(\mu \). For any given \(\epsilon >0\) it holds that
5.2 Making BM implementable
The algorithms we have described in this section suffer from a major drawback. They are all based on unlimited accumulation of information, in terms of number of generated linearization or, equivalently, of bundle size. Convergence properties we have discussed are in fact valid under such hypothesis. This makes such methods, at least in theory, not implementable. In the sequel, focusing in particular on PBM, we briefly review two strategies to overcome such difficulty, introduced in Kiwiel (1983), Kiwiel (1985), named subgradient selection and aggregation, respectively.
The strategies are both based on thorough analysis of the dual formulation (48) of the problem to be solved at Step 3 of Conceptual BM. Observe, in fact, that strict convexity of problem (45) ensures that the optimal solution \(\mathbf {d}_k\) is unique and it is a (scaled) convex combination of the \(\mathbf {g}_i\)s, see (49). Note also that the optimal solution of the dual (48) is not necessarily unique, but there exists (by Carathéodory’s Theorem) a set of at most \(n+1\) optimal dual multipliers \(\lambda _i^{(k)} > 0\), \(i \in I_k\), \(|I_k| \le n+1\) such that
They can be calculated, in fact, by finding an optimal basic solution of the following linear program
which is characterized by \((n+1)\) constraints.
On the basis of previous observation there is an obvious possibility, once such set of subgradients has been detected, to select the corresponding bundle couples and to cancel the remaining ones, while the solutions of (48) and (45) remain unchanged. In this way the bundle size can be kept finite, without impairing overall convergence. It is worth noting that ad hoc algorithms for solving (48) are designed to automatically satisfy the condition that no more than \((n+1)\) subgradients are “active” in the definition of \(d_k\), so that solution of problem (63) is not necessary for subgradient selection purposes.
In many practical cases, however, \(n+1\) is still too large in view of the need of solving at each iteration the quadratic program (48) of corresponding size. In such a case, a very strong reduction in bundle size can be obtained by means of the subgradient aggregation mechanism. Once the optimal solution \(\varvec{\lambda }^{(k)}\) to (48) has been found, the aggregate couple \((\mathbf {g}_a, \alpha _a)\) is obtained by letting
In addition, define the single-constraint aggregate quadratic program
and observe that it is equivalent to the simple unconstrained quadratic problem
Hence, the optimal solution \((\mathbf {d}_a,v_a)\) to (64) coincides with the solution to (48) since it can be obtained in closed form as
and
Summing up, the aggregate problem (64) retains the fundamental properties of (48), so that, when point \(\mathbf {x}_{k+1}\) is generated, all past bundle couples \((\mathbf {g}_i, \alpha _i)\) can be replaced by the unique \((\mathbf {g}_a,\alpha _a)\), and the new couple \((\mathbf {g}_{k+1}, \alpha _{k+1})\), with \(\mathbf {g}_{k+1} \in \partial f(\mathbf {x}_{k+1})\) is added to the bundle. Under such aggregation scheme, with the bundle containing just two elements, it is possible to show convergence. Such version of proximal BM is sometimes referred to as the “poorman” bundle. Of course many other selection-aggregation schemes have been discussed in the literature. Their treatment is, however, beyond the scope of this paper.
6 Miscellaneous algorithms
In Sect. 5 we have mostly discussed about bundle methods, a family of NSO algorithms related to cutting plane, which is a model function grounded on information coming from many points spread throughout the objective function domain. Such a feature keeps bundle methods somehow apart from the smooth optimization mainstream, where most of the popular iterative methods (Gradient type, Conjugate Gradient, Newton, quasi–Newton etc.) are based on information on the objective function related to the current iterate or, sometimes, also to the previous one. Several scientists have thus tried to convey to NSO, and in particular to cutting-plane based area, some ideas coming from smooth optimization, upon appropriate modifications to cope with nonsmoothness. In this section we briefly survey some of such attempts.
6.1 Variable metric
In discussing the proximal BM we have already observed that tuning of the proximity parameter \(\gamma _k\) in problem (45) has a strong impact on the numerical performance of such class of algorithms. The problem has been addressed by many authors (see, e.g., Kiwiel 1990) and several heuristic techniques are available. More in general, setting of \(\gamma _k\) is related to the attempt of capturing some kind of second order approximation of the objective function. After all, the quadratic term \(\frac{1}{2}\gamma _k\Vert \mathbf {d}\Vert ^2\), in case f is twice differentiable, would be seen as a single–parameter positive definite approximation \(\gamma _k I\) of the Hessian at point \(\overline{\mathbf {x}}_k\), I being the identity matrixFootnote 1.
Thus, the simplest idea, see (Lemaréchal 1978), is to replace (45) with the following problem
where \(B_k\) is a positive definite matrix in \({\mathbb {R}}^{n \times n}\) to be updated any time the stability center changes, according to some rule inspired by the Quasi–Newton updates for smooth minimization. We recall that in all Quasi–Newton methods the Hessian (or its inverse) approximation is updated, in correspondence to the iterate \(\overline{\mathbf {x}}_k\), on the basis of the following differences in points and gradients between two successive iterates
A straightforward and practical way to adopt a Quasi-Newton approach in the nonsmooth environment would be to use any classic variable metric algorithm based on updating formulae (e.g., DFP, BFGS, etc.), with \(\mathbf {q}_k\) defined as difference of subgradients instead of gradients. Note, in passing, that due to possible discontinuities in derivatives, large \(\mathbf {q}_k\) may correspond to small \(\mathbf {s}_k\). This, however, is not a reportedly serious drawback in terms of practical applications (see classic Lemaréchal 1982 and Vlček and Luksǎn 2001 for an accurate analysis).
As a consequence of previous observation, research has focused on the definition of some differentiable object, related to f, thus suitable for application of Quasi-Newton methods. Such an object, the Moreau-Yosida regularization of f, is the function \(\phi _{\rho }:{\mathbb {R}}^n \rightarrow {\mathbb {R}}\), defined as
for some \(\rho >0\), whose minimizer is denoted by
and referred to as the proximal point of \(\mathbf {x}\), see (Rockafellar 1976). Function \(\phi _{\rho }\) enjoys the following properties:
-
The sets of minima of f and \(\phi _{\rho }\) coincide;
-
\(\phi _{\rho }\) is differentiable (see Hiriart-Urruty and Lemaréchal 1993);
-
\(\nabla \phi _{\rho }(\mathbf {x})=\rho (\mathbf {x}-p_{\rho }(\mathbf {x})) \in \partial f(p_{\rho }(\mathbf {x}))\), since at \(p_\rho (\mathbf {x})\) it is \(0 \in \partial h(\mathbf {y})\), where \(h(\mathbf {y}) = f(\mathbf {y})+ \frac{\rho }{2}\Vert \mathbf {y}-\mathbf {x}\Vert ^2\) is a strictly convex function.
The latter properties allow to find a minimum of f by solving the following (smooth) problem
Here, we note that smoothness is not gathered for free, as calculation of the new objective function \(\phi _\rho \) requires solution of a convex (nonsmooth) optimization problem.
Straightforward application of any Quasi-Newton paradigm (equipped with a line search) to minimize \(\phi _\rho \) leads to the following iteration scheme:
where \(B_k\) is the classic approximation of the Hessian, and a line search is accommodated into the iteration scheme to fix the stepsize \(t_k>0\) along the Quasi–Newton direction \(\mathbf {d}_k=- B_k^{-1} \nabla \phi _{\rho } (\overline{\mathbf {x}}_k)\)
Matrix \(B_k\) comes from updating of \(B_{k-1}\) (usually choosing \(B_1=I\)), by means of one of the effective Quasi–Newton formulae. A popular one is BFGS, according to which it is
with \(\mathbf {s}_k=\overline{\mathbf {x}}_k- \overline{\mathbf {x}}_{k-1}\) and \(\mathbf {q}_k=\nabla \phi _{\rho }(\overline{\mathbf {x}}_k)- \nabla \phi _{\rho }(\overline{\mathbf {x}}_{k-1})\). In fact, matrix \(B_k\) satisfies the secant equation
A (simplified) algorithmic scheme is reported in Algorithm 3.

The QN scheme of Algorithm 3 leaves open several relevant issues. We note first that the inner loop deals with minimization of a (strictly) convex nonsmooth function. Thus, it is quite natural to apply in such framework the machinery we have discussed in previous sections (e.g., any bundle-type algorithm would be in order). On the other hand, the idea of exactly solving at each iteration a problem of the same difficulty as the original one does not appear viable in terms of computation costs. In fact, it is appropriate to settle for an approximate solution of problem (66) in the inner loop, which results in inexact calculation of \(\overline{\mathbf {x}}_{k+1}\) as, instead of the exact optimality condition \(\rho (\overline{\mathbf {x}}_{k+1} - p_{\rho }(\overline{\mathbf {x}}_{k+1})) \in \partial f(p_{\rho }(\overline{\mathbf {x}}_{k+1})\), the approximate one \(\rho (\overline{\mathbf {x}}_{k+1} - p_{\rho }(\overline{\mathbf {x}}_{k+1})) \in \partial _{\epsilon } f(p_{\rho }(\overline{\mathbf {x}}_{k+1})\), for some \(\epsilon >0\), is enforced. We note in passing that the Quasi–Newton framework is one of the areas that have solicited the development of a convergence theory for NSO algorithms with inexact calculation of function and/or subgradient (see Sect. 7).
The need of accommodating for inexact calculation of the Moreau-Yosida regularization \(\phi _{\rho }\) (consider that also tuning of \(\rho \) is a significant issue), has also an impact on the implementation of the choice of \(\overline{\mathbf {x}}_{k+1}\) in the outer loop, irrespective of whether a line search is executed, as evoked by formula (68), or the constant stepsize \(t_k=1\) is adopted. We do not enter into the technicalities of the above mentioned issues. Possible choices are relevant in establishing the theoretical convergence rate of QN type algorithms. Discussion on such topics can be found in Bonnans et al. (1995), Lemaréchal and Sagastizábal (1997), Chen and Fukushima (1999).
6.2 Methods of centers (MoC)
We have already seen how fecund was the cutting plane idea of using many linearizations, generated all over the function domain, in order to obtain a global, not just local, model of the objective function. Yet another approach deriving from cutting plane is a class of methods known as Methods of Centres, whose connection with interior methods for Linear Programming is apparent. To explain the basic ideas it is convenient to assume a set-oriented viewpoint instead of a function-oriented one.
In solving the (constrained) problem (34), the same framework as CP (or BM) is adopted. Given the cutting plane function \(f_k\), available at iteration k, we denote by \(F_k(z_k)\) the following subset of \(\mathbb {R}^{n+1}\)
where \(z_k\) is any upper bound on the optimal value of \(f_k\) (e.g., the value of f calculated at any feasible point). The set \(F_k(z_k)\), next referred to as the localization set, is contained in \(epi f_k\), being obtained by horizontally cutting \(epi f_k\), and it contains the point \((\mathbf {x}^*, f^*)\).
The basic idea of MoC is to construct a nested sequence of sets \(F_k(z_k)\) shrinking as fast as possible around the point \((\mathbf {x}^*,f^*)\), by introducing a cut at each iteration. To obtain substantial volume reduction in passing from \(F_k(z_k)\) to \(F_{k+1}(z_{k+1})\), one looks for a central cut, i.e., a cut generated on the basis of some notion of center of \(F_k(z_k)\). Several proposals in this context can be found in the literature, stemming from Levin’s “Center of Gravity” method (Levin 1965), which is based on the property that for a given convex set C with nonempty interior, any hyperplane passing through the center of gravity generates a cut which reduces the volume of C by a factor of at least \( (1- e^{-1})\). However, such substantial reduction in the volume of \(F_k\) can only be obtained by solving the hard problem of locating the center of gravity.
Next we particularly focus on a more practical proposal, the Analytic Center Cutting Plane Method (ACCPM), see (Goffin et al. 1992, 1997; Ouorou 2009), which is based on the notion of “analytic center” introduced in Sonnevend (1985) as a point that maximizes the product of distances to all faces of \(F_k(z_k)\).
Thus, in the ACCPM the required central point of the localization set is calculated as the unique maximizer of the potential function
Once the analytic center
has been obtained, function \(f_k\) is updated thanks to the new cut generated at \(\mathbf {x}_{k+1}\), and the value \(z_k\) is possibly updated. A stopping condition is tested, which is based on the difference between the upper bound and a lower bound obtained by minimizing \(f_{k+1}\) over Q, and the procedure possibly iterated. Calculation of the analytic center can be performed by adapting interior point algorithms for Linear Programming based on the use of potential functions (see, e.g., de Ghellinck and Vial 1986). Complexity estimates of the method, with possible embedding of a proximal term in calculating the analytic center, are presented in Nesterov (1995)
Yet another possibility is to adopt, instead of the analytic center, the Chebyshëv center, defined as the center of the largest sphere contained in \(F_k(z_k)\). The approach, originally proposed in Elzinga and Moore (1975), has been equipped with a quadratic stabilizing term in Ouorou (2009).
An original approach somehow related to this area can be finally found in Bertsimas and Vempala (2004).
6.3 Gradient sampling
The fundamental fact behind most of NSO method is that satisfaction of an angle condition, that of forming an obtuse angle with a subgradient, is not enough for a direction to be a descent one. The angle condition, in fact, must be robust, that is the direction has to make an obtuse angle with many subgradients around the point. Based on this observation, and considering that for most practical problems the objective function is differentiable almost everywhere, gradient sampling algorithms have been introduced, see Kiwiel (2007), whose key feature is the evaluation of subgradient (i.e., gradient with probability 1) on a set of random points close to the current iterate. All such gradients are then used to obtain a search direction.
A sketch of an iteration of gradient sampling algorithm is reported in Algorithm 4, see (Burke et al. 2005, 2020). We do not report, for simplicity of notation, the iteration counter and thus we indicate by \(\mathbf {x}\) the current iterate. The algorithm works on the basis of two couples of stationarity/sampling-radius tolerances, the overall \((\eta , \epsilon )\) and the iteration–dependent \((\theta , \delta )\), respectively.

It can be proved that an algorithm based on the above iteration scheme provides a sequence of points \(\{\mathbf {x}_k\}\) converging to a Clarke stationary point with probability 1, unless \(f(\mathbf {x}_k) \rightarrow -\infty \). A necessary assumption is that the set of points where f is continuously differentiable is open, dense and full measure in \({\mathbb {R}}^n\), while no convexity assumption is required for ensuring convergence.
7 Inexact calculation of function and/or subgradient
We have already seen a case where it is advisable to dispose of a method for minimizing a convex function without requiring its exact calculation, see Sect. 6.1. This is a typical case in the wide application field of Lagrangian relaxation for hard ILP problems.
Next we briefly recall some basic facts, see (Gaudioso 2020). Suppose the following ILP problem is to be solved
with \( \mathbf {c} \in {\mathbb {R}}^n \), \(A \in {\mathbb {R}}^{m \times n}\), \(B \in {\mathbb {R}}^{p \times n}\), \(\mathbf {b} \in {\mathbb {R}}^m\), \(\mathbf {d} \in {\mathbb {R}}^p\), and \(\mathbb {Z}^n\) denoting the set of n-dimensional vectors. We assume that the problem is feasible and that the set
is finite, that is \(X= \{\mathbf {x}_1,\,\mathbf {x}_2, \ldots , \mathbf {x}_K\}\) and \(\mathcal {K} = \{1,2,\ldots , K \}\) is the corresponding index set.
Assume also that constraints are partitioned into two families, those defined through \(A\mathbf {x}= \mathbf {b}\) being the complicating ones. A Lagrangian relaxation of (69) is obtained by relaxing complicating constraints as follows
where \(\varvec{\lambda } \in {\mathbb {R}}^m\). Problem (70), which is still an ILP, provides an upper bound for problem (69), namely,
Moreover, denoting by \(\mathbf {x}(\varvec{\lambda }) \in \{\mathbf {x}_1,\,\mathbf {x}_2, \ldots , \mathbf {x}_K\}\) the optimal solution of (70), it holds that
\(z(\varvec{\lambda })\) being often referred to as the dual function. We note that, in case \(\mathbf {x}(\varvec{\lambda })\) is feasible (i.e., \(A\mathbf {x}(\varvec{\lambda })=\mathbf {b}\)), then it is also optimal for (69).
Aiming for the best among the upper bounds (i.e., the one closest to \(z_{I}\)), we define the Lagrangian dual problem as
\(z_{LD}\) being the best upper bound obtainable through Lagrangian relaxation.
Problem (72) consists in the minimization of a convex function defined as the pointwise maximum of K affine functions of \(\varvec{\lambda }\), one for each feasible point in X. In fact, it is a convex nonsmooth optimization problems which can be tackled by means of any of the methods described in previous sections.
Very often, once the complicating constraints have been removed, the Lagrangian relaxation is easy to solve. If this is not the case, however, any iterative NSO method which requires at each iteration its exact solution may lead to prohibitive computation time. Now suppose we are able to solve approximately the Lagrangian relaxation (70), that is, we are able to obtain for any given \(\bar{\varvec{\lambda }}\) an approximation of \(z(\bar{\varvec{\lambda }})\), say \(\tilde{z}(\bar{\varvec{\lambda }}) = z(\bar{\varvec{\lambda }})-\epsilon \), for some \(\epsilon \ge 0\). Suppose, in particular, that
for some \(\widetilde{\mathbf {x}}(\bar{\varvec{\lambda }}) \in \{\mathbf {x}_1,\,\mathbf {x}_2, \ldots , \mathbf {x}_K\}\). Hence, for every \(\varvec{\lambda } \in {\mathbb {R}}^m\) the following inequality holds
which indicates that \(\big (\mathbf {b} - A\widetilde{\mathbf {x}}(\bar{\varvec{\lambda }})\big ) \in \partial _{\epsilon } z (\bar{\varvec{\lambda }})\).
Lagrangian relaxation and corresponding solution of the (convex and nonsmooth) Lagrangian dual problem is a very common example of the general case where, in minimizing a convex function f, at any point \(\mathbf {x}\) we have at hand both an approximate value of the function \(\tilde{f}(\mathbf {x})=f(\mathbf {x})+\epsilon _f\), and an approximate subgradient \(\tilde{g}(\mathbf {x}) \in \partial _{\epsilon _g} f(\mathbf {x})\), for some positive \(\epsilon _f\) and \(\epsilon _g\). Convergence analysis of algorithms based on such an approximation has been extensively used both in subgradient (see Kiwiel 2004; D’Antonio and Frangioni 2009; Astorino et al. 2019) and in bundle methods (see Hintermüller 2001; Kiwiel 2006; de Oliveira et al. 2014; van Ackooij and Sagastizábal 2014). In particular, in de Oliveira et al. (2014) a taxonomy of possible kinds of inexactness in function and/or subgradient evaluation is provided, together with a classification of the methods. It is relevant, in fact, the distinction between cases where \(\epsilon _f\) and \(\epsilon _g\) are completely unknown and those where such errors can be estimated or, sometimes, even controlled.
8 Nonconvex NSO: a bundle view
The extension of the cutting plane idea and, consequently, of bundle methods to (local) minimization of nonconvex functions is not straightforward. In fact, in such a case it is still possible to define the convex piecewise affine function \(f_k\), exactly as in (25), provided that vectors \(\mathbf {g}_i\) are now elements of Clarke’s subdifferential \(\partial _C f(\mathbf {x})\). Nevertheless, two fundamental properties valid in the convex framework get lost:
-
it is no longer ensured that \(f_k\) is a lower approximation of f;
-
\(f_k\) does not necessarily interpolates f at points \(\mathbf {x}_i\), \(i \in \{1,\ldots ,k\}\).
If we adopt the stability center viewpoint and rewrite \(f_k\), see (39), as
it may happen that \(f_k\) does not even interpolate f at point \(\overline{\mathbf {x}}_k\), in case some \(\alpha _i\) takes a negative value, which is likely to occur since f is nonconvex. Note that such drawback is independent of the nonsmoothness assumption. Several authors, see (Kiwiel 1996; Mäkelä and Neittaanmäki 1992; Schramm and Zowe 1992), have handled it by embedding into a standard bundle scheme possible downward shifting of one or more of the affine pieces which give rise to the cutting plane function. This can be obtained by replacing the definition (40) of the linearization error \(\alpha _i\) with
for some \(\sigma >0\). Such modification, although somehow arbitrary, ensures the interpolation \(f_k(\overline{\mathbf {x}}_k)=f(\overline{\mathbf {x}}_k)\).
An alternative way to handle possibly negative linearization errors is based on the idea of bundle splitting, see (Fuduli et al. 2004; Gaudioso and Gorgone 2010). It is based on the distinction between affine pieces that exhibit a kind of convex or nonconvex behavior relative to the stability center. The approach requires a slightly different definition of the elements of the bundle, which is now
Letting \(I=\{1,\ldots ,k \}\) be the index set of \(B_k\), we introduce the partition \(I= I^+ \cup I^-\) with \(I_+\) and \(I_{-}\) defined as follows
The bundles defined by the index sets \(I_+\) and \(I_{-}\) are related to points that somehow exhibit, respectively, a “convex behavior” and a “concave behavior” with respect to \(\overline{\mathbf {x}}_k\). We observe that \(I_+\) is never empty as at least the element \((\overline{\mathbf {x}}_k, f(\overline{\mathbf {x}}_k), \mathbf {g}_k, 0, 0)\) belongs to the bundle.
The basic idea is to treat differently the two bundles in the construction of a piecewise affine model. The following two piecewise affine functions are thus defined
and
Function \(\varDelta ^+(\mathbf {d})\) is intended as an approximation to the difference function \(f(\overline{\mathbf {x}}_k+\mathbf {d}) - f(\overline{\mathbf {x}}_k)\), and interpolates it at \(\mathbf {d}=\mathbf {0}\) as it is \(\varDelta ^+(\mathbf {0})=0\), being \(k \in I_+\). On the other hand, \(\varDelta ^- (\mathbf {d})\) is a locally pessimistic approximation of the same difference function, since at \(\mathbf {d}=\mathbf {0}\) it is \(\varDelta ^-(\mathbf {0}) = \min \left\{ -\alpha _i: \, i \in I_{-}\right\} >0\). Summing up, around \(\mathbf {d}=\mathbf {0}\) (i.e., around the stability center \(\overline{\mathbf {x}}_k\)) it is
Consequently, it appears reasonable to consider significant the difference function approximation \(\varDelta ^+(\mathbf {d})\) as far as condition (75) is fulfilled. Thus, we come out with a kind of trust region model \({{\mathcal {S}}}_k\) defined as
As in all bundle methods, the building block of the double–bundle approach is the subproblem to be solved in order to find a (tentative) displacement \(\mathbf {d}_k\) from the stability center \(\overline{\mathbf {x}}_k\). Under the trust region constraint \(\mathbf {d} \in S_k\), the choice in Fuduli et al. (2004) is to solve
which, by introducing also in this case the classic proximity term, can be put in the form
We do not enter into the (rather technical) details on how subproblem above can be cast into a working bundle scheme. Implementations of the algorithm described in Fuduli et al. (2004) have been fruitfully used in many nonconvex optimization applications.
9 Bibliography, complements, and reading suggestions
We discuss, without the ambition of being exhaustive, a number of bibliographic references, some already cited throughout the paper, on various topics touched in this survey. We also open some windows on certain research sub-areas, that it has been impossible to treat for the sake of brevity. From time to time we draw the reader’s attention to some contributions we feel of particular interest.
Mathematical background Convex analysis is the well-grounded theoretical basis of numerical NSO. Cornerstone references are the (unpublished but well known) 1951 Lecture notes by W. Fenchel at Princeton Fenchel (1951), the Moreau paper Moreau (1965), Rockafellar’s “Convex Analysis” Rockafellar (1970), the book by Hiriart-Urruty and Lemaréchal (1993), which covers both theoretical and algorithmic aspects, and the books by Bertsekas (1995, 2009) and Mordukhovich (2006).
Historical Contributions Some books provide a complete view of the well advanced state of the art of numerical NSO, mainly in former Soviet Union, during the 70s of last century. Most of the successive developments have their roots there. We cite Demyanov and Malozemov book on minmax problems (Demyanov and Malozemov 1974), the book by Pshenichnyi and Danilin (1975) which covers both smooth and nonsmooth optimization, Shor’s book (Shor 1985) on subgradient method and its variants, Polyak’s complete presentation (Polyak 1987), both in deterministic and in stochastic setting, and Nemirovski and Yudin book (Nemirovski and Yudin 1983), where the complexity and efficiency issues are treated in depth. A real milestone in the development of numerical NSO was the workshop held in spring 1977 at IIASA, in Laxenburg, near to Wien, were for the first time scientists from both sides of what, at that time, was named the iron curtain had the opportunity of a long and fruitful debate. In particular, the meeting represented the starting point of a rapid development of the NSO area in western countries. The Proceedings of the workshop (Lemaréchal and Mifflin 1978) contain a number of fine contributions. To our knowledge, the term bundle method was coined by Lemaréchal in that occasion (Lemaréchal 1978) and it is very interesting to note that similar ideas, independently developed, were present in other contributions, see (Pshenichnyi 1978).
Comprehensive books and surveys Among books which give a complete overview of both theory and practice of NSO, apart the already mentioned (Hiriart-Urruty and Lemaréchal 1993), we recall here (Kiwiel 1985; Mäkelä and Neittaanmäki 1992; Shor 1998; Bagirov et al. 2020). We suggest, in particular, (Bagirov et al. 2014) for its admirable clarity. Excellent surveys are Lemaréchal (1989), Mäkelä (2002), Frangioni (2020). We also suggest the reading of Ben-Tal and Nemirovski (2001) for the original approach to convex optimization.
Subgradient methods The methods discussed in Sect. 4 were, to our knowledge, introduced in a note by N.Z. Shor (1962). From the very beginning several other scientists gave their contributions (Ermoliev 1966; Eremin 1967; Polyak 1978). As far as the classic approach is concerned, reference books, whose reading is strongly suggested, are Shor (1985), Polyak (1987). In more recent years, the interest in subgradient–type methods was renewed, thanks to the Mirror Descent Algorithm introduced by Nemirowski and Yudin (see also Beck and Teboulle 2003), and to some papers by Nesterov (2005, 2009a, 2009b) (see also the variant Frangioni et al. 2018). Very recent developments are in Dvurechensky et al. (2020). Apart from subgradient methods, we recall that also the concept of \(\epsilon \)-subdifferential has been at the basis of some early algorithms (see, e.g., Bertsekas and Mitter 1973; Nurminski 1982).
Cutting plane and bundle methods The cutting plane method stems, as already mentioned, from the seminal papers by Kelley (1960) and Cheney and Goldstein (1959), where the reader finds much more than just the description of the algorithm. A similar approach was independently devised by Levitin and Levitin and Polyak (1966). As for bundle method, fundamental references are the papers by Lemaréchal (1975) and by Wolfe (1975). The approach known as Method of Linearisations also embedding the proximity concept was independently proposed at about the same time by Pshenichnyi, see (Pshenichnyi 1970) and (Pshenichnyi and Danilin (1975), Chapter 3, §5). Since the beginning of the 80s the interest towards bundle methods has flourished within the mathematical programming community, and a large number of papers has appeared in outstanding journals. It is impossible to provide a complete list. We just mention the early papers (Lemaréchal et al. 1981; Mifflin 1982; Fukushima 1984). As examples of the use of the three stabilizing strategies described in Sect. 5.1 we recall Kiwiel’s paper (Kiwiel 1990) for a deep view on the proximal point BM; trust region BM is analysed in Schramm and Zowe (1992), with possible application also to nonconvex functions and, finally, the level bundle variant of BM, somehow already evoked in Pshenichnyi (1978), is presented in Lemaréchal et al. (1995), Brännlund et al. (1995). Apart from the three main classes of BM described in Sect. 5.1, we wish to mention some other proposals.
-
Methods based on possible decomposition of function domain into a subspace where the function is smooth, while nonsmoothness is confined into the orthogonal subspace, see (Mifflin and Sagastizábal 2005). Such approach is usually referred to as VU decomposition. A fine historical note about it (and much more) is in Mifflin and Sagastizábal (2012).
-
Methods which adopt different stabilization strategies. We cite, in particular, the Generalized BM Frangioni (2002), the use of Bregman distance (Kiwiel 1999), and the doubly stabilized BM de Oliveira and Solodov (2016).
-
Methods where the condition that the model function \(f_k\) is a lower approximation of f is removed, by replacing the \(\alpha _i\)s in (45) with adjustable (non negative) parameters,see (Gaudioso and Monaco 1982, 1992; Astorino et al. 2017).
-
Methods where bundle update takes place every time a new stability center \(\overline{\mathbf {x}}_{k+1}\) is found, through simultaneous moves of all points \(\mathbf {x}_i\)s towards \(\overline{\mathbf {x}}_{k+1}\), see (Demyanov et al. 2007).
-
Methods based on piecewise quadratic approximations of the objective function, see (Gaudioso and Monaco 1991; Astorino et al. 2011).
-
Spectral BM for dealing with eigenvalue optimization and semidefinite relaxations of combinatorial problems, see (Helmberg and Rendl 2000).
-
The Volume Algorithm which is midway between subgradient and simplified bundle methods, thus appearing suitable for large scale applications, see (Barahona and Anbil 2000; Bahiense et al. 2002).
Line searches Line searches tailored on nonsmooth (not necessarily convex) functions constitute an important chapter of NSO. A line search algorithm embedded into any BM method must accommodate for possible null-step. We have already mentioned in Sect. 5.1 the Armijo’s rule (Armijo 1966). In the literature, specific line searches have been designed, and we recall here the method due to Wolfe (1975), the Lemarechal’s survey (Lemaréchal 1981), and the Mifflin’s paper (Mifflin 1984), where a method with superlinear convergence rate for locally Lipschitz functions is discussed.
Solving the quadratic subproblem In bundle methods a quadratic subproblem is to be solved at each iteration and, consequently, the overall performance is strongly affected by the quality of the correspondent quadratic solver. In particular, in proximal BM either problem (45) or (48) are to be tackled to provide the direction \(\mathbf {d}_k\). The special structure of the latter has suggested the design of ad hoc algorithms. Efficient methods are described in Kiwiel (1986, 1994), Monaco (1987), Frangioni (1996). We also mention the historical paper (Wolfe 1976), where the quadratic problem (48) is treated for the case when \(\alpha _i\)s are all equal to zero, in the framework of classic Wolfe’s conjugate subgradient method (Wolfe 1975).
Variable metric methods As for the extension to NSO of Quasi-Newton formulae, we have already cited Lemaréchal (1982) and Vlček and Luksǎn (2001), the latter being also able to deal with nonconvex objective functions. A different way to embed QN ideas in the bundle framework is presented in Luksǎn and Vlček (1998). References for QN methods based on Moreau-Yosida regularization and bundle-QN methods are Qi and Sun (1993), Bonnans et al. (1995), Lemaréchal and Sagastizábal (1997), Fukushima and Qi (1996), Mifflin (1996), Mifflin et al. (1998), Rauf and Fukushima (1998), Chen and Fukushima (1999). An interesting area where QN ideas have been fruitfully employed, mainly to deal with large scale NSO, is the Limited memory BM Haarala et al. (2007), Gaudioso et al. (2018c) where ideas coming from Luksǎn and Vlček (1998), Vlček and Luksǎn (2001) have been employed in the framework of the limited memory QN for smooth problems (Byrd et al. 1994). The method has been extended to very large scale problems, also nonconvex, by adopting a sparse (diagonal, in fact) form for the QN matrix (Karmitsa 2015). We wish to mention, finally, that celebrated Shor’s subgradient with space dilatation algorithm can be viewed as a QN method with symmetric rank-one update formula, see (Todd 1986; Burke et al. 2008).
Minmax problems A large part of NSO problems arising in practical applications are of the minmax type, mainly in consideration that the worst case analysis, which naturally leads to minmax (or maxmin) model, is an increasingly popular paradigm in decision making. We recall here the already cited fundamental book (Demyanov and Malozemov 1974) and the papers (Di Pillo et al. 1993, 1997) where minmax problems are dealt with by transformation into smooth problems. Some basic references are Hald and Madsen (1981), Polak et al. (1991), Nedić and Bertsekas (2001). Minmaxmin optimization is revisited in Demyanov et al. (2002) (see also Gaudioso et al. 2018a). Inexact calculation of the \(\max \) function has been considered in both cases of finite and semi-infinite convex minmax in Gaudioso et al. (2006) and Fuduli et al. (2014), respectively; an application to a minmax problem in a Lagrangian relaxation setting is presented in Gaudioso et al. (2009).
Nonconvex NSO and DC programming There exist numerous bundle type algorithms applicable to nonconvex functions. We recall here (Nurminski 1982; Schramm and Zowe 1992; Qi and Sun 1994; Kiwiel 1996; Noll and Apkarian 2005; Hare and Sagastizábal 2010; Akbari et al. 2014). Papers (Bagirov et al. 2008; Kiwiel 2010; Fasano et al. 2014) are examples of derivative free NSO methods capable to cope with nonconvexity. In recent years the class of DC (Difference of Convex) functions (Hiriart-Urruty 1986; Strekalovsky 1998; Tuy 2016) has received considerable attention. A DC function \(f(\mathbf {x})\) is expressed in the form:
where both \(f^{(1)}\) and \(f^{(2)}\) are convex. The well established algorithm DCA (An and Tao 2005) works as follows. Letting \(\mathbf {x}_k\) be the current iterate, point \(\mathbf {x}_{k+1}\) is obtained as
where \(\mathbf {g}^{(2)}(\mathbf {x}_k) \in \partial f^{(2)}(\mathbf {x}_k)\). In other words, the linearization of function \(f^{(2)}\) gives rise, at each iteration, to a convex program to be solved in order to obtain the next iterate. The bundle philosophy has been extensively used in handling DC optimization, introducing the cutting plane model for \(f^{(1)}\) and/or \(f^{(2)}\). Some recent references are Astorino and Miglionico (2016), de Oliveira (2019), de Oliveira (2020), Gaudioso et al. (2018b), Gaudioso et al. (2020a), Gaudioso et al. (2020b), Joki et al. (2018).
Notes
Given the features of the adopted machinery, we keep on denoting the current iterate (i.e., the estimate of a minimizer) by \(\overline{\mathbf {x}}_k\), although the methods involved in this class are not necessarily of the bundle type.
References
Akbari, Z., Yousefpour, R., & Reza Peyghami, M. (2014). A new nonsmooth trust region algorithm for locally Lipschitz unconstrained optimization problems. Journal of Optimization Theory and Applications, 164, 733–754.
An, L. T. H., & Tao, P. D. (2005). The DC (difference of convex functions) programming and DCA revisited with DC models of real world nonconvex optimization problems. Journal of Global Optimization, 133, 23–46.
Armijo, L. (1966). Minimization of functions having Lipschitz continuous first partial derivatives. Pacific Journal of Mathematics, 16, 1–3.
Astorino, A., Frangioni, A., Gaudioso, M., & Gorgone, E. (2011). Piecewise quadratic approximations in convex numerical optimization. SIAM Journal on Optimization, 21, 1418–1438.
Astorino, A., Fuduli, A., & Gaudioso, M. (2019). A Lagrangian relaxation approach for binary Multiple Instance Classification. IEEE Transactions on Neural Networks and Learning Systems, 30, 2662–2671.
Astorino, A., Gaudioso, M., & Gorgone, E. (2017). A method for convex minimization based on translated first-order approximations. Numerical Algorithms, 76, 745–760.
Astorino, A., & Miglionico, G. (2016). Optimizing sensor cover energy via DC programming. Optimization Letter, 10, 355–368.
Bagirov, A. M., Gaudioso, M., Karmitsa, N., Mäkelä, M. M., & Taheri, S. (Eds.). (2020). Numerical nonsmooth optimization: State of the art algorithms. New York: Springer.
Bagirov, A. M., Karasözen, B., & Sezer, M. (2008). Discrete gradient method: Derivative-free method for nonsmooth optimization. Journal of Optimization Theory and Applications, 137, 317–334.
Bagirov, A. M., Karmitsa, N., & Mäkelä, M. M. (2014). Introduction to nonsmooth optimization: Theory, practice and software. New York: Springer.
Bahiense, L., Maculan, N., & Sagastizábal, C. (2002). The volume algorithm revisited: Relation with bundle methods. Mathematical Programming, 94, 41–69.
Barahona, F., & Anbil, R. (2000). The volume algorithm: Producing primal solutions with a subgradient method. Mathematical Programming, 87, 385–399.
Barzilai, J., & Borwein, J. M. (1988). Two-point step size gradient methods. IMA Journal of Numerical Analysis, 8, 141–148.
Beck, A., & Teboulle, M. (2003). Mirror descent and nonlinear projected subgradient methods for convex optimization. Operations Research Letters, 31, 167–175.
Ben-Tal, A., & Nemirovski, A. (2001). Lectures on modern optimization. MPS/SIAM series on optimization. Philadelphia: SIAM.
Bertsekas, D. P. (1995). Nonlinear programming. Belmont, MA: Athena Scientific.
Bertsekas, D. P. (2009). Convex optimization theory. Belmont: Athena Scientific.
Bertsekas, D. P., & Mitter, S. K. (1973). A descent numerical method for optimization problems with nondifferentiable cost functionals. SIAM Journal on Control, 11, 637–652.
Bertsimas, D., & Vempala, S. (2004). Solving convex programs by random walks. Journal of the ACM, 51, 540–556.
Bonnans, J., Gilbert, J., Lemaréchal, C., & Sagastizábal, C. (1995). A family of variable metric proximal methods. Mathematical Programming, 68, 15–47.
Brännlund, U., Kiwiel, K. C., & Lindberg, P. O. (1995). A descent proximal level bundle method for convex nondifferentiable optimization. Operations Research Letters, 17, 121–126.
Burke, J. V., Curtis, F. E., Lewis, A. S., Overton, M. L., & Simões, L. E. A. (2020). Gradient sampling methods for nonsmooth optimization. In A. M. Bagirov, M. Gaudioso, N. Karmitsa, M. Mäkelä, & S. Taheri (Eds.), Numerical nonsmooth optimization: State of the art algorithms. New York: Springer.
Burke, J. V., Lewis, A. S., & Overton, M. L. (2005). A robust gradient sampling algorithm for nonsmooth, nonconvex optimization. SIAM Journal on Optimization, 15, 751–779.
Burke, J. V., Lewis, A. S., & Overton, M. L. (2008). The speed of Shor’s R-algorithm. IMA Journal of Numerical Analysis, 28, 711–720.
Byrd, R. H., Nocedal, J., & Schnabel, R. B. (1994). Representations of quasi-Newton matrices and their use in limited memory methods. Mathematical Programming, 63, 129–156.
Chebyshëv, P. L. (1961). Sur les questions de minima qui se rattachent a la représentation approximative des fonctions, 1859. In Oeuvres de P. L. Tchebychef, (Vol. 1, pp. 273–378). New York: Chelsea.
Cheney, E. W., & Goldstein, A. A. (1959). Newton’s method for convex programming and Tchebycheff approximation. Numerische Mathematik, 1, 253–268.
Chen, X., & Fukushima, M. (1999). Proximal quasi-Newton methods for nondifferentiable convex optimization. Mathematical Programming, 85, 313–334.
Clarke, F. H. (1983). Optimization and nonsmooth analysis (pp. 357–386). New York: Wiley.
D’Antonio, G., & Frangioni, A. (2009). Convergence analysis of deflected conditional approximate subgradient methods. SIAM Journal on Optimization, 20, 357–386.
de Ghellinck, G., & Vial, J.-P. (1986). A polynomial Newton method for linear programming. Algorithmica, 1, 425–453.
de Oliveira, W. (2019). Proximal bundle methods for nonsmooth DC programming. Journal of Global Optimization, 75, 523–563.
de Oliveira, W. (2020). The ABC of DC programming. Set-Valued and Variational Analysis, 28, 679–706.
de Oliveira, W., Sagastizábal, C., & Lemaréchal, C. (2014). Convex proximal bundle methods in depth: A unified analysis for inexact oracles. Mathematical Programming, 148, 241–277.
de Oliveira, W., & Solodov, M. (2016). A doubly stabilized bundle method for nonsmooth convex optimization. Mathematical Programming, 156, 125–159.
Demyanov, A. V., Demyanov, V. F., & Malozemov, V. N. (2002). Minmaxmin problems revisited. Optimization Methods and Software, 17, 783–804.
Demyanov, A. V., Fuduli, A., & Miglionico, G. (2007). A bundle modification strategy for convex minimization. European Journal of Operational Research, 180, 38–47.
Demyanov, V. F., & Malozemov, V. N. (1974). Introduction to minimax. New York: Wiley.
Demyanov, V. F., & Rubinov, A. M. (1995). Constructive nonsmooth analysis. Berlin: Verlag Peter Lang.
Di Pillo, G., Grippo, L., & Lucidi, S. (1993). A smooth method for the finite minimax problem. Mathematical Programming, 60, 187–214.
Di Pillo, G., Grippo, L., & Lucidi, S. (1997). Smooth transformation of the generalized minimax problem. Journal of Optimization Theory and Applications, 95, 1–24.
Dvurechensky, P. E., Gasnikov, A. V., Nurminski, E. A., & Stonyakin, F. S. (2020). Advances in low-memory subgradient optimization. In A. Bagirov, M. Gaudioso, N. Karmitsa, M. Mäkelä, & S. Taheri (Eds.), Numerical nonsmooth optimization: State of the art algorithms. New York: Springer.
Elzinga, J., & Moore, T. G. (1975). A central cutting plane algorithm for the convex programming problem. Mathematical Programming, 8, 134–145.
Eremin, I. I. (1967). The method of penalties in convex programming. Dokladi Academii Nauk USSR, 173, 748–751.
Ermoliev, Yu. M. (1966). Methods of solution of nonlinear extremal problems. Cybernetics, 2, 1–16.
Fasano, G., Liuzzi, G., Lucidi, S., & Rinaldi, F. (2014). A linesearch-based derivative-free approach for nonsmooth constrained optimization. SIAM Journal on Optimization, 24, 959–992.
Fenchel, W. (1951). Convex cones, sets and functions. Lectures at Princeton University. Princeton: Princeton University Press.
Frangioni, A. (1996). Solving semidefinite quadratic problems within nonsmooth optimization algorithms. Computers and Operations Research, 23, 1099–1118.
Frangioni, A. (2002). Generalized bundle methods. SIAM Journal on Optimization, 13, 117–156.
Frangioni, A. (2020). Standard bundle methods: Untrusted models and duality. In A. M. Bagirov, M. Gaudioso, N. Karmitsa, M. Mäkelä, & S. Taheri (Eds.), Numerical nonsmooth optimization: State of the art algorithms. New York: Springer.
Frangioni, A., Gendron, B., & Gorgone, E. (2018). Dynamic smoothness parameter for fast gradient methods. Optimization Letters, 12, 43–53.
Fuduli, A., Gaudioso, M., & Giallombardo, G. (2004). Minimizing nonconvex nonsmooth functions via cutting planes and proximity control. SIAM Journal on Optimization, 14, 743–756.
Fuduli, A., Gaudioso, M., Giallombardo, G., & Miglionico, G. (2014). A partially inexact bundle method for convex semi-infinite minmax problems. Communications in Nonlinear Science and Numerical Simulation, 21, 172–180.
Fukushima, M. (1984). A descent algorithm for nonsmooth convex optimization. Mathematical Programming, 30, 163–175.
Fukushima, M., & Qi, L. (1996). A globally and superlinearly convergent algorithm for nonsmooth convex minimization. SIAM Journal on Optimization, 6, 1106–1120.
Gaudioso, M. (2020). A view of Lagrangian relaxation and its applications. In A. M. Bagirov, M. Gaudioso, N. Karmitsa, M. Mäkelä, & S. Taheri (Eds.), Numerical nonsmooth optimization—State of the art algorithms. New York: Springer.
Gaudioso, M., Giallombardo, G., & Miglionico, G. (2006). An incremental method for solving convex finite min-max problems. Mathematics of Operations Research, 31, 173–187.
Gaudioso, M., Giallombardo, G., & Miglionico, G. (2009). On solving the Lagrangian dual of integer programs via an incremental approach. Computational Optimization and Applications, 44, 117–138.
Gaudioso, M., Giallombardo, G., & Miglionico, G. (2018). Minimizing piecewise concave functions over polyhedra. Mathematics of Operations Research, 43, 580–597.
Gaudioso, M., Giallombardo, G., & Miglionico, G. (2020). Essentials of numerical nonsmooth optimization. 4OR, 18, 1–47.
Gaudioso, M., Giallombardo, G., Miglionico, G., & Bagirov, A. M. (2018). Minimizing nonsmooth DC functions via successive DC piecewise-affine approximations. Journal of Global Optimization, 71, 37–55.
Gaudioso, M., Giallombardo, G., Miglionico, G., & Vocaturo, E. (2020). Classification in the multiple instance learning framework via spherical separation. Soft Computing, 24(7), 5071–5077.
Gaudioso, M., Giallombardo, G., & Mukhametzhanov, M. (2018). Numerical infinitesimals in a variable metric method for convex nonsmooth optimization. Applied Mathematics and Computation, 318, 312–320.
Gaudioso, M., & Gorgone, E. (2010). Gradient set splitting in nonconvex nonsmooth numerical optimization. Optimization Methods and Software, 25, 59–74.
Gaudioso, M., Hiriart-Urruty, J.-B., & Gorgone, E. (2020). Feature selection in SVM via polyhedral \(k\)-norm. Optimization Letters, 14(1), 19–36.
Gaudioso, M., & Monaco, M. F. (1982). A bundle type approach to the unconstrained minimization of convex nonsmooth functions. Mathematical Programming, 23, 216–223.
Gaudioso, M., & Monaco, M. F. (1991). Quadratic approximations in convex nondifferentiable optimization. SIAM Journal on Control and Optimization, 29, 1–10.
Gaudioso, M., & Monaco, M. F. (1992). Variants to the cutting plane approach for convex nondifferentiable optimization. Optimization, 25, 65–75.
Goffin, J.-L. (1977). On convergence rates of subgradients optimization methods. Mathematical Programming, 13, 329–347.
Goffin, J.-L., Gondzio, J., Sarkissian, R., & Vial, J.-P. (1997). Solving nonlinear multicommodity flow problems by the analytic center cutting plane method. Mathematical Programming, 76B, 131–154.
Goffin, J.-L., Haurie, A., & Vial, J.-P. (1992). Decomposition and nondifferentiable optimization with the projective algorithm. Management Science, 38, 284–302.
Grippo, L., Lampariello, F., & Lucidi, S. (1991). A class of nonmonotone stabilization methods in unconstrained optimization. Numerische Mathematik, 59, 779–805.
Haarala, N., Miettinen, K., & Mäkelä, M. M. (2007). Globally convergent limited memory bundle method for large-scale nonsmooth optimization. Mathematical Programming, 109, 181–205.
Hald, J., & Madsen, K. (1981). Combined LP and Quasi-Newton methods for minimax optimization. Mathematical Programming, 20, 49–62.
Hare, W., & Sagastizábal, C. (2010). A redistributed proximal bundle method for nonconvex optimization. SIAM Journal on Optimization, 20, 2242–2473.
Helmberg, C., & Rendl, F. (2000). A spectral bundle method for semidefinite programming. SIAM Journal on Optimization, 10, 673–696.
Hintermüller, M. (2001). A proximal bundle method based on approximate subgradients. Computational Optimization and Applications, 20, 245–266.
Hiriart-Urruty, J.-B. (1986). Generalized differentiability/duality and optimization for problems dealing with differences of convex functions. Lecture notes in economic and mathematical systems (Vol. 256, pp. 37–70). New York: Springer.
Hiriart-Urruty, J. B., & Lemaréchal, C. (1993). Convex analysis and minimization algorithms (Vol. I and II). Berlin: Springer.
Joki, K., Bagirov, A. M., Karmitsa, N., Mäkelä, M. M., & Taheri, S. (2018). Double bundle method for finding Clarke stationary points in nonsmooth DC programming. SIAM Journal on Optimization, 28, 1892–1919.
Karmitsa, N. (2015). Diagonal bundle method for nonsmooth sparse optimization. Journal of Optimization Theory and Applications, 166, 889–905.
Kelley, J. E. (1960). The cutting plane method for solving convex programs. Journal of SIAM, 8, 703–712.
Kiwiel, K. C. (1983). An aggregate subgradient method for nonsmooth convex minimization. Mathematical Programming, 27, 320–341.
Kiwiel, K. C. (1985). Methods of descent for nondifferentiable optimization. Lecture notes in mathematics (Vol. 1133). Berlin: Springer.
Kiwiel, K. C. (1986). A method for solving certain quadratic programming problems arising in nonsmooth optimization. IMA Journal of Numerical Analysis, 6, 137–152.
Kiwiel, K. C. (1990). Proximity control in bundle methods for convex nondifferentiable minimization. Mathematical Programming, 46, 105–122.
Kiwiel, K. C. (1994). A Cholesky dual method for proximal piecewise linear programming. Numerische Mathematik, 68, 325–340.
Kiwiel, K. C. (1996). Restricted step and Levenberg-Marquardt techniques in proximal bundle methods for nonconvex nondifferentiable optimization. SIAM Journal on Optimization, 6, 227–249.
Kiwiel, K. C. (1999). A bundle Bregman proximal method for convex nondifferentiable minimization. Mathematical Programming, 85, 241–258.
Kiwiel, K. C. (2004). Convergence of approximate and incremental subgradient methods for convex optimization. SIAM Journal on Optimization, 14, 807–840.
Kiwiel, K. C. (2006). A proximal bundle method with approximate subgradient linearizations. SIAM Journal on Optimization, 16, 1007–1023.
Kiwiel, K. C. (2007). Convergence of the gradient sampling algorithm for nonsmooth nonconvex optimization. SIAM Journal on Optimization, 18, 379–388.
Kiwiel, K. C. (2010). A nonderivative version of the gradient sampling algorithm for nonsmooth nonconvex optimization. SIAM Journal on Optimization, 20, 1983–1994.
Lemaréchal, C. (1978). Nonsmooth optimization and descent methods. Report RR-78-4, IIASA, Laxenburg, Austria.
Lemaréchal, C. (1974). An algorithm for minimizing convex functions. In J. L. Rosenfeld (Ed.), Proceedings IFIP ’74 congress (pp. 20–25). Amsterdam: North-Holland.
Lemaréchal, C. (1975). An extension of Davidon methods to nondifferentiable problems. Mathematical Programming Study, 3, 95–109.
Lemaréchal, C. (1981). A view of line-searches. In A. Auslender, W. Oettli, & J. Stoer (Eds.), Optimization and optimal control. Lecture notes in control and information sciences (Vol. 30). Berlin: Springer.
Lemaréchal, C. (1982). Numerical experiments in nonsmooth optimization. In E. A. Nurminski (Ed.), Progress in nondifferentiable optimization CP-82-S8 (pp. 61–84). Laxenburg: IIASA.
Lemaréchal, C., et al. (1989). Nondifferentiable optimization. In G. L. Nemhauser (Ed.), Handbooks in OR& MS (Vol. 1). New York: North-Holland.
Lemaréchal, C., & Mifflin, R. (Eds.). (1978). Nonsmooth optimization. Oxford: Pergamon Press.
Lemaréchal, C., Nemirovskii, A., & Nesterov, Y. (1995). New variants of bundle methods. Mathematical Programming, 69, 111–147.
Lemaréchal, C., & Sagastizábal, C. (1997). Variable metrics bundle methods: From conceptual to implementable forms. Mathematical Programming, 76, 393–410.
Lemaréchal, C., Strodiot, J.-J., & Bihain, A. (1981). On a bundle algorithm for nonsmooth optimization. In O. L. Mangasarian, R. R. Meyer, & S. M. Robinson (Eds.), Nonlinear programming 4 (pp. 245–282). New York: Academic Press.
Levin, AYu. (1965). On an algorithm for minimization of convex functions. Soviet Mathematical Doklady, 6, 286–290.
Levitin, E. C., & Polyak, B. T. (1966). Constrained minimization methods. Journal of Computational Mathematics and Mathematical Physics, 6, 787–823 ((in Russian)).
Luksǎn, L., & Vlček, J. (1998). A bundle-Newton method for nonsmooth unconstrained minimization. Mathematical Programming, 83, 373–391.
Mäkelä, M. M. (2002). Survey of bundle methods for nonsmooth optimization. Optimization Methods and Software, 17, 1–29.
Mäkelä, M. M., & Neittaanmäki, P. (1992). Nonsmooth optimization. Singapore: World Scientific.
Mifflin, R., & Sagastizábal, C. (2012). A science fiction story in nonsmooth optimization originating at IIASA. Documenta Mathematica Extra Volume: Optimization Stories (pp. 291–300).
Mifflin, R. (1982). A modification and an extension of Lemaréchal’s algorithm for nonsmooth minimization. Mathematical Programming Study, 17, 77–90.
Mifflin, R. (1984). Stationarity and superlinear convergence of an algorithm for univariate locally Lipschitz constrained minimization. Mathematical Programming, 28, 50–71.
Mifflin, R. (1996). A quasi-second order proximal bundle algorithm. Mathematical Programming, 73, 51–72.
Mifflin, R., & Sagastizábal, C. (2005). A VU-algorithm for convex minimization. Mathematical Programming, 104, 583–608.
Mifflin, R., Sun, D., & Qi, L. (1998). Quasi-Newton bundle-type methods for nondifferentiable convex optimizations. SIAM Journal on Optimization, 8, 583–603.
Monaco, M. F. (1987). An algorithm for the minimization of a convex quadratic function over a simplex. Technical Report, Dipartimento di Sistemi, Universitá della Calabria (Vol. 56).
Mordukhovich, B. S. (2006). Variational analysis and generalized differentiation. Berlin: Springer.
Moreau, J.-J. (1965). Proximité et dualité dans un espace hilbertien. Bulletin de la Société Mathématique de France, 93, 272–299.
Nedić, A., & Bertsekas, D. P. (2001). Incremental subgradient methods for nondifferentiable optimization. SIAM Journal on Optimization, 12, 109–138.
Nemirovski, A., & Yudin, D. (1983). Problem complexity and method efficiency in optimization. New York: Wiley.
Nesterov, Yu. (1995). Complexity estimates of some cutting plane methods based on the analytic barrier. Mathematical Programmming, 69, 149–176.
Nesterov, Yu. (2005). Smooth minimization of non-smooth functions. Mathematical Programming, 103, 127–152.
Nesterov, Yu. (2009). Primal-dual subgradient methods for convex problems. Mathematical Programming, 120, 221–259.
Nesterov, Yu. (2009). Universal gradient methods for convex optimization problems. Mathematical Programming, 152, 381–404.
Noll, D., & Apkarian, P. (2005). Spectral bundle methods for non-convex maximum eigenvalue functions: First-order methods. Mathematical Programming, 104, 701–727.
Nurminski, E. A. (1982). Subgradient method for minimizing weakly convex functions and \(\epsilon \)-subgradient methods of convex optimization. In E. A. Nurminski (Ed.), Progress in nondifferentiable optimization CP-82-S8 (pp. 97–123). Laxenburg: IIASA.
Ouorou, A. (2009). A proximal cutting plane method using Chebychev center for nonsmooth convex optimization. Mathematical Programmming, 119, 239–271.
Polak, E., Mayne, D. Q., & Higgins, J. E. (1991). Superlinearly convergent algorithm for min-max problems. Journal of Optimization Theory and Applications, 69, 407–439.
Polyak, B. T. (1978). Subgradient methods: A survey of Soviet research. In C. Lemaréchal & R. Mifflin (Eds.), Nonsmooth optimization (pp. 5–29). Oxford: Pergamon Press.
Polyak, B. T. (1987). Introduction to optimization. New York: Optimization Software Inc.
Pshenichnyi, B. N. (1970). An algorithm for general problems of mathematical programming. Kybernetika, 5, 120–125 ((in Russian)).
Pshenichnyi, B. N. (1978). Nonsmooth optimization and nonlinear programming. In C. Lemaréchal & R. Mifflin (Eds.), Nonsmooth optimization (pp. 71–78). Oxford: Pergamon Press.
Pshenichnyi, B. N., & Danilin, Yu. M. (1975). Numerical methods for extremum problems. Moscow: Nauka.
Qi, L., & Sun, J. (1993). A nonsmooth version of Newton’s method. Mathematical Programming, 58, 353–368.
Qi, L., & Sun, J. (1994). A trust region algorithm for minimization of locally Lipschitzian functions. Mathematical Programming, 66, 25–43.
Rauf, A. I., & Fukushima, M. (1998). Globally convergent BFGS method for nonsmooth convex optimization. Journal of Optimization Theory and Applications, 104, 539–558.
Rockafellar, R. T. (1970). Convex analysis. Princeton: Princeton University Press.
Rockafellar, R. T. (1976). Monotone operators and the proximal point algorithm. SIAM Journal on Control and Optimization, 14, 877–898.
Schramm, H., & Zowe, J. (1992). A version of the bundle idea for minimizing a nonsmooth function: Conceptual idea, convergence analysis, numerical results. SIAM Journal on Optimization, 2, 121–152.
Shor, N. Z. (1962). Application of the gradient method for the solution of network transportation problems. Notes, scientific seminar on theory and application of cybernetics and operations research, Academy of Science, Kiev (in Russian).
Shor, N. Z. (1985). Minimization methods for nondifferentiable functions. Berlin: Springer.
Shor, N. Z. (1998). Nondifferentiable optimization and polynomial problems. Boston: Kluwer Academic Publishers.
Sonnevend, G. (1985). An analytic center for polyhedrons and new classes of global algorithms for linear (smooth, convex) programming. In A. Prekopa (Ed.), Lecture notes in control and information sciences 84 (pp. 866–876). New York: Springer.
Strekalovsky, A. S. (1998). Global optimality conditions for nonconvex optimization. Journal of Global Optimization, 12, 415–434.
Todd, M. J. (1986). The symmetric rank-one quasi-Newton algorithm is a space-dilation subgradient algorithm. Operations Research Letters, 5, 217–219.
Tuy, H. (2016). Convex analysis and global optimization. Berlin: Springer.
van Ackooij, W., & Sagastizábal, C. (2014). Constrained bundle methods for upper inexact oracles with application to joint chance constrained energy problems. SIAM Journal on Optimization, 24, 733–765.
Vlček, J., & Luksǎn, L. (2001). Globally convergent variable metric method for nonconvex nondifferentiable unconstrained minimization. Journal of Optimization Theory and Applications, 111, 407–430.
Wolfe, P. (1975). A method of conjugate subgradients for minimizing nondifferentiable functions. Mathematical Programming Study, 3, 143–173.
Wolfe, P. (1976). Finding the nearest point in a polytope. Mathematical Programming, 11, 128–149.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This is an updated version of the paper that appeared in 4OR, 18, pp. 1–47, 2020.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gaudioso, M., Giallombardo, G. & Miglionico, G. Essentials of numerical nonsmooth optimization. Ann Oper Res 314, 213–253 (2022). https://doi.org/10.1007/s10479-021-04498-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-021-04498-y