Multi-issue bankruptcy problems with crossed claims

Abstract

In this paper, we introduce a novel model of multi-issue bankruptcy problem inspired from a real problem of abatement of emissions of different pollutants in which pollutants can have more than one effect on atmosphere. In our model, therefore, several perfectly divisible goods (estates) have to be allocated among certain set of agents (claimants) that have exactly one claim which is used in all estates simultaneously. In other words, unlike of the multi-issue bankruptcy problems already existent in the literature, this model study situations with multi-dimensional states, one for each issue and where each agent claims the same to the different issues in which participates. In this context, we present an allocation rule that generalizes the well-known constrained equal awards rule from a procedure derived from analyzing this rule for classical bankruptcy problems as the solution to a sucession of linear programming problems. Next, we carry out an study of its main properties, and we characterize it using the well-known property of consistency.

1 Introduction

A bankruptcy poblem describes a situation in which an endowment, perfectly divisible, must be distributed among a set of agents who have claims on it but the endowment is not enough to completely satisfy all of them. An allocation for such a problem should meet two reasonable conditions: (1) agents can neither receive more than they claim nor less than nothing, (2) the endowment should be fully distributed. These problems were first studied by O’Neill (1982) and Aumann and Maschler (1985) . Since then this problem and their extensions have been widely studied (see Thomson 2003, 2015, 2019) for an excellent analysis of bankruptcy problems from an axiomatic perspective) and many applications of them can be found in the literature (see, for example, Gallastegui et al. 2002; Pulido et al. 2008, 2002; Niyato and Hossain 2006; Casas-Méndez et al. 2011; Bergantiños et al. 2012; Gozálvez et al. 2012; Hu et al. 2012; Lucas-Estañ et al. 2012; Giménez-Gómez et al. 2016; Sánchez-Soriano et al. 2016; Gutiérrez et al. 2018; Bergantiños et al. 2018; Duro et al. 2020; Wickramage et al. 2020, among others).

To illustrate our model, consider now that a certain authority is interested in reducing the emission of pollutants into the atmosphere. However, there are many pollutants, each with different effects and consequences. There are pollutants that contribute to the greenhouse effect and thus to climate change, and others that are harmful to health because they are carcinogenic, cause respiratory problems or other diseases. On the one hand, water vapour (H2O), carbon dioxide (CO2), nitrous oxide (NO2), methane (CH4), and ozone (O3) are the primary greenhouse effect gases (GHG’s), but also sulphur hexafluoride (SF6), hydrofluorocarbons (HFCs) and perfluorocarbons (PFCs) are relevant according to the Kyoto Protocol. On the other hand, carbon monoxide (CO), sulphur dioxide (SO2), nitrous oxide (NO2), ozone (O3), ammonia (NH3), particulate matter (PM), polycyclic aromatic hydrocarbon (PAH) and volatile organic compounds (VOCs) among others are considered very harmful to health. Thus, for example, the Gothenburg Protocol sets emission ceilings for SO2, NO2, VOCs and NH3. Therefore, we can find international, European, national and regional directives, laws, and regulations in order to control their emissions. Some examples are the well-known Paris Agreement or the Kyoto Protocol for the global reduction of GHGs or the Gothenburg Protocol to abate the acidification, eutrophication and ground-level ozone. Furthermore, we can observe that there are gases that contribute to both the greenhouse effect and the air pollution. For details on these and other topics related to the protection of the environment and health visit the webpage https://greenfacts.org.

The entire system for the abatement of pollutants could be represented in a hierarchical structure of two levels (see Fig. 1). In the first level, we would have the effect of pollutants, and in the second level the pollutants themselves. The ultimate goal of that authority is for emissions per year of the different pollutants to be below certain levels (for example, emitted tons per year) in order to better control the pollution and their effects. In this sense, the authority fixes certain levels of emissions (total tons per year) for each effect of pollutants. However, pollutants could contribute to more than one effect as we have shown above. Thus, we consider the particular situation in which there are different amounts of emissions of different pollutants and the authority fixes maximum levels of emissions (total tons per year) for each effect of pollutants according, for example, to their effects on air quality or contribution to climate change, in order to abate these emissions and keep them below certain levels (tons per year). The approach of setting a level of emissions per year is the usual one in the directives and protocols in this regard, so the particular impact of a pollutant in each effect in the atmosphere is not considered, it is simply a matter of reducing its emissions and with it, its negative impact on air quality or the greenhouse effect. Moreover, in this context, if we set global emission levels for greenhouse gases and for air polluting gases separately, it seems reasonable that when distributing efforts to abate the different pollutants, more emphasis should be placed on those that are being emitted the most, for example, this is what happens with CO2 or NO2, and therefore, those that are being emitted least are less affected. Therefore, if we allocate the emission quotas among the different pollutants, this allocation would have to be as egalitarian as possible to the quantity claimed by the atmospheric pollutant that pollutes the least to keep controlled the pollution levels. This is reminiscent of the constrained equal award rule (CEA) in bankruptcy problems. Therefore, we have a kind of multi-issue bankruptcy problem which is different from other multi-issue bankruptcy problems as the multi-issue problems as we will explain below. Of course, if we were only interested in a particular effect of pollutants, we obtain a classical bankruptcy problem, where the estate is the amount fixed for the effect (total tons per year) and the claims are the current emission levels of pollutants (tons per year).

Fig. 1

Example of a two level hierarchical structure for the abatement of GHGs and air pollutants

This problem remembers a multi-issue bankruptcy problem in which the issues are the effects of pollutants. Multi-issue bankruptcy problems introduced by Calleja et al. (2005) describe situations in which there are a perfect divisible estate which can be divided between various issues, and a number of claimants that have claims on each of those issues.¹ Therefore, there are a perfect divisible estate, several issues, and claimants with vectors of claims with as many coordinates as issues, such that the total amount of claims is above the estate. The central question for these problems is how the estate should be allocated. This problem is solved by means of allocation rules and there are several approaches to it (see, for example, Calleja et al. 2005; Borm et al. 2005; Izquierdo and Timoner 2016). However, we have ex ante one estate for each effect on atmosphere, and the claimants are the pollutants, and each pollutant has just one claim which is the same for each of the estates of the effects which it contributes to. This approach is different from the multi-issue bankruptcy problems in the literature.

In our case, we have several perfectly divisible estates, and claimants have exactly one claim which is used in all estates simultaneously. Now, again, the question is how the estate should be allocated in a reasonable way. As far as we know this approach is totally novel in the literature and then fills a gap in the bankruptcy problems that have been dealt until now. Moreover, we study a generalization of the constrained equal awards (CEA) rule (Maimonides, twelfth century) to this context, and provide an axiomatic analysis of it.

The CEA rule has been studied in multi-issue bankruptcy problems in different settings. Lorenzo-Freire et al. (2010) introduce the two-stage constrained equal awards rule. In the first stage, the estate is distributed among the issues taking into account the total claims for each issue and applying the CEA rule. In the second stage, the part of the estate assigned to each issue is distributed among the claimants by applying again the CEA rule. This rule is characterized by some known axioms, in this context, and a kind of consistency property that connects the first and second stage, among others. Bergantiños et al. (2011) provide three new characterizations of the two-stage CEA rule for multi-issue bankruptcy problems by adapting known properties for bankruptcy problems to the multi-issue case. Bergantiños et al. (2018) introduce and characterize a two-stage allocation rule for multi-issue bankruptcy problems by combining the CEA rule and the proportional rule. Izquierdo and Timoner (2016) propose the CEA rule for constrained multi-issue bankruptcy problems by using the so-called multi-issue reference systems and a quadratic optimization problem. They characterize their CEA rule by using consistency and Lorez-domination properties. In this paper, we introduce the CEA rule for multi-issue bankruptcy problems with crossed claims by using two different iterative procedures. One of them is based on linear programming and the other is related to the CEA rule for one issue bankrutcy problems. We characterize our CEA rule by means of Pareto efficiency, conditional equal division and consistency, showing that is uniquely determined by conditional equal division and consistency. Finally, we provide another characterization following the obtained in Yeh (2006).

The rest of the paper is organized as follows. In Sect. 2, multi-issue bankruptcy problems with crossed claims (MBC) are introduced and the concept of rule in this context is formally established. In Sect. 3, the constrained equal awards rule for multi-issue bankruptcy problems with crossed claims is defined as the optimal solution of a succession of linear programs and it is shown that satisfies the concept of Lorenz week dominance. In Sect. 4, an analysis of the behavior of the CEA rule in this context, according to principles like equity, efficiency monotonicity or consistency is carried out. In fact, the study of all these properties is determinant to make a choice of a reasonable rule to different situations. As a result of the properties satisfied by this rule, it can be deduced that it is a good choice when looking for allocations equitables or consistent, in particular, in the situation illustrated of abatement of emissions of different pollutants into the atmosphere. Additionally, in Sect. 5, we get a better insight of the CEA rule for multi-issue bankruptcy problems with crossed claims characterizing it by means of the combination of three of these principles, namely, Pareto efficiency, conditional equal division and consistency. Additionally, we obtain another characterization of CEA in this setting with similar properties to the characterization of CEA given in Yeh (2006). Section 6 concludes.

2 Multi-issue bankruptcy problems with crossed claims

We consider a situation where there are a finite set of issues (effects of pollutants) $M=\{1,2,\ldots ,m\}$ such that each issue j has a perfectly divisible estate $e_j$ (maximum level of emissions for that effect of pollutans). Let $E =(e_1,e_2,\ldots ,e_m)$ be the vector of estates. There are a finite set of claimants (pollutants) $N=\{1,2,\ldots ,n\}$ such that each claimant i claims $c_i$ (emissions of pollutant i) of those estates which belongs to. Let $c=(c_{1},c_{2},\ldots ,c_{n})$ be the vector of claims. Now, each claimant claims to different set of issues. Thus, $\alpha$ is a set-valued function that associates with every $i \in N$ a subset $\alpha (i) \subset M$. In fact, $\alpha (i)$ represents the issues to which claimant i asks for. Furthermore, $\sum _{i:j \in \alpha (i)} c_i > e_j$, for all $j \in M$, otherwise, those estates could be discarded from the problem because they do not impose any limitation, and so the allocation would be trivial. Therefore, a multi-issue bankruptcy problem with crossed claims (MBC in short) is defined by a 5-tuple $(M,N,E,c,\alpha )$, and the family of all these problems is denoted by $\mathcal {MBC}$.

We illustrate the structure of these problems in the following example.

Example 1

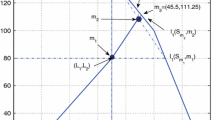
Consider the following multi-issue bankruptcy problem with crossed claims $MBC=(M,N,E,c,\alpha )$ with $M=\{1,2,3\}$; $N=\{1,2,3,4,5,6,7,8\}$; $E=(40,60,70)$; $c=(20,30,20,40,30,8,50,40)$; and $\alpha (1) = \{1\}$, $\alpha (2) = \{1,2\}$, $\alpha (3) = \{1\}$, $\alpha (4) = \{2\}$, $\alpha (5) = \{1,2\}$, $\alpha (6) = \{2\}$, $\alpha (7) = \{2,3\}$, and $\alpha (8) = \{3\}$. This situation is depicted in Fig. 2.

Fig. 2

Example 1

At first sight, a simplistic approach could be to solve three bankruptcy problems, one for each issue, but this is not so simple, because there are claimants with claims to different issues and this could lead to unfeasible or incompatible allocations. Therefore, a more detailed analysis of this type of problem is necessary.

In Example 1, we can clearly observe the structure of our model of multi-issue bankruptcy problem. This model differs from other multi-issue models in three elements. First, there are several issues, each one with their own endowments (this feature would be similar to the approach in Izquierdo and Timoner (2016) to multi-issues bankruptcy problems), i.e., in our model the estate, E, is a vector while in other multi-issue models the estate E is a single number. Second, we do not have a vector of claims for each issue as in all approches to multi-issues bankruptcy problems have, but a single vector of claims for all issues simultaneously. And finally, this vector of claims can result in the same claim to be considered in several issues at the same time.

On the other hand, when there is a single issue in multi-issue bankruptcy problems with crossed claims correspond to the well-known bankruptcy problems ($\mathcal {B}$) (O’Neill 1982; Aumann and Maschler 1985). In this case, we have a triplet (N, E, c) instead of 5-tuple $(M,N,E,c,\alpha )$, because we only have a single issue and M and $\alpha$ become irrelevant for the analysis of this problem. Therefore, multi-issue bankruptcy problems are a possible extension of bankruptcy problems.

Given a problem $(M,N,E,c,\alpha ) \in \mathcal {MBC}$, a feasible allocation for it, it is a vector $x \in \mathbb {R}^N$ such that:

• 1. $0 \le x_i \le c_i$, for all $i \in N$.

• 2. $\sum _{i \in N:j \in \alpha (i)}x_i \le e_j$, for all $j \in M$,

and we denote by $A(M,N,E,c,\alpha )$ the set of all its feasible allocations.

Requirement 1 means that each agent receives at most her claim but not less than nothing. Requirement 2 means that no estates can be overpassed with the allocation. Therefore, a feasible allocation $x \in \mathbb {R}^N$ represents an allocation to the claimants which is simultaneously feasible for all issues.

A rule for multi-issue bankruptcy problems with crossed claims is a mapping R that associates with every $(M,N,E,c,\alpha ) \in \mathcal {MBC}$ a unique feasible allocation $R(M,N,E,c,\alpha ) \in A(M,N,E,c,\alpha )$.

Example 2

Consider again the MBC problem in Example 1. Two possible allocations are the following:

• $R(M,N,E,c,\alpha ) = \left( 12.5,7.5, 12.5, 7.5, 7.5, 7.5, 30, 40\right)$.

• $R(M,N,E,c,\alpha ) = \left( 13.75,6.25, 13.75, 6.25, 6.25, 6.25, 35, 35\right)$.

Both allocations given in Example 2 satisfy the two requirements and, additionally, it is easy to check that they are efficient for all issues, i.e., Requirement 2 is satisfied with equality. However, this is not possible, in general, as the following example shows.

Remark 1

Consider again the MBC in Example 1 but only changing $c_7=65$ and $e_3=105$. In this situation, it is obvious that if an allocation is efficient for Issue 3, then it is unfeasible for Issue 2.

Therefore, in view of Remark 1, we cannot make Requirement 2 more demanding if we want to achieve at least one possible allocation.

3 The constrained equal awards rule for MBC problems

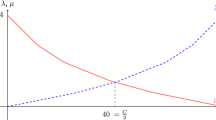
The constrained equal awards rule (CEA) is one of the main rules to solve bankruptcy problems (see Herrero and Villar 2001). This rule simply divides as equally as possible the estate among the claimants. The question here is what as equally as possible means. In the context of one-issue bankruptcy problems, as equitably as possible means that no claimant can get more than those with smaller claims, except that the latter have already received their entire claim. This can be formulated mathematically as follows:

For each $(N,E,c) \in \mathcal {B}$,

$$\begin{aligned} \textit{CEA}_i(N,E,c)=\min \{c_i,\beta \},\qquad i\in N, \end{aligned}$$

(1)

where $\beta$ is a positive real number satisfying $\sum _{i \in N} \textit{CEA}_i(N,E,c)=E$.

How to extrapolate this to the MBC situations. To do this, in this paper, we introduce the CEA rule as the result of the optimal solution of a succession of linear programs.²

Given a problem $(N,E,c) \in \mathcal {B}$, in order to allocate E among the claimants according to CEA, we proceed as follows:

$$\begin{aligned} (P_1) \begin{array}{ll} max &{} z^1 \\ s.a: &{} \sum _{i \in N} x_i \le E \\ &{} x_i \le c_i, \text { for all } i \in N \\ &{} x_i \ge z^1, \text { for all } i \in N \\ &{} x_i \ge 0, \text { for all } i \in N, \text { and } z^1 \ge 0 \end{array} \end{aligned}$$

Let $z^{*1}$ be the optimal value of the linear problem ($P_1$). If $nz^{*1} = E$, then $\textit{CEA}_i(N,E,c) = z^{*1}$. Otherwise, the following linear problem must be solved:

$$\begin{aligned} (P_2) \begin{array}{ll} max &{} z^2 \\ s.a: &{} \sum _{i \in N} x_i \le E \\ &{} x_i \le c_i, \text { for all } i \in N \\ &{} x_i \ge z^{*1} + \mu ^0(c_i - z^{*1})z^2, \text { for all } i \in N \\ &{} x_i \ge 0, \text { for all } i \in N, \text { and } z^2 \ge 0 \end{array} \end{aligned}$$

where for each $a \in \mathbb {R}$,

$$\begin{aligned} \mu ^0(a)= {\left\{ \begin{array}{ll} 0 &{} \textit{if } a \le 0,\\ 1&{} otherwise. \end{array}\right. } \end{aligned}$$

Let $z^{*2}$ be the optimal value of the linear problem ($P_2$). If $nz^{*1} + \sum _{i \in N}\mu ^0(c_i - z^{*1})z^{*2}= E$, then $\textit{CEA}_i(N,E,c) = z^{*1} + \mu ^0(c_i - z^{*1})z^{*2}$. Otherwise, a new linear problem must be solved. In the general step k, we have the following linear problem:

$$\begin{aligned} (P_k) \begin{array}{ll} max &{} z^k \\ s.a: &{} \sum _{i \in N} x_i \le E \\ &{} x_i \le c_i, \text { for all } i \in N \\ &{} x_i \ge \sum _{h=1}^{k-1}\mu ^0(c_i - \sum _{l=1}^{h-1}z^{*l})z^{*h} + \mu ^0(c_i - \sum _{l=1}^{k-1}z^{*l})z^k, \text { for all } i \in N \\ &{} x_i \ge 0, \text { for all } i \in N, \text { and } z^k \ge 0 \end{array} \end{aligned}$$

Again, let $z^{*k}$ be the optimal value of the linear problem ($P_k$). If $\sum _{i \in N}\sum _{h=1}^{k}\mu ^0(c_i - \sum _{l=1}^{h-1}z^{*l})z^{*h} =E$, then $\textit{CEA}_i(N,E,c) = \sum _{h=1}^{k}\mu ^0(c_i - \sum _{l=1}^{h-1}z^{*l})z^{*h}$. Otherwise, the linear problem ($P_{k+1}$) must be solved. And so on and so forth, until the estate is fully distributed or all claims are completely granted. It is obvious that this procedure ends in a finite number of steps and the final allocation is CEA.

Note that when the last linear problem of the procedure is solved, then we have that its optimal solution is $x^{*k} = \textit{CEA}(N,E,c)$. We illustrate this procedure in the following example.

Example 3

Consider $(N,E,c) \in \mathcal {B}$ with $N=\{1,2,3,4,5,6,7,8\}$; $E=170$; $c=(20,30,20,40,30,8,50,40)$. We now apply the procedure described above to calculate the CEA rule of this problem.

• 1. First we solve ($P_1$). The optimal value of this linear problem is $z^{*1}= 8$. Therefore, all claimants receive 8 units of the estate. In total 64 units of the estate have been distributed, therefore another round is necessary. Since claimant 6 has obtained her claim, this will not take part in the distribution of the estate in the next step.

• 2. In this step,we first guarantee claimants all what they have obtained until the previous step. The optimal value of ($P_2$) is $z^{*2}=12$. Thus, all claimants except claimant 6 are allocated 12 extra units of the estate. In total 148 units of the estate have been distributed, therefore another round is necessary. Since claimants 1 and 3 have already obtained their claims, these will not take part in the distribution of the estate in the next step.

• 3. Again, we first guarantee claimants all what they have obtained until the previous step. The optimal value of ($P_3$) is $z^{*3}=4.4$. Thus, all claimants except claimants 1, 3 and 6 are allocated 4.4 extra units of the estate. Since the estate has been fully distributed, the procedure ends and $\textit{CEA}(N,E,c) = \left( 20,24.4,20,24.4,24.4,8,24.4,24.4\right)$.

Note that this procedure perfectly fits to the following description of CEA in Thomson (2015):

At first, equal division takes place until each claimant receives an amount equal to the smallest claim. The smallest claimant drops out, and the next increments of the endowment are divided equally among the others until each of them receives an amount equal to the second smallest claim. The second smallest claimant drops out, and so on.

Therefore, following this same procedure we can define the CEA rule for MBC problems. Given a problem $(M,N,E,c,\alpha ) \in \mathcal {MBC}$, in the general step k of the procedure, the linear problem to be solved is given by:

$$\begin{aligned} (P_k) \begin{array}{ll} max &{} z^k \\ s.a: &{} \sum _{i \in N:j \in \alpha (i)} x_i \le e_j, \text { for all } j \in M \\ &{} x_i \le c_i, \text { for all } i \in N \\ &{} x_i \ge \sum _{h=1}^{k-1}\mu ^0(a_{i}^{h})z^{*h} + \mu ^0(a_{i}^{k})z^k, \text { for all } i \in N \\ &{} x_i \ge 0, \text { for all } i \in N, \text { and } z^k \ge 0 \end{array} \end{aligned}$$

where

$$\begin{aligned} a_{i}^{h}=\min \left\{ c_i - \sum _{l=1}^{h-1}\mu ^{0}(a_{i}^{l})z^{*l},min_{j \in \alpha (i)}\left\{ e_j - \sum _{t \in N:j \in \alpha (t)}\sum _{s=1}^{h-1}\mu ^{0}(a_{t}^{s})z^{*s}\right\} \right\} . \end{aligned}$$

Note that $a_{i}^{h}$ measures whether claimant i can take part in the distribution of step h taking into account what she received before and whether there is still something to distribute in every issue she claims.

In this case, the procedure also ends in a finite number of steps, but not necessarily when all estates are fully distributed or all claims are completely granted. In this situation the procedure stops when $z^{*k}=0$, and it holds that

$$\begin{aligned} \textit{CEA}_i(M,N,E,c,\alpha ) = \sum _{h=1}^{k}\mu ^0(a_{i}^{h})z^{*h}. \end{aligned}$$

Likewise, we also have that for the last linear problem solved its optimal solution $x^{*k}$ is exactly $\textit{CEA}(M,N,E,c,\alpha )$.

It is important to emphasize that we have introduced CEA rule for bankruptcy problems as the solution to a sucession of linear programming problems and we have extended this procedure to MBC. So, it is easy to check that when we have exactly only one issue both coincide. The only difference is that we additionally take into account how much remains in each of the estates to which claimants ask for. However, this procedure for MBC problems does not guarantee that all estates are fully distributed, even when they could be. The next example illustrates this.

Example 4

Consider again the MBC problem in Example 1. We now calculate the CEA rule of this problem by applying the procedure described above.

• 1. The optimal value of ($P_1$) is $z^{*1}=8$ and this amount is allocated to each claimant. None of the estates have been fully distributed, so a next step is necessary. However, claimant 6 has obtained her claim, so this will not take part in the distribution of the estates in the next step.

• 2. In this step, we guarantee claimants all what they have obtained until the previous step. The optimal value of ($P_2$) is $z^{*2}=2$, and this amount is allocated to all claimants except claimant 6. Now, the estate $e_1$ has been fully distributed, therefore, claimants requesting part of this estate cannot continue to receive anything else. Otherwise, the quantity available in that estate would be exceeded. However, the other two estates have not been fully distributed, hence another step is needed.

• 3. In this step, we guarantee claimants all what they have obtained until the previous step. The optimal value of ($P_3$) is $z^{*3}=6$, and this amount is only allocated to claimants 4, 7, and 8. Now, the estate $e_2$ has been fully distributed, so claimants 4, and 7 cannot continue to receive anything else. Again, otherwise, the quantity available in that estate would be exceeded.

• 4. In this step, we again guarantee claimants all what they have obtained until the previous step, and claimant 8 is the only one that can receive something else in this step. The optimal value of ($P_4$) is $z^{*4}=24$, and this amount is only allocated to claimant 8. However, the estate $e_3$ has not been fully distributed, in fact, there are still 14 units to be distributed. Furthermore $x^{*4}=\left( 10,10,10,16,10,8,16,40\right)$ that coincides with $\textit{CEA}(M,N,E,c,\alpha )$.

$\textit{CEA}(M,N,E,c,\alpha )$ is calculated in four steps, and the allocations in each step are the following:

$$\begin{aligned} \begin{array}{cccccc} Claimant &{} Step-1 &{} Step-2 &{} Step-3 &{} Step-4 &{}Row-total \\ 1 &{} 8 &{} 2 &{} - &{} - &{} 10 \\ 2 &{} 8 &{} 2 &{} - &{} - &{} 10 \\ 3 &{} 8 &{} 2 &{} - &{} - &{} 10 \\ 4 &{} 8 &{} 2 &{} 6 &{} - &{} 16 \\ 5 &{} 8 &{} 2 &{} - &{} - &{} 10 \\ 6 &{} 8 &{} - &{} - &{} - &{} 8 \\ 7 &{} 8 &{} 2 &{} 6 &{} - &{} 16 \\ 8 &{} 8 &{} 2 &{} 6 &{} 24 &{} 40 \\ Column-total &{} 64 &{} 14 &{} 18 &{} 24 &{} 120 \end{array} \end{aligned}$$

This allocation does not fully distribute all estates, but it is possible to obtain feasible allocations for this particular MBC problem which do. For example, the allocations given in Example 2 fully distribute all estates for this problem, but they are not as egalitarian as this. Furthermore, although the claimants have received 120 units in total, of the 170 units that make up the three estates, 156 have been actually distributed. This difference is because some claimants asked for in several issues simultaneously.

If we look carefully at the application of the procedure in Example 4, we observe that first a estate is fully distributed, then another estate is completely distributed, and finally the last estate cannot be distributed in its entirety. Therefore, we can design another procedure based on the CEA rule itself which follows this scheme. We illustrate it in the following example.

Example 5

Consider once again the MBC problem in Example 1. In order to calculate $\textit{CEA}(M,N,E,c,\alpha )$, we proceed as follows:

• 1. First we calculate the CEA rule for each of the three bankruptcy problems defined by each issue.

  • $(N^{1,1},E^{1,1},c^{1,1})$. $N^{1,1}= \{1,2, 3, 5\}$, $E^{1,1}=40$, and $c^{1,1}=\left( 20, 30, 20, 30\right)$. $\textit{CEA}(N^{1,1},E^{1,1},c^{1,1}) = \left( 10, 10, 10, 10\right)$, and $\beta ^{1,1}=10$.

  • $(N^{2,1},E^{2,1},c^{2,1})$. $N^{2,1} = \{2, 4, 5, 6, 7\}$, $E^{2,1}=60$, and $c^{2,1}=\left( 30, 40, 30, 8, 50\right)$. $\textit{CEA}(N^{2,1},E^{2,1},c^{2,1}) = \left( 13,13,13,8,13\right)$, and $\beta ^{2,1}=13$.

  • $(N^{3,1},E^{3,1},c^{3,1})$. $N^{3,1} = \{7, 8\}$, $E^{3,1}=70$, and $c^{3,1}=\left( 50, 40\right)$. $\textit{CEA}(N^{3,1},E^{3,1},c^{3,1}) = \left( 35,35\right)$, and $\beta ^{3,1}=35$.

• 2. Next, we take $\beta ^{*1}=\min \{\beta ^{1,1},\beta ^{2,1},\beta ^{3,1}\}=10$, and we allocate each claimant i $\min \{c_i,\beta ^{*1}\}$. Therefore, we obtain the allocation vector $\left( 10,10,10,10,10,8,10,10\right)$.

Now, it is obvious that estate $e_1$ has been fully distributed, and in the next step this bankruptcy problem and the claimants associated with it are excluded. Moreover, claimant 6 is also excluded because she has got her claim. The other two problems are updated in claimants, and decreasing estates and claims according to the allocation previously obtained.

• 1. We calculate the CEA rule for each of the two bankruptcy problems remaining.

  • $(N^{2,2},E^{2,2},c^{2,2})$. $N^{2,2} = \{4, 7\}$, $E^{2,2}=12$, and $c^{2,2}=\left( 30, 40\right)$. $\textit{CEA}(N^{2,2},E^{2,2},c^{2,2}) = \left( 6,6\right)$, and $\beta ^{2,2}=6$.

  • $(N^{3,2},E^{3,2},c^{3,2})$. $N^{3,2} = \{7, 8\}$, $E^{3,2}=50$, and $c^{3,2}=\left( 40, 30\right)$. $\textit{CEA}(N^{3,2},E^{3,2},c^{3,2}) = \left( 25,25\right)$, and $\beta ^{3,2}=25$.

• 2. Next, we take $\beta ^{*2}=\min \{\beta ^{2,2},\beta ^{3,2}\}=6$, and we allocate each claimant i $\min \{c_i,\beta ^{*2}\}$. Therefore, we obtain the allocation vector $\left( 0,0,0,6,0,0,6,6\right)$.

Now, it is obvious that estate $e_2$ has been fully distributed, and in the next step this bankruptcy problem and the claimants associated with it are excluded. The third problem is updated in claimants, and decreasing estates and claims according to the allocation previously obtained.

• 1. We calculate the CEA rule for each of the bankruptcy problem remaining.

  • $(N^{3,3},E^{3,3},c^{3,3})$. $N^{3,3} = \{8\}$, $E^{3,3}=38$, and $c^{3,3}=\left( 24\right)$. $\textit{CEA}(N^{3,3},E^{3,3},c^{3,3}) = \left( 24\right)$, and $\beta ^{3,3}=24$.

• 2. Next, we take $\beta ^{*3}=\min \{\beta ^{3,3}\}=24$, and we allocate each claimant i $\min \{c_i,\beta ^{*3}\}$. Therefore, we obtain the allocation vector $\left( 0,0,0,0,0,0,0,24\right)$.

The procedure stops because either estates have been completely distributed or claimants have obtained their claims. Finally, by adding the allocation vectors obtained in the procedure, we obtain that $\textit{CEA}(M,N,E,c,\alpha )=\left( 10,10,10,16,10,8,16,40\right)$.

The procedure based on the CEA rule is as follows. In general step k, we calculate the CEA rule for all bankruptcy problems defined by the available estates in the step k, for each we determine the values $\beta ^{j,k}$, and take the minimum $\beta ^{*k}$ of all of them. We allocate $\beta ^{*k}$ to all active claimants in step k and nothing to the others. Next, we update the problem by revising downwards estates, claimants, and claims. After updating the problem, if no bankruptcy problem can be defined, we stop. Otherwise we go to the next step with the updated problem, and so on. Finally, the CEA rule of the MBC is the sum of all allocation vectors obtained.

The following theorem states that both procedures introduced coincide for all MBC problems.

Theorem 1

Given a problem $MBC=(M,N,E,c,\alpha ) \in \mathcal {MBC}$, the allocation vectors obtained by the procedure based on linear programming and the procedure based on the CEA rule of classical bankrupcty problems coincide, and their outcome corresponds to the rule $\textit{CEA}(M,N,E,c,\alpha )$.

Proof

In order to prove this result, it suffices to demonstrate that there is a step in the procedure based on linear programming that coincides with the first step of the procedure based on the one-issue CEA rule, because after that step we can repeat the same reasoning again.

Given a problem $MBC=(M,N,E,c,\alpha )$, we consider, without loss of generality, that $c_1 \le c_2 \le c_3 \le \ldots \le c_n$. Let $\beta ^{*1}$ be the first value in the procedure based on the standard CEA rule. We distinguish three cases:

• 1. $\beta ^{*1} \le c_1$. In this case, $x_i = \beta ^{*1}$, for all $i \in N$ and $z^1 = \beta ^{*1}$ is a feasible solution of linear program ($P_1$). Moreover, it is optimal because if we increase $z^1$, some estate would be exceeded by the definition of $\beta ^{*1}$.

• 2. $c_h \le \beta ^{*1} < c_{h+1}$. In this situation, $x_i =\min \{c_i, \beta ^{*1}\}$, for all $i \in N$ and $z = \beta ^{*1}$ is a feasible solution of some linear program ($P_k$), because $\beta ^{*1}$ determines the first estate which will be fully distributed. Indeed, after a number of steps of the procedure based on linear programming a first estate must have been distributed. Let k be that step, then the solution given above is a feasible one for linear problem ($P_k$) and also optimal by using the same reasoning as in the previous case.

• 3. $c_n \le \beta ^{*1}$. In this case, there is no problem and all claims are granted in both procedures.

For the remaining steps of the procedure based on the one-issue CEA rule the reasoning is the same as above by only taking into account that in the procedure based on linear programming we guarantee claimants all what they have obtained until the previous step, and in the procedure based on the one-issue CEA rule we update the problem. Thus, for obtaining feasible solutions for the linear programs from the procedure based on CEA, we just have to accumulate the allocations. $\square$

An interesting property of CEA for bankruptcy problems is that it is the most egalitarian allocation in the sense of Lorenz. This result can be extended to the context of MBC problems. To do this, we first introduce the well-known concept of Lorenz dominance adapted to the context of multi-issue bankruptcy problems with crossed claims.

Given a problem $MBC=(M,N,E,c,\alpha ) \in \mathcal {MBC}$, and two feasible vectors $x,y \in \mathbb {R}_{+}^{N}$, we say that x Lorenz weakly dominates y, $x \succeq _{wL} y$, if $\sum _{j=1}^{k} x_{(j)} \ge \sum _{j=1}^{k} y_{(j)}$, for all $k=1,2,\ldots ,h$, $h \le n$, where for a vector $z\in \mathbb {R}_{+}^{N}$, $z_{(1)},\ldots ,z_{(n)}$ represent its coordinates rewritten in increasing order.

Theorem 2

Given a problem $MBC=(M,N,E,c,\alpha ) \in \mathcal {MBC}$, the rule $\textit{CEA}(M,N,E,c,\alpha )$ Lorenz weakly dominates all feasible allocations.

Proof

The proof follows from the procedure based on linear programing to calculate $\textit{CEA}(M,N,E,c,\alpha )$. Indeed, since the minimum amount that all active claimants have to receive is maximized in each step, and the estates are successively exhausted during the application of the procedure, no other allocation can improve the equality of the distribution. If so, in some of the steps the solution would not be optimal, and this is a contradiction. $\square$

4 Properties

In this section, we present several properties which are interesting in the context of MBC problems. These properties are related to efficiency, fairness, consistency or monotonicity, among others.

First, we define when two claimants are considered equal. In our context, claimants are characterized by two features: their claims and the issues to which they claim. Therefore, both should be taken into account in the definition of equal agents. Given a problem $MBC=(M,N,E,c,\alpha ) \in \mathcal {MBC}$, and two claimants $i,j \in N$, we say they are equal, if $c_i=c_j$ and $\alpha (i) = \alpha (j)$.

Next, we give a set of properties which are very natural and reasonable for an allocation rule.

Property

(EFF) Given a rule R, it satisfies efficiency, if for every problem $MBC=(M,N,E,c,\alpha ) \in \mathcal {MBC}$, $\sum _{i: j \in \alpha (i)}R_i(M,N,E,c,\alpha )= e_j$, for all $j \in M$.

EFF simply says that the estates must be fully distributed, we know that this property is very demanding in the context of multi-issue bankruptcy problems with crossed claims as Remark 1 shows. However, a weaker version of efficiency can be defined by considering Pareto efficiency. A feasible allocation is Pareto efficient if there is no other feasible allocation in which some individual is better off and no individual is worse off. Formally, given a problem $MBC=(M,N,E,c,\alpha ) \in \mathcal {MBC}$, an allocation $x \in A(M,N,E,c,\alpha )$ is Pareto efficient if there is no other allocation $x' \in A(M,N,E,c,\alpha )$ such that $x'_i \ge x_i, \forall i \in N$, with at least one strict inequality. Now Pareto efficiency is defined as follows:

Property

(PEFF) Given a rule R, it satisfies Pareto efficiency, if for every problem $MBC=(M,N,E,c,\alpha ) \in \mathcal {MBC}$, $R(M,N,E,c,\alpha )$ is Pareto efficient.

Note that PEFF implies that at least one estate is fully distributed, but not EFF. However, EFF implies PEFF. Therefore, PEFF is a weaker property than EFF.

Property

(ETE) Given a rule R, it satisfies equal treatment of equals, if for every problem $MBC=(M,N,E,c,\alpha )\in \mathcal {MBC}$ and every pair of equal claimants $i,j \in N$, $R_i(M,N,E,c,\alpha )=R_j(M,N,E,c,\alpha )$.

ETE is related to impartiality and says that claimants with the same claims and the same set of issues must be treated equally in the final allocation.

Property

(CTI) Given a rule R, it satisfies claims truncation invariance, if for every problem $MBC=(M,N,E,c,\alpha )\in \mathcal {MBC}$, when considering the problem $MBC'=(M,N,E,c',\alpha ) \in \mathcal {MBC}$ such that $c'_i = \min \left\{ c_i,\min \{e_j|j \in \alpha (i)\}\right\}$, for all $i \in N$; then $R(M,N,E,c,\alpha )=R(M,N,E,c',\alpha ).$

CTI says that if the claims are truncated by the estates, then the final allocation does not change. This property appears in Curiel et al. (1987) and it is used to characterize the so-called game theoretical rules for one-issue bankruptcy problems. Dagan and Volij (1993) were the first to propose this property as an axiom.

Property

(RMR) Given a rule R, it satisfies respect of minimal rights, if for every problem $MBC=(M,N,E,c,\alpha )\in \mathcal {MBC}$, for all $i \in N$,

$$\begin{aligned} R_i(M,N,E,c,\alpha ) \ge \min _{j : j \in \alpha (i)}\max \{0,e_j - \sum _{k \in N\backslash \{i\}:j \in \alpha (k)}c_k\}. \end{aligned}$$

Property

(CED) Given a rule R, it satisfies conditional equal division, if for every problem $MBC=(M,N,E,c,\alpha )\in \mathcal {MBC}$, for all $i \in N$,

$$\begin{aligned} R_i(M,N,E,c,\alpha ) \ge \min _{j : j \in \alpha (i)}\min \left\{ c_i,\frac{e_j}{|k:j \in \alpha (k)|}\right\} . \end{aligned}$$

Property

(SEC) Given a rule R, it satisfies securement, if for every problem $MBC=(M,N,E,c,\alpha )\in \mathcal {MBC}$, for all $i \in N$,

$$\begin{aligned} R_i(M,N,E,c,\alpha ) \ge \min _{j : j \in \alpha (i)}\min \left\{ \frac{c_i}{|k:j \in \alpha (k)|},\frac{e_j}{|k:j \in \alpha (k)|}\right\} . \end{aligned}$$

RMR, CED and SEC are related to the minimum amount that should reasonably be guaranteed to each claimant. The concept of minimal right was introduced by Tijs (1981) in the context of cooperative games to define the $\tau$-value. Thus, RMR says that a claimant should receive at least what is left when all the other claimants are completely satisfied in their claims. CED was introduced by Moulin (2000) for rationing problems. In our context, this property means that an agent should obtain her claim if this is less than any egalitarian distribution of the estates of the issues she claims, and in other case, at least the minimal egalitarian distribution of the estates of all issues she claims. Finally, SEC was introduced for bankruptcy problems by Moreno-Ternero and Villar (2004). They use this property along with other properties to characterize the Talmud rule (Aumann and Maschler 1985). In the environment of MBC problems, this property means that a rule should guarantee to agents at least the minimal egalitarian distribution of the estates of all issues they claims when they are feasible, and the minimal egalitarian distribution of the estates of all issues they claims otherwise.

Property

(CFC) Given a rule R, it satisfies conditional full compensation, if for every problem $MBC=(M,N,E,c,\alpha )\in \mathcal {MBC}$ and each $i \in N$, such that $\sum _{k: j \in \alpha (k)}\min \{c_k,c_i\} \le e_j$, for all $j \in M$, then $R_i(M,N,E,c,\alpha ) = c_i$.

CFC means that if the claim of a claimant is so small that if all claimants with higher claims asked for the same amount as her, all claims would be fully honored, then it seems reasonable that said claimant receives her claim. This property was introduced by Herrero and Villar (2002) and used to characterize the CEA rule.

Property

(CM) Given a rule R, it satisfies claim monotonicity, if for every pair of problems $MBC=(M,N,E,c,\alpha )\in \mathcal {MBC}$ and $MBC'=(M,N,E,c',\alpha )\in \mathcal {MBC}$, such that $c_i \ge c'_i$ and $c_j = c'_j$, for all $j \in N\backslash \{i\}$, then $R_i(M,N,E,c,\alpha ) \ge R_i(M,N,E,c',\alpha )$.

CM means that if the claim of a claimant increasing she cannot receive less than she received in the previous situation. In Kasajima and Thomson (2011) monotonicity properties are studied in the context of the adjudication of conflicting claims.

Before introducing the last property we need to introduce the concept of reduced problem. Given a problem $MBC=(M,N,E,c,\alpha )\in \mathcal {MBC}$, and $N' \subset N$, the reduced problem associated with $N'$, $MBC^{N'}=(M',N',E'^R,c|_{N'},\alpha )\in \mathcal {MBC}$, where $M'=\{j \in M:\text { there exists } i \in N' \text { such that }j \in \alpha (i)\}$, $E'^R=\left( e'^R_j\right) _{j \in M'}$ with $e'^R_j=e_j- \sum _{i \in N\backslash N':j \in \alpha (i)}R_i(M,N,E,c,\alpha )$, for all $j \in M'$, and $c|_{N'}$ is the vector whose coordinates correspond to the claimants in $N'$.

Property

(CONS) Given a rule R, it satisfies consistency, if for every problem $MBC=(M,N,E,c,\alpha )\in \mathcal {MBC}$, and $N' \subset N$, it holds that

$$\begin{aligned} R_i(M,N,E,c,\alpha ) = R_i(M',N',E'^R,c|_{N'},\alpha ), \text { for all } i \in N'. \end{aligned}$$

CONS means that if a subset of claimants leave the problem respecting what had been assigned to those who remain, then what those players get in the new reduced problem is the same as what they got in the whole problem. Consistency properties have been used to characterize many bankruptcy rules, because they represents a requirement of robustness when some agents leave the problem with their allocations (see Thomson (2011, 2018) for surveys about the application of consistency properties and their principles behind.)

The CEA rule for MBC problems satisfies all properties above mentioned but efficiency as Example 4 shows. We establish this in the following theorem.

Theorem 3

The CEA rule for multi-issue bankruptcy problems with crossed claims satisfies PEFF, ETE, CTI, RMR, CED, SEC, CFC, CM, and CONS.

Proof

We prove the result property by property.

• CEA satisfies PEFF by definition.

• ETE. If two claimants are symmetric, then CEA allocates both the same, since the procedure to calculate the rule treats, in each step, all active claimants egalitarianly, so if two claimants are symmetric, they stop receiving at the same step.

• CTI. Since the claims are used as upperbounds in the procedure based on linear programming and the estates cannot be exceeded, the CEA rule satisfies CTI because upperbounds are not relevant for solving the linear programs when they are above the estates.

• RMR. CEA satisfies this property by definition of the rule.

• CED. Given a problem $MBC=(M,N,E,c,\alpha )\in \mathcal {MBC}$, and $i \in N$. We distinguish three cases:

  • 1. $R_i(M,N,E,c,\alpha ) = c_i \ge \min _{j : j \in \alpha (i)}\min \left\{ c_i,\frac{e_j}{|k:j \in \alpha (k)|}\right\}$.

  • 2. $R_i(M,N,E,c,\alpha ) < c_i$ and there exists $j \in \alpha (i)$ which is fully distributed. Consider that the first issue in $\alpha (i)$ whose associated estate was fully distributed was $j^{*}$ in the k-th step of the procedure based on the standard CEA rule. Until step $(k-1)$-th claimant i has received the same as those active claimants in the step k-th and more than those inactive claimants in step $(k-1)$-th. Now in the step k-th, claimant i is going to receive exactly the same as the other active claimants in the issue $j^{*}$, and they can be less than the beginning, therefore, $R_i(M,N,E,c,\alpha ) \ge \min \left\{ c_i,\frac{e_j^{}}{|k:j^{*} \in \alpha (k)|}\right\}$.

  • 3. $R_i(M,N,E,c,\alpha ) < c_i$ and there does not exist $j \in \alpha (i)$ which is fully distributed. This case is not possible because if there does not exist $j \in \alpha (i)$ which is fully distributed, then claimant i gets her claim.

• SEC. CED implies SEC.

• CFC. This property follows from the structure of the linear programs in the procedure to calculate CEA.

• CM. This property also follows from the structure of the linear programs in the procedure to calculate CEA.

• CONS. Given $MBC=(M,N,E,c,\alpha )\in \mathcal {MBC}$ and $MBC^{N'}=(M',N',E'^{CEA},c|_{N'},\alpha )\in \mathcal {MBC}$ the reduced game associated with $N' \subset N$, let r be the number of steps needed to calculate CEA of the problem $MBC=(M,N,E,c,\alpha )$ by applying the procedure based on the standard CEA rule. We define the following two sequences of sets:

  $$\begin{aligned} N = N_1 \supset N_2 \supset \cdots \supset N_r, \text { and } N' = N'_1 \supset N'_2 \supset \cdots \supset N'_r, \end{aligned}$$

  where $N_k$ is the subset of claimants of N who were active in step k, and, $N'_k$ is the subset of claimants of $N'$ who were active in step k. Obviously, $N'_k \subset N_k$, for all $k=1,2,\ldots ,r$. Note that, in the application of the procedure based on the standard CEA rule, at least one estate is fully distributed in each step, and if at the end of the procedure some estates are not fully distributed, then if feasible the last active claimants will receive as much as possible until the limit of their claims. Now, let f be the last step in which at least one estate was fully distributed, $f \le r$. We distinguish three cases:

  • 1. $f<1$. In this case, all claimants get their claims in the problem $MBC=(M,N,E,c,\alpha )$, and, obviously, claimants in $N'$ also get their claims in $MBC^{N'}=(M',N',E'^{CEA},c|_{N'},\alpha )$. In fact, this case is not considered as a problem according to the definition of MBC problems.

  • 2. $1\le f < r$. Since the CEA rule for standard bankruptcy problems is consistent, and $N'_k \subset N_k$, for all $k=1,2,\ldots ,f$, claimants in $N'$ will get until that step the same in the application of the procedure based on the standard CEA rule in both problems, $MBC=(M,N,E,c,\alpha )$ and $MBC^{N'}=(M',N',E'^{CEA},c|_{N'},\alpha )$. Thus, in the case of some $N'_k$, $k \le f$, to be empty, then the result immediately follows. Therefore, we consider now that $N'_k \ne \varnothing$ for some $k > f$. In this case, active claimants in $N'_{f+1}$ will get their claims both in $MBC^{N}$ and $MBC^{N'}$. Consequently, $\textit{CEA}_i(M,N,E,c,\alpha ) = \textit{CEA}_i(M',N',E'^{CEA},c|_{N'},\alpha )$, for all $i \in N'$.

  • 3. $f=r$. Since the CEA rule for standard bankruptcy problems is consistent, and $N'_k \subset N_k$, for all $k=1,2,\ldots ,f=r$, claimants in $N'$ will get the same in both problems when CEA is applied.

$\square$

5 Characterization

In this section, the aim is to get a better knowledge of the CEA rule for MBC by describing it in a unique way as a combination of some reasonable axioms. This combination of principles is very important to understand the behavior of this rule and be able to make a good choice. The characterization given uses three appealing axioms: Pareto efficiency, conditional equal division and consistency. In particular, consistency is a robust axiom that describes the invariance of a rule with respect to any change in the number of agents. In fact, this symbolic principle focus on the reduction in the number of agents and reflects not only fairness but also stability and its role in characterizations is significant, an interesting introduction to the literature on the “consistency principle” and its“converse”can be found in Thomson (2011).

Lemma 1

For each problem $(M,N,E,c,\alpha ) \in \mathcal {MBC}$, and each Pareto efficient allocation $x \in A(M,N,E,c,\alpha )$, if for each $N' \subset N$ with $|N'|=|N|-1$, we have $x_i =\textit{CEA}_i(M',N',E'^x,c|_{N'},\alpha )$ for all $i \in N'$, then $x = \textit{CEA}(M,N,E,c,\alpha )$.

Proof

We first prove that if there is $x_i=\textit{CEA}_i(M,N,E,c,\alpha )$, then the result holds. Indeed, let us consider x in the conditions of the statement, and $x_i = \textit{CEA}_i(M,N,E,c,\alpha )$. We now consider $N' = N \backslash \{i \}$, since $x_i = \textit{CEA}_i(M,N,E,c,\alpha )$,

$$\begin{aligned} (M',N',E'^x,c|_{N'},\alpha ) =(M',N',E'^{CEA},c|_{N'},\alpha ). \end{aligned}$$

By hypothesis, we have that

$$\begin{aligned} x_k =\textit{CEA}_k(M',N',E'^x,c|_{N'},\alpha ) \text { for all } k \in N'. \end{aligned}$$

Moreover, since CEA satisfies consistency,

$$\begin{aligned} \textit{CEA}_k(M,N,E,c,\alpha ) = \textit{CEA}_k(M',N',E'^{CEA},c|_{N'},\alpha ) \text { for all } k \in N'. \end{aligned}$$

Therefore, $\textit{CEA}_k(M',N',E'^{CEA},c|_{N'},\alpha )=x_k$ for all $k \in N'$.

Let us consider x in the conditions of the statement and we assume without loss of generality that $x_1 \le x_2 \ldots \le x_{|N|}$. We are going to prove that $x_1 = \textit{CEA}_1(M,N,E,c,\alpha )$ always holds. We distinguish two cases:

• $x_1=c_1$. We take any $N' \subset N$ with $1 \in N'$ and $|N'|=|N|-1$. By definition of CEA, in the first step the following linear program has to be solved:

  $$\begin{aligned} \begin{array}{ll} max &{} z^1 \\ s.a: &{} \sum _{i \in N':j \in \alpha (i)} x_i \le e'^x_j, \text { for all } j \in M' \\ &{} x_i \le c_i, \text { for all } i \in N' \\ &{} x_i \ge z^1, \text { for all } i \in N' \\ &{} x_i \ge 0, \text { for all } i \in N', \text { and } z^1 \ge 0 \end{array} \end{aligned}$$

  By hypothesis, we know that $c_1= \textit{CEA}_1(M',N',E'^x,c|_{N'},\alpha )$. Therefore, since $c_1$ is the minimum value of the allocation x, the solution $x_i = c_1$ for all $i \in N'$ is a feasible solution of the linear program above, and also optimal because $x_1 \le c_1$. Therefore $z^{*1}=c_1$. On the other hand, for the original problem $(M,N,E,c,\alpha )$, in the first step the linear program to be solved is given by

  $$\begin{aligned} \begin{array}{ll} max &{} z^1 \\ s.a: &{} \sum _{i \in N:j \in \alpha (i)} x_i \le e_j, \text { for all } j \in M \\ &{} x_i \le c_i, \text { for all } i \in N \\ &{} x_i \ge z^1, \text { for all } i \in N \\ &{} x_i \ge 0, \text { for all } i \in N, \text { and } z^1 \ge 0 \end{array} \end{aligned}$$

  Now, since $e'^x_j \le e_j$ for all $j \in M'$ and $c_1 \le x_j$ for all $j \in N$, $z^{*1}=c_1$ is a feasible solution of this linear program and also optimal for the same reasons as before. Therefore, $\textit{CEA}_1(M,N,E,c,\alpha ) = c_1$.

• $x_1 < c_1$. We take any $N' \subset N$ with $1 \in N'$ and $|N'|=|N|-1$. By definition of CEA, in the first step the following linear program has to be solved:

  $$\begin{aligned} \begin{array}{ll} max &{} z^1 \\ s.a: &{} \sum _{i \in N':j \in \alpha (i)} x_i \le e'^x_j, \text { for all } j \in M' \\ &{} x_i \le c_i, \text { for all } i \in N' \\ &{} x_i \ge z^1, \text { for all } i \in N' \\ &{} x_i \ge 0, \text { for all } i \in N', \text { and } z^1 \ge 0 \end{array} \end{aligned}$$

  By hypothesis, we know that $x_1= \textit{CEA}_1(M',N',E'^x,c|_{N'},\alpha )$. Therefore, since $x_1$ is the minimum value of the allocation x, the solution $x_i = x_1$ for all $i \in N'$ is a feasible solution of the linear program above. Moreover, it must be optimal because otherwise, since $x_1 < c_1$, $\textit{CEA}_1(M',N',E'^x,c|_{N'},\alpha ) > x_1$ which leads to a contradiction with the hypothesis. Furthermore, for the same reason, at least one of the inequalities $\sum _{i \in N':j \in \alpha (i)} x_i \le e'^x_j, j \in M'$, must be saturated in the optimal solution $x_i = x_1$ for all $i \in N'$. Eventually, for each $N' \subset N$ with $1 \in N'$ and $|N'|=|N|-1$, the saturated issue could be different. Note that all claimants i in $N'$ such that the saturated issue belongs to $\alpha (i)$ are allocated the same, $x_1$. Now, we take $N'$ such that $1 \in \{i \in N: j^* \in \alpha (i)\} \subset N'$ such that $j^*$ is a saturated item in the first step of the calculation of CEA. Note that each claimant i in $N'$ such that $j^* \in \alpha (i)$ receive exactly $x_1$ in $\textit{CEA}(M',N',E'^x,c|_{N'},\alpha )$. On the other hand, for the original problem $(M,N,E,c,\alpha )$, in the first step the linear program to be solved is given by

  $$\begin{aligned} \begin{array}{ll} max &{} z^1 \\ s.a: &{} \sum _{i \in N:j \in \alpha (i)} x_i \le e_j, \text { for all } j \in M \\ &{} x_i \le c_i, \text { for all } i \in N \\ &{} x_i \ge z^1, \text { for all } i \in N \\ &{} x_i \ge 0, \text { for all } i \in N, \text { and } z^1 \ge 0 \end{array} \end{aligned}$$

  Now, since $e'^x_{j^*} = e_{j^*}$, $e'^x_j \le e_j$ for all $j \in M \backslash \{j^*\}$ and $x_1 \le x_j$ for all $j \in N$, $z^{*1}=x_1$ is a feasible solution of this linear program and also optimal for the same reasons as before. Therefore, $\textit{CEA}_1(M,N,E,c,\alpha ) = x_1$. If $N'$ such that $1 \in \{i \in N: j^* \in \alpha (i)\} \subset N'$ with $j^*$ a saturated item in the first step of the calculation of CEA does not exist, then there will be $j' \in M$ such that $j' \in \alpha (i)$ for all $i \in N$ which will be saturated for all $N' \subset N$ with $1 \in N'$ and $|N'|=|N|-1$. Therefore, taking into account that each claimant i in $N'$ such that $j^* \in \alpha (i)$ receive exactly $x_1$ in $\textit{CEA}(M',N',E'^x,c|_{N'},\alpha )$, we obtain that $x_i = x_1$ for all $i \in N$. Once again, following similar arguments as before, we have that $\textit{CEA}_1(M,N,E,c,\alpha ) = x_1$.

$\square$

Theorem 4

The CEA rule for multi-issue bankruptcy problems with crossed claims is the only rule that satisfies PEFF, CED, and CONS.

Proof

We proceed by induction in the number of claimants in the problem.

• 1. $|N|=1$. If a rule R satisfies CED then, it is obvious that for all problem $(M,N,E,c,\alpha )$, such that $|N|=1$,

  $$\begin{aligned} R_1(M,N,E,c,\alpha ) = \min _{j : j \in \alpha (1)}\min \left\{ c_1,e_j\right\} . \end{aligned}$$

• 2. $|N|=2$. We distinguish two cases:

  • a. $\alpha (1) \cap \alpha (2) = \varnothing$. In this case, by the definition of rule and PEFF,

    $$\begin{aligned} R_1(M,N,E,c,\alpha )= & {} \min _{j : j \in \alpha (1)}\min \left\{ c_1,e_j\right\} \text { and }\\ R_2(M,N,E,c,\alpha )= & {} \min _{j : j \in \alpha (2)}\min \left\{ c_2,e_j\right\} . \end{aligned}$$

  • b. $\alpha (1) \cap \alpha (2) \ne \varnothing$. By the definition itself of allocation rule,

    $$\begin{aligned} R_1(M,N,E,c,\alpha )\le & {} \min _{j : j \in \alpha (1)\backslash \alpha (2)}\min \left\{ c_1,e_j\right\} = c'_1,\\ R_2(M,N,E,c,\alpha )\le & {} \min _{j : j \in \alpha (2)\backslash \alpha (1)}\min \left\{ c_1,e_j\right\} = c'_2. \end{aligned}$$

    We now take

    $$\begin{aligned} e^{*} = \min \left\{ e_j:j \in \alpha (1) \cap \alpha (2)\right\} . \end{aligned}$$

    Next, two cases are distinguished:

    • i. $c'_1 + c'_2 \le e^{*}$. Since $R_1(M,N,E,c,\alpha ) \le c'_1$, $R_2(M,N,E,c,\alpha ) \le c'_2$, and R satisfies PEFF,

      $$\begin{aligned} R_1(M,N,E,c,\alpha ) = c'_1 \text { and } R_2(M,N,E,c,\alpha ) = c'_2. \end{aligned}$$

      .

    • ii. $c'_1 + c'_2 > e^{*}$. If a rule satisfies CED, then

      $$\begin{aligned} R_i(M,N,E,c,\alpha )&\ge \min \left\{ c_i,\min _{j : j \in \alpha (i)}\left\{ \frac{e_j}{|\{k:j \in \alpha (k)\}|}\right\} \right\} \\&=\min \left\{ c'_i,\frac{e^{*}}{2}\right\} , i=1,2. \end{aligned}$$

      Finally, we assume, without loss of generality, that $c'_1\le c'_2$ and distinguish three cases:

      • A. $\frac{e^{*}}{2}\le c'_1\le c'_2$. Then,

        $$\begin{aligned} R_i(M,N,E,c,\alpha ) \ge \frac{e^{*}}{2}, i = 1,2. \end{aligned}$$

        By the definition of rule,

        $$\begin{aligned} R_i(M,N,E,c,\alpha ) = \frac{e^{*}}{2}, i = 1,2. \end{aligned}$$

      • B. $c'_1\le \frac{e^{*}}{2} \le c'_2$. Then,

        $$\begin{aligned} R_1(M,N,E,c,\alpha ) \ge c'_1 \text { and } R_2(M,N,E,c,\alpha ) \ge \frac{e^{*}}{2}. \end{aligned}$$

        Now, since $R_1(M,N,E,c,\alpha ) \le c'_1$, $R_1(M,N,E,c,\alpha ) = c'_1$; and by PEFF,

        $$\begin{aligned} R_2(M,N,E,c,\alpha ) = \min \{c'_2, e^{*}-c'_1\} = e^{*}-c'_1. \end{aligned}$$

      • C. $c'_1 \le c'_2 \le \frac{e^{*}}{2}$. Then $R_i(M,N,E,c,\alpha ) \ge c'_i, i = 1,2$. Hence,

        $$\begin{aligned} R_i(M,N,E,c,\alpha ) = c'_i, i = 1,2. \end{aligned}$$

  Therefore, if a rule satisfies PEFF and CED is also completely determined when $|N|=2$. Since CEA satisfies PEFF and CED, any other rule that satisfies these properties coincides with CEA when $|N|\le 2$

• 3. $|N|= 3$. Let R be a rule that satisfies PEFF, CED and CONS, and let $(M,N,E,c,\alpha ) \in \mathcal {MBC}$, then we have that

  $$\begin{aligned} R(M,N,E,c,\alpha ) = \textit{CEA}(M,N,E,c,\alpha ). \end{aligned}$$

  Indeed, for each $N'=\{i_1,i_2\} \subset N$ such that $|N'|=2$, since R satisfies CONS,

  $$\begin{aligned} R_{i_k}(M',N',E'^R,c|_{N'},\alpha ) = R_{i_k}(M,N,E,c,\alpha ), k =1,2, \end{aligned}$$

  and since $|N'|=2$, we have that

  $$\begin{aligned} R_{i_k}(M',N',E'^R,c|_{N'},\alpha ) = \textit{CEA}_{i_k}(M',N',E'^R,c|_{N'},\alpha ), k =1,2. \end{aligned}$$

  Since we can take all possible $N'=\{i_1,i_2\} \subset N$, by Lemma 1

  $$\begin{aligned} R(M,N,E,c,\alpha )=\textit{CEA}(M,N,E,c,\alpha ). \end{aligned}$$

• 4. $|N|\le k$. Let us suppose that for each $(M,N,E,c,\alpha )$ with $|N| \le k$, $R(M,N,E,c,\alpha )=\textit{CEA}(M,N,E,c,\alpha )$.

• 5. $|N|= k+1$. For each $N' \subset N$ such that $|N'|=k$, since R satisfies CONS,

  $$\begin{aligned} R_{i}(M',N',E'^R,c|_{N'},\alpha ) = R_{i}(M,N,E,c,\alpha ), i \in N'. \end{aligned}$$

  and since $|N'|\le k$, we have that

  $$\begin{aligned} R_{i}(M',N',E'^R,c|_{N'},\alpha ) = \textit{CEA}_{i}(M',N',E'^R,c|_{N'},\alpha ), i \in N'. \end{aligned}$$

  Finally, since we can take all possible $N'\subset N$ with $|N'|=k$, by Lemma 1,

  $$\begin{aligned} R(M,N,E,c,\alpha )=\textit{CEA}(M,N,E,c,\alpha ). \end{aligned}$$

$\square$

Note that from Theorem 4, we know that for $|N| = 2$, CEA is the only rule satisfying PEFF and CED for multi-issue bankruptcy problems with crossed claims. Next, in the following propositions, we show the role of each property in Theorem 4. We first prove that CED and CONS imply PEFF, then, we show that CED and CONS are necessary, and that any other combination of two properties do not imply the remaining third. Therefore, CEA can also be characterized by only CED and CONS. This is established below in Corollary 1. However, we have preferred to keep the characterization with PEFF because this way we obtain a different characterization of CEA for the case of two agents as described above.

Proposition 1

If a rule satisfies CED and CONS then it satisfies PEFF.

Proof

Let us suppose by contradiction that a rule R satisfies CED and CONS but not PEFF. Therefore, there is a problem $(M,N,E,c,\alpha ) \in \mathcal {MBC}$ such that $R(M,N,E,c,\alpha )$ is not Pareto efficient. Since $R(M,N,E,c,\alpha )$ is not Pareto effcient, there exists $x \in A(M,N,E,c,\alpha )$ such that $x_i \ge R_i(M,N,E,c,\alpha ), \forall i \in N$, with at least one strict inequality. Le $i_0$ be such that $x_{i_0} > R_{i_0}(M,N,E,c,\alpha )$. We now take $N'=\{i_0\}$ and its associated reduced problem $(M',N',E',c|_{N'},\alpha )$. For each $j \in M'$,

$$\begin{aligned} e'_j=e_j - \sum _{i \in N \backslash \{i_0\}:j \in \alpha (i)}R_i(M,N,E,c,\alpha ). \end{aligned}$$

Since $x \in A(M,N,E,c,\alpha )$ and satisfies that $x_{i_0} > R_{i_0}(M,N,E,c,\alpha )$, then $x_{i_0} \le e'_j, \forall j \in \alpha (x_{i_0})$. Moreover, by CED,

$$\begin{aligned} R_{i_0}(M',N',E',c,\alpha ) \ge \min \left\{ c_{i_0},\min _{j : j \in \alpha (i_0)}\left\{ e'_j \right\} \right\} . \end{aligned}$$

Therefore, we have the following chain of inequalities

$$\begin{aligned} R_{i_0}(M,N,E,c|_{N'},\alpha ) \ge \min \left\{ c_{i_0},\min _{j : j \in \alpha (i_0)}\left\{ e'_j \right\} \right\} \ge x_{i_0} > R_{i_0}(M,N,E,c,\alpha ), \end{aligned}$$

which is a contradiction with the fact that R satisfies CONS. $\square$

Corollary 1

The CEA rule for multi-issue bankruptcy problems with crossed claims is the only rule that satisfies CED, and CONS.

Proposition 2

The properties CED and CONS in Theorem 4 (and Corollary 1) are necessary.

Proof

We consider the two possible situations:

• For each problem $(M,N,E,c,\alpha ) \in \mathcal {MBC}$, we define the following rule:

  $$\begin{aligned} R^*_i(M,N,E,c,\alpha )= \min \left\{ c_i,\min _{j \in \alpha (i)}\left\{ e_j - \sum _{k:k<i;j \in \alpha (k)}R*_k(M,N,E,c,\alpha )\right\} \right\} , \forall i \in N, \end{aligned}$$

  which is calculated recursively allocating from the agent with the lowest number to the agent with the highest number. By definition this rule satisfies PEFF and CONS, but not CED.

• For each problem $(M,N,E,c,\alpha ) \in \mathcal {MBC}$, we define the following rule in two steps. We first allocate to each agent the following:

  $$\begin{aligned} F_i(M,N,E,c,\alpha )=\min \left\{ c_i,\min _{j : j \in \alpha (i)}\left\{ \frac{e_j}{|\{k:j \in \alpha (k)\}|}\right\} \right\} , \forall i \in N. \end{aligned}$$

  Then we consider the following problem $(M,N,E',c',\alpha )$:

  $$\begin{aligned} e'_j = e_j - \sum _{i:j \in \alpha (i)} F_i(M,N,E,c,\alpha ), \forall j \in M, \end{aligned}$$
  $$\begin{aligned} c'_i = c_i - F_i(M,N,E,c,\alpha ), \forall i \in N. \end{aligned}$$

  Finally, the rule is given by

  $$\begin{aligned} R_i(M,N,E,c,\alpha )=F_i(M,N,E,c,\alpha )+R^*_i(M,N,E',c',\alpha ), \forall i \in N. \end{aligned}$$

  By definition this rule satisfies CED and PEFF, but not CONS as the following example shows. We consider the problem $M=\{1\}, N=\{1,2,3\}, E=(12), c=(3,6,6), \alpha (i) =1, \forall i \in N$. We have that

  $$\begin{aligned} F_1(M,N,E,c,\alpha ) = 3, F_2(M,N,E,c,\alpha ) = 4, F_3(M,N,E,c,\alpha ) = 4, \end{aligned}$$

  and

  $$\begin{aligned} R_1(M,N,E,c,\alpha ) = 3, R_2(M,N,E,c,\alpha ) = 5, R_3(M,N,E,c,\alpha ) = 4. \end{aligned}$$

  Let us consider $N'=\{2,3\}$, it is easy to check that

  $$\begin{aligned} R_2(M',N',E',c|_{N'},\alpha ) = 4.5, \text { and } R_3(M',N',E',c|_{N'},\alpha ) = 4.5. \end{aligned}$$

$\square$

Note that CED for MBC problems is the equivalent of conditional equal division lower bound (Moulin 2000) for bankruptcy problems, but it is not the same as conditional equal division full compensation (this was called exemption by Herrero and Villar (2001)). In bankruptcy problems, for $|N| = 2$, CEA is the only rule satisfying the conditional equal division lower bound (Thomson 2015), we do not mention efficiency because all bankruptcy rules satisfy it. Here, we obtain the same result for MBC problems by using PEFF and CED (see the proof of the case $|N|=2$ in Theorem 4). However, when using conditional equal division full compensation an extra property is necessary to characterize CEA in bankruptcy problems with $|N|=2$. In addition, for bankruptcy problems when $|N|=2$, conditional full compensation (this was called sustainability by Herrero and Villar (2002)) and conditional equal division full compensation coincide.

Proposition 3

For multi-issue bankruptcy problems with crossed claims, CFC and CM imply CED.

Proof

Let R be a rule satisfying CFC and CM, and $(M,N,E,c,\alpha ) \in \mathcal {MBC}$. For each $i \in N$, we consider the following problem $(M,N,E,c'^i,\alpha )$ ,

$$\begin{aligned} c'^i_i=\min \left\{ c_i,\min _{j : j \in \alpha (i)}\left\{ \frac{e_j}{|\{k:j \in \alpha (k)\}|}\right\} \right\} , c'^i_k=c_k, \forall k \in N\backslash \{i\}. \end{aligned}$$

By CFC, it holds that $R_i(M,N,E,c'^i,\alpha ) = c'^i_i, \forall i \in N$. Since R satisfies CM,

$$\begin{aligned} R_i(M,N,E,c,\alpha ) \ge R_i(M,N,E,c'^i,\alpha ), \forall i \in N. \end{aligned}$$

Therefore, R satisties CED. $\square$

Corollary 2

The CEA rule for multi-issue bankruptcy problems with crossed claims is the only rule that satisfies PEFF, CFC, CM and CONS.

Corollary 2 corresponds to the characterization of CEA in MBC problems equivalent to the characterization of CEA in Yeh (2006) (see, Thomson 2015, Th. 4b and Th. 14). Of course, other characterizations of the classical constrained equal awards rule could try to be extended to this context, for example the characterization of CEA in Herrero and Villar (2002). In the latter case, we would first have to define what composition down (Moulin 2000) means in this context. Since we have many issues, it could be extended in different ways. In any case, this last characterization and others in the literature would be interesting for further research in this framework.

6 Conclusions and further research

This paper is related to one of the earliest problems arised in the economic literature. In fact, this problem already appeared in primal documents as the Talmud, or in essays of Aristotle or Maimonides. However, their mathematical modelization was first carried out by O’Neill (1982). The common and central question in these problems is how to divide when there is not enough. An extension of the classical bankcruptcy problems appears with the introductin of multi-issue bankruptcy problems (Calleja et al. 2005) allowing that claims of agents can be referred to different issues.

In this paper, we go beyong of it with the purpose of solving a real problem of abatement of emissions of different pollutants in which pollutants can contribute to more than one effect. To do this, we establish a new and original model based on multi-issues bankrupcy problem (MB) called multi-issue bankruptcy problems with crossed claims (MBC). This novel model presents a multi-dimensional state, one for each issue and each agent claims the same to the different issues in which participates, these are essential differences with respect to MB problems.

Similar as for MB problems, in this new framework, problems are solved through rules that assigns to each MB problem a distribution pointing out the amount obtained for each agent in each issue. In this paper, we have allocated according to the CEA rule for bankruptcy problems introducing it as the solution to a sucession of linear programming problems and extending this procedure to this framework. Currently, we are working to solve this problem through other possible allocations or rules. In particular, futher research will include to extent to this context other rules already studied for MB problems as the proportional rule³(Moreno-Ternero 2009; Bergantiños et al. 2010), the constrained equal losses (CEL) analyzed for MB problems in Lorenzo-Freire et al. (2010), the ramdon arrival rule (O’Neill 1982) based on the Shapley value (Shapley 1953) (see Algaba et al. 2019b for an updating on theoretical and applied aspects about this outstanding value), or the Talmud rule studied in the setting of bankrupcy problems (see, for instance, Moreno-Ternero and Villar 2006), among others.

Finally, in the literature of Operations Research (OR) there exist problems that could fit well in this theoretical model, for example, set covering problems. Bergantiños et al. (2020) study the problem of how to allocate costs in set covering problems when a reasonable cover is given in advance. These problems are described by a 4-tuple (N, M, c, A), where N is the set of agents, M is the set of facilities open, $c \in \mathbb {R}_{+}^{M}$ is the vector costs associated with the facilities, and $A=\{A_j\}_{j \in M}$ with $A_j \subset N$ for each $j \in M$ denotes the agents covered by each facility. The question to be answered is how to allocate the total costs among the agents. If we look carefully at the structure of the problem, we can observe a certain similarity with multi-issue bankruptcy problems with crossed claims in the following way. We first identify agents with pollutants and issues with facilities (regions). Thus, we have a set of pollutants that affect several regions, this is described by A that plays the role of function $\alpha$. On the other hand, we consider that each region fixes a maximum level of pollution which is given by vector c that plays the role of vector E. Thus, the following problem arises: How to set pollutant emission levels when pollutants affect different regions? But one extra element is necessary in this problem: the pollutant emissions to be abated, i.e., the claims. Therefore, the set covering problem is the following. When we have a set of regions that impose limits on pollutant emissions, and these emissions come from several pollutants that can affect several of the regions simultaneously, the question to be answered is, how to set the emission limits of pollutants in such a way that the limits established by the regions are covered? This problem can be analyzed as a multi-issue bankruptcy problem with crossed claims. However, what happens if no reference on the ex-ante emissions of the pollutants are given? In this case, the problem have exactly four elements, (N, M, c, A), and the question to be answered is, how to set maximal limits of emissions of pollutants such that the regional limits are not exceeded? Therefore, these relationships between set covering problems and multi-issue bankruptcy problems with crossed claims would be interesting to study them in greater detail in further research.