1 Introduction

Designing electoral districts has been a wide studied subject of research in the literature of the last 60 years. Since the first Multi-Kernel Growth procedure introduced by Vickrey (1961), and the location-allocation model provided by Hess et al. (1965), the challenging task of obtaining a fair division of the territory, with respect to specific electoral criteria, has motivated the production of a variety of Political Districting (PD) models and methods which follow different, exact and heuristic, optimization approaches. A general picture of the state-of-the-art on this subject is provided in Ricca et al. (2013, 2017) and Ricca and Scozzari (2020) were the main models and criteria for PD are surveyed and discussed. Other interesting survey papers on the topic are those by Duque et al. (2007) and Kalcsics et al. (2005) and the very recent volume edited by Rios-Mercado (2020). All provide surveys of methods and models for the general Territory Design problem which includes PD.

Typically PD models are integer or mixed integer mathematical programs. Differences among models depend on which objective function is minimized (or maximized) and on the number and type of restrictions imposed in each formulation. They follow from the particular features deemed relevant in each specific model, according to the principles established in the electoral law of each country. The complexity of the solution process also derives from such elements, according to which of them are considered in the PD problem and how they are actually formulated in the corresponding mathematical model. The classical PD criteria are population equality (or balance), contiguity, compactness, and conformity to administrative boundaries, see Grilli di Cortona et al. (1999). All these criteria pursue desirable properties of the districts, but it is generally impossible to include all of them in an algebraic model, since, due to the binary nature of the decision variables, this may lead to PD models which cannot be solved in reasonable computational time.

Other criteria have been suggested in the literature on PD, referring to particular aspects which may be considered valid only in very special cases. In this view, George et al. (1997) propose conformity to the natural configuration of the territory, that is, a criterion which requires to avoid that electoral districts’ boundaries cross rivers, high mountains, and all such natural barriers of the territory which may prevent reachability between two sites located inside the same district. This criterion is generally well-accepted, but frequently it is discarded in order to avoid that the model complexity increases too much.

A different issue is related to the idea of trying to avoid the split of communities of common interests (also referred to as respect of minority groups, or communities representation).

This last criterion is widely discussed in the literature and, although there are authors that strongly criticize its inclusion in a PD model, others support it. Morril (1987) mentions the importance of considering respect of minority groups in PD and Williams (1995) discusses some examples where the lack of communities’ representation produces an unfair solution. Even more, the “Erice Decalogue” (unanimously signed in 2005 by relevant researchers in this area) explicitly established in its eighth point that: “A system using electoral districts should respect existing communities of interest”, see Simeone and Pukelsheim (2006). In this sense, in Cameron et al. (1996), the authors suggest non linear estimation techniques and simulate districting strategies trying to solve the under-representation of minority interests in the political process. On the other side, using surveys that sampled minorities in the U.S. and New Zealand, both these countries modified their electoral systems, so that the minority groups will have sufficient power to elect their representatives. In Banducci et al. (2004) it is showed that giving this option to minorities in U.S. these groups also improves their knowledge about representation and the contact with their representatives; in the case of New Zealand this also increases the electoral participation.

In our opinion, the representation of minority groups must be included in the PD model only when the electoral law of a country explicitly prescribes this kind of requirement, and given that the communities under consideration are well defined and can be easily located over the territory. This is in fact a way to pursue a better representation of the minorities in the Parliament, with positive implications on public policies concerning socio-economic problems. This is the case of our application to Mexico, where the resident population is characterized by the presence of community of indigenous people having very well defined cultural and social characteristics which allow to identify with a high level of precision the community to represent.

According to the Mexican law, seven criteria must be considered in the political districting process. They are: 1. balancing districts’ populations, 2. guaranteeing a prefixed number of indigenous districts in which the indigenous population is at least 40% of the total (respect of the indigenous minorities), 3. guaranteeing integrity of municipalities (respect of administrative boundaries), 4. optimize compactness, 5. minimizing traversing time from one municipality to another within the same district, 6. contiguity, 7. respecting socio-economic factors and geographic features. To be more precise, the first two criteria have a priority over the others, since they are acknowledged by the Constitution.Footnote 1. Population balance is established in Articles 53 and 116, paragraph II of the Constitution, while the respect of indigenous minorities is established in Article 2. Differently, the other five criteria are stated in the Mexican Electoral Law.Footnote 2 For the two main principles stated above some precise rules are given: for population balance the requirement is that each district has a population which does not differ more than the 15% from the average one; for respect of indigenous minorities, a prefixed number of districts must be formed by collecting together the indigenous municipalities.

In the paper we propose an automatic procedure which solves the PD problem in two successive stages, both adopting integer mathematical models, which can be equivalently formulated as Mixed Integer Linear Programs (MILP), and by applying ordinary optimization techniques. We consider the classical, PD criteria, such as population balance and districts’ contiguity. To follow the principles stated in the Mexican law, we also include respect of minority groups, but, to give it a major importance, we model it as an objective, with the aim of collecting together as many indigenous municipalities as possible in the established-by-the-law indigenous districts. Besides this, also respect of municipal boundaries is considered, which, together with the specific purpose for which it is conceived, is also useful to avoid the splitting of indigenous municipalities. This was possible in our model since respect of municipal boundaries was considered as a hard constraint. We point out that this is an innovative aspect for PD in Mexico, since even if this criterion is clearly stated by the law, it seems to be ignored in the institutional district map.

The methodology proposed in this paper is motivated by the idea that optimization procedures can be a valid decision support for lawmakers in the delicate process of designing electoral districts. The automatic nature of the method is also a guarantee of “fairness”, provided that decision makers agree on formulating the PD problem by a mathematical model. Electoral districts satisfying many desirable criteria simultaneously can be obtained efficiently by a super-partes automated tool, which can be easily implemented in the computers of an electoral office. If, on the one hand, the solution procedures (which, in any case, are a matter of the optimization solver) are not within everyone’s reach, on the other hand, MILP models can be easily understood by everyone, also with the possibility of evaluating the output solution and, possibly, modifying it, if this is deemed necessary. In this view, basic principles of electoral problems, like simplicity, transparency, and impartiality, can be pursued while providing useful tools to solve efficiently problems which are technically difficult. Since considering too many criteria in a MILP leads to the impossibility of solving it in reasonable times, not all PD criteria can be included in the model, and, in our approach, we chose to give a secondary role to compactness. There are different reasons supporting this choice which we illustrate in what follows. The first one is that unlikely a country imposes compactness explicitly in the electoral law. As in Mexico, it is generally recommended that electoral districts have a “round” shape, but it is well-known that translating this into a formal constraint is difficult and it is generally impossible to model the many facets of compactness, see Horn et al. (1993) or Grilli di Cortona et al. (1999) and the references therein. A second problem is related to the fact that it is generally not correct to judge the compactness of the districts looking directly at their geographical shape on the map, since the actual compactness also depends on the distribution of the population over the territory. Also the geographical orientation of the state may affect the compactness level which can be actually reached in a district map. Therefore, even if compactness is a deterrent for gerrymandering, when an automatic procedure is adopted, fair district maps can be obtained also without imposing compactness, provided that the procedure is not biased a priori.

Finally, in the particular case of our PD problem in Mexico, a priority is respecting municipal boundaries, that is, municipalities must not be divided into more than one district. Since the Mexican municipalities have highly non regular geographical shapes, it is very hard to find districts with regular shapes without dividing them in smaller parts. This means that geographical compactness and respect of municipal boundaries are conflicting criteria and, between the two, we gave priority to the second. This choice also depends on an additional consideration, which is very important when coping with the delicate criterion of respect of minorities. Following the principle that indigenous representation must be guaranteed in the Parliament, the idea of this criterion is that indigenous must be collected in the same districts to gain representation power. Depending on where the indigenous are actually located in the country’s territory, this task may become really hard. Imposing compactness in this framework may produce conflicts in the model tasks, and this may prevent the formation of suitable indigenous districts. For this reason we do not consider compactness when designing the indigenous districts in Phase 1 of our procedure.

In our second phase the situation is completely different, since we have just to produce non-indigenous districts, and we do not care any more about the criterion related to the minorities. Therefore, in this case, compactness could be considered, even if, together with population balance and contiguity, this results in a very hard model. To manage this aspect, in our second phase we include compactness and try to solve the model. As we will see, the model becomes impossible to solve to optimality in short times. For this reason we resorted to a successive divisions approach by applying the districting model with compactness and dividing the territory into two parts in successive steps. This is a classical approach in territory design and in PD literature, see, for example, Forrest (1964).

In the paper we test our procedure on Chiapas and on some additional artificial data sets with size ranging from 100 to 200 territorial units (municipalities). For Chiapas and the other territories of similar size (120 units) we manage to solve the problem by applying our MILP models, while for the cases with 210 units the computational time for solution becomes too long and an heuristic procedure is required.

The paper is organized as follows. Section 2 outlines the main characteristics of the classical PD problem and the traditional PD criteria. Section 3 introduces the notation and illustrates the mathematical programs used in our procedure to solve the problem exactly. On the other hand, Sect. 4 illustrates an alternative heuristic approach which can be used when the exact solution becomes a hard task. Section 5 reports on the results of the application to the Mexican state of Chiapas and to a set of fictitious territories with size similar to Chiapas or larger. Finally, Sect. 6 draws some conclusions and final thoughts, as well as possible extensions of our approach.

2 Criteria

Classical criteria in political districting are population equality (or balance), conformity to administrative boundaries, contiguity and compactness. In our model we also include the respect of minority groups. We briefly recall each of them in what follows.

Population equality Under the assumption that the electoral system is a plurality one, all districts should have the same proportion of representation (according to the “one person, one vote” principle); in particular, in case of single member districts, they should have nearly the same population. This criterion could be implemented as a constraint in the model, by fixing a maximum tolerance on the deviation of the population of each district from the average district population, and imposing each district population to be within the tolerance thresholds. The ideal situation would be having exactly the same population in each district, but this is obviously impossible to get, and typically the maximum absolute deviation is fixed as a percentage of the average district population. In this way, the model rigidly bounds the districts’ populations from above and below.

As for any other criteria, in a mathematical program, population balance can be pursued also by means of the objective function. In this case, a measure of the total deviation of population over all districts must be established (for example one can compute the \(L_1\)-norm or \(L_2\)-norm of the districts’ populations), and the model tries to minimize it. This leads to different mathematical models according to the algebraic form of the objective function.

Conformity to administrative boundaries According to this criterion, one should avoid as much as possible that already existing administrative or normative zones (such as counties or municipalities) are split among two or more electoral districts. Actually, splitting a municipality into two or more parts does not affect conformity to its administrative boundaries if each of these parts corresponds to a single district. In fact, even if in this case the integrity of the municipality is broken, its separated parts are not included in a district together with portions of other municipalities. This last situation must be avoided instead. On the other hand, if integrity of municipalities is imposed, the districts automatically satisfy conformity to municipal boundaries, too. This is in fact the way in which we pursued this criterion at best in our model.

Compactness Compactness is a very intuitive concept, but, unfortunately, a rigorous definition of this notion does not exist. A district may be considered compact if it spans a round region, without straggling or rambling. Deviation from compactness has been classified by Taylor (1973) according to the shape of the district in the following four categories: elongation, indentation, separation, and puncturedness. Notice that Taylor’s definition of compactness is very strong, since it implies both contiguity (non-separation) and absence of holes (non-puncturedness). Caution should be taken when dealing with this criterion because every attempt to define a correct measure of compactness turns out to be strongly related to only one of the above categories, and each indicator is able to detect only some types of non-compactness. An idea could be to consider more than one compactness measure at the same time. This implies a careful measurement of compactness at the expense of a very complicated mathematical model which could become unmanageable if there are also other criteria. This is why, in the end, the most practical thing to do is to measure compactness, as every other criterion, with a single index. This is the typical approach in the literature on PD where compactness is frequently measured as the total inertia of the district map, see Grilli di Cortona et al. (1999).

Contiguity A district is contiguous if it is possible to reach any place in the district from any other one in the same district without leaving it. In any territorial districting problem, contiguity is a crucial aspect, since it provides a structural feature aimed at guaranteeing well defined responsibility areas (whichever the activity related to the district: political vote, commercial activities, the distribution of a service). The difficulty with this criterion is that it is hard to be implemented in an algebraic model. For these reasons, the PD problem is frequently modeled via the use of a connected graph, called contiguity graph, which represents the territory, see Ricca et al. (2008) and Ricca and Simeone (2008), among others. After a discretization of the territory into a fixed number of elementary territorial units, in the contiguity graph, nodes correspond to territorial units and an edge between node i and node j exists if i and j are neighbors. In this context, contiguity can be guaranteed by searching for a partition of the graph into connected components. An organized presentation of the main issues related to contiguity in territorial districting can be found in Duque et al. (2007) and in Ricca and Scozzari (2020).

In this paper we consider population balance, conformity to administrative boundaries, contiguity and respect of the Mexican indigenous community.

We basically control population balance by imposing lower and upper thresholds for the district populations.

Conformity to municipal boundaries is considered as a hard condition, and, in principle, our aim is to maintain integral the territory of all municipalities. Unfortunately, as we will see in the application to Chiapas reported in Sect. 5, this is not always possible, since some municipalities with population much larger than the average district population may exist. This evidently prevents perfect respect of municipal boundaries, but, in any case, our approach aims at avoiding as much as possible the division of a municipality into many pieces assigned to different districts.

Districts’ contiguity is a main issue in the methodology proposed in this paper. We apply the approach provided by Shirabe (2009) who introduces a set of flow constraints able to enforce the contiguity of the districts. Even if this requires a polynomial number of constraints, the mathematical models for PD have binary variables, so that the solving the problem to optimality is computationally hard and only problems of small size can be solved in reasonable time.

We point out that there is a variety of approaches for managing contiguity when a graph representation of the territory is adopted. There are three typical approaches based on the following three ideas, see Duque et al. (2007) and Miyazawa et al. (2021): (1) imposing order constraints on the assigning variables related to nodes lying on specific paths; (2) exploiting tree structures to guarantee the contiguity of each district; (3) using networks flow formulations. Among these methods, flow constraints have the best performance since they are able to solve problems with up to 100 nodes. However, this is generally possible only for the basic problem of partitioning a graph into connected components (without other constraints). When, on the contrary, some additional constraints are included in the model even small problems become difficult to solve to optimality. Attempts to overcome this problem are present in the current literature on the subject, and some interesting results are provided for example in Validi et al. (2020), Rios-Mercado and Lopez-Perez (2013) and Oehlein and Haunert (2017). Unfortunately, efficiency in the design of contiguous district maps can be obtained at the price of using high sophisticated technical tools, such as cutting planes strategies, or adding extra constraints to formulate separation problems. On the contrary, a districting method has to be as simple as possible in order to be understood and used by politicians, legislators, public administrators, etc. This is a long-standing question in the mathematics of electoral systems, which always leads to the evaluation of the compromise between efficiency and user-friendlyness of the proposed procedures. In our approach we model contiguity as a hard constraint since we believe that it is a fundamental aspect of the problem, not easily manageable by non technicians. Including it in the model guarantees that lawmakers have a procedure which produces a balanced and contiguous district map, without any need of additional intervention for fixing possible non-contiguity.

Respect of minority groups Given a specific and recognizable type of community, which can be reasonably considered a minority w.r.t. the rest of the population of a country, when designing the electoral districts, one should collect as much as possible people from the minority group in the same districts. In other words, electoral districts’ populations should be as much homogeneous as possible w.r.t. the group identity.

As already discussed, in the Mexican case, maintaining the identity and the representation power of the indigenous community is a main issue. This is the reason why, in our approach, we focus our attention on this aspect and try to design a model approach aimed at guaranteeing respect of communities.

Finally, as we will see in Sect. 3, we consider the compactness criterion in our second phase model by modeling it in the objective function.

3 A two-phase districting procedure for political districting with minority groups

The methodology proposed in this paper is tailored for PD in Mexico, but can be applied in general when the population of a given country is characterized by the presence of a well defined minority group and the law supports the representation of such minority. The method is based on Mathematical Programming, and works in two successive stages: in the first one, districts including the minority groups are designed; then the district map is completed in the second stage with the formation of non-indigenous districts. The method is tested on real-life data referring to the territory of Chiapas and on some fictitious territories represented by grid graphs with size similar to Chiapas or larger. A successive divisions approach is applied when the MILP cannot be solved to optimality. In these cases, even if the solutions of the models are not exact, we manage to obtain a good solution w.r.t. to all the PD criteria considered in the model. This provides a practical solution tool for political districting able to give automated decision support to lawmakers and to electoral offices. A heuristic variant of the method is also developed to solve problem instances of larger size.

The PD problem is the following one. A division of the territory into municipalities is given. Each municipality represents an elementary territorial unit and is characterized by its resident population. Municipalities are classified into two types according to how large is the number of residents belonging to the minority. A threshold \(\tau \) (fixed in advance by the Government) is used to obtain this classification. A municipality is classified as a minority municipality if at least \(\tau \%\) of its population belongs to the minority. We also consider a graph representation of the territory which is useful for visualizing the results on a map and helpful to formulate and understand the contiguity constraints, which in our model are implemented by means of network flow constraints, see Ahuja et al. (1993).

The connection structure of the graph is also exploited in the heuristic procedure that follows a constructive strategy of the districts and works by adding municipalities one at a time.

In the contiguity graph G, nodes represent municipalities and there exists an edge between nodes i and j if the corresponding municipalities share a common boundary (different from a single point). As we will see, in order to implement the flow constraints in the model, we have also to consider the network \({\mathcal {G}}\) which can be obtained from G in the ordinary way, i.e., by maintaining the set of nodes and replacing each edge \(<i,j>\) of G by a pair of (directed) arcs (i, j) and (j, i).

The PD problem is formulated as partitioning the set of the municipalities (nodes of the graph G) into a prefixed number k of contiguous districts (connected components of G), taking into account the basic PD criteria. Aggregating nodes of G, the municipal boundaries are automatically respected by the fact that a municipality (node of G) is never split among more than one district. No other administrative boundaries are considered.

The special situation given by the existence of the indigenous minority also requires that only a part of the k districts contains the minority group population, so that a number \(k_I\) is given as an input parameter providing the number of minority districts to design.

3.1 Basic notation and parameters’ definitions

We introduce here all the notation necessary to formulate the mathematical programming models presented in the next sections. Considering the Mexican case, we have indigenous and non-indigenous population.

Sets

M:

Municipalities

\(M_{I}\):

Indigenous municipalities

\(M_{NI}\):

Non-indigenous municipalities

K:

Districts

\(K_{I}\):

Indigenous districts

\(K_{NI}\):

Non-indigenous districts

Parameters

\(p_{i}\):

Population of municipality i

m:

Number of municipalities

\( m_I\):

Number of indigenous municipalities

\( m_{NI}\):

Number of non-indigenous municipalities

k:

Number of districts

\( k_I \):

Number of indigenous districts

\( k_{NI} \):

Number of non-indigenous districts;

\({\bar{P}}=\displaystyle \sum _{i \in M} p_i / k\):

Average district population (target population)

\(P_{h}\):

Population of district h

\(\alpha \):

Maximum absolute deviation for each district population to \({\bar{P}}\)(\(\%\))

\(d_{ij}\):

Distance between municipality i and municipality j (in km)

Decision variables

\(x_{ih}\):

: Equals 1 if municipality i is assigned to district h, 0 otherwise

\(w_{ih}\):

: Equals 1 if municipality i is chosen as the center of district h, 0 otherwise

\(y_{ijh}\):

: Amount of flow from municipality i to municipality j for district h

3.2 Mathematical programming models

In this section we introduce the mathematical programming models which we apply to build a PD map taking into account minority groups in Mexico. We propose Integer Programming formulations with non linear objective functions which are then linearized to obtain the corresponding Mixed Integer Linear Programs.

Our approach applies in two successive phases. The first one is dedicated to the design of the \(k_I\) indigenous districts, which should include all the indigenous municipalities. In the second phase, the remaining municipalities are considered to form the rest of the districts (\(k_{NI}\)). Note that in the first phase all municipalities are considered, but the model does not force those in \(M_{NI}\) to be assigned to some districts. This is motivated by the idea of giving flexibility to the model in the first phase, when population from the minority group must be collected together as much as possible, but provided that all PD constraints are satisfied.

$$\begin{aligned} \min _{x}\left( \displaystyle \max _{h \in K_{I}} \displaystyle \sum _{i\in M_{NI}} x_{ih} \right) \\ \text{ s.t. } \end{aligned}$$
$$\begin{aligned}&\displaystyle \sum _{h\in K_I}x_{ih} = 1 \qquad \forall i\in M_{I} \end{aligned}$$
(1)
$$\begin{aligned}&\displaystyle \sum _{h\in K_{I}}x_{ih} \le 1 \qquad \forall i\in M_{NI} \end{aligned}$$
(2)
$$\begin{aligned}&\displaystyle \sum _{i\in M} w_{ih}=1 \qquad \forall h \in K_{I} \end{aligned}$$
(3)
$$\begin{aligned}&w_{ih}\le x_{ih} \qquad \forall i \in M, \forall h \in K_{I} \end{aligned}$$
(4)
$$\begin{aligned}&\displaystyle \sum _{j|(i,j)\in A}y_{ijh}-\displaystyle \sum _{j|(j,i)\in A}y_{jih}\ge x_{ih}-\left[ \;|M|-|K_{I}|+1\right] w_{ih} \quad \forall h \in K_{I}, \forall i \in M \end{aligned}$$
(5)
$$\begin{aligned}&\displaystyle \sum _{j|(j,i)\in A}y_{jih}\le [\;|M|-|K_{I}| \;]x_{ih} \quad \forall h \in K_{I}, \forall i \in M \end{aligned}$$
(6)
$$\begin{aligned}&(1-\alpha ){\bar{P}}\le \displaystyle \sum _{i\in M}p_{i}x_{ih}\le (1+\alpha ){\bar{P}} \quad \forall h \in K_{I} \end{aligned}$$
(7)
$$\begin{aligned}&y_{ijh}\ge 0 \quad \forall h\in K_{I}, \quad \forall (i,j) \in A \\&x_{ih}, \; w_{ih} \in \{0,1\}, \quad \forall h\in K_{I}, \quad \forall i \in M \end{aligned}$$

The formation of the \(k_I\) districts of the first phase is performed via restrictions (1) and (2) in the model, according to which a municipality \(i \in M_I\) should be assigned to some districts in \(K_I\) (the constraint is an equality), and a municipality \(i \in M_{NI}\) could be assigned to one of them (the constraint is an inequality). Constraints (3) state that each district in \(K_I\) should have exactly one center, while constraints (4) model the dependency between variables \(x_{ih}\) and \(w_{ih}\). Restrictions (5) and (6) are the flow constraints proposed by Shirabe (2009) for districts’ contiguity and involve variables \(y_{ijh}\) representing the flow from municipality i to municipality j related to contiguity for the hth district. Note that the use of these flow constraints requires the model to identify one center per district. The role of such centers is merely technical and in our application it has no specific political, territorial, or demographic meaning. Constraints (7) limit the population of the districts between two bounds whose level can be modulated by changing the percentage \(\alpha \) that establishes the maximum and minimum absolute population deviations from the average district population \({\bar{P}}\). The respect of minority groups is considered in the objective function which tries to minimize the maximum number of non-indigenous municipalities belonging to the districts in \(K_I\). This objective function can be linearized using some well-known techniques in order to obtain an equivalent MILP. A new variable \(\lambda \ge 0\) is introduced representing the maximum number of non-indigenous municipalities in an indigenous district. Therefore, the objective of the model is to minimize \(\lambda \) under the following set of constraints which guarantees that \(\lambda \) is the above defined maximum:

$$\begin{aligned} \lambda \ge \sum _{i\in M_{NI}} x_{ih} \; \; \; \forall h\in K_I \end{aligned}$$

Once the indigenous districts have been formed, a second mathematical model is applied to complete the district map. At this stage only non-indigenous municipalities are involved and, in particular, only those which were not assigned to any district in the first phase. Even if they actually are a subset of \(M_{NI}\), for the sake of simplicity, in the following we refer to this subset (of only non-indigenous municipalities) still as \(M_{NI}\).

$$\begin{aligned} \max \left( \displaystyle \min _{h \in K_{NI}} \displaystyle \sum _{i\in M_{NI}} p_{i}x_{ih} \right) \\ \text{ s.t. } \end{aligned}$$
$$\begin{aligned}&\displaystyle \sum _{h\in K_{NI}}x_{ih} = 1 \quad \forall i\in M_{NI} \end{aligned}$$
(1)
$$\begin{aligned}&\displaystyle \sum _{i\in M_{NI}} w_{ih}=1 \quad \forall h \in K_{NI} \end{aligned}$$
(2)
$$\begin{aligned}&w_{ih}\le x_{ih} \quad \forall i \in M_{NI}, \forall h \in K_{NI} \end{aligned}$$
(3)
$$\begin{aligned}&\displaystyle \sum _{j|(i,j)\in A}y_{ijh}-\displaystyle \sum _{j|(j,i)\in A}y_{jih}\ge x_{ih}-\left[ \;|M_{NI}|-|K_{NI}|+1\right] w_{ih} \quad \forall h \in K_{NI}, \forall i \in M_{NI} \nonumber \\\end{aligned}$$
(4)
$$\begin{aligned}&\displaystyle \sum _{j|(j,i)\in A}y_{jih}\le [\;|M_{NI}|-|K_{NI}| \;]x_{ih} \quad \forall h \in K_{NI}, \forall i \in M_{NI} \end{aligned}$$
(5)
$$\begin{aligned}&\displaystyle \sum _{i\in M_{NI}}p_{i}x_{ih}\le (1+\alpha ){\bar{P}} \quad \forall h \in K_{NI} \end{aligned}$$
(6)
$$\begin{aligned}&y_{ijh}\ge 0 \quad \forall h\in K_{NI}, \quad \forall (i,j) \in A \\&x_{ih}, \; w_{ih} \in \{0,1\} \quad \forall h\in K_{NI}, \quad \forall i \in M_{NI} \end{aligned}$$

This second model has a structure similar to the previous one, but now the territorial units are all of the same type (all non-indigenous), so that the objective function can be exploited in order to reduce the number of constraints in the model. Therefore, now we bound districts’ populations only by above, and we control them by below with a max–min objective that can be linearized as before, by introducing a new variable \(\mu \ge 0\) representing the minimum district population, as well as the related set of constraints:

$$\begin{aligned} \mu \le \sum _{i\in M_{NI}} p_{i}x_{ih} \; \; \; \forall h\in K_{NI} \end{aligned}$$

In order to take into account also compactness, an alternative model was considered in which both lower and upper bounds on population are included in the set of constraints, while total inertia is minimized as objective function. This leads to a Phase II model which analogous to the one by Hess et al. (1965), but including also the contiguity constraints. Using our model variables the inertia objective is formulated as a quadratic function:

$$\begin{aligned} \sum _{h\in K_{NI}}\sum _{i\in M_{NI}}\sum _{j\in M_{NI}} p_{i}d_{ij}^2x_{ih}w_{jh} \end{aligned}$$

and the Phase II model becomes a Quadratic Program. It is worth noting that, even if the objective function is quadratic, the constraints remain linear, and the model can be solved with the standard optimization solver for this type of programs, by applying a successive division approach, we were able to solve this quadratic program at each stage for the territories of smallest size.

To conclude this section, we point out that, after Phase I, some non-indigenous municipalities which were not assigned to a district may form enclaves, i.e., they can be isolated from the rest of non-indigenous municipalities which will be processed altogether in Phase II. This is a physiological consequence of the two-phase procedure which sometimes may arise. As we will see in Sect. 5, if this happens, only few territorial units remain isolated.

4 Heuristics for the two-phase PD approach

In the application of our exact procedure to Chiapas we encountered some problems of different nature. On the one hand, we detected some irregularities in the structure of the territory which prevented the possibility of exploiting the contiguity graph in the best way. On the other hand, some difficulties arose in the solution of some MILP due to the excessive computational effort required by the procedure, especially when solving Phase II.

The first problem is due to the preexisting territory subdivision into municipalities, which in our model correspond to the elementary territorial units (nodes of the contiguity graph). As already discussed, the model input should be given by elementary units having more or less similar populations. The huge population of Tuxtla in Chiapas shows that this condition is not satisfied in our real case. Since Tuxtla population is not enough to form two districts, we were forced to operate some manual preprocessing on this municipality. This kind of situations does not generally arise if the given administrative division of the territory into municipalities is population balanced. This was one of the reasons why, we decided to extend our experimental analysis and test our procedure also on fictitious territories with balanced municipalities’ populations.

A second problem was detected during the solution of our programs, especially in Phase II, when considering the large-size problems for which the exact approach required too much computational time. This was probably due to the presence of connectivity constrains combined with those on population bounds. To overcome these problems efficiently we developed a heuristic procedure in which we tried to maintain the same two-phase approach as the exact one. It is a constructive procedure which aggregates municipalities one at a time to form the non-indigenous districts. The basic principles of the two-phase approach are still satisfied, but the heuristic procedure allows to solve the second phase faster than before.

As we will see in the section dedicated to the experiments, there is also an additional problem that may require a particular computational effort. It is related to the spatial distribution of the indigenous population on the territory. In fact, even if in most cases the minority groups are all located in a specific well defined part of the state, it may also happen that different communities are found far from each other. In our experiments on fictitious data we generated different configurations in which indigenous municipalities are concentrated, or they spread all over the territory. It is natural to expect that, when the communities are sparse, the districting problem becomes harder, but we will see that some difficulties arise also when they are concentrated in the same zone, but geographically located in the center of the territory.

In all cases in which the computational effort to solve the problem optimally becomes too heavy, we resort to the heuristic method. The empirical study of these cases permitted us to better understand the PD problem with minorities, and also to provide a reference scheme about which cases, for size and territory configuration, can be solved optimally and which necessarily require a heuristic approach.

4.1 The heuristic procedure

The procedure works on the contiguity graph by forming one district at a time. For each district a heavy node (in terms of population) is selected and the algorithm follows a sequential kernel-growth strategy. In order to avoid premature arrests and to satisfy district population bounds, a parameter \(P_{low}\) is introduced to control the amount of population of the districts under construction. The idea is to obtain first the kernels of the districts with a population which is smaller than the imposed lower bound. Next, in the growth step, these partial districts are completed by adding the unassigned municipalities to the districts with smallest population and taking into account contiguity.

At the end, all the municipalities are assigned to some districts. Thanks to the use of parameter \(P_{low}\), which must be carefully calibrated, in our experiments we are able to obtain districts whose population is either in the range of the bounds imposed at the beginning (15%), or it is not too far from such bounds. Therefore, if some districts exceed the maximum possible population, the municipality in the district with the smallest population is removed and it is assigned to an adjacent district with the smallest population. Similarly, a district h may have a population size smaller than the minimum allowed, so that the district adjacent to h with the largest population is selected and, among its municipality adjacent to h, the one with the smallest population is removed from it and assigned to h. In our experiments this kind of situations arises, but, in all cases, they are solved by performing just few of these steps. This is due to the fact that districts with population outside the imposed bounds are, in fact, not too far from such limits, and also thanks to the fact that elementary territorial units are population balanced.

The heuristic algorithm was implemented by using the software Mathematica.Footnote 3 We briefly illustrate the main steps of the procedure.

figure a

The above heuristics is mainly thought for solving the second phase problem, since this is typically the computationally hardest. However, in the larger data sets we encountered computational problems also in solving the MILP model of Phase I, so that the heuristic approach was exploited also in this phase for the hardest problems.

In particular, we resorted to the heuristics for solving the PD problem on fictitious territories when indigenous municipalities have the configuration of being spread over the territory. In this case, the task of collecting all indigenous municipalities in the indigenous districts becomes, in fact, too challenging, and imposing this as a hard constraint may lead to an unfeasible model. This problem arises for all data sets when indigenous are spread-located and, in order to find the indigenous districts, in our Phase I model we have to relax into inequalities the assignment constraints for indigenous municipalities (which before were formulated as equalities) as follows:

$$\begin{aligned} \sum _{h\in K_{I}}x_{ih}\le 1\quad \forall i\in M_{I} \end{aligned}$$
(1)

The MILP is then solved with these relaxed constraints and lowering the average district population to a value equal to \(P_{low}<{\bar{P}}\). This implies that in Phase I only partial districts are produced, for which the population is maintained smaller than the final district population (typically, it is under the lower bound imposed in the model). The partial districts are then completed heuristically by adding adjacent municipalities in order to bring districts’ populations within the prefixed bounds.

A natural consequence of this procedure is that not necessarily all indigenous municipalities are assigned to some indigenous districts in Phase I. With indigenous population spread over the territory this is unavoidable, but thanks to the objective function of our Phase I MILP, we are still able to assign as many indigenous municipalities as possible in such districts.

The above illustrated strategies showed to be effective, since for all our grids we were able to obtain a final contiguous district map with all district populations within the imposed bounds. For spread indigenous configurations, it happened that a single indigenous municipality (or just few) is assigned to a non-indigenous district.

5 Application and experiments

The Mexican Chamber of Deputies is elected by a mixed electoral system. The Chamber of Deputies, is composed by 500 representatives: 300 are elected by a first-past-the-post method in single-member districts; the other 200 are elected through a proportional method in five electoral constituencies with 40 representatives each. The Mexican Electoral Institute recognizes the peculiarity of the Mexican population to have indigenous communities and a municipality is considered indigenous if at least 40% of its population is indigenous, according to INEGI (National Institute of Statistics and Geography, Mexico). We applied our model to design single-member districts in real territory of the municipality of Chiapas, but also to solve the same PD problem on a set of fictitious territories. It is worth mentioning that in the Mexican mixed electoral system the allocation of proportional seats depends on the results of the election by the plurality system. In fact, the votes obtained by a party in a single member district are also used to get seats in the electoral constituencies where the proportional method is applied.

We solved our models by using the AMPL modeling languageFootnote 4 and the available solver CPLEX 12.6.1.0. All our runs could be solved within 15 min on a processor Intel(R) Core(TM) i7-4810MQ CPU @ 2.80 GHZ.

5.1 Application to the State of Chiapas

The state of Chiapas has a total population of 4.8 million people, and a considerable part of it is indigenous. The number of municipalities in Chiapas is 118 and the percentage of indigenous municipalities is 39.8 (47 municipalities).

The number of districts in Chiapas is 13, 5 of which should be indigenous according to the INE/CG59/2017 (total population data and indigenous population per municipality was taken from INEGI’s websiteFootnote 5). In order to visualize the solutions on the map, we used the open-source software R.

In order to implement our model on these real data, it is necessary to perform a preprocessing on those municipalities which show some structural features that do not fit our modeling framework. In Chiapas we detected three situations which need in fact a specific treatment. We illustrate them in the following special cases.

Tuxtla municipality

This municipality is the capital of the state of Chiapas with a population size equal to 555,374. The average district population in Chiapas is \({\bar{P}}=368,969\). Hence, depending on the value fixed for the parameter \(\alpha \), this municipality alone may exceed the upper limit imposed on the district population. Unfortunately, this already happens when considering a maximum percentage of deviation about 15%, but it still happens if it is increased up to 30%.

San Cristobal de las Casas municipality

This municipality is geographically divided into two separated parts. Therefore, it is structurally non contiguous by itself.

Tapachula municipality

Tapachula has a population of 320, 450 inhabitants. Therefore, it alone could form a district respecting the population bounds of a maximum deviation of 15% from the target \({\bar{P}}=368,969\). In spite of this, municipality of Tapachula is geographically located in a position that isolates a group of six municipalities (Suchiate, Frontera de Hidalgo, Metapa, Tuxtla Chico, Cacahuatán and Unión Juárez). These municipalities can be connected among them, but obtaining a total population about 148, 391 which alone is not enough to produce a district. Alternatively, they can be connected to the rest of the Chiapas municipalities, but only through Tapachula. In fact, for this set of municipalities Tapachula represents a barrier of connection with the rest of the territory. Therefore, when it is left alone, it provides a feasible district, but this prevents the formation of other contiguous districts satisfying the population bounds.

Fig. 1
figure 1

Chiapas municipalities not fitting basic data requirements for the application of our models

Full size image

The particular features of each of the three cases listed above (shown in Fig. 1) do not allow to satisfy the modeling prerequisites to apply our methodology. Therefore each situation must be treated in some way before the application of the models.

Since respect of municipal boundaries is a hard constraint in this models, it is not possible to split a municipality (elementary unit) among two or more electoral districts. If a municipality alone exceeds the upper bound on the district population, it could be divided in more than one part, provided that the exceeding population is sufficient to form another district (i.e., it reaches at least the lower bound). Since this is not possible for Tuxtla, perfect respect of municipal boundaries is not possible for Chiapas. To cope with this problem, without dividing Tuxtla into too many pieces, we split it a priori into two parts. One has population equal to the upper bound over the district population and forms a district completely included in Tuxtla; the other covers the rest of the population of this municipality and is assigned to another district. Given the structure of this big municipality, which in any case requires to split Tuxtla, this is a simple way to optimize respect of municipal boundaries since the municipality is divided only in two pieces rather than in many.

For San Cristobal de las Casas, which is an indigenous municipality, we have a strange situation in which the territory of the municipality covers two separated portions of land. These are in fact two elementary territorial units in our data set (obtained from the INEGI data base), labeled by number 78 and 120, respectively. In order to avoid unexpected and undesired districts configurations, in our data we maintained the two separated territorial units, but we included in the model an additional constraint which forces these two municipalities to be always in the same district. Therefore, given that \(x_{78 k}\) and \(x_{120 k}\) are the assignment variables for district k and municipality 78 and 120 respectively, the restrictions to impose are the following:

$$\begin{aligned} x_{78 k}=x_{120 k} \; \; \forall k \in K_I \end{aligned}$$
(2)

Only districts in \(K_I\) are involved in this set of constraints, since the two units belong to an indigenous municipality. Combined with contiguity, these additional constraints act to guarantee that in any output district map the two units are always included in the same (connected) district.

Finally, for Tapachula municipality we have another technical problem, since this municipality geographically configures as a physical barrier between a set of municipalities and the rest of the territory. The set, which we denote by S, includes six municipalities, i.e., Suchiate, Frontera de Hidalgo, Metapa, Tuxtla Chico, Cacahuatán and Unión Juárez, which in total do not reach the minimum district population when the threshold of 15% is adopted. On the other hand, by adding also Tapachula the district population upper limit is exceeded. It is then impossible to form a set of contiguous districts, all within the 15% population limit, without dividing Tapachula. Hence, we separated a priori a piece of territory from Tapachula to get one district formed by this part and the 6 municipalities. After this, the rest of the territory of Tapachula forms a new territorial unit to be included in some other districts. By this preprocessing of Tuxla and Tapachula, even if perfect respect of municipal boundaries cannot be reached in Chiapas, we manage to optimize it since only two municipalities are split, and in only two parts. Operating in this way produces two advantages: (1) the structural problems of Chiapas municipalities is overcome; (2) two districts are formed a priori and the number of districts to be formed by the MILP is reduced by 2.

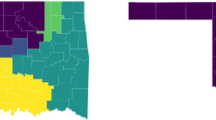
Figure 2 shows the results obtained in the first phase of the proposed model. In this first phase all the 47 indigenous municipalities in Chiapas were assigned to some indigenous districts. After the application of the first phase, three non-indigenous municipalities remained non assigned. Since they formed enclaves enclosed in one of the indigenous districts, they were added a posteriori to that district.

Fig. 2
figure 2

Map of the indigenous districts in Chiapas formed after Phase I

Full size image

Figure 3 shows the non-indigenous districts formed after Phase II is completed. First of all, one can visualize the two districts formed a priori. For Tapachula, one part is included in District 13, together with Suchiate, Frontera de Hidalgo, Metapa, Tuxtla Chico, Cacahuatán and Unión Juárez, while the rest formed a territorial unit which was then included in District 6. On the other hand, one can easily visualize that District 12 is cut from the municipality of Tuxtla, the rest of which is included in District 11.

In this phase 6 districts were actually formed out of the total 8 non-indigenous districts, since, as already discussed, a part Tuxtla forms one district on its own, while another is given by a part of Tapachula and the 6 municipalities of the set S.

These 6 districts are the output of our successive division approach. We first divided the territory into 2 districts, and, successively, we further divided each of the two parts into 3 districts. Therefore we got in total 6 districts in which one can appreciate also the effect of considering compactness. In fact, 4 out of 6 districts have a quite compact shape, while the other two, namely district 7 and 10, have an elongated shape. We point out here that also the institutional districts map shown in Fig. 5 has elongated districts, although with a different shape. In Chiapas this is an unavoidable output for some districts, since some municipalities in the western part of the country have small population density, and elongation derives from the effort of collecting together a sufficient amount of residents to get a district. We point out in any case that, what is guaranteed by our approach is that mathematical programs do not pursue gerrymandering on their own, so that lack of shape compactness cannot be attributed to lack of fairness in the division process.

Fig. 3
figure 3

Map of the non-indigenous districts in Chiapas formed after Phase II

Full size image

The final 13 districts obtained for Chiapas with our procedure are presented in Fig. 4. The population of all the districts satisfies the imposed bounds which, according to a maximum 15% absolute deviation from \({\bar{P}}\), correspond to \(P_{min}=313,624\) and \(P_{max}=424,314\). Figure 5 shows the institutional districts currently adopted in Chiapas.

Fig. 4
figure 4

Complete district map for Chiapas provided by our method

Full size image
Fig. 5
figure 5

Institutional district map for Chiapas

Full size image

Comparing the two maps, we see that both are contiguous and with balanced districts’ populations. On the contrary, we guarantee that municipal boundaries are respected by the districts in Fig. 4, while this is not true for those showed in Fig. 5. Finally, the main criterion related to respect of minority groups is fully satisfied by districts in Fig. 4, since here indigenous municipalities are all collected inside the prefixed 5 indigenous districts. Differently, in the institutional map in Fig. 5 they spread outside such districts (see also Figs. 6 and 7).

In fact, as expected, the main difference between the two solutions appears in the formation of indigenous districts. Both maps satisfy the requirement that at least 40% of the population of these districts is indigenous, but in our map this aspect is optimized since it concentrates in these districts as many indigenous municipalities as possible. Figure 6 for our map and Fig. 7 for the institutional one illustrate the composition of the districts w.r.t. which municipalities they include, showing a clear distinction in our solution between indigenous and non-indigenous districts: indigenous municipalities are all collected inside the prefixed 5 indigenous districts and are well separated from the non-indigenous ones. On the contrary, in the institutional solution they spread outside such districts and district 11, which is non-indigenous, includes many indigenous municipalities.

Fig. 6
figure 6

Indigenous and non-indigenous Chiapas municipalities distribution in the districts provided by our method

Full size image
Fig. 7
figure 7

Indigenous and non-indigenous Chiapas municipalities distribution in the institutional districts

Full size image

The characteristics of the indigenous districts in the two maps can be further illustrated by computing the actual percentage of indigenous inhabitants in each of the five districts for both layouts, which, however may be a bit misleading. In fact, on the one hand, we see that the percentages of indigenous people in indigenous districts are high in both cases, and for both maps there is a district with a clearly lower percentage: District 1 in our solution (65.6%), and District 4 in the institutional one (58.8%). On the other hand, one can realize that this is due to some indigenous municipalities (those labeled as 7, 38, 64, 78, 94 appear in both low percentage indigenous districts) which themselves have probably a low percentage of indigenous. In the end, the result is that the configuration in Fig. 6 has indigenous districts with more homogeneous percentages of indigenous residents, and no indigenous people in the non-indigenous districts. On the contrary in Fig. 7 we see a big difference between the lowest (58.8%) and the highest (87.5%) percentage, and, most all, we have a number of indigenous included in a non-indigenous district (21.8% in District 6).

Basing on optimization, we can maximize the concentration of indigenous into their districts, without leaving any indigenous municipalities outside them. This is very important in view of the representation power which the law wants to guarantee to the indigenous population. Actually, the fact that indigenous population is concentrated in the same districts is meaningful, not only at the moment of the expression of the vote, but also under a territorial administrative viewpoint, when the representatives elected by the indigenous community become operational in the practical implementation of public policies.

5.2 Application to fictitious data

We test our exact and heuristic procedures also on fictitious territories. We choose territories with a very regular structure for which the corresponding contiguity graph is a rectangular grid. As known, and frequently exploited in the applications, see Ricca et al. (2008) and Miyazawa et al. (2021), grids resemble real territories, since they are planar graphs with node degree between 2 and 4. In the pictures shown in the rest of the paper, the elementary units of the grids are represented as adjacent cells.

Table 1 Fictitious problem size
Full size table

In our experimental plan we consider rectangular grids of different size m (number of nodes/municipalities), and the corresponding subdivision into a number (\(m_I\)) of indigenous municipalities and the rest (\(m_{NI}\)) of non-indigenous ones. We also consider different values for the number of districts (k, \(k_I\), \(k_{NI}\)). Table 1 shows the numerical characteristics of our test problems. It can be seen that we test first fictitious territories of size similar to that of Chiapas, then we try to solve the problem on larger size data sets. Results on even larger graphs are not reported since, already with 210 nodes we had some difficulties which forced us to switch from the exact procedure to the (partially) heuristic one. We generate randomly the population of the municipalities of the test problems by choosing populations with size ranging between 100 and 350.

To take into account the existence of indigenous and non-indigenous municipalities, we consider three different configurations for the indigenous distribution over the territory. Thus, in each grid graph, for the location of the \(m_I\) nodes corresponding to the indigenous municipalities we have three situations: (1) all indigenous nodes are inside a smaller subgrid located in the center of the original grid; (2) all are in a smaller subgrid located at a corner of the original grid; (3) all indigenous nodes randomly spread all over the original grid.

In the pictures showing our fictitious territories the subgrids where indigenous are located are visualized within a rectangle (in bold), and the indigenous municipalities are labeled by white numbers (on the contrary, the black numbers refer to non-indigenous). In each figure we also report a table showing the populations of indigenous and non-indigenous districts.

First we illustrate the results obtained on the first three grids with \(M=120\) municipalities, among which \(M_{NI}=46\) are indigenous. In this data sets we have 13 districts, 5 indigenous and 8 non-indigenous. With respect to population, we have \({\bar{P}} = 1532 \) and, considering a value \(\alpha =0.15\), \(P_{min}=1302\) and \(P_{max}=1762\). Computational times required for the solution of the optimization models of Phase I for the grid with 120 nodes and the indigenous communities located in a corner were similar to those for Chiapas. As for Chiapas, we were also able to consider compactness in Phase II and to obtain a good map in reasonable times by applying a successive division approach (see Fig. 8).

Figures 8, 9 and 10 show the results on grids with 120 nodes. One can verify that the bounds on the district population are fully satisfied in all cases. With respect to the distribution of the indigenous municipalities in the territory, with the first two configurations the procedure was able collect all of them within the indigenous districts. On the contrary, when the indigenous municipalities are spread, as expected, in the final solution some indigenous municipalities belong to non-indigenous districts (see Fig. 10). When indigenous are sparse over the territory, in Phase I we are forced to relax the assignment constraint for indigenous and to use the MILP model only to find partial districts which are then completed heuristically. The spread configuration produces some additional difficulties also for solving Phase II, since, after the formation of indigenous districts, in this case the remaining municipalities to be still assigned are sparse as well. In our experiments, this implied that only the heuristic procedure could be applied to complete the district map.

A similar problem was encountered with the configuration in which the indigenous municipalities are located in the center. In this case, for the 120 node grid we were able to apply the exact approach in Phase I, and assign all indigenous municipalities to indigenous districts, but, after this, the remaining non-indigenous municipalities had a ring configuration, and this again made hard the task of solving the MILP model of Phase II.

Fig. 8
figure 8

Case 1: \(M=120\), indigenous located in a corner

Full size image
Fig. 9
figure 9

Case 2: \(M=120\), indigenous located in the center

Full size image
Fig. 10
figure 10

Case 3: \(M=120\), indigenous spread

Full size image

For the grid with 210 nodes we have \({\bar{P}}=1876\), and, using \(\alpha =0.15\), we have \(P_{min}=1594\) and \(P_{max}=2157\). The results for this case are shown in Figs. 11, 12, and 13. It can be seen that, when indigenous population is spread, relaxing the assignment constraints in the model of Phase I unavoidably implies that some indigenous municipalities are assigned to a non-indigenous district (Fig. 13).

Fig. 11
figure 11

Case 4: \(M=210\), indigenous located in the corner

Full size image
Fig. 12
figure 12

Case 5: \(M=210\), indigenous located in a center

Full size image
Fig. 13
figure 13

Case 6: \(M=210\), indigenous spread

Full size image

For all cases with 210 nodes we had computational problems in solving the MILP models exactly. Therefore, it was necessary to exploit the heuristic procedure to get solutions in reasonable times by constructing partial (kernel) districts in Phase I and then using the heuristic to complete them, and then also to produce the non-indigenous ones. In any case, for all grids we were able to obtain a contiguous district map with all district populations within the imposed bounds. In addition, thanks to the integral nature of the municipalities, represented as nodes of the graph, perfect conformity is always guaranteed.

The increasing difficulties found in the solution of PD on territories when the number of units becomes large suggests that it is not possible to apply our MILP models further. Our experiments made us understand up to which size our MILP models can be exploited at best. We also tried to solve the PD problem on territories with 500 municipalities, but, as expected, in these cases only a heuristic approach can be applied.

The results in this section provide district maps which satisfy population equality, contiguity, and guarantee perfect conformity to municipal boundaries. In addition, they optimize the criterion of respecting minority groups. This goal is fully reached for the small-size territories, for which all indigenous municipalities are assigned to indigenous districts, while it is optimized in the larger data sets, or when indigenous are spread, by collecting as much as possible indigenous in their districts.

6 Conclusions

In this paper we propose an optimization approach for Political Districting in Mexico. The aim is to obtain a procedure for designing electoral districts taking into account that in this country there exist minority groups which, according to the law, have a special right to be represented in the Parliament. The approach is tailored for the Mexican case, but it is applicable to any PD problem in which respect of minority groups is a main issue. It was motivated by the observation that in Mexico the law considers the existence of the minority groups and prescribes explicitly that a fixed number of districts should be designed with the precise aim of supporting their representation. For this reason, we focus our attention on minorities and suggest a procedure which collects together in the prescribed number of indigenous districts as many indigenous municipalities as possible. We also consider the basic PD criteria of contiguity, which is treated as a strict constraint, together with population equality and conformity to municipal boundaries, which are satisfied at best. In particular, population equality is satisfied according to the bounds on district populations imposed by the law, while, by considering municipalities as elementary (indivisible) territorial units, conformity to municipal boundaries is automatically satisfied by the districts. This is one aspect of the more general conformity to administrative boundaries criterion which, in our opinion, is fundamental in any territorial zoning problem with an institutional role.

The solution procedure is performed in two stages: the first one is devoted to the design of indigenous districts, the second is aimed at completing the map with the construction of the non-indigenous districts. Our experimental experience showed the pros and cons of the procedure, but the general performance is good, especially for the results w.r.t. respect of indigenous minorities and conformity to municipal boundaries.

In particular, for the solution of the specific Mexican PD problem, we have the following results:

The application of our method to Chiapas produces a district map which matches the law requirements of balancing population and having a fixed number of indigenous districts; under this point of view, our solutions outperforms the institutional district map, since in such map indigenous municipalities are not concentrated only in the indigenous districts, but they spread also in some non-indigenous ones. In our solution they are all collected in the \(K_{I}\) indigenous districts, providing a map in which the separation between the two types of districts is clear.

The districts map provided by our procedure outperforms the institutional one also w.r.t. conformity to municipal boundaries, which is one of the most important criteria according to the Mexican law. Actually, in the institutional district map, several municipalities are split between more than one district, and this is an evident consequence of pursuing population balance without caring of municipalities’ borders. This splitting does not appear in our map, except for only two cases in which the territory of a municipality is divided between only two districts. This is, in fact, unavoidable for Chiapas, due to some structural problems in the already existing administrative division of its territory into municipalities. If population equality must be satisfied within the bounds imposed by the law on district populations, at least two splits must be performed.

The good performance of the exact two-phase districting procedure is confirmed when applied to our artificial data sets, but only if the size of the problem is within a maximum which corresponds more or less to the size of Chiapas. For these problems, as for Chiapas, we also managed to take into account the compactness criterion when designing the non-indigenous districts, without loosing anything in conformity to municipalities boundaries. On the contrary, we discarded compactness in the formation of the indigenous districts, basically because it is conflicting with respect of minority groups. These results suggest that the method can be successfully used for practical application of PD problems.

On territories of larger size good district maps can be still obtained in reasonable times by resorting to the heuristic procedure. The two-phase approach shows some difficulties when the distribution of the indigenous population over the territory has a very particular (non-concentrated) configuration. Unfortunately, in PD with minority groups, if this is the case, the problem becomes harder for any procedure, and typically this requires ad hoc intervention and additional computational effort. In our approach, we were able to cope with this by applying our kernel-growth procedure.

We finally point out that our procedure is conceptually simple and easy to apply (of course, with suitable computer aid) by the electoral offices who have to implement the operations prescribed by the law. We think that this is an important aspect when mathematical models and methods are applied in the social science context and, in our opinion, this should be promoted also in view of the principles of transparency and simplicity which are at the basis of the electoral law in any country.

We conclude the paper by meditating on our heuristics which is clearly very simple and straightforward, but this was mainly due to the fact that it was developed when experiments demonstrated the impossibility of applying our MILP for large size problems. We think that our future work may be headed towards developing a most sophisticated heuristic procedure which is still able to exploit the two-phase approach proposed in this work.