Abstract
In this paper, we examine the effect of relative/absolute firm efficiency on weighted average cost of capital (WACC). Using a sample of Korean listed firms, we find that WACC is negatively associated with relative firm efficiency (operational performance) suggesting that firms with higher (lower) relatively efficiency are expected to pay lower (higher) capital costs. When we repeat our analysis using absolute firm efficiency (ROA), we do not find a statistically significant relationship. Our results suggest relative efficiency which is estimated as output (sales) divided by the resources that are directly under the control of management is assessed by capital providers and impounded into a firm’s capital costs. Absolute efficiency (ROA) which is estimated as sales divided by total assets is not. Our results suggest that simple accounting ratios used in the accounting literature are not considered as informative to explain borrowing costs compared to relative efficiency that captures managerial operational performance.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The efficiency-risk hypothesis implies efficient firms have a higher concentration of debt in their capital structure, suggesting that inefficient firms face financing limitations based on perceived risk (Margaritis & Psillaki, 2010). However, the efficiency measurements employed by capital providers to measure risk is not well-established in the literature. Efficiency studies are divided into two methodological approaches (1) absolute efficiency (AFE) and (2) relative efficiency (RFE). AFE is estimated using variations of simple accounting ratios, such as sales (output) divided by assets and/or capital (input). RFE is a more sophisticated technique that is estimated using two techniques: (1) Data Envelopment Analysis (DEA) using linear programming, and (2) econometric techniques such as Stochastic Frontier Analysis. Increasingly, studies report that RFE is inherently more informative compared to simple accounting ratios because it has the potential to capture managerial performance (Combs et al., 2005; Crook et al., 2008; Demerjian et al., 2012a, 2012b; Frijns et al., 2012). Recent studies use DEA to develop RFE models that measure operational efficiency (Demerjian et al., 2012a, 2012b; Lim & Mali, 2018a, 2018b). Operational RFE measures capture efficiency as relative sales generated (output) from resources/costs under the direct control of management (input). Based on the extant literature, RFE can be considered a superior estimation model compared to AFE. However, from a real-world application standpoint, whether firm stakeholders and market participants interpret that both types of efficiency are equal is a question left unanswered.
There is evidence that rating agencies provide higher credit ratings to firms with higher relative efficiency, implying RFE is a specific form of information that can be used as an indicator of whether a firm is likely to survive a business cycle (Lim & Mali, 2019). Mali and Lim (2021) demonstrate that audit clients (firms) are incentivised to signal operational performance (RFE) is genuine by securing increasing audit effort. The results indicate that client firms believe that there are economic benefits to signalling robust performance to market participants based on RFE. Thus, in this study, we are motivated to establish whether previously unknown economic benefits associated with RFE can be ascertained by firms, and empirically demonstrated. We are also motivated to illustrate whether capital providers differentiate between more sophisticated RFE techniques and simple AFE techniques, hence adjust borrowing costs accordingly based on the perceived information quality of both measurements.
Using OLS regression, we find a negative relation between WACC and RFE. The results demonstrate that firms with higher RFE are required to pay lower capital costs compared to less efficient firms. We interpret that the ability of a firm to generate sales based on resources that are directly under the control of management are considered by capital providers as a robust measurement of operational performance (risk); thus, WACC is reduced. Next, we test whether RFE and AFE are considered equal by capital providers. We find a statistically insignificant relation between WACC and ROA (AFE measure). When we add both AFE and RFE into regressions, RFE is still statistically significant with WACC, AFE remains statistically insignificant. The results suggest that RFE has an incremental effect on WACC, but AFE does not. Our results are consistent to various forms of additional analyses including the division of WACC into its two individual components; Cost of Debt (COD) and Cost of Equity (COE), 'risk criteria', persistency tests, stochastic frontier analysis and Fama and MacBeth (1973) year, industry regressions and endogeneity tests.
Our study is important for several reasons. First, Yatsenko and Hritonenko (2016) report that there is a connection between the production process and capital costs. We extend this argument by clearly demonstrating that after controlling for known firm risk determinants, higher levels of RFE reduces WACC. We interpret that capital providers have the sophistication to monitor operational performance and impound the associated risk into WACC. Securing inexpensive WACC is the most important function of a firm’s finance department. Thus, we expand the literature by demonstrating a specific example where robust tactical management has an explicit organizational advantage. Second, the productivity literature identifies two forms of efficiency, AFE and RFE. However, specific examples of the relative informativeness of both efficiency measures are rarely captured empirically. The extant literature acknowledges that RFE is considered more informative compared to AFE based on its various computational advantages (Demerjian et al., 2012a, 2012b; Leverty & Grace, 2012; Barr & Siems, 1997; Andersen & Petersen, 1993; Cook & Zhu, 2006). Our results demonstrate a specific example where RFE is considered incrementally informative by capital providers, but AFE is not. To the best of our knowledge, we are the very first to capture a different relationship between RFE and AFE with any dependent variable based on performance/risk. To avoid repetition, we provide a detailed explanation of the numerous reasons why RFE can be considered a more informative efficiency measure by capital providers in the hypothesis development (H.2.) and conclusion Sect. 6).
Finally, there are conflicting views in the productivity literature about the usefulness of absolute accounting numbers as a measure of firm performance. Proponents consider AFE to be the most important measure of success (Rangone, 1997), with critics suggesting that AFE is uninformative (Chamber, 1960; Athanassopoulos & Thanassoulis, 1995). In our study, we show AFE is not as informative to capital provides, suggesting that firm operational performance (RFE) is a more important measure of risk compared to ratios that signal accounting profit (AFE). Because both efficiency measures can be considered different by market participants, we would encourage future studies to include both RFE and AFE measures into regressions to enhance the predictive validity of empirical models.
The remainder of our paper is structured as follows. In the next section, we review literature and investment theories relevant to our hypotheses. In Sect. 3, we explain our research design, and provide information about model design. In Sect. 4, we analyse empirical results. In Sect. 5, we explain our additional analysis. Section 6 concludes.
2 Literature review and hypothesis
2.1 Literature review
McWilliams and Smart (1993) suggest that more efficient firms have a comparative advantage relative to inefficient industry peers. Consistent with the efficient structure hypothesis, Demsetz (1973) surmises that firms with the ability to make robust decisions to optimize efficiency will earn higher profits, increase market share and become larger. Efficiency ratios capture the resource management effectiveness of firms, with higher efficiency demonstrating effective strategic management (Neely et al., 1995). Management can improve efficiency by implementing two different strategies: Firstly, sales maximization (output). Management that are able increase sales demonstrate an ability to understand; the needs of their customers; market trends; and technological developments. Secondly, firms that optimize resource expenditure (input) without reducing sales can also be considered efficient. Efficient firms utilize available resources to optimize sales including production, advertising, marketing, staff and capital expenditure. However, given management can employ different strategies to optimize efficiency, there is an increasing impetus in the literature to define efficiency as an organizational construct.
The productivity literature divides firm efficiency into two methodological approaches, AFE and RFE. AFE calculates a firm's efficiency as the ratio of output divided by inputs. Examples of absolute accounting ratios include the value of total earnings divided by total assets (ROA) or equity (ROE) and ATO (asset turnover ratio) amongst others. In empirical studies, ROA is the most commonly used AFE measure because it is simple to estimate and easily interpreted. Countless studies capture a positive relation between AFE and numerous forms of organizational performance (Abarbanell & Bushee, 1997; Lev & Thiagarajan, 1993; Ou & Penman, 1989; Soliman, 2008). Whilst AFE is simple to calculate and interpret, there is a vast literature suggesting that RFE is a more robust measure of firm efficiency compared to AFE (Callen, 1991; Demerjian et al., 2012a, 2018; Frijns et al., 2012). Critics argue AFE is an inferior measure compared to frontier analysis because (1) AFE can be influenced using accounting treatments and policies that reduce the levels of assets (denominator) relative to sales (numerator), (2) all values are considered as equivalent inputs to generate sales when some inputs will yield higher sales, and (3) absolute measures such as ROA are considered equivalent market/industry measures when the profit margins are almost certainly different in different industries (Combs et al., 2005; Crook et al., 2008; Demerjian et al., 2012a, 2018).
Because AFE can be considered a less robust measurement of efficiency compared to RFE, increasingly, studies have adopted RFE to add robustness to empirical models. Numerous studies use frontier analyses to capture firm effectiveness (Bergendahl, 1998; Berenguer et al., 2016; Bendoly, et al., 2009; Ross & Droge, 2002; Thompson et al., 1996; Sherman & Zhu, 2006; Sun, 2004). Moreover, studies demonstrate a positive relation between relative efficiency and various forms of organizational performance (Alam & Sickles, 1998; Cummins et al., 2010; Greene & Segal, 2004). Lim and Mali (2018a, 2018b) show RFE influences the propensity of market participants to invest/disinvest. Mali and Lim (2019) demonstrate that firms with higher RFE are likely to achieve higher credit ratings. A study by Baik et al. (2013) shows that after controlling for absolute efficiency, relative efficiency has a positive and statistically significant relation with profitability changes without the existence of a collinearity problem. The findings show that both RFE and AFE can represent different forms of efficiency. Baik's (2013) study raises important questions whether RFE and AFE are considered equally by market participants or whether they differentiate between both types of efficiency.
Whilst Tsolas (2015) suggests that there is no association between operational performance and firm risk, in this study, we consider capital providers are likely to consider firm performance based on both RFE and AFE. Both debt and equity providers issue capital cost terms to firms based on performance/risk. Therefore, they have a high incentive to monitor clients to optimize capital investment. To estimate whether capital providers consider efficiency performance when providing capital, we utilize WACC. WACC is the average rate a firm is expected to pay to secure capital indicating the minimum return that a company needs to earn on an existing asset base to satisfy its shareholders, creditors, and other capital providers. WACC is subdivided into two measures; the cost of debt (COD), and the cost of equity (COE) calculated using the Capital Asset Pricing Model (CAPM). COD is calculated as the aggregated value of interest demanded from a bank, bondholders and other forms of debt financing institutions. The two main forms of debt available for firms are private debt markets (banks) and public debt markets (bondholders). Banks and credit rating agencies offer more favourable credit terms based on a robust analysis of firm level risk (Francis et al., 2005; Bharath, 2008). Evidence suggests that despite high profile financial crises, banks and credit rating agencies are effective monitors of firm level risk, and banks are effective monitors for the debt market (Dhaliwal et al., 2011). Based on the literature, debt providers are likely to conduct a robust analysis of firm fundamentals including RFE, thus have the potential to include RFE inferences into COD.
COE is estimated using the Capital Asset Pricing Model. CAPM has been developed to explain the positive linear relationship between risk and market returns (Markowitz, 1952; Sharpe, 1964; Lintner, 1965; Black & Scholes, 1973). To improve the predictive validity of the model, Fama and French (1992) add variables known to influence risk, size and market-to-book ratio. Carhart (1997) enhance the model by considering the momentum factor for stocks. Fama and French (2016) develop the model again by including profitability and investment proxies. Critics of CAPM suggest it is not a complete model (Pastor and Stambaugh, 2003; Easley et al., 2002). Fama and French (2004) suggest the model is miss-specified because beta does not differentiate in the direction of stock movements; and French (2016) criticize that CAPM risk estimates are time constant. However, despite the criticisms of CAPM, the model is accepted by analysts and investors as a measure of the returns that income maximising investors would require for bearing additional risk (Gregory et al., 2018). Therefore, based on the efficient market hypothesis, investors are risk sensitive and are likely to conduct a robust analysis of firm fundamentals when issuing capital. As with CAPM, whilst there is evidence that WACC has limitations (Barth et al., 2013), WACC is used on a daily basis in international markets to measure risk. Thus, there is a strong potential that firm characteristics such as RFE and potentially AFE are impounded into this WACC.
2.2 Hypotheses
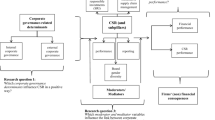
Previous studies suggest that market participants are motivated to interpret operational performance (RFE) (Lim & Mali, 2018a, 2018b; Mali & Lim, 2019), with RFE reducing firm level uncertainty and having a positive effect on credit ratings. As a result, there is also the potential that capital equity and debt providers consider RFE when issuing capital. Whilst high levels of efficiency are important for firms, a firm’s primary function in financing is to reduce capital costs. Therefore, capturing whether firms can achieve the double comparative advantage of lower WACC and higher RFE is an important discovery for firms, as well as the literature.
Firms can maximize efficiency using two different strategies. (1) a firm can increase sales to maximize efficiency (output maximization), implying experienced managers have developed strategies to increase output (sales), for example; effective advertising; marketing campaigns; competitive pricing strategies; and an ability to keep up to date with technological developments and industry trends, relative to peers. (2) A firm can reduce expenditure to increase their efficiency (input minimization) by optimizing resources. Such firms are likely to have the ability to; keep their staff motivated without incurring unnecessary expenses; optimize their production processes and; are unlikely to waste resources on inefficient projects that do not generate sales. Because RFE is a relative measurement of the effectiveness of the above strategies, we would expect to find a negative relationship between RFE and WACC based on capital providers impounding RFE information into WACC as a form of firm risk, after controlling for other known measures of risk. Thus, we develop the following hypothesis:
H1
Relative efficiency levels reduce a firm’s WACC
In our second hypothesis, we test whether RFE is a more informative measurement of investment risk compared to AFE. There is the potential that RFE and AFE can have different effects on WACC based on the analysis of capital providers. Based on the following methodology advantages, we consider that capital providers may impound RFE into WACC, but not AFE for the following reasons, (1) whilst American evidence suggests that ROE has a negative relation with capital costs (Safdar, 2018), AFE as a measure is subject to a mathematical limitation. It is likely that accounting treatments and financial decisions can influence values such as ROE and ROA. For example, an increased dividend improves the ROE ratio, and land revaluation or patent depreciation enhances ROA performance. Thus, AFE performance ratios subject to accounting treatments can be considered as an inferior measure to RFE, which is not subject to the same level of variation as a result of accounting treatments or modifications. (2) Our RFE measure which captures operational performance is estimated only using (inputs) resources and costs that are directly under the control of management (PPE + Operating Lease + Goodwill + Other Intangibles/Cost of goods sold + SG&A). On the other hand, AFE estimates efficiency using values recorded on annual reports such as land, cash and equivalents (shares) that are not used by managers to generate sales.
(3) RFE is calculated using frontier analysis (Data Envelopment Analysis) to discover the optimum efficiency of a firm within an industry known as a decision-making unit (DMU). Therefore, whilst ROA considers all inputs to be equal, the most effective utilization of $1 resource to maximize sales can be captured using RFE (Demerjian et al., 2012a, 2012b; Jacobs et al., 2016). All firms within a specific industry must decide on the most effective utilization of resources to maximize sales. RFE shows the optimum ratio of cost of goods sold, PPE and all other inputs for a manufacturing firm and identifies the most efficient firm resource utilization from all available inputs. AFE considers all inputs as equal. (4) RFE develops a maximum efficiency vector for all firms within an industry. However, through scaling, RFE avoids the benchmarking problem that exists in traditional methods (Barr & Siems, 1997; Leverty & Grace, 2012). Efficiency values of service firms will be inherently different to manufacturing/merchandising firms. Thus, a like for like AFE ratio can be considered as having inherent industry bias because of the higher margins in some industries. RFE incorporates a weighting structure that provides a relative measure of efficiency for all firms ranging from 0 to 1. (5) Previous studies suggest that increased transparency can reduce information asymmetry and lower WACC (Baik et al., 2013; Barth et al., 2013). AFE considers firms with equal absolute values to have identical performance. However, virtually all possible combinations of inputs for each DMU can be considered using RFE. Therefore, RFE has the potential to reduce information asymmetry because it is a significantly more informative measure of managerial decision making compared to AFE. Based on the above, we develop the following hypothesis:
H2
Relative efficiency has a different effect on WACC compared to accounting book value efficiency.
3 Research design
3.1 Variable definition
3.1.1 WACC
We calculate weighted average cost of capital (WACC) in Eq. (1). WACC is the 'weighted' combination of cost of debt (COD) in Eq. (2) and cost of equity (COE) in Eq. (3). To estimate WACC, we multiply both values; COE and COD with the weightings in Eq. (4) and (5) to aggregate our values consistent with market values recognized on the Korean Stock Exchange and previous Korean literature. We provide details of how WACC is calculated below:
where \({R}_{f}\) the average interest rate for a 3-year treasury bond (the risk-free rate of interest), \({\beta }_{i}\) market beta, calculated using the Equally Weighted Index (EWI), \({MP}_{i}\) market premium; we use 3.3%, following the Korea Stock Exchange report, a value used in previous Korean studies.
The COD weighting is the average IBDC (interest-bearing debts for cost) divided by IBDC plus AMC (average annual market capitalization of common and preferred stock) in Eq. (4). The weighting for COE is AMC divided by IBDC and AMC in Eq. (5). For clarity, we list the below weighting:
3.2 Relative efficiency
Next, we estimate relative efficiency using Data Envelopment Analysis (DEA). To calculate relative efficiency, we borrow from Mali and Lim’s (2018) modified Demerjian et al. (2012a, 2012b) managerial ability (relative efficiency) model which is explicitly designed to capture operational performance using the following procedure. First, we construct a strongly balanced panel by firm and year from 2000 to 2015. Second, we sort firms by year and industry. Third, we classify each firm as an individual decision-making unit (DMU). Each firm listed on the Korean Stock Exchange is considered a DMU. Each DMU is divided by industry to estimate efficiency by industry. We estimate RFE for each individual DMU using Eq. (6). In Eq. (6), the numerator is gross sales (output), consistent with prior research (Verma, 1993). Fourth, we estimate our denominator, the resoues that are directly under the control of a manager (input). Input is divided into 'given resources' and 'costs'. Given resources are equity items listed on a firm's financial statements that are under the control of managers (PPE + Operating Lease + Goodwill + Other Intangibles). Costs are classed as expenses a manager can utilize to generate sales. Costs include R&D, advertising expenses, admin expenses and cost of goods sold (Cost of goods sold + SG&A).
where Sales: (Output) Gross Sales, Given Resources: PPE + Operating Lease + Goodwill + Other Intangibles, Costs: Cost of goods sold + SG&A, PPE: net property, plant, and equipment, Operating lease: net operating lease, Goodwill: purchased goodwill.
Fifth, to estimate DEA, we discover the most efficient firm in each industry by optimizing the efficiency of each firm. This value captures an aggregate of the most efficient expenditure of each given resource and cost per unit of sales. Based on DEA estimations, a value can be estimated for the most efficient utilization aggregate for each firm (efficiency frontier horizon) in each industry. In Eq. (7), sales are represented by s and given resources and costs are represented by m for all DMUs. This is necessary to demonstrate that different industries are required to utilize different combinations of inputs to achieve outputs. We also add weightings for our input and output levels. The weightings for our input and output values are denoted by u and v. The weighting determines the efficiency frontier by varying the weights of u and v and enables a sample and market comparison. After performing Eq. (7) for each firm in each industry, a specific DEA vector for that industry is established.
Finally, we use the industry measures to estimate the efficiency of each firm within a specific industry compared to the market. Thus, the derived optimal weights (DEA vector) are multiplied by the corresponding output and input quantities for scaling purposes to yield a ratio-based efficiency score for each DMU. An ordinal value of 1 is given to the firm with the optimal efficiency on the efficiency frontier. A scaled value for the optimally efficient firm has the potential to be represented 5.5/5.5 (1 scaled). By comparison a scaled less efficient firm has the potential to be represented as 2/5.5 (0.3815 scaled). The scaling procedure allows all firms within an industry to be compared with the market using an ordinal rank. The scaling process allows us to compare how efficiency is achieved in specific industries and in the entire sample of listed firms. Our given resources and costs in Eq. (6) are estimated as x in Eq. (7). Sales in Eq. (6) are represented by y in Eq. (7).
The classical Data Envelopment Analysis (DEA) model by Charnes et al. (1978) assumes constant returns to scale. Conversely, the BBC (Banker et al., 1984) model presents a concave downward efficiency frontier that presumes variable returns to scale. As a benchmark, we assume constant return to scale based on Afzal and Lawrey (2012). Also based on the mechanical relationship between output (sales) and input (costs and operating assets), we believe our DEA model is a robust and felicitous model to report returns-to-scale. In our additional analysis section, we conduct an isotonic regression analysis (see Sect. 5.7) suggesting that there is a strong positive association between output (sales) and each component of input (costs and given resources), providing evidence of constant returns to scale. However, we infer that firms that have increasing returns to scale compared to industry peers are relatively efficient firms, as output increases to a greater extent compared to industry peers (increasing returns to scale). On the contrary, we consider firms that have decreasing returns to scale compared to industry peers, as relatively inefficient firms (decreasing returns to scale).
The DEA variable illustrated in Eq. (7) is listed as our dependent variable \({\beta }_{1}{Relative\_Effi}_{i,t}\) in Eq. (8). In Eq. (8), we perform OLS regression to determine whether our ordinal estimation of relative efficiency using DEA has a negative influence on a firm's WACC. Based on our first hypothesis, we would expect managers that make effective operational decisions to maximize output from given resources to secure lower capital costs. This relation would be modelled as a negative relation between relative efficiency and WACC in Eq. (8).
Absolute efficiency is our second variable of interest. As explained in our literature review, various studies use simple accounting ratios to proxy for absolute efficiency. Absolute efficiency is calculated as overall firm efficiency, computed by dividing EBITDA /prior year total assets. There is the potential that the relation between absolute performance and WACC is negative suggesting capital providers reward firms with higher book value efficiency with lower borrowing costs. If the result is insignificant, absolute efficiency does not provide capital providers with information about investment risk, and has no effect on WACC.
We include important control variables to enhance the explanatory power of our model. The definition for each variable is included in Table 1. The first control variable is Market_Risk, defined as market beta. Beta is the systematic risk of a security in comparison to the market as a whole. Whilst beta is used in estimating COE in CAPM, we also include beta as an important control variable to control for market risk because beta represents the return an investor would expect for bearing additional risk. Therefore, a higher beta is expected to be significantly positively associated with our dependent variable WACC, because higher market risk naturally increases cost of capital. For robustness, in our additional analysis, we exclude beta and repeat our analysis using stock price volatility as a different market risk proxy. Size is calculated as the natural logarithm of total assets. Larger firms are likely to have more resources and lower levels of downside risk; as a result, they are likely to pay lower capital costs. Leverage is calculated as total assets divided by total liabilities. Leverage is expected to have a negative relation with WACC because firms with lower assets relative to debt are risker. Cash performance is proxied by CFO, calculated as cashflow from operations divided by total assets. We expect firms with superior cash performance to have lower borrowing rates compared to firms with inferior cash performance. Earnings management, a form of managerial opportunism is estimated as the absolute value of discretionary accruals suggested by Dechow et al. (1995). We expect firms that engage in earning management should have higher capital costs.
Next, we control for ownership structures using the percentage ownership of the largest shareholder. There is conflicting evidence whether concentrated ownership has a negative, (see Dann & DeAngelo, 1983; Bhojraj Sengupta, 2003; Tran, 2014) or positive (Datta et al., 2005; Shleifer & Vishny, 1997) relation based on large shareholders having the power to expropriate wealth / demanding the implementation of robust governance systems. However, based on Lim and Mali’s (2018a, 2018b) Korean evidence, increasing ownership power enhances monitoring. Thus increasing ownership can be expected to reduce WACC. We provide an ordinal rank for a firm's credit rating from 1 (D) to 10 (AAA) based on the assumption that WACC is decreasing with credit risk. We expect to find a negative association between WACC and credit ratings because a credit rating is designed to capture default risk. Audit hours are shown to be positively associated with relative efficiency (Mali & Lim, 2020). Therefore, we would expect a negative relation between WACC and audit hours based on audit demand theory. All variables are winsorized at the top and bottom 1% to control for the effect of outliers.
3.3 Sample
In Table 2, we provide information about our sample selection process. We download all firm financial data for Korean listed firms, listed on the Korean Stock Exchange (KRX) from KIS-value and TS-2000 databases. After excluding financial firms, we have a potential sample of 14,745 firm year observations. We then discard 3913 observations with insufficient financial data to conduct necessary analyses, leaving a final sample of 10,823. The mean level of our sample's weighted cost of capital and relative efficiency is estimated every year in Panel B. From 2000 to 2015, we show the results of 921 firm observations. In the year 2000, the sample's mean WACC is 8.77 and the sample's mean relative efficiency is 0.53. From 2001 to 2015 the overall trend shows that mean WACC has been decreasing by 71% to 5.12. The sample's mean relative efficiency has increased by 45% to 0.77. The results are consistent with our expectation. We would expect relative efficiency to increase due to market forces including competition and globalization. A decrease in WACC suggests that Korean firms have become relatively less risky since 2000.
4 Empirical results
4.1 Univariate analysis
In Table 3, we provide descriptive statistics and Person Correlations. The means and medians are consistent for all variables, demonstrating a normal sample. The mean value for relative efficiency is 0.64, a positive number. The mean value of absolute efficiency is 0.00. Our results of interest for the Person Correlations are bold in column 1. We find there is a negative relation between WACC, relative efficiency (− 0.12) and absolute efficiency and WACC (− 0.05), both statistically significant at the 0.01% level. Without controlling for firm risk values, the results suggest that more efficient firms are expected to pay lower borrowing costs.
The remainder of our Pearson Correlations show the correct signs and are all statistically significant at the 1% level. Consistent with our expectation, there is a positive relation between relative market risk (0.51), leverage (0.08), earnings management (0.15) and WACC. Likewise, we find a negative relation between size (− 0.11), CFO (− 0.06), large ownership (− 0.03), credit risk (− 0.11), audit hour (− 0.18) and WACC.
4.2 Multivariate analysis
In Table 4, we provide results of OLS regression to test the relationship between relative efficiency and weighted average cost of capital. In row 2, Table 4 we find a negative relation between WACC and relative efficiency (coeff − 0.33, t − 8.35). The result suggests that RFE, a measure that captures the utilization of resources and costs under the direct control of management is considered by capital providers and investors as a form of operational performance that reduces capital costs. We interpret that the management of firms that do not possess the capability of maximizing sales from ‘given resources’ and ‘costs’ must therefore pay a premium based on their relative inefficiency. On the other hand, efficient firms are rewarded by capital providers with lower borrowing costs, allowing us to accept our first hypothesis. All our control variables are statistically significant and demonstrate the expected signs. Market risk (coeff 2.54, t value 74.92), leverage (coeff 0.52, t value 5.78) and earnings management (coeff 2.03, t value 11.40) are shown to increase WACC. Large (coeff − 0.04, t value 3.71), cash rich firms (coeff − 0.81, t value − 6.86) with large ownership (coeff − 0.83, t value − 9.96), higher credit ratings (coeff − 0.06, t value − 5.70) and increased audit effort in hours (coeff − 0.29, t value − 22.85) are also expected to pay lower WACC.
Next, we perform an empirical test to determine whether relative efficiency has a different effect on WACC compared to absolute efficiency. In Table 5, model 1, we list the results from Table 4 to enable a comparison. In model 2, we use OLS regression to establish whether there is a relation between AFE and WACC. Our results demonstrate that there is an insignificant relationship between AFE and WACC. In model 3, we demonstrate relative efficiency has incrementally more explanatory power compared to absolute measures to explain a firm’s WACC. We find that after controlling for absolute efficiency, relative efficiency still has a statistically significant negative relation with WACC (coeff − 0.27, t value − 5.29). The results allow us to accept our second hypothesis. We contribute to the literature by demonstrating for the first time, relative efficiency measuring operational performance, and absolute efficiency measured using a simple accounting ratios are not equivalent measures of firm risk, thus interpreted differently by capital providers.
5 Additional analysis
5.1 Cost of debt versus cost of equity
In our additional analysis, we aggregate a firm's borrowing costs into the two separate components of WACC. We provide details of two separate regressions to estimate the relation between 1, COD with relative efficiency: and 2, COE with relative efficiency. We estimate the values for COD in Eq. (2) and COE in Eq. (3) using the CAPM model. The efficiency-risk hypothesis underpins the development of the main hypotheses for this study, as it provides the link from efficiency to the cost of capital. Under the hypothesis, more efficient firms select lower equity ratios than other firms because higher efficiency reduces the expected costs of financial distress (Margaritis & Psillaki, 2010). Hence more efficient firms may face a lower cost of capital, recognising all else equal. To add further robustness to our analysis, we test whether the cost of debt has a more pronounced association with efficiency compared to cost of equity. In Table 6, we provide the results of our regressions. In column 2, we find a negative relation between relative efficiency and cost of debt (coeff − 0.55, t value − 3.84). In column 3 we find a negative relation between relative efficiency and cost of equity (coeff − 0.41, t value − 21.32). Taken together, the results show that the debt coefficient is more negative (economic significance is larger and both are statistically significance at 1%) compared to cost of equity, implying that as efficiency increases, cost of debt is likely to decrease at a higher rate compared to cost of equity. However, taken together, the results suggest that banks and other financial intermediaries that provide firms with debt expect higher capital cost premiums from firms with lower RFE compared to relatively more efficient peers, consistent with the our main findings.
5.2 Risk criteria
Next, we divide our sample based on risk criteria. In our main analysis, the results suggest that operational performance can be interpreted as a form of risk that increases WACC. Therefore, we divide our groups into 3 'risk criteria' and repeat to see whether it is possible capture consistent results. Our first criterion is a firm’s age; we expect older firms to pay lower WACC based on reputation and market presence. The second risk criterion is firm size; larger firms have more resources compared to smaller firms that are less able to deal with market shocks. The third risk criterion, credit rating is based on the assumption that credit ratings provide a meaningful representation of credit risk (Faure‐Grimaud et al., 2009; Mathis et al., 2009; Skreta & Veldkamp, 2009).
We conduct both univariate mean/median difference tests and multivariate OLS regression analysis to compare different groups. We partition our entire sample into (1) old and young firms, (2) Big and small firms, (3) investment and non-investment grade firms. We define old/young as firms with a ‘firm age’ that is above/below the median. Big/small firms are firms that are listed in KOSPI (large) /KOSDAQ (small) stock exchanges. Investment/non-investment grade firms are the firms with credit rating scores of 5 or/and above/below. In Table 7 Panel A, we illustrate the results of our univariate analysis, the first two columns compare the mean/median of WACC and relative efficiency for two different groups divided by ‘risk criteria’; (1) old and young, (2) KOSPI and KOSDAQ, (3) IG and NIG. The third column titled 'Diff test' shows the difference test results between WACC and relative efficiency based on 'risk criteria'.
Based on firm age, we find that older firms have lower WACC (t − 1.86, z value − 2.88) and relative efficiency (t − 2.67, z value − 5.08) compared to smaller firms. This would suggest that larger firms have more complex business operations; however, are able to retain cheaper capital. Moreover, the results suggest that market participants reward older firms with lower capital costs consistent with business survival theory, (long-term sustainability of organization) that implies older firms can run more complex organizations. Similarly, we find that larger KOSPI firms have lower WACC (t − 7.17, z value − 15.54) and lower relative efficiency (t − 13.14, z value − 8.67) compared to smaller KOSDAQ firms, suggesting that KOSPI listed firms are perceived as less risky, but KOSDAQ firms are relatively more efficient. Finally, we find that IG firms have lower WACC (t − 10.90, z value − 8.57) and higher relative efficiency (t 7.63, z value 13.16) compared to investment grade firms, suggesting that credit rating agencies consider relative efficiency when issuing investment/non-investment grade credit ratings, consistent with Mali and Lim (2019).
In Table 7 Panel B, we use multivariate analysis using 6 different samples based on 'risk criteria'. Overall, there is a negative relation between relative efficiency and WACC consistent with our mean/median different tests and main analyses. After partitioning our sample into two different groups, we find that the negative relationship between relative efficiency and WACC is stronger for: (1) older firms (Coeffi − 0.45, t value − 7.74) compared younger firms (Coeffi − 0.18, t value − 3.34): (2) KOSPI (bigger) firms (Coeffi − 0.41, t value − 7.40) compared to KOSDAQ (smaller) firms (Coeffi − 0.17, t value − 3.05): 3) and NIG firms (Coeffi − 0.27, t value − 7.50) compared to IG firms (Coeffi − 0.48, t value − 5.97). However, regardless of our risk status partitioning, we find consistent evidence that RFE is a statistically significant predictor in reducing WACC.
5.3 Persistency tests
Next, we perform persistency tests. We perform various regressions estimating the relation between relative efficiency and WACC in various periods in period t + 1 (and t + 2). In Table 8, relative efficiency has a persistent effect on a firm's WACC in subsequent periods (t + 1 and t + 2). We interpret that relative efficiency not only predicts the current WACC value, it also predicts WACC in subsequent periods, suggesting that RFE has an incremental effect on WACC in subsequent calendar years.
5.4 Consideration of other control variables
In our main analysis, we use a linear regression model where our independent variable to proxy for market risk is market beta (relative market risk). Although market beta is a robust proxy for risk, we repeat our analysis after replacing market beta with stock price volatility (absolute market risk) based on Lim and Mali (2018a, 2018b) who show that both beta and stock price volatility capture market risk in efficiency models. Untabulated results are consistent with our main analysis using both risk proxies, suggesting our model is robust to both forms of market risk. Secondly, we estimate relative efficiency using SFA instead of DEA. Some studies exclusively use SFA (Callen et al., 2005) to measure efficiency. However, SFA and DEA frontier analyses are commonly and interchangeably used in business academic research (Baik et al., 2013; Dopuchet al., 2003), and both have a high correlation coefficient (Kendall’s Tau). DEA is a non-parametric approach that establishes an efficiency frontier using mathematical programming. SFA is a parametric approach that hypothesizes an efficiency frontier and estimates parameters econometrically using the entire set of DMUs. When we repeat our analysis by replacing DEA with SFA, as expected, our results are consistent with our main hypothesis.
5.5 Firm fixed effect and Fama–Macbeth two-step procedure
Due to market forces, relative efficiency may not be consistent over time due to the accumulation of corporate knowledge and technological developments. For robustness we cross-sectionally estimate relative efficiency for each year in the dataset and examine the relationship between WACC and relative efficiency for each year using the technique suggested by Fama and MacBeth (1973). Thus, to control for year/firm effects, we include dummy variables for each firm and year, and repeat our regressions. We report untabulated results that results are consistent with previous findings.
5.6 Endogeneity tests
Next, we test for endogeneity using the two stage least square model listed in Eq. (9). In stage one of the model, relative efficiency (endogenous variable) is set as a dependent variable with all key determinants included as control variables (period t). The two instruments (independent variables) that are likely to have an influence on relative efficiency are (i) relative efficiency in the previous year (t − 1), because the values are inherently associated, and (ii) 2) absolute efficiency (ATO = Sales/Assets) at time t. We also control for variables that are likely to influence relative efficiency including market risk, size, leverage, CFO, EM, Bigown, credit risk, and audit quality. Our results suggest that relative efficiency is persistent, largely influenced by relative efficiency in the previous year (Coeff 0.65, t value 92.19), and positively associated with absolute firm efficiency (Assets Turn Over ratio) (Coeff 0.02, t value 4.52). Moreover, relatively efficient firms are likely to be relatively smaller (Coeff − 0.01, t value − 4.25) and have higher leverage (Lev) (Coeff 0.06, t value 3.40). Furthermore, they have relatively higher cash performance (CFO) (Coeff 0.09, t value 4.34), have higher ownership concentration (Bigown) (Coeff 0.04, t value 2.74) and higher audit quality (Coeff 0.02, t value 8.34).
After deriving a value of relative efficiency in Eq. (9), we compute Eq. (10) where the computed predicted value of relative efficiency from Eq. (9) is used as a control variable, with other control variable being held constant. Untabulated results demonstrate that our results are qualitatively indifferent (Predicted Relative_effi Coeff − 0.39, t value − 6.53). Next, we conduct the Durbin and Wu-Hausman test. The null hypothesis implies that the variable (relative efficiency) is exogenous. The Wooldridge’s score is insignificant, implying that the model (the positive relationship between the two main dimensions) is free from endogeneity (score = 1.58, p = 0.21).
5.7 Isotonic regression
To justify the selection of variables in our DEA model, we conduct an isotonic regression analysis. For brevity, we only discuss untabulated results. As expected, cost of goods sold and SG&A are strongly positively associated with output (sales), since these are the direct costs to achieve a certain level of sales. Furthermore, tangible resources (net property, plant, and equipment) also show a positive relationship with sales, since larger firms with high level of fixed assets tend to produce a high level of sales. However, intangible assets (operating lease, good will and other intangibles) have a weak relationship with sales, suggesting that intangible assets alone do not directly increase sales.
6 Conclusions
In this study, we question the argument whether capital providers perceive relative firm efficiency (RFE) differently compared to absolute firm efficiency (AFE). Our results show that capital providers demand a higher capital cost premium based on lower levels of RFE. However, interestingly we do not find a consistent relationship when we replace RFE with AFE. We find that ROA (AFE) is not likely to have any influence on a firm’s WACC, suggesting that capital providers do not impound AFE into WACC. Our study is important for several reasons. First, previous studies suggest that credit rating agencies reward firms with higher operational performance (RFE) with higher credit ratings (Lim & Mali, 2019). There is also evidence that RFE has a direct influence on market participants' propensity to invest and disinvest. Our results show that debt and equity providers are also effective monitors of operational performance and reward firms with higher RFE with lower WACC. This result is important to the extant literature because linking managerial performance and firm organizational benefit is referred to as a ‘blackbox’ in the management literature (Combs et al., 2006; Venkatraman, & Ramanujam, 1986). We clearly link managerial decision making and related benefits. The results are important for industry because lowering capital costs is the primary function of a firm’s finance department. We interpret that capital providers consider RFE as a form of firm risk and demand higher WACC based on firm risk status, extending previous studies that suggest that operational performance and firm risk are linked (Hendricks & Singhal, 2005; Jacobs et al., 2016; Kleindorfer & Saad, 2005; Seshadri & Subrahmanyam, 2005).
Second, to our knowledge, we are the very first to show that AFE and RFE are not perceived as equivalent risk measures by market participants. Numerous studies suggest that RFE is a more robust measure of firm performance compared to AFE (Demerjian et al., 2012a, b; Leverty & Grace, 2012; Barr & Siems, 1997; Mali & Lim, 2019; Lim & Mali, 2021). Baik et al. (2013) demonstrate that both RFE and AFE are potentially both informative based on evidence both variables can be included in a single regression analysis without the existence of collinearity problems. We expand the literature by showing that capital providers consider operational efficiency (RFE) when issuing capital costs, but not (AFE). As suggested in our second hypothesis, we surmise that capital providers consider RFE to be a firm risk indicator but not AFE: because, (1) AFE (ROA) has a mathematical limitation because writing off assets/equity improves AFE ratios, leading to bias; (2) RFE uses values that are under the direct control of management to generate sales whilst AFE uses all asset values whether they have been utilized to generate sales or not; (3) RFE calculates the most effective utilization of a $1 input to generate sales from a combination of resources, AFE considered all inputs equal; (4) RFE considers the efficiency margins as relative amongst firms with the same industry and the market as a whole, but AFE considers all industries equal, and (5) RFE can be considered as enhancing transparency and reducing information asymmetry because it is an informative measure of managerial decision making.
Third, there are conflicting views in the literature regarding the relevance of accounting information to measure firm performance. Rangone (1997) suggest that linking organizational strategic effectiveness and accounting numbers is important. However, Chamber (1960) posits the accounting process has been formalized to a point to where accounting values misinterpret a firm's financial position. This argument is consistent with Athanassopoulos and Thanassoulis (1995) who consider financial ratios to be misleading, and many others who advocate that the literature move beyond an accounting approach. Based on our results, we surmise that analysts and market participants may interpret both types of efficiency differently. We find RFE, but not AFE can be considered a measure of risk by capital providers. However, countless studies utilize ROA/ROE (amongst other AFE measures) to capture the influence of efficiency on upside performance but exclude RFE. As a result, we show that analysts should consider AFE and RFE as different forms of efficiency in specific situations especially in relation to risk. Firm risk analyses should therefore include operational performance (RFE) in regressions as a firm risk control. Furthermore, we would encourage empirical studies to differentiate and include both types of efficiency to improve the predictive validity of regression models. Future studies can enhance the literature by demonstrating instances in which RFE differs from AFE based on the perceptions of market participants.
Finally, we list avenues for future research and limitations. Using a South Korean dataset, our results demonstrate that relatively more efficient firms should have lower WACC. South Korea is a developed country based on economic power, but a developing country based on legal infrastructure (Wood, 2013; WTO, 2021). Following major financial collapses, South Korea strives to protect market participants by implementing value adding financial policies (Choi et al., 2017). Therefore, we utilize a unique dataset to provide valuable insights to the academic community, market participants and legislators in both developing and developed countries. However, whether our results are consistent using an international firm sample is a question left unanswered. We would therefore encourage future studies to use international datasets to test whether our results are generalizable in an international context. Due to data unavailability (interest spread), we do not use implied cost of capital or equivalent WACC measures that are used as substitutes for WACC in previous literature (Gebhardt et al., 2001; Hou et al, 2012). Instead we use the WACC measure listed in Eq. (1), a value acknowledged in previous Korean studies as the most commonly accepted measurement of WACC. We encourage future studies to capture whether the relationship between WACC and RFE is consistent based on alternative WACC measures.
Change history
26 July 2021
A Correction to this paper has been published: https://doi.org/10.1007/s10479-021-04206-w
References
Abarbanell, J. S., & Bushee, B. J. (1997). Fundamental analysis, future earnings, and stock prices. Journal of Accounting Research, 35(1), 1–24.
Afzal, M. N. I., & Lawrey, R. (2012). Evaluating the comparative performance of technical and scale efficiencies in knowledge-based economies (KBEs) in ASEAN: A data envelopment analysis (DEA) application. European Journal of Economics, Finance and Administrative Sciences, 51, 81–95.
Alam, I. M. S., & Sickles, R. C. (1998). The relationship between stock market returns and technical efficiency innovations: Evidence from the US airline industry. Journal of Productivity Analysis, 9(1), 35–51.
Andersen, P., & Petersen, N. C. (1993). A procedure for ranking efficient units in data envelopment analysis. Management Science, 39(10), 1261–1264.
Athanassopoulos, A. D., & Thanassoulis, E. (1995). Separating market efficiency from profitability and its implications for planning. Journal of the Operational Research Society, 46(1), 20–34.
Baik, B., Chae, J., Choi, S., & Farber, D. B. (2013). Changes in operational efficiency and firm performance: A frontier analysis approach. Contemporary Accounting Research, 30(3), 996–1026.
Barr, R. S., & Siems, T. F. (1997). Bank failure prediction using DEA to measure management quality. In Interfaces in computer science and operations research (pp. 341–365). Springer, Boston, MA.
Barth, M. E., Konchitchki, Y., & Landsman, W. R. (2013). Cost of capital and earnings transparency. Journal of Accounting and Economics, 55(2–3), 206–224.
Bendoly, E., Rosenzweig, E. D., & Stratman, J. K. (2009). The efficient use of enterprise information for strategic advantage: A data envelopment analysis. Journal of Operations Management, 27(4), 310–323.
Berenguer, G., Iyer, A. V., & Yadav, P. (2016). Disentangling the efficiency drivers in country-level global health programs: An empirical study. Journal of Operations Management, 45, 30–43.
Bergendahl, G. (1998). DEA and benchmarks—An application to Nordic banks. Annals of Operations Research, 82, 233–250.
Bharath, S. T., Sunder, J., & Sunder, S. V. (2008). Accounting quality and debt contracting. The Accounting Review, 83(1), 1–28.
Bhojraj, S., & Sengupta, P. (2003). Effect of corporate governance on bond ratings and yields: The role of institutional investors and outside directors. The Journal of Business, 76(3), 455–475.
Black, F., & Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of Political Economy, 81(3), 637–654.
Burkert, M., Fischer, F. M., & Schäffer, U. (2011). Application of the controllability principle and managerial performance: The role of role perceptions. Management Accounting Research, 22(3), 143–159.
Callen, J. L., Morel, M., & Fader, C. (2005). Productivity measurement and the relationship between plant performance and JIT intensity. Contemporary Accounting Research, 22(2), 271–309.
Carhart, M. M. (1997). On persistence in mutual fund performance. The Journal of Finance, 52(1), 57–82.
Chambers, R. J. (1960). Measurement and misrepresentation. Management Science, 6(2), 141–148.
Choi, J. S., Lim, H. J., & Mali, D. (2017). Mandatory audit firm rotation and Big4 effect on audit quality: Evidence from South Korea. Asian Academy of Management Journal of Accounting and Finance 13(1):1–40
Combs, J. G., Russell Crook, T., & Shook, C. L. (2005). The dimensionality of organizational performance and its implications for strategic management research. In Research methodology in strategy and management (pp. 259–286). Emerald Group Publishing Limited.
Cook, W. D., & Zhu, J. (2006). Rank order data in DEA: A general framework. European Journal of Operational Research, 174(2), 1021–1038.
Crook, T. R., Ketchen, D. J., Combs, J. G., & Todd, S. Y. (2008). Strategic resources and performance: A meta-analysis. Strategic Management Journal, 29(11), 1141–1154.
Cummins, J. D., Weiss, M. A., Xie, X., & Zi, H. (2010). Economies of scope in financial services: A DEA efficiency analysis of the US insurance industry. Journal of Banking & Finance, 34(7), 1525–1539.
Dann, L. Y., & DeAngelo, H. (1983). Standstill agreements privately negotiated stock repurchases, and the market for corporate control. Journal of Financial Economics, 11(1–4), 275–300.
Datta, S., Iskandar-Datta, M., & Raman, K. (2005). Managerial stock ownership and the maturity structure of corporate debt. The Journal of Finance, 60(5), 2333–2350.
Dechow, P. M., Sloan, R. G., & Sweeney, A. P. (1995). Detecting earnings management. Accounting Review, 70(2), 193–225.
Demerjian, P. (2018). Calculating efficiency with financial accounting data: Data envelopment analysis for accounting researcher. Working paper.
Demerjian, P. R., Lev, B., Lewis, M. F., & McVay, S. E. (2012a). Managerial ability and earnings quality. The Accounting Review, 88(2), 463–498.
Demerjian, P., Lev, B., & McVay, S. (2012b). Quantifying managerial ability: A new measure and validity tests. Management Science, 58(7), 1229–1248.
Demsetz, H. (1973). Industry structure, market rivalry, and public policy. The Journal of Law and Economics, 16(1), 1–9.
Dhaliwal, D., Hogan, C., Trezevant, R., & Wilkins, M. (2011). Internal control disclosures, monitoring, and the cost of debt. The Accounting Review, 86(4), 1131–1156.
Dopuch, N., Gupta, M., Simunic, D. A., & Stein, M. T. (2003). Production efficiency and the pricing of audit services. Contemporary Accounting Research, 20(1), 47–77.
Easley, D., Hvidkjaer, S., & O’hara, M. (2002). Is information risk a determinant of asset returns? The Journal of Finance, 57(5), 2185–2221.
Fairfield, P. M., & Yohn, T. L. (2001). Using asset turnover and profit margin to forecast changes in profitability. Review of Accounting Studies, 6(4), 371–385.
Fama, E. F., & French, K. R. (1992). The cross-section of expected stock returns. The Journal of Finance, 47(2), 427–465.
Fama, E. F., & French, K. R. (2004). The capital asset pricing model: Theory and evidence. Journal of Economic Perspectives, 18(3), 25–46.
Fama, E. F., & French, K. R. (2016). Dissecting anomalies with a five-factor model. The Review of Financial Studies, 29(1), 69–103.
Fama, E. F., & MacBeth, J. D. (1973). Risk, return, and equilibrium: Empirical tests. Journal of Political Economy, 81(3), 607–636.
Faure-Grimaud, A., Peyrache, E., & Quesada, L. (2009). The ownership of ratings. The RAND Journal of Economics, 40(2), 234–257.
Francis, J., LaFond, R., Olsson, P., & Schipper, K. (2005). The market pricing of accruals quality. Journal of Accounting and Economics, 39(2), 295–327.
French, J. (2016). Estimating time-varying beta coefficients: An empirical study of US and ASEAN portfolios. In The spread of financial sophistication through emerging markets worldwide (pp. 19–34). Emerald Group Publishing Limited.
Frijns, B., & Margaritis, D. M. (2012). Firm efficiency and stock returns. Journal of Productivity Analysis, 37(3), 295–306.
Gebhardt, W. R., Lee, C. M. C., & Swaminathan, B. (2001). Toward an Implied Cost of Capital. Journal of Accounting Research., 39(1), 135–176.
Greene, W. H., & Segal, D. (2004). Profitability and efficiency in the US life insurance industry. Journal of Productivity Analysis, 21(3), 229–247.
Gregory, A., Hua, S., & Tharyan, R. (2018). In search of beta. The British Accounting Review, 50(4), 25–441.
Hendricks, K. B., & Singhal, V. R. (2005). An empirical analysis of the effect of supply chain disruptions on long-run stock price performance and equity risk of the firm. Production and Operations Management, 14(1), 35–52.
Hou, K., Dijk, M. A. V., & Zang, Y. (2012). The implied Cost of Capital: A new approach. Journal of Accounting and Economics, 53(3), 504–526.
Jacobs, B. W., Kraude, R., & Narayanan, S. (2016). Operational productivity, corporate social performance, financial performance, and risk in manufacturing firms. Production and Operations Management, 25(12), 2065–2085.
Kleindorfer, P. R., & Saad, G. H. (2005). Managing disruption risks in supply chains. Production and Operations Management, 14(1), 53–68.
Kwon, S. Y., Lim, Y., & Simnett, R. (2014). The effect of mandatory audit firm rotation on audit quality and audit fees: Empirical evidence from the Korean audit market. Auditing: A Journal of Practice and Theory, 33(4), 167–196.
Lev, B., & Thiagarajan, S. R. (1993). Fundamental information analysis. Journal of Accounting Research, 31(2), 190–215.
Leverty, J. T., & Grace, M. F. (2012). Dupes or incompetents? An examination of management’s impact on firm distress. Journal of Risk and Insurance, 79(3), 751–783.
Lim, H. J., & Mali, D. (2018a). Does market risk predict credit risk? An analysis of firm risk sensitivity, evidence from South Korea. Asia-Pacific Journal of Accounting & Economics, 25(1–2), 235–252.
Lim, H. J., & Mali, D. (2018b). Does relative efficiency matter? An analysis of market uncertainty. Investment Analysts Journal, 47(2), 127–148.
Lintner, J. (1965). Security prices, risk, and maximal gains from diversification. The Journal of Finance, 20(4), 587–615.
Lozano, S., Soltani, N., & Dehnokhalaji, A. (2020). A compromise programming approach for target setting in DEA. Annals of Operations Research, 288(1), 363–390.
Mali, D., & Lim, H. J. (2018). Conservative reporting and the incremental effect of mandatory audit firm rotation policy: A comparative analysis of audit partner rotation vs audit firm rotation in South Korea. Australian Accounting Review, 28(3), 446–463.
Mali, D., & Lim, J. H. (2019). The influence of firm efficiency on agency credit ratings. Journal of Credit Risk, 15(1), 1–36.
Mali, D., & Lim, H. J. (2020). Can audit effort (hours) reduce a firm's cost of capital? Evidence from South Korea. In Accounting Forum (pp. 1--29). Routledge
Mali, D., & Lim, H. J. (2021). Do relatively more efficient firms demand additional audit effort (hours)? Australian Accounting Review, 31(2), 108–127.
Margaritis, D., & Psillaki, M. (2010). Capital structure, equity ownership and firm performance. Journal of Banking & Finance, 34(3), 621–632.
Markowitz, H. (1952). Portfolio Selection. The Journal of Finance, 7(1), 77–91.
Mathis, J., McAndrews, J., & Rochet, J. C. (2009). Rating the raters: Are reputation concerns powerful enough to discipline rating agencies? Journal of Monetary Economics, 56(5), 657–674.
McWilliams, A., & Smart, D. L. (1993). Efficiency v. structure-conduct-performance: Implications for strategy research and practice. Journal of Management, 19(1), 63–78.
Neely, A., Gregory, M., & Platts, K. (1995). Performance measurement system design: A literature review and research agenda. International Journal of Operations & Production Management, 15(4), 80–116.
Ou, J. A., & Penman, S. H. (1989). Financial statement analysis and the prediction of stock returns. Journal of Accounting and Economics, 11(4), 295–329.
Pástor, Ľ, & Stambaugh, R. F. (2003). Liquidity risk and expected stock returns. Journal of Political Economy, 111(3), 642–685.
Rangone, A. (1997). Linking organizational effectiveness, key success factors and performance measures: An analytical framework. Management Accounting Research, 8(2), 207–219.
Ross, A., & Droge, C. (2002). An integrated benchmarking approach to distribution center performance using DEA modeling. Journal of Operations Management, 20(1), 19–32.
Safdar, I. (2018). The information content of aggregate profitability. The British Accounting Review, 50(5), 497–515.
Seshadri, S., & Subrahmanyam, M. (2005). Introduction to the special issue on “Risk Management in Operations.” Production and Operations Management, 14(1), 1–4.
Sharpe, W. F. (1964). Capital asset prices: A theory of market equilibrium under conditions of risk. The Journal of Finance, 19(3), 425–442.
Sherman, H. D., & Zhu, J. (2006). Benchmarking with quality-adjusted DEA (Q-DEA) to seek lower-cost high-quality service: Evidence from a US bank application. Annals of Operations Research, 145(1), 301–319.
Shleifer, A., & Vishny, R. W. (1997). A survey of corporate governance. The Journal of Finance, 52(2), 737–783.
Skreta, V., & Veldkamp, L. (2009). Ratings shopping and asset complexity: A theory of ratings inflation. Journal of Monetary Economics, 56(5), 678–695.
Soliman, M. T. (2008). The use of DuPont analysis by market participants. The Accounting Review, 83(3), 823–853.
Sun, S. (2004). Assessing joint maintenance shops in the Taiwanese Army using data envelopment analysis. Journal of Operations Management, 22(3), 233–245.
Thompson, R. G., Dharmapala, P. S., Humphrey, D. B., Taylor, W. M., & Thrall, R. M. (1996). Computing DEA/AR efficiency and profit ratio measures with an illustrative bank application. Annals of Operations Research, 68(3), 301–327.
Tran, D. H. (2014). Multiple corporate governance attributes and the cost of capital–Evidence from Germany. The British Accounting Review, 46(2), 179–197.
Tsolas, I. E. (2015). Firm credit risk evaluation: A series two-stage DEA modeling framework. Annals of Operations Research, 233(1), 483–500.
Venkatraman, N., & Ramanujam, V. (1986). Measurement of business performance in strategy research: A comparison of approaches. Academy of Management Review, 11(4), 801–814.
Verma, K. (1993). Managerial efficiency: A study of management buyouts. Contemporary Accounting Research, 10(1), 179–204.
World Trade organization/WTO. (2021). Groups in negotiations. Retrieved on the 20/4/2021. https://www.wto.org/english/tratop_e/dda_e/negotiating_groups_e.htm#grp002b
Yatsenko, Y., & Hritonenko, N. (2016). Asset replacement under improving operating and capital costs: A practical approach. International Journal of Production Research, 54(10), 2922–2933.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mali, D., Lim, HJ. Does relative (absolute) efficiency affect capital costs?. Ann Oper Res 315, 1037–1060 (2022). https://doi.org/10.1007/s10479-021-04159-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-021-04159-0