1 Introduction

Modern supply chains have started transforming from integrated networks to dynamic systems to cope with rising customer expectations. Augmented services and unique experience for products that are sent swiftly have compelled companies to collaborate with all supply chain stakeholders. Supply chains should indeed be agile and adaptive enough to withstand competition as well as to be able to compensate for disruptions and any ripple effects that could challenge both their performance and stability (Dolgui et al. 2019). The enormous volume of products offered and delivered by companies in conjunction with the “common” logistics-related problems such as demand fluctuations, environmental and political challenges requires innovative and high-performance supply chains.

Over the years the ultimate goal of supply chain management to serve customers has become not only imperative but also a unified strategy to efficiently manage the flow of information and products delivered and returned to/from customers. Reverse logistics (RL) and closed-loop supply chains (CLSC) have become more and more common as manufacturers, distributors and retailers orchestrate a backward logistics network to support product recovery or returns (Govindan and Soleimani 2017). RL and CLSC models were in the past deployed mainly to highlight and support business engagement towards waste minimisation, pollution prevention and circular economy (Hazen et al. 2017). However, as more customers are embracing the online purchasing of products, RL and CLSC may merely support product returns for in-store or online purchases. Retailers such as Asos and Harrods have only recently adopted measures to deal with “serial” returners (customers that intentionally buy several items knowing that they will return some or all of them) who add complexity to supply chain processes and governance (Espinosa et al. 2019). Although more evident in the fashion retail sector, product returns are an inevitable part of operations in almost all industries [see indicatively (Figueira et al. 2013; Senthil et al. 2014; Hames et al. 2018)]. The present work assumes that returned products are “good as new” and thus constitute part of the serviceable inventory.

Product returns induce high complexity in replenishment policies, having a huge impact on inventory decision-making and management  (Fleischmann and Minner 2004; De Giovanni 2017). Assid et al. (2019) argue that uncertainties of demand and returns can significantly deteriorate the reverse flows while lack of information on returned product quantities and timing impede return policies (Alinovi et al. 2012). The number of returned products operates as a disruption to inventory levels in forward supply chains, and, thus effectual inventory management not only very often becomes an increasing challenge for many companies but also forces them to constantly amend or optimise their replenishment policies (Chen and Bell 2013; Mallidis et al. 2018). Although there is extant literature on linking product return rates to the bullwhip effect and inventory management, the relationship between product return rates and replenishment policies has not been dealt with. The present work attempts to bridge this gap as it investigates this relationship in explicit terms and identifies the conditions under which the bullwhip effect exists. To the best of author’s knowledge, no research to date examines or formulates the relationship between replenishment policies and product return rates. Nevertheless, there are situations where supply chain managers would wish to know whether their ordering policies exhibit bullwhip effect when product return rates are known,in order to modify them.

The impact of demand uncertainty on supply chains was first studied by Forrester (1961) who noticed that demand variability is amplified towards the upstream levels of supply chains. P&G executives coined the term “bullwhip effect” to describe and study the effect of this phenomenon on supply chain dynamics within the retail industry (Lee et al. 1997). Since then, a considerable number of researchers have considered the presence of the bullwhip effect on both Reverse Logistics (RL) and closed-loop supply chains (CLSC). Braz et al. (2018) conducted a comprehensive literature review of 56 articles addressing the bullwhip effect in CLSC within a 14-year period (2004–2018). More than half of the articles deal with system dynamics and simulation methods (29). Seventeen (17) of all the papers apply control theory-based approaches and have been used extensively to study the bullwhip effect as they are capable to capture the dynamics of the supply chain systems with the aid of a controller and control action (see early papers (Riddalls and Bennett 2001; Dejonckheere et al. 2003) as well as more recent ones (Fu et al. 2018; Xiong et al. 2019).

One of the methodological contributions of the present work is the development of a stochastic state-space control model which depicts the full dynamics of CLSC. The proposed model is represented in a compact parametric form, outlining the evolution of the dynamic CLSC state processes. At the same time it provides detailed information on the interaction between the various CLSC key variables (i.e., inventory levels, order and product flows, replenishment policies, product return rates). This helps for a formula representation to be derived, which characterises the bullwhip effect with respect to product return rates and replenishment policies. Furthermore, the model allows for optimal techniques to be implemented to eliminate the bullwhip effect; and finally useful insights are offered in understanding the effects of the different parameters in the resulting time-varying variances and covariances. Also, in contrast to most studies which investigate the bullwhip effect with a focus on remanufacturing or recycling processes, this work provides an alternative (yet relatively new) approach to studying closed-loop supply chain dynamics by closing the loop downstream of the CLSC.

Product returns should be supported by extensive supply networks, which are usually the same and used for forward movements. In most cases, companies apply particular strategies to minimise returns as much as possible. When this is not achievable, companies apply strategic decisions to improve their returns operations by using specifically designed practices to fully utilise their supply networks (Prakash et al. 2018). Very often, these networks require closer collaboration between manufacturers, distributors and retailers as products travel forwards and backwards concurrently (Shaharudin et al. 2017).

One of the most common features of the collaboration with the aim to alleviate the bullwhip effect is information sharing between supply chain participants. Thus, in the context of RL and CLSC, traditional sharing approaches should be extended to encompass strategies to collect and share information on product returns. However, most of the literature dealing with the benefit of collaboration and integration usually involves sharing of valuable information on customer demand and inventory levels. The value of information related to supply chains with product returns has not been studied extensively while most studies assume that return distribution is fully observable (Brito et al. 2009). However, supply chain participants in non-integrated CLSC, may not have strong incentives to share information due to factors concerning competitiveness, as well as uncertainty on pricing decisions (Fallah et al. 2015). In addition, information sharing, without a strong technology-based infrastructure, increases the risk of leakage whether accidentally or deliberately by third parties to obtain proprietary information (Kong et al. 2017; Taleizadeh et al. 2019).

The present study aims to fill this gap in the literature by proposing a sophisticated information sharing platform that is grounded in the concept of the Internet of Things (IoT). In contrast to the traditional information sharing solutions proposed in supply chain literature, this paper considers IoT technology as a well-established interoperable infrastructure beyond ERP/IT/IS architecture. This allows supply chain participants to share real-time complex information by utilising cloud computing technology for the data stored in ERP systems, GPS position tracking of transport fleets, RFID based shipment tracking at warehouses and last but not least a middleware which communicates and integrates all individual devices with a very high level of encryption and security. In addition, one of the highest priorities in supply chains is to deliver the products on time to the customer in good condition. The model presented in this study, provides complete visibility and transparent (real-time) information of the product condition and location across the supply networks.

This paper considers a four-echelon series CLSC (Customer, Retailer, Distributor, Manufacturer) similar to the one presented by Pati et al. (2010), allowing customer product returns to the retailers. Initially, it is assumed that ordering policies are decentralised and based on local information (inventory levels and downstream demand). Replenishment decisions of the Retailer and Distributor follow continuous base stock policies, which are tuned by a proportional gain controller. Also, the impact product returns has on inventory variance is investigated because the bullwhip effect is also associated with inventory fluctuations. A further contribution of this paper is to investigate whether a centralised approach - reinforced by an integrated CLSC infrastructure based on Internet of Things - can effectively suppress the bullwhip effect.

2 Literature review

2.1 Bullwhip effect on reverse logistics

Closed-loop supply chains help organisations reduce waste and maximise resources by allowing products to travel backwards. These products are returned usually at the participants’ warehouses resulting in constant changes at inventory levels. Turrisi et al. (2013) showed that the higher the variability of reverse flow, the greater inventory fluctuations that CLSCs participants see Zhou and Disney (2006) first studied the impact of returned products on inventory variations by means of the bullwhip effect. Their study showed that CLSCs tend to alleviate the bullwhip effect in comparison to forward supply chains. Likewise they found that the greater the return product rate the lesser the bullwhip effect, a finding also supported by Zhao et al. (2018) and Dominguez et al. (2019). Some scholars argue that remanufacturing can improve the reuse ratio and alleviate the bullwhip of closed-loop systems (Da et al. 2008; Corum et al. 2014). Zanoni et al. (2006) found that even with longer lead times pull policies can in turn mitigate the bullwhip effect.

In contrast to the research discussed in the previous paragraph, there are works in the literature indicating that closed loop supply chains may actually reinforce the bullwhip effect and inventory variance. Khiavi et al. (2019) studied closed loop supply chains with stochastic noise and found that demand amplification occurs. Huang and Liu (2008) argued that the bullwhip effect is higher in CLSC than in forward supply chains, which does not depend on collection rates or lead times. Hosoda et al. (2015) considered a CLSC with stochastic product returns that are correlated to each other. Based on a mathematical model and numerical study, they concluded that a CLSC is more likely than a forward supply chain to experience a bullwhip effect. Chatfield and Pritchard (2013) built a hybrid discrete-event/agent-based simulation model of a five-stage serial supply chain and showed that CLSC with product returns exhibit a significantly larger bullwhip effect. They also found that the increase in order variance due to product returns has more impact on the upstream supply chain. Adenso-Díaz et al. (2012) considered a simulation instrument similar to the Beer Game and showed that the bullwhip effect depends on the percentage of material returned.

The contradictory findings suggest that further empirical investigation is required in order to more fully understand the presence of the bullwhip effect within CLSC. There may be a number of causes for this discrepancy in the literature, including different bullwhip effect constructs and divergent perspectives regarding CLSC characteristics (Adenso-Díaz et al. 2012); it could be due to distinct modelling assumptions (Cannella et al. 2016), or different CLSC structure and configuration (Zhou et al. 2018). Still, for products as good as new, as regards quality, which is what this study examines - it is not clear whether the return rates (or yields) mitigate or amplify the bullwhip effect. Some scholars argue that the relationship between product rates and the bullwhip effect also depends on the quality of the information shared (Hosoda et al. 2015; Cannella et al. 2016; Linda and Imam 2020). In their study, Ponte et al. (2020) claim that increasing the product rates may improve or worsen the bullwhip effect, depending on the degree of CLSC visibility and the types of information (transparent or opaque) being shared between echelons. Thus, as the dynamics of CLSC tend to be prone to different information sharing practices (and information per se) there is a need for an innovative CLSC configuration which overcomes those limitations and exemplifies an explicit relationship between product return rates and the bullwhip effect. The inherent aspects of such a configuration are discussed in more detail in Sect. 2.3.

2.2 Control theory and bullwhip effect mitigation strategies in CLSC

At present, a considerable number of modelling studies on supply chain dynamics are based on the control and systems theoretical approaches. The main reason for this is because control theory is based on a mathematical approach that describes the relationship between the inputs, states and outputs of a complex system such as a supply chain (Ivanov et al. 2012). Various control theory-based research has been developed to study the bullwhip effect in CLSC. Within the remanufacturing context, most scholars consider the automatic pipeline inventory and order based production control system (APIOBPCS) as the basis to facilitate ordering policy. Indicatively, Zhou and Disney (2006) implemented a replenishment rule that can be tuned by a proportional controller. Different versions or extensions of APIOBPCS have also been applied to study the dynamic behaviour of a remanufacturing system by setting certain control parameters (Tang and Naim 2004; Zhou et al. 2017; Lin and Naim 2019).

State space methods by means of mathematical structures which contain key variables sufficient to describe the CLSC systems’ future responses in a unique way - as this paper suggests - have only recently been introduced. In most research articles, H-infinity (H\(\infty \)) control strategies have been offered to achieve certain performance specifications in addition to providing stability. Zhang et al. (2011) implemented an H\(\infty \) control method to reduce the bullwhip effect in a CLSC under uncertainties by examining the quality of returned products, demand fluctuations and market demand forecast. Guo and Sun (2010) presented a two-chain cooperation in a CLSC configuration by applying H\(\infty \) control methods to mitigate the bullwhip effect. In order to reduce the bullwhip effect, Guo (2007) and Guo and Sun (2010) demonstrated linear state-space approaches to design an H\(\infty \) control strategy in the worst-case scenario when a customer’s demand in a CLSC exhibits the highest fluctuations. Guo (2015) applied a convex optimisation problem involving linear matrix inequalities (LMIs) to quantify the bullwhip effect in a CLSC served by third-party reverse providers (3PRLP). Model predictive control methods within a CLSC dynamic system providing state estimations to restrain the bullwhip effect have also been investigated (Guo 2017; Yuan et al. 2019). It is interesting to note that most of the articles which use state space methods provide similar insights with regards to the influence of CLSC on dynamic behaviour (Cannella et al. 2016).

2.3 Information sharing practices and internet of things technology in CLSC

Even a recent review of the literature suggests that the bullwhip effect cannot be completely eliminated even though various methods and techniques have been tested on CLSC networks. Studies on inventory management and the bullwhip effect on CLSCs assert that information sharing and information transparency for product returns help the overall SC performance to restrain the bullwhip effect (Tang and Naim 2004; Ketzenberg 2009; Hosoda et al. 2015). Brito et al. (2009) argue that the value of information is crucial and that sharing policies assume “perfect” information between supply chain echelons. In fact, the value of information can be reinforced with the use of technology. Dominguez et al. (2019) state that investing in technologies to process product returns helps managers to absorb the uncertainty in terms of quality and reduce the bullwhip effect. Recent technological innovations, such as radio-frequency identification (RFID), distributed systems and cloud computing have been investigated as to whether they can reduce information distortion through data acquisition, data analytics, and real-time communication systems (Lindner et al. 2010; Zhigang 2012; Gowda and Subramanya 2017).

Since information sharing alone is insufficient to completely eliminate the bullwhip effect, CLSCs require effective coordination, sharing of key information at different locations and no losses or delays in transmitted data. Thus, more sophisticated synergies than RFID practices should be adopted to link all key information with regards to supply chain management. Internet of Things (IoT) technology has only recently been explored as a technological solution to address those issues. Paksoy et al. (2016) conducted experimental research and found that IoT not only reduces uncertainty, waste and costs but also provides vital information of returned products throughout the CLSC network. The benefits of IoT for manufacturers within the CLSC context have been studied in terms of optimal production planning (Fang et al. 2016) and better inventory management.

IoT can be used as a safe and reliable way of exchanging information related to goods and services in a global supply chain. IoT, obviously, uses the Internet as a carrier to integrate all interconnected and independently addressable “things” through wireless communication technology and radio frequency technology (Jiang 2019). Ivanov et al. (2018) argue that Industry 4.0 systems can benefit from control theory by integrating crucial information feedbacks and dynamics leading to robust, stable and resilient supply chains. An exploratory literature review on the applications and challenges of IoT, including the supply chain context is given by Mishra et al. (2016).

Xu et al. (2012) introduced the concept of the smart reverse supply chain (SRSC), which enables an intelligent combination of recycling, ERP, CRM and SCM systems. In an SRSC, each returned product is assigned a unique code, which is stored on the internet. IoT then enables the gathering and management of real-time information regarding the returned product. In contrast to the common information sharing methods, this paper considers that product return rates and replenishment policies are shared with the aid of an IoT infrastructure between two neighbouring CLSC echelons. An optimisation method is applied involving the minimisation of inventory fluctuations in such an infrastructure to study whether the bullwhip effect can be completely eliminated.

3 State-space model formulation

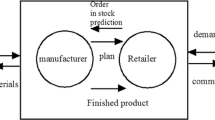
A series of four-echelon CLSC is considered in this study as shown in Fig. 1. The CLSC is segmented in three parts (upstream, midstream and downstream). It is assumed that in the upstream and midstream parts of the CLSC, the flow of information (orders) is backward, while the flow of products is forward; whereas in the downstream part the flow of products is bidirectional. Figure 1 depicts a typical decentralised CLSC where product replenishment decisions are made locally. Customer demand, which is placed on the Retailer site (R), is considered a normally distributed signal as \(N(\mu ,\sigma ^2)\). Given that the order-setup costs in the midstream parts are usually small compared to other costs, both Distributor (D) and Retailer (R) follow a simple (installation) base-stock for continuous inventory review policy. Under this base-stock policy, the inventory level is updated at every time step and is a function of on-hand inventory levels and projected material quantities that are sent and received to and from the downstream and upstream echelon, respectively (Ignaciuk 2017).

Fig. 1
figure 1

Four-echelon series closed-loop supply chain model

Full size image

It is assumed that all four echelons always have sufficient inventory to meet the downstream demand (typically the production capacity of the factory has no limits whereas Distributor and Retailer echelons always have sufficient levels of specific products). This research refrains from studying the impact of lead-time on the bullwhip effect as this has been examined extensively in the CLSC literature (see indicatively (Turrisi et al. 2013; Chatfield and Pritchard 2013; Hosoda et al. 2015). Hence, for simplicity throughout this paper, we assume that \(L = 1\). By denoting with \(Q_{R,C}(t)\) the quantities of products delivered by the Retailer at time t and with \(O_{C,R}(t-1)\) the orders placed from the Customer (C) to the Retailer at time \(t-1\), then:

$$\begin{aligned} Q_{R,C}(t) = O_{C,R}(t-1) \end{aligned}$$
(1)

As long as product returns are allowed in the downstream part of the CLSC, product return rate is represented by the variable \(\alpha \) with \(\{\alpha \in {\mathbb {R}} \, | \, \alpha \ge 0 \}\). The variable \(\alpha \) expresses the percentage of products returned to the Retailer echelon from the Customer.

The inventory level \(I_R(t)\) in the Retailer echelon (R) at time t is given by:

$$\begin{aligned} I_{R}(t)=I_{R}(t-1)-Q_{R,C}(t)+Q_{D,R}(t-L)+ \alpha Q_{C,R}(t-L) \end{aligned}$$
(2)

Note that essentially the Retailer receives an \(\alpha \) percentage of the \(Q_{R,C}\) products that were sent to the Customer in the past. The variable \(Q_{D,R}(t-L)\) indicates the quantities sent to the Retailer by the Distributor (echelon D). Note also, that the quantities dispatched by the neighbouring echelon have lead time \(L=1\).

As long as the Retailer follows a base-stock policy, inventory levels are reviewed continuously against inventory (pre) set points while order decisions are based on local information. To better model the continuous replenishment policy - followed by the Retailer site - a proportional control algorithm is introduced by means of proportional gain \(k_R \ge 0 \), which (continuously) adjusts the difference between the inventory set-point \(SP_R\), which is assumed to be constant throughout this analysis, and actual inventory level \(I_R\). Thus, the orders placed by the Retailer site to the Distributor can be written as:

$$\begin{aligned} O_{R,D}(t)=k_{R}[SP_R-I_R(t)] \end{aligned}$$
(3)

Note that the Retailer experiences backorders \(B_R(t)\), which at time t are given by: \(B_R(t)= B_R(t-1) + O_{C,R}(t) -- Q_{R,C}(t)\). Similarly, the Distributor attempts to minimise the inventory fluctuations while maintaining sufficient on hand stock. The inventory level of the Distributor \(I_D(t)\) at time t is depleted by \(Q_{D,R}(t)\) and increased by the quantities received by the Manufacturer (echelon (M) \(Q_{M,D}(t)\), with \(L=1\), as:

$$\begin{aligned} I_{D}(t)=I_{D}(t-1)-Q_{D,R}(t)+Q_{M,D}(t) \end{aligned}$$
(4)

The orders placed by the Distributor to the Manufacturer \(O_{D,M}(t)\) at time t is the discrepancy between the set-point \(SP_D\) and the inventory level \(I_D(t)\), compensated by a replenishment gain factor \(k_D \ge 0\), which again signifies the base-stock policy followed by the Distributor. Hence,

$$\begin{aligned} O_{D,M}(t)=k_{D}[SP_D-I_D(t)] \end{aligned}$$
(5)

while backorders at the Distributor site \(B_D(t)\), are given by: \(B_D(t)= B_D(t-1) + O_{R,D}(t) -- Q_{D,R}(t)\). Since the Manufacturer (echelon M) always has enough inventory to cover downstream demand, the quantities sent to the Distributor are always equal to the number of orders placed in the previous time unit. Thus,

$$\begin{aligned} Q_{M,D}(t)=O_{D,M}(t-1) \end{aligned}$$
(6)

Equations (1–6) demonstrate the dynamics of the four-echelon CLSC model and can be compactly written in a state-space form by selecting \(I_{R}(t-1)\), \(I_{D}(t-1)\), \(Q_{M,D}(t)\), \(Q_{D,R}(t)\), \(Q_{R,C}(t)\) and \(Q_{R,C}(t-1)\) as state-space variables. The input and output variables are also selected as \(O_{C,R}(t)\) (customer demand) and \(Q_{R,C}(t)\) (quantities dispatched to Customer by Retailer). Then the state-space model can be written as:

$$\begin{aligned} \left[ \begin{array}{c} I_R(t)\\ Q_{R,C}(t+1) \\ I_D(t)\\ Q_{D,R}(t+1) \\ Q_{M,D}(t+1) \\ Q_{R,C}(t) \\ \end{array} \right] = \left[ \begin{array}{cccccc} 1 &{}\quad -1 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad \alpha \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad -1 &{}\quad 1 &{}\quad 0 \\ -k_{R} &{}\quad k_{R} &{}\quad 0 &{}\quad -k_{R} &{}\quad 0 &{}\quad -\alpha \,k_{R}\\ 0 &{}\quad 0 &{}\quad -k_{D} &{}\quad k_{D} &{}\quad -k_{D} &{}\quad 0\\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array}\right] \nonumber \\ \left[ \begin{array}{c} I_R(t-1)\\ Q_{R,C}(t) \\ I_D(t-1)\\ Q_{D,R}(t) \\ Q_{M,D}(t) \\ Q_{R,C}(t-1) \\ \end{array} \right] + \left[ \begin{array}{c} 0\\ \alpha \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} \right] O_{C,R}(t) + \left[ \begin{array}{cc} 0 &{}\quad 0\\ 0 &{}\quad 0\\ 0 &{}\quad 0\\ k_R &{}\quad 0\\ 0 &{}\quad k_D \\ 0 &{}\quad 0\\ \end{array} \right] \left[ \begin{array}{cc} SP_R \\ SP_D \\ \end{array} \right] \end{aligned}$$
(7)

and

$$\begin{aligned} Q_{R,C}(t)= \left[ \begin{array}{cccccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \end{array} \right] \left[ \begin{array}{c} I_R(t-1)\\ Q_{R,C}(t) \\ I_D(t-1)\\ Q_{D,R}(t) \\ Q_{M,D}(t) \\ Q_{R,C}(t-1) \end{array} \right] \end{aligned}$$
(8)

which is of the form \(x(t+1)=Ax(t)+Bu(t)+GSP\) and \(y(t) = Cx(t)\)

4 Delineation of the bullwhip effect

The stochastic state space representation in Eqs. (7–8) provides all necessary information to continuously measure, learn and update the inventory level and movement of products. It also allows the integration of historical data from past state variables and formalises the causation from the past to the future. Although the state-space representation of the elements and the supply chain system’s dynamics given in Eqs. (7–8) offers many advantages, the CLSC model presented here can also be used to study undesired phenomena such as the bullwhip effect. This can be achieved by calculating the covariance matrix of the state vector of the overall supply chain model in parametric form.

Equations (7, 8) can be rewritten in the generic form: \(x_{k+1}=Ax_k+Ce_k + DSP\) and \(y_k=Hx_k\), where \(e_k\) is a random uncorrelated Gaussian random sequence (applied as the input to the model from the infinite past) with zero mean and \(cov\{e_k\}=1\) for all k. Provided that A is stable (all eigenvalues are inside the unit circle), the steady state covariance matrix P is given by the unique solution of the Lyapunov equation \(P=A P A^T + C C^T \), Davis (2013). Note that \(cov\{y_k,y_{k-j}\}=H P A^j H^T \), for \(j>0\) and \(cov\{y_k,y_{k-j}\}=H P H^T\), for \(j=0\). Then, the state variable \(x_{k+1}\) and state matrix A are expressed as a linear combination of \(k_R\), \(k_D\) and \(\alpha \), which are assumed to be parameters. The covariance matrix P corresponding to the CLSC model is given by:

$$\begin{aligned} P=\left[ \begin{array}{cccccc} -\frac{\varLambda }{k_{R}\,\left( k_{R}-2\right) } &{}\quad 0 &{}\quad \frac{\varTheta \, \varGamma }{\left( k_{R}-2\right) \,\varDelta } &{}\quad \frac{\varLambda }{k_{R}-2} &{}\quad -\frac{k_{D}\,\varTheta \,\varGamma }{\left( k_{R}-2\right) \,\varDelta } &{}\quad -1\\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \frac{\varTheta \,\varGamma }{\left( k_{R}-2\right) \,\varDelta } &{}\quad 0 &{}\quad \frac{k_{R}\{\varDelta -\alpha \left[ \alpha \left( \varDelta -2\right) +2\left( 2-k_{R}-k_{D}\right) \right] -2 \}}{k_{D}\,\left( k_{D}-2\right) \,\left( k_{R}-2\right) \,\varDelta } &{}\quad -\frac{k_{R}\,\varTheta \,\varGamma }{\left( k_{R}-2\right) \,\varDelta } &{}\quad -\frac{k_{R}\{\varDelta -\alpha \left[ \alpha \left( \varDelta -2\right) +2\left( 2-k_{R}-k_{D}\right) \right] -2 \}}{\left( k_{D}-2\right) \,\left( k_{R}-2\right) \,\varDelta } &{}\quad 0\\ \frac{\varLambda }{k_{R}-2} &{}\quad 0 &{}\quad -\frac{k_{R}\,\varTheta \,\varGamma }{\left( k_{R}-2\right) \,\varDelta } &{}\quad -\frac{k_{R}\,\varLambda }{k_{R}-2} &{}\quad \frac{k_{D}\,k_{R}\,\varTheta \,\varGamma }{\left( k_{R}-2\right) \,\varDelta } &{}\quad k_{R}\\ -\frac{k_{D}\,\varTheta \,\varGamma }{\left( k_{R}-2\right) \,\varDelta } &{}\quad 0 &{}\quad -\frac{k_{R}\{\varDelta -\alpha \left[ \alpha \left( \varDelta -2\right) +2\left( 2-k_{R}-k_{D}\right) \right] -2 \}}{\left( k_{D}-2\right) \,\left( k_{R}-2\right) \,\varDelta } &{}\quad \frac{k_{D}\,k_{R}\,\varTheta \,\varGamma }{\left( k_{R}-2\right) \,\varDelta } &{}\quad \frac{k_{D}\,k_{R}\,\{\varDelta -\alpha \left[ \alpha \left( \varDelta -2\right) +2\left( 2-k_{R}-k_{D}\right) \right] -2 \}}{\left( k_{D}-2\right) \,\left( k_{R}-2\right) \,\varDelta } &{}\quad 0\\ -1 &{}\quad 0 &{}\quad 0 &{}\quad k_{R} &{}\quad 0 &{}\quad 1\\ \end{array}\right] ,\nonumber \\ \end{aligned}$$
(9)

where:

$$\begin{aligned} \varLambda&= 2\alpha k_{R}-2\alpha +\alpha ^2+1 \\ \varTheta&= \alpha k_{R}-\alpha +1 \\ \varGamma&= \alpha + k_{R}-1 \\ \varDelta&= k_{D}+ k_{R}-k_{D}\,k_{R} \end{aligned}$$

Note that since \(\varLambda >0\), the diagonal elements (variances) of the positive semi-definite P denote that the system is stable if \(\varDelta >0\), \(\alpha geq 0\), \(k_R < 2\) and \(k_D < 2\). The bullwhip effect (demand amplification) towards the Manufacturer echelon (M) can be quantified by calculating the variability in orders faced by the Manufacturer and compare it with the variability of demand \(O_{C,R}(t)\) placed by the Customer. Thus, the demand at the Manufacturer site may be calculated easily from the covariance matrix P. Equation (6) with the aid of Eqs. (4) and (5) can be rewritten by assuming a time-shift, \(t-1\rightarrow t\), as:

$$\begin{aligned} \begin{aligned} Q_{M,D}(t+1)&= O_{D,M}(t) \Leftrightarrow O_{D,M}(t) \\&= -k_{D}\,I_D(t-1) + k_{D}\,Q_{D,R}(t)-k_{D}\,Q_{M,D}(t)+k_{D}SP_D \end{aligned} \end{aligned}$$
(10)

It can be inferred that \(O_{D,M}(t)\) in Eq. (10) is a linear function of the state variables and constant \(SP_D\) in the form \(O_{D,M}(t)=\varXi '\,x(t) +k_D\,SP_D\), where x(t) is the state vector and \(\varXi '=[0\; 0 \; -k_{D} \; k_{D} \; -k_{D} \; 0]\). Then, the demand amplification factor DAF is expressed as a fraction between the two order variances \(Var\{O_{D,M}(t)\}\) and \(Var\{O_{C,R}(t)\}\) as in Simchi-Levi et al. (2008):

$$\begin{aligned} DAF=\frac{Var\{O_{D,M}(t)\}}{Var\{O_{C,R}(t)\}}=\varXi ' P \varXi = \frac{k_{D}\,k_{R}\,\{\varDelta -\alpha \left[ \alpha \left( \varDelta -2\right) +2\left( 2-k_{R}-k_{D}\right) \right] -2 \}}{\sigma \left( k_{D}-2\right) \,\left( k_{R}-2\right) \,\varDelta }\nonumber \\ \end{aligned}$$
(11)

In order to find the regions in the \((\alpha ,k_R,k_D)\) plane where the bullwhip effect occurs, Eq. (11) was set to one so that \(k_D\) can be expressed as a function of \(k_R\) and \(\alpha \) leading to the Eq. (12) with \(\sigma =1\). Due to the rather complex calculations involved, \(\alpha \) was set to 0.5 (50% of product returns).

$$\begin{aligned} k_D=f(k_R,\alpha \equiv 0.5)=\frac{34\,k_{R}-13\,{k_{R}}^2-16\pm 4\,\sqrt{\frac{\left( k_{R}-2\right) \, \left( 119\,{224\,k_{R}-k_{R}}^3-130\,{k_{R}}^2-128\right) }{16}}}{2\,\left( 9\,{k_{R}}^2-13\,k_{R}+8\right) }\nonumber \\ \end{aligned}$$
(12)

Equation (12) has two solutions, however, given that \(k_D\ge 0\) and \(\alpha \ge 0\), the positive square root part should be chosen. Note, that the root expression and the denominator have positive values for \(0 \le k_R<2\). Figure 2 depicts the region where the amplification (bullwhip effect) exists, which resides in the upper part of the mesh surface, whereas the area under the mesh signifies the region where the bullwhip effect is attenuated. It can be seen that large values of \(\alpha \) reinforce the bullwhip effect, a finding that agrees with previous studies (Huang and Liu 2008; Chatfield and Pritchard 2013; Khiavi et al. 2019). Thus, products with very high return rates provide limited flexibility for both the Retailer and the Distributor to opt for replenishment policies that do not cause the bullwhip effect. Note that Fig. 2 provides the theoretical values of \(\alpha \) where the bullwhip effect does exist. Later, it will be shown that under stationary conditions, \(0 \le \alpha \le 1\).

Similarly, large values of the proportional controller bolster the bullwhip effect. Hence, when “aggressive” replenishment policies are followed for some products (\(k_R > 1\) or \(k_D >1\)), even small return rates for those products may cause a bullwhip effect. Note that both proportional gain factors \(k_R\) and \(k_D\) are lying in the interval (0, 2), which denotes that when the Retailer experiences high product return rates, even with smoothed ordering policies \(k_R<1\) the Distributor site has limited flexibility to compensate the downstream demand and avoid the bullwhip effect. This type of control action is typical in proportional controllers since the orders \(O_{D,M}(t)\) placed by the Distributor are simply related to the proportional algebraic difference \(SP_D-I_D(t)\).

Fig. 2
figure 2

The bullwhip effect regions in the \((k_D,k_R,\alpha )\) hyperplane

Full size image

5 Employing Internet of Things to alleviate the bullwhip effect

Next, an integrated supply chain is considered, where information sharing regarding the products returned by customers to retailers is reinforced by the Internet of Things (IoT) frameworks presented by Abdel-Basset et al. (2018) and Garrido-Hidalgo et al. (2019). A typical framework consists of database middleware, a software (HTML, CSS, JavaScript) and a hardware (RFID technology, GIS and GPS, sensors) gateway implementation. The returned products are interconnected with IoT devices through long-range communication technologies. RFID tags are attached to products usually by the retailer or manufacturer and contain all necessary (data-encrypted) information allowing the tracking and classification of products. Hence, the IoT-based CLSC infrastructure helps supply chain echelons to gain accurate real-time information on the number of products returned, and, subsequently product return rates.

The sharing of ordering policies in real-time within the IoT framework presented in this paper can be achieved by allowing the Retailer to connect automatic replenishment systems (APS) to distribution sensors technology that collect and transform valuable data. These data, through the communication process, reach the Distributor’s end (see Fig. 3) in real-time. Thus, the IoT framework may realise (automatic) information interactions between intelligent sensing devices and the Retailer’s replenishment systems that can be easily set up according to the Retailer’s choice of replenishment programme or ordering policy tuned by \(k_R\). As a result, the Retailer shares ordering policies \(k_R\) with the Distributor at real-time t, and, therefore, the Distributor also knows whether the Retailer is applying an aggressive ordering policy (\(k_R > 1\)) or not.

It is also assumed that the Distributor (along with the Retailer) can track the rate of product returns \(\alpha \) leaving the Customer site at real-time t. In fact, both the Retailer and the Distributor are informed about product return rates at each time step. Last but not least, the Distributor receives at time t the number of orders \(O_{R,D}(t)\) placed by the Retailer. As a result, thanks to the IoT framework, the Distributor now has at each time step a full picture of the key parameters that govern the dynamics of the CLSC (i.e., product return rates, replenishment policies, and the number of orders placed by the downstream echelon).

The revised CLSC model is shown in Fig. 3. For modelling purposes and to assess the efficiency of the IoT-based CLSC in terms of bullwhip effect elimination, it is assumed that \(\alpha Q_{C,R}(t)\) is the aggregated number of return products at time t (e.g., return products per day). Also, it is assumed that the returned products can be immediately resold without the need for remanufacturing or refurbishment.

Note, that most of the suggested strategies for reducing the magnitude of the bullwhip effect focus the centralisation of “on-demand” information by making customer demand data available to the upstream stage of the supply chain (see Tang and Naim (2004); Hosoda et al. (2015)). The present study goes beyond this “remedy” by allowing both parties to communicate and interact with each other over the Internet by collecting all necessary information from physical things, which helps to identify and share the exact (actual) value of \(\alpha \).

Fig. 3
figure 3

Four-stage CLSC model with IoT framework

Full size image

Let’s assume that the system is stable (\({k_R,k_D}<2\)) and the demand from the Customer site \(O_{C,R}(t)\) consists of independent and identically distributed random variables of mean \(\mu \) and variance \(\sigma ^2\). Then, if all echelons in the CLSC always have enough inventory to satisfy downstream demand, all signals are stationary. The state space model given in Eq. (7) can be written in compact form as:

$$\begin{aligned} \begin{aligned} x(t+1)&=Ax(t)+ Bu(t) + G \times [SP_R\; SP_D]' \\ y(t)&=Cx(t) \end{aligned} \end{aligned}$$
(13)

where u(t) is customer demand and \(SP_R\), \(SP_D\) are the deterministic values of inventory set-points at the Retailer and the Distributor sites, respectively. By means of the equilibrium state (\(t \rightarrow \infty \)) the state space model becomes: \(x(t)=Ax(t)+ Bu(t) + G\times [SP_R\; SP_D]' \Leftrightarrow x(t)=(I-A)^{-1}Bu(t)+(I-A)^{-1}G \times [SP_R\; SP_D]'\). The expected values of the state variable can be easily calculated as:

$$\begin{aligned} E\{x(t)\}=\mu (I-A)^{-1}B+(I-A)^{-1}G \times [SP_R\; SP_D]' \end{aligned}$$
(14)

So long as the state space model in Eq. (13) is an LTI model, then it satisfies the condition that \(x(t-t_1)=A[y(t-t_1)]\), which provides stationarity in time (Strejc 1981). The five state variables are distributed as follows (note that under stationary conditions the state variables \(Q_{R,C}(t)\) and \(Q_{R,C}(t+1)\) are distributed equally):

$$\begin{aligned} \begin{aligned} I_R(t)&\thicksim \mathrm {N}\left( SP_{R}+\frac{\mu \,(\alpha -1)}{k_{R}},-\sigma ^2\,\frac{\varLambda }{k_{R}\,\left( k_{R}-2\right) }\right) \\ Q_{R,C}(t)&\thicksim \mathrm {N} \left( \mu ,\sigma ^{2}\right) \\ I_D(t)&\thicksim \mathrm {N}\left( SP_{D}+\frac{\mu \,(\alpha -1)}{k_{D}},-\sigma ^{2}\frac{k_{R}\{\varDelta -\alpha \left[ \alpha \left( \varDelta -2\right) +2\left( 2-k_{R}-k_{D}\right) \right] -2 \}}{k_{D}\,\left( k_{D}-2\right) \,\left( k_{R}-2\right) \,\varDelta }\right) \\ Q_{D,R}(t)&\thicksim \mathrm {N} \left( -\mu (\alpha -1),-\sigma ^{2}\,\frac{k_{R}\,\varLambda }{k_{R}-2}\right) \\ Q_{M,D}(t)&\thicksim \mathrm {N} \left( -\mu (\alpha -1), \sigma ^2\,\frac{k_{D}\,k_{R}\,\{\varDelta -\alpha \left[ \alpha \left( \varDelta -2\right) +2\left( 2-k_{R}-k_{D}\right) \right] -2 \}}{\left( k_{D}-2\right) \,\left( k_{R}-2\right) \,\varDelta }\right) \end{aligned} \end{aligned}$$
(15)

Since \(Q_{D,R}(t)\) and \(Q_{M,D}(t\)), and their means, may always take positive values, Eq. (15) signify that under stationarity \(0 \le \alpha \le 1\). To study the benefit of employing the IoT framework in terms of inventory management performance, a new variable (sufficient inventory), \(SI_D(t)=I_D(t-1)-O_{R,D}(t)\) is introduced, which denotes the ability of the Distributor to meet the demand placed by the Retailer. Then the sufficient inventory is distributed as:

$$\begin{aligned} SI_D(t) \thicksim \mathrm {N} \left( SP_D -\mu + \frac{\mu (\alpha -1)}{k_D}, -\sigma ^{2}\frac{k_{R}\{\varDelta -\alpha \left[ \alpha \left( \varDelta -2\right) +2\left( 2-k_{R}-k_{D}\right) \right] -2 \}}{k_{D}\,\left( k_{D}-2\right) \,\left( k_{R}-2\right) \,\varDelta }\right) \nonumber \\ \end{aligned}$$
(16)

From Eq. (16), it can be inferred that under step input demand, \(I_D(t)\) tracks the set-point \(SP_D\) with a steady state error \(-\mu + \frac{\mu (\alpha -1)}{k_D}\), which applies to zero-type feedback systems. Thus, the magnitude of the discrepancy between the actual inventory level and the target level at the Distributor site clearly depends on replenishment strategies and the product return rate.

When the Retailer dispatches returned products, the Distributor attempts to promptly fulfill backorders based on the new inventory balance. Any backorders are updated through the demand signal and as a result the Distributor follows an aggressive replenishment policy \(k_D>1\). As long as the Distributor site is responsible for managing returns of any missing products, the necessary arrangements need be made as to how to bring back returned product quantities to their place of origin. This leads to higher transportation costs, while often these are proportional to the number of returned products, they can, however, be better estimated if quantities are known beforehand (Hosoda et al. 2015).

The overall costs become even higher due to fluctuations in the inventory levels leading to an increase in holding costs. However, if \(\alpha \) and \(k_R\) are shared between supply chain participants in real-time using the IoT framework presented here, the Distributor can use this information to minimise costs associated with excessive inventory levels. In fact, the Distributor site can avert additional costs by eliminating both the average and the fluctuations in inventory levels. Note, that Distributor can control the inventory level average by setting \(SP_D\) to a desired position, which can be used to shift \(SI_D(t)\) to any optative level, too. The following analysis deals with the costs associated with fluctuations in inventory levels.

5.1 Optimal policies in the internet of things context

The information in covariance matrix P, given in Eq. (9), can be used to obtain the variance of inventory level \(I_D(t)\) at the Distributor site. Then, for any given \(0 \le \alpha \le 1\) and \(0<k_R<2\) an optimal choice of \(k_D\), \({k_D}^*=f^*(\alpha ,k_R)\) is sought to minimise the variance of \(I_D(t)\) subject to \(Prob\{SI_D(t)<0\} \le \zeta \), where \(\zeta \) is considered to be a very small parameter. This can be achieved by taking the first derivative of \(Var\{I_D(t)\}\) with respect to \(k_R\) and \(\alpha \) and setting it equal to zero. Since this again involves some complex calculations we derive the resulting equation by setting \(\alpha =0.5\). Then, the optimal choice for \(k_D\), (\({k_D}^*\)) is given by:

$$\begin{aligned} \begin{aligned} {k_D}^*&=f^*(k_D,k_R,\alpha \equiv 0.5)\\&=\frac{k_{R}\,\left( 5\,{k_{D}}^3\,{k_{R}}^2-6\,{k_{D}}^3\,k_{R}+{k_{D}}^3-9\,{k_{D}}^2\,{k_{R}}^2+11\,{k_{D}}^2\,k_{R}-4\,{k_{D}}^2+3\,k_{D}\,{k_{R}}^2-8\,k_{D}\,k_{R}+4\,k_{D}-{k_{R}}^2+2\,k_{R}\right) }{2\,{k_{D}}^2\,{\left( k_{D}-2\right) }^2\,\left( k_{R}-2\right) \,{\left( k_{D}+k_{R}-k_{D}\,k_{R}\right) }^2} \end{aligned}\nonumber \\ \end{aligned}$$
(17)

Then, by setting Eq. (17) as being equal to zero, we can express \(k_R\) as a function of \(k_D=f^*(k_R)\) given that Eq. (17) is continuous in the interval \(0\le k_R<2\) and \(0<k_D<2\). Figure 4a shows the plot of \({k_D}^*=f^*(k_R)\) (solid line) alongside the regions where the bullwhip effect exists when \(\alpha =0\), \(\alpha =0.5\) and \(\alpha =1\) (dotted line). Figure 4a also provides a schematic comparison of the bullwhip effect regions for the original CLSC (dotted line) as well as the one reinforced by IoT technology (solid line).

It can clearly be seen that a CLSC with an IoT infrastructure for any value of \(\alpha \) does not allow the bullwhip effect to occur, as the curve (solid line) is always to be found in the attenuation region, which is the area marked out underneath the dotted line. Note also that when all products ordered in the previous period are returned (\(\alpha = 1\)), the region where the bullwhip effect occurs (the area above the dotted line in Fig. 4a) is greater than the corresponding area when \(\alpha =0.5\) (half of the products have been returned from the Retailer to the Customer). Similarly, with \(\alpha = 0.5\) the bullwhip effect region is bigger than that with no returns \((\alpha = 0)\). In fact, the results of this study indicate that the bigger the product return rates, the smaller the range for the replenishment gain factor \(k_D\) at the Distributor site, which guarantees minimum inventory fluctuations as well as elimination of the bullwhip effect. This supports the findings in Sect. 4 where even without the implementation of the proposed IoT infrastructure, the Distributor has less flexibility to follow a replenishment policy, leading to a complete elimination of the bullwhip effect when product return rates are high.

Another useful observation from Fig. 4a is that optimal inventory fluctuation policies always guarantee the elimination of the bullwhip effect even when the Distributor is enforcing aggressive ordering policies. Thus, with the sharing information strategies reinforced by the IoT framework which this paper presents, not only is the Distributor able to minimise inventory fluctuations, but the bullwhip effect in CLSCs can also be fully avoided. In the long-run, the proposed model may lead to significant cost savings, which can depreciate the high costs currently associated with IoT solutions. Figure 4b shows the optimal (minimum) variance of inventory fluctuations at Distributor \(Var^*{I_D(t)}\) for the three values of \(\alpha \). The optimal variance can be derived by substituting the optimal policy \(k_D=f^*(k_R,\alpha )\) into P(3, 3) an element of the covariance matrix P. It can be inferred that (\(Var^*{I_D(t)}\) is a monotonically increasing function of \(k_R\). Interestingly, there is a positive analogy between \(Var^*{I_D(t)}\) and \(\alpha \). Hence, the more product returns, the more inventory fluctuations the Distributor experiences. In fact, the practical implication, which can be seen in Fig. 4b is that the higher the product returns rates, the less the flexibility for the Distributor to minimise the inventory variance for bigger values of \(k_R\) e.g., \(k_R> 1.5\).

Fig. 4
figure 4

a Optimal policies \(k_D=f^*(k_R)\) and boundaries of bullwhip effect, b plot of \(Var^*{I_D(t)}\) versus \(k_R\)

Full size image

6 Conclusion

This article presents a model for analysing the effect on product return rates with continuous replenishment polices based on a four-echelon series closed-loop supply chain structure. The idea was to initially obtain a covariance matrix of the model in parametric form as a function of product rates and replenishment policies. This helps to characterise and quantify the bullwhip effect under certain parameter values. The present results indicate that higher product return rates and aggressive ordering policies exhibit a larger bullwhip effect. This finding is in agreement with other studies suggesting that there is a positive correlation between product returns and the bullwhip effect (Guo and Sun 2010; Chatfield and Pritchard 2013).

The impact of returned products on the bullwhip effect appears to be contradictory in the literature. It is important to emphasise here that closed-loop supply chains, reverse logistics and the stock management in circular economy models can be examined in several ways. Product returns are associated with recycling, refurbishing, reusing or remanufacturing processes and, thus, they may feedback into the supply chain network at different levels. There are also different aspects of returns with regards to their source, such as end-customer or intermediaries (e.g., 3PL’s). The findings of this research are based on a CLSC model which considers the returns process of previously purchased products from the end customer through the retailer-distributor supply channel and not directly through the distributor or manufacturer. As also found in other studies, it is valid that the absence of common ground in CLSCs brings contradictory results and, for this reason further research should be conducted to unify different constructs and settings.

An additional contribution of this paper is the formulation and solution of an optimisation problem involving the minimisation of inventory fluctuations in closed loop supply chains reinforced by an IoT platform. It has been shown that initially sharing replenishment-related information eliminates demand amplification a finding that has been also derived in (Derakhshan et al. 2019). The proposed model provides useful insights into how IoT are linked with replenishment policies and product return rates. The findings also indicate that IoT infrastructure eliminates the bullwhip effect even if the product return rates are high. Despite the high cost of IoT implementation, CLSCs (especially those impacted by the boom in online shopping) have started to convert to integration by adopting sophisticated technological means. Besides this, many companies more and more are considering platforms that can homogenise and share data gathered from disparate sources.

As this research work effectively deals with information asymmetry problem in closed-loop supply chains, it may help organisations to develop CLSC structures based on IoT technology. Although the model proposed in this paper is based on a series supply chain structure, the closed-loop supply chain can become divergent on the assumption that all mathematical formulas pertain to a single product. Thus, for more realistic CLSC representations involving the movement of multiple products, the number of series supply chains should be equal to the number of products. Last but not least, the proposed structure of the CLSC model allows the required covariance analysis to be extended to models with an arbitrary number of echelons.