Abstract
Although there is a growing number of research articles investigating the performance in the banking industry, research on Chinese banking efficiency is rather focused on discussing rankings to the detriment of unveiling its productive structure in light of banking competition. This issue is of utmost importance considering the relevant transformations in the Chinese economy over the last decades. This is a development of a two-stage network production process (production and intermediation approaches in banking, respectively) to evaluate the efficiency level of Chinese commercial banks. In the second stage regression analysis, an integrated Multi-Layer Perceptron/Hidden Markov model is used for the first time to unveil endogeneity among banking competition, contextual variables, and efficiency levels of the production and intermediation approaches in banking. The competitive condition in the Chinese banking industry is measured by Panar–Rosse H-statistic and Lerner index under the Ordinary Least Square regression. Findings reveal that productive efficiency appears to be positively impacted by competition and market power. Second, credit risk analysis in older local banks, which focus the province level, would possibly be the fact that jeopardizes the productive efficiency levels of the entire banking industry in China. Thirdly, it is found that a perfect banking competition structure at the province level and a reduced market power of local banks are drivers of a sound banking system. Finally, our findings suggest that concentration of credit in a few banks leads to an increase in bank productivity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The financial system in China is supported by four pillars including the banking industry, the insurance industry, the trust industry, and the securities industry. Among these, the banking industry has specific advantages over the other three because its operations involve both enterprises and government. More specifically, the banks are supported and protected by the government and they mainly engage in providing services to different types and sizes of enterprises, while some competitive Chinese banks have engaged in insurance investment and the finance department of these banks has gradually provided trust-related money management services to customers. We can forecast that in the near future, big Chinese commercial banks will become “all-round” financial institutions that provide a variety of different businesses covering the functions of trust companies, insurance companies, and securities companies. Previous researches on the Chinse banking industry, which is the focus of this study, are rather scarce and limited to discussing rankings under the traditional “black-box” productive approach (Asmild & Matthews, 2012; Avkiran, 2011; Avkiran & Morita, 2010; Gattoufi et al., 2014; Luo et al., 2012; Tan & Anchor, 2017; Tan & Floros, 2013 among others).
Therefore, this research significantly contributes to the empirical literature in banking by focusing on the banking industry of China in light its productive and competition structures. Precisely, a GMSS-DEA (General Multi-Stage Structure-Data Envelopment Analysis) model is proposed here to capture the productive structure in the Chinese banking industry in terms of the well-known production and intermediation approaches in banking. Our method is completely different from other efficiency studies and compared to the empirical Chinese efficiency studies (Dong et al., 2016; Du et al., 2018; among others). The GMSS-DEA model is capable of simultaneously handling income statement and balance sheet related variables in different production stages so that we can produce more accurate results for the efficiency levels. GMSS has the advantage of computing in a simultaneous way the efficiency level of the overall production stage and the internal stages. Furthermore, the assumption that exogenous inputs are not consumed, and exogenous outputs are not produced during the internal processes (Kao, 2014) have been relaxed in GMSS. Particularly in this research, different assets are considered as the exogenous outputs in the first stage (production approach in banking), while deposits from the central bank and other institutions are the exogenous inputs in the second stage (intermediation approach in banking). Analogously, equity is regarded as an exogenous input in the production approach, while cash and deposits at central banks and other institutions are treated as exogenous outputs in the intermediation approach, altogether with provisions and fee/interest expenses.
Additionally, an integration of these results with Multi-Layer Perceptron (MLP) models is adopted to unveil the endogeneity between banking efficiency, contextual variables, and major market competition metrics such as the Herfindahl–Hirschman index, the Panzar–Rosse H-statistic, and the Lerner-index. Hidden Markov Models (HMM) are used as a basis for bootstrapping such variables while preserving their endogeneity within the ambit of MLP models. We are also the pioneer study to use this method to address competition and efficiency relationship in the banking literature.
This study has two main innovative motivations. It decomposes the efficiency of Chinese banks with a multi-stage system structure that encompasses the production and intermediation approaches. Meanwhile, it adopts a novel integrated MLP/HMM model to stochastically unveil the feedback processes that may exist among these approaches, macro-economic variables, and competition structures. We have the following findings: (1) productive efficiency appears to be positively impacted by competition and market power; (2) credit risk analysis in older local banks that focus the province level, would possibly be the factor that jeopardizes the productive efficiency levels of the entire banking industry in China; (3) a perfect banking competition structure at the province level and a reduced market power of local banks are drivers of a sound banking system in China; (4) increased banking productivity is a direct consequence of the concentration of credit into fewer banks as a form of maintaining scale and reducing transaction costs.
2 Banking sector overview in China
The main purposes of banking reform in China since the 1970s are to improve profitability, productivity, and efficiency while reducing the level of market power and enhancing the banking stability for the multi-layer bank structure. Non-performing loans is still a historical issue. To solve this problem, a number of different measurements have been taken by the Chinese government to reduce the risk level of Chinese commercial banks, including non-performing loan write-offs (Bonin & Huang, 2001), establishment of the China Banking Regulatory Commission (CBRC) (Liang et al., 2013), and the introduction of strategic foreign investors (Wu et al., 2012).
Lower level competition is the second issue. There are hundreds of banking and non-banking financial institutions in China and CBRC statistics report that among the different ownership types of Chinese banks, state-owned banks still dominate the industry, though the proportion of assets held by this bank type has declined over recent years. Foreign banks were allowed to provide financial services in mainland China with some restriction at the beginning with the restrictions being completely removed by the end of 2006 (Hsiao et al., 2015). The level of competition is supposed to further increase due to the fact that private banks were allowed to operate in China and there are few private banks operating in China since 2015 (Lu, 2016).
The Chinese banking industry has encouraged banks to engage in Initial Public Offering (IPO), which does not only increase the source of funding for their operation, but it also provides more incentive for the Chinese banks to optimize their resource, improve their management, and further improve performance (Okazaki, 2017). There have been two large IPO listings in the Chinese banking industry. One was the Industrial and Commercial Bank of China listed on the Hong Kong and Shanghai stock exchange and the other was the Agricultural Bank of China listed on the Hong Kong and Shanghai stock exchange in 2011.
The Chinese banking industry is still facing some challenges and difficulties. First, credit risk, as reflected by the non-performing loan ratios, is still the issue. Second, the operation and in particular how to keep the customer and sustain a good relationship between bank and customer is another difficulty faced by Chinese commercial banks derived from interest rate liberalization. In addition, Chinese commercial banks also face competition from Internet giants including Alibaba and Tencent, both of which provide financial services to customers. The financial products they offer strongly affect commercial banks and they need to keep innovating in order to have a competitive position.
3 Literature review
Efficiency in the Chinese banking industry is dispersed in terms of scope, but there has been a growing number of research in the last decade revealing a growing importance in the study of this issue, mostly due to the emergence of China as a relevant global player.
Berger et al. (2009) used a stochastic frontier analysis to examine efficiency in Chinese banks during 1994–2013. Their findings suggest that the state-owned commercial banks are least efficient while the foreign banks are most efficient. The results indicate that minority foreign ownership can improve the efficiency of Chinese banks. Fu and Heffernan (2009) extended the work of Berger et al. (2009) by investigating the X-efficiency and scale efficiency during 1985–2002. The results reported that X-efficiency had been declining on average and that most banks operated under the optional scale. The results further reported that the X-efficiency of joint-stock commercial banks were improved by banking reforms with no evidence supporting the quite-life hypothesis that the higher level of market power reduces the efficiency level of Chinese commercial banks. A number of studies have used the stochastic frontier analysis to assess the efficiency level in the Chinese banking industry (Berger et al, 2010; Dong et al., 2016; Jiang et al., 2013; Sun et al., 2013).
Besides using stochastic frontier analysis, the second method is the non-parametric Data Envelopment Analysis. Tan and Floros (2013) used this method to examine efficiency and productivity during 2003–2009 and to further examine their interrelationships with risk and capital. Their findings suggest that risk and efficiency are significantly related, and risk and capital are significantly and negatively related with each other. Wang et el. (2014) extended the work of Tan and Floros (2013) by innovatively dividing the banking production process into two stages, namely a deposit producing stage and a profit earning stage. The results from this two-stage DEA show that the source of inefficiency of Chinese banks is derived from the first stage production process. In addition, the results report that the overall efficiency level has improved and the difference in the efficiency level of state-owned banks and joint-stock banks decreased over the period. Similar research has also been conducted by Matthews, (2013), An et al., (2015), Zha et al., (2016), Zhou et al., (2018), Du et al., (2018), Liu et al. (2018), Liu et al. (2018), Liu et al., (2019); among others.
As far as we could find, there are only two pieces of research to apply the GMSS-DEA to economic sectors for efficiency analysis. One of them assessed the productivity of 17 major Chinese ports over the period 2006–2015 (Wanke et al., 2018a, 2018b). Another piece of research analyzed the efficiency level in the Portuguese banking sector (Alves et al., 2020). Our study significantly extends these two papers, in particular the latter one, by controlling bank-specific risks, capital indicators, as well as ownership variables.
4 Data and methodology
4.1 The data
Analyses were performed based on data obtained from Fitch Connect and annual financial statements from 27 Commercial banks operating in China with data available from 2007 to 2017. Table 1 shows the descriptive variables of the inputs, outputs, and intermediate resources used in the GMSS-DEA. A detailed discussion on the variable type is given in the next two subsequent subsections, where the GMSS-DEA model is presented and the alternative productive approaches in banking are discussed. Nevertheless, as regards variable selection with respect to physical and monetary productive resources, the data availability and inputs, outputs, and intermediate variables found in previous studies (Martinez-Campillo et al., 2020; Wanke Azad et al., 2019; Wanke et al., 2019; Wanke, dos Henrique, et al., 2019) constitute the two major criteria used. Monetary inputs and outputs considered in this paper are given in current dollars adjusted to China´s yearly consumer price index. Besides, descriptive for the major contextual variables considered are also given.
According to Berger and Humphrey (1997), there are two distinct approaches to input and output selection in the banking sector, which vary mainly in their consideration of deposits as inputs or outputs, i.e. the production approach and the intermediation approach.
Under the production approach, banks are assumed to produce financial services for the customers. Hence the loans, deposits, and services associated with deposits are all considered as outputs of banks. Meanwhile, the capital and work required to carry out the transactions and processes are considered as inputs of banks.
On the contrary, under the intermediation approach, banks are regarded as financial intermediaries between the savings and investments of their customers. Therefore, deposits and the interest costs are classified as inputs. According to Kumar and Gulati (2014), the intermediation approach can be further subdivided into the following approaches: assets, cost, and value added.
The assets approach focuses on the bank’s role of intermediating between depositors and the bank assets. The inputs include deposits, labor, physical capital, and other liabilities while the outputs consist of the income-earning assets such as loans and securities.
Under the cost approach, the input/output classification is based on its contribution to the bank's revenue. The value-added approach differs from the previous ones since it considers inputs and outputs in terms of their contribution to the bank's added value, allowing for a non-mutually exclusive choice.
Berger and Humphrey (1997) argue that neither the production approach, nor the intermediation approach is perfect since they do not fully consider the dual role of institutions as transaction and intermediary providers of financial products. However, the authors consider the production approach to be the most adequate for analyzing the efficiency of bank branches, while the intermediation approach is the most adequate for evaluating the efficiency of banking institutions. Indeed, the difference between the two approaches stems from the role that deposits assume in each of them. In the production approach, deposits are considered as outputs, while in the intermediation approach, they are considered as inputs.
In the controversy regarding the role of deposits in the productive process of banks, some authors present alternatives in order to dispense with their use. With Avkiran (2009a, 2009b), for example, interest expenses are incorporated as inputs. Sealey and Lindley (1977) use an asset-oriented model considering only income-earning assets as outputs. Other authors consider the deposits simultaneously as inputs and outputs (Tortosa-Ausina, 2002), but most studies consider deposits as inputs (Fethi & Pasiouras, 2010).
In order to overcome the problem of classifying deposits as inputs or outputs, a new approach has emerged that corresponds with the current orientation towards profitability and focuses mainly on operating results (profit-oriented approach). This approach considers revenues such as interest received and non-financial income as outputs, while cost components such as personnel expenses and interest paid (Drake et al., 2006) are inputs with the aim of minimizing costs and maximizing the bank revenues.
In general, the inputs used are mainly fixed assets and personnel measured in absolute value or money, as seen for example in Isik and Hassan (2002), Maudos and Pastor (2003), Casu and Girardone (2004), Havrylchyk (2006), and Diallo (2018). Several authors also use the number of branches (Chen, 2001) and provisions and equity (Pasiouras, 2008a) as inputs. The most commonly used outputs are loans and income-earning assets such as by Casu and Molyneux (2003), Casu and Girardone (2004), and Tzeremes (2015). Other research includes non-financial income or off-balance sheet resources as outputs such as Isik and Hassan (2002), Sturm and Williams (2004), Havrylchyk (2006), Pasiouras (2008b), and Degl'Innocenti et al. (2017).
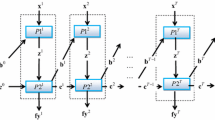
In this research, we propose reconciling the production and intermediation approaches within the ambit of the GMSS-DEA model, situating them as two consecutive stages of the productive process of Chinese banks. In stage 1, following the production approach, these banks were regarded as firms producing loans, deposits, and other assets with labor and capital. In contrast, in stage 2, under the intermediation approach, these banks were considered to be financial intermediaries with the role of transforming deposits and purchased funds into loans, income, and revenues. More specifically, deposits are assumed to be an output under the production approach, while they are regarded as an input under the intermediation approach. As a distinctive feature of this study, both approaches are followed in a complimentary fashion in the network productive structure of the Chinese banking sector, as depicted in Fig. 1.
Readers should note the role played by the exogenous inputs and outputs in both stages. Although they are not directly involved in the core activities of each stage, they may affect the efficiency levels of each stage as long as these exogenous variables can be considered as by-products in the case of outputs or auxiliary resources in the case of the inputs.
4.2 GMSS-DEA
DEA is a linear programming approach applied to compute the efficiency scores of DMUs or Decision Making Units based on efficiency frontiers that constitute a convex envelope on the data set. Efficiency score is a value that normally ranges between 0 and 1 with 0 corresponding to an inefficient unit and 1 to an efficient unit. An efficiency frontier corresponds to a set of best practices in which actual or virtual combination of DMUs can obtain a greater quantity of outputs when considering fixed inputs (output orientation) or can reduce the quantity of inputs used when considering fixed outputs (input orientation). Thus, an efficiency frontier is formed on the convex set of production possibilities by linearly combining efficient DMUs. Suppose \(s = 1 \ldots S\) productive DMUs consuming inputs \(x_{s}^{T} = (x_{s1} , \ldots ,x_{sm} )\) and generating outputs \(y_{s}^{T} = (y_{s1} , \ldots ,y_{sn} )\). Additionally suppose that \(\lambda^{T} = (\lambda_{1} , \ldots ,\lambda_{s} )\) is non-negative and \(e^{T} = (1, \ldots ,1) \in R^{S}\) is an unitary value vector (Wanke & Barros, 2016). The dual LP are given next. The virtual input and output sums of \(\sum\nolimits_{i = 1}^{m} {v_{i} x_{ij} }\) and \(\sum\nolimits_{r = 1}^{s} {u_{r} y_{rj} }\) consist of weighted resources and products by decision variables endogenously optimized when solving the linear problem. The respective constant-returns to scale known as CCR (Charnes et al., 1978), and variable returns to scale known as BCC (Banker et al., 1984), are given in models (1) to (3):
Frontier type | Input-oriented | Output-oriented |
|---|---|---|
\(\begin{gathered} \max \sum\limits_{r = 1}^{s} {u_{r} y_{ro} + u_{o} } \hfill \\ s.t. \hfill \\ \sum\limits_{r = 1}^{s} {u_{r} y_{rj} } - \sum\limits_{i = 1}^{m} {v_{i} x_{ij} + u_{o} \le 0} \hfill \\ \sum\limits_{i = 1}^{m} {v_{i} x_{io} = 1} \hfill \\ u_{r} ,v_{i} \ge 0 \hfill \\ \end{gathered}\)(1) | \(\begin{gathered} \min \sum\limits_{i = 1}^{m} {v_{i} x_{io} + v_{o} } \hfill \\ s.t. \hfill \\ \sum\limits_{i = 1}^{m} {v_{i} x_{ij} } - \sum\limits_{r = 1}^{s} {u_{r} y_{rj} + v_{o} \ge 0} \hfill \\ \sum\limits_{r = 1}^{s} {u_{r} y_{ro} = 1} \hfill \\ u_{r} ,v_{i} \ge 0 \hfill \\ \end{gathered}\)(2) | |
CCR | \(u_{o} = 0\) | \(v_{o} = 0\)(3) |
BCC | \(u_{o}\) free in sign | \(v_{o}\) free in sign |
The major drawback of the DEA model is the “black box” representation of the internal processes of a given DMU. As a matter of fact, a DMU may be formed by diverse sub-substructures that contribute differently to overall levels of efficiency. Network DEA has been designed to handle this drawback. The first and more basic DEA network structure encompasses two distinct stages, which are connected in series and represent specific processes (or substructures) that cooperate for achieving maximal overall efficiency. Explaining it differently, DMUs are structured as a two-stage linear network where the products generated in the first process enter as resources into the subsequent stage (Golany et al., 2006). The two-stage structures are in fact a reduced case derived from a broader network structure composed by multiple stages (Fare, 1991; Fare & Grosskopf, 1996, 2000; Fare & Whittaker, 1995;). Here the general network structure departs from Kao (2014) and Wanke et al. (2018a, 2018b). The productive system is allowed to consume m inputs that are exogenous, \(i = 1,2, \ldots ,m|i \in I^{\left( p \right)}\) to deliver s outputs that are exogenous, \(r = 1,2, \ldots ,s|r \in O^{\left( p \right)}\). Besides, the g endogenous intermediate variables \(f = 1,2, \ldots ,g|f \in M^{\left( p \right)}\) link subsequent stages. The X exogenous resources, Y exogenous products, and Z intermediate endogenous variables are weighted, respectively, by \(v_{i}\), \(u_{r}\), and \(w_{f}\). The efficiency estimation of the whole system (\(\theta_{k}\)) for unit k, considering a total of \(n\) DMUs, given q individual stages, \(p = 1,2, \ldots ,q\), is defined as:
The set \(\left( {u_{r}^{*} ,v_{i}^{*} ,w_{f}^{*} } \right)\) represents an optimal solution while \(s_{k}^{*}\) and \(s_{k}^{\left( p \right)*}\) refer to the constraint slacks and the index p denotes the subset of elements encompassed in a given stage. The efficiency of each stage (\(\theta_{k}^{\left( p \right)}\)) can be computed as follows:
Finally, the system slacks are defined by the summation of the individual slacks calculated for each stage \(s_{k}^{*} = \mathop \sum \nolimits_{p = 1}^{q} s_{k}^{\left( p \right)*}\). This implies that system efficiency depends directly on the efficiency of the individual stages, therefore assuring that efficiency estimation bias regarding the single-stage “black box” DEA are eliminated.
4.2.1 Banking efficiency approach
In accordance to the seminal paper of Berger and Humphrey (1997), two alternative approaches for selecting inputs and outputs in the banking sector exist, which mainly vary in the consideration of deposits as resources or products: the production and the intermediation approaches, respectively.
This research proposes to reconcile the intermediation and production approaches within the ambit of the GMSS-DEA structure, placing them as two consecutive stages of the productive process of Chinese banks. In stage 1 (production approach), banks are considered to produce loans, deposits, and other assets while using capital and labor. On the other hand, in stage 2 (intermediation approach), banks are treated as financial intermediaries that convert deposits and purchase funds into income and revenues. Precisely, deposits are considered as a product within the production approach and as a productive resource within the intermediation one. As a distinctive feature of this paper, both approaches are viewed as complementary in the productive network structure of the banking industry in China, as is depicted in Fig. 1. Readers should note the role played by the exogenous inputs and outputs in both stages. Although they are not directly involved in the core activities of each stage, they may affect the efficiency levels of each stage as long as these exogenous variables can be considered as by-products when considering the outputs of stage 1 or auxiliary resources when considering the inputs of stage 2.
The aggregate results obtained using the GMSS-DEA structure for the Chinese banks are presented in Fig. 2. It depicts the distributions for the overall system and the two individual stages: production approach (stage 1) and intermediation approach (stage 2). Banks in China seem to be less efficient in converting physical and human resources and equity into deposits, loans, and assets than in converting deposits and loans into several types of income. This scenario may suggest that competition level of Chinese banks in generating assets based on physical and monetary resources is low and that they tend to operate in a quasi-monopolistic fashion at the province level, although it is a highly fragmented industry at the country level focused on the front-office of the banking operation (intermediation approach). These competitiveness issues are further explored in the next sections.
4.3 Measures of banking competition
Since one key aim of this paper, as reflected in its title, is to investigate the endogeneity between competition and efficiency, so obviously the measurement of competition is essential. This section provides three different measurements of competition widely adopted in the banking literature. Our main focuses are: (1) estimate and present the results of bank competition accompanied by relevant discussion; (2) use the results to examine its relationship with efficiency.
4.3.1 Herfindahl–Hirschman index
The Herfindahl–Hirschman Index (HHI or sometimes HHI-score) computes the scale of the firm with respect to a given sector. In this research, two alternative measures of the HHI are computed to assess the concentration of the Chinese banks: HHI as a function of total deposits and HHI as a function of the total credit. The distributions of these indexes are depicted in Fig. 3. Results indicate that the banking industry in China is extremely fragmented over the examined period of 2007–2017 both in terms of deposits and credits. The fact that deposits are slightly less concentrated than credits may be reflected in the fact that efficiency is higher in the intermediation approach when compared to that in the production approach. This is a very interesting finding. It shows that commercial banks in China are better in keeping relationships with borrowers rather than depositors. This can be further traced back to the issue of corruption in such an industry. Different borrowers tried to bribe bank managers in order to get loans, which further promoted the relationship between the bank and borrowers. A sustainable relationship between banks and borrowers further contributes to a more concentrated credit market. In addition, this is also related to the issue that different banks normally engage in providing credits to different types of businesses. For example, state-owned banks usually provide loans to big state enterprises in comparison to city commercial banks that usually concede loans to city level enterprises and small and medium sized enterprises, which will be served by joint-stock commercial banks.
4.3.2 Panzar and Rosse (1987) H-statistic
The Panzar and Rosse H-statistic is computed via the following reduced revenue equation form for panel data of Chinese banks. The respective Ordinary Least Squares considering fixed bank-specific effects and time dummies is given in Eq. (17). Logarithmics were taken for all variables. Subscripts i and t respectively refer to bank i at time t. Hausman test was conducted to confirm the choice of the fixed effects model (Casu & Girardone, 2006; Claessens & Laeven, 2004).
In this research, TRit is calculated by the following quotient: [Gross Revenue/Total Assets] while PL, PF,it, and PC,it are, respectively:
-
Cost of labor given by the quotient between personnel expenses and total assets [Personnel Expenses/Total Assets]it.
-
Cost of funds computed via the quotient between interest expenses and total deposits [Interest Expenses/Total Deposits]it.
-
Cost of fixed capital calculated using the quotient between other operating and administrative expenses to total assets [Overhead Costs/Total Assets]it.
EARit is the quotient between total equity and total assets, which indicates the capitalization level of the bank [Equity Capital/Total Assets]it.; STAit is total assets, which captures bank size [Total Assets]it; and finally LARit is the quotient between total loans and total assets proxying the portfolio mix of the bank [Total Loans/Total Assets]it. The H-statistics is computed by the sum of the coefficients for the input prices, which are β1, β2, and β3 in Eq. (17). If H is equal to 1, there is perfect competition, but if it lies between 0 and 1, then there is monopolistic competition. However, if H is less than 0, then there is monopoly.
4.3.3 Lerner (1934) index
Different from the H-statistic as explained above, the Lerner index makes it possible to measure the degree of market power for a specific bank on a yearly basis. It can be computed using the relative difference between price and marginal cost. The Lerner index usually ranges from 0 to 1 with higher figures indicating higher levels of market power and lower competition levels, while lower figures underline that there is a lower market-power level and a higher degree of competition (Fare et al., 2015; Fungacova et al., 2013; Tan & Floros, 2014; Tan, 2016; Tan et al., 2017; Liu et al., 2018; Liu et al., 2018; among others). In some scenarios, the value of the Lerner index can be negative. We use Ordinary Least Square to estimate the Lerner index while controlling for bank fixed effects and time dummies. The specification can be expressed as below:
where ln represents natural logarithm, cost represents the total cost, and Q stands for bank output. Here the sum of interest income, non-interest income, and net income are the proxy for the bank output. P stands for the three input prices, which are the same as the ones used in the previous section. Again, subscripts t and i read similarly. Equation 18 is differentiated to derive the marginal cost with respect to the output Q as below:
Therefore, the Lerner index is given by:
where P stands for price that is measured by the quotient between total revenue and total assets. MC stands for marginal cost, and TA is total assets. In some scenarios when the Lerner index is negative, the price level is lower than the marginal cost. This can be explained by the Chinese banking industry with a special characteristic of higher level of government subsidy. Negative Lerner index is good for the Chinese banking industry on the one hand due to the fact that higher marginal cost will deter entry, which is good for the improvement of profit of the existing banks. On the other hand, higher marginal cost than the price level indicates that the banks are suffering losses in the short run. Results for the OLS regression for the H-statistic and Lerner index are displayed in Table 2. In terms of H-statistic, the findings suggest, based upon the summation of coefficients β1, β2, and β3 (0.34), that the Chinese banking industry is not operating in a monopolistic competition when taken in aggregate. Results for the OLS regression for the Lerner Index also indicate that the market power of Chinese banks is low, thus confirming that these banks operate under a very fragmented fashion and are not so selective with regards to customer loans. The distribution of the weighted H-statistic per bank i and time t and Lerner index is depicted in Fig. 4. This weighted H-statistic allows an individual assessment for banks suggesting that there are a few institutions operating in virtual monopolies, possibly larger banks that operate in niche segments or present dominant positions at the province level. This is associated to the structure of the banking sector in China. As discussed before, Commercial banks that are state-owned usually provide loan services to state and large companies, while city level government normally focuses on providing services to the enterprises at the city level.
4.4 Multi-layer perceptron–Hidden Markov Model (MLP-HMM) approach
Artificial Neural Networks (ANNs) are computational algorithms based on the human thinking paradigm. ANNs are formed of processing units (neurons) that are weight connected. These connections motivate the estimation of non-linear models by using a training data set. Athanassopoulos and Curram (1996) is the first literature insight on combining ANNs and DEA for predicting efficiency levels. Other ANN applications in DEA can be found in Santin and Delgado (2004); Wu et al. (2006); Emrouznejad and Shale (2009); Misiunas et al. (2016); Shokrollahpour et al. (2016); Olanrewaju et al. (2012); Bashiri et al. (2013); Modhej et al. (2017).
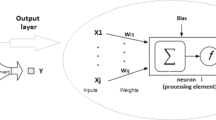
In this research, a specific focus is placed on the MLP network that has been extensively studied in forecasting applications (Mubiru & Banda, 2008). Within the ambit of an MLP, neurons are pooled in layers and just forward connections are allowed. These features provide a robust architecture capable of learning upon any kind of continuous nonlinear mapping. A typical MLP is represented in Fig. 5.
MLP constituents encompass neurons, weights, and transfer functions. An input \(x_{j}\) is transmitted via connections that multiplies its respective strength by \(w_{ij}\) weights, yielding the product \(x_{j} w_{ij}\) used in the transfer function f to compute a specific output \(y_{i}\) given as \(y_{i = } f\left( {\mathop \sum \nolimits_{j = 1}^{n} x_{j} w_{ij} } \right)\). i is the neuron index in the hidden layer and j is the input index in the MPL. The modification of the weights of each connection observing some orderly fashion is known as training. During the training, an input is assigned to the network along with the desired output and the weights are adjusted so that the MLP catches up with the desired output value.
Here, the focus is on unveiling endogeneity between efficiency and competition in Chinese banks by means of MLP, taking contextual variables as the control ones. This paper departs from previous research in the banking sector by using an MLP network structure to explore endogeneity between these variables in terms of the following models:
-
Model 1: Production Efficiency = Intermediation Efficiency + HHc + HHd + H-Stat + Lemer + Contextual Variables.
-
Model 2: Intermediation Efficiency = Production Efficiency + HHc + HHd + H-Stat + Lemer + Contextual Variables.
-
Model 3: HHc = Production Efficiency + Intermediation Efficiency + HHd + H-Stat + Lemer + Contextual Variables.
-
Model 4: HHd = Production Efficiency + Intermediation Efficiency + HHc + H-Stat + Lemer + Contextual Variables.
-
Model 5: H-Stat = Production Efficiency + Intermediation Efficiency + HHc + HHd + Lemer + Contextual Variables.
-
Model 6: Lerner = Production Efficiency + Intermediation Efficiency + HHc + HHd + H-Stat + Contextual Variables.
The relative importance of each model in explaining the competition and the efficiency levels in the Chinese banking industry, besides the endogenous nature of these variables, were explored, respectively, by the variances of each model and the covariances between models. Variances and covariances of the residuals (\(R_{i}\)) of these six models are simultaneously minimized by a non-linear stochastic optimization problem, as presented in Eq. (21), where \(w_{i}\) stands for the weights, which range from 0 to 1, assigned respectively to the residual vectors of each one of the six models previously described. The values of w are optimized so that the variance (Var) and covariance (Covar) of the pooled residuals is minimal. Model (21) was solved by means of differential evolution (DE). DE is a research stream of genetic algorithms also emulating the natural selection and evolution. Readers should refer to Ardia et al. (2011) and Mullen et al. (2011) for further details. Results are discussed in the next section.
Residuals of the MLP models were bootstrapped 200 times based on HMM. The HMM bootstrapping allowed the collection of a distributional profile of w for the most accurate prediction of the network efficiency scores and competition indexes. The stochastic HMM used in this research enables the assessment of endogeneity between efficiency and competitiveness variables by means of the respective transition probabilities for each state. Consider that there are j observations for each bank X at time t that are given as {Xtj: t = 1, …, T; j = 1,…, J}. Also assume that these random vectors are mutually independent. The HMM is structured upon choosing a proper distributional assumption of the random vectors Xtj at each one of the m states of the HMM. Therefore, transition probabilities should be determined for t = 1, 2, …, T, i = 1, 2, …, m, and for all relevant xtj, like in Wanke, dos Henrique et al. (2019), Wanke et al. (2019), Wanke et al. (2019)). Here, the stochastic HMM is modelled as a multinomial distribution for each bank j at each state i over time t. The likelihood function is given as (Zucchini et al., 2016):
Equation (22) holds for continuous-valued series, where \({\text{P}}_{{\text{m}}} \left( {{\text{X}}_{{{\text{tj}}}} } \right)\) is the probability that observation of bank j on time t belongs to state m. The following definitions are now observed:
T = {1…OBS}, where OBS is the number of observations of the sample for each bank.
J = {production approach efficiency (pae), intermediation approach efficiency (iae), HHI for credit (hhic), HHI for deposits (hhid), weighted H-statistic (whs), Lerner Index (li), Age (age), State-Owned Bank (sob), Listed Bank (lb), Impaired Loans ratio (ilr), Total Capital Ratio (tcr), Top 10 Customer Loan Ratio (ttclr)}.
M = {m1….m4096}, each stage m is defined upon the quantile combinations (above median, below median) for each individual vector of observations, as displayed in Table 3.
5 Results and discussion
While alternative DEA models have made a great contribution to better apprehend the productive network of the banking industry over time, the methods proposed in the NEIO research stream achieved relevant findings for mapping its competitive behavior. Still, these different research streams have not yet been cross-checked against each other in terms of temporal dependence and mutual feedback (endogeneity). This cross-checking is deemed relevant because hidden feedbacks between the competitive structure and the productive efficiency may devise important policy and strategic implications for the Chinese banks.
Overall efficiency and sub-efficiencies of the sample are given in Appendix B. The endogenous nature of this dataset is presented in Figs. 6 and 7. It shows that banking efficiency levels are correlated to contextual variables and to competition structure metrics. Also, the time dependent nature between these relationships is noteworthy.
Figures 8, 9 and Tables 4 and 5 report the results regarding the fifteen most probable states and their respective transition matrices. It is noteworthy that, although 120 out of the 4096 individual states showed non-zero probabilities, only 178 out of the 14,400 (120^2) transition matrix possible combinations presented non-zero probabilities. These initial findings indicate that when efficiency, competition structure, and contextual variables are modelled in terms of boostrapped HMM, only a small fraction of all possible transitions actually exist. This feature may be explained by the presence of strong feedback mechanisms between efficiency and competition structure in parallel with time-series auto correlation within the observations of each bank, which also limits the probability of abrupt transitions between two disparate states.
Figures 10 and 11 report on, respectively, the variance/covariance minimization results using differential evolution for weighted Models 1 to 6 based on 100 data series replications generated with HMM. Residuals from Models 1 to 6 were obtained solving MLP networks for each model for each HMM realization. Model 1, where productive efficiency is the dependent variable, presents isolate as of the highest importance in terms of the minimization of variance/covariance of the residuals. The weight of production efficiency is higher than the sum of the weights of all other models combined and this result suggests that converting physical and human resources into loan and deposits is the key for understanding efficiency and competitiveness in Chinese banks. Besides, productive efficiency is the key for understanding endogeneity as long as it is linked with intermediation efficiency (as expected), the level of concentration of credit and deposits (HHc and HHd), the banking industry competition type (H-Stat), and the market power of each bank (Lerner Index). All other endogenous relations are negligible, as reported in Fig. 11. As regards the competition structure variables, productive efficiency appears to be positively impacted by competition and market power in the sense that market concentration and quasi-monopolistic operation at the province level may favor the conversion of physical and human resources into deposits and loans. There is, however, a trade-off between production and intermediation efficiency levels, which may be explained by risk analysis in credit concession and other provisions for default loans. According to Fig. 12, as regards the contextual variables, the most relevant feedbacks related to productive efficiency occur in order of the impaired loans ratio, age, local bank, top ten customer loans ratio, and total capital ratio. With the exception of tcr, all remaining contextual variables presented a negative feedback, on average, with productive efficiency levels (cf. Table 6). These results suggest that credit risk analysis in older local banks with focused actuation at the province level can possibly be the factor that jeopardizes the productive efficiency levels of the entire banking industry in China. However, at this stage we cannot be assured that definitely it is the credit risk analysis in older local banks that jeopardizes the productive efficiency because the NPL ratio is primarily the metric of ex-post credit risk or the materialized credit risk and not necessarily the outcome of the bank's credit scoring, but may be the result of a deteriorating economic activity in the macro-environment. Productive efficiency of Chinese banks positively impacts, and it is impacted by, these variables, which suggests that a movement towards a perfect banking competition structure at the province level and reduced market power of local banks are drivers of a sound banking system in China. Although less important, HHc presents a positive feedback with production efficiency, thus suggesting that increased banking productivity is a direct consequence of the concentration of credit into fewer banks as a form of maintaining scale and reducing transaction costs.
We can see from the table that the production approach efficiency feeds back in a stronger manner on the intermediation approach efficiency rather than the other way around. This can be explained by the fact that the production approach efficiency mainly measures efficiency using relevant variables related to physical units as reflected in Table 1, i.e. the inputs used include number of employees and equity capital and the output variables are fixed assets, liquid assets, and total assets. In comparison, the intermediation approach efficiency mainly measures the level of efficiency using variables related to currency units such as using interest and non-interest expenses as inputs and interest and non-interest income as the outputs. This finding reflects the fact that in the Chinese banking industry, fixed assets, liquid assets, and total assets are strongly related to the interest and non-interest income of Chinese commercial banks, whereas larger amount of interest and non-interest income is not necessarily used to increase the volume of fixed assets and liquid assets.
We can further notice from Table 6 that the production approach efficiency for state-owned banks is 20, which is significantly different and smaller than the intermediate approach efficiency, which is 66.67. As discussed above, the intermediate approach efficiency focuses on the currency unit, whereas the production approach efficiency concentrates more on physical units. These results show that Chinese state-owned banks are more concerned about “money” related issues in the production process and do not pay enough attention to physical issues, although some of which are very important for the bank stability, such as liquid assets and equity capital. Both state-owned banks and local banks focus on producing monetary units related to outputs rather than physical units. However, local banks pay more attention on generating physical units of outputs. This is because small local banks are more concerned about their safety rather than income.
This finding is very interesting and important for the Chinese banking industry to make relevant policies. Obviously, there is still a room for the Chinese banking industry to increase the level of efficiency through allocating resources in a more optimal way in the production process, but compared to the state-owned banks, the local banks should pay more attention to using the resources to maximize the monetary unit production. It is recommended that both state-owned banks and local banks make more effort to focus on generating important physical units such as capital and liquid assets, which will further promote stability in the Chinese banking industry.
6 Robustness check
First of all, customer loans were incorporated in the NDEA model as an intermediate variable, altogether with SME loans and total loans. Results for the Kullback–Leibler (KL) divergence between previous scores (w/o customer loans) and new scores (w/ customer loans) were found to be negligible: Overall = 7.916239e−07; Stage 1 = 0.006994322; Stage 2 = 0.00944464. Therefore, it can be posited that the impact of customer loans on score differences is minimal for the Chinese banking productive process, which also can be confirmed by visual inspection on Fig. 13.
Subsequently, the other two ratios of liquidity and year-to-year increase in provision were incorporated as additional contextual variables to be used in the neural network models. Analogously, the results for Stage 1 (the most relevant for explaining endogeneity and total variance reduction) and its interactions with other competition structure variables revealed substantially small values for their respective Mean Squared Error (MSE), thus supporting that the previous results still hold in terms of isotonicity despite the addition of these two new variables. In fact, MSE for Stage 1 weight between both analyses was 0.0861, while as for each one of the five Stage 1 interactions, the MSEs were respectively 0.00092, 0.00196, 0.0029, 0.0045, and 0.00156.
7 Sensitivity to risk analysis
An additional sensitivity analysis was performed repeating all steps described so far, but now including two risk-related variables: insolvency risk and capital risk. The insolvency risk is measured by the widely used Z-score (Tan & Floros, 2013), which is calculated using the steps as follows: (1) calculate the ratio of equity capital to total assets; (2) add up the return on assets with (1); (3) use (2) to divide by the standard deviation of return on assets. Higher values of Z-score indicates a lower level of insolvency risk, while lower values indicate a higher level of risk. In terms of the measurement of capital risk, we use the ratio of equity capital to total assets. The literature has used this measurement to reflect the level of capital adequacy (Altunbas et al., 2007; Fiordelisi et al., 2011). Higher values of this ratio indicate a lower level of capital risk, lower values indicate a higher level of capital risk. Table 7 reports on the changes verified in Table 6 results. One can easily verify that the most impacted relationships were those related to H-Statistics, Local Bank, and Total Capital Ratio, for which signs presented reversion with respect to efficiency scores. These results may indicate that local Chinese banks may be operating more leveraged and exposed to financial risks which may be affecting the banking efficiency levels of this particular segment. In fact, this segment is highly concentrated in the hand of local banks with low governance levels. Our results are in line with the findings of Sun et al. (2013) who report that higher levels credit risk of city commercial banks is mainly attributed to the fact that city commercial banks are established with the purpose of supporting regional economic growth and development without assessing the level of credit risk in a strict way. Lower level of governance existed in this specific bank ownership type is mainly reflected by the absolute ownership control from the local government, which impedes the effective and efficient decision making process through the involvement of different shareholders. This coincides with the finding of Sun et al. (2013) showing that strategic investors are supposed to significantly improve the efficiency of Chinese city commercial banks.
8 Conclusions and direction for future research
This paper explored efficiency in Chinese banks using a novel two-stage DEA approach to capture the impact of endogenous and exogenous variables. A specific stochastic HMM and neural network analysis was also developed in this analysis to be able to reduce the fitting bias with this analysis having the advantage of improving the accuracy of the model, in particular when the competition structure and contextual variables are included. Our model significantly contributes to the banking literature as well as to the literature on the operational research in efficiency analysis.
Our findings suggest that the local action of older banks can possibly be the factor that sets the performance threshold in the Chinese banking industry. Regarding concentration indexes, their overall effect on productive efficiency was positive, so we could argue that in the period under analysis that banking concentration was positively related with efficiency. Further research should be directed to use an alternative competition indicator (Boone indicator) to measure the level of competition in the Chinese banking industry. In addition, our method can be applied to other countries to see whether the result will hold.
References
Altunbas, Y., Carbo, S., Gardener, E. P. M., & Molynuex, P. (2007). Examining the relationships between capital, risk and efficiency in European banking. European Financial Management, 13(1), 49–70.
Alves, A. B., Wanke, P., Antunes, J., & Chen, Z. (2020). Endogenous network efficiency, macroeconomy, and competition: evidence from the Portuguese banking industry. The North American Journal of Economics and Finance, 52, 1–20.
An, Q., Chen, H., Wu, J., & Liang, L. (2015). Measuring slacks-based efficiency for commercial banks in China by using a two-stage DEA model with undesirable output. Gbn Rations Research, 235(1), 13–35.
Ardia, D., Boudt, K., Carl, P., Mullen, K., & Peterson, B. G. (2011). Differential evolution with DEoptim: an application to non-convex portfolio optimization. The R Journal, 3(1), 27–34.
Asmild, M., & Matthews, K. (2012). Multi-directional efficiency analysis patterns in Chinese banks 1997–2008. European Journal of Operational Research, 219, 434–441.
Athanassopoulos, A. D., & Curram, S. (1996). A comparison of data envelopment analysis and artificial neural networks as tools for assessing the efficiency of decision making units. Journal of the Operational Research Society, 47(8), 1000–1017.
Avkiran, N. K. (2009a). Opening the black-box of efficiency analysis: an illustration with UAE banks. Omega, 37, 930–941.
Avkiran, N. K. (2009b). Removing the impact of environment with units-invariant efficient frontier analysis: an illustrative case study with intertemporal panel data. Omega, 37, 534–544.
Avkiran, N. K. (2011). Association of DEA super-efficiency estimates with financial ratios: investigating the case for Chinese banks. Omega, 39, 323–334.
Avkiran, N. K., & Morita, H. (2010). Benchmarking firm performance from a multiple-stakeholder perspective with an application to Chinese banking. Omega, 38, 501–508.
Banker, R. D., Charnes, A., & Cooper, W. W. (1984). Some models for estimating technical and scale inefficiencies in data envelopment analysis. Management Science, 30(9), 1078–1092.
Bashiri, M., Farshbaf-Geranmayeh, A., & Mogouie, H. (2013). A neuro-data envelopment analysis approach for optimization of uncorrelated multiple response problems with smaller the better type controllable factors. Journal of Industrial Engineering International, 9(30), 1–10.
Berger, A. N., Hasan, I., & Zhou, M. (2009). Bank ownership and efficiency in China: What will happen in the world’s largest nation? Journal of Banking and Finance, 33(1), 13–130.
Berger, A. N., Hasan, I., & Zhou, M. (2010). The effects of focus versus diversification on bank performance: evidence from Chinese banks. Journal of Banking and Finance, 34(7), 1417–1435.
Berger, A. N., & Humphrey, D. B. (1997). Efficiency of financial institutions: international survey and directions for future research. European Journal of Operational Research, 98(2), 175–212.
Bonin, J. P., & Huang, Y. (2001). Dealing with the bad loans of the Chinese banks. Journal of Asian Economics, 12, 197–214.
Casu, B., & Girardone, C. (2004). Large banks’ efficiency in the single European market. Service Industries Journal, 24(6), 129–142.
Casu, B., & Girardone, C. (2006). Bank competition, concentration and efficiency in the single European market. The Manchester School, 74(4), 441–468.
Casu, B., & Molynuex, P. (2003). A comparative study of efficiency in European banking. Applied Economics, 35(7), 1865–1876.
Charnes, A., Cooper, W. W., & Rhodes, E. (1978). Measuring the efficiency of decision making units. European Journal of Operational Research, 2(6), 429–444.
Chen, T. Y. (2001). An estimation of X-efficiency in Taiwan’s banks. Applied Financial Economics, 11, 237–242.
Claessens, S., & Laeven, L. (2004). What drives bank competition? Some international evidence. Journal of Money, Credit and Banking, 36(3), 563–583.
Degl’Innocenti, M., Matousek, R., Sevic, Z., & Tzeremes, N. G. (2017). Bank efficiency and financial centres: Does geographical location matter? Journal of International Financial Markets, Institutions and Money, 46, 188–198.
Diallo, B. (2018). Bank efficiency and industry growth during financial crises. Economic Modelling, 68, 11–22.
Dong, Y., Firth, M., Hou, W., & Yang, W. (2016). Evaluating the performance of Chinese commercial banks: a comparative analysis of different types of banks. European Journal of Operational Research, 252(1), 280–295.
Drake, L., Hall, M. J. B., & Simper, R. (2006). The impact of macroeconomic and regulatory factors on bank efficiency: a non-parametric analysis of Hong Kong’s banking system. Journal of Banking and Finance, 30(5), 1443–1466.
Du, K., Worthington, A. C., & Zelenyuk, V. (2018). Data envelopment analysis, truncated regression and double-bootstrap for panel data with application to Chinese banking. European Journal of Operational Research, 265(2), 748–764.
Emrouznejad, A., & Shale, E. A. (2009). A combined neural network and DEA for measuring efficiency of large scale data sets. Computers and Industrial Engineering, 56(1), 249–254.
Fare, R. (1991). Measuring Farrell efficiency for a firm with intermediate inputs. Academia Economic Papers, 19(2), 329–340.
Fare, R., & Grosskopf, S. (1996). Productivity and intermediate products: a frontier approach. Economics Letters, 50(1), 65–70.
Fare, R., & Grosskopf, S. (2000). Network DEA. Socio-Economic Planning Sciences, 34(1), 35–49.
Fare, R., Grosskopf, S., Maudos, J., & Tortsa-Ausina, M. (2015). Revisiting the quiet life hypothesis in banking using nonparametric techniques. Journal of Business Economics and Management, 16, 159–187.
Fare, R., & Whittaker, G. (1995). An intermediate input model of dairy production using complex survey data. Journal of Agricultural Economics, 46(2), 201–213.
Fethi, M. D., & Pasiouras, F. (2010). Assessing bank efficiency and performance with operational research and artificial intelligence techniques: a survey. European Journal of Operational Research, 204(2), 189–198.
Fiordelisi, F., Marques-Ibanez, D., & Molyneux, P. (2011). Efficiency and risk in European banking. Journal of Banking and Finance, 35(5), 1315–1326.
Fu, X., & Heffernan, S. (2009). The effects of reform on China’s bank structure and performance. Journal of Banking and Finance, 33(1), 39–52.
Fungacova, Z., Pessarossi, P., & Weill, L. (2013). Is bank competition detrimental to efficiency? Evidence from China. China Economic Review, 27, 121–134.
Gattoufi, S., Amin, G. R., & Emrouznejad, A. (2014). A new inverse DEA method for merging banks. IMA Journal of Management Mathematics, 25, 73–87.
Golany, B., Hackman, S. T., & Passy, U. (2006). An efficiency measurement framework for multi-stage production system. Annals of Operations Research, 145(1), 51–68.
Havrylchyk, O. (2006). Efficiency of the Polish banking industry: foreign versus domestic banks. Journal of Banking and Finance, 30(7), 1975–1996.
Hsiao, C., Shen, Y., & Bian, W. (2015). Evaluating the effectiveness of China’s financial reform—the efficiency of China’s domestic banks. China Economic Review, 35, 70–82.
Isik, I., & Hassan, M. K. (2002). Technical, scale and allocative efficiencies of Turkish banking industry. Journal of Banking and Finance, 26(4), 719–766.
Jiang, C., Yao, S., & Feng, G. (2013). Bank ownership, privatization, and performance: evidence from a transition economy. Journal of Banking and Finance, 37(9), 3364–3372.
Kao, C. (2014). Efficiency decomposition for general multi-stage systems in data envelopment analysis. European Journal of Operational Research, 232(1), 17–124.
Kumar, S., & Gulati, R. (2014). Deregulation and efficiency of Indian banks. Springer.
Lerner, A. P. (1934). The concept of monopoly and the measurement of monopoly power. The Review of Economic Studies, 1(3), 157–175.
Liang, Q., Xu, P., & Jiraporn, P. (2013). Board characteristics and Chinese bank performance. Journal of Banking and Finance, 37, 2953–2968.
Liu, B., Liu, C., & Peng, J. (2018). Interest rate pass-through in China: an analysis of Chinese commercial banks. Emerging Markets Finance and Trade, 54, 3051–3063.
Liu, X., Sun, J., Yang, F., & Wu, J. (2018). How ownership structure affects bank deposits and loan efficiencies: an empirical analysis of Chinese commercial banks. Annals of Operations Research. https://doi.org/10.1007/s10479-018-3106-6
Liu, X., Yang, F., & Wu, J. (2019). DEA considering technological heterogeneity and intermediate output target setting: the performance analysis of Chinese commercial banks. Annals of Operations Research. https://doi.org/10.1007/s10479-019-03413-w
Lu, L. (2016). Private banks in China: origin, challenges and regulatory implications. Banking and Finance Law Review, 31, 585–599.
Luo, Y., Bi, G., & Liang, L. (2012). Input/output indicator selection for DEA efficiency evaluation: an empirical study of Chinese commercial banks. Expert Systems with Applications, 39, 1118–1123.
Martinez-Campillo, A., Wijesiri, M., & Wanke, P. (2020). Evaluating the double bottom-line of social banking in an emerging country: how efficient are public banks in supporting priority and non-priority sector in India. Journal of Business Ethics, 162, 399–420.
Matthews, K. (2013). Risk management and managerial efficiency in Chinese banks: a network DEA framework. Omega, 41, 207–215.
Maudos, J., & Pastor, M. (2003). Cost and profit efficiency in the Spanish banking sector (1985–1996): a non-parametric approach. Applied Financial Economics, 13(1), 1–12.
Misiunas, N., Oztekin, A., Chen, Y., & Chandra, K. (2016). DEANN: a healthcare analytic methodology of data envelopment analysis and artificial neural networks for the prediction of organ recipient functional status. Omega, 58, 46–54.
Modhej, D., Sanei, M., Shoja, N., & Hosseinzadeh Lotfi, F. (2017). Integrating inverse data envelopment analysis and neural network to preserve relative efficiency values. Journal of Intelligent and Fuzzy Systems, 32(6), 4047–4058.
Mubiru, J., & Banda, E. (2008). Estimation of monthly average daily global solar irradiation using artificial neural networks. Solar Energy, 82(2), 181–187.
Mullen, K. M., Ardia, D., Gil, D. L., Windover, D., & Cline, J. (2011). DEoptim: an R package for global optimization by differential evolution. Journal of Statistical Software, 40(6), 1–26.
Okazaki, K. (2017). Banking system reform in China: the challenges to improving its efficiency in serving the real economy. Asian Economic Policy Review, 12, 303–320.
Olanrewaju, O., Jimoh, A., & Kholopan, P. (2012). Integrated IDA–ANN–DEA for assessment and optimization of energy consumption in industrial sectors. Energy, 46(1), 629–635.
Panzar, J. C., & Rosse, J. N. (1987). Testing for monopoly equilibrium. Journal of Industrial Economics, 35(4), 443–456.
Pasiouras, F. (2008a). International evidence on the impact of regulations and supervision on banks’ technical efficiency: an application of two-stage data envelopment analysis. Review of Quantitative Finance and Accounting, 30, 187–223.
Pasiouras, F. (2008b). Estimating the technical and scale efficiency of Greek commercial banks: the impacts of credit risk, off-balance-sheet activities, and international operations. Research in International Business and Finance, 22, 301–318.
Santin, D., & Delgado, F. J. (2004). The measurement of technical efficiency: a neural network approach. Applied Economics, 36(6), 627–635.
Sealey, C., & Lindley, J. (1977). Inputs, outputs, and the theory of production and cost of depository financial institutions. Journal of Finance, 32, 1251–1266.
Shokrollahpour, E., Hosseinzadeh Lotfi, F., & Zandieh, M. (2016). An integrated data envelopment analysis–artificial neural network approach for benchmarking of bank branches. Journal of Industrial Engineering International, 12(2), 137–143.
Sturm, J. E., & Williams, B. (2004). Foreign bank entry, deregulation and bank efficiency: lessons from Australian experience. Journal of Banking and Finance, 28(7), 1775–1799.
Sun, J., Harimaya, K., & Yamori, N. (2013). Regional economic development, strategic investors and efficiency of Chinese city commercial banks. Journal of Banking and Finance, 37(5), 1602–1611.
Tan, Y. (2016). The impacts of risk and competition on bank profitability in China. Journal of International Financial Markets, Institutions and Money, 40, 85–110.
Tan, Y., & Anchor, J. (2017). The impacts of risk-taking behaviour and competition on technical efficiency: evidence from the Chinese Banking Industry. Research in International Business and Finance, 41, 90–104.
Tan, Y., & Floros, C. (2013). Risk, capital and efficiency in Chinese banking. Journal of International Financial Markets, Institutions and Money, 26, 378–393.
Tan, Y., & Floros, C. (2014). Risk, profitability, and competition: evidence from the Chinese banking industry. Journal of Developing Areas, 48, 303–319.
Tan, Y., Floros, C., & Anchor, J. (2017). The profitability of Chinese banks: impacts of risk, competition and efficiency. Review of Accounting and Finance, 16, 86–105.
Tortosa-Ausina, E. (2002). Bank cost efficiency and output specification. Journal of Productivity Analysis, 18, 199–222.
Tzeremes, N. G. (2015). Efficiency dynamics in Indian banking: a conditional directional distance approach. European Journal of Operational Research, 240(3), 807–818.
Wang, K., Huang, W., Wu, J., & Liu, Y. (2014). Efficiency measures of the Chinese commercial banking system using an additive two-stage DEA. Omega, 44, 5–20.
Wanke, P., dos Henrique, O., & Moreira Antunes, J. J. (2019). Unveiling endogeneity and temporal dependence between tourism revenues/expenditures and macroeconomic variables in Brazil: a stochastic hidden Markov model approach. Tourism Economics, 25(1), 3–21.
Wanke, P., Azad, M. A. K., & Correa, H. (2019b). Mergers and acquisitions strategic fit in middle Eastern banking: an NDEA approach. International Journal of Service and Operations Management, 33(1), 1–25.
Wanke, P., Azad, M. A. K., Emrouznejad, A., & Antunes, J. (2019c). A dynamic network DEA model for accounting and financial indicators: a case of efficiency in MENA banking. International Review of Economics and Finance, 61, 52–68.
Wanke, P. F., & Barros, C. P. (2016). Evaluating returns to scale and convexity in DEA via bootstrap: a case study with Brazilian port terminals. In S. N. Hwang, H. S. Lee, & J. Zhu (Eds.), Handbook of operations analytics using data envelopment analysis (Vol. 239, pp. 187–214). Springer.
Wanke, P., Chen, Z., Antunes, J., & Barros, C. (2018a). Malmquist productivity indexes in Chinese ports: a fuzzy GMSS DEA approach. International Journal of Shipping and Transport Logistics, 10(2), 202–236.
Wanke, P., Chen, Z., Antunes, J., & Barros, C. (2018b). Malmquist productivity indexes in Chinese ports: a fuzzy GMM DEA approach. International Journal of Shipping and Transport Logistics, 10, 202–236.
Wu, D., Yang, Z., & Liang, L. (2006). Using DEA-neural network approach to evaluate branch efficiency of a large Canadian bank. Expert Systems with Applications, 31(1), 108–115.
Wu, M., Shen, C., Lu, C., & Chan, C. (2012). Impact of foreign strategic investors on earnings management in Chinese banks. Emerging Markets Finance and Trade, 48, 115–133.
Zha, Y., Liang, N., Wu, M., & Bian, Y. (2016). Efficiency evaluation of banks in China: a dynamic two-stage slacks-based measure approach. Omega, 60, 60–72.
Zhou, X., Xu, Z., Chai, J., Yao, L., Wang, S., & Lev, B. (2018). Efficiency evaluation for banking systems under uncertainty: a multi-period three-stage DEA model. Omega, 85, 68–82.
Zucchini, W., MacDonald, I. L., & Kangrock, R. (2016). Hidden Markov models for time series: an introduction using R (2nd ed.). Taylor and Francis.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: List of Chinese banks researched
Bank Code | Full name |
|---|---|
ICB | Industrial & Commercial Bank of China (The)—ICBC |
CCB | China Construction Bank Corporation Joint Stock Company |
ACL | Agricultural Bank of China Limited |
BCL | Bank of China Limited |
PSB | Postal Savings Bank of China Co Ltd |
CMB | China Merchants Bank Co Ltd |
BCC | Bank of Communications Co. Ltd |
SPD | Shanghai Pudong Development Bank |
CBC | China CITIC Bank Corporation Limited |
CMB | China Minsheng Banking Corporation |
IBC | Industrial Bank Co Ltd |
CEB | China Everbright Bank Company Limited |
HXB | Hua Xia Bank co., Limited |
BOB | Bank of Beijing Co Ltd |
CZB | China Zheshang Bank Co Ltd |
BOJ | Bank of Jiangsu Co Ltd |
BOS | Bank of Shanghai |
BON | Bank of Nanjing |
CRC | Chongqing Rural Commercial Bank |
HBC | Huishang Bank Co Ltd |
HB | Harbin Bank |
BOH | Bank of Hangzhou Co Ltd |
GRC | Guangzhou Rural Commercial Bank Co., Ltd |
ZBC | Zhongyuan Bank Co Ltd |
BOZ | Bank of Zhengzhou Co., Ltd |
BOC | Bank of Chongqing |
CRC | Jiangsu Changshu Rural Commercial Bank Co., Ltd-Changshu Rural Commercial Bank |
WRC | Wuxi Rural Commercial Bank Co., Ltd |
JWR | Jiangsu Wujiang Rural Commercial Bank |
Appendix B: Overall efficiency and sub-efficiencies of the sample
Bank name | Full name | Year | Overall | Stage 01 | Stage 02 |
|---|---|---|---|---|---|
ICB | Industrial & Commercial Bank of China (The)—ICBC | 2007 | 1 | 1 | 1 |
ICB | Industrial & Commercial Bank of China (The)—ICBC | 2008 | 1 | 1 | 1 |
ICB | Industrial & Commercial Bank of China (The)—ICBC | 2009 | 0.9909 | 0.9191 | 0.9909 |
ICB | Industrial & Commercial Bank of China (The)—ICBC | 2010 | 1 | 0.9017 | 1 |
ICB | Industrial & Commercial Bank of China (The)—ICBC | 2011 | 1 | 0.9486 | 1 |
ICB | Industrial & Commercial Bank of China (The)—ICBC | 2012 | 1 | 0.9182 | 1 |
ICB | Industrial & Commercial Bank of China (The)—ICBC | 2013 | 1 | 0.9758 | 1 |
ICB | Industrial & Commercial Bank of China (The)—ICBC | 2014 | 0.9227 | 0.9432 | 0.8845 |
ICB | Industrial & Commercial Bank of China (The)—ICBC | 2015 | 0.9463 | 0.9463 | 0.6522 |
ICB | Industrial & Commercial Bank of China (The)—ICBC | 2016 | 1 | 1 | 0.7695 |
ICB | Industrial & Commercial Bank of China (The)—ICBC | 2017 | 1 | 1 | 0.7313 |
CCB | China Construction Bank Corporation Joint Stock Company | 2007 | 1 | 1 | 1 |
CCB | China Construction Bank Corporation Joint Stock Company | 2008 | 1 | 0.9629 | 1 |
CCB | China Construction Bank Corporation Joint Stock Company | 2009 | 1 | 0.783 | 1 |
CCB | China Construction Bank Corporation Joint Stock Company | 2010 | 1 | 0.9349 | 1 |
CCB | China Construction Bank Corporation Joint Stock Company | 2011 | 1 | 0.8521 | 1 |
CCB | China Construction Bank Corporation Joint Stock Company | 2012 | 0.8976 | 0.8748 | 0.9481 |
CCB | China Construction Bank Corporation Joint Stock Company | 2013 | 0.8926 | 0.8293 | 0.8926 |
CCB | China Construction Bank Corporation Joint Stock Company | 2014 | 0.9118 | 0.88 | 1 |
CCB | China Construction Bank Corporation Joint Stock Company | 2015 | 0.8865 | 0.8998 | 0.9462 |
CCB | China Construction Bank Corporation Joint Stock Company | 2016 | 0.8304 | 0.9294 | 0.7989 |
CCB | China Construction Bank Corporation Joint Stock Company | 2017 | 0.8188 | 0.8367 | 0.7553 |
ACL | Agricultural Bank of China Limited | 2007 | 0.9106 | 0.9207 | 0.9106 |
ACL | Agricultural Bank of China Limited | 2008 | 0.9463 | 0.8785 | 0.9463 |
ACL | Agricultural Bank of China Limited | 2009 | 1 | 0.9625 | 1 |
ACL | Agricultural Bank of China Limited | 2010 | 0.9534 | 0.9918 | 0.949 |
ACL | Agricultural Bank of China Limited | 2011 | 0.9958 | 0.9912 | 1 |
ACL | Agricultural Bank of China Limited | 2012 | 0.9998 | 0.9655 | 1 |
ACL | Agricultural Bank of China Limited | 2013 | 0.9432 | 0.9598 | 0.9581 |
ACL | Agricultural Bank of China Limited | 2014 | 0.8657 | 0.865 | 0.95 |
ACL | Agricultural Bank of China Limited | 2015 | 0.8233 | 0.8248 | 0.8803 |
ACL | Agricultural Bank of China Limited | 2016 | 0.7902 | 0.8861 | 0.7558 |
ACL | Agricultural Bank of China Limited | 2017 | 0.7842 | 0.9095 | 0.7368 |
BCL | Bank of China Limited | 2007 | 1 | 1 | 0.9522 |
BCL | Bank of China Limited | 2008 | 0.9609 | 0.9609 | 0.9291 |
BCL | Bank of China Limited | 2009 | 0.9951 | 0.8563 | 0.9951 |
BCL | Bank of China Limited | 2010 | 1 | 0.9675 | 1 |
BCL | Bank of China Limited | 2011 | 0.9686 | 0.8178 | 0.9686 |
BCL | Bank of China Limited | 2012 | 1 | 0.8465 | 1 |
BCL | Bank of China Limited | 2013 | 1 | 0.8408 | 1 |
BCL | Bank of China Limited | 2014 | 0.8648 | 0.8792 | 0.9278 |
BCL | Bank of China Limited | 2015 | 0.8258 | 0.8601 | 0.8812 |
BCL | Bank of China Limited | 2016 | 0.8506 | 0.8506 | 0.6992 |
BCL | Bank of China Limited | 2017 | 0.9061 | 0.9061 | 0.683 |
PSB | Postal Savings Bank of China Co Ltd | 2007 | 1 | 1 | 1 |
PSB | Postal Savings Bank of China Co Ltd | 2008 | 1 | 0.9398 | 1 |
PSB | Postal Savings Bank of China Co Ltd | 2009 | 1 | 0.8501 | 1 |
PSB | Postal Savings Bank of China Co Ltd | 2010 | 0.9465 | 0.7821 | 0.9465 |
PSB | Postal Savings Bank of China Co Ltd | 2011 | 1 | 0.7493 | 1 |
PSB | Postal Savings Bank of China Co Ltd | 2012 | 0.9764 | 0.7139 | 0.9764 |
PSB | Postal Savings Bank of China Co Ltd | 2013 | 0.9232 | 0.6819 | 0.9232 |
PSB | Postal Savings Bank of China Co Ltd | 2014 | 0.9165 | 0.3333 | 0.9165 |
PSB | Postal Savings Bank of China Co Ltd | 2015 | 0.9026 | 0.3078 | 0.9026 |
PSB | Postal Savings Bank of China Co Ltd | 2016 | 1 | 0.2893 | 1 |
PSB | Postal Savings Bank of China Co Ltd | 2017 | 0.9986 | 0.3241 | 0.9986 |
CMB | China Merchants Bank Co Ltd | 2007 | 0.8216 | 0.8492 | 0.8624 |
CMB | China Merchants Bank Co Ltd | 2008 | 0.8442 | 0.8721 | 0.8971 |
CMB | China Merchants Bank Co Ltd | 2009 | 0.8832 | 0.9096 | 0.9191 |
CMB | China Merchants Bank Co Ltd | 2010 | 0.903 | 0.8974 | 0.9083 |
CMB | China Merchants Bank Co Ltd | 2011 | 0.9408 | 0.9753 | 0.9492 |
CMB | China Merchants Bank Co Ltd | 2012 | 0.9672 | 0.7648 | 0.9672 |
CMB | China Merchants Bank Co Ltd | 2013 | 0.8599 | 0.8329 | 0.9059 |
CMB | China Merchants Bank Co Ltd | 2014 | 0.8619 | 0.8263 | 0.9652 |
CMB | China Merchants Bank Co Ltd | 2015 | 0.8578 | 0.8238 | 0.9651 |
CMB | China Merchants Bank Co Ltd | 2016 | 0.8427 | 0.9543 | 0.8002 |
CMB | China Merchants Bank Co Ltd | 2017 | 0.7726 | 0.7726 | 0.695 |
BCC | Bank of Communications Co. Ltd | 2007 | 0.9741 | 0.9741 | 0.9555 |
BCC | Bank of Communications Co. Ltd | 2008 | 1 | 0.9041 | 1 |
BCC | Bank of Communications Co. Ltd | 2009 | 1 | 0.9746 | 1 |
BCC | Bank of Communications Co. Ltd | 2010 | 1 | 0.9704 | 1 |
BCC | Bank of Communications Co. Ltd | 2011 | 1 | 1 | 1 |
BCC | Bank of Communications Co. Ltd | 2012 | 0.905 | 0.8976 | 0.9375 |
BCC | Bank of Communications Co. Ltd | 2013 | 0.9021 | 0.9261 | 0.9403 |
BCC | Bank of Communications Co. Ltd | 2014 | 0.8729 | 0.8637 | 0.9666 |
BCC | Bank of Communications Co. Ltd | 2015 | 0.9194 | 0.9328 | 0.9364 |
BCC | Bank of Communications Co. Ltd | 2016 | 0.927 | 0.927 | 0.5814 |
BCC | Bank of Communications Co. Ltd | 2017 | 1 | 1 | 0.5775 |
SPD | Shanghai Pudong Development Bank | 2007 | 0.7329 | 0.8062 | 0.7493 |
SPD | Shanghai Pudong Development Bank | 2008 | 0.7512 | 0.8651 | 0.7797 |
SPD | Shanghai Pudong Development Bank | 2009 | 0.7847 | 0.8712 | 0.8418 |
SPD | Shanghai Pudong Development Bank | 2010 | 0.7925 | 0.8973 | 0.8087 |
SPD | Shanghai Pudong Development Bank | 2011 | 0.8432 | 0.9621 | 0.8502 |
SPD | Shanghai Pudong Development Bank | 2012 | 0.8755 | 0.9201 | 0.914 |
SPD | Shanghai Pudong Development Bank | 2013 | 0.932 | 0.9417 | 0.964 |
SPD | Shanghai Pudong Development Bank | 2014 | 0.8519 | 0.8729 | 0.9084 |
SPD | Shanghai Pudong Development Bank | 2015 | 0.8284 | 0.8176 | 0.9157 |
SPD | Shanghai Pudong Development Bank | 2016 | 0.7986 | 0.7986 | 0.7301 |
SPD | Shanghai Pudong Development Bank | 2017 | 0.7848 | 0.7848 | 0.6357 |
CBC | China CITIC Bank Corporation Limited | 2007 | 0.9703 | 0.8715 | 0.9703 |
CBC | China CITIC Bank Corporation Limited | 2008 | 1 | 0.7033 | 1 |
CBC | China CITIC Bank Corporation Limited | 2009 | 0.9443 | 0.8326 | 0.9443 |
CBC | China CITIC Bank Corporation Limited | 2010 | 0.9512 | 0.9143 | 0.9512 |
CBC | China CITIC Bank Corporation Limited | 2011 | 0.9439 | 0.9044 | 0.9439 |
CBC | China CITIC Bank Corporation Limited | 2012 | 0.8627 | 0.8954 | 0.9198 |
CBC | China CITIC Bank Corporation Limited | 2013 | 0.9533 | 0.9154 | 1 |
CBC | China CITIC Bank Corporation Limited | 2014 | 0.9636 | 0.937 | 1 |
CBC | China CITIC Bank Corporation Limited | 2015 | 0.95 | 0.9134 | 1 |
CBC | China CITIC Bank Corporation Limited | 2016 | 0.8594 | 0.9219 | 0.8833 |
CBC | China CITIC Bank Corporation Limited | 2017 | 0.782 | 0.8444 | 0.7823 |
CMB | China Minsheng Banking Corporation | 2007 | 0.9555 | 0.9359 | 1 |
CMB | China Minsheng Banking Corporation | 2008 | 0.9035 | 0.9987 | 0.8818 |
CMB | China Minsheng Banking Corporation | 2009 | 0.8466 | 0.872 | 0.916 |
CMB | China Minsheng Banking Corporation | 2010 | 0.8611 | 0.9013 | 0.8983 |
CMB | China Minsheng Banking Corporation | 2011 | 0.8959 | 0.9364 | 0.9157 |
CMB | China Minsheng Banking Corporation | 2012 | 0.9095 | 0.9323 | 0.941 |
CMB | China Minsheng Banking Corporation | 2013 | 0.9137 | 0.9259 | 0.9515 |
CMB | China Minsheng Banking Corporation | 2014 | 0.7678 | 0.7707 | 0.8565 |
CMB | China Minsheng Banking Corporation | 2015 | 0.7418 | 0.7418 | 0.7046 |
CMB | China Minsheng Banking Corporation | 2016 | 0.849 | 0.849 | 0.5009 |
CMB | China Minsheng Banking Corporation | 2017 | 0.8564 | 0.8564 | 0.4952 |
IBC | Industrial Bank Co Ltd | 2007 | 0.7697 | 0.8226 | 0.7929 |
IBC | Industrial Bank Co Ltd | 2008 | 0.7642 | 0.7888 | 0.8702 |
IBC | Industrial Bank Co Ltd | 2009 | 0.754 | 0.7655 | 0.8747 |
IBC | Industrial Bank Co Ltd | 2010 | 0.7266 | 0.7519 | 0.8578 |
IBC | Industrial Bank Co Ltd | 2011 | 0.7848 | 0.8278 | 0.8671 |
IBC | Industrial Bank Co Ltd | 2012 | 0.86 | 0.7347 | 1 |
IBC | Industrial Bank Co Ltd | 2013 | 0.8526 | 0.7593 | 0.9863 |
IBC | Industrial Bank Co Ltd | 2014 | 0.8439 | 0.7312 | 1 |
IBC | Industrial Bank Co Ltd | 2015 | 0.837 | 0.6752 | 1 |
IBC | Industrial Bank Co Ltd | 2016 | 0.8441 | 0.8441 | 0.7908 |
IBC | Industrial Bank Co Ltd | 2017 | 0.8591 | 0.8591 | 0.5592 |
CEB | China Everbright Bank Company Limited | 2007 | 0.926 | 0.8631 | 1 |
CEB | China Everbright Bank Company Limited | 2008 | 0.8522 | 0.8743 | 0.9252 |
CEB | China Everbright Bank Company Limited | 2009 | 0.8279 | 0.7866 | 0.9762 |
CEB | China Everbright Bank Company Limited | 2010 | 0.8146 | 0.7975 | 0.9464 |
CEB | China Everbright Bank Company Limited | 2011 | 0.8263 | 0.7514 | 1 |
CEB | China Everbright Bank Company Limited | 2012 | 0.8292 | 0.7782 | 0.9836 |
CEB | China Everbright Bank Company Limited | 2013 | 0.8101 | 0.7381 | 0.961 |
CEB | China Everbright Bank Company Limited | 2014 | 0.783 | 0.7422 | 0.9184 |
CEB | China Everbright Bank Company Limited | 2015 | 0.7425 | 0.725 | 0.8789 |
CEB | China Everbright Bank Company Limited | 2016 | 0.7672 | 0.7672 | 0.6655 |
CEB | China Everbright Bank Company Limited | 2017 | 0.7109 | 0.7109 | 0.5733 |
HXB | Hua Xia Bank co., Limited | 2007 | 0.9238 | 0.8344 | 1 |
HXB | Hua Xia Bank co., Limited | 2008 | 0.9131 | 0.6986 | 0.9198 |
HXB | Hua Xia Bank co., Limited | 2009 | 0.8337 | 0.6924 | 0.8455 |
HXB | Hua Xia Bank co., Limited | 2010 | 0.7727 | 0.787 | 0.8602 |
HXB | Hua Xia Bank co., Limited | 2011 | 1 | 0.7255 | 1 |
HXB | Hua Xia Bank co., Limited | 2012 | 0.7685 | 0.8396 | 0.8336 |
HXB | Hua Xia Bank co., Limited | 2013 | 0.833 | 0.8426 | 0.9104 |
HXB | Hua Xia Bank co., Limited | 2014 | 0.8448 | 0.8307 | 0.9416 |
HXB | Hua Xia Bank co., Limited | 2015 | 0.8058 | 0.8714 | 0.8413 |
HXB | Hua Xia Bank co., Limited | 2016 | 0.7086 | 0.767 | 0.7812 |
HXB | Hua Xia Bank co., Limited | 2017 | 0.7009 | 0.7179 | 0.6997 |
BOB | Bank of Beijing Co Ltd | 2007 | 0.7974 | 0.7974 | 0.6801 |
BOB | Bank of Beijing Co Ltd | 2008 | 0.8407 | 0.8407 | 0.5718 |
BOB | Bank of Beijing Co Ltd | 2009 | 0.8382 | 0.8382 | 0.5437 |
BOB | Bank of Beijing Co Ltd | 2010 | 0.8492 | 0.8492 | 0.6076 |
BOB | Bank of Beijing Co Ltd | 2011 | 0.9176 | 0.9176 | 0.6235 |
BOB | Bank of Beijing Co Ltd | 2012 | 0.8268 | 0.8268 | 0.8334 |
BOB | Bank of Beijing Co Ltd | 2013 | 0.9324 | 0.9324 | 0.8308 |
BOB | Bank of Beijing Co Ltd | 2014 | 0.9045 | 0.9045 | 0.973 |
BOB | Bank of Beijing Co Ltd | 2015 | 0.8369 | 0.8369 | 0.9102 |
BOB | Bank of Beijing Co Ltd | 2016 | 0.849 | 0.849 | 0.7794 |
BOB | Bank of Beijing Co Ltd | 2017 | 0.9418 | 0.9418 | 0.7069 |
CZB | China Zheshang Bank Co Ltd | 2007 | 1 | 1 | 1 |
CZB | China Zheshang Bank Co Ltd | 2008 | 0.9898 | 0.9832 | 1 |
CZB | China Zheshang Bank Co Ltd | 2009 | 1 | 1 | 0.9487 |
CZB | China Zheshang Bank Co Ltd | 2010 | 0.9482 | 0.9511 | 0.9548 |
CZB | China Zheshang Bank Co Ltd | 2011 | 0.9104 | 0.8476 | 0.9957 |
CZB | China Zheshang Bank Co Ltd | 2012 | 0.8925 | 0.8743 | 0.9572 |
CZB | China Zheshang Bank Co Ltd | 2013 | 0.9055 | 0.9055 | 0.9031 |
CZB | China Zheshang Bank Co Ltd | 2014 | 0.9811 | 0.9811 | 0.6761 |
CZB | China Zheshang Bank Co Ltd | 2015 | 0.7533 | 0.7533 | 0.7108 |
CZB | China Zheshang Bank Co Ltd | 2016 | 0.9008 | 0.9008 | 0.8424 |
CZB | China Zheshang Bank Co Ltd | 2017 | 0.834 | 0.834 | 0.787 |
BOJ | Bank of Jiangsu Co Ltd | 2007 | 0.8507 | 0.8507 | 0.6512 |
BOJ | Bank of Jiangsu Co Ltd | 2008 | 0.7762 | 0.8113 | 0.7016 |
BOJ | Bank of Jiangsu Co Ltd | 2009 | 0.7636 | 0.8782 | 0.7545 |
BOJ | Bank of Jiangsu Co Ltd | 2010 | 0.7784 | 0.8979 | 0.75 |
BOJ | Bank of Jiangsu Co Ltd | 2011 | 0.7665 | 0.8739 | 0.7653 |
BOJ | Bank of Jiangsu Co Ltd | 2012 | 0.7578 | 0.8658 | 0.775 |
BOJ | Bank of Jiangsu Co Ltd | 2013 | 0.7744 | 0.8502 | 0.8225 |
BOJ | Bank of Jiangsu Co Ltd | 2014 | 0.814 | 0.9038 | 0.8242 |
BOJ | Bank of Jiangsu Co Ltd | 2015 | 0.8728 | 0.8728 | 0.908 |
BOJ | Bank of Jiangsu Co Ltd | 2016 | 0.9308 | 0.9308 | 0.6483 |
BOJ | Bank of Jiangsu Co Ltd | 2017 | 0.9253 | 0.9253 | 0.7308 |
BOS | Bank of Shanghai | 2007 | 0.8468 | 0.8763 | 0.738 |
BOS | Bank of Shanghai | 2008 | 0.8018 | 0.8088 | 0.7005 |
BOS | Bank of Shanghai | 2009 | 0.7699 | 0.7699 | 0.76 |
BOS | Bank of Shanghai | 2010 | 0.8366 | 0.8366 | 0.7588 |
BOS | Bank of Shanghai | 2011 | 0.8139 | 0.8192 | 0.799 |
BOS | Bank of Shanghai | 2012 | 0.8782 | 0.9788 | 0.8362 |
BOS | Bank of Shanghai | 2013 | 0.8702 | 0.8702 | 0.8494 |
BOS | Bank of Shanghai | 2014 | 0.8769 | 0.8769 | 0.8947 |
BOS | Bank of Shanghai | 2015 | 0.9182 | 0.9182 | 0.7637 |
BOS | Bank of Shanghai | 2016 | 1 | 1 | 0.6859 |
BOS | Bank of Shanghai | 2017 | 1 | 1 | 0.5645 |
BON | Bank of Nanjing | 2007 | 0.6052 | 0.6669 | 0.6861 |
BON | Bank of Nanjing | 2008 | 0.6672 | 0.7039 | 0.8275 |
BON | Bank of Nanjing | 2009 | 0.6934 | 0.7102 | 0.8289 |
BON | Bank of Nanjing | 2010 | 0.6695 | 0.6478 | 0.7305 |
BON | Bank of Nanjing | 2011 | 0.7306 | 0.6149 | 0.7959 |
BON | Bank of Nanjing | 2012 | 0.7675 | 0.6744 | 0.8346 |
BON | Bank of Nanjing | 2013 | 0.8631 | 0.826 | 0.8631 |
BON | Bank of Nanjing | 2014 | 1 | 1 | 1 |
BON | Bank of Nanjing | 2015 | 0.9697 | 0.8774 | 1 |
BON | Bank of Nanjing | 2016 | 0.9309 | 0.9773 | 0.8821 |
BON | Bank of Nanjing | 2017 | 0.9402 | 0.9402 | 0.3233 |
CRC | Chongqing Rural Commercial Bank | 2007 | 0.7884 | 0.7884 | 0.3885 |
CRC | Chongqing Rural Commercial Bank | 2008 | 0.6877 | 0.5681 | 0.6877 |
CRC | Chongqing Rural Commercial Bank | 2009 | 0.8213 | 0.6692 | 0.8213 |
CRC | Chongqing Rural Commercial Bank | 2010 | 0.7748 | 0.7014 | 0.7748 |
CRC | Chongqing Rural Commercial Bank | 2011 | 0.8501 | 0.8364 | 0.8501 |
CRC | Chongqing Rural Commercial Bank | 2012 | 1 | 0.919 | 1 |
CRC | Chongqing Rural Commercial Bank | 2013 | 0.7886 | 0.825 | 0.8319 |
CRC | Chongqing Rural Commercial Bank | 2014 | 0.7581 | 0.8232 | 0.8302 |
CRC | Chongqing Rural Commercial Bank | 2015 | 0.797 | 0.9366 | 0.7337 |
CRC | Chongqing Rural Commercial Bank | 2016 | 0.7535 | 0.7489 | 0.8643 |
CRC | Chongqing Rural Commercial Bank | 2017 | 0.737 | 0.7845 | 0.8137 |
HBC | Huishang Bank Co Ltd | 2007 | 1 | 1 | 0.1981 |
HBC | Huishang Bank Co Ltd | 2008 | 0.7554 | 0.9582 | 0.7328 |
HBC | Huishang Bank Co Ltd | 2009 | 0.7989 | 1 | 0.6533 |
HBC | Huishang Bank Co Ltd | 2010 | 0.8072 | 0.9895 | 0.6582 |
HBC | Huishang Bank Co Ltd | 2011 | 0.7539 | 0.829 | 0.7541 |
HBC | Huishang Bank Co Ltd | 2012 | 0.896 | 0.944 | 0.896 |
HBC | Huishang Bank Co Ltd | 2013 | 0.7415 | 0.8964 | 0.7743 |
HBC | Huishang Bank Co Ltd | 2014 | 0.7142 | 0.7421 | 0.8486 |
HBC | Huishang Bank Co Ltd | 2015 | 0.7279 | 0.8409 | 0.6778 |
HBC | Huishang Bank Co Ltd | 2016 | 0.7323 | 0.7675 | 0.7932 |
HBC | Huishang Bank Co Ltd | 2017 | 0.8302 | 0.8302 | 0.2664 |
HB | Harbin Bank | 2007 | 1 | 1 | 1 |
HB | Harbin Bank | 2008 | 0.9806 | 1 | 0.9188 |
HB | Harbin Bank | 2009 | 1 | 1 | 0.5778 |
HB | Harbin Bank | 2010 | 0.9558 | 0.9558 | 0.6566 |
HB | Harbin Bank | 2011 | 1 | 1 | 0.7534 |
HB | Harbin Bank | 2012 | 1 | 1 | 0.9252 |
HB | Harbin Bank | 2013 | 1 | 1 | 0.972 |
HB | Harbin Bank | 2014 | 1 | 0.9067 | 1 |
HB | Harbin Bank | 2015 | 1 | 1 | 1 |
HB | Harbin Bank | 2016 | 0.9742 | 0.9742 | 0.6795 |
HB | Harbin Bank | 2017 | 1 | 1 | 0.738 |
BOH | Bank of Hangzhou Co Ltd | 2007 | 0.7929 | 0.3948 | 0.7929 |
BOH | Bank of Hangzhou Co Ltd | 2008 | 0.9209 | 0.1214 | 0.9209 |
BOH | Bank of Hangzhou Co Ltd | 2009 | 0.8455 | 0.4237 | 0.8455 |
BOH | Bank of Hangzhou Co Ltd | 2010 | 1 | 0.1348 | 1 |
BOH | Bank of Hangzhou Co Ltd | 2011 | 1 | 0.288 | 1 |
BOH | Bank of Hangzhou Co Ltd | 2012 | 1 | 0.3139 | 1 |
BOH | Bank of Hangzhou Co Ltd | 2013 | 0.9231 | 0.4616 | 0.9231 |
BOH | Bank of Hangzhou Co Ltd | 2014 | 0.7111 | 0.6515 | 0.8167 |
BOH | Bank of Hangzhou Co Ltd | 2015 | 0.7072 | 0.6893 | 0.8044 |
BOH | Bank of Hangzhou Co Ltd | 2016 | 1 | 1 | 0.7443 |
BOH | Bank of Hangzhou Co Ltd | 2017 | 1 | 1 | 1 |
GRC | Guangzhou Rural Commercial Bank Co., Ltd | 2007 | 0.7893 | 0.4462 | 0.7893 |
GRC | Guangzhou Rural Commercial Bank Co., Ltd | 2008 | 0.9935 | 0.1795 | 0.9935 |
GRC | Guangzhou Rural Commercial Bank Co., Ltd | 2009 | 0.9393 | 0.152 | 0.9393 |
GRC | Guangzhou Rural Commercial Bank Co., Ltd | 2010 | 1 | 0.1495 | 1 |
GRC | Guangzhou Rural Commercial Bank Co., Ltd | 2011 | 1 | 0.1519 | 1 |
GRC | Guangzhou Rural Commercial Bank Co., Ltd | 2012 | 1 | 0.1732 | 1 |
GRC | Guangzhou Rural Commercial Bank Co., Ltd | 2013 | 0.8842 | 0.418 | 0.8842 |
GRC | Guangzhou Rural Commercial Bank Co., Ltd | 2014 | 0.7627 | 0.7876 | 0.8463 |
GRC | Guangzhou Rural Commercial Bank Co., Ltd | 2015 | 0.8801 | 0.8801 | 0.5534 |
GRC | Guangzhou Rural Commercial Bank Co., Ltd | 2016 | 0.7456 | 0.7456 | 0.3813 |
GRC | Guangzhou Rural Commercial Bank Co., Ltd | 2017 | 0.7889 | 0.8338 | 0.7929 |
ZBC | Zhongyuan Bank Co Ltd | 2007 | 1 | 1 | 1 |
ZBC | Zhongyuan Bank Co Ltd | 2008 | 1 | 1 | 1 |
ZBC | Zhongyuan Bank Co Ltd | 2009 | 1 | 1 | 1 |
ZBC | Zhongyuan Bank Co Ltd | 2010 | 1 | 1 | 0.4062 |
ZBC | Zhongyuan Bank Co Ltd | 2011 | 0.9978 | 0.9971 | 1 |
ZBC | Zhongyuan Bank Co Ltd | 2012 | 0.9971 | 0.8996 | 1 |
ZBC | Zhongyuan Bank Co Ltd | 2013 | 1 | 1 | 1 |
ZBC | Zhongyuan Bank Co Ltd | 2014 | 0.6045 | 0.6091 | 0.7741 |
ZBC | Zhongyuan Bank Co Ltd | 2015 | 0.7363 | 0.7363 | 0.2636 |
ZBC | Zhongyuan Bank Co Ltd | 2016 | 0.6828 | 0.6828 | 0.2248 |
ZBC | Zhongyuan Bank Co Ltd | 2017 | 0.648 | 0.648 | 0.3504 |
BOZ | Bank of Zhengzhou Co., Ltd | 2007 | 1 | 0.51 | 1 |
BOZ | Bank of Zhengzhou Co., Ltd | 2008 | 0.9718 | 0.6504 | 0.9718 |
BOZ | Bank of Zhengzhou Co., Ltd | 2009 | 0.8088 | 0.7411 | 0.9966 |
BOZ | Bank of Zhengzhou Co., Ltd | 2010 | 0.9417 | 0.7212 | 0.9417 |
BOZ | Bank of Zhengzhou Co., Ltd | 2011 | 0.9728 | 0.6855 | 0.9728 |
BOZ | Bank of Zhengzhou Co., Ltd | 2012 | 0.7633 | 0.6956 | 0.7633 |
BOZ | Bank of Zhengzhou Co., Ltd | 2013 | 0.7288 | 0.6084 | 0.7852 |
BOZ | Bank of Zhengzhou Co., Ltd | 2014 | 0.7777 | 0.674 | 0.8669 |
BOZ | Bank of Zhengzhou Co., Ltd | 2015 | 0.7573 | 0.5277 | 1 |
BOZ | Bank of Zhengzhou Co., Ltd | 2016 | 0.7689 | 0.7689 | 0.4337 |
BOZ | Bank of Zhengzhou Co., Ltd | 2017 | 0.7829 | 0.7829 | 0.4777 |
BOC | Bank of Chongqing | 2007 | 1 | 0.7368 | 1 |
BOC | Bank of Chongqing | 2008 | 1 | 0.3854 | 1 |
BOC | Bank of Chongqing | 2009 | 1 | 0.4446 | 1 |
BOC | Bank of Chongqing | 2010 | 1 | 0.5282 | 1 |
BOC | Bank of Chongqing | 2011 | 0.9081 | 0.8291 | 0.9081 |
BOC | Bank of Chongqing | 2012 | 0.9404 | 0.8946 | 0.9884 |
BOC | Bank of Chongqing | 2013 | 0.7993 | 0.7933 | 0.8963 |
BOC | Bank of Chongqing | 2014 | 0.8858 | 0.8858 | 0.8443 |
BOC | Bank of Chongqing | 2015 | 0.7372 | 0.7372 | 0.8438 |
BOC | Bank of Chongqing | 2016 | 0.8039 | 0.8039 | 0.6361 |
BOC | Bank of Chongqing | 2017 | 0.9359 | 0.9359 | 0.5201 |
CRC | Jiangsu Changshu Rural Commercial Bank Co., Ltd-Changshu Rural Commercial Bank | 2007 | 0.7797 | 0.7797 | 0.6457 |
CRC | Jiangsu Changshu Rural Commercial Bank Co., Ltd-Changshu Rural Commercial Bank | 2008 | 1 | 1 | 0.8227 |
CRC | Jiangsu Changshu Rural Commercial Bank Co., Ltd-Changshu Rural Commercial Bank | 2009 | 0.9083 | 0.9083 | 0.69 |
CRC | Jiangsu Changshu Rural Commercial Bank Co., Ltd-Changshu Rural Commercial Bank | 2010 | 0.9268 | 0.9268 | 0.9603 |
CRC | Jiangsu Changshu Rural Commercial Bank Co., Ltd-Changshu Rural Commercial Bank | 2011 | 1 | 1 | 1 |
CRC | Jiangsu Changshu Rural Commercial Bank Co., Ltd-Changshu Rural Commercial Bank | 2012 | 1 | 1 | 1 |
CRC | Jiangsu Changshu Rural Commercial Bank Co., Ltd-Changshu Rural Commercial Bank | 2013 | 0.9143 | 0.8996 | 0.9566 |
CRC | Jiangsu Changshu Rural Commercial Bank Co., Ltd-Changshu Rural Commercial Bank | 2014 | 0.9409 | 0.7465 | 1 |
CRC | Jiangsu Changshu Rural Commercial Bank Co., Ltd-Changshu Rural Commercial Bank | 2015 | 0.8422 | 0.5821 | 0.9541 |
CRC | Jiangsu Changshu Rural Commercial Bank Co., Ltd-Changshu Rural Commercial Bank | 2016 | 0.5087 | 0.546 | 0.7471 |
CRC | Jiangsu Changshu Rural Commercial Bank Co., Ltd-Changshu Rural Commercial Bank | 2017 | 0.5135 | 0.5561 | 0.7394 |
WRC | Wuxi Rural Commercial Bank Co., Ltd | 2007 | 1 | 1 | 1 |
WRC | Wuxi Rural Commercial Bank Co., Ltd | 2008 | 1 | 1 | 1 |
WRC | Wuxi Rural Commercial Bank Co., Ltd | 2009 | 1 | 1 | 1 |
WRC | Wuxi Rural Commercial Bank Co., Ltd | 2010 | 0.9626 | 0.9626 | 0.7115 |
WRC | Wuxi Rural Commercial Bank Co., Ltd | 2011 | 0.9862 | 1 | 0.8971 |
WRC | Wuxi Rural Commercial Bank Co., Ltd | 2012 | 0.9931 | 0.9698 | 0.9942 |
WRC | Wuxi Rural Commercial Bank Co., Ltd | 2013 | 1 | 0.9685 | 1 |
WRC | Wuxi Rural Commercial Bank Co., Ltd | 2014 | 1 | 0.9949 | 1 |
WRC | Wuxi Rural Commercial Bank Co., Ltd | 2015 | 1 | 1 | 1 |
WRC | Wuxi Rural Commercial Bank Co., Ltd | 2016 | 0.9703 | 0.9703 | 0.2753 |
WRC | Wuxi Rural Commercial Bank Co., Ltd | 2017 | 1 | 1 | 1 |
JWR | Jiangsu Wujiang Rural Commercial Bank | 2007 | 0.8042 | 0.6323 | 0.8042 |
JWR | Jiangsu Wujiang Rural Commercial Bank | 2008 | 0.8356 | 0.8356 | 0.7192 |
JWR | Jiangsu Wujiang Rural Commercial Bank | 2009 | 0.7954 | 0.7954 | 0.5232 |
JWR | Jiangsu Wujiang Rural Commercial Bank | 2010 | 0.9077 | 0.8446 | 0.9077 |
JWR | Jiangsu Wujiang Rural Commercial Bank | 2011 | 1 | 0.9127 | 1 |
JWR | Jiangsu Wujiang Rural Commercial Bank | 2012 | 1 | 1 | 0.9599 |
JWR | Jiangsu Wujiang Rural Commercial Bank | 2013 | 1 | 1 | 0.8207 |
JWR | Jiangsu Wujiang Rural Commercial Bank | 2014 | 1 | 1 | 0.6132 |
JWR | Jiangsu Wujiang Rural Commercial Bank | 2015 | 1 | 1 | 0.3769 |
JWR | Jiangsu Wujiang Rural Commercial Bank | 2016 | 0.8645 | 0.8645 | 0.3554 |
JWR | Jiangsu Wujiang Rural Commercial Bank | 2017 | 0.9476 | 0.9476 | 0.3435 |
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tan, Y., Wanke, P., Antunes, J. et al. Unveiling endogeneity between competition and efficiency in Chinese banks: a two-stage network DEA and regression analysis. Ann Oper Res 306, 131–171 (2021). https://doi.org/10.1007/s10479-021-04104-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-021-04104-1