Financing and coordination strategies for a manufacturer with limited operating and green innovation capital: bank credit financing versus supplier green investment

Abstract

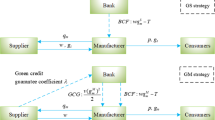
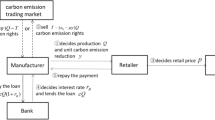
Green product development depends on the green innovation behavior of upstream and downstream companies in the supply chain. This paper focuses on a green supply chain consisting of a supplier and a manufacturer and considers two financing schemes wherein the manufacturer’s operating capital and green innovation capital are both constrained: bank credit financing (BCF) and supplier green investment (SGI). We investigate the financing strategy of a manufacturer with different financing decision preferences and supply chain coordination contract designs. The results show that when the manufacturer’s financing decision preference is low bankruptcy risk, it should choose BCF when the bank loan interest rate is lower than a threshold and SGI when the bank loan interest rate is higher than this threshold; when the manufacturer’s financing decision preference is high R&D benefit, it should choose BCF when the initial capital is lower than another threshold and choose SGI when the initial capital is higher than this threshold. Then, we compare whether cost-sharing, quantity discount and revenue-sharing contracts can coordinate the supply chain, and discuss the selection strategies of supply chain members for coordination contracts. Research shows that revenue-sharing contracts fail to coordinate; however, when the cost-sharing ratio and quantity discount rate are appropriate, both cost-sharing and quantity discount contracts can achieve supply chain coordination. The lower the supplier’s unit production cost, the stronger its motivation to accept a higher cost-sharing ratio and quantity discount rate. For the supplier, the key to choosing any coordination contract lies in the relative height of the cost-sharing ratio and quantity discount rate while the manufacturer should always choose a quantity discount contract when the quantity discount rate is high enough.

Appendix A

Proof of Proposition 1

From Eq. (2), we obtain the first-order and second-order derivative of ${{\pi }_{m}}$ with respect to ${{q}_{m}}$.

$$\begin{aligned} \frac{\partial {{\pi }_{m}}}{\partial {{q}_{m}}}= & {} p\left[ 1-F(q_{m}^{{}},g_{m}^{{}}) \right] -w(1+{{r}_{b}})\left[ 1-F(q_{m,t}^{{}},g_{m}^{{}}) \right] \end{aligned}$$

(A.1)

$$\begin{aligned} \frac{{{\partial }^{2}}{{\pi }_{m}}}{\partial q_{m}^{2}}= & {} -pf(q_{m}^{{}},g_{m}^{{}})+\frac{{{w}^{2}}{{(1+{{r}_{b}})}^{2}}}{p}f(q_{m,t}^{{}},g_{m}^{{}}) \end{aligned}$$

(A.2)

As $\frac{\partial {{\pi }_{m}}}{\partial {{q}_{m}}}=0$, we obtain $\frac{{{\partial }^{2}}{{\pi }_{m}}}{\partial q_{m}^{2}}=-p{\overline{F}}({{q}_{m}},{{g}_{m}})\left[ h({{q}_{m}},{{g}_{m}})-h({{q}_{m,t}},{{g}_{m}})A \right]$, where $A=\frac{w(1+{{r}_{b}})}{p}$. If the distribution of demand is IFR, the inequality of $h({{q}_{m}},{{g}_{m}})/h({{q}_{m,t}},{{g}_{m}})>1$ holds for $f(q_{m}^{{}},g_{m}^{{}})/f(q_{m,t}^{{}},g_{m}^{{}})>1$. As $A\le 1$, we obtain $h({{q}_{m}},{{g}_{m}})-h({{q}_{m,t}},{{g}_{m}})A>0$, i.e., ${{\partial }^{2}}{{\pi }_{m}}/\partial q_{m}^{2}\le 0$. From $\partial {{\pi }_{m}}/\partial {{q}_{m}}=0$, we obtain Eq. (3). From Eq. (2), we obtain the first-order derivative of ${{\pi }_{m}}$ with respect to ${{g}_{m}}$.

$$\begin{aligned} \frac{\partial {{\pi }_{m}}}{\partial {{g}_{m}}}=p\phi F({{q}_{m}},{{g}_{m}})-p\phi F({{q}_{m,t}},{{g}_{m}})-v{{g}_{m}}(1+{{r}_{b}}){\overline{F}}({{q}_{m,t}},{{g}_{m}}) \end{aligned}$$

(A.3)

From Eqs. (3) and (A.3), we obtain Eq. (4). $\square$

Proof of Corollary 1

Using the Implicit Function Derivation Rule to find the partial derivative with respect to w on both sides of $p\left[ 1-F({{q}_{m}},{{g}_{m}}) \right] \text {=}w(1+{{r}_{b}})\left[ 1-F({{q}_{m,t}},{{g}_{m}}) \right]$, we obtain:

$$\begin{aligned} -f(q_{m}^{*},g_{m}^{*})\left( \frac{\partial q_{m}^{*}}{\partial w}+\frac{{{\phi }^{2}}}{v}\right) =\frac{A}{w}{\overline{F}}\left( q_{m,t}^{*},g_{m}^{*}\right) -Af\left( q_{m,t}^{*},g_{m}^{*}\right) \left[ A\frac{\partial q_{m}^{*}}{\partial w}+q_{m}^{*}\frac{A}{w}-\frac{{{\phi }^{2}}(1-A)-{{\phi }^{2}}}{v} \right] \end{aligned}$$

(A.4)

Equation (A.4) can be rewritten as $\frac{\partial q_{m}^{B*}}{\partial w}=\frac{-{{\phi }^{2}}}{v}\text {+}\frac{A}{w}\frac{\left[ -{\overline{F}}(q_{m,t}^{*},g_{m}^{*}\phi )p+Aq_{m}^{*}f(q_{m,t}^{*},g_{m}^{*}) \right] }{-f(q_{m,t}^{*},g_{m}^{*}){{A}^{2}}+f(q_{m}^{*},g_{m}^{*})}$.

Let $B=\frac{A}{w}\frac{\left[ -{\overline{F}}(q_{m,t}^{*},g_{m}^{*})p+Aq_{m}^{B*}f(q_{m,t}^{*},g_{m}^{*}) \right] }{-{{A}^{2}}f(q_{m,t}^{*},g_{m}^{*})+f(q_{m}^{*},g_{m}^{*})}=\frac{1-Aq_{m}^{*}h(q_{m,t}^{*},g_{m}^{*})}{w\left[ Ah(q_{m,t}^{*},g_{m}^{*})-h(q_{m}^{*},g_{m}^{*}) \right] }$. Similar to Chen and Wang (2012) and Yan et al. (2016), we can use contradiction to prove $B<0$. Therefore, we obtain $\frac{\partial q_{m}^{B*}}{\partial w}<0$.

Using the Implicit Function Derivation Rule to find the partial derivative with respect to M on both sides of $p\left[ 1-F({{q}_{m}},{{g}_{m}}) \right] \text {=}w(1+{{r}_{b}})\left[ 1-F({{q}_{m,t}},{{g}_{m}}) \right]$, we have:

$$\begin{aligned} -pf(q_{m}^{*},g_{m}^{*})\frac{\partial q_{m}^{*}}{\partial M}=-w(1+{{r}_{b}})f(q_{m,t}^{*},g_{m}^{*})\left[ \frac{w(1+{{r}_{b}})}{p}\frac{\partial q_{m}^{*}}{\partial M}-\frac{(1+{{r}_{b}})}{p} \right] \end{aligned}$$

(A.5)

From Eq. (A.5), we obtain $\frac{\partial q_{m}^{B*}}{M}=\frac{f(q_{m,t}^{*},g_{m}^{*}){{(1+{{r}_{b}})}^{2}}w}{f(q_{m,t}^{*},g_{m}^{*}){{(1+{{r}_{b}})}^{2}}{{w}^{2}}-f(q_{m}^{*},g_{m}^{*}){{p}^{2}}}<0$.

Using the Implicit Function Derivation Rule to find the partial derivative with respect to ${{g}_{s}}$ on both sides of $p\left[ 1-F({{q}_{m}},{{g}_{m}}) \right] \text {=}w(1+{{r}_{b}})\left[ 1-F({{q}_{m,t}},{{g}_{m}}) \right]$, we have:

$$\begin{aligned} -pf(q_{m}^{*},g_{m}^{*})(\frac{\partial q_{m}^{*}}{\partial {{g}_{s}}}-\phi )=-w(1+{{r}_{b}})f(q_{m,t}^{*},g_{m}^{*})\left[ \frac{w(1+{{r}_{b}})}{p}\frac{\partial q_{m}^{*}}{\partial {{g}_{s}}}-\phi \right] \end{aligned}$$

(A.6)

From Eq. (A.6), we obtain $\frac{\partial q_{m}^{B*}}{\partial {{g}_{s}}}=\frac{\left[ -f(q_{m,t}^{B*},g_{m}^{B*})(1+{{r}_{b}})w+f(q_{m}^{B*},g_{m}^{B*})p \right] p\phi }{-f(q_{m,t}^{B*},g_{m}^{B*}){{(1+{{r}_{b}})}^{2}}{{w}^{2}}+f(q_{m}^{B*},g_{m}^{B*}){{p}^{2}}}>0$. $\square$

Proof of Corollary 2

From Eq. (4), we obtain $\frac{\partial g_{m}^{B*}}{\partial w}=-\frac{\phi }{v}<0$, $\frac{\partial g_{m}^{B*}}{\partial M}=0$ and $\frac{\partial g_{m}^{B*}}{\partial {{g}_{s}}}=0$. $\square$

Proof of Proposition 2

From Eq. (5), we get the first-order derivative of ${{\pi }_{s}}$ with respect to w

$$\begin{aligned} \frac{\partial \pi _{m}^{{}}}{\partial w}=(w-c-\frac{kg_{s}^{2}}{2})\frac{\partial q_{m}^{B*}}{\partial w}+q_{m}^{B*} \end{aligned}$$

(A.7)

Similar to the prove progress of the Yan et al. (2016) and Yan et al. (2019), we obtain the rational supplier would charge w and no less than ${{{\widehat{c}}}^{B}}$, which guarantees a nonnegative profit for the supplier. We called ${{{\widehat{c}}}^{B}}$ is unit efficient cost under BCF. It should be noted that the unit effective cost under BCF is equal to the unit production cost, i.e., ${{{\widehat{c}}}^{B}}={\widetilde{c}}=c+\frac{kg_{s}^{2}}{2}$. Let $\frac{\partial \pi _{m}^{{}}}{\partial w}=0$, we have $w_{{}}^{B*}\text {=}{{{\widehat{c}}}^{B}}-\frac{q_{m}^{B*}}{\partial q_{m}^{B*}/\partial w}$. Substituting $\frac{\partial q_{m}^{B*}}{\partial w}$ into the above formula, we have the optimal w. $\square$

Proof of Proposition 3

Proof of Proposition 3 is similar to Proposition 1. $\square$

Proof of Corollary 3

Using the Implicit Function Derivation Rule to find the partial derivative with respect to $\alpha$ on both sides of $\alpha p\left[ 1-F({{q}_{m}},{{g}_{m}}) \right] \text {=}w\left[ 1-F({{q}_{m,t}},{{g}_{m}}) \right]$, we have:

$$\begin{aligned} \begin{aligned}&p{\overline{F}}(q_{m}^{*},g_{m}^{*})-\alpha pf(q_{m}^{*},g_{m}^{*})\left( \frac{\partial q_{m}^{*}}{\partial \alpha }-\frac{\partial g_{m}^{*}}{\partial \alpha }\phi \right) \\&=-wf(q_{m,t}^{*},g_{m}^{*})\left( \frac{w}{\alpha p}\frac{\partial q_{m}^{*}}{\partial \alpha }-\frac{wq_{m}^{*}}{{{\alpha }^{2}}p}+\frac{vg_{m}^{*}}{\alpha p}\frac{\partial g_{m}^{*}}{\partial \alpha }-\frac{1}{2}\frac{vg_{m}^{2}}{{{\alpha }^{2}}p}-\frac{\partial g_{m}^{*}}{\partial \alpha }\phi +\frac{M}{{{\alpha }^{2}}p}\right) \\ \end{aligned} \end{aligned}$$

(A.8)

Equation (A.8) can be rewritten as:

$$\begin{aligned} \begin{aligned} \frac{\partial q_{m}^{S*}}{\partial \alpha }\text {=}\frac{\left[ \begin{aligned}&2{{\alpha }^{3}}{{p}^{3}}f(q_{m}^{*},g_{m}^{*}){{\phi }^{2}} \\&-({{\alpha }^{2}}{{p}^{2}}w+{{w}^{3}}){{\phi }^{2}}f(q_{m,t}^{*},g_{m}^{*}) \\ \end{aligned} \right] +\left[ \begin{aligned}&2f(q_{m,t}^{*},g_{m}^{*})Mvw \\&+2{{\alpha }^{2}}{{p}^{2}}v{\overline{F}}(q_{m,t}^{*},g_{m}^{*})-2f(q_{m,t}^{*},g_{m}^{*})v{{w}^{2}}q_{m}^{*} \\ \end{aligned} \right] }{2\alpha v\left[ {{\alpha }^{2}}{{p}^{2}}f(q_{m}^{*},g_{m}^{*})-f(q_{m,t}^{*},g_{m}^{*}){{w}^{2}} \right] } \\ \end{aligned} \end{aligned}$$

(A.9)

In order to proof the positive or negative of $\frac{\partial q_{m}^{S*}}{\partial \alpha }$, we proof the positive or negative of $\frac{\partial q_{m}^{S*}}{\partial w}$. Taking the partial derivatives of $\left[ 1-F({{q}_{m}},{{g}_{m}}) \right] ap=w\left[ 1-F({{q}_{m}},{{g}_{m}}) \right]$ with respect to w, we obtain:

$$\begin{aligned} \alpha pf(q_{m}^{*},g_{m}^{*})\left( \frac{\partial q_{m}^{*}}{\partial \alpha }-\frac{\partial g_{m}^{*}}{\partial \alpha }\phi \right) ={\overline{F}}(q_{m}^{*},g_{m}^{*})-wf(q_{m,t}^{*},g_{m}^{*})\left( \frac{w}{\alpha p}\frac{\partial q_{m}^{*}}{\partial w}+\frac{q_{m}^{*}}{\alpha p}+\frac{vg_{m}^{*}}{\alpha p}\frac{\partial g_{m}^{*}}{\partial w}-\frac{\partial g_{m}^{*}}{\partial w}\phi \right) \end{aligned}$$

(A.10)

Equation (A.10) can be rewritten as $\frac{\partial q_{m}^{S*}}{\partial w}=\frac{-{{\alpha }^{2}}{{p}^{2}}f(q_{m}^{*},g_{m}^{*}){{\phi }^{2}}+f(q_{m}^{*},g_{m}^{*})w(q_{m}^{*}v+{{\phi }^{2}}w)-\alpha pv{\overline{F}}(q_{m,t}^{*},g_{m}^{*})}{v{{\alpha }^{2}}{{p}^{2}}f(q_{m}^{*},g_{m}^{*})-f(q_{m,t}^{*},g_{m}^{*}){{w}^{2}}v}$. Similar to the proof progress of $\frac{\partial q_{m}^{B*}}{\partial w}$, we obtain $\frac{\partial q_{m}^{S*}}{\partial w}<0$, i.e., $\alpha p{\overline{F}}(q_{m,t}^{*},g_{m}^{*})-f(q_{m}^{*},g_{m}^{*})wq_{m}^{*}>0$.

From $2{{\alpha }^{2}}{{p}^{2}}v{\overline{F}}(q_{m}^{*},g_{m}^{*})>2f(q_{m}^{*},g_{m}^{*})v{{w}^{2}}q_{m}^{*}$ and $2{{\alpha }^{3}}{{p}^{3}}f(q_{m}^{*},g_{m}^{*}){{\phi }^{2}}>({{\alpha }^{2}}{{p}^{2}}w+{{w}^{3}}){{\phi }^{2}}f(q_{m,t}^{*},g_{m}^{*})$, we obtain $\frac{\partial q_{m}^{S*}}{\partial \alpha }>0$. From Eq. (10), we obtain $\frac{\partial g_{m}^{*}}{\partial \alpha }=\frac{p\phi }{v}>0$. $\square$

Proof of Proposition 4

From Eq. (11), we obtain the first-order derivative of ${{\pi }_{s}}$ with respect to w:

$$\begin{aligned} \frac{\partial \pi _{s}^{{}}}{\partial w}=(w-c-kg_{s}^{2}/2)\frac{\partial q_{m}^{*}}{\partial w}+q_{m}^{*}\text {+}\frac{\text {(}1-\alpha )}{\alpha }\frac{\partial \pi _{m}^{{}}}{\partial {{q}_{m}}}\frac{\partial q_{m}^{*}}{\partial w}-p(\frac{\partial q_{m,t}^{*}}{\partial w}-\frac{\partial g_{m}^{*}}{\partial w}\phi )F(q_{m,t}^{*},g_{m}^{*}) \end{aligned}$$

(A.11)

From Eqs. (7), (A.11) can be rewritten as

$$\begin{aligned} \begin{aligned} \frac{\partial \pi _{s}^{S}}{\partial w}&=\left( 1 -\frac{F(q_{m,t}^{*},g_{m}^{*})}{\alpha }\right) q_{m}^{*}\\&\quad +\left[ w\left( 1-\frac{F\left( q_{m,t}^{*},g_{m}^{*}\right) }{\alpha }\right) \right. \\&\quad \left. -{\widetilde{c}}+\frac{\text {(}1-\alpha )}{\alpha }\frac{\partial {{\pi }_{m}}}{\partial {{q}_{m}}} \right] \frac{\partial q_{m}^{*}}{\partial w}\\&\quad -\left( \frac{vg_{m}^{*}}{\alpha }-p\phi \right) \frac{\partial g_{m}^{*}}{\partial w}F\left( q_{m,t}^{*},g_{m}^{*}\right) \\&\quad =\left( 1-\frac{F\left( q_{m,t}^{*},g_{m}^{*}\right) }{\alpha }\right) q_{m}^{*}+\frac{\partial q_{m}^{*}}{\partial w}\left( 1-\frac{F\left( q_{m,t}^{*},g_{m}^{*}\right) }{\alpha }\right) \\&\qquad \left[ w-\left( \frac{{\widetilde{c}}}{1-\frac{F\left( q_{m,t}^{*},g_{m}^{*}\right) }{\alpha }} +\frac{F\left( q_{m,t}^{*},g_{m}^{*}\right) }{1-\frac{F\left( q_{m,t}^{*},g_{m}^{*}\right) }{\alpha }}\frac{\frac{w{{\phi }^{2}}}{\alpha v}}{\frac{\partial q_{m}^{*}}{\partial w}}-\frac{\frac{\text {(}1-\alpha )}{\alpha }\frac{\partial {{\pi }_{m}}}{\partial {{q}_{m}}}}{1-\frac{F\left( q_{m,t}^{*},g_{m}^{*}\right) }{\alpha }}\right) \right] \\ \end{aligned} \end{aligned}$$

(A.12)

Let $\left[ 1-\frac{F(q_{m,t}^{*},g_{m}^{*})}{\alpha } \right] \text {=}\eta$ and ${{{\widehat{c}}}^{S}}=\frac{{\widetilde{c}}}{1-\frac{F(q_{m,t}^{*},g_{m}^{*})}{\alpha }}\text {+}\frac{F(q_{m,t}^{*},g_{m}^{*})}{1-\frac{F(q_{m,t}^{*},g_{m}^{*})}{\alpha }}\frac{\frac{w{{\phi }^{2}}}{\alpha v}}{\frac{\partial q_{m}^{*}}{\partial w}}-\frac{\frac{\text {(}1-\alpha )}{\alpha }\frac{\partial \pi _{m}^{{}}}{\partial {{q}_{m}}}}{1-\frac{F(q_{m,t}^{*},g_{m}^{*})}{\alpha }}$, the above equation can be rewritten as $\frac{\partial \pi _{s}^{S}}{\partial w}\text {=}\eta q_{m}^{*}+\frac{\partial q_{m}^{*}}{\partial w}\eta (w-{{{\widehat{c}}}^{S}})$. It is straight that $0<\eta <1$. Therefore, the rational manufacturer would charge w no less than ${{{\widehat{c}}}^{S}}$ when ${{{\widehat{c}}}^{S}}>{\widetilde{c}}$. From the first-order condition of $\frac{\partial \pi _{s}^{S}}{\partial w}\text {=}0$, we finally get the optimal w. $\square$

Proof of Corollary 4

By comparing the bankruptcy threshold of supplier in BCF and SGI scenarios, we obtain:

$$\begin{aligned} q_{m,t}^{B}-q_{m,t}^{S}=\frac{\left[ wq_{m}^{B*}-M+\frac{v{{(g_{m}^{B\text {*}})}^{2}}}{2} \right] (1+{{r}_{b}})}{p}-\frac{wq_{m}^{S*}-M+\frac{v{{(g_{m}^{S\text {*}})}^{2}}}{2}}{\alpha p} \end{aligned}$$

(A.13)

From Eq. (A.13), we obtain $\frac{\partial (q_{m,t}^{B}-q_{m,t}^{S})}{\partial {{r}_{b}}}\text {=}\frac{wq_{m}^{B*}-M+\frac{v{{(g_{m}^{B\text {*}})}^{2}}}{2}}{p}+\frac{(w\frac{\partial q_{m}^{B*}}{\partial {{r}_{b}}}+vg_{m}^{B\text {*}}\frac{\partial g_{m}^{B*}}{\partial {{r}_{b}}})(1+{{r}_{b}})}{p}$ . To determine the monotony of $\frac{\partial (q_{m,t}^{B}-q_{m,t}^{S})}{\partial {{r}_{b}}}$, we need to determine the monotony of $\frac{\partial q_{m}^{B*}}{\partial {{r}_{b}}}$.

Taking the partial derivatives of $\left[ 1-F({{q}_{m}},{{g}_{m}}) \right] p=w(1+{{r}_{b}})\left[ 1-F({{q}_{m,t}},{{g}_{m}}) \right]$ with respect to ${{r}_{b}}$, we obtain:

$$\begin{aligned}&-f(q_{m}^{B*},g_{m}^{B*})\left( \frac{\partial q_{m}^{B*}}{\partial {{r}_{b}}}-\frac{\partial g_{m}^{B*}}{\partial {{r}_{b}}}\phi \right) p\nonumber \\&\quad =w{\overline{F}}\left( q_{m,t}^{B*}-g_{m}^{B*}\phi )-w(1+{{r}_{b}}\right) f(q_{m,t}^{B*},g_{m}^{B*})\left( \frac{\partial q_{m,t}^{B*}}{\partial {{r}_{b}}}-\frac{\partial g_{m}^{B*}}{\partial {{r}_{b}}}\phi \right) \end{aligned}$$

(A.14)

Therefore, $\frac{\partial q_{m}^{B*}}{\partial {{r}_{b}}}=\frac{\left[ -2{{p}^{3}}f(q_{m}^{B*},g_{m}^{B*}){{\phi }^{2}}-2p{{(1+{{r}_{b}})}^{2}}vw{\overline{F}}(q_{m,t}^{B*},g_{m}^{B*}) \right] +f(q_{m,t}^{B*},g_{m}^{B\text {*}})(1+{{r}_{b}})w\left[ {{p}^{2}}{{\phi }^{2}}-{{(1+{{r}_{b}})}^{2}}(2Mv-2wq_{m}^{B*}v-{{\phi }^{2}}{{w}^{2}}) \right] }{2{{(1+{{r}_{b}})}^{2}}v\left[ f(q_{m}^{B*},g_{m}^{B*})-f(q_{m,t}^{B*},g_{m}^{B*}){{w}^{2}}{{(1+{{r}_{b}})}^{2}} \right] }$. From $\frac{\partial q_{m}^{B*}}{\partial w}<0$, we obtain $f(q_{m,t}^{B*},g_{m}^{B*})w{{(1+{{r}_{b}})}^{2}}q_{m}^{B*}v-(1+{{r}_{b}})vp{\overline{F}}(q_{m,t}^{B*},g_{m}^{B*})<0$. Multiply the above formula by $2w(1+{{r}_{b}})$, we have $f(q_{m,t}^{B*},g_{m}^{B*})2{{w}^{2}}{{(1+{{r}_{b}})}^{3}}q_{m}^{B*}v-{{(1+{{r}_{b}})}^{2}}wvp{\overline{F}}(q_{m,t}^{B*},g_{m}^{B*})<0$, i.e., $f(q_{m,t}^{B*},g_{m}^{B*})2w{{(1+{{r}_{b}})}^{3}}(wq_{m}^{B*}-M)v-{{(1+{{r}_{b}})}^{2}}wvp{\overline{F}}(q_{m,t}^{B*},g_{m}^{B*})<0$. In addition, since $-2f(q_{m}^{B*},g_{m}^{B*}){{p}^{3}}{{\phi }^{2}}+f(q_{m,t}^{B*},g_{m}^{B*})(1+{{r}_{b}})w{{\phi }^{2}}\left[ {{p}^{2}}+{{w}^{2}}{{(1+{{r}_{b}})}^{2}} \right] <0$, we finally obtain $\frac{\partial q_{m}^{B*}}{\partial {{r}_{b}}}<0$.

Since $\frac{\partial q_{m}^{B*}}{\partial {{r}_{b}}}<0$ and $\frac{\partial g_{m}^{B*}}{\partial {{r}_{b}}}<0$, we obtain that $\frac{\partial (q_{m,t}^{B}-q_{m,t}^{S})}{\partial {{r}_{b}}}=0$ has at most one solution in the domain of ${{r}_{b}}$. Therefore, $q_{m,t}^{B}-q_{m,t}^{S}\text {=}0$ has at most two solution in the domain of ${{r}_{b}}$. Let $q_{m,t}^{B}-q_{m,t}^{S}\text {=}0$, we have ${{r}_{b}}<\widehat{{{r}_{b}}}({{r}_{b}})$, then $q_{m,t}^{B}<q_{m,t}^{S}$ and ${{r}_{b}}>\widehat{{{r}_{b}}}({{r}_{b}})$, then $q_{m,t}^{B}>q_{m,t}^{S}$; where $\widehat{{{r}_{b}}}=\frac{2M-2\alpha M+\alpha v{{(g_{m}^{B*})}^{2}}-v{{(g_{m}^{S*})}^{2}}+2\alpha q_{m}^{B*}w-2q_{m}^{S*}w}{2\alpha M-\alpha v{{(g_{m}^{B*})}^{2}}-2\alpha q_{m}^{B*}w}$. $\square$

Proof of Corollary 5

By comparing the profit of manufacturer in BCF and SGI scenarios, we obtain

$$\begin{aligned} \begin{aligned}&\pi _{m}^{B}-\pi _{m}^{S}=p\int _{q_{m,t}^{B*}-({{g}_{s}}+g_{m}^{B*})\phi }^{q_{m}^{B*}-({{g}_{s}}+g_{m}^{B*})\phi }{\left[ x+({{g}_{s}}+g_{m}^{B*})\phi -q_{m,t}^{B*} \right] f(x)dx}\\&\quad +p\int _{q_{m}^{B*}-({{g}_{s}}+g_{m}^{B*})\phi }^{\infty }{(q_{m}^{B*}-q_{m,t}^{B*})f(x)dx}-M \\&\quad -\alpha p\int _{q_{m,t}^{S*}-({{g}_{s}}+g_{m}^{S*})\phi }^{q_{m}^{S*}-({{g}_{s}}+g_{m}^{S*})\phi }{\left[ x+({{g}_{s}}+g_{m}^{S*})\phi -q_{m,t}^{S*} \right] f(x)dx}\\&\quad -\alpha p\int _{q_{m}^{S*}-({{g}_{s}}+g_{m}^{S*})\phi }^{\infty }{(q_{m}^{S*}-q_{m,t}^{S*})f(x)dx}+\alpha M \\ \end{aligned} \end{aligned}$$

(A.15)

Equation (A.15) can be rewritten as:

$$\begin{aligned} p(q_{m}^{B*}-\alpha q_{m}^{S*}-q_{m,t}^{B*}+\alpha q_{m,t}^{S*})-p\int _{q_{m,t}^{B*}-({{g}_{s}}+g_{m}^{B*})\phi }^{q_{m}^{B*}-({{g}_{s}}+g_{m}^{B*})\phi }{F(x)dx}+\alpha p\int _{q_{m,t}^{S*}-({{g}_{s}}+g_{m}^{S*})\phi }^{q_{m}^{S*}-({{g}_{s}}+g_{m}^{S*})\phi }{F(x)dx}-M+\alpha M \end{aligned}$$

(A.16)

Since $\frac{\partial (q_{m}^{B*}-q_{m,t}^{B*})}{\partial M}=\frac{\partial q_{m}^{B*}}{\partial M}-\frac{\partial q_{m}^{B*}}{\partial M}\frac{w(1+{{r}_{b}})}{p}+\frac{1}{p}>0$ and $\frac{\partial (q_{m}^{S*}-q_{m,t}^{S*})}{\partial M}=\frac{\partial q_{m}^{S*}}{\partial M}-\frac{\partial q_{m}^{S*}}{\partial M}\frac{w}{\alpha p}+\frac{1}{\alpha p}>0$, we have $\frac{\partial (\pi _{m}^{B}-\pi _{m}^{S})}{\partial M}$ has at most one solution in the domain of M. Therefore, $\pi _{m}^{B}-\pi _{m}^{S}\text {=}0$ has at most two solution in the domain of M. Let $\pi _{m}^{B}-\pi _{m}^{S}\text {=}0$, we have $M>{\widehat{M}}(M)$, then $\pi _{m}^{B*}<\pi _{m}^{S*}$ and $M<{\widehat{M}}(M)$ then $\pi _{m}^{B*}>\pi _{m}^{S*}$; where ${\widehat{M}}=p\left[ \int _{q_{m,t}^{B*}-({{g}_{s}}+g_{m}^{B*})\phi }^{q_{m}^{B*}-({{g}_{s}}+g_{m}^{B*})\phi }{F(x)dx}-q_{m}^{B*}+q_{m,t}^{B*}-\alpha (\int _{q_{m,t}^{S*}-({{g}_{s}}+g_{m}^{S*})\phi }^{q_{m}^{S*}-({{g}_{s}}+g_{m}^{S*})\phi }{F(x)dx}-q_{m}^{S*}+q_{m,t}^{S*}) \right] /(\alpha -1)$.

Proof of Corollary 6

For the B-CS scenario, we obtain $\frac{\partial g_{m}^{B-CS*}}{\partial \theta }=\frac{\phi (w+{{r}_{b}}w-p)}{(1+{{r}_{b}}){{\theta }^{2}}v}<0$. Using the Implicit Function Derivation Rule to find the partial derivative with respect to $\theta$ on both sides of $p\left[ 1-F\left[ {{q}_{m}}-({{g}_{s}}+{{g}_{m}})\phi \right] \right] \text {=}w(1+{{r}_{b}})\left[ 1-F\left[ {{q}_{m,t}}-({{g}_{s}}+{{g}_{m}})\phi \right] \right]$, we have:

$$\begin{aligned} \begin{aligned}&f(q_{m}^{B-CS*},g_{m}^{B-CS*})(\frac{\partial q_{m}^{B-CS*}}{\partial \theta }-\phi \frac{\partial g_{m}^{B-CS*}}{\partial \theta }) \\&=\frac{A}{w}f(q_{m,t}^{B-CS*},g_{m}^{B-CS*})\left[ A\frac{\partial q_{m}^{B-CS*}}{\partial \theta }+\frac{v{{(g_{m}^{B-CS*})}^{2}}}{2}\frac{A}{w}+(g_{m}^{B-CS*}\theta v-\phi )\frac{\partial g_{m}^{B-CS*}}{\partial \theta } \right] \\ \end{aligned} \end{aligned}$$

(A.17)

Therefore, $\frac{\partial q_{m}^{B-CS*}}{\partial \theta }\text {=}\frac{{{\phi }^{2}}(-p+w+{{r}_{b}}w)\left[ -2{{p}^{2}}f(q_{m}^{B-CS*},g_{m}^{B-CS*})+f(q_{m,t}^{B-CS*},g_{m}^{B-CS*})w(p+w+{{r}_{b}}w) \right] }{2(1+{{r}_{b}}){{\theta }^{2}}v\left[ -{{p}^{2}}f(q_{m}^{B-CS*},g_{m}^{B-CS*})+f(q_{m,t}^{B-CS*},g_{m}^{B-CS*}){{w}^{2}}{{(1+{{r}_{b}})}^{2}} \right] }<0$ and $\frac{\partial q_{m,t}^{B-CS*}}{\partial \theta }=\frac{p{{\phi }^{2}}f(q_{m}^{B-CS*},g_{m}^{B-CS*}){{\left[ p-(1+{{r}_{b}})w \right] }^{2}}}{(1+{{r}_{b}}){{\theta }^{3}}v\left[ -{{p}^{2}}f(q_{m}^{B-CS*},g_{m}^{B-CS*})+f(q_{m,t}^{B-CS*},g_{m}^{B-CS*}){{w}^{2}}{{(1+{{r}_{b}})}^{2}} \right] }<0$. Therefore, we obtain $\frac{\partial g_{m}^{B-CS*}}{\partial (1-\theta )}>0$, $\frac{\partial q_{m}^{B-CS*}}{\partial (1-\theta )}>0$, and $\frac{\partial q_{m,t}^{B-CS*}}{\partial (1-\theta )}>0$.

For the S-CS scenario, we can also obtain $\frac{\partial g_{m}^{S-CS*}}{\partial (1-\theta )}>0$, $\frac{\partial q_{m}^{S-CS*}}{\partial (1-\theta )}>0$, and $\frac{\partial q_{m,t}^{S-CS*}}{\partial (1-\theta )}>0$. $\square$

Proof of Corollary 7

For the B-QD scenario, we have $\frac{\partial g_{m}^{B-QD*}}{\partial b}=\frac{2\phi ({{q}_{m}}+b\partial {{q}_{m}}/\partial b)}{v}$. Using the Implicit Function Derivation Rule, we find the partial derivative with respect to b on both sides of $p\left[ 1-F({{q}_{m}},{{g}_{m}}) \right] \text {=(}w-2{{q}_{m}}b)(1+{{r}_{b}})\left[ 1-F({{q}_{m,t}},{{g}_{m}}) \right]$. Therefore, we obtain

$$\begin{aligned} \begin{aligned}&pf(q_{m}^{\text {*}},g_{m}^{\text {*}})\left( \frac{\partial q_{m}^{*}}{\partial b}-\phi \frac{\partial g_{m}^{*}}{\partial b}\right) \text {=}2\left( q_{m}^{*}+b\frac{\partial q_{m}^{*}}{\partial b}\right) (1+{{r}_{b}}){\overline{F}}(q_{m,t}^{*},g_{m}^{*})\text {+} \\&\text {(}w-2bq_{m}^{*})(1+{{r}_{b}})f(q_{m,t}^{*},g_{m}^{*})\left[ \left[ (w-2bq_{m}^{*})\frac{\partial q_{m}^{*}}{\partial b}-{{(q_{m}^{*})}^{2}} \right] \frac{A}{w}\text {+}g_{m}^{*}v\frac{\partial g_{m}^{*}}{\partial b}/p-\phi \frac{\partial g_{m}^{*}}{\partial b} \right] \\ \end{aligned} \end{aligned}$$

(A.18)

From Eq. (A.18), we obtain $\frac{\partial q_{m}^{B-QD*}}{\partial b}>0$, and then $\frac{\partial g_{m}^{B-QD*}}{\partial b}=2\phi ({{q}_{m}}+b\frac{\partial {{q}_{m}}}{\partial b})/v>0$. From Eq. (20), we obtain $\frac{\partial q_{m}^{B-QD*}}{{{q}_{m}}}=\frac{(w-2q_{m}^{B-QD*})(1+{{r}_{b}})}{p}$. For the S-QD scenario, we also have $\frac{\partial q_{m}^{S-QD*}}{\partial b}>0$, $\frac{\partial g_{m}^{S-QD*}}{\partial b}>0$ and $\frac{\partial q_{m}^{S-QD*}}{{{q}_{m}}}=\frac{(w-2q_{m}^{S-QD*})}{\alpha p}$. $\square$

Proof of Table 3

From Eq. (13), we obtain the Hessian matrix:

$H=\left[ \begin{array}{ll} \frac{{{\partial }^{2}}\pi _{sc}^{{}}}{\partial q_{m}^{2}} &{} \frac{{{\partial }^{2}}\pi _{sc}^{{}}}{\partial {{q}_{m}}\partial {{g}_{m}}} \\ \frac{{{\partial }^{2}}\pi _{sc}^{{}}}{\partial {{g}_{m}}\partial {{q}_{m}}} &{} \frac{{{\partial }^{2}}\pi _{sc}^{{}}}{\partial g_{m}^{2}} \\ \end{array} \right] \text {=}\left[ \begin{array}{ll} -pf(q_{m}^{C},g_{m}^{C}) &{} p\phi f(q_{m}^{C},g_{m}^{C}) \\ p\phi f(q_{m}^{C},g_{m}^{C}) &{} -p{{\phi }^{2}}f(q_{m}^{C},g_{m}^{C})-v \\ \end{array} \right] =vpf(q_{m}^{C},g_{m}^{C})>0$. Therefore, H is negative definite. From $\frac{\partial \pi _{sc}^{C}}{\partial {{q}_{m}}}=0$ and $\frac{\partial \pi _{sc}^{C}}{\partial {{q}_{m}}}=0$, we obtained optimal greenness and order quantity in the centralized scenario. The rest of the proof is similar to Proposition 1 and Proposition 2. The wholesale prices in different scenarios are as follows:

${{w}^{B-CS*}}={{{\widehat{c}}}^{B-CS}}+\frac{q_{m}^{*}\theta v\left[ f(q_{m}^{*},g_{m}^{*}){{p}^{2}}-f(q_{m,t}^{*},g_{m}^{*}){{w}^{2}}{{(1+{{r}_{b}})}^{2}} \right] }{(1+{{r}_{b}})pv\theta {\overline{F}}(q_{m,t}^{*},g_{m}^{*})+f(q_{m}^{*},g_{m}^{*}){{p}^{2}}{{\phi }^{2}}-f(q_{m,t}^{*},g_{m}^{*})w{{(1+{{r}_{b}})}^{2}}(q_{m}^{*}v\theta +{{\phi }^{2}}w)}$, ${{w}^{B-QD*}}={{{\widehat{c}}}^{B-QD}}+\frac{q_{m}^{*}\left[ (v-2b{{\phi }^{2}})\left[ f(q_{m}^{*},g_{m}^{*}){{p}^{2}}-f(q_{m,t}^{*},g_{m}^{*}){{(w-2bq_{m}^{*})}^{2}}{{(1+{{r}_{b}})}^{2}} \right] -2bp(1+{{r}_{b}})v{\overline{F}}(q_{m,t}^{*},g_{m}^{*}) \right] }{(1+{{r}_{b}})pv{\overline{F}}(q_{m,t}^{*},g_{m}^{*})+f(q_{m}^{*},g_{m}^{*}){{p}^{2}}{{\phi }^{2}}-f(q_{m,t}^{*},g_{m}^{*})(w-2bq_{m}^{*}){{(1+{{r}_{b}})}^{2}}(q_{m}^{*}v+{{\phi }^{2}}w-2b{{\phi }^{2}}q_{m}^{*})}$, ${{w}^{S-CS*}}={{{\widehat{c}}}^{S-CS}}+\frac{q_{m}^{*}\theta v\left[ f(q_{m}^{*},g_{m}^{*}){{\alpha }^{2}}{{p}^{2}}-f(q_{m,t}^{*},g_{m}^{*}){{w}^{2}} \right] }{\alpha pv\theta {\overline{F}}(q_{m,t}^{*},g_{m}^{*})+f(q_{m}^{*},g_{m}^{*}){{\alpha }^{2}}{{p}^{2}}{{\phi }^{2}}-f(q_{m,t}^{*},g_{m}^{*})w(q_{m}^{*}\theta v+{{\phi }^{2}}w)}$ and ${{w}^{S-QD*}}={{{\widehat{c}}}^{S-QD}}+\frac{q_{m}^{*}\left[ (v-2b{{\phi }^{2}})\left[ f(q_{m}^{*},g_{m}^{*}){{\alpha }^{2}}{{p}^{2}}-f(q_{m,t}^{*},g_{m}^{*}){{(w-2bq_{m}^{*})}^{2}} \right] -2bp\alpha v{\overline{F}}(q_{m,t}^{*},g_{m}^{*}) \right] }{\alpha pv{\overline{F}}(q_{m,t}^{*},g_{m}^{*})+f(q_{m}^{*},g_{m}^{*}){{\alpha }^{2}}{{p}^{2}}{{\phi }^{2}}-f(q_{m,t}^{*},g_{m}^{*})(w-2bq_{m}^{*})(q_{m}^{*}v+{{\phi }^{2}}w-2b{{\phi }^{2}}q_{m}^{*})}$; where ${{{\widehat{c}}}^{B-CS}}\text {=}{\widetilde{c}}-\frac{{{\phi }^{2}}(1-\theta )\left[ p-w(1+{{r}_{b}}) \right] }{(1+{{r}_{b}}){{\theta }^{2}}v}/\frac{\partial q_{m}^{*}}{\partial w}$, ${{{\widehat{c}}}^{B-QD}}\text {=}{\widetilde{c}}+2b{{q}_{m}}$, ${{{\widehat{c}}}^{S-CS}}=\frac{{\widetilde{c}}}{1-\frac{F(q_{m,t}^{*},g_{m}^{*})}{\alpha }}\text {+}\frac{F(q_{m,t}^{*},g_{m}^{*})\frac{w{{\phi }^{2}}}{\alpha \theta v}-\frac{{{\phi }^{2}}\left( 1-\theta \right) \left[ \alpha p-w \right] }{{{\theta }^{2}}v}}{1-\frac{F(q_{m,t}^{*},g_{m}^{*})}{\alpha }}/\frac{\partial q_{m}^{*}}{\partial w}-\frac{\frac{\text {(}1-\alpha )}{\alpha }\frac{\partial \pi _{m}^{{}}}{\partial {{q}_{m}}}}{1-\frac{F(q_{m,t}^{*},g_{m}^{*})}{\alpha }}$ and ${{{\widehat{c}}}^{S-QD}}=\frac{{\widetilde{c}}+2bq_{m}^{*}-2bq_{m}^{*}F(q_{m,t}^{*},g_{m}^{*})/a}{1-\frac{F(q_{m,t}^{*},g_{m}^{*})}{\alpha }}\text {+}\frac{F(q_{m,t}^{*},g_{m}^{*})\left[ \frac{vg_{m}^{*}}{\alpha }-p\phi \right] \frac{\partial g_{m}^{*}}{\partial w}}{1-\frac{F(q_{m,t}^{*},g_{m}^{*})}{\alpha }}/\frac{\partial q_{m}^{*}}{\partial w}-\frac{\frac{\text {(}1-\alpha )}{\alpha }\frac{\partial \pi _{m}^{{}}}{\partial {{q}_{m}}}}{1-\frac{F(q_{m,t}^{*},g_{m}^{*})}{\alpha }}$. $\square$

Proof of Corollary 8 and Corollary 9

By comparing the profit of supplier in B and B-CS scenarios, we obtain

$$\begin{aligned} \pi _{s}^{B}-\pi _{s}^{B-CS}=(w-{\widetilde{c}})(q_{m}^{B*}-q_{m}^{B-CS*})+{{(g_{m}^{B-CS*})}^{2}}(1-\theta )v/2 \end{aligned}$$

(A.19)

We can check that the RHS is increasing with ${\widetilde{c}}$ i.e., $\frac{\partial (\pi _{s}^{B}-\pi _{s}^{B-CS})}{\partial {\widetilde{c}}}\text {=}q_{m}^{B-CS*}-q_{m}^{B*}>0$ since $\frac{\partial q_{m}^{B-CS*}}{\partial (1-\theta )}>0$. Furthermore, $\pi _{s}^{B}-\pi _{s}^{B-CS}$ equals to zero when ${{{\overline{c}}}^{B-CS}}={\frac{{{(g_{m}^{B-CS*})}^{2}}(1-\theta )v+2(q_{m}^{B*}-q_{m}^{B-CS*})w}{2(q_{m}^{B*}-q_{m}^{B-CS*})w}}$, where ${{{\overline{c}}}^{B-CS}}>\frac{kg_{s}^{2}}{2}$. Hence, when ${\widetilde{c}}>{{{\overline{c}}}^{B-CS}}$, $\pi _{s}^{B-CS}<\pi _{s}^{B}$ and when ${\widetilde{c}}<{{{\overline{c}}}^{B-CS}}$, $\pi _{s}^{B-CS}>\pi _{s}^{B}$.

By comparing the profit of supplier in S and S-CS scenarios, we obtain

$$\begin{aligned} \begin{aligned}&\pi _{s}^{S}-\pi _{s}^{S-CS}=(w-{\widetilde{c}})(q_{m}^{S*}-q_{m}^{S-CS*})+(1-\alpha )p(q_{m}^{S*}-q_{m,t}^{S*}-q_{m}^{S-CS*}+q_{m,t}^{S-CS*}) \\&-(1-\alpha )p\int _{q_{m,t}^{S*}-({{g}_{s}}+g_{m}^{S*})\phi }^{q_{m}^{S*}-({{g}_{s}}+g_{m}^{S*})\phi }{F(x)dx}-p\int _{0}^{q_{m,t}^{S*}-({{g}_{s}}+g_{m}^{S*})\phi }{F(x)dx} \\&+(1-\alpha )p\int _{q_{m,t}^{S-CS*}-({{g}_{s}}+g_{m}^{S-CS*})\phi }^{q_{m}^{S-CS*}-({{g}_{s}}+g_{m}^{S-CS*})\phi }{F(x)dx}\\&\quad +p\int _{0}^{q_{m,t}^{S-CS*}-({{g}_{s}}+g_{m}^{S-CS*})\phi }{F(x)dx}+{{(g_{m}^{S-CS*})}^{2}}(1-\theta )v/2 \\ \end{aligned} \end{aligned}$$

(A.20)

We can check that the RHS is increasing with ${\widetilde{c}}$ i.e., $\frac{\partial (\pi _{s}^{S}-\pi _{s}^{S-CS})}{\partial {\widetilde{c}}}\text {=}q_{m}^{S-CS*}-q_{m}^{S*}>0$ since $\frac{\partial q_{m}^{S-CS*}}{\partial (1-\theta )}>0$. Furthermore, $\pi _{s}^{S}-\pi _{s}^{S-CS}$ equals to zero when , where ${{{\overline{c}}}^{S-CS}}>\frac{kg_{s}^{2}}{2}$. Hence, when ${\widetilde{c}}>{{{\overline{c}}}^{S-CS}}$, $\pi _{s}^{S-CS}<\pi _{s}^{S}$ and when ${\widetilde{c}}<{{{\overline{c}}}^{S-CS}}$, $\pi _{s}^{S-CS}>\pi _{s}^{S}$.

By comparing the profit of supplier in B and B-QD scenarios, we obtain

$$\begin{aligned} \pi _{s}^{B}-\pi _{s}^{B-QD}=(w-{\widetilde{c}})q_{m}^{B*}-(w-bq_{m}^{B-QD*}-{\widetilde{c}})q_{m}^{B-QD*} \end{aligned}$$

(A.21)

We can check that the RHS is increasing with ${\widetilde{c}}$ i.e., $\frac{\partial (\pi _{s}^{B}-\pi _{s}^{B-QD})}{\partial {\widetilde{c}}}\text {=}q_{m}^{B-QD*}-q_{m}^{B*}>0$ since $\frac{\partial q_{m}^{B-QD*}}{\partial b}>0$. Furthermore, $\pi _{s}^{B}-\pi _{s}^{B-QD}$ equals to zero when ${{{\overline{c}}}^{B-QD}}=\frac{b{{(q_{m}^{B-QD*})}^{2}}+(q_{m}^{B*}-q_{m}^{B-QD*})w}{(q_{m}^{B*}-q_{m}^{B-QD*})}$, where ${{{\overline{c}}}^{B-QD}}>\frac{kg_{s}^{2}}{2}$. Hence, when ${\widetilde{c}}>{{{\overline{c}}}^{B-QD}}$, $\pi _{s}^{B-CS}<\pi _{s}^{B}$ and when ${\widetilde{c}}<{{{\overline{c}}}^{B-QD}}$, $\pi _{s}^{B-QD}>\pi _{s}^{B}$.

By comparing the profit of supplier in S and S-QD scenarios, we obtain

$$\begin{aligned} \begin{aligned}&\pi _{s}^{S}-\pi _{s}^{S-QD}=(w-{\widetilde{c}})q_{m}^{S*}-(w-{\widetilde{c}}-bq_{m}^{S-QD*})q_{m}^{S-QD*}\\&\quad +(1-\alpha )p(q_{m}^{S*}-q_{m,t}^{S*}-q_{m}^{S-QD*}+q_{m,t}^{S-QD*}) \\&\quad -(1-\alpha )p\int _{q_{m,t}^{S*}-({{g}_{s}}+g_{m}^{S*})\phi }^{q_{m}^{S*}-({{g}_{s}}+g_{m}^{S*})\phi }{F(x)dx}-p\int _{0}^{q_{m,t}^{S*}-({{g}_{s}}+g_{m}^{S*})\phi }{F(x)dx} \\&\quad +(1-\alpha )p\int _{q_{m,t}^{S-QD*}-({{g}_{s}}+g_{m}^{S-QD*})\phi }^{q_{m}^{S-QD*}-({{g}_{s}}+g_{m}^{S-QD*})\phi }{F(x)dx}+p\int _{0}^{q_{m,t}^{S-QD*}-({{g}_{s}}+g_{m}^{S-QD*})\phi }{F(x)dx} \\ \end{aligned} \end{aligned}$$

(A.22)

We can check that the RHS is increasing with ${\widetilde{c}}$ i.e., $\frac{\partial (\pi _{s}^{S}-\pi _{s}^{S-QD})}{\partial {\widetilde{c}}}\text {=}q_{m}^{S-QD*}-q_{m}^{S*}>0$ since $\frac{\partial q_{m}^{S-QD*}}{\partial b}>0$. Furthermore, $\pi _{s}^{S}-\pi _{s}^{S-QD}$ equals to zero when

$$\begin{aligned}{{{\overline{c}}}^{S-QD}}=\frac{p\left[ \begin{aligned}&(\alpha -1)\int _{q_{m,t}^{S*}-g_{m}^{S*}\phi -q_{m,t}^{S-QD*}+g_{m}^{S-QD*}\phi }^{q_{m}^{S*}-g_{m}^{S*}\phi -q_{m}^{S-QD*}+g_{m}^{S-QD*}\phi }{F(x)dx} \\&+\int _{0}^{q_{m,t}^{S-QD*}-g_{m}^{S-QD*}\phi -q_{m,t}^{S*}+g_{m}^{S*}\phi }{F(x)dx} \\ \end{aligned} \right] +\left[ \begin{aligned}&b{{(q_{m}^{S-QD*})}^{2}}+(q_{m}^{S*}-q_{m}^{S-QD*})w \\&+p(1-\alpha )(q_{m}^{S*}-q_{m}^{S-QD*}-q_{m,t}^{S*}+q_{m,t}^{S-QD*}) \\ \end{aligned} \right] }{(q_{m}^{S*}-q_{m}^{S-QD*})}, \end{aligned}$$

where ${{{\overline{c}}}^{S-QD}}>\frac{kg_{s}^{2}}{2}$. Hence, when ${\widetilde{c}}>{{{\overline{c}}}^{S-QD}}$, $\pi _{s}^{S-QD}<\pi _{s}^{S}$ and when ${\widetilde{c}}<{{{\overline{c}}}^{S-QD}}$, $\pi _{s}^{S-QD}>\pi _{s}^{S}$. $\square$

Proof of Corollary 10

From Eq. (A.19), we obtain $\frac{\partial (\pi _{s}^{B}-\pi _{s}^{B-CS})}{\partial (1-\theta )}\text {=}-(w-{\widetilde{c}})\frac{\partial q_{m}^{B-CS*}}{\partial (1-\theta )}\text {+}\frac{v{{(g_{m}^{B-CS*})}^{2}}}{2}+vg_{m}^{B-CS*}(1-\theta )\frac{\partial g_{m}^{B-CS*}}{\partial (1-\theta )}$. Since $\frac{\partial q_{m}^{B-CS*}}{\partial (1-\theta )}>0$ and $\frac{\partial g_{m}^{B-CS*}}{\partial (1-\theta )}>0$, we obtain that when $0<(1-\theta )<1$, $\frac{\partial (\pi _{s}^{B}-\pi _{s}^{B-CS})}{\partial (1-\theta )}\text {=}0$ has at most one solution. From ${{{\overline{c}}}^{B-CS}}$, we obtain that for a given ${\widetilde{c}}$ and ${\widetilde{c}}>\frac{kg_{s}^{2}}{2}$, GM cost proportion borne by the supplier that makes the B-CS coordinated contract establishment should satisfy $0<1-\theta <Min[{{\overline{1-\theta }}^{B-CS}},1]$, where ${{\overline{1-\theta }}^{B-CS}}\text {=}\frac{2(w-{\widetilde{c}})(q_{m}^{B-CS*}-q_{m}^{B*})}{{{(g_{m}^{B-CS*})}^{2}}v}$.

Smiliar to the above proof process, we also obtain GM cost proportion borne by the supplier that makes the S-CS coordinated contract establishment should satisfy $0<1-\theta <Min[{{\overline{1-\theta }}^{S-CS}},1]$, where

$$\begin{aligned} {{\overline{1-\theta }}^{S-CS}}\text {=}\frac{2\left[ \begin{aligned}&(w-{\widetilde{c}})(q_{m}^{S-CS*}-q_{m}^{S*}) \\&-p(1-\alpha )(q_{m}^{S*}-q_{m}^{S-CS*}-q_{m,t}^{S*}+q_{m,t}^{S-CS*}) \\ \end{aligned} \right] +2p\left[ \begin{aligned}&(1-\alpha )\int _{q_{m,t}^{S*}-g_{m}^{S*}\phi -q_{m,t}^{S-CS*}+g_{m}^{S-CS*}\phi }^{q_{m}^{S*}-g_{m}^{S*}\phi -q_{m}^{S-CS*}+g_{m}^{S-CS*}\phi }{F(x)dx} \\&+\int _{0}^{q_{m,t}^{S*}-g_{m}^{S*}\phi -q_{m,t}^{S-CS*}+g_{m}^{S-CS*}\phi }{F(x)dx} \\ \end{aligned} \right] }{{{(g_{m}^{S-CS*})}^{2}}v}. \end{aligned}$$

From Eq. (A.21), we obtain $\frac{\partial (\pi _{s}^{B}-\pi _{s}^{B-QD})}{\partial b}\text {=}(w-bq_{m}^{B-QD*}-{\widetilde{c}})\frac{\partial q_{m}^{B-QD*}}{\partial b}-{{(q_{m}^{B-QD*})}^{2}}-bq_{m}^{B-QD*}\frac{\partial q_{m}^{B-QD*}}{\partial b}$. Since $\frac{\partial q_{m}^{B-QD*}}{\partial b}>0$, we obtain that when $0<b<\frac{w-{\widetilde{c}}}{q_{m}^{B-QD*}}$, $\frac{\partial (\pi _{s}^{B}-\pi _{s}^{B-QD})}{\partial b}\text {=}0$ has at most one solution. From ${{{\overline{c}}}^{B-QD}}$, we obtain that for a given ${\widetilde{c}}$ and ${\widetilde{c}}>\frac{kg_{s}^{2}}{2}$, the quantity discount rate that makes the B-QD coordinated contract establishment should satisfy $0<b<Min[{{{\overline{b}}}^{B-QD}},\frac{w-{\widetilde{c}}}{q_{m}^{B-QD*}}]$, where ${{{\overline{b}}}^{B-QD}}=\frac{(w-{\widetilde{c}})(q_{m}^{B-QD*}-q_{m}^{B*})}{{{(q_{m}^{B-QD*})}^{2}}}$.

Smiliar to the above proof process, we also obtain the quantity discount rate that makes the S-QD coordinated contract establishment should satisfy $0<b<Min[{{{\overline{b}}}^{S-QD}},\frac{w-{\widetilde{c}}}{q_{m}^{B-QD*}}]$, where

$$\begin{aligned} {{{\overline{b}}}^{S-QD}}=\frac{\left[ \begin{aligned}&(w-{\widetilde{c}})(q_{m}^{S-QD*}-q_{m}^{S*}) \&p(1-\alpha )(q_{m}^{S*}-q_{m}^{S-QD*}-q_{m,t}^{S*}+q_{m,t}^{S-QD*}) \\ \end{aligned} \right] +p\left[ \begin{aligned}&(1-\alpha )\int _{q_{m,t}^{S*}-g_{m}^{S*}\phi -q_{m,t}^{S-QD*}+g_{m}^{S-QD*}\phi }^{q_{m}^{S*}-g_{m}^{S*}\phi -q_{m}^{S-QD*}+g_{m}^{S-QD*}\phi }{F(x)dx} \\&+\int _{0}^{q_{m,t}^{S*}-g_{m}^{S*}\phi -q_{m,t}^{S-QD*}+g_{m}^{S-QD*}\phi }{F(x)dx} \\ \end{aligned} \right] }{{{(q_{m}^{S-QD*})}^{2}}}. \end{aligned}$$

By comparing the profit of supplier in B-CS and B-QD scenarios, we obtain:

$$\begin{aligned} \pi _{s}^{B-CS}-\pi _{s}^{B-QD}=(w-{\widetilde{c}})(q_{m}^{B-CS*})-{{(g_{m}^{B-CS*})}^{2}}(1-\theta )v/2-(w-bq_{m}^{B-QD*}-{\widetilde{c}})q_{m}^{B-QD*} \end{aligned}$$

(A.23)

From Eq. (A.23), we obtain $\frac{\partial (\pi _{s}^{B-CS}-\pi _{s}^{B-QD})}{\partial (1-\theta )}\text {=}(w-{\widetilde{c}})\frac{\partial q_{m}^{B-CS*}}{\partial (1-\theta )}-\frac{v{{(g_{m}^{B-CS*})}^{2}}}{2}-vg_{m}^{B-CS*}(1-\theta )\frac{\partial g_{m}^{B-CS*}}{\partial (1-\theta )}$. Since $\frac{\partial q_{m}^{B-CS*}}{\partial (1-\theta )}$ and $\frac{\partial g_{m}^{B-CS*}}{\partial (1-\theta )}>0$, we obtain that $\frac{\partial (\pi _{s}^{B-CS}-\pi _{s}^{B-QD})}{\partial (1-\theta )}\text {=}0$ has at most one solution in the domain. Therefore, $\pi _{s}^{B-CS}-\pi _{s}^{B-QD}$ has at most two solution in the domain of $(1-\theta )$. Furthermore, $\pi _{s}^{B-CS}-\pi _{s}^{B-QD}$ equals to zero when ${{\widetilde{1-\theta }}^{B}}=\frac{2\left[ b{{(q_{m}^{B-QD*})}^{2}}+(w-{\widetilde{c}})(q_{m}^{B-CS*}-q_{m}^{B-QD*}) \right] }{{{(g_{m}^{B-CS*})}^{2}}v}$. Hence, if $1-\theta <\widetilde{1-\theta }{{(1-\theta ,b)}^{B}}$, $\pi _{s}^{B-CS}>\pi _{s}^{B-QD}$ and if $1-\theta >\widetilde{1-\theta }{{(1-\theta ,b)}^{B}}$, $\pi _{s}^{B-CS}<\pi _{s}^{B-QD}$.

By comparing the profit of supplier in S-CS and S-QD scenarios, we obtain:

$$\begin{aligned} \begin{aligned}&\pi _{s}^{S-CS}-\pi _{s}^{S-QD}=(w-{\widetilde{c}})q_{m}^{S-CS*}+(1-\alpha )p(q_{m}^{S-CS*}-q_{m,t}^{S-CS*})-(1-\alpha )p\\&\quad \int _{q_{m,t}^{S-CS*}-({{g}_{s}}+g_{m}^{S-CS*})\phi }^{q_{m}^{S-CS*}-({{g}_{s}}+g_{m}^{S-CS*})\phi }{F(x)dx} -p\int _{0}^{q_{m,t}^{S-CS*}-({{g}_{s}}+g_{m}^{S-CS*})\phi }{F(x)dx}-\frac{{{(g_{m}^{S-CS*})}^{2}}(1-\theta )v}{2}\\&-(w-{\widetilde{c}}-bq_{m}^{S-QD*})q_{m}^{S-QD*} -(1-\alpha )p(q_{m}^{S-QD*}-q_{m,t}^{S-QD*})\\&+(1-\alpha )p\int _{q_{m,t}^{S-QD*}-({{g}_{s}}+g_{m}^{S-QD*})\phi }^{q_{m}^{S-QD*}-({{g}_{s}}+g_{m}^{S-QD*})\phi }{F(x)dx}\quad +p\int _{0}^{q_{m,t}^{S-QD*}-({{g}_{s}}+g_{m}^{S-QD*})\phi }{F(x)dx} \\ \end{aligned} \end{aligned}$$

(A.24)

From Eq. (A.24), we obtain

$$\begin{aligned} \begin{aligned}&\frac{\partial (\pi _{s}^{S-CS}-\pi _{s}^{S-QD})}{\partial (1-\theta )}\text {=}(w-{\widetilde{c}})\frac{\partial q_{m}^{S-CS*}}{\partial (1-\theta )}\text {+(}1-\alpha )p\left[ \frac{\partial q_{m}^{S-CS*}}{\partial (1-\theta )}-\frac{\partial q_{m,t}^{S-CS*}}{\partial (1-\theta )} \right] \\&-\text {(}1-\alpha )p\left[ F(q_{m}^{S-CS*},g_{m}^{S-CS*})-F(q_{m,t}^{S-CS*},g_{m}^{S-CS*}) \right] (\frac{\partial q_{m}^{S-CS*}}{\partial (1-\theta )}-\frac{\partial q_{m,t}^{S-CS*}}{\partial (1-\theta )}) \\&-pF(q_{m,t}^{S-CS*},g_{m}^{S-CS*})(\frac{\partial q_{m}^{S-CS*}}{\partial (1-\theta )}-\frac{\partial g_{m}^{S-CS*}}{\partial (1-\theta )})-\frac{v{{(g_{m}^{S-CS*})}^{2}}}{2}-vg_{m}^{S-CS*}(1-\theta )\frac{\partial g_{m}^{S-CS*}}{\partial (1-\theta )} \\ \end{aligned} \end{aligned}$$

(A.25)

Since $\frac{\partial q_{m}^{S-CS*}}{\partial (1-\theta )}>0$, $\frac{\partial g_{m}^{S-CS*}}{\partial (1-\theta )}>0$, $\frac{\partial q_{m}^{S-CS*}}{\partial (1-\theta )}>\frac{\partial g_{m}^{S-CS*}}{\partial (1-\theta )}$ and $0<F(q_{m}^{S-CS*},g_{m}^{S-CS*})-F(q_{m,t}^{S-CS*},g_{m}^{S-CS*})<1$, we obtain $\frac{\partial (\pi _{s}^{S-CS}-\pi _{s}^{S-QD})}{\partial (1-\theta )}\text {=}0$ has at most one solution in the domain. Therefore, $\pi _{s}^{S-CS}-\pi _{s}^{S-QD}$ has at most two solution in the domain of $(1-\theta )$. Furthermore, $\pi _{s}^{S-CS}-\pi _{s}^{S-QD}$ equals to zero when

$$\begin{aligned} {{\widetilde{1-\theta }}^{S}}=\frac{\left[ \begin{aligned}&b{{(q_{m}^{S-QD*})}^{2}}+(w-{\widetilde{c}})(q_{m}^{S-CS*}-q_{m}^{S-QD*}) \\&+p\int _{0}^{q_{m,t}^{S-QD*}-g_{m}^{S-QD*}\phi -q_{m,t}^{S-CS*}+g_{m}^{S-CS*}\phi }{F(x)dx} \\ \end{aligned} \right] +p(\alpha -1)\left[ \begin{aligned}&\int _{q_{m,t}^{S-CS*}-g_{m}^{S-CS*}\phi -q_{m,t}^{S-QD*}+g_{m}^{S-QD*}\phi }^{q_{m}^{S-CS*}-g_{m}^{S-CS*}\phi -q_{m}^{S-QD*}+g_{m}^{S-QD*}\phi }{F(x)dx} \\&-(q_{m}^{S-CS*}-q_{m}^{S-QD*}-q_{m,t}^{S-CS*}+q_{m,t}^{S-QD*}) \\ \end{aligned} \right] }{{{(g_{m}^{S-CS*})}^{2}}v/2}. \end{aligned}$$

Hence, if $1-\theta <\widetilde{1-\theta }{{(1-\theta ,b)}^{S}}$, $\pi _{s}^{S-CS}>\pi _{s}^{S-QD}$ and if $1-\theta >\widetilde{1-\theta }{{(1-\theta ,b)}^{S}}$, $\pi _{s}^{S-CS}<\pi _{s}^{S-QD}.$ $\square$