Abstract
In this paper, we consider standard as well as instrumental variables regression. Specification problems related to autocorrelation, heteroskedasticity, neglected non-linearity, unsatisfactory out-of-small performance and endogeneity can be addressed in the context of multi-criteria optimization. The new technique performs well, it minimizes all these problems simultaneously, and eliminates them for the most part. Markov Chain Monte Carlo techniques are used to perform the computations. An empirical application to NASDAQ returns is provided.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Multi-objective optimization is an important methodology when we face conflicting objectives (see Das and Dennis 1998; Handi et al. 2007). Portfolio analysis, for example, can be presented in terms of multiobjective programming instead of the classical mean-variance approach. The nature of the problem as multicriteria decision making has been emphasized by many authors (e.g. Mavrotas et al. 2008; Xidonas and Psarras 2009; Xidonas et al. 2009a, b, 2010a, b; Steuer et al. 2005, 2006a, b, 2007a, b; Zopounidis and Doumpos 2002; Zopounidis 1999; Hurson and Zopounidis 1993, 1995, 1997; Spronk and Hallerbach 1997; Zeleny 1977, 1981, 1982; Colson and Zeleny 1979, 1980). For deep reviews of other solution methods, consider the below references: Awasthi and Omrani (2019), Duan et al. (2018), Dubey et al. (2015), Gharaei et al. (2019a, 2019b, 2019c), Giri and Bardhan (2014), Giri and Masanta (2018), Hao et al. (2018), Kazemi et al. (2018), Rabbani et al. (2019, 2020), Sarkar and Giri (2018), Sayyadi and Awasthi (2018a, 2018b), Shah et al. (2020). Shakarabi et al. (2019), Tsao (2015) and Yin et al. (2016).
Narula and Wellington (2007) consider a multi-criteria formulation in regression with a single explanatory variable. Their motivation is different from this paper, as they want to minimize the sum of squared and absolute errors simultaneously, or minimize the sum of absolute errors and the maximum absolute error simultaneously. We are not aware of further applications or extensions of this method. Hwang et al. (2010) propose using regression in a special context (collaborative filtering in engineering) to obtain weights and then use multi-criteria analysis and find that experimental results showed that the proposed approach outperformed the single-criterion collaborative filtering method. Priya and Venkatesh (2012) follow the same approach but first they use regression and principal components to identify important objectives and then use the Analytic Hierarchy Process. For a variation of this technique see Nilashi et al. (2016).
This paper is based on the idea that obtaining parameter estimates in regression is, indeed, a multi-criteria decision making problem, but the objectives should include criteria that can deal with the standard problems of regression, viz. autocorrelation, heteroskedasticity, possible nonlinearities, out-of-sample forecasting, as well as endogeneity (correlation between errors and explanatory variables). It is known that the Ordinary Least Squares (OLS) estimator is consistent even when autocorrelation and heteroskedasticity are present but inconsistent when we have nonlinearities and endogeneity. When autocorrelation, heteroskedasticity and the other problems are absent, the OLS estimator is known to be the best linear unbiased estimator (BLUE), a property that holds for finite samples (whereas consistency is associated with infinitely large data sets). In practice, researchers have used a number of criteria to obtain parameter estimates. The OLS estimator is known as \(L_{2}\) estimator as it minimizes the sum of squared residuals. The \(L_{1}\) estimator minimizes the sum of absolute errors, and it is popular when researchers want to mitigate the problem of outliers. The \(L_{\infty }\) estimator minimizes (with respect to \(\beta \)) the maximum absolute error and depends sensitively on outliers (Stam 1997). In the operations research community, practical problems associated with OLS are, to a large extent, ignored, despite the fact that in small or finite samples, autocorrelation, heteroskedasticity, and the other problems mentioned, can have a significant effect on estimates and thus, in measurement and interpretations.
This becomes even more important, when we realize that even “simple” violations of the assumptions in OLS (like autocorrelation and heteroskedasticity) can be viewed as misspecification errors: When a heteroskedastic or autocorrelated variable is erroneously omitted from the regression model, the OLS estimates of the parameters are biased and inconsistent, but the residuals can be informative for these problems as the omitted variable becomes part of the error term. Of course, both autocorrelation and heteroskedasticity can be present in a missing variable, so a systematic investigation of the residuals is called for. In practically every empirical situation, tests are performed for autocorrelation and heteroskedasticity and, if problems are found, the standard errors of OLS are replaced by Heteroskedastic and Autocorrelation Consistent (HAC) standard errors. HAC retains OLS estimates and corrects only standard errors. This practice, however, ignores the fact that it is the rule, rather than the exception, that autocorrelation and heteroskedasticity may, in fact, be due to omitted variables which happen to be autocorrelated and / or heteroscedastic. In such instances, the OLS estimator is biased and inconsistent, and application of HAC standard errors is misguided. To summarize, autocorrelation and heteroskedasticity may, in fact, detect misspecification problems .
From the empirical viewpoint, this problem is important as in most applications, measurement of effects and interpretation of coefficients may, in fact, be compromised under conditions of misspecification. From another point of view, datasets with outliers pose a serious challenge in regression analysis and many solution techniques have been proposed (e.g. Panagopoulos et al. 2019, and Zioutas et al. 2009). Mielke and Berry (1997) have proposed \(L_{1}\) regression when errors are generated from fat-tailed or outlier-producing distributions, which are common in operations research. Moreover, these authors developed a chance-corrected goodness-of-fit measure between observed and predicted values. Dielman and Rose (1997) proposed \(L_{1}\) regression with autocorrelated errors. Bowlin et al. (1984) compare Data Envelopment Analysis and regression approaches to efficiency measurement, which shows the importance of estimation procedure in efficiency analysis: Without model problems, efficiency estimates will be accurate enough. See also Ouenniche and Carrales (2018). However, under heteroskedasticity and /or autocorrelation, such estimates will not even be consistent. Desai and Bharati (1998) investigated whether the predictive power of economic and financial variables can be enhanced if regression is replaced by feedforward neural networks with back-propagation of error. These authors find that the neural networks forecasts are conditionally efficient with respect to the linear regression forecasts. In fact, this finding may be due to misspecification of functional form or other diagnostic failures in regressions and reinforces our arguments. More recent approaches (Wang and Zhu 2018) employ support vector regression for financial time series forecasting. The authors applied their technique to forecast the S&P500 and the NASDAQ market indices with promising results.
Stam (1997) correctly argued that: “there is a need to forge a link between researchers active in statistical discriminant analysis and researchers in the area of \(L_{p}\)-norm classification. Such a link would be beneficial for both groups. Particularly, \(L_{p}\)-norm classification may well be of considerable interest to researchers in areas where nonparametric classification analysis is traditionally used successfully, such as discrete variable classification, mixed variable classification, and in application areas which are often susceptible to data analytical problems, such as medical diagnosis, psychology, marketing, financial analysis, engineering and pattern recognition. Without reaching out, the \(L_{p}\)-norm classification field will remain limited to a small group of researchers with interesting new methodologies that are hardly used where they may be most needed” (pp. 28–29). This statement illustrates the importance of alternative criteria, other than OLS, in the context of linear (or nonlinear) models with an emphasis on potential applications in the fields mentioned by Stam (1997). This paper contributes to this general research agenda by focusing not only on \(L_{p}\)-norm regression but also in the area of providing estimators that are robust to potential problems such as autocorrelation, heteroskedasticity, endogeneity, nonlinearity, etc.
2 The model
In this paper, we consider regression models of the form:
where \(x_{t}\in {\mathbb {R}}^{k}\) is a vector of explanatory variables, \(\beta \in {\mathbb {R}}^{k}\) is a vector of coefficients (parameters) and \(u_{t}\) is an error term whose properties are not specified for the moment except that \(E(u_{t}|x_{t})=0\). Let \(y=[y_{1},\ldots ,y_{T}]'\) and \(X=[x'_{t},t=1,\ldots ,T]\). Common regression problems include (i) heteroskedasticity, (ii) autocorrelation, (iii) misspecified functional form, (iv) outliers, and (v) relatively unacceptable out-of-sample forecasting performance. The modern econometric approach in heteroskedasticity and autocorrelation, is to retain the same Ordinary Least Squares (OLS) coefficients but provide so-called robust standard errors derived from Heteroskedasticity and Autocorrelation Consistent (HAC) covariance matrices. This practice is justified when the model is correctly specified, that is there are no important omitted variables, the functional form is correctly specified, etc. In such cases, under heteroskedasticity and / or autocorrelation, the OLS estimator remains consistent so OLS estimates are reliable but OLS standard errors are biased. More often than not, researchers are not comfortable with the assumption of correct specification in terms of variables included and the linearity assumption as in (1). In such cases, residuals are informative about misspecification problems. For example, if the omitted variables are heteroskedastic and / or autocorrelated, standard diagnostic tests will revel the existence of heteroskedasticity and / or autocorrelation. This, in fact, shows that heteroskedasticity and /or autocorrelation are not merely “nuisances” that can be dealt away using robust-HAC standard errors. The diagnostic tests, actually, provide guidance as to the problems of model specification itself. In this paper, we propose a multi-criteria decision-making approach to regression by developing an estimator which minimizes, simultaneously, the sum of least-squares errors and \(L_{p}\)-objective (as measures of fit, for some \(p>0\)), as well as the extent of heteroskedasticity, autocorrelation, nonlinearity in the functional form, outliers, and out-of-sample forecast errors.
In practical applications we face several econometric problems which can be summarized as follows:
Autocorrelation: This happens when:
where, typically, \(\varepsilon _{t}\sim iid(0,\sigma ^{2})\), and L is the number of lags in the autoregressive process.
Heteroskedasticity: This is the case when:
for some function \(f(\cdot )\) and parameters \(\delta \in {\mathbb {R}}^{K}\).
Nonlinearity: When nonlinear functions of the explanatory variables have been omitted from (1).
Endogeneity: When the assumption \(E(u_{t}|x_{t})=0\) is violated.
Failure in out-of-sample forecasting: When actual and predicted values out-of-sample (or in a hold-out sample) are not “close” enough.
Autocorrelation and heteroskedasticity are not considered as problems, per se, as one can always use “robust”-HAC standard errors. However, this practice of correcting standard errors but not ordinary least squares (OLS) estimates is misguided. Autocorrelation and heteroskedasticity, more often than not, are, in reality, specification problems and, as such, they indicate misspecification in some direction(s). Therefore, they really call for re-examining the specification in (1). Moreover, we often have to deal with the problem of outliers.
In this paper, we want to provide an estimator of parameters that satisfies multiple criteria: Specifically, additionally to minimizing the sum of squared residuals in (1), we also need to minimize simultaneously the presence of autocorrelation, heteroskedasticity, misspecification arising from nonlinearities, endogeneity, and failure in out-of-sample forecasting.
3 The multi-objective nature of regression problems
Suppose the model in (1) has been estimated using a certain technique (not necessarily OLS) and the resulting estimates are \({\hat{\beta }}\). Then, autocorrelation can be tested via the hypothesis \(H_{0}:\gamma _{1}=\cdots =\gamma _{L}=0\) under the specification in (2) where \({\hat{u}}_{t}=y_{t}-x'_{t}{\hat{\beta }}\) is used in place of \(u_{t}\).
Heteroskedasticity is traditionally tested using White’s form:
for some error term \(\xi _{t}\). Moreover, \(\otimes \) is the Kronecker product of two vectors, viz. \(a\otimes b=[a_{i}b,i=1,\ldots ,dim(a)]\), and vech removes all duplicate elements. This is a second order approximation to an arbitrary variance function, and \(h(\hat{u_{t}})={\hat{u}}_{t}^{2}\).
Functional form misspecification is traditionally tested using Ramsey’s Regression Specification Error Test (RESET) . If \({\hat{y}}_{t}=x'_{t}{\hat{\beta }}\), the RESET test uses the regression:
with an error term \(\zeta _{t}\). If \(a_{1}=a_{2}=a_{3}=0\) we conclude there is no neglected nonlinearity.
Endogeneity is trickier and cannot be tested using OLS regressions (notice that all the above tests can be effectively implemented using OLS residuals and fitted values). All we can do, practically, is to find a vector of instruments (say \(z_{t}\in {\mathbb {R}}^{d_{z}}\)) such that \(E(u_{t}|z_{t})=0\) and \(E(z_{t}x_{t}')\ne \mathbf {0}\) to implement the so called Instrumental Variables (IV) estimator or the Generalized Method of Moments (GMM) estimator.
Out-of-sample forecasts, say \(\{{\hat{y}}_{T+h},h=1,\ldots ,H\}\), can be compared to actual values \(y_{T+h}\) to \({\hat{y}}_{T+h}\) using a metric such as root-mean-squared-error (RMSE), mean absolute error (MAE), etc. Finally, outliers can be avoided by adopting a norm other than \(L_{2}\) when minimizing the average deviation of \(u_{t}(\beta )=y_{t}-x'_{t}\beta \), as we explain in the next section.
4 Multi-criteria OLS and IV
In the absence of endogeneity, we propose a new formulation of OLS which takes explicitly into account, autocorrelation, heteroskedasticity, possible nonlinearity, and out-of-sample forecasts as follows:
The first criterion is the usual OLS criterion for fit. The second minimizes the \(L_{p}\)-norm (for example \(p=1\) provides the Least Absolute Deviations (LAD) estimator and \(p\rightarrow \infty \) provides the maximum absolute residual, i.e. the Chebyshev norm). Here \(\delta =[\delta '_{1},\delta _{2}']'\), \(a=[a_{1},a_{2},a_{3}]'\) and \(\gamma \) is defined by (2). Therefore, \(\delta '\delta \) deals with heteroskedasticity, \(\gamma '\gamma \) with autocorrelation, \(a'a\) with problems of neglected nonlinearity, and the last criterion minimizes the average absolute error of out-of- sample forecasting using a hold out sample \(\{y_{T+1},...,y_{T+H}\}\). To avoid heteroskedasticity, autocorrelation, and nonlinearity, ideally, we should have \(\delta '\delta =\gamma '\gamma =a'a=0\).
Moreover, we may have problems with outlying observations which are taken care of by using \(p=1\) or similar. In addition, if a set of linear restrictions must be imposed, the minimization above is subject to:
where R is a \(J\times k\) matrix of coefficients representing the J restrictions, and b is a \(J\times 1\) vector of constants.
If endogeneity is thought to be a problem, and instruments \(z_{t}\in {\mathbb {R}}^{d_{z}}\) are available, the problem in (6) can be reformulated as follows:
where Z is the \(T\times d_{z}\) matrix of instrumental variables, \({\tilde{y}}_{t}=z_{t}y_{t}\), \({\tilde{x}}_{t}=z_{t}x'_{t}\). A more convenient expression results if we express (1) in vector form:
Given the matrix of instruments, we have:
where by definition \(E(Z'u)=\mathbf {0}\). This can be written as
where \(e=Z'u\). The IV estimator is \({\hat{\beta }}_{IV}=(Z'X)^{-1}Z'y\) when \(d_{z}=k\). When \(d_{z}>k\) one can use the OLS estimator:
Since
the Generalized Instrumental Variables Estimator (GIVE) is the Generalized Least Squares (GLS) estimator applied to (10):
Of course, using (8) is more transparent. If we define \({\tilde{u}}_{t}(\beta )={\tilde{y}}_{t}-{\tilde{x}}_{t}\beta \), and \({\tilde{u}}(\beta )=[{\tilde{u}}_{t}(\beta ),t=1,...,T]'\) the GIVE form of (8) is:
possibly subject to (7). To obtain \(\delta ,a,\gamma \) which implicitly depend on the estimator \(\beta \) we perform regressions in (4), (5), and (2). Similarly, for the hold-out-sample we define: \({\hat{y}}_{T+1:T+h}=x_{T+1:T+h}'\beta \).
Additionally, one may wish to avoid OLS altogether in (15) and use Rousseeauw’s (1984) least median of squares (LMS) technique:
This formulation begins directly with LMS and then proceeds with autocorrelation, heteroskedasticity, neglected non-linearity, endogeneity, and out-of sample forecasting. Relative to (15), (16) deals with endogeneity in a somewhat clumsy way as it does not take account of the covariance of errors given by (13). Choosing between (15) and (16) is an empirical issue that we try to resolve on the basis of Monte Carlo simulations.
Suppose now \(\theta =[\delta ',a',\gamma ']'\) denotes the corresponding parameters for heteroskedasticity, neglected nonlinearity and autocorrelation. It may not be enough to make the Euclidean norm \(||\theta ||\) as small as possible as in (6), (15) or (16). What is of interest is to be able to accept the hypothesis: \(H:\theta =\mathbf {0}\). To this purpose, we would like to minimize the maximum coefficient of determination (\(R^{2}\)) in (6), (15), and (16). If the maximum coefficient of determination in regressions (2), (4), and (5) is denoted by \(R_{\theta }^{2}\) then the modified multi-criteria IV problems can be stated as follows:
Additionally, if we target statistical insignificance of \(\delta ,a,\gamma \) we can consider the maximum absolute value of the t-statistics for these coefficients, which we denote by \(t_{\theta }\). Therefore, we can modify (17) and (18) as follows:
Therefore, we have eight objectives in (19) and seven objectives in (20), possibly subject to (7). Additional restrictions that we may want to impose are as follows:
The expression in the last constraint is Mean Absolute Relative Error (MARE). The other two constraints imply that (i) the maximum absolute value of t-statistics in diagnostic regressions, which is denoted by \(t_{\theta }\), is less than the 95% critical value (1.96 which is close to 2), and (ii) the maximum coefficient of determination in diagnostic regressions is less than 10%. The value of the coefficient of determination in diagnostic regressions, shows the explanatory power of such regressions. If large then the presence of autocorrelation. heteroskedasticity and misspecified functional form cannot be excluded. Clearly, in practice, we want to avoid this.
Under these constraints, a solution may not exist so one may want to remove (21) and examine their values at a Pareto optimal solution. We examine the behavior of estimators in both (19) and (20). We use 10,000 simulations. In all cases we have \(T+H\) observations where \(H=20\) is the length of the hold-out sample.
5 Solution technique
Due to the presence of absolute values the multi-criteria problems in (19) and (20) are not differentiable so, finding a Pareto optimal solution is difficult, and, clearly, not available in closed form. For the solution technique, we rely heavily on Tsionas (2017) although we avoid the use of cumbersome Sequential Monte Carlo or Particle Filtering techniques. A significant advantage of the technique proposed here is that it delivers (posterior) standard deviations of parameters of interest and, therefore, confidence bands can be constructed as well. This is in contrast to other multi-objective optimization techniques which, if applied to the present problem, would not deliver measures of statistical uncertainty such as standard errors. Standard errors would have to be computed via sub-sampling or bootstrap methods which would increase the complexity of existing multi-objective methods and, at any rate, they would put them at par with our MCMC technique for Bayesian inference.
Suppose \(F(\beta )=(F_{1}(\beta ),...,F_{n}(\beta ))'\in {\mathbb {R}}^{n}\), \({\underline{F}}=({\underline{F}}_{1},...,{\underline{F}}_{n})'\in {\mathbb {R}}^{n}\). The objective is to solve the problem:
where \(\beta \) incorporates all restriction on \(\beta \). As in Qu et al. (2014) we settle for global Pareto optimality, meaning that \(\beta ^{*}\) is a solution if and only if there does not exist \(\beta \in X\) and \({\hat{\beta }}_{GIVE}=[X'Z(Z'Z)^{-1}Z'X)^{-1}X'Z(Z'Z)^{-1}Z'y.F(\beta )\le F(\beta ^{*})\), \(F(\beta )\ne F(\beta ^{*})\).
In multi-criteria decision making the problem is:
for a certain vector of Pareto weights \(\alpha =(\alpha _{1},...,\alpha _{n})'\) which belong to the unit simplex, \(S=\{\alpha \in {\mathbb {R}}^{n}:\alpha _{i}\ge 0,\;i=1,...,n,\;\sum _{i=1}^{n}\alpha _{i}=1\}\). In this problem, we can get a solution for any given set of \(\alpha \)s. Moreover, if we solve (23) for a range of values of \(\alpha \in S\) we can trace out the Pareto frontier. Therefore, we proceed as follows. Problem (23) is equivalent to finding the mean of the following posterior distributionFootnote 1:
for a given positive constant h and a prior for \(\beta \) , denoted by \(p(\beta )\). For this prior, it is reasonable to assume:
where \({\hat{\beta }}_{OLS}=(X'X)^{-1}X'Y\), \({\hat{u}}=(y-X{\hat{\beta }}_{OLS})'(y-X{\hat{\beta }}_{OLS})\), and \((n-k)s^{2}={\hat{u}}'{\hat{u}}\), and \(\varphi =10\). This prior depends on the data so, strictly speaking, it is not a pure, coherent Bayes prior. Nevertheless, it is reasonable in our context which can, in fact, be given an empirical Bayes interpretation. Here, we re-emphasize that we can condition on the \(\alpha \)s. Then, the posterior mean is:
This result goes back to Pincus (1968) and it is known that h must be “large”. If we consider the non-normalized posterior:
for a certain prior p(h) then h becomes part of the parameter vector. For example, we can use a gamma prior of the form:
where the parameters a and b can be chosen so that the prior mean \(E(h)=\frac{a}{c}\) is small and the prior variance \(Var(h)=\frac{E(h)}{c}\) is also small. For example, we can set \(a=0.01\) and \(c=\frac{a}{100}\). In this way, we do not have to consider different values of h, although it might be useful to perform sensitivity analysis. An alternative is to integrate analytically h out of (27) using (28) to obtain:
Further analytical integration with respect to \(\alpha \) (when unknown and assigned a prior distribution) is not possible. Therefore, the posterior mean has to be computed numerically. Here, we use a standard random-walk Metropolis-algorithm (a well known Markov Chain Monte Carlo [MCMC] technique). This MCMC technique produces a set of draws \(\{\beta ^{(s)},s=1,...,S\}\) that converges (as S increases) to the posterior whose non-normalized density is (29). To construct this sequence suppose we have \(\beta ^{(s)}\) and we generate a candidate, say, \(\beta ^{c}\) as follows:
where \(\tau \) is a certain parameter. Then we accept the candidate, that is \(\beta ^{(s+1)}=\beta ^{c}\) with the Metropolis-Hastings probability:
otherwise we set \(\beta ^{(s+1)}=\beta ^{(s)}\). We select \(\tau \) so that the acceptance ratio is between 20-30% during the “burn in” phase, as the optimal acceptance ratio for a multivariate normal posterior is close to 24%.
On an average personal computer, the algorithm does not take more than about a few minutes of wall clock time to perform full posterior analysis in samples of size 1,000. Convergence is examined using two techniques: i) Geweke’s (1992) t-statistic for convergence of posterior means, and ii) by running separate chains starting from randomly chosen different initial conditions. Ten such chains are used here and computation is implemented in parallel. This parallel implementation does not contribute to increases in computation timing.
Convergence of MCMC algorithms like the ones described here can be tested by starting the algorithm from different sets of initial conditions and testing convergence using Geweke’s (1992) diagnostic which is asymptotically distributed (in the number of MCMC draws) as standard normal. Using the settings reported here and starting from ten randomly selected sets of initial conditions, Geweke’s z-test indicated that our MCMC chains are not incompatible with the hypothesis of convergence.
6 Monte Carlo study
We consider the following model. First, \(k=5\) so that we have five regressors. The specification is \(y_{t}=1+x_{t1}+x_{t2}+x_{t3}+x_{t4}+x_{t3}x_{t4}+u_{t},\,u_{t}\sim iid\mathcal {\,N}(0,0.1^{2}),t=1,\ldots ,T\). The regressors \(x_{t3},x_{t4}\) are omitted and they are generated as follows:
Equation (32) implies that \(x_{t1}\) is autocorrelated. Equation (33) implies that \(x_{t2}\) is heteroskedastic and depends on \(x_{t1}\) in a nonlinear way. In fact, the first term is a sigmoid. Notice that to allow for endogeneity both (32) and (33) depend on \(u_{t}\).
By omitting \(x_{t3},x_{t4},x_{t1}x_{t2}\) all the problems we mentioned are simultaneously present. We construct five instruments as follows:
and \(\beta _{i1},\beta _{i2},\,i=1,\ldots ,5\), are generated from a uniform distribution in \(\left[ -1,1\right] \).Footnote 2 We implement MCMC using 15,000 passes, the first 5000 of which are discarded to mitigate possible start-up effects. The initial conditions are obtained from OLS. We assume that all Pareto weights are equal.
From the results in Table 1, it turns out that OLS always has a bias as expected and the RMSE remains approximately constant for all sample sizes. The multi-criteria OLS does better but still it is biased and inconsistent. In contrast, both multi-criteria IV techniques have much lower bias and RMSE which decrease as the sample size increases, showing that they have great potential in large samples. Autocorrelation is eliminated in, approximately, 75-80% of Monte Carlo samples, while heteroskedasticity is eliminated in over 80% of the samples. The multi-criteria OLS is not equally successful and, of course, this can be attributed to the fact that it does not deal with the endogeneity problem. From Fig. 1, it is evident that multi-criteria IV provides estimators which are much closer to the true values compared to OLS and multi-criteria OLS. It seems that there is no ground to choose between multi-criteria IV as in (19) and (20). However, from Table 1, it is evident that average mean absolute relative error is much lower for the multi-criteria IV estimator in (19).
Sampling distributions of the different estimators are reported in Fig. 1. Notably the sampling distribution of multi-criteria OLS is non-normal even in large samples. Multi-criteria IV has a non-normal sampling distribution only when \(T=100\).
To examine more closely the behavior of the two IV estimators, we present the sampling distributions of \(t_{\theta }\), \(R_{\theta }^{2}\) and MARE in Fig. 2.
For both multi-criteria IV estimators, maximum absolute t-statistics are less than 1.96 for multi-criteria IV-1 but they exceed this critical value for nearly 1% of the samples when we consider multi-criteria IV-2. Values of \(R_{\theta }^{2}\) are less than 0.10 in both cases (although lower for multi-criteria IV-1). Finally, the sampling distribution of MARE is concentrated around 0.70% for multi-criteria IV-1. Although there is some concentration around this value for multi-criteria IV-2, its sampling distribution allows for values as large as over 8%. From this point of view, multi-criteria IV-1 performs better than multi-criteria IV-2.
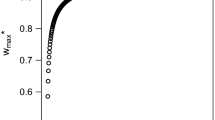
To visualize the Pareto front, we assume a simple model where:
where \(\beta =1\), \(x_{t}\sim iid\mathcal {\,N}(0,1)\), and \(\rho =0.7\). The weight for the OLS criterion is \(\lambda \in (0,1)\) and the weight for autocorrelation is \(1-\lambda \). As \(\lambda \rightarrow 1\) we obtain OLS, and as \(\lambda \rightarrow 0\) we focus exclusively on autocorrelation. As the latter case does not make sense, we restrict \(\lambda \) to [0.20, 1] and we examine 100 points in this interval. We also examine the heteroskedastic case where
In both cases the sample size is \(T=100\). The Pareto front is presented in panel (a) of Fig. 3, where b denotes the estimate of \(\beta \).
As the choice of \(\lambda \) is not obvious from panel (a), in panel (b) we report MARE across different values of \(\lambda \) for the autocorrelation and heteroskedasticity cases. Out-of-sample prediction is implemented using a hold-out sample of size 20. Clearly, MARE attains a minimum value close to 0.55 for autocorrelation, and 0.47 for heteroskedasticity, showing that some balance between in-sample fit and autocorrelation / heteroskedasticity is required. The Pareto weights are not far from 0.5, at least in this example. It is possible that in some cases MARE does not attain a minimum for the chosen values of \(\lambda \). In such cases, one can use leave-one-out cross-validation similarly to bandwidth selection in non-parametric estimation.
7 Empirical application
To illustrate the usefulness of the new techniques, we use the same data-construction methodology as in Wang and Zhu (2010). We use data for 2,014 trading days from 11/June/2011 to 12/June/2019, which covers nearly eight years, for the NASDAQ index. From the daily closing prices of NASDAQ indices, Wang and Zhu (2010) proposed to compute the 5 (weekly), 10 (biweekly), 20 (monthly), and 50-day (quarterly) moving averages, which are widely used technical indicators by traders. Let \(P_{t}\) denote the closing price on day t and \(A_{t,T}\) be the T -day moving average on day t, where \(A_{t,T}\) is computed as follows:
Next, the moving average log-return \(R_{t,T}\) (including the daily log-return) for each day t, is as follows:
In turn, we have five time series: (1) \(R_{t,1}\), (2) \(R_{t,5}\), (3) \(R_{t,10}\), (4) \(R_{t,20}\), and (5) \(R_{t,50}\). The dependent variable is \(y_{t}=R_{t+1,1}\), the next day’s log-return. Then we constructed the input features. For the jth time series, we extract \(p_{j}\) data points to construct the input features. Specifically, let
where \(T_{1}=1\), \(T_{2}=5\), \(T_{3}=10\), \(T_{4}=20\), \(T_{5}=50\). The overall input features for day t are:
As in Wang and Zhu (2010) , \(\mathbf {x}_{t}^{1}\) and \(\mathbf {x}_{t}^{2}\) capture the short-term (daily and weekly) behaviors of the market, while \(\mathbf {x}_{t}^{4}\) and \(\mathbf {x}_{t}^{5}\) capture the long-term (monthly and quarterly) trends. Moreover, “[i]t is not clear a priori which features are important for predicting the next day return, neither how they should be combined to predict (Wang and Zhu 2010, p. 110). The problem with the specification of explanatory variables in (40) is that, since they are constructed from functions of lagged values of \(y_{t}\), they introduce, autocorrelation as well as heteroskedasticity in the error term. The error term is also expected to be heteroskedastic because of the well-known stylized fact that we have time-varying second-order moments in financial data.
To compare the various alternatives, we consider buy-and-hold strategy, artificial neural network (ANN)Footnote 3 , OLS and MCDR for the last 100 trading days which have not been taken into account in estimations.
In the upper left panel of Fig. 4, we present NASDAQ log-returns. In the upper right panel we compare buy-and-hold, ANN, OLS, and MCDMR. OLS, clearly, does not do well relative to buy-and-hold and ANN. MCDMR, for the most part, does quite well in terms of cumulative returns, even when compared to ANN. In the lower panel we report results from Multi-criteria IV along with 95% Bayes probability intervals which can be computed easily, once MCMC draws from the posterior in (29) are available. It turns out that Multi-criteria IV delivers rather tight error bounds so, the performance in terms of cumulative returns, is statistically, important.
8 Managerial implications
That linear regression is used in many managerial decision making processes, is well-known and beyond any doubt. Stam (1997) succinctly pointed out the relevance in discrete variable classification, mixed variable classification, and in application areas which are often susceptible to data analytical problems, such as medical diagnosis, psychology, marketing, financial analysis, engineering and pattern recognition. In this paper, we provide an estimator of parameters in linear regression or instrumental-variable models that satisfies multiple criteria: In addition to minimizing the sum of squared residuals in (1), we also need to minimize simultaneously the presence of autocorrelation, heteroskedasticity, misspecification arising from nonlinearities, endogeneity, and failure in out-of-sample forecasting. These problems are commonly encountered in applications, but they are addressed, for the most part, in an ad hoc way. A formulation of linear regression estimation as a multi-criteria decision-making problem, addresses these problems in a common and principled framework, also permitting the user to assign different importance to different objectives, if so desired. Managers often need to understand how a process work by using the framework of linear regression. We have argued that autocorrelation and heteroskedasticity are not incidental problems that can be treated in a mechanical way by using, for example, so-called robust standard errors, which are now part of commonly available statistical software. Autocorrelation and heteroskedasticity rather indicate misspecification of the model as it is quite likely that autocorrelated and / or heteroskedastic variables, have been omitted from the model, becoming part of the error term. Our new multi-criteria decision making for OLS and IV regression, is found to perform well in a Monte Carlo study. An application to NASDAQ daily returns shows that the cumulative predicted returns are higher than buy-and-hold strategies and even artificial neural networks, whereas least-squares regression fails to deliver acceptable results.
These particular aspects of the model as it relates to forecasting performance are encouraging and deserve further investigation in future research.
9 Concluding remarks
In this paper, we consider OLS and IV regression. We argue that specification problems related to autocorrelation, heteroskedasticity, neglected non-linearity, unsatisfactory out-of-small performance and endogeneity can be addressed in the context of multi-criteria optimization. We show that the new technique performs well, it minimizes all these problems simultaneously, and effectively eliminates them for the most part. Markov Chain Monte Carlo techniques are used to perform the computations. An application to NASDAQ daily returns shows that cumulative predicted returns are higher than buy-and-hold strategies and even an artificial neural network, whereas OLS regression fails to deliver acceptable results. As such, the new techniques are likely to be of interest for practitioners in most applied fields dealing with estimation, misspecification and interpretation of regression models. In particular, the method may relevant in portfolio optimization and prediction, as it minimizes the effect of regression problems, simultaneously. Although we use Bayesian analysis and MCMC methods to solve the multi-criteria OLS and IV problems, it is possible to use several other techniques (see Footnote 1). The downside is that computation of standard errors and confidence bands are not straightforward to derive, and it is likely that the use of the sub-sampling bootstrap and other variants becomes imperative thus increasing computational complexity and timing . From this point of view, as simulation techniques are required, the use of Bayesian MCMC may be more straightforward, in practice.
The new techniques allow dealing with outliers in a straightforward way, as appropriate norms of errors are introduced among the objectives in multi-criteria OLS / IV. Out-of-sample fit is also taken into account so that the techniques deliver the best predictions possible when commonly encountered regression problems are also taken into account.
In terms of future research several problems are open. First, a generalization to Generalized Method of Moments estimation is possible to deal with specification problems of regressions. Second, it would be worthwhile to address the same problems in non-linear regression models, which seems to be quite easy. Third, methods for selecting valid instruments in practical situations should be developed. One such technique in the big-data context is provided by Bai and Ng (2010).
Change history
20 July 2021
A Correction to this paper has been published: https://doi.org/10.1007/s10479-021-04203-z
Notes
One may proceed in two ways. One is the scalarization approach where a single objective is formulated and corresponding Pareto optima are determined numerically (Das and Dennis (1998)). The alternative is to solve the first-order conditions for Pareto optimality in multiobjective programming (see Fliege et al. 2009; Vieira et al. 2012). Qu et al. (2011) present a quasi-Newton method for smooth problems. Qu et al. (2013) and Neto et al. (2013) consider methods for non-smooth objectives. Qu et al. (2014) propose an extension of the quasi-Newton method in Qu et al. (2011) to the non-smooth case along with a new algorithm to compute the critical point under non-convexity. Other techniques are presented in Angilella et al. (2017), Chica et al. (2016), Cardoso et al. (2016), Kadziński et al. (2017), Mavrotas et al. (2015), Paul et al. (2017), and Tsai and Chen (2017). It is not the purpose of this study to compare different solution techniques for multi-criteria decision-making problems.
Several different parameter values have been tried and the results were the same.
Our formulation is \(y_{t}=x_{t}'\beta _{0}+\sum _{g=1}^{G}\lambda _{g}\varphi \left( x_{t}'\beta _{g}\right) \), where \(\varphi (\cdot )\) is the sigmoidal activation function, \(\varphi (z)=(1+e^{-z})^{-1},\,z\in {\mathbb {R}}.\) Our selection of G was based on the ANN model that delivers the best out-of-sample mean absolute prediction error, and we found \(G=4\).
Abbreviations
- IV:
-
Instrumental Variables.
- GIVE:
-
Generalized Instrumental Variables Estimation.
- GLS:
-
Generalized Least Squares.
- GMM:
-
Generalized Method of Moments.
- HAC:
-
Heteroskedasticity and Autocorrelation Consistent (HAC) covariance matrix.
- LAD:
-
Least Absolute Deviations.
- LMS:
-
Least Median of Squares.
- MAE:
-
Mean Absolute Error.
- MARE:
-
Mean Absolute Relative Error.
- MCMC:
-
Markov Chain Monte Carlo.
- LAD:
-
Least Absolute Deviations.
- OLS:
-
Ordinary Least Squares.
- RMSE:
-
Root Mean Squared Error.
References
Angilella, S., Corrente, S., Greco, S., & Słowiński, R. (2017). Robust ordinal regression and stochastic multiobjective acceptability analysis in multiple criteria hierarchy process for the choquet integral preference model. Omega, 63, 154–169.
Awasthi, A., & Omrani, H. (2019). A goal-oriented approach based on fuzzy axiomatic design for sustainable mobility project selection. International Journal of Systems Science: Operations and Logistics, 6(1), 86–98.
Bai, J., & Ng, S. (2010). Instrumental variable estimation in a data rich environment. Econometric Theory, 26(6), 1577–1606.
Bowlin, W. F., Charnes, A., Cooper, W. W., & Sherman, H. D. (1984). Data envelopment analysis and regression approaches to efficiency estimation and evaluation. Annals of Operations Research, 2(1), 113–138.
Cardoso, T., Duarte Oliveira, M., Barbosa-Póvoa, A., & Nickel, S. (2016). Moving towards an equitable long-term care network: A multi-objective and multi-period planning approach. Omega, 58, 69–85.
Chica, M., Bautista, J., Cordón, Ó., & Damas, S. (2016). A multiobjective model and evolutionary algorithms for robust time and space assembly line balancing under uncertain demand. Omega, 58, 55–68.
Colson, G., & Zeleny, M. (1979). Uncertain Prospects Ranking and Portfolio Analysis Under the Condition of Partial Information Mathematical Systems in Economics (Vol. 44). Maisenheim: Verlag Anton Hain.
Das, I., & Dennis, J. E. (1998). Normal-boundary intersection: A new method for generating the Pareto surface in nonlinear multicriteria optimization problem. SIAM Journal on Optimization, 8(3), 931–967.
Desai, V. S., & Bharati, R. (1998). A comparison of linear regression and neural network methods for predicting excess returns on large stocks. Annals of Operations Research, 78, 127–163.
Dielman, T. E., & Rose, E. L. (1997). Estimation and testing in least absolute value regression with serially correlated disturbances. Annals of Operations Research, 74, 239–25.
Duan, C., Deng, C., Gharaei, A., Wu, J., & Wang, B. (2018). Selective maintenance scheduling under stochastic maintenance quality with multiple maintenance actions. International Journal of Production Research, 56(23), 7160–7178.
Dubey, R., Gunasekaran, A., & Singh, S. T. (2015). Building theory of sustainable manufacturing using total interpretive structural modelling. International Journal of Systems Science: Operations and Logistics, 2(4), 231–247.
Fliege, L., Graña Drummond, L. M., & Svaiter, B. F. (2009). Newton’s method for multiobjective optimization. SIAM Journal on Optimization, 2, 602–626.
Geweke, J. (1992). Evaluating the accuracy of sampling-based approaches to calculating posterior moments. In M. Bernado, J. O. Berger, A. P. Dawid, & A. F. M. Smith (Eds.), Bayesian Statistics 4 (J) (pp. 169–193). Oxford, UK: Clarendon Press.
Gharaei, A., Karimi, M., & Shekarabi, S. A. H. (2019a). An integrated multi-product, multi-buyer supply chain under penalty, green, and quality control polices and a vendor managed inventory with consignment stock agreement: The outer approximation with equality relaxation and augmented penalty algorithm. Applied Mathematical Modelling, 69, 223–254.
Gharaei, A., Shekarabi, S. A. H., & Karimi, M. (2019). Modelling and optimal lot-sizing of the replenishments in constrained, multi-product and bi-objective EPQ models with defective products: Generalised Cross Decomposition. International Journal of Systems Science: Operations and Logistics. https://doi.org/10.1080/23302674.2019.1574364.
Gharaei, A., Karimi, M., & Shekarabi, S. A. H. (2019b). Joint Economic Lot-sizing in Multi-product Multi-level Integrated Supply Chains: Generalized Benders Decomposition. International Journal of Systems Science: Operations and Logistics. https://doi.org/10.1080/23302674.2019.1585595.
Gharaei, A., Shekarabi, S. A. H., Karimi, M., Pourjavad, E., & Amjadian, A. (2019c). An integrated stochastic EPQ model under quality and green policies: generalised cross decomposition under the separability approach. International Journal of Systems Science: Operations and Logistics. https://doi.org/10.1080/23302674.2019.1656296.
Giri, B. C., & Bardhan, S. (2014). Coordinating a supply chain with backup supplier through buyback contract under supply disruption and uncertain demand. International Journal of Systems Science: Operations and Logistics, 1(4), 193–204.
Giri, B. C., & Masanta, M. (2018). Developing a closed-loop supply chain model with price and quality dependent demand and learning in production in a stochastic environment. International Journal of Systems Science: Operations and Logistics. https://doi.org/10.1080/23302674.2018.1542042.
Handi, J., Kell, D. B., & Knowles, J. (2007). Multiobjective optimization in bioinformatics and computational biology. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 4(2), 279–290.
Hao, Y., Helo, P., & Shamsuzzoha, A. (2018). Virtual factory system design and implementation: Integrated sustainable manufacturing. International Journal of Systems Science: Operations and Logistics, 5(2), 116–132.
Hurson, C., & Zopounidis, C. (1993). Return, risk measures and multicriteria decision support for portfolio selection. In: Papathanassiou, B., Paparrizos, K. (eds.) Proceedings of the 2nd Balkan conference on operational research, pp. 343–357.
Hurson, C., & Zopounidis, C. (1995). On the use of multicriteria decision aid methods to portfolio selection. Journal of Euro-Asian Management, 1(2), 69–94.
Hurson, C., & Zopounidis, C. (1997). Gestion de portefeuille et analyse multicritere. Paris: Economica.
Hwang, C-S., Kao, Y-C., & Yu, P. (2010). Integrating Multiple Linear Regression and Multicriteria Collaborative Filtering for Better Recommendation. 2010 International Conference on Computational Aspects of Social Networks. https://doi.org/10.1109/CASoN.2010.59. IEEE.
Kadziński, M., Tervonen, T., Tomczyk, M. K., & Dekker, R. (2017). Evaluation of multi-objective optimization approaches for solving green supply chain design problems. Omega, 68, 168–184.
Kazemi, N., Abdul-Rashid, S. H., Ghazilla, R. A. R., Shekarian, E., & Zanoni, S. (2018). Economic order quantity models for items with imperfect quality and emission considerations. International Journal of Systems Science: Operations and Logistics, 5(2), 99–115.
Mavrotas, G., Figueira, J. R., & Siskos, E. (2015). Robustness analysis methodology for multi-objective combinatorial optimization problems and application to project selection. Omega, 52, 142–155.
Mavrotas, G., Xidonas, P., & Psarras, J. (2008). An integrated multiple criteria methodology for supporting common stock portfolio selection decisions. In: Lahdelma, R.,Miettinen, K., Salminen, P., Salo,A. (eds.) Proceedings of the 67th meeting of the European working group on multiple criteria decision aiding. pp. 56–71. Rovaniemi, Finland
Mielke, P. W., & Berry, K. J. (1997). Permutation-based multivariate regression analysis: The case for least sum of absolute deviations regression. Annals of Operations Research, 74, 259–268.
Narula, S. C., & Wellington, J. F. (2007). Multiple criteria linear regression. European Journal of Operational Research, 181, 767–772.
Nilashi, M., Dalvi-Esfahani, M., Roudbaraki, M. Z., Ramayah, T., & Ibrahim, P. (2016). A Multi-Criteria Collaborative Filtering Recommender System Using Clustering and Regression Techniques. Journal of Soft Computing and Decision Support Systems, 3(5), 24–30.
Neto, J. X. D. C., Silva, G. J. P. D., Ferreira, O. P., & Lopes, J. O. (2013). A subgradient method for multiobjective optimization. Computational Optimization and Applications, 54, 461–472.
Ouenniche, J., & Carrales, S. (2018). Assessing efficiency profiles of UK commercial banks: a DEA analysis with regression-based feedback. Annals of Operations Research, 266(1–2), 551–587.
Panagopoulos, O. P. P., Xanthopoulos, T. Razzaghi., & Şeref, O. (2019). Relaxed support vector regression. Annals of Operations Research, 276(1–2), 191–210.
Paul, N. R., Lunday, B. J., & Nurre, S. G. (2017). A multiobjective, maximal conditional covering location problem applied to the relocation of hierarchical emergency response facilities. Omega, 66, 147–158.
Pincus, M. (1968). A Closed-Form Solution of Certain Programming Problems. Operations Research, 16, 690–694.
Priya, P., & Venkatesh, A. (2012). Integration of Analytic Hierarchy Process with Regression Analysis to Identify Attractive Locations for Market Expansion. Journal of Multi-Criteria Decision Making, 19(3–4), 143–153.
Qu, S. J., Goh, M., & Chan, F. T. S. (2011). Quasi-Newton methods for solving multiobjective optimization. Operations Research Letters, 39, 397–399.
Qu, S. J., Goh, M., & Liang, B. (2013). Trust region methods for solving multiobjective optimisation. Optimization Methods and Software, 28, 796–811.
Qu, S., Liu, C., Goh, M., Li, Y., & Ji, Y. (2014). Nonsmooth multiobjective programming with quasi-Newton methods. European Journal of Operational Research, 235, 503–510.
Rabbani, M., Foroozesh, N., Mousavi, S. M., & Farrokhi-Asl, H. (2019). Sustainable supplier selection by a new decision model based on interval-valued fuzzy sets and possibilistic statistical reference point systems under uncertainty. International Journal of Systems Science: Operations and Logistics, 6(2), 162–178.
Rabbani, M., Hosseini-Mokhallesun, S. A. A., Ordibazar, A. H., & Farrokhi-Asl, H. (2020). A hybrid robust possibilistic approach for a sustainable supply chain location-allocation network design. International Journal of Systems Science: Operations and Logistics, 7(1), 60–75.
Rousseeauw, P. J. (1984). Least Median of Squares Regression. Journal of the American Statistical Association December 1984, 79(388), 871–880.
Sarkar, S., & Giri, B. C. (2018). Stochastic supply chain model with imperfect production and controllable defective rate. International Journal of Systems Science: Operations and Logistics, 7(2), 133–146.
Sayyadi, R., & Awasthi, A. (2018a). A simulation-based optimisation approach for identifying key determinants for sustainable transportation planning. International Journal of Systems Science: Operations and Logistics, 5(2), 161–174.
Sayyadi, R., & Awasthi, A. (2018b). An integrated approach based on system dynamics and ANP for evaluating sustainable transportation policies. International Journal of Systems Science: Operations and Logistics, 7(2), 181–191.
Shah, N. H., Chaudhari, U., & Cárdenas-Barrón, L. E. (2020). Integrating credit and replenishment policies for deteriorating items under quadratic demand in a three echelon supply chain. International Journal of Systems Science: Operations and Logistics, 7(1), 34–45.
Shekarabi, S. A. H., Gharaei, A., & Karimi, M. (2019). Modelling and optimal lot-sizing of integrated multi-level multi-wholesaler supply chains under the shortage and limited warehouse space: generalised outer approximation. International Journal of Systems Science: Operations and Logistics, 6(3), 237–257.
Spronk, J., & Hallerbach, W. G. (1997). Financial modelling: where to go? With an illustration for portfolio management. European Journal of Operational Research, 99(1), 113–127.
Stam, A. (1997). Nontraditional approaches to statistical classification: Some perspectives on \(L_{p}\)-norm methods. Annals of Operations Research, 74(1), 1–36.
Steuer, R. E., Qi, Y., & Hirschberger, M. (2005). Multiple objectives in portfolio selection. Journal of Financial Decision Making, 1(1), 11–26.
Steuer, R. E., Qi, Y., & Hirschberger, M. (2006a). Developments in multi-attribute portfolio selection. In T. Trzaskalik (Ed.), Multiple Criteria Decision Making ‘05 (pp. 251–262). Katowice Poland: Karol Adamiecki Press.
Steuer, R. E., Qi, Y., & Hirschberger, M. (2006b). Portfolio optimization: new capabilities and future methods. Zeitschrift für Betriebswirtschaft, 76(2), 199–219.
Tsai, S. C., & Chen, S. T. (2017). A simulation-based multi-objective optimization framework: A case study on inventory management. Omega, 70, 148–159.
Tsao, Y.-C. (2015). Design of a carbon-efficient supply-chain network under trade credits. International Journal of Systems Science: Operations and Logistics, 2(3), 177–186.
Tsionas, M. G. (2017). A Bayesian approach to find Pareto optima in multiobjective programming problems using Sequential Monte Carlo algorithms. Omega, 77(C), 73–79.
Vieira, D. A. G., Takahashi, R. H. C., & Saldnha, R. R. (2012). Multicriteria optimization with a multiobjective golden section line search. Mathematical Programming, Series A, 131, 131–161.
Xidonas, P., & Psarras, J. (2009). Equity portfolio management within the MCDM frame: A literature review. International Journal of Banking, Accounting, and Finance, 1(3), 285–309.
Xidonas, P., Askounis, D., & Psarras, J. (2009a). Common stock portfolio selection: A multiple criteria decision making methodology and an application on the Athens stock exchange. Operations Research, 9(1), 55–79.
Xidonas, P., Mavrotas, G., & Psarras, J. (2009b). A multicriteria methodology for equity selection using financial analysis. Computers and Operations Research, 36(12), 3187–3203.
Xidonas, P., Mavrotas, G., & Psarras, J. (2010a). A multiple criteria decision making approach for the selection of stocks. Journal of the Operations Research Society, 61(8), 1273–1278.
Xidonas, P., Mavrotas, G., & Psarras, J. (2010b). Portfolio construction on the Athens stock exchange: A multiobjective optimization approach. Optimization, 59(8), 1211–1229.
Zeleny, M. (1977). Multidimensional measure of risk: The prospect ranking vector. In S. Zionts (Ed.), MultipleCriteria Problem Solving (pp. 529–548). Heidelberg: Springer.
Zeleny, M. (1981). Satisficing optimization, and risk in portfolio selection. In F. G. H. Derkindreen & R. L. Crum (Eds.), Readings in Strategies for Corporate Investment (pp. 200–219). Boston: Pitman Publishing.
Zeleny, M. (1982). Multiple Criteria Decision Making. New York: McGraw Hill.
Yin, S., Nishi, T., & Zhang, G. (2016). A game theoretic model for coordination of single manufacturer and multiple suppliers with quality variations under uncertain demands. International Journal of Systems Science: Operations and Logistics, 3(2), 79–91.
Zioutas, G., Pitsoulis, L., & Avramidis, A. (2009). Quadratic mixed integer programming and support vectors for deleting outliers in robust regression. Annals of Operations Research, 166(1), 339–353.
Zopounidis, C. (1999). Multicriteria decision aid in financial management. European Journal of Operational Research, 119(2), 404–415.
Zopounidis, C., & Doumpos, M. (2002). Multicriteria decision aid in financial decision making: methodologies and literature review. Journal of Multicriteria Decision Analysis, 11, 167–186.
Wang, L., & Zhu, J. (2018). Financial market forecasting using a two-step kernel learning method for the support vector regression. Annals of Operations Research, 174(1), 103–120.
Acknowledgements
The author is grateful to two anonymous referees for useful comments on an earlier version.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
FOR SPECIAL ISSUE OF ANNALS OF OPERATIONS RESEARCH ON “Operations Research, Regression Techniques, and Computational Aspects in Management, Economics, and Finance”.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tsionas, M.G. Multi-criteria optimization in regression. Ann Oper Res 306, 7–25 (2021). https://doi.org/10.1007/s10479-021-03990-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-021-03990-9
Keywords
- Regression
- Instrumental variables
- Autocorrelation
- Heteroskedasticity
- Specification error
- Multi-criteria optimization