Characterizing NTU-bankruptcy rules using bargaining axioms

Abstract

This paper takes an axiomatic bargaining approach to bankruptcy problems with nontransferable utility, by using properties from bargaining theory in order to characterize bankruptcy rules. In particular, we derive new axiomatic characterizations of the proportional rule, the truncated proportional rule, and the constrained relative equal awards rule, using properties which concern changes in the estate or in the claims.

1 Introduction

In a bankruptcy problem with nontransferable utility, claimants have incompatible claims on an insufficient estate, which is represented by a set of attainable utility allocations. Such bankruptcy problems arise when claimants have individual utility functions over their monetary payoffs. Bankruptcy rules assign to any such bankruptcy problem a feasible utility allocation, i.e., an allocation for which the individual utility payoffs are bounded by the corresponding claims. On the one hand, bankruptcy problems with nontransferable utility generalize monetary bankruptcy problems, as introduced by O’Neill (1982). On the other hand, they can be considered as bargaining problems with claims (cf. Chun and Thomson 1992) under a somewhat different interpretation.

Orshan et al. (2003), Dietzenbacher (2018), and Estévez-Fernández et al. (2020) took a game theoretic approach to bankruptcy problems with nontransferable utility by defining an appropriate coalitional bankruptcy game and focusing on the structure of the core. Moreover, Dietzenbacher (2018) showed that the class of game theoretic bankruptcy rules coincides with the class of bankruptcy rules satisfying truncation invariance, i.e., invariance under truncation of the claims by the estate.

Recently, Dietzenbacher et al. (2020a, (2020b) took an axiomatic approach to bankruptcy problems with nontransferable utility, by characterizing bankruptcy rules in terms of adequately generalized properties from bankruptcy theory. To explore the proportional rule, the truncated proportional rule, and the constrained relative equal awards rule, they proposed the relative symmetry axiom, which imposes relatively equal treatment of relatively equal claimants.

This paper takes an axiomatic bargaining approach to bankruptcy problems with nontransferable utility by characterizing bankruptcy rules using properties from bargaining theory. Similar to Chun and Thomson (1992), we interpret the estate of a bankruptcy problem as the feasible set of a bargaining problem, as introduced by Nash (1950), which is enriched by a claims vector. However, we adopt the standard assumption from bankruptcy theory that individual utility is normalized in such a way that allocating nothing corresponds to a utility level of zero. Therefore, it is convenient to consider the zero vector as a natural benchmark for allocations, instead of an exogenous disagreement point as in bargaining problems. Although not addressed in this paper, this still allows for the approach of Herrero (1997), which interprets the vector of minimal rights of a bankruptcy problem, i.e., the maximal individual payoffs in the estate when all other claimants are allocated their claims, as the corresponding endogenous disagreement point of a bargaining problem with claims.

We consider the role of the claims vector in bankruptcy problems as being ‘dual’ to the role of the disagreement point in bargaining problems.¹ Where the disagreement point serves as a lower bound for rational payoff allocations in a bargaining problem, the claims vector serves as an upper bound for feasible payoff allocations in a bankruptcy problem. Following the classical axiomatic theory of bargaining, we formulate several properties which concern changes in the estate or in the claims, where the latter ones are based on axioms concerning changes in the disagreement point, and study their implications. In particular, we translate several axioms from bargaining theory to the domain of bankruptcy problems with nontransferable utility, study their relations, and combine them with the axioms of relative symmetry and truncation invariance from bankruptcy theory, in order to derive new axiomatic characterizations of the proportional rule, the truncated proportional rule, and the constrained relative equal awards rule.

This paper is organized as follows. Section 2 provides an overview of notions for bankruptcy problems with nontransferable utility. In Sect. 3, we introduce and study the implications of axioms concerning changes in the estate. In Sect. 4, we introduce and study the implications of axioms concerning changes in the claims. Section 5 concludes.

2 Preliminaries

Let N be a nonempty and finite set of claimants. For $x,y\in {\mathbb {R}}^N$, $x\ge y$ denotes $x_i\ge y_i$ for all $i\in N$, and $x>y$ denotes $x_i>y_i$ for all $i\in N$. The notations $\le$ and < are defined analogously. Further, ${\mathbb {R}}_+^N=\{x\in {\mathbb {R}}^N\mid x\ge 0_N\}$ and ${\mathbb {R}}_{++}^N=\{x\in {\mathbb {R}}^N\mid x>0_N\}$. The comprehensive hull of $E\subseteq {\mathbb {R}}_+^N$ is the set $\mathrm{comp}(E)=\{x\in {\mathbb {R}}_+^N\mid x\le y\ \text {for some}\ y\in E\}$. A set $E\subseteq {\mathbb {R}}_+^N$ is comprehensive if $E=\mathrm{comp}(E)$. The weak Pareto set of $E\subseteq {\mathbb {R}}_+^N$ is the set $\mathrm{WP}(E)=\{x\in E\mid y\not >x\ \text {for all}\ y\in E\}$. A set $E\subseteq {\mathbb {R}}_+^N$ is nonleveled if for all $x,y\in \mathrm{WP}(E)$ with $x\ge y$, we have $x=y$.

A bankruptcy problem with nontransferable utility (cf. Orshan et al. 2003) is a triple (N, E, c) in which the estate $E\subseteq {\mathbb {R}}_+^N$ with $E\cap {\mathbb {R}}_{++}^N\ne \emptyset$ is compact, comprehensive, and nonleveled, and where $c\in (\mathrm{WP}(E)\cup ({\mathbb {R}}^N\setminus E))\cap {\mathbb {R}}_{++}^N$ is the vector of claims.² Let $\mathrm{BR}^N$ denote the class of all bankruptcy problems with claimant set N. For convenience, an NTU-bankruptcy problem is denoted by $(E,c)\in \mathrm{BR}^N$. It is easy to see that both $(E\cup E',c)\in \mathrm{BR}^N$ and $(E\cap E',c)\in \mathrm{BR}^N$ for all $(E,c),(E',c)\in \mathrm{BR}^N$.

Note that the estate is not required to be convex. This means that we allow for utility functions which are not necessarily of the Von Neumann-Morgenstern type. However, most of our results do not rely on the admission of nonconvex estates and can therefore be reformulated on the domain of bankruptcy problems with convex estates.

Let $(E,c)\in \mathrm{BR}^N$. The truncated estate ${\hat{E}}_c\subseteq {\mathbb {R}}_+^N$ is given by

$$\begin{aligned} {\hat{E}}_c=\{x\in E\mid x\le c\}. \end{aligned}$$

The vector of utopia values $u^E\in {\mathbb {R}}_{++}^N$ is given by

$$\begin{aligned} u^E=\left( \max \{x_i\mid x\in E\}\right) _{i\in N}. \end{aligned}$$

The vector of truncated claims ${\hat{c}}^E\in {\mathbb {R}}_{++}^N$ is given by

$$\begin{aligned} {\hat{c}}^E=\left( \min \{c_i,u_i^E\}\right) _{i\in N}. \end{aligned}$$

Note that $u^{{\hat{E}}_c}={\hat{c}}^E$ and ${\hat{E}}_c={\hat{E}}_{{\hat{c}}^E}$.

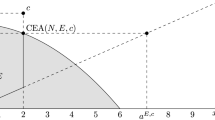
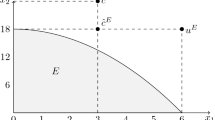
Example 1

Let $N=\{1,2\}$ and consider the bankruptcy problem $(E,c)\in \mathrm{BR}^N$ given by $E=\{x\in {\mathbb {R}}_+^N\mid x_1^2+12x_2\le 36\}$ and $c=(3,4)$. Then ${\hat{E}}_c=\{x\in {\mathbb {R}}_+^N\mid x_1^2+12x_2\le 36,x_1\le 3\}$, $u^E=(6,3)$, and ${\hat{c}}^E=(3,3)$. This is illustrated as follows.

$\square$

A bankruptcy rule $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ assigns to any $(E,c)\in \mathrm{BR}^N$ a payoff allocation $f(E,c)\in \mathrm{WP}(E)$ with $f(E,c)\le c$.³ A bankruptcy rule $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ satisfies

• relative symmetry if $\frac{f_i(E,c)}{u_i^E}=\frac{f_j(E,c)}{u_j^E}$ for all $(E,c)\in \mathrm{BR}^N$ and any $i,j\in N$ with $\frac{c_i}{u_i^E}=\frac{c_j}{u_j^E}$;

• truncation invariance if $f(E,c)=f(E,{\hat{c}}^E)$ for all $(E,c)\in \mathrm{BR}^N$.

Relative symmetry imposes relatively equal treatment of claimants with relatively equal claims, i.e., equal proportions of their claims with respect to their utopia values. Truncation invariance states that it is not relevant to claim more than your utopia value, supported by the fact that claimants are not allocated more than their utopia values in any feasible estate allocation. The following three bankruptcy rules all satisfy relative symmetry.

The proportional rule $\mathrm{Prop}:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ assigns to any $(E,c)\in \mathrm{BR}^N$ the payoff allocation

$$\begin{aligned} \mathrm{Prop}(E,c)=\lambda ^{E,c}c, \end{aligned}$$

where $\lambda ^{E,c}=\max \{t\in (0,1]\mid tc\in E\}$. The proportional rule satisfies relative symmetry, but does not satisfy truncation invariance.

The truncated proportional rule $\mathrm{TProp}:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ assigns to any $(E,c)\in \mathrm{BR}^N$ the payoff allocation

$$\begin{aligned} \mathrm{TProp}(E,c)=\mathrm{Prop}(E,{\hat{c}}^E). \end{aligned}$$

The truncated proportional rule satisfies both relative symmetry and truncation invariance.

The constrained relative equal awards rule $\mathrm{CREA}:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ assigns to any $(E,c)\in \mathrm{BR}^N$ the payoff allocation

$$\begin{aligned} \mathrm{CREA}(E,c)=\left( \min \{c_i,\alpha ^{E,c}u_i^E\}\right) _{i\in N}, \end{aligned}$$

where $\alpha ^{E,c}=\max \{t\in (0,1]\mid (\min \{c_i,tu_i^E\})_{i\in N}\in E\}$. The constrained relative equal awards rule satisfies both relative symmetry and truncation invariance.

Example 2

Let $N=\{1,2\}$ and consider the bankruptcy problem $(E,c)\in \mathrm{BR}^N$ given by $E=\{x\in {\mathbb {R}}_+^N\mid x_1^2+12x_2\le 36\}$ and $c=(3,4)$ as in Example 1. Then $\mathrm{Prop}(E,c)=(2,2\frac{2}{3})$

$\square$

3 Estate axioms

In this section, we introduce and study the implications of axioms concerning changes in the estate. Starting from the well-known independence of irrelevant alternatives axiom introduced by Nash (1950), several axioms concerning changes in the feasible set of bargaining problems have been proposed in the literature. Kalai (1977) introduced a strong monotonicity axiom and Thomson and Myerson (1980) introduced the axiom independence of undominating alternatives. Peters (2010) introduced the axiom independence of individually irrational outcomes to describe solutions for bargaining problems which only depend on the individually rational payoff allocations in the feasible set. As exploited by Roth (1977) for the independence of irrelevant alternatives axiom, in the formulation of these properties the disagreement point is required to be fixed. We translate these properties to the domain of bankruptcy problems with nontransferable utility in such a way that the vector of claims is required to be fixed.

Definition 3.1

A bankruptcy rule $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ satisfies

• estate monotonicity if $f(E,c)\ge f(E',c)$ for all $(E,c),(E',c)\in \mathrm{BR}^N$ with $E'\subseteq E$;

• independence of irrelevant alternatives if $f(E,c)=f(E',c)$ for all $(E,c),(E',c)\in \mathrm{BR}^N$ with $E'\subseteq E$ and $f(E,c)\in \mathrm{WP}(E')$;

• independence of undominating alternatives if $f(E,c)=f(E',c)$ for all $(E,c),(E',c)\in \mathrm{BR}^N$ with $E'\subseteq E$ and $f(E',c)\in \mathrm{WP}(E)$;

• independence of unclaimed alternatives if $f(E,c)=f(E',c)$ for all $(E,c),(E',c)\in \mathrm{BR}^N$ with ${\hat{E}}'_c={\hat{E}}_c$.

Estate monotonicity requires that no claimant is worse off when the estate turns out to be larger than expected. Independence of irrelevant alternatives states that the solution should not change when the estate becomes smaller while the solution remains feasible. Independence of undominating alternatives states that the solution should not change when the estate becomes larger while none of the new payoff allocations is better for all claimants. The independence of unclaimed alternatives axiom, also invoked by Chun and Thomson (1992), describes bankruptcy rules which only depend on the feasible payoff allocations in the estate. The following lemma presents the relations between the estate axioms. The proof is provided in the appendix.

Lemma 3.1

Let $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ be a bankruptcy rule.

• (i) If f satisfies estate monotonicity, then f satisfies independence of irrelevant alternatives.

• (ii) If f satisfies estate monotonicity, then f satisfies independence of undominating alternatives.

• (iii) If f satisfies independence of irrelevant alternatives, then f satisfies independence of unclaimed alternatives.

• (iv) If f satisfies independence of undominating alternatives, then f satisfies independence of unclaimed alternatives.

As shown by the following two bankruptcy rules, the axioms independence of irrelevant alternatives and independence of undominating alternatives are independent.

Let $N=\{1,2\}$. The bankruptcy rule $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ which assigns to any $(E,c)\in \mathrm{BR}^N$ the payoff allocation

$$\begin{aligned} f(E,c)= {\left\{ \begin{array}{ll} ({\hat{c}}_1^E,\max \{x\mid ({\hat{c}}_1^E,x)\in E\}) &{} \quad \text {if }{\hat{c}}_1^E\ge {\hat{c}}_2^E; \\ (\max \{x\mid (x,{\hat{c}}_2^E)\in E\},{\hat{c}}_2^E) &{} \quad \hbox { if}\ {\hat{c}}_1^E<{\hat{c}}_2^E \end{array}\right. } \end{aligned}$$

satisfies independence of irrelevant alternatives, but does not satisfy independence of undominating alternatives.

Let $N=\{1,2\}$. The bankruptcy rule $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ which assigns to any $(E,c)\in \mathrm{BR}^N$ the payoff allocation

$$\begin{aligned} f(E,c)= {\left\{ \begin{array}{ll} ({\hat{c}}_1^E,\max \{x\mid ({\hat{c}}_1^E,x)\in E\}) &{} \text {if } {\hat{c}}_1^E\le {\hat{c}}_2^E;\\ (\max \{x\mid (x,{\hat{c}}_2^E)\in E\},{\hat{c}}_2^E) &{} \hbox { if}\ {\hat{c}}_1^E>{\hat{c}}_2^E \end{array}\right. } \end{aligned}$$

satisfies independence of undominating alternatives, but does not satisfy independence of irrelevant alternatives.

The relations between all estate axioms can be summarized by the following diagram.

The axioms independence of irrelevant alternatives and independence of undominating alternatives are independent. However, if relative symmetry is required, then the two properties become equivalent and are only satisfied by the proportional rule.

Theorem 3.2

The proportional rule is the unique bankruptcy rule satisfying relative symmetry and independence of irrelevant alternatives.

Proof

The proportional rule satisfies relative symmetry. By Lemmas 3.1 and A.1,⁴ the proportional rule satisfies independence of irrelevant alternatives. Let $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ be a bankruptcy rule satisfying relative symmetry and independence of irrelevant alternatives. Let $(E,c)\in \mathrm{BR}^N$. Denote

$$\begin{aligned} t=\max _{i\in N}\left\{ \frac{u_i^E}{c_i}\right\} \ \text {and}\ \varepsilon =\min _{i\in N}\left\{ \mathrm{Prop}_i(E,c)\right\} . \end{aligned}$$

Define

$$\begin{aligned} E'=\bigcup _{i\in N}\mathrm{comp}\left( \mathrm{conv}\left( \left\{ \left( tc_i,0_{N\setminus \{i\}}\right) \right\} \cup \left\{ \left( \varepsilon ,0_{N\setminus \{j\}}\right) \ \Big |\ j\in N\setminus \{i\}\right\} \right) \right) \cup E. \end{aligned}$$

Then $(E',c)\in \mathrm{BR}^N$ and $E\subseteq E'$. Moreover, $u^{E'}=tc$ and $\lambda ^{E',c}=\lambda ^{E,c}$. For all $i,j\in N$, $\frac{c_i}{u_i^{E'}}=\frac{1}{t}=\frac{c_j}{u_j^{E'}}$. By relative symmetry, $f(E',c)=\lambda ^{E',c}c=\lambda ^{E,c}c=\mathrm{Prop}(E,c)$. By independence of irrelevant alternatives, $f(E,c)=f(E',c)=\mathrm{Prop}(E,c)$. $\square$

In contrast to all further results, Theorem 3.2 exploits the fact that the estate of a bankruptcy problem is not required to be convex. All further results do not rely on the admission of nonconvex estates and can therefore be reformulated on the domain of bankruptcy problems with convex estate.

Theorem 3.3

The proportional rule is the unique bankruptcy rule satisfying relative symmetry and independence of undominating alternatives.

Proof

The proportional rule satisfies relative symmetry. By Lemmas 3.1 and A.1, the proportional rule satisfies independence of undominating alternatives. Let $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ be a bankruptcy rule satisfying relative symmetry and independence of undominating alternatives. Let $(E,c)\in \mathrm{BR}^N$. If $|N|=1$, then $f(E,c)=u^E=\mathrm{Prop}(E,c)$. Suppose that $|N|\ge 2$. Denote

$$\begin{aligned} t=\min _{i\in N}\left\{ \frac{u_i^E}{c_i}\right\} . \end{aligned}$$

Let $\varepsilon \in {\mathbb {R}}_{++}^N$ be defined by

$$\begin{aligned} \varepsilon _i=\frac{1}{|N|-1}\left( tc_i-\mathrm{Prop}_i(E,c)\right) \quad \text {for all }\quad i\in N. \end{aligned}$$

Define

$$\begin{aligned} E'=\mathrm{comp}\left( \mathrm{conv}\left( \left\{ \left( \left( \mathrm{Prop}_i(E,c)+|N\setminus S|\varepsilon _i\right) _{i\in S},0_{N\setminus S}\right) \ \Big |\ S\in 2^N\setminus \{\emptyset \}\right\} \right) \right) \cap E. \end{aligned}$$

Then $(E',c)\in \mathrm{BR}^N$ and $E'\subseteq E$. Moreover, $u^{E'}=tc$ and $\lambda ^{E',c}=\lambda ^{E,c}$. For all $i,j\in N$, $\frac{c_i}{u_i^{E'}}=\frac{1}{t}=\frac{c_j}{u_j^{E'}}$. By relative symmetry, $f(E',c)=\lambda ^{E',c}c=\lambda ^{E,c}c=\mathrm{Prop}(E,c)$. By independence of undominating alternatives, $f(E,c)=f(E',c)=\mathrm{Prop}(E,c)$. $\square$

To show that relative symmetry is independent of any estate axiom, we introduce the constrained equal awards rule $\mathrm{CEA}:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$, which assigns to any $(E,c)\in \mathrm{BR}^N$ the payoff allocation

$$\begin{aligned} \mathrm{CEA}(E,c)=\left( \min \{c_i,a\}\right) _{i\in N}, \end{aligned}$$

where $a\in {\mathbb {R}}_+$ is such that $\mathrm{CEA}(E,c)\in \mathrm{WP}(E)$. Where the constrained relative equal awards rule aims to allocate payoffs relatively equal among the claimants, the constrained equal awards rule aims to allocate payoffs absolutely equal among the claimants. The constrained relative equal awards rule satisfies relative symmetry, but does not satisfy independence of unclaimed alternatives. The constrained equal awards rule satisfies estate monotonicity, but does not satisfy relative symmetry. This is summarized in the following table.

	$\mathrm{Prop}$	$\mathrm{CREA}$	$\mathrm{CEA}$
Relative symmetry	$+$	$+$	−
Estate monotonicity	$+$	−	$+$
Independence of irrelevant alternatives	$+$	−	$+$
Independence of undominating alternatives	$+$	−	$+$
Independence of unclaimed alternatives	$+$	−	$+$

The observations in this table imply that relative symmetry is independent of any of the four estate axioms. Also, the properties in Theorem 3.2 are independent and remain independent when independence of irrelevant alternatives is strengthened to estate monotonicity, and the properties in Theorem 3.3 are independent and remain independent when independence of undominating alternatives is strengthened to estate monotonicity.

The proportional rule is not the unique bankruptcy rule satisfying relative symmetry and independence of unclaimed alternatives, since the truncated proportional rule also satisfies these two properties. Nevertheless, these two properties lead to the proportional rule for a large class of problems.

Lemma 3.4

Let $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ be a bankruptcy rule. If f satisfies relative symmetry and independence of unclaimed alternatives, then $f(E,c)=\mathrm{Prop}(E,c)$ for all $(E,c)\in \mathrm{BR}^N$ with $c<u^E$.

Proof

Assume that f satisfies relative symmetry and independence of unclaimed alternatives. Let $(E,c)\in \mathrm{BR}^N$ be such that $c<u^E$. Then $|N|\ge 2$. Denote

$$\begin{aligned} t=\min _{i\in N}\left\{ \frac{u_i^E}{c_i}\right\} . \end{aligned}$$

Let $\varepsilon \in {\mathbb {R}}_{++}^N$ be defined by

$$\begin{aligned} \varepsilon _i=\frac{t-1}{|N|-1}c_i\ \text {for all}\,\,i\in N. \end{aligned}$$

Define

$$\begin{aligned} E'=\mathrm{comp}\left( \mathrm{conv}\left( \left\{ \left( \left( c_i+|N\setminus S|\varepsilon _i\right) _{i\in S},0_{N\setminus S}\right) \Big | S\in 2^N\setminus \{\emptyset \}\right\} \right) \right) \cap E. \end{aligned}$$

Then $(E',c)\in \mathrm{BR}^N$ and ${\hat{E}}'_c={\hat{E}}_c$. Moreover, $u^{E'}=tc$ and $\lambda ^{E',c}=\lambda ^{E,c}$. For all $i,j\in N$, $\frac{c_i}{u_i^{E'}}=\frac{1}{t}=\frac{c_j}{u_j^{E'}}$. By relative symmetry, $f(E',c)=\lambda ^{E',c}c=\lambda ^{E,c}c=\mathrm{Prop}(E,c)$. By independence of unclaimed alternatives, $f(E,c)=f(E',c)=\mathrm{Prop}(E,c)$. $\square$

If we combine independence of unclaimed alternatives with the axioms relative symmetry, truncation invariance, and claims continuity, we obtain an axiomatic characterization of the truncated proportional rule, by using Lemma 3.4.

Definition 3.2

A bankruptcy rule $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ satisfies claims continuity if f(E, c) is continuous in c for all $(E,c)\in \mathrm{BR}^N$.

Theorem 3.5

The truncated proportional rule is the unique bankruptcy rule satisfying relative symmetry, truncation invariance, independence of unclaimed alternatives, and claims continuity.

Proof

The truncated proportional rule satisfies relative symmetry and truncation invariance. By Lemmas A.2 and A.3, the truncated proportional rule satisfies independence of unclaimed alternatives and claims continuity. Let $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ be a bankruptcy rule satisfying relative symmetry, truncation invariance, independence of unclaimed alternatives, and claims continuity. Let $(E,c)\in \mathrm{BR}^N$. If $|N|=1$, then $f(E,c)=u^E=\mathrm{TProp}(E,c)$. Suppose that $|N|\ge 2$. Let $\{x^k\}_{k\in {\mathbb {N}}}$ be defined by $x^k=\frac{1}{k}\mathrm{Prop}(E,{\hat{c}}^E)+(1-\frac{1}{k}){\hat{c}}^E$ for all $k\in {\mathbb {N}}$. Then $x^k<u^E$ for all $k\in {\mathbb {N}}$ and $\lim _{k\rightarrow \infty }x^k={\hat{c}}^E$. By relative symmetry and independence of unclaimed alternatives, Lemma 3.4 implies that $f(E,x^k)=\mathrm{Prop}(E,x^k)=\mathrm{Prop}(E,{\hat{c}}^E)=\mathrm{TProp}(E,c)$ for all $k\in {\mathbb {N}}$. By claims continuity, $f(E,{\hat{c}}^E)=\lim _{k\rightarrow \infty }f(E,x^k)=\mathrm{TProp}(E,c)$. By truncation invariance, $f(E,c)=f(E,{\hat{c}}^E)=\mathrm{TProp}(E,c)$. $\square$

To show that the properties in Theorem 3.5 are independent, we introduce the restricted truncated proportional rule $\mathrm{RTProp}:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$, which assigns to any $(E,c)\in \mathrm{BR}^N$ the payoff allocation

$$\begin{aligned} \mathrm{RTProp}(E,c)= {\left\{ \begin{array}{ll} \mathrm{Prop}(E,c) &{} \quad \text {if}\,\,c<u^E; \\ (tu_S^E,0_{N\setminus S}) &{} \quad \text {otherwise,} \end{array}\right. } \end{aligned}$$

where $S=\{i\in N\mid c_i\ge u_i^E\}$ and $t\in (0,1]$ is such that $\mathrm{RTProp}(E,c)\in \mathrm{WP}(E)$. The restricted truncated proportional rule satisfies relative symmetry, truncation invariance, and independence of unclaimed alternatives, but does not satisfy claims continuity. The constrained relative equal awards rule satisfies relative symmetry, truncation invariance, and claims continuity, but does not satisfy independence of unclaimed alternatives. The proportional rule satisfies relative symmetry, independence of unclaimed alternatives, and claims continuity, but does not satisfy truncation invariance. The constrained equal awards rule satisfies truncation invariance, independence of unclaimed alternatives, and claims continuity, but does not satisfy relative symmetry. This is summarized in the following table.

	$\mathrm{TProp}$	$\mathrm{RTProp}$	$\mathrm{CREA}$	$\mathrm{Prop}$	$\mathrm{CEA}$
Relative symmetry	$+$	$+$	$+$	$+$	−
Truncation invariance	$+$	$+$	$+$	−	$+$
Independence of unclaimed alternatives	$+$	$+$	−	$+$	$+$
Claims continuity	$+$	−	$+$	$+$	$+$

Thus, the properties in Theorem 3.5 are independent.

4 Claims axioms

In this section, we introduce and study the implications of axioms concerning changes in the claims. Several axioms concerning changes in the disagreement point of bargaining problems have been proposed in the literature. We translate these properties to the domain of bankruptcy problems with nontransferable utility in such a way that they concern similar changes in the vector of claims while the estate is required to be fixed.

Definition 4.1

A bankruptcy rule $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ satisfies

• claims linearity if $f(E,c)=f(E,\theta c+(1-\theta )c')$ for all $(E,c),(E,c')\in \mathrm{BR}^N$ with $f(E,c)=f(E,c')$ and any $\theta \in {\mathbb {R}}$ with $(E,\theta c+(1-\theta )c')\in \mathrm{BR}^N$;

• weak claims linearity if $f(E,c)=f(E,\theta c+(1-\theta )f(E,c))$ for all $(E,c)\in \mathrm{BR}^N$ and any $\theta \in {\mathbb {R}}_+$;

• claims convexity if $f(E,c)=f(E,\theta c+(1-\theta )c')$ for all $(E,c),(E,c')\in \mathrm{BR}^N$ with $f(E,c)=f(E,c')$ and any $\theta \in [0,1]$;

• weak claims convexity if $f(E,c)=f(E,\theta c+(1-\theta )f(E,c))$ for all $(E,c)\in \mathrm{BR}^N$ and any $\theta \in [0,1]$.

The claims linearity axiom describes bankruptcy rules for which all claim vectors on the line connecting two claim vectors with equal outcomes lead to the same payoff allocation. The claims convexity axiom is based on a bargaining axiom of Livne (1988) and Chun and Thomson (1990). If there is uncertainty about which of the two claim vectors with equal outcomes applies, then any expected value leads to the same payoff allocation. The corresponding weaker axioms of claims linearity and claims convexity, which only require that linear or convex combinations of the claim vector and its outcome lead to the same payoff allocation, are based on bargaining axioms of Peters and Van Damme (1991) and Peters (2010). The following lemma presents the relations between the claims axioms. The straightforward proof is omitted.

Lemma 4.1

Let $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ be a bankruptcy rule.

• (i) If f satisfies claims linearity, then f satisfies claims convexity.

• (ii) If f satisfies claims linearity, then f satisfies weak claims linearity.

• (iii) If f satisfies claims convexity, then f satisfies weak claims convexity.

• (iv) If f satisfies weak claims linearity, then f satisfies weak claims convexity.

As shown by the following two bankruptcy rules, the axioms claims convexity and weak claims linearity are independent.

Let $N=\{1,2\}$. The restricted constrained relative equal awards rule $\mathrm{RCREA}:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$, which assigns to any $(E,c)\in \mathrm{BR}^N$ the payoff allocation

$$\begin{aligned} \mathrm{RCREA}(E,c)= {\left\{ \begin{array}{ll} \mathrm{CREA}(E,c) &{} \text {if }c<u^E{ or}c\ge \lambda ^{E,u^E}u^E; \\ (tu_S^E,0_{N\setminus S}) &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$

where $S=\{i\in N\mid c_i\ge u_i^E\}$ and $t\in (0,1]$ is such that $\mathrm{RCREA}(E,c)\in \mathrm{WP}(E)$, satisfies claims convexity, but does not satisfy weak claims linearity.

Let $N=\{1,2,3\}$. The bankruptcy rule $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ which assigns to any $(E,c)\in \mathrm{BR}^N$ the payoff allocation

$$\begin{aligned} f(E,c)= {\left\{ \begin{array}{ll} ({\hat{c}}_1^E,\min \{c_2,tu_2^E\},\min \{c_3,tu_3^E\}) &{} \text {if }\frac{c_2}{u_2^E}=\frac{c_3}{u_3^E}; \\ \mathrm{CREA}(E,c) &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$

where $t\in [0,1]$ is such that $f(E,c)\in \mathrm{WP}(E)$, satisfies weak claims linearity, but does not satisfy claims convexity.

The relations of all claims axioms can be summarized by the following diagram.

The axioms claims convexity and weak claims linearity are independent. The constrained relative equal awards rule and the restricted constrained relative equal awards rule both satisfy relative symmetry, truncation invariance, and claims convexity. By replacing claims convexity by weak claims linearity, however, we obtain a characterization of the constrained relative equal award rule.

Theorem 4.2

The constrained relative equal awards rule is the unique bankruptcy rule satisfying relative symmetry, truncation invariance, and weak claims linearity.

Proof

The constrained relative equal awards rule satisfies relative symmetry and truncation invariance. By Lemma A.4, the constrained relative equal awards rule satisfies weak claims linearity. Let $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ be a bankruptcy rule satisfying relative symmetry, truncation invariance, and weak claims linearity. Let $(E,c)\in \mathrm{BR}^N$. If $c\in E$, then $f(E,c)=c=\mathrm{CREA}(E,c)$. Suppose that $c\notin E$. Denote $S=\{i\in N\mid f_i(E,c)<c_i\}$. Then $S\ne \emptyset$. Let $x\in {\mathbb {R}}_+^N$ with $x=\theta c+(1-\theta )f(E,c)$ for some $\theta \in {\mathbb {R}}_+$ be such that $x_S\ge u_S^E$. Then ${\hat{x}}_S^E=(\min \{x_i,u_i^E\})_{i\in S}=u_S^E$ and $\frac{{\hat{x}}_i^E}{u_i^E}=1=\frac{{\hat{x}}_j^E}{u_j^E}$ for all $i,j\in S$. By relative symmetry, $f_S(E,{\hat{x}}^E)=tu_S^E$ for some $t\in [0,1]$. By truncation invariance, $f_S(E,x)=f_S(E,{\hat{x}}^E)=tu_S^E$. By weak claims linearity, $f_S(E,c)=f_S(E,x)=tu_S^E$. Since E is nonleveled, this implies that $f_S(E,c)\le \alpha ^{E,c}u_S^E$.

Suppose that there exists $i\in N\setminus S$ such that $f_i(E,c)>\alpha ^{E,c}u_i^E$. Then $\frac{f_i(E,c)}{u_i^E}>\alpha ^{E,c}\ge \frac{f_j(E,c)}{u_j^E}$ for all $j\in S$. Let $y\in {\mathbb {R}}_+^N$ be such that $y=\theta c+(1-\theta )f(E,c)$ for some $\theta \in {\mathbb {R}}_{++}$ and $\frac{f_i(E,c)}{u_i^E}=\frac{y_j}{u_j^E}$ for some $j\in S$. Then $\frac{y_i}{u_i^E}=\frac{y_j}{u_j^E}$. By relative symmetry, $\frac{f_i(E,y)}{u_i^E}=\frac{f_j(E,y)}{u_j^E}$. By weak claims linearity, $\frac{f_i(E,c)}{u_i^E}=\frac{f_j(E,c)}{u_j^E}$. This is a contradiction, so $f(E,c)\le \alpha ^{E,c}u^E$. This means that $f(E,c)\le \mathrm{CREA}(E,c)$. Since E is nonleveled, this implies that $f(E,c)=\mathrm{CREA}(E,c)$. $\square$

The truncated proportional rule satisfies relative symmetry and truncation invariance, but does not satisfy weak claims linearity. The proportional rule satisfies relative symmetry and weak claims linearity, but does not satisfy truncation invariance. The constrained equal awards rule satisfies truncation invariance and weak claims linearity, but does not satisfy relative symmetry. This is summarized in the following table.

	$\mathrm{CREA}$	$\mathrm{TProp}$	$\mathrm{Prop}$	$\mathrm{CEA}$
Relative symmetry	$+$	$+$	$+$	−
Truncation invariance	$+$	$+$	−	$+$
Weak claims linearity	$+$	−	$+$	$+$

Thus, the properties in Theorem 4.2 are independent.

The axioms concerning changes in the claims can also be combined with the axioms concerning changes in the estate. The proportional rule and the truncated proportional rule both satisfy relative symmetry and independence of unclaimed alternatives. However, if weak claims linearity is required in addition, then these properties are only satisfied by the proportional rule.

Theorem 4.3

The proportional rule is the unique bankruptcy rule satisfying relative symmetry, independence of unclaimed alternatives, and weak claims linearity.

Proof

The proportional rule satisfies relative symmetry. By Lemmas 3.1, 4.1, A.1, and A.5, the proportional rule satisfies independence of unclaimed alternatives and weak claims linearity. Let $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ be a bankruptcy rule satisfying relative symmetry, independence of unclaimed alternatives, and weak claims linearity. Let $(E,c)\in \mathrm{BR}^N$. If $|N|=1$, then $f(E,c)=u^E=\mathrm{Prop}(E,c)$. Suppose that $|N|\ge 2$. Let $x\in {\mathbb {R}}_+^N$ with $x=\theta c+(1-\theta )\mathrm{Prop}(E,c)$ for some $\theta \in (0,1]$ be such that $x<u^E$. By relative symmetry and independence of unclaimed alternatives, Lemma 3.4 implies that $f(E,x)=\mathrm{Prop}(E,x)=\mathrm{Prop}(E,c)$. By weak claims linearity, $f(E,c)=f(E,\frac{1}{\theta }x+(1-\frac{1}{\theta })f(E,x))=f(E,x)=\mathrm{Prop}(E,c)$.$\square$

To show that relative symmetry and independence of unclaimed alternatives are independent of any claims axiom, we introduce two classes of bankruptcy rules.

Let $N=\{1,2\}$ and let $\Psi$ denote the set of all continuous functions $\psi :{\mathbb {R}}_{++}^N\rightarrow {\mathbb {R}}_{++}$ for which

• $\lim _{x_1\rightarrow 0}\psi (x_1,x_2)=\infty$ for all $x_2\in {\mathbb {R}}_{++}$;

• $\lim _{x_2\rightarrow 0}\psi (x_1,x_2)=0$ for all $x_1\in {\mathbb {R}}_{++}$;

• $\psi (x)\ge \psi (y)$ for all $x,y\in {\mathbb {R}}_{++}^N$ with $x_1<y_1$ and $x_2>y_2$.

For any $\psi \in \Psi$ and any $(E,c)\in \mathrm{BR}^N$ with $c\notin E$, let $\xi \in \mathrm{WP}(E)$ be defined such that $\psi (\xi )=\frac{c_2-\xi _2}{c_1-\xi _1}$. Note that $\xi$ exists and is uniquely defined.

For any $\psi \in \Psi$ with $\psi (\frac{1}{2},\frac{1}{2})=1$, the bankruptcy rule $f_1^\psi :\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ assigns to any $(E,c)\in \mathrm{BR}^N$ the payoff allocation

$$\begin{aligned} f_1^\psi (E,c)= {\left\{ \begin{array}{ll} \xi &{} \text {if }E=\{x\in {\mathbb {R}}_+^N\mid x_1+x_2\le 1\},\,{ and}c\notin E; \\ \mathrm{Prop}(E,c) &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Note that $f_1^\psi =\mathrm{Prop}$ if and only if $\psi (x)=\frac{x_2}{x_1}$ for all $x\in {\mathbb {R}}_{++}^N$.

For any $\psi \in \Psi$, the bankruptcy rule $f_2^\psi :\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ assigns to any $(E,c)\in \mathrm{BR}^N$ the payoff allocation

$$\begin{aligned} f_2^\psi (E,c)= {\left\{ \begin{array}{ll} \xi &{} \text {if }c\notin E; \\ \mathrm{Prop}(E,c) &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Note that $f_2^\psi =\mathrm{Prop}$ if and only if $\psi (x)=\frac{x_2}{x_1}$ for all $x\in {\mathbb {R}}_{++}^N$.

The truncated proportional rule satisfies relative symmetry and independence of unclaimed alternatives, but does not satisfy weak claims convexity. Any bankruptcy rule $f_1^\psi \ne \mathrm{Prop}$ with $\psi \in \Psi$ and $\psi (\frac{1}{2},\frac{1}{2})=1$ satisfies relative symmetry and claims linearity, but does not satisfy independence of unclaimed alternatives. Any bankruptcy rule $f_2^\psi \ne \mathrm{Prop}$ with $\psi \in \Psi$ satisfies independence of unclaimed alternatives and claims linearity, but does not satisfy relative symmetry.

	$\mathrm{Prop}$	$\mathrm{TProp}$	$f_1^\psi \ne \mathrm{Prop}$	$f_2^\psi \ne \mathrm{Prop}$
Relative symmetry	$+$	$+$	$+$	−
Independence of unclaimed alternatives	$+$	$+$	−	$+$
Claims linearity	$+$	−	$+$	$+$
Weak claims linearity	$+$	−	$+$	$+$
Claims convexity	$+$	−	$+$	$+$
Weak claims convexity	$+$	−	$+$	$+$

The observations in this table imply that relative symmetry and independence of unclaimed alternatives are independent of any of the four claims axioms. Also, the properties in Theorem 4.3 are independent and remain independent when weak claims linearity is strengthened to claims linearity.

The proportional rule is not the unique bankruptcy rule satisfying relative symmetry, independence of unclaimed alternatives, and claims convexity. Let $N=\{1,2\}$. The restricted proportional rule $\mathrm{RProp}:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$, which assigns to any $(E,c)\in \mathrm{BR}^N$ the payoff allocation

$$\begin{aligned} \mathrm{RProp}(E,c)= {\left\{ \begin{array}{ll} \mathrm{Prop}(E,c) &{} \quad \text {if}\,\,c<u^E; \\ (tc_S,0_{N\setminus S}) &{} \quad \text {otherwise,} \end{array}\right. } \end{aligned}$$

where $S=\{i\in N\mid \forall _{j\in N}:\frac{c_j}{u_j^E}\le \frac{c_i}{u_i^E}\}$ and $t\in [0,1]$ is such that $\mathrm{RProp}(E,c)\in \mathrm{WP}(E)$, also satisfies relative symmetry, independence of unclaimed alternatives, and claims convexity. However, if claimants are required to get positive awards, then these properties are only satisfied by the proportional rule.

Definition 4.2

A bankruptcy rule $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ satisfies positive awards if $f_i(E,c)>0$ for all $(E,c)\in \mathrm{BR}^N$ and any $i\in N$.

Theorem 4.4

The proportional rule is the unique bankruptcy rule satisfying relative symmetry, independence of unclaimed alternatives, weak claims convexity, and positive awards.

Proof

The proportional rule satisfies relative symmetry. By Lemmas 3.1, 4.1, A.1, A.5, and A.6, the proportional rule satisfies independence of unclaimed alternatives, weak claims convexity, and positive awards. Let $f:\mathrm{BR}^N\rightarrow {\mathbb {R}}_+^N$ be a bankruptcy rule satisfying relative symmetry, independence of unclaimed alternatives, weak claims convexity, and positive awards. Let $(E,c)\in \mathrm{BR}^N$. If $|N|=1$, then $f(E,c)=u^E=\mathrm{Prop}(E,c)$. Suppose that $|N|\ge 2$. By positive awards, there exists $x\in {\mathbb {R}}_+^N$ with $x=\theta c+(1-\theta )f(E,c)$ for some $\theta \in (0,1]$ such that $x<u^E$. By relative symmetry and independence of unclaimed alternatives, Lemma 3.4 implies that $f(E,x)=\mathrm{Prop}(E,x)$. By weak claims convexity, $f(E,c)=f(E,x)=\mathrm{Prop}(E,x)=\mathrm{Prop}(E,c)$.

The restricted proportional rule satisfies relative symmetry, independence of unclaimed alternatives, and claims convexity, but does not satisfy positive awards. The truncated proportional rule satisfies relative symmetry, independence of unclaimed alternatives, and positive awards, but does not satisfy weak claims convexity. The constrained relative equal awards rule satisfies relative symmetry, claims convexity, and positive awards, but does not satisfy independence of unclaimed alternatives. The constrained equal awards rule satisfies independence of unclaimed alternatives, claims convexity, and positive awards, but does not satisfy relative symmetry. This is summarized in the following table.

	$\mathrm{Prop}$	$\mathrm{RProp}$	$\mathrm{TProp}$	$\mathrm{CREA}$	$\mathrm{CEA}$
Relative symmetry	$+$	$+$	$+$	$+$	−
Independence of unclaimed alternatives	$+$	$+$	$+$	−	$+$
Claims convexity	$+$	$+$	−	$+$	$+$
Weak claims convexity	$+$	$+$	−	$+$	$+$
Positive awards	$+$	−	$+$	$+$	$+$

Thus, the properties in Theorem 4.4 are independent and remain independent when weak claims convexity is strengthened to claims convexity.

5 Concluding remarks

In this paper, we derived new axiomatic characterizations of the proportional rule, the truncated proportional rule, and the constrained relative equal awards rule for bankruptcy problems with nontransferable utility using axioms from bargaining theory. An overview of the corresponding properties, including the axioms relative symmetry and truncation invariance, the axioms concerning changes in the estate, the axioms concerning changes in the claims, and the weak technical requirements claims continuity and positive awards, is provided in the following table. The constrained equal awards rule is included for illustrative purposes.

	$\mathrm{Prop}$	$\mathrm{TProp}$	$\mathrm{CREA}$	$\mathrm{CEA}$
Relative symmetry	$+$	$+$	$+$	−
Truncation invariance	−	$+$	$+$	$+$
Estate monotonicity	$+$	−	−	$+$
Independence of irrelevant alternatives	$+$	−	−	$+$
Independence of undominating alternatives	$+$	−	−	$+$
Independence of unclaimed alternatives	$+$	$+$	−	$+$
Claims continuity	$+$	$+$	$+$	$+$
Claims linearity	$+$	−	−	−
Weak claims linearity	$+$	−	$+$	$+$
Claims convexity	$+$	−	$+$	$+$
Weak claims convexity	$+$	−	$+$	$+$
Positive awards	$+$	$+$	$+$	$+$

The following table provides an overview of the axiomatic characterizations derived in this paper.

	$\mathrm{Prop}$	$\mathrm{Prop}$	$\mathrm{Prop}$	$\mathrm{Prop}$	$\mathrm{TProp}$	$\mathrm{CREA}$
Relative symmetry	$\star$	$\star$	$\star$	$\star$	$\star$	$\star$
Truncation invariance					$\star$	$\star$
Indep. of irrelevant alternatives	$\star$
Indep. of undominating alternatives		$\star$
Indep. of unclaimed alternatives			$\star$	$\star$	$\star$
Claims continuity					$\star$
Weak claims linearity			$\star$			$\star$
Weak claims convexity				$\star$
Positive awards				$\star$

Alternatively, in line with Albizuri et al. (2020), solutions for bargaining problems can be interpreted as rules for bankruptcy problems with nontransferable utility by explicitly incorporating the claims as upper bounds. The constrained Kalai and Smorodinsky (1975) solution coincides with the constrained relative equal awards rule. This approach could also be further studied in future research to elaborate on the connection between bankruptcy problems and bargaining problems.

Another research direction connecting bankruptcy problems and bargaining problems studies strategic justifications of bankruptcy rules through bargaining protocols. Recent work on this topic was presented by Hagiwara and Hanato (2019).

Appendix

Proof of Lemma 3.1

Proof

(i) Assume that f satisfies estate monotonicity. Let $(E,c),(E',c)\in \mathrm{BR}^N$ be such that $E'\subseteq E$ and $f(E,c)\in \mathrm{WP}(E')$. Then $f(E,c)\ge f(E',c)$. Since E is nonleveled, this implies that $f(E,c)=f(E',c)$. Hence, f satisfies independence of irrelevant alternatives.

(ii) Assume that f satisfies estate monotonicity. Let $(E,c),(E',c)\in \mathrm{BR}^N$ be such that $E'\subseteq E$ and $f(E',c)\in \mathrm{WP}(E)$. Then $f(E,c)\ge f(E',c)$. Since E is nonleveled, this implies that $f(E,c)=f(E',c)$. Hence, f satisfies independence of undominating alternatives.

(iii) Assume that f satisfies independence of irrelevant alternatives. Let $(E,c),(E',c)\in \mathrm{BR}^N$ be such that ${\hat{E}}_c={\hat{E}}'_c$. Then $f(E,c),f(E',c)\in \mathrm{WP}(E\cap E')$. This implies that $f(E,c)=f(E\cap E',c)=f(E',c)$. Hence, f satisfies independence of unclaimed alternatives.

(iv) Assume that f satisfies independence of undominating alternatives. Let $(E,c),(E',c)\in \mathrm{BR}^N$ be such that ${\hat{E}}_c={\hat{E}}'_c$. Then $f(E,c),f(E',c)\in \mathrm{WP}(E\cup E')$. This implies that $f(E,c)=f(E\cup E',c)=f(E',c)$. Hence, f satisfies independence of unclaimed alternatives. $\square$

Lemma A.1

The proportional rule satisfies estate monotonicity.

Proof

Let $(E,c),(E',c)\in \mathrm{BR}^N$ be such that $E'\subseteq E$. Then $\lambda ^{E,c}\ge \lambda ^{E',c}$. This means that

$$\begin{aligned} \mathrm{Prop}(E,c)=\lambda ^{E,c}c\ge \lambda ^{E',c}c=\mathrm{Prop}(E',c). \end{aligned}$$

Hence, the proportional rule satisfies estate monotonicity. $\square$

Lemma A.2

The truncated proportional rule satisfies independence of unclaimed alternatives.

Proof

Let $(E,c),(E',c)\in \mathrm{BR}^N$ be such that ${\hat{E}}_c={\hat{E}}'_c$. Then ${\hat{E}}_{{\hat{c}}^E}={\hat{E}}_c={\hat{E}}'_c={\hat{E}}'_{{\hat{c}}^{E'}}$ and ${\hat{c}}^E=u^{{\hat{E}}_c}=u^{{\hat{E}}'_c}={\hat{c}}^{E'}$. By Lemmas 3.1 and A.1, the proportional rule satisfies independence of unclaimed alternatives. Then

$$\begin{aligned} \mathrm{TProp}(E,c)=\mathrm{Prop}(E,{\hat{c}}^E)=\mathrm{Prop}(E',{\hat{c}}^{E'})=\mathrm{TProp}(E',c). \end{aligned}$$

Hence, the truncated proportional rule satisfies independence of unclaimed alternatives $\square$ .

Lemma A.3

The truncated proportional rule satisfies claims continuity.

Proof

Let $(E,c)\in \mathrm{BR}^N$. Then $\lim _{x\rightarrow c}{\hat{x}}^E={\hat{c}}^E$, $\lim _{x\rightarrow c}\lambda ^{E,{\hat{x}}^E}=\lambda ^{E,{\hat{c}}^E}$, and

$$\begin{aligned} \lim _{x\rightarrow c}\mathrm{TProp}(E,x)&= \lim _{x\rightarrow c}\mathrm{Prop}(E,{\hat{x}}^E)&= \lim _{x\rightarrow c}\lambda ^{E,{\hat{x}}^E}{\hat{x}}^E&= \lim _{x\rightarrow c}\lambda ^{E,{\hat{x}}^E}\lim _{x\rightarrow c}{\hat{x}}^E\\&= \lambda ^{E,{\hat{c}}^E}{\hat{c}}^E&= \mathrm{Prop}(E,{\hat{c}}^E)&= \mathrm{TProp}(E,c). \end{aligned}$$

Hence, the truncated proportional rule satisfies claims continuity. $\square$

Lemma A.4

The constrained relative equal awards rule satisfies weak claims linearity.

Proof

Let $(E,c)\in \mathrm{BR}^N$ and let $\theta \in {\mathbb {R}}_+$. Suppose that $\alpha ^{E,\theta c+(1-\theta )\mathrm{CREA}(E,c)}\ge \alpha ^{E,c}$. For all $i\in N$,

$$\begin{aligned}&\mathrm{CREA}_i(E,\theta c+(1-\theta )\mathrm{CREA}(E,c)) \\ =&\min \{\theta c_i+(1-\theta )\mathrm{CREA}_i(E,c),\alpha ^{E,\theta c+(1-\theta )\mathrm{CREA}(E,c)}u_i^E\} \\ =&\min \{\mathrm{CREA}_i(E,c)+\theta (c_i-\mathrm{CREA}_i(E,c)),\alpha ^{E,\theta c+(1-\theta )\mathrm{CREA}(E,c)}u_i^E\} \\ \ge&\min \{\mathrm{CREA}_i(E,c),\alpha ^{E,c}u_i^E\} \\ =&\mathrm{CREA}_i(E,c). \end{aligned}$$

Since E is nonleveled, this implies that $\mathrm{CREA}(E,c)=\mathrm{CREA}(E,\theta c+(1-\theta )\mathrm{CREA}(E,c))$.

Now, suppose that $\alpha ^{E,\theta c+(1-\theta )\mathrm{CREA}(E,c)}\le \alpha ^{E,c}$. For all $i\in N$,

$$\begin{aligned}&\mathrm{CREA}_i(E,\theta c+(1-\theta )\mathrm{CREA}(E,c)) \\ =&\min \{\theta c_i+(1-\theta )\mathrm{CREA}_i(E,c),\alpha ^{E,\theta c+(1-\theta )\mathrm{CREA}(E,c)}u_i^E\} \\ =&\min \{\mathrm{CREA}_i(E,c)+\theta (c_i-\mathrm{CREA}_i(E,c)),\alpha ^{E,\theta c+(1-\theta )\mathrm{CREA}(E,c)}u_i^E\} \\ \le&\min \{\mathrm{CREA}_i(E,c)+\theta (c_i-\mathrm{CREA}_i(E,c)),\alpha ^{E,c}u_i^E\} \\ =&\mathrm{CREA}_i(E,c). \end{aligned}$$

Since E is nonleveled, this implies that $\mathrm{CREA}(E,c)=\mathrm{CREA}(E,\theta c+(1-\theta )\mathrm{CREA}(E,c))$. Hence, the constrained relative equal awards rule satisfies weak claims linearity. $\square$

Lemma A.5

The proportional rule satisfies claims linearity.

Proof

Let $(E,c),(E,c')\in \mathrm{BR}^N$ be such that $\mathrm{Prop}(E,c)=\mathrm{Prop}(E,c')$, and let $\theta \in {\mathbb {R}}$ be such that $(E,\theta c+(1-\theta )c')\in \mathrm{BR}^N$. Then $\lambda ^{E,c}c=\lambda ^{E,c'}c'$ and

$$\begin{aligned} \mathrm{Prop}(E,\theta c+(1-\theta )c')=\lambda ^{E,\theta c+(1-\theta )c'}(\theta c+(1-\theta )c')=\lambda ^{E,\theta c+(1-\theta )c'}\left( \theta +(1-\theta )\frac{\lambda ^{E,c}}{\lambda ^{E,c'}}\right) c. \end{aligned}$$

This means that $\mathrm{Prop}(E,c)=\mathrm{Prop}(E,\theta c+(1-\theta )c')$. Hence, the proportional rule satisfies claims linearity. $\square$

Lemma A.6

The proportional rule satisfies positive awards.

Proof

Let $(E,c)\in \mathrm{BR}^N$. Then $\lambda ^{E,c}>0$ and $\mathrm{Prop}_i(E,c)=\lambda ^{E,c}c_i>0$ for all $i\in N$. Hence, the proportional rule satisfies positive awards. $\square$