1 Introduction

A supply chain includes all activities related to the flow of products and information from the point of raw materials to delivery to final consumers. Technically, a supply chain is a network among suppliers, companies, distributers and consumers. Another example of a supply chain framework would be a service supply chain, such as the services provided by hospitals and banks. In the recent decades, healthcare industry has witnessed an increasing competition in which medical institutions including hospitals face challenges to improve patient treatment and boost the service quality along with minimizing the operational costs. Therefore, higher capabilities of the belonging medical organizations and hospitals to the healthcare supply chain (HSC) is a critical task to secure competitiveness and survival (Kim and Kim 2019). The process of service provision consists of different stages from start to end, including multilayered internal linking activities and multiple entities. Therefore, it is essential to assess the performance of supply chain partners to enhance the supply chain surplus. Therefore, performance evaluation is of great importance in a supply chain. Ever increasing demand for higher service quality and lower cost in the medical institutions, forces hospitals to improve the efficiency of their operations (Fong et al. 2016). They suggest that medical institutions might standardize their works, collection and usage of data, and establish effective collaboration and communication among teams to improve their operational efficiency.

Data envelopment analysis (DEA) is a popular method for performance evaluation in the supply chain context. Conventional DEA models are no longer useful for performance evaluation when the supply chain has an internal structure; because they consider each decision making unit (DMU) as a black-box which take into account just the initial inputs and the final outputs. Although previous studies evaluated the efficiency of hospitals using DEA models, they have not addressed the implications of ratio data for efficiency analysis. Network data envelopment analysis (NDEA) models can consider the internal relationships of supply chains for efficiency measurement purposes (Löthgren and Tambour 1999; Prieto and Zofío 2007). To overcome the shortcomings of the NDEA models in service supply chains especially healthcare supply chains, this paper proposes a novel NDEA with ratio data (NDEA-R) model for evaluating the performance of hospital supply chains. This paper evaluates the efficiency of the overall supply chains and its divisions using NDEA. Compared with the previous studies, the major contributions of this research are summarized as follows:

  • The proposed model obtains the overall efficiency of each division in a multi-stage network and demonstrates the relationships between the overall efficiency and the efficiency of each division. Using the proposed model, the importance of each division is considered in evaluating the overall efficiency of the network.

  • The proposed model looks at the internal structure of the networks by considering the two assumptions of free-link and fixed-link to calculate the efficiency scores.

  • The models proposed in this paper use constant return to scale technology. They incorporate the importance of all output-to-input ratios to calculate the overall and divisional efficiencies. The advantage of the proposed models over the current models is that the overall efficiency of the supply chain and the efficiency of all divisions are calculated solving a single NDEA model.

  • This research develops the NDEA-R models in both multiplicative and envelopment forms to evaluate the efficiency of the supply chains.

The remainder of this paper is organized as follows: Sect. 2 reviews the literature of healthcare supply chain and NDEA. Section 3 develops novel NDEA models for evaluating the supply chains based on ratio data. Section 4 illustrates the case study of 19 hospitals and discusses the findings. Finally, Sect. 5 concludes the paper.

2 Literature review

2.1 Data envelopment analysis (DEA)

Data envelopment analysis (DEA) is a technique based on mathematical programming for evaluating the relative efficiency of a set of homogenous DMUs that initially proposed by Charnes et al. (1978) and extended by Banker et al. (1984). A variety of techniques have been developed for efficiency analysis but evaluating the efficiency of service providers with ratio data is not well researched. The efficiency of each DMU is determined by the efficiency frontier. The DMUs on the efficiency frontier are assumed efficient; otherwise, they are referred to inefficient. DEA sets up a production possibility set (PPS) and considers its frontier as the efficient frontier made according to the non-domination condition.

DEA models are used to evaluate the supply chain structure including buyers and sellers by developing a nonlinear form with a leader–follower structure (Liang et al. 2006). Two-stage DEA models can calculate technical efficiency and cost efficiency in a supply chain to allocate resources (Wong and Wong 2007). Wong et al. (2008) proposed a DEA-based model in a random environment and applied the Monte Carlo simulation to assess the supply chain performance. Shabani et al. (2012) developed an integrated DEA and goal programming (GP) approach for sustainable supplier selection. Using separation approaches, Tone and Tsutsui (2009) proposed the slacks-based measure (SBM) model to reflect the internal structure of a supply chain while measuring efficiency. Network DEA models are applied to measure supply chain efficiency by extending to super-efficiency models (Farzipoor Saen 2008); including centralized, decentralized and mixed models in order to ruminate the internal relationships of the supply chain management (Chen and Yan 2011); developing an epsilon-based network DEA model (Tavana et al. 2013); using directional measures to deal with negative data (Izadikhah and Farzipoor Saen 2016); and developing a common set of weight with goal programming approach (Kiani Mavi et al. 2019a) and ideal point method (Kiani Mavi et al. 2019b; Kiani Mavi and Kiani Mavi 2019; Tavana et al. 2015; Kiani Mavi et al. 2013).

The input-oriented efficiency scores of DEA-R models are greater than or equal to conventional DEA models (Wei et al. 2011a). DEA-R models are able to prevent pseudo-inefficiency as well as underestimated efficiency (Wei et al. 2011b). In cases with ratio data, conventional DEA models are not helpful. Therefore, ratio-based DEA models should be developed. For instance, in a hospital case, researchers could only have access to a ratio of recovered patients to admitted patients or a percentage of successful surgeries to all performed operations. In such a situation, decision-makers should enter the ratio of inputs to outputs or the ratio of outputs to inputs into DEA model. Researchers applied analytic network process (ANP) technique (Supeekit et al. 2016) and DEA models (Chen et al. 2005; Goncalves et al. 2007; Zere et al. 2006) to evaluate the performance of hospital supply chains.

2.2 Data envelopment analysis with ratio data (DEA-R)

To evaluate the efficiency of DMUs with DEA, two types of ratio data are considered:

  1. 1.

    Consider \( DMU_{j} = \left( {X_{j}^{V} ,X_{j}^{R} ,Y_{j}^{V} ,Y_{j}^{R} } \right) \) where \( X_{j}^{V} \) and \( Y_{j}^{V} \) are the cardinal and non-ratio inputs and outputs, respectively. \( X_{j}^{R} \) and \( Y_{j}^{R} \) are the ratio inputs and outputs, respectively. For instance, the rate of population growth, relative profits, and the percentage of discharged patients are ratio data, while the number of students and amount of deposits in a bank are cardinal data. The major problem of DEA to deal with ratio data is the convexity axiom which does not apply to ratio data. Olesen et al. (2015, 2017) developed radial and non-radial models considering ratio data under constant and variable return to scale technologies. Hatami-Marbini and Toloo (2019) developed a DEA model with ratio data to evaluate the efficiency of DMUs for the input- and output orientations regardless of the assumed technology.

  2. 2.

    Consider \( DMU_{j} = \left( {X_{j}^{V} ,Y_{j}^{V} } \right) \) where \( X_{j}^{V} \) and \( Y_{j}^{V} \) are the inputs and outputs, respectively, which adopt cardinal scores ​​and are not of ratio type. However, the ratios \( \frac{{X_{j}^{V} }}{{Y_{j}^{V} }} \) or \( \frac{{Y_{j}^{V} }}{{X_{j}^{V} }} \) are defined based on inputs and outputs. For example, in a hospital, the ratio of discharged patients to the total number of admitted patients over a period is calculated by dividing the two corresponding variables. In this category, the values of input and output variables are available, and their division gives the ratio data. The ratio data in category 1 are ratio by nature like the rate of population growth, while the ratio data in category 2 are made up by dividing cardinal data like the ratio of discharged patients to the total number of admitted patients. Despic et al. (2007) presented DEA models for the ratio of inputs to outputs and vice versa as DEA-R models, in which performance is defined as the sum of the weighted outputs to the sum of weighted inputs. Liu et al. (2011) developed DEA-R models in the form of BCC (Banker–Charnes–Cooper) model without explicit inputs. Mozaffari et al. (2014a, b) proposed relationship among the DEA models without explicit inputs and DEA-R models.

In many circumstances, managers tend to use the ratio of inputs and outputs instead of original data. For example, the ratio of discharged patients to the total number of patients in a hospital, or the ratio of loans paid-off to the total amount of loans in a bank. To evaluate the efficiency of a set of DMUs in the presence of ratio data, DEA-R models outperform the traditional models. The DEA-R models in the input-oriented form, have larger or equal efficiency scores than their corresponding scores obtained from the traditional DEA models (Wei et al. 2011a, b, c). The traditional DEA models face with the issue of underestimation of efficiency and pseudo-inefficiency during efficiency appraisal. Underestimation of efficiency occurs when the efficiency scores of DMUs are not calculated correctly. This problem originates from the fact that the corresponding weights of some inputs and outputs are computed as zero. Therefore, the importance of that variable is not considered in the efficiency score of the DMUs. DEA-R models prevent the underestimation of efficiency and pseudo-inefficiency (Wei et al. 2011a, b, c; Mustaffa and Potter 2009, 2014). Therefore, they correctly calculate the efficiency score of DMUs. DEA-R models have a larger feasible space to choose the corresponding weight of the output-to-input ratios or vice versa. Therefore, all the output-to-input ratios or vice versa are included to measure the DMU efficiency.

2.3 Healthcare supply chain

Healthcare Supply Chain Management (HSCM) is defined as “the information, supplies and finances involved with the acquisition and movement of goods and services from the supplier to the end-user in order to enhance clinical outcomes while controlling costs” (De Vries and Huijsman 2011). The internal supply chain of hospitals are highly complex, unique and operationally challenging (Moons et al. 2019; Lewis et al. 2010). As healthcare supply chains deal with human lives, their operations have higher complexity and they use more valuable products, they are different from usual supply chains (Aldrighetti et al. 2019). Typically, the major partners of a healthcare supply chain are healthcare providers or hospitals which are composed of different departments with the complex flow of information and products between them (Kitsiou et al. (2007). Since the HSC deals with the health and safety of patients, and hospitals are major players in this supply chain, it is highly important to efficiently manage the hospitals to accomplish both the high quality of medical services and reasonable cost. A hospital supply chain includes all activities aimed at providing healthcare services and supporting processes to patients (Mustaffa and Potter 2009; Kumar et al. 2008). For example, a shortage of drugs in a hospital more likely requires an emergency delivery. These emergency replenishments escalate cost and may disrupt the recovery process for the patients (Kochan et al. 2018). Therefore, the healthcare industry is under continuous societal pressure to provide high quality, safe, and reasonable patient care while keeping the overall service cost as low as possible (Dobrzykowski et al. 2014). In the healthcare industry, effective supply chain management increases operational efficiency which in turns improves efficient utilization of healthcare resources (Chen et al. 2013). Like other supply chains, a healthcare supply chain is a network of partnering organizations that aim to deliver supplies in the right quantity, at the right place, at the right price, and at the right time (Kochan et al. 2018). Generally, managing inventory and capacity in the healthcare supply chain is more complex compared to other industries because (1) hospitals handle a significant amount of high-value healthcare items like drugs, medical devices, tools and other supplies (Chen et al. 2013), (2) several stakeholders such as medical doctors and pharmacists, who usually possess conflicting perspectives about the supply chain operations, decide on inventory management strategies (Bhakoo et al. 2012; De Vries 2011), (3) lead-times of medical devices, supplies and drugs are usually long (Bhakoo et al. 2012) and (4) demands of patients, especially emergency demands, are difficult to forecast precisely (Bhakoo et al. 2012).

The ultimate goal of a healthcare supply chain is to provide patient care services. Performance of a hospital supply chain should be evaluated to ensure that the patient safety objective of the chain is achieved (Battini et al. 2009). However, some studies measure the performance of hospital supply chains independently, means that safety of patients is evaluated regardless of analysing the efficiency of clinical care and supporting processes which are the backbone of a hospital supply chain (Supeekit et al. 2016). The patient care, clinical care, and supporting processes are not independent because clinical care divisions provide services to patient care while supporting divisions enable the clinical care divisions to deliver successful patent care and safety services (Singh 2008). These interactions make the components of a healthcare supply chain interconnected so their efficiencies are interdependent, too. Holmberg (2000) points out that the performance of all divisions in an interconnected system are interrelated, either directly or indirectly, which make it difficult or even impossible to individually evaluate the performance of a division.

Therefore, efficiency management is interpreted differently by different stakeholders as they have conflicting goals for performance evaluation and they do not collectively agree upon what constitutes efficiency and what actions are needed to improve it (Melo 2012). However, the definitive goal is to accomplish “a well-coordinated system that delivers care with great efficiency and quality, at a reasonable cost, matching the resources for care to where (and when) they are needed most” (Hall 2012). To evaluate the performance of medical institutions, not only the costs through the whole supply chain should be considered, but also the efficiency of the operations needs to be assessed which looks at both cost and performance simultaneously. Schneller et al. (2006) point out that healthcare supply chain does not include just hospitals but also encompasses other organizations which are responsible for product design, transportation, inventory, warehousing and packaging.

3 The proposed models

In this section, at first, we develop DEA-R model presented by Wei et al. (2011a) in output-oriented context. Then, we present a new NDEA-R model for evaluating the performance of supply chains.

3.1 DEA-R model

Assume n DMUs; \( \left( {{\text{X}}_{\text{j}} , {\text{Y}}_{\text{j}} } \right), {\text{j}} = 1,..,{\text{n}} \) in which the input vector \( {\text{X}}_{\text{j}} = \left( {{\text{x}}_{{1{\text{j}}}} ,{\text{x}}_{{2{\text{j}}}} , \ldots ,{\text{x}}_{\text{mj}} } \right)^{\text{T}} \) and output vector \( {\text{Y}}_{\text{j}} = \left( {{\text{y}}_{{1{\text{j}}}} ,{\text{y}}_{{2{\text{j}}}} , \ldots ,{\text{y}}_{\text{sj}} } \right)^{\text{T}} . \) Wei et al. (2011a) developed the output-oriented DEA-R (DEA-R-O) model for calculating the efficiency of a set of DMUs as Model (1):

$$ \begin{aligned} &\gamma^{*} = \hbox{Min}\, \gamma \\ s.t. & \quad \mathop \sum \limits_{r = 1}^{s} \mathop \sum \limits_{i = 1}^{m} w_{ri} \left( {\frac{{\frac{{y_{rj} }}{{x_{ij} }}}}{{\frac{{y_{ro} }}{{x_{io} }}}}} \right) \le \gamma ,\quad j = 1, \ldots ,n, \\ & \quad \mathop \sum \limits_{r = 1}^{s} \mathop \sum \limits_{i = 1}^{m} w_{ri} = 1, \\ & w_{ri} \ge 0,\,\,r = 1, \ldots , s, \,\,i = 1, \ldots ,m,\,\,\gamma \ge 0. \\ \end{aligned} $$
(1)

where \( x_{ij} \): \( i \)th input variable for \( DMU_{j} \). \( y_{rj} \): \( rth \) output variable for \( DMU_{j} \). \( w_{ri} \): The weight corresponding with the ratio of \( \frac{{{\text{the }}i{\text{th input variable }}x_{i} }}{{{\text{the }}r{\text{th input variable }}y_{r} }} \). \( \mathop \sum \limits_{r = 1}^{s} \mathop \sum \limits_{i = 1}^{m} w_{ri} \left( {\frac{{\frac{{y_{rj} }}{{x_{ij} }}}}{{\frac{{y_{ro} }}{{x_{io} }}}}} \right) \): The relative efficiency score corresponding with \( DMU_{j} \).

For each DMU under evaluation (\( DMU_{0} \)), this model considers the lowest score obtained from different sets of weights as the efficiency of \( DMU_{0} \). Since each unit can achieve its optimal weights, then if a unit’s efficiency score is lower than 1 that unit is inefficient. The output-oriented Model (1) has been defined based on the ratio of outputs to inputs. The ratio of inputs to outputs will lead to the input-oriented model. Wei et al. (2011b, c) demonstrated that the abovementioned models would prevent the pseudo-inefficiency and underestimations common to CCR (Charnes–Cooper–Rhodes) and BCC models.

The dual of Model (1) is Model (2).

$$ \begin{aligned} & \theta^{*} = \hbox{Max}\, \theta \\ s.t. & \quad \mathop \sum \limits_{j = 1}^{n} \lambda_{j} \left( {\frac{{\frac{{y_{rj} }}{{x_{ij} }}}}{{\frac{{y_{ro} }}{{x_{io} }}}}} \right) \ge \theta ,\quad i = 1, \ldots , m, \quad r = 1, \ldots ,s, \\ & \quad \mathop \sum \limits_{j = 1}^{n} \lambda_{j} = 1,\quad \lambda_{j} \ge 0. \\ \end{aligned} $$
(2)

3.2 NDEA-R-O model

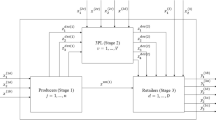
In this section, the DEA-R models are extended to evaluate the supply chain internal structure. Consider a general structure of a supply chain as Fig. 1.

Fig. 1
figure 1

The general structure of a supply chain

Full size image

This structure consists of \( k \) divisions, each division contains separate inputs, outputs and intermediate measures, as depicted by Fig. 1. For performance evaluation, each supply chain is regarded as a DMU.

Definition of notations:

\( x_{ij}^{h} \) is the \( i \)th input and \( y_{rj}^{h} \) is the \( r \)th output from the \( h \)th division in the jth supply chain \( \left( {j = 1, \ldots ,n} \right) \).

\( z_{{f_{{\left( {h,h^{\prime}} \right)}} j}}^{{\left( {h,h^{\prime}} \right)}} \) represents the intermediate products between \( h \)th and \( h^{\prime} \)th divisions of the jth supply chain.

\( f\left( {h, h^{\prime}} \right) \) shows the number of intermediate products transferred from the \( h \)th division to \( h^{\prime} \)th division, \( f_{{\left( {h,h^{\prime}} \right)}} = 1, \ldots , F\left( {h,h^{\prime}} \right) \).

\( \left( {zout} \right)_{fj}^{h} \) represents the intermediate products exiting division \( h \) and entering other divisions \( \left( {j = 1, \ldots ,n} \right) \). \( f = 1, \ldots ,F \).

\( \left( {zin} \right)_{{f^{\prime}j}}^{h} \) is considered as the intermediate products entering the \( h \)th division of the jth supply chain \( \left( {j = 1, \ldots ,n} \right) \). \( f^{\prime} = 1, \ldots ,F^{\prime} \).

In situations where DMUs cannot control the linking activities (nondiscretionary), then they are kept unchanged by applying fixed link case. On the other hand, when the linking activities are freely determined (discretionary) by the DMU, they are called free link cases. The continuity of link values between divisions is guaranteed in both free link and fixed link cases (Shamsijamkhaneh et al. 2018).

Here, the output-oriented network DEA (NDEA-R-O) model is proposed for evaluating the efficiency of a set of \( n \) DMUs based on Model (2). By contemplating the internal relationships among different divisions of a supply chain, Model (3) is proposed under the free link assumption (Tone and Tsutsui 2009).

$$ \theta^{*} = \hbox{Max} \mathop \sum \limits_{h = 1}^{k} w_{h} \theta_{h} $$
(3)
$$ s.t.\quad \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{h} \left( {\frac{{y_{rj}^{h} }}{{x_{ij}^{h} }}} \right) \ge \theta_{h} \left( {\frac{{y_{ro}^{h} }}{{x_{io}^{h} }}} \right),\quad i = 1, \ldots , m_{h} ,\quad r = 1, \ldots ,s_{h} $$
(3-1)
$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{h} \left( {\frac{{\left( {zout} \right)_{fj}^{h} }}{{x_{ij}^{h} }}} \right) \ge \theta_{h} \left( {\frac{{\left( {zout} \right)_{fo}^{h} }}{{x_{io}^{h} }}} \right),\quad i = 1, \ldots , m_{h} ,\quad f = 1, \ldots ,F, $$
(3-2)
$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{h} \left( {\frac{{y_{rj}^{h} }}{{\left( {zin} \right)_{{f^{\prime}j}}^{h} }}} \right) \ge \theta_{h} \left( {\frac{{y_{ro}^{h} }}{{\left( {zin} \right)_{{f^{\prime}o}}^{h} }}} \right),\quad r = 1, \ldots ,s_{h} ,\quad f^{\prime} = 1, \ldots ,F^{\prime}, $$
(3-3)
$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{h} \left( {\frac{{\left( {zout} \right)_{fj}^{h} }}{{\left( {zin} \right)_{{f^{\prime}j}}^{h} }}} \right) \ge \theta_{h} \left( {\frac{{\left( {zout} \right)_{fo}^{h} }}{{\left( {zin} \right)_{{f^{\prime}o}}^{h} }}} \right),\quad f = 1, \ldots ,F,\quad f^{\prime} = 1, \ldots ,F^{\prime}, $$
(3-4)
$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{h} z_{{f_{{\left( {h,h^{\prime}} \right)}} j}}^{{\left( {h,h^{\prime}} \right)}} = \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{{h^{\prime}}} z_{{f_{{\left( {h,h^{\prime}} \right)}} j}}^{{\left( {h,h^{\prime}} \right)}} ,\quad f_{{\left( {h,h^{\prime}} \right)}} = 1, \ldots , F\left( {h,h^{\prime}} \right), $$
(3-5)
$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{h} = 1,\;\;\theta_{h} \ge 1,\;\;\lambda_{j}^{h} \ge 0,\;\;h = 1, \ldots ,k,\quad j = 1, \ldots ,n. $$
(3-6)

Constraints (3-5) ensure that the links flow among divisions, then the shadow prices for the corresponding intermediate products are free (Shamsijamkhaneh et al. 2018).

To develop Model (3) under fixed link assumption, we can replace constraint (3-5) with constraint (3-7):

$$ \left\{ {\begin{array}{*{20}l} {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{h} z_{{f_{{\left( {h,h^{\prime}} \right)}} j}}^{{\left( {h,h^{\prime}} \right)}} = z_{{f_{{\left( {h,h^{\prime}} \right)}} o}}^{{\left( {h,h^{\prime}} \right)}} , f_{{\left( {h,h^{\prime}} \right)}} = 1, \ldots , F\left( {h,h^{\prime}} \right) , \forall \left( {h,h^{\prime}} \right) } \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{{h^{\prime}}} z_{{f_{{\left( {h,h^{\prime}} \right)}} j}}^{{\left( {h,h^{\prime}} \right)}} = z_{{f_{{\left( {h,h^{\prime}} \right)}} o}}^{{\left( {h,h^{\prime}} \right)}} , f_{{\left( {h,h^{\prime}} \right)}} = 1, \ldots , F\left( {h,h^{\prime}} \right)} \hfill \\ \end{array} } \right. $$
(3-7)

Clearly, the linking constraints in fixed link case are tighter than free link case. It means that feasible region for the model is bigger than that for the model with free links. Therefore, the overall efficiency score of DMUs under fixed link case are greater than or equal to the overall efficiency of DMUs under free link assumption.

Model (3) is linear, in which \( w_{h} \left( {h = 1, \ldots ,k} \right) \) is the weight of \( h \)th objective function related to the efficiency of division \( h \) in the supply chain under evaluation, and is determined by the decision-maker. Constraints (3-1)–(3-4) are the ratio of outputs to inputs for division \( h \) in the jth supply chain \( \left( {j = 1, \ldots ,n} \right) \).

Constraint (3-5) is related to the intermediate products; the right-hand side is the number of products sent from the \( h \)th division in the jth supply chain \( \left( {j = 1, \ldots ,n} \right) \), and left-hand side shows the number of products entered the division \( h^{\prime} \) in the jth supply chain \( \left( {j = 1, \ldots ,n} \right) \), this amount is both the input flow to division \( h^{\prime} \) and the output flow from division \( h \).

Constraint (3-6) corresponds with the productions of division \( h \) being sent to other divisions. Moreover, constraint (3-7) is related to the input flow of products sent from the \( h \)th division to division \( h^{\prime} \); these two values are the same. These two constraints demonstrate that the number of intermediate products for the DMU under evaluation equals a convex combination of intermediate products of all the other DMUs. In conclusion, constraints (3-5), (3-6), (3-7) reveal the interdependencies between different divisions of the supply chain in free and fixed link situations. Therefore, any of them can be used to obtain the overall efficiency of DMUs based on the decision-maker’s preferences.

The dual of Model (3) is as Model (4):

Case 1:

under free link assumption

$$ \gamma^{*} = \mathop {\hbox{Min} }\limits_{{}} \mathop \sum \limits_{h = 1}^{k} \gamma^{h} $$
$$ \begin{aligned} & s.t.\quad \mathop \sum \limits_{r = 1}^{{s_{h} }} \mathop \sum \limits_{i = 1}^{{m_{h} }} w_{ri}^{h} \left( {\frac{{\frac{{y_{rj}^{h} }}{{x_{ij}^{h} }}}}{{\frac{{y_{ro}^{h} }}{{x_{io}^{h} }}}}} \right) + \mathop \sum \limits_{f = 1}^{F} \mathop \sum \limits_{i = 1}^{{m_{h} }} v_{fi}^{h} \left( {\frac{{\frac{{\left( {zout} \right)_{fj}^{h} }}{{x_{ij}^{h} }}}}{{\frac{{\left( {zout} \right)_{fo}^{h} }}{{x_{io}^{h} }}}}} \right) \\ & + \mathop \sum \limits_{r = 1}^{{s_{h} }} \mathop \sum \limits_{{f^{\prime} = 1}}^{{F^{\prime}}} u_{{rf^{\prime}}}^{h} \left( {\frac{{\frac{{y_{rj}^{h} }}{{\left( {zin} \right)_{{f^{\prime}j}}^{h} }}}}{{\frac{{y_{ro}^{h} }}{{\left( {zin} \right)_{{f^{\prime}o}}^{h} }}}}} \right) + \mathop \sum \limits_{f = 1}^{F} \mathop \sum \limits_{{f^{\prime} = 1}}^{{F^{\prime}}} \mu_{{ff^{\prime}}}^{h} \left( {\frac{{\frac{{\left( {zout} \right)_{fj}^{h} }}{{\left( {zin} \right)_{{f^{\prime}j}}^{h} }}}}{{\frac{{\left( {zout} \right)_{fo}^{h} }}{{\left( {zin} \right)_{{f^{\prime}o}}^{h} }}}}} \right) \\ & + \mathop \sum \limits_{{f_{{\left( {h,h^{\prime}} \right)}} }}^{{F_{{\left( {h,h^{\prime}} \right)}} }} \rho_{{f_{{\left( {h,h^{\prime}} \right)}} }} z_{{f_{{\left( {h,h^{\prime}} \right)}} j}}^{{\left( {h,h^{\prime}} \right)}} \le \gamma^{h} ,\quad h = 1, \ldots ,k,\quad j = 1, \ldots ,n, \\ & \mathop \sum \limits_{r = 1}^{{s_{h} }} \mathop \sum \limits_{i = 1}^{{m_{h} }} w_{ri}^{h} + \mathop \sum \limits_{f = 1}^{F} \mathop \sum \limits_{i = 1}^{{m_{h} }} v_{fi}^{h} + \mathop \sum \limits_{r = 1}^{{s_{h} }} \mathop \sum \limits_{{f^{\prime} = 1}}^{{F^{\prime}}} u_{{rf^{\prime}}}^{h} \\ & \quad + \mathop \sum \limits_{f = 1}^{F} \mathop \sum \limits_{{f^{\prime} = 1}}^{{F^{\prime}}} \mu_{{ff^{\prime}}}^{h} = w^{h} ,\quad w_{ri}^{h} \ge 0,\quad i = 1, \ldots , m_{h} ,\quad r = 1, \ldots ,s_{h} , \\ & v_{fi}^{h} \ge 0,\,i = 1, \ldots , m_{h} ,\,f = 1, \ldots ,F,\, u_{{rf^{\prime}}}^{h} \ge 0,\,r = 1, \ldots ,s_{h} ,\, f^{\prime} = 1, \ldots ,F^{\prime} \\ & \mu_{{ff^{\prime}}}^{h} \ge 0,\,\,f = 1, \ldots ,F,\,\,f^{\prime} = 1, \ldots ,F^{\prime},\,\,\rho_{{f_{{\left( {h,h^{\prime}} \right)}} }} \,\,{\text{is}}\;{\text{free}}\;{\text{in}}\;{\text{sign}} .\\ \end{aligned} $$
(4)

This model can easily be extended to fixed link situation by replacing (4-1) with the objective function of model (4).

Case 2

Under fixed link assumption

$$ \mathop {\gamma^{*} = \hbox{Min} }\limits_{{}} \mathop \sum \limits_{h = 1}^{k} \gamma^{h} + \mathop \sum \limits_{{f_{{\left( {h,h^{\prime}} \right)}} = 1}}^{{F\left( {h,h^{\prime}} \right)}} \rho_{{f_{{\left( {h,h^{\prime}} \right)}} }} z_{{f_{{\left( {h,h^{\prime}} \right)}} o}}^{{\left( {h,h^{\prime}} \right)}} $$
(4-1)

Definition 1

\( {\text{DMU}}_{\text{j}} \) is considered NDEA-R-O efficient when \( \theta_{j}^{*} = 1 \).

Definition 2

Division h is considered NDEA-R-O efficient when \( \theta_{h}^{*} = 1 \).

Note: \( {\text{DMU}}_{\text{j}} \) will not be NDEA-R-O efficient unless all its corresponding divisions are efficient.

4 Case study

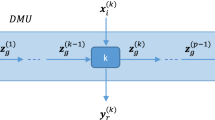
The supply chains considered in this study consist of 19 public hospitals in Fars province of Iran, evaluated during July–August 2016. These hospitals provide medical services to patients. Due to the similar structure of the hospitals, they are considered as the patient service supply chains. Each supply chain consists of 5 divisions, including medicine, nutrition, laboratory, pharmacy and radiology, as illustrated in Fig. 2.

Fig. 2
figure 2

The supply chain structure

Full size image

The first division is the hospital’s medical ward; all patients initially enter this division and either get directly treated there and leave the hospital or get referred to the other divisions. The medical division consists of the emergency room, the internal ward and the clinic. Patients are hospitalized in the internal ward and visit the clinic with previous appointments to be examined and treated by specialist doctors. The emergency room admits and treats patients without previous appointments. In this study, the number of all patients admitted during the research period is considered as the input for the medical division. The output of this division is the hospital’s revenue including the income from the emergency room, the internal ward and clinic, which is either paid directly by the patients or received from insurance companies after subtracting tax. This income is called the gross revenue of the medical division.

The second division is the hospital kitchen. Expenses are the only input for this division, including the costs of ingredients, installations and personnel salary; the only output is revenue which directly received from patients for the meals sold.

The hospital’s third division is the laboratory facilities. In this division, expenses are the only input, including the costs related to lab equipment, raw materials and personnel salary. The output includes earnings received from patients or insurance companies after tax deductions.

The fourth division is the pharmacy, with expenses as its input which includes the cost of drug purchases, facilities and personnel salary. The outputs of this division are income received either from patients for medication or from insurance companies for prescriptions after tax deductions.

The radiology unit is the hospital’s fifth division. In this division, input expenses are related to raw materials, installations and personnel salary while the output includes earnings received from patients and insurance companies after tax deductions.

Intermediate measures (products) include the number of patients being referred to nutritional, laboratory, pharmacy and radiology divisions from the medical division. All the parameters used in Model (3) for hospital evaluation are as follows:

\( x_{1j}^{1} \)::

Number of all patients admitted to jth hospital.

\( y_{1j}^{1} \)::

Revenue earned in the medical division (ER, internal ward & clinic) of jth hospital.

\( x_{1j}^{2} \)::

Expenses of the nutritional division in jth hospital.

\( y_{1j}^{2} \)::

Revenue of the nutritional division in jth hospital.

\( x_{1j}^{3} \)::

Expenses of the laboratory facilities in jth hospital.

\( y_{1j}^{3} \)::

Revenue of the laboratory facilities in jth hospital.

\( x_{1j}^{4} \)::

Expenses of the pharmacy division in jth hospital.

\( y_{1j}^{4} \)::

Revenue of the pharmacy division in jth hospital.

\( x_{1j}^{5} \)::

Expenses of the radiology division in jth hospital.

\( y_{1j}^{5} \)::

Revenue of the radiology division in jth hospital.

All revenues and expenses are presented as total revenues and total expenses of the period under study.

\( \left( {Zout} \right)_{fj}^{1} \)::

Number of all patients referred from the medical division of jth hospital to other divisions during the period under study,\( f = 1, 2, 3, 4. \)

\( \left( {zin} \right)_{{f^{\prime}j}}^{{h_{s} }} \)::

Number of patients entering the \( h_{s} \)th division of jth hospital, \( f^{\prime} = 1 \), \( h_{s} = 2,3,4,5 \).

\( Z_{{f\left( {h,h^{\prime}} \right)j}}^{{\left( {h,h^{\prime}} \right)}} \)::

Number of patients transferred from the \( h \)th division of jth hospital to its \( h^{\prime} \)th division during the period under study, \( h = 1 \), \( h^{\prime} = 2,3,4,5 \), \( f_{{\left( {1,h^{\prime}} \right)}} = F_{{\left( {1,h^{\prime}} \right)}} = 1 \).

Note that in this research, patients are only referred from the medical division to the other divisions for services.

\( {\raise0.7ex\hbox{${Z_{1j}^{{\left( {1,h^{\prime}} \right)}} }$} \!\mathord{\left/ {\vphantom {{Z_{1j}^{{\left( {1,h^{\prime}} \right)}} } {x_{1j}^{1} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${x_{1j}^{1} }$}} \)::

Ratio of patients entering division \( h^{\prime} \) from the first division of hospital \( j \) to all patients visiting the hospital during the period under study, \( h^{\prime} = 2,3,4,5. \)

\( \frac{{y_{ij}^{1} }}{{x_{ij} }} \)::

Ratio of the revenue earned in the medical division of jth hospital to all patients entering the hospital for serviced during the period under study.

\( \frac{{y_{ij}^{hs} }}{{x_{ij}^{hs} }} \)::

Ratio of the revenue earned in \( h_{s} \)th division of the jth hospital to all expenses related to this division, \( h_{s} = 2,3,4,5 \).

\( \frac{{y_{1j}^{{h_{s} }} }}{{\left( {zin} \right)_{1j}^{{h_{s} }} }} \)::

Ratio of the revenue earned in \( h_{s} \)th division of the jth hospital to all patients entering this division for services during the period under study, \( h_{s} = 2,3,4,5. \)

\( \frac{{\left( {Zout} \right)_{fj}^{1} }}{{x_{1j}^{1} }} \):

Ratio of all patients exiting the medical division of jth hospital and entering the \( f \)th division for services during the period under study, \( f = 2, 3, 4, 5 \).

All divisions have only one input and one output, and the intermediate measure is the number of patients being referred from the medical division to other divisions. \( j = 1, \ldots ,19 \), \( s_{h} = 1 \), \( m_{h} = 1 \), \( h = 1, 2, 3, 4, 5 \), \( f = F = f^{\prime} = F^{\prime} = 1 \). Data are shown in Tables 1 and 2.

Table 1 Dataset
Full size table
Table 2 Efficiency scores of the supply chains
Full size table

Considering the ratio data and the fact that those ratios matter to hospital administrations, output-oriented DEA-R models are implemented in this study. There are a variety of methods for selecting the weight of objective functions in multi-objective linear programming (MOLP) context (Torabi and Hassini 2009). In order to solve model (3), we initially select the same weights for the importance of all objective functions. Then, the initial vector is \( w_{0} \) = (0.2, 0.2, 0.2, 0.2, 0.2). Each objective function provides the efficiency score for a division and overall efficiency is defined as a weighted sum of divisional efficiency scores in a hospital. Overall and divisional efficiencies are obtained by Model (2) under two assumptions of free link and fixed link. Table 3 presents the overall and divisional efficiencies in the free and fixed link situations.

Table 3 Efficiency scores of the supply chains under the free link assumption
Full size table

Findings show that only DMU-14 is DEA-R efficient, as all divisions of this DMU are efficient. All the other units are inefficient. For example, although 4 out of 5 divisions of DMU-9 are efficient, this DMU is called an inefficient unit.

Figure 3 depicts the efficiency scores of 19 DMUs under free and fixed link assumptions for the weight vector \( w_{0} \). Figure 3 illustrates that overall efficiency score of all DMUs under the fixed link situation is greater than or equal to their efficiency score under the free link situation.

Fig. 3
figure 3

Overall efficiency scores with \( w_{0} \) = (0.2, 0.2, 0.2, 0.2, 0.2)

Full size image

Figures 4, 5, 6, 7 and 8 illustrate the comparison of divisional efficiency scores under the fixed and free link assumptions for the weight vector \( w_{0} \). Similarly, for all divisions, the efficiency score obtained by Model (3) under the fixed link assumption is greater than or equal to its corresponding scores under the free link assumption.

Fig. 4
figure 4

Efficiency scores for division 1 with \( {\text{w}}_{0} \) = (0.2, 0.2, 0.2, 0.2, 0.2)

Full size image
Fig. 5
figure 5

Efficiency scores for division 2 with \( {\text{w}}_{0} \) = (0.2, 0.2, 0.2, 0.2, 0.2)

Full size image
Fig. 6
figure 6

Efficiency scores for division 3 with \( {\text{w}}_{0} \) = (0.2, 0.2, 0.2, 0.2, 0.2)

Full size image
Fig. 7
figure 7

Efficiency scores for division 4 with \( {\text{w}}_{0} \) = (0.2, 0.2, 0.2, 0.2, 0.2)

Full size image
Fig. 8
figure 8

Efficiency scores for division 5 with \( {\text{w}}_{0} \) = (0.2, 0.2, 0.2, 0.2, 0.2)

Full size image

4.1 Sensitivity analysis

Sensitivity analysis is undertaken in order to realize the effect of change in weight vector on the overall and divisional efficiency of DMUs. Tables 5 and 6 present the results for the overall and divisional efficiency under the free link assumption using arbitrary weight vectors \( w_{1} , w_{2} , w_{3} \) where: \( w_{1} = \left( {0.4, 0.1, 0.2, 0.2, 0.1} \right) \), \( w_{2} = \left( {0.5, 0.1, 0.15, 0.15, 0.1} \right) \), \( w_{3} = \left( {0.5, 0.125, 0.125, 0.125, 0.125} \right) \).

It is evident that the overall efficiency score of DMUs with weight vector \( w_{3} \) is greater than or equal to that of all DMUs with weight vectors \( w_{1} \) and \( w_{2} \). Table 4 presents efficiency scores of all hospitals and their divisions under fixed link assumption. These efficiency values are obtained with weight vectors \( w_{1} , w_{2} \), and \( w_{3} \).

Table 4 Efficiency scores of the supply chains under the fixed link assumption
Full size table

It is clear that for all DMUs, efficiency scores obtained with weight vector \( w_{3} \) are greater than or equal to their corresponding scores obtained with \( w_{1} \) and \( w_{2} \). Since the revenue is the only output in all divisions of the hospitals, the proposed models (3) and (4) are all output-oriented. On the other hand, a hospital’s revenue mainly comes from the medical division which is the most important division in all hospitals. Therefore, increasing the importance of the objective function for this division in Model (3) will increase the hospital’s overall efficiency. Because the first objective function (the medical division) has higher importance in the weight vector \( w_{3} \) compared to \( w_{1} \) and \( w_{2} \), then it leads to higher efficiency score of DMUs.

As another case, assume the weight vector \( w_{4} = \left( {0.1, 0.1, 0.3, 0.3, 0.2} \right) \) in which first objective function (the medical division) has lower importance weight compared to the 3rd, 4th and 5th divisions. Table 5 presents the efficiency scores calculated by the weight vector \( w_{4} \) under free and fixed link assumptions, respectively.

Table 5 Efficiency score of the supply chains under the free link assumption with \( w_{4} \)
Full size table

Furthermore, Figs. 9 and 10 compare the overall efficiency score of DMUs obtained by Model (3) using weight vectors \( w_{0} \) and \( w_{4} \) under free and fixed link assumptions, respectively. In this case, all efficiency scores related to the weight vector \( w_{0} \) are greater than or equal to the scores related to \( w_{4} \). This result can also be attributed to the high importance weight of the revenue.

Fig. 9
figure 9

Overall efficiency score of supply chains with weight vectors \( w_{0} \) and \( w_{4} \) under the free link assumption

Full size image
Fig. 10
figure 10

Overall efficiency score of supply chains with weight vectors \( w_{0} \) and \( w_{4} \) under the fixed link assumption

Full size image

Table 2 shows that DMU 14 is the only efficient DMU out of 19 DMUs under the free link assumption. On the other hand, DMU 14 is the only efficient DMU under the fixed link assumption. In addition to its overall efficiency which is unity, the efficiencies of all five divisions are unity. Table 2 also pinpoints that the overall efficiency of DMUs and the efficiency of each division under the fixed link assumption are greater than or equal to those under the free link assumption. Mathematically, since the feasible region of the proposed model under the fixed link assumption is bigger than the feasible region under the free link assumption, the overall efficiency scores of DMUs under the fixed link case are greater than or equal to the overall efficiency of DMUs under the free link assumption. This is the case for the divisional efficiencies as well.

To validate the proposed model, findings are compared with the results obtained by Model (5). Model (5) is the output-oriented network data envelopment analysis (NDEA-O) model. This model extends the study of Tone and Tsutsui (2009) by considering the internal relationships among different divisions of a supply chain under free link and fixed link assumptions.

$$ \theta^{*} = \mathop {\hbox{Max} }\limits_{{}} \mathop \sum \limits_{h = 1}^{k} w_{h} \theta_{h} $$
(5)
$$ s.t.\quad \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{h} x_{ij}^{h} \le x_{io}^{h} ,\quad i = 1, \ldots , m_{h} ,\quad h = 1, \ldots ,k, $$
(5-1)
$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{h} y_{rj}^{h} \ge \theta_{h} y_{ro}^{h} ,\quad r = 1, \ldots ,s_{h} ,\quad h = 1, \ldots ,k $$
(5-2)
$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{h} z_{{f_{{\left( {h,h^{\prime}} \right)}} j}}^{{\left( {h,h^{\prime}} \right)}} = \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{{h^{\prime}}} z_{{f_{{\left( {h,h^{\prime}} \right)}} j}}^{{\left( {h,h^{\prime}} \right)}} ,\quad f_{{\left( {h,h^{\prime}} \right)}} = 1, \ldots , F\left( {h,h^{\prime}} \right)\quad \left( {{\text{free}}\;\;{\text{link}}} \right) $$
(5-3)
$$ \left\{ \begin{aligned} \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{h} z_{{f_{{\left( {h,h^{\prime}} \right)}} j}}^{{\left( {h,h^{\prime}} \right)}} = z_{{f_{{\left( {h,h^{\prime}} \right)}} o}}^{{\left( {h,h^{\prime}} \right)}} , f_{{\left( {h,h^{\prime}} \right)}} = 1, \ldots , F\left( {h,h^{\prime}} \right) , \forall \left( {h,h^{\prime}} \right) \hfill \\ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{{h^{\prime}}} z_{{f_{{\left( {h,h^{\prime}} \right)}} j}}^{{\left( {h,h^{\prime}} \right)}} = z_{{f_{{\left( {h,h^{\prime}} \right)}} o}}^{{\left( {h,h^{\prime}} \right)}} , f_{{\left( {h,h^{\prime}} \right)}} = 1, \ldots , F\left( {h,h^{\prime}} \right) \, \left( {\text{fixed link}} \right) \hfill \\ \end{aligned} \right. $$
(5-4)
$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{h} = 1,\;\theta_{h} \ge 1,\lambda_{j}^{h} \ge 0,\quad h = 1, \ldots ,k,\quad j = 1, \ldots ,n $$
(5-5)

The efficiency scores of 19 hospital supply chains are calculated using Model (5) and the results are shown in Table 6.

Table 6 The efficiency score of the supply chains under the free link assumption [obtained by Model (5)]
Full size table

Assuming the free link, the overall efficiency score of DMUs obtained by proposed NDEA-R-O Model (3) are greater than or equal to the corresponding scores obtained by NDEA-O Model (5). The average overall efficiency of DMUs by Model (5) and Model (3) are 0.707 and 0.827, respectively. This suggests that the proposed NDEA-R-O model calculates higher efficiency scores for DMUs compared to the NDEA-O model provided by Tone and Tsutsui (2009). Therefore, contrary to the traditional models, the proposed model prevents the problems of underestimation of efficiency and pseudo-inefficiency. With the same analysis, the proposed NDEA-R-O model provides greater or equal efficiency score for DMUs under the fixed link assumption. In this case, the average overall efficiency of DMUs obtained from Model (5) and Model (3) are 0.751 and 0.870, respectively.

Although the average efficiency of DMUs obtained from the proposed models is greater than or equal to Model (5), this might not be true for all divisions. For example, the average efficiency of division 3 calculated by the proposed model under the free link assumption is 0.917 which is greater than the average efficiency of division 3 obtained from Model (5), i.e. 0.757. At the same time, the proposed model has not provided a greater average for division 3 in the case of the fixed link (0.938 vs. 0.941). Given the merits of the proposed NDEA-R-O models in preventing the pseudo-inefficiency, they are a good alternative to the previous NDEA-O models.

In this research, a sensitivity analysis was performed to investigate the effect of changes in the importance of objective functions on the overall and divisional efficiency of DMUs. As mentioned earlier, the proposed model can take into account the preferences of managers in efficiency evaluation. The case study showed that when the importance of division 1 is increased, the overall efficiency is increased as division 1 is the most important one in a hospital supply chain. Since the proposed model has the output orientation, therefore, the divisions with more important outputs have a higher impact on the overall efficiency of the supply chains.

4.2 Managerial implications

Healthcare supply chain management is different from industrial supply chain management because it includes physical products such as drugs, pharmaceuticals and medical devices and tools, on the other hand, the flow of patients between departments, communication, allocation of the medical team (e.g. doctors and nurses). Since HSC and healthcare providers are on the front line of providing health services to people, the efficiency and effectiveness of HSC operations are significant. Life and death of patients depend on the continuous and uninterrupted supply of medical services and medical products such as pharmaceutical products. Therefore, hospitals are required to guarantee 100% product availability at the right time, at the right cost, in good condition to right patients. Clearly, the pharmaceutical department will incur higher costs because of their responsibility, which adds to the total cost of that hospital.

Institutions such as hotels and hospitals play a major role in the food system because of their high power to procure food and ingredients, usage of resources, and waste generation. Food systems in addition to providing nutrients to the patients are important in achieving sustainable development goals because they add to the environmental challenges by producing food wastage. Hence, efficient management of the kitchen department of the hospitals provides healthy diets, cuts the food-related costs, reduces food wastage, and contributes to environmental sustainability. Therefore, improving the performance of this division can improve the performance of the whole system.

Since HSC is a high-cost industry in which the cost of labour and medical supplies are the top two cost factors (Kwon et al. 2016), hospitals need a sophisticated planning and forecasting systems to minimize their cost. Furthermore, the efficiency of a healthcare supply chain can reduce 2–8% of operating costs of hospitals (Haavik 2000) and offer a high level of customer service by promoting the loyalty of medical staffs, which leads to the improvement in revenues of the hospital (Storey et al. 2006). Performance evaluation to improve the operational efficiency of the hospitals lead to lean and agile healthcare practices. On the other hand, effective management of hospital operations will positively influence disaster management, for example, managing the supply of blood for critical situations. Therefore, evaluating the performance of hospitals enables them to benchmark best practices to improve their technical efficiency in order to provide better services to the public.

5 Conclusions

Performance evaluation is of great importance for any supply chain especially for the hospital supply chains which provide health and safety services in an interconnected network of divisions. The existing NDEA models suffer from the underestimated efficiency. To overcome this problem, we developed a ratio-based NDEA-R-O model for measuring the efficiency of supply chains under the free link and fixed link assumptions. The proposed model prevents the pseudo-inefficiency problem of the traditional DEA models. Our research prevents the underestimation of efficiency by decreasing unnecessary and unreasonable weights of inputs/outputs and by providing a realistic weight vector. Since stakeholders may have conflicting interests and different objectives for efficiency analysis, the proposed model is able to get the decision-makers’ preferences on the weight of objective functions. Therefore, managers and policy-makers can be involved in the performance evaluation process to achieve optimal results. Using the hospital supply chain as the case study, we found that the medical division, which is the biggest source of income in hospitals, has the highest impact on the overall efficiency score of DMUs. The proposed model can present the optimal ratio of revenues to the expense and the optimal ratio of revenues to the number of admitted patients for each hospital in all divisions.

Future studies can be devoted to developing NDEA-R models under variable returns to scale assumption. In some cases, data of inputs and outputs of a supply chain are uncertain or imprecise. Therefore, future research can consider extending the proposed model with fuzzy and interval data.