Abstract
As a result of its liberalization, the European gas market is organized as an entry-exit system in order to decouple the trading and transport of natural gas. Roughly summarized, the gas market organization consists of four subsequent stages. First, the transmission system operator (TSO) is obliged to allocate so-called maximal technical capacities for the nodes of the network. Second, the TSO and the gas traders sign mid- to long-term capacity-right contracts, where the capacity is bounded above by the allocated technical capacities. These contracts are called bookings. Third, on a day-ahead basis, gas traders can nominate the amount of gas that they inject or withdraw from the network at entry and exit nodes, where the nominated amount is bounded above by the respective booking. Fourth and finally, the TSO has to operate the network such that the nominated amounts of gas can be transported. By signing the booking contract, the TSO guarantees that all possibly resulting nominations can indeed be transported. Consequently, maximal technical capacities have to satisfy that all nominations that comply with these technical capacities can be transported through the network. This leads to a highly challenging mathematical optimization problem. We consider the specific instantiations of this problem in which we assume capacitated linear as well as potential-based flow models. In this contribution, we formally introduce the problem of Computing Technical Capacities (CTC) and prove that it is NP-complete on trees and NP-hard in general. To this end, we first reduce the Subset Sum problem to CTC for the case of capacitated linear flows in trees. Afterward, we extend this result to CTC with potential-based flows and show that this problem is also NP-complete on trees by reducing it to the case of capacitated linear flow. Since the hardness results are obtained for the easiest case, i.e., on tree-shaped networks with capacitated linear as well as potential-based flows, this implies the hardness of CTC for more general graph classes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The European gas market is organized as a so-called entry-exit market system, which has been the outcome of the European gas market liberalization; see Directive (1998, (2009, (2003). The main goal of the entry-exit system is to decouple the trading and transport of gas. The current market organization that should achieve this goal is mainly split into different stages in which the transmission system operator (TSO) and the gas traders interact with each other. First, the TSO is obliged to allocate so-called maximal technical capacities at all nodes of the network at which gas can be injected or withdrawn. After determining the maximal technical capacities, the TSO and the gas traders sign mid- to long-term capacity-right contracts, called bookings, in which the traders buy rights for the maximal injection or withdrawal at certain entry and exit nodes of the network. In doing so, the maximal bookable capacities are bounded from above by the maximal technical capacities. These mid- to long-term booking contracts bound the amounts of gas that traders can nominate on a day-ahead market. On this day-ahead basis, the traders nominate the amount of gas that they inject or withdraw on the next day while the nominated amount of gas is bounded above by the beforehand determined bookings. Finally, the TSO has to operate the network such that the nominated amount of gas is transported as requested. By signing the booking contract, the TSO has to guarantee the feasibility of transport for every booking-compliant nomination, i.e., every nomination below the booked capacity. Since the gas traders can sign any booking below the maximal technical capacities, the TSO has to guarantee that all technical-capacities-compliant nominations, i.e., infinitely many flow situations, can be transported through the network. Thus, computing maximal technical capacities in the European gas market leads to a challenging mathematical problem. A mathematical model of the European entry-exit gas market system that models the described market organization has been developed in Grimm et al. (2019). The model is a four-level model and it is shown that, under suitable assumptions, it can be reformulated as an equivalent bilevel model. Here, we focus on the first stage where the maximal technical capacities need to be computed. For doing so, we consider passive networks, i.e., no controllable network devices like valves or compressors exist. We further focus on stationary models of gas transport with capacitated linear flow models as well as on potential-based flows as used in, e.g., Schewe et al. (2020), Groß et al. (2019). One of the main differences between capacitated linear flows and the more accurate potential-based flow models is that, in the latter, no cyclic flows are possible. On the one hand, this provides additional structure that can be exploited for analyzing the feasibility of nominations and bookings as well as the maximization of technical capacities. However, on the other hand, the coupling between node potentials and arc flows usually is nonlinear and thus, leads to a harder class of optimization problems.
Mathematical optimization methods for gas transport networks have been studied with great interest in the last decades. For a comprehensive overview of this field see, e.g., the book (Koch et al. 2015) and the survey article (Ríos-Mercado and Borraz-Sánchez 2015) as well as the references therein. Most of the literature focuses on checking the feasibility of a single nomination as well as its transport through the network. In Bakhouya and De Wolf (2007) and De Wolf and Smeers (2000), the cost-optimal gas transport in the Belgian network before and after the European market liberalization is discussed. In these papers, the gas physics is approximated by piecewise-linear functions, leading to mixed-integer linear programs (MILPs). Alternative approaches that are also based on MILP techniques can be found in Geißler (2011), Geißler et al. (2013), Martin et al. (2006). Further, purely continuous and physically accurate nonlinear optimization models are, e.g., studied in Schmidt et al. (2015a, (2015b, (2016). Even more sophisticated nonlinear mixed-integer models are considered, e.g., in Geißler et al. (2015, (2018), Humpola (2017). Checking the feasibility of a nomination considering a capacitated linear flow model is in P, since the task can be modeled as a linear program. Additionally, the same holds in case of potential-based networks; see Collins et al. (1978), Maugis (1977). In case of networks with active elements, deciding the feasibility of a nomination is NP-hard for the potential-based flow model; see Szabó (2012).
In contrast to the rich literature on nominations, there is much less published research on the feasibility of bookings. Deciding the feasibility of a given booking consists of checking the feasibility of all booking-compliant nominations, i.e., of all infinitely many nominations within the given booking bounds. Thus, this problem can also be seen as a two-stage or adjustable robust optimization problem, see, e.g., Ben-Tal and El Ghaoui (2009), where the uncertainty set is given by the booking-compliant nominations. First results about the mathematical analysis of bookings are obtained in the PhD theses (Hayn 2016; Willert 2014). Moreover, the reservation-allocation problem studied in Fügenschuh et al. (2014) is also related to the feasibility of bookings. Considering the robust side, a set containment approach to decide the robust feasibility and infeasibility of bookings with an application to the Greek gas transport network is studied in Aßmann et al. (2018). In general, structural properties such as (non-)convexity and star-shapedness of the set of feasible nominations and bookings for different gas transport models are considered in Schewe et al. (2020). For networks consisting of pipes only together with potential-based flows, the feasibility of bookings can be characterized by conditions on nominations with maximal potential difference; see Labbé et al. (2020). Further, there it is shown that in case of a linear potential-based flow model, this characterization enables us to check the feasibility of a booking in polynomial time. Additionally, this is also possible in case of nonlinear potential-based flows in tree-shaped networks; see Labbé et al. (2020), Robinius et al. (2019). Using special structures of the nomination with maximal potential difference together with techniques from real algebraic geometry enables the authors of Labbé et al. (2019) to show that checking the feasibility of a booking in a single cycle network is in P. For the general case, i.e., a nonlinear potential-based flow model on arbitrary networks, the complexity of checking the feasibility of a booking is not yet decided and an open question for research. In the linear case, deciding the feasibility of a booking is shown to be in coNP in Labbé et al. (2020), Hayn (2016). For the case of a capacitated linear flow model, checking the feasibility of a booking is coNP-complete for cyclic networks, but it can be solved in polynomial time for trees; see Hayn (2016). An illustrative overview about the computational complexity of checking the feasibility of a booking is given in Section 6 of Labbé et al. (2020).
For computing maximal technical capacities as introduced in, e.g., Martin et al. (2011), there is much less in the literature compared to the results for nominations and even less compared to the feasibility of bookings. First results about technical capacities are again obtained in the PhD theses Willert (2014), Hayn (2016). Further, for the case of a capacitated linear flow model, exponential upper bounds for computing technical capacities are given in Hayn (2016).
Our contribution is the following. We prove that computing maximal technical capacities is NP-complete for capacitated linear flows as well as potential-based flow models even in tree-shaped networks. The proof is obtained by reducing the Subset Sum problem to computing maximal technical capacities for capacitated linear flows on trees. Afterward, we reduce computing maximal technical capacities with potential-based flows to the case of capacitated linear flows. Consequently, computing maximal technical capacities is significantly harder than checking the feasibility of bookings, since the latter can be done in polynomial time on trees. Note that our complexity results are obtained on trees. Thus, computing technical capacities remains hard on more complex graph classes like on general graphs. We summarize our contribution, together with a review of the results from the literature, in Table 1.
The remainder of this paper is structured as follows. In Sect. 2, the problem of computing maximal technical capacities is formally defined. The NP -completeness of computing maximal technical capacities for capacitated linear flow models on trees is shown in Sect. 3. Afterward, in Sect. 4 we extend this result by showing that this problem is also NP-complete for potential-based instead of capacitated linear flows. Finally, we close with a conclusion in Sect. 5.
2 Problem description
In general, our problem description follows the one in Labbé et al. (2019). We consider a directed and connected graph \(G=(V,A)\) with nodes \(V\) and arcs \(A\). The set of nodes is partitioned into the set \(V_{+}\) of entry nodes, at which gas is supplied, the set \(V_{-}\) of exit nodes, where gas is withdrawn, and the set \(V_{0}\) of the remaining inner nodes. We abbreviate the set \(V_{+}\cup V_{-}\) by \(V_{\mathrm{b}}\). The node types are also encoded in a vector \(\sigma =(\sigma _u)_{u\in V}\) defined by
We now introduce basic definitions that we use in the following.
Definition 2.1
A load flow is a vector \(\ell =(\ell _u)_{u\in V} \in \mathbb {R}_{\ge 0}^{V}\), with \(\ell _u=0\) for all \(u\in V_{0}\). The set of load flow vectors is denoted by \(L\).
A load flow thus corresponds to an actual situation at a single point in time by specifying the amount of gas that is supplied (\(\ell _u\) for \(u\in V_{+}\)) or withdrawn (\(\ell _u\) for \(u\in V_{-}\)). Since we only consider stationary flows, we need to impose that the supplied amount of gas equals the withdrawn amount, which leads to the definition of a nomination.
Definition 2.2
A nomination is a balanced load flow \(\ell \), i.e., \(\sigma ^\top \ell = 0\). The set of nominations is given by \(N{:}{=}\{\ell \in L:\sigma ^\top \ell = 0\}\).
Nominations and bookings are connected as follows.
Definition 2.3
A booking is a vector \(b=(b_u)_{u\in V} \in \mathbb {R}_{\ge 0}^{V}\), with \(b_u=0\) for all \(u\in V_{0}\). A nomination \(\ell \) is called booking-compliant w.r.t. the booking \(b\) if \(\ell \le b\) holds, where “\(\le \)” is meant component-wise. The set of booking-compliant (or \(b\)-compliant) nominations is given by \(N(b) {:}{=}\{\ell \in N:\ell \le b\}\).
Obviously, \(N(b) \subseteq N\subseteq L\) holds for finite \(b\).
We now define feasible nominations and feasible bookings, where “feasible” is meant w.r.t. technical, physical, and legal constraints of gas transport. To this end, let \(c_{\varepsilon }(x;\ell ) = 0\) and \(c_{\mathcal {I}}(x;\ell ) \ge 0\) be the possibly nonlinear, nonconvex, and nonsmooth constraints that model the full problem of gas transport.
Definition 2.4
A nomination \(\ell \in N\) is feasible if a vector \(x\in \mathbb {R}^n\) exists such that
holds. The set of feasible nominations is denoted by \(F_{N}\).
We note that the set of feasible nominations \(F_{N}\) depends on the chosen model of gas transport. The only constraint that we need in all formulations is mass conservation at each node of the network, i.e.,
where \(q _{u} \ge 0\) for entries, \(q _{u} \le 0\) for exits, and \(q _{u} = 0\) for inner nodes.
The dependence of the feasible set defined in (1) on the nomination is given by a fixation of the entry and exit flows according to the nomination \(\ell \), i.e.,
These constraints are part of \(c_{\varepsilon }(x;\ell ) = 0\) in (1).
For a nomination \(\ell \in N\), we say that \(q \in \mathbb {R} ^A\) is an \(\ell \)-flow if and only if \(q \) satisfies Condition (2). We note that to check whether a given nomination is feasible may lead to a nonlinearand nonconvex problem depending on the constraints \(c_{\varepsilon }\) and \(c_{\mathcal {I}}\). For more information on this problem, see, e.g., Koch et al. (2015), Pfetsch et al. (2015) and the references therein.
Definition 2.5
We say that a booking \(b\) is feasible if all booking-compliant nominations \(\ell \in N(b)\) are feasible. The set of feasible bookings is denoted by \(F_{B}\).
Due to the liberalization of the European gas market, trading and transport are decoupled. This is mainly ensured by the so-called technical capacities. The TSO is obliged to allocate such capacities while guaranteeing the feasibility of transport for any balanced injections at entry nodes and withdrawals at exit nodes within these capacities.
Definition 2.6
Technical capacities are a vector \(q^{{\text {C}}}= (q^{{\text {C}}}_u)_{u\in V} \in \mathbb {R}_{\ge 0}^{V}\) with \(q^{{\text {C}}}_u= 0\) for \(u\in V_{0}\). The set of technical capacities is denoted by \(C\).
We note that technical capacities \(q^{{\text {C}}}\) can also be seen as a booking.
Definition 2.7
We say that technical capacities \(q^{{\text {C}}}\) are feasible if all bookings \(b\in B\) with \(b\le q^{{\text {C}}}\) are feasible. The set of feasible technical capacities is denoted by \(F_{{\text {C}}}\).
From the previous definitions it follows that given technical capacities \(q^{{\text {C}}}\in C\) are feasible if and only if all nominations \(\ell \in N(q^{{\text {C}}})\) are feasible.
In the following, we analyze the complexity of computing maximal feasible technical capacities for different Constraints (1) of gas transport. To avoid unbounded technical capacities, we require that feasible technical capacities satisfy the conditions
Conditions (3a) ensure that for every entry node, a technical-capacities-compliant nomination exists such that the entry supplies its total capacity to the grid, i.e., a nomination \(\ell \in N(q^{{\text {C}}})\) with \(\ell _{w} = q^{{\text {C}}}_{w}\) exists. Consequently, the complete capacity of an entry node can be nominated in a nomination. In analogy, Conditions (3b) ensure that for every exit node a technical-capacities-compliant nomination exists such that the exit demands its total capacity. Conditions (3) ensure that we do not allocate “unusable” node capacities, i.e., capacities that are not completely used in any technical-capacities-compliant nomination. This prevents that the problem of computing technical capacities is unbounded by setting a single technical capacity to an arbitrary large value and the remaining capacities to zero. The latter technical capacities only contain the zero nomination as technical-capacities-compliant nomination which is usually feasible.
We finally describe the problem of computing (optimal) technical capacities for a fixed weight vector \(d\in \mathbb {R} ^V\) by
Note that feasibility of (4) implicitly contains feasibility of the actual flows of every technical-capacities-compliant nomination; see (1). Moreover, let us briefly discuss that Problem (4) is slightly more general than the problem that TSOs actually face in practice. The reason is that we consider arbitrary weight vectors \(d\in \mathbb {R} ^V\), whereas these may be restricted to be nonnegative in practice. The proof of our complexity result is already rather technical without this restriction. Thus, we keep the assumption \(d\in \mathbb {R} ^V\) throughout the paper and postpone the nonnegative case to future research.
We define two variants of CTC as the threshold problem associated with optimization problem (4). Note that the used specific constraints \(c_{\varepsilon }^{\text {lin}}(x;\ell )\) and \(c_{\mathcal {I}}^{\text {lin}}(x;\ell )\) as well as \(c_{\varepsilon }^{\text {pot}}(x;\ell )\) and \(c_{\mathcal {I}}^{\text {pot}}(x;\ell )\) will be specified in detail later.
Computing Technical Capacities (CTC) –capacitated linear flows. | |
Input: | Graph \(G=(V,A)\) with entries \(V_{+}\), exits \(V_{-}\), inner nodes \(V_0\), |
constraints \(c_{\varepsilon }^{\text {lin}}(x;\ell )\) and \(c_{\mathcal {I}}^{\text {lin}}(x;\ell )\), | |
arc flow bounds \({q}^-_{a} \le {q}^+_{a}, {q}^-_{a}, {q}^+_{a} \in \mathbb {Q} \) for all \(a \in A\), | |
a weight vector \(d\in \mathbb {Q} ^{{V}}\), and threshold value \(T\in \mathbb {Q} _+\). | |
Question: | Do feasible technical capacities \(q^{{\text {C}}}\in F_{{\text {C}}}\) with \(d^\top q^{{\text {C}}}\ge T\) exist? |
Computing Technical Capacities (CTC) – potential-based flows. | |
Input: | Graph \(G=(V,A)\) with entries \(V_{+}\), exits \(V_{-}\), inner nodes \(V_0\), |
constraints \(c_{\varepsilon }^{\text {pot}}(x;\ell )\) and \(c_{\mathcal {I}}^{\text {pot}}(x;\ell )\), | |
potential bounds \({p}^-_{u} \le {p}^+_{u}, {p}^-_{u}, {p}^+_{u} \in \mathbb {Q} _+\) for all \(u\in V\), | |
a weight vector \(d\in \mathbb {Q} ^{{V}}\), and threshold value \(T\in \mathbb {Q} _+\). | |
Question: | Do feasible technical capacities \(q^{{\text {C}}}\in F_{{\text {C}}}\) with \(d^\top q^{{\text {C}}}\ge T\) exist? |
3 Computing technical capacities for capacitated linear flows
As in the last section, we follow the notation introduced in Labbé et al. (2019). In the remainder of the paper, we focus on tree-shaped networks and thus assume that the graph \(G= (V,A)\) is a tree.
We first introduce some notation. We choose to use directed graphs to represent gas networks. This modeling choice allows us to interpret the direction of flows. However, actual physical flow in a gas network is not influenced by the direction of the arcs. Thus, for \(u,v \in V\), we introduce the so-called flow-path  in which
in which  contains the nodes of the path from u to v in the undirected version of the graph \(G\) and
contains the nodes of the path from u to v in the undirected version of the graph \(G\) and  contains the corresponding arcs of this path. Moreover, we call
contains the corresponding arcs of this path. Moreover, we call  a directed flow-path from \(u\) to \(v \) if
a directed flow-path from \(u\) to \(v \) if  is a directed path from \(u\) to \(v \) in \(G\). For another pair of nodes \(u',v ' \in V\), we say that
is a directed path from \(u\) to \(v \) in \(G\). For another pair of nodes \(u',v ' \in V\), we say that  is a flow-subpath of
is a flow-subpath of  if
if  , i.e.,
, i.e.,  and
and  holds, and if
holds, and if  is itself a flow-path. In particular, this allows us to define an order on the nodes of a flow-path. For
is itself a flow-path. In particular, this allows us to define an order on the nodes of a flow-path. For  and
and  , we define \(u' \preceq _{P} v '\) if and only if a flow-subpath
, we define \(u' \preceq _{P} v '\) if and only if a flow-subpath  exists. If \(u'\ne v '\) holds, we write \(u'\prec _{P} v '\).
exists. If \(u'\ne v '\) holds, we write \(u'\prec _{P} v '\).
We note that if we reverse arcs in \(G\), then \(\ell \)-flows can be adapted by switching the sign for flows on each arc with different orientation. For a given \(\ell \)-flow \(q \), we say that node \(u\in V\) supplies node \(v \in V\setminus \left\{ {u} \right\} \) if for each arc  , the conditions
, the conditions
hold. We now introduce two sub-graphs for an arc \(a = (u,v) \in A\). If we delete arc \(a \) in \(G\), then the tree decomposes into two sub-trees. We define the sub-tree that includes node \(u\) as  and the other sub-tree that contains \(v\) as
and the other sub-tree that contains \(v\) as  . By construction,
. By construction,  holds. Note that considering the reversed arc \((v, u)\) does not change the sub-trees \(G_{u}\) and \(G_{v}\).
holds. Note that considering the reversed arc \((v, u)\) does not change the sub-trees \(G_{u}\) and \(G_{v}\).
We now present the capacitated linear flow model considered in this section. We consider lower and upper flow bounds \({q}^-_{a} \le {q}^+_{a} \) that are given for every arc \(a \in A\) and assume no other flow constraints. This means, we consider a standard capacitated linear flow model. Consequently, for a nomination \(\ell \in N\), Constraints (1) are given by (2) and the flow bounds
i.e.,
and \(c_{\varepsilon }\) stays the same as in Sect. 2, i.e.,
We note that checking the feasibility of a nomination \(\ell \in N\) w.r.t. Conditions (1) of this section is a standard \(\ell \)-transshipment problem; see, e.g., Chapter 11 of the book (Schrijver 2003).
We first show that we can validate the feasibility of given technical capacities for a tree-shaped network in polynomial time. Afterward, in Sect. 3.2 we prove that CTC for capacitated linear flows is NP-hard even for trees.
3.1 Checking feasibility of technical capacities
Due to the tree structure of the graph, we know that for every nomination \(\ell \in N\), there exists a unique \(\ell \)-flow.
Lemma 3.1
(Lemma 1 in Robinius et al. (2019)) Let \(\ell \in N\) be a nomination. Then, a unique \(\ell \)-flow exists and this flow can be computed in \(O(|V|)\).
With the next lemma, we bound the arc flow for a given \(\ell \)-flow in dependence of the technical capacities by using the uniqueness of the flow-path between two nodes. Thus, the arc flow is bounded by the minimum of the aggregated capacities of the entries on one side of the arc and of the aggregated capacities of the exits on the other side of the arc.
Lemma 3.2
Let \(q^{{\text {C}}}\in C\) be technical capacities, \(\ell \in N(q^{{\text {C}}})\) a nomination, and \(q \) its unique \(\ell \)-flow. Then, for every arc \(a = (u,v) \in A\), the flow \(q _{a} \) is bounded by

Proof
The claim follows from the tree structure of \(G\), Lemma 3.1, and the flow conservation constraints (2) that are satisfied by \(q \). \(\square \)
With an adaption of the approach developed in Robinius et al. (2019), we can show that the lower and upper arc flow bounds (6) are tight w.r.t. \(N(q^{{\text {C}}})\). This means that for every arc at least one nomination exists such that the corresponding flow is at the bound. To this end, we state the auxiliary lemma that directly follows from the tree structure of \(G\).
Lemma 3.3
Let \(u\ne w\in V\). Further, let  hold for the first arc \((u, i)\) of the unique flow-path
hold for the first arc \((u, i)\) of the unique flow-path  . Then, an entry
. Then, an entry  exists such that
exists such that  holds and additionally, no entry
holds and additionally, no entry  with
with  exists.
exists.
In particular, this implies  for the first arc \((\tilde{u},k)\) of the unique flow-path
for the first arc \((\tilde{u},k)\) of the unique flow-path  .
.
We now show that the upper arc flow bound in (6) is tight w.r.t. \(N(q^{{\text {C}}})\). We even show a stronger result: For any node pair, a nomination with unique flows exists so that for every arc of the unique flow-path between these two nodes the arc flow is at its upper bound.
Lemma 3.4
Let \(q^{{\text {C}}}\in C\) be technical capacities and \(u\ne w\in V\). Furthermore, let  be a directed flow-path from \(u\) to \(w\). Then, a nomination \(\ell \in N(q^{{\text {C}}})\) with unique flows \(q \) exists such that for every arc
be a directed flow-path from \(u\) to \(w\). Then, a nomination \(\ell \in N(q^{{\text {C}}})\) with unique flows \(q \) exists such that for every arc  the corresponding arc flow is at its upper bound in (6), i.e.,
the corresponding arc flow is at its upper bound in (6), i.e.,
holds for every  . Additionally, we can compute this nomination \(\ell \) in polynomial time.
. Additionally, we can compute this nomination \(\ell \) in polynomial time.
Proof
For directly applying the results of Theorem 4 in Robinius et al. (2019) and its proof, we make the following additional assumption. If \(u\) is no entry, then we interpret \(u\) as an entry with technical capacity of zero. In analogy, if \(w\) is no exit, then we interpret \(w\) as an exit with technical capacity of zero. These assumptions do not affect the upper bound in (6). Further, let arc  be the first arc of the flow-path
be the first arc of the flow-path  . We distinguish between two cases.
. We distinguish between two cases.
-
(i)
Let
 . This means that no flow can be supplied to \(u\) without using arcs of flow-path
. This means that no flow can be supplied to \(u\) without using arcs of flow-path  . Thus, the claim directly follows from Theorem 4 in Robinius et al. (2019) and its proof.
. Thus, the claim directly follows from Theorem 4 in Robinius et al. (2019) and its proof. -
(ii)
Let
 holds. We apply Lemma 3.3 and Case 1 for \(\tilde{u}\) and \(w\). In doing so, we can w.l.o.g. assume that
holds. We apply Lemma 3.3 and Case 1 for \(\tilde{u}\) and \(w\). In doing so, we can w.l.o.g. assume that  is a directed flow-path from \(\tilde{u}\) to \(w\). Consequently, (7) is satisfied for
is a directed flow-path from \(\tilde{u}\) to \(w\). Consequently, (7) is satisfied for  . Due to this and
. Due to this and  , the claim follows.
, the claim follows.
We can compute the corresponding nominations of Case 1 and 2 in polynomial time due to Lemma 11 in Robinius et al. (2019). \(\square \)
Using Lemma 3.4, we now prove that also the lower arc flow bound of (6) is tight.
Lemma 3.5
Let \(q^{{\text {C}}}\in C\) be technical capacities and \(u\ne w\in V\). Furthermore, let  be a directed flow-path from \(u\) to \(w\). Then, a nomination \(\ell \in N(q^{{\text {C}}})\) with unique flows \(q \) exists such that for every arc
be a directed flow-path from \(u\) to \(w\). Then, a nomination \(\ell \in N(q^{{\text {C}}})\) with unique flows \(q \) exists such that for every arc  the corresponding arc flow is at the lower bound in (6), i.e.,
the corresponding arc flow is at the lower bound in (6), i.e.,
holds for every  . Additionally, we can compute this nomination \(\ell \) in polynomial time.
. Additionally, we can compute this nomination \(\ell \) in polynomial time.
Proof
We consider the graph \(\tilde{G}=({V}, \tilde{A})\), which is a copy of \(G=(V,A)\) except that arcs of  are reversed so that
are reversed so that  is a directed flow-path from \(w\) to \(u\). We now apply Lemma 3.4 for \(w\) and \(u\) in \(\tilde{G}\). Consequently, a nomination \(\ell \in N(q^{{\text {C}}})\) with unique \(\ell \)-flow \(\tilde{q}\) in \(\tilde{G}\) exist such that for
is a directed flow-path from \(w\) to \(u\). We now apply Lemma 3.4 for \(w\) and \(u\) in \(\tilde{G}\). Consequently, a nomination \(\ell \in N(q^{{\text {C}}})\) with unique \(\ell \)-flow \(\tilde{q}\) in \(\tilde{G}\) exist such that for  , it holds
, it holds
Let \({q}\) be the unique flows in \(G\) corresponding to nomination \(\ell \). Due to the different orientation of arc \(a =(k,l)\) of  in \(G\) and \(\tilde{G}\) and the tree structure of \(G\),
in \(G\) and \(\tilde{G}\) and the tree structure of \(G\),

holds. This shows the claim. \(\square \)
Using the previous two lemmas, we can efficiently check the feasibility of technical capacities.
Lemma 3.6
Let \(q^{{\text {C}}}\in C\) be technical capacities. Then, \(q^{{\text {C}}}\) are feasible technical capacities if and only if for every arc \(a =(u, v) \in A\), the conditions
are satisfied.
Proof
Let \(q^{{\text {C}}}\) be feasible technical capacities and \(a \in A=(k, l)\) an arbitrary arc. Applying Lemmas 3.4 and 3.5 for \(u= k\) and \(w= l\) as well as using the feasibility of every nomination in \(N(q^{{\text {C}}})\) implies Conditions (9).
Let Condition (9) be valid. Then, \(q^{{\text {C}}}\) are feasible technical capacities due to Lemma 3.2. \(\square \)
We finally prove that checking the feasibility of given technical capacities can be done in polynomial time.
Theorem 3.7
Let \(q^{{\text {C}}}\) be technical capacities in a tree. Then, it can be decided in polynomial time if \(q^{{\text {C}}}\) is feasible and if it satisfies Conditions (3). In particular, this implies that CTC with capacitated linear flows on trees is in NP .
Proof
For given technical capacities, we can check Conditions (3), and for every arc, the Condition (9), in polynomial time. \(\square \)
We note that the result of the previous theorem is also shown in a different way by Theorem 3.2.3 and Proposition 3.2.7 in Hayn (2016). We have proven the same result differently here because we need the special structure considered in Lemmas 3.4 and 3.5 for the potential-based case, which is not considered in Hayn (2016).
3.2 Hardness
We prove that CTC for the case of capacitated linear flows is NP-complete on trees. In the remainder of this section, we require that feasible technical capacities satisfy Definition 2.6 and Conditions (3), i.e., feasible technical capacities are always feasible for Problem (4).
In what follows, we reduce the Subset Sum problem to CTC. To this end, we consider the following variant of the Subset Sum problem.
Subset Sum (SSP). | |
Input: | \(M\in \mathbb {N} \), \(Z_1,\dotsc ,Z_n \in \mathbb {N} \) with \(Z_i \le M\) for \( i \in \left\{ {1,\dotsc ,n} \right\} \), \(n\ge 2\), \(\sum _{i=1}^n Z_i \ge M\). |
Question: | Does \( I \subseteq \left\{ {1,\dotsc ,n} \right\} \) with \( \sum _{i \in I}Z_i = M\) exist? |
This definition of the SSP slightly deviates from the original definition in Garey and Johnson (1990). The requirements \(n\ge 2, \sum _{i=1}^n Z_i \ge M\), and \(Z_i \le M\) for \(i \in \left\{ {1,\dotsc ,n} \right\} \) can be checked in polynomial time and, thus, the considered SSP variant is still NP-hard .
The proof is structured as follows. We first construct a CTC instance on a tree based on a given SSP instance. We then prove sufficient conditions for feasibility of a solution and show a lower bound of the objective; see Lemma 3.8. This can be used to prove that the optimal value of the CTC instance exceeds a specific threshold value if the corresponding SSP instance is feasible; see Lemma 3.9. The bulk of the proof characterizes optimal solutions of the specific CTC instance; see Lemmas 3.10–3.15. We finally use these properties to prove that if the SSP is infeasible, optimal technical capacities in the specific CTC instance do not exceed the threshold value.
For an arbitrary SSP instance, we construct an instance of (4) using capacitated linear flows as follows. The graph \(G({{\textsf {SSP}}})\) is given by
We specify entries \(V_{+}\), exits \(V_{-}\), and inner nodes \(V_0\) by
In the following, we use the abbreviation \(\delta = (n+1)^{-1}\). We now define the lower and upper arc flow bounds \({q}^-_{a} \), \({q}^+_{a} \) for \(a \in A\) in \(G({{\textsf {SSP}}})\) as follows
These arc flow bounds satisfy \({q}^-_{a} \le 0 \le {q}^+_{a} \) for \(a \in A\) due to \(Z_i \le M\) for \(i \in \left\{ {1,\dotsc ,n} \right\} \). A graphical representation of \(G({{\textsf {SSP}}})\) is given in Fig. 1.
We denote nonnegative technical capacities by \(q^{{\text {C}}}\). We note that the capacity of inner nodes is set to zero and, thus, we neglect these nodes w.r.t. technical capacities. We determine the nonzero coefficients of the weight vector \(d\) as follows:
We note that \(G({{\textsf {SSP}}})\) is a tree and \(q^{{\text {C}}}=0\) are feasible technical capacities for \(G({{\textsf {SSP}}})\) because of \(q ^-_a \le 0 \le q ^+_a \) for all \(a \in A\). Further, we note that for a given instance of SSP, we can build \(G({{\textsf {SSP}}})\) in polynomial time and its coding length is polynomially bounded above by the coding length of the given SSP instance.
Due to the tree structure of \(G({{\textsf {SSP}}})\), we can check the feasibility of technical capacities in \(G({{\textsf {SSP}}})\) in polynomial time; see Theorem 3.7. Lemma 3.6 implies that for checking the feasibility of technical capacities in \(G({{\textsf {SSP}}})\) we have to verify the conditions
for \(i \in \left\{ {1,\dotsc ,n} \right\} \).
The instance \(G({{\textsf {SSP}}})\) is constructed in such a way that the threshold of the objective value for deciding the feasibility of SSP is given by
We next prove sufficient conditions for the feasibility of technical capacities in \(G({{\textsf {SSP}}})\).
Lemma 3.8
Let \(\tilde{q}^{\text {C}}\in C\) be technical capacities in \(G({{\textsf {SSP}}})\) that satisfy the conditions
and
for \(i \in \left\{ {1,\dotsc ,n} \right\} \). Then, \(\tilde{q}^{\text {C}}\) are feasible technical capacities in \(G({{\textsf {SSP}}})\) and \(d^\top \tilde{q}^{\text {C}}\ge T-M\) holds. Furthermore, such a \(\tilde{q}^{\text {C}}\) always exists.
Proof
To construct such a \(\tilde{q}^{\text {C}}\), one can use any fractional solution of the SSP. It is easy to verify that the capacities \(\tilde{q}^{\text {C}}\) satisfy Conditions (3). For checking the feasibility of \(\tilde{q}^{\text {C}}\), it is left to verify Conditions (11). Due to the construction of \(\tilde{q}^{\text {C}}\), the Conditions (11a) and (11c)–(11f) are satisfied. For Condition (11b), we now distinguish for \(i \in \left\{ {1,\dotsc ,n} \right\} \) two cases depending on \(\tilde{q}^{\text {C}}_{h_i}\).
First, let \(\tilde{q}^{\text {C}}_{h_i} = Z_i\). Consequently,
which implies Condition (11b). Second, let \(\tilde{q}^{\text {C}}_{h_i} < Z_i\). Consequently,
which implies Condition (11b). Thus, the feasibility of \(\tilde{q}^{\text {C}}\) follows from Lemma 3.6 and the objective value of \(\tilde{q}^{\text {C}}\) satisfies
\(\square \)
We can directly use the previous lemma to show that if the given SSP instance is feasible, then optimal technical capacities in \(G({{\textsf {SSP}}})\) exceed the threshold value \(T\).
Lemma 3.9
Let the given SSP be feasible, i.e., there exists \( I \subseteq \left\{ {1,\dotsc ,n} \right\} \) with \(\sum _{i \in I} Z_i = M\). Further, let \(q^{{\text {C}}}\in C\) be optimal technical capacities in \(G({{\textsf {SSP}}})\). Then, \(d^\top q^{{\text {C}}}\ge T\) holds.
Proof
Let I be a feasible solution of SSP, then we construct the following technical capacities:
The technical capacities \(\bar{q}^{\text {C}}\) are feasible because they satisfy the conditions of Lemma 3.8. Let \(i \in \left\{ {1,\dotsc ,n} \right\} \). We now compute the objective value of the \(i\)th branch of \(G({{\textsf {SSP}}})\), i.e.,
If \(i \in I\) holds, then from the construction of \(\bar{q}^{\text {C}}\) the \(i\)th branch (12) evaluates to
which also holds for \(i \notin I\). Thus, the objective value of \(\bar{q}^{\text {C}}\) is given by
Consequently, the claim follows because \(\bar{q}^{\text {C}}\) are feasible technical capacities. \(\square \)
In what follows, we characterize optimal solutions; see Lemmas 3.10–3.15. Using the obtained properties we prove that if SSP is infeasible, the threshold \(T\) value is not exceeded by optimal technical capacities in \(G({{\textsf {SSP}}})\).
We first bound the technical capacity of certain nodes.
Lemma 3.10
Let \(q^{{\text {C}}}\in C\) be optimal technical capacities in \(G({{\textsf {SSP}}})\). Then,
Proof
The claim follows from the explicit structure of tree \(G({{\textsf {SSP}}})\), Conditions (3), the arc flow bounds (10), and Lemmas 3.4 and 3.5. \(\square \)
Additionally, we prove that the technical capacity of entry \(h_i\) is bounded above by \(Z_i\) in an optimal solution.
Lemma 3.11
Let \(q^{{\text {C}}}\in C\) be optimal technical capacities in \(G({{\textsf {SSP}}})\). Then, \(q^{{\text {C}}}_{h_i} \le Z_i\) holds for all \(i \in \left\{ {1,\dotsc ,n} \right\} \).
Proof
We prove the claim by contraposition, i.e., we now assume that \(i \in \left\{ {1,\dotsc ,n} \right\} \) with \(q^{{\text {C}}}_{h_i} > Z_i\) exists and then prove that \(q^{{\text {C}}}\) are not optimal technical capacities. From Condition (11a) it follows \(\sum _{u\in V_{-}\setminus \left\{ { v_i} \right\} } q^{{\text {C}}}_{u} \le Z_i\). Thus, we obtain the bounds \(q^{{\text {C}}}_{s} \le Z_i\) and \( q^{{\text {C}}}_{v_j} \le Z_i\) for \(j \in \left\{ {1,\dotsc ,n} \right\} \setminus \left\{ {i} \right\} \).
Using Lemma 3.10, we can bound the objective value corresponding to \(q^{{\text {C}}}\) from above as follows:
For the latter inequality, we also used that \(Z_i \le M\) holds. The upper bound (13) of the objective value for \(q^{{\text {C}}}\) and the objective value of the feasible point in Lemma 3.8 show that \(q^{{\text {C}}}\) is not optimal. \(\square \)
We next prove that the optimal technical capacity of entry \(t\) is at its upper bound \(\delta \).
Lemma 3.12
Let \(q^{{\text {C}}}\in C\) be optimal technical capacities in \(G({{\textsf {SSP}}})\). Then, \(q^{{\text {C}}}_t= \delta \) holds.
Proof
Let \(q^{{\text {C}}}\) be feasible technical capacities. Due to Lemma 3.10, \(q^{{\text {C}}}_{t} \le \delta \) holds. We now prove the claim by contraposition, i.e., we show that if \(q^{{\text {C}}}_t< \delta \) holds, then we can construct a better solution \(\bar{q}^{\text {C}}\). We set \(\varepsilon \ge 0\) such that \(q^{{\text {C}}}_t+ \varepsilon = \delta \) holds and construct a new solution \(\bar{q}^{\text {C}}\) by
We now check the feasibility of \(\bar{q}^{\text {C}}\). To this end, we first verify that \(\bar{q}^{\text {C}}\) satisfies Conditions (3). Conditions (3a) are satisfied due to \(\bar{q}^{\text {C}}_s\ge \bar{q}^{\text {C}}_u\) for \(u\in V_{+}\). We next show that Conditions (3b) hold. To this end, we distinguish between two cases.
First, assume \({q^C_w} \le n \varepsilon \) for all \(w\in V_{-}\). Consequently, \(\bar{q}^{\text {C}}_{s} = \max \left\{ {\bar{q}^{\text {C}}_{u}:u\in V_{+}} \right\} \) and \(\bar{q}^{\text {C}}_{v_i} = 0\) for \(i \in \left\{ {1,\dotsc ,n} \right\} \) are satisfied, which implies Conditions (3b). Second, assume there exists \(v \in V_- \) with \(q^{{\text {C}}}_{v} > n \varepsilon \). If additionally
holds, then Conditions (3b) directly follow. Otherwise, from the feasibility of \(q^{{\text {C}}}\) and the construction of \(\bar{q}^{\text {C}}\),
follows, which implies (3b). Thus, Conditions (3) are satisfied by \(\bar{q}^{\text {C}}\). For checking the feasibility of \(\bar{q}^{\text {C}}\), it is left to show that Conditions (11) are satisfied for \(\bar{q}^{\text {C}}\). Due to the optimality of \(q^{{\text {C}}}\), we can apply Lemma 3.11 and, thus, \(q^{{\text {C}}}_{h_i} \le Z_i\) for \(i \in \left\{ {1,\dotsc ,n} \right\} \). Due to this and the construction of \(\bar{q}^{\text {C}}\), Conditions (11a) are satisfied. Thus, \(\bar{q}^{\text {C}}_{t} \le \delta \) as well as Conditions (11c) and (11e) are satisfied. We next show that (11d) holds for \(\bar{q}^{\text {C}}\). The construction of \(\bar{q}^{\text {C}}\) and \(q^{{\text {C}}}_{h_i} \le Z_i \le M\) for \(i \in \left\{ {1,\dotsc ,n} \right\} \) leads to
This, together with the feasibility of Condition (11d) for \(q^{{\text {C}}}\), leads to
which implies the feasibility of Condition (11d) for \(\bar{q}^{\text {C}}\). From Lemma 3.10, the construction of \(\bar{q}^{\text {C}}\), and the feasibility of \(q^{{\text {C}}}\) Condition (11f) follows.
We now show the feasibility of Condition (11b). For \(i \in \left\{ {1,\dotsc ,n} \right\} \), we prove
If \( u\in V_{+}\setminus \left\{ {t, h_i} \right\} \) with \( q^{{\text {C}}}_u> \varepsilon \) does not exist, then
holds. Otherwise, an entry \(w\in V_{+}\setminus \left\{ {t, h_i} \right\} \) with \(q^{{\text {C}}}_{w} > \varepsilon \) exists and
is satisfied.
Using (14), the feasibility of \(q^{{\text {C}}}\), and the construction of \(\bar{q}^{\text {C}}\), we show the feasibility w.r.t. Condition (11b) for \(\bar{q}^{\text {C}}\) by
Consequently, Conditions (11) are satisfied by \(\bar{q}^{\text {C}}\) and, thus, \(\bar{q}^{\text {C}}\) are feasible technical capacities due to Lemma 3.6.
Lastly, we compare the objective values of \(\bar{q}^{\text {C}}\) and \(q^{{\text {C}}}\) by
Consequently, \(\bar{q}^{\text {C}}\) is a strictly better solution if \(\varepsilon >0\). \(\square \)
In what follows, we show that the aggregated capacity of certain entries is bounded for optimal technical capacities in \(G({{\textsf {SSP}}})\).
Lemma 3.13
Let \(q^{{\text {C}}}\in C\) be optimal technical capacities in \(G({{\textsf {SSP}}})\). Then, \(\sum _{u\in V_{+}\setminus \left\{ {t} \right\} } q^{{\text {C}}}_u\le M\) is satisfied.
Proof
We prove the claim by contraposition. To this end, we assume that \(\sum _{u\in V_{+}\setminus \left\{ {t} \right\} } q^{{\text {C}}}_u> M\) holds. This together with Lemma 3.12 implies \(q^{{\text {C}}}_t= \delta \) and, hence,
By Lemma 3.6, the feasible technical capacities \(q^{{\text {C}}}\) satisfy Conditions (11). Because of the assumption, the inequality \(q^{{\text {C}}}_{s} \le M\) follows from Condition (11d). Due to Lemma 3.11, \(q^{{\text {C}}}_{h_i} \le Z_i\) for \(i \in \left\{ {1,\dotsc ,n} \right\} \). This, Inequality (15), and Condition (11b), imply \(q^{{\text {C}}}_{v_i} \le M+\delta - Z_i\) for \(i \in \left\{ {1,\dotsc ,n} \right\} \).
We now bound the objective value of \(q^{{\text {C}}}\) by
Thus, from Lemma 3.8 it follows that \(q^{{\text {C}}}\) is not optimal. \(\square \)
With the next two lemmas, we bound the objective value of the \(i\)th branch of \(G({{\textsf {SSP}}})\) in optimal technical capacities depending on the amount of flow, which is supplied to this branch. In doing so, the \(i\)th branch consists of the subtree that includes the nodes \(o, h_i\), and \(v_i\).
Lemma 3.14
Let \(q^{{\text {C}}}\in C\) be optimal technical capacities and \(i \in \left\{ {1,\dotsc ,n} \right\} \). If \(\sum _{u\in V_{+}\setminus \left\{ {h_i} \right\} } q^{{\text {C}}}_u> M+ \delta - Z_i\) holds, then
holds.
Proof
Let \(q^{{\text {C}}}\in C\) be optimal technical capacities and \(i \in \left\{ {1,\dotsc ,n} \right\} \). Due to \(\sum _{u\in V_{+}\setminus \left\{ {h_i} \right\} } q^{{\text {C}}}_u> M+\delta -Z_i\) and the feasibility of \(q^{{\text {C}}}\), it follows from Conditions (11b) that \(q^{{\text {C}}}\) is only feasible if \( q^{{\text {C}}}_{v_i} \le M+\delta - Z_i\) holds. Using this, \(Z_i \le M+ \delta \), the optimality of \(q^{{\text {C}}}\), \( d_{v_i} > 0\), Lemmas 3.10–3.12, and Conditions (11) leads to \(q^{{\text {C}}}_{v_i} = M+ \delta - Z_i\), which shows the claim. \(\square \)
Lemma 3.15
Let \(q^{{\text {C}}}\in C\) be optimal technical capacities and \(i \in \left\{ {1,\dotsc ,n} \right\} \). If \(\sum _{u\in V_{+}\setminus \left\{ {h_i} \right\} } q^{{\text {C}}}_u\le M+ \delta - Z_i\) holds, then
holds.
Proof
Let \(q^{{\text {C}}}\in C\) be optimal technical capacities, which satisfy the requirements and \(i \in \left\{ {1,\dotsc ,n} \right\} \). Due to Conditions (3b), the inequality \(q^{{\text {C}}}_{v_i} \le \sum _{u\in V_{+}} q^{{\text {C}}}_u\) is satisfied. For any assignment \(q^{{\text {C}}}_{v_i} \in [0,\sum _{u\in V_{+}} q^{{\text {C}}}_u]\), the Conditions (11) are satisfied by \(q^{{\text {C}}}\) due to \(\sum _{u\in V_{+}\setminus \left\{ {h_i} \right\} } q^{{\text {C}}}_u\le M+ \delta - Z_i\) and Lemmas 3.10–3.12. Thus, the optimality of \(q^{{\text {C}}}\), and \(d_{v_i} > 0\), \(q^{{\text {C}}}_{v_i} = \sum _{u\in V_{+}} q^{{\text {C}}}_u\) holds and the claim follows. \(\square \)
We now derive an upper bound for the objective value if the given SSP instance is infeasible while the aggregated entry capacity is \(M+ q^{{\text {C}}}_{t}\).
Lemma 3.16
Let the given SSP be infeasible, i.e., there exists no subset \(I \subseteq \left\{ {1,\dotsc ,n} \right\} \) with \(\sum _{i \in I} Z_i = M\). Let \(q^{{\text {C}}}\in C\) be optimal technical capacities in \(G({{\textsf {SSP}}})\) with \(\sum _{u\in V_{+}\setminus \left\{ {t} \right\} } q^{{\text {C}}}_{u} = M\). Then, \(d^\top q^{{\text {C}}}< T\) holds.
Proof
Due to Lemma 3.12, \(q^{{\text {C}}}_{t} = \delta \) holds. Consequently, \(\sum _{u\in V_{+}} q^{{\text {C}}}_{u} = M+ \delta \) is satisfied. We now compute an upper bound for the \(i\)th branch (12) in \(G({{\textsf {SSP}}})\) depending on \(i \in \left\{ {1,\dotsc ,n} \right\} \). Due to Lemma 3.11, \(q^{{\text {C}}}_{h_i} \le Z_i\) holds.
If \(q^{{\text {C}}}_{h_i} < Z_i\) holds, then
Hence, we apply Lemma 3.14, and thus, (12) evaluates to \(- q^{{\text {C}}}_{h_i} + M+ \delta - Z_i. \) If \(q^{{\text {C}}}_{h_i} = Z_i\) holds, then
Consequently, we can apply Lemma 3.15 and, thus, (12) evaluates to \(M+ \delta - Z_i. \) From Lemma 3.11, it follows \(q^{{\text {C}}}_{h_i} \in [0, Z_i]\) for \(i \in \left\{ {1,\dotsc ,n} \right\} \). Due to this, the infeasibility of SSP, \(q^{{\text {C}}}_{t} = \delta \), and \(\sum _{u\in V_{+}\setminus \left\{ {t} \right\} } q^{{\text {C}}}_u= M\), an index \(j \in \left\{ {1,\dotsc ,n} \right\} \) exists with \(q^{{\text {C}}}_{h_j} \in (0, Z_j)\). Also using Lemma 3.10, we can bound the objective value of \(q^{{\text {C}}}\) by
\(\square \)
We now prove an upper bound for the objective value of optimal technical capacities independent of the SSP being feasible while the aggregated entry capacity is below \(M+ q^{{\text {C}}}_{t}\).
Lemma 3.17
Let \(q^{{\text {C}}}\in C\) be optimal technical capacities in \(G({{\textsf {SSP}}})\) and \(\sum _{u\in V_{+}\setminus \left\{ {t} \right\} } q^{{\text {C}}}_{u} = M- \varepsilon \) for a fixed \(\varepsilon \in (0,M]\). Then, \(d^\top q^{{\text {C}}}< T\) holds.
Proof
Due to Lemma 3.12, \(q^{{\text {C}}}_{t} = \delta \) holds, which implies \(\sum _{u\in V_{+}} q^{{\text {C}}}_{u} = M+ \delta - \varepsilon \). We now compute an upper bound for the \(i\)th branch (12) of \(G({{\textsf {SSP}}})\) depending on \(i \in \left\{ {1,\dotsc ,n} \right\} \). Let \(i \in \left\{ {1,\dotsc ,n} \right\} \). If \(q^{{\text {C}}}_{h_i} < Z_i - \varepsilon \) holds, then
We apply Lemma 3.14 and, thus, the ith branch (12) evaluates to \( - q^{{\text {C}}}_{h_i} + M+ \delta - Z_i.\) If, on the other hand, \(q^{{\text {C}}}_{h_i} \ge Z_i - \varepsilon \) holds, then
We now apply Lemma 3.15, which together with \(q^{{\text {C}}}_{h_i} \ge Z_i - \varepsilon \), Conditions (3), and the requirements implies that the objective of the \(i\)th branch (12) is bounded by
From \(\sum _{u\in V_{+}} q^{{\text {C}}}_u= M+ \delta - \varepsilon \) and Condition (3b), it follows \(q^{{\text {C}}}_{s} \le M+ \delta - \varepsilon \). Due to this and the above, we can bound the objective value of \(q^{{\text {C}}}\) from above by
\(\square \)
The next theorem describes the relation between deciding the feasibility of a given SSP instance and computing optimal technical capacities in \(G({{\textsf {SSP}}})\).
Lemma 3.18
The SSP problem is solvable if and only if the optimal technical capacities \(q^{{\text {C}}}\in C\) in \(G({{\textsf {SSP}}})\) satisfy
Proof
Let the SSP problem be solvable and \(q^{{\text {C}}}\) be optimal technical capacities in \(G({{\textsf {SSP}}})\). We apply Lemma 3.9 and, thus, (16) is satisfied.
Let now \(q^{{\text {C}}}\in C\) be optimal technical capacities in \(G({{\textsf {SSP}}})\) that satisfy (16). We now assume that SSP is infeasible. Due to the optimality of \(q^{{\text {C}}}\) and Lemma 3.13, we know that \(\sum _{u\in V_{+}\setminus \left\{ {t} \right\} } q^{{\text {C}}}_u\le M\) holds. If \(\sum _{u\in V_{+}\setminus \left\{ {t} \right\} } q^{{\text {C}}}_u= M\) holds, then we apply Lemma 3.16, which is a contradiction to \(q^{{\text {C}}}\) satisfying (16). If \(\sum _{u\in V_{+}\setminus \left\{ {t} \right\} } q^{{\text {C}}}_{u}= M-\varepsilon \) for a fixed \( \varepsilon \in (0,M]\) holds, we apply Lemma 3.17, which is a contradiction to \(q^{{\text {C}}}\) satisfying (16). \(\square \)
We finally prove that CTC is NP-complete on trees.
Theorem 3.19
CTC with capacitated linear flows is NP-complete on trees. On general graphs, it is at least NP-hard .
Proof
The feasibility of given technical capacities can be verified in polynomial time on trees; see Theorem 3.7.
For a given SSP instance, we can construct the CTC instance \(G({{\textsf {SSP}}})\) in polynomial time and its coding length is polynomially bounded above by the coding length of the given SSP instance. Hence, from Lemma 3.18 it follows that CTC is NP-hard on trees, since \(G({{\textsf {SSP}}})\) is a tree. \(\square \)
4 Computing technical capacities for nonlinear potential-based flows
We now consider a nonlinear potential-based flow model of gas transport. Thus, the flows depend on the potentials at the incident nodes. In contrast to the capacitated linear flow case, the flows in potential-based networks follow additional physical laws that make it unique. On the one hand, the potentials provide additional structure for the analysis of nominations, bookings, and technical capacities. On the other hand, the coupling between potentials and flows is usually nonlinear, which results in a harder class of optimization problems. For capacitated linear flows it is shown that checking the feasibility of technical capacities, respectively bookings, is coNP-complete on general networks; see Hayn (2016). In Labbé et al. (2020), it is shown that verifying the feasibility of technical capacities, respectively bookings, can be solved in polynomial time on networks with linear potential-based flows. Moreover, checking the feasibility of technical capacities, respectively bookings, can be done in polynomial time on trees and single cycle networks in case of nonlinear potential-based flows; see Labbé et al. (2019, (2020). For the complexity of CTC with potential-based flows, only exponential upper complexity bounds are known so far; see Hayn (2016).
In this section, we prove that CTC is NP-complete for nonlinear as well as linear potential-based flows. We first prove this for the nonlinear potential-based case. Afterward, we show that the linear potential-based case can be proven in analogy with the help of minor adaptions.
We now explicitly state the considered nonlinear potential-based flow model. To this end, we introduce a bounded potential variable \(p_u\) for every node \(u\in V\). Additionally, the potentials are coupled to arc flows. Thus, for a nomination \(\ell \in N\) the Constraints (1) are given by (2) and the classical Weymouth pressure drop conditions
where \(\Lambda _a > 0\) is a constant for every arc \(a \in A\); see Weymouth (1912); Ríos-Mercado and Borraz-Sánchez (2015) and the chapter Fügenschuh et al. (2015) in the book Koch et al. (2015). Furthermore, the pressures are bounded, i.e.,
Consequently, the Constraints (1) are given by
as well as
with
In contrast to the capacitated linear flow model, no arc flow bounds exist in the potential-based model. Instead, potential bounds are now included.
We can check the feasibility of technical capacities in tree-shaped networks with potential-based flows in polynomial time due to Labbé et al. (2020).
Lemma 4.1
Let \(q^{{\text {C}}}\in C\) be technical capacities in the tree \(G=(V, A)\). Then, we can decide if \(q^{{\text {C}}}\) is feasible and satisfies Condition (3) in polynomial time. In particular, this implies that CTC with nonlinear potential-based flows on trees is in NP .
Proof
Conditions (3) can obviously be checked in polynomial time. The feasibility of \(q^{{\text {C}}}\) can be checked in \(O(|V|^2)\) due to Theorem 20 in Labbé et al. (2020). \(\square \)
We note that checking the feasibility of \(q^{{\text {C}}}\) in polynomial time also follows from adapting Theorem 4 in Robinius et al. (2019).
Considering a nonlinear potential-based flow model, we now prove that CTC is NP-hard in tree-shaped networks. To this end, we reduce CTC with capacitated linear flows to CTC with nonlinear potential-based flows. The case of capacitated linear flows is NP-hard due to the results of Sect. 3. Thus, we now focus on the reduction instances \(G({{\textsf {SSP}}})\) of the capacitated linear flow case; see Sect. 3.
We now transform a given \(G({{\textsf {SSP}}})\) instance of the capacitated linear flow to the potential-based case. To this end, we take the same graph \(G({{\textsf {SSP}}})=(V, A)\) and the objective coefficients \(d\) as in the previous section. We remove the flow bounds. Moreover, we set \(\Lambda _{(t, s)} = (M+ \delta )^2 10^2 d_{t}^2\) and \(\Lambda _{a} = 1\) for all remaining arcs \(a \in A\setminus \left\{ {(t, s)} \right\} \). The squared potential bounds are given in Table 2. Intuitively, \(K= 2(M+ \delta )\) is a pressure value that is chosen high enough such that the pressure never drops below zero in the network. We denote the constructed instance by \(G^{\text {pot}}({{\textsf {SSP}}})\). We further note that for a given instance of \(G({{\textsf {SSP}}})\), we can build \(G^{\text {pot}}({{\textsf {SSP}}})\) in polynomial time and its coding length is polynomially bounded above by the coding length of the given \(G({{\textsf {SSP}}})\) instance.
We first prove that feasible technical capacities in \(G({{\textsf {SSP}}})\) with capacitated linear flow are also feasible for \(G^{\text {pot}}({{\textsf {SSP}}})\) in the potential-based case.
Lemma 4.2
Let \(q^{{\text {C}}}\in C\) be feasible technical capacities in \(G({{\textsf {SSP}}})\) with capacitated linear flow. Then, \(q^{{\text {C}}}\) are feasible technical capacities in \(G^{\text {pot}}({{\textsf {SSP}}})\) in the potential-based model.
Proof
Since \(q^{{\text {C}}}\) are feasible technical capacities for \(G({{\textsf {SSP}}})\), they satisfy Conditions (3). Let \(\ell \in N(q^{{\text {C}}})\) be a nomination and \(q \) its corresponding flow, which is unique due to the tree structure of the underlying graph. We now prove that this nomination is also feasible in \(G^{\text {pot}}({{\textsf {SSP}}})\). To this end, we construct the potentials corresponding to \(q \) and \(i \in \left\{ {1,\dotsc ,n} \right\} \) as follows:
Since \(\ell \) with its unique flows \(q \) is feasible for \(G({{\textsf {SSP}}})\), they satisfy the flow bounds (10). Replacing the arc flows in (19) by the upper, respectively lower, arc flow bounds of \(G({{\textsf {SSP}}})\), given by (10), shows that for any arc flows satisfying (10) the potentials given in (19) are within the lower and upper potential bounds of Table 2. Consequently, \((q, p)\) satisfy Constraints (1) for the potential-based case and thus, \(\ell \) is a feasible nomination for \(G^{\text {pot}}({{\textsf {SSP}}})\). Since \(\ell \) is an arbitrary booking-compliant nomination w.r.t. \(q^{{\text {C}}}\), this shows the claim. \(\square \)
We note that not all feasible technical capacities in \(G^{\text {pot}}({{\textsf {SSP}}})\) for the potential-based case are also feasible in \(G({{\textsf {SSP}}})\) with capacitated linear flow. For instance, technical feasible capacities with \(q^{{\text {C}}}_{t} > \delta \) exist that are feasible for \(G^{\text {pot}}({{\textsf {SSP}}})\) but not for \(G({{\textsf {SSP}}})\).
In contrast to feasible points, we now show that all optimal technical capacities in \(G^{\text {pot}}({{\textsf {SSP}}})\) are also feasible in \(G({{\textsf {SSP}}})\). To this end, we prove an upper bound for \(q^{{\text {C}}}_{t}\) and an analogous result to Lemma 3.11 for the potential-based case.
Lemma 4.3
Let \(q^{{\text {C}}}\in C\) be feasible technical capacities in \(G^{\text {pot}}({{\textsf {SSP}}})\). Then, \(q^{{\text {C}}}_{t} \le \delta + 1/(10 d_{t})\) holds.
Proof
From Conditions (3), the squared potential bounds of Table 2, (17), and \(t\) being a leaf node of \(G^{\text {pot}}({{\textsf {SSP}}})\), it follows
Due to \(\sqrt{a+b} \le \sqrt{a} + \sqrt{b}\) for \(a,b \ge 0\) and the choice of \(\Lambda _{(t, s)}\), we obtain
\(\square \)
Lemma 4.4
Let \(q^{{\text {C}}}\in C\) be optimal technical capacities in \(G^{\text {pot}}({{\textsf {SSP}}})\). Then, \(q^{{\text {C}}}_{h_i} \le Z_i\) holds for all \(i \in \left\{ {1,\dotsc ,n} \right\} \).
Proof
We prove the claim by contraposition. Thus, we assume that \(i \in \left\{ {1,\dotsc ,n} \right\} \) with \(q^{{\text {C}}}_{h_i} > Z_i\) exists. From the tree structure of \(G^{\text {pot}}({{\textsf {SSP}}})\), Lemmas 3.4 and 3.5, Conditions (3), and the potential bounds in Table 2, it follows that \(\sum _{j=1, j \ne i}^n q^{{\text {C}}}_{v_j} + q^{{\text {C}}}_{s} \le Z_i\). Thus, we obtain the bounds \(q^{{\text {C}}}_{s} \le Z_i,\) and \(q^{{\text {C}}}_{v_j} \le Z_i\) for \(j \in \left\{ {1,\dotsc ,n} \right\} \setminus \left\{ {i} \right\} \). Moreover, we obtain
Due to Lemma 4.3, \(q^{{\text {C}}}_{t} \le \delta + 1/(10 d_{t})\) holds. Furthermore, \(d_{h_j} q^{{\text {C}}}_{h_j} \le 0\) holds for \(j \in \left\{ {1,\ldots ,n} \right\} \setminus \left\{ {i} \right\} \) and, thus, we can neglect these terms for bounding the objective value corresponding to \(q^{{\text {C}}}\) by
A comparison of the upper bound (20) for the objective value corresponding to \(q^{{\text {C}}}\) and the objective value of the feasible solution \(\tilde{q}^{\text {C}}\) in Lemma 3.8, which is also feasible for the potential-based case due to Lemma 4.2, leads to
if \(n \ge 2\). Hence, \(q^{{\text {C}}}\) is not optimal. \(\square \)
We now prove that in an optimal solution \(q^{{\text {C}}}_{t}\) is bounded above by \(\delta \), which is also the case for the capacitated linear flow model; see Lemma 3.12.
Lemma 4.5
Let \(q^{{\text {C}}}\in C\) be optimal technical capacities in \(G^{\text {pot}}({{\textsf {SSP}}})\). Then, \(q^{{\text {C}}}_{t} \le \delta \) holds.
Proof
We prove the claim by contraposition. Thus, we assume \(q^{{\text {C}}}_{t} > \delta \). Due to this, Lemmas 3.4 and 3.5, and the potential bounds in Table 2, it follows \(\sum _{u\in V_{-}\setminus \left\{ {s} \right\} } q^{{\text {C}}}_u\le \delta \). Consequently, \(\sum _{u\in V_{-}\setminus \left\{ {s} \right\} } d_{u} q^{{\text {C}}}_{u} \le \delta \) holds due to \(d_{u} \le 1\) for all \(u\in V_{-}\setminus \left\{ {s} \right\} \). Further, from the potential bounds, Lemma 4.3, and Conditions (3), the inequality \(q^{{\text {C}}}_{s} \le M+ \delta + 1/(10 d_{t})\) follows. We now compare the objective value of \(q^{{\text {C}}}\) with the corresponding objective value of the solution \(\tilde{q}^{\text {C}}\) of Lemma 3.8.
First, assume that \(q^{{\text {C}}}_{s} \ge M+ \delta \) holds. Due to Conditions (3) and \(q^{{\text {C}}}_{t} \le \delta + 1/(10 d_{t})\), which follows from Lemma 4.3, \(\sum _{u\in V_{+}\setminus \left\{ {t} \right\} } q^{{\text {C}}}_{u} \ge M- 1/(10 d_{t}) > 0\) holds. Consequently, a comparison of the objective values of \(q^{{\text {C}}}\) and \(\tilde{q}^{\text {C}}\) of Lemma 3.8 leads to
Since \(n \ge 2\) holds, \(q^{{\text {C}}}\) is not optimal. Second, assume that \(q^{{\text {C}}}_{s} < M+ \delta \) holds. Thus, \(\varepsilon > 0\) with \(q^{{\text {C}}}_{s} + \varepsilon = M+ \delta \) exists. Due to Conditions (3) and \(q^{{\text {C}}}_{t} \le \delta + 1/(10 d_{t})\), which follows from Lemma 4.3, \(\sum _{u\in V_{+}\setminus \left\{ {t} \right\} } q^{{\text {C}}}_{u} \ge \max \left\{ {0, M- \varepsilon - 1/(10 d_{t})} \right\} \) holds. Consequently, a comparison of the objective values of \(q^{{\text {C}}}\) and \(\tilde{q}^{\text {C}}\) of Lemma 3.8 leads to
If \(\max \{0, M- \varepsilon - 1/(10 d_{t})\} = 0\) is satisfied, then \(\varepsilon \ge 0.9\) holds. Thus, (21) is positive for \(n \ge 2\). Otherwise, (21) results in
Hence, \(q^{{\text {C}}}\) is not optimal. \(\square \)
Lemma 4.6
Let \(q^{{\text {C}}}\in C\) be optimal technical capacities in \(G^{\text {pot}}({{\textsf {SSP}}})\). Then, \(q^{{\text {C}}}\) are feasible technical capacities in \(G({{\textsf {SSP}}})\).
Proof
Since \(q^{{\text {C}}}\) are feasible technical capacities for the potential-based case, they satisfy Conditions (3). We now check if \(q^{{\text {C}}}\) satisfies Conditions (11). Due to Lemma 4.4, \(q^{{\text {C}}}_{h_i} \le Z_i\) holds for all \(i \in \left\{ {1,\dotsc ,n} \right\} \). Consequently, Condition (11a) is satisfied. Due to Lemma 4.5, \(q^{{\text {C}}}_{t} \le \delta \) holds as well. Thus, Conditions (11c) and (11e) are satisfied. From Conditions (3), the potential bounds in Table 2, Lemmas 3.4 and 3.5, and \(q^{{\text {C}}}_{h_i} \le Z_i\), it follows \({q^{{\text {C}}}_{v_i} \le M+ \delta }\) for \(i \in \left\{ {1,\dotsc ,n} \right\} \). Consequently, Condition (11f) is satisfied.
The potential bounds in Table 2 imply that the flow on arc \((o, s)\) is bounded from the above by \(M\) and the arc flow \((o, h_i)\) is bounded from below by \(-Z_i\) as well as from above by \(M+ \delta - Z_i\) for \(i \in \left\{ {1,\dotsc ,n} \right\} \). Due to this and Lemmas 3.4 and 3.5, Conditions (11d) and (11b) are satisfied. In total, \(q^{{\text {C}}}\) satisfies Conditions (11) and thus, the claim follows from Lemma 3.6. \(\square \)
Lemma 4.7
The optimal technical capacities in \(G({{\textsf {SSP}}})\) and in \(G^{\text {pot}}({{\textsf {SSP}}})\) are identical.
Proof
The claim follows from Lemmas 4.2 and 4.6. \(\square \)
As a consequence of the last lemma, the Lemmas 3.10–3.17 are also valid in the potential-based case. Thus, we can also adapt Lemma 3.18, which implies that CTC on trees with a nonlinear potential-based model is NP-hard .
Lemma 4.8
The SSP problem is solvable if and only if the optimal technical capacities \(q^{{\text {C}}}\) of \(G^{\text {pot}}({{\textsf {SSP}}})\) satisfy \(d^\top q^{{\text {C}}}\ge T.\)
Proof
The claim follows from Lemmas 4.7 and 3.18. \(\square \)
Theorem 4.9
CTC with nonlinear potential-based flows is NP-complete on trees. On general graphs, it is at least NP-hard .
Proof
The validation of a given technical capacities of a tree can be done in polynomial time due to Lemma 4.1. Then, the claim follows from Lemma 4.8. \(\square \)
Sometimes linear potential-based flow models are preferred instead of the nonlinear potential-based model here considered, since it simplifies the resulting optimization problem. The only difference between a linear and our nonlinear potential-based model is that the Weymouth equations (17) are replaced by
The remaining Constraints (1) stay the same. We conclude this section with proving that CTC for linear potential-based flows is also NP-complete on trees. This can be shown in analogy to the nonlinear potential-based case considering only a few small adaption.
Theorem 4.10
CTC with linear potential-based flows is NP-complete on trees. On general graphs, it is NP-complete as well.
Proof
(Sketch) Checking the feasibility of technical capacities with linear potential-based flows in a general graph can be done in polynomial time due to Theorem 12 in Labbé et al. (2020). Consequently, CTC with linear potential-based flow is in NP .
For proving NP -hardness, we adapt the previous results for the nonlinear potential-based case. We first replace the original value \(\Lambda _{(t, s)}= (M+ \delta )^2 10^2 d_{t}^2\) by \(\Lambda _{(t, s)}= (M+ \delta ) 10 d_{t}\). In analogy, we replace in Table 2 every squared value by its non-squared value. Furthermore, Table 2 now represents the potential bounds \(p^{-}\) and \(p^{+}\) instead of \((p^{-})^2\) and \((p^{+})^2\). Finally, we replace the terms \(|q _{a} | q _{a} \) by \(q _{a} \) and \(p^2_u\) by \(p_u\) in (19). After these modifications, we can prove Lemmas 4.2–4.8 for the linear potential-based case in analogy to the nonlinear case—keeping in mind that the potentials are now coupled by (22), which simplifies some of the calculations.
This implies that CTC for linear potential-based flows is NP-hard on general graphs. \(\square \)
5 Conclusion
In this paper, we proved that computing maximal technical capacities in the European entry-exit gas market is NP-hard . To this end, we showed that the problem is NP-complete on trees for a capacitated linear flow model as well as for potential-based flows. We first reduced the Subset Sum problem to computing maximal technical capacities with capacitated linear flows on trees. Afterward, we used this result to reduce the case of capacitated linear flows to the case of potential-based flows. In contrast to the situation in the literature on the feasibility of bookings, our hardness results for CTC are already obtained for the easiest case, i.e., on tree-shaped networks and capacitated linear flow models as well as potential-based flows. Consequently, computing technical capacities is also hard for more general graph classes including trees, i.e., especially for general graphs. Another interesting question regarding the complexity of CTC is whether it is \(\Sigma _2^\mathsf {P}\)-complete for capacitated linear or nonlinear potential-based flows.
References
Aßmann, D., Liers, F., Stingl, M., & Vera, J. C. (2018). Deciding Robust Feasibility and Infeasibility Using a Set Containment Approach: An Application to Stationary Passive Gas Network Operations. SIAM Journal on Optimization, 28(3), 2489–2517. https://doi.org/10.1137/17M112470X.
Bakhouya, B., & De Wolf, D. (2007). The gas transmission problem when the merchant and the transport functions are disconnected. Technical Report. Université catholique de Lille, Jan. https://www.researchgate.net/publication/253816284_The_gas_transmission_problem_when_ the_merchant_and_the_transport_functions_are_disconnected. Accessed 5 Aug 2020.
Ben-Tal, A., El Ghaoui, L., & Nemirovski, A. (2009). Robust optimization. Princeton: Princeton University Press.
Collins, M., Cooper, L., Helgason, R., Kennington, J., & LeBlanc, L. (1978). Solving the pipe network analysis problem using optimization techniques. Management Science, 24(7), 747–760. https://doi.org/10.1287/mnsc.24.7.747.
De Wolf, D., & Smeers, Y. (2000). The gas transmission problem solved by an extension of the simplex algorithm. Management Science, 46(11), 1454–1465. https://doi.org/10.1287/mnsc.46.11.1454.12087.
Directive 98/30/EC of the European Parliament and of the Council of 22 June 1998 concerning common rules for the internal market in natural gas (OJ L 204, pp. 1–12).
Directive 2003/55/EC of the European Parliament and of the Council of 26 June 2003 concerning common rules for the internal market in natural gas and repealing Directive 98/30/EC (OJ L 176, pp. 57–78).
Directive 2009/73/EC of the European Parliament and of the Council concerning common rules for the internal market in natural gas and repealing Directive 2003/55/EC (OJ L 211, pp. 36–54).
Fügenschuh, A., Geißler, B., Gollmer, R., Morsi, A., Rövekamp, J., Schmidt, M., et al. (2015). Chapter 2: Physical and technical fundamentals of gas networks. In Evaluating gas network capacities. SIAM (pp. 17–43). https://doi.org/10.1137/1.9781611973693.ch2. Accessed 5 Aug 2020.
Fügenschuh, A., Junosza-Szaniawski, K., & Kwasiborski, S. (2014). The reservation-allocation network flow problem. Technical report, https://www.researchgate.net/publication/265126185_The_Reservation-Allocation_Network_Flow_Problem. Accessed 5 Aug 2020.
Garey, M. R., & Johnson, D. S. (1990). Computers and intractability; A guide to the theory of NP-completeness. New York, NY: W. H. Freeman & Co.
Geißler, B. (2011). Towards globally optimal solutions for MINLPs by discretization techniques with applications in gas network optimization. Ph.D. thesis, Friedrich-Alexander Universität Erlangen-Nürnberg.
Geißler, B., Morsi, A., & Schewe, L. (2013). A new algorithm for MINLP applied to gas transport energy cost minimization. In Facets of Combinatorial Optimization (pp. 321–353). Berlin: Springer. https://doi.org/10.1007/978-3-642-38189-8_14.
Geißler, B., Morsi, A., Schewe, L., & Schmidt, M. (2015). Solving power-constrained gas transportation problems using an MIP-based alternating direction method. Computers & Chemical Engineering, 82, 303–317. https://doi.org/10.1016/j.compchemeng.2015.07.005.
Geißler, B., Morsi, A., Schewe, L., & Schmidt, M. (2018). Solving highly detailed gas transport MINLPs: Block separability and penalty alternating direction methods. INFORMS Journal on Computing, 30(2), 309–323. https://doi.org/10.1287/ijoc.2017.0780.
Grimm, V., Schewe, L., Schmidt, M., & Zöttl, G. (2019). A multilevel model of the European entry-exit gas market. Mathematical Methods of Operations Research, 89(2), 223255. https://doi.org/10.1007/s00186-018-0647-z.
Groß, M., Pfetsch, M. E., Schewe, L., Schmidt, M., & Skutella, M. (2019). Algorithmic results for potential-based flows: Easy and hard cases. Networks, 73(3), 306–324. https://doi.org/10.1002/net.21865.
Hayn, C. (2016). Computing maximal entry and exit capacities of transportation networks. Ph.D. thesis. Friedrich-Alexander Universität Erlangen-Nürnberg.
Humpola, J. (2017). Gas network optimization by MINLP. Ph.D. thesis, Technische Universität Berlin
Koch, T., Hiller, B., Pfetsch, M. E., & Schewe, L. (Eds.). (2015). Evaluating gas network capacities. SIAM-MOS series on Optimization. Philadelphia: SIAM. https://doi.org/10.1137/19781611973693.
Labbé, M., Plein, F., & Schmidt, M. (2020). Bookings in the European gas market: Characterisation of feasibility and computational complexity results. Optimization and Engineering, 21(1), 305–334. https://doi.org/10.1007/s11081-019-09447-0.
Labbé, M., Plein, F., Schmidt, M.,&, Thürauf, J. (2019). Deciding feasibility of a booking in the European gas market on a cycle is in P. Technical report. http://www.optimization-online.org/DB_HTML/2019/ 11/7472.html. Accessed 5 Aug 2020.
Martin, A., Geißler, B., Hayn, C., Morsi, A., Schewe, L., Hiller, B., et al. (2011). Optimierung Technischer Kapazitäten in Gasnetzen. In Optimierung in der Energiewirtschaft. VDI-Berichte 2157 (pp. 105–114). https://opus4.kobv.de/opus4-zib/frontdoor/index/index/docId/1512.
Martin, A., Möller, M., & Moritz, S. (2006). Mixed integer models for the stationary case of gas network optimization. Mathematical Programming, 105(2), 563–582. https://doi.org/10.1007/s10107-005-0665-5.
Maugis, J. J. (1977). Étude de réseaux de transport et de distribution de fluide. RAIRO - Operations Research, 11(2), 243–248. https://doi.org/10.1051/ro/1977110202431.
Pfetsch, M. E., Fügenschuh, A., Geißler, B., Geißler, N., Gollmer, R., Hiller, B., et al. (2015). Validation of nominations in gas network optimization: Models, methods, and solutions. Optimization Methods and Software, 30(1), 15–53. https://doi.org/10.1080/10556788.2014.888426.
Ríos-Mercado, R. Z., & Borraz-Sánchez, C. (2015). Optimization problems in natural gas transportation systems: A state-of-the-art review. Applied Energy, 147, 536–555. https://doi.org/10.1016/j.apenergy.2015.03.017.
Robinius, M., Schewe, L., Schmidt, M., Stolten, D., Thürauf, J., & Welder, L. (2019). Robust optimal discrete arc sizing for tree-shaped potential networks. Computational Optimization and Applications, 73(3), 791–819. https://doi.org/10.1007/s10589-019-00085-x.
Schewe, L., Schmidt, M., & Thürauf, J. (2020). Structural properties of feasible bookings in the European entry-exit gas market system. 4OR, 18, 197–218. https://doi.org/10.1007/s10288-019-00411-3.
Schmidt, M., Steinbach, M. C., & Willert, B. M. (2015a). High detail stationary optimization models for gas networks. Optimization and Engineering, 16(1), 131–164. https://doi.org/10.1007/s11081-014-9246-x.
Schmidt, M., Steinbach, M. C., & Willert, B. M. (2015b). The precise NLP model. In T. Koch, B. Hiller, M. E. Pfetsch, & L. Schewe (Eds.), Evaluating gas network capacities (pp. 181–210). Philadelphia: SIAM. https://doi.org/10.1137/1.9781611973693.ch10.
Schmidt, M., Steinbach, M. C., & Willert, B. M. (2016). High detail stationary optimization models for gas networks: Validation and results. Optimization and Engineering, 17(2), 437–472. https://doi.org/10.1007/s11081-015-9300-3.
Schrijver, A. (2003). Combinatorial optimization—Polyhedra and efficiency. Berlin: Springer.
Szabó, J. (2012). The set of solutions to nomination validation in passive gas transportation networks with a generalized flow formula. Technical report 11-44. ZIB. URN: urn:nbn:de:0297-zib-15151.
Weymouth, T. R. (1912). Problems in natural gas engineering. Transactions of the American Society of Mechanical Engineers, 34(1349), 185–231.
Willert, B. (2014). Validation of nominations in gas networks and properties of technical capacities. Ph.D. thesis, Gottfried Wilhelm Leibniz Universität Hannover
Acknowledgements
Open Access funding provided by Projekt DEAL. This research has been performed as part of the Energie Campus Nürnberg and is supported by funding of the Bavarian State Government. The authors also thank the DFG for their support within projects A05, B07, and B08 in CRC TRR 154. We also want to thank Julia Grübel for many fruitful discussions on the topic of this paper. Finally, we thank an anonymous reviewer for pointing out an issue in a former version of Sect. 4.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schewe, L., Schmidt, M. & Thürauf, J. Computing technical capacities in the European entry-exit gas market is NP-hard. Ann Oper Res 295, 337–362 (2020). https://doi.org/10.1007/s10479-020-03725-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-020-03725-2
Keywords
- European entry-exit gas market
- Technical capacities
- Potential-based flows
- Computational complexity
- NP-hardness


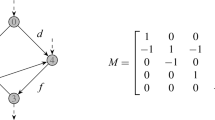

 . This means that no flow can be supplied to
. This means that no flow can be supplied to  . Thus, the claim directly follows from Theorem 4 in Robinius et al. (
. Thus, the claim directly follows from Theorem 4 in Robinius et al. ( holds. We apply Lemma
holds. We apply Lemma  is a directed flow-path from
is a directed flow-path from  . Due to this and
. Due to this and  , the claim follows.
, the claim follows.