1 Introduction

While hub-and-spoke operation has been exercised in practice (especially in telecommunications) for over a half decade now, in the last two decades (and in particular in transportation systems of the post-2008 crisis) it has received a very significant attention from researchers. The research directions have become widespread in alignment with the variety of contemporary logistics and transportation business models of the post-2008 era and the agenda of Industry 4.0 (which focuses on collaborative and cooperative aspects) in parallel with the emergence of big data and Internet of Things (IoT).

The hub-and-spoke structures aim at exploiting economies of scale resulting in minimized total costs, maximized utilization of transporters and improved/maintained service levels among other advantages. In such structures the flows among origin–destination (O–D) pairs are routed via some consolidation/redistributon/redirection centers, which are referred to as hub nodes and are connected among themselves using inter-hub connections known as hub edges. The inter-hub connections have special features such as higher performance (increased bandwidth in telecommunications, faster trains in public transport or higher capacity of mega-vessels in liner shipping) and a potential to exploit economies of scale. While in single allocation models every spoke node is allocated to one unique hub node, in the general form of multiple allocation scheme, there are no constraints on the number of hub nodes to which a spoke node can be allocated. Such networks can be seen as two nested networks: a hub-level network and a spoke-level one.

In classical models of hub location—irrespective of single allocation or multiple allocation—it is often assumed that the flows will only traverse one or two hub nodes along every O–D path (Hall 1989; O’Kelly and Lao 1991; O’Kelly 1987). This assumption leads to models with very limited applicability such as in air transport while in almost all other application areas are considered as less a realistic approximation of operative networks in practice.

Apart from this, a typical vulnerability of hub-and-spoke networks in general is that such structures encourage a sort of non-uniform concentration of volumes (stress) with high variance among different hub edges and across the hub-level network, which puts a lot of pressure on a small number of segments or entities in this sub-network. The hub nodes and hub edges in this small subset process/carry much higher volumes compared to other hub facilities.

This work has been inspired by the issues encountered by the authors in various consultancy projects in telecommunication, land and maritime transport wherein the single objective optimal hub-and-spoke network solutions were practically unrealistic in terms of variance of distribution of flow and could be a cause of inefficiencies in service design and asset management—given the level of abstraction required to model the network design problem. The approach proposed in this paper aims to generate practice-friendly outputs by providing a small number of alternative solutions that illustrate the trade-off between minimization of cost and load balancing.

Fig. 1
figure 1

The cost and flow structures of AP-n10 (derived from Australian Post dataset)

Full size image
Fig. 2
figure 2

The red circles correspond to the hub nodes and the edge colors are proportional to the flow density. (Color figure online)

Full size image

Figures 1 and 2 shed more light on the aforementioned issue in the context of a multiple allocation hub location problem where O–D flows can traverse any number of hub nodes and hub edges based on the service design on the hub-level structure [see Gelareh and Nickel (2011)].

Figure 1a, b correspond to the flow and cost matrices, respectively, of an instance with \(n=10\) generated using the techniques proposed in Ernst and Krishnamoorthy (1996). The flow matrix is not symmetric, as in Fig. 1a, and contains a node with a supply/demand that is significantly higher than others. However, the cost structure is indeed symmetric and in particular, the cost of sending one unit of flow between node 0 and nodes 7, 8 and 9 is relatively high. This can be due to several reasons such as natural and geographical barrier in land transport or even security and insurance measures in maritime transport. For the same reason, the cost of installing a hub edge between those nodes has been devised to reflect this feature.

Figure 2, depicts the optimal solution of an instance of a multiple allocation hub location problem [see Gelareh and Nickel (2011)]. The red nodes correspond to the hub nodes and the blue ones represent the spoke nodes. In the spoke-level network, in Fig. 2a, we observe a relatively balanced distribution of total flow on the spoke/access edges with the exception of the spoke edge 4–6. The latter is because as can be observed in the confusion map Fig. 1, the node 6 has an exceptionally high supply/demand in this instance, along with almost all the instances derived from the Australian Post (AP) dataset (Ernst and Krishnamoorthy 1996). This is the pattern for the multiple allocation scheme wherein every spoke node is allowed to send different portions of its flow via as many hub nodes as necessary.

However, in the hub-level network the volume of flow on hub edges is influenced by the way the spoke nodes split their receiving/sending flows among the hub nodes at which they are allocated. In Fig. 2b, one observes that the flow is not uniformly distributed across the network and certain edges and their end-points are receiving much more pressure (due to such a variance) compared to the other components. Such a pressure is a serious issue in practice, especially if the end-nodes are in charge of some sort of processing, whether human factors are involved or sustainability measures play a role. In Fig. 2b, there is a highly saturated hub edge 0–4 and four other moderately exploited edges such as 4–8, 4–9, 3–9 and 8–9. The other hub edges are significantly under utilized.

A Decision Maker (DM) may not be convinced by such a solution and may think that the current structure imposes a lot of risks on their operation due to the saturation of 0-4. Moreover, they may argue that such a high pressure on this leg and the end points will significantly increase their costs of predictive and preventive maintenance while the other low utilized edges still require regular maintenance. In general, in this solution, the return on investment may hence be sub-optimal in practice. Our initial computational experiments show that this is a common phenomenon that median-type single objective hub location (hub-and-spoke network design) models are faced with.

The problem we are dealing with in this work is of a bi-objective nature as often two distinct stakeholder are involved each with its specific objective function—network owner willing to install elements on the network aiming at minimizing huge installation costs while satisfying the demands and network operators for whom the traffic management on the rented capacities is the vital part and they have not much to do with the huge strategic installation costs and investments. In some application areas such as telecommunications, two levels of network design are observed: Physical and Logical. The physical network design belongs to the infrastructure owners where they establish physical links (e.g. fiber optic cables etc.) and determine the location of hub nodes (e.g. routers, switching centers etc.). But the network operators do not make any significant investment on installing facilities and often only lease residual capacities. They mainly focus on the choice of a set of facilities and links from among existing ones and deploy their logical network. Here, the infrastructure owners are only in charge of establishing and maintaining the infrastructure and operators are in charge of efficiently routing the O–D demands. The former see themselves as the ones to provide strategically sufficient capacity ensuring the possibility for a balanced use of their infrastructures and the latter are in charge of avoiding congestion through different (congestion) pricing strategies at the tactical and operational levels.

1.1 Literature review

In the seminal work of Hakimi (1964), it has been shown that for finding the optimal location of a single switching center that minimizes the total wire length in a communication network, one can limit oneself to find the vertex median of the corresponding graph. Goldman (1969) generalized this result.

Assuming that every origin–destination (O–D) path traverses no more than two hub nodes dates back to the models in O’Kelly (1986a, b), which were the first continuous location models for the hub-and-spoke location problems dealing with locating two hub nodes in the plane and the discrete models proposed later by e.g. O’Kelly (1987). While this assumption is valid for the applications such as air passenger transport due to the aspects of service level, customer satisfaction, business models etc., it is rather hard to justify it in applications such as land transport, air cargo transport, maritime transport, public transport and many other sort of transport activities we observe in daily life.Footnote 1

From the first round of works that started relaxing the classical assumptions of the Hub Location Problem, this topic has evolved significantly and more realistic models with better approximation of real practice have emerged. O’Kelly and Bryan (1998) dealt with flow-dependent costs and congestion cost was considered by de Camargo et al. (2009), De Camargo et al. (2011) , de Camargo and Miranda (2012) among others. Rodríguez-Martín et al. (2014) proposed a model of hub location and routing; Correia et al. (2014) dealt with multi-product and capacity; and Sasaki et al. (2014) studied a competitive hub location based on Stackelberg games.

Very few multi-period hub location models have been proposed in the literature, that includes Campbell (1990), for a continuous approximation model of a general freight carrier serving a fixed region with an increasing density of demand, Gelareh (2008), Gelareh et al. (2015) for a HLP model within which the transport service provider starts with an initial configuration of the hub-level structure at the first period and then the network evolves in the course of a planning horizon and Contreras et al. (2011) for a dynamic uncapacitated hub location problem.

Very recently, Monemi et al. (2017) proposed a hub location problem in a co-opetitive setting. Interested readers are also referred to the recent HLPs literature review in Alumur and Kara (2008), Campbell and O’Kelly (2012) and Farahani et al. (2013) as well as other contributions by Campbell et al. (2002) and Kara and Taner (2011).

Concerning control of density of flow across the network, we can refer to the following works. Rahimi et al. (2016) dealt with a bi-objective model for a multi-modal hub location problem under uncertainty considering congestion in the hubs. Their objective functions attempt to minimize the total transportation cost as well as minimize the maximum transportation time between each pair of O–D in the network. Their proposed model is a nonlinear one and they resorted to metaheuristic approaches. De Camargo et al. (2011) dealt with a single allocation hub location problem under congestion, which is formulated as a nonlinear program and proposed a hybrid of outer approximation and a Benders approach to solve it. de Camargo and Miranda (2012) addressed a single allocation hub location problem under congestion and proposed a nonlinear formulation. de Camargo et al. (2009) studied the multiple allocation case with a nonlinear convex objective function. Elhedhli and Hu (2005a) dealt with a single allocation p-hub location problem and obtained an objective function with a non-linear cost term in it. They linearized the model, and provided an efficient Lagrangean heuristic. Elhedhli and Wu (2010) formulated congestion as a nonlinear mixed-integer program that explicitly minimizes congestion, capacity acquisition, and transportation costs. Congestion at hubs is modeled as the ratio of total flow to surplus capacity by viewing the hub-and-spoke system as a network of M/M/1 queues. They used a Lagrangean heuristic on a linearized version of the nonlinear subproblems.

Table 1 summarizes the key features in some of the closely related contributions.

Table 1 A summary of main elements of the relevant contributions in literature
Full size table

From the infrastructure owner perspective, a balanced distribution of flow across the hub-and-spoke network structure is a critical issue, which has received little attention in the literature (while congestion pricing from the operator viewpoints has received more attention). We study both capacitated and uncapacitated variants of the Multiple Allocation Hub Location Problem with fixed charge cost of hub nodes and edge. We consider two objective functions and deal with these in a compromise programming framework. To the best of our knowledge, this is the first approach of its type dealing with de-stressing in a hub-and-spoke structure in the literature and we are unaware of any similar work.

1.2 Contribution and scope

This paper looks at the problem from the infrastructure owner’s point of view and distinguishes between a load balancing (de-stressing) at the strategic level and congestion pricing in the lower levels. It is distinct from all other works by taking into account network design and hub-level flow balance (both at hub nodes and hub edges) in a bi-objective model. If we assume that once the infrastructure owner establish their facilities, the network operators will address their own problem of choosing among those hub nodes and hub edges to define their own sub-network and control their traffic by incorporating congestion cost. From the real-life application point of view, this work lies between these two levels. This paper presents the first generalized framework to deal with bi-objective models of capacitated and uncapacitated multiple allocation hub location problems, which take into account load balancing in the strategic level. This work is inspired by some of the authors’ consultancy projects with applications in liner shipping, land transport and traffic engineering in telecommunication applications. A compromise programming approach to the problem leads to non-linearities that are handled through perspective reformulation (leading to second order conic counterparts) and linearization for the capacitated and uncapacitated cases. In addition, by exploiting the structure of models and problems, we propose a very efficient matheuristic capable of producing effective high quality and practice-friendly solutions in reasonable time. We also validate our results and the efficiency of our approach on a real-life instance from the land transport industry.

This paper is organized as follows: the mathematical models are proposed in Sect. 2, together with the techniques to transform the models to the more tractable counterparts. In Sect. 3, we describe our approach for dealing with the bi-objective model. Section 4 describes and elaborates on the design of our matheuristic. Section 5 reports some computational experiments and gives insights into the effectiveness of proposed approach. In Sect. 6, we summarize, draw conclusions and provide suggestions for further research directions.

2 Mathematical models

A Multiple Allocation Hub Location Problemwhich is referred to as HLPPT in Gelareh and Nickel (2011) constitute the starting point of our modeling. The variables and parameters in the proposed model are defined as in the following. It much be noted that for the ease of notation and without loss of generality we assume dealing with a complete graph, otherwise one can simply fix the variable corresponding to the non-existing elements to 0.

Variables \(x_{ijkl}, ~\forall i,j\ne i, k, l\notin \{k,i\}\) represent the fraction of flow from i to j that traverses the hub edge \(\{k,l\}\). Also, \(a_{ijk} , \forall j\ne i, k\ne i,j\) stands for the fraction of flow from i to j that traverses spoke edge (i, k), where i is not a hub and k is a hub node, and \(b_{ijk}, \forall j\ne i, k\notin \{ i,j\}\) represents the optimal path from i to j traversing (k, j), where k is a hub node and j is not a hub. In addition, \(e_{ij}, \forall i\ne j\) represents the fraction of flow from i to j that traverses (i, j) where at most one of i and j is a spoke node (see Fig. 3). For the hub-level variables, \(y_{kl}= 1, k<l\) if the hub edge \(\{k,l\}\) is established, 0 otherwise and \(h_{k}= 1\) if node k is chosen to be a hub, 0 otherwise. We also define \(\ddot{g}_{kl}(.)\) and \({\dot{g}}_{k}(.)\) to represent the stress-related functions for the hub edge \(k-l\) and hub node k, respectively.

Fig. 3
figure 3

The correspondence between variables and network elements. The boxes represent hub nodes and circles represent spoke nodes

Full size image

Parameters The transportation cost per unit of flow with origin i and destination j amounts to the sum of: (i) the cost of sending flow from i to the first hub node (if i is a spoke node assigned to a hub node) in the path to j, (ii) the cost incurred by traversing one or more hub edges in the hub-level network discounted by the factor \(\alpha \), \(0<\alpha < 1\), and, (iii) the cost of transition on the last spoke edge (if destination is a spoke node). We introduce \(W_{ij}\) as the flow from i to j, \(C_{ij}\) the cost per unit of flow on link i to j, \(F_k\) fixed cost for establishing hub at node k and \(I_{kl}\) the fixed cost for establishing hub link between nodes k and l.

The De-stressing Hub Location Problem (DSHLP) in its general form follows: (DSHLP)

$$\begin{aligned} \min ~~~ Z_1=&\sum _i\sum _{j\ne i}\sum _k\sum _{l\ne k} \alpha W_{ij}C_{kl} x_{ijkl} + \sum _i\sum _{j\ne i}\sum _{k\ne i,j} W_{ij}C_{ik} a_{ijk} + \nonumber \\&\sum _i\sum _{j\ne i}\sum _{k\ne i,j} W_{ij}C_{kj} b_{ijk} + \sum _i\sum _{j\ne i} W_{ij}C_{ij} e_{ij} +\nonumber \\&\sum _k F_k h_k + \sum _k \sum _{l>k} I_{kl} y_{kl} \end{aligned}$$
(1)
$$\begin{aligned} \min ~~~Z_2=&\sum _k \sum _{l>k}{\ddot{g}_{kl}}+\sum _{k}{{\dot{g}}_{kl}}\end{aligned}$$
(2)
$$\begin{aligned} s.t.&\nonumber \\&\sum _{l\ne i} x_{ijil}+\sum _{l\ne i,j} a_{ijl} + e_{ij} = 1 ,&i,j\ne i, \end{aligned}$$
(3)
$$\begin{aligned}&\sum _{l\ne j} x_{ijlj}+\sum _{l\ne i,j} b_{ijl} + e_{ij} = 1,&i,j\ne i, \end{aligned}$$
(4)
$$\begin{aligned}&\sum _{l\ne k, i}x_{ijkl}+ b_{ijk}= \sum _{l\ne k, j}x_{ijlk} + a_{ijk},&i,j\ne i,k\ne i,j, \end{aligned}$$
(5)
$$\begin{aligned}&y_{kl}\le h_k,&k,l>k, \end{aligned}$$
(6)
$$\begin{aligned}&y_{kl}\le h_l,&k,l>k, \end{aligned}$$
(7)
$$\begin{aligned}&x_{ijkl}+x_{ijlk}\le y_{kl},&i,j\ne i,k,l>k, \end{aligned}$$
(8)
$$\begin{aligned}&\sum _{l\ne i} x_{ijil} \le h_i,&j,i\ne j, \end{aligned}$$
(9)
$$\begin{aligned}&\sum _{k\ne j} x_{ijkj} \le h_j,&i,j\ne i, \end{aligned}$$
(10)
$$\begin{aligned}&e_{ij} \le 2-(h_i+h_j),&i,j\ne i, \end{aligned}$$
(11)
$$\begin{aligned}&a_{ijk} \le 1-h_i,&i,j\ne i,k\ne i,j, \end{aligned}$$
(12)
$$\begin{aligned}&b_{ijl} \le 1 -h_j,&i,j\ne i,l\ne i,j, \end{aligned}$$
(13)
$$\begin{aligned}&a_{ijk}+\sum _{l\ne j, k} x_{ijlk} \le h_k,&i,j\ne i,k\ne i,j, \end{aligned}$$
(14)
$$\begin{aligned}&b_{ijk}+\sum _{l\ne k, i} x_{ijkl} \le h_k,&i,j\ne i,k\ne i,j, \end{aligned}$$
(15)
$$\begin{aligned}&e_{ij}+2x_{ijij}+\sum _{l\ne j, i}x_{ijil}+\sum _{l\ne i, j}x_{ijlj}\le h_i+h_j,&i,j\ne i, \end{aligned}$$
(16)
$$\begin{aligned}&\sum _{k,l}y_{kl} \ge 1, \end{aligned}$$
(17)
$$\begin{aligned}&\ddot{g}_{kl}(.) \ge 0,&\forall k,l>k,\end{aligned}$$
(18)
$$\begin{aligned}&{\dot{g}}_{k}(.) \ge 0,&\forall k,\end{aligned}$$
(19)
$$\begin{aligned}&x_{ijkl},a_{ijk},b_{ijk},e_{ij} \in (0,1), h_k,y_{kl} \in \{0,1\} . \end{aligned}$$
(20)

The first objective (1) accounts for the total cost of transportation plus hub node and hub edge setup costs while the second objective function (2) corresponds to the stress functions for hub nodes and hub edges. Constraints (3)–(5) are the flow conservation constraints. Constraints (6)–(7) ensure that both end-points of a hub edge are hub nodes. The constraints (8) ensure that a hub edge should exist before being used in any flow path. In (9) (resp. (10) ) it is ensured that only a flow with origin (destination) of hub type is allowed to select a hub edge to leave the origin (arrive at the destination). Constraints (12)–(13) check the end-points of spoke edges. Any flow from i to j that enters to (departs from) a node other than i and j, must make sure that the node is a hub node. This is ensured by (14) ((15)). The choice of edges on the path between origin and destination (i and j) depends on the status of i and j: whether both, none or just one of them is a hub. This is checked by (16). Constraint (17) ensure that there will be at least one hub edge in every feasible solution. Constraints (18) and (19) stand for the stress-related functions for the capacitated/uncapacitated versions.

2.1 Uncapacitated de-stressed fixed cardinality hub location problem (UDSFCHLP)

In the uncapacitated case, de-stressing is done by allocating the volume of flow in such a way that the variance of flow volume on the hub facilities is minimized.

The general form of such a load balancing objective function for the hub edges (\({\ddot{U}}_{kl}\)) follows (Altın et al. 2009):

$$\begin{aligned}&\zeta \sum _{k,l>k} \left( {\ddot{U}}_{kl}-{\ddot{U}}^{mean}\right) ^2+\beta \sum _{k,l>k} {\ddot{U}}_{kl}^2 \end{aligned}$$
(21)

where \({\ddot{U}}_{kl}\) represents the load of edge \(\{k,l\}\) and \({\ddot{U}}^{mean}\) stands for the average load among the hub edges. The first term measures the sum of squared deviations from the mean over the hub edges and the second term controls the impact on the shortest path. As our first objective function already takes care of the transportation cost and distance, to avoid double counting, we set \(\beta =0\) while \(\zeta =1\).

For the hub edges, the load is equivalent to the total flow transported on the hub edges:

$$\begin{aligned} {\ddot{U}}^{mean}&= \frac{1}{|E|}\sum _{\{k,l\}}{\ddot{U}}_{kl} = \frac{1}{\sum _{k,l>k}y_{kl}}\sum _{k,l>k}{\ddot{U}}_{kl} , \end{aligned}$$
(22)
$$\begin{aligned} {\ddot{U}}_{kl}&= \sum _{i,j\ne i}w_{ij}x_{ijkl},&\forall k,l>k, \end{aligned}$$
(23)

and for the hub nodes, the load, \({\dot{U}}_{k}\), is equal to the flows arrived (sent or relayed) via adjacent hub nodes plus the ones received from the spoke nodes toward any destination other than the hub itself (using variables \(a_{ijk}\)). The average load of hub nodes, \({\dot{U}}^{mean}\), is equivalent to the sum of flows arriving to all hub nodes divided by the total number of them.

$$\begin{aligned} {\dot{U}}^{mean}&= \frac{1}{|H|}\sum _{k}{\dot{U}}_{k} = \frac{1}{\sum _{k}h_{k}}\sum _{k}{\dot{U}}_{k} , \end{aligned}$$
(24)
$$\begin{aligned} {\dot{U}}_{k}&= \sum _{i,j\ne i}\sum _{l\notin \{ j,k\}}w_{ij}x_{ijlk}+\sum _{i, j\ne i}w_{ij}a_{ijk},&\forall k. \end{aligned}$$
(25)

The non-smooth optimization problems induced by constraints (22) and (24) is not efficiently handled by general-purpose black-box solvers such as CPLEX. We therefore, resort to a fixed cardinality approach and add the following two constraints to the formulation:

$$\begin{aligned} \sum _{k,l>k}y_{kl}=q.&\end{aligned}$$
(26)
$$\begin{aligned} \sum _{k}h_{k} = p.&\end{aligned}$$
(27)

Now, we define \(\ddot{g}_{kl}, {\dot{g}}_{k}\ge 0\) for the hub edge and hub nodes, respectively:

$$\begin{aligned}&\displaystyle \ddot{g}_{kl} \ge \left( \sum _{i,j\ne i}w_{ij}x_{ijkl}-\frac{\sum _{k,l>k}\sum _{i,j\ne i}w_{ij}x_{ijkl}}{q}\right) ^2, \forall k,l>k, \end{aligned}$$
(28)
$$\begin{aligned}&\displaystyle {\dot{g}}_{k} \ge \left( \sum _{i,j\ne i}\sum _{l\notin \{ j,k\}}w_{ij}x_{ijlk}+\sum _{i, j\ne i}w_{ij}a_{ijk}-\frac{\sum _{k}\left( \sum _{i,j\ne i}\sum _{l\notin \{ j,k\}}w_{ij}x_{ijlk}+\sum _{i, j\ne i}w_{ij}a_{ijk}\right) }{p}\right) ^2, \qquad \forall k. \end{aligned}$$
(29)

Therefore, the complete mathematical model for UDSFCHLP as follows:

$$\begin{aligned}&(1)\\&(2)\\ s.t.&\\&(3){-}(20)\\&(26){-}(27), \\&(28)\text{, } \text{ and } (29). \end{aligned}$$

Often the standard commercial general-purpose solvers have difficulties to handle this model in which case it can be reformulated as follows. Constraints (28) and (29) are quadratic and semi-positive definite, which (after introducing the required auxiliary variables \( \ddot{\nu }_{kl} \in \mathbb {R}\) and \(\ddot{f}_{kl}\in \mathbb {R}^+\)) can be represented as a second order conic form as follows.

For hub edges, the reformulation yields:

$$\begin{aligned}&\ddot{f}_{kl} \ge \frac{\sum _{k,l>k}\sum _{i,j\ne i}w_{ij}x_{ijkl}}{q} - {\ddot{M}}(1-y_{kl}),&\forall k,l>k, \end{aligned}$$
(30)
$$\begin{aligned}&\ddot{f}_{kl} \le \frac{\sum _{k,l>k}\sum _{i,j\ne i}w_{ij}x_{ijkl}}{q} ,&\forall k,l>k, \end{aligned}$$
(31)
$$\begin{aligned}&\ddot{\nu }_{kl} = \ddot{f}_{kl} - \sum _{i,j\ne i}w_{ij}x_{ijkl},&\forall k,l>k, \end{aligned}$$
(32)
$$\begin{aligned}&\ddot{g}_{kl} \ge \left( \ddot{\nu }_{kl}\right) ^2,&\forall k,l>k, \end{aligned}$$
(33)
$$\begin{aligned}&\ddot{\nu }_{kl} \in \mathbb {R}, \ddot{f}_{kl}\in \mathbb {R}^+, \forall k,l>k. \end{aligned}$$
(34)

where \({\ddot{M}}\) is a sufficiently large instance-dependent number no larger than \(\sum _{i,j\ne i}w_{ij}\).

For the hub nodes we have:

$$\begin{aligned}&{\dot{f}}_{k} \ge \frac{\sum _{k}\left( \sum _{i,j\ne i}\sum _{l\notin \{ j,k\}}w_{ij}x_{ijlk}+\sum _{i, j\ne i}w_{ij}a_{ijk}\right) }{p} - {\dot{M}}(1-h_{k}),&\forall k, \end{aligned}$$
(35)
$$\begin{aligned}&{\dot{f}}_{k} \le \frac{\sum _{k}\left( \sum _{i,j\ne i}\sum _{l\notin \{ j,k\}}w_{ij}x_{ijlk}+\sum _{i, j\ne i}w_{ij}a_{ijk}\right) }{p},&\forall k, \end{aligned}$$
(36)
$$\begin{aligned}&{\dot{\nu }}_{k} = {\dot{f}}_{k} - \left( \sum _{i,j\ne i}\sum _{l\notin \{ j,k\}}w_{ij}x_{ijlk}+\sum _{i, j\ne i}w_{ij}a_{ijk} \right) ,&\forall k, \end{aligned}$$
(37)
$$\begin{aligned}&{\dot{g}}_{k} \ge \left( {\dot{\nu }}_{k}\right) ^2,&\forall k,\end{aligned}$$
(38)
$$\begin{aligned}&{\dot{\nu }}_{k} \in \mathbb {R}, {\dot{f}}_{k}\in \mathbb {R}^+, \forall k. \end{aligned}$$
(39)

where \({\dot{M}}\) is a sufficiently large instance-dependent number no larger than \(\sum _{i,j\ne i}w_{ij}\).

It must be noted that for the (load balancing \(Z_2\)) single objective UDSFCHLP, the optimal objective value is always 0 as, for any hub-level structure, it is always possible to route the flow such that the load on all the hub edges be equal.

2.2 Capacitated de-stressed hub location problem (CDSHLP)

In a capacitated environment, the congestion cost of a hub facility (edge or node) is proportional to the gap between volume of occupation and the nominal capacity of the network component. We introduce \(\Gamma _{kl}\) to be the capacity associated to the hub edge \(k-l\) and \(\Upsilon _k\) the capacity of hub nodes k. We assume that the congestion is an average delay of an M/M/1 queue (as in Elhedhli and Wu 2010) and minimize the sum of convex delay cost functions associated with each hub facility.

We need to introduce a new set of capacity constraints to constrain the volume of flow that can be accommodated/processed by every hub facility (hub edge \(k-l\) and hub node k).

$$\begin{aligned}&\sum _{i,j\ne i} w_{ij}x_{ijkl} \le \Gamma _{kl}y_{kl} ,&\forall k,l> k. \end{aligned}$$
(40)
$$\begin{aligned}&\sum _{i,j\ne i}\sum _{l\notin \{ j,k\}}w_{ij}x_{ijlk}+\sum _{i, j\ne i}w_{ij}a_{ijk} \le \Upsilon _{k}h_k ,&\forall k. \end{aligned}$$
(41)

For hub edges, the stress function \(\ddot{g}_{kl}\) follows the following form:

$$\begin{aligned} \ddot{g}_{kl}&\ge \frac{ {\ddot{U}}_{kl} }{\left( 1-\frac{\sum _{k,l\ne k} {\ddot{U}}_{kl} }{\Gamma _{kl}}\right) } = \frac{\sum _{i,j\ne i} w_{ij}x_{ijkl} }{\left( 1-\frac{\sum _{i,j\ne i} w_{ij}x_{ijkl} }{\Gamma _{kl}}\right) },&\forall k,l> k, \end{aligned}$$
(42)

which can be written as:

$$\begin{aligned}&\ddot{g}_{kl} \ge \frac{\Gamma _{kl}\sum _{i,j\ne i} w_{ij}x_{ijkl} }{\left( \Gamma _{kl}-\sum _{i,j\ne i} w_{ij}x_{ijkl} \right) },&\forall k,l> k,\end{aligned}$$
(43)
$$\begin{aligned}&\ddot{g}_{kl}\left( \Gamma _{kl}-\sum _{i,j\ne i} w_{ij}x_{ijkl} \right) \ge \Gamma _{kl}\sum _{i,j\ne i} w_{ij}x_{ijkl},&\forall k,l> k. \end{aligned}$$
(44)

After some algebra, one obtains:

$$\begin{aligned}&(\ddot{g}_{kl} - \sum _{i,j\ne i} w_{ij}x_{ijkl})(\Gamma _{kl}- \sum _{i,j\ne i} w_{ij}x_{ijkl}) \ge \left( \sum _{i,j\ne i} w_{ij}x_{ijkl}\right) ^2,&\forall k,l>k, \end{aligned}$$
(45)

and as \(\ddot{g}_{kl} \ge \sum _{i,j\ne i} w_{ij}x_{ijkl}\) and \(\Gamma _{kl}\ge \sum _{i,j\ne i} w_{ij}x_{ijkl}\), (45) is a rotated second order conic form.

In CDSHLP, if \(y_{kl}=0\), no flow is transported on this edge \(k-l\), otherwise constraints (40) must be satisfied. Constraints (45) can therefore be replaced by the following rotated second order cone constraints:

$$\begin{aligned}&(\ddot{g}_{kl} - \sum _{i,j\ne i} w_{ij}x_{ijkl})(\Gamma _{kl}y_{ij}- \sum _{i,j\ne i} w_{ij}x_{ijkl}) \ge \left( \sum _{i,j\ne i} w_{ij}x_{ijkl}\right) ^2,&\forall k,l>k, \end{aligned}$$
(46)

given that \(\ddot{g}_{kl} \ge \sum _{i,j\ne i} w_{ij}x_{ijkl}\) and \(\Gamma _{kl}y_{ij} \ge \sum _{i,j\ne i} w_{ij}x_{ijkl}\).

For the hub nodes, we have a similar development:

$$\begin{aligned}&({\dot{g}}_{k} - \sum _{i,j\ne i}\sum _{l\notin \{ j,k\}}w_{ij}x_{ijlk}-\sum _{i, j\ne i}w_{ij}a_{ijk})(\Upsilon _{k}h_{k}\nonumber \\&\quad - \sum _{i,j\ne i}\sum _{l\notin \{ j,k\}}w_{ij}x_{ijlk}-\sum _{i, j\ne i}w_{ij}a_{ijk}) \ge \left( \sum _{i,j\ne i}\sum _{l\notin \{ j,k\}}w_{ij}x_{ijlk}+\sum _{i, j\ne i}w_{ij}a_{ijk}\right) ^2,&\forall k, \end{aligned}$$
(47)

The complete mathematical model for CDSHLP follows:

$$\begin{aligned}&(1)\\&(2)\\ s.t.&\\&(3){-}(20)\\&(46)\text{, } \text{ and } (47). \end{aligned}$$

Again, most of the solvers have difficulties to deal with this form and this needs to be re-written by introducing some auxiliary variables.

For hub edges, we require \(\ddot{\nu }_{kl}^{(3)}, \ddot{\nu }_{kl}^{(4)}, \ddot{\nu }_{kl}^{(5)} \ge 0\):

$$\begin{aligned}&\ddot{\nu }_{kl}^{(3)} = \ddot{g}_{kl} - \sum _{i,j\ne i} w_{ij}x_{ijkl},&\forall k,l>k, \end{aligned}$$
(48)
$$\begin{aligned}&\ddot{\nu }_{kl}^{(4)} = \Gamma _{kl}y_{ij}- \sum _{i,j\ne i} w_{ij}x_{ijkl},&\forall k,l>k, \end{aligned}$$
(49)
$$\begin{aligned}&\ddot{\nu }_{kl}^{(5)} = \left( \sum _{i,j\ne i} w_{ij}x_{ijkl}\right) ,&\forall k,l>k, \end{aligned}$$
(50)
$$\begin{aligned}&\left( \ddot{\nu }_{kl}^{(5)}\right) ^2 \le v_{kl}^{(3)} v_{kl}^{(4)} ,&\forall k,l>k, ,\end{aligned}$$
(51)
$$\begin{aligned}&\ddot{\nu }_{kl}^{(3)}, \ddot{\nu }_{kl}^{(3)}, \ddot{\nu }_{kl}^{(3)} \ge 0,&\forall k,l>k. \end{aligned}$$
(52)

For the hub nodes, let \({\dot{f}}_k = \left( \sum _{i,j\ne i}\sum _{l\notin \{ j,k\}}w_{ij}x_{ijlk}+\sum _{i, j\ne i}w_{ij}a_{ijk}\right) \), we have:

$$\begin{aligned}&{\dot{\nu }}_{k}^{(3)} = {\dot{g}}_{k} - {\dot{f}}_k,&\forall k, \end{aligned}$$
(53)
$$\begin{aligned}&{\dot{\nu }}_{k}^{(4)} = \Upsilon _{k}h_{k}- {\dot{f}}_k,&\forall k, \end{aligned}$$
(54)
$$\begin{aligned}&{\dot{\nu }}_{k}^{(5)} = \left( {\dot{f}}_k\right) ,&\forall k, \end{aligned}$$
(55)
$$\begin{aligned}&\left( \ddot{v}_{k}^{(5)}\right) ^2 \le {\dot{v}}_{k}^{(3)} {\dot{v}}_{k}^{(4)} ,&\forall k, \end{aligned}$$
(56)
$$\begin{aligned}&{\dot{\nu }}_{k}^{(3)}, {\dot{\nu }}_{k}^{(3)}, {\dot{\nu }}_{k}^{(3)} \ge 0,&\forall k. \end{aligned}$$
(57)

2.3 Illustrative examples and some reduction

In this section, we report the optimal solutions of four single objective problems corresponding to the capacitated and uncapacitated for cost and load balancing objective functions.

For the uncapacitated case, in Fig. 4, the optimal solutions of the single objective problems are depicted. The red circles represent the hub nodes and the blue ones stand for the spoke nodes. The node sizes (the diameter of nodes) are proportional to the volume of flow they process (supply, demand and transshipment) and the edge colors are proportional to the volume of flow on they carry (as shown by the color-map bar in each figure).

Expectedly, the network structures (in Fig. 4a, b) are quite different while also sharing some elements. As can be seen in Fig. 4a, the edges carry significantly different volumes of flow. For example, the edges 10–12 and 1–4 are on the extreme ends of the scale. However, in Fig. 4b the edges carry almost similar volumes and stick around an average.

Fig. 4
figure 4

Optimal solution of AP instance \(n=15\) with \(q=9\), \(p=7\) and \(\alpha =0.75\) in an uncapacitated environment

Full size image

For the capacitated case, Fig. 5, we observe again a similar pattern—the network structures are very different. Moreover, as the hub edges are subject of load balancing (not the spoke edges) therefore, often a very few and even very often only a single hub edge appears in an optimal solution of the load balancing problem (e.g. Fig. 5b) as this solution is the one that minimizes a hub-edge load balancing objective function.

Fig. 5
figure 5

Optimal solution of AP instance \(n=15\) and \(\alpha =0.75\) in a capacitated environment

Full size image

An important observation out of an extensive preliminary computational experiments is the following, which is very helpful in reducing the computational burden.

Observation 1

In a single objective model of load balancing, the balancing on the hub edges implies (with a very high precision) a load balancing on the hub nodes as well (but not vice versa). Therefore, the node-related variable and constraints can be safely removed in favor of a better computational behavior while the solution quality remains balanced and practice-friendly. However, still there is a constraint on the number of hub nodes that can appear in an optimal solution. This number cannot be larger than \(\frac{n}{2}\)—i.e. at most half of the nodes can become a hub. Therefore the constraints (27) will be modified to:

$$\begin{aligned} \sum _{k}h_{k} \le \frac{n}{2}.&\end{aligned}$$
(58)

Therefore, based on this preliminary extensive computational experiments, we opt to remove all the node-related variables and stick to the edge-based ones.

3 Bi-objective optimization: compromise programming

There is a large body of literature on method for dealing with the multi-objective optimization problems including goal programming, Pareto set construction, and compromise programming. In the case of our problem, Compromise Programming seems to be a viable approach compared to the goal programming techniques (because no information about the goal target values is available) and Pareto frontier generation approach (due to the nonlinearity in both CDSHLP and UDSFCHLP). Moreover Romero et al. (1998) also showed that the CP method works well with the two objective functions.

CP was first introduced by (Zeleny 1973) and relies on the reasonable assumption that DMs choice of solution is biased towards proximity the ideal point (Romero and Rehman 2003). This is formalized by the choice of a solution that minimizes an LP distance metric of the difference between the achieved and ideal values of the objectives.

This approach relies on minimizing the scaled distance between the ideal and efficient solutions Jones and Tamiz (2010). The relationship between the aforementioned approaches to deal with the multi-objective optimization problems is elaborated in Romero et al. (1998). On the other hand, Ballestero (2007) regards CP method as the maximization of the decision maker’s additive utility.

Some successful applications of the CP approach include: (Anton and Bielza 2003) for a road project selection in Madrid, Spain; (André et al. 2008) for an application in macro-economic policy making in a general equilibrium framework for a case-study of Spain; (Fattahi and Fayyaz 2010) for an urban water management problem; (Amiri et al. 2011) for a multi-objective portfolio problem; (Liberatore et al. 2014) for a optimizing recovery operations and distribution of emergency goods; (Kanellopoulos et al. 2015) for scenario assessment; and recently Irawan et al. (2017) applied this technique on a model for installation scheduling in offshore wind-farms.

The general formulation of a CP approach is expressed as follows:

$$\begin{aligned} Min~~&Lp = \left( \sum _{1}^n \left| {\widehat{w}}_i \frac{Z_i(x)- Z_i^*}{Z_{i*}- Z_i^*} \right| ^p\right) ^\frac{1}{p} \end{aligned}$$
(59)

wherein, \(p\in [1,\infty ]\) represents the distance metric and n is the number of objective functions. The \(p=1\) solution represents pure optimization of the objectives, whereas the \(p=\infty \) solution represents balance between the objectives. The intermediate solutions in the range \(p\in (1,\infty )\) therefore represent the transition from a pure optimization to a balanced solution. Moreover, \(Z_i^*\) represents the ideal value of objective i, \(Z_{i*}\) stands for the anti-ideal value of objective i, \(Z_i(x)\) represents the achieved values of the i’th objective and \({\widehat{w}}_i\) stands for the weight/importance of objective i relative to the others. An anti-ideal solution for the load balancing model corresponds to a solution that installs some hub nodes/edges and routes the flow through shortest path causing a huge volume of flow traversing a few hub-level edges and an anti-ideal solution for the cost minimization model corresponds to a solution that installs many hub edges with very low utilization resulting.

Although the problems at hand are mostly non-linear ones, we may be still consider the properties that are known for the linear cases: One may limit oneself to \(p\in \{1,\infty \}\), which can be used to derive a good approximation of intermediate compromise set points given that the problem is a bi-objective one (i.e. \(n=2\)) [see Romero et al. (1998)]. The CP objective function of CDSHLP and UDSFCHLP for \(p\in \{1,\infty \}\) are developed in the following:

Case I \(p=1\)

(60)

which is equivalent to following linear objective function (in the bi-objective case).

$$\begin{aligned} \min&~~~ \left( \sum _i\sum _{j\ne i}\sum _k\sum _{l\ne k} \alpha W_{ij}C_{kl} x_{ijkl} + \sum _i\sum _{j\ne i}\sum _{k\ne i,j} W_{ij}C_{ik} a_{ijk}\right. \nonumber \\&+ \sum _i\sum _{j\ne i}\sum _{k\ne i,j} W_{ij}C_{kj} b_{ijk} + \sum _i\sum _{j\ne i} W_{ij}C_{ij} e_{ij} \nonumber \\&\left. +\sum _k F_k h_k + \sum _k \sum _{l>k} I_{kl} y_{kl}\right) \frac{{\widehat{w}}_1}{|Z_{1*}- Z_1^*|} + \left( \frac{{\widehat{w}}_2\sum _{k,l>k}g^a_{kl}}{|Z_{2*}- Z_2^*|}\right) + \alpha _1 +\alpha _2 \end{aligned}$$
(61)

where \(\alpha _i=-\frac{{\widehat{w}}_iZ_i^*}{Z_{i*}- Z_i^*},~~\forall i\in \{1,2\}\).

Case II \(p=\infty \) The objective function (59) minimizes the maximum deviation (\(\pi \)) as follows:

(62)

which is equivalent (in the bi-objective case) to:

$$\begin{aligned} \min ~~&\pi \end{aligned}$$
(63)
$$\begin{aligned}&\left( \sum _i\sum _{j\ne i}\sum _k\sum _{l\ne k} \alpha W_{ij}C_{kl} x_{ijkl} + \sum _i\sum _{j\ne i}\sum _{k\ne i,j} W_{ij}C_{ik} a_{ijk}\right. \nonumber \\&+ \sum _i\sum _{j\ne i}\sum _{k\ne i,j} W_{ij}C_{kj} b_{ijk} + \sum _i\sum _{j\ne i} W_{ij}C_{ij} e_{ij} \nonumber \\&\left. +\sum _k F_k h_k + \sum _k \sum _{l>k} I_{kl} \right) \frac{{\widehat{w}}_1}{|Z_{1*}- Z_1^*|} + \alpha _1 \le \pi \end{aligned}$$
(64)
$$\begin{aligned}&\left( \frac{{\widehat{w}}_2\sum _{k,l>k}g^a_{kl}}{|Z_{2*}- Z_2^*|}\right) +\alpha _2 \le \pi \end{aligned}$$
(65)

Figure 6 depicts the compromise objective function values for our bi-objective load balancing multiple allocation hub location problem. A and B are optimal objective values of cost and stress minimization problems, respectively. While E is the nadir or an anti-ideal point, node F is the idea point wherein both single objectives are at their optimal. The line segment connecting points C and D sets an upper envelop on all the compromise solutions, i.e. \(\overrightarrow{DC}\), is a representation of the compromise set. Towards the end point D the load balance is improved while the cost function will deteriorate and as we move further towards C, the cost objective function will improve and the load balancing objective function will deteriorate. As expected, the point C provides a better balance between the two objectives than point D.

Fig. 6
figure 6

Compromise solutions in the bi-objective load balancing multiple allocation hub location problem

Full size image

4 Solution method

Compromise programming is an approach parameterized by weight factors \({\widehat{w}}_i\). In a transition from to , the computational behavior of the problem changes dramatically from a linear combination of objective functions to a minimax objective function, which is known to be computationally challenging Florentino et al. (2017). In addition, our initial computational experiments with different decomposition techniques revealed that different combinations of \({\widehat{w}}_i\) in both and cases, lead to models with significantly different computational behavior. As a result, an exact (decomposition) approach, which perform very efficiently on one combination, often performs poorly with another combination of weights. It must be noted that although the polyhedral structure is not altered, the gradient of objective function becomes different for every combination of weights.

More precisely, although both problems possess structures that make primal decompositions such as Benders decomposition (Benders 2005) an obvious candidate, however, constraints (30) discourage Benders-like approaches for UDSFCHLP and . Because from among load balancing constraints (30)–(34) only constraints (30) (in addition to the subproblem described in Gelareh and Nickel (2011)) depend on the integer variables of the master and given the nature of such big-M constraints, the resulting Benders cuts become very weak—even after sharpening—and convergence tends to be very slow. For UDSFCHLP with , a combinatorial Benders Codato and Fischetti (2006) is a potential candidate rather than the classical Benders ( Benders (1962)) but even that did not report any good performance (with all sorts of tweaking, variable fixing, heuristic injections etc.).

For CDSHLP and , a very sophisticated Benders decomposition (equipped with variable elimination, specialized branching and various cut separations etc.) has not reported any particular efficiency. For CDSHLP and , we observed the same issues as with the case of UDSFCHLP with .

Likewise, some sophisticated dual approaches such as Lagrangian and column generation-like approaches have also been examined with very limited success being reported.

Nevertheless, the same properties that suggest a primal-type relaxation can be exploited to propose a heuristic approach.

4.1 Variable neighborhood methods

Variable Neighborhood Search (VNS) (Mladenović and Hansen 1997) is a flexible framework for building heuristics to solve combinatorial and continuous global optimization problems approximately. The idea is to systematically alternate exploring different neighborhood structures while seeking an optimal (or near-optimal) solution. The philosophy of VNS relies on the following facts: (i) a local optimum relative to one neighborhood structure is not necessarily the local optimum for another neighborhood structure; (ii) a global optimum is a local optimum with respect to all neighborhood structures; and (iii) for many problems, empirical evidence shows that all local optima are relatively close to each other.

In VNS, we alternate between improvement methods that are based on exploring different neighborhoods in a systematic way seeking better solutions and a shaking method in charge of injecting some noises (perturbation) before reaching predefined stopping condition(s).

In what concerns the Improvement methods, several systematic ways of exploring the neighborhood have been proposed in the literature: sequential Variable Neighborhood Descent (seqVND) [see e.g., (Hansen et al. 2010) for more details]; Composite (Nested) VND [see e.g., Todosijević et al. (2015) where full Nested VND was applied for the first time]; and Mixed Nested VND [see e.g., Ilić et al. (2010) for a recent application of Mixed Nested VND]. The so called General Variable Neighborhood Search (GVNS) (Hansen et al. 2010) is the one that incorporates advanced procedures in the improvement phase.

The Shaking procedure is applied to help escape from local optima where improvement procedures get stuck and the search process stagnates. Traditionally, two parameters are being used as stopping criteria: maxIter, the maximum number of iterations and \(t_{max}\), the maximum allowed CPU time. Additionally, we terminate the process if maxNoImprove has been passed and no improvement has been observed.

Interested readers are referred to (Hansen et al. 2010; Mladenović et al. 2016) for survey of successful applications of variants of VNS for solving different optimization problems.

Our approach that is elaborated in the following integrates an MIP solver as a part of the solution process whether for solving the purely continuous part of the problem or for recreating a partially ruined solution resulted by the operators. In such case, we use CPLEX as a component of the solution method. In this way, one may wish to consider this approach a matheuristic-like method.

4.2 Initial solution

Let for fixed values of variables h and y, \({\textit{CDSHLP}}({\overline{h}},{\overline{y}})\) and \({\textit{UDSFCHLP}}({\overline{h}},{\overline{y}})\) be called \({\overline{{\textit{CDSHLP}}}}\) and \({\overline{{\textit{UDSFCHLP}}}}\), respectively. For fixed set of hub nodes and hub edges, \({\overline{{\textit{UDSFCHLP}}}}\) has always a feasible solution for any \(1\le p\le n\) and \(0\le q \le \frac{p(p-1)}{2}\). For \({\overline{{\textit{CDSHLP}}}}\), a trivial solution is the one wherein all the edges are of hub type.

A naïve initial solution for any of the two problems can be constructed as in the following: (1) UDSFCHLP: choose any q edges among them (resulting in a connected hub-level sub-network). The q hub edges characterize the hub nodes and the hub-level structure of a solution and the remaining problem is solved using an LP solver, CPLEX in this case. Note that due to the availability of hub-level network structure, a preprocessing on the flow variables results in a significantly smaller LP, which can be solved very efficiently. (2) CDSHLP: set all the nodes as hub nodes with a complete graph. One then iteratively removes the hub edges carrying the least traffic one by one, and stop when the next removal will cause infeasibility. Again, the problem after fixing hub-level structure is solved as an LP by (with a similar preprocessing applied to it) and in each iteration we warm start the optimal LP basis of the previous iteration, even further improving the efficiency in solution.

A more clever initial solution can be created as follows:

  • UDSFCHLP: sort the O–D demands by their O–D flow volumes. Start from the busiest O–D, connect them with a direct hub edge and then choose the remaining edges from the top of the ordered list in such a way that the resulting hub level sub-network remains connected and the number of edges is .

  • CDSHLP: solve the LP relaxation of the single objective median problem without load-balancing constraints. One then fixes the fractional (variable that takes a value between 0 and 1) hub nodes and hub edges (e.g. using a threshold) iteratively until reaches an integer feasible solution, which may not necessarily take into account load-balancing constraints. As a rule of thumb, a threshold of 0.85 and 0.15 for fixing to 1 and 0 is used. We give priority to fixing to 1 first.

In what follows, we opted to use the pair of clever algorithms as the quality of initial solutions generated by them are very often much better than the one from the alternative naïve method.

In all the aforementioned cases in this section and in what follows, unless stated otherwise, a reduced problem (wherein part of the variables are fixed by the local search operator) is being solved. The constraint sets for these problems are those of UDSFCHLP or CDSHLP and the objective function is that of compromise programming developed in Sect. 3, i.e., (61) for \(p=1\) and (63) with two constraints (64) and (65) for \(p=\infty \).

4.3 Neighborhood structures

In general two types of neighborhood structures are suggested. The first type deals with neighborhoods with respect to the location of hub nodes and the second type is concerned with the neighborhoods in relation with the edges.

4.3.1 Node-based neighborhoods

The location neighborhoods used within our VNS are based on the following moves, which are defined with respect to a given solution s:

Fig. 7
figure 7

An example of a feasible solution. The node sizes are proportional to the total supply/demand/transshipment volumes and the (hub) edges colors correspond to the intensity of flow on the hub edges according to the color map. The red nodes represent the hub nodes and the blue ones represent the spoke nodes

Full size image

  • Drop_Hub( i ): it removes a hub node i from the current solution s. If the gap between the highest (\(\mathscr {L}^h\)) and the lowest (\(\mathscr {L}_l\)) volume of flow transiting through hub nodes is significant (\(\frac{\mathscr {L}^h}{\mathscr {L}^l}>2\)) then the less busy node is turned into a spoke node. Otherwise, if the variance of loads is not significantly high, the candidate hub node is normally chosen randomly (with equal probability) from among the 50% hub nodes with the lowest utilization following. The logic behind this is that dropping a hub node will anyway result in the reduction of setup cost and given the bi-objective nature of the problem one can use this opportunity to move aligned with the load balancing objective function as well. Looking at Fig. 7b, one realizes that in this example, the nodes 5 and 6 (when compared to the node 10) are the candidates for such a move. In the case that the cardinality of hub edges is fixed to q, one can either introduce a busy node such as node 9 to be the new hub node or leave it to CPLEX to continue and complete the solution with a better one in the neighborhood of the partial solution (ruined one). However, using CPLEX, on one hand can be quite expensive and on the other hand, within a given time limit, may deliver high quality solutions that would be hard to find otherwise.

  • Add_Hub: if we give a higher weight to the median-type part of the objective function, it has been regularly observed through extensive computational experiments that a trade-off between cost and flow balance often (except in some extreme cases) encourages nodes with highest supply/demand to be among the hub nodes. Figure 7a also depicts another example of such nodes (#10 and #11 ) that appear as hub nodes. In practice, it is often the case that a hub is located at or very close to the location of major clients (one or more clients with maximum inward/outward flows). Therefore, one can either search for a hub node in the neighborhood of the busiest nodes or resort to a heuristic approach in which case one constructs a convex hull of the top 3 busiest (hub or non-hub) nodes and add one hub from among the ones closest to the perimeter of this set, if any, as a hub node. In the uncapacitated fixed cardinality version, when a new hub is added one must connect this new hub node to the other set and remove at least one edge in order to make sure that only q edges will remain in the network. The later can be selected from among those edges that have the least flow and whose removal does not split the hub-level network in two components. Alternatively, one can add local search constraints. Let \({\overline{Y}}\) and \({\underline{Y}}\) be the set of existing and potential (but currently non-hub) hub edges, respectively. A local search constraint \(\sum _{\{k,l\}\in {\overline{Y}}}(1-y_{kl}) + \sum _{\{k,l\}\in {\underline{Y}}}y_{kl} \le k\) for \(k=2 \text{ or } 3\) can be added and CPLEX can be called for a time limit to find a new good feasible solution. For the capacitated case, the addition of one hub node does not harm feasibility but may alter the objective function.

  • Swap_Hubs: chooses a node to leave the set of hub nodes and a spoke to become a hub node. In Fig. 7a, the node #2, which is a hub node and connected to only one other hub node will become a spoke node and node #5 becomes a hub node. The primary edge encompassed from the new hub node connects the closest hub node (i.e. #11) from among the existing nodes. Once the hub node and the connection to the closest node have been identified, the other promising outgoing edges to the existing hub nodes (e.g. 5–4) may be identified by carrying out a heuristic local search within the edge-based neighborhoods or calling CPLEX by adding a local search constraint.

When using CPLEX to solve the reduced problem, we fix the lower/upper bounds on those variables where the corresponding elements is fixed by the heuristic.

4.3.2 Edge-based neighborhood

  • Drop_Edge \((i-j)\): removes a hub edge \(i-j\) from the current solution s. The hub edge is normally chosen from among the hub edges with the lowest ratio \(\frac{\mathrm{utilization}}{\mathrm{fixed cost}}\) or \(\frac{\mathrm{utilization}}{\mathrm{capacity}}\) and with an equal probability.

  • Add_Edge: in the case of UDSFCHLP, this operator follows a call to Drop_Edge \((i-j)\). A prudent choice of a hub edge to be added is the one that can de-stress the hub edges with highest traffic by introducing a sort of redundancy. If possible, this can be done by adding an edge between the existing hub nodes that are receiving significant traffic. The second situation is when a hub must also be added. One then introduces a new hub node and adds an edge from that node to one of the closest hub nodes, which is chosen according to a uniform distribution. Again, our extensive computational experiments show that it is unlikely that this node is the closest node to the current set of hubs because the added value of introducing this edge (fixed cost for the new hub node and the hub edge) is rather negligible or even negative. Therefore, this new hub edge should have some meaningful minimum length. Our empirical conclusion arising from extensive computational experiments is that it must have a length at least equal to 10% of the distance between the two most remote nodes (diameter) of the network.

  • Swap_Edge: an under utilized hub edge with the lowest ratio \(\frac{\text {utilization}}{\hbox {fixed cost}}\) can be removed in favor of adding a direct connection between hub nodes i and k where \(i-j-k\) represent a sequence of two hub edges with the highest traffic on them. This introduces a redundancy and will de-stress \(i-j-k\).

In all the aforementioned local search methods, in the initial iterations of the solution algorithm we try to avoid using CPLEX (mainly due to the computational overheads) as we still have several unseen feasible solutions in the search space that can improve the current solution. But as iterations continue and the success rate of heuristic raises, the use of CPLEX becomes much more viable as it can often find solutions that are not found by the other method.

4.3.3 Feasibility and objective value

If the hub-level network is connected and composed of only one component, we can then discuss the feasibility of \({\overline{{\textit{CDSHLP}}}}\) and \({\overline{{\textit{UDSFCHLP}}}}\). \({\overline{{\textit{CDSHLP}}}}\) and \({\overline{{\textit{UDSFCHLP}}}}\), which are then pure nonlinear programming formulations that can be solved by any solver for the second order cone programming such as CPLEX. In the case of \({\textit{UDSFCHLP}}\), the feasibility is always guaranteed as long as constraints (26) are satisfied, but in \({\textit{CDSHLP}}\) the capacity constraint is the only source of infeasibility.

Note 1

It must be noted that as the flow subproblem is an expensive one to solve for every candidate solution, a hashing system can guarantee the efficiency and the success of this solution method.

4.4 Adaptive variable neighborhood descent (AVND)

AVND works as following: Create and order a list of neighborhood structures and examine them in a linear order defined below. A state-transition matrix () is introduced where represents the reward attributed when neighborhood j is examined after the neighborhood i. After exploring the neighborhoods using a given order, a reward proportional to its performance is attributed to that operator and in the state-transition matrix influencing the chance of that operator for being solicited in the future iterations.

Let \(\ell _{max}\)-tuple \({\mathcal {N}}=({\mathcal {N}}_1, \dots , {\mathcal {N}}_{\ell _{max}})\) be an ordered set of operators defining the neighborhood structures. The sequential version works as following: we start with the first operator (\(l=1\)) and continue until all the operators are visited. Let l be the current operator and s be the current solution. We find the best solution in the neighborhood of s explored by the operator l. If this best neighbor improves the current solution, the current solution gets updated and we go back to the first operator \(l=1\), otherwise we move to the next operator. The process terminates when in a given iteration the current operator is \(l_{max}\) and no improvement is observed.

Our initial extensive computational experiments show that the most promising order of operators is (Add_Hub, Add_Edge, Drop_Hub, Drop_Edge, Swap_Hub, Swap_Edge).

In the first round of our solution algorithm as we do not have any reward attributed to the operators, we run a sequential VND and calculate rewards. Once the rewards are calculated, we switch to an Adaptive VND (AVND) mode and thereupon the operators are selected based on the accumulated rewards attributed to them in the state-transition matrix . If rewards do not change significantly in the transition from one iteration to another, we call on the shaking phase.

4.5 Shaking procedure

The shaking function Shake(s, k) is called whenever the search is stagnated and no improvement is observed. It basically take two parameters—the solution s and an integer number k. There are two types of shaking: node shaking and edge shaking.

4.5.1 Node shaking

Let \({\overline{H}}(s)\) be the set of hub nodes in s and \({\underline{H}}(s)\) be the set of non-hub nodes in s. Shake randomly chooses k elements from \({\overline{H}}\) and adds them to \({\underline{H}}\) and at the same time chooses k nodes from \({\underline{H}}\) and adds them to \({\overline{H}}\). The k new hub nodes are connected to their closest hub nodes using hub edges. We give higher weights to locate new hub nodes among the locations with less history of hub facilities among the visited solutions so far.

4.5.2 Edge shaking

The edge shaking follows the same strategy as the node shaking but we also need to make sure that the resulting hub level remains connected.

4.6 Steps of the proposed AVND

Algorithm 1 outlines the major steps of our AVND. The algorithm described in Sect. 4.4 serves as the local search part and the perturbation introduced in Sect. 4.5 acts as the diversification and shaking procedure.

AVND accepts two parameters, as shown in Algorithm 1: \(t_{max}\), the total CPU time as time limit and \(k_{max}\) as the maximum number of iterations of the inner loop before resorting to the shaking procedure. Algorithm 1 shows that the starting solution is obtained using the procedure detailed in Sect. 4.2 and it is subjected to some improvement using the sequential VND/AVND elaborated in Sect. 4.4.

figure a

5 Computational experiments

All the reported algorithms were coded and compiled under VC++ compiler in Windows 10 and run on a personal computer with an Intel Core i7-6700K CPU, 4.0 GHz and 32 GB of RAM. CPLEX 12.7.1 is used as an MIP solver.

In all our computational experiments we assumed that \(\alpha =0.75\). The parameter IloCplex::BarQCPEpComp has been set to \(10^{-9}\) and IloCplex::MIPEmphasis has been set to CPX_MIPEMPHASIS_BALANCED. The default value for IloCplex::Param::MIP::Strategy::MIQCPStrat is maintained. The custom termination criteria for CPLEX (UserAbort) is the following: we terminate CPLEX if a maximum of 10 h (36,000 s) of CPU time is passed and an incumbent solution has been identified. If within this 10 h no solution is found then it continues until either the first feasible solution is found or CPLEX crashes due to an exception. While this 36,000 s is imposed, CPLEX only checks the CPU time upon termination of the current node LP resolve. This may result in a CPU time slightly larger than 36,000 s in our tables. For the heuristic approach, we also use the same time limit, although the process terminates in much less time.

The capacity of hub edges is chosen uniformly by \(U[0.1, 0.15]\times \sum _{i,j}w_{ij}\). For the heuristic, \(k_{max}\) is set to n and \(t_{max}\) is set to 7,200 s. maxNoImprove is also set to 1000. For the uncapacitated case, the constraint (58) has been added to the model. The first problem being solved is the cost optimization problem and its solution is being used to warm start the other problem with \(w_1=0.1\). For every other w, the CPLEX is warm-started using the solution for the previous \(w_i\). Note that \(w_i\in \{0.1,0.3,0.5,0.7, 0.9\}\). A hashing system has been used to retrieve the objective solution should the problem has been solved previously.

5.1 Testbed

To carry out our computational experiments, we use the instances from a real practice data set of a telecommunication operator. The operator is a major one—with an extended network from central Europe to the Suez Canal and widespread across Africa—that also owns a major part of the national infrastructure. Therefore, almost any operator in this country is leasing capacity on the network maintained by this major operator. The clients are of two categories: other equally popular operators that have acquired their own dedicated bandwidths on long-term lease contracts and the low-cost ones that are dynamically leasing residual capacities from the unused segments of the operational networks. Therefore, the infrastructure owner is not in charge of congestion pricing but a longer term strategic network design capable of assuring a balanced load to cope with all such demands given some historical information, the current trend of technology/demand and the forecast and prediction for the future.

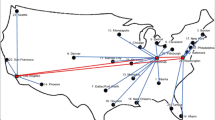
Our main instance is a network composed of 30 nodes scattered across the country within the national-level network. These 30 nodes include the major hubs (hub nodes) and secondary hubs (spoke nodes) which are the subject of this network design problem. To create smaller instances, we use a kind of aggregation [akin to the one proposed by Ernst and Krishnamoorthy (1996)] to establish grids on the map and introduce new virtual nodes as the centers of gravity of cells in the grid with a demand equal to that of all the nodes within the grid cell.

No more than half of these nodes are expected to be used as hub nodes and the number of edges (technological connections) is always limited to at most 30 edges. Therefore, in practice the optimal number of hub is between 5 and \(\frac{n}{2}\). For every n, the corresponding q values are indicated in Table 2.

Table 2 The n values and their corresponding q values
Full size table
Fig. 8
figure 8

The CP frontiers corresponding to the CDSHLP and DSHLP instances with \(n=10\)

Full size image

5.2 Analysis

In Fig. 8a, b, the CP frontiers corresponding to Fig. 6 are depicted. In Fig. 8b, we plot all the values for q in Table 2.

The curve corresponding to the capacitated version defines a smoother representation of the frontier. In the case of uncapacitated, clearly \(q=5\) absolutely dominates \(q=10\) in terms of cost and flow balance. It can be concluded that adding more than 5 hub edges will not necessarily result in a better trade-off between cost and load balancing for this instance.

Similar behavior can be observed in Fig. 9a, b (respectively, in Fig. 11a, b). Again the capacitated version defines a smoother curve. In Fig. 9b (Fig. 11b), the image combines plots for all the values of q corresponding to this instance in Table 2. As it can be observed, again \(q=5\) dominates all the other values of q for this instance in Table 2.

Fig. 9
figure 9

The CP frontiers corresponding to the CDSHLP and DSHLP instances with \(n=15\)

Full size image

Figure 10 depicts a decision space representation of a solution on the frontier in Fig. 9a.

Fig. 10
figure 10

The decision space representation of the promising member of frontier for n15 in Fig. 9a

Full size image
Fig. 11
figure 11

The CP frontiers corresponding to the CDSHLP and DSHLP instances with \(n=20\)

Full size image

For \(n=20\), a similar observation is depicted in Fig. 11.

5.3 CPLEX versus heuristic

Tables 3, 4, 5 and 6 report the computational results for instance of 10, 15 and 20 nodes in CDSHLP and DSHLP, respectively. Every table is divided into two blocks: CPLEX results and Heuristic results. In the first block, the first column indicates the instance name in the format “nX-c-wY-ZZZ” (“nX-wY-ZZZ” for the uncapacitated case ) where ‘X’ represent number of nodes, ‘Y’ stands for the coefficient of w in the CP model and ‘ZZZ’ to identify whether it was , , the cost or load balancing objective functions. The second column (‘TimeIP’) reports the CPU time (in seconds) for solving that case. The next column (‘Nnodes’) indicates the number of branch-and-bound nodes processed followed by the column reporting the gap (‘Gap’) reached during the time. The column (‘IPStatus’) stands for the status of CPLEX upon termination followed by the reported objective value in the next column (‘IPobj’). The columns (‘\(Z_1\)’) and (‘\(Z_2\)’) report the split objective values for cost and load balancing separately. The last two columns (‘#Hubs’) and (‘#Edges’) indicate the number of hub nodes and hub edges reported by the corresponding solution delivered by CPLEX. The tables are composed of blocks for every instance and different objective function corresponding to (cost, load balancing and different values of \(w_i\)). In the second block, the first column (‘TimeH’) represents the time (in second) within which the heuristic methods has terminated. The second column (‘TimeHB’) represent the time (in seconds) at which the best solution of heuristic has been identified and the last column (‘GapH (%)’) represents the gap between the solution of heuristic relative to the best reported bound of the exact method.

For every instance configuration (n with given parameters) there are four rows appended to report a summary of results for the given set of instances. The first row reports the average CPU time spent in CPLEX solving reduce problem for the given n. In the second to fourth rows depending on whether it is capacitated or uncapacitated case, we report different values. For UDSFCHLP, the second to the fourth rows report the ratio of volumes on the less loaded hub edge and the busiest one and the variance of loads on hub nodes (separated by a slash) for the cases of cost-only (VarH (C)), load balancing (VarH (L)) and the average over all other cases (i.e. VarH (, )). For CDSHLP, three consecutive lines report the minimum, maximum and average utilization (separated by slash) as well as variance of loads for the cases of cost-only, load balancing and the average over all other cases.

As one observes, the ideal load balancing objective function tends to install the minimum required number of hub edges, i.e. one. A similar behavior can be observed in when the weight corresponding to the load balancing objective function increases and that of cost decreases.

In the CP objective function as in (59), \(w_i\) refers to the weight of cost objective function and \(1-w_i\) to the load balancing objective. In Table 3, for every n, the higher coefficient \(w_i\) suggest opening more hub nodes and hub edges and the smaller values tends to open less number of hub nodes. The computational times are relatively moderate and the number of processed branch-and-bound nodes are very few indicating that processing nodes in the branch-and-bound tree is the most time consuming task. All instances, except one, were solved to the optimality. Often the solution found in the early iterations were optimal but it has taken long for CPLEX to prove the optimality. Therefore, given that our heuristic also did not find any better solution for this particular instance, we expect this also to be the optimal even though the proof is not at hand.

It must be noted that in (59), except for case of ‘idealCost’, no more than 5 hub nodes has been opened in any solution.

Table 3 Numerical experiments for the CDSHLP instances (\(n=10,~ 15\) and 20)
Full size table

In Tables 4, 5 and 6, we deal with the uncapacitated version which takes into account a fixed cardinality of hub edges and an upper bound on the number of possible hub nodes (at most half the number of nodes). As one observes the computational times for instances are significantly less than those for . In general, computational time increases exponentially as the instance size increases. The smaller number of processed branch-and-bound nodes confirms that the problem being solved at every node is indeed a challenging one resulting in less number of nodes being processed within the time limit. Sometimes in this column values larger than our time limit are reported this is because when the time limit has been reached, CPLEX was in the middle of solving the node sub-problem and termination process for that node took very long time.

As before we solve the problems in this order: first ‘idealCost’ was solved and then the obtained optimal solution was used to warm start CPLEX for solving ‘idealLdBlncng’. After that, this warm start style has been repeated for all other problems of and , respectively, in the given order. Our computational experiments confirm that the use of the previous solution to help warm-start CPLEX indeed reduced the required computational efforts very significantly. Often such solutions were optimal or very close to optimal but it took very long time for CPLEX to prove that. In this table, all instances, except six, were solved to optimality within the time limit. Allowing longer run time showed that indeed some of the six cases reported solutions even though showing high gap in this table, they are indeed either optimal or within less than 5% of the optimality when optimality was proven beyond the time limit.

For the uncapacitated problem, UDSFCHLP, for any feasible network structure, there is always an optimal solution with the objective value of 0. When comparing the number of hub nodes and hub edges among different instances of uncapacitated version, one observes that while for the cases of \(n=10, 15\) for the given q, the maximum number of hub nodes (i.e. \(\frac{n}{2}\)) is being opened, for \(n20,~ q=10, 15\), always 8 and 9, hub nodes (i.e. less than \(\frac{n}{2}\)), respectively, were opened for CP approach and the given values of \(q=10, 15\) (the two other exceptions for every \(q\in \{10,15\}\) are the single objective cases corresponding to ‘idealCost’ and ‘idealLdBlncng’). However, again starting from \(q=20\) the number of hub nodes being opened increases as q increases.

Table 4 Numerical experiments for the UDSFCHLP instances
Full size table
Table 5 Numerical experiments for the UDSFCHLP instances
Full size table
Table 6 Numerical experiments for the UDSFCHLP instances
Full size table

5.4 Variable neighborhood methods

Our VNS reports optimal solutions for all instances for which the optimal solutions and objective values are obtained via CPLEX. The only bottleneck of this heuristic approach seems to be its dependency on CPLEX for solving the continuous part of the problem. Therefore, it is very vital for its performance to employ a sophisticated hashing system in order to avoid resolving a problem solved previously.

Due to such a large neighborhood structure, the heuristic was always terminated with the time limit.

For \(n=25\) and \(n=30\) (and the values of q for each instance given in Table 2) for the uncapacitated version we could only use the heuristic approach as CPLEX performed very inefficient. Within the time limit, we have obtained solutions that essentially confirmed the results for aggregated smaller instances (i.e. \(n=10, 15\) and 20). The conclusion is therefore that dominance of instance with \(q=5\) is re-stated.

For the capacitated case, as it can be seen in Fig. 12 and Fig. 13, a smooth boundary has been generated. However, in a couple of cases, the solutions reported by the heuristic (perhaps due to the sub-optimality) did not lie on the smooth curve and are therefore non-efficient solutions.

Fig. 12
figure 12

The CP frontiers corresponding to the CDSHLP instances with \(n=25, 30\) using the VNS approach

Full size image

5.5 Random instance with \(n=40\) and 50

Our algorithm was also tested on a set of random instances without any particular structure. Again for all the cases where the optimal solution was at hand, the heuristic reported that solution.

For the uncapacitated case, given different fixed cost and flow structures, we did not observe any tendency towards installing smaller number of hub edges as we could observe in the real-life data.

In the capacitated case, again we see that for a couple of cases, the solution reported by the heuristic are dominated ones and are not part of the frontier.

Fig. 13
figure 13

The CP frontiers corresponding to the CDSHLP instances with \(n=40, 50\) using the VNS approach

Full size image

6 Summary and conclusion

The infrastructure owners (in telecommunication and transportation sectors) usually have a longer term plan and a couple of major objectives. They seek solutions that are close to the optimal solution with respect to each objective. Investment in routing and switching centers and the technological connections among them in telecommunications and transforming some platforms to the uni-modal/multi-modal hub nodes and establishing transport corridors are part of the decisions to be made.

In all such applications, the main question is to how design the strategic network such that it has the sufficient capacity and can be resilient and responsive with respect to the current and future demands. This is independent of what operators will be operating the infrastructures.

We have proposed mathematical models for Capacitated and Uncapacitated versions of the problem. These models are intrinsically nonlinear, which are transformed to second order conic counter-parts. The bi-objective model is approached using the Compromise Programming technique. The resulting models are very computationally challenging and hence exact methods have very limited success. We therefore, proposed a very efficient adaptive variable neighborhood search wherein CPLEX is used to solve the resulting subproblems. We then applied the methodology on a case-study from a telecommunication operator that also owns major part of the national infrastructure and obtained practically high quality solutions. The CP has been used to provide a visual illustration of the trade-off between cost and load balance for the problem instances studied.

The future directions include reformulation of the models to models with particular structures to be exploited in exact decomposition techniques, identifying some valid inequalities and proposing some hyper-heuristic approaches and conducting learning-based local search techniques.