Abstract
Entrepreneurial, innovative entry can have devastating effects disrupting a market. However, the many players involved including all current producers, sellers and suppliers and the often non-technological but organizational nature of the innovation may lead to a gradual restoration of the market, viz., to a new equilibrium. Entrepreneurial entry can be regarded as a disaster while the restoration towards a new equilibrium as disaster management. Hardly any empirical models have been developed in order to test these ideas. This paper conducts the first empirical dynamic simultaneous equilibrium analysis of the role of entry and exit of firms, the number of firms in an industry, and profit levels in industry dynamics. Our model enables to discriminate between the entrants’ entrepreneurial function of creating disequilibrium and their conventional role of moving the industry to a new equilibrium. Using a rich data set of the retail industry, we find that indeed entrants perform an entrepreneurial function causing long periods of disequilibrium after which a new equilibrium is attained. Notably, shocks to the entry rate have permanent effects on the industry, emphasizing the entrepreneurial function of entrants rather than their passive reactive function as postulated in classical economics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The field of disaster management studies how communities and governments respond to a catastrophic situation such as a hurricane, bushfire, flood, volcanic eruption or an earthquake. Two central elements of study in this field of literature are the magnitude of disasters and the recovery from disasters which includes taking care of refugees (Oloruntoba and Banomyong 2018). The magnitude of disasters is often measured in terms of the economic losses they cause,Footnote 1 while the recovery of disasters is typically being measured in terms of the time it takes to return to a sustainable post-disaster level of economic activity (Prasad et al. 2017). However, Xie et al. (2018) argue this only provides a partial picture of recovery as there is an (underanalyzed) connection between the time-path of disaster recovery and disaster losses in terms of economic output and employment. In particular, these authors make a distinction between the repair of buildings and infrastructure, essentially a stock of production factors, and the lost flow of economic activity between the point at which the disaster strikes and the point at which recovery is completed. Xie et al. (2018) argue that particularly this lost flow of economic activity is interconnected with the time-path of recovery. For instance, a time-path with vast and efficient investments in repair and reconstruction may be associated with smaller economic losses than a time-path with smaller investments. Different time-paths may also lead to different post-disaster equilibria having lasting impact on the economy. However, at present we don’t know much yet about how different time-paths of recovery are related to economic losses following a disaster.
In this paper we study economic markets and build a dynamic equilibrium model at the level of economic markets, which we then estimate using real world data. In particular, when modelling a shock to the existing equilibrium (analogous to a ‘disaster’), the model is able to accurately describe the features of both the new equilibrium and the time-path leading to that new equilibrium. Thus, we use economic modelling in order to inform disaster management literature how different time-paths following a shock may be related to different post-shock equilibria. In this analogy, a shock (disruption or ‘disaster’) to an economic market is usually attributed to some technological innovation. For instance, in the copying industry, Xerox was the dominant player until the 1970s, mainly selling big copy machines to large firms. When Canon entered the market with smaller, cheaper machines, Xerox could not respond because of their high cost structure hampering adaptation to the new technology. Similarly, CDC (Control Data Corporation) who dominated the 14-in. drive market for mainframe computers were unable to respond when the 8-in. drive market emerged (Bower and Christensen 1995). When a new technology is introduced as in the above examples, the functioning of the entire market including all current producers, sellers and suppliers can be affected. For all these incumbent players the advent of a disruptive innovation can be interpreted as a disaster because its consequences can be a threat to their survival. In that sense, the advent of a technological innovation is similar to a classical disaster such as a natural one in the form of a flood or an earthquake or the outbreak of a contagious disease or a situation of political or humanitarian conflict.
The advent of a technological innovation may also produce winners such as consumers or incumbent players that are able to adapt and new players which enter the market immediately using the new technology. The same may happen after classical disasters which may lead to a restoration in the form of a new and possibly better structure or environment,Footnote 2 possibly through the help of social entrepreneurs (Ibrahim and El Ebrashi 2017). Much may depend upon the goals and effects of disaster management, in particular the level of (dynamic) economic resilience (Duhamel et al. 2016). Market disasters, just as classical ones, are taken to have significant and long-lasting effects. But unlike classical disasters, where costs and damage tend to be huge even in the presence of human action trying to avoid or mitigate such costs (Tatham and Houghton 2011), the consequences of market disasters can be mitigated due to the many players involved and the often non-technological but organizational nature of the innovation. This then leads to a gradual restoration, or in other words, to the gradual creation of a new equilibrium. What may seem gradual in the short term can work out to be profound in the longer run and be classified as disruptive nonetheless.
The entry of entrepreneurial, innovative firms in an industry can be classified as such a gradual disaster where the entrants are a threat to the incumbents, which leads to exits (i.e., casualties) but maybe also to a different number of firms and, more importantly, to a different profit level (the new equilibrium). All the dynamic simultaneous interrelationships between entry, exit, and industry profits can be interpreted as the disaster management function, and together determine the time-path and new equilibrium following an exogenous shock (disaster) to the system.
Entry and exit of firms constantly change the number of firms in an industry. Entry and exit as well as other economic conditions determine the total profit levels in an industry. In turn, the economic conditions and profit levels also impact entry and exit of firms. This interactive and dynamic process may converge to an equilibrium and induce economic progress. However, it is not immediately clear how either are reached as different economics schools of entrepreneurial thought exist where new firms can serve to crowd as well as grow markets.
While Schumpeter’s (1947) driver of economic progress is about how entrepreneurs generate shocks which disrupt existing market equilibrium, that of Schultz (1975) is about how entrepreneurs adjust to these shocks. Schumpeter (1947) simply assumes that equilibrium is quickly restored after disruption. For Schultz (1975) disequilibria are inevitable features of economic progress. It takes time to regain equilibrium and the adjustment patterns may vary according to the opportunities and restrictions of entrepreneurial behavior, just like adjustment after a classical disaster may depend on human action as well, including the extent of cooperation between government and private firms and the amount of investments made to recover from the disaster (Hausken and Zhuang 2016; Wang et al. 2016).
In the conventional framework, entry and exit of firms, rather than the entrepreneurial behavior of people, play the role of adjustment mechanisms which restore market equilibrium. Net-entry rises when incumbents’ profits are supernormal and falls when they are at unsustainable low levels. In this framework, the only economic function of entrepreneurs is to be reactive and to respond to disequilibrium profit levels. In equilibrium, when profits are at normal levels, entry and exit have no role and are assumed to be in a steady state where entry equals exit. However, reality seems to be different, as many empirical examples from the field of industry life cycle theory show. For many industries, it has been shown that the number of firms follows an inverted U-shaped relation with market age, where entry exceeds exit in the early stages of the industry life cycle due to innovation opportunities, and exit exceeds entry (shake-out) in the later stages due to a decline in product variety and an associated shift from product R&D to process R&D (Klepper 1997). Moreover, adjustment may not be immediate, for instance due to information asymmetries between entries and incumbent firms. The present paper is about all three phenomena which Schumpeter and Schultz identify as the essence of economic progress: the effect of entry and exit on market equilibrium, duration of disequilibrium, and patterns of adjustment.
Baumol (2002) points out that one of the most disappointing shortcomings in the neo-classical approach is that it does not explain the enduring success of capitalism in generating economic growth. This might have to do with the invisibility of the role of the entrepreneur in this approach (Barreto 1989). As Schumpeter (1947) argues, neo-classical analysis is preoccupied with competition without innovation and by consequence is focused on the adjustment process around any given equilibrium. It also does not enlighten our understanding of the main mystery which surrounds the determinants of the long-term dynamic equilibrium itself (Baumol 2002). Moving the focus of attention to this question clearly involves the role of entrepreneurship. Specifically, the potential for an entrepreneurial function for entrants, i.e., to discover, experiment, refine, and exploit new products or new production processes. When we allow for such an entrepreneurial function, entrants are no longer assumed to be imitative ‘me too’ aspiring firms that seize their moment only when incumbents’ profits have become excessive. Instead, entrants may bring innovation and differentiation to the market and in the process introduce new profit opportunities. In such a framework they reverse the causation so that equilibrium normal profit levels are determined by entry and exit rather than the other way around. In terms of entrepreneurial roles: it is the combination of the Schumpeterian entrepreneur creating instability and destruction and the Austrian entrepreneur combining resources to recreate stability (Wennekers and Thurik 1999). The Schumpeterian entrepreneur creates potential and the Austrian entrepreneur realizes it (De Jong and Marsili 2015). This realization hinges around the process of market dynamics with the interplay of not just entry and exit but also profit as the indicators of competition (Kirzner 1973).Footnote 3 Implementing this view in the world of economic modeling immediately raises the question how the interplay of entry, exit and profits works; particularly distinguishing between short term relationships where the neo-classical assumption of fixed technology may be more realistic and the longer term where entrants may introduce new disruptive technologies to the market (Beesley and Hamilton 1984).
The present paper specifies a full equilibrium model explaining entry, exit, the number of firms, and industry profit while also capturing the duration of disequilibrium and patterns of adjustment (analogous to the duration and time-path of recovery following a disaster; Xie et al. 2018). The model accounts for both short- and long-run effects. A unique feature of our model is that it allows for replacement in equilibrium, i.e., we not only specify an equilibrium function for the number of firms, but also equilibrium functions for entry and exit (which levels are consistent with the change in the equilibrium number of firms). We make use of a rich data set on Dutch retailing which encompasses varied dynamic markets such as florists, baby clothes shops and bakeries. We construct a dynamic simultaneous equilibrium model of entry, exit, the number of firms, and profits allowing for both short- and long-run effects in order to capture the Schumpeterian disequilibrium effects as well as the Austrian equilibrium effects of entrepreneurial entry, exit and profit. In this fashion we also discriminate between three aspects of industry dynamics: the effect of entry and exit on market equilibrium, the duration of disequilibrium, and the patterns of adjustment. Based on these aspects we test the main features of three seminal theories on the economic role of entry and exit: neoclassical theory, Schumpeter, and Schultz. In particular, we investigate three research questions. First, if the economy is exposed to an exogenous shock in the number of entrants, do we, in time, get back at the old equilibrium (consistent with neo-classical theory), or do we arrive at a new equilibrium (consistent with an entrepreneurial function of entrants à la Schumpeter)? Second, regardless of whether we return to the old or a new equilibrium following an entry shock, how long does the adjustment process take? Is equilibrium restored quickly after disruption (Schumpeter), or does it take longer so that disequilibrium is the norm rather than the exception (Schultz)? Third, is the adjustment process towards equilibrium monotonic and gradual (neo-classical theory) or is it non-monotonic, stressing the complex nature of adjustment (Schultz)?
To our knowledge our study is the first empirical analysis of the dynamic simultaneous interrelationship between entry, exit, and industry profits. It contributes to disaster management literature by examining an understudied phase of the disaster management lifecycle, i.e. the phase of recovery.Footnote 4 Specifically, our model can be used to inform disaster management literature how different time-paths following a shock (‘disaster’) may be related to different post-shock equilibria. As we use a sophisticated simulation analysis to uncover these time paths, our paper also contributes to the emerging trend within disaster management literature to use simulation modelling as an analytical tool (Mishra et al. 2018).
The next section of the paper provides a description of the data. This is followed by the specification of the model in Sect. 3. The estimation results are discussed in Sect. 4. In Sect. 5 we carry out simulations of entry and exit shocks based on the estimated parameters of our model. These simulations enable us to answer the three research questions formulated above. Section 6 concludes.
2 Data
At an empirical level we investigate the interrelation between entry and exit levels, the number of firms, and profit levels. These four variables will be the key variables in the error-correction model which we will develop in the next section. The model parameters are estimated using data for a panel of shop types in a comprehensive series of markets within the Dutch retail sector.Footnote 5 The current section describes the measurement and data sources for the key variables in our analysis as well as for some other covariates. This section also provides descriptive statistics and a series of tests on stationarity and cointegration for the key variables. The results of these tests are used to develop our error-correction model in the next section.
2.1 Our data set
We use a data base for 41 shop types in the retail sector over the period 1980–2000. Our data base combines variables from two major sources: the Dutch Central Registration Office (CRK) and a panel of independent Dutch retailers (establishments) called ‘Bedrijfssignaleringssysteem’ (BSS) (interfirm comparison system) which was operated by EIM Business and Policy Research in Zoetermeer. The data are complemented by information from several other sources. As the number of shop types investigated in BSS has varied in the 1980s and 1990s, our data base is an unbalanced panel. By and large, we have 28 shop types with data for the 1980s and 1990s and 13 shop types with data for the 1990s only.Footnote 6 The exact data period per shop type is given in Table 1. This table also contains averages for some key variables in our model. Details on the measurement and source for each variable are given below. We apply several corrections to the raw data in order to make the data ready for analysis.
Raw data on the number of firms (N) and the numbers of entries (E) and exits (X) in a shop type are obtained from the Dutch Central Registration Office (CRK). CRK provides data on the number of new registrations and deregistrations of establishments for each shop type. Over time the sectoral classification of shop types used by CRK changed several times and we correct for trend breaks because of these changes.
Total industry profits \( \left( \pi \right) \) are computed by multiplying average profits per firm by the total number of firms in a shop type. Raw data on average (net) profit per firm are taken from BSS. This panel was started by EIM in the 1970s and each year a large number of firms were asked for their financial performance. Although the panel changes from year to year (each year some firms exit the panel while some others enter), it is important to note that we compute the relative change in average profit based on only those firms present in the panel in two consecutive years. Hence, the dynamics of these variables are not influenced by changes in the composition of the panel.Footnote 7 Until the beginning of the 1990s average profit levels are computed based on about seventy individual retail stores per shop type but from the beginning of the 1990s the coverage of the panel decreases, i.e., less firms participate so that shop type averages become less reliable. Fortunately, the timing of this decrease coincides with the start of average financial performance registration by Statistics Netherlands (CBS) at low sectoral aggregation levels. Hence, from the early 1990s onwards, we have information on the development over time of these variables from two sources: BSS and CBS. Differences between these two sources are small which supports the reliability of our constructed times series. From 1994 onwards we use the average of the annual relative change implied by these two sources.Footnote 8
Data on total consumer spending (CS) on the products and services sold in a certain shop type is taken from Statistics Netherlands (publication ‘Budgetonderzoeken’ or Budget statistics).Footnote 9 Modal income and unemployment are also obtained from Statistics Netherlands, while the (nominal) interest rates are taken from Thomson Reuters Datastream, a provider of financial data.Footnote 10 Finally, for total industry profits, modal income, consumer spending, and the nominal interest rate, we use a consumer price index to correct for inflation.
In Table 1 we give an overview of the available data. Table 1 shows that some shop types have grown in terms of the number of shops over the sample period, while other shop types have shrunk. For instance, the average number of entrants for the shop type “grocers/supermarkets” is 743 while over the same period of time the average number of exits equals 932. This implies that the category shrunk with, on average, 189 shops each year. Over the entire sample period of 21 years this category shrunk with about 189 × 21 = 3969 stores. Note that at the same time this category witnessed an inflation-corrected yearly profit decrease of about 0.7% and an increase in consumer spending of about 0.3%. In all shop types there are many stores entering the market and many shops leaving the market (relative to the number of firms). In some shop types entry dominates exit, while in others exit dominates entry. Remarkably, even in shop types where there is no net change in the number of stores, there are still entrants and exits. For example, the category “fish shops” has on average 114 stores entering and 114 stores exiting the market each year, corresponding to 11% of the population of firms. Table 1 clearly shows that entry and exit levels are significantly positive over a long period of time. This suggests that the neo-classical idea of a steady-state level with entry and exit rates equal to zero is not a sufficient account of the patterns in the data. It seems that there exists a long-term persistent level of entry and exit in each shop type. As explained earlier, the current paper develops a model where these long-term entry and exit levels are explicitly specified.
2.2 Testing for stationarity and cointegration
Before we specify our model we test the key series for stationarity. The key variables in the analysis below are the log of the number of firms in a shoptype, the log of total profit in a shoptype, and log entry and log exit relative to the number of firms. The main reason to use entry and exit rates is that this allows for an easier comparison across shoptypes. We define the entry rate (e) and exit rate (x) as
where Et and Xt denote the numbers of entries and exits in year t, respectively, and Nt denotes the number of firms at the beginning of year t. Note that the exit rate is defined relative to the previous number of firms plus net-entry (as \( N_{t + 1} = N_{t} + E_{t} - X_{t} \)). In other words, new entrants are allowed to exit in the same year. For both rates it holds that higher values indicate more entries or more exits. This formulation also yields a convenient relation between et, xt, Nt and the number of firms in the next year (Nt+1), that is,Footnote 11
To test for stationarity of the log profit and log entry and log exit rates we use panel unit root tests. There exist basically two sets of panel unit root tests. The first set assumes a common AR structure across panel members under the null and a common AR structure under the alternative. Popular examples are the Levin et al. (2002) test and the Breitung (2000) t-statistic. The second set of tests assumes individual AR structures. Popular examples in this class are the Im et al. (2003) W-statistic, and the Fisher-type tests (Maddala and Wu 1999; Choi 2001). The alternative hypothesis in this second class of tests is that some of the panel members are stationary. We use the tests as they are implemented in EViews 7.1, with all the “automatic” options for lag and bandwidth selection. If the majority of the shop types show a trend for a particular series we use the tests with the option of individual deterministic trends. Our final conclusion is based on the combined results of the tests.Footnote 12
We summarize the test results in Table 2. The log entry and log exit rates do not appear to have a trend and the test results clearly indicate that the log entry rate and log exit rate do not contain a unit root. Note that this fits with expectations based on economic theory. For the number of firms we do have to correct for possible deterministic trends. The tests clearly show that the log of the number of firms is not stationary. Note that entry and exit together measure the change in number of firms. For the log total profit and the log consumer spending in a shop type the presence of a trend is less easy to judge. Therefore, we present the results for the tests without correcting for trends as well as those where the trend correction is made. Table 2 clearly shows that the log consumer spending does not contain a unit root. For the log of total industry profit the results are less clear. We decide to classify this series as non-stationary.
We next test for cointegration between the log number of firms and log profits. In our panel set-up we test for cointegration by testing the hypothesis of a unit root in the residuals of a panel regression of log profit on log number of firms. Note that this hypothesis corresponds to no cointegration. More specifically we apply the procedure of Pedroni (1999, 2004). This procedure is similar to the Engle and Granger (1987) method for a single time series. Again we use this method as implemented in EViews with all the automatic options. After correcting for trends the Panel PP-Statistic as well as the Panel ADF-Statistic give a p value of 0. Hence, the null hypothesis of no cointegration is rejected. We conclude that total industry profits and the number of firms are indeed cointegrated. The conclusion of cointegration matches with the economic reasoning that, in the long run, the number of firms is tied to the profit level.
3 The model
In this section we develop our model in which we discriminate between the short term disequilibrating and long term equilibrating roles of entry and exit. We explicitly make room for an analysis of the net change, the duration, and the pattern of the move from an initial to the next equilibrium. The model is constructed in order to account for the insights on dynamic equilibrium from both the economics and organizational ecology literatures. At the core of industrial economics and organizational ecology theories is the common concept that every market has a long run limit on the number of firms that it can sustain at any point in time (Geroski 2001). In the economics literature this limit is depicted as an equilibrium which can be dynamic or static depending on the model in question (Audretsch et al. 2001). In organizational ecology it is dynamic (with an emphasis on evolutionary processes) and referred to as carrying capacity of an industry (Hannan and Freeman 1989).
In this paper we seek to ascertain the importance of this dynamic point of gravitation in the market. We want to ascertain the strength with which a market forces the actual number of firms to converge to its carrying capacity or equilibrium. If this force is sufficiently weak, so that disequilibrium or deviation from the carrying capacity is the norm rather than the exception, then both the scale of deviation between the actual number of firms and the steady state equivalent as well as the rate and path of the adjustment process become key dimensions of business performance. From a public policy perspective, it is important to know the strength of such market gravity. If market gravity is weak and if there are market failures associated with the supply of new ventures then it raises the question of whether enterprise policy should run counter to crowding so that it is more active when the market is below its carrying capacity and less/in active when it is above. But to have the full answer to that we need to know the extent to which firm entry serves a passive economic function of restoring a dynamic equilibrium or whether it delivers an entrepreneurial function of altering the carrying capacity of a market. Put differently, do entrants crowd or create market space? The following model is constructed in order to provide some answers which will help inform this debate.
Denote by πit the total profit in shop type i = 1, …, N during year t = 1, …,Ti. Next, eit and xit give the entry and exit rate for shop type i in year t, respectively, as defined in Eqs. (1.1) and (1.2). Finally, Nit gives the number of firms in market i at the beginning of year t. As shown in Eq. (2), the log number of firms at the beginning of year t + 1 is by definition equal to log Nit+1 = log Nit + log eit − log xit. In this section we develop a model describing the log of total industry (shop type) profits as well as the log of the number of entrants and the log of the number of exits. The model therefore also implicitly describes the number of firms.
We specify a model in which the changes in entry, exit and profit are related to short-term dynamics, changes in exogenous variables and to deviations from the steady-state of the market. The exogenous variables related to market i in year t are denoted by Zit. We specify a vector error-correction model [VECM] (see Hendry et al. 1984). Although our VECM specifies the short-term change in entry, exit and profit, the error-correction framework also gives insight into the long-run relationships (Granger 1993). We specify the VECM for the three endogenous variables such that it is consistent with the earlier findings that log entry and log exit are stationary and that log profits and log number of firms are cointegrated. We first specify the long-run steady state equations
where log e*it, log x*it, log N*it, and log π*it denote the steady state levels for log entry rate, log exit rate, log number of firms, and log industry profit, respectively. The steady state levels depend on exogenous variables describing the market situations. These variables are denoted by \( W_{it}^{e} \), \( W_{it}^{x} \), and \( W_{it}^{N} \). In other words, in the long-run steady state entry and exit rates are constant, and the carrying capacity of a shop type is a function of the total profit in that shop type. The relationship between carrying capacity and total profits possibly contains a trend. This allows the long-term profits to change without a compensating change in the carrying capacity. Conversely, the number of firms could change in the equilibrium without an effect on the profits. The latter case would correspond to a difference in the equilibrium levels of entry and exit.
An interesting hypothesis to test is κi = 0, which implies no trend in the equilibrium relationship between number of firms and profits. Another interesting hypothesis is whether “on average” Δlog N*it = log e* it− log x*it = 0. This would imply that in the steady state the market does not grow or shrink. To formalize this hypothesis, we will mean center the variables in Wit such that the hypothesis can be stated as γ1i = γ2i.
In case entry and exit do not cancel each other log N has a trend in equilibrium. From (3.3) we can obtain whether profits will also show a trend in equilibrium. The slope of the equilibrium trend in profits is given by \( \frac{{\gamma_{1i} - \gamma_{2i} - \kappa_{i} }}{\lambda } \): with this trend the drift on the left hand side of (3.3) equals the drift on the right-hand side of (3.3) as
Note that, if λ ≠ 0, we can also define the equilibrium relationship (3.3) between the number of firms and profits the other way around, that is,
In Eq. (5.1), the total profit instead of the carrying capacity is seen as the focal variable, while in (5.2) the left hand side indicates log average profit if λ = 1.
The short term changes in entry rate, exit rate and total industry profit are related to lagged changes, exogenous changes in the economy and the deviation from the steady state in the last period. We capture all these effects in a VECM. In this model we ensure that Eqs. (3.1)–(3.3) indeed represents the steady state. Our VECM becomes
where Zit denotes a vector of exogenous variables related to the economic conditions. The first term on the right-hand side of (1) makes sure that in equilibrium profits indeed grow with rate equal to \( (\gamma_{1i} - \gamma_{2i} - \kappa_{i} )/\lambda \). Note that the inclusion of this term has no impact on the fit of the model as all three equilibrium relations in (3) contain a market-specific intercept. This term is only included to facilitate an easy interpretation of the parameters. Next Γ is a matrix and contains the speed of adjustment of entry, exit and profits to a potential disequilibrium in all three equilibrium relations. Note that a disequilibrium in one dimension can be corrected through a change in another dimension. For example, if profit levels are above equilibrium the market can (partly) correct this through additional entry.
The error terms are expected to be correlated within a market. In particular, we expect a positive correlation between entry and exit. We assume that there is no correlation over time or across markets. That is, we specify
To economize on the number of parameters we restrict the covariance structure such that the correlations are the same across markets. We parameterize the variance such that
The ρ-parameters now denote the correlations between different error terms, while for example \( \sigma_{\varepsilon ,i}^{2} \) gives the variance of the error term associated with log entry for shop type i.
3.1 Further insight in the steady-state relations
The VECM allows for various equilibrium relations. The model can capture a market where in equilibrium nothing changes, but also markets where, for example, in equilibrium entry exceeds exit and average profits per firm decline.
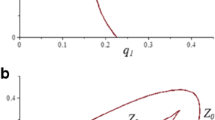
In Fig. 1 we illustrate four steady state combinations for profits and the number of firms. For convenience we ignore exogenous variables and we set λ = 1. Under these conditions the steady-state relation between the number of firms and total industry profits can be represented by a straight line. In the top left and top right plots of Fig. 1, there is no trend in the carrying capacity of the market \( (\kappa = 0) \), so that the steady-state relationship between profits and number of firms remains constant. In this setting, we compare the case where, in equilibrium, entry and exit cancel each other (top left plot) to the case where in equilibrium exit dominates (top right plot). In the bottom left and bottom right plots of Fig. 1, there is a trend in the carrying capacity of the market \( (\kappa \ne 0) \), so that the steady-state relationship between profits and number of firms moves over time. In this setting we consider the case where the number of firms remains constant (bottom left plot) versus the case where exit dominates entry (bottom right plot).Footnote 13
In the top left plot entry equals exit and there is no time trend, therefore the number of firms and the profit level are constant in equilibrium. This very much depicts a fairly static industry with an ongoing rejuvenation process where entrants replace exits. The retail high street for public houses (pubs serving alcohol) in some sleepy semi-rural towns might be the nearest empirical equivalent of this possible scenario. In essence the number of pubs and the profitability of this retail market remain constant over time—replacement and displacement rates of entrants and exits equate holding the number of pubs in the market fixed. In ecological terms this fixed carrying capacity could resemble a flower bed of limited size that can accommodate a fixed number of plants—maintained by dying (exits) plants being replaced/displaced by an equal number of new ones (entrants).
In the top right plot, there is no trend in the relation between profits and carrying capacity, but exit dominates entry. Over time we move along the line to a lower number of firms and consequently lower profits. This situation depicts declining retail sector industry much like the decline of candle shops following the diffusion of electric light to homes. More recently, it is capable of depicting a situation like the decline of music high street record stores caused by the emergence of online music retailers.
In the bottom left plot, entry and exit cancel each other but there is a negative trend in the carrying capacity, or conversely a positive trend in profits when we keep the number of firms constant. The increased market opportunities (reflected by higher industry profits) are captured by the incumbent firms. Most likely, these firms grow.
In the final example (bottom right), there is net exit and a decrease in the carrying capacity given constant profits. We move along the equilibrium line while the line itself also moves. In this example the composite outcome is such that the profits increase. This situation is very much synonymous with a situation where the retail sector is experiencing a rise in minimum efficient scale (MES). Increased economies of scale cause net exit and result in a smaller number of more monopolistic and profitable retailers. Although outside of our sample period, the advent of the internet and the creation of online retail sectors would be examples of cases where minimum efficient scale rises causing a smaller number of online monopolistic firms and greater sector profits.
These four examples highlight the agnostic and flexible nature of the model. In fact, all different situations can be distinguished based on the individual intercepts in γ1 and γ2 (3.1) and (3.2) and the trend coefficient κ in (3.3). In Table 3 we enumerate all 9 combinations of declining, stable or increasing number of firms and profits in equilibrium. In each cell of the table we indicate the corresponding parameter restrictions.
3.2 Operationalization of variables
We estimate our model for the earlier mentioned collection of shop types (industries) in the retail sector in the Netherlands, for the period 1980–2000. Below we summarize the key variables and list the control variables we use:
3.2.1 Key variables
- e it :
-
Entry rate in shop type i during year t.
- x it :
-
Exit rate in shop type i during year t.
- N it :
-
Number of firms in shop type i at start of year t.
- π it :
-
Total industry profit in shop type i in year t (in 1990 prices).
3.2.2 Variables included in vector W
log modal income: log average modal income (in 1990 prices).
log consumer spending: log total consumer spending in shop type (in 1990 prices).
log unemployment: log number of unemployed (in millions).
3.2.3 Variables included in vector Z
Vector Z contains the same variables as vector W. In addition, the real interest rate is included.
3.3 Explanation of expected relations between model variables
Equation (6) of our model describes the interrelations between entry, exit, and total industry profits. Many empirical studies of industrial organization model the interrelation between entry and exit (e.g. Carree and Thurik 1996; Burke and van Stel 2014; Samaniego 2010). When more firms leave the market, there is room for more entry (replacement). When more firms enter the market, some other firms may be forced to leave the market because it is no longer competitive enough (displacement). Also, when profits in an industry increase, this attracts more firms (positive effect on entry) and incentives for firms to leave the market are low (negative effect on exit). Furthermore, when entry, exit or profits are above or below equilibrium carrying capacity, error-correction will cause these variables to move towards the steady-state level again. All these type of interactions between entry, exit and profits are captured by the coefficients contained in matrices A (short-term effects) and Γ (adjustment effects) in (6).
The vector Z in (6) contains exogenous explanatory variables for (changes in) entry, exit, and profit levels. In our application this vector includes the variables modal income, consumer spending, unemployment, and real interest rate. Modal income acts as an opportunity cost for running a retail shop, and hence this variable is expected to have a negative impact on entry and a positive impact on exit. Furthermore, an increase in modal income level may signal an overall upturn of the economy from which shopkeepers benefit as well (Carree and Thurik 1994). Hence the expected impact on profits is positive. The growth rate of consumer expenditure on the goods and services sold in a shop type is an indicator for demand growth. This variable is expected to have a positive impact on entry, a negative impact on exit (Bergin and Bernhardt 2008), and a positive impact on profits. Changes in unemployment may have a positive effect on entry as the (newly) unemployed may have limited alternative employment options in the wage sector (Thurik et al. 2008). Increasing unemployment rates are also a disincentive to exit as economic circumstances are not favorable to find a different occupation. Increasing unemployment will also put pressure on profit levels (expected effect on profits negative). High interest rates, finally, make running a business more expensive, hence the expected impact on entry is negative. Also, profit levels may be lower when interest rates are high.
With the exception of the real interest rate, the variables from vector Z are also included in the vector W capturing the long-term influences on entry, exit, and profits. In other words, the variables in W can move the equilibrium relations. By and large, the arguments are the same as for the short-term impacts described above. The interest rate is not included in the long-run relationships for two reasons. First, the interest rate appears to be non-stationary. Therefore this variable cannot be a determinant of the steady state levels of the stationary variables entry and exit. Second, the interest rate is expected to only affect the markets in the short run. That is, the interest rate mainly influences the moment to start a business (hence an impact in the short run) but not the decision as such to start a business. To the contrary modal income (indicator of opportunity costs), consumer spending (indicator of shop type-specific demand) and unemployment (indicator of general business conditions) may be seen as more structural, long-run, impacts on entry and exit. Note that the effects of unemployment in the long-run equations may be different from those in the short-term. In particular, the positive effect of unemployment on entry may be a short-term effect only, primarily relating to individuals who have just recently become unemployed, and want to start a business. In the long-term though, a structurally high level of unemployment indicates bad conditions for running businesses, implying a negative relation with entry.
As mentioned earlier, the steady-state relation for the number of firms also contains total industry profits. A market with higher total profits can facilitate more firms hence the expected relationship is positive. What is interesting is whether the parameter for profits in the long-run relation (Eq. 3.3 in the model) is bigger or smaller than one. This can clearly be seen by writing the long-run relation for total profit in yet another way,
The left hand side of this equilibrium relation now gives the average profit per firm. A λ-coefficient smaller than one suggests a positive relation between the equilibrium profit per firm and the number of firms. This implies that more firms are associated with larger profits per firm. In other words, total industry profits increase disproportionally with an increase in the number of firms. On the contrary, a coefficient in excess of one corresponds to decreasing average profits per firm.Footnote 14
4 Results
We use the model as described in Eqs. (3)–(8) to analyze 41 different shop types in the Dutch retail sector. Parameter estimation is done by numerically maximizing the log likelihood function using Ox 7 (Doornik 2007). The likelihood function can straightforwardly be obtained from the model specification.
We present the estimation results in Tables 4 and 5. First we comment on the long-run relationships as represented in Table 4. The λ-parameter in the equilibrium relation between number of firms and total industry profits is significantly different from 0, but not significantly different from 1. This implies that the equilibrium relation between profits and number of firms actually dictates an equilibrium level for the average profits. In other words, average profits per firm are independent of the number of firms, see Eq. (9).
Modal income is negatively related to the long-run level of entry. This implies that if the modal income is high there are fewer firms entering the market in equilibrium. This perfectly corresponds to our conjecture that modal income acts as opportunity costs of entrepreneurship. In contrast, the equilibrium level of exit seems to be unaffected by modal income. This may reflect the existence of a labor market penalty where former business owners re-entering wage-employment experience a lower return (in terms of earnings) to their business ownership experience compared with the return to the experience as wage-employee (Baptista et al. 2012). This, in turn, may lead the marginal entrepreneur to remain in business, even when wages increase.
Modal income and consumer spending have a negative impact on the carrying capacity of a market (given a certain level of total industry profits). Both variables indicate good economic conditions. Keeping total profits constant, in good economic conditions the market can hold fewer firms. Stated otherwise, profitability (average profits per firm) increases in such conditions. The consumer spending is not significantly related to the long run entry and exit levels. High unemployment signals bad business conditions. Hence few firms enter the market and few firms exit. Turbulence in this case will be low.Footnote 15 High unemployment also seems to lower the average profit per firm in equilibrium.Footnote 16
The estimates presented in Table 5 give insight in the short-term changes. The adjustment parameters indicate the way an out-of-equilibrium situation is corrected. If the entry level is too high relative to the equilibrium level, this leads to a short-term decrease in entrants in the next period and a short-term increase in the number of exits. At the same time, the total profit level increases. If the exit level is too high, this mainly gets corrected by a lower exit level in the next period. Excess exit is also associated with a decrease in profit levels. The entry rate is affected only slightly (though significantly at 10%). Finally, excessive profits are corrected through a change in profits itself and, to a small extent, by a (temporarily) higher number of entrants, who are attracted by the high profit level.
The short-run effects of the (lagged) endogenous variables can be best shown using impulse response functions. Such functions give insight on how external shocks affect all variables. We will present such functions in the next subsection. The short-run effects of the exogenous variables are easier to evaluate as they correspond to the direct impact of a particular change. The direct impact of an increase in modal income is that entry levels drop and profit levels increase, consistent with theoretical expectations. The magnitude of these effects is relatively large. An increase in consumer spending only leads to a direct increase in profits. An increase in unemployment directly leads to an increase in entry, and decrease in exit and profit. Finally, the interest rate only has a direct impact on entry: an increase in the interest rate corresponds to lower entry levels as expected.
Finally, we discuss the estimated correlation structure. We find a relatively large correlation (0.35) between the error terms associated with entry and exit. This positive correlation implies that many shocks lead to a change in both variables, that is, many shocks tend to affect turbulence. The correlation between the errors in entry or exit and profit are rather small.
4.1 Tests on trends
For each shop type we tested whether on average the long-run steady state entry rate exactly offsets the average long-run exit, such that the number of firms is constant in equilibrium. In terms of the model parameters this means testing the restriction γ1i = γ2i. The corresponding hypothesis is not rejected in 58% of the cases. On the other hand, this result implies that for a large part of the shop types there is a positive or negative trend in the number of firms, this matches the reported data described in Table 2.
Next, for each shoptype we test whether the long-run relation between industry profit and number of firms contains a trend. We test the significance of the individual trends and find that in 73% of the cases the trend is not significant. Therefore, in the majority of cases the relationship between profits and number of firms does not move over time. A joint test on both hypothesis (entry offsets exit, no trend) is not rejected in 44% of the cases. So, about half of the shoptypes are stable in the sense that in the long-run, both total industry profits and the number of firms remain constant.
Next, for the cases where the number of firms shows a trend we test whether the profits are stable. The corresponding hypothesis is κ = γ1 − γ2 (compare Table 3). The results are given in Table 6. For the cases where the hypothesis is rejected we distinguish between declining profits and increasing profits. The table shows that in 20% of the shop types (industries), both the number of firms and industry profits decline.
Table 6 shows that, on average over the period 1980–2000, the majority of shop types (44%) in Dutch retailing showed no major changes in equilibrium industry structure. For about one-third of shop types, the equilibrium number of firms declined significantly over this period. For some industries, this finding corresponds with a development of increased scale and scope in Dutch retailing over this period, associated with increased average firm size. Explanations for this increase in average firm size include consolidation into retail chains, horizontal integration and ICT developments altering logistic operations in the retail trade (Creusen et al. 2006). For some other industries, the declining number of firms goes together with declining industry profits. This is likely associated with the end of the industry life cycle of certain shop types, reflecting the finite life of certain submarkets (Klepper 1997). This may for instance be the case for dairy shops (where the selling of dairy products was taken over by supermarkets) and for the sewing-machines industry (see Table 1).
5 Simulations and discussion
Having established a model with realistic features (both in terms of estimated model parameters and in terms of the distribution of industries over different types of steady state behavior as depicted in Table 6), we now move on to perform a simulation analysis based on our estimated model, which will enable us to answer the three research questions formulated in the introduction.
In this section we use impulse response functions to investigate the impact of entry and exit shocks to a market in equilibrium. We measure the impact of the shock relative to the market development without a shock. By considering relative measures the impulse response functions become independent of the market-specific intercepts and trend. Furthermore, we assume that all exogenous variables are constant and equal to their observed mean values over time. We consider a one-time purely exogenous shock (analogous to a ‘disaster’) to an otherwise stable system. The size of the shock is taken to be 1%.
In each case we investigate three dimensions of the adjustment process to equilibrium caused by the impact of these shocks: net change, time of adjustment and the pattern of adjustment.Footnote 17 ‘Net change’ measures the total effect of the shock comparing the initial and the new equilibrium states. It is the Schumpeterian element of our investigation, and it measures the permanent impact of the shock (the ‘disaster’) after recovery to the new equilibrium (i.e. the sustainable post-disaster level of economic activity) has been completed. ‘Time’ is about the duration of disequilibrium between these states (i.e. the time of recovery). It tests Schultz’s assumption that disequilibrium is the norm rather than a rarity. ‘Pattern’ is about the route that the adjustment process takes from the initial to the new equilibrium. Its analysis is important because economic analyses are often based upon comparative statics and the assumption of monotonic adjustment processes.Footnote 18 This part of our analysis is particularly relevant for disaster management as we show that different routes or time-paths of recovery are associated with different post-disaster equilibria having lasting impact on the economy (Xie et al. 2018).
Figure 2 shows the result of a 1% shock to entry on the five elements of the model including relative change in entry, exit, total profit, number of firms and profit per firm. The result of this shock is to cause more exit for at least 15 years,Footnote 19 and permanently higher levels of total industry profits and the number of firms. Since the increase in the number of firms seems to be slightly larger than the increase in total profits, the figure suggests that average profit per firm is somewhat lower in the new steady state. However, since the estimate for parameter λ is not significantly different from unity (see Table 4), we know that the difference in average profit per firm between the initial and new equilibrium does not significantly differ from zero (see also Eq. (9), where, for λ = 1, equilibrium average profits are independent of the number of firms).
Hence, as a result of the positive shock to entry, total profits as well as the number of firms permanently increase. In terms of the three dimensions of the adjustment process to equilibrium, the shock to entry provides several insights. First we note that while there are no long term changes to entry and exit, the short term rise in net entry causes a permanent increase in the number of firms. This is associated with higher total industry profits. Therefore, in terms of net change the shock to entry has a permanent effect on the economic size of the retail industry. Second, the timing of this adjustment process is far from instantaneous lasting approximately 10–15 years between the initial and the new equilibrium. Thirdly, the pattern of the adjustment process is non-monotonic and oscillates before it settles on a convergent path towards the new equilibrium. This is particularly noticeable with profits per firm which first ‘overshoots’ and then ‘undershoots’ before finally converging towards the new equilibrium.
This pattern of adjustment following the shock to entry is consistent with an entrepreneurial function of entrants as predicted by Schumpeter (1947) and Schultz (1975), and similar to a disaster management function where the interaction between entrants and other actors in the system together determine the time-path and new equilibrium following an exogenous shock (disaster) to the system. Entrants have a disruptive impact on the market, causing destruction of businesses and turbulence, a long period of disequilibrium, and importantly a permanent change in the market equilibrium or carrying capacity. Put differently, the market does not return to the original pre-entry shock equilibrium carrying capacity and total industry profits are permanently changed. Notably, total industry profits are at a permanently higher level so in this case, the level of dynamic economic resilience seems to have been quite high (Duhamel et al. 2016).
The entry shock also causes an oscillating pattern for the average profit level per firm. At first, average profits rise, but after a few years, a sharp decrease is visible, after which the average profit level stabilizes. The question now is how this oscillating pattern can be explained, where average profits per firm initially rise above the pre-shock equilibrium level and then sharply decrease. The first part of this adjustment process is consistent with innovation which expands market size by making the retail sector more attractive to consumers through effects such as expanding product variety (Krugman 1979) and creating new market segments. Looking at this from a product differentiation perspective the entrants’ innovation expands market space thereby creating disequilibrium. The emergence in supernormal profits then attracts new entrants and the competitive process is then akin to models of product differentiation (e.g. Hotelling’s 1929 model of spatial competition) where average profits per firm decline. There are several alternative possibilities as to why the parameters estimated in our model illustrate this effect. These include the possibility that a shock increase in entry is associated with a fall in barriers to entry so that both the number of firms and the level of competition (not only on the product market but also on the factor market for employees; Roessler and Koellinger 2012) temporarily increase. Another alternative view is that entry shocks might be associated with reductions in resource constraints for entrants such as lack of finance (Evans and Jovanovic 1989; Burke et al. 2000) thereby causing a period of excess entry which let average profits decline. Many other explanations and indeed associated counter arguments for these can be advanced (e.g. Cressy 1996) but as we noted earlier our research contribution is uncovering the adjustment process and highlighting its economic significance. A definitive interpretation of the estimated parameters is beyond the scope of this paper and hence is raised as an area for future research.
The impact of an exogenous shock to the number of exits is shown in Fig. 3. The figure shows that the entry rate increases for 10–15 years. However, the size of this impact is relatively small (note the different scales on the vertical axes for entry and exit). In the new steady state profit levels have decreased by more than 1.74%, the number of firms has decreased by about 1.86%.
In terms of the three dimensions of the adjustment process to equilibrium, we observe the following. First we note that there is again no permanent change to the equilibrium rate of entry and exit. These results match the stationary nature of the entry and exit rate. However, again consistent with an entrepreneurial role of firms, an exit shock causes a net decrease in the equilibrium number of firms and industry profit meaning that the industry does not recover to its initial equilibrium. Second, the timing of the adjustment process to the new equilibrium is again slow taking between 10 and 15 years. Thirdly, the pattern of the adjustment process is not monotonic. Initially the shock to exit has a sustained affect causing the exit rate to stay above equilibrium for 6 years. The entry rate stays above the long run equilibrium for an even longer time, however this increase is not very large. Hence, in the case of a positive shock to exit the striking result is that the market never fully recovers: the size of the market decreases, both in terms of the number of firms, and in terms of total industry profit.
In general, the entry and exit shocks simulations of the empirically estimated parameters of the model manifest permanent changes in the industry, i.e., there is a dynamic equilibrium. In these processes entrants are found to play two roles. Initially, they perform an entrepreneurial function of creating disequilibrium; permanently undermining the existing equilibrium. Thereafter they play the conventional equilibrating role of moving the industry to a new equilibrium. For instance, a shock to exit has a permanent effect in that the market does not recover as opposed to one in entry which has a permanent positive effect on the size of the market. These shocks cause a long period of disequilibrium, typically 10–15 years, indicating the importance of the entrepreneurial function of entry and exit. This provides support for the Schultzian view that disequilibrium is the norm rather than the oddity. Moreover, we observe not only long periods of disequilibrium but also many non-monotonic adjustment processes which highlight their complexity. Frequently these processes are initially ‘erratic’ before earnest convergence to the new equilibrium sets in.
6 Conclusion
A huge theoretical literature exists on the role of entrepreneurial entry in disrupting or restoring market equilibrium yet hardly any empirical models have been developed in order to test these theories. In this paper we explored the role of entry in the context of the field of disaster management while also drawing insights from the economics of entrepreneurship literature. We constructed a dynamic model capable of testing these insights where entrants are entrepreneurial and bring innovation that affects the long run equilibrium carrying capacity of a market (à la Schumpeter). The model also encompasses more traditional classical perspectives on entry and exit where firms can be easily replaced and where entry and exit respond to market equilibrium causing a swift return to equilibrium. Hence, our model enables to discriminate between the entrants’ role of performing the entrepreneurial function of creating disequilibrium (causing a gradual ‘disaster’ to incumbent players in the market) and their conventional equilibrating role of moving the industry to a new equilibrium. In terms of the field of disaster management, entrepreneurial entry can be regarded as a (gradual) disaster while the restoration towards a new equilibrium as disaster management. Moreover, the model allows for an analysis of three aspects of industry dynamics: the effect of entry and exit on market equilibrium, the duration of disequilibrium (time of recovery), and the patterns of adjustment (route of recovery). Based on these aspects we test the main features of three seminal theories on the economic role of entry and exit: neoclassical theory, Schumpeter and Schultz.
We apply our dynamic model to a rich dataset on Dutch retailing—a sector with extensive diversity. For many retail markets (44%) we find a stable equilibrium, that is, in equilibrium profits do not change and the number of firms stays constant. Note that in such an equilibrium there may still be a replacement of firms, that is, the entry and exit rates are equal but not necessarily zero. On the other hand, for 20% of the markets we established an equilibrium in which both total industry profits and the number of firms decline. Such markets are becoming less important overall, a likely example of such a market are music stores. In these markets exit (and entry) have an important role of maintaining equilibrium by reducing the number of firms to keep trend with the decrease in total industry profits.
Using simulation analysis, we also find that entry plays an entrepreneurial role and when in disequilibrium, a market does not simply gravitate back towards the previous equilibrium carrying capacity in the market. Instead, we find that a shock to entry causes disequilibrium, the resulting adjustment process to equilibrium is sufficiently slow so that, in line with economics theorists of entrepreneurship (most notably, Schultz), markets spend long protracted periods in disequilibrium. In this process they undergo turbulence and a non-monotonic adjustment towards equilibrium. Notably, in line with Schumpeter, it is a new equilibrium as the disruptive effect of entry grows markets so that a shock to the entry rate has a permanent long term positive effect on the number of firms and total industry profits. These effects are proportionate so that average profit per firm in the new equilibrium does not significantly differ from that in the old equilibrium. Our simulation analysis provides support for the claims by Xie et al. (2018) that the time-path of disaster recovery, the disaster losses and the post-disaster equilibrium are strongly connected.
Correspondingly, a shock to exit causes a long term permanent decrease in the number of firms and industry profits with average profits per firm again remaining stable. The results provide some new insights and likely challenges for public policy aimed at enhancing economic performance; particularly those concerned with limiting the downside of business closures (exits) and the benefits of new entrants. Our findings illustrate that entry and exit are more important for long term economic performance than implied by more conventional analysis which overlooks the entrepreneurial role of firms.
In terms of the three different theories on the economic role of entry and exit, our empirical findings show that industry dynamics in Dutch retailing show features of all three theories: a shock in entry causes a new market equilibrium à la Schumpeter and the adjustment process is non-monotonic and slow causing long periods of disequilibrium à la Schultz. Regarding neo-classical theory, although our simulation analysis of the consequences of shocks to entry and exit do not lend much support to neo-classical theory (as the old equilibrium is not restored, and the adjustment to the new equilibrium follows a non-monotonic path), the majority (44%) of markets that remain in a stable equilibrium does seem to be more consistent with neo-classical theory, as the role of entry and exit in these markets is relatively limited. Hence, our empirical results suggest that, although to some extent the three theories contradict each other, they are also compatible with each other.
The field of disaster management is expanding rapidly and new insights from other disciplines are increasingly being added to inform disaster management literature. For instance, recent studies have added perspectives from project management (Prasad et al. 2017), commercial supply chain management (Olaogbebikan and Oloruntoba 2017; Behl and Dutta 2018) and internet of things (IoT) technology (Sinha et al. 2017; Han et al. 2018) literatures. In a similar vein, the current study adds new insights from the economics of entrepreneurship literature. Future research may focus on distinguishing between different types of firm entry and exit at the industry level, e.g. in terms of de novo entry versus entrants that relocate from another industry, and exiting firms that cease operations versus exiting firms that relocate to another industry (Plehn-Dujowich 2009). Another useful distinction may be based on the size of the firm entries and exits (Manjón-Antolín 2010).
In sum, studying economic markets and using economic modelling, our paper has contributed to disaster management literature by showing how different time-paths following a shock may be related to different post-shock equilibria.
Notes
Akter and Wamba (2017) provide various estimates of total economic losses caused by recent natural disasters.
This may include a better preparedness for new disasters through learning by private enterprises and government organizations from each other’s disaster responses (Hausken and Zhuang 2016; Wang et al. 2016). However, other researchers dispute if it is in fact possible to increase preparedness for future disasters (Goldschmidt and Kumar 2017).
The Kirznerian notion of entrepreneurial activity originates from the existence of disequilibria characterized by profit opportunities.
There are four stages in the disaster management life cycle: mitigation, preparedness, response, and recovery (Waugh and Hy 1990; Galindo and Batta 2013). A literature review by Altay and Green (2006) revealed that only 11% of studies in disaster operations management literature dealt with the stage of disaster recovery.
The industries in our data base are defined at (approximately) fourth digit level. Hence, these industries are quite narrowly defined. Because firms in the retail sector are almost always shops, we use the terms shop type and industry interchangeably throughout this paper.
A small part of an early version of this data set (22 shop types for the 1981–1988 period) is used explaining entry and exit flows: in Carree and Thurik (1996) for their analysis of the role of incentives, barriers, replacement and displacement and in Carree and Thurik (1999) for their analysis of the role of carrying capacity.
Hence we choose a base year to compute the level of average profits or turnover, and next we compute the levels for the other years making use of the relative changes of only those firms present in two consecutive years. As most firms stayed in the panel for many years, these relative changes are also based on a substantial number of firms, but this way we correct for trend breaks introduced by a changing composition of the panel (e.g. when a firm with exceptionally high profits would enter or exit the panel). For the base year we always choose a year for which the number of participating firms in the panel is high.
Ideally, one would like to use information from Statistics Netherlands (CBS) as this is the national statistical office in the Netherlands. However, as the number of firms in a shop type (which is approximately fourth digit level) is often small, and the number of firms is rounded to thousands in CBS statistics, using the CBS data also implies some extent of measurement error. Therefore we use information from both sources to estimate the dynamic pattern of the profit and turnover variables.
Total consumer spending was computed by multiplying the variables average household spending, the total number of households in the Netherlands and the share of a certain shop type in total household spending.
See www.datastream.com. In particular we used the series HOLIB1Y.
This can be seen as follows. It holds that \( e_{t} = 1 + \frac{{E_{t} }}{{N_{t} }} = \frac{{N_{t} + E_{t} }}{{N_{t} }} \). Also, \( x_{t} = 1 + \frac{{X_{t} }}{{N_{t + 1} }} = \frac{{N_{t + 1} + X_{t} }}{{N_{t + 1} }} = \frac{{N_{t} + E_{t} - X_{t} + X_{t} }}{{N_{t + 1} }} = \frac{{N_{t} + E_{t} }}{{N_{t + 1} }} \). Hence it follows that \( \frac{{e_{t} }}{{x_{t} }} = \frac{{N_{t + 1} }}{{N_{t} }} \).
As is well known in the econometric literature, in practice it may happen that the tests contradict each other. Furthermore, given sample size we should not expect a very large power of the tests.
Turbulence is the sum of entry and exit.
Note that the third dependent variable in Table 4 is an inverse measure of average profits.
The importance of accounting for the timing of the adjustment process in empirical models of entry and exit is also stressed by Manjón-Antolín (2010).
This may be interpreted as the magnitude of the disaster in terms of lost flows of economic activity between the time of disaster and the time post-disaster equilibrium is reached (Xie et al. 2018).
References
Akter, S., & Wamba, S. F. (2017). Big data and disaster management: A systematic review and agenda for future research. Annals of Operations Research(forthcoming). https://doi.org/10.1007/s10479-017-2584-2.
Altay, N., & Green, W. G., III. (2006). OR/MS research in disaster operations management. European Journal of Operational Research,175(1), 475–493.
Audretsch, D. B., Baumol, W. J., & Burke, A. E. (2001). Competition policy in dynamic markets. International Journal of Industrial Organization,19, 613–634.
Baptista, R., Lima, F., & Torres Preto, M. (2012). How former business owners fare in the labor market? Job assignment and earnings. European Economic Review,56, 263–276.
Barreto, H. (1989). The entrepreneur in microeconomic theory: Disappearance and explanation. London: Routledge.
Baumol, W. J. (2002). The free-market innovation machine: Analyzing the growth miracle of capitalism. Princeton, NJ: Princeton University Press.
Beesley, M. E., & Hamilton, R. T. (1984). Small firms’ seedbed role and the concept of turbulence. Journal of Industrial Economics,33, 217–231.
Behl, A., & Dutta, P. (2018). Humanitarian supply chain management: A thematic literature review and future directions of research. Annals of Operations Research(forthcoming). https://doi.org/10.1007/s10479-018-2806-2.
Bergin, J., & Bernhardt, D. (2008). Industry dynamics with stochastic demand. RAND Journal of Economics,39(1), 41–68.
Bower, J. L., & Christensen, C. M. (1995). Disruptive technologies: Catching the wave. Harvard Business Review,73, 43–53.
Breitung, J. (2000). The local power of some unit root tests for panel data. In B. Baltagi (Ed.), Advances in econometrics: Nonstationary panels, panel cointegration, and dynamic panels (Vol. 15, pp. 161–177). Stamford: JAI Press.
Burke, A. E., FitzRoy, F. R., & Nolan, M. A. (2000). When less is more: Distinguishing between entrepreneurial choice and performance. Oxford Bulletin of Economics and Statistics,62, 565–587.
Burke, A. E., & Van Stel, A. (2014). Entry and exit in disequilibrium. Journal of Business Venturing,29(1), 174–192.
Carree, M. A., & Thurik, A. R. (1994). The dynamics of entry, exit and profitability: An error correction approach for the retail industry. Small Business Economics,6, 107–116.
Carree, M. A., & Thurik, A. R. (1996). Entry and exit in retailing: Incentives, barriers, displacement and replacement. Review of Industrial Organization,11, 155–172.
Carree, M. A., & Thurik, A. R. (1999). Carrying capacity and entry and exit flows in retailing. International Journal of Industrial Organization,17, 985–1007.
Choi, I. (2001). Unit root tests for panel data. Journal of International Money and Finance,20, 249–272.
Cressy, R. C. (1996). Are business startups debt-rationed? The Economic Journal,106, 1253–1270.
Creusen, H., Vroomen, B., Van der Wiel, H., & Kuypers, F. (2006). Dutch retail trade on the rise?, CPB Document No. 137. The Hague, Netherlands: CPB Netherlands Bureau for Economic Policy Analysis.
De Jong, J. P. J., & Marsili, O. (2015). The distribution of Schumpeterian and Kirznerian opportunities. Small Business Economics,44(1), 19–35.
Doornik, J. A. (2007). Object-oriented matrix programming using Ox, 3rd edn. London: Timberlake Consultants Press. www.doornik.com.
Duhamel, C., Santos, A. C., Brasil, D., Châtelet, E., & Birregah, B. (2016). Connecting a population dynamic model with a multi-period location-allocation problem for post-disaster relief operations. Annals of Operations Research,247(2), 693–713.
Engle, R. F., & Granger, C. W. J. (1987). Co-integration and error correction: Representation, estimation, and testing. Econometrica,55, 251–276.
Galindo, G., & Batta, R. (2013). Review of recent developments in OR/MS research in disaster operations management. European Journal of Operational Research,230(2), 201–211.
Geroski, P. A. (2001). Exploring the niche overlaps between organizational ecology and industrial economics. Industrial and Corporate Change,10(2), 507–540.
Goldschmidt, K. H., & Kumar, S. (2017). Reducing the cost of humanitarian operations through disaster preparation and preparedness. Annals of Operations Research(forthcoming). https://doi.org/10.1007/s10479-017-2587-z.
Granger, C. W. J. (1993). What are we learning about the long-run? The Economic Journal,103, 307–317.
Han, S., Huang, H., Luo, Z., & Foropon, C. (2018). Harnessing the power of crowdsourcing and internet of things in disaster response. Annals of Operations Research(forthcoming). https://doi.org/10.1007/s10479-018-2884-1.
Hannan, M. T., & Freeman, J. (1989). Organizational ecology. Cambridge, MA: Harvard University Press.
Hausken, K., & Zhuang, J. (2016). The strategic interaction between a company and the government surrounding disasters. Annals of Operations Research,237(1–2), 27–40.
Hendry, D. F., Pagan, A. R., & Sargan, J. D. (1984). Dynamic specification. In Z. Griliches & M. D. Intriligator (Eds.), Handbook of econometrics (Vol. 2, pp. 1023–1100). Amsterdam: Elsevier.
Hotelling, H. H. (1929). Stability in competition. The Economic Journal,39, 41–57.
Ibrahim, S. E., & El Ebrashi, R. (2017). How social entrepreneurship can be useful in long-term recovery following disasters. Journal of Humanitarian Logistics and Supply Chain Management,7(3), 324–349.
Im, K., Pesaran, M. H., & Shin, Y. (2003). Testing for unit roots in heterogeneous panels. Journal of Econometrics,115, 53–74.
Jovanovic, B., & MacDonald, G. M. (1994). The life cycle of a competitive industry. Journal of Political Economy,102, 322–347.
Kim, W Ch., & Mauborgne, R. (2005). Blue ocean strategy: How to create uncontested market space and make the competition irrelevant. Boston, MA: Harvard Business School Press.
Kirzner, I. M. (1973). Competition and entrepreneurship. Chicago: University of Chicago Press.
Klepper, S. (1997). Industry life cycles. Industrial and Corporate Change,6, 145–182.
Krugman, P. R. (1979). Increasing returns, monopolistic competition and international trade. Journal of International Economics,9, 469–479.
Levin, A., Lin, C., & Chu, C. (2002). Unit root tests in panel data: Asymptotic and finite-sample properties. Journal of Econometrics,108, 1–24.
Maddala, G., & Wu, S. (1999). A comparative study of unit root tests with panel data and a new simple test. Oxford Bulletin of Economics and Statistics,61, 631–652.
Manjón-Antolín, M. C. (2010). Firm size and short-term dynamics in aggregate entry and exit. International Journal of Industrial Organization,28, 464–476.
Mishra, D., Kumar, S., & Hassini, E. (2018). Current trends in disaster management simulation modelling research. Annals of Operations Research(forthcoming). https://doi.org/10.1007/s10479-018-2985-x.
Olaogbebikan, J. E., & Oloruntoba, R. (2017). Similarities between disaster supply chains and commercial supply chains: A SCM process view. Annals of Operations Research(forthcoming). https://doi.org/10.1007/s10479-017-2690-1.
Oloruntoba, R., & Banomyong, R. (2018). Humanitarian logistics research for the care of refugees and internally displaced persons: A new area of research and a research agenda. Journal of Humanitarian Logistics and Supply Chain Management,8(3), 282–294.
Pedroni, P. (1999). Critical values for cointegration tests in heterogeneous panels with multiple regressors. Oxford Bulletin of Economics and Statistics,61, 653–670.
Pedroni, P. (2004). Panel cointegration; Asymptotic and finite sample properties of pooled time series tests with an application to the PPP hypothesis. Econometric Theory,20, 597–625.
Plehn-Dujowich, J. M. (2009). Entry and exit by new versus existing firms. International Journal of Industrial Organization,27, 214–222.
Porter, M. E. (1980). Competitive strategy. New York: Free Press.
Prasad, S., Woldt, J., Tata, J., & Altay, N. (2017). Application of project management to disaster resilience. Annals of Operations Research(forthcoming). https://doi.org/10.1007/s10479-017-2679-9.
Reid, G. C. (2007). The foundations of small business enterprise: An entrepreneurial analysis of small business inception and growth. London: Routledge.
Roessler, C., & Koellinger, P. (2012). Entrepreneurship and organization design. European Economic Review,56, 888–902.
Samaniego, R. M. (2010). Entry, exit, and investment-specific technical change. American Economic Review,100(1), 164–192.
Schultz, T. W. (1975). The value of the ability to deal with disequilibria. Journal of Economic Literature,13(6), 827–846.
Schumpeter, J. A. (1947). Theoretical problems of economic growth. Journal of Economic History,7, 1–9.
Sinha, A., Kumar, P., Rana, N. P., Islam, R., & Dwivedi, Y. K. (2017). Impact of internet of things (IoT) in disaster management: A task-technology fit perspective. Annals of Operations Research(forthcoming). https://doi.org/10.1007/s10479-017-2658-1.
Tatham, P., & Houghton, L. (2011). The wicked problem of humanitarian logistics and disaster relief aid. Journal of Humanitarian Logistics and Supply Chain Management,1(1), 15–31.
Thurik, A. R., Carree, M. A., Van Stel, A. J., & Audretsch, D. B. (2008). Does self-employment reduce unemployment? Journal of Business Venturing,23(6), 673–686.
Wang, X., Wu, Y., Liang, L., & Huang, Z. (2016). Service outsourcing and disaster response methods in a relief supply chain. Annals of Operations Research,240(2), 471–487.
Waugh, W. L., & Hy, R. J. (Eds.). (1990). Handbook of emergency management: Programs and policies dealing with major hazards and disasters. New York, NY: Greenwood Press.
Wennekers, S., & Thurik, A. R. (1999). Linking entrepreneurship to economic growth. Small Business Economics,13(1), 27–55.
Xie, W., Rose, A., Li, S., He, J., Li, N., & Ali, T. (2018). Dynamic economic resilience and economic recovery from disasters: A quantitative assessment. Risk Analysis,38(6), 1306–1318.
Acknowledgements
Comments by Gavin Reid, Italo Colantone, Philipp Koellinger, Christian Roessler and Rameshwar Dubey are gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fok, D., van Stel, A., Burke, A. et al. How entry crowds and grows markets: the gradual disaster management view of market dynamics in the retail industry. Ann Oper Res 283, 1111–1138 (2019). https://doi.org/10.1007/s10479-019-03322-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-019-03322-y