Skip to main content
SpringerLink
Log in

Comonotonicity and low volatility effect

  • S.I.: Recent Developments in Financial Modeling and Risk Management
  • Published:
Annals of Operations Research Aims and scope Submit manuscript

Abstract

Discussions on low volatility effects often highlight the advantage of low volatility stocks outperforming high volatility stocks. Using comonotonicity tests, our study provides evidence of the downside of this effect: stock returns do not increase monotonically with low volatility, but volatility increases monotonically with specific risks. We find that, counterintuitively, the low volatility effect is mostly driven by high volatility stocks with high specific risks. Our empirical analysis addresses a cross section of stock returns across 23 developed countries and employs comonotonicity tests to show that expected stock returns do not increase monotonically with lower volatility. In addition, by decomposing volatility into its individual risk components, we show that volatility increases monotonically with its specific risk component. Finally, we also confirm that returns obtained from the low volatility effect in stocks are principally driven by the specific risk component rather than the systematic risk component.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. See Novy-Marx (2014) for a detailed discussion of defensive equity strategies.

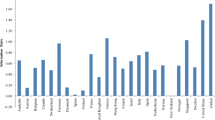
  2. Source: TrackInsight.com.

  3. Haugen and Heins (1975) Haugen and Baker (1996, 2010) and Baker et al. (2011).

  4. The calibration period and portfolio formation methodology follows the work of Baker et al. (2011) and Baker and Wurgler (2015), except that their portfolios are based on U.S. CRSP data.

  5. See results reported in Baker et al. (2011), Blitz and Van Vliet (2007), Bali and Cakici (2008), Chen et al. (2019) and Lin et al. (2018).

References

  • Ang, A., Hodrick, R. J., Xing, Y., & Zhang, X. (2006). The cross-section of volatility and expected returns. The Journal of Finance, 61(1), 259–299.

    Google Scholar 

  • Ang, A., Hodrick, R. J., Xing, Y., & Zhang, X. (2009). High idiosyncratic volatility and low returns: International and further us evidence. Journal of Financial Economics, 91(1), 1–23.

    Google Scholar 

  • Baker, M., Bradley, B., & Wurgler, J. (2011). Benchmarks as limits to arbitrage: Understanding the low-volatility anomaly. Financial Analysts Journal, 67(1), 40–54.

    Google Scholar 

  • Baker, M., & Wurgler, J. (2015). Do strict capital requirements raise the cost of capital? Banking regulation and the low risk anomaly. American Economic Review: Papers and Proceedings, 105(5), 315–320.

    Google Scholar 

  • Bali, T. G., Brown, S., Murray, S., & Tang, Y. (2016). A lottery demand-based explanation of the beta anomaly. Working paper (2408146).

  • Bali, T. G., & Cakici, N. (2008). Idiosyncratic volatility and the cross section of expected returns. Journal of Financial and Quantitative Analysis, 43(01), 29–58.

    Google Scholar 

  • Black, F. (1972). Capital market equilibrium with restricted borrowing. Journal of Business, 45, 444–455.

    Google Scholar 

  • Blitz, D., & Van Vliet, P. (2007). The volatility effect: Lower risk without lower return. Journal of Portfolio Management, 34(1), 102–113.

    Google Scholar 

  • Carhart, M. M. (1997). On persistence in mutual fund performance. The Journal of Finance, 52(1), 57–82.

    Google Scholar 

  • Chen, C., & Zhou, Z.-G. (2001). Portfolio returns, market volatility, and seasonality. Review of Quantitative Finance and Accounting, 17(1), 27–43.

    Google Scholar 

  • Chen, Y.-T., Lai, W., & Sun, E. (2019). Jump detection and noise separation by a singular wavelet method for predictive analytics of high-frequency data. Computational Economics, 54(2), 809–844.

    Google Scholar 

  • Chen, Y.-T., Sun, E., & Yu, M.-T. (2015). Improving model performance with the integrated wavelet denoising method. Studies in Nonlinear Dynamics and Econometrics, 19(4), 445–467.

    Google Scholar 

  • Chen, Y.-T., Sun, E., & Yu, M.-T. (2018). Risk assessment with wavelet feature engineering for high-frequency portfolio trading. Computational Economics, 52, 653–684.

    Google Scholar 

  • Cheung, K. (2007). Characterization of conditional comonotonicity. Journal of Applied Probability, 44, 607–617.

    Google Scholar 

  • Cheung, K. (2008). Improved convex upper bound via conditional comonotonicity. Insurance: Mathematics and Economics, 42, 651–655.

    Google Scholar 

  • Cheung, K. (2009). Applications of conditional comonotonicity to some optimization problems. Insurance: Mathematics and Economics, 45, 89–93.

    Google Scholar 

  • Clarke, R. G., De Silva, H., & Thorley, S. (2010). Know your VMS exposure. The Journal of Portfolio Management, 36(2), 52–59.

    Google Scholar 

  • Dhaene, J., Denuit, M., Goovaerts, M. J., Kaas, R., & Vyncke, D. (2002a). The concept of comonotonicity in actuarial science and finance: Applications. Insurance: Mathematics and Economics, 31(2), 133–161.

    Google Scholar 

  • Dhaene, J., Denuit, M., Goovaerts, M. J., Kaas, R., & Vyncke, D. (2002b). The concept of comonotonicity in actuarial science and finance: Theory. Insurance: Mathematics and Economics, 31(1), 3–33.

    Google Scholar 

  • Dhaene, J., Vanduffel, S., Goovaerts, M. J., Kaas, R., Tang, Q., & Vyncke, D. (2006). Risk measures and comonotonicity: A review. Stochastic Models, 22, 573–606.

    Google Scholar 

  • Dutt, T., & Humphery-Jenner, M. (2013). Stock return volatility, operating performance and stock returns: International evidence on drivers of the ‘low volatility’ anomaly. Journal of Banking & Finance, 37(3), 999–1017.

    Google Scholar 

  • Fama, E. F., & French, K. R. (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics, 33(1), 3–56.

    Google Scholar 

  • Fama, E. F., & French, K. R. (2015). A five-factor asset pricing model. Journal of Financial Economics, 116(1), 1–22.

    Google Scholar 

  • Fama, E. F., & French, K. R. (2016). Dissecting anomalies with a five-factor model. Review of Financial Studies, 29(1), 69–103.

    Google Scholar 

  • Frazzini, A., & Pedersen, L. H. (2014). Betting against beta. Journal of Financial Economics, 111(1), 1–25.

    Google Scholar 

  • Fu, F. (2009). Idiosyncratic risk and the cross-section of expected stock returns. Journal of Financial Economics, 91(1), 24–37.

    Google Scholar 

  • Gangopadhyay, P., Yook, K. C., & Shin, Y. (2014). Insider trading and firm-specific return volatility. Review of Quantitative Finance and Accounting, 43(1), 1–19.

    Google Scholar 

  • Harvey, C. R., Liu, Y., & Zhu, M.-T. (2016). \(\ldots \) and the cross-section of expected returns. Review of Financial Studies, 29(1), 5–68.

    Google Scholar 

  • Haugen, R. A., & Baker, N. L. (1996). Commonality in the determinants of expected stock returns. Journal of Financial Economics, 41(3), 401–439.

    Google Scholar 

  • Haugen, R. A., & Baker, N. L. (2010). Case closed. In J. Guerard (Ed.), Handbook of portfolio construction (pp. 601–619). Boston, MA: Springer.

    Google Scholar 

  • Haugen, R. A., & Heins, A. J. (1975). Risk and the rate of return on financial assets: Some old wine in new bottles. Journal of Financial and Quantitative Analysis, 10, 775–784.

    Google Scholar 

  • Huang, W., Liu, Q., Rhee, S. G., & Zhang, L. (2009). Return reversals, idiosyncratic risk, and expected returns. The Review of Financial Studies, 23(1), 147–168.

    Google Scholar 

  • Jacod, J., & Shiryaev, A. (2013). Limit theorems for stochastic processes (Vol. 288). Berlin: Springer.

    Google Scholar 

  • Jegadeesh, N., & Titman, S. (1993). Returns to buying winners and selling losers: Implications for stock market efficiency. The Journal of Finance, 48(1), 65–91.

    Google Scholar 

  • Jordan, B. D., & Riley, T. B. (2015). Volatility and mutual fund manager skill. Journal of Financial Economics, 118(2), 289–298.

    Google Scholar 

  • Kaas, R., Dhaene, J., & Goovaerts, M. (2000). Upper and lower bounds for sums of random variables. Insurance: Mathematics and Economics, 27, 151–168.

    Google Scholar 

  • Kosowski, R., Timmermann, A., Wermers, R., & White, H. (2006). Can mutual fund “stars” really pick stocks? New evidence from a bootstrap analysis. The Journal of Finance, 61(6), 2551–2595.

    Google Scholar 

  • Lee, S., & Mykland, P. (2008). Jumps in financial markets: A new nonparametric test and jump dynamics. Review of Financial Studies, 21(6), 2535–2563.

    Google Scholar 

  • Leote de Carvalho, R., Lu, X., & Moulin, P. (2012). Demystifying equity risk-based strategies: A simple alpha plus beta description. The Journal of Portfolio Management, 38(3), 56–70.

    Google Scholar 

  • Lin, E., Sun, E., & Yu, M.-T. (2018). Systemic risk, financial markets, and performance of financial institutions. Annals of Operations Research, 262, 579–603.

    Google Scholar 

  • Nartea, G. V., & Wu, J. (2013). Is there a volatility effect in the hong kong stock market? Pacific-Basin Finance Journal, 25, 119–135.

    Google Scholar 

  • Novy-Marx, R. (2014). Understanding defensive equity. Working paper 20591, National Bureau of Economic Research.

  • Patton, A. J., & Timmermann, A. (2010). Monotonicity in asset returns: New tests with applications to the term structure, the capm, and portfolio sorts. Journal of Financial Economics, 98(3), 605–625.

    Google Scholar 

  • Scherer, B. (2011). A note on the returns from minimum variance investing. Journal of Empirical Finance, 18(4), 652–660.

    Google Scholar 

  • Stambaugh, R. F., Yu, J., & Yuan, Y. (2015). Arbitrage asymmetry and the idiosyncratic volatility puzzle. The Journal of Finance, 70(5), 1903–1948.

    Google Scholar 

  • Sullivan, R., Timmermann, A., & White, H. (1999). Data-snooping, technical trading rule performance, and the bootstrap. Journal of Finance, 54, 1647–1691.

    Google Scholar 

  • Sun, E., & Meinl, T. (2012). A new wavelet-based denoising algorithm for high-frequency financial data mining. European Journal of Operational Research, 217, 589–599.

    Google Scholar 

  • Sun, W., Rachev, S., Fabozzi, F., & Kalev, P. (2009). A new approach to modeling co-movement of international equity markets: Evidence of unconditional copula-based simulation of tail dependence. Empirical Economics, 36, 201–229.

    Google Scholar 

  • White, H. (2000). A reality check for data snooping. Econometrica, 68(5), 1097–1126.

    Google Scholar 

  • Xu, Z. (2014). A new characterization of comonotonicity and its application in behavioral finance. Journal of Mathematical Analysis and Applications, 418(2), 612–625.

    Google Scholar 

  • Yin, S., Mazouz, K., Benamraoui, A., & Saadouni, B. (2018). Stock price reaction to profit warnings: The role of time-varying betas. Review of Quantitative Finance and Accounting, 50(1), 67–93.

    Google Scholar 

Download references

Funding

Chen was supported by the research project funded by InfoTech Frankfurt am Main, Germany under USt-IdNr. DE320245686 and DAAD (Grant No. ST34-AP).

Author information

Authors and Affiliations

  1. SKEMA Business School, Université Côte d’Azur, Nice, France

    Wan-Ni Lai

  2. InfoTech Frankfurt, Frankfurt am Main, Germany

    Yi-Ting Chen

  3. School of Computer Science, National Chiao Tung University, Hsinchu, Taiwan

    Yi-Ting Chen

  4. KEDGE Business School, 680 Cours de la Libèration, 33405, Talance Cedex, France

    Edward W. Sun

Authors
  1. Wan-Ni Lai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yi-Ting Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Edward W. Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Edward W. Sun.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The authors would like to thank Philippe Bertrand, Kris Boudt, Felix Goltz, Bertrand Groslambert, Marie Lambert, Florencio Lopez de Silanes, Armin Schwienbacher and conference participants of the 33rd International Conference of the French Finance Association for their valuable comments and discussion.

Appendix

Appendix

Tables 9, 10 and 11 present the results of the time-series linear regressions of the volatility sorted quintile portfolios against different risk factors in their respective regions. The complete set of risk factors are consolidated from the standard single factor and four factor models with (low) risk-based factors, namely, a low beta factor and a low IV factor computed using the methodology described in Sect. 3.2. We then assess the factor exposures of the lowest and highest volatility portfolio returns, as well as the lowest minus highest volatility portfolio returns for the cross section of stocks listed in Europe, Asia Pacific and North America.

Table 9 Volatility sorted portfolios in Europe
Full size table
Table 10 Volatility sorted portfolios in Asia Pacific
Full size table
Table 11 Volatility sorted portfolios in North America
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lai, WN., Chen, YT. & Sun, E.W. Comonotonicity and low volatility effect. Ann Oper Res 299, 1057–1099 (2021). https://doi.org/10.1007/s10479-019-03320-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10479-019-03320-0

Keywords

JEL Classifications

Search

Navigation