If you cannot prove your theorem, keep shifting parts of the conclusion to the assumptions, until you can.
(Ennio di Giorgi)
Abstract
Pairwise comparison matrices often exhibit inconsistency, therefore many indices have been suggested to measure their deviation from a consistent matrix. A set of axioms has been proposed recently that is required to be satisfied by any reasonable inconsistency index. This set seems to be not exhaustive as illustrated by an example, hence it is expanded by adding two new properties. All axioms are considered on the set of triads, pairwise comparison matrices with three alternatives, which is the simplest case of inconsistency. We choose the logically independent properties and prove that they characterize, that is, uniquely determine the inconsistency ranking induced by most inconsistency indices that coincide on this restricted domain. Since triads play a prominent role in a number of inconsistency indices, our results can also contribute to the measurement of inconsistency for pairwise comparison matrices with more than three alternatives.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Pairwise comparisons play an important role in a number of decision analysis methods such as the Analytic Hierarchy Process (AHP) (Saaty 1977, 1980). They also naturally emerge in country (Petróczy 2019) and higher education (Csató and Tóth 2019) rankings, in voting systems (Čaklović and Kurdija 2017), as well as in sport tournaments (Bozóki et al. 2016; Chao et al. 2018; Csató 2013, 2017b). Theoretically, an appropriate set of \(n-1\) pairwise comparisons would be sufficient to derive a set of weights or to rank all alternatives. However, usually, more information is available in real-life situations. For example, the decision makers are asked further questions because it increases the robustness of the result. It is also clear that a round-robin tournament can be fairer than a knockout format as a loss does not lead to the elimination of a player.
Nonetheless, the knowledge of extra pairwise comparisons has a price. First, processing this additional information is time-consuming. Second, the set of comparisons may become inconsistent: if alternative A is better than B, and B is better than C, then C still might turn out to be preferred over A. While consistent preferences do not automatically imply the rationality of the decision maker, it is plausible to assume that strongly inconsistent preferences indicate a problem. Perhaps the decision maker has not understood the elicitation phase, or the strength of players varies during the tournament.
Thus it is necessary to measure the deviation from consistency. The first concept of inconsistency has probably been presented in Kendall and Smith (1940). Since then, several inconsistency indices have been proposed (Saaty 1977; Koczkodaj 1993; Duszak and Koczkodaj 1994; Barzilai 1998; Aguaron and Moreno-Jiménez 2003; Peláez and Lamata 2003; Fedrizzi and Ferrari 2018), and compared with each other (Bozóki and Rapcsák 2008; Brunelli et al. 2013; Brunelli and Fedrizzi 2019; Cavallo 2019). Brunelli (2018) offers a comprehensive overview of inconsistency indices and their ramifications.
Recently, some authors have applied an axiomatic approach by suggesting reasonable properties required from an inconsistency index (Brunelli and Fedrizzi 2011, 2015; Brunelli 2016, 2017; Cavallo and D’Apuzzo 2012; Koczkodaj and Szwarc 2014; Koczkodaj and Urban 2018). There is also one characterization in this topic: Csató (2018a) introduces six independent axioms that uniquely determine the Koczkodaj inconsistency ranking induced by the Koczkodaj inconsistency index (Koczkodaj 1993; Duszak and Koczkodaj 1994). In the case of such characterizations, the appropriate motivation of the properties is not crucial. The result only says that there remains a single choice if one accepts all axioms.
This work aims to connect these two research directions by placing the axioms of Brunelli (2017)—which is itself an extended set of the properties proposed by Brunelli and Fedrizzi (2015)—and Csató (2018a) into a single framework. They will be considered on the domain of triads, that is, pairwise comparison matrices with only three alternatives. Bozóki and Rapcsák (2008) have already proved that there exists a differentiable one-to-one correspondence between the inconsistency indices of Saaty (1977), Koczkodaj (1993) and Duszak and Koczkodaj (1994) on this set, furthermore, almost all inconsistency indices are functionally dependent for triads (Cavallo 2019). We will show that the inconsistency ranking induced by this so-called natural triad inconsistency index is the unique inconsistency ranking satisfying all properties on the set of triads. Since triads play a prominent role in a number of inconsistency indices, our results can also contribute to the measurement of inconsistency for pairwise comparison matrices with more than three alternatives.
The paper is structured as follows. Section 2 presents the setting and the properties of inconsistency indices suggested by Brunelli (2017). This axiomatic system is revealed in Sect. 3 to be not exhaustive. Section 4 introduces two new axioms and discusses logical independence. The natural triad inconsistency ranking is characterized in Sect. 5. Finally, Section 6 summarizes our results.
2 Preliminaries
A matrix \({\mathbf {A}} = \left[ a_{ij} \right] \in {\mathbb {R}}^{n \times n}\) is called a pairwise comparison matrix if \(a_{ij} > 0\) and \(a_{ij} = 1 / a_{ij}\) for all \(1 \le i,j \le n\). A pairwise comparison matrix \({\mathbf {A}}\) is said to be consistent if \(a_{ik} = a_{ij} a_{jk}\) for all \(1 \le i,j,k \le n\).
Let \({\mathcal {A}}\) denote the set of pairwise comparison matrices. Inconsistency index\(I: {\mathcal {A}} \rightarrow {\mathbb {R}}\) associates a value for each pairwise comparison matrix.
Brunelli and Fedrizzi (2015) have suggested and justified five axioms for inconsistency indices. They are briefly recalled here.
Axiom 1
Existence of a unique element representing consistency (URS): An inconsistency index \(I: {\mathcal {A}} \rightarrow {\mathbb {R}}\) satisfies axiom URS if there exists a unique \(v \in {\mathbb {R}}\) such that \(I({\mathbf {A}}) = v\) if and only if \({\mathbf {A}} \in {\mathcal {A}}\) is consistent.
Axiom 2
Invariance under permutation of alternatives (IPA): Let \({\mathbf {A}} \in {\mathcal {A}}\) be any pairwise comparison and \({\mathbf {P}}\) be any permutation matrix on the set of alternatives considered in \({\mathbf {A}}\). An inconsistency index \(I: {\mathcal {A}} \rightarrow {\mathbb {R}}\) satisfies axiom IPA if \(I({\mathbf {A}}) = I({\mathbf {P}} {\mathbf {A}} {\mathbf {P}}^\top )\).
Axiom 3
Monotonicity under reciprocity-preserving mapping (MRP): Let \({\mathbf {A}} = \left[ a_{ij} \right] \in {\mathcal {A}}\) be any pairwise comparison matrix, \(b \in {\mathbb {R}}\) and \({\mathbf {A}}(b) = \left[ a_{ij}^b \right] \in {\mathcal {A}}\). An inconsistency index \(I: {\mathcal {A}} \rightarrow {\mathbb {R}}\) satisfies axiom MRP if \(I({\mathbf {A}}) \le I \left( {\mathbf {A}}(b) \right) \) if and only if \(b \ge 1\).
Axiom 4
Monotonicity on single comparisons (MSC): Let \({\mathbf {A}} \in {\mathcal {A}}\) be any consistent pairwise comparison matrix, \(a_{ij} \ne 1\) be a non-diagonal element and \(\delta \in {\mathbb {R}}\). Let \({\mathbf {A}}_{ij}(\delta ) \in {\mathcal {A}}\) be the inconsistent pairwise comparison matrix obtained from \({\mathbf {A}}\) by replacing the entry \(a_{ij}\) with \(a_{ij}^\delta \) and \(a_{ji}\) with \(a_{ji}^\delta \). An inconsistency index \(I: {\mathcal {A}} \rightarrow {\mathbb {R}}\) satisfies axiom MSC if
Axiom 5
Continuity (CON): Let \({\mathbf {A}} = \left[ a_{ij} \right] \in {\mathcal {A}}\) be any pairwise comparison matrix. An inconsistency index \(I: {\mathcal {A}} \rightarrow {\mathbb {R}}\) satisfies axiom CON if it is a continuous function of the entries \(a_{ij}\) of \({\mathbf {A}} \in {\mathcal {A}}\).
Brunelli (2017) has introduced a further reasonable property.
Axiom 6
Invariance under inversion of preferences (IIP): Let \({\mathbf {A}} \in {\mathcal {A}}\) be any pairwise comparison matrix. An inconsistency index \(I: {\mathcal {A}} \rightarrow {\mathbb {R}}\) satisfies axiom IIP if \(I({\mathbf {A}}) = I \left( {\mathbf {A}}^\top \right) \).
The six properties above do not contradict each other and none of them are superfluous.
Proposition 1
Axioms URS, IPA, MRP, MSC, CON, and IIP are independent and form a logically consistent axiomatic system.
Proof
See Brunelli (2017, Theorem 1). \(\square \)
A triad is a pairwise comparison matrix with three alternatives, the smallest pairwise comparison matrix which can be inconsistent. Therefore, triads play a prominent role in the measurement of inconsistency. For instance, the Koczkodaj inconsistency index (Koczkodaj 1993; Duszak and Koczkodaj 1994), the Peláez–Lamata inconsistency index (Peláez and Lamata 2003), and the family of inconsistency indices proposed by Kułakowski and Szybowski (2014) are all based on triads.
In this paper, we will focus on the set of triads \({\mathcal {T}}\), and inconsistency will be measured by a triad inconsistency index\(I: {\mathcal {T}} \rightarrow {\mathbb {R}}\). Note that a triad \({\mathbf {T}} \in {\mathcal {T}}\) can be described by its three elements above the diagonal such that \({\mathbf {T}} = (t_{12}; \,t_{13}; \,t_{23})\) and \({\mathbf {T}}\) is consistent if and only if \(t_{13} = t_{12} t_{23}\).
3 Motivation
The axiomatic system suggested by Brunelli (2017) is not guaranteed to be exhaustive in the sense that it may allow for some strange inconsistency indices. Consider the following one.
Definition 1
Scale-dependent triad inconsistency index: Let \({\mathbf {T}} = \left[ t_{ij} \right] \in {\mathcal {T}}\) be any triad. Its inconsistency according to the scale-dependent triad inconsistency index\(I^{SD}\) is
The scale-dependent triad inconsistency index sums the differences of all non-diagonal matrix elements from the value exhibiting consistency.
Proposition 2
The scale-dependent triad inconsistency index \(I^{SD}\) satisfies axioms URS, IPA, MRP, MSC, CON, and IIP.
Proof
It is straightforward to show that \(I^{SD}\) satisfies URS, IPA, CON, and IIP.
Consider MRP. Due to the properties IIP and IPA, it is enough to show that \(\left| t_{13}^b - t_{12}^b t_{23}^b \right| \ge \left| t_{13} - t_{12} t_{23} \right| \) for every possible (positive) value of \(t_{12}\), \(t_{13}\), and \(t_{23}\) if and only if \(b \ge 1\). It can be assumed without loss of generality that \(t_{13} - t_{12} t_{23} \ge 0\), which implies \(t_{13}^b - t_{12}^b t_{23}^b \ge 0\). Let \(f(b) = t_{13}^b - t_{12}^b t_{23}^b\), so
in other words, f(b) is a monotonically increasing (decreasing) function for \(b \ge 1\) (\(b \le 1\)).
Consider MSC. It can be assumed that \(t_{13}\) is the entry to be changed because of the axiom IPA. \(I^{SD} ({\mathbf {T}}) = 0\) if \(t_{13} = t_{12} t_{23}\), and all terms in the formula of \(I^{SD} \left( {\mathbf {T}}_{ij}(\delta ) \right) \) increase gradually when \(\delta \) goes away from 1. \(\square \)
According to the example below, the scale-dependent triad inconsistency index \(I^{SD}\) may lead to questionable conclusions.
Example 1
Take two alternatives A and B such that the decision maker is indifferent between them. Assume that a third alternative C appears in the comparison, and A is judged three times better than C, while B is assessed to be two times better than C. Suppose that C is a divisible alternative and is exchanged by its half.
The two situations can be described by the triads:
Here \(I^{SD}({\mathbf {S}}) = 19/6 \approx 3.167\) and \(I^{SD}({\mathbf {T}}) = 5\). In other words, the scale-dependent inconsistency index suggests that triad \({\mathbf {S}}\) is less inconsistent than triad \({\mathbf {T}}\), contrary to the underlying data as inconsistency is not expected to be influenced by the ‘amount’ of alternative C.
Example 1 clearly shows that the axioms of Brunelli (2017) should be supplemented even on the set of triads.
4 An improved axiomatic system
We propose two new axioms of inconsistency indices for triads.
Axiom 7
Homogeneous treatment of alternatives (HTA): Let \({\mathbf {T}} = (1; \,t_{13}; \,t_{23})\) and \(\mathbf {T'} = (1; \,t_{13} / t_{23}; \,1)\) be any triad. A triad inconsistency index \(I: {\mathcal {T}} \rightarrow {\mathbb {R}}\) satisfies axiom HTA if \(I({\mathbf {T}}) = I \left( \mathbf {T'} \right) \).
According to homogeneous treatment of alternatives, if the first and the second alternatives are equally important on their own, but they are also compared to a third alternative, then the inconsistency of the resulting triad should not be influenced by the relative importance of the new alternative.
Axiom 8
Scale invariance (SI): Let \({\mathbf {T}} = (t_{12}; \,t_{13}; \,t_{23})\) and \(\mathbf {T'} = (k t_{12}; \,k^2 t_{13}; \,k t_{23})\) be any triads such that \(k > 0\). A triad inconsistency index \(I: {\mathcal {T}} \rightarrow {\mathbb {R}}\) satisfies axiom SI if \(I({\mathbf {T}}) = I \left( \mathbf {T'} \right) \).
Scale invariance implies that inconsistency is independent of the mathematical representation of the preferences. For example, consider the following pairwise comparisons: the first alternative is ‘moderately more important’ than the second and the second alternative is ‘moderately more important’ than the third. It makes sense to expect the level of inconsistency to be the same if ‘moderately more important’ is coded by the numbers 2, 3, or 4, and so on, even allowing for a change in the direction of the two preferences. If the encoding is required to preserve consistency, one arrives at the property SI.
Note that Example 1 shows the violation of SI by the scale-dependent triad inconsistency index \(I^{SD}\).
HTA and SI have been introduced in Csató (2018a) for inconsistency rankings (and HTA has been called homogeneous treatment of entities there).
In order to understand the implications of the extended axiomatic system, the logical consistency and independence of the eight properties should be discussed.
For this purpose, let us introduce the natural triad inconsistency index.
Definition 2
Natural triad inconsistency index: Let \({\mathbf {A}} = \left[ a_{ij} \right] \in {\mathbb {R}}^{3 \times 3}_+\) be a triad. Its inconsistency according to the natural triad inconsistency index\(I^T\) is
This inconsistency index was considered first probably in Bozóki and Rapcsák (2008), where it is denoted by T.
On the domain of triads, most inconsistency indices induce the same inconsistency ranking as the natural triad inconsistency index because they are functionally related (Bozóki and Rapcsák 2008; Cavallo 2019).
Proposition 3
Axioms URS, IPA, MRP, MSC, CON, IIP, HTA, and SI form a logically consistent axiomatic system on the set of triads.
Proof
The Koczkodaj inconsistency index satisfies all properties. See Brunelli (2017, Proposition 1) for the axioms URS, IPA, MRP, MSC, CON, and IIP. Homogeneous treatment of alternatives and scale invariance immediately follow from Csató (2018a, Theorem 1). \(\square \)
However, some axioms can be implied by a conjoint application of the others.
Lemma 1
Axioms IIP, HTA, and SI imply IPA on the set of triads.
Proof
Let \({\mathbf {T}} = (t_{12}; \,t_{13}; \,t_{23})\) be a triad, \({\mathbf {P}}\) be a permutation matrix and \({\mathbf {S}} = {\mathbf {P}} {\mathbf {T}} {\mathbf {P}}^\top = (s_{12}; \,s_{13}; \,s_{23})\). Let \(I: {\mathcal {T}} \rightarrow {\mathbb {R}}\) be a triad inconsistency index satisfying IIP, HTA, and SI.
Consider \(\mathbf {T_1} = (1; \,t_{13} / t_{12}^2; \,t_{23} / t_{12})\) and \(\mathbf {S_1} = (1; \,s_{13} / s_{12}^2; \,s_{23} / s_{12})\). Then \(I(\mathbf {T_1}) = I({\mathbf {T}})\) and \(I (\mathbf {S_1}) = I({\mathbf {S}})\) according to SI.
Consider \(\mathbf {T_2} = \left( 1; \,t_{13} / (t_{12} t_{23}); \,1 \right) \) and \(\mathbf {S_2} = \left( 1; \,s_{13} / (s_{12} s_{23}); \,1 \right) \). HTA leads to \(I(\mathbf {T_2}) = I(\mathbf {T_1})\) and \(I (\mathbf {S_2}) = I(\mathbf {S_1})\).
\(t_{13} / (t_{12} t_{23}) \ge 1\) and \(s_{13} / (s_{12} s_{23}) \ge 1\) can be assumed without loss of generality because of the property IIP.
To summarize, \(I({\mathbf {T}}) = I(\mathbf {T_1}) = I(\mathbf {T_2})\) and \(I({\mathbf {S}}) = I(\mathbf {S_1}) = I(\mathbf {S_2})\).
The natural triad inconsistency index \(I^T\) satisfies IPA, therefore \(t_{13} / (t_{12} t_{23}) = s_{13} / (s_{12} s_{23})\), hence \(\mathbf {T_2} = \mathbf {S_2}\), that is, \(I(\mathbf {T_2}) = I(\mathbf {S_2})\) and \(I({\mathbf {T}}) = I({\mathbf {S}})\). \(\square \)
Lemma 2
Axioms URS, MSC, IIP, HTA, and SI imply MRP on the set of triads.
Proof
Let \({\mathbf {T}} = (t_{12}; \,t_{13}; \,t_{23})\) and \({\mathbf {T}}(b) = (t_{12}^b; \,t_{13}^b; \,t_{23}^b)\) be any triads. Let \(I: {\mathcal {T}} \rightarrow {\mathbb {R}}\) be a triad inconsistency index satisfying URS, MSC, IIP, HTA, and SI.
Consider \(\mathbf {T_1} = (1; \,t_{13} / t_{12}^2; \,t_{23} / t_{12})\) and \(\mathbf {T_1}(b) = (1; \,t_{13}^b / t_{12}^{2b}; \,t_{23}^b / t_{12}^b)\). Then \(I(\mathbf {T_1}) = I({\mathbf {T}})\) and \(I \left( \mathbf {T_1}(b) \right) = I({\mathbf {T}}(b))\) according to SI.
Consider \(\mathbf {T_2} = \left( 1; \,t_{13} / (t_{12} t_{23}); \,1 \right) \) and \(\mathbf {T_2}(b) = \left( 1; \,t_{13}^b / (t_{12}^b t_{23}^b); \,1 \right) \). HTA leads to \(I(\mathbf {T_2}) = I(\mathbf {T_1})\) and \(I \left( \mathbf {T_2}(b) \right) = I \left( \mathbf {T_1}(b) \right) \).
It can be assumed without loss of generality that \(t_{13} / (t_{12} t_{23}) \ge 1\) because of IIP.
To summarize, \(I({\mathbf {T}}) = I(\mathbf {T_1}) = I(\mathbf {T_2})\) and \(I \left( {\mathbf {T}}(b) \right) = I \left( \mathbf {T_1}(b) \right) = I \left( \mathbf {T_2}(b) \right) \).
If \(t_{13} / (t_{12} t_{23}) > 1\), then \(\mathbf {T_2}\) differs only in one non-diagonal element from the consistent triad with all entries equal to 1. Therefore, \(I(\mathbf {T_2}) \le I \left( \mathbf {T_2}(b) \right) \) if and only if \(b \ge 1\) because of the property MSC. Otherwise, \(\mathbf {T_2}\) is consistent, and \(I({\mathbf {T}}) = I \left( {\mathbf {T}}(b) \right) = I(\mathbf {T_2}) = v\) due to URS. \(\square \)
There exists no further direct implication among the remaining six properties.
Theorem 1
Axioms URS, MSC, CON, IIP, HTA, and SI are independent on the set of triads.
Proof
Independence of a given axiom can be shown by providing a triad inconsistency index that satisfies all axioms except the one at stake:
- \(\fbox {1}\) :
-
URS: The triad inconsistency index \(I^1: {\mathcal {T}} \rightarrow {\mathbb {R}}\) such that \(I^1({\mathbf {T}}) = 0\) for all triads \({\mathbf {T}} \in {\mathcal {T}}\).
- \(\fbox {2}\) :
-
MSC: The triad inconsistency index \(I^2: {\mathcal {T}} \rightarrow {\mathbb {R}}\) such that
$$\begin{aligned} I^2({\mathbf {T}}) = - \max \left\{ \frac{t_{13}}{t_{12} t_{23}}; \, \frac{t_{12} t_{23}}{t_{13}} \right\} \end{aligned}$$for all triads \({\mathbf {T}} \in {\mathcal {T}}\). \(I^2\) can be called the inverse natural triad inconsistency index.
- \(\fbox {3}\) :
-
CON: The triad inconsistency index \(I^3: {\mathcal {T}} \rightarrow {\mathbb {R}}\) such that
$$\begin{aligned} I^3({\mathbf {T}}) = \left\{ \begin{array}{ll} 0 &{} \text {if }\quad {\mathbf {T}}\text { is consistent }\\ \max \left\{ t_{13} / \left( t_{12} t_{23} \right) ; \, \left( t_{12} t_{23} \right) / t_{13} \right\} + 1 &{} \text {otherwise} \end{array} \right. \end{aligned}$$for all triads \({\mathbf {T}} \in {\mathcal {T}}\). \(I^3\) is essentially the index \(I^T\), but it is not continuous in the environment of consistent matrices.
- \(\fbox {4}\) :
-
IIP: The triad inconsistency index \(I^4: {\mathcal {T}} \rightarrow {\mathbb {R}}\) such that
$$\begin{aligned} I^4({\mathbf {T}}) = \frac{t_{13}}{t_{12} t_{23}} \end{aligned}$$for all triads \({\mathbf {T}} \in {\mathcal {T}}\). \(I^4\) is essentially the natural triad inconsistency index \(I^T\), but takes only the entries above the diagonal into account.
- \(\fbox {5}\) :
-
HTA: The triad inconsistency index \(I^5: {\mathcal {T}} \rightarrow {\mathbb {R}}\) such that
$$\begin{aligned} I^5({\mathbf {T}}) = \left( \frac{t_{12}}{t_{23}} + \frac{t_{23}}{t_{12}} \right) \cdot \left( \max \left\{ \frac{t_{13}}{t_{12} t_{23}}; \, \frac{t_{12} t_{23}}{t_{13}} \right\} - 1 \right) \end{aligned}$$(1)for all triads \({\mathbf {T}} \in {\mathcal {T}}\).
- \(\fbox {6}\) :
-
SI: The triad inconsistency index \(I^6: {\mathcal {T}} \rightarrow {\mathbb {R}}\) such that
$$\begin{aligned} I^6({\mathbf {T}}) = \left| t_{12} - \frac{t_{13}}{t_{23}} \right| + \left| \frac{1}{t_{12}} - \frac{t_{23}}{t_{13}} \right| \end{aligned}$$for all triads \({\mathbf {T}} \in {\mathcal {T}}\).
Proving that the triad inconsistency index \(I^i\) satisfies all axioms except for the ith is straightforward if \(1 \le i \le 4\), therefore left to the reader.
Consider the triad inconsistency index \(I^5\). It is easy to see that this function is continuous, nonnegative and equals to zero if and only if a triad is consistent (\(t_{13} = t_{12} t_{23}\)), as well as it meets invariance under inversion of preferences and scale invariance. \(I^5\) also satisfies monotonicity on single comparisons because the second term in formula (1) is essentially the natural triad inconsistency index, and the first term is increasing in both \(t_{12}\) and \(t_{23}\) ceteris paribus, while it is independent of \(t_{13}\). Finally, take the triads \({\mathbf {T}} = (1; \,8; \,4)\) and \(\mathbf {T'} = (1; \,2; \,1)\), which lead to \(I^5({\mathbf {T}}) = 17/4 \ne 5/2 = I^5(\mathbf {T'})\), showing the violation of HTA.
Now look at the triad inconsistency index \(I^6\). It is trivial to verify that \(I^6\) satisfies URS, MSC, CON, and IIP. HTA is also met as \(I^6({\mathbf {T}}) = I^6(\mathbf {T'})\) when \({\mathbf {T}} = (1; \,t_{13}; \,t_{23})\) and \(\mathbf {T'} = (1; \,t_{13} / t_{23}; \,1)\). Take the triads \({\mathbf {T}} = (1; \,8; \,4)\) and \(\mathbf {T'} = (2; \,32; \,8)\), which result in \(I^6({\mathbf {T}}) = 3/2 \ne 9/4 = I^6(\mathbf {T'})\), presenting the violation of SI. \(\square \)
To conclude, the axiomatic system consisting of URS, MSC, CON, IIP, HTA, and SI satisfies logical consistency and independence on the set of triads \({\mathcal {T}}\).
5 Characterization
It still remains a question whether the extended set of properties is exhaustive on the set of triads \({\mathcal {T}}\) or not. We will show that the axioms are closely related to the natural triad inconsistency index: they mean that \(I^T\) is the only appropriate index for measuring the inconsistency of triads.
Theorem 2
Let \({\mathbf {S}},{\mathbf {T}} \in {\mathcal {T}}\) be any triads and \(I: {\mathcal {T}} \rightarrow {\mathbb {R}}\) be a triad inconsistency index satisfying MSC, IIP, HTA, and SI. Then \(I^T({\mathbf {S}}) \ge I^T({\mathbf {T}})\) implies \(I({\mathbf {S}}) \ge I({\mathbf {T}})\).
Proof
Assume that \(I^T({\mathbf {S}}) \ge I^T({\mathbf {T}})\). The idea is to gradually simplify the comparison of the inconsistencies of the two triads by using the axioms that are satisfied by the arbitrary triad inconsistency index \(I: {\mathcal {T}} \rightarrow {\mathbb {R}}\).
Consider the triads \(\mathbf {S_1} = (1; \,s_{13} / s_{12}^2; \,s_{23} / s_{12})\) and \(\mathbf {T_1} = (1; \,t_{13} / t_{12}^2; \,t_{23} / t_{12})\). Since the natural triad inconsistency index satisfies SI, it is guaranteed that \(I^T({\mathbf {S}}) = I^T(\mathbf {S_1})\) and \(I^T({\mathbf {T}}) = I^T(\mathbf {T_1})\).
Consider the triads \(\mathbf {S_2} = (1; \,s_{13} / (s_{12} s_{23}); \,1)\) and \(\mathbf {T_2} = (1; \,t_{13} / (t_{12} t_{23}); \,1)\). As the natural triad inconsistency index meets HTA, it is known that \(I^T(\mathbf {S_1}) = I^T(\mathbf {S_2})\) and \(I^T(\mathbf {T_1}) = I^T(\mathbf {T_2})\).
\(s_{13} / (s_{12} s_{23}) \ge 1\) and \(t_{13} / (t_{12} t_{23}) \ge 1\) can be assumed without loss of generality due to IIP. Consequently, \(I^T(\mathbf {S_2}) = I^T(\mathbf {S_1}) = I^T({\mathbf {S}}) \ge I^T({\mathbf {T}}) = I^T(\mathbf {T_1}) = I^T(\mathbf {T_2})\), which means that \(s_{13} / (s_{12} s_{23}) \ge t_{13} / (t_{12} t_{23}) \ge 1\).
Starting from this inequality and using the properties of the triad inconsistency index \(I:{\mathcal {T}} \rightarrow {\mathbb {R}}\), MSC leads to \(I(\mathbf {S_2}) \ge I(\mathbf {T_2})\), HTA results in \(I(\mathbf {S_1}) = I(\mathbf {S_2}) \ge I(\mathbf {T_2}) = I(\mathbf {T_1})\), and SI implies that \(I({\mathbf {S}}) = I(\mathbf {S_1}) = I(\mathbf {S_2}) \ge I(\mathbf {T_2}) = I(\mathbf {T_1}) = I({\mathbf {T}})\), which completes the proof. \(\square \)
Remark 1
As Theorem 2 shows, axioms MSC, IIP, HTA, and SI allow for some odd triad inconsistency indices, for example, the flat triad inconsistency index\(I^F: {\mathcal {T}} \rightarrow {\mathbb {R}}\) such that \(I^F({\mathbf {T}}) = 0\) for any triad \({\mathbf {T}} \in {\mathcal {T}}\). By attaching properties URS and CON, inconsistency index \(I^F\) is excluded, but they still allow for a ‘discretised’ natural triad inconsistency index\(I^{DT}: {\mathcal {T}} \rightarrow {\mathbb {R}}\) defined as
for any triad \({\mathbf {T}} \in {\mathcal {T}}\).
The proof of Theorem 2 does not work in the reverse direction of \(I({\mathbf {S}}) \ge I({\mathbf {T}}) \Rightarrow I^T({\mathbf {S}}) \ge I^T({\mathbf {T}})\) because monotonicity on single comparisons has been introduced without strict inequalities by Brunelli and Fedrizzi (2015).
Axiom 9
Strong monotonicity on single comparisons (SMSC): Let \({\mathbf {A}} \in {\mathcal {A}}^{n \times n}\) be any consistent pairwise comparison matrix, \(a_{ij} \ne 1\) a non-diagonal element and \(\delta \in {\mathbb {R}}\). Let \({\mathbf {A}}_{ij}(\delta ) \in {\mathcal {A}}^{n \times n}\) be the inconsistent pairwise comparison matrix obtained from \({\mathbf {A}}\) by replacing the entry \(a_{ij}\) with \(a_{ij}^\delta \) and \(a_{ji}\) with \(a_{ji}^\delta \). An inconsistency index \(I: {\mathcal {R}}^n \rightarrow {\mathbb {R}}\) satisfies axiom SMSC if
With the introduction of SMSC, there is no need for all of the six axioms.
Lemma 3
Axioms SMSC, CON, HTA, and SI imply URS on the set of triads.
Proof
Let \({\mathbf {S}} = (s_{12}; \,s_{13}; \,s_{23})\) and \({\mathbf {T}} = (t_{12}; \,t_{13}; \,t_{23})\) be any triads. Let \(I: {\mathcal {T}} \rightarrow {\mathbb {R}}\) be a triad inconsistency index satisfying SMSC, CON, HTA, and SI.
First, it is shown that \(I({\mathbf {S}}) = I({\mathbf {T}})\) if triads \({\mathbf {S}}\) and \({\mathbf {T}}\) are consistent. Consider the triads \(\mathbf {S_1} = (1; \,s_{13} / s_{12}^2; \,s_{23} / s_{12})\) and \(\mathbf {T_1} = (1; \,t_{13} / t_{12}^2; \,t_{23} / t_{12})\). Then \(I({\mathbf {S}}) = I(\mathbf {S_1})\) and \(I({\mathbf {T}}) = I(\mathbf {T_1})\) due to SI. Consider the triads \(\mathbf {S_2} = (1; \,s_{13} / (s_{12} s_{23}); \,1)\) and \(\mathbf {T_2} = (1; \,t_{13} / (t_{12} t_{23}); \,1)\). Then \(I(\mathbf {S_1}) = I(\mathbf {S_2})\) and \(I(\mathbf {T_1}) = I(\mathbf {T_2})\) because of HTA. Furthermore, \(\mathbf {S_2} = \mathbf {T_2}\), so \(I({\mathbf {S}}) = I({\mathbf {T}})\).
Second, it is proved that \(I({\mathbf {S}}) \ne I({\mathbf {T}})\) if triad \({\mathbf {S}}\) is consistent but \({\mathbf {T}}\) is inconsistent. Consider the triads \(\mathbf {S_1} = (1; \,s_{13} / s_{12}^2; \,s_{23} / s_{12})\) and \(\mathbf {T_1} = (1; \,t_{13} / t_{12}^2; \,t_{23} / t_{12})\). Then \(I({\mathbf {S}}) = I(\mathbf {S_1})\) and \(I({\mathbf {S}}) = I(\mathbf {S_1})\) due to SI. Consider the triads \(\mathbf {S_2} = (1; \,s_{13} / (s_{12} s_{23}); \,1\) and \(\mathbf {T_2} = (1; \,t_{13} / (t_{12} t_{23}); \,1)\). Then \(I(\mathbf {S_1}) = I(\mathbf {S_2})\) and \(I(\mathbf {T_1}) = I(\mathbf {T_2})\) because of HTA. Furthermore, \(s_{13} / (s_{12} s_{23}) = 1\) and \(t_{13} / (t_{12} t_{23}) \ne 1\). Let \(\delta \in {\mathbb {R}}\) and \({\mathbf {T}}_{ij}(\delta ) \in {\mathcal {T}}\) be the inconsistent triad obtained from \(\mathbf {T_2}\) by replacing the entry \(t_{13} / (t_{12} t_{23})\) with \(\left[ t_{13} / (t_{12} t_{23}) \right] ^\delta \). Assume, for contradiction, that \(I({\mathbf {T}}) = I({\mathbf {S}})\). Then \(I \left( {\mathbf {T}}(\delta ) \right)< I \left( {\mathbf {T}}(1/2) \right) < I({\mathbf {S}})\) for any \(0< \delta < 1/2\) due to strong monotonicity on single comparisons, which contradicts to continuity because \(\lim _{\delta \rightarrow 0} {\mathbf {T}}(\delta ) = {\mathbf {S}}\). \(\square \)
As Theorem 1 has already revealed, the weaker property of MSC cannot substitute SMSC in the proof of Lemma 3.
Proposition 4
Axioms SMSC, CON, IIP, HTA, and SI form a logically consistent and independent axiomatic system on the set of triads \({\mathcal {T}}\).
Proof
For consistency, it is sufficient to check that the natural triad inconsistency index \(I^T\) satisfies strong monotonicity on single comparisons.
For independence, see the proof of Theorem 1. The inconsistency indices \(I^3\), \(I^4\), \(I^5\), and \(I^6\) satisfy SMSC, too. \(\square \)
With this strengthening of MSC, we are able to characterize the natural triad inconsistency index on the set of triads.
Proposition 5
Let \({\mathbf {S}},{\mathbf {T}} \in {\mathcal {T}}\) be two triads and \(I:{\mathcal {T}} \rightarrow {\mathbb {R}}\) be a triad inconsistency index satisfying SMSC, IIP, HTA, and SI. Then \(I({\mathbf {S}}) \ge I({\mathbf {T}})\) if and only if \(I^T({\mathbf {S}}) \ge I^T({\mathbf {T}})\).
Proof
For the direction \(I^T({\mathbf {S}}) \ge I^T({\mathbf {T}}) \Rightarrow I({\mathbf {S}}) \ge I({\mathbf {T}})\), see Theorem 2.
For \(I({\mathbf {S}}) \ge I({\mathbf {T}}) \Rightarrow I^T({\mathbf {S}}) \ge I^T({\mathbf {T}})\), the proof of Theorem 2 can be followed in the reverse direction with the assumption \(I({\mathbf {S}}) \ge I({\mathbf {T}})\). The key point is the implication \(I(\mathbf {S_2}) \ge I(\mathbf {T_2}) \Rightarrow s_{13} / (s_{12} s_{23}) \ge t_{13} / (t_{12} t_{23}) \ge 1\), which is guaranteed if the triad inconsistency index I satisfies strong monotonicity on single comparisons, but not necessarily true if it meets only MSC. \(\square \)
On the basis of Proposition 5, our main result can be formulated.
Theorem 3
The natural triad inconsistency index is essentially the unique triad inconsistency index satisfying strong monotonicity on single comparisons, invariance under inversion of preferences, homogeneous treatment of alternatives, and scale invariance.
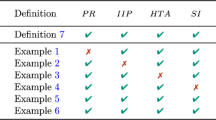
The term essentially refers to the fact that the four axioms SMSC, IIP, HTA, and SI characterize only the inconsistency ranking induced by the natural triad inconsistency index. Nonetheless, Csató (2018a) argues that it does not make sense to distinguish inconsistency indices which rank pairwise comparison matrices uniformly. Naturally, continuity can also be attached to these four axioms but it is rather a technical property.
Remark 2
Remark 1 remains valid in the case of Csató (2018a, Theorem 1) which is true only in the following revised form:
Let \({\mathbf {A}}\) and \({\mathbf {B}}\) two pairwise comparison matrices. If \(\succeq \) is an inconsistency ranking satisfying positive responsiveness, invariance under inversion of preferences, homogeneous treatment of entities, scale invariance, monotonicity, and reducibility, then \({\mathbf {A}} \succeq ^K {\mathbf {B}}\) implies \({\mathbf {A}} \succeq {\mathbf {B}}\).
Contrary to Csató (2018a, Theorem 1) the implication does not hold in the other direction. This problem can be easily solved by introducing the first axiom, positive responsiveness (PR) in a more powerful version called strong positive responsiveness (SPR) with strict inequalities:
Consider two triads \({\mathbf {S}} = (1; \,s_2; \,1)\) and \({\mathbf {T}} = (1; \,t_2; \,1)\) such that \(s_2,t_2 \ge 1\). Inconsistency ranking \(\succeq \) satisfies SPR if \({\mathbf {S}} \succ {\mathbf {T}} \iff s_2 < t_2\).
Then the Koczkodaj inconsistency ranking would be the unique inconsistency ranking satisfying strong positive responsiveness, invariance under inversion of preferences, homogeneous treatment of entities, scale invariance, monotonicity, and reducibility.
6 Conclusions
Axiomatic discussion of inconsistency measurement seems to be fruitful. While it is a well-established research direction in the choice of an appropriate weighting method (Fichtner 1984, 1986; Barzilai et al. 1987; Barzilai 1997; Cook and Kress 1988; Bryson 1995; Csató 2017a, 2018b, 2019; Bozóki and Tsyganok 2019; Csató and Petróczy 2019), formal studies of inconsistency indices has not been undertaken until recently (Brunelli and Fedrizzi 2015, 2019; Brunelli 2017; Koczkodaj and Szwarc 2014; Koczkodaj and Urban 2018; Csató 2018a).
The contribution of this paper can be shortly summarized as a unification of the two axiomatic approaches. The first aims to justify reasonable properties and analyse indices in their light (Brunelli and Fedrizzi 2015; Brunelli 2017). The second concentrates on the exact derivation of certain indices without spending too much time on the motivation of the axioms (Csató 2018a). In particular, the axiomatic system of Brunelli (2017) has been presented to be not exhaustive even for only three alternatives. However, by the introduction of two new properties, a unique triad inconsistency ranking can be identified.
Although most inconsistency indices are functionally related on this domain (Cavallo 2019), hence they induce the same inconsistency ranking, our main finding is a powerful argument against indices which violate some of the axioms on the set of triads, like the Ambiguity Index (Salo and Hämäläinen 1995, 1997), the Relative Error (Barzilai 1998), or the Cosine Consistency Index (Kou and Lin 2014). This fact illustrates that it is worth discussing inconsistency indices on special classes of pairwise comparison matrices, similarly to Čerňanová et al. (2018). The results derived here can serve as a solid basis for measuring the inconsistency of pairwise comparison matrices for order greater than three.
References
Aguaron, J., & Moreno-Jiménez, J. M. (2003). The geometric consistency index: Approximated thresholds. European Journal of Operational Research, 147(1), 137–145.
Barzilai, J. (1997). Deriving weights from pairwise comparison matrices. Journal of the Operational Research Society, 48(12), 1226–1232.
Barzilai, J. (1998). Consistency measures for pairwise comparison matrices. Journal of Multi-Criteria Decision Analysis, 7(3), 123–132.
Barzilai, J., Cook, W. D., & Golany, B. (1987). Consistent weights for judgements matrices of the relative importance of alternatives. Operations Research Letters, 6(3), 131–134.
Bozóki, S., Csató, L., & Temesi, J. (2016). An application of incomplete pairwise comparison matrices for ranking top tennis players. European Journal of Operational Research, 248(1), 211–218.
Bozóki, S., & Rapcsák, T. (2008). On Saaty’s and Koczkodaj’s inconsistencies of pairwise comparison matrices. Journal of Global Optimization, 42(2), 157–175.
Bozóki, S., & Tsyganok, V. (2019). The (logarithmic) least squares optimality of the arithmetic (geometric) mean of weight vectors calculated from all spanning trees for incomplete additive (multiplicative) pairwise comparison matrices. International Journal of General Systems, 48(4), 362–381.
Brunelli, M. (2016). Recent advances on inconsistency indices for pairwise comparisons—A commentary. Fundamenta Informaticae, 144(3–4), 321–332.
Brunelli, M. (2017). Studying a set of properties of inconsistency indices for pairwise comparisons. Annals of Operations Research, 248(1), 143–161.
Brunelli, M. (2018). A survey of inconsistency indices for pairwise comparisons. International Journal of General Systems, 47(8), 751–771.
Brunelli, M., Canal, L., & Fedrizzi, M. (2013). Inconsistency indices for pairwise comparison matrices: A numerical study. Annals of Operations Research, 211(1), 493–509.
Brunelli, M., & Fedrizzi, M. (2011). Characterizing properties for inconsistency indices in the AHP. In Proceedings of the international symposium on the analytic hierarchy process (ISAHP) (pp. 15–18).
Brunelli, M., & Fedrizzi, M. (2015). Axiomatic properties of inconsistency indices for pairwise comparisons. Journal of the Operational Research Society, 66(1), 1–15.
Brunelli, M., & Fedrizzi, M. (2019). A general formulation for some inconsistency indices of pairwise comparisons. Annals of Operations Research, 274(1–2), 155–169.
Bryson, N. (1995). A goal programming method for generating priority vectors. Journal of the Operational Research Society, 46(5), 641–648.
Čaklović, L., & Kurdija, A. S. (2017). A universal voting system based on the Potential Method. European Journal of Operational Research, 259(2), 677–688.
Cavallo, B. (2019). Functional relations and Spearman correlation between consistency indices. Journal of the Operational Research Society (in press). https://doi.org/10.1080/01605682.2018.1516178.
Cavallo, B., & D’Apuzzo, L. (2012). Investigating properties of the \(\odot \)-consistency index. In S. Greco, B. Bouchon-Meunier, G. Coletti, M. Fedrizzi, B. Matarazzo, & R. R. Yager (Eds.), Advances in computational intelligence: 14th international conference on information processing and management of uncertainty in knowledge-based systems, IPMU 2012, Catania, Italy, July 9–13, 2012, Proceedings, Part IV, Vol. 300 of communications in computer and information science (pp. 315–327). Berlin: Springer.
Čerňanová, V., Koczkodaj, W. W., & Szybowski, J. (2018). Inconsistency of special cases of pairwise comparisons matrices. International Journal of Approximate Reasoning, 95, 36–45.
Chao, X., Kou, G., Li, T., & Peng, Y. (2018). Jie Ke versus AlphaGo: A ranking approach using decision making method for large-scale data with incomplete information. European Journal of Operational Research, 265(1), 239–247.
Cook, W. D., & Kress, M. (1988). Deriving weights from pairwise comparison ratio matrices: An axiomatic approach. European Journal of Operational Research, 37(3), 355–362.
Csató, L. (2013). Ranking by pairwise comparisons for Swiss-system tournaments. Central European Journal of Operations Research, 21(4), 783–803.
Csató, L. (2017a). Eigenvector Method and rank reversal in group decision making revisited. Fundamenta Informaticae, 156(2), 169–178.
Csató, L. (2017b). On the ranking of a Swiss system chess team tournament. Annals of Operations Research, 254(1–2), 17–36.
Csató, L. (2018a). Characterization of an inconsistency ranking for pairwise comparison matrices. Annals of Operations Research, 261(1–2), 155–165.
Csató, L. (2018b). Characterization of the row geometric mean ranking with a group consensus axiom. Group Decision and Negotiation, 27(6), 1011–1027.
Csató, L. (2019). A characterization of the logarithmic least squares method. European Journal of Operational Research, 276(1), 212–216.
Csató, L., & Petróczy, D. G. (2019). On the monotonicity of the eigenvector method. Manuscript. arXiv:1902.10790.
Csató, L., & Tóth, C. S. (2019). University rankings from the revealed preferences of the applicants. Manuscript. arXiv:1810.04087.
Duszak, Z., & Koczkodaj, W. W. (1994). Generalization of a new definition of consistency for pairwise comparisons. Information Processing Letters, 52(5), 273–276.
Fedrizzi, M., & Ferrari, F. (2018). A chi-square-based inconsistency index for pairwise comparison matrices. Journal of the Operational Research Society, 69(7), 1125–1134.
Fichtner, J. (1984). Some thoughts about the mathematics of the analytic hierarchy process. Technical report, Institut für Angewandte Systemforschung und Operations Research, Universität der Bundeswehr München.
Fichtner, J. (1986). On deriving priority vectors from matrices of pairwise comparisons. Socio-Economic Planning Sciences, 20(6), 341–345.
Kendall, M. G., & Smith, B. B. (1940). On the method of paired comparisons. Biometrika, 31(3/4), 324–345.
Koczkodaj, W. W. (1993). A new definition of consistency of pairwise comparisons. Mathematical and Computer Modelling, 18(7), 79–84.
Koczkodaj, W. W., & Szwarc, R. (2014). On axiomatization of inconsistency indicators for pairwise comparisons. Fundamenta Informaticae, 132(4), 485–500.
Koczkodaj, W. W., & Urban, R. (2018). Axiomatization of inconsistency indicators for pairwise comparisons. International Journal of Approximate Reasoning, 94, 18–29.
Kou, G., & Lin, C. (2014). A cosine maximization method for the priority vector derivation in AHP. European Journal of Operational Research, 235(1), 225–232.
Kułakowski, K., & Szybowski, J. (2014). The new triad based inconsistency indices for pairwise comparisons. Procedia Computer Science, 35, 1132–1137.
Peláez, J. I., & Lamata, M. T. (2003). A new measure of consistency for positive reciprocal matrices. Computers & Mathematics with Applications, 46(12), 1839–1845.
Petróczy, D. G. (2019). An alternative quality of life ranking on the basis of remittances. Manuscript. arXiv:1809.03977.
Saaty, T. L. (1977). A scaling method for priorities in hierarchical structures. Journal of Mathematical Psychology, 15(3), 234–281.
Saaty, T. L. (1980). The analytic hierarchy process: Planning, priority setting, resource allocation. New York: McGraw-Hill.
Salo, A. A., & Hämäläinen, R. P. (1995). Preference programming through approximate ratio comparisons. European Journal of Operational Research, 82(3), 458–475.
Salo, A. A., & Hämäläinen, R. P. (1997). On the measurement of preferences in the analytic hierarchy process. Journal of Multi-Criteria Decision Analysis, 6(6), 309–319.
Acknowledgements
Open access funding provided by MTA Institute for Computer Science and Control (MTA SZTAKI). We would like to thank Sándor Bozóki, Matteo Brunelli and Miklós Pintér for inspiration.
Tamás Halm and two anonymous reviewers provided valuable comments and suggestions on an earlier draft.
The research was supported by OTKA grant K 111797 and by the MTA Premium Postdoctoral Research Program.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Csató, L. Axiomatizations of inconsistency indices for triads. Ann Oper Res 280, 99–110 (2019). https://doi.org/10.1007/s10479-019-03312-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-019-03312-0
Keywords
- Pairwise comparisons
- Analytic Hierarchy Process (AHP)
- Inconsistency index
- Axiomatic approach
- Characterization