Modelling and forecasting the kurtosis and returns distributions of financial markets: irrational fractional Brownian motion model approach

Abstract

This paper reports a new methodology and results on the forecast of the numerical value of the fat tail(s) in asset returns distributions using the irrational fractional Brownian motion model. Optimal model parameter values are obtained from fits to consecutive daily 2-year period returns of S&P500 index over [1950–2016], generating 33-time series estimations. Through an econometric model, the kurtosis of returns distributions is modelled as a function of these parameters. Subsequently an auto-regressive analysis on these parameters advances the modelling and forecasting of kurtosis and returns distributions, providing the accurate shape of returns distributions and measurement of Value at Risk.

Introduction

Researchers have put much effort into developing ways of accurately modelling the returns distributions for financial market indices. The literature is so enormous that to quote a few papers would lead to consider that the present authors are biased, thus, it is assumed that the reader is aware that indeed there are many papers available. Nevertheless, let us stress that among the stylized facts of returns distributions in financial markets, one of the most well-known is the early recognized so-called fat tail (Mandelbrot 1963). It is still somewhat unclear why a fat tail exists, with some decay exponent values in limited ranges, even in presence of varied volatility occurrences or origins, like time lags (Ausloos and Ivanova 2003; Castellano et al. 2018). An often mentioned argument stems from the asymmetry of information, but not easily accepted if one sticks to the “efficient market hypothesis” (EMH) (Borges 2010; Schinckus et al. 2016). Nevertheless, we do assume that an asymmetric information flow exists, not yet discounting an asymmetric time lag for such flows.

A classical Bachelier random walk model would suggest a Brownian motion analogy for the returns r_t at time t, the so called Geometric Brownian Motion (GBM) (Mandelbrot 1963; Mills and Markellos 2008; Rachev et al. 2005; Birge and Linetsky 2007).

$$ r_{t} = \ln \left( {\frac{{P_{t} }}{{P_{t - 1} }}} \right) = \mu + \varepsilon_{t} \quad \varepsilon_{t} \sim NID(0,\sigma^{2} ) $$

(1)

where $\mu$ is the averaged returns over the time interval [0, t], and ε_t is assumed to be normally independently distributed with zero mean and constant variance. The above equation can be written as

$$ P_{t + \delta t} = P_{t} { \exp }(\mu \delta t + \sigma Z_{t} \sqrt {\delta t} ) $$

(2)

where Z_t is a random number drawn from the standardised normal distribution, $\delta t$ is a small-time step and $\sigma$ is the standard deviation of the returns over the time interval [0, t]. This equation is deployed to run simulations and construct the modelled returns distributions based on the GBM.

Usually, the distribution of returns generated from GBM model does not match the distribution of historical returns data which often show leptokurtosis. The usual returns fat-tailed distributions show a power law decay in the tail: if the skewness is greater than 1.0 (or less than − 1.0), the skewness is substantial and the distribution is far from symmetrical. Moreover, a flat distribution has a negative kurtosis, while a distribution which is more peaked than a Gaussian distribution has a positive kurtosis (Mills 1995).

It is widely recognized that the use of distribution higher moments, such as skewness and kurtosis, can be important for improving the performance of various financial models (Mills 1995; Harvey and Siddique 1999; Peiró 1999; Bera and Premaratne 2001). Responding to this recognition, researchers and practitioners have started to incorporate these high moments into models, mostly using conventional measures, e.g. the sample skewness and/or the sample kurtosis. Models of conditional counterparts of the sample skewness and the sample kurtosis, based on extensions of the generalized autoregressive conditional heteroskedasticity (GARCH) model (Engle 1982), have also been developed and used; see, for example, Leon et al. (2004).

Moments of asset returns of order higher than 2 are important because these permit recognitions of the multi-dimensional nature of the concept of risk (Das and Sundaram 1999). Such higher order moments have been proved useful for asset pricing, portfolio construction, and risk assessment. See, for example, Hwang and Satchell (1999) and Harvey and Siddique (2000). High order moments that have received particular attention are the skewness and kurtosis, which involve moments of order three and four, respectively. Indeed, it is widely held as a “stylized fact” that the distributions of stock returns exhibits both left skewness and excess kurtosis (fat tails); there is a large amount of empirical evidence to this effect. See for example, Groeneveld and Meeden (1984) or Critchley and Jones (2008).

Furthermore, distributions containing parameters that control skewness and/or kurtosis are attractive since they can accommodate asymmetry and “flexible tail” behaviour (Rubio and Steel 2015). These distributions are typically obtained by adding parameters to a known symmetric distribution through a parametric transformation. General representations of parametric transformations have been proposed in Ferreira and Steel (2006) as “probability integral transformations”, Ley and Paindaveine (2010) as “transformations of random variables” and Jones (2014) as “transformations of scale”. Transformations that include a parameter that controls skewness are usually referred to as “skewing mechanisms” (Ferreira and Steel 2006; Ley and Paindaveine 2010), while those that add a kurtosis parameter have been called “elongations” (Fischer and Klein 2004), due to the effect produced on the shoulders and the tails of the distributions. Some members of this class are the Johnson SU family (Johnson 1949), Tukey-type transformations such as the g-and-h transformation and the Lambert W transformation (Hoaglin et al. 1985; Goerg 2011), and the sinh–arcsinh transformation (Jones and Pewsey 2009). These sorts of transformations are typically, but not exclusively, applied to the normal distribution. Alternatively, distributions that can account for skewness and kurtosis can be obtained by introducing skewness into a symmetric distribution that already contains a shape parameter. Examples of distributions obtained by this method are skew-t distributions (Hansen 1994; Fernandez and Steel 1998; Azzalini and Capitanio 2003; Rosco et al. 2011), and skew-exponential power distributions (Azzalini 1986; Fernandez et al. 1995). Other distributions containing shape and skewness parameters have been proposed in different contexts such as the generalized hyperbolic distribution (Barndorff-Nielsen et al. 1982; Aas and Haff 2006), the skew-t proposed in Jones and Faddy (2003); and the α-stable family of distributions. With the exception of the so called “two-piece” transformation (Fernandez and Steel 1998; Arellano-Valle et al. 2005), the aforementioned transformations produce distributions with different shapes and/or different tail behaviour in each direction. Surveys on families of “flexible tail” distributions can be found in Jones (2014) and Ley (2015). Other approaches used to produce so called flexible models are semi-parametric models (Quintana et al. 2009) or fully nonparametric models (e.g. kernel density estimators and Bayesian nonparametric density estimation).

Understanding what is happening as well as risk control and management is and continues to be an urgent challenge for investors and researchers alike. One should mention here that numerous problem-solving strategies can be drawn from Operations Research to apply in Finance and related sub-categories. Financial Engineering takes on the developing and implementation of innovative ideas for financial products. For example exploring the financial risk of temperature index by Castellano et al. (2018). In Portfolio Theory minimising risk and maximising returns; (classic optimisation scenario) like Value at Risk (VAR) measure for managing risk (Elliott and Siu 2010). In Financial Instruments pricing and risk management of complex financial instruments, the seminal Black–Scholes Model and its numerous variations including the one developed by Guillaume (2018) and Elliott and Siu (2010) is the one of many examples, also application of Monte Carlo simulations (applied in this paper simulate returns) to analyse the behaviour of these financial instruments. High-Frequency Trading probably the prime example of OR being put into use in Finance. Certain strategies consider optimal order size, optimal trading signal, optimal trading times, etc. to calculate tiny statistical discrepancies in the market and trade on them as explained in Kürüm et al. (2018). Moreover, the Brownian Motion and its different variations/extensions have been extensively applied to model the various operations research, management science and computational problems as highlighted in Ormeci et al. (2008), Harrison et al. (1983), Zacharias and Armony (2016), Lucheroni and Mari (2018), Miao et al. (2016), Zheng et al. (2016) amongst others.

Moving theories away from classical Geometric Brownian Motion has become a necessity. Hence asset modelling has been also addressed by the development of Normal Inverse Gaussian Levy Process providing the explanation of the empirical scaling power law as in Barndorff-Nielsen (1997a, b, 1998), Barndorff-Nielsen and Prause (1999). Levy processes combined with jump models have been developed and applied for financial asset modelling as in Leon et al. (2002) and Corcuera et al. (2005). In fact, Levy walks (Mantegna 1991) were discovered as potential causes ruling the stock market noticing a breaking of the central limit theorem (further to be replaced by the Levy–Khinchine one). This discovery meant that the world could enter an age of significantly increasing risk of financial market investments: not only huge losses but also colossal profits could be possible. The Mantegna discovery (Mantegna 1991) opened the eyes to non-Gaussian processes on financial markets focusing on the non classical Brownian or non-Wiener random walks. Among these is the identification of empirical regularities and canonical stylized facts (Dacorogna et al. 2001) bearing upon new scaling laws (Di Matteo et al. 2003, 2005) emphasizing long term memories. Alongside these numerous studies have also applied Fractal Brownian Motion, which takes into account the dependant increments and possesses long-range dependence and self-similarity properties, to model the underlying asset. Some of these works include Castellano et al. (2018), Kloeden et al. (2011), Funahashi and Higuchi (2018), Siu (2012), Elliott and Siu (2010), Puu (1992), Tapiero and Vallois (2018) amongst others.

However, recent papers use a quite innovative approach for doing so (Dhesi et al. 2011, 2016; Dhesi and Ausloos 2016). This is achieved by adding an extra stochastic function, with only two parameters (k and c) to be estimated, to the GBM, incorporating a weighting factor [see Eq. (5) here below]. The introduction of such (up to now) parameters can be easily argued, see below in Sect. 1. Interestingly, this type of modelling is endogenous and part of some coherent understanding of the market process, i.e. taking into account some so called irrationality of agents. Feedback and success of “irrational investors” are for example reported in Hirshleifer et al. (2006). Such a psychological behaviour is sometimes accepted as common knowledge that is as a realistic possibility, but hardly included in models.

The irrational fractional Brownian motion (IFBM) modelling captures the fat tails and overall leptokurtosis (Dhesi et al. 2016; Dhesi and Ausloos 2016). Therefore, it can be claimed that the model makes a fully pertinent connection between the extra function and so called irrational behaviour of financial markets.

In light of such premises, and in view of predicting/explaining the exponent of the fat tails, the paper is organized as follows. Section 2 briefly outlines the Geometric Brownian motion model, for completeness, while Sect. 3 explains the novel irrational fractional Brownian motion model. Section 4 explains the methodology of using the irrational fractional Brownian motion for modelling and forecasting the kurtosis of returns distributions. The fine results obtained from this method are summarized and further discussed in Sect. 5.

Geometric Brownian motion model

Equation (2) can be also written as

$$ \frac{dP}{P} = \exp (\mu dt + \sigma Z\sqrt {dt} ) - 1 $$

(3)

Applying Ito’s Lemma (Merton 1975; Gardiner 1985; Heston 1993), the equivalent form of Eq. (3) is expressed as

$$ \frac{dP}{P} = \alpha dt + \sigma Z\sqrt {dt} \quad {\text{where}}\;\alpha = \mu + \frac{1}{2}\sigma^{2} $$

(4)

The above model, Eqs. (1)–(4), provides the foundations of classical quantitative finance. As mentioned here above, the problem is that the distributions of returns generated from this GBM model does not match the distributions of historical returns data,—which often show leptokurtosis.

Irrational fractional Brownian motion model

Continuously compounded returns over k periods are given by

$$ r_{t} (k) = \ln \left( {\frac{{P_{t} }}{{P_{t - k} }}} \right) = \ln \left( {\frac{{P_{t} }}{{P_{t - 1} }}\frac{{P_{t - 1} }}{{P_{t - 2} }} \cdots \frac{{P_{t - k - 2} }}{{P_{t - k - 1} }}\frac{{P_{t - k - 1} }}{{P_{t - k} }}} \right) $$

The following additivity equation shows that the continuously compounded return over k periods can be written as

$$ r_{t} (k) = \ln \left( {\frac{{P_{t} }}{{P_{t - 1} }}} \right) + \ln \left( {\frac{{P_{t - 1} }}{{P_{t - 2} }}} \right) + \cdots + \ln \left( {\frac{{P_{t - k - 2} }}{{P_{t - k - 1} }}} \right) + \ln \left( {\frac{{P_{t - k - 1} }}{{P_{t - k} }}} \right) $$

Also, this sum also comes in useful when returns may diverge from normal distribution. As in this case the central limit theorem shows that the sample average of the sum will converge to the normal distribution.

However, this is only the case over the longest of time periods, such as annual returns (Ausloos and Ivanova 2003). One argument could be as follows. Price-influencing events may be normally distributed, but the likelihood of said events being reported in the news increases with the magnitude of the impact of the event. For the latter distribution, one can factor in the tendency for the media to simplify and exaggerate the news implication. When multiplying the normal distribution by the distribution according to a function modelling, the likelihood/duration/impact of such news reports leads to a much fatter-tailed distribution than a Gaussian (Dhesi et al. 2011).

After extensive simulations and analyses, Dhesi et al. (2016) proposed the irrational fractional Brownian motion (IFBM): in order to manage such aspects; it reads

$$ P_{t + \delta t} = P_{t} \exp \left( {\mu \delta t + \sigma Z_{t} \sqrt {\delta t} + \mu Kf\left( {Z_{t} } \right)\delta t} \right) $$

or

$$ P_{t + \delta t} = P_{t} \exp \left( {\mu \delta t + \sigma Z_{t} \sqrt {\delta t} - kf\left( {Z_{t} } \right)\delta t} \right) k = - \mu K $$

(5)

By comparing Eqs. (4) and (5) one can observe that the GBM modifying function is

$$ f(Z) = \left( {2\exp \left( { - c\frac{{Z^{2} }}{2}} \right) - 1} \right)\arctan (Z) $$

(6)

shown in Fig. 1.

Fig. 1

Source: Dhesi and Ausloos (2016)

Plot of the response/feedback f(Z) function, Eq. (6) emphasizing the various regions of interest.

In understanding how the function f(Z) is achieved one needs to look at the shape of the function that is desirable. The shape of the function that is desirable is presented in Fig. 1. An analytic expression of a function that achieves such a shape is expressed by Eq. 6.

Part of the function f(Z) that is bounded by the roots, the so-called negative feedback area, will peak the returns distribution whereas the parts of the function f(Z) beyond the roots, the so-called positive feedback area will fatten the tails. Hence overall turning a mesokurtic (normal) distribution into a leptokurtic distribution. Full details regarding this can be found in Dhesi and Ausloos (2016).

The function f(Z) contains two parameters namely k and c. Parameter k increases the amplitude of the function whereas the parameter c changes the positioning of the roots of the function. Optimal k and c are selected by performing extensive simulations, such as to find the best possible fit using Chi squared goodness of fit calculations to the specific data set. Full details regarding this can be found in Dhesi et al. (2011).

There could be many other such non-linear combinations which would generate similar shapes. However, it was found (Dhesi et al. 2011) that simulations based on this model [Eqs. (5) and (6)] provided the best k and c tail parameterization, by using Chi square test. As an example, Fig. 2 illustrates the GBM and IFBM (with optimal k and c) best fitted on 2-year daily S&P500 data over 2010–2011.

Fig. 2

Source: Dhesi et al. (2016)

GBM and IFBM, with optimal k and c, best fitted 2-year daily S&P500 data over 2010–2011.

It can be seen that the (red) IFBM curve is very close to the historical histogram leading to a much better fit than the (green) GBM curve. This was verified by running a Chi square goodness of fit test on the historical data (observed frequency) with respect to simulations from the GBM and the IFBM (corresponding expected frequencies).

One possible explanation as of why GBM is transformed into IFBM can be deduced by looking into the shape of $f\left( Z \right)$, on Fig. 1. For simplicity, we may notate that the values bounded by the Z-roots are “small” values of Z and “large” values to be away from roots in either direction. Therefore, the returns generated by “small” Z-values cause the peak of the distribution as the magnitude of returns is diminished; this can be linked to the negative feedback region of f(Z); on the other hand, the returns generated by “large” Z-values shape the fat tails of the distribution.

Forecasting kurtosis and returns distribution

As IFBM seems to capture the leptokurtosis or fat tails of returns distributions, a question arises about the link between the distribution kurtosis and the parameters k and/or c.

In order to determine such a link, we present analysis on daily S&P500 index data from 1950 to 2015 as follows. The sample consists of 33 “2-year daily data” non-overlapping windows, from the time interval [1950–2015]. In the notation below “t [1, 33]” refers to the tth data window.

$$ { \ln }(Kurt_{t} ) = 1.66 + 0.078{ \ln }(k_{t} ) - 0.079{ \ln }(c_{t} ) $$

$$ \begin{array}{*{20}l} {\text{standard errors:}} \hfill & (0.10) \hfill & \quad (0.02) \hfill & \quad (0.03) \hfill \\ {\text{t-statistics:}} \hfill & {16.47} \hfill & \quad {4.97} \hfill & \quad {2.74} \hfill \\ \end{array} $$

The data set is reduced to 32 points¹ (up to 2013) in view of forecasting the kurtosis of 2014–2015 and comparing with the actually realized value (refer to Table 1). A significant statistical econometric relationship is found between the logarithmic kurtosis and the logarithmic $k$ and $c$ values as given by:

Table 1 Comparison of kurtosis from historical returns data, with GBM and IFBM

$$ { \ln }\left( {Kurt_{t} } \right) = 1.66 + 0.078\ln \left( {k_{t} } \right) - 0.081\ln \left( {c_{t} } \right) $$

(7)

$$ \begin{array}{*{20}l} {\text{standard errors:}} \hfill & (0.10) \hfill & \quad (0.03) \hfill & \quad (0.02) \hfill \\ {\text{t-statistics:}} \hfill & {16.05} \hfill & \quad {4.89} \hfill & \quad {2.73} \hfill \\ \end{array} $$

In order to complete the model and verify its robustness, we explore whether there is an autoregressive process on k and c, i.e. whether future k and c values can be forecasted from the past values.

It is found that a basic time series analysis for values of k does not produce an AR process on k due to a small t-statistics on lagged value of k; one finds

$$ k_{t} = 0.002 + 0.259k_{t - 1} $$

$$ \begin{array}{*{20}l} {\text{standard errors:}} \hfill & (0.0006) \hfill & \quad (0.174) \hfill \\ {\text{t-statistics:}} \hfill & {3.02} \hfill & \quad {1.49} \hfill \\ \end{array} $$

However, it is found that there is an AR process on c with a significant t-statistics test on one period lagged c:

$$ c_{t} = 0.180 + 0.422c_{t - 1} $$

(8)

$$ \begin{array}{*{20}l} {\text{standard errors:}} \hfill & (0.06) \hfill & \quad (0.17) \hfill \\ {\text{t-statistics:}} \hfill & {3.04} \hfill & \quad {2.53} \hfill \\ \end{array} $$

The non-significance of the AR processes on k proves a stumbling block in using the forecast model Eq. (7), which leads to request some further investigation. One possibility is to check the AR process on the ratio k/c,—since c is AR and k is not. This is also inspired by a further analysis of Eq. (7). This is also confirmed by modelling the logarithmic kurtosis by the logarithmic ratio (k/c), which produces the following results:

$$ \ln \left( {Kurt_{t} } \right) = 1.66 + 0.08ln\left( {\frac{{k_{t} }}{{c_{t} }}} \right) $$

(9)

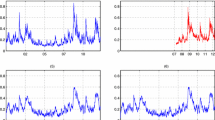
The ratio (k/c) when interestingly plotted over time for the sample (see Fig. 3) produces a picture indicating a smooth pattern with occasional outliers.

Fig. 3

Scatter plot of (k/c) values with corresponding 2-year time periods, between t = 1 (for Jan 01, 1950–Dec 31, 1951) till t = 33 (for Jan 01, 2014–Dec. 31, 2015)

These outliers occur at market crash years, that is the Cuban missile crisis (1962), the financial crisis (1987) and the subprime mortgage crisis (2008), i.e., extreme events indicating an a priori unexpected high ratio. This means that extreme events are well modelled by an IFBM with large $\left( {\frac{k}{c}} \right)$ value. The results are summarised in Table 1.

However, there does not seem to be an AR process on (k/c) with insignificant t-stat. In fact, a graph of (k/c) with one period lagged values (see Fig. 4) presents a fanning out process, hinting the presence of heteroscedasticity like effect. Therefore, we perform the variable transformation to eradicate this heteroscedasticity like effect.

Fig. 4

Scatter plot of k/c versus one period lagged k/c

In so doing, the transformed version of (k/c) does have an AR process on ratio (k/c) with a significant t-stat of 5.18; the result reads:

$$ \frac{{\left[ {k/c} \right]_{t + 1} }}{{\sqrt {\left[ {k/c} \right]_{t} } }} = 0.004\sqrt {\left[ {k/c} \right]_{t} }^{ - 1} + 0.465\sqrt {\left[ {k/c} \right]_{t} } $$

(10)

Applying the 1-step forecast for the kurtosis of 2014–2015 using Eqs. (8), (9) and (10). A 3.53 kurtosis value is predicted; this is in very good agreement with the kurtosis equal to 3.58 generated by the IFBM model (see last row of Table 1) for the same time period.

Also since there are AR processes on c and (k/c), thereby meaning that one can forecast c and (k/c) using the 1-step forecast method, one can use these values to forecast k. In other words, we prove that one can forecast the signature of the returns distribution, with known mean and standard deviation, by forecasting the values of k and c. Table 2 presents a comparison of forecast and IFBM simulated values and forecast values of k, c, (k/c) for Jan 01, 2014–Dec 31, 2015. IFBM simulated values can be seen in the last row of Table 1 and forecast values are obtained from Eqs. (8) and (10).

Table 2 Comparison: between simulated values from IFBM (column 2) and forecasted values from Eqs. (8) and (10) (column 3). (Jan 01, 2014–Dec 31, 2015)

Based on these forecast values, the returns distribution for 2014–2015 generates the theoretical distribution displayed in Fig. 5. Precisely, the grey bars are the historical returns, while the green distribution represents the GBM values; the red distribution represents the simulated distribution from IFBM (using c and k of the last row of Table 1). It is easily observed that, the blue curve, the forecasted distribution using the forecast values of c and k (second column of Table 2) finely overlaps the simulated distribution.

Fig. 5

Distribution of S&P500 returns for 2014–2015 with GBM, IFBM simulation and IFBM forecast

For a normally distributed data set, the 5% probability in left tail will yield a Z-value (Z measures the number of standard deviations away from the mean value) of − 1.64, whereas the historical distribution of S&P500 index for 2014–2015 data set has 5% probability to left of − 1.86; however by applying IFBM on same data accurately forecasts a 5% Z-value of − 1.85 in agreement with historical data.

Conclusion

In the present paper, we provide a theoretical analysis and a numerical investigation of financial data in order to demonstrate that the response function so introduced in the IFBM model in order to render the GBM model “more flexible” is of great validity and forecasting power. In particular, the best proof stems in Fig. 5 which shows that our methodology, justified in Sect. 1 and analytically introduced in Sect. 3, allows to finely forecast returns distributions.

It can be concurred that this process as modelled in Eqs. (8), (9) and (10) significantly adds to the forecasting of financial time series and provides further and novel directions to academics working in this field. Frequency distribution of returns taken ad hoc from the normal distribution or leptokurtic distribution from previous period will inaccurately measure risk signature for the period under forecast investigation. However, this accurate forecasting of the fat tailed frequency distribution for returns provides a major benefit for practitioners, for example, in Value at Risk (VaR) management.

Risk managers will be able to apply the accurate forecasted returns distribution to accurately calculate the p% VaR loss of the desired untraded asset/index.