A modified distance friction minimization approach in data envelopment analysis

Abstract

A multi-step distance friction minimization (DFM) approach has been developed to assist a decision making unit to improve its efficiency. This approach contracts inputs and expands outputs simultaneously through the minimization of distance friction relative to the strongly efficient frontier based on a weighted Euclidean norm. In this paper, we point out that the DFM approach has a problem by means of two numerical examples and then show how to solve the problem. Using a real data set, we not only confirm the occurrence of this problem inherent in the original formulation, but also demonstrate how our modification works.

1 Introduction

Recently, Suzuki et al. (2010) have proposed a multi-step distance friction minimization (DFM) approach to assist a decision making unit (DMU) to improve its efficiency that is computed relative to the strongly efficient frontier of the production possibility set (PPS). The original DFM approach is developed based on data envelopment analysis (DEA), which is a nonparametric method to assess the relative efficiency of the DMUs that consume some inputs to produce some outputs (Cooper et al. 2011). In standard DEA, the efficiency assessment and target setting are carried out relative to the efficient frontier that comprises the strongly efficient frontier and the weakly efficient boundary.

For an inefficient DMU, it is possible to determine a projection on the efficient frontier through decreasing its inputs and/or augmenting its outputs. The coordinates of this projection on the efficient frontier will be the target for the mentioned DMU. Target setting of traditional DEA models is based upon a linear proportional projection. But some non-radial efficiency measures such as the slack-based measure pursues the furthest projection for an inefficient unit, since they consider the maximization of the potential improvements. There are many cases which show that their obtained targets are not realistic or useful. However, the closer the efficient projection to the DMU under evaluation, the easier it is to reach the efficient frontier with less variation in its inputs and outputs. Therefore, the models dealing with the closest targets have made a considerable progress over the traditional ones. DFM model is one of the newly developed models which searches for a point on the strong efficient frontier that is as close as possible to the assessed DMU. DFM method has some advantages, so that it retains the property of the standard DEA approach. That is, it does not confine itself to the proportional improvement by adopting simultaneous input reduction and output expansion. In the target setting, since a priori information can be wrong or biased or there may be a lack of consensus among decision makers, by taking into account the DMU’s preference, a wrong direction to efficiency measurement may be chosen. That’s why the challenge is to develop a method that does not necessarily include a priori information. An additional advantage of DFM projection is that it does not need to incorporate a prior information and the weights related to inputs and outputs are directly determined through the CCR model.

To generate efficiency targets that are easy for DMUs to achieve, several authors developed least distance DEA methods. With the oriented framework, i.e. models that aim at increasing the outputs or decreasing the inputs but not both, Coelli (1998) presented a multi-stage method which carries out a sequence of radial movements for determining closest projection points. Cherchye and Van Puyenbroeck (2001) defined the deviation of the observed input vector and the corresponding reference point in terms of the cosine of the angle, and maximized the cosine to obtain the efficient target. In the same year, Gonzalez and Alvarez (2001) introduced the concept of input-specific contractions and found a relevant benchmark for inefficient units by minimizing this contraction in the inputs required to reach the efficient subset. Nevertheless, it does not guarantee to reach the strong efficient frontier and more recently Aparicio et al. (2017a) developed an approach based on bi-level linear programming by means of special ordered set (SOS) for setting the closest targets.

In earlier studies for finding out the closest projection of inefficient unit, Briec (1998) determined the least distance from each DMU to the weakly efficient boundary based upon Hölder distance functions or $\ell_{p}$ norms. Frei and Harker (1999) found Euclidean projection points by minimizing the distance from an inefficient DMU to a hyperplane associated with the efficient frontier. Portela et al. (2003) analyzed the issue of obtaining closest targets for both convex DEA and nonconvex free disposal hull PPS using a multi-stage procedure. Later, Aparicio et al. (2007) introduced a well-known single-stage procedure that solves a unique zero–one mixed-integer LP problem and Jahanshahloo et al. (2012b) presented a linear bi-level programming problem for calculating the minimum distance of DMUs relative to the strongly efficient frontier. Jahanshahloo et al. (2012a) provided two linear models based on l₁ and l_∞ norms to evaluate the group performance of DMUs relative to the efficient frontier which includes the weakly efficient boundary. Based on the least effort in obtaining the strong efficient projections, Aparicio et al. (2017b, c) introduced Luenberger productivity change indicator.

An interesting property of monotonicity regarding the least distance measure, has motivated in recent times several authors. In this context, Ando et al. (2012) gave weakly monotonic least distance measure with the incorporation of a free disposable set and showed that it satisfies weak monotonicity over the strongly efficient frontier. Aparicio and Pastor (2013, 2014a) proposed an output-oriented strongly monotonic measure based on least distance. Fukuyama et al. (2014a) by extending the free disposable set and introducing the so-called tradeoff set, developed a least distance p-norm efficiency measure satisfying strong monotonicity over the strongly efficient frontier. Fukuyama et al. (2014b) analyzed the possibility of multiple optimal targets as well as the property of monotonicity. Moreover, Fukuyama et al. (2016) focused on investigating the monotonicity based on the FDH (free disposable hull) technologies. Ando et al. (2017) proved the strong monotonicity based on the Hölder norms in the oriented framework for some classes of DEA models. Finally, Zhu et al.’s (2018) paper is a newly published paper based on mixed integer linear program (MILP) that is free from the several disadvantages of previously developed models without requiring the existence of FDEFs (full dimensional efficient facets) or multi stage procedures.

Recently, the authors such as Baek and Lee (2009) and Aparicio and Pastor (2014b) have focused on the determination of a weighted Euclidean distance ($\ell_{2}$ norm) with respect to the strongly efficient frontier. Along this line, Suzuki et al. (2010) introduced the original DFM approach to generate an appropriate efficiency improving projection of an inefficient DMU to the strongly efficient frontier. Because of its practically implementable algorithm, the original DFM approach has recently been adopted for empirical analysis by several authors, such as Wanke et al. (2014) and Suzuki and Nijkamp (2017).

For recent and up-to-date developments on the least distance projections, the reader is referred to Aparicio (2016) and Aparicio et al. (2017d).

The purpose of this paper is twofold. First, we show that Suzuki et al.’s original DFM approach (Suzuki et al. 2010) has a problem that the DFM projection may be located outside the PPS in some circumstances. Second, we solve this problem by appending some constraints to the original DFM model.

The paper is organized as follows: A brief review of the DFM approach is given in Sect. 2. Section 3 shows the problem associated with the original DFM approach by two numerical examples and then suggests how the problem can be solved. In Sect. 4, the proposed modified DFM methodology is empirically checked and compared with the original DFM by using a recent data on 30 European airports used in Suzuki et al.’s (2010) paper. The final section summarizes this paper.

2 The DFM model

In this section, the original DFM approach is reviewed. Let {DMU₁, DMU₂, …, DMU_n} be a set of n observed DMUs where DMU_j, j = 1, 2, …, n produces s outputs y_rj(r = 1, 2, …, s), using m inputs x_ij(i = 1, 2, …, m). Also, let x_j = (x_1j, x_2j, …, x_mj)^t and y_j = (y_1j, y_2j, …, y_sj)^t be the input and output vectors, respectively, where t represents the transpose. The performance of DMU_j, j = 1, 2, …, n, is evaluated relative to the efficient frontier of the constant returns to scale (CRS) PPS:

$$ T_{C} = \left\{ {({\mathbf{x}},{\mathbf{y}}) \in \Re_{ + }^{m} \times \Re_{ + }^{s} :\sum\limits_{j = 1}^{n} {\lambda_{j} {\mathbf{y}}_{j} \ge {\mathbf{y}}\,,\sum\limits_{j = 1}^{n} {\lambda_{j} {\mathbf{x}}_{j} \le {\mathbf{x}},\,\;{\varvec{\uplambda}} \ge {\mathbf{0}}} } } \right\}, $$

where ${\varvec{\uplambda}} = \left( {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{n} } \right) \in \Re_{ + }^{n}$ and 0 is a zero vector of appropriate dimension. Let DMU_o= (x_o, y_o) be an input–output vector under assessment. The input-oriented CCR envelopment and multiplier models take the following forms:

$$ \begin{aligned} LP_{o} :\quad \theta^{*} = & \,\hbox{min} \;\,\,\theta \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad DLP_{o} :\quad \theta^{*} = \hbox{max} \,\,{\mathbf{u}}^{t} {\mathbf{y}}_{o} \\ & \,\,{\text{s.t.}}\quad\sum\limits_{j = 1}^{n} {\lambda_{j} {\mathbf{x}}_{j} } + {\mathbf{s}}^{ - } = \theta {\mathbf{x}}_{o} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {\text{s.t.}}\quad {\mathbf{v}}^{t} {\mathbf{x}}_{o} = 1, \\ & \quad \;\;\;\;\sum\limits_{j = 1}^{n} {\lambda_{j} {\mathbf{y}}_{j} } - {\mathbf{s}}^{ + } = {\mathbf{y}}_{o} ,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\,{\mathbf{u}}^{t} {\mathbf{y}}_{j} - {\mathbf{v}}^{t} {\mathbf{x}}_{j} \le 0,\,j = 1,2, \ldots ,n, \\ & \quad \quad \,{\mathbf{s}}^{ - } \ge {\mathbf{0}},\;\;{\mathbf{s}}^{ + } \ge {\mathbf{0}},\;\;{\varvec{\uplambda}} \ge {\mathbf{0}},\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,{\mathbf{v}} \ge {\mathbf{0}},\,{\mathbf{u}} \ge {\mathbf{0}}, \\ \end{aligned} $$

(1)

where s⁻ and s⁺ are vectors of excess inputs and output shortfalls, respectively.

An optimal solution provides the value of technical inefficiency for DMU_o as well as a projection point on the boundary of technology. In other words, for the CCR strong efficient projection, firstly the radial projection is obtained and secondly the Pareto-efficient targets are obtained through the maximization of slacks which may yield the furthest projections points on the frontier (Banker et al. 1984; Charnes et al. 1978, 1985; Cook and Seiford 2009; Pastor et al. 1999).

Suzuki et al. (2010) proposed the following procedure to determine a closest strongly efficient projection for $\left( {{\mathbf{x}}_{o} ,{\mathbf{y}}_{o} } \right) \in T_{C}$.

Step 1:

Obtain an optimal solution $\left( {\theta^{*} ,{\mathbf{u}}^{*} ,{\mathbf{v}}^{*} } \right)$ from DLP_o in (1)

Step 2:

Solve (2) for $\left( {\theta^{*} {\mathbf{x}}_{o} ,{\mathbf{y}}_{o} } \right)$

$$ \begin{aligned} &\mathop {\hbox{max} }\limits_{{{\varvec{\uplambda}},\;{\mathbf{s}}^{ - } ,\;{\mathbf{s}}^{ + } }} \,\;\mathop w\limits = {\mathbf{e}}^{t} {\mathbf{s}}^{ - } + {\mathbf{e}}^{t} {\mathbf{s}}^{ + } \hfill \\ &{\text{s.t.}}\quad{\mathbf{s}}^{ - } = \theta^{*} {\mathbf{x}}_{o} - \sum\limits_{j = 1}^{n} {\lambda_{j} {\mathbf{x}}_{j} } ,\,\, \hfill \\ &\quad \quad \quad {\mathbf{s}}^{ + } = \sum\limits_{j = 1}^{n} {\lambda_{j} {\mathbf{y}}_{j} } - {\mathbf{y}}_{o} ,\;\, \hfill \\ &\quad \quad \quad {\mathbf{s}}^{ - } \ge {\mathbf{0}},\;\;{\mathbf{s}}^{ + } \ge {\mathbf{0}},\;\;{\varvec{\uplambda}} \ge {\mathbf{0}}, \hfill \\ \end{aligned} $$

(2)

where ${\mathbf{e}}^{t} = \left( {1,1, \ldots ,1} \right)$. Let the optimal solution to (2) be $\left( {{\varvec{\uplambda}}^{*} ,{\mathbf{s}}^{ - *} ,{\mathbf{s}}^{ + *} } \right)$, then the DMUs are classified as follows:

• (1) If θ^* = 1 and for all optimal solutions to (2), ${\mathbf{s}}^{ - *} = {\mathbf{0}}$ and ${\mathbf{s}}^{ + *} = {\mathbf{0}}$. Then $\left( {{\mathbf{x}}_{o} ,{\mathbf{y}}_{o} } \right)$ is strongly efficient.

• (2) If $\theta^{*} = 1$ and ${\mathbf{s}}^{ - *} \ne {\mathbf{0}}$ or ${\mathbf{s}}^{ + *} \ne {\mathbf{0}}$, then $\left( {{\mathbf{x}}_{o} ,{\mathbf{y}}_{o} } \right)$ is weakly efficient and the projections are generated as: ${\hat{\mathbf{x}}}_{o} = \theta^{*} {\mathbf{x}}_{o} - {\mathbf{s}}^{ -*} \,\;\;{\text{and}}\quad {\hat{\mathbf{y}}}_{o} = {\mathbf{y}}_{o} + {\mathbf{s}}^{ + *} .$

• (3) If $0 < \theta^{*} < 1$, then $\left( {{\mathbf{x}}_{o} ,{\mathbf{y}}_{o} } \right)$ is inefficient and projections are generated by Steps 3, 4 and 5 below.

Step 3:

Solve:

$$ \begin{aligned} & \hbox{min} \;\;\,Fr^{x} = \sqrt {\sum\limits_{i = 1}^{m} {\left( {v_{i}^{*} x_{io} - v_{i}^{*} d_{io}^{x} } \right)^{2} } } \,\, \\ & \hbox{min} \;\;Fr^{y} = \sqrt {\sum\limits_{r = 1}^{s} {\left( {u_{r}^{*} y_{ro} - u_{r}^{*} d_{ro}^{y} } \right)^{2} } } \\ & {\text{s.t.}}\quad\sum\limits_{i = 1}^{m} {v_{i}^{*} \left( {x_{io} - d_{io}^{x} } \right)} = \frac{{2\theta^{*} }}{{1 + \theta^{*} }},\, \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{r}^{*} \left( {y_{ro} + d_{ro}^{y} } \right)} = \frac{{2\theta^{*} }}{{1 + \theta^{*} }},\;\, \\ & \quad \quad {\mathbf{x}}_{o} - {\mathbf{d}}_{o}^{x} \ge 0, \\ & \quad \;\;\;{\mathbf{d}}_{o}^{x} \ge {\mathbf{0}},\,\;\;{\mathbf{d}}_{o}^{y} \ge {\mathbf{0}}, \\ \end{aligned} $$

(3)

where ${\mathbf{d}}_{o}^{x} = \mathop (\nolimits d_{1o}^{x} ,d_{2o}^{x} ,\ldots,d_{mo}^{x} \mathop )\nolimits^{t}$ and ${\mathbf{d}}_{o}^{y} = \mathop (\nolimits d_{1o}^{y} ,d_{2o}^{y} ,\ldots,d_{so}^{y} \mathop )\nolimits^{t}$ are the decision variables.

Step 4:

From (3), obtain:

$$ {\mathbf{x}}_{o}^{*} = {\mathbf{x}}_{o} - {\mathbf{d}}_{o}^{{x^{*} }} \quad {\text{and}}\quad {\mathbf{y}}_{o}^{*} = {\mathbf{y}}_{o} + {\mathbf{d}}_{o}^{{y^{*} }} . $$

(4)

Step 5:

Solve:

$$ \begin{aligned} & \mathop {\hbox{max} }\limits_{{{\varvec{\uplambda}},\;{\mathbf{s}}^{ - } ,\;{\mathbf{s}}^{ + } }} \,\;\mathop w\limits = {\mathbf{e}}^{t} {\mathbf{s}}^{ - } + {\mathbf{e}}^{t} {\mathbf{s}}^{ + } \\ & {\text{s.t.}}\quad{\mathbf{s}}^{ - } = {\mathbf{x}}_{o}^{*} - \sum\limits_{j = 1}^{n} {\lambda_{j} {\mathbf{x}}_{j} } ,\,\, \\ & \quad \quad \;\;{\mathbf{s}}^{ + } = \sum\limits_{j = 1}^{n} {\lambda_{j} {\mathbf{y}}_{j} } - {\mathbf{y}}_{o}^{*} ,\;\, \\ & \quad \quad \;\;{\mathbf{s}}^{ - } \ge {\mathbf{0}},\;\;{\mathbf{s}}^{ + } \ge {\mathbf{0}},\;\;{\varvec{\uplambda}} \ge {\mathbf{0}}. \\ \end{aligned} $$

(5)

Let $\left( {{\varvec{\uplambda}}^{**} ,{\mathbf{s}}^{ - **} ,{\mathbf{s}}^{ + **} } \right)$ be an optimal solution to (5). Then, a strongly efficient projection for inefficient DMU_o is:

$$ \begin{aligned} & {\mathbf{x}}_{io}^{**} = {\mathbf{x}}_{io}^{*} - {\mathbf{s}}^{ - **} , \\ & {\mathbf{y}}_{ro}^{**} = {\mathbf{y}}_{ro}^{*} + {\mathbf{s}}^{ + **} . \\ \end{aligned} $$

(6)

It is notable that according to (Suzuki et al. 2010), the major advantages of the DFM method over the radial projection method is simultaneous treatment of input selection and output choices. In other words, this method provides a balanced allocation between input and output efforts as compared with the oriented models. Moreover, in spite of the radial projections, DFM method allows to change several inputs and/or outputs to achieve efficiency for inefficient units in some cases, while other inputs or outputs could be left unaltered. DFM method is not based on priori information by a DMU and the measurement units of the multiple input and outputs need not be identical.

3 The main results

3.1 Counterexample

Although the original DFM approach is an attractive tool for efficiency measurement and targeting, it is not without any drawback. In this section, we show the cases that may lead to the infeasibility of DFM projection and then the deficiency of the original DFM approach two numerical examples are presented to show and a remedy is provided.

As mentioned in the previous section, we need optimal weights of CCR model (i.e. $\left( {{\mathbf{u}}^{*} ,{\mathbf{v}}^{*} } \right)$) in step 3 to solve Model (3). We now discuss two possible status regarding the CCR optimal weights that may lead to the infeasibility of DFM projection.

The first case consists of optimal weights with at least one zero. Precisely, if at least one of the inputs or outputs weight be assigned zero, a projection in step 4 (i.e. $(x_{o}^{*} ,\,y_{o}^{*} )$) may locate outside of the PPS. For instance, suppose $v_{k}^{*} = 0\,$ for some $k \in \{ 1,2,\ldots,m\}$. So, the first constraint of Model (3) is written as:

$$ v_{1}^{*} (x_{1o} - d_{1o}^{x} ) + v_{2}^{*} (x_{2o} - d_{2o}^{x} ) + \cdots + v_{k}^{*} (x_{ko} - d_{ko}^{x} ) + \cdots + v_{m}^{*} (x_{mo} - d_{mo}^{x} ) = \frac{{2\theta^{*} }}{{1 + \theta^{*} }} $$

Considering $v_{k}^{*} = 0\,$ and $x_{ko} - d_{ko}^{x} \ge 0$, variable $d_{ko}^{x}$ can take a number between 0 and $x_{ko}$. Different optimal value for $d_{ko}^{x}$ then is obtained depending on the software used, which may leads to infeasibility of the projection point as we will show through Example 1. The second case where the DFM projection is made infeasible is associated with the situation when the CCR projection of an inefficient DMU becomes an extreme efficient point.

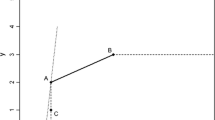
In other words, occurrence of alternative optimal solutions of the CCR model may lead to infeasibility of $(x_{o}^{*} ,\,y_{o}^{*} )$. Changing the optimal solutions of the CCR model may imply the different DFM projections and this may lead to the infeasibility of $(x_{o}^{*} ,\,y_{o}^{*} )$. Figure 1 shows in detail the presence of alternative optimal weights in evaluating DMU_E through CCR-I model. Each weight corresponds to one of the supporting hyperplanes passing through the reference point (DMU_B). Regarding the balanced allocation for the total improvement of inefficiency, we have:

$$ \sum\limits_{r = 1}^{s} {u_{r}^{*} \left( {y_{ro} + d_{ro}^{y} } \right)} = \sum\limits_{i = 1}^{m} {v_{i}^{*} \left( {x_{io} - d_{io}^{x} } \right)} = \frac{{2\theta^{*} }}{{1 + \theta^{*} }} $$

Fig. 1

Supporting hyperplanes and faces

And as a result,

$$ \sum\limits_{r = 1}^{s} {u_{r}^{*} \left( {y_{o}^{*} } \right)} - \sum\limits_{i = 1}^{m} {v_{i}^{*} \left( {x_{o}^{*} } \right)} = 0 $$

Since the normalized coefficient $\left( {{\mathbf{u}}^{*} ,{\mathbf{v}}^{*} } \right)$ of the supporting hyperplane at B gives an optimal solution of the CCR model, it can easily be seen that $(x_{o}^{*} ,\,y_{o}^{*} )$ exactly lies on the same supporting hyperplane obtained through the CCR-I model. Among all of points on the supporting hyperplane by the normalized coefficient $\left( {{\mathbf{u}}^{*} ,{\mathbf{v}}^{*} } \right)$, only DMU_B and segments AB and BC belong to the PPS. Since Model (3), in contrast with CCR model, obtains a non-radial projection by reducing inputs and increasing outputs, movements reaching DMU_B and segments AB and BC give us a feasible projection. Model (3) does not consider the directions ending up with the mentioned parts, the projection would not belong to the PPS. Example 2 depicts the deficiency of DFM in such cases.

Example 1

Consider four DMUs {DMU_A, DMU_B, DMU_C, DMU_D} with one input and two outputs. The data values are given in Table 1. Note that all DMUs consume the same amount of input, i.e., x = 1. Figure 2 shows the projection of PPS on the plane x = 1.

Table 1 Data of the observed DMUs

Fig. 2

Production possibilities on the plane x = 1

In Fig. 2, the solid and the dashed lines represent the strongly efficient and the weakly efficient boundaries, respectively. The efficiency score for DMU_B is $\theta_{B}^{*} = \frac{7}{10}$ and the optimal weights are $v_{1}^{*} = 1$,$u_{1}^{*} = \frac{1}{10}$ and $u_{2}^{*} = 0$. Let $B^{*} \left( {CCR} \right)^{\prime } = \left( {x,y_{1} ,y_{2} } \right)^{t} = \left( {\frac{7}{10},7,4} \right)^{t}$ be the CCR projection of DMU_B. Figure 2 shows that $B^{*} \left( {CCR} \right) = \frac{10}{7} \times B^{*} \left( {CCR} \right)^{\prime } = \frac{10}{7}\left( {\frac{7}{10},7,4} \right)^{t}$ is a point on plane x = 1, and $B^{*} \left( {CCR} \right) \in T_{C}$. Given multipliers $v^{*} = 1,\,\,u_{1}^{*} = 0.1$ and $u_{2}^{*} = 0$, Model (3) has alternative optimal solutions, one of which is:

$$ d_{B}^{{x^{*} }} = \frac{3}{17},\,\;d_{1B}^{{y^{*} }} = \frac{21}{17},\,\;d_{2B}^{{y^{*} }} = \frac{72}{17}. $$

Therefore, the DFM projection of DMU_B based on step 4 is:

$$ B^{*} \left( {DFM} \right)^{\prime } = \left( {x_{B} - d_{B}^{{x^{*} }} ,\;y_{1B} + d_{1B}^{{y^{*} }} ,\;y_{2B} + d_{2B}^{{y^{*} }} } \right)^{t} = \left( {\frac{14}{17},\frac{140}{17},\frac{140}{17}} \right)^{t} . $$

(7)

Since the input value of B*(DFM)′ is less than one, i.e.,$x_{B}^{*} = \frac{14}{17}$, and DMU_B exhibits CRS by assumption, the original DFM projection of DMU_B is $B^{*} \left( {DFM} \right) = \frac{17}{14} \times B^{*} \left( {DFM} \right)^{\prime } = \left( {1,10,10} \right)^{t}$, as is depicted in Fig. 2.

To show that B*(DFM)′ does not belong to PPS, it is sufficient to show that the optimal value of (8) is greater than one. Substituting the values of (7) into (8), we obtain:

$$ \begin{aligned} & \theta_{{B^{*} \left( {DFM} \right)^{\prime } }}^{*} = \hbox{max} \,\,\frac{140}{17}u_{1} + \frac{140}{17}u_{2} \, \\ & \quad \quad \quad \quad \quad {\text{s}} . {\text{t}} .\;\;1u_{1} + 8u_{2} - v \le 0, \\ & \quad \quad \quad \quad \quad \quad \;\,7u_{1} + 4u_{2} - v \le 0, \\ & \quad \quad \quad \quad \quad \quad \,\,10u_{1} + 6u_{2} - v \le 0, \\ & \quad \quad \quad \quad \quad \quad \;4u_{1} + 6u_{2} - v \le 0, \\ & \quad \quad \quad \quad \quad \quad \,\frac{14}{17}v = 1, \\ & \quad \quad \quad \quad \quad \quad v \ge 0,\;\;u_{1} \ge 0,\;\;u_{2} \ge 0. \\ \end{aligned} $$

(8)

The optimal solution and objective value of (8) are:

$$ \left( {v^{*} ,\,\,u_{1}^{*} ,u_{2}^{*} } \right) = \frac{17}{14}\left( {1,\frac{2}{74},\frac{9}{74}} \right),\,\,\;\theta_{{B^{*} \left( {DFM} \right)^{\prime } }}^{*} = \frac{110}{74} \approx 1.49. $$

We have shown that the original DFM projection of DMU_B does not belong to the PPS.

In the next example we show that this kind of drawback occurs in the two-input and one output case as well.

Example 2

Assume that the data are given in Table 2. For DMU_D, $u^{*} ,\,\,v_{1}^{*}$ and $v_{2}^{*}$ are the optimal output weight and input weights, respectively. All optimal solutions of DLP_o in (1) are:

$$ \begin{aligned} & u^{*} = \frac{1}{2}, \\ & v_{1}^{*} = \lambda \left( {\frac{1}{5}} \right) + \left( {1 - \lambda } \right)\left( {\frac{1}{24}} \right),\quad 0 \le \lambda \le 1, \\ & v_{2}^{*} = \frac{1}{4} - v_{1}^{*} . \\ \end{aligned} $$

(9)

Table 2 Data of the observed DMUs

The DFM projection is obtained for each $\lambda \in [0,1]$. Based on step 4, for λ = 0, the original DFM projection is $D_{1} = \left( {3,\frac{9}{5},1} \right)$ which lies on the $\overline{BC}$ segment according to Fig. 3. For λ = 1, we have $D_{2} = \left( {\frac{7}{4},3,1} \right)$ which is located on the $\overline{AB}$ segment. If $\lambda = \frac{1}{4}$, then $D_{3} = \left( {3,\frac{41}{27},1} \right)$. It follows that D₃ is outside the PPS.

Fig. 3

Production possibility on the y = 1 plane

3.2 Solution

We have shown that the original DFM approach has a flaw via Examples 1 and 2. The main problem about this approach is the use of ${\mathbf{x}}_{o} - {\mathbf{d}}_{o}^{x} \ge 0$ in (3). This set of input constraints should have been replaced by $\sum\nolimits_{j = 1}^{n} {\lambda_{j} {\mathbf{x}}_{j} \le \,{\mathbf{x}}_{o} - {\mathbf{d}}_{o}^{x} }$ so that the projection points are on the input frontier. Moreover, the set of output constrains $\sum\nolimits_{j = 1}^{n} {\lambda_{j} {\mathbf{y}}_{j} \ge {\mathbf{y}}_{o} + {\mathbf{d}}_{o}^{y} }$ should also have been appended in order to guarantee the feasibility of the projection of step 4 in the original DFM method. In other words, our proposed approach replaces model (3) by model (10) all else being the same.

That is, our modified bi-objective quadratic programming problem for the original DFM approach is:

$$ \begin{aligned} & \hbox{min} \;\,Fr^{x} = \sqrt {\sum\limits_{i = 1}^{m} {\left( {v_{i}^{*} x_{io} - v_{i}^{*} d_{io}^{x} } \right)^{2} } } \,\, \\ & \hbox{min} \;\,Fr^{y} = \sqrt {\sum\limits_{r = 1}^{s} {\left( {u_{r}^{*} y_{ro} - u_{r}^{*} d_{ro}^{y} } \right)^{2} } } \,\, \\ & {\text{s.t.}}\quad\sum\limits_{i = 1}^{m} {v_{i}^{*} \left( {x_{io} - d_{io}^{x} } \right)} = \frac{{2\theta^{*} }}{{1 + \theta^{*} }},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {10.1} \right) \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{r}^{*} \left( {y_{ro} + d_{ro}^{y} } \right)} = \frac{{2\theta^{*} }}{{1 + \theta^{*} }},\;\,\,\,\,\,\,\,\,\,\,\,\left( {10.2} \right) \\ & \quad \quad \sum\limits_{j = 1}^{n} {\lambda_{j} {\mathbf{x}}_{j} } \le \,{\mathbf{x}}_{o} - {\mathbf{d}}_{o}^{x} ,\,\,\,\,\quad \quad \quad \;\quad \left( {10.3} \right) \\ & \quad \quad \sum\limits_{j = 1}^{n} {\lambda_{j} {\mathbf{y}}_{j} } \ge {\mathbf{y}}_{o} + {\mathbf{d}}_{o}^{y} ,\,\;\quad \quad \quad \;\;\,\,\,\,\left( {10.4} \right) \\ & \quad \quad {\mathbf{d}}_{o}^{x} \ge {\mathbf{0}},\,\;\;{\mathbf{d}}_{o}^{y} \ge {\mathbf{0}},\;\;{\varvec{\uplambda}} \ge {\mathbf{0}}. \\ \end{aligned} $$

(10)

The constraints (10.3) and (10.4) guarantee that the vector $\left( {{\mathbf{x}}_{o} - {\mathbf{d}}_{o}^{x} ,{\mathbf{y}}_{o} + {\mathbf{d}}_{o}^{y} } \right)$ belongs to the PPS. We can obtain this result without changing Steps 4 and 5 of the original DFM method. Now, it is proved by the following lemma that the modified model (10) is feasible.

Lemma 1

The modified DFM model (10) is feasible.

Proof

Let $\theta^{*}$ be the optimal value of input-oriented CCR multiplier model (DLP_o) in the evaluation of the inefficient unit DMU_o and let $({\mathbf{u}}^{*} ,{\mathbf{v}}^{*} )$ denote the optimal weights. Therefore, $(\theta^{*} \,{\mathbf{x}}_{o} \,,\,{\mathbf{y}}_{o} )$ lies on the efficient frontier and the linear-fractional programming problem (11) has the optimal value of 1 and $({\mathbf{u}}^{*} ,{\mathbf{v}}^{*} )$ is one of its optimal solutions.

$$ \begin{aligned}& 1 = \hbox{max} \;\frac{{{\mathbf{u}}^{t} {\mathbf{y}}_{o} }}{{{\mathbf{v}}^{t} (\theta^{*} {\mathbf{x}}_{o} )}} \hfill \\ &\quad{\text{ s}} . {\text{t}} . \quad {\mathbf{u}}^{t} {\mathbf{y}}_{j} - {\mathbf{v}}^{t} {\mathbf{x}}_{j} \le 0,\,\;j = 1,2,\ldots,n,\,\, \hfill \\ &\qquad \quad \quad {\mathbf{v}} \ge {\mathbf{0}},\,\;{\mathbf{u}} \ge {\mathbf{0}}.\quad \,\,\,\,\, \hfill \\ \end{aligned} $$

(11)

Setting ${\mathbf{v}}^{t} {\mathbf{x}}_{o} = \frac{{1 + \theta^{*} }}{{2\theta^{*} }}\,\,$, we obtain the equivalent Model (12) as follows.

$$ \begin{aligned} &1 = \hbox{max} \,\,{\mathbf{u}}^{t} {\mathbf{y}}_{o} \left( {\frac{2}{{1 + \theta^{*} }}} \right) \hfill \\ &\quad{\text{ s}} . {\text{t}} .\quad { }{\mathbf{v}}^{t} {\mathbf{x}}_{o} = \frac{{1 + \theta^{*} }}{{2\theta^{*} }} \hfill \\ &\quad \qquad \quad {\mathbf{u}}^{t} {\mathbf{y}}_{j} - {\mathbf{v}}^{t} {\mathbf{x}}_{j} \le 0,\,\;j = 1,2,\ldots,n,\,\, \hfill \\ &\qquad \quad \quad \,{\mathbf{v}} \ge {\mathbf{0}},\,\;{\mathbf{u}} \ge {\mathbf{0}}.\quad \,\,\,\,\, \hfill \\ \end{aligned} $$

(12)

It is clear that Model (12) is the input-oriented CCR multiplier model and, for the input–output vector $\left( {\frac{{2\theta^{*} }}{{1 + \theta^{*} }}{\mathbf{x}}_{o} ,\frac{2}{{1 + \theta^{*} }}{\mathbf{y}}_{o} } \right)$, the vector $\left( {\frac{{1 + \theta^{*} }}{{2\theta^{*} }}{\mathbf{u}}^{*} ,\frac{{1 + \theta^{*} }}{{2\theta^{*} }}{\mathbf{v}}^{*} } \right)$ is an optimal solution to (12). Since (12) has the optimal objective value of 1, the vector $\left( {\frac{{2\theta^{*} }}{{1 + \theta^{*} }}{\mathbf{x}}_{o} ,\frac{2}{{1 + \theta^{*} }}{\mathbf{y}}_{o} } \right)$ belongs to PPS and there exists ${\varvec{\uplambda}}^{ *} = (\mathop {{\lambda }}\nolimits_{ 1}^{ *} ,\mathop {{\lambda }}\nolimits_{ 2}^{ *} , \ldots ,\mathop {{\lambda }}\nolimits_{\text{n}}^{ *} ) \in \Re_{ + }^{n}$ such that

$$ \begin{aligned} & \sum\limits_{j = 1}^{n} {\mathop \lambda \nolimits_{j}^{*} {\mathbf{x}}_{j} } \le \,\frac{{2\theta^{*} }}{{1 + \theta^{*} }}{\mathbf{x}}_{o} , \\ & \sum\limits_{j = 1}^{n} {\mathop \lambda \nolimits_{j}^{*} {\mathbf{y}}_{j} } \ge \frac{2}{{1 + \theta^{*} }}{\mathbf{y}}_{o} . \\ \end{aligned} $$

Now, let $\,{\mathbf{x}}_{o} - {\mathbf{d}}_{o}^{x} = \frac{{2\theta^{*} }}{{1 + \theta^{*} }}{\mathbf{x}}_{o}$ and $\,{\mathbf{y}}_{o} + {\mathbf{d}}_{o}^{y} = \frac{2}{{1 + \theta^{*} }}{\mathbf{y}}_{o}$. The vector $({\mathbf{d}}_{o}^{x} ,{\mathbf{d}}_{o}^{y} ,{\varvec{\uplambda}}) = \left( {\frac{{1 - \theta^{*} }}{{1 + \theta^{*} }}{\mathbf{x}}_{o} ,\frac{{1 - \theta^{*} }}{{1 + \theta^{*} }}{\mathbf{y}}_{o} ,{\varvec{\uplambda}}^{ *} } \right)$ is a feasible solution to (10). The proof is completed.□

Although Suzuki et al.’s (Suzuki et al. 2010) attempt, associated with the least distance efficiency measurement, is interesting, it has the drawback as mentioned above. Next, we show that Eq. (10) is free from the drawback in Examples 1 and 2. In Example 1, $\theta_{B}^{*} = \frac{7}{10},\,u_{1}^{*} = \frac{1}{10},\,u_{2}^{*} = 0$ and v* = 1 is the optimal solution to the input-oriented CCR multiplier model corresponding to DMU_B and $d_{B}^{x*} = \frac{3}{17},\;\,d_{1B}^{y*} = \frac{21}{17},$ and $\,d_{2B}^{y*} = \frac{593}{1240}$ forms an optimal solution to (10). It follows that the projection obtained by (10) is:

$$ DMU_{B}^{*} = \left( {x_{B}^{*} ,y_{1B}^{*} ,y_{2B}^{*} } \right) = \left( {x_{B} - d_{B}^{x*} ,y_{1B} + d_{1B}^{y*} ,y_{2B} + d_{2B}^{y*} } \right) = \left( {\frac{14}{17},\frac{140}{17},\frac{5553}{1240}} \right), $$

which lies on the weakly efficient boundary. Solving (5) for $DMU_{B}^{*}$, we obtain $s^{ - **} = 0,\,s_{1}^{ + **} = 0$ and $s_{2}^{ + **} = \frac{706}{1525}$. Consequently, the modified DFM projection obtained by (10) is $\left( {x_{B}^{**} ,\,y_{1B}^{**} ,\,y_{2B}^{**} } \right) = \left( {\frac{14}{17},\frac{140}{17},\frac{84}{17}} \right)$, which is an activity in PPS. The modified DFM projection point corresponding to the plane x = 1 is $\left( {1,\,10,\,6} \right) = \frac{17}{4}\left( {\frac{14}{17},\frac{140}{17},\frac{84}{17}} \right)$.

Similarly, the problem associated with DMU_D in Example 2, can be solved. For the circumstance of $\lambda = \frac{1}{4}$, we have $\left( {v_{1D}^{*} ,\,v_{2D}^{*} ,\,u_{D}^{*} } \right) = \left( {\frac{13}{160},\frac{27}{160},\frac{1}{2}} \right)$, $\theta_{D}^{*} = \frac{1}{2}$ and $DMU_{D}^{**} = \left( {x_{1D}^{**} ,\,x_{1D}^{**} ,\,y_{D}^{**} } \right) = \left( {\frac{8}{3},\frac{8}{3},\frac{4}{3}} \right)$. Henceforth, the modified DFM projection corresponding to plane y = 1 is (2, 2, 1).

4 The empirical example

In the previous section, we showed that the projection point obtained by Suzuki et al.’s original DFM approach doesn’t necessarily belong to the PPS using the two numerical examples. In this section, we investigate whether or not this problem occurs in a real situation by comparing the results obtained from the original and the modified DFM approaches. For this purpose, we examine the data set of selected thirty European airports employed by Suzuki et al. (Suzuki et al. 2010). This data set includes four inputs and two outputs. Six out of the thirty airports are deemed efficient according to the input-oriented CCR model.¹ None of the computations in Table A1 of Suzuki et al. (Suzuki et al. 2010) showed infeasibility.² However, this does not mean that their method is free from the limitation. According to the original DFM approach based on Eq. (3), the data produces multiple solutions that may lead to infeasibility of projection.

We solve a multi-objective quadratic programming problem (model (3) in Step 3 of the original DFM approach) for investigating the above example through implementing the algorithm in MATLAB. Evidence shows that some of the airports exhibited infeasibility for the case of the original DFM approach. We apply the CCR model to each of the original DFM solutions in order to check the feasibility of the solutions. Note that the feasibility can be checked by computing the input-oriented CCR score: if the score is greater than one,³ then the projected point is outside the production possibility set (indicating technological infeasibility relative to the production possibility set). In order to demonstrate the well-definedness of the modified DFM approach, we also evaluated each projection point obtained by the modified DFM approach.

Now consider the airport CPH. Based on Step 4 of the original DFM approach, we obtained the multipliers (weights) are shown as follows:

$$ \left( {v_{1}^{*} ,\;v_{2}^{*} ,\;v_{3}^{*} ,\;v_{4}^{*} ,\;u_{1}^{*} ,u_{2}^{*} } \right) = \left( {1.2e - 1,\;\;3.7e - 6,\;\;0,\;\;2.2e - 4,\;\;0,\;\;2.6e - 6 \, } \right) $$

and the corresponding projection point using MATLAB as follows:

$$ \begin{aligned} & RN\;(x_{1}^{*} ) = 2.0 \hfill \\ & TS\;(x_{2}^{*} ) = 90101.9 \hfill \\ & GN\;(x_{3}^{*} ) = 1.2 \hfill \\ & EN\;(x_{4}^{*} ) = 1087.5 \hfill \\ & PN\;(y_{1}^{*} ) = 17714008.1 \hfill \\ & AM\;(y_{2}^{*} ) = 308088.9 \, \hfill \\ \end{aligned} $$

(13)

See the column 5 of Table 3. Based on the projection point given in Eq. (13), we obtain the input-oriented CCR score of $\theta_{{(x_{o}^{*} ,y_{o}^{*} )}}^{*} = 32.6 > 1$, which indicates the projection point based on the original DFM approach is located outside the PPS. Now we turn to the modified DFM approach, of which results are shown in the columns 7–11 of Table 3. Clearly, the projection points based on the modified DFM are all feasible, which is shown by the input-oriented CCR scores of one.

Table 3 Evaluation of optimal solutions based on MATLAB

A further analysis shows that the original and modified approaches produce the same results for AMS, ARN, CDG, CIA, HEL, IST, LIS and ORY. For some other airports (BRU, DUS, FRA, MUC, MXP, OSL), the projection points are the same across the six airports except for the second input of TS. We can observe a significant difference between the two DFM approaches for the airports such as BHX, CGN, CPH, FCO, GVA, HAM, MAN, PRG,VIE and ZRH. In summary, the projections of the original DFM measure lied outside the PPS in 37.5% of cases for the entire set of airports. See Appendix. More details are available upon request.

However, as we know, adding new constraints to the programming problem may not improve the optimal value. Therefore, the modified DFM approach obtains either the same projection or a farther projection compared to the original DFM. As a result, if the decision maker looks for the closer projection, the original DFM method can be solved unless the projection lies out of the PPS. It is notable that the goal of this paper is providing a remedy for the infeasibility of projections and therefore, rectifying the mentioned drawbacks to return the exterior points back onto the original efficient frontier of DFM method by choosing the suitable weights of CCR model can be an interesting future work.

5 Summary

In this paper we considered Suzuki et al.’s original DFM approach (Suzuki et al. 2010) for generating efficiency improvement projections. Using two numerical examples, we showed that the obtained projection point can be technologically infeasible in the sense that it can be located outside the production possibility set. Therefore, we rectified the drawback inherent to the original DFM approach, not only by replacing the set of input constraints but also by adding the set of output constraints to the bi-objective quadratic programming model in the original DFM approach. Perhaps a non-radial super-efficient projection would be suitable and interesting as a future work to return the exterior points back onto the original efficient frontier.

Appendix

See Table 4.

Table 4 The modified DFM projection results for the projections of the original DFM lying outside the PPS