A manufacturer’s responsible sourcing strategy: going organic or participating in fair trade?

Abstract

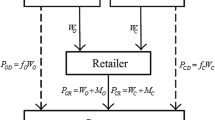
We consider a bilateral supply chain with a downstream manufacturer and an upstream farmer. The manufacturer makes two sourcing decisions: Whether to join the fair trade movement and whether to use organic or conventional (non-organic) cotton in her product. The manufacturer’s sourcing strategy affects the determination of the wholesale price, the farmer’s production cost, and consumers’ purchasing decisions. We characterize the supply chain parties’ subgame perfect Nash equilibrium decisions, finding that the manufacturer participates in fair trade or uses organic cotton only when the non-organic cotton commodity price is sufficiently high. Moreover, increases in the cotton commodity price may not necessarily benefit the farmer. Finally, the manufacturer’s participation in fair trade can yield the highest profit for both supply chain parties. Such a win–win outcome always occurs when the fair trade manufacturer also chooses organic cotton but never occurs if the manufacturer does not participate in fair trade.

Appendix

1.1 A.1. Proofs

Proof of Lemma 1

We begin by determining the manufacturer’s optimal retail price in different sourcing scenarios. We use the function $D_{i} = k - \inf \left\{ {v:U_{i} \ge 0} \right\}$ to derive consumer demand $D_{i}$ under sourcing scenario $i$, finding that $D_{i} = k + \delta_{i} - p$. Replacing $D_{i}$ into $\pi_{i}^{M}$, it is straightforward to show that $\pi_{i}^{M}$ is concave in $p$. Then, the optimal price without quantity constraint can be derived from solving the first-order condition for $\pi_{i}^{M} = \left( {p - w_{i} } \right) \cdot D_{i}$, which leads to case (2) of the lemma. $\hat{Q}_{i}$ is then $D_{i}$ with the optimal price given in case (2). When $Q \le \hat{Q}_{i}$, the optimal price is obtained by solving $Q = k + \delta_{i} - p$ due to the concavity of $\pi_{i}^{M}$.□

Proof of Lemma 2

We now solve the farmer’s optimal choice of growing quantity with manufacturer’s choice of the retail price.

• (i) In the NC and FC scenarios, $c_{i} \left( Q \right) = aQ$, which implies $\pi_{i}^{F} = w_{i} \cdot min\left( {Q,D_{i} } \right) - aQ$. If $Q \ge \hat{Q}_{i}$, $\pi_{i}^{F} = w_{i} \cdot \hat{Q}_{i} - aQ$, which is decreasing in $Q$, therefore $Q_{i}^{*} = \hat{Q}_{i} = \frac{{k - w_{i} + \delta_{i} }}{2}$. If $Q \le \hat{Q}_{i}$, $\pi_{i}^{F} = w_{i} \cdot Q - aQ$, which is increasing in $Q$, which implies $Q_{i}^{*} = \hat{Q}_{i} = \frac{{k - w_{i} + \delta_{i} }}{2}$.

• (ii) In the NO and FO scenarios, $c_{i} \left( Q \right) = \left( {a + bQ} \right)Q$, $\pi_{i}^{F} = w_{i} \cdot min\left( {Q, D_{i} } \right) - \left( {a + bQ} \right)Q$. Because $\pi_{i}^{F}$ is non-increasing in $Q$ when $Q > D_{i}$, the optimal solution must satisfy $Q_{i}^{*} \le D_{i}$. This implies that we can reduce the problem to maximizing $\pi_{i}^{F} = w_{i} \cdot Q - \left( {a + bQ} \right)Q$, which is concave in $Q$ so the first-order condition leads to $Q_{i}^{*} = \bar{Q}_{i} = \frac{{w_{i} - a}}{2b}$. If $\bar{Q}_{i} < \hat{Q}_{i}$ (i.e., $w_{i} < \hat{w}_{i} = \frac{{b \left( {k + \delta_{i} } \right) + a}}{1 + b}$), $Q_{i}^{*} = \bar{Q}_{i} = \frac{{w_{i} - a}}{2b}$. If $\bar{Q}_{i} \ge \hat{Q}_{i}$ (i.e., $w_{i} \ge \hat{w}_{i} = \frac{{b \left( {k + \delta_{i} } \right) + a}}{1 + b}$), $Q_{i}^{*} = \hat{Q}_{i} = \frac{{k - w_{i} + \delta_{i} }}{2}$.□

Proof of Lemma 3

We now focus on the optimal wholesale price $w_{i}^{*}$ in each scenario $i$.

• (i) In the FC scenario, the farmer determines his wholesale price. According to Lemma 2, $\pi_{i}^{F} = w_{i} \cdot \frac{{k - w_{i} + \delta_{i} }}{2} - a \cdot \frac{{k - w_{i} + \delta_{i} }}{2}$, which is concave in $w_{i}$. Hence then farmer’s optimal wholesale price in FC scenario can be derived by solving the first-order condition, leading to $w_{i}^{*} = \frac{{k + a + \delta_{i} }}{2}$ (i.e., $w_{FC}^{*} = \frac{k + a + s}{2}$).

• (ii) In the FO scenario, farmer also determines his wholesale price. If $w_{i} \le \hat{w}_{i} = \frac{{b \left( {k + \delta_{i} } \right) + a}}{1 + b}$, $\pi_{i}^{F} = w_{i} \cdot \frac{{w_{i} - a}}{2b} - \left( {a + b \cdot \frac{{w_{i} - a}}{2b}} \right) \cdot \frac{{w_{i} - a}}{2b} = \frac{{\left( {w_{i} - a} \right)^{2} }}{4b}$, which is increasing in $w_{i}$ that implies $w_{i}^{*} = \hat{w}_{i} = \frac{{b \left( {k + \delta_{i} } \right) + a}}{1 + b}$, and farmer’s corresponding profit is $\pi_{i}^{F} = \frac{{b\left( {k + \delta_{i} - a} \right)^{2} }}{{4\left( {1 + b} \right)^{2} }}$. If $w_{i} > \hat{w}_{i} = \frac{{b \left( {k + \delta_{i} } \right) + a}}{1 + b}$, $\pi_{i}^{F} = w_{i} \cdot \frac{{k - w_{i} + \delta_{i} }}{2} - \left( {a + b \cdot \frac{{k - w_{i} + \delta_{i} }}{2}} \right) \cdot \frac{{k - w_{i} + \delta_{i} }}{2}$, which is concave in $w_{i}$. Hence the farmer’s optimal wholesale price can be derived by solving the first-order condition, we can derive that $w_{i}^{*} = \frac{{\left( {b + 1} \right) \left( {k + \delta_{i} } \right) + a}}{b + 2}$ which satisfies the condition that $w_{i} > \hat{w}_{i}$, and farmer’s corresponding profit is $\pi_{i}^{F} = \frac{{\left( {k + \delta_{i} - a} \right)^{2} }}{{4\left( {2 + b} \right)}}$. Comparing the farmer’s two profit $\pi_{i}^{F} = \frac{{b\left( {k + \delta_{i} - a} \right)^{2} }}{{4\left( {1 + b} \right)^{2} }}$ and $\pi_{i}^{F} = \frac{{\left( {k + \delta_{i} - a} \right)^{2} }}{{4\left( {2 + b} \right)}}$, we have that $\frac{{b\left( {k + \delta_{i} - a} \right)^{2} }}{{4\left( {1 + b} \right)^{2} }} < \frac{{\left( {k + \delta_{i} - a} \right)^{2} }}{{4\left( {2 + b} \right)}}$. Then the farmer’s optimal wholesale price is $w_{i}^{*} = \frac{{\left( {b + 1} \right) \left( {k + \delta_{i} } \right) + a}}{b + 2}$ (i.e., $w_{FO}^{*} = \frac{{\left( {b + 1} \right) \left( {k + q + \alpha s} \right) + a}}{b + 2}$).

• (iii) In the NO scenario, the manufacturer determines her wholesale price. According to Lemmas 1 and 2, $\pi_{i}^{M} = \left( {p - w_{i} } \right) \cdot min\left( {Q,D_{i} } \right) = \left( {p - w_{i} } \right) \cdot Q = \left( {k - Q + \delta_{i} - w_{i} } \right) \cdot Q$. If $w_{i} \le \hat{w}_{i} = \frac{{b \left( {k + \delta_{i} } \right) + a}}{1 + b}$, $\pi_{i}^{M} = \left( {k - \frac{{w_{i} - a}}{2b} + \delta_{i} - w_{i} } \right) \cdot \frac{{w_{i} - a}}{2b}$ which is concave in $w_{i}$, solving the first-order condition and we can derive that $w_{i}^{*} = \frac{{b\left( {k + \delta_{i} } \right) + a\left( {1 + b} \right)}}{1 + 2b}$, and it satisfies the condition that $w_{i} \le \hat{w}_{i}$. And manufacturer’s corresponding profit is $\pi_{i}^{M} = \frac{{\left( {k + \delta_{i} - a} \right)^{2} }}{{4\left( {1 + 2b} \right)}}$. If $w_{i} \ge \hat{w}_{i} = \frac{{b \left( {k + \delta_{i} } \right) + a}}{1 + b}$, $\pi_{i}^{M} = \left( {k - \frac{{k - w_{i} + \delta_{i} }}{2} + \delta_{i} - w_{i} } \right) \cdot \frac{{k - w_{i} + \delta_{i} }}{2} = \frac{{\left( {k - w_{i} + \delta_{i} } \right)^{2} }}{4}$, which is decreasing in $w_{i}$ that implies $w_{i}^{*} = \hat{w}_{i} = \frac{{b \left( {k + \delta_{i} } \right) + a}}{1 + b}$. The manufacturer’s corresponding profit is $\pi_{i}^{M} = \frac{{\left( {k + \delta_{i} - a} \right)^{2} }}{{4\left( {1 + b} \right)^{2} }}$. Comparing the manufacturer’s two profit $\pi_{i}^{M} = \frac{{\left( {k + \delta_{i} - a} \right)^{2} }}{{4\left( {1 + 2b} \right)}}$ and $\pi_{i}^{M} = \frac{{\left( {k + \delta_{i} - a} \right)^{2} }}{{4\left( {1 + b} \right)^{2} }}$, we have that $\frac{{\left( {k + \delta_{i} - a} \right)^{2} }}{{4\left( {1 + 2b} \right)}} > \frac{{\left( {k + \delta_{i} - a} \right)^{2} }}{{4\left( {1 + b} \right)^{2} }}$. Then $w_{i}^{*} = \frac{{b\left( {k + \delta_{i} } \right) + a\left( {1 + b} \right)}}{1 + 2b}$. As $w_{NO} \ge w_{c}$, manufacturer’s optimal wholesale price is $w_{NO}^{*} = max\left( {\frac{{b\left( {k + \delta_{i} } \right) + a\left( {1 + b} \right)}}{1 + 2b},w_{c} } \right)$ (i.e., $max\left( {\frac{{b\left( {k + q + s} \right) + a\left( {1 + b} \right)}}{1 + 2b},w_{c} } \right)$).□

Proof of Corollary 1

In this part, we will compare the subgame perfect growing quantity $Q_{i}^{*}$ with the manufacturer’s preferred quantity $\hat{Q}_{i}$ in each scenario. We obtain the result that $Q_{i}^{*} = \hat{Q}_{i} \left( {i = NC,FC} \right)$ from the first part of Lemma 2, and $Q_{FO}^{*} = \hat{Q}_{NO}$ from the second part of Lemma 2. From the second part of Lemma 2, if $w_{NO}^{*} = max\left( {\frac{{b\left( {k + q + s} \right) + a\left( {1 + b} \right)}}{1 + 2b}, w_{c} } \right) < \hat{w}_{NO} = \frac{{b \left( {k + q + s} \right) + a}}{1 + b}$, then $Q_{NO}^{*} < \hat{Q}_{NO}$, and the condition is equivalent to $w_{c} < \frac{{b \left( {k + q + s} \right) + a}}{1 + b}$).□

Proof of Proposition 1

In this part, we will continue to determine the manufacturer’s optimal sourcing strategy. First, we apply Lemmas 1–3 and Corollary 1 to derive the manufacturer’s equilibrium profit. We know that $Q_{i}^{*} = \hat{Q}_{i} = \frac{{k - w_{i} + \delta_{i} }}{2} \left( {i = FC,FO,NC,NO\,if\,w_{c} \ge \frac{{b \left( {k + q + s} \right) + a}}{1 + b} } \right)$ from Corollary 1, then replace $p^{*}$ and $Q_{i}^{*}$ into manufacturer’s profit, we can get that $\pi_{i}^{M} = \left( {p^{*} - w_{i}^{*} } \right) \cdot Q_{i}^{*} = \left( {k - Q_{i}^{*} + \delta_{i} - w_{i}^{*} } \right) \cdot Q_{i}^{*} = \frac{{\left( {k + \delta_{i} - w_{i}^{*} } \right)^{2} }}{4}$. And we also know that $Q_{NO}^{*} < \hat{Q}_{NO}$$\left( {if\,w_{c} < \frac{{b \left( {k + q + s} \right) + a}}{1 + b} } \right)$ and $Q_{NO}^{*} = \frac{{w_{NO} - a}}{2b}$, then $\pi_{NO}^{M} = \left( {p^{*} - w_{NO}^{*} } \right) \cdot Q_{NO}^{*} = \left( {k - Q_{NO}^{*} + \delta_{NO} - w_{NO}^{*} } \right) \cdot Q_{NO}^{*} = \frac{{\left[ {2b\left( {k + q + s} \right) + a - \left( {2b + 1} \right) \cdot w_{NO}^{*} } \right] \cdot \left( {w_{NO}^{*} - a} \right)}}{{4b^{2} }}$. By replacing Lemma 3’s optimal wholesale price into the manufacturer’s profit, we can obtain her equilibrium profit:

• (i) $\pi_{FC}^{M} = \frac{{\left( {k - a + s} \right)^{2} }}{16}$.

• (ii) $\pi_{FO}^{M} = \frac{{\left( {k + q + \alpha s - a} \right)^{2} }}{{4\left( {b + 2} \right)^{2} }}$.

• (iii) $\pi_{NC}^{M} = \frac{{\left( {k - w_{c} } \right)^{2} }}{4}.$

• (iv) If $w_{c} \ge \frac{{b \left( {k + q + s} \right) + a}}{1 + b}$, $\pi_{NO}^{M} = \frac{{\left( {k + q + s - w_{c} } \right)^{2} }}{4}$; If $\frac{{b\left( {k + q + s} \right) + a\left( {1 + b} \right)}}{1 + 2b} \le w_{c} < \frac{{b \left( {k + q + s} \right) + a}}{1 + b}$, $\pi_{NO}^{M} = \frac{{\left[ {2b\left( {k + q + s} \right) + a - \left( {2b + 1} \right)w_{c} } \right] \cdot \left( {w_{c} - a} \right)}}{{4b^{2} }}$; If $w_{c} < \frac{{b\left( {k + q + s} \right) + a\left( {1 + b} \right)}}{1 + 2b}$, $\pi_{NO}^{M} = \frac{{\left( {k + q + s - a} \right)^{2} }}{{4\left( {1 + 2b} \right)}}$.

We now compare the manufacturer’s equilibrium profits across the four scenarios to identity the most profitable sourcing strategies. First, we compare every two scenarios’ profit to identity the manufacturer’s switch boundary between them.

We determine that the boundary between FC and FO is $\alpha_{1} \left( {a,b,k,q,s} \right) = \frac{ - ab + bk - 2q + 2s + bs}{2s}$, if $\alpha \ge \alpha_{1}$, the manufacturer chooses FO, otherwise FC.

The boundary between FC and NO is as follows: First, we set ${\text{b}}1 = \frac{3}{2} + \frac{{2q\left( { - 2a + 2k + q + 2s} \right)}}{{\left( { - a + k + s} \right)^{2} }}$, ${\text{b}}2 = \frac{a - k - 2q - s}{a - k - s}$. Then, if $b \ge b1$, $\pi_{NC}^{M} > max\left( {\pi_{NO}^{M} } \right) = \frac{{\left( {k + q + s - a} \right)^{2} }}{{4\left( {1 + 2b} \right)}}$, then NC’s profit will always dominate NO; if $b2 \le b < b1$, FC gets across NO in the area $\frac{{b\left( {k + q + s} \right) + a\left( {1 + b} \right)}}{1 + 2b} \le w_{c} < \frac{{b \left( {k + q + s} \right) + a}}{1 + b}$, and the manufacturer’s choice will switch from NO to FC in the point $wc5 = \frac{{2a\left( {1 + b} \right) + b\left( {2\left( {k + q + s} \right) + \sqrt {\left( {3 - 2b} \right)\left( {k - a + s} \right)^{2} + 4q\left( {2k - 2a + 2s + q} \right)} } \right)}}{2 + 4b}$; if $0 < b < b2$, FC gets across NO in the area $w_{c} > \frac{{b \left( {k + q + s} \right) + a}}{1 + b}$, and manufacturer’s choice will switch from NO to FC in the point $wc6 = \frac{{\left( {a + k + 2q + s} \right)}}{2}$.

The boundary between FC and NC is $wc8 = \frac{1}{2}\left( {a + k - s} \right)$. If $wc < wc8$, the manufacturer chooses NC, otherwise FC.

The boundary between FO and NO is as follows: We first set $\alpha 2 = \frac{{\left( {2 + b} \right)\left( {\frac{a}{2 + b} - \frac{k}{2 + b} - \frac{q}{2 + b} + \frac{ - a + k + q + s}{{\sqrt {1 + 2b} }}} \right)}}{s}$ and $\alpha 3 = \frac{ - a + k + q + 2s + bs}{{\left( {1 + b} \right)s}}$. Then, if $\alpha \ge \alpha 2$, $\pi_{FO}^{M} > max\left( {\pi_{NO}^{M} } \right) = \frac{{\left( {k + q + s - a} \right)^{2} }}{{4\left( {1 + 2b} \right)}}$, then FO’s profit will always dominate NO; if $\alpha 3 \le \alpha < \alpha 2$, FO gets across NO in the area $\frac{{b\left( {k + q + s} \right) + a\left( {1 + b} \right)}}{1 + 2b} \le w_{c} < \frac{{b \left( {k + q + s} \right) + a}}{1 + b}$, and manufacturer’s choice will switch from NO to FO in the point $wc3 = \frac{{\left( {a + ab + bk + bq + bs + b\sqrt {\left( {3 + 2b + b^{2} } \right)\left( {k - a + q + s} \right)^{2} - \left( {2b + 1} \right)\left( {\alpha - 1} \right)\left( {2ks - 2as + 2qs + \left( {\alpha + 1} \right)s^{2} } \right)} /\left( {2 + b} \right)} \right)}}{1 + 2b}$. If $\alpha < \alpha 3$, FO gets across NO in the area $w_{c} > \frac{{b \left( {k + q + s} \right) + a}}{1 + b}$, and manufacturer’s choice will switch from NO to FO in the point $wc4 = \frac{a + k + bk + q + bq + 2s + bs - s\alpha }{2 + b}$.

The boundary between FO and NC is $wc7 = \frac{a + k + bk - q - s\alpha }{2 + b}$. If $wc < wc7$, the manufacturer chooses NC, otherwise FO.

The boundary between NO and NC is as follows: We first set $k1 = a + \frac{q + s}{{ - 1 + \sqrt {1 + 2b} }}$ and $k2 = a + \frac{{\left( {1 + b + \sqrt {1 + 2b} } \right)\left( {1 + b\left( {2 + \sqrt {1 + 2b} } \right)} \right)\left( {q + s} \right)}}{{b^{2} \sqrt {1 + 2b} }}$. Then, if $a \le k < k1$, $\pi_{NC}^{M} < max\left( {\pi_{NO}^{M} } \right) = \frac{{\left( {k + q + s - a} \right)^{2} }}{{4\left( {1 + 2b} \right)}}$, NO’s profit will always dominate NC; if $k1 \le k < k2$, manufacturer’s choice will switch from NC to NO in the area $w_{c} > \frac{{b\left( {k + q + s} \right) + a\left( {1 + b} \right)}}{1 + 2b}$ with the point $wc1 = k - \frac{k + q + s - a}{{\sqrt {1 + 2b} }}$; if $k \ge k2$, manufacturer’s choice will switch from NC to NO in the area $\frac{{b\left( {k + q + s} \right) + a\left( {1 + b} \right)}}{1 + 2b} \le w_{c} < \frac{{b \left( {k + q + s} \right) + a}}{1 + b}$ with the point $wc2 = \frac{{a\left( {1 + b} \right) + b\left( {k + bk + q + s - \sqrt {\left( {q + s} \right)\left( { - 2a\left( {1 + b} \right) + 2\left( {1 + b} \right)k + q + s} \right)} } \right)}}{{\left( {1 + b} \right)^{2} }}$.

When $\alpha 3 \le \alpha < \alpha 2$, there exists $\alpha 4 = \frac{{ - a\left( {1 + b} \right) + k - q + b\left( {k + \left( {2 + b} \right)\left( { - 2q - s + \sqrt {\left( {q + s} \right)\left( { - 2a\left( {1 + b} \right) + 2\left( {1 + b} \right)k + q + s} \right)} } \right)} \right)}}{{\left( {1 + b} \right)^{2} s}}$ which satisfies $\alpha 3 \le \alpha 4 < \alpha 2$. If $\alpha 4 \le \alpha < \alpha 2$, FO intersects with NC before NO. The manufacturer’s choice will switch from NC to FO directly. If $\alpha 3 \le \alpha < \alpha 4$, FO intersects with NC after NO. The manufacturer’s choice will switch from NC to NO then to FO.

When $b2 \le b < b1$, there exists $b3 = \frac{{\left( {a - k - 2q - 3s} \right)\left( {a - k + s} \right) + 2\sqrt { - \left( {a - k - q - 2s} \right)\left( {a - k + s} \right)^{2} \left( {q + s} \right)} }}{{\left( { - a + k + s} \right)^{2} }}$ which satisfies $b2 \le b3 < b1$. If $b3 \le b < b1$, FC intersects with NC before NO. The manufacturer’s choice will switch from NC to FC directly. If $b2 \le b < b3$, FC intersects with NC after NO. The manufacturer’s choice will switch from NC to NO then to FC.

Comparing these boundaries, we can derive thresholds $w_{1}$, $w_{2}$, which influence the manufacturer’s strategies as follows: $w_{1}$ is the boundary at which the manufacturer switches from NC to another scenario when $w_{c}$ gets higher. $w_{2}$ is the boundary at which the manufacturers switch from NO to another scenario when $w_{c}$ gets higher:

$$ \begin{aligned} w_{2} & = \left\{ {\begin{array}{*{20}l} {max(a,wc8)} \hfill & { \alpha < \alpha 1\,and\,( b > b1\,or\,(b3 \le b < b1\,and\,k > k2))} \hfill \\ { wc5} \hfill & {\alpha < \alpha 1\,and\,((b2 \le b < b3\,and\,k > k2)\,or\,( b2 \le b < b1\,and\,a < k < k2))} \hfill \\ { wc3} \hfill & {\alpha > \alpha 1\,and\,((\alpha 3 < \alpha < \alpha 4\,and\,k > k2)\,or\,(\alpha 3 < \alpha < \alpha 2\,and\,a < k < k2))} \hfill \\ {max(a,wc7)} \hfill & {\alpha > \alpha 1\,and\,(\alpha > \alpha 2\,or\,(\alpha 4 < \alpha < \alpha 2\,and\,k > k2))} \hfill \\ { wc6} \hfill & {\alpha < \alpha 1\,and\,b < b2} \hfill \\ { wc4} \hfill & {\alpha > \alpha 1\,and\,\alpha < \alpha 3} \hfill \\ \end{array} } \right. \\ w_{1} & = \left\{ {\begin{array}{*{20}l} {max(a,wc8)} \hfill & { \alpha < \alpha 1\,and\,( b > b1\,or\,(b3 \le b < b1\,and\,k > k2))} \hfill \\ {max(a,wc1)} \hfill & {((\alpha < \alpha 1\,and\,b < b1)\,or\,(\alpha > \alpha 1\,and\,\alpha < \alpha 2))\,and\,a < k < k2} \hfill \\ { wc2} \hfill & {((\alpha < \alpha 1\,and\,b < b1)\,or\,(\alpha > \alpha 1\,and\,\alpha < \alpha 4))\,and\,k > k2} \hfill \\ {max(a,wc7)} \hfill & {\alpha > \alpha 1\,and\,(\alpha > \alpha 2\,or\,(\alpha 4 < \alpha < \alpha 2\,and\,k > k2))} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

We then compare $\alpha 2,$$\alpha 3$, and $\alpha 4$ with $\alpha 1$ separately to simplify $w_{1}$ and $w_{2}$. First, $\alpha 2 - \alpha 1 = \frac{{\left( {2 + b} \right)f\left( b \right)}}{{2\sqrt {1 + 2b} s}}$, where $f\left( b \right) = \left( {a\left( { - 2 + \sqrt {1 + 2b} } \right) - \sqrt {1 + 2b} \left( {k + s} \right) + 2\left( {k + q + s} \right)} \right)$, and $f\left( b \right)$ is decreasing in $b$. Solving $f\left( b \right) = 0$, we obtain $b = \frac{3}{2} + \frac{{2q\left( { - 2a + 2k + q + 2s} \right)}}{{\left( { - a + K + s} \right)^{2} }} = b1$. When $b \le b1$, $\alpha 2 \ge \alpha 1$, when $b > b1$, $\alpha 2 < \alpha 1$.

Similarly, we can demonstrate that when $b \le b2$, $\alpha 3 \ge \alpha 1$; when $b > b2$, $\alpha 3 < \alpha 1$; and when $b \le b3$, $\alpha 4 \ge \alpha 1$, when $b > b3$, $\alpha 4 < \alpha 1$.

We can then simplify $w_{1}$, $w_{2}$, and define $w_{c1}$, $w_{c2}$ and $\alpha_{1}$ as follows:

• (i) For $b \ge b1\,or\,( b3 \le b < b1\,and\,k \ge k2)$

  $$ \begin{aligned} w_{1} & = w_{2} = \left\{ {\begin{array}{*{20}c} {max\left( {a,wc8} \right)} & {\alpha < \alpha 1} \\ {max\left( {a,wc7} \right)} & {\alpha \ge \alpha 1} \\ \end{array} } \right. \\ w_{c1} & = w_{1} ,\quad w_{c2} = max\left( {a,wc8} \right),\alpha_{1} = \alpha 1 \\ \end{aligned} $$

• (ii) For $b2 \le b < b1\,and\,a \le k < k2$

  $$ \begin{aligned} w_{1} & = \left\{ {\begin{array}{*{20}c} {max\left( {a,wc1} \right)} & {\alpha < \alpha 2} \\ {max\left( {a,wc7} \right)} & {\alpha \ge \alpha 2} \\ \end{array} } \right. \\ w_{2} & = \left\{ {\begin{array}{*{20}l} {wc5} \hfill & {\alpha < \alpha 1} \hfill \\ {wc3} \hfill & {\alpha 1 \le \alpha < \alpha 2} \hfill \\ {max(a,wc7)} \hfill & {\alpha \ge \alpha 2} \hfill \\ \end{array} } \right. \\ w_{c1} & = w_{1} ,\quad w_{c2} = wc5 \\ \end{aligned} $$
  $$ \alpha_{1} = \left\{ {\begin{array}{*{20}l} {\alpha 1} \hfill & {\alpha = \alpha 1} \hfill \\ {wc3^{ - 1} (\alpha ) } \hfill & {\alpha 1 < \alpha < \alpha 2} \hfill \\ {\alpha 2} \hfill & {\alpha = \alpha 2} \hfill \\ \end{array} } \right. $$

  where

  $$ wc3^{ - 1} \left( \alpha \right) = \frac{{a - \left( {k + q} \right) + \left( {2 + b} \right)\sqrt {(w_{c} - a)(a + 2b(k + q + s) - (2b + 1)w_{c} )} /b}}{s} $$

• (iii) For $0 < b < b2\,and\,a \le k < k2$

  $$ \begin{aligned} w_{1} & = \left\{ {\begin{array}{*{20}c} {max\left( {a,wc1} \right)} & {\alpha < \alpha 2} \\ {max\left( {a,wc7} \right)} & {\alpha \ge \alpha 2} \\ \end{array} } \right. \\ w_{2} & = \left\{ {\begin{array}{*{20}l} {wc6} \hfill & {\alpha < \alpha 1} \hfill \\ {wc4} \hfill & { \alpha 1 \le \alpha < \alpha 3} \hfill \\ {wc3} \hfill & {\alpha 3 \le \alpha < \alpha 2} \hfill \\ {max\left( {a,wc7} \right)} \hfill & {\alpha \ge \alpha 2} \hfill \\ \end{array} } \right. \\ w_{c1} & = w_{1} , w_{c2} = wc6 \\ \end{aligned} $$
  $$ \alpha_{1} = \left\{ {\begin{array}{*{20}l} {\alpha 1} \hfill & {\alpha = \alpha 1} \hfill \\ {wc4^{ - 1} \left( \alpha \right)} \hfill & {\alpha 1 < \alpha \le \alpha 3} \hfill \\ {wc3^{ - 1} \left( \alpha \right)} \hfill & {\alpha 3 < \alpha \le \alpha 2} \hfill \\ {\alpha 2} \hfill & {\alpha = \alpha 2} \hfill \\ \end{array} } \right. $$

  And

  $$ wc4^{ - 1} \left( \alpha \right) = \frac{{a + \left( {1 + b} \right)k + \left( {1 + b} \right)q + \left( {2 + b} \right)\left( {s - w_{c} } \right)}}{s} $$

• (iv) For $b2 \le b < b3\,and\,k \ge k2$

  $$ \begin{aligned} w_{1} & = \left\{ {\begin{array}{*{20}l} {wc2} \hfill & {\alpha < \alpha 4} \hfill \\ { max\left( {a,wc7} \right)} \hfill & {\alpha \ge \alpha 4} \hfill \\ \end{array} } \right. \\ w_{2} & = \left\{ {\begin{array}{*{20}l} {wc5} \hfill & {\alpha < \alpha 1} \hfill \\ {wc3} \hfill & {\alpha 1 \le \alpha < \alpha 4} \hfill \\ {max\left( {a,wc7} \right)} \hfill & {\alpha \ge \alpha 4} \hfill \\ \end{array} } \right. \\ w_{c1} & = w_{1} ,\quad w_{c2} = wc5 \\ \end{aligned} $$
  $$ \alpha_{1} = \left\{ {\begin{array}{*{20}l} {\alpha 1} \hfill & {\alpha = \alpha 1} \hfill \\ {wc3^{ - 1} \left( \alpha \right)} \hfill & {\alpha 1 < \alpha < \alpha 4} \hfill \\ {\alpha 4} \hfill & {\alpha = \alpha 4} \hfill \\ \end{array} } \right. $$

• (v) For $0 < b < b2\,and\,k \ge k2$

  $$ \begin{aligned} w_{1} & = \left\{ {\begin{array}{*{20}l} {wc2} \hfill & {\alpha < \alpha 4} \hfill \\ {max(a,wc7)} \hfill & {\alpha \ge \alpha 4} \hfill \\ \end{array} } \right. \\ w_{2} & = \left\{ {\begin{array}{*{20}l} {wc6} \hfill & {\alpha < \alpha 1} \hfill \\ {wc4} \hfill & {\alpha 1 \le \alpha < \alpha 3} \hfill \\ {wc3} \hfill & {\alpha 3 \le \alpha < \alpha 2} \hfill \\ {max\left( {a,wc7} \right)} \hfill & {\alpha \ge \alpha 2} \hfill \\ \end{array} } \right. \\ w_{c1} & = w_{1} ,\quad w_{c2} = wc6 \\ \end{aligned} $$
  $$ \alpha_{1} = \left\{ {\begin{array}{*{20}l} {\alpha 1} \hfill & {\alpha = \alpha 1} \hfill \\ {wc4^{ - 1} \left( \alpha \right)} \hfill & {\alpha 1 < \alpha \le \alpha 3} \hfill \\ {wc3^{ - 1} \left( \alpha \right)} \hfill & {\alpha 3 < \alpha \le \alpha 4} \hfill \\ {\alpha 4} \hfill & {\alpha = \alpha 4} \hfill \\ \end{array} } \right. $$

When $w_{c} < w_{c1}$, the manufacturer chooses NC. When $w_{c} \ge w_{c1}$, if $w_{c} < w_{c2}$ and $\alpha < \alpha_{1}$ the manufacturer chooses NO; if $w_{c} \ge w_{c2}$ and $\alpha < \alpha_{1}$, the manufacturer chooses FC. Otherwise, the manufacturer chooses FO.

There always exists an area in which $w_{c1} > 0$ if and only if $wc1 = k - \frac{k + q + s - a}{{\sqrt {1 + 2b} }} > a$, which is $q + s < \left( {k - a} \right)\left( {\sqrt {1 + 2b} - 1} \right)$.□

Proof of Proposition 2

Before we demonstrate Proposition 2, we will analyze the impact of each parameter to the manufacturer’s profit under her optimal choice of sourcing strategy:

• (i) $\pi_{FC}^{M} = \frac{{\left( {k - a + s} \right)^{2} }}{16} \cdot \frac{{d\left( {\pi_{FC}^{M} } \right)}}{dk} = \frac{{\left( {k - a + s} \right)}}{8} > 0$; $\frac{{d\left( {\pi_{FC}^{M} } \right)}}{da} = \frac{{ - \left( {k - a + s} \right)}}{8} < 0$; $\frac{{d\left( {\pi_{FC}^{M} } \right)}}{ds} = \frac{{\left( {k - a + s} \right)}}{8} > 0$; $\frac{{d\left( {\pi_{FC}^{M} } \right)}}{dq} = \frac{{d\left( {\pi_{FC}^{M} } \right)}}{d\alpha } = \frac{{d\left( {\pi_{FC}^{M} } \right)}}{db} = \frac{{d\left( {\pi_{FC}^{M} } \right)}}{{dw_{c} }} = 0$.

• (ii) $\pi_{FO}^{M} = \frac{{\left( {k + q + \alpha s - a} \right)^{2} }}{{4\left( {b + 2} \right)^{2} }} \cdot \frac{{d\left( {\pi_{FO}^{M} } \right)}}{dk} = \frac{ - a + k + q + s\alpha }{{2\left( {2 + b} \right)^{2} }} > 0$; $\frac{{d\left( {\pi_{FO}^{M} } \right)}}{dq} = \frac{ - a + k + q + s\alpha }{{2\left( {2 + b} \right)^{2} }} > 0$; $\frac{{d\left( {\pi_{FO}^{M} } \right)}}{ds} = \frac{{\alpha \left( { - a + k + q + s\alpha } \right)}}{{2\left( {2 + b} \right)^{2} }} > 0$; $\frac{{d\left( {\pi_{FO}^{M} } \right)}}{d\alpha } = \frac{{s\left( { - a + k + q + s\alpha } \right)}}{{2\left( {2 + b} \right)^{2} }} > 0$; $\frac{{d\left( {\pi_{FO}^{M} } \right)}}{da} = \frac{{ - \left( { - a + k + q + s\alpha } \right)}}{{2\left( {2 + b} \right)^{2} }} < 0$; $\frac{{d\left( {\pi_{FO}^{M} } \right)}}{db} = - \frac{{\left( { - a + k + q + s\alpha } \right)^{2} }}{{2\left( {2 + b} \right)^{3} }} < 0$; $\frac{{d\left( {\pi_{FO}^{M} } \right)}}{{dw_{c} }} = 0$.

• (iii) $\pi_{NC}^{M} = \frac{{\left( {k - w_{c} } \right)^{2} }}{4} \cdot \frac{{d\left( {\pi_{NC}^{M} } \right)}}{dk} = \frac{{k - w_{c} }}{2} > 0$; $\frac{{d\left( {\pi_{NC}^{M} } \right)}}{{dw_{c} }} = \frac{{w_{c} - k}}{2} < 0$; $\frac{{d\left( {\pi_{NC}^{M} } \right)}}{dq} = \frac{{d\left( {\pi_{NC}^{M} } \right)}}{ds} = \frac{{d\left( {\pi_{NC}^{M} } \right)}}{d\alpha } = \frac{{d\left( {\pi_{NC}^{M} } \right)}}{da} = \frac{{d\left( {\pi_{NC}^{M} } \right)}}{db} = 0$.

• (iv) If $w_{c} \ge \frac{{b \left( {k + q + s} \right) + a}}{1 + b}$, $\pi_{NO}^{M} = \frac{{\left( {k + q + s - w_{c} } \right)^{2} }}{4}$, $\frac{{d\left( {\pi_{NO}^{M} } \right)}}{dk} = \frac{{d\left( {\pi_{NO}^{M} } \right)}}{dq} = \frac{{d\left( {\pi_{NO}^{M} } \right)}}{ds} = \frac{{k + q + s - w_{c} }}{2} > 0$, $\frac{{d\left( {\pi_{NO}^{M} } \right)}}{{dw_{c} }} = - \frac{{k + q + s - w_{c} }}{2} < 0$, $\frac{{d\left( {\pi_{NO}^{M} } \right)}}{d\alpha } = \frac{{d\left( {\pi_{NO}^{M} } \right)}}{da} = \frac{{d\left( {\pi_{NO}^{M} } \right)}}{db} = 0$; If $\frac{{b\left( {k + q + s} \right) + a\left( {1 + b} \right)}}{1 + 2b} \le w_{c} < \frac{{b \left( {k + q + s} \right) + a}}{1 + b}$, $\pi_{NO}^{M} = \frac{{\left[ {2b\left( {k + q + s} \right) + a - \left( {2b + 1} \right)w_{c} } \right] \cdot \left( {w_{c} - a} \right)}}{{4b^{2} }}$, $\frac{{d\left( {\pi_{NO}^{M} } \right)}}{dk} = \frac{{d\left( {\pi_{NO}^{M} } \right)}}{dq} = \frac{{d\left( {\pi_{NO}^{M} } \right)}}{ds} = \frac{{w_{c} - a}}{2b} > 0$, $\frac{{d\left( {\pi_{NO}^{M} } \right)}}{d\alpha } = 0$, $\frac{{d\left( {\pi_{NO}^{M} } \right)}}{da} = - \frac{{a + b\left( {k + q + s} \right) - \left( {1 + b} \right)w_{c} }}{{2b^{2} }} < 0$, $\frac{{d\left( {\pi_{NO}^{M} } \right)}}{db} = \frac{{\left( {a - w_{c} } \right)\left( {a + b\left( {k + q + s} \right) - \left( {1 + b} \right)wc} \right)}}{{2b^{3} }} < 0$, $\frac{{d\left( {\pi_{NO}^{M} } \right)}}{{dw_{c} }} = \frac{{a\left( {1 + b} \right) + b\left( {k + q + s} \right) - \left( {2b + 1} \right)wc}}{{2b^{2} }} < 0$; If $w_{c} < \frac{{b\left( {k + q + s} \right) + a\left( {1 + b} \right)}}{1 + 2b}$, $\pi_{NO}^{M} = \frac{{\left( {k + q + s - a} \right)^{2} }}{{4\left( {1 + 2b} \right)}}$, $\frac{{d\left( {\pi_{NO}^{M} } \right)}}{dk} = \frac{{d\left( {\pi_{NO}^{M} } \right)}}{dq} = \frac{{d\left( {\pi_{NO}^{M} } \right)}}{ds} = \frac{{2\left( {k + q + s - a} \right)}}{{4\left( {1 + 2b} \right)}} > 0$, $\frac{{d\left( {\pi_{NO}^{M} } \right)}}{da} = 0$, $\frac{{d\left( {\pi_{NO}^{M} } \right)}}{da} = - \frac{{2\left( {k + q + s - a} \right)}}{{4\left( {1 + 2b} \right)}} < 0$, $\frac{{d\left( {\pi_{NO}^{M} } \right)}}{db} = - \frac{{\left( {k + q + s - a} \right)^{2} }}{{2\left( {1 + 2b} \right)^{2} }} < 0$, $\frac{{d\left( {\pi_{NO}^{M} } \right)}}{{dw_{c} }} = 0$.

We then focus on the farmer’s profit change when the manufacturer switches from one strategy to another. First, we apply Lemmas 1–3 and Corollary 1 to derive the farmer’s equilibrium profit.

• (i) $\pi_{FC}^{F} = \left( {w_{FC} - a} \right) \cdot \frac{{k - w_{FC} + \delta_{FC} }}{2} = \frac{{\left( {k - a + s} \right)^{2} }}{4}$.

• (ii) $\pi_{FO}^{F} = \frac{{\left( {k + \delta_{FO} - a} \right)^{2} }}{{4\left( {2 + b} \right)}} = \frac{{\left( {k + q + \alpha s - a} \right)^{2} }}{{4\left( {2 + b} \right)}}$.

• (iii) $\pi_{NC}^{F} = \frac{{\left( {w_{c} - a} \right)\left( {k - w_{c} } \right)}}{2}$.

• (iv) If $w_{c} \ge \frac{{b \left( {k + q + s} \right) + a}}{1 + b}$, $Q_{NO}^{*} = \frac{{k - w_{NO} + \delta_{NO} }}{2}$, $\pi_{NO}^{F} = \frac{1}{2}\left( {k + q + s - w_{c} } \right) \cdot \left[ {w_{c} - a - \frac{b}{2}\left( {k + q + s - w_{c} } \right)} \right]$; When $w_{c} < \frac{{b \left( {k + q + s} \right) + a}}{1 + b},Q_{NO}^{*} = \frac{{w_{NO}^{*} - a}}{2b}$, $\pi_{NO}^{F} = \frac{{\left( {w_{NO}^{*} - a} \right)^{2} }}{4b}$, so if $\frac{{b\left( {k + q + s} \right) + a\left( {1 + b} \right)}}{1 + 2b} \le w_{c} < \frac{{b \left( {k + q + s} \right) + a}}{1 + b}$, $\pi_{NO}^{F} = \frac{{\left( {w_{c} - a} \right)^{2} }}{4b}$; If $w_{c} < \frac{{b\left( {k + q + s} \right) + a\left( {1 + b} \right)}}{1 + 2b}$, $\pi_{NO}^{F} = \frac{{b\left( {k + q + s - a} \right)^{2} }}{{4\left( {1 + 2b} \right)^{2} }}$.

We then examine the farmer’s profit change when the manufacturer switches from NC to NO. As stated in proof of Proposition 1, when $k1 \le k < k2$, the switch point is $wc1$, farmer’s corresponding profit in the switch point is $\pi_{NO}^{F} = \frac{{b\left( {k + q + s - a} \right)^{2} }}{{4\left( {1 + 2b} \right)^{2} }}$, $\pi_{NC}^{F} = \frac{{\left( { - a + k + q + s} \right)\left( { - a + k - \frac{ - a + k + q + s}{{\sqrt {1 + 2b} }}} \right)}}{{2\sqrt {1 + 2b} }}$. We set $\hat{k}_{1} = a - \frac{{\sqrt {1 + 2b} \left( {2 + 5b} \right)\left( {q + s} \right)}}{{2\left( { - 1 + \sqrt {1 + 2b} } \right) + b\left( { - 8 - 8b + 5\sqrt {1 + 2b} } \right)}}$ and derive that when $\hat{k}_{1} < k < k2$, $\pi_{NC}^{F} > \pi_{NO}^{F}$; when $k1 \le k \le \hat{k}_{1}$, $\pi_{NC}^{F} < \pi_{NO}^{F}$. If $k \ge k2$, the switch point $wc2$, comparing the farmer’s corresponding profit in the switch point, we can derive that $\pi_{NC}^{F} > \pi_{NO}^{F}$. So, when $k1 \le k \le \hat{k}_{1}$, $\pi_{NC}^{F} < \pi_{NO}^{F}$; $k > \hat{k}_{1}$, $\pi_{NC}^{F} > \pi_{NO}^{F}$.

We continue to examine the farmer’s profit change when the manufacturer switches from NO to FC. Note that $0 \le b < b2$, which corresponds to $k < a - s + \frac{2q}{b - 1}$. And the switch point is $wc6$, farmer’s corresponding profit at the switch point is $\pi_{NO}^{F} = \frac{1}{16}\left( {k - a + s} \right)\left( {\left( {2 - b} \right)\left( {k - a + s} \right) + 4q} \right)$, $\pi_{FC}^{F} = \frac{{\left( {k - a + s} \right)^{2} }}{8}$. Comparing the farmer’s profit at the switch point, we obtain that $\pi_{NO}^{F} > \pi_{FC}^{F}$ if $b > 2$. If $b \le 2$, $\pi_{NO}^{F} \ge \pi_{FC}^{F}$ when $k \le a - s + \frac{4q}{b}$; $\pi_{NO}^{F} < \pi_{FC}^{F}$ when $k > a - s + \frac{4q}{b}$. When $b2 \le k < b1$, we can derive that if $b \le 2$, $\pi_{NO}^{F} \le \pi_{FC}^{F}$; If $b > 2$, $\pi_{NO}^{F} \ge \pi_{FC}^{F}$ when $k \le a - s + \frac{4\sqrt 2 \sqrt b q}{2 - 4\sqrt 2 \sqrt b + 5b}$; $\pi_{NO}^{F} < \pi_{FC}^{F}$ when $k > a - s + \frac{4\sqrt 2 \sqrt b q}{2 - 4\sqrt 2 \sqrt b + 5b}$. So, the threshold value $\hat{k}_{2} = a - s + \frac{4q}{b}$ for $0 < b \le 2$; and $\hat{k}_{2} = a - s + \frac{{4\sqrt {2b} q}}{{2 - 4\sqrt {2b} + 5b}}$ for $b > 2$. Then, when $k \le \hat{k}_{2}$, $\pi_{NO}^{F} \ge \pi_{FC}^{F}$; $k > \hat{k}_{2}$, $\pi_{NO}^{F} < \pi_{FC}^{F}$.

We continue to examine the farmer’s profit change when the manufacturer switches from NC to FO. When the manufacturer switches from NC to FO when $\alpha \ge \alpha 2$ and the switch point is $wc7$, the farmer’s corresponding profit at the switch point is $\pi_{NC}^{F} = \frac{{\left( {a - k - q - s\alpha } \right)\left( {a\left( {1 + b} \right) - \left( {1 + b} \right)k + q + s\alpha } \right)}}{{2\left( {2 + b} \right)^{2} }}$, $\pi_{FO}^{F} = \frac{{\left( {k + q + s\alpha - a} \right)^{2} }}{{4\left( {2 + b} \right)}}$.$\pi_{NC}^{F} - \pi_{FO}^{F} = \frac{{\left( {a - k - q - s\alpha } \right)\left( {4\left( {q + s\alpha } \right) + b\left( {a - k + q + s\alpha } \right)} \right)}}{{4\left( {2 + b} \right)^{2} }}$ is decreasing in $\alpha$, when $\alpha \ge \alpha 2$, $\pi_{NC}^{F} < \pi_{FO}^{F}$.

We now examine the farmer’s profit change when the manufacturer switches from NO to FO. From the farmer’s profit function, we can obtain that in the NO scenario, the farmer can achieve his maximum profit $max\left( {\pi_{NO}^{F} } \right) = \frac{{\left( { - a + k + q + s} \right)^{2} }}{{4\left( {2 + b} \right)}}$ when $w_{c} = \frac{a + k + bk + q + bq + s + bs}{2 + b}$. While $max\left( {\pi_{NO}^{F} } \right) \le \frac{{\left( {k + q + s\alpha - a} \right)^{2} }}{{4\left( {2 + b} \right)}} = \pi_{FO}^{F}$, then $\pi_{FO}^{F}$ always dominates $\pi_{NO}^{F}$.□

Proof of Proposition 3

As stated in Proposition 2, $\pi_{FO}^{F}$ always dominates $\pi_{NO}^{F}$, then the farmer will never choose the NO strategy. And $\pi_{NC}^{F} = \frac{{\left( {w_{c} - a} \right)\left( {k - w_{c} } \right)}}{2} \le \frac{{\left( {k - a} \right)^{2} }}{4} \le \pi_{FC}^{F}$, so the farmer also will never choose the NC strategy. As such, win–win scenarios arise only when the manufacturer participates in fair trade.

• (i) When the manufacturer chooses the FO strategy, $\pi_{FO}^{M} \ge \pi_{FC}^{M}$, which is equivalent to $\alpha \ge \alpha_{1} = \frac{ - ab + bk - 2q + 2s + bs}{2s}$. From the manufacturer’s profit function, we can know that $\pi_{FO}^{M} \ge \pi_{FC}^{M}$ equals to $\frac{{\left( {k + q + \alpha s - a} \right)^{2} }}{{4\left( {b + 2} \right)^{2} }} \ge \frac{{\left( {k - a + s} \right)^{2} }}{16}$, which is equivalent to $\frac{{\left( {k + q + \alpha s - a} \right)^{2} }}{{4\left( {b + 2} \right)}} \ge \frac{{\left( {b + 2} \right)\left( {k - a + s} \right)^{2} }}{16} \ge \frac{{\left( {k - a + s} \right)^{2} }}{8}$, so $\pi_{FO}^{F} \ge \pi_{FC}^{F}$. Then when $\alpha \ge \alpha_{1}$, FO is a win–win scenario.

• (ii) When the manufacturer chooses the FC strategy, $\pi_{FC}^{M} \ge \pi_{FO}^{M}$, which is equivalent to $\alpha < \alpha_{1}$. The condition that the farmer will choose the FC strategy is $\alpha < \alpha_{2} = \frac{{2a - 2\left( {k + q} \right) + \sqrt {2\left( {2 + b} \right)} \left( {k - a + s} \right)}}{2s}$, where $\alpha_{2} < \alpha_{1}$. Then when $\alpha < \alpha_{2}$, FC is a win–win scenario.□