Abstract
This paper analyzes the valuation and pricing of physical electricity delivery contracts from the viewpoint of a producer with given capacities for production and fuel-storage. Using stochastic optimization problems in discrete time with general state space, the dual problems of production problems are used to derive no-arbitrage conditions for fuel and electricity prices as well as superhedging values and prices of bilaterally traded electricity delivery contracts. In particular we take the perspective of an electricity producer, who serves contractual deliveries but avoids unacceptable losses. The resulting no-arbitrage conditions, stochastic discount factors and superhedging prices account for typical frictions like limitation of storage and production capacity and for the fact that it is possible to produce electricity from fuel, but not to produce fuel from electricity. Similarities, but also substantial differences to purely financial results can be demonstrated in this way. Furthermore, using acceptability measures, we analyze capital requirements and acceptability prices for delivery contracts, when the producer accepts some risk.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This work aims at the analysis of valuation and pricing for electricity delivery contracts, bilaterally traded between a producer and a consumer of delivered electrical energy. On the one hand valuation and pricing of contracts is a typical problem from finance, and therefore many authors apply classical financial results in a direct way to pricing and valuation of electricity contracts, see e.g. most chapters and cited literature in Eydeland and Wolyniec (2003). Clearly this is also an important option for practical applications. On the other hand, electricity markets show many frictions, not present at financial or other commodity markets. From this point of view, one should be careful about applying well known results from other markets to electricity markets.
In this paper we use an alternative approach and consider pricing and valuation as decision problems closely related to production decisions of an electricity producer. The producer is able to generate electricity from fuel (within certain physical constraints) and faces random spot prices for electricity and fuel. When entering into a contract for delivering some load pattern of power consumption, the producer has to fix a delivery price (or a value for a contract with given delivery price) and later on takes further decisions on power production and buying and/or selling fuel and electricity at the markets. The aim here is to meet all contractual obligations and to end up with an acceptable wealth (asset value) at the end.
We analyze a number of stochastic optimization formulations in discrete time but possibly continuous state space. Similar problems have already been treated numerically in e.g. Vayanos et al. (2011) and Kovacevic and Paraschiv (2014). However, in the present paper we want to give a deeper theoretical analysis of the properties of prices and values obtained in such a way. The main results are derived from the Lagrange duals of the underlying production problems. In particular it turns out that—based on this dualization—similarities and distinctions between classical financial results and prices obtained from production problems can be analyzed in a convenient way.
1.1 Some financial background
The notions of arbitrage and market completeness—cornerstones of modern finance—are relevant also in our context. A market is arbitrage free if riskless profits are possible and it is complete if any relevant payoff can be replicated from the underlying securities, contracts or commodities, traded at this market. Essentially, a financial market is arbitrage free if and only if there exists an equivalent (local) martingale measure \({\mathbb {Q}}\), such that all underlying securities can be priced correctly by taking expectation under the equivalent measure, i.e. the underlying’s price \(S_{t}\) fulfills \(S_{t}={\mathbb {E}}_{t}^{{\mathbb {Q}}}\left[ e^{r\!(T-t)}S_{T}\right] \). An arbitrage free market is complete if and only if there is a unique equivalent martingale measure. See e.g. Delbaen and Schachermayer (1994, 1998) for more detailed statements and proofs. In complete markets, every contingent claim is attainable by hedging portfolios, and financial derivatives can be priced by calculating the expected discounted value of the derivatives payoff w.r.t. the unique martingale measure. Briefly sketched, in the situation of a complete market (and constant interest rate), at time t the value \(p_{t}(\cdot )\) of a claim receivable at time T, can be calculated as the expectation
where \({\mathbb {Q}}\) denotes the unique martingale measure related to the process \(X_{t}\). The same value can also be expressed in terms of the physical measure \({\mathbb {P}}\) by using a (likewise unique) stochastic discount factor \(\xi _{T}\) closely related to the risk neutral measure \({\mathbb {Q}}\), i.e.
On incomplete markets, not every contingent claim can be attained by hedging with traded assets. Still, under no-arbitrage there exist equivalent martingale measures (respectively stochastic discount factor processes) and at least one of them, \(Q^{*}\) (respectively \(\xi ^{*}\)) fulfills (1) [respectively (2)]. Although, \(Q^{*}\) is not known in advance (there is no unique martingale measure) and the value \(p_{t}\) therefore cannot be calculated just from (1) or (2), it is possible to calculate the minimal and the maximal discounted expectation under all expectations w.r.t. any equivalent martingale measure, the lower and upper arbitrage bounds. If the analyzed security is traded at an exchange, one can try to estimate the market price of risk, which leads to a price within the arbitrage bounds. For bilaterally traded contracts this is not possible because data are not easily available. Because the interval defined by arbitrage bounds can be quite large, several methods for finding reasonable bounds on prices for incomplete markets have been developed. Classical financial approaches are discussed e.g. in Hao (2008). Important alternatives are good deal bounds (Cochrane and Saá-Roquejo 2000), local risk minimization (Pansera 2012) or convex hedging (Rudloff 2007). Such methods search for stochastic discount factors with restricted or minimal risk, where the exact notion of risk is different for each approach. Basically this leads to optimization of the expectation (1) or (2) with respect to the measure \({\mathbb {Q}}\) or the discount factor \(\xi _{T}\), where \({\mathbb {Q}}\) or \(\xi _{T}\) are restricted to ensure absence of arbitrage.
1.2 From finance to energy markets
In the present paper we leave the sphere of purely financial markets and analyze bilaterally traded electricity delivery contracts from the viewpoint of an electricity producer. Electricity markets nowadays are very liquid and in many regards comparable with financial markets. Therefore, absence of arbitrage seems to be reasonable. On the other hand it is well known that electricity markets are incomplete with unique frictions, not existent on financial markets (or on other commodity markets). In particular, electricity is produced from fuels but cannot be converted back to fuels. Moreover, electricity cannot be stored in large quantities (as would be possible commodities like e.g. oil or gas). Therefore produced and used electric power has to be balanced immediately in an electrical network, because differences between demanded and produced power may lead to damaged equipment or even breakdown of the net. Furthermore, all kinds of restrictions on physical fuel storage and generation capacity are relevant for the production process. Some sub-markets for electricity (in particular futures markets) are organized as financial markets, but even in this case the delivery profiles of traded futures [although hedging by futures contracts is an important approach in practice, see e.g. Deng et al. (2001)] cannot fully replicate typical bilaterally-traded delivery profile.
We start our analysis with a study of arbitrage and ask the question: Given the above frictions, how can we characterize arbitrage in a simple market model with electricity produced from fuel? In particular we search for analogues to equivalent martingale measures and the related stochastic discount factors in the context of fuel and electricity prices. Later on, absence of arbitrage (respectively its characterization) is also used as a technical condition for strong duality, on which most of the pricing and valuation results are based.
Based on our analysis of arbitrage we proceed to valuation and pricing of electricity delivery contracts, which is our main goal. Due to incompleteness and the frictions discussed above it is not possible to calculate a unique market price from observable data. It may not even be possible to observe market prices for certain bilaterally traded contracts. In this situation we take the viewpoint of an electricity producer and analyze several types of valuation and pricing principles.
When a producer aims at finding a price or a value of a delivery contract, he has to account for his production possibilities. This may comprise e.g. the used generators and their characteristics and the size and costs of fuel storage. Moreover, all price/value decisions should be taken with the optimal use of the equipment in view. Therefore the pricing/valuation problems in this paper (their primal formulation) are similar to typical planning problems for electricity production.
Optimization for electricity production has been discussed in literature over a long time and is used as a practical planning tool by generating companies. While deterministic optimization is still an important option, in view of the random nature of energy prices, stochastic optimization models are increasingly used. Without by any means claiming to be exhaustive, we mention Takriti et al. (1996), Gollmer et al. (2000), Philpott and Schultz (2006), Sen et al. (2006), Sagastizabal (2012), Kovacevic and Paraschiv (2014) and Zephyr and Anderson (2018), the overview Wallace and Fleten (2003) and the collections Bertocchi et al. (2011) and Kovacevic et al. (2013). A multitude of numerical solution approaches has been applied in the cited paper, e.g. tree based stochastic programming, Lagrange decomposition methods and approximate dynamic programming. In the present paper we aim at analytical results in a very general setup and use the related duality theory as our main tool. However, in the last section we sketch the implementation and numerical results for an illustrative valuation example, using tree based stochastic programming.
When valuating a specified contract with a stochastic process of deliveries and a fixed delivery price, it is reasonable for the producer to look at the smallest value or up-front payment such that all contractual obligations can be satisfied at the given delivery price, and the asset value (consisting of cash and the value of fuel) at the end of the planning horizon is for sure not negative. In this way the producer is able to find the smallest up-front payment at which he is able to contract a delivery pattern at a given price without the risk of a loss. This approach resembles what is called superhedging in finance and therefore we call the resulting value the superhedging value. The method can also be applied to pricing by searching for the smallest delivery price such that, starting with an asset value of zero, all contractual obligations can be fulfilled with a nonnegative end value. Here the producer finds the smallest delivery price at which he is able to contract a given pattern without any upfront payment. Still there will be no risk of any loss. The resulting price is the superhedging price of the contract. Superhedging prices are not market prices (as superhedging values are not market values) but mark an important boundary: if delivery is agreed at a smaller price (or the producer starts with cash reserve smaller than the superhedging value), the producer definitely has to take some risk.
Superhedging values and superhedging prices depend on the production equipment but do not depend on the preferences of the producer. They are very loose boundaries for feasible upfront payments (cash reserves) or delivery prices, because if a payment or price within these boundaries is contracted, any risk of a negative end value is eliminated. In practical situations however, producers usually are willing to take some risk in order to achieve potentially higher profit. We therefore also analyze the smallest upfront payment leading to an acceptable distribution of the end value as well as the smallest delivery price that leads to an acceptable distribution of the end value when starting at zero capital. In the first case (following Pennanen 2012) we speak of the capital requirement. The delivery price in the second case will be called the acceptability price. In the present paper we measure acceptability by concave acceptability functionals, see e.g. Pflug and Römisch (2007) [and Kovacevic (2012) for conditional versions] , which are (up to sign) closely related to coherent risk measures, Artzner et al. (1999).
Again, capital requirements and acceptability prices are not market figures. They depend on the production equipment and preferences with respect to risk of the producer and define another boundary: if the delivery price is agreed below, the producer will either not enter the contract or has to accept a less acceptable outcome than originally intended. In a competitive situation this means that producers with lower efficiency might be driven out of the market by participants with higher efficiency, because the latter are able to deliver at small prices and still keep acceptable outcome distributions.
1.3 Back to finance?
We formulate these production-based valuation and pricing problems in terms of stochastic optimization in discrete time with general state space.
Subsequently, we use duality theory for cone constraint optimization in Banach spaces to derive Lagrange dual problems. This allows for analyzing further the properties of superhedging prices and values, as well as of capital requirements and acceptability prices. The approach is consistent with basic financial principles: similar methods have been applied to purely financial problems e.g. in King (2002) and Flåm (2008), where it was shown that classical results on no-arbitrage pricing can be replicated in a discrete time, discrete state space stochastic optimization framework. In particular dual formulations can be used to characterize no-arbitrage and to derive the classical risk-free pricing results and arbitrage bounds. Pennanen (2011a, b) analyzes superhedging in a very general framework. In addition, Pennanen (2012) derives basic facts of capital requirements and acceptability pricing (in particular indifference pricing, see Remark 3.3 below) in the context of convex analysis. Again both papers are aim at a purely financial context.
Superhedging on (incomplete) electricity markets has been applied from a modeling perspective and with numerical results in Vayanos et al. (2011), which however does not consider production and storage. Numerical superhedging for delivery contracts with electricity production and storage was applied in Kovacevic and Paraschiv (2014).
Concrete no-arbitrage conditions and pricing principles are derived in the complex situation with storage and production restrictions (e.g. random outages of generators), asymmetric production possibilities between fuel and electricity, and non-storability of electricity. These results allow comparisons with the purely financial situation. In particular it turns out that it is still meaningful to speak about arbitrage, stochastic discount factors and equivalent measures and some of the results can be interpreted in a generalized context of good deal bounds. However the concrete formulation, in particular the requirements for discount factors or equivalent measures deviate severely from classical financial results.
The details are worked out in the following sections as follows: Sect. 2 uses a basic optimization problem to derive and analyze no-arbitrage conditions for a model with spot prices for fuel and electricity, when electricity can be produced with given efficiency. In the main part, Sect. 3, the optimization problem of a minimum up-front payment for a delivery contract is used to derive valuation formulas in terms of stochastic discount factors and equivalent measures. As a second application we analyze the smallest feasible delivery price. In both cases we aim at almost surely nonnegative end value. Finally we relax this requirement and consider the minimum capital requirement and the acceptability price. In Sect. 4 we give a numerical example, analyzing the superhedging value and its sensitivity to parameter changes in the context of a stylized vector-autoregressive price model. Section 5 concludes the paper.
2 No-arbitrage conditions
In the following all relevant risk factors (in particular prices) and the related decisions are considered as stochastic processes, defined on a filtered probability space \(\mathfrak {Y=}\left( \varOmega ,\mathcal {{\mathcal {F}}},{\mathfrak {F}}=\left\{ {\mathcal {F}}_{t}\right\} _{t\ge 0},{\mathbb {P}}\right) \) in discrete time \(t=0,1,\ldots ,T\). For simplicity we use constant time increments, e.g. hours, days or weeks. However, all statements can easily be adapted to more general time models. Time zero represents here and now and the related \(\sigma \)-algebra \({\mathcal {F}}_{0}\) is the trivial \(\sigma \)-algebra \({\mathcal {F}}_{0}=\left\{ \emptyset ,\varOmega \right\} \). Time T denotes the end of the planning horizon. In order to simplify notation we use the sets \({\mathcal {T}}=\{0,1,\ldots ,T\}\), \({\mathcal {T}}_{0}=\{0,1,\ldots ,T-1\}\), \({\mathcal {T}}_{1}=\{1,\ldots ,T\}\) and \({\mathcal {T}}_{1}^{T-1}=\left\{ 1,\ldots ,T-1\right\} \).
As the basic stochastic risk factors, we consider fuel prices and electricity prices at some power exchange (implicitly assuming that market participants are price takers with little market power). Prices observed at points in time t and represented by real valued stochastic processes \(X_{t}^{f}(\omega )\) for fuel and \(X_{t}^{e}(\omega )\) for electricity, both adapted to the filtration \({\mathfrak {F}}\). Fuel prices are assumed to be almost surely nonnegative, whereas electricity prices may also take negative values with positive probability. Both prices are given in currency units per MWh. Note that it is not assumed that the filtration \({\mathfrak {F}}\) is necessarily generated by the price processes \(X_{t}^{f}\) and \(X_{t}^{e}\): additional information like e.g. prices of further fuels, weather, or general business activity may play a role.
The producer is able to generate electrical energy from fuel with efficiency \(\eta >0\). For simplicity we measure quantities of electric energy and quantities of fuel (the related energy content) both in MWh. At time t, immediately before taking all decisions, the producer owns a cash position \(c_{t}\) with a fixed interest rate \(r\ge 0\) (per period) and an amount of fuel \(s_{t}\) [MWh]. We will also use the notation \(R=(1+r)\). The producer then (still at time t) makes his decisions. First he decides the amount \(z_{t}\) [MWh] of fuel traded at the fuel market at price \(X_{t}^{f}\) [currency units per MWh]. This trade happens at (or immediately after) time t. Positive values of \(z_{t}\) indicate that an amount of fuel is bought, negative values indicate a selling of fuel. Then the amount \(y_{t}\) [MWh] of electricity produced over the period \([t,t+1]\) decided. It is sold at time \(t+1\) at price \(X_{t+1}^{e}\), immediately before observing the new cash position. The amount of fuel burned for electricity production then is given by \(\eta ^{-1}y_{t}\) [MWh].
The decision processes \(y_{t}\) and \(z_{t}\) as well as the decision processes \(c_{t}\) and \(s_{t}\) are considered as real valued random processes defined on \({\mathfrak {Y}}\) and adapted to the filtration \({\mathfrak {F}}\). This means that decisions at time t have to rely on information available at time t. Other specifications may be possible, but as sketched above in the present paper we assume that fuel \(z_{t}\) is bought at time t at a known fuel price \(X_{t}^{f}\). On the other hand we assume that electricity production over the period \(\left[ t,t+1\right] \) is planned in advance at time t but the electricity price \(X_{t+1}^{e}\)(currency units per MWh) at which the planned amount is sold is revealed only at the end, \(t+1\), of the period. Keep in mind that \(c_{0},s_{0},y_{\text {0}},z_{0}\) are deterministic, as \({\mathcal {F}}_{0}\) is assumed to be the trivial \(\sigma \)-algebra.
In the following, all equations involving random variables are understood in the sense of holding almost surely. Furthermore, all inequalities are considered as inequalities with respect to the cone of almost surely nonnegative random variables. Fuel prices and electricity prices are assumed to be essentially bounded and all decision variables are considered as integrable. More precisely, we assume \(X_{t}^{f},X_{t}^{e}\in L^{\infty }\left( \varOmega ,{\mathcal {F}}_{t},{\mathbb {P}}\right) \) and \(y_{t},z_{t},c_{t},s_{t}\in L^{1}\left( \varOmega ,{\mathcal {F}}_{t},{\mathbb {P}}\right) \) with state space \(\varOmega \), \(\sigma \)-algebra \({\mathcal {F}}_{t}\) and probability measure \({\mathbb {P}}\) as discussed above. Here \(L^{1}\left( \varOmega ,{\mathcal {F}}_{t},{\mathbb {P}}\right) \) denotes the space of integrable random variables, defined on the probability space \(\left( \varOmega ,{\mathcal {F}}_{t},{\mathbb {P}}\right) \). This means that \(y_{t}(\omega ),z_{t}(\omega ),c_{t}(\omega ),s_{t}(\omega )\) are defined for \(\omega \in \varOmega ,\) are measurable with respect to \({\mathcal {F}}_{t}\), and their expectations under the measure \({\mathbb {P}}\) is finite. Moreover, \(L^{\infty }\left( \varOmega ,{\mathcal {F}}_{t},{\mathbb {P}}\right) \) denotes the space of essentially bounded random variables, defined on the probability space \(\left( \varOmega ,{\mathcal {F}}_{t},{\mathbb {P}}\right) \). If a random variable Y belongs to the space \(L^{\infty }\left( \varOmega ,{\mathcal {F}}_{t},{\mathbb {P}}\right) \), then it is \({\mathcal {F}}_{t}\)-measurable and there exists a bounded \({\mathcal {F}}_{t}\)-measurable random variable Z, such that Y and Z may take different values only on a set with \({\mathbb {P}}\)-probability zero.
With this specification the left hand side of all equations and inequalities in this paper (when brought into standard form \(g(y_{t},z_{t},c_{t},s_{t})\le 0\)) take values in \(L^{1}(\varOmega ,{\mathcal {F}}_{t},{\mathbb {P}})\). Therefore it is possible to apply arguments from optimization in vector (Banach) spaces and related duality arguments to the production-based valuation problems discussed later, see e.g. Luenberger (1969) and Bot et al. (2009) for the theoretical background. In particular, when duality arguments are applied, the Lagrange multipliers are chosen from \(L^{\infty }\left( \varOmega ,{\mathcal {F}}_{t},{\mathbb {P}}\right) \), which can be identified with the dual space of \(L^{1}\left( \varOmega ,{\mathcal {F}}_{t},{\mathbb {P}}\right) \).
For physical reasons, electricity production \(y_{t}\) and fuel storage \(s_{t}\) are almost surely restricted to nonnegative values. We do not use storage for electrical energy, see the discussion on frictions at electricity market above.
This basic setup will be extended later, when we consider the full production problem and contractual deliveries and delivery prices are introduced. In particular, then it will be necessary to account for upper bounds on production and storage. For the moment however, we use it as it is to derive no-arbitrage conditions. Extending the usual Definitions (see e.g. Björk (2009) Definitions 2.14, 2.15 in a financial context, and Vayanos et al. (2011) on electricity markets, but still without fuel storage) we now define self financing strategies and arbitrage. Self financing strategies basically are strategies without external in- or outflows of money and (in our case) fuel: storage is changed only by buying from the market and burning fuel for production and the cash position is changed by paying for fuel, selling electricity to the market and interest on cash.
Definition 1
In the basic model, a strategy \(\left\{ y_{t},z_{t}\right\} _{t\ge 0}\) with cash position \(c_{t}\) and fuel storage \(s_{t}\), where \(y_{t}\ge 0\) and \(s_{t}\ge 0\), is self financing if the following conditions hold almost surely for all \(t\in {\mathcal {T}}_{1}\):
At any time t the asset value of a strategy is given by
Remark 1
Slightly abusing common usage, we use the term asset value for the sum of the cash position and the storage value (mark to market) and exclude the (fixed) value of the generator.
A market allows arbitrage, if there exists a strategy with riskless profit, in particular if there is a strategy that starts at a nonpositive value but leads to a nonnegative end value with probability one which is even positive with positive probability. In case of electricity markets the possibility of arbitrage depends on the available technology (efficiency) and can be formulated as follows:
Definition 2
An \(\eta \)-arbitrage for a market \(\left\{ X_{t}^{e},X_{t}^{f}\right\} \) is a self financing strategy \(\left\{ y_{t},z_{t}\right\} _{t\ge 0}\) with
We call a market \(\left\{ X_{t}^{e},X_{t}^{f}\right\} \)\(\eta \)-arbitrage free, if no \(\eta \)-arbitrage exists. A market \(\left\{ X_{t}^{e},X_{t}^{f}\right\} \) is arbitrage free if it is \(\eta \)-arbitrage free for any \(0\le \eta \le \eta _{max}\), where \(\eta _{max}\) denotes the maximum efficiency available to the producers.
Remark 2
Clearly an \(\eta \)-arbitrage free market is \(\eta ^{\prime }\)-arbitrage free for any \(\eta ^{\prime }\le \eta \).
Based on the previous definitions and assumptions, the following optimization problem can be used to detect the existence of an arbitrage strategy.
Remark 3
In order to avoid too much numbering, we refer to parts of the constraint sets as “constraint groups”. As an example, the first line of constraints in (8) will be referred to as “constraint group 1”.
Remark 4
The set of feasible solutions is not empty for problem (8), because setting all decision variables to zero is feasible. This also implies that the feasible set is a pointed cone.
It might sound strange that test problem (8) is formulated without upper bounds on storage and production. However, because of positive homogeneity, a strategy which leads to a positive end value with positive probability can be scaled in a way such that either the scaled solution leads to an infinite expectation without upper bounds or such that all upper bounds are observed and at least one upper bound is reached with positive probability at some point in time. Therefore for a pure test of \(\eta \)-arbitrage the upper bounds are not relevant.
The following observation is a key to characterizing \(\eta \)-arbitrage.
Lemma 1
An \(\eta \)-arbitrage for a market \(\left\{ X_{t}^{e},X_{t}^{f}\right\} \) exists if and only if (8) is unbounded.
Proof
The first two constraints of (8) correspond to Conditions (3) and (4) for a self financing portfolio. The third and fourth constraints enforce Conditions (5) and (6). The last two constraints are the nonnegativity constraints on electricity production and fuel storage. Because of (6) , \({\mathbb {E}}^{{\mathbb {P}}}\left[ c_{T}+X_{t}^{f}s_{T}\right] >0\) if and only if \(c_{T}+X_{T}^{f}s_{T}>0\) on a set with positive probability. Furthermore, because the objective function and the constraints are positively homogeneous in the decision variables \(\left\{ y_{t},z_{t},c_{t},s_{t}\right\} \), the optimal value is unbounded if and only if a positive expectation can be fulfilled by a feasible strategy. Hence Conditions (5)–(7) can be achieved by a self financing strategy if and only if problem (8) is unbounded.\(\square \)
We can now apply duality theory to problem (8) in order to characterize arbitrage further.
Lemma 2
A market \(\left\{ X_{t}^{e},X_{t}^{f}\right\} \) is \(\eta \)-arbitrage free in the described setup if and only if there exist adapted stochastic processes \(\left\{ \xi _{t},\lambda _{t}\right\} \) with the following properties:
-
A1:
For each \(t\in {\mathcal {T}}_{1}\) the random variables \(\xi _{t}, \lambda _{t}\in L^{\infty }(\varOmega ,{\mathcal {F}}_{t},{\mathbb {P}})\).
-
A2:
\(\xi _{T}>0\) and \(\lambda _{T}\ge X_{T}^{f}\cdot \xi _{T}\)
-
A3:
\(R\,{\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{t+1}|{\mathcal {F}}_{t}\right] =\xi _{t}\) for \(t\in {\mathcal {T}}_{1}^{T-1}\), and \(R\,{\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{1}\right] =1\)
-
A4:
\({\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{t+1}X_{t+1}^{e}|{\mathcal {F}}_{t}\right] \le \eta ^{-1}X_{t}^{f}\xi _{t}\) for \(t\in {\mathcal {T}}_{0}\)
-
A5:
\({\mathbb {E}}^{{\mathbb {P}}}\left[ \lambda _{t+1}|{\mathcal {F}}_{t}\right] =X_{t}^{f}\xi _{t}\) for \(t\in {\mathcal {T}}_{0}\)
-
A6:
\({\mathbb {E}}^{{\mathbb {P}}}\left[ \lambda _{t+1}|{\mathcal {F}}_{t}\right] \le \lambda _{t}\) for \(t\in {\mathcal {T}}_{1}^{T-1}\)
Proof
The Lagrangian of (8) is given by
where \(\gamma \ge 0\) is a real number, \(\zeta \ge 0\) a \({\mathcal {F}}_{T}\)-measurable essentially bounded random variable, \(\xi _{t}\) and \(\lambda _{t}\) are \({\mathcal {F}}_{t}\)-measurable and essentially bounded, i.e. \(\zeta \in L^{\infty }(\varOmega ,{\mathcal {F}}_{T},{\mathbb {P}})\) and \(\xi _{t},\lambda _{t}\in L^{\infty }(\varOmega ,{\mathcal {F}}_{t},{\mathbb {P}})\).
After some reordering, (9) can be rearranged as follows:
Using (10), the tower property of conditional expectation and keeping in mind \(y_{t},s_{t}\ge 0\), the dual function
is bounded (in fact zero almost surely) if and only if the following conditions hold:
Hence, the dual problem is a feasibility problem and (by weak duality) it follows that the original problem is unbounded if and only if conditions (12)-(23) hold.
Equations (18) and (22), respectively (19) and (23) can be consolidated to
if the fact that \({\mathcal {F}}_{0}\) is the trivial \(\sigma \)-algebra is taken into account.
From (12) and (13) we can infer \(\xi _{T}\ge 1>0\). Applying (20) recursively and keeping in mind \(R>0\), it follows that
for \(t\in {\mathcal {T}}_{1}\). Immediately we get
from (16).
Therefore it is possible to divide inequalities by \(\gamma \) without changing their direction. It follows that processes \(\xi ^{\prime }\) and \(\lambda ^{\prime }\) fulfill the system (12)–(23) if and only if the processes \(\xi _{t}=\frac{\xi _{t}^{\prime }}{\gamma }\) and \(\lambda _{t}=\frac{\lambda _{t}^{\prime }}{\gamma }\) fulfill the modified system
(31) is superfluous. Clearly, from (29) and (30) we have \(\lambda _{T}\ge \xi _{t}X_{t}^{f}\). Furthermore, (28) and (27) are equivalent to \(\xi _{T}>0\). Together this gives property A2 of the Lemma. Equations (32) and (36) lead to property A3 and (37) is property A6.
It turns out that (33) is automatically fulfilled and can therefore be omitted: Using (35) it is possible to replace \({\mathbb {E}}^{{\mathbb {P}}}\left[ \lambda _{1}\right] \) by \({\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{1}\right] X_{0}^{f}\) in (33). Furthermore
can be inferred from (36). Together this leads to
which is a tautology, given that \(R\ge 1\) and \(X_{0}^{f}\) are nonnegative.
Finally, we see that property A4 and (34) are equivalent if (35) holds (and A3 is applied). Hence all properties, A1–A6, of the Lemma can be derived from the Lagrangian of the test problem.
Note also that
holds for \(t=0,\ldots ,T-1\) (and \(\lambda _{T}>0\)) because of \(X_{t}^{f}\ge 0\) and A2, A6. \(\square \)
So far we have characterized arbitrage in terms of (rescaled) shadow prices \(\xi _{t}\) and \(\lambda _{t}\). However, this representation can also be used to derive no-arbitrage conditions in terms of equivalent martingale measures. In the financial context arbitrage is not possible, if equivalent martingale measures exist. For electricity and fuel the no-arbitrage conditions are more complicated.
Proposition 1
A market \(\left\{ X_{t}^{e},X_{t}^{f}\right\} \) is \(\eta \)-arbitrage free if and only if there exist an equivalent measure \(\mathfrak {{\mathbb {Q}}}\) and a process \(\lambda _{t}\in L^{\infty }(\varOmega ,{\mathcal {F}}_{t},{\mathbb {P}})\) with the following properties:
-
B1:
\(\frac{1}{R}{\mathbb {E}}^{{\mathbb {Q}}}\left[ X_{t+1}^{e}|{\mathcal {F}}_{t}\right] \le \eta ^{-1}X_{t}^{f}\) for \(t\in {\mathcal {T}}_{0}\).
-
B2:
\(\lambda _{T}\ge X_{T}^{f}\)
-
B3:
\(\frac{1}{R}{\mathbb {E}}^{{\mathbb {Q}}}\left[ \lambda _{t+1}|{\mathcal {F}}_{t}\right] \le \lambda _{t}\) for \(t\in {\mathcal {T}}_{1}^{T-1}\)
-
B4:
\(\frac{1}{R}{\mathbb {E}}^{{\mathbb {Q}}}\left[ \lambda _{t+1}|{\mathcal {F}}_{t}\right] =X_{t}^{f}\) for \(t\in {\mathcal {T}}_{0}\)
Proof
Assume that the market is \(\eta \)-arbitrage free. Hence there exist processes \(\xi ^{\prime },\lambda ^{\prime }\) fulfilling conditions A1–A6 of Lemma 2. From A2 and A3 we have that \(\xi _{t}^{\prime }>0\). Define now
Furthermore note that from property A3 we can infer \({\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{t}^{\prime }\right] =\frac{1}{R^{t}}\) by recursively applying property A3 and taking expectation. It follows immediately that
In particular, \(\xi _{T}\) is almost surely positive and \(\mathbb {E^{{\mathbb {P}}}}\left[ \xi _{t}\right] =1.\) This allows to define a measure \({\mathbb {Q}}\) (equivalent to the original measure \({\mathbb {P}}\)) such that
for any \(A\in {\mathcal {F}}_{T}\). Hence the Radon–Nikodym derivative of \({\mathbb {Q}}\) with respect to \({\mathbb {P}}\) is given by
From \(\lambda _{T}^{\prime }\ge X_{T}^{f}\cdot \xi _{T}^{\prime }\) (property A2 of Lemma 2) it is possible to conclude \(\lambda _{T}\ge X_{T}^{f}\), i.e. B2.
By the above definition of \(\xi \) the inequality
property A4 of Lemma 2, is equivalent to
Properties A2, A3 also imply that \(\xi _{t}\) is a positive martingale, in particular
Hence accounting for
we get
from (42). Finally [using (41) and applying the abstract Bayes rule, see e.g. Björk (2009), Proposition B.41] this reduces to
which is B1.
In similar manner, starting with \({\mathbb {E}}^{{\mathbb {P}}}\left[ \lambda _{t+1}^{\prime }|{\mathcal {F}}_{t}\right] =X_{t}^{f}\xi _{t}^{\prime }\) (property A5 of Lemma 2) we get
and therefore
which is property B4 of the Proposition.
Finally, property A6 of Lemma 2, \({\mathbb {E}}^{{\mathbb {P}}}\left[ \lambda _{t+1}^{\prime }|{\mathcal {F}}_{t}\right] \le \lambda _{t}^{\prime }\) is equivalent to
and hence (again by Bayes’s rule)
which is property B3.
For the converse start with a measure \({\mathbb {Q}}\) and a process \(\lambda \) fulfilling conditions B1–B4 of the Proposition. Then use the density of \({\mathbb {Q}}\) w.r.t. \({\mathbb {P}}\), see (41), to define a random variable \(\xi _{T}\) and the positive martingale
as well as the processes
Using the same equivalent transformation as above one can show that \(\xi ^{\prime },\lambda ^{\prime }\) fulfills 1–6 of Lemma 2 if \(\xi ,\lambda \) fulfills B1–B4 of the Proposition.\(\square \)
Condition B1 can be interpreted as a consistency condition between fuel and electricity prices: under the equivalent measure \({\mathbb {Q}}\) the expected proceeds of selling one MWh of electricity at the end of the period must be less or equal to the compounded costs \(R\,\eta ^{-1}X_{t}^{f}\) for producing one MWh electricity over the time period. Comparison of the spark spread (the difference between contemporaneous efficiency-corrected electricity prices and fuel prices) can be seen as a rule of thumb related to B1. Properties B2–B4 can be restated as \(\lambda _{t}\ge X_{t}^{f}\) together with B4: under the measure \({\mathbb {Q}}\) the discounted expectation of \(\lambda \) equals the fuel price and at each point in time \(\lambda \) is not less than the fuel price.
Moreover, conditions B2–B4 can be used to derive further properties of fuel prices under the measure \({\mathbb {Q}}\):
Corollary 1
If a market \(\left\{ X_{t}^{e},X_{t}^{f}\right\} \) is \(\eta \)-arbitrage free then there exists an equivalent measure such that B1 holds together with
Proof
From B3, B4 one can infer \(X_{t}^{f}\le \lambda _{t}\) for \(t\in {\mathcal {T}}_{0}\). Taking expectation and using B4 a second time leads to
for \(t\in {\mathcal {T}}_{0}\).
In similar manner (43) can be derived from B2 and B4.\(\square \)
The necessary condition (43) states that under the no-arbitrage assumption the discounted fuel price must be a supermartingale under any feasible \({\mathbb {Q}}\). This ensures that the expected revenue from storing fuel and selling it later does not exceed the proceeds from immediately selling the fuel, if interest is taken into account.
The equivalent systems A1–A6 of Lemma 2 and B1–B4 of Proposition 1 include inequalities. Depending on the processes \(X_{t}^{f}\) and \(X_{t}^{e}\), those systems will not in general lead to a unique process \(\xi _{t}\) respectively a unique measure \({\mathbb {Q}}\). Moreover, keep in mind that Proposition 1 does not require \({\mathbb {Q}}\) to be a martingale measure, like in purely financial models: neither the (discounted) fuel price, nor the electricity price are necessarily martingales under a feasible measure \({\mathbb {Q}}\). Nevertheless it can be shown that the existence of a martingale measure for the fuel price process together with consistency between fuel and electricity price is sufficient for the exclusion of arbitrage.
Corollary 2
If there exists an equivalent measure \({\mathbb {Q}}\) such that B1 holds together with
then the market is \(\eta \)-arbitrage free.
Proof
B1 holds by assumption. Set \(\lambda _{t}=X_{t}^{f}\) for all t. This choice fulfills B2. Substituting \(\lambda _{t+1}\) for \(X_{t+1}^{f}\) at the left side of (45) leads to B4. Finally, using the same substitution on both sides, and observing \(r>0\) leads to B3.\(\square \)
Remark 5
We note that Lemma 2 and Proposition 1 can be generalized, if several production units \(i\in \{1,\ldots ,K\}\) with different efficiencies are introduced. If \(y_{t}^{i}\) denotes the energy produced by unit i and \(\eta _{i}\) denotes the efficiency of unit i it is possible to reformulate the basic accounting Eqs. (3) and (4) as
which leads to a corresponding reformulation of the test problem (8). Let \(\eta _{max}\) denote the largest efficiency. Analyzing the related dual formulation then shows that the market is \(\eta \)-arbitrage free for any \(\eta _{i}\le \eta _{max}\) if and only if conditions A1–A6 (respectively B1–B4) hold for \(\eta =\eta _{max}\).
3 Contract pricing and valuation
Consider now a delivery contract for electrical energy, agreed between a producer and a customer and specified in the following way: the producer has the obligation to deliver amounts \(D_{t}\) [MWh] of electric energy at a price of K currency units per MWh over each period \(\left[ t,t+1\right] \), \(t\in {\mathcal {T}}_{0}\). The demand \(D_{t}\) is a stochastic process adapted to the filtration \(\left\{ {\mathcal {F}}_{t}\right\} \) while K is a fixed price, agreed in advance. This is a quite general setup, \(D_{t}\) might be just a constant delivery or may depend in any measurable way on some \(\left\{ {\mathcal {F}}_{t}\right\} \)-adapted process, in particular on the price processes.
Such contracts have to be distinguished from contracts like swing options, where the demand can be optimized by the contract buyer as a reaction to the delivery price. For swing option pricing by dynamic stochastic optimization see e.g. Haarbrücker and Kuhn (2009) and Vayanos et al. (2011), for a method that accounts for the (multistage stochastic) bilevel aspects of swing option valuation see Kovacevic and Pflug (2014) and Gross and Pflug (2016), further approaches can be found e.g. in Thompson (1995) and Carmona and Touzi (2008).
Two natural questions arise, when designing a contract:
-
(1)
What is the value of the contract, when the delivery price K is given.
-
(2)
What is an adequate delivery price?
Given the no-arbitrage conditions, derived above, in general there is no hope that a unique arbitrage free price (or values) can be derived, even if the market is \(\eta \)-arbitrage free. Therefore, still taking into account the these arbitrage conditions, we analyze valuation and pricing from the standpoint of a producer. As discussed in the introduction, a variant of the first question then can be stated as: What is the minimum initial asset value or upfront-payment \(V_{0}=c_{0}+s_{0}X_{0}^{f}\) such that the producer is able to fulfill all contractual obligations and the distribution of the asset value at the end of the planning horizon, i.e. \(V_{T}=c_{T}+s_{T}X_{T}^{f}\), still stays “acceptable”. The second question can be restated in similar manner: Given an asset value of zero at the beginning, what is the minimum delivery price K such that the producer is able to fulfill all contractual obligations and the distribution of the asset value at the end of the planning horizon, i.e. \(V_{T}=c_{T}+s_{T}X_{T}^{f}\), still stays “acceptable”. Both, the minimum upfront payment and the minimum delivery price are not market prices or market values. However, when the delivery price has to be agreed below the firms minimum acceptable price (or value), then the producer will not enter the contract or at least has to take some additional risk.
In the following we consider two approaches to acceptability. The first interpretation requires that the asset value is almost surely not negative at the end. In finance this strict approach is called superhedging. In the second case, the producer measures acceptability by applying an acceptability functional to the end distribution and accepts the contract only if the value of the functional, applied to the distribution of the end value exceeds some bound. In what follows, we call this approach “acceptability pricing”.Footnote 1
3.1 The superhedging value
The basic setup is the same as in the previous section. However, in contrast to the pure no-arbitrage arguments, an individual producer cannot neglect that fuel storage and production capacity is restricted. So \(S>0\) will denote the upper bound on storage and \(P_{t}\) is an \(\left\{ {\mathcal {F}}_{t}\right\} \)-adapted process of upper bounds on the production of a generator with efficiency \(\eta \). While from a technical point of view the generator may have a fixed production capacity, the usage of an (adapted) process \(P_{t}\ge 0\) of production capacities allows to consider the effects of reserve-requirements or preferential demand, not related to the contract under consideration. Furthermore, it is possible to handle (random) outages in this way. Again we assume that the producer is a price-taker at both the fuel and the electricity market.
Because of the contractual obligations, only a part of the produced energy \(y_{t}\) can be sold at the electricity spot market after entering into the agreement. We therefore now have to make a difference between produced energy and energy sold to the market. Moreover, in addition to selling electricity at the market, it may also be useful for the producer to buy electricity from the market in order to meet obligations, either because such trades are expected to be cheaper than producing or because the deliverable amount exceeds the production boundary. The amount \(w_{t}\) of electricity sold at the market is an \(\left\{ {\mathcal {F}}_{t}\right\} \)-adapted stochastic process of decisions that can take values in \({\mathbb {R}}\). If \(w_{t}\) is negative, an amount of energy is bought.
We start with the superhedging value \(V_{0}^{*}\), the smallest up-front payment the producer would accept for a contract with delivery \(D_{t}\) and delivery price K if he aims at an almost surely nonnegative end value. The superhedging value can be calculated as the optimal value of the following optimization problem for a producer with efficiency \(\eta \), where the objective is to minimize the asset value \(V_{0}^{*}=c_{\text {0}}+X_{0}^{f}s_{0}\) at the beginning (funded as an upfront payment or as an initial reserve).
About the prices \(X_{t}^{e},X_{t}^{f}\) and the decision variables \(c_{t},y_{t},s_{t},z_{t}\) we make the same assumptions as in the previous section. In addition we assume that S is a real number and \(P_{t}\in L^{\infty }(\varOmega ,{\mathcal {F}}_{t},{\mathbb {P}})\) and \(D_{t}\in L^{1}(\varOmega ,{\mathcal {F}}_{t},{\mathbb {P}}).\) This ensures again that in the following we can use Lagrange multipliers from \(L^{\infty }(\varOmega ,{\mathcal {F}}_{t},{\mathbb {P}})\), the dual space of \(L^{1}(\varOmega ,{\mathcal {F}}_{t},{\mathbb {P}})\).
The first group of constraints is an adapted self financing condition for the cash position, taking into account that parts of the production are sold at the market. Note that under the contractual obligations the cash position develops according to
Here we assume that the delivery price K is payable at the end of each delivery period. Produced energy splits into energy traded on the market and contractual energy delivery, i.e. \(w_{t}+D_{t}=y_{t}\). Therefore the first constraint of (48) follows by substituting \(y_{t}-D_{t}\) for \(w_{t}\) in the basic cash Eq. (49). The second constraint group describes storage accounting. In contrast to the no-arbitrage problem, now we have a restriction on the end value instead of a restriction on the start value. Finally, constraint groups 4 and 5 specify the lower and upper bounds on production and storage.
In order to analyze the superhedging problem (48) we use again the related dual problem. The valuation problem (48) and the no-arbitrage test problem (8) look quite different at first glance. However it turns out that the related dual problems have similar constraints as the following Lemma shows.
Lemma 3
The Lagrange dual of the valuation problem (48) is given by
where \(\xi _{t}, \lambda _{t},\mu _{t}, \nu _{t}\in L^{\infty }(\varOmega ,{\mathcal {F}}_{t},{\mathbb {P}})\).
Proof
The Lagrangian of (48) can be written as
where \(\zeta \ge 0\) is an essentially bounded \({\mathcal {F}}_{T}\)-measurable random variable, and \(\xi _{t}\), \(\lambda _{t}\) , \(\mu _{t}\ge 0,\nu _{t}\ge 0\) are chosen \({\mathcal {F}}_{t}\)-measurable and essentially bounded.
After reordering, (51) yields
The dual problem then reads
where the constraints ensure that the Lagrange function \(\min _{y\ge 0,z,c,s\ge 0}L(y,z,c,s;\xi ,\lambda ,\zeta ,\gamma )\) stays bounded.
Constraint groups 3–6 of (53) already coincide with the constraint groups 2–5 of (50).Using \(\xi _{T}=\zeta \ge 0\) the multiplier \(\zeta \) can be eliminated, which [using the first line of constraints in (50)] leads to \(\xi _{T}\ge 0\) and \(\lambda _{T}+\nu _{T}\ge X_{T}^{f}\cdot \xi _{T}\) . This resembles the first line of constraints in (50). The second constraint of (53) can be reformulated as
and taking into account \(\nu _{t}\ge 0\) shows that it is superfluous.\(\square \)
Absence of \(\eta \)-arbitrage ensures feasibility and the existence of inner solutions of (50), which in turn leads to strong duality, i.e. the optimal value of the primal and the dual problems coincide.
Proposition 2
If a market \(\left\{ X_{t}^{e},X_{t}^{f}\right\} \) is \(\eta \)-arbitrage free, then (48) has an optimal solution and
Proof
The constraints of Lemma 3 consist of (linear) equations and inequalities w.r.t. the cone of nonnegative, essentially bounded random variables. The (linear) equations define a convex set S of processes \(\lambda \) and \(\xi \). Clearly the equations coincide with the equations in A1-A6 of Lemma 2. Consequently, if the market is arbitrage free then S must be nonempty because any arbitrage free \(\xi ,\lambda \) together with \(\mu _{t}=\nu _{t}=0\) is feasible for (50).
Furthermore, if the market is arbitrage free, each \(\lambda ,\xi \) in S also fulfills (by Lemma 2) the inequalities
as well as \(\xi _{t}>0\). It follows that for such \(\xi ,\lambda \) and any \(\mu ,\nu \) with \(\mu _{t}>0\),\(\nu _{t}>0\) we have
Summarizing, there exist processes \(\xi ,\lambda ,\mu ,\nu \) in S such that the inequality constraints of 3 are strictly fulfilled.
Noting that the domain of the objective function imposes no relevant restriction, we see that it is possible to apply the Slater condition for cone constrained vector optimization, see e.g. Bot et al. (2009) p. 80. Theorem 3.2.9 of Bot et al. (2009) then implies strong duality and the optimal values of (50) and its dual (48) coincide. Moreover, (48) has an optimal solution.\(\square \)
Proposition 2 shows that the shadow prices \(\xi \) related to the cash position, which occurs in Lemma 3, can be interpreted as a process of stochastic discount factors applied to the opportunity costs of delivering amounts \(D_{t}\) of electricity at price K instead of selling them at the market at prices \(X_{t}^{e}\). In particular \(R^{t}\xi _{t}\) is a martingale and the relation
can be derived easily, which underpins this interpretation. The processes \(\mu \) and \(\nu \) can be understood as special discount factors for available production and storage capacities (“value of available capacity”). It is deducted from the opportunity costs, because larger production or storage capacity increase the possibilities to produce and sell electricity when it is favorable.
On the other hand, the process \(\lambda \) (the shadow prices for storage accounting) does not occur in the dual objective function and therefore cannot be interpreted as a process of discount factors. However, it becomes apparent that \(\lambda \) is closely related to fuel prices. In particular, constraint group 4 shows that the conditional expectation of \(\lambda _{t+1}\) is equal to the (stochastically) discounted fuel price at time t, i.e. \({\mathbb {E}}^{\mathbb {P}}\left[ \lambda _{t+1}|{\mathcal {F}}_{t}\right] =X_{t}^{f}\xi _{t}\). Taking expectation then implies
which means that the expectation of \(\lambda \) equals the expected discounted fuel price plus a risk loading, which is given by the covariance between the stochastic discount factor \(\xi \) and the fuel price.
The idea of risk loadings can also be applied to the superhedging price as a whole. Given the stochastic discount factors one can derive the following decomposition of the superhedging price into expectations and covariances.
Corollary 3
If a market is \(\eta \)-arbitrage free, there exist stochastic discount factors \(\xi ,\lambda ,\mu ,\nu \) such that the superhedging value can be decomposed as follows:
Proof
For \(\eta \)-arbitrage free market, it is possible to apply Proposition 2. The assertion then can be obtained easily from the objective function of (50), by applying the relation \(Cov(X,Y)={\mathbb {E}}^{{\mathbb {P}}}\left[ XY\right] -{\mathbb {E}}^{{\mathbb {P}}}\left[ X\right] {\mathbb {E}}^{{\mathbb {P}}}\left[ Y\right] \) and (55).\(\square \)
The first term at the right hand side of (56) is the expected present value of a pure trader, fulfilling the contractual obligations by electricity bought on the market. Further expectation terms correct for the risks of production outages and (limited) storage. The first covariance term can be interpreted as a risk loading for a pure trader, while the second covariance term is related to the effects of uncertain production capacities. Because the covariances may have any sign and the effects of production and storage are subtracted from the expectation, all kinds of contango and backwardation may arise.
Corollary 4
If a market \(\left\{ X_{t}^{e},X_{t}^{f}\right\} \) is \(\eta \)-arbitrage free, then the optimal value function \(V_{0}^{*}(K,D,\eta )\) is convex, both in K and in D.
Proof
Let F denote the (convex) set of feasible \(\xi ,\)\(\lambda ,\;\mu ,\;\nu \) for formulation (59) and define
We then have
which is equal to \(V_{0}^{*}(K,D,\eta )\) by Proposition 3. For fixed K the combined objective in (57) is linear, hence convex in D. Therefore, \(U_{0}^{*}(K,D,\eta )\) is obtained as a pointwise maximum over an infinite set of convex functionals, which shows that \(U_{0}^{*}(K,D,\eta )\) is convex in D. A similar argument can be applied to show convexity in K.\(\square \)
An important difference between the constraints of (50) and the no-arbitrage conditions A1-A6 is the fact that in the first case we have \(\xi _{T}\ge \) 0, whereas in the second case the stricter \(\xi _{T}>0\) is demanded. For \(\eta \)-arbitrage free markets the dual problem can be restated by using equivalent measures in the following way:
Proposition 3
If the market \(\left\{ X_{t}^{e},X_{t}^{f}\right\} \) is \(\eta \)-arbitrage free, then the superhedging value \(V_{0}^{*}(K,D,\eta )\) can be calculated as
where \(\lambda _{t},\mu _{t},\nu _{t}\in L^{\infty }(\varOmega ,{\mathcal {F}}_{t},{\mathbb {P}})\)
Proof
Starting from (50) the dual problem can be reformulated as
If the market is \(\eta \)-arbitrage free then by Lemma 2 the feasible set of (59) is not empty. Let \(\xi ^{\prime },\lambda ^{\prime },\mu ^{\prime },\nu ^{\prime }\) be feasible for (59) and define again
In addition, now set
Clearly we then have \(\mu _{t}\ge 0\)\(\nu _{t}\ge 0\). The arguments used in the proof of Proposition 1 can be applied again to derive the following dual feasibility conditions for \(\lambda ,\mu ,\nu \) together with and an equivalent measure \({\mathbb {Q}}\) with \(\frac{d{\mathbb {Q}}}{d{\mathbb {P}}}=\xi _{T}\):
-
C1
: \({\mathbb {E}}^{{\mathbb {Q}}}\left[ X_{t+1}^{e}|{\mathcal {F}}_{t}\right] \le R\,\eta ^{-1}X_{t}^{f}+\mu _{t}\) for \(t\in {\mathcal {T}}_{0}\)
-
C2
: \(\lambda _{T}+\nu _{T}\ge X_{T}^{f}\)
-
C3
: \({\mathbb {E}}^{{\mathbb {Q}}}\left[ \lambda _{t+1}|{\mathcal {F}}_{t}\right] \le \left( \lambda _{t}+\nu _{t}\right) R\) for \(t\in {\mathcal {T}}_{1}^{T-1}\)
-
C4
: \({\mathbb {E}}^{{\mathbb {Q}}}\left[ \lambda _{t+1}|{\mathcal {F}}_{t}\right] =R\,X_{t}^{f}\) for \(t\in {\mathcal {T}}_{0}\)
-
C5
: \(\mu _{t}\ge 0\),\(\nu _{t}\ge 0\text { for }t\in {\mathcal {T}}\)
The second group of constraints in (50), i.e. \(R{\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{t+1}|{\mathcal {F}}_{t}\right] =\xi _{t}\) is equivalent to \(\xi _{t+1}=R{}^{T-t-1}{\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{T}|{\mathcal {F}}_{t+1}\right] \). Together with definitions (62) this fact can be used to reformulate the dual objective function as
Applying now (61) and the relation \(\frac{d{\mathbb {Q}}}{d{\mathbb {P}}}=\xi _{T}\) it is possible to reformulate the objective function again and one gets the reformulated dual
If the market is \(\eta \)-arbitrage free we have \(V_{0}^{*}(K,D,\eta )=U_{0}^{*}(K,D,\eta )\) by Proposition 2.\(\square \)
3.2 Superhedging prices
We keep the basic setup of a producer with bounded storage and production. As discussed above superhedging prices ensure that - starting from an asset value of zero - all contractual obligations are fulfilled and the asset value stays nonnegative at the end. In particular the objective now is to minimize the delivery price, and the asset value starts at zero. This leads to the following modification of (48)
Again the dual problem of (63) reveals important properties of the superhedging price.
Proposition 4
The Lagrange dual of the pricing problem (63) is given by
where for each \(t=1,\ldots ,T\) the random variables \(\xi _{t}, \lambda _{t},\mu _{t}\) and \(\nu _{t}\) are essentially bounded and measurable w.r.t. \({\mathcal {F}}_{t}\).
If the market is \(\eta \)-arbitrage free then
Proof
The Lagrangian of (64) is
where \(\zeta \ge 0\) is an essentially bounded \({\mathcal {F}}_{T}\)-measurable random variable, and \(\xi _{t}\), \(\lambda _{t}\) , \(\mu _{t}\ge 0,\;\nu _{t}\ge 0\) are chosen \({\mathcal {F}}_{t}\)-measurable and essentially bounded.
After reordering (67) yields
The Lagrange dual problem then can be written as
where the constraints ensure that the Lagrange function
stays bounded.
Constraint groups 3–6 of (69) already coincide with constraint groups 2–5 of (50). Using \(\xi _{T}=\zeta \ge 0\) we can eliminate \(\zeta \) which leads to \(\xi _{T}\ge 0\) and \(\lambda _{T}+\nu _{T}\ge X_{T}^{f}\cdot \xi _{T}\) from the first line of constraints of (64). This resembles the first line of constraints in (64). Finally, the second constraint of (69) can be reformulated as
Taking into account \(\nu _{t}\ge 0\) shows that this constraint is superfluous. Altogether we have the dual (69).
Now, because of \(R>0\) and \(R{\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{1}\right] =\gamma \) the multiplicator \(\gamma \) must be nonnegative. Moreover, the assumption \(\gamma =0\) would imply \({\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{1}\right] =0\) and hence \(\xi _{1}=0\) with probability one, which (using the second constraint and \(\xi _{t}\ge 0\)) implies \(\xi _{t}=0\) a.s. for all t. This contradicts \(\sum _{t=0}^{T-1}{\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{t+1}D_{t}\right] =1\) and hence we can conclude \(\gamma >0\).
If now the market is \(\eta \)-arbitrage free, there exists a nonempty set of processes \(\xi ^{\prime },\lambda ^{\prime }\) fulfilling conditions A1-A6. By multiplying all equations and inequalities by \(\gamma >0\), one sees that the rescaled processes \(\xi =\kappa \xi ^{\prime }\text {and }\lambda =\kappa \lambda ^{\prime }\) fulfill A1-A6 with the exception that the equation \(R{\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{1}\right] =1\) is replaced by \(R{\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{1}\right] =\gamma \). It is possible then to choose \(\gamma \) such that \(\sum _{t=0}^{T-1}{\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{t+1}D_{t}\right] =1\). Using these facts, the arguments of in the proof of Proposition then can be used again, to show strong duality. \(\square \)
From the objective function of dual problem (64) one sees that, given strong duality, the process of Lagrange multipliers \(\xi \) can again be interpreted as some kind of stochastic discount factor process. The superhedging price then can be regarded as the expected present value of the costs of buying the contracted electricity delivery from the market, corrected by the effects of storage, production capacity and related risk loadings. There is also a decomposition into expected present values and risk premia.
Corollary 5
If a market \(\left\{ X_{t}^{e},X_{t}^{f}\right\} \) is \(\eta \)-arbitrage free, then there exist stochastic discount factors \(\xi ,\lambda ,\mu ,\nu \) and \(\gamma \) such that the superhedging price can be decomposed into
Proof
This is a straightforward application of the equation \(Cov(X,Y)={\mathbb {E}}^{{\mathbb {P}}}\left[ XY\right] -{\mathbb {E}}^{{\mathbb {P}}}\left[ X\right] {\mathbb {E}}^{{\mathbb {P}}}\left[ Y\right] \) to the objective of (69).\(\square \)
The interpretation of the stochastic discount factor \(\xi \) in Proposition 4 is quite different from the interpretation of \(\xi \) in the case of superhedging, despite the fact that both processes can be viewed as stochastic discount factors. While (55) holds for valuations, this is not true in Proposition 4. Here \(\xi \) is normalized to ensure \(\sum _{t=0}^{T-1}{\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{t+1}D_{t}\right] =1\), which means that \(\xi \) must have dimensionality [1 / MWh]. Nonetheless, it is possible to reformulate the dual problem such that the stochastic discount factors can be interpreted in the same way as in the previous subsection on valuation. However, this leads away from the linear objective function in (64): the superhedging price then can be interpreted as expected (and adjusted) present value of the opportunity costs divided by the expected discounted demand, where both expectations use \(\xi \) as stochastic discount factors. In this formulation \(\xi \) is dimensionless and (55) is valid.
Corollary 6
The dual problem (64) is equivalent to the fractional optimization problem
Proof
Suppose \(\xi ^{\prime },\lambda ^{{\prime }},\mu ^{\prime },\nu ^{\prime }\) and \(\gamma \) fulfill the constraints of the dual problem (64). As \(\gamma >0\), define
Dividing all constraints of the dual (64) by \(\gamma \) and using the rescaled variables \(\xi ,\lambda ,\mu ,\nu \), one gets the constraints of (71) plus the constraint
On the other hand, the dual objective function can be rewritten with scaled multiplicators:
Substituting \(\gamma \) from (72) into (73) leads to the objective of (71).\(\square \)
3.3 Capital requirement and acceptability pricing
Superhedging-based approaches lead to price bounds for delivery contracts, comparable to the rough no-arbitrage bounds for financial derivatives. The related strategy is riskless from the producer’s perspective but usually contract cannot be sold at the superhedging price: the smallest riskless price for the producer still may be expensive for the potential customers. This problem intensifies for producers with smaller efficiency \(\eta \). In order to offer the contract at a reasonable price (or value) the producer definitely has to take some risk.
In the following we consider a producer who deviates from complete superhedging but nevertheless wants to control the risk: instead of aiming at an almost surely nonnegative asset value at the end, the producer accepts some risk but bounds the acceptability of the final wealth distribution. In terms of optimization the third constraint group of the original problem (48) [or the fourth of (63)] is replaced by the constraint
where \({\mathcal {A}}\) denotes an acceptability functional which maps integrable random variables to the real line, and \(\alpha \) is a real number. In the following we analyze the two main issues, valuation and pricing in this new context.
-
(CR): If we search for the smallest capital such that (74) holds together with the production and trading constraints of (48) (without constraint group four), this is the problem of acceptability valuation (capital requirement). We denote this problem by (CR) and the related optimal value by \(V_{0}^{*}(K,D,\eta )\).
-
(AP): If we search instead for the minimum delivery price, using (74) within (63) (replacing constraint group 4), then we call this an acceptability pricing problem, which we denote by (AP). The related optimal value is \(K_{0}^{*}(D,\eta )\).
Acceptability valuation and pricing in the strict sense aims at the case \(\alpha =0\). However, \(\alpha \ne 0\) may also be a sensible choice in certain situations. In particular, electricity producers usually optimize their production and trading activities. Such producers therefore are able to maximize the acceptability of their portfolio without the contract and then to calculate a capital requirement or acceptability price for the new contract (keeping all existing production and trading possibilities) with an acceptability not below the previously calculated optimal value. For the second step it is necessary to calculate a (CR) or (AP) problem with \(\alpha \) different from zero. This idea is often called indifference pricing (see Carmona 2009; Pennanen 2012 for the general idea, and Kovacevic and Paraschiv 2014; Analui and Kovacevic 2014 for some applications to electricity production and trading).
Different notions of acceptability exist in literature. In the following we use acceptability functionals (see e.g. Pflug and Römisch 2007), also known as monetary utility functions (e.g. Jouini et al. 2008). Acceptability functionals are mappings \({{\mathcal {A}}}:\varXi \subseteq L^{1}(\varOmega ,{\mathfrak {F}},{\mathbb {P}})\rightarrow \overline{{\mathbb {R}}}\) (where \(\varXi \) is a subspace), satisfying the following properties
-
(MA1) Concavity. The functional \(Y\mapsto {{\mathcal {A}}}(Y)\) is concave.
-
(MA2) Monotonicity. If \(X,Y\in L^{1}(\varOmega ,{\mathfrak {F}},{\mathbb {P}})\) and \(X\le Y\) holds a.s., then \({{\mathcal {A}}}(X)\le {{\mathcal {A}}}(Y).\)
-
(MA3) Translation Equivariance. If \(X\in L^{1}(\varOmega ,{\mathfrak {F}},{\mathbb {P}})\) and \(a\in {\mathbb {R}}\) then \({{\mathcal {A}}}(X+a)={{\mathcal {A}}}(X)+\beta a\).
It should be kept in mind that—up to sign—such functionals are identical with convex risk measures, e.g. Fritelli and Rosazza (2002). For simplicity we restrict the analysis to positive homogeneous functionals centered at zero, i.e.
-
(MA4) If \(X\in L^{1}(\varOmega ,{\mathfrak {F}},{\mathbb {P}})\) and \(a\in {\mathbb {R}},\,a\ge 0\) then \({{\mathcal {A}}}(aX)=a{{\mathcal {A}}}(X)\).
-
(MA5) \({{\mathcal {A}}}(0)=0\)
Recall that any positive homogeneous acceptability functional functional \({\mathcal {A}}\) on \(\varXi \) can be rewritten in terms of the conjugate representation
for some set \(\varUpsilon _{{\mathcal {A}}}\subseteq \left\{ \zeta :\;Z\in \varXi ^{*}\text {and }\mathbb {E^{{\mathbb {P}}}}\left[ \zeta \right] =\beta ,\;\ \zeta \ge 0 \right\} \) where \(\varXi ^{*}\) is the dual space of \(\varXi \). In this formulation \(\beta \) can be interpreted as a (deterministic) discount factor. The infimum is attained. See e.g. Pflug (2006) and Pflug and Römisch (2007), 2.22 for more details and many examples of relevant functionals as well as Eichhorn et al. (2004) for a related class of risk functionals used in electricity planning.
In the following we denote the set dual processes \(\xi ,\lambda \) fulfilling the no-arbitrage requirements by
which means that \({\mathbb {A}}\) is nonempty if the market is \(\eta \)-arbitrage free. In addition we will use the specification \(\varXi =L^{1}\left( \varOmega ,{\mathfrak {F}},{\mathbb {P}}\right) \) because our assumptions about the relevant processes (integrable or essentially bounded as discussed before) implies that the end value is integrable. The dual variable \(\zeta \) then is in the space \(L^{\infty }\left( \varOmega ,{\mathfrak {F}},{\mathbb {P}}\right) \).
Based on the above setup, capital requirements calculated by acceptability valuation lead to a slight modification of the superhedging results. The acceptability valuation problem can be stated as the superhedging problem plus an additional constraint that states that the discount factor \(\xi _{T}\) lies in the defining set \(\varUpsilon _{{\mathcal {A}}}\) of the used acceptability functional.
Proposition 5
Consider an acceptability valuation problem (CR) based on a positive homogeneous acceptability functional \({\mathcal {A}}\) with conjugate representation (75) and \(\beta =\frac{1}{R^{T}}\). The dual problem then is given by
If in addition the market \(\left\{ X_{t}^{e},X_{t}^{f}\right\} \) is arbitrage free and \(\varUpsilon _{{\mathcal {A}}}\cap \mathbb {A\ne \emptyset }\), then the capital requirement equals the dual value, i.e.
Proof
Define the Lagrangian of (CR) by
where \(\kappa \ge 0\) is a real number, \(\zeta =\kappa \zeta ^{\prime }\) for some \(\zeta ^{\prime }\in \varUpsilon _{{\mathcal {A}}}\), and the processes \(\xi _{t}\), \(\lambda _{t}\) , \(\mu _{t}\ge 0,\;\nu _{t}\ge 0\) are adapted and essentially bounded. Recall that \(\zeta ^{\prime }\) is the (attained) minimizer in (75). Because of \(-{\mathbf {inf}}\left\{ {\mathbb {E}}\left( \zeta X\right) :\zeta \in \varUpsilon _{{\mathcal {A}}}\right\} =\sup \left\{ -{\mathbb {E}}\left( \zeta X\right) :\zeta \in \varUpsilon _{{\mathcal {A}}}\right\} \) the optimal value \(V_{0}^{*}(K,D,\eta )\) of the acceptability pricing problem is \(V_{0}^{*}(K,D,\eta )=\underset{y,z,c,s}{\min }\underset{\xi .\lambda ,\mu ,\nu ,\gamma ,\zeta }{\max }L(y,z,c,s;\xi ,\lambda ,\zeta ,\mu ,\nu ,\gamma ,\zeta )\) w.r.t. the above restrictions.
After reordering, (77) yields
Ensuring boundedness, the dual problem then is given by
Using \({\mathbb {E}}^{{\mathbb {P}}}\left[ \zeta ^{\prime }\right] =\frac{1}{R^{T}}\) (which follows from translation equivariance of \({\mathcal {A}}\)) and \({\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{t}\right] =\frac{1}{R^{t}}\), we can conclude \(\kappa \frac{1}{R^{T}}=\kappa \cdot {\mathbb {E}}^{{\mathbb {P}}}\left[ \zeta ^{\prime }\right] ={\mathbb {E}}^{{\mathbb {P}}}\left[ \zeta \right] ={\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{T}\right] =\frac{1}{R^{T}}\), hence \(\kappa =1\) and therefore \(\xi _{T}=\zeta \in \varUpsilon _{{\mathcal {A}}}\). The same arguments as at the end of the proof for Lemma 3 then lead to (76).
If \(\varUpsilon _{{\mathcal {A}}}\cap \mathbb {A\ne \emptyset }\), then the arguments of Proposition 2 can be used to show strong duality.
\(\square \)
Interpreting Proposition 5, capital requirements (or acceptability valuation) can be considered as an application of the idea of good deal bounds to energy markets. Good-deal bounds were used in several papers for pricing of standard financial contracts, traded on incomplete markets. The upper bound is given by the maximum contract price using nonnegative stochastic discount factors that price the basic assets (which leads to the no-arbitrage bound) and additionally fulfill some additional restrictions. A special case with a restriction on the variance of discount factors was derived as the dual of minimizing the variance of discount factors that correctly price a set of assets in Hansen and Jagannathan (1991). Cochrane and Saá-Roquejo (2000) proposed good deal bounds as a general method for pricing in incomplete markets and also coined the term. Different restrictions on the discount factors were proposed e.g. in Bernardo and Ledoit (2000). In the present context of electricity markets with production, the problem of acceptability valuation leads to a generalized good deal bound with the appropriate no-arbitrage conditions and a restriction on the stochastic discount factor, namely \(\xi _{T}\in \varUpsilon _{{\mathcal {A}}}\), which comes from the used acceptability functional.
In the same manner a dual representation of the acceptability pricing problem (AP) can be derived.
Proposition 6
Consider an acceptability pricing problem based on a positive homogeneous acceptability functional \({\mathcal {A}}\) with conjugate representation (75) and \(\beta =\frac{1}{R^{T}}\). The dual problem is
If \(\varUpsilon _{{\mathcal {A}}}\cap \mathbb {A\ne \emptyset }\), then the minimum upfront payment based on acceptability pricing equals the optimal dual value, i.e.
Proof
Defining the Lagrangian like in the proof of Proposition 5 leads to the dual problem
Using \({\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{t}\right] =\frac{\gamma }{R^{t}}\), we then can conclude
hence \(\kappa =\gamma \) and therefore \(\xi _{T}={\gamma }\zeta ^{\prime }\).
The further arguments of the proofs for Propositions 5 and 6 then can be applied in a direct way to derive (80) and the further statement of the current proposition.\(\square \)
Proposition 6 also implies a fractional representation. The proof repeats the arguments of Corollary 6.
Corollary 7
The dual problem (80) is equivalent to the fractional optimization problem
Proof
Again, it can be shown that \(\gamma >0\). Assume that \(\xi ^{\prime },\lambda ^{\prime },\mu ^{\prime },\nu ^{\prime }\) is feasible for (80) and define rescaled variables \(\xi _{t}=\xi ^{\prime }/\gamma \), \(\lambda _{t}=\lambda ^{\prime }/\gamma \), \(\mu _{t}=\mu ^{\prime }/\gamma \), \(\nu _{t}=\nu ^{\prime }/\gamma \), leads to a dual objective function with scaled multiplicators
and the first line of constraints reads \(\xi _{T}\in \varGamma _{{\mathcal {A}}}\). Furthermore the rescaled variables fulfill \(R{\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{1}\right] =1\) and \(\sum _{t=0}^{T-1}{\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{t+1}D_{t}\right] =1/\gamma \). Solving for \(\gamma \) and plugging the result into (82), leads to the objective function in (81).\(\square \)
Remark 6
Given the optimal stochastic discount processes \(\xi ,\mu ,\nu ,\lambda \) capital requirements can be decomposed according to Corollary 3 and acceptability prices can be decomposed according to Corollary 5.
Remark 7
It is also possible to analyze valuation and pricing of delivery contracts if the producer has available several generators. Using the setup of Remark 5, the constraints of Lemma 3, Corollary 6 and Propositions 5, 6 have to be reformulated with \(\eta =\eta _{max}\). Moreover, each expression \(\sum _{t=0}^{T-1}{\mathbb {E}}^{{\mathbb {P}}}\left[ \mu _{t}P_{t}\right] \) in the respective objective functions has to be replaced with \(\sum _{i=1}^{K}\sum _{t=0}^{T-1}{\mathbb {E}}^{{\mathbb {P}}}\left[ \mu _{t}^{i}P_{t}^{i}\right] \), where \(P_{t}^{i}\) denotes the production restriction of generator i and \(\mu ^{i}\) is the related process of (essentially bounded) shadow prices.
4 An illustrative numerical example
As an example for a possible implementation of our results, we consider a producer who uses a single gas turbine in order to produce electricity. The generator produces with a maximum power capacity of 50 MW and an efficiency of 0.43. Fuel can be stored up to an amount of 2800 MWh. Storage starts empty. Interest is neglected, as often done in electricity applications, i.e. we set \(R=1\).
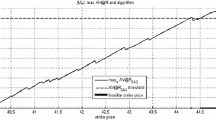
We analyze the superhedging value of a contract that delivers 500 MWh for 10 days over the time period 7:00–21:00 of a day, if the average electricity price of the previous day over these hours is larger or equal to 40 Euro. If the average price of the previous day is smaller, then no power is delivered.
In order to model the joint price process of gas and electricity we estimated a vector-autoregressive model over the period 9/2017–11/2017 for the relative price differences (returns) of GPL spot gas prices (daily, Bloomberg) and EEX Phelix electricity day ahead spot prices (aggregated from hourly prices, Bloomberg). The model equation is given by
where \(x_{t}^{i}=\frac{X_{t}^{i}-X_{t-1}^{i}}{X_{t-1}^{i}}\) for \(i\in \left\{ f,e\right\} \) denotes the relative price differences for fuel and electricity,
is the matrix of autoregressive parameters,
is an intercept vector, and \(\varepsilon _{t}=\left( \varepsilon _{t}^{f},\varepsilon _{t}^{e}\right) ^{\prime }\) are i.i.d. random vectors which are normally \(N(0,\varOmega )\)-distributed with
In the present paper we do not compete with the rich literature on electricity and gas price forecasting (see e.g. Nowotarski and Weron (2018) for an overview of recent models). Our aim for this example is just to use an easily tractable price model which leads to reasonable price distributions. The model therefore does not include long term equilibrium effects (cointegration of prices) a more complicated lag-structure (e.g. weekly dependencies) or important exogenous variables like e.g. wind force.
Estimation (using the R-package vars, see Pfaff (2008)) of the model for our price data led to the values
and
While the theoretical results of this paper are obtained for very general probability spaces, in the following we use tree based multistage stochastic optimization in order to formulate discretized versions of our valuation problems which leads to a reformulation on “tractable” finite state spaces. In particular, scenario trees are used in order to model the discretized processes as well as the information flow over time. We use the approach described in Pflug and Pichler (2014), 1.4. (for an alternative see e.g. Alonso-Ayuso et al. 2009), which can be sketched as follows: the original time oriented formulation of (50), respectively (69), (76) or (80), is replaced by a node oriented formulation. In our case this leads to an LP, which means that standard software can be used in order to solve the approximating problem.
Consider a finite probability space \(\varOmega =(\omega _{1},\ldots ,\omega _{S})\) which contains S scenario paths. Any stochastic process defined on this sample space can be represented as a finite tree with node set \({{\mathcal {N}}}=\{0,1,\ldots ,N\}\). The levels of the tree correspond to the decision stages. Let \({{\mathcal {N}}}_{t}\) be the set of nodes at level t, for \(t=0,\ldots ,T\). The last level \({{\mathcal {N}}}_{T}\) contains the S leafs of the tree which can be identified with the scenario paths. The tree structure represents the filtration of the process and can be defined by stating the (unique) predecessor node \(n_{-}\) for each node n. There is a unique root node, by convention denoted with 0, which represents the present. By construction there is a one to one relation between any node n and an assigned pair \((\omega ,t\)), which means that each node is related to the state of the system at time t in sample path \(\omega \) and vice versa.
The price processes \(X^{e},X^{f}\) are represented w.r.t. the nodes of the tree, i.e. we write \(X_{n}^{e},X_{n}^{f}\) instead of \(X_{t}^{e}(\omega ),X_{t}^{f}(\omega )\) if node n refers to scenario \(\omega \) at time t. In similar manner the decision processes x, c, s, z, y are related to the nodes: So far \(s_{t}(\omega )\) denoted the random amount of fuel stored at time t. In the discretized model, \(s_{n}\) denotes the value of produced energy planned at node n, which can be identified with a point in time t and a scenario \(\omega \). Almost sure constraints are obtained by formulating the same constraint for all nodes of a stage \({\mathcal {N}}_{t}\). Moreover, constraints between points in time can be rewritten with node indices instead of time indices, using the predecessor relation \(n_{-}\). As an example consider the cash Eq. (3), which can be rewritten as
in the node oriented formulation. The node structure defines the filtration in the discretized model and the fact that all decision variables are dependent on nodes n ensures that decisions are based on the information available in this node.
Finally, probabilities \(\pi _{n}\) can be assigned to all leaf nodes \(n\in {\mathcal {N}}\)(T), which also implies probabilities \(\pi _{n}\) for all other nodes. These probabilities then can be used to formulate the expectations occurring in the objective functions of (50), respectively (69), (76) or (80): Let X denote a random variable with values \(X_{n}\) in nodes \(n\in {\mathcal {N}}_{t}\) for some stage t, then we calculate
in the discretized model. With known probabilities related to nodes, it easily possible to assign conditional probabilities \(\pi _{nm}\) for going to node m given that node n is reached. In fact these conditional probabilities are used to formulate the dual constraints involving conditional expectations: in the discretized model the conditional expectation \({\mathbb {E}}\left[ X_{t+1}|{\mathcal {F}}_{t}\right] \) for some random variable \(X_{t+1}\) (measurable with respect to \({\mathcal {F}}_{t+1}\)) is replaced by a random variable \(E_{t}\) that takes values \(E_{n}\) with probabilities \(\pi _{n}\) in nodes \(n\in {\mathcal {N}}_{t}\) such that
Several methods have been proposed to construct approximating scenario trees (with given tree structure) for stochastic processes, see e.g. Dupacova et al. (2003), Heitsch and Römisch (2010), Kovacevic and Pichler (2015) and Pflug and Pichler (2015). In the following we use optimal quadratic quantization for modeling the discretized distribution of the (i.i.d.) residuals \(\varepsilon _{t}\) in (83), from which the discretized conditional distribution of the price process \((X_{t}^{f},X_{t}^{e})\) can be derived. To this end consider a standard normally distributed random vector \(Z=\left( \begin{array}{c} Z_{1}\\ Z_{2} \end{array}\right) \), i.e. \(Z\sim N(0,I_{2})\) where \(I_{2}\) denotes the \(2\times 2\) identity matrix. In a first step we approximate this continuously distributed random variable by a discretely distributed random variable \({\hat{Z}}=\left( \begin{array}{c} {\hat{Z}}_{1}\\ {\hat{Z}}_{2} \end{array}\right) \) which may take finitely many values from the \(n-\)tupel \(z=(z_{1},\ldots ,z_{n})=(\left( \begin{array}{c} z_{11}\\ z_{21} \end{array}\right) ,\ldots ,\left( \begin{array}{c} z_{1n}\\ z_{2n} \end{array}\right) )\). Optimal quadratic quantization chooses z such that the quadratic distortion (or quantization error)
(where \(u=\left( \begin{array}{c} u_{1}\\ u_{2} \end{array}\right) \) and \(\phi \) denotes the density of the standard normal distribution) is minimized. The approximating random variable \({\hat{Z}}\) then can be described by the two dimensional vectors \(z_{i}\) and the related probabilities \(p_{i}\), which can be calculated as
where \(C_{i}(z)\) is the Voronoi tessel that contains \(z_{i}\) , see e.g. Pagès and Printems (2003).
Our numerical example is based on a tree such that each node (except the leaf nodes) has three successors, therefore we use a quantization of the two dimensional standard normal distribution with \(n=3\). The related quantizers and probabilities have been calculated in Pagès and Printems (2003) and can be downloaded at http://www.quantize.maths-fi.com: the three quantizers (scenarios) are given by
and the related probabilities are \(p_{1}\thickapprox 0.3334\), \(p_{2}\thickapprox 0.3330\), \(p_{3}\thickapprox 0.3336\). Given that z represents three approximating scenarios for a two dimensional standard normal distribution, we can obtain three approximating scenarios \(\varepsilon ^{q}\) for the i.i.d. residuals \(\varepsilon _{i}\) with estimated covariance matrix \({\hat{\varOmega }}\) by using the Cholesky decomposition \({\hat{\varOmega }}=LL^{\prime }:\)
Based on these considerations the i.i.d. random variables and their distribution \(\varepsilon _{t}\) can be approximated by \(\varepsilon ^{q}=\left( \varepsilon _{1}^{q},\varepsilon _{2}^{q},\varepsilon _{3}^{q}\right) \) and the related probabilities \(p_{1},\,p_{2},\,p_{3}.\) In particular we can use this fact in order to construct a scenario tree for the discretized price process in the following way: Given a node n, the related price values \(X_{n}^{f},\,X_{n}^{e}\) and returns
price scenarios at three successor nodes s(n, i) such that \(s(n,i)_{-}=n\) and \(i\in \left\{ 1,2,3\right\} \) are obtained by
\(e_{2}\) is the two dimensional vector of ones, \(\circ \) denotes the component-wise multiplication (Hadamard product) between vectors. The related probabilities \(p_{1},\,p_{2},\,p_{3}\) are then used as conditional probabilities of going to node s(n, i) in the next step, given that node n is reached. In our example we used the initial values (root node 0) \(X_{0}^{f}=16.05,\,X_{0}^{e}=39.4\) and \(x_{0}^{f}=0.02578797,\,x_{0}^{e}=0.31791383.\)
In this way the scenario tree and the related prices can be constructed in an iterative way and one can easily calculate unconditional probabilities for the nodes, in particular the leaf nodes, from the conditional probabilities defined between the nodes. For the 10 days under considerations, this leads to a tree structure with 88573 nodes and 59049 scenarios (leaf nodes).
Based on the described setup and the concrete values used above, we implemented the dual acceptability valuation problem (76). As the underlying acceptability functional we chose a version of the average value at risk [see e.g. Pflug and Römisch (2007), 2.2.3] that allows for correct discounting, namely the average value at risk of the discounted random variable (“discounted average value at risk”) with parameter \(0\le \theta \le 1\), i.e.
In fact this is a trivial modification of the average value at risk. The only reason for defining it separately, comes from the fact that (unlike the original average value at risk) it fulfills the requirement of Propositions 5 and 6. From the conjugate representation of the average value at risk (Pflug and Römisch 2007, Theorem 2.34) it can be easily derived that the conjugate representation of the discounted value at risk is given by
with
As a heritage from the average value at risk, the discounted average value at risk is a homogeneous acceptability measure and centered at zero. Moreover, for \(\theta =1\) the discounted average value at risk equals the discounted expectation of the random variable and for \(\theta =0\) we get the essential supremum of the discounted values. Note that it is not needed to ensure \({\mathbb {E}}[Z]=\frac{1}{R^{T}}\) by a separate equation in (76), because this requirement is already implied by the constraints \(R{\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{t+1}|{\mathcal {F}}_{t}\right] =\xi _{t}\text { for }t=1,\ldots ,T-1,\text { and }R{\mathbb {E}}^{{\mathbb {P}}}\left[ \xi _{1}\right] =1\). Therefore only the constraint \(\,0\le \xi _{T}\le \frac{1}{R^{T}\theta }\) has to be added in order to ensure \(\xi _{T}\in \varUpsilon _{{\mathcal {A}}}\).
We choose \(\alpha =0\) in (74) for defining the lower bound of acceptable outcomes. Then the acceptability valuation includes the superhedging value as a special case. This is achieved by setting \(\theta =0\).
The described approaches for tree construction and optimization were implemented in Matlab™, using YALMIP (see Lofberg 2005) for formulating the discretized dual valuation problem (76) on the constructed tree. Here Gurobi™was used as linear optimization solver.
We calculated the valuation problem for 101 (equidistant) values of the acceptability parameter \(\theta \). While the capital requirement or acceptability value (which is the minimum payment that the producer would accept for contracting) can also be calculated by using the primal formulation, the dual problem allows to analyze the composition of the valuation, based on Corollary (56), which is valid also in the acceptability context, compare remark 3.3.
The results are shown in Fig. 1. In the left diagram one can see the acceptability value \(U^{*}(\theta )\) (red line) and the sum of all expectations in the decomposition (56) (blue dashed line),
where
are the effects of the turbine limits and the storage. Keep in mind that the processes \(\mu \) and \(\nu \) are results of the optimization problem and depend on the acceptability parameter \(\theta \). The difference between these two lines reveals the risk loading
Note that the production capacity P is a deterministic constant in our example, therefore the sum of covariances \(\sum _{t=0}^{T-1}{\textit{Cov}}^{{\mathbb {P}}}\left[ \mu _{t},P_{t}\right] \) vanishes.
Acceptability valuation with acceptability defined by \(AV@R_{\theta }^{R_{T}}.\) In the upper picture the acceptability value and the related expected part \(E(\theta )\) are plotted versus the parameter value \(\theta \). The lower picture shows the decomposition of the equipment effect into the effect of the generator size (EPL) and the effect of the storage size (ESL). (Color figure online)
The acceptability value goes down with increasing parameter \(\theta \). This is understandable, because the constraint \(\,0\le \xi _{T}\le \frac{1}{R^{T}\theta }\) is more restrictive for larger values of \(\theta ,\) than for smaller values, so the optimal value \(U^{*}(\theta )\) must be smaller for larger values of \(\theta \). Moreover it can be seen that the risk loading \(C(\cdot )\) goes to zero when \(\theta \) goes to 1: the acceptability value with \(\theta =1\) is exactly the the expectation part \(E(\theta )\) and no risk loading is added at this point. This comes from the fact that an agent with \(\theta =1\) uses the expectation for measuring acceptability and is therefore risk neutral. For \(\theta =0\) the agent uses the essential infimum as acceptability measure (which means that the acceptability value equals the superhedging value as discussed above) and is therefore highly risk averse. However the risk loading does not decrease monotonically in \(\theta \).
The right part of Fig. 1 shows (depending on \(\theta \)) the overall benefit of the equipment (solid blue line) and decomposes the total effect into the partial effects for availability of the turbine (production limit, dashed light blue) and for availability of storage (difference between the solid blue and the dashed light blue line). In our example the effect of the available equipment (production capacity and storage size) is large, because the efficiency of the generator is in the upper range (for gas turbines) and the storage size allows to store the energy equivalent of 500 MWh (the contract size) for roughly 2.4 days.
5 Conclusion
In the present paper we analyzed basic differences regarding the characterization of arbitrage and the pricing of bilateral contracts between electricity markets and financial markets. Tools from convex analysis and duality theory in a stochastic optimization framework were used for this purpose. While keeping a fundamentally financial view, the models used account for typical frictions like storage restrictions, production efficiency and asymmetric production possibilities that are important for energy markets but not relevant for financial markets.
Using this setup, arbitrage can be characterized by the feasibility of a system of equations and inequalities, which ensures consistency between fuel and electricity prices and the possibilities of storage, cash accumulation and production. While the characterizing system can be stated in terms of equivalent measures, the existence of equivalent martingale measures are neither necessary nor sufficient like in the classical financial results.
If the market is arbitrage free, valuation and pricing problems can be restated in terms of discount factors. The dual problems for superhedging pricing and valuation maximize the expected present value of the respective opportunity costs, where the stochastic discount factors are derived from the Lagrange multipliers and the costs account for the restrictions on storage and production capacity. The dual feasible sets are a supersets of the no-arbitrage set. Besides the stochastic discount factor process, the Lagrange multiplier for storage plays also an important role: if rescaled properly, its expectation can be interpreted as a risk adjusted version of the expected fuel price.
Finally, we considered capital requirements and acceptability prices, where the acceptability of the wealth distribution at the end was measured by concave, positive homogeneous acceptability functionals. It shows that the dual representation of those quantities is quite similar to the superhedging quantities, but that the set of feasible discount factors has to be restricted even further, depending on the concrete acceptability functional. The results show the similarities and dissimilarities between financial and energy markets quite well. In particular, the dual problems follow the same principles as superhedging prices and good deal bounds in finance, however the set of feasible discount factors is quite different from the financial case (equivalent martingales).
Of course this paper restricts the analysis to a simple, stylized market model: further frictions like storage costs, the usage of several fuels and production dependent efficiencies may be considered in future research.
Notes
It must be mentioned that in practice one often tries to estimate the value or price of a a contract by replicating it as good as possible by electricity futures. While clearly it is possible to incorporate futures into the overall approach of the current paper, we will leave this for future research. If we assume consistency between spot and futures prices, our stylized model is still sufficient for valuation and pricing. Moreover, complete hedging is not possible, because delivery patterns of futures are much more restricted than possible delivery patterns of bilateral delivery contracts. So even if one sticks to hedging with futures, there will be some residual demand that can be treated as demand \(D_{t}\) in the above terminology and valuated or priced by the proposed methods.
References
Alonso-Ayuso, A., Escudero, L. F., & Pizarro-Romero, C. (2009). Introduction to stochastic programming. Madrid: Ciencias Experimentales Y Tecnologia: Universidad Rey Juan Carlos.
Analui, B., & Kovacevic, R. (2014). Medium term hydroelectric production planning–a multistage stochastic optimization problem. Civil Engineering Infrastructures Journal (CEIJ), 47(1), 139–152.
Artzner, P., Delbaen, F., Eber, J. M., & Heath, D. (1999). Coherent measures of risk. Mathematical Finance, 9, 203–228.
Bernardo, A., & Ledoit, O. (2000). Gain, loss, and asset pricing. Journal of Political Economy, 108, 144–172.
Bertocchi, M., Consigli, G., & Dempster, M. A. (Eds.). (2011). Stochastic optimization methods in finance and energy., International series in operations research and management science Berlin: Springer.
Björk, (2009). Arbitrage theory in continuous time (3rd ed.). Oxford: Oxford University Press.
Bot, R. I., Grad, S.-M., & Wanka, G. (2009). Duality in vector space optimization. Dordrecht: Springer.
Carmona, R. (2009). Indifference pricing: Theory and applications. Princeton: Princeton University Press.
Carmona, R., & Touzi, N. (2008). Optimal multiple stopping and valuation of swing options. Mathematical Finance, 18(2), 239–268.
Cochrane, J. H., & Saá-Roquejo, J. (2000). Beyond arbitrage; good deal asset price bounds in incomplete markets. Journal of Political Economy, 108, 79–119.
Delbaen, F., & Schachermayer, W. (1994). A general version of the fundamental theorem of asset pricing. Mathematische Annalen, 300, 463–520.
Delbaen, F., & Schachermayer, W. (1998). The fundamental theorem for unbounded processes. Mathematische Annalen, 312, 212–250.
Deng, S.-J., Johnson, B., & Sogomonian, A. (2001). Exotic electricity options and the valuation of electricity generation and transmission assets. Decision Support Systems, 30, 383–392.
Dupacova, J., Gröwe-Kuska, N., & Römisch, W. (2003). Scenario reduction in stochastic programming: An approach using probability metrics. Mathematical Programming, Series A, 95, 493–511.
Eichhorn, A., Römisch, W., & Wegner, I. (2004). Polyhedral risk measures in electricity portfolio optimization. Proceedings in Applied Mathematics and Mechanics, 4(1), 7–10.
Eydeland, A., & Wolyniec, K. (2003). Energy and power risk management. New York: Wiley.
Flåm, S . D. (2008). Option pricing by mathematical programming. Optimization: A Journal of Mathematical Programming and Operations Research, 57(1), 165–182.
Fritelli, M., & Rosazza, G. E. (2002). Putting order in risk measures. Journal of Banking and Finance, 2, 1473–1486.
Gollmer, R., Nowak, W., Römisch, W., & Schultz, R. (2000). Unit commitment in power generation, a basic model and some extensions. Annals of Operations Research, 96, 167–189.
Gross, P., & Pflug, G. C. (2016). Behavioral pricing of energy swing options by stochastic bilevel optimization. Energy Systems,. https://doi.org/10.1007/s12667-016-0190-z.
Haarbrücker, G., & Kuhn, D. (2009). Valuation of electricity swing options by multistage stochastic programming. Automatica, 45, 889–899.
Hansen, L. P., & Jagannathan, R. (1991). Implications of security market data for models of dynamic economics. Journal of Political Economy, 99, 225–262.
Hao, T. (2008). Option pricing and hedging bounds in incomplete markets. Journal of Derivatives and Hedge Funds, 14(2), 89.
Heitsch H., & Römisch W. (2010) Stability and scenario trees for multistage stochastic programs. In G. Infanger (Ed.), Stochastic programming. International series in operations research & management science (Vol. 150). New York: Springer.
Jouini, E., Schachermayer, W., & Touzi, N. (2008). Optimal risk sharing for law invariant monetary utility functions. Mathematical Finance, 18(2), 269–292.
King, A. J. (2002). Duality and martingales: A stochastic programming perspective on contingent claims. Mathematical Programming, Series B, 91, 543–562.
Kovacevic, R., & Paraschiv, F. (2014). Medium term planning for thermal electricity production. Operations Research Spectrum, 36(3), 723–759.
Kovacevic, R. M. (2012). Conditional risk and acceptability mappings as banach lattice valued mappings. Statistics & Risk Modeling, 29(1), 1–18.
Kovacevic, R. M., & Pflug, G. C. (2014). Electricity swing option pricing by stochastic bilevel optimization: A survey and new approaches. European Journal of Operational Research, 237(2), 389–403.
Kovacevic, R. M., Pflug, G. C., & Vespucci, M. (Eds.). (2013). Handbook of risk management in energy production and trading., International series in operations research and management science Berlin: Springer.
Kovacevic, R. M., & Pichler, A. (2015). Tree approximation for discrete time stochastic processes–a process distance approach. Annals of OR, 235(1), 395–421.
Lofberg, J. (2005). Yalmip: A toolbox for modeling and optimization in MATLAB. In: 2004 IEEE international symposium on computer aided control systems design. https://doi.org/10.1109/CACSD.2004.1393890.
Luenberger, D. G. (1969). Optimization by vector space methods. New York: Wiley.
Nowotarski, J., & Weron, R. (2018). Recent advances in electricity price forecasting: A review of probabilistic forecasting. Renewable and Sustainable Energy Reviews, 81(1), 1548–1568.
Pagès, G., & Printems, J. (2003). Optimal quadratic quantization for numerics: The Gaussian case. Monte Carlo Methods and Applications, 9(2), 135–165.
Pansera, J. (2012). Discrete-time local risk minimization of payment processes and applications to equity linked life-insurance contracts. Insurance: Mathematics and Economics, 50, 1–11.
Pennanen, T. (2011a). Dual representation of superhedging costs in illiquid markets. Mathematics and Financial Economics, 5(4), 233–248.
Pennanen, T. (2011b). Superhedging in illiquid markets. Mathematical Finance, 21(3), 519–540.
Pennanen, T. (2012). Introduction to convex optimization in financial markets. Mathematical Programming, Series B, 134(1), 157–186.
Pfaff, B. (2008). VAR, SVAR and SVEC models: Implementation within R package vars. Journal of Statistical Software, 27(4), 1–32.
Pflug, G. C. (2006). Subdifferential representations of risk measures. Mathematical Programming, 108, 339–354.
Pflug, G. C., & Pichler, A. (2014). Multistage stochastic optimization., Springer series in operations research and financial engineering Berlin: Springer.
Pflug, G. C., & Pichler, A. (2015). Dynamic generation of scenario trees. Computational Optimization and Applications, 62(3), 641–668.
Pflug, G. C., & Römisch, W. (2007). Modeling, measuring and managing risk. Singapore: World Scientific.
Philpott, A., & Schultz, R. (2006). Unit commitment in electricity pool markets. Mathematical Programming, 108, 313–337.
Rudloff, B. (2007). Convex hedging in incomplete markets. Applied Mathematical Finance, 14(5), 437–452.
Sagastizabal, C. (2012). Divide to conquer: Decomposition methods for energy optimization. Mathematical Programming, Series B, 134(1), 187–222.
Sen, S., Yu, L., & Genc, T. (2006). A stochastic programming approach to power portfolio optimization. Operations Research, 54(1), 55–72.
Takriti, S., Birge, J., & Long, E. (1996). A stochastic model for the unit commitment problem. IEEE Transactions on Power Systems, 11, 1497–1508.
Thompson, A. (1995). Valuation of path-dependent contingent claims with multiple exercise decisions over time. Journal of Financial and Quantitative Analysis, 30(2), 271–293.
Vayanos, P., Wiesemann, W., & Kuhn, D. (2011). Hedging electricity swing options in incomplete markets. In Preprints of the 18th IFAC World Congress Milano, pp. 846–853.
Wallace, S. W., & Fleten, S. E. (2003). Stochastic programming. Vol. 10 of Handbooks in operations research and management science. Ch. Stochastic programming models in energy (pp. 637–677). Elsevier: Amsterdam.
Zephyr, L., & Anderson, C. L. (2018). Stochastic dynamic programming approach to managing power system uncertainty with distributed storage. Computational Management Science, 15(1), 87–110.
Acknowledgements
Open access funding provided by TU Wien (TUW).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kovacevic, R.M. Valuation and pricing of electricity delivery contracts: the producer’s view. Ann Oper Res 275, 421–460 (2019). https://doi.org/10.1007/s10479-018-3010-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-018-3010-0