Rivalry and uncertainty in complementary investments with dynamic market sharing

Abstract

We study the effects of revenue and investment cost uncertainty, as well non-preemption duopoly competition, on the timing of investments in two complementary inputs, where either spillover-knowledge is allowed or proprietary-knowledge holds. We find that the ex-ante and ex-post revenue market shares play a very important role in firms’ behavior. When competition is considered, the leader’s behavior departs from that of the monopolist firm of Smith (Ind Corp Change 14:639–650, 2005). The leader is justified in following the conventional wisdom (i.e., synchronous investments are more likely), whereas, the follower’s behavior departs from that of the conventional wisdom (i.e., asynchronous investments are more likely).

1 Introduction

Sometimes it pays to put the (new) cart before the (new) horse. Conventional wisdom says that “when a production process requires two extremely complementary inputs, a firm should upgrade (or replace) them simultaneously”.¹ When raising the quality of one input, a firm should upgrade its complement at the same time. These guidelines are corroborated by the deterministic models of Milgrom and Roberts (1990, 1995) and Colombo and Mosconi (1995).

However, the above literature neglects the effect of uncertainty. Smith (2005) considers operating cost and investment cost uncertainty, using a real option model, and concludes that the conventional wisdom described above does not necessarily hold if the costs are uncertain and their growth rates differ significantly. However, she neglects the effect of competition.

We provide a somewhat richer model, which considers the effect of uncertainty, as well as duopoly non-preemption competition, on the timing of the investment in two complementary inputs. We rely on the Siddiqui and Takashima (2012) leader–follower duopoly model setting, which comprises two alternative market structures: first, where spillover-knowledge (SK) is allowed, and second, where there is proprietary-knowledge (PK).

In line with Smith (2005), we find that when the costs of two inputs are uncertain and decreasing at different rates, it may pay, for both firms, to invest first in the input whose cost is falling more slowly and wait to invest in the input whose cost is falling more rapidly. However, this guideline applies more to the follower, and is dependent on the market structures and assumptions on the ex-ante and ex-post market shares of the two firms. The leader is more prone than the monopolistic firm of Smith (2005) to invest in the two inputs at the same time (follows the behavior suggested by the conventional wisdom), whereas the follower is more likely to invest in the two inputs sequentially (follows the behavior of the monopolist firm of Smith 2005)—see Fig. 13 in “Appendix C”.

Our model setting is for a non-preemption game, therefore, the leader invests at the time as a monopolist, and gets 100% of the market while operating alone, regardless of with which input(s) she operates (input 1 alone, input 2 alone, or input 1 and input 2 at the same time). Thus, the degree of competition (i.e., how the market share is divided between the two firms when both are active) does not affect the timing of the leader’s investment in the two inputs at the same time. However, we find that it influences significantly the timing of the follower’s investment. The more asymmetric is the ex-post market share between the two firms, favouring the leader, the later the follower invests, which makes more likely asynchronous input-investments. This finding is somewhat surprising, because in a leader–follower investment game as soon as the game ends for the leader, the follower is in a monopoly-like position.

Furthermore, we show that: (i) in non-preemption duopoly SK and PK markets, an increase in the input cost growth rate differences makes both firms more likely to invest in the two inputs sequentially, (ii) for an inactive firm, a decrease in the cost growth rate of one input and an increase in the cost growth rate of another input accelerates the investment in the input whose cost growth rate is increasing, deters the investment in the input whose cost growth rate is decreasing, but may have no effect on the timing of the investment in the two inputs at the same time. We also find that sequential investments are more likely: (iii) when firms are inactive and the cost growth rate of one input is increasing and the cost growth rate of another input is decreasing, so there is a negative change in the cost growth rate of the two inputs together.

Finally, we conclude that, for both the SK and the PK markets: (iv) for simultaneous-input investments, the sensitivity of the follower’s investment threshold to changes in the degree of complementarity is greater than that of the leader, and (v) an increase in the degree of complementarity between input 1 and input 2, accelerates the investments of both firms in the two inputs at the same time, if they are inactive, and the investment in input 2(1) if they are active with 1(2).

The real options literature for monopoly markets neglects the effect of competition on firms’ investment behavior, but it is very extensive and diverse in terms of practical applications (Martzoukos 2000; Smith 2005; Koussis et al. 2007; Bastian-Pinto et al. 2010; Franklin 2015; Chronopoulos and Siddiqui 2015; Farzan et al. 2015). Smets (1993) initiated a new branch of literature, now named “real option game” models, which study firms’ investment behavior considering uncertainty and (duopoly) competition (Dixit and Pindyck 1994, Ch. 9; Grenadier 1996; Huisman 2001; Weeds 2002; Huisman and Kort 2003, 2004; Paxson and Pinto 2005; Pawlina and Kort 2006; Hsu and Lambrecht 2007; Moretto 2008; Thijssen 2010; Femminis and Martini 2011; Leung and Kwok 2012; Pereira and Rodrigues 2014).²

Yet, the above literature neglects the existence of complementarity between investments. Furthermore, with few exceptions (Huisman 2001, Ch. 9; Smith 2005; Decamps et al. 2006; Nishihara 2012; Siddiqui and Takashima 2012), firms are usually assumed to hold (ex-ante) only one option to invest.

However, firms often use inputs whose qualities are complements. Therefore, investment decisions on upgrades or replacements must consider the degree of complementarity between the inputs and the possibility of sequential-input investments. In this article “complementarity” exists if the investment in one input increases the marginal or incremental return to another input in terms of “net cost savings”. More generally, in industrial organization contexts, complementarity exists if the implementation of one practice increases the marginal return to another practice (see, e.g., Carree et al. 2011). When the implementation of a technology/practice decreases the marginal return to the other technology/practice, there is “substitutability” (or subadditivity).³

Notice that, due to technological progress, input costs are usually uncertain and might follow different evolution patterns. For instance, according to a joint report by the U.S. Solar Energy Industries Association (SEIA) and GTM Research, the cost of solar power (technology) in the U.S. is now 60% cheaper than in early 2011, but the cost of the solar panel sites may have increased.⁴ Therefore, it might be optimal to invest in the solar panel sites first and defer the investment in the solar panels. Similar guidelines apply to wind energy investments, if the cost growth rates of the wind towers and wind farm sites differ significantly. Furthermore, wind towers comprise several components (e.g., the tower, rotor hub, blades, etc.) whose cost growth rates may differ significantly. Therefore, it might be optimal to replace the components of old wind farms sequentially, starting with those whose cost is decreasing more slowly.⁵

There are also industries whose production is organized in sub-industries, with each sub-industry corresponding to a production stage of the overall industry. This is the case of the textile industry, which is organized in four main sub-industries: spinning, weaving, finishing and making up, where there is high (production quality/efficiency) complementarity. The adoption of a more advanced spinning technology increases not only the efficiency of the spinning mill but also the efficiency of the weaving mills which use yarns produced by the spinning mill whose technology was upgraded. But asynchronous investments might be possible if there is a high cost growth rate asymmetry between the technologies used in each of these sub-industries. Thus, we can see firms operating with highly advanced spinning technologies and relatively obsolete weaving mills, or vice-versa (Griffiths et al. 1992; Conrad and James 1995).

The concept of complementarity is also used to study economic decisions in other contexts. For instance, when planning R&D activities, firms make strategic decisions regarding the degree of complementarity (sometimes called compatibility) between the incumbent products and the new products they aim to launch in the future since the diffusion of an innovation depends, to some extent, on the diffusion of complement innovations which amplify its value.⁶

It has been also argued that the pace of modernization of industries is often influenced by the degree of technological complementarity between the technologies adopted in the industries. Milgrom and Roberts (1994) study the Japanese economy between 1940 and 1995 to interpret the characteristic features of Japanese economic organization in terms of the complementarity between some of the most important elements of its economic structure. Colombo and Mosconi (1995) examine the diffusion of flexible automation production and design/engineering technologies in the Italian metalworking industry, giving particular attention to the role of the technological complementarity and the learning effects associated with the experience of previously available technologies. From Milgrom and Roberts (1990, 1995) models, we infer that it is relatively unprofitable to adopt only one part of the modern manufacturing technologies. Milgrom and Roberts (1990, p. 524) suggest that “we should not see an extended period of time during which there are substantial volumes of both highly flexible and highly specialized equipment being used side-by-side”.

The rest of the article is organized as follows. In Sect. 2, we outline the model assumptions and describe the two market structures. In Sect. 3, we derive the value functions and investment thresholds for the two firms and each of the market structures, and provide some illustrative sensitivity analysis. In Sect. 4, we show some further results. In Sect. 5, we conclude and offer guidelines for future research.

2 The model

Suppose a market consists of two idle⁷ firms (i and j), where $i,j=\left\{ {L,F} \right\}$ with “L” meaning “leader” and “F” meaning “follower”, considering the investment in two (available) complementary inputs (input 1 and input 2), one after the other or both at the same time depending on which of these choices maximizes value. The instantaneous “net cost savings” (NCS) of firm i from the investment in input k is:

$$\begin{aligned} X(t)\gamma _k D_{k_i k_j } \end{aligned}$$

(1)

where X(t) is the market revenue at time t; $\gamma _k \in ({0,1})$ is the “proportion of the revenue of firm i that is expected to be saved if investing in input k”, with $k=\{ {0,1,2,12}\}$, where “0” means that firm i is not yet active and “1”, “2” and “12” mean that firm i operates with input 1, input 2, or the two inputs at the same time, respectively; and $D_{k_i k_j }$ is the market share of firm i for when the two firms operate with input(s) k.

Market revenue, X(t), follows a geometric Brownian motion (gBm) process given by:⁸

$$\begin{aligned} dX=\mu _{X} Xdt+\sigma _{X} Xdz_{X} \end{aligned}$$

(2)

where $\mu _{X}$ is the revenue growth rate, $\sigma _{X}$ is the revenue volatility and $dz_{X}$ is the increment of a standard Wiener process. For convergence reasons $r-\mu _{X} >0$ holds, where r is the risk free interest rate.

Operating with input 1 provides a NCS ($S_1$) which is a fraction ($\gamma _1 )$ of the firm i’s revenue ($X.D_{k_i k_j }$):

$$\begin{aligned} S_1 =\gamma _1 X.D_{k_i k_j } \end{aligned}$$

(3)

Since NCS is proportional to revenue and this follows a gBm process, so NCS also follows a gBm process. Similarly, the use of input 2 alone provides NCS equal to:

$$\begin{aligned} S_2 =\gamma _2 X.D_{k_i k_j } \end{aligned}$$

(4)

The simultaneous use of the two inputs yields a NCS equal to:⁹

$$\begin{aligned} S_{12} =\gamma _{12} X.D_{k_i k_j } \end{aligned}$$

(5)

The complementarity between the two inputs, $\xi$, with $\xi =\gamma _{12} -(\gamma _1 +\gamma _2 )$ and $\xi \in ({0,1} )$, is shown as:

$$\begin{aligned} \gamma _{12} >(\gamma _1 +\gamma _2 ) \end{aligned}$$

(6)

The investment (sunk) cost of the inputs 1 and 2, respectively $I_1$ and $I_2$, also follows gBm processes:

$$\begin{aligned} dI_1 =\mu _{I_1 } I_1 dt+\sigma _{I_1 } I_1 dz_{I_1 } \end{aligned}$$

(7)

and

$$\begin{aligned} dI_2 =\mu _{I_2 } I_2 dt+\sigma _{I_2 } I_2 dz_{I_2 } \end{aligned}$$

(8)

where $\mu _{I_1 }$ and $\mu _{I_2 }$ are the growth rates of the cost of input 1 and input 2, respectively; $\sigma _{I_1 }$ and $\sigma _{I_2 }$ are the cost volatilities of inputs 1 and 2, respectively; and $dz_{I_1 }$ and $dz_{I_2 }$ are the increments of the standard Wiener processes for the cost of input 1 and input 2, respectively.

If firms invest in the two inputs at the same time, the investment cost is $I_{12}$ which we assume also follows an independent gBm process, given by:¹⁰

$$\begin{aligned} dI_{12} =\mu _{I_{12} } I_{12} dt+\sigma _{I_{12} } I_{12} dz_{I_{12} } \end{aligned}$$

(9)

where $\mu _{I_{12} }$ is the instantaneous cost growth rate; $\sigma _{I_{12} }$ is the cost volatility; and $dz_{I_{12} }$ is the increment of the standard Wiener process.

Following Smets (1993), we impose the following constraints on the parameter $D_{k_i k_j }$, where i represents the “leader” and j the “follower”:

$$\begin{aligned} (D_{12_L 0_F } =D_{1_L 0_F } =D_{2_L 0_F } )>(D_{12_L 1_F } =D_{12_L 2_F } )>(D_{12_L 12_F } =D_{1_L 1_F } =D_{2_L 2_F } ) \end{aligned}$$

(10)

with $D_{12_L 0_F } =D_{1_L 0_F } =D_{2_L 0_F } =1.0$, $D_{12_L 12_F } =D_{1_L 1_F } =D_{2_L 2_F } =0.5$ and $D_{12_L 1_F } =D_{12_L 2_F } \in (0.5,1.0)$, which ensures that: (i) the leader gets 100% of the market share if active alone; (ii) the two firms get the same market share (50%) if active with the same input(s); (iii) the leader gets more than 50% of the market share if operating with the two inputs and the follower operates with one input only.¹¹ Additionally, the sum of the market shares of the two firms equals 100% if at least one of the firms is active.

The “partial differential equation” (PDE) (11) describes the evolution of the value $F_k^{i,j}$ of an inactive firm (i, j) that holds the option to invest in input(s) k:

$$\begin{aligned}&\frac{1}{2}\sigma _{X} ^{2}X^{2}\frac{\partial ^{2}F_k^{i,j} }{\partial X^{2}}+\frac{1}{2}\sigma _{I_k }^2 I_k ^{2}\frac{\partial ^{2}F_k^{i,j} }{\partial I_k ^{2}}+XI_k \sigma _{X} \sigma _{I_k } \rho _{XI_k } \frac{\partial ^{2}F_k^{i,j} }{\partial X\partial I_k }+\,\mu _{X} X\frac{\partial F_k^{i,j} }{\partial X}\nonumber \\&\quad +\,\mu _{I_k } I_k \frac{\partial F_k^{i,j} }{\partial I_k }-rF_k^{i,j} = 0 \end{aligned}$$

(11)

where $\rho _{XI_k }$ is the correlation coefficient between the market revenue (X) and the cost of input(s) k ($I_k$), with $k\in \left\{ {1,2,12} \right\}$, r is the riskless interest rate, and $\rho _{XI_K = 0}$.

A useful analytical simplification of (11) is achieved by taking advantage of the natural homogeneity of degree one of the investment problem—i.e., $F_k^{i,j} (X,I_k )=I_k f_k^{i,j} (X/I_k )$, where $f_{12}^{i,j}$ is the variable to be determined.¹² We reduce the dimensionality of the PDE (11) from two to one using the following variable change: $\phi _k =X/I_k$.¹³ Substituting $\phi _k$ in (11) yields (12):¹⁴

$$\begin{aligned} \frac{1}{2}\sigma _{m_k }^2 (\phi _k )^{2}\frac{\partial ^{2}f_k^{i,j} (\phi _k )}{\partial \phi _k ^{2}}+\left( {\mu _{X} -\mu _{I_k } } \right) (\phi _k )\frac{\partial f_k^{i,j} (\phi _k )}{\partial \phi _k }-(r-\mu _{I_k } )f_k^{i,j} (\phi _k )=0 \end{aligned}$$

(12)

where $\sigma _{m_k }^2 =\sigma _{X}^2 +\sigma _{I_k }^2 -2\rho _{XI_k } \sigma _{X} \sigma _{I_k }$.

Equation (12) is a homogeneous second-order linear ordinary differential equation (ODE) whose general solution has the form:

$$\begin{aligned} f_k^{i,j} (\phi _k )=A_k^{i,j} (\phi _k )^{\psi _1 }+B_k^{i,j} (\phi _k )^{\psi _2 } \end{aligned}$$

(13)

where $\psi _1$ ($\psi _2$) is the positive (negative) solution of the characteristic quadratic function of the ODE: $0.5(\sigma _{m_k } )^{2}\psi _1 (\psi _1 -1)+(\mu _{X} -\mu _{I_k } )\psi _1 -(r-\mu _{I_k } )=0$. Solving this equation for $\psi _1$ ($\psi _2$) we get:

$$\begin{aligned} \psi _{1(2)} =\frac{1}{2}-\frac{\mu _{X} -\mu _{I_k } }{\sigma _{m_k }^2 }+(-)\sqrt{\left( {\frac{(\mu _{X} -\mu _{I_k } )}{\sigma _{m_k }^2 }-\frac{1}{2}} \right) ^{2}+\frac{2(r-\mu _{I_k } )}{\sigma _{m_k }^2 }} \end{aligned}$$

(14)

Notice that as the ratio of market revenue over cost of input k ($\phi _k$) approaches 0, the value of the option to invest in input k becomes worthless. Therefore, in (13) $B_k^{i,j} =0$. Using the appropriate “value matching” (VM) and “smooth pasting” (SP) conditions for each investment scenario, in the next section, we determine the constants ($A_k^{i,j}$) and the investment thresholds for both firms.

2.1 Industry settings

We formulate a leader–follower investment problem for two specific industry scenarios, following Siddiqui and Takashima (2012, p. 585): (i) symmetric non-preemptive duopoly with “spillover-knowledge” (SK); and (ii) symmetric non-preemptive duopoly with “proprietary-knowledge” (PK). The difference between these two scenarios is that, in the former, due to a weak patent-protection, the follower is allowed to proceed with his first-stage investment (in input 1) immediately after the leader’s entry (with input 1) and, in the latter, due to a strong patent-protection, the leader invests in the two inputs sequentially (first in input 1 and then in input 2) with the follower inactive.

2.1.1 Non-preemptive duopoly with SK

This industry setting considers a duopoly where the leader cannot be pre-empted by the follower in the first move. After the leader’s first move, the follower is allowed to proceed, since he obtains knowledge of the leader investment (input 1) via spillover-knowledge. The diagram in Fig. 1 indicates both investment approaches for the two firms: sequential-input investment (solid lines) and simultaneous-input investment (dotted lines). From state (1,1) the competition for establishing a dominant position remains sequential until the investment cycle is completed in state (2,2). Similarly, in the direct approach (simultaneous-input investment-dotted line), the leader invests first, before the follower is allowed to proceed. We add to the Siddiqui and Takashima (2012) investment problem the effects of both the investment cost uncertainty and the complementarity between the inputs in the two stages.

We tried to use a max-option analysis (see Decamps et al. 2006; Nishihara 2012) for the optimization of the first-stage of the investment game, where firms solve the following optimal stopping problem: $\sup \limits _{\tau }\hbox {E}[ {e^{-r\tau }V( {X(\tau ),I_1 (\tau ),I_2 (\tau ),I_{12} (\tau )} )} ]$. Yet such framework is more suitable for mono-factor real option game models. When applied to our multi-factor real option game model, it increases significantly the complexity of the derivations, since our assumption regarding the homogeneity of degree one for PDE (11) would not hold—we would have to solve a three-dimensional stochastic problem which would require complex numerical solutions.

Fig. 1

Duopoly state transition with SK. Note: Due to SK the follower invests in input 1 before the leader investment in input 2. The dotted lines in the diagram represent the direct approach where the two firms invest, one after the other, in the two inputs at the same time. The solid lines represent the sequential-input investment approach for the two firms. $\phi _{1_L }^{*}$ and $\phi _{1_F }^{*}$ are the leader and the follower thresholds to invest in input 1 alone, respectively; $\phi _{1+2_L }^{*}$ and $\phi _{1+2_F }^{*}$ are the leader and the follower thresholds to invest in input 2 if active with input 1, respectively; $\phi _{12_L }^{*}$ and $\phi _{12_F }^{*}$ are the leader and the follower thresholds to invest in the two inputs at the same time, respectively. The information in between brackets refers to the equation provided in Sect. 3 for the investment thresholds

2.1.2 Non-preemptive duopoly with PK

In this scenario the leader is allowed to invest in inputs 1 and 2, sequentially or simultaneously, with the follower inactive, due to proprietary-knowledge.

3 Analytical results

3.1 Simultaneous-input investments

3.1.1 SK market

In this section we consider that both firms are inactive at stage (0,0) and invest, one after the other, in the two inputs at the same time if optimal to do so. $I_{12}$ is the investment cost if firms invest in the two inputs at the same time.

Follower

ODE (12), with $i=F$ and $k=12$, describes the follower value if inactive in a SK market, whose general solution is given by:¹⁵

$$\begin{aligned} f_{12}^{\mathrm{F,SK}} =A_{12}^{\mathrm{F,SK}} \phi _{12}^{\eta _1 }+B_{12}^{\mathrm{F,SK}} \phi _{12}^{\eta _2 } \end{aligned}$$

(15)

where $\eta _1 (\eta _2 )$ is the positive (negative) solution of the characteristic quadratic function of the ODE: $\frac{1}{2}(\sigma _{m_{12} } )^{2}\eta (\eta -1)+(\mu _{X} -\mu _{I_{12} } )\eta -(r-\mu _{I_{12} } )=0$. Solving this equation for $\eta _1 (\eta _2 )$ leads to:

$$\begin{aligned} \eta _{1(2)} =\frac{1}{2}-\frac{\mu _{X} -\mu _{I_{12} } }{\sigma _{m_{12} }^2 }+(-)\sqrt{\left( {\frac{(\mu _{X} -\mu _{I_{12} } )}{\sigma _{m_{12} }^2 }-\frac{1}{2}} \right) ^{2}+\frac{2(r-\mu _{I_{12} } )}{\sigma _{m_{12} }^2 }} \end{aligned}$$

(16)

where $\sigma _{m_{12} }^2 =\sigma _{X}^2 +\sigma _{I_{12} }^2 -2\rho _{XI_{12} } \sigma _{X} \sigma _{I_{12} }$.

Notice that as $\phi _{12}$ approaches 0, the value of the option to invest in input 1 and input 2 at the same time becomes worthless. Therefore, in (15) $B_{12} =0$.¹⁶

The VM condition:

$$\begin{aligned} F_{12}^{\mathrm{F,SK}} (X^{*},I_{12}^*)=\frac{X^{*}\gamma _{12} D_{12_F 12_L } }{r-\mu _{X} }-I_{12_F }^*\end{aligned}$$

(17)

has the following economic interpretation: before investing in input 1 and input 2 at the same time the follower holds the option to invest whose value is given by the left-hand side of Eq. (17). This option will be exercised at the moment the option value equals the present value of the cash flows obtained from operating with the two inputs forever less the investment cost (right-hand side of Eq. 17).

Dividing (17) by $I_{12_F }^*$, replacing $f_{12}^{\mathrm{F,SK}} (\phi _{12}^{*})$ by $A_{12}^{\mathrm{F,SK}} {\phi _{12}^*}^{\eta _1 }$ and rewriting gives,

$$\begin{aligned} A_{12}^{\mathrm{F,SK}} \phi _{12_F }^{*\mathrm{SK}\eta _{1}}=\frac{\phi _{12_F }^{*\mathrm{SK}} \gamma _{12} D_{12_F 12_L } }{r-\mu _{X} }-1 \end{aligned}$$

(18)

The SP condition is:

$$\begin{aligned} \eta _1 A_{12}^{\mathrm{F,SK}} \phi _{12_F }^{*\mathrm{SK}} {}^{(\eta _1 -1)}=\frac{\gamma _{12} D_{12_F 12_L } }{r-\mu _{X} } \end{aligned}$$

(19)

Solving together Eqs. (18) and (19) and rearranging we get the follower threshold to invest in the inputs 1 and 2 at the same time, $\phi _{12_F }^{*\mathrm{SK}}$, and the constant $A_{12}^{\mathrm{F,SK}}$, respectively:

$$\begin{aligned} \phi _{12_F }^{*\mathrm{SK}}= & {} \frac{\eta _1 }{\eta _1 -1}\frac{r-\mu _{X} }{\gamma _{12} D_{12_F 12_L } } \end{aligned}$$

(20)

$$\begin{aligned} A_{12}^{\mathrm{F,SK}}= & {} \frac{\phi _{12}^{*\mathrm{SK}} {}^{(1-\eta _1 )}}{\eta _1 }\frac{\gamma _{12} D{ }_{12_F 12L}}{r-\mu _{X} } \end{aligned}$$

(21)

The follower value function is given by:

$$\begin{aligned} f_{12}^{\mathrm{F,SK}} (\phi _{12} )=\left\{ {\begin{array}{ll} A_{12}^{\mathrm{F,SK}} \phi _{12} ^{\eta _1 } &{} \hbox { if }\phi _{12} <\phi _{12_F }^{*\mathrm{SK}} \\ \frac{\phi _{12} \gamma _{12} D_{12_F 12_L } }{r-\mu _{X} }-1 &{} \hbox { if }\phi _{12} \ge \phi _{12_F }^{*\mathrm{SK}} \\ \end{array}} \right. \end{aligned}$$

(22)

The first row of (22) represents the follower option to invest in the two inputs at the same time; the second row is the perpetual payoff the follower attains from operating in the market with the leader (both with the two inputs) from the instant $\phi _{12_F }^*$ is reached.

Leader

Assuming that the follower invests in the two inputs at the same time when $\phi _{12_F }^{*\mathrm{SK}}$ is reached, the leader’s payoff is given by:

$$\begin{aligned} F_{12}^{L,SK} \left( {X,I_{12} } \right)= & {} \left. E \right| _{X\left( 0 \right) =X} \left[ \mathop {\smallint }\nolimits _{t=\tau }^{T_{12_F } } X_\tau \gamma _{12} D_{12_L 0_F } e^{-r\tau }d\tau -I_{12_L }^*\right. \nonumber \\&\left. +\mathop {\smallint }\nolimits _{T_{12_{F}}}^{\infty } X_\tau \gamma _{12} D_{12_L 12_F } e^{-r\tau }d\tau \right] \end{aligned}$$

(23)

where the first integral represents the payoff attained from the instant of the investments in inputs 1 and 2 at the same time made before the follower invests in inputs 1 and 2 at the same time; $I_{12_L }^*$ is the cost of the two inputs at the time of the investment; and the second integral represents the leader payoff from operating with the follower (both firms with the two inputs) from the moment the follower invests in inputs 1 and 2 at the same time.

The leader value function is given by:

$$\begin{aligned} f_{12}^{L,SK} \left( {\emptyset _{12} } \right) \left\{ {\begin{array}{ll} A_{12}^{\mathrm{L},\mathrm{SK}} \emptyset _{12} ^{\eta _1 }+\frac{\emptyset _{12_F }^{*\mathrm{SK}} \gamma _{12} \left( {D_{12_L 12_F } -D_{12_L 0_F } } \right) }{r-\mu _{X} }\left( {\frac{\emptyset _{12} }{\emptyset _{12_F }^{*\mathrm{SK}} }} \right) ^{\eta _1 } &{} if\,\emptyset _{12} <\emptyset _{12_L }^{*SK} \\ \frac{\emptyset _{12} \gamma _{12} D_{12_L 0_F } }{r-\mu _{X} }-1+\frac{\emptyset _{12_F }^{*\mathrm{SK}} \gamma _{12} \left( {D_{12_L 12_F } -D_{12_L 0_F } } \right) }{r-\mu _{X} }\left( {\frac{\emptyset _{12} }{\emptyset _{12_F }^{*\mathrm{SK}} }} \right) ^{\eta _1}&{}if\,\emptyset _{12}\epsilon \left[ {\emptyset _{12_L }^{*\mathrm{SK}} , \emptyset _{12_F }^{*\mathrm{SK}} } \right) \\ \frac{\emptyset _{12} \gamma _{12} D_{12_L 12_F } }{r-\mu _{X} }-1 &{} if\,\emptyset _{12} \ge \emptyset _{12_F }^{*\mathrm{SK}} \\ \end{array}} \right. \nonumber \\ \end{aligned}$$

(24)

In the first row, the first term is the leader option value to invest in the two inputs at the same time, which is the same as that of a monopolist, and the second term is a correction factor which incorporates the fact that in the future if $\phi _{12_F }^{*\mathrm{SK}}$ is reached the follower will invest in inputs 1 and 2 and the leader payoff will be reduced (in markets where there is fear of pre-emption, this term does not exists because, at this stage, both firms have equal chances of being the leader).¹⁷ It is negative given that $(D_{12_L 12_F } -D_{12_L 0_F } )<0$—see inequality 10.¹⁸ In the second row, the first two terms represent the leader payoff from operating with the two inputs from $\phi _{12_L }^{*\mathrm{SK}}$ onwards (with the follower inactive) less the investment cost, the third term is the correction factor described above. The third row is the leader’s perpetual payoff, while operating with the follower (both firms with the two inputs), from the instant the follower invests in the two inputs, less the investment cost.¹⁹

This is a non-preemption game and, therefore, the leader enters the market at the moment her payoff is maximized. ODE (12), with $k=12$, describes the leader’s value if inactive, whose solution is given by:

$$\begin{aligned} f_{12}^{\mathrm{L,SK}} =A_{12}^{\mathrm{L,SK}} \phi _{12} ^{\eta _1 } \end{aligned}$$

(25)

The constant $A_{12}^{\mathrm{L,SK}}$ and the leader threshold, $\phi _{12_L }^{*\mathrm{SK}}$, are determined using the following VM and SP conditions. The VM condition is given by:²⁰

$$\begin{aligned} A_{12}^{\mathrm{L,SK}} {\phi _{12_L }^{*\mathrm{SK}}}^{\eta _1 }=\frac{\phi _{12_L }^{*\mathrm{SK}} \gamma _{12} D_{12_L 0_F } }{r-\mu _{X} }-1 \end{aligned}$$

(26)

SP condition:

$$\begin{aligned} \eta _1 A_{12}^{\mathrm{L,SK}} {\phi _{12_L }^{*\mathrm{SK}}} ^{(\eta _1 -1)}=\frac{\gamma _{12} D_{12_L 0_F } }{r-\mu _{X} } \end{aligned}$$

(27)

Solving together (26) and (27) we obtain $A_{12}^{L,\mathrm{SK}}$ and $\phi _{12_L }^{*\mathrm{SK}}$, given by:

$$\begin{aligned} A_{12}^{\mathrm{L,SK}}= & {} \frac{\gamma _{12} D_{12_L 0_F } }{(r-\mu _{X} )\eta _1 {\phi _{12_L }^{*\mathrm{SK}}} ^{(\eta _1 -1)}} \end{aligned}$$

(28)

$$\begin{aligned} \phi _{12_L }^{*\mathrm{SK}}= & {} \frac{\eta _1 (r-\mu _{X} )}{\eta _1 \gamma _{12} D_{12_L 0_F } -\gamma _{12} D_{12_L 0_F } } \end{aligned}$$

(29)

Notice that although the leader’s investment threshold for a duopoly non-preemption market is the same as that of a monopolistic firm, its value is lower because the follower may enter the market later, eroding its market share.²¹

3.1.2 PK market

“Simultaneous-input” investments are “one-shot” games for the two firms in both the PK and the SK markets. Therefore, the investment behavior of the leader and the follower is the same for the two markets and the following proposition holds:²²

Proposition 1

$$\begin{aligned} f_{12}^{\mathrm{L,PK}} (\phi _{12})= & {} f_{12}^{\mathrm{L,SK}} (\phi _{12} )\, \text {---}\,\textit{given by expression}\,24 \end{aligned}$$

(29a)

$$\begin{aligned} f_{12}^{\mathrm{F,PK}} (\phi _{12} )= & {} f_{12}^{\mathrm{F,SK}} (\phi _{12} )\,\text {---} \textit{given by expression}\,22 \end{aligned}$$

(29b)

$$\begin{aligned} \phi _{12_L }^{*\mathrm{PK}}= & {} \phi _{12_L }^{*S\mathrm{K}} \,\text {---}\,\textit{given by Eq.}\,29 \end{aligned}$$

(29c)

$$\begin{aligned} \phi _{12_F }^{*\mathrm{PK}}= & {} \phi _{12_F }^{*S\mathrm{K}} \,\text {---}\,\textit{given by Eq.}\,20 \end{aligned}$$

(29d)

where $f_{12}^{\mathrm{L,PK}} (\phi _{12} )$ and $\phi _{12_L }^{*\mathrm{PK}}$ are the leader’s value function and investment threshold for the PK market, respectively; $f_{12}^{\mathrm{F,PK}} (\phi _{12} )$ and $\phi _{12_F }^{*P\mathrm{K}}$ are the follower’s value function and investment threshold for the PK market, respectively. Proof: see “Appendix B”.

3.1.3 Illustrative results (base parameter values are in Tables 1, 2 and 3)

The results above show that for both markets, ceteris paribus: (i) an increase in $\rho _{X/I_{12} }$, or $\xi$, or $\mu _{I_{12} }$ accelerates the investment in the two inputs at the same time for both firms, with the follower slightly more sensitive than the leader to these changes; and (ii) an increase in $D_{12_L 12_F }$ delays the investment of the follower and has no effect on the investment threshold of the leader. This latter result means that the more asymmetric the competition between the two firms (in terms of ex-post market share) the later the investment in the two inputs simultaneously for the follower.

Table 1 Market variables

Table 2 Firms’ market revenue share, $D_{k_i k_j }$

Table 3 Complementarity related factors, $\xi$ and $\gamma _k$

However, input cost uncertainty can make such behavior unlikely for the follower (in Sect. 4.1 we discuss this finding further). We also find that an increase in the revenue volatility or the investment cost volatility delays the investment for both firms.²³

3.2 “Sequential-input” investments

3.2.1 SK market

SK market, terminal-state: follower

We start by deriving the follower’s value function and investment threshold for the state where he is active with input 1 and the leader is active with both inputs. Therefore, the follower is in a monopoly-like position and his behavior replicates that of a monopolist.²⁴ His value comprises the option value to invest in input 2, $f_{1+2}^{\mathrm{F,SK}} (\phi _2 )$, plus the cost savings attained from operating with input 1 forever, $X\gamma _1 D_{1_F 12_L } /(r-\mu _{X} )$. Following similar procedures as those described in the previous section, we get the homogeneous second-order linear ODE (12), with $k=2$, whose general solution has the form:

$$\begin{aligned} f_{1+2}^{\mathrm{F,SK}} (\phi _2 )=A_{1+2}^{\mathrm{F,SK}} \phi _2 ^{\psi _1 } \end{aligned}$$

(30)

where $\psi _1$ is the positive solution of the characteristic quadratic function of the homogeneous part of Eq. (12): $0.5(\sigma _{m_2 } )^{2}\psi (\psi -1)+(\mu _{X} -\mu _{I_2 } )\psi -(r-\mu _{I_2 } )=0$. Solving this equation for $\psi _1$ we get:

$$\begin{aligned} \psi _1 =\frac{1}{2}-\frac{\mu _{X} -\mu _{I_2 } }{\sigma _{m_2 }^2 }+\sqrt{\left( {\frac{(\mu _{X} -\mu _{I_2 } )}{\sigma _{m_2 }^2 }-\frac{1}{2}} \right) ^{2}+\frac{2(r-\mu _{I_2 } )}{\sigma _{m_2 }^2}} \end{aligned}$$

(31)

where $\sigma _{m_2 }^2 =\sigma _{X}^2 +\sigma _{I_2 }^2 -2\rho _{XI_2 } \sigma _{X} \sigma _{I_2 }$.

The VM condition is:

$$\begin{aligned} F_{1+2}^{\mathrm{F,SK}} (X^{*},I_2^*)+\frac{X^{*}\gamma _1 D_{1_F 12_L } }{r-\mu _{X} }=\frac{X^{*}\gamma _{12} D_{12_F 12_L } }{r-\mu _{X} }-I_{2_F }^{*} \end{aligned}$$

(32)

Before investing in input 2 the follower’s payoff is equal to the value of the option to invest in input 2 plus the present value from operating with input 1 forever, with the leader active with the two inputs (left-hand side of 32). The option to invest in input 2 is exercised at the moment its value equals the present value of the cash flows the follower obtains from operating with the two inputs forever less the cost of input 2 (right-hand side of 32).

Dividing (32) by $I_{2_F }^{*}$, replacing $f_{1+2}^{\mathrm{F,SK}} (\phi _2^{*})$ by $A_{1+2}^{\mathrm{F,SK}} {\phi _{1+2}^{*\mathrm{SK}}} ^{\psi _1 }$ and rewriting gives:²⁵

$$\begin{aligned} A_{1+2}^{\mathrm{F,SK}} {\phi _{1+2_F }^{*\mathrm{SK}}} ^{\psi _1 }=\frac{\phi _{1+2_F }^{*\mathrm{SK}} \gamma _{12} D_{12_F 12_L } -\phi _1 \gamma _1 D_{1_F 12_L } }{r-\mu _{X} }-1 \end{aligned}$$

(33)

The SP condition is given by:

$$\begin{aligned} \psi _1 A_{1+2}^{\mathrm{F,SK}} {\phi _{1+2_F }^{*\mathrm{SK}}} ^{(\psi _1 -1)}=\frac{\gamma _{12} D_{12_F 12_L } }{r-\mu _{X} } \end{aligned}$$

(34)

Solving together Eqs. (33) and (34) we get the follower threshold for investing in input 2 if active with input 1, $\phi _{1+2_F }^{*\mathrm{SK}}$, and the constant $A_{1+2}^{\mathrm{F,SK}}$, respectively:

$$\begin{aligned} \phi _{1+2_F }^{*\mathrm{SK}}= & {} \frac{\psi _1 (\mu _{X} -r)-\psi _1 \phi _1 \gamma _1 D_{1_F 12_L } }{\gamma _{12} D_{12_F 12_L } (1-\psi _1 )} \end{aligned}$$

(35)

$$\begin{aligned} A_{1+2}^{\mathrm{F,SK}}= & {} \frac{\gamma _{12} D_{12_F 12_L } }{(r-\mu _{X} )\psi _1 {\phi _{1+2_F }^{*\mathrm{SK}}} ^{(\psi _1 -1)}} \end{aligned}$$

(36)

SK market, first-state: follower

Now we derive the follower’s value function and investment threshold for the state where he is inactive and the leader is active with input 1. Following similar procedures as those of the previous subsections we get the homogeneous second-order linear ODE (12), with $k=1$, whose general solution in this case has the form:

$$\begin{aligned} f_1^{\mathrm{F,SK}} (\phi _1 )=A_1^{\mathrm{F,SK}} \phi _1 ^{\beta _1 } \end{aligned}$$

(37)

where $\beta _1$ is the positive solution of the characteristic quadratic function of the homogeneous part of Eq. (12): $0.5(\sigma _{m_1 } )^{2}\beta (\beta -1)+(\mu _{X} -\mu _{I_1 } )\beta -(r-\mu _{I_1 } )=0$. Solving this equation for $\beta _1$ we get:

$$\begin{aligned} \beta _1 =\frac{1}{2}-\frac{\mu _{X} -\mu _{I_1 } }{\sigma _{m_1 }^2 }+\sqrt{\left( {\frac{(\mu _{X} -\mu _{I_1 } )}{\sigma _{m_1 }^2 }-\frac{1}{2}} \right) ^{2}+\frac{2(r-\mu _{I_1 } )}{\sigma _{m_1 }^2}} \end{aligned}$$

(38)

where $\sigma _{m_1 }^2 =\sigma _{X}^2 +\sigma _{I_1 }^2 -2\rho _{XI_1 } \sigma _{X} \sigma _{I_1 }$.

The VM condition is:

$$\begin{aligned} F_1^{\mathrm{F,SK}} (X,I_1 )=\frac{X^{*}\gamma _1 D_{1_F 1_L } }{r-\mu _{X} }-I_{1_F }^*\end{aligned}$$

(39)

Before investing in input 1 the follower’s payoff is equal to the value of the option to invest in input 1 (left-hand side of Eq. 39). This option will be exercised at the moment its value equals the follower’s present value of the cash flows from operating with input 1 forever less the investment cost (right-hand side of Eq. 39).

Dividing (39) by $I_{1_F }^{*}$, replacing $f_1^{\mathrm{F,SK}} (\phi _1 )$ by $A_1^{\mathrm{F,SK}} {\phi _1^{*\mathrm{SK}}} ^{\beta _1 }$ and rewriting gives:

$$\begin{aligned} A_1^{\mathrm{F,SK}} {\phi _{1_F }^{*\mathrm{SK}}} ^{\beta _1 }=\frac{\phi _{1_F }^{*\mathrm{SK}} \gamma _1 D_{1_F 1_L } }{r-\mu _{X} }-1 \end{aligned}$$

(40)

The SP condition is:

$$\begin{aligned} \beta _1 A_1^{\mathrm{F,SK}} {\phi _{1_F }^{*\mathrm{SK}}} ^{(\beta _1 -1)}=\frac{\gamma _1 D_{1_F 1_L } }{r-\mu _{X} } \end{aligned}$$

(41)

Solving together Eqs. (40) and (41) we get the follower’s threshold for investing in input 1 if inactive, $\phi _{1_F }^{*\mathrm{SK}}$, and the constant $A_1^{\mathrm{F,SK}}$:

$$\begin{aligned} \phi _{1_F }^{*\mathrm{SK}}= & {} \frac{\beta _1 }{\beta _1 -1}\frac{r-\mu _{X} }{\gamma _1 D_{1_F 1_L } } \end{aligned}$$

(42)

$$\begin{aligned} A_1^{\mathrm{F,SK}}= & {} \frac{{\phi _{1_F }^{*\mathrm{SK}}} ^{(1-\beta _1 )}}{\beta _1 }\frac{\gamma _1 D_{1_F 1_L } }{r-\mu _{X} } \end{aligned}$$

(43)

SK market-terminal state: leader

At the instant the leader invests in input 2, $\tau$, her payoff is given by:

$$\begin{aligned} F_{1+2}^{\mathrm{L,SK}} (X,I_2 )=E\left[ {\int _\tau ^{T_{2_F } } {X_t \gamma _{12} D_{12_L 1_F } e^{-r\tau }d\tau -I_{2_L }^*+} \int _{T_{2_F } }^\infty {X_t \gamma _{12} D_{12_L 12_F } e^{-r\tau }d\tau } } \right] \end{aligned}$$

(44)

where the first integral represents the leader’s payoff from the moment of the investment in input 2 until the instant before the follower invests in input 2; and the second integral represents the leader’s payoff from the moment the follower invests in input 2 onwards.

This is a non-preemption game, hence the leader, if active with input 1, invests in input 2 at the point her payoff is maximized. ODE (12), with $k=2$, describes the leader’s value whose solution is given, in this case, by:

$$\begin{aligned} f_{1+2}^{L,\mathrm{SK}} (\phi _2 )=A_{1+2}^{L,\mathrm{SK}} \phi _2 ^{\psi _1 } \end{aligned}$$

(45)

The constant $A_{1+2}^{L,\mathrm{SK}}$ and the leader’s threshold are determined using the following VM and SP conditions:

Fig. 2

Duopoly state transition with PK. Note: The dotted lines refer to the direct approach where the two firms invest, one after the other, in the two inputs at the same time; the solid lines refer to the scenario where the two firms invest, one after the other, in the two inputs sequentially. The information in between brackets refers to the equation provided in Sect. 3 for the investment thresholds

VM condition:

$$\begin{aligned} \frac{\phi _1 \gamma _1 D_{1_L 1_F } }{r-\mu _{X} }+A_{1+2}^{L,\mathrm{SK}} {\phi _{1+2_L }^{*\mathrm{SK}_{\psi _1}}}=\frac{\phi _{1+2_L }^{*\mathrm{SK}} \gamma _{12} D_{12_L 1_F } }{r-\mu _{X} }-1 \end{aligned}$$

(46)

with the following economic interpretation: the leader, if active with input 1, invests in input 2 at the moment the value attained from operating with input 1 forever plus the value of the option to invest in input 2 equals the present value of the perpetual cash flow obtained from operating with the two inputs forever less the investment cost (cost of input 2) (Fig. 2).

SP condition:

$$\begin{aligned} \psi _1 A_{1+2}^{L,\mathrm{SK}} {\phi _{1+2_L }^{*\mathrm{SK} \,(\psi _1 -1)}}=\frac{\gamma _{12} D_{12_L 1_F } }{r-\mu _{X} } \end{aligned}$$

(47)

Solving together (46) and (47) we obtain the constant $A_{1+2}^{\mathrm{L,SK}}$:

$$\begin{aligned} A_{1+2}^{L,\mathrm{SK}} =\frac{\gamma _{12} D_{12_L 1_F } }{(r-\mu _{X} )\psi _1 {\phi _{1+2_L }^{*\mathrm{SK}\,(\psi _1 -1)}}} \end{aligned}$$

(48)

and the leader’s threshold:

$$\begin{aligned} \phi _{1+2_L }^{*\mathrm{SK}} =\frac{\phi _1 \psi _1 \gamma _1 D_{1_L 1_F } +\psi _1 (r-\mu _{X} )}{\gamma _{12} D_{12_L 1_F } (\psi _1 -1)} \end{aligned}$$

(49)

SK market, first-state: leader

The leader enters the market with input 1 at the point her payoff is maximized. ODE (12), with $k=1$, describes the leader’s value if inactive, whose solution is given by:

$$\begin{aligned} f_1^{\mathrm{L,SK}} (\phi _1 )=A_1^{\mathrm{L,SK}} \phi _1 ^{\beta _1} \end{aligned}$$

(50)

The constant $A_1^{\mathrm{L,SK}}$ and the leader’s threshold are determined using the following VM and SP conditions:

VM condition:

$$\begin{aligned} A_1^{\mathrm{L,SK}} {\phi _{1_L }^{*\mathrm{SK}}} ^{\beta _1 }=\frac{\phi _{1_L }^{*\mathrm{SK}} \gamma _1 D_{1_L 0_F } }{r-\mu _{X} }-1 \end{aligned}$$

(51)

The leader should invest in input 1 at the moment the option value to invest in input 1 equals the value she obtains from operating with input 1 alone forever less the investment cost (cost of input 1).

SP condition:

$$\begin{aligned} \beta _1 A_1^{L,\mathrm{SK}} \emptyset _{1_L }^{*SK\,(\beta _1 -1)} =\frac{\gamma _1 D_{1_L 0_F } }{r-\mu _{X} } \end{aligned}$$

(52)

Solving together (51) and (52) we obtain the constant $A_{1+2}^L$, given by:

$$\begin{aligned} A_1^{\mathrm{L,SK}} =\frac{\gamma _1 D_{1_L 0_F } {\phi _{1_L }^{*\mathrm{SK}}} ^{(1-\beta _1 )}}{\beta _1 (r-\mu _{X} )} \end{aligned}$$

(53)

and the leader’s threshold, given by:²⁶

$$\begin{aligned} \phi _{1_L }^{*\mathrm{SK}} =\frac{\beta _1 (r-\mu _{X} )}{\beta _1 \gamma _1 D_{1_L 0_F } -\gamma _1 D_{1_L 0_F } } \end{aligned}$$

(54)

Proposition 2

two inactive firms in a non-preemption duopoly (SK or PK) market invest in two complementary inputs (input 1 and input 2) sequentially if and only if there is a time t, $t\in [ {0,\infty } )$, where $\phi _1 (t)$ reaches $\phi _{1_L }^{*} (t)$ and $\phi _{1_F }^{*} (t)$ the first time with $\phi _{12} (t)<\phi _{12_L }^{*} (t)$ and $\phi _{12} (t)<\phi _{12_F }^{*} (t)$. Proof: see “Appendix B”.

Fig. 3

This figure shows the effect on the investment thresholds of the leader (Eq. 29) and the follower (Eq. 20) of changes in the correlation between market revenue and the cost of the two inputs, $\rho _{X/I_{12} }$, (left-hand side) and the degree of complementarity between the two inputs, $\xi =\gamma _{12} -(\gamma _1 +\gamma _2 )$, (right-hand side) for the SK and PK markets. Given that, according to Proposition 1, the investment threshold expressions for the SK and PK markets are the same, we use $\Phi *\hbox {12L},\hbox {SK} \& \hbox {PK}$ and $\Phi *\hbox {12F},\hbox {SK} \& \hbox {PK}$ to represent the investment thresholds for both markets, for the leader and the follower, respectively

3.2.2 Illustrative results

The above results show that an increase in $\sigma _{X}$ delays the investment for both firms and an increase in $\rho _{X/I_1 }$ accelerates the investment in input 1 for both firms, with the follower slightly more sensitive than the leader to changes in these variables (Fig. 3).

The above results show that an increase in $\mu _{I_1 }$ accelerates the investment for both firms and an increase in $D_{1_L 1_F }$ delays the investment of the follower and has no effect on the investment threshold of the leader (Fig. 4).

The above results are like those of Fig. 5 and, therefore, similar comments apply.

The above results show that an increase in $\xi$ accelerates the investment in the second input for both firms and an increase in $D_{1_L 1_F }$ delays the investment of the leader in the second input (input 2) and has no effect on the investment threshold of the follower (Fig. 6).

The above results show that an increase in $D_{12_L 1_F }$ accelerates the investment in the second input (input 2) for both firms and an increase in $D_{12_L 12_F }$ delays significantly the investment of the follower in the second input (input 2) and has no effect on the investment threshold of the leader (Fig. 7).

Fig. 4

This figure shows, for the SK and PK markets, the effect on firms’ investment thresholds of changes in the cost growth rate of the two inputs, $\mu _{I_{12} }$, (left-hand side) and the leader’s market share when both firms are active with the two inputs, $D_{12_L 12_F }$, (right-hand side)

Fig. 5

This figure shows the sensitivity of the thresholds of the leader (Eq. 54) and the follower (Eq. 42) to invest in input 1 if in a SK market, to changes in the market revenue volatility (left-hand side) and the correlation between the market revenue and the cost of input 1 (right-hand side)

Fig. 6

This figure shows the sensitivity of the thresholds of the leader (Eq. 54) and the follower (Eq. 42) to invest in input 1 if in a SK market, to changes in the cost growth rate of input 1 (left-hand side) and the leader’s market share if both firms are active with the input 1 (right-hand side)

Fig. 7

This figure shows the sensitivity of the thresholds of the leader (Eq. 49) and the follower (Eq. 35) to invest in input 2 if active with input 1 in the SK market, to changes in the market revenue volatility (left-hand side) and the correlation between the market revenue and the cost of input 2 (right-hand side)

3.2.3 PK market

PK market, terminal-state: follower

For the terminal state of sequential-input investments with the leader active with the two inputs, the threshold expression of the follower is the same for both the PK and the SK markets. Therefore, the following condition holds:

Proposition 3

$$\begin{aligned} \phi _{1+2_F }^{*\mathrm{PK}} =\phi _{1+2_F }^{*S\mathrm{K}}\,\text {-}\,\textit{given by Eq.}\,35 \end{aligned}$$

(55)

where $\phi _{1+2_F }^{*\mathrm{PK}}$ and $\phi _{1+2_F }^{*S\mathrm{K}}$ are the follower’s thresholds to invest in input 2 if active with input 1 in the PK and the SK markets, respectively. Proof: See “Appendix B”.

PK market, first-state: follower

In the first-state the follower optimizes the timing of the investment in input 1, with the leader active with the two inputs.²⁷ Following similar procedures as those of the previous sections we get the homogeneous second-order linear ODE (12), with $k=1$, whose general solution has the form:

$$\begin{aligned} f_1^{\mathrm{F,PK}} (\phi _1 )=A_1^{\mathrm{F,PK}}\phi _1 ^{\lambda _1} \end{aligned}$$

(56)

where $\lambda _1$ is the positive solution of the characteristic quadratic function of the homogeneous part of Eq. (12): $0.5(\sigma _{m_1 } )^{2}\lambda (\lambda -1)+(\mu _{X} -\mu _{I_1 } )\lambda -(r-\mu _{I_1 } )=0$. Solving this equation for $\lambda _1$ we get:

$$\begin{aligned} \lambda _1 =\frac{1}{2}-\frac{\mu _{X} -\mu _{I_1 } }{\sigma _{m_1 }^2 }+\sqrt{\left( {\frac{(\mu _{X} -\mu _{I_1 } )}{\sigma _{m_1 }^2 }-\frac{1}{2}} \right) ^{2}+\frac{2(r-\mu _{I_1 } )}{\sigma _{m_1 }^2}} \end{aligned}$$

(57)

where $\sigma _{m_1 }^2 =\sigma _{X}^2 +\sigma _{I_1 }^2 -2\rho _{XI_1 } \sigma _{X} \sigma _{I_1 }$.

The following VM condition is:

$$\begin{aligned} A_1^{\mathrm{F,PK}} {\phi _{1_F }^{*\mathrm{PK}}} ^{\lambda _1 }=\frac{\phi _{1_F }^{*\mathrm{PK}} \gamma _1 D_{1_F 12_L } }{r-\mu _{X} }-1 \end{aligned}$$

(58)

Before investing in input 1, the follower’s payoff is equal to the value of the option to invest in input 1 (left-hand side of Eq. 58). This option is exercised at the moment its value equals the present value of the follower’s cash flows from operating with input 1 forever (with the leader active with the two inputs) less the investment cost (right-hand side of Eq. 58).

The SP condition is:

$$\begin{aligned} \lambda _1 A_1^{\mathrm{F,PK}} {\phi _{1_F }^{*\mathrm{PK}}} ^{(\lambda _1 -1)}=\frac{\gamma _1 D_{1_F 12_L } }{r-\mu _{X} } \end{aligned}$$

(59)

Solving together Eqs. (58) and (59) we get the follower’s threshold for investing in input 1 if inactive, $\phi _{1_F }^{*\mathrm{PK}}$, and the constant $A_1^{\mathrm{F,PK}}$:

$$\begin{aligned} \phi _{1_F }^{*\mathrm{PK}}= & {} \frac{\lambda _1 }{\lambda _1 -1}\frac{r-\mu _{X} }{\gamma _1 D_{1_F 12_L } } \end{aligned}$$

(60)

$$\begin{aligned} A_1^{\mathrm{F,PK}}= & {} \frac{{\phi _{1_F }^{*\mathrm{PK}}} ^{(1-\lambda _1 )}}{\lambda _1 }\frac{\gamma _1 D_{1_F 12_L } }{r-\mu _{X} } \end{aligned}$$

(61)

PK market, terminal-state: leader

This is a non-preemption game and therefore the leader, if active with input 1, invests in input 2 at the moment her payoff is maximized. ODE (12), with $k=2$, describes the leader’s option value to invest in input 2 if active with input 1, whose solution is given by:

$$\begin{aligned} f_{1+2}^{\mathrm{L,PK}} (\phi _2 )=A_{1+2}^{\mathrm{L,PK}} \phi _2 ^{\upsilon _1 } \end{aligned}$$

(62)

where $\upsilon _1$ is the positive solution of the characteristic quadratic function of the homogeneous part of Eq. (12) given by: $\frac{1}{2}(\sigma _{m_2 } )^{2}\upsilon (\upsilon -1)+(\mu _{X} -\mu _{I_2 } )\upsilon -(r-\mu _{I_2 } )=0$. Solving the equation above for $\upsilon _1$ leads to:

$$\begin{aligned} \upsilon _1 =\frac{1}{2}-\frac{\mu _{X} -\mu _{I_2 } }{\sigma _{m_2 }^2 }+\sqrt{\left( {\frac{(\mu _{X} -\mu _{I_2 } )}{\sigma _{m_2 }^2 }-\frac{1}{2}} \right) ^{2}+\frac{2(r-\mu _{I_2 } )}{\sigma _{m_2 }^2}} \end{aligned}$$

(63)

The constant $A_{1+2}^{\mathrm{L,PK}}$ and the leader’s threshold are determined using the following VM and SP conditions:

VM condition:

$$\begin{aligned} \frac{\phi _1 \gamma _1 D_{1_L 0_F } }{r-\mu _{X} }+A_{1+2}^{\mathrm{L,PK}} {\phi _{1+2_L }^{*\mathrm{SK}\upsilon _{1}}}=\frac{\phi _{1+2_L }^{*\mathrm{PK}} \gamma _{12} D_{12_L 0_F } }{r-\mu _{X} }-1 \end{aligned}$$

(64)

The leader should invest in input 2 at the moment the value she attains from operating with input 1 alone forever plus the value of the option to invest in input 2 (left-hand side of Eq. 64) equals the present value of the cash flows she obtains from operating with the two inputs forever less the investment cost (right-hand side of Eq. 64).

SP condition:

$$\begin{aligned} \upsilon _1 A_{1+2}^{L,\mathrm{SK}} {\phi _{1+2_L }^{*\mathrm{SK}(\upsilon _1 -1)}} =\frac{\gamma _{12} D_{12_L 0_F } }{r-\mu _{X} } \end{aligned}$$

(65)

Solving together (62), (64) and (65) we obtain the constant $A_{1+2}^{\mathrm{L,SK}}$:

$$\begin{aligned} A_{1+2}^{\mathrm{L,PK}} =\frac{\gamma _{12} D_{12_L 0_F } }{(r-\mu _{X} )\upsilon _1 {\phi _{1+2_L }^{*P\mathrm{K}(\upsilon _1 -1)}}} \end{aligned}$$

(66)

and the leader’s threshold:

$$\begin{aligned} \phi _{1+2_L }^{*\mathrm{PK}} =\frac{\phi _1 \upsilon _1 \gamma _1 D_{1_L 0_F } +\upsilon _1 (r-\mu _{X} )}{\gamma _{12} D_{12_L 0_F } (\upsilon _1 -1)} \end{aligned}$$

(67)

PK market-first state: leader

In the first-state of “sequential-input investments” the investment threshold expression of the leader for the PK and SK markets are the same. Therefore, the following proposition holds:

Proposition 4

$$\begin{aligned} \phi _{1_L }^{*\mathrm{PK}} =\phi _{1_L }^{*S\mathrm{K}} \,\text {-}\,\textit{given by Eq.}\,54 \end{aligned}$$

(68)

where $\phi _{1_L }^{*\mathrm{PK}}$ and $\phi _{1_L }^{*S\mathrm{K}}$ are the leader’s investment threshold to invest in input 1 if inactive in the PK and SK markets, respectively. Proof: See “Appendix B”.

Fig. 8

This figure shows the sensitivity of the thresholds of the leader (Eq. 49) and the follower (Eq. 35) to invest in input 2 if active with input 1, to changes in $\xi$ (left-hand side) and the leader’s market share if both firms are active with input 1, $D_{1_L 1_F }$ (right-hand side)

3.2.4 Illustrative results

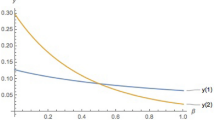
The results show that the investment threshold of the leader is lower than that of the follower (as expected) and that both increase with the revenue volatility. Comparing the thresholds of the left-hand side with those of the right-hand side, we conclude that for both firms, the threshold to invest in input 1 if active with input 2 is lower than the threshold to invest in input 2 if active with input 1. This is because in our base parameters we use $\mu _{I_1 } =-\,0.05$ and $\mu _{I_2 } =-\,0.10$ (i.e. the cost of input 2 decreases more rapidly than the cost of input 1). This result supports the conclusion that when the cost of two complementary inputs decreases at different rates it might be optimal to invest sequentially, first, in the input with the cost decreasing less rapidly, a result which is in line with that of Smith (2005).

The above results show that an increase in $D_{12_L 1_F }$ delays the investment of the follower in input 1 if inactive and has no effect on the investment threshold of the leader. The sensitivity of the investment thresholds of both firms to changes in $\xi$ are similar to those described in the previous subsections for the SK market (Fig. 8) and therefore similar comments apply.

4 Results

In this section we provide further sensitivity analysis regarding the most relevant model parameters. As for the previous results, we use the following base parameters where for simplicity of notation $\delta =\mu _{I_1 } -\mu _{I_2 }$.

In our model, ex-ante, firms hold three options to invest (in input 1 alone, input 2 alone and inputs 1 and 2 at the same time) whose values are driven by independent (stochastic) underlying variables. Therefore, in order to characterize the market conditions that (at a given time t) imply sequentially-input and/or simultaneously-input investments for each firm and market structures, we should analyse if the investment thresholds related to each of the above options are crossed. If firms are inactive and the threshold to invest in input 1 (or input 2) alone is crossed before the threshold to invest in the two inputs at the same time, they invest sequentially, starting with input 1 (or input 2). If firms are inactive and the threshold to invest in input 1 and input 2 at the same time is crossed before the threshold to invest in the input 1 (or input 2) alone, they invest in the two inputs at the same time.²⁸ Therefore, comparing the threshold values stated in Tables 4 and 5 below with the value of the (respective) underlying variable ($\phi _{12}(t)=1$, $\phi _1(t)=2$ or $\phi _2(t)=2)$ we can identify the market conditions (in terms of $\xi$ and $\delta )$ that determine whether the investments in the two inputs are sequential or simultaneous.

Table 4 shows a sensitivity analysis for the thresholds to invest in the two inputs at the same time to changes in $\xi$ and $\delta$, using the base parameter values.

Table 4 This table provides complementary results for the combined effect of changes in $\xi =\gamma _{12} -(\gamma _1 +\gamma _2 )$ and $\delta =(\mu _1 -\mu _2 )$ on the threshold to invest in the two inputs at the same time, for the leader (top panel) and the follower (bottom panel)

Table 5 This table provides further results on the effect the difference between the cost growth rates of the two inputs on the threshold to invest in input 1 alone, input 2 alone and input 1 and input 2 at the same time

The above results show that while the leader’s thresholds were crossed for most scenarios, the follower’s thresholds were crossed for few scenarios only, which suggests that simultaneous-input investments are less likely for the follower. We can also see that $\xi$ and $\delta$ have opposite effects on the investment thresholds of both firms. An increase in $\xi$ accelerates the investment and an increase in $\delta$ delays the investment.

These contrasting effects make the conventional wisdom, which says that “when a production process requires two extremely complementary inputs, a firm should upgrade (or replace) them simultaneously...”, less likely to hold for the follower when input drift differences are large, a result which was highlighted by Smith (2005) for a monopoly market. Notice that the marginal changes used for $\xi$ and $\delta$ are of the same size ($\Delta \xi =\Delta \delta =0.05)$ and yet the threshold values of the diagonals of both matrices decrease slightly as $\xi$ and $\delta$ increase (see threshold values underlined), which means that the effect of changes in the former parameter values slightly dominates that of the latter.

Table 5 shows a sensitivity analysis for all the investment thresholds, using $\mu _{I_1} =0$, and changing $\mu _{I_2 }$, from $-\,0.05$ to 0.30, ceteris paribus, in order to illustrate more clearly our findings (Fig. 9).

The above results show that both $\phi _{12_\mathrm{L} }^{*\mathrm{PK} \& \mathrm{SK}}$ and $\phi _{1_\mathrm{L} }^{*\mathrm{PK} \& \mathrm{SK}}$ are crossed for the whole range of $\delta$ values, whereas $\phi _{2_\mathrm{L} }^{*\mathrm{PK} \& \mathrm{SK}}$ is crossed when $\delta =\{ {0.05,0.10} \}$. Therefore, the leader invests in the two inputs at the same time in all scenarios. For the follower, $\phi _{12_\mathrm{F} }^{*\mathrm{PK} \& \mathrm{SK}}$ is crossed in two scenarios only, and $\phi _{1_F }^{*\mathrm{SK}}$ is not crossed for all scenarios. Specifically, as the cost growth rates difference increases, $\phi _{1_F }^{*\mathrm{SK}}$ does not change but $\phi _{12_\mathrm{F} }^{*\mathrm{PK} \& \mathrm{SK}}$ increases significantly, making the investment in the two inputs at the same time less likely. This latter result contradicts the conventional wisdom for complementary investments, and corroborates Smith (2005) findings for a monopolist firm (Fig. 10).

Fig. 9

This figure shows the sensitivity of the thresholds of the leader (Eq. 49) and the follower (Eq. 35) to invest in input 2 if active with input 1, to changes in the leader’s market share when she is active with the two inputs and the follower is active with input 1, $D_{12_L 1_F }$ (left-hand side) and when both firms are active with the two inputs, $D_{12_L 12_F }$ (right-hand side)

Fig. 10

This figure shows the sensitivity of the investment thresholds of the leader (Eq. 67) and the follower (Eq. 35) to invest in input 2 if active with input 1 (left-hand side) or invest in input 1 if active with input 2 (right-hand side) to changes in the market revenue volatility

Fig. 11

The two figures at the top show the sensitivity of the thresholds of the leader (Eq. 67) and the follower (Eq. 35) to invest in input 2 if active with input 1, to changes in $\rho _{X/I_{12} }$ (left-hand side) and $\xi$ (right-hand side). The figure at the bottom shows the sensitivity of the thresholds of the leader (Eq. 60) and the follower (Eq. 54) to invest in input 1 if inactive, to changes in the leader’s market share when she is active with the two inputs and the follower is active with input 1 ($D_{12_L 1_F }$)

4.1 Further analysis

In most real option models such as those of Decamps et al. (2006), Nishihara (2012) and Siddiqui and Takashima (2012), the value of the ex-ante real options are driven by the same stochastic variable. However, in our model, the value of the ex-ante real options (to invest in input 1 alone, or input 2 alone or input 1 and input 2 at the same time) are driven by three independent stochastic variables ($\phi _1 (t)$, $\emptyset _2 (t)$ and $\phi _{12} (t)$, respectively). While this modelling setting is more realistic, it complicates significantly the characterization of the market conditions that justify sequential-input or simultaneous-input investments for the two firms because the investment thresholds (related to $\phi _1 (t)$, $\emptyset _2 (t)$ and $\phi _{12} (t)$) are not directly comparable. In this section we summarize some further relevant insights on the effect of $\mu _{I_1 }$, $\mu _{I_2 }$ and $\delta$ on firms’ investment behavior (Fig. 11).

4.1.1 Input cost growth rates

As shown in Sect. 3, the cost growth rate of the two inputs play a very important role in firms’ investment behavior. Below we explore with further detail some of the results of Sect. 3 (Fig. 12).

Fig. 12

This figure illustrates the most likely investment behavior (sequential-input vs simultaneous-input) for the leader and the follower according to the relative values of $\mu _{I_1 }$ and $\mu _{I_2 }$, for both the SK and PK markets

We start our analysis by the scenarios where the set of ($\mu _{I_1 }$,$\mu _{I_2 }$) points are in the south-east or north-west quadrants, and conclude, respectively: if $\mu _{I_1 } \downarrow$, with $\mu _{I_1 } \in ( {-\,\infty ,0} ]$, and $\mu _{I_2 } \uparrow$, with $\mu _{I_2 } \in [ {0,+\,\infty } )$, $\phi _{1_L }^{*} \uparrow$, $\phi _{1_F }^{*} \uparrow$, $\phi _{2_L }^{*} \downarrow$ and $\phi _{2_F }^{*} \downarrow$, and sequential-input investments (starting with input 2) are more likely for both firms. If $\mu _{I_1 } \uparrow$, with $\mu _{I_1 } \in [ {0,+\,\infty } )$, and $\mu _{I_2 } \downarrow$, with $\mu _{I_2 } \in ( {-\,\infty ,0} ]$, $\phi _{1_L }^{*} \downarrow$, $\phi _{1_F }^{*} \downarrow$, $\phi _{2_L }^{*} \uparrow$ and $\phi _{2_F }^{*} \uparrow$, and sequential-input investments (starting with input 1) are more likely for both firms. When the set of ($\mu _{I_1 }$,$\mu _{I_2 }$) points are in the north-east or south-west quadrants, we conclude, respectively: if $\mu _{I_1 } \downarrow$, with $\mu _{I_1 } \in [ {0,+\,\infty } )$, and $\mu _{I_2 } \uparrow$, with $\mu _{I_2 } \in [ {0,+\,\infty } )$, $\phi _{1_L }^{*} \uparrow$, $\phi _{1_F }^{*} \uparrow$, $\phi _{2_L }^{*} \downarrow$ and $\phi _{2_F }^{*} \downarrow$, and sequential-input investments (starting with input 2) are more likely for both firms. If $\mu _{I_1 } \uparrow$, with $\mu _{I_1 } \in ( {-\,\infty ,0} ]$, and $\mu _{I_2 } \downarrow$, with $\mu _{I_2 } \in ( {-\,\infty ,0} ]$, $\phi _{1_L }^{*} \downarrow$, $\phi _{1_F }^{*} \downarrow$, $\phi _{2_L }^{*} \uparrow$ and $\phi _{2_F }^{*} \uparrow$, and sequential-input investments (starting with input 1) are more likely for both firms.

Notice that if the set of ($\mu _{I_1 } ,\mu _{I_2 }$) points are in the north-west or south-east quadrants, sequential-input investments are more likely than if these are in the south-west or north-east quadrants. This is because, in the former cases, $\mu _{I_1 }$ and $\mu _{I_2 }$ have different signs which means that the cost of one input is decreasing whereas the cost of the other input is increasing and, therefore, sequential-input investments, starting with the input whose growth rate is positive, are more likely. Finally, if the set of ($\mu _{I_1 } ,\mu _{I_2 }$) points are on the 45 degree dotted line, $\delta =0$, simultaneous-input investments are more likely regardless of the relative values of $\mu _{I_1 }$ and $\mu _{I_2 }$. This is because, in these cases, the cost growth rates of the two inputs are the same (either positive or negative).²⁹

Proposition 5

In non-preemption duopoly SK and PK markets, ceteris paribus, an increase in the difference between the cost growth rates of the two inputs ($\delta$), makes both firms more likely to invest in the two inputs sequentially. Proof: See “Appendix B”.

Corollary 5.1

For an inactive leader (follower), ceteris paribus, if there is a $+\Delta \mu _{I_1 }$ and a $-\Delta \mu _{I_2 }$ so $\mu _{I_{12} }$ is kept unchanged, $\phi _{1_L }^{*} \downarrow$ ($\phi _{1_F }^{*} \downarrow$), $\phi _{2_L }^{*} \uparrow$ ($\phi _{2_F }^{*} \uparrow$ ) and $\phi _{12_L }^{*}$ ($\phi _{12_F }^{*}$ ) is kept unchanged—and sequential-input investments, starting with input 1, are more likely for both firms. Proof: See “Appendix B”.

Corollary 5.2

For an inactive leader (follower), ceteris paribus, if there is a $-\Delta \mu _{I_1 }$ and a $+\Delta \mu _{I_2 }$ so $\mu _{I_{12} }$ is kept unchanged, $\phi _{1_L }^{*} \uparrow$ ($\phi _{1_F }^{*} \uparrow$), $\phi _{2_L }^{*} \downarrow$ ($\phi _{2_F }^{*} \downarrow$) and $\phi _{12_L }^{*}$ ($\phi _{12_F }^{*}$) is kept unchanged—and sequential-input investments, starting with input 2, are more likely for both firms. Proof: See “Appendix B”.

Corollary 5.3

For an inactive leader (follower), ceteris paribus, if there is a $+\Delta \mu _{I_1 }$ and a $-\Delta \mu _{I_2 }$ so as there is a $+\Delta \mu _{I_{12} }$, $\phi _{1_L }^{*} \downarrow$ ($\phi _{1_F }^{*} \downarrow$), $\phi _{2_L }^{*} \uparrow$ ($\phi _{2_F }^*\uparrow$) and $\phi _{12_L}^{*} \downarrow$ ($\phi _{12_F }^{*} \downarrow$), and both sequential-input investments starting with input 1 and simultaneous-input investments are possible, with the predominant investment behavior dependent on the (ex-ante) relative values of $\mu _{I_1 }$ and $\mu _{I_{12} }$ and (ex-ante) how far away $\phi _1 (t)$ and $\phi _{12} (t)$ are from $\phi _{1_L }^{*} (t)$ and $\phi _{12_L }^{*} (t)$, respectively. Proof: See “Appendix B”.

Notice that, although in general the quadrant where the set of ($\mu _{I_1 } ,\mu _{I_2 }$) points is located determine to some extent firms behavior (sequential-input or simultaneous-input investments), in all quadrants the thresholds of the leader and the follower have different sensitivities to changes in the input cost growth rates, as shown in Sect. 3.

4.1.2 Input complementarity

As shown in Sect. 3, the complementarity between the two inputs plays a very important role in firms’ behavior. Below we discuss with further detail some of the results of Sect. 3.

Proposition 6

For the SK and PK markets, ceteris paribus: (i) an increase in $\xi$ accelerates the investments of the leader and the follower in the two inputs at the same time and the investments of both firms in input 2 if active with input 1; (ii) for investments in the two inputs at the same time, the sensitivity of the threshold of the follower to changes in $\xi$ is greater than that of the leader. Proof: See “Appendix B”.

Corollary 6.1

As $\gamma _{12} \rightarrow 0$: (i) the follower tends to delay forever the investment in input 2 if he is active with input 1; (ii) both firms tend to delay forever the investment in the two inputs at the same time. Proof: See “Appendix B”.

Corollary 6.2

As $\gamma _{12} \rightarrow 1$: (i) the leader behaves as if she was in a monopoly regarding the investment in the two inputs at the same time; (ii) when the two firms are active with the two inputs and their market shares are symmetric ($D_{12_L 12_F } =D_{12_F 12_L } =0.5$), the threshold of the follower to invest in the two inputs at the same time is twice that of the leader. Proof: See “Appendix B”.

Corollary 6.3

(i) As $\gamma _1 (\gamma _2 )\rightarrow 0$, the leader tends to delay forever her investment in input 1(2); (ii) as $\gamma _1 (\gamma _2 )\rightarrow 1$ the leader tends to behave as if she was in a monopoly regarding her first-stage investment in input 1(2); (iii) an increase in $\gamma _1 (\gamma _2)$ accelerates the follower’s first-stage investment in input 1(2) and delays the follower’s second-stage investment in input 2 (1). Proof: See “Appendix B”.

Proposition 7

(i) For the SK and PK markets where the leader is active with input 1 (input 2), an increase in $\gamma _{12}$ accelerates the investment in input 2 (input 1); (ii) when the leader is active with input 1 (input 2), the threshold to invest in input 2 (input 1) is more sensitive to changes in $\gamma _{12}$ if the leader is in a SK market. Proof: See “Appendix B”.

Proposition 8

(i) For the SK and PK markets where the leader is active with input 1 (input 2), an increase in $\gamma _1 (\gamma _2 )$ accelerates the second-stage investment in input 2 (input 1); (ii) when the leader is active with input 1 (input 2) the threshold to invest in input 2 (input 1) is more sensitive to changes in $\gamma _1 (\gamma _2 )$ if the leader is in a SK market. Proof: See “Appendix B”.

Proposition 9

(i) For the SK and PK markets where the leader is inactive, an increase in $\gamma _1 (\gamma _2 )$ accelerates her first-stage investment in input 1 (input 2); (ii) if the leader is inactive, her threshold to invest in input 1 (input 2) is more sensitive to changes in $\gamma _1 (\gamma _2 )$ if in a PK market. Proof: See “Appendix B”.

Table 6 below provides further illustrative results regarding our model.

Table 6 This table provides information on the investment thresholds of both firms for all the investment scenarios

The results above show that, for both firms and the SK and PK markets, in sequential-input investments, the thresholds to invest in input 2 if active with input 1 ($\phi _{1+2_L }^{*}$ and $\phi _{1+2_F }^{*}$) are higher than the thresholds to invest in input 1 if active with input 2 ($\phi _{2+1_L }^{*}$ and $\phi _{2+1_F }^{*}$). This occurs because we assume in our base parameters that the cost of input 1 decreases more slowly than the cost of input 2 ($\mu _{I_1 } =-\,0.05$ and $\mu _{I_1 } =-\,0.10$). Furthermore, in sequential-input investments, the timing of the first-stage investment of the leader is the same for both markets, but the leader invests earlier in the second-stage if in a PK market and the follower invests earlier in the first-stage if in a SK market. The above results also support Propositions 3 and 4.

4.1.3 Competition factor

We show that when competition is taken into account, the conventional wisdom described above does not necessarily hold, particularly for the follower. This investment behavior of the follower is more likely when the competition asymmetry (in terms of market shares) between the two firms is high (Fig. 4, right-hand side). Thus, we conclude that competition has a negligible effect on the leader’s behavior and affects significantly the timing of the follower’s investment in the two inputs at the same time.

Regarding the first-stage of the sequential input-investments, we find that the leader’s threshold is not affected by its market share, whereas the follower’s threshold increases with the leader’s market share for both the SK and PK markets (see, respectively, Fig. 6, right-hand side, and Fig. 11 at the bottom). With respect to the second-stage of sequential input-investments, there is a more diverse set of investment behavior for both firms if in a SK market. The leader delays the investment in the second input as $D_{1_L 1_F }$ increases, whereas the follower’s threshold is not affected by changes in $D_{1_L 1_F }$(see Fig. 8, right-hand side). In addition, both firms invest earlier in the second-input if $D_{12_L 1_F }$ increases (see Fig. 9, left-hand side), the follower delays the investment in the second input if $D_{12_L 12_F }$ increases, and the leader’s threshold is not affected by changes in $D_{12_L 12_F}$ (see Fig. 9, right-hand side). Furthermore, we also conclude that:

Proposition 10

For the SK and PK markets where the leader is active with the two inputs, ceteris paribus: (i) if the follower is inactive, an increase in $D_{12_F 12_L }$, accelerates the investment in the two inputs at the same time; (ii) if the follower is active with input 1(2), an increase in $D_{1_F 12_L } (D_{2_F 12_L } )$, accelerates the second-stage investment in input 2(1); (iii) if the follower is active with input 1(2), $D_{12_F 12_L }$, accelerates the second-stage investment in input 2(1). Proof: See “Appendix B”.

5 Conclusions

We study the combined effect of uncertainty and competition on the timing optimization of investments in complementary inputs, for a leader–follower non-preemption duopoly market where both revenue and input costs are uncertain, and either spillover-knowledge is allowed or proprietary-knowledge holds. We develop a multi-factor real option game model where, ex-ante, the two firms hold the option to invest in input 1 alone, input 2 alone, or input 1 and 2 at the same time.

Our results show that, for both firms, the threshold to invest in the two inputs at the same time is significantly affected by the degree of complementarity between the two inputs (Fig. 3, right-hand side) and the input cost growth rates (Fig. 4, left-hand side). Also, the leader’s market share when both firms are active with the two inputs has no effect on the timing of the investment of the leader and affects significantly the timing of the investment of the follower (the higher the leader’s market share, the later the follower invests), see Fig. 4, right-hand side. Thus, we conclude that when we mix revenue and input costs uncertainty with duopoly competition, the two firms can have very distinct behavior regarding the investment in the two inputs at the same time.

Notice that our model setting is for a non-preemption game, thus the leader invests at the same time as a monopolist, and gets 100% of the market while active alone, regardless of which input she adopts. Therefore, competition (i.e., how the ex-post market share is divided between the two firms when both are active) does not affect the leader’s threshold to invest in the two inputs at the same time, but it influences significantly the timing of the follower’s investment. The more asymmetric is the ex-post market share between the two firms, favoring the leader, the later the follower invests, which implies that asynchronous input-investments are more likely.

Smith (2005) shows that input cost uncertainty makes a monopolistic firm less likely to follow the conventional wisdom regarding the investment in two complementary inputs. From our results we conclude that the leader is more prone to behave according to what is suggested by the conventional wisdom, synchronous input-investments are more likely, and the follower is more prone to behave according to what is advised for the monopolistic firm of Smith (2005), asynchronous input-investments are more likely (see Fig. 13 in the “Appendix C”). However, our findings also show that revenue market share competition reinforces an asynchronous input-investment behaviour for the follower, who is more likely than the monopolistic firm of Smith (2005) to invest in the two inputs sequentially.

The above behaviour is somewhat surprising, because in a leader–follower investment game as soon as the leader invests the follower is like a monopolist. Nevertheless, because the follower is exposed to competition, and the more asymmetric is the ex-post market share between the two firms, favoring the leader, the later the follower invests, which makes synchronous input-investments less likely.

We also show that asymmetric changes in the cost growth rates of the two inputs accelerate the investment in the input whose cost growth rate change is positive, deters the investment in the input whose cost growth rate is negative, and may not affect the timing of the investment in the two inputs at the same time (Figs. 4 and 6, left-hand side, and Table 5). Also, for both firms, we find that an increase in the degree of complementarity between the two inputs, enhances the investment in the two inputs at the same time, if the firm is inactive, and the investment in the second input if the firm is active with one input (see, respectively, Fig. 3, right-hand side, Fig. 8, left-hand side, and Fig. 11, right-hand side). Finally, we conclude that, for simultaneous-input investments, the sensitivity of the follower’s investment threshold to changes in the degree of complementarity is slightly greater than that of the leader (Fig. 3, right-hand side), dependent on the input growth rate differentials (Table 4).

By taking advantage of the natural homogeneity of degree one of our investment problem (regarding PDE 11) and the use of other standard real option modelling assumptions, we arrive at analytical solutions for both the firms’ value and the investment thresholds, for several realistic investment scenarios, which make a very complex (three-dimensional) multi-factor real option game model analysis tractable.

This research can be extended in several ways. For instance, it would be interesting to consider markets where pre-emption is allowed, or there is a second-mover advantage, or the degree of complementarity between the investment inputs and the ex-post market shares is stochastic.

Appendices

Appendix A

Proof of homogeneity of degree-one

If the value-matching relationship can be expressed as the equality between the option value denoted by $F_{12}^{\mathrm{F,SK}}({\bar{{X}},\bar{{I}}_2 })$ and the difference between the two functions, $f_2^{\mathrm{F,SK}} (\bar{{X}})$ and $f_3^{\mathrm{F,SK}} (\bar{{I}}_2 )$, representing the net value generated from exercising the option, where the vectors $\bar{{X}}$ and $\bar{{I}}_2$, of size n and m respectively are defined by $\bar{{X}}=\{ {X_1 , X_2 , \ldots , X_n } \}$ and $\bar{{I}}_2 =\{ {I_2^1 ,I_2^2 ,\ldots ,I_2^m } \}$, then Euler’s theorem on homogenous functions applies (see Sydsaeter and Hammond 2006). The value matching relationship is:

$$\begin{aligned} F_{12}^{\mathrm{F,SK}} \left( {\bar{{X}},\bar{{I}}_2 } \right) =f_2^{\mathrm{F,SK}} (\bar{{X}})-f_3^{\mathrm{F,SK}} (\bar{{I}}_2) \end{aligned}$$

The associated smooth pasting conditions are:

$$\begin{aligned} \frac{\partial F_{12}^{\mathrm{F,SK}} }{\partial X_i }= & {} \frac{\partial f_2^{\mathrm{F,SK}} }{\partial X_i } \forall i \\ \frac{\partial F_{12}^{\mathrm{F,SK}} }{\partial I_{2 _j}}= & {} -\frac{\partial f_3^{\mathrm{F,SK}} }{\partial I_{2 _j} } \forall j \end{aligned}$$

These conditions imply:

$$\begin{aligned} \sum _{i=1}^n {X_i } \frac{\partial F_{12}^{\mathrm{F,SK}} }{\partial X_i }+\sum _{j=1}^m {I_{2 _j} } \frac{\partial F_{12}^{\mathrm{F,SK}} }{\partial I_{2 _j} }=\sum _{i=1}^n {X_i } \frac{\partial f_2^{\mathrm{F,SK}} }{\partial X_i }-\sum _{j=1}^m {I_{2 _j} } \frac{\partial f_3^{\mathrm{F,SK}} }{\partial I_{2 _j} } \end{aligned}$$

If the two functions, $f_2^{\mathrm{SK}} (\bar{{X}})$ and $f_3^{\mathrm{SK}} (\bar{{I}}_2 )$, possess the homogeneity of degree-one property, then by Euler’s theorem:

$$\begin{aligned} \sum _{i=1}^n {X_i } \frac{\partial F_{12}^{\mathrm{F,SK}} }{\partial X_i }+\sum _{j=1}^m {I_j } \frac{\partial F_{12}^{\mathrm{F,SK}} }{\partial I_{2 _j} }=f_2^{\mathrm{F,SK}} -f_3^{\mathrm{F,SK}} =F_{12}^{\mathrm{F,SK}} \end{aligned}$$

which implies that $F_{12}^{\mathrm{F,SK}}$ is a homogenous function of degree one. The assertion that the option value is represented by a homogenous degree-one function can be tested by the value matching relationship and its associated smooth pasting conditions. Examining the value “matching conditions” we can easily prove that homogeneity exists. The value matching condition given by Eq. (17) is reproduced here as Eq. (A.1),

$$\begin{aligned} F_{12}^{\mathrm{F,SK}} (X^{*},I_2^*)=\frac{\gamma _{12} X^{*}.D_{12_F 12_L } }{r-\mu _{X} }-I_{2_F }^{*} \end{aligned}$$

(A.1)

If the option value is $F_{12}^{\mathrm{F,SK}} (X,I_2)$ and the value after exercising the option is $\gamma _{12} X^{*}.D_{12_F 12_L } /(r-\mu _{X} )-I_{2_F }^{*}$, with both X and $I_2$ stochastic, then if $F_{12}^{\mathrm{F,SK}} (X,I_2 )=\gamma _{12} X^{*}.D_{12_F 12_L } /(r-\mu _{X} )-I_{2_F }^{*}$ holds, doubling $X^{*}$ and $I_{2_F }^{*}$ doubles $F_{12}^{\mathrm{F,SK}} (X,I_2)$, there is homogeneity of degree-one. If the “value matching” relationship exhibits homogeneity of degree-one, then the two variables $(X,I_2 )$ can be replaced by, in this case, the ratio $\phi _2 =X/I_2$.³⁰

Derivation of ODE (12)

Rewriting Eq. (11) as (A.2):³¹

$$\begin{aligned}&\frac{1}{2}\frac{\partial ^{2}F_{12} }{\partial X^{2}}\sigma _{X} ^{2}X^{2}+\frac{1}{2}\frac{\partial ^{2}F_{12} }{\partial I_2 ^{2}}\sigma _{I_2 }^2 I_2 ^{2}+\frac{\partial ^{2}F_{12} }{\partial X\partial I_2 }XI_2 \sigma _{X} \sigma _{I_2 } \rho _{XI_2 } +\frac{\partial F_{12} }{\partial X}\mu _{X} X\nonumber \\&\quad +\frac{\partial F_{12} }{\partial I_2 }\mu _{I_2 } I_2 -rF_{12} =0 \end{aligned}$$

(A.2)

In order to reduce the homogeneity of degree two in the underlying variables to homogeneity of degree one, similarity methods can be used, as in Paxson and Pinto (2005). Let $\phi _2 =X/I_2$, so:

$$\begin{aligned} F(X,I_2)= & {} f\left( {X/I_2 } \right) I_2 =f(\phi _2 )I_2 \\ \frac{\partial F(X,I_2 )}{\partial I_2 }= & {} f(\phi _2 )-\frac{X}{I_2 }\frac{\partial f(\phi _2 )}{\partial \phi _2 }\\ \frac{\partial F(X,I_2 )}{\partial X}= & {} \frac{\partial f(\phi _2 )}{\partial \phi _2 } \\ \frac{\partial ^{2}F(X,I_2 )}{\partial I^{2}}= & {} \frac{\partial ^{2}f(\phi _2 )}{(\partial \phi )^{2}}\frac{X^{2}}{(I_2 )^{3}}\\ \frac{\partial ^{2}F(X,I_2 )}{\partial X^{2}}= & {} \frac{\partial ^{2}f(\phi _2 )}{\partial \phi _2 ^{2}}\frac{1}{I_2 } \\ \frac{\partial ^{2}F(X,I_2 )}{\partial X\partial I_2 }= & {} -\frac{\partial ^{2}f(\phi _2 )}{\partial \phi _2 ^{2}}\frac{X}{(I_2 )^{2}} \\ \end{aligned}$$

Substituting back to Eq. (A.2) we obtain Eq. (12), rewritten here as (A.3):

$$\begin{aligned}&\frac{1}{2}\sigma _{m_2 }^2 (\phi _2 )^{2}\frac{\partial ^{2}f_{12} (\phi _2 )}{\partial \phi _2 ^{2}}+\left( {\mu _{X} -\mu _{I_2 } } \right) (\phi _2 )\frac{\partial f_{12} (\phi _2 )}{\partial \phi _2 }+\gamma _1 X.D_{1_L 1_F } \nonumber \\&\quad -\,(r-\mu _{I_2 } )f_{12} (\phi _2 )=0 \end{aligned}$$

(A.3)

where $\sigma _{m_2 }^2 =\sigma _{X}^2 +\sigma _{I_2 }^2 -2\rho _{XI_2 } \sigma _{X} \sigma _{I_2 }$.

Appendix B

Proof of Proposition 1

In simultaneous-input investments both firms play a “one-shot” game, regardless of the market structure, i.e. the investment game ends for the two firms at the moment they exercise the option to invest in the two inputs at the same time. Consequently, firms’ value, if inactive, equals the option value to invest in the two inputs at the same time (which is the same for the SK and PK markets), and, if active with the two inputs, equals the present value of the cost savings from operating with the two inputs forever (which is the same for the SK and PK markets). Therefore, conditions (29A) and (29B) are proved. From the above rationale we also conclude that the boundary conditions used to derive the threshold expressions are the same for the two markets. Therefore, conditions (29C) and (29D) are also proved. $\square$

Proof of Proposition 2

In our framework the investment thresholds are trigger points which, if reached the first time, justify investment, otherwise firms should defer investment. It also results from our modelling setting that firms lose the option to invest in the two inputs at the same time if they exercise the option to invest in one of the inputs alone (input 1 or input 2). Consequently, if the thresholds that justify the leader and the follower investing in input 1 alone ($\phi _{1_L }^{*} (t)$ and $\phi _{1_F }^{*} (t)$ respectively) or input 2 alone ($\phi _{2_L }^{*} (t)$ and $\phi _{2_F }^{*} (t)$ respectively) are reached before those which justify the leader and the follower investing in the two inputs at the same time ($\phi _{12_L }^{*} (t)$ and $\phi _{12_F }^{*} (t)$ respectively), both firms should invest in the two inputs sequentially. $\square$

Proof of Proposition 3

In sequential-input investments, in the terminal-state where the follower operates with input 1 and the leader operates with the two inputs, the follower plays a “one-shot” game regarding the investment in the second input, regardless of the market structure (i.e., the game ends at the moment the follower exercises the option to invest in input 2). Therefore, the boundary conditions used to derive the follower’s threshold expression are the same for the SK and PK markets and, if so, condition (55) is proved. $\square$

Proof of Proposition 4

In sequential-input investments the leader invests before the follower in one of the inputs (input 1 or input 2), regardless of the market structure. Using the same rationale as for the proofs of propositions 1 and 2 we prove condition (68). $\square$

Proof of Proposition 5 and Corollaries 5.1 and 5.2

In order to prove proposition 5 we have to prove that $\phi _{1_L }^{*}$ and $\phi _{1_F }^{*}$ decrease with $\delta$, and/or $\phi _{12_L }^{*}$ and $\phi _{12_F }^{*}$ increase with $\delta$. The most obvious way to do this would be to determine the first derivative of the threshold expressions with respect to $\delta$ (i.e., $\partial \phi _{k_{i,j} }^{*} /\partial \delta$). Yet, $\delta$ is not in the threshold expressions and, therefore, this approach is not feasible. Nevertheless, from Sect. 3 we know that, ceteris paribus: if $\mu _{I_1} \uparrow$ and $\mu _{I_2 } \downarrow$ so as $\delta \uparrow$, $\phi _{1_L }^{*} \downarrow$, $\phi _{1_F }^{*} \downarrow$, $\phi _{2_L }^{*} \uparrow$ and $\phi _{2_F }^{*} \uparrow$, both firms invest earlier in input 1 and later in input 2, and therefore sequential-input investments (starting with input 1) are more likely. If $\mu _{I_1 } \downarrow$ and $\mu _{I_2 } \uparrow$ so as $\delta \uparrow$, $\phi _{1_L }^{*} \uparrow$, $\phi _{1_F }^{*} \uparrow$, $\phi _{2_L }^{*} \downarrow$ and $\phi _{2_F }^{*} \downarrow$ , both firms invest earlier in input 2 and later in input 1, and therefore sequential-input investments (starting with input 2) are more likely. $\square$

Proof of Corollary 5.3

Following the rationale used above for the proof of corollaries 5.1 and 5.2, we conclude that when simultaneous changes in the cost growth rates of the two inputs lead to a decrease in the threshold to invest in one input alone (input 1 or input 2) and the threshold to invest in the two inputs at the same time, both sequential-input investments and simultaneous-input investments are likely. It is not possible to determine the predominant investment behavior, since the thresholds to invest in input 1 alone, input 2 alone, and inputs 1 and 2 at the same time, decrease. The occurrence of sequential-input or simultaneous-input investments depends on the relative values of the thresholds, the size of the changes in $\mu _{I_1 }$, $\mu _{I_2 }$ and $\mu _{I_{12} }$, and (ex-ante) how far away $\phi _1 (t)$, $\phi _2 (t)$ and $\phi _{12} (t)$ are from $\phi _{1_L }^{*} (t)$, $\phi _{2_L }^{*} (t)$ and $\phi _{12_L }^{*} (t)$, respectively. $\square$

Proof of Proposition 6

Proposition 1 shows that $\phi _{12_L }^{*\mathrm{SK}} =\phi _{12_L }^{*\mathrm{PK}} \equiv \phi _{12_L }^{*\mathrm{SK} \& \mathrm{PK}}$ and $\phi _{12_F }^{*\mathrm{SK}} =\phi _{12_F }^{*\mathrm{PK}} \equiv \phi _{12_F }^{*\mathrm{SK} \& \mathrm{PK}}$. To study the relationship between $\xi$ and the above thresholds we determine the first derivative of $\phi _{12_L }^{*\mathrm{SK} \& \mathrm{PK}}$ and $\phi _{12_F }^{*\mathrm{SK} \& \mathrm{PK}}$ with respect to $\xi$—see Eqs. (20) and (29). Yet, $\xi$ is not in the above threshold expressions, and so we use the first derivatives of (29) and (20) with respect to the complementarity-related parameter(s) that belongs to the threshold expression ($\gamma _{12}$):

$$ \begin{aligned}&\frac{\partial \phi _{12_L }^{*\mathrm{SK} \& \mathrm{PK}} }{\partial \gamma _{12} }=-\frac{\eta _1 (r-\mu _{X} )\left( {\eta _1 D_{12_L 0_F } -D_{12_L 0_F } } \right) }{\left( {\eta _1 \gamma _{12} D_{12_L 0_F } -\gamma _{12} D_{12_L 0_F } } \right) ^{2}}<0 \end{aligned}$$

(B.1)

$$ \begin{aligned}&\frac{\partial \phi _{12_F }^{*\mathrm{SK} \& \mathrm{PK}} }{\partial \gamma _{12} }=-\frac{\eta _1 \left( {r-\mu _{X} } \right) \left( {\eta _1 -1} \right) D_{12_F 12_L } }{\left[ {\left( {\eta _1 -1} \right) \gamma _{12} D_{12_F 12_L } } \right] ^{2}}<0 \end{aligned}$$

(B.2)

$$ \begin{aligned}&\frac{\partial \phi _{1+2_F }^{*\mathrm{SK} \& \mathrm{SP}} }{\partial \gamma _{12} }=-\frac{\left[ {\psi _1 (\mu _{X} -r)-\psi _1 \phi _1 \gamma _1 D_{1_F 12_L } } \right] \left[ {D_{12_F 12_L } (1-\psi _1 )} \right] }{\left[ {\gamma _{12} D_{12_F 12_L } (1-\psi _1 )} \right] ^{2}}<0 \end{aligned}$$

(B.3)

$$ \begin{aligned}&\frac{\partial \phi _{1+2_L }^{*\mathrm{SK} \& \mathrm{SP}} }{\partial \gamma _{12} }=-\frac{\phi _1 \nu _1 \gamma _1 D_{12_L 0_F } }{\gamma _{12} D_{12_F 0_L } (\nu -1)^{2}}<0 \end{aligned}$$

(B.4)

B.1, B.2, B.3 and B.4 are all negative, therefore (i) is proved. To prove (ii) we have to show that $\frac{\partial \phi _{12_L }^{*\mathrm{SK} \& \mathrm{PK}} /\partial \xi }{\partial \phi _{12_F }^{*\mathrm{SK} \& \mathrm{PK}} /\partial \xi }=\Delta <1$, $\forall \gamma _{12}$. Using the above expression and simplifying, yields:$\Delta =\frac{( {\eta _1 D_{12_L 0_F } -D_{12_L 0_F } } )( {\eta _1 -1} )\gamma _{12} ^{2}D_{12_F 12_L } }{( {\eta _1 \gamma _{12} D_{12_L 0_F } -\gamma _{12} D_{12_L 0_F } } )^{2}}$ , with $\gamma _{12} \in ( {0,1} )$. Taking the limits we get: $\mathop {Lim}\nolimits _{\gamma _{12}\rightarrow 0} \Delta =0$ and $\mathop {Lim}\nolimits _{\gamma _{12} \rightarrow 1} \Delta =\frac{\eta _1 D_{12_F 12_L } -D_{12_F 12_L } }{\eta _1 D_{12_L 0_F } -D_{12_L 0_F } }$. Since $D_{12_L 0_F } =1$ and $D_{12_F 12_L } \in ( {0,0.5} ]$, $\Delta <1$, $\forall \gamma _{12}$. Therefore (ii) is proved. $\square$

Proof of Corollary 6.1

$\gamma _{12} \in ({0,1} )$, $\mathop {Lim}\nolimits _{\gamma _{12}\rightarrow 0} \phi _{1+2_F }^{*\mathrm{SK} \& \mathrm{PK}} =\infty$ and $\mathop {Lim}\nolimits _{\gamma _{12} \rightarrow 0} \phi _{12_L }^{*\mathrm{SK} \& \mathrm{PK}} =\infty$, therefore, corollary 6.1 is proved. $\square$

Proof of Corollary 6.2

$\gamma _{12} \in ( {0,1} )$, $\mathop {Lim}\nolimits _{\gamma _{12}\rightarrow 1} \phi _{12_L }^{*\mathrm{SK} \& \mathrm{PK}} =\frac{\eta _1 (r-\mu _{X} )}{\eta _1 -1}$, $\mathop {Lim}\nolimits _{\gamma _{12}\rightarrow 1} \phi _{12_F }^{*\mathrm{SK} \& \mathrm{PK}} =\frac{\eta _1 (r-\mu _{X} )}{(\eta _1 -1)D_{12_F 12_L } }$. Notice that $\eta _1 (r-\mu _{X} )/(\eta _1 -1)$ is the threshold mark-up normalized by the investment cost for a monopoly market, therefore (i) is proved. The follower’s threshold differs from that of the leader by a factor: $1/D_{12_F 12_L }$. Notice that $D_{12_F 12_L } \in ( {0,0.5} ]$ and if the ex-post market shares of the two firms are symmetric, $D_{12_F 12_L } =0.5$. Replacing $D_{12_F 12_L }$ in the above expression by 0.5, we conclude that the $\mathop {Lim}\nolimits _{\gamma _{12}\rightarrow 1} \phi _{12_F }^{*\mathrm{SK} \& \mathrm{PK}}$ is twice the $\mathop {Lim}\nolimits _{\gamma _{12}\rightarrow 1} \phi _{12_L }^{*\mathrm{SK} \& \mathrm{PK}}$. Therefore (ii) is proved. $\square$

Proof of Corollary 6.3

note that $\gamma _1 \in ({0,1})$ and $\mathop {Lim}\nolimits _{\gamma _1\rightarrow 0} \phi _{1_L }^{*\mathrm{SK} \& \mathrm{PK}} =\infty$, therefore (i) is proved; $\mathop {Lim}\nolimits _{\gamma _1 \rightarrow 1} \phi _{1_L }^{*\mathrm{SK} \& \mathrm{PK}} =\frac{\beta _1 (r-\mu _{X} )}{\beta _1 -1}$ and corresponds to the threshold mark-up normalized by the investment cost for a monopoly market, therefore (ii) is proved; to prove (iii) we need to prove that the first derivatives of $\phi _{1_L }^{*\mathrm{SK} \& \mathrm{PK}}$ and $\phi _{1+2_F }^{*\mathrm{SK} \& \mathrm{PK}}$ with respect to $\gamma _1$ are negative and positive, respectively, which we show below. Therefore (iii) is also proved.

$$ \begin{aligned} \frac{\partial \phi _{1_L }^{*\mathrm{SK} \& \mathrm{PK}} }{\partial \gamma _1 }= & {} -\frac{\beta _1 (r-\mu _{X} )\left( {\beta _1 D_{1_L 0_F } -D_{1_L 0_F } } \right) }{\left( {\beta _1 \gamma _1 D_{1_L 0_F } -\gamma _1 D_{1_L 0_F } } \right) ^{2}}<0 \end{aligned}$$

(B.5)

$$ \begin{aligned} \frac{\partial \phi _{1+2_F }^{*\mathrm{SK} \& \mathrm{SP}} }{\partial \gamma _1 }= & {} -\frac{\psi _1 \phi _1 D_{1_F 12_L } }{\gamma _{12} D_{12_F 12_L } (1-\psi _1 )}>0 \end{aligned}$$

(B.6)

$\square$

Proof of Proposition 7

to prove (i) we need to show that the first derivatives of $\phi _{1+2_L }^{*S\mathrm{K}}$ and $\phi _{1+2_L }^{*\mathrm{PK}}$ with respect $\gamma _{12}$ are negative, which is shown by (B.7) and (B.8) below. Therefore (i) is proved.

$$\begin{aligned} \frac{\partial \phi _{1+2_L }^{*\mathrm{SK}} }{\partial \gamma _{12} }= & {} -\frac{\phi _1 \psi _1 \gamma _1 D_{1_L 1_F } +\psi _1 (r-\mu _{X} )+D_{12_L 0_F } (\psi _1 -1)}{\left[ {\gamma _{12} D_{12_L 0_F } (\psi _1 -1)} \right] ^{2}}<0 \end{aligned}$$

(B.7)

$$\begin{aligned} \frac{\partial \phi _{1+2_L }^{*\mathrm{PK}} }{\partial \gamma _{12} }= & {} -\frac{\phi _1 \upsilon _1 \gamma _1 D_{1_L 0_F } +\upsilon _1 (r-\mu _{X} )+D_{12_L 0_F } (\upsilon _1 -1)}{\left[ {\gamma _{12} D_{12_L 0_F } (\upsilon _1 -1)} \right] ^{2}}<0 \end{aligned}$$

(B.8)

To prove (ii) we need to compare (B.7) with (B.8) and show that $\frac{\partial \phi _{1+2_L }^{*\mathrm{PK}} }{\partial \gamma _{12} }>\frac{\partial \phi _{1+2_L }^{*\mathrm{SK}} }{\partial \gamma _{12} }, \forall \gamma _{12}$, or that $\frac{\partial \phi _{1+2_L }^{*\mathrm{PK}} }{\partial \gamma _{12} }/\frac{\partial \phi _{1+2_L }^{*\mathrm{SK}} }{\partial \gamma _{12} }=\Pi <1, \forall \gamma _{12}$. Replacing the terms of this inequality by their respective expressions and simplifying yields:$\frac{(\upsilon _1 -1)^{2}\phi _1 \psi _1 \gamma _1 D_{1_L 1_F } +(\upsilon _1 -1)^{2}\psi _1 (r-\mu _{X} )+(\upsilon _1 -1)^{2}D_{12_L 0_F } (\psi _1 -1)}{(\psi _1 -1)^{2}\phi _1 \upsilon _1 \gamma _1 D_{1_L 0_F } +(\psi _1 -1)^{2}\upsilon _1 (r-\mu _{X} )+(\psi _1 -1)^{2}D_{12_L 0_F } (\upsilon _1 -1)}=\Pi$. If the market conditions (revenue volatility, input cost volatility, etc) are the same for the SK and PK markets, $\psi _1 =\upsilon _1$, the above expression yields: $\frac{\phi _1 \psi _1 \gamma _1 D_{1_L 1_F } +\psi _1 (r-\mu _{X} )+D_{12_L 0_F } (\psi _1 -1)}{\phi _1 \psi _1 \gamma _1 D_{1_L 0_F } +\psi _1 (r-\mu _{X} )+D_{12_L 0_F } (\psi _1 -1)}=\Pi$. Since $D_{1_L 1_F } <D_{12_L 0_F }$ and $\gamma _{12} \in ( {0,1} )$, $\Pi <1$, $\forall \gamma _{12}$. Therefore, (ii) is also proved. $\square$

Proof of Proposition 8

To prove (i) we need to show that the first derivative of $\phi _{1+2_L }^{*S\mathrm{K}}$ and $\phi _{1+2_L }^{*\mathrm{PK}}$ with respect to $\gamma _1$ is negative. This is shown below by (B.9) and (B.10) and therefore (i) is proved.

$$\begin{aligned} \frac{\partial \phi _{1+2_L }^{*\mathrm{SK}} }{\partial \gamma _1 }= & {} -\frac{\phi _1 \psi _1 \gamma _1 D_{1_L 1_F } }{\gamma _{12} D_{12_L 0_F } (\psi _1 -1)}<0 \end{aligned}$$

(B.9)

$$\begin{aligned} \frac{\partial \phi _{1+2_L }^{*\mathrm{PK}} }{\partial \gamma _1 }= & {} -\frac{\phi _1 \upsilon _1 D_{1_L 0_F } }{\gamma _{12} D_{12_L 0_F } (\upsilon _1 -1)}<0 \end{aligned}$$

(B.10)

To prove (ii) we need to compare (B.12) with (B.13) and show that $\frac{\partial \phi _{1+2_L }^{*\mathrm{PK}} }{\partial \gamma _1 }>\frac{\partial \phi _{1+2_L }^{*\mathrm{SK}} }{\partial \gamma _1 }, \forall \gamma _1$, or that $\frac{\partial \phi _{1+2_L }^{*\mathrm {PK}} }{\partial \gamma _1 }/\frac{\partial \phi _{1+2_L }^{*\mathrm{SK}} }{\partial \gamma _1 }=\Omega <1,\forall \gamma _1$. Replacing the terms of the inequality by the respective expressions and proceeding as for proposition 7 (i.e., $\psi _1 =\upsilon _1$ if the same market conditions hold for the SK and PK markets) we obtain: $\frac{\gamma _1 D_{1_L 1_F } }{D_{1_L 0_F } }=\Omega$. Since $D_{1_L 0_F } >D_{1_L 1_F }$ and $\gamma _1 \in ( {0,1} )$, $\Omega <1,\forall \gamma _1$, therefore (ii) is proved. $\square$

Proof of Proposition 9

To prove (i) we need to show that the first derivatives of $\phi _{1+2_L }^{*S\mathrm{K}}$ and $\phi _{1+2_L }^{*\mathrm{PK}}$ with respect to $\gamma _1$ are negative. This is shown below by (B.14) and (B.15), therefore (i) is proved.

$$\begin{aligned} \frac{\partial \phi _{1_F }^{*\mathrm{SK}} }{\partial \gamma _1 }= & {} -\frac{\beta _1 (r-\mu _{X} )\left( {\beta _1 -1} \right) D_{1_F 1_L } }{\left[ {(\beta _1 -1)\gamma _1 D_{1_F 1_L } } \right] ^{2}}<0\end{aligned}$$

(B.11)

$$\begin{aligned} \frac{\partial \phi _{1_F }^{*\mathrm{PK}} }{\partial \gamma _1 }= & {} -\frac{\lambda _1 (r-\mu _{X} )\left( {\lambda _1 -1} \right) D_{1_F 12_L } }{\left[ {(\lambda _1 -1)\gamma _1 D_{1_F 12_L } } \right] ^{2}}<0 \end{aligned}$$

(B.12)

To prove (ii) we need to compare (B.11) with (B.12) and show that $\frac{\partial \phi _{1_F }^{*\mathrm{PK}} }{\partial \gamma _1 }>\frac{\partial \phi _{1_F }^{*\mathrm{SK}} }{\partial \gamma _1 }, \forall \gamma _1$, or that $\frac{\partial \phi _{1_F }^{*\mathrm{PK}} }{\partial \gamma _1 }/\frac{\partial \phi _{1_F }^{*\mathrm{SK}} }{\partial \gamma _1 }=\Upsilon <1,\forall \gamma _1$. Replacing the terms of the inequality by the respective expressions and proceeding as for propositions 7 and 8 (i.e., $\beta _1 =\lambda _1$ if the same market conditions hold for the SK and PK markets) we obtain: $\frac{D_{1_F 1_L } }{D_{1_F 12_L } }=\Upsilon$. Since $D_{1_L 1_F } >D_{1_F 12_L }$, $\Upsilon >1$, and therefore (ii) is proved. $\square$

Proof of Proposition 10

$D_{12_F 12_L }$ is the follower’s market share when both firms are active with the two inputs and $D_{1_F 12_L }$ is the follower’s market share if active with input 1 and the leader is active with the two inputs. To prove (i) and (ii) we need to show that the first derivative of $\phi _{12_F }^{*\mathrm{SK} \& \mathrm{PK}}$ with respect to $D_{12_F 12_L }$ and the first derivative of $\phi _{1+2_F }^{*\mathrm{SK} \& \mathrm{SP}}$ with respect to $D_{1_F 12_L }$, respectively, are negative. This is shown by (B.13) and (B.14). Therefore (i) and (ii) are proved. To prove (iii) we need to show that the first derivative of $\phi _{1+2_F }^{*\mathrm{SK} \& \mathrm{SP}}$ with respect to $D_{12_F 12_L }$ is negative. This is shown by (B.14) and therefore (iii) is also proved.

$$ \begin{aligned}&\displaystyle \frac{\partial \phi _{12_F }^{*\mathrm{SK} \& \mathrm{PK}} }{\partial D_{12_F 12_L } }=-\frac{\eta _1 (r-\mu _{X} )(\eta _1 -1)\gamma _{12} }{\left[ {(\eta _1 -1)\gamma _{12} D_{12_F 12_L } } \right] ^{2}}<0 \end{aligned}$$

(B.13)

$$ \begin{aligned}&\displaystyle \frac{\partial \phi _{1+2_F }^{*\mathrm{SK} \& \mathrm{SP}} }{\partial D_{1_F 12_L } }=\frac{-\psi _1 \phi _1 D_{1_F 12_L } }{\left[ {\gamma _{12} D_{12_F 12_L } (1-\psi _1 )} \right] ^{2}}<0\end{aligned}$$

(B.14)

$$ \begin{aligned}&\displaystyle \frac{\partial \phi _{1+2_F }^{*\mathrm{SK} \& \mathrm{SP}} }{\partial D_{12_F 12_L } }=-\frac{\left[ {\psi _1 (\mu _{X} -r)-\psi _1 \phi _1 \gamma _1 D_{1_F 12_L } } \right] \gamma _{12} (1-\psi _1 )}{\left[ {\gamma _{12} D_{12_F 12_L } (1-\psi _1 )} \right] ^{2}}<0 \end{aligned}$$

(B.15)

$\square$

Appendix C

See Fig. 13.

Fig. 13

This figure contextualizes one of our main findings within the available investment literature