Optimal capacity allocation in a production–inventory system with base stock

Abstract

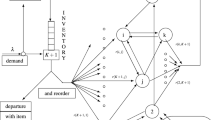
We address the optimal allocation of a given capacity in a multi-product inventory–production system with base stock. In the system, the base stock level is equal to the sum of the finished goods and work-in-process inventory. Each exogenous demand releases production of a new unit and increases the level of work-in-process. Unsatisfied demand is backordered. Using an open single-server queueing network, we model the behavior of the work-in-process in the manufacturing system in order to determine the cost-optimal base stock level. We focus on the utilizations in the network and compare balanced and unbalanced systems regarding their base stock level. In particular, we analyze the effect of capacity reallocation and show that a manufacturing system consisting of production stations with constant utilization rates, results in the lowest base stock level. With the combined application of queueing network theory and majorization theory, we are able to provide analytical explanations of the network’s behavior.

Proof of Proposition 1

In the proof, we use

Lemma 1

For $j \in \overline{J}$ the jth partial derivative (of order 1) is

$$\begin{aligned} \frac{\partial }{\partial \rho _j} G(n,\overline{J})(\rho _1,...,\rho _J)=G(n-1,\overline{J})(\rho _1,...,\rho _J)+\rho _j \frac{\partial }{\partial \rho _j}G(n-1,\overline{J})(\rho _1,...,\rho _J). \end{aligned}$$

Proof of Proposition 1

From the definition of $G(n,\overline{J})(\rho _1,...,\rho _J)$, the functions $\phi ^{(z)}$ are symmetric on $A=(0,1)^J$. Thus, we have to show

$$\begin{aligned} \frac{\frac{\partial }{\partial \rho _1}\phi ^{(z)}\left( \rho _1,...,\rho _J\right) -\frac{\partial }{\partial \rho _2}\phi ^{(z)}\left( \rho _1,...,\rho _J\right) }{\rho _1 - \rho _2} \overset{!}{\le } 0. \end{aligned}$$

(10)

Using Lemma 1, we firstly calculate the numerator of the fraction. (For shorthand notation we abbreviate $G(n,\overline{J})(\rho _1,...,\rho _J) =G(n,\overline{J})$ whenever the argument $(\rho _1,...,\rho _J)$ is obvious.)

$$\begin{aligned}&\frac{\partial }{\partial \rho _1} \phi ^{(z)}(\rho _1,...,\rho _J) - \frac{\partial }{\partial \rho _2}\phi ^{(z)}(\rho _1,...,\rho _J)\\&\quad =\left( \prod _{i \in \overline{J}-\left\{ 1\right\} }(1-\rho _i)\right) \left[ (-1)\sum ^z_{n=0}\sum _{k_1+...+k_J=n}\prod _{j\in \overline{J}}\rho _j^{k_j}\right. \\&\qquad +\left. (1-\rho _1)\sum ^z_{n=0}\frac{\partial }{\partial \rho _1}\left\{ \sum _{k_1+...+k_J=n}\prod _{j\in \overline{J}}\rho _j^{k_j}\right\} \right] \\&\qquad -\left( \prod _{i \in \overline{J}-\left\{ 2\right\} }(1-\rho _i)\right) \left[ (-1)\sum ^z_{n=0}\sum _{k_1+...+k_J=n}\prod _{j\in \overline{J}}\rho _j^{k_j}\right. \\&\qquad +\left. (1-\rho _2)\sum ^z_{n=0}\frac{\partial }{\partial \rho _2}\left\{ \sum _{k_1+...+k_J=n}\prod _{j\in \overline{J}}\rho _j^{k_j}\right\} \right] \\&\quad =\left( \prod _{i \in \overline{J}-\left\{ 1,2\right\} }(1-\rho _i)\right) \left[ (\rho _2-1)\sum ^z_{n=0}\sum _{k_1+...+k_J=n}\prod _{j\in \overline{J}}\rho _j^{k_j}\right. \\&\qquad +\left. (1-\rho _1)\sum ^z_{n=0}\sum _{k_1+...+k_J=n}\prod _{j\in \overline{J}}\rho _j^{k_j}\right. \\&\qquad +\left. (1-\rho _1)(1-\rho _2)\left( \sum ^z_{n=0}\frac{\partial }{\partial \rho _1}\left\{ \sum _{k_1+...+k_J=n}\prod _{j\in \overline{J}}\rho _j^{k_j}\right\} \right. \right. \\&\qquad -\left. \left. \sum ^z_{n=0}\frac{\partial }{\partial \rho _2}\left\{ \sum _{k_1+...+k_J=n}\prod _{j\in \overline{J}}\rho _j^{k_j}\right\} \right) \right] \\ \end{aligned}$$

$$\begin{aligned}&\quad =\left( \prod _{i \in \overline{J}-\left\{ 1,2\right\} }(1-\rho _i)\right) \left[ (\rho _2-\rho _1)\sum ^z_{n=0}\sum _{k_1+...+k_J=n}\prod _{j\in \overline{J}}\rho _j^{k_j}\right. \\&\quad \quad +\left. (1-\rho _1)(1-\rho _2)\left( \sum ^z_{n=1}\left( \frac{\partial }{\partial \rho _1}\left\{ \sum _{k_1+...+k_J=n}\prod _{j\in \overline{J}}\rho _j^{k_j}\right\} \right. \right. \right. \\&\quad \quad -\left. \left. \left. \frac{\partial }{\partial \rho _2}\left\{ \sum _{k_1+...+k_J=n}\prod _{j\in \overline{J}}\rho _j^{k_j}\right\} \right) \right) \right] \\&\quad {\overset{\text {Lemma 1}}{=}}\left( \prod _{i \in \overline{J}-\left\{ 1,2\right\} }(1-\rho _i)\right) \left[ (\rho _2-\rho _1)\sum ^z_{n=0}\sum _{k_1+...+k_J=n}\prod _{j\in \overline{J}}\rho _j^{k_j}\right. \\&\quad \quad +\left. (1-\rho _1)(1-\rho _2)\left( \sum ^{z-1}_{n=1}\left( \rho _1\frac{\partial }{\partial \rho _1}\left\{ \sum _{k_1+...+k_J=n}\prod _{j\in \overline{J}}\rho _j^{k_j}\right\} \right. \right. \right. \\&\quad \quad -\left. \left. \left. \rho _2\frac{\partial }{\partial \rho _2}\left\{ \sum _{k_1+...+k_J=n}\prod _{j\in \overline{J}}\rho _j^{k_j}\right\} \right) \right) \right] \\&\quad = \left( \prod _{i \in \overline{J}-\left\{ 1,2\right\} }(1-\rho _i)\right) \left[ (\rho _2-\rho _1)\sum ^z_{n=0} \sum _{k_1+...+k_J=n} \prod _{j\in \overline{J}}\rho _j^{k_j} \right. \\&\quad \quad +\left. (1-\rho _1)(1-\rho _2)\sum ^{z-1}_{n=1}\left( \rho _1 \sum _{\begin{array}{c} k_1+...+k_J=n \\ k_1>0 \end{array}}k_1\prod _{j\in \overline{J}- \left\{ 1\right\} }\rho _j^{k_j}\rho _1^{k_1-1}\right. \right. \\&\quad \quad -\left. \left. \rho _2 \sum _{\begin{array}{c} k_1+...+k_J=n \\ k_2>0 \end{array}}k_2\prod _{j\in \overline{J}-\left\{ 2\right\} }\rho _j^{k_j}\rho _2^{k_2-1}\right) \right] \\ \end{aligned}$$

$$\begin{aligned}&\quad = \left( \prod _{i \in \overline{J}-\left\{ 1,2\right\} }(1-\rho _i)\right) \left[ (\rho _2-\rho _1)\sum ^z_{n=0} \sum _{k_1+...+k_J=n} \prod _{j\in \overline{J}}\rho _j^{k_j} \right. \\&\quad \quad +\left. (1-\rho _1)(1-\rho _2)\sum ^{z-1}_{n=1}\left( \sum _{\begin{array}{c} k_1+...+k_J=n \\ k_1\ge 0 \end{array}}k_1\prod _{j\in \overline{J}}\rho _j^{k_j}\right. \right. \\&\quad \quad -\left. \left. \sum _{\begin{array}{c} k_1+...+k_J=n \\ k_2\ge 0 \end{array}}k_2\prod _{j\in \overline{J}}\rho _j^{k_j}\right) \right] \\&\quad = \left( \prod _{i \in \overline{J}-\left\{ 1,2\right\} }(1-\rho _i)\right) \left[ (\rho _2-\rho _1)\sum ^z_{n=0} \sum _{k_1+...+k_J=n} \prod _{j\in \overline{J}}\rho _j^{k_j} \right. \\&\quad \quad +\left. (1-\rho _1)(1-\rho _2)\sum ^{z-1}_{n=1}\left( \sum _{k_1+...+k_J=n}k_1\left( \prod _{j\in \overline{J}}\rho _j^{k_j}\right) G(n,J)^{-1}\right. \right. \\&\quad \quad -\left. \left. \sum _{k_1+...+k_J=n}k_2\left( \prod _{j\in \overline{J}}\rho _j^{k_j}\right) G(n,J)^{-1}\right) G(n,J)\right] \\&\quad = \left( \prod _{i \in \overline{J}-\left\{ 1,2\right\} }(1-\rho _i)\right) \left[ (\rho _2-\rho _1)\sum ^z_{n=0} \sum _{k_1+...+k_J=n} \prod _{j\in \overline{J}}\rho _j^{k_j} \right. \\&\quad \quad +\left. (1-\rho _1)(1-\rho _2)\sum ^{z-1}_{n=1}\left( \sum _{k_1=1}^n \rho _1^{k_1}G(n-k_1,\overline{J})G(n,J)^{-1}\right. \right. \\&\quad \quad -\left. \left. \sum _{k_2=1}^n \rho _2^{k_2}G(n-k_2,\overline{J})G(n,J)^{-1}\right) G(n,J)\right] \\&\quad = \left( \prod _{i \in \overline{J}-\left\{ 1,2\right\} }(1-\rho _i)\right) \left[ (\rho _2-\rho _1)\sum ^z_{n=0} \sum _{k_1+...+k_J=n} \prod _{j\in \overline{J}}\rho _j^{k_j} \right. \\&\quad \quad +\left. (1-\rho _1)(1-\rho _2)\sum ^{z-1}_{n=1}\left( \sum _{k=1}^n G(n-k,J)G(n,J)^{-1}\left( \rho _1^{k}-\rho _2^{k}\right) \right) G(n,J)\right] \\&\quad = \left( \prod _{i \in \overline{J}-\left\{ 1,2\right\} }(1-\rho _i)\right) \left[ (\rho _2-\rho _1)\sum ^z_{n=0} \sum _{k_1+...+k_J=n} \prod _{j\in \overline{J}}\rho _j^{k_j} \right. \\&\quad \quad +\left. (1-\rho _1)(1-\rho _2)\sum ^{z-1}_{n=1}\left( \sum _{k=1}^n G(n-k,J)G(n,J)^{-1}\right. \right. \\&\quad \qquad \left. \left. \left( \sum ^{k-1}_{l=0}\rho _1^{l}\rho _2^{k-1-l}\right) (\rho _1-\rho _2)\right) G(n,J)\right] \\ \end{aligned}$$

Consequently, we have

$$\begin{aligned}&\frac{\frac{\partial }{\partial \rho _1} \phi ^{(z)}(\rho _1,...,\rho _J) - \frac{\partial }{\partial \rho _2}\phi ^{(z)}(\rho _1,...,\rho _J)}{\rho _1-\rho _2}\\= & {} \left( \prod _{i \in \overline{J}-\left\{ 1,2\right\} }(1-\rho _i)\right) \left[ -\sum ^z_{n=0} \sum _{k_1+...+k_J=n} \prod _{j\in \overline{J}}\rho _j^{k_j} \right. \\&+\left. (1-\rho _1)(1-\rho _2)\sum ^{z-1}_{n=1}\left( \sum _{k=1}^n G(n-k,J)\left( \sum ^{k-1}_{l=0}\rho _1^{l}\rho _2^{k-1-l}\right) \right) \right] . \end{aligned}$$

Since we started from an ergodic Jackson network, we have $\rho _i \in (0,1)$, $\forall i \in \overline{J}$. So $\phi ^{(z)}$ is Schur-concave if

$$\begin{aligned} \sum ^z_{n=0}G(n,\overline{J})&\ge (1-\rho _1)(1-\rho _2)\sum ^{z-1}_{n=1}\left( \sum _{k=1}^n G(n-k,\overline{J})\left( \sum ^{k-1}_{l=0}\rho _1^{l}\rho _2^{k-1-l}\right) \right) \\ \sum ^z_{n=0}G(n,\overline{J})\left( \sum ^\infty _{k_1=0}\rho _1^{k_1}\right) \left( \sum ^\infty _{k_2=0}\rho _2^{k_2}\right)&\ge \sum ^{z-1}_{n=1}\left( \sum _{k=1}^n G(n-k,\overline{J})G(k-1,\left\{ 1,2\right\} )\right) \\ \sum ^z_{n=0}G(n,\overline{J})\left( \sum ^\infty _{k=0}\sum _{k_1+k_2=k}\rho _1^{k_1}\rho _2^{k_2}\right)&\ge \sum ^{z-1}_{n=1}\left( \sum _{k=1}^n G(n-1-(k-1),\overline{J})G(k-1,\left\{ 1,2\right\} )\right) \\ \sum ^z_{n=0}G(n,\overline{J})\left( \sum ^\infty _{k=0}G(k,\left\{ 1,2\right\} \right)&\ge \sum ^{z-1}_{n=1}\left( \sum _{k=0}^{n-1} G(n-1-k,\overline{J})G(k,\left\{ 1,2\right\} )\right) \\ \sum ^z_{n=0}G(n,\overline{J})\left( \sum ^\infty _{k=0}G(k,\left\{ 1,2\right\} \right)&\ge \sum ^{z-2}_{n=0}\left( \sum _{k=0}^{n} G(n-k,\overline{J})G(k,\left\{ 1,2\right\} )\right) .\\ \end{aligned}$$

For the right side of the inequality, we have

$$\begin{aligned}&\sum ^{z-2}_{n=0}\left( \sum _{k=0}^{n} G(n-k,\overline{J})G(k,\left\{ 1,2\right\} )\right) =\sum ^{z-2}_{k=0}\sum _{n=k}^{z-2} G(n-k,\overline{J})G(k,\left\{ 1,2\right\} )\\&=\sum ^{z-2}_{k=0}G(k,\left\{ 1,2\right\} )\sum _{n=0}^{z-2-k} G(n,\overline{J}).\\ \end{aligned}$$

With the last equation, we can complete our proof with

$$\begin{aligned}&\sum ^{z-2}_{k=0}G(k,\left\{ 1,2\right\} )\sum _{n=0}^{z-2-k} G(n,\overline{J})\le \sum ^{z-2}_{k=0}G(k,\left\{ 1,2\right\} )\sum _{n=0}^{z-2} G(n,\overline{J}) \\&\le \left( \sum ^{z}_{n=0}G(n,\overline{J})\right) \left( \sum _{k=0}^\infty G(k,\left\{ 1,2\right\} )\right) . \end{aligned}$$

Thus, $\phi ^{(z)}$ is Schur-concave on A. $\square$