Abstract
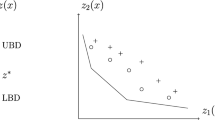
This paper considers a family of bi-objective discrete facility location problems with a cost objective and a bottleneck objective. A special case is, for instance, a bi-objective version of the (vertex) p-centdian problem. We show that bi-objective facility location problems of this type can be solved efficiently by means of an \(\varepsilon \)-constraint method that solves at most \((n-1)\cdot m\) minisum problems, where n is the number of customer points and m the number of potential facility sites. Additionally, we compare the approach to a lexicographic \(\varepsilon \)-constrained method that only returns efficient solutions and to a two-phase method relying on the perpendicular search method. We report extensive computational results obtained from several classes of facility location problems. The proposed algorithm compares very favorably to both the lexicographic \(\varepsilon \)-constrained method and to the two phase method.

Similar content being viewed by others
References
Achterberg, T., Koch, T., & Martin, A. (2005). Branching rules revisited. Operations Research Letters, 33(1), 42–54.
Balinski, M. (1965). Integer programming: Methods, uses, computations. Management Science, 12(3), 253–313.
Bérubé, J.-F., Gendreau, M., & Potvin, J.-Y. (2009). An exact \(\epsilon \)-constraint method for bi-objective combinatorial optimization problems: Application to the traveling salesman problem with profits. European Journal of Operational Research, 194(1), 39–50.
Chalmet, L., Lemonidis, L., & Elzinga, D. (1986). An algorithm for the bi-criterion integer programming problem. European Journal of Operational Research, 25(2), 292–300.
Cornuejols, G., Nemhauser, G., & Wolsey, L. A. (1990). The uncapacitated facility location problem. In P. Mirchandani & R. Francis (Eds.), Discrete Location Theory. New York: Wiley-Interscience.
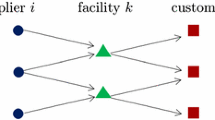
Current, J., & Weber, C. (1994). Application of facility location modeling constructs to vendor selection problems. European Journal of Operational Research, 76(3), 387–392.
Dearing, P., & Newruck, F. (1979). A capacitated bottleneck facility location problem. Management Science, 25(11), 1093–1104.
Díaz, J., & Fernández, E. (2002). A branch-and-price algorithm for the single source capacitated plant location problem. Journal of the Operational Research Society, 53, 728–740.
Ehrgott, M. (2005). Multicriteria Optimization (2nd ed.). Berlin, Heidelberg: Springer.
Farahani, R., SteadieSeifi, M., & Asgari, N. (2010). Multiple criteria facility location problems: A survey. Applied Mathematical Modelling, 34(7), 1689–1709.
Fernández, E., & Puerto, J. (2003). Multiobjective solution of the uncapacitated plant location problem. European Journal of Operational Research, 145(3), 509–529.
Filippi, C., & Stevanato, E. (2013). Approximation schemes for bi-objective combinatorial optimization and their application to the TSP with profits. Computers & Operations Research, 40(10), 2418–2428.
Gadegaard, S., Klose, A., & Nielsen, L., (2016). A bi–objective approach to discrete cost–bottleneck location problems. https://github.com/SuneGadegaard/BOCBLP, commit: 384088cd374e7629c29dbe97b8d07f0a2c0dfbdb.
Garfinkel, R. S., & Rao, M. (1971). The bottleneck transportation problems. Naval Research Logistics Quarterly, 18(4), 465–472.
Hakimi, S. (1965). Optimum distribution of switching centers in a communication network and some related graph theoretic problems. Operations Research, 13(3), 462–475.
Hakimi, S. L. (1964). Optimum locations of switching centers and the absolute centers and medians of a graph. Operations Research, 12(3), 450–459.
Halpern, J. (1976). The location of a center-median convex combination on an undirected tree*. Journal of Regional Science, 16(2), 237–245.
Halpern, J. (1978). Finding minimal center-median convex combination (cent-dian) of a graph. Management Science, 24(5), 535–544.
Hamacher, H., Labbé, M., & Nickel, S. (1999). Multicriteria network location problems with sum objectives. Networks, 33(2), 79–92.
Hamacher, H. W., & Nickel, S. (1996). Multicriteria planar location problems. European Journal of Operational Research, 94(1), 66–86.
Hamacher, H. W., Pedersen, C. R., & Ruzika, S. (2007). Finding representative systems for discrete bicriterion optimization problems. Operations Research Letters, 35(3), 336–344.
Hammer, P. (1969). Time minimizing transportation problems. Naval Research Logistics Quarterly, 16(3), 345–357.
Hansen, P. (1980). Bicriterion path problems. In G. Fandel & T. Gal (Eds.), Multiple Criteria Decision Making Theory and Application. Vol. 177 of Lecture Notes in Economics and Mathematical Systems (pp. 109–127). Berlin Heidelberg: Springer.
Holmberg, K., Rönnqvist, M., & Yuan, D. (1999). An exact algorithm for the capacitated facility location problems with single sourcing. European Journal of Operational Research, 113(3), 544–559.
Klose, A., & Görtz, S. (2007). A branch-and-price algorithm for the capacitated facility location problem. European Journal of Operational Research, 179(3), 1109–1125.
Mavrotas, G. (2009). Effective implementation of the \(\varepsilon \)-constraint method in multi-objective mathematical programming problems. Applied Mathematics and Computation, 213(2), 455–465.
Nickel, S., Puerto, J., & Rodríguez-Chía, A. (2005). Multiple Criteria Decision Analysis: State of the Art Surveys. International Series in Operations Research and Management Science. In J. Figueira, S. Greco, & M. Ehrgott (Eds.), Mcdm location problems (Vol. 19, pp. 761–795). Berlin, Heidelberg: Springer.
Pandian, P., & Nataraja, G. (2011). A new method for solving bottleneck-cost transportation problems. International Mathematical Forum, 6(10), 451–460.
Pérez-Brito, D., Moreno-Pérez, J., & Rodríguez-Martín, I. (1997). Finite dominating set for the p-facility cent-dian network location problem. Studies in Locational Analysis, 11, 27–40.
Przybylski, A., Gandibleuz, X., & Ehrgott, M. (2011). The two phase method for multiobjective combinatorial optimization problems. In R. Mahjoub (Ed.), Progress in Combinatorial Optimization (pp. 559–595). Hoboken: ISTE Ltd and John Wiley Sons Inc.
Ralphs, T., Saltzman, M., & Wiecek, M. (2006). An improved algorithm for solving biobjective integer programs. Annals of Operations Research, 147(1), 43–70.
Reese, J. (2006). Solution methods for the p-median problem: An annotated bibliography. Networks, 48(3), 125–142.
Revelle, C., Eiselt, H., & Daskin, M. (2008). A bibliography for some fundamental problem categories in discrete location science. European Journal of Operational Research, 184(3), 817–848.
Ross, G., & Soland, R. (1980). A multicriteria approach to the location of public facilities. European Journal of Operational Research, 4(5), 307–321.
Acknowledgements
The authors would like to thank Professor Kim Allan Andersen for insightful comments and suggestions. This work was supported by a grant from Købmand Ferdinand Sallings Mindefond.
Author information
Authors and Affiliations
Corresponding author
Appendix: A link to the weighted p-centdian problem
Appendix: A link to the weighted p-centdian problem
The p-centdian problem is a combination of the p-median and the p-center problems where the objective function is a convex combination of the median/cost and the center/bottleneck objectives. Given a graph \(G=(V,E)\), let P(G) be the set of all points on G and d(l, h) be the distance of a shortest path between points l and h on G (note that the points l and h might be interior points on the edges of G). Furthermore, given a set of points \(S\subseteq {P(G)}\) we define  . In addition, let \(w_j\ge 0\) and \(v_j \ge 0\) be weights of the node \(j\in V\) representing, for example, the number of customers or some other measure of attractiveness of the node j. For \(0\le \lambda \le 1\) the p-centdian problem may then be stated as
. In addition, let \(w_j\ge 0\) and \(v_j \ge 0\) be weights of the node \(j\in V\) representing, for example, the number of customers or some other measure of attractiveness of the node j. For \(0\le \lambda \le 1\) the p-centdian problem may then be stated as
It has been shown in Pérez-Brito et al. (1997) that there exists a finite set of points on G containing an optimal solution to the p-centdian. In what follows, the problem

is denoted the bi-objective p-centdian problem. It turns out that there can be infinitely many Pareto optimal solutions to this problem.
Theorem 2
The set of Pareto optimal solutions to the bi-objective p-centdian problem on a network can be uncountably infinite even for \(p=1\) when \(S\subseteq P(G)\).
Proof
We show the result by giving an example having this property. Consider the graph given in Fig. 2a, where the edge lengths are given by \(d(1,2)=d(2,1)=1\) and \(d(2,3)=d(3,2)=2\). Furthermore, suppose \(p=1\), that is, we want to place one facility on G. The intersection points on G are denoted by \(n_4\), \(n_5\), and \(n_6\). It is easily verified that locating a facility at node 2 is an optimal solution to the 1-median problem with outcome vector (3, 2) whereas placing a facility at \(n_5\) is an optimal solution for the 1-center problem, resulting in the outcome vector (3.5, 1.5). As the solutions are unique optimal solutions they are efficient. In Fig. 2b the outcome vectors for all points on the graph G have been plotted. All points on the edge (1, 2) map into the dashed line, while all solutions on the edges \((n_5,n_6)\) and \((n_6,3)\) map into the dotted line. However, all points on the edge \((2,n_5)\) map into the solid line which is non-dominated. As there are an uncountable infinite number of points on this edge, the result follows. \(\square \)
Note that the bi-objective p-centdian is not covered by the general BO–CBLP as the set I of potential facility sites has to be finite in the definition of the BO–CBLP. However, letting the sets I and J equal the set V, the (vertex) p-centdian problem (8) can be stated as the following scalarized version of the BO–CBLP:

where  ,
,  , \(f_i=0\), \(c_{ij}=w_jd(i,j)\), and \(t_{ij}=v_jd(i,j)\) for all \(i\in I\) and \(j\in J\). In many practical applications it will suffice to consider placing facilities only at the nodes of the graph. For \(0< \lambda < 1\) a solution to the vertex-p-centdian problem corresponds to a supported efficient solution of the BO–CBLP (3) with the sets I, J, \(\mathcal {X} _i\), \(\mathcal {Y} \) and the coefficients \(f_i\), \(c_{ij}\), and \(t_{ij}\) defined as above. This means that solving the BO–CBLP yields a solution to the vertex-p-centdian problem for each value of \(\lambda >0\). Most literature considers special structured graphs such as trees when solving the p-centdian problem. This approach offers a means to solve the vertex-p-centdian problem for all values of \(0<\lambda <1\) on a general graph with no assumption other than that facilities should be located on nodes only.
, \(f_i=0\), \(c_{ij}=w_jd(i,j)\), and \(t_{ij}=v_jd(i,j)\) for all \(i\in I\) and \(j\in J\). In many practical applications it will suffice to consider placing facilities only at the nodes of the graph. For \(0< \lambda < 1\) a solution to the vertex-p-centdian problem corresponds to a supported efficient solution of the BO–CBLP (3) with the sets I, J, \(\mathcal {X} _i\), \(\mathcal {Y} \) and the coefficients \(f_i\), \(c_{ij}\), and \(t_{ij}\) defined as above. This means that solving the BO–CBLP yields a solution to the vertex-p-centdian problem for each value of \(\lambda >0\). Most literature considers special structured graphs such as trees when solving the p-centdian problem. This approach offers a means to solve the vertex-p-centdian problem for all values of \(0<\lambda <1\) on a general graph with no assumption other than that facilities should be located on nodes only.
Rights and permissions
About this article
Cite this article
Gadegaard, S.L., Klose, A. & Nielsen, L.R. A bi-objective approach to discrete cost-bottleneck location problems. Ann Oper Res 267, 179–201 (2018). https://doi.org/10.1007/s10479-016-2360-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-016-2360-8