Network models and biproportional rounding for fair seat allocations in the UK elections

Abstract

Systems for allocating seats in an election offer a number of socially and mathematically interesting problems. We discuss how to model the allocation process as a network flow problem, and propose a wide choice of objective functions and allocation schemes. Biproportional rounding, which is an instance of the network flow problem, is used in some European countries with multi-seat constituencies. We discuss its application to single seat constituencies and the inevitable consequence that seats are allocated to candidates with little local support. However, we show that variants can be selected, such as regional apportionment, to mitigate this problem. In particular, we introduce a parameter based family of methods, which we call balanced majority voting, that can be tuned to meet the public’s demand for local and global “fairness”. Using data from the 2010 to 2015 UK general elections, we study a variety of network models and implementations of biproportional rounding, and address conditions of existence and uniqueness.

1 Introduction

The fundamental ideal of a functioning democracy, namely “one person, one vote” is easy to understand but has never been perfectly met (Balinski and Young 2001). There are myriad systems for electing governments in use throughout the world. In particular, most countries in Europe use some form of proportional representation (PR) as a means of allocating members to parliaments and councils at both local and national level, though there are many competing arguments as to the best way to achieve a fair system Nurmi (2014). The UK is a latecomer to PR but a number of recent elections (e.g., European, Scottish) have adopted it, at least in part. Among the systems tried are the Alternative Vote (AV) system, for one seat constituencies; and the Single Transferrable Vote (STV), for multi-seat constituencies. In both systems the voter ranks candidates in order of preference and candidates are elected once their support reaches a certain quota (an absolute majority in the case of AV). In STV, surplus votes of the elected candidates are transferred to the remaining candidates according to second preferences and anyone pushed over the quota is then elected. If no-one reaches the necessary threshold, the least popular candidate is eliminated and their votes are reallocated. This process is iterated until all seats are filled. In AV, only the second reallocation stage is necessary.

Still there is strong resistance to bringing it into the election for members of parliament (MPs) to Westminster, as the 2011 referendum on AV indicates (White 2011). Currently, UK elections are fought on the first past the post (FPTP) system, where the winner takes all in each constituency. In a multi-party election, this can skew results significantly from proportionality. For example, in the 2005 and 2015 general elections, Labour and Conservatives each gained a majority of the seats (57 and 51 %, respectively) with a minority share of votes (36 and 37 %, respectively). Conversely, in 2010 the Liberal Democrats received 23 % of the votes but only 9 % of the seats (Thrasher et al. 2011) and in 2015 UKIP received 13 % of the votes but won just one of the 614 seats they contested (The Electoral Commission 2015).

FPTP is also alleged to be responsible for effectively disenfranchising many voters, as the demographics of some constituencies means that they almost never change hands. For example, Gower, Normanton and Makerfield have elected Labour MPs without exception since 1906. If the result is a foregone conclusion voter turnout can be expected to be adversely affected. A similar problem in Switzerland led a disgruntled voter to sue (successfully) providing impetus for a subsequent change in the local electoral law (Balinski and Pukelsheim 2006).

One of the main objections to PR for the UK parliamentary elections is that it breaks the link of MPs with individual constituencies: as well as being members of a party, MPs have traditionally represented the interests of individual voters in the towns or districts they have been elected to. Suppose that a voting area has n districts, where $\sigma _i$ seats are to be allocated to district $i = 1,\ldots ,n$, and a list system typically allocates the $\sigma _i$ seats proportionally to party shares in i. If $\sigma _i=1$ as in the UK, then this simply becomes FPTP, whereas using a single transferable vote reduces to AV. If we are to devise a model of PR which retains a constituency link, a balance must be made between nationwide and local voting patterns. In particular, it should accommodate the strong support for nationalist parties in certain regions and the consistent levels of support for other smaller parties.

Any electoral system implicitly attempts to solve an optimization problem: given a set of votes, one allocates seats to parties based on their proportionate strength at regional or national level while minimizing a particular objective function.¹ For some systems, such as FPTP, the minimization part of the problem is trivial; however, explicitly framing electoral systems in the language of optimization offers insight. In particular, we choose to interpret electoral systems as instances of network flow, taking care when translating continuous models to the integer problem underlying the allocation of MPs. Pukelsheim et al. (2012) provides an excellent review of network models in this area for the interested reader. In our work, we look at a wide range of objective functions that we can attempt to optimize, chosen to promote criteria that seem reasonable for PR to achieve. If the proportional strengths are calculated at constituency level we simply recover FPTP. If proportionality at national level is too great a leap, our methods offer a halfway house that may prove more satisfactory to the general populace than AV.

For one particular choice of objective function, network flow can be viewed as a well known linear algebra problem, namely of finding a diagonal scaling of the matrix with prescribed row and column sums which respects (as far as possible) the proportionality of the original matrix of votes. This process is commonly known as biproportional rounding (Zachariasen 2006) and has formed the mathematical basis for reforming PR systems with multi-seat districts, as epitomised by research groups such as BAZI.² Biproportional rounding applies a global scaling, which means that each individual influences the result in every constituency. In elections over regions with multi-seat districts, biproportional rounding can be applied to ensure that, as closely as possible, the number of seats awarded to a district is proportional to its population while simultaneously ensuring that the number of seats awarded to a party over the whole region is proportional to the total number of votes it receives. Finding the closest fit is known as the biproportional apportionment problem. It was first proposed as a system for proportional representation in (Balinski and Demange 1989) and has since been adopted successfully in a number of legislatures (Balinski and Pukelsheim 2006; Maier et al. 2010). It is possible to apply biproportional rounding to single seat constituencies. For example, in (Balinski 2008) an implementation is presented for the House of Representatives in the USA. Balinski’s method, which he calls fair majority voting, exploits the fact that the US constitution insists that states should be awarded a quota of representatives proportionate to the population but no such condition applies in the UK. The size of the electorate of individual constituencies can vary widely³: in the 2015 General Election, the electorate for the Isle of Wight was 108,804 while that for Na h-Eileanan an Iar was just 21,744 (The Electoral Commission 2015). This means that no allocation will be a biproportional apportionment but biproportional rounding is still applicable. To some extent, Balinski’s method is also reliant on the fact that US elections are essentially between two parties, which doesn’t fit the UK model. If biproportional rounding is applied to elections involving many smaller parties then it can result in seats being awarded to candidates with a very small constituency vote. To mitigate against this, Balinski suggests that parties must reach a certain threshold in their overall popularity before they are legible for seats, a feature common to many PR systems. Choosing an appropriate threshold is difficult in the UK, where some small parties are closely tied to particular regions while others have a broad national level of support, and we will discuss a number of methods for accommodating these parties while avoiding the award of a large number of seats to candidates without a strong constituency mandate.

We believe that this paper is the first to look at biproportional rounding and network flow models in the UK context. As in fair majority voting, we ensure that each party receives seats proportionate to its total vote by scaling the votes in each constituency. Because of its links to Balinski’s method, we will call our proposed family of allocations “balanced majority voting” (or BMV). We will investigate in detail the feasibility of BMV as a means of distributing seats in any election where each constituency has a single representative. We discuss some aspects of implementation of algorithms for finding a biproportional rounding in this case and, in a corollary to the results in (Balinski and Demange 1989), we give an existence result.

To apply BMV we need a list of parties, a list of constituencies and an array of votes, $A = (a_{ij})$ where $a_{ij}$ is the number of votes party j received in constituency i. There are then two stages to the allocation in BMV. First we use the national results to calculate an appropriate proportional distribution of seats amongst parties. We arrive at a vector of global seat assignments, s, whose entries indicate the number of seats to be awarded nationally to each party. Next we must divide the constituencies amongst the parties to match this distribution. We observe that each stage can be implemented in many different ways.

Typically in an electoral system employing biproportional rounding, s is chosen to match as closely as possible the proportion of votes won at the national level. However, this isn’t the only way to proceed and we observe that FPTP is an implementation of biproportional rounding with seat allocations matched to constituency results (we will prove this is true later). One feature of our proposed allocation is that s can be tuned to lie anywhere between these two extremes to match a perceived desire for proportionality and to ease the transition to PR.

The main flexibility in the second stage comes in the choice of objective function; however, we can also apply a hierarchical approach to try and deal sensitively with regional voting patterns. We will expound this approach in more detail in our analysis. We will show that broad classes of allocation methods work (in the sense of existence and uniqueness of solutions) under only the mildest of assumptions.

To test our models, we use the voting data from both the 2010 and 2015 General Elections (The Electoral Commission 2015), for which the constituencies were identical. Note that we excluded Northern Ireland from our electoral map, due to significant difference in constituency sizes and the popular parties in comparison with the rest of the UK. For simplicity and consistency, we also assigned the votes for the Speaker in Buckingham to the Conservative party and amalgamated Green party votes although they are different parties in different nations. Since we primarily aim to highlight the possibility of applying such a system and justify its use, we leave treatment of smaller parties and other implementation details to the electoral decision makers. Biproportional rounding is performed in MATLAB, and all network optimization problems are implemented and solved using $\hbox {FICO}^\circledR$ Xpress Optimization Suite (Mosel version 3.6.0, Xpress-MP v7.7 released in 2014). Additional examples can be found in an earlier technical report available on-line (Akartunalı and Knight 2012).

2 Biproportional rounding

Before applying biproportional rounding to General Election data, we briefly consider the more general problem of equilibration in order to give some context to our consideration of algorithms and existence results for BMV. In the equilibration problem we are not forced to deal with integer variables, making some of the analysis easier.

Suppose $A\in {\mathbb {R}}^{m \times n}, t \in {\mathbb {R}}^m$ and $s \in {\mathbb {R}}^n$ are all nonnegative and that $\Vert t\Vert _1 = \Vert s\Vert _1$. Equilibration involves finding diagonal matrices $D_1$ and $D_2$ (whose diagonals are positive) such that the ith row sum of $X = D_1 A D_2$ is $t_i$ and the jth column sum of X is $s_j$. The problem has many applications (including interpreting economic data (Bacharach 1970), understanding traffic circulation (Lamond and Stewart 1981), mapping the human genome (Rao et al. 2014) and ordering nodes in a graph (Knight 2008)), particularly when A is square and X is doubly stochastic. Existence and uniqueness of solutions is well understood (Brualdi 1968; Pukelsheim 2014) and relates to the nonzero pattern of A. We can calculate X by a very straightforward iterative process: given starting vectors $r_1 \in {\mathbb {R}}^m$ and $c_1 \in {\mathbb {R}}^n$ we form the sequence of vectors

$$\begin{aligned} r_{k+1} = \frac{t}{Ac_k}, \ \ c_{k+1} = \frac{s}{A^Tr_{k+1}}, \end{aligned}$$

(1)

where the division of vectors is applied componentwise.⁴ If a solution exists, then the iterates converge linearly: $\mathrm{diag}(r_k) \rightarrow D_1, \mathrm{diag}(c_k) \rightarrow D_2$. It is usual to set all of the elements of $r_1$ and $c_1$ to 1. We will do so, too, and we use e to denote a vector of ones (whose dimension should be clear from context).

In biproportional rounding, the entries of t, s and X (not necessarily those of A) must be integers and our aim is to find real diagonal matrices $D_1$ and $D_2$ so that

$$\begin{aligned} X = \mathrm{round}(D_1 A D_2). \end{aligned}$$

(2)

Simply rounding the solution to the continuous equilibration problem is rarely the answer (usually it is far from it) however algorithms for computing X generally start by applying a number of steps of (1). In our experiments, we have found that only one or two such steps are needed. (Maier et al. 2010) describe a number of algorithms for the integer problem including a discrete version of (1) based on alternating iterative vector apportionment of the multipliers to achieve the desired row and column sums. We have adapted their algorithm to take advantage of the fact that since UK constituencies each elect a single MP $x_{ij} \in \{0,1\}$ which removes the guesswork needed to find initial estimates of the multipliers at each step. The algorithm can be found in (Akartunalı and Knight 2012). At each step we calculate a range of multipliers which give a rounding to the desired sum, from which we take the midpoint. Typically, we need no more than 50 steps of the integer algorithm to find the solution. This can be reduced with a more aggressive choice of multiplier at an endpoint of the interval, though at the risk of failure as it has a tendency to create ties in rounding (a phenomenon we have never seen with midpoint multipliers). Even on a modest PC the computations to find $D_1$ and $D_2$ (and hence X) can be performed almost instantaneously.

The question of how to round has been discussed by a number of authors. We use MATLAB’s standard rounding rule, assuming that the computations have been performed in binary floating point arithmetic.⁵ Note that this is a different problem to that of the rounding needed to determine the seats allocated to each party (i.e., the elements of the vector s for which the d’Hondt method, for example, can be used).

Conditions for existence of an allocation, X, are given by (Balinski and Demange 1989), where the authors consider the more general problem of finding allocations satisfying inequality constraints. When we want equality, as we do in our case, the conditions are almost exactly the same as those established by (Brualdi 1968) when rounding is not used, and are stated below. The difference is simply that a strong inequality becomes weak. We make use of the following definition.

Definition 1

The sets $I\subseteq \{1,2,\ldots ,m\}$ and $J\subseteq \{1,2,\ldots ,n\}$ are a reducible partition of $A \in {\mathbb {R}}^{m \times n}$ if $a_{ij}=0$ for all $i\in I$ and $j\notin J$.

Note that we can use a reducible partition to induce a permutation of A of the form

$$\begin{aligned} \left[ \begin{array}{ll} A_1 &{} 0\\ A_2 &{} A_3 \end{array}\right] \end{aligned}$$

where $A_1 = A(I,J)$. $I=\{1,2,\ldots ,m\}$ and $J=\{1,2,\ldots ,n\}$ forms a reducible partition for any A.

Theorem 1

(Balinski and Demange 1989) Suppose $A \in {\mathbb {R}}^{m \times n}$ is a nonnegative matrix, $t\in {\mathbb {N}}^m$ and $s \in {\mathbb {N}}^n$. Then there exist nonnegative diagonal matrices $D_1$ and $D_2$ such that if $X =\mathrm{round}(D_1 A D_2)$ then $Xe = t$ and $X^Te = s$ if and only if

$$\begin{aligned} \sum _{j\in J} s_j \ge \sum _{i\in I} t_i \end{aligned}$$

(3)

for any reducible partition of A (with equality if $a_{ij}=0$ for all $i\notin I$ and $j\in J$).

In terms of single seat constituencies, the consequence of this theorem is that any reasonable choice of global seat assignment will do.

Corollary 1

So long as no party is awarded more seats than it has candidates who win votes, then an allocation exists for an election for m single member constituencies contested by n parties for any distribution of seats $s \in {\mathbb {Z}}_+^n$ such that $\sum _i s_i = m$.

Proof

Clearly, a total of m seats must be allocated to parties. Now suppose a reducible partition, (I, J) exists that allows a permutation of the matrix of votes into the form

$$\begin{aligned} \left[ \begin{array}{ll} A_1 &{} 0\\ A_2 &{} A_3 \end{array}\right] \end{aligned}$$

where $A_1 \in {\mathbb {R}}^{k\times l}$. Since parties cannot be awarded seats where they did not receive votes, $\sum _{j\notin J} s_j \le m-k$ so

$$\begin{aligned} \sum _{j\in J} s_j \ge k= \sum _{i\in I} t_i \end{aligned}$$

(as $t = e$). If $A_2 = 0$ then $\sum _{j\in J} s_j \le k$, thus (3) becomes an equality. $\square$

While existence criteria can be unambiguously stated, uniqueness is not necessarily guaranteed. In particular, in any election there is the possibility of ties: consider how any system, whether FPTP or proportional, fairly allocates seats in an election where all parties earn the same number of votes in every constituency. Maier et al. (2010) analysed realistic data for districts with multiple representatives and found no instances of non-uniqueness. We revisit uniqueness in the context of network flow later in the paper and find that for single seat constituencies a judicious choice of objective function seems to prevent a threat of multiple solutions.

3 Biproportional rounding in UK general elections

The 2010 and 2015 General Elections were fought over the same $m=632$ constituencies in England, Scotland and Wales. Each election involved more than 100 parties and 300 independent candidates, and of the order of 30 million votes were cast. As we mentioned earlier, there are many ways of choosing a share of seats, s, to allocate to each party in such elections. In the first instance, we follow the approach used in both the biproportional apportionment problem and fair majority voting by simply summing the total votes for each party/independent nationally and applied the d’Hondt method (Balinski and Young 1978), also known as the Jefferson method. In the d’Hondt method, the votes cast for each party are divided by $1, 2, \ldots , m$ and the values are tabulated. A seat is then assigned to each party for each of the m largest such values. Roughly speaking, a seat is awarded by this method for every 45,000 votes won. No minimum threshold of national support was stipulated at this stage. Applying the method to the 2015 General Election, $n=7$ parties should be awarded seats—the same seven who actually won seats using FPTP. These are listed in Table 2. In 2010 two additional parties (the British National Party and the English Democrats) received sufficient support to be awarded seats under PR. The actual value of n makes little difference in implementing BMV. More detail of the 2010 allocations can be found in Akartunalı and Knight (2012).

It is well known that the d’Hondt method is biased towards larger parties (Schuster et al. 2003) but given the huge bias towards larger parties in FPTP we do not see this as a significant issue (in fact it ameliorates to some degree the extent of change caused by our proposed approach). Table 1 compares the global seat assignments, s, when the d’Hondt method is applied nationally against the actual FPTP allocation in both 2010 and 2015.

Table 1 FPTP and d’Hondt allocation of parliamentary seats

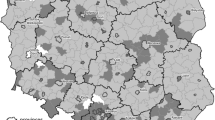
Ignoring parties who have not won enough votes to be awarded seats, we use the $m \times n$ matrix of votes, A, the vector s and $t=e$ as the input data for forming an equilibrated allocation X that satisfies (2), $Xe=t$ and $X^Te=s$. Note that with the allocation methods we have used, incorporating the votes and seat allocations of unrepresented parties in A and s would make no difference to our results, simply resulting in additional zero columns in X. The results of using BMV with the global seat assignments prescribed by the d’Hondt values on the 2015 data is compared with the actual result in Fig. 1. We also show the result of a blended approach to be described in Sect. 3.1. Each constituency is coloured according to the party awarded the seat according to the colour coding presented in Table 2.

Fig. 1

Allocation of constituencies according to FPTP (left), BMV (centre) and a blend (right)

The effects can be characterised as taking the excess seats of the two main parties and redistributing them among the smaller parties. Table 3 quantifies the number of seats assigned to each party in terms of their ranking in constituency votes (for example, 41 of the BMV Liberal Democrats were runners up according to FPTP). The sum of each column in Table 3 matches the d’Hondt values in Table 1, as intended.

Table 2 Parties and colour coding for figures

Table 3 2015 FPTP rank of seats awarded under BMV using d’Hondt rounding

While over 70 % of constituencies retain the same MP as with FPTP and nearly 90 % have a top two finisher, the fact that the candidate who comes fourth or fifth can become the MP may not sit well with some voters: the result of the AV referendum in 2011 suggests an overwhelming resistance from the populace to PR in Westminster elections, and such a radical realignment of parties may suggest that BMV is unpalatable.

Using d’Hondt exclusively to determine s means that with $m=632$, as in the UK, a party would be awarded a constituency even if it only wins around 0.2 % of the vote nationally and this low level of popularity may also be reflected locally. Thus it may be desirable to manipulate the vector s before allocating constituencies to respect local trends. However, BMV gives us a freedom that other methods of proportional representation, such as STV and AV, do not have when applied to single seat constituencies. We can tune the global seat assignments in order that the redistributive nature of BMV matches popular sentiment. We note that it is common for electoral systems to impose minimum levels of popular support before representation is permitted. The precise method for calculating is a choice to be made by policy makers (and indirectly by the public). We note that however we choose a “fair” seat allocation, our methods will still produce an apportionment; and that this method can be changed incrementally if necessary.

We first note that FPTP is itself an extreme example of BMV.

Theorem 2

Suppose BMV is used in an election with single seat constituencies where the global seat assignments are given by the FPTP results and that there are no ties for first place in any constituency. Then the resulting allocation exactly matches that of FPTP.

Proof

Suppose A is the matrix of votes and let $D_1 = \mathrm{diag}(r)$ where $1/r_i = 2\max _j a_{ij}$. Then precisely one entry in each row of $X = \mathrm{round}(D_1A)$ equals one: the entry corresponding to the largest value in row i of A. Thus BMV matches FPTP.

Furthermore, in this case the biproportional rounding given by BMV is unique. For suppose there exist diagonal matrices R and C such that $Y = \mathrm{round}(RAC)$ satisfies the marginals provided by FPTP and $X \ne Y$. Since $Xe = Ye$ and the entries of X and Y are binary, there must exist sets of indices I and J of equal length ($l\ge 2$, say) such that

$$\begin{aligned} x_{i_kj_k} = 1,\, \, x_{i_kj_{k+1}} = 0, \, \, y_{i_kj_k} = 0,\, \, y_{i_kj_{k+1}} = 1, \, \, 1\le k\le l \end{aligned}$$

where $j_{l+1} = j_1$. Since we know that $a_{i_kj_k}$ is the largest element in row $i_k$ we end up with the sequence of inequalities amongst the column scalings

$$\begin{aligned} c_{j_1}< c_{j_2}< \cdots < c_{j_{l+1}} = c_{j_1}, \end{aligned}$$

hence no such Y exists. $\square$

Suppose d is the vector of party assignments according to a d’Hondt apportionment and f is that given by FPTP. Let $0 \le \alpha \le 1$; then we can mitigate the effects of our original model of PR by choosing

$$\begin{aligned} s(\alpha ) = \mathrm{round}(\alpha f + (1-\alpha )d) \end{aligned}$$

(4)

where we choose a rounding that ensures that $\Vert s(\alpha )\Vert _1$ matches the number of seats being contested.

An illustration of allocations with $\alpha = 0.25, 0.5, 0.75$ on the 2010 election can be found in (Akartunalı and Knight 2012). One measure of the effect of changing s is given in Table 4 where we indicate the total number of seats won according to FPTP rank for a range of values for $\alpha$ for the 2015 election. The low ranking of some allocations is exclusively due to the need to assign constituencies to smaller parties, in particular the Greens.

Table 4 2015 FPTP rank of seat allocations for different values of $\alpha$

Note that if we choose $\alpha > 0.5$ then, subject to resolving ties in rounding favourably, any party that wins a seat through FPTP will win a seat through BMV. Thus we can guarantee that any constituency election that is dominated by local issues (sleaze and the need to elect a Speaker are two of the diverse examples from recent General Elections) will not be swamped by the national mood.

3.1 Balanced majority voting on regions

Comparing the results of BMV and FPTP, one can see that large areas of the country are unaffected by the reallocation. In particular, the Conservative and Labour parties remain tightly wedded to their traditional heartlands: Gower, Normanton and Makerfield remain Labour seats under BMV. In essence, BMV finds that the simplest way to deal with the iniquities of FPTP is to remove the surplus seats. However, this means that regional imbalances remain: Scotland has only two Conservative MPs out of 60 and the South and East of England are almost Labour-free outside London; both factors that run counter to proportionality. Frustrated constituents can console themselves that their vote has made a difference somewhere in the country, but this effect is rather intangible.

To mitigate against this, we can divide the country into groups of constituencies and then apply BMV separately on each: if each group contains a single constituency we are back at FPTP. We propose a grouping based on eleven regions commonly used in electoral maps, as illustrated (along with the number of seats in each region).

Rather than determining seat assignments globally, for each region we now need a vector of regional seat assignments. As with the global approach, we are free to choose the regional seat assignments as we please. As an example, we choose them by applying the d’Hondt method on each region in turn. The d’Hondt method’s inherent bias against smaller parties is amplified when used on smaller regions, although this bias is slight when compared to FPTP. The results with the May 2015 election data are shown in Table 5.

Table 5 Allocation of constituencies and party ranking according to 2015 regional BMV

Our approach ensures that the conditions of Theorem 1 hold at both the regional and national level so we can be sure an allocation exists.

Another way to apply BMV regionally is to calculate the allocation vector (4) on each region. The right hand map in Fig. 1 shows the allocation if we use $\alpha = 0.5$ on each region. We think this makes for a reasonable balance between proportionality and local representation. More detailed results are given in Table 6.

Table 6 Allocation of constituencies and party ranking according to 2015 regional BMV ($\alpha =0.5$)

Note that the number of seats handed to very poorly supported candidates has been reduced at the expense of rewarding an increased number of runners-up. Only one seat (Hereford and Herefordshire South) is awarded to a candidate outside of the top three in the constituency vote.

There are many other ways of determining the MPs. As well as varying the regional seat assignments, we can add additional constraints (for example, a minimum threshold that parties must achieve locally/nationally to be awarded seats). The main aim of this paper is to show the viability of BMV and we fear that looking at ever more intricate allocation methods will obfuscate this aim. One benefit of using BMV, however it is implemented, is that once the scaling factors r and c are calculated it is straightforward for anyone to validate the results by confirming that the entries of X are the correct scalings of A.

4 Network models for seat allocation

Of course, there are many different ways of defining target allocations for a supposedly fair electoral system. BMV fits into a general framework that can be analysed with the tools of network flow. The connection between BMV and network flow means that the insights we gain in studying one problem inform our understanding of the other. In particular, existence and uniqueness results can be understood more clearly by looking at the two different facets of the same problem.

Consider an election over the set of m constituencies (set denoted by I), contested by the set of n political parties (set denoted by J). Suppose that each party $j \in J$ gets $a_{ij}$ votes in the constituency $i \in I$, and let $x_{ij}$ indicate the number of seats allocated to party $j \in J$ in the constituency $i \in I$.

In the UK electoral system, each constituency is allocated exactly one seat, hence $x_{ij} \in \{0,1\}$ for all i and j. The current allocation system of FPTP ensures that the winner in a constituency simply takes the seat. Our aim is to prescribe a fairer allocation of the $x_{ij}$ incorporating overall votes regionally/nationally. Our proposal is to choose an objective function f(x), that is minimized when some criteria based on fairness are met subject to certain constraints placed on x.

Let $q_{ij}$ be the “target seat allocation” in constituency i to party j. An obvious choice is

$$\begin{aligned} q_{ij} = \frac{a_{ij}}{\sum _{j' \in J} a_{ij'}} \end{aligned}$$

This quantity is going to be part of the objective function, and is therefore crucial for the optimal allocation. Note that one can also define a normalized version of this, as follows:

$$\begin{aligned} \ \widehat{q}_{ij} = \frac{a_{ij}}{\max _{j' \in J} a_{ij'}} \end{aligned}$$

$\widehat{q}_{ij}$ simply denotes the ratio of a particular party’s vote to the highest vote of any party in the constituency, and there will be always a party $j'$ in each constituency with $\widehat{q}_{ij'}=1$. We also note the ranking of party j in constituency i, denoted by $r_{ij}$, is an alternative measure of fairness.

Based on these measures, we propose the following objective functions for minimization to achieve a fair seat allocation. This list is by no means exhaustive.

• 1. $f_1(x) = \sum _{i \in I} \sum _{j \in J} (1-q_{ij}) x_{ij}$

• 2. $f_2(x) = \sum _{i \in I} \sum _{j \in J} (1-\widehat{q}_{ij}) x_{ij}$

• 3. $f_3(x) = \sum _{i \in I} \sum _{j \in J} (1/q_{ij}) x_{ij}$

• 4. $f_4(x) = \sum _{i \in I} \sum _{j \in J} (r_{ij}-1) x_{ij}$

• 5. $f_5(x) = \sum _{i \in I} \sum _{j \in J} |x_{ij}-q_{ij}|$

• 6. $f_6(x) = \sum _{i \in I} \sum _{j \in J} |x_{ij}-\widehat{q}_{ij}|$

• 7. $f_7(x) = \max _{i \in I,j \in J} |x_{ij}-q_{ij}|$

• 8. $f_8(x) = \max _{i \in I,j \in J} |x_{ij}-\widehat{q}_{ij}|$

Note that the first four functions consider only the tuples (i, j) that are given a seat allocation at the end. On the other hand, the function 5 to 8 consider all tuples: these are $\ell _1$ and $\ell _\infty$ norms, respectively. A significant observation in our context is that since all variables are binary, $\ell _2$ is redundant in the case of first four objective functions above. We also note that (Serafini and Simeone 2012) discusses the $\ell _\infty$ case as presented here in $f_7(x)$, and the work of (Ricca et al. 2012) investigates the properties of the $\ell _1$ case as presented in $f_5(x)$. The advantage of $f_2(x)$ over $f_1(x)$ is that it considers zero penalty when the winner of a constituency is given the seat, which might be preferable in some electoral settings due to its emphasis on the winner. With $f_3(x)$, the penalties are anti-proportional to the amount of votes received, making it virtually impossible for a low-ranked party to win a seat, again a possible choice of electorates. In a similar fashion, $f_4(x)$ aims to avoid low-ranked parties winning seats, though it doesn’t differentiate according to the volume of votes and only considers ranking. The functions $f_7(x)$ and $f_8(x)$ are different from the others in the sense that only the “extreme case” is considered. That is, if the electorate is simply sensitive to the chance of an extreme winner/loser, then these functions would be appropriate. An electorate might want to consider a number of these criteria simultaneously in which case a multi-objective approach would be better. Finally, we note the paper of (Pukelsheim et al. 2012) as an excellent review of network modelling approaches for various electoral problems including seat allocation and political districting; the work of (Gaffke and Pukelsheim 2008a, b) on treating the fairness problem by convex integer optimization and duality to structure algorithms; and Pretolani’s quadratic knapsack approach to apportionment (Pretolani 2014).

We also consider the objective function $f_9(x) = \sum _{i \in I} \sum _{j \in J} x_{ij}(-\ln (q_{ij}) - 1)$. This can be viewed as a measure of entropy and it is well known that solving the network flow problem with this objective function is equivalent to solving biproportional rounding (Lamond and Stewart 1981; Rote and Zachariasen 2007) and so can be used to reproduce the results of the last two sections.

The usual choice of entropy measure is $\sum _{i \in I} \sum _{j \in J} x_{ij} \left( \ln \frac{x_{ij}}{a_{ij}} - 1 \right)$. Since the $x_{ij}$ can take only binary values in our model, this is equivalent to $f_9(x)$ (the scaling by ${\sum _{j' \in J} a_{ij'}}$ in the definition of $q_{ij}$ makes no difference).

Having chosen an objective function to minimise we must then determine our constraints. Obviously each constituency must be assigned to one party. We insist that a seat can only be assigned to a party that has a candidate standing there. We also need to fix the number of seats each party should be awarded. As with the objective function, we have a number of choices depending on what we consider to be fair. We could simply apply the d’Hondt method to derive our constraints but we can also look at a broader range of possibilities.

The simplest idea is to allocate $s_j$ seats to party j so that

$$\begin{aligned} \frac{s_j}{S} \approx \frac{\sum _{i \in I} a_{ij} }{\sum _{i \in I} \sum _{j' \in J} a_{ij'}} \end{aligned}$$

(5)

where S is the total number of seats (i.e., $\sum _{j \in J} s_j$). We can define the (probably) fractional seat allocation to the party j as:

$$\begin{aligned} s_j = \frac{\sum _{i \in I} a_{ij} }{\sum _{i \in I} \sum _{j' \in J} a_{ij'}} S. \end{aligned}$$

Another alternative to this measure is that we can define it based on constituencies, as follows (since each constituency has a single seat):

$$\begin{aligned} s_j = \sum _{i \in I} q_{ij}. \end{aligned}$$

Once we have defined the values of s we need to deal with their fractionality. A common alternative to the d’Hondt method to handle fractional $s_j$ values is to round them to the nearest integer according to the largest remainder rule, i.e., round down all $s_j$ values first and then round up the remaining fractional parts from the largest to the smallest fraction, until $\sum _{j \in J} s_j = S$. We will refer to this rounding with the notation $|\bullet |_{LRR}$. Alternatively, rather than constraining $s_j$ to a specific value, we can also accept allocations where the seats awarded to party j lies in an interval $[\underline{s}_j, \overline{s}_j]$, where these values are set to integer values. A particularly simple example is to choose $\underline{s}_j = \lfloor s_j \rfloor$ and $\overline{s}_j = \lceil s_j \rceil$.

Given f(x) and s our network optimization problem with integer variables is as follows:

$$\begin{aligned}&min&f(x) \end{aligned}$$

(6)

$$\begin{aligned}&s.t.&\sum _{j \in J} x_{ij} = 1&i \in I \end{aligned}$$

(7)

$$\begin{aligned}&\underline{s}_j \le \sum _{i \in I} x_{ij} \le \overline{s}_j&j \in J \end{aligned}$$

(8)

$$\begin{aligned}&x_{ij} \in \{0,1\}&i \in I, j \in J \end{aligned}$$

(9)

Note that the problem defined by (6)–(9) is essentially a network flow problem on a bipartite graph, and with integer capacities. Indeed, this problem with the previously defined objective functions can be reduced to an instance of the minimum cost flow problem. On the other hand, if a fixed value $\underline{s}_j = \overline{s}_j$ is used in (8), it reduces to an assignment problem, as one can create $\underline{s}_j$ identical nodes for each j. We will discuss these aspects further in the next section.

5 Properties of different objective functions

To gain additional insight into the process, particularly with respect to uniqueness of apportionments, we return to the general problem of apportionment through network flow. We first observe that the choice of objective function is critical. In Fig. 2 we show the apportionments when we solve Eqs. (6)–(9) with different objectives. We have computed the $s_j$ using (5) and used $\underline{s}_j = \lfloor s_j \rfloor$ and $\overline{s}_j = \lceil s_j \rceil$ in (8). This results in a small change from the party allocations given by d’Hondt.

Fig. 2

Allocation of constituencies according to (from left to right) $f_1(x), f_2(x), f_3(x)$ and $f_7(x)$

There are clear differences between each of the pictures, in particular in the way they allocate parties in Scotland. Here it is clear that the reluctance of $f_3(x)$ to give seats to low-ranked parties concentrates UKIP and the Green party to England while the $\infty$-norm measure, $f_7(x)$, is the most effective in spreading the allocations of the Conservatives and Labour nationwide without resorting to explicit regional weighting. Of all the measures, $f_3(x)$ seems to have most (visual) similarity to the biproportional rounding ($f_9(x)$) illustrated in the centre of Fig. 1. Interestingly, the picture changes somewhat when we use the 2010 data [see Akartunalı and Knight (2012)] when $f_1, f_2, f_3$ and $f_9$ all look roughly similar. To understand the connections between objective functions we first present some straightforward results.

Proposition 1

$f_5(x) \equiv f_1(x)$.

This follows from the fact that we can pick only one party (say $j'$) in each constituency i, i.e., $x_{ij'}=1$, and hence the value of $f_5(x)$ for i is simply $2(1-q_{ij'})$ (since $\sum _{j\in J, j \ne j'} q_{ij} = 1-q_{ij'}$). Therefore, $f_5(x) = \sum _{i \in I} \sum _{j \in J} 2(1-q_{ij}) x_{ij}$. $\square$

Proposition 2

$f_6(x) \equiv f_2(x)$.

This follows from the fact that when we pick one party (say $j'$) in constituency i, i.e., $x_{ij'}=1$, then the the value of $f_6(x)$ for i is: $(1-\widehat{q}_{ij'}) + \sum _{j\in J, j \ne j'} \widehat{q}_{ij}$. Therefore, $f_6(x) = \sum _{i \in I} \sum _{j \in J} (1 + \sum _{j' \in J} \widehat{q}_{ij'} - 2 \widehat{q}_{ij}) x_{ij}$, where $1 + \sum _{j' \in J} \widehat{q}_{ij'}$ is simply a constant. $\square$

Any seat allocation system should produce a unique solution for a given election, and this uniqueness property is even more significant than the fairness. Next, we will present two simple numerical examples to initiate discussion about solution uniqueness of the proposed objective functions. Small examples are used in order to allow the reader have a better understanding on apparent issues. Recall that each row of a vote matrix represents a constituency whereas each column represents a party. For simplicity, we will assume fair seat allocation to a party follows the largest remainder rule. Note that we present more examples with different scenarios in (Akartunalı and Knight 2012) and refer the interested reader there.

Example 1

Suppose votes for an election with 3 constituencies and 3 parties as in $V_1$.

$$\begin{aligned} \ V_1 = \left[ \begin{array}{lll} 5 &{} 1 &{} 4\\ 1 &{} 5 &{} 4\\ 5 &{} 2 &{} 3 \end{array} \right] \quad X_{1,1} = \left[ \begin{array}{lll} 0 &{} 0 &{} 1\\ 0 &{} 1 &{} 0\\ 1 &{} 0 &{} 0 \end{array} \right] \quad X_{1,2} = \left[ \begin{array}{lll} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1 \end{array} \right] \end{aligned}$$

By the largest remainder rule, fair seat allocation dictates that all parties earn a seat, where the first and third party got each 11 votes total, and the second party got 8 votes. The objective functions $f_4(x)$ and $f_8(x)$ will reach multiple solutions as presented in $X_{1,1}$ and $X_{1,2}$, with $f_4(x) = 1$ and $f_8(x) = 1$. The functions $f_1(x), f_2(x), f_3(x), f_7(x)$ and $f_9(x)$ all have a unique solution given by $X_{1,1}$. The optimal objective function values are $f_1(x)=\frac{8}{5}, f_2(x)=\frac{1}{5}, f_3(x)=\frac{13}{2}, f_7(x)=\frac{3}{5}$ and $f_9(x) = \ln (10)-3$. We note that the two previous corollaries imply that $f_5(x)$ and $f_6(x)$ also have unique solutions; we omit this trivial result here and in the following discussion. $\square$

Here we note that the objective function $f_8(x)$ has more than 2 solutions, since any solution x satisfying the row and column equations also satisfies $f_8(x) = 1$ for this problem. This is the key weakness of this function, as it loses sensitivity whenever a winner in a constituency is not given a seat. This insensitivity is natural for $\ell _\infty$ (or “minimax”) solutions, as also pointed out by (Serafini and Simeone 2012) for $f_7(x)$ (though $f_7(x)$ is much more successful at generating unique solutions than $f_8(x)$, as seen in other examples). This uniqueness problem can be dealt with by using strongly optimal solutions and unordered lexico minima, and we refer the interested reader to (Serafini and Simeone 2012) for details.

Example 2

Consider an election with 2 constituencies and 3 parties, with votes presented as in $V_2$ (first two parties deserving one seat each):

$$\begin{aligned} V_2 = \left[ \begin{array}{lll} 9 &{} 8 &{} 1 \\ 9 &{} 8 &{} 0 \end{array} \right] \quad X_{2,1} = \left[ \begin{array}{lll} 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 \end{array} \right] \quad X_{2,2} =\left[ \begin{array}{lll} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \end{array} \right] \end{aligned}$$

For objective functions $f_2(x), f_4(x), f_8(x)$ and $f_9(x)$, the optimal seat allocation is not unique, obtainable with $X_{2,1}$ and $X_{2,2}$. On the other hand, the objective function $f_1(x)$ has a unique optimal seat allocation as given by $X_{2,1}$, and $f_3(x)$ and $f_7(x)$ have a unique optimal seat allocation given by $X_{2,2}$. $\square$

This interesting example raises the question of “which objective function provides a better/fairer seat allocation”, as they do not necessarily provide the same allocation even when they generate a unique seat allocation. This, in turn, gives a decision maker different options to choose from. Different societies can have different perspectives and this can be reflected in their preferred objective function.

As these examples and further examples from (Akartunalı and Knight 2012) indicate, different objective functions generate unique results in different cases, and none of these objective functions seem in particular superior to the others in this aspect, although it is clear that $f_8(x)$ consistently generates multiple solutions. Similarly, $f_4(x)$ can generate multiple solutions, though not as often. From a social point of view, one can easily argue that each of these objective functions has its own merits and use of them in combination could provide the “fairest” seat allocation. Finally, we note that an electoral system might combine a number of these criteria in a multi-objective or multi-level approach.

The only theoretical uniqueness result we are aware of stems from the max algebra literature, as discussed in detail in (Burkard and Butkoviç 2003) and (Burkard et al. 2009), for our case of having an assignment problem, i.e., $\underline{s}_j = \overline{s}_j$. The uniqueness of the linear assignment problem with a cost matrix $A \in \mathbb {R}^{n \times n}$ is proven to be equivalent to the matrix A being strongly regular (or the max algebraic system $A \bigotimes x = b$ having a unique solution). However, this result is limited to square matrices only, and therefore offers very limited applicability for a general election setting as stated in our problem, with the only exceptional case of dividing the country into regions containing as many constituencies as number of parties. We are not aware of any other uniqueness result in a general setting, however we note this as a possibility for extension in the future.

To gain additional insight into uniqueness, we tested the different objective functions presented using the UK election setting (excluding the Northern Ireland for reasons previously mentioned). We used FICO Xpress 7.7 to implement and solve the network optimization problems. First, we generated 1000 random election results (with [0.1,0.3] of votes $v_{ij}$ being zero, to be comparable with the last election results). In each constituency we matched the total number of votes cast to those in the 2105 election. We then optimized each of the objective functions (except $f_5(x)$ and $f_6(x)$ due to the equivalence result presented earlier). After the optimal solution $x^*$ is found, we add the following cover cut [see e.g., (Nemhauser and Wolsey 1999)] before re-solving:

$$\begin{aligned} \sum _{\mathop { s.t. x^*_{ij}=1}\limits ^{i \in I, j \in J}} x_{ij} \le |I| - 1 \end{aligned}$$

This ensures that the first solution is eliminated from the solution space and a different solution will be found, whether with the same optimal value or not, hence showing us uniqueness. From 1000 instances, the objective functions $f_4(x)$ and $f_8(x)$ had multiple optimal solutions for each of the 1000 instances, whereas $f_7(x)$ achieved a unique optimal solution for 19 of the instances but failed to do so for the remaining 981 instances. On the other hand, the objective functions $f_1(x)$ and $f_2(x)$ had a unique optimal solution for each of the 1000 instances, whereas $f_3(x)$ and $f_9(x)$ failed to do so only for one instance each (not for the same instance, though). Details are presented in the first row of the Table 7. The results are very similar when we repeat the simulation with the 2010 data (and 9 parties).

Table 7 Number of unique solutions for 1000 instances with different votes (first row) and with $s_j$ differentiation (second and third rows)

Another interesting aspect is how different objective functions would handle $s_j$ differentiation, i.e., given election results, the effects of varying $s_j$ values (not necessarily perfected values such as using largest remainder rule but any values) and also the effects of alternative $(\underline{s}_j,\overline{s}_j)$ values (fixed as $\underline{s}_j = \overline{s}_j = |s_j|_{LRR}$, or in interval of $\underline{s}_j = \lfloor s_j \rfloor$ and $\overline{s}_j = \lceil s_j \rceil$). Using the last UK election results, we generated 1000 random feasible seat allocations to parties. As the results in Table 7 indicate, the objective functions $f_4(x)$ and $f_8(x)$, in line with the previous results, had multiple optimal seat allocations for all cases. Although using $(\lfloor s_j \rfloor , \lceil s_j \rceil )$ increases the solution space and hence theoretically one would expect more solutions (less uniqueness), the effect of this has been very minimal for most of the objective functions: There was only one instance out of 1000 for $f_2(x)$ that resulted in multiple optimal solutions. However, $f_7(x)$ presents the more interesting case here (again, similar to previous tests) that observation of uniqueness decreases with this dimension increase. Therefore, we conclude the uniqueness is in general more dependent on the matrix of votes as well as the objective function used, whereas for $f_7(x)$, the $s_j$ differentiation also affects it significantly. Again, the table entries differ only slightly if we repeat the experiment with the 2010 data suggesting that our observations can be applied in a fairly general setting.

Finally, we refer to (Ahuja et al. 1993) for sensitivity analysis of networks, as this is also an interesting aspect regarding different levels of votes, and we conclude this section with an example that generated non-unique solutions no matter which method is chosen.

Example 3

Consider an election with 3 constituencies and 3 parties, votes as in $V_3$.

$$\begin{aligned} V_3 = \left[ \begin{array}{lll} 5 &{} 1 &{} 4 \\ 1 &{} 5 &{} 4 \\ 5 &{} 1 &{} 4 \end{array} \right] \quad X_{3,1} = \left[ \begin{array}{lll} 0 &{} 0 &{} 1 \\ 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 \end{array} \right] \quad X_{3,1} = \left[ \begin{array}{lll} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right] \end{aligned}$$

In a fair allocation, all parties would earn a seat. Solutions presented as $X_{3,1}$ and $X_{3,2}$ are both optimal for all objective functions proposed. Moreover, biproportional apportionment would not generate a unique solution either. Hence the tie break needs to be handled specially here. $\square$

6 Conclusions

In this paper we have introduced a number of tuneable methods of proportional representation appropriate to single seat constituencies. We have shown that existence of allocations is guaranteed for any vote metric. Uniqueness is not always guaranteed: as with any other voting system, a tie breaking system must be employed when two parties get matching vote numbers. However, our simulations using realistic data show that for certain choices of objective function such ties are (almost) nonexistent. Single seat constituencies prove not to be an insurmountable challenge for network flow models and the binary nature of some of the variables makes the properties of some objective functions more amenable to analysis.

Our family of proposed voting systems, balanced majority voting, offer a continuum between pure proportional representation at a national level through to FPTP. Indeed, if we constrain our party allocations to match those of FPTP, our methods reproduce the constituency allocations exactly.

At the same time as trying to introduce a degree of fairness in the sense of proportionality, any electoral system should be simple to explain, to implement, and to validate. These four criteria (and we could add more) are tricky to satisfy simultaneously. In particular, we admit that our models may fail some of the simplicity tests. However we feel that our focus on fairness outweighs any perceived limitations.

There is still an issue with how to deal with smaller parties. If the fourth or fifth ranked party is handed a constituency, it is likely to prove unpopular with the local electorate. We have shown how to mitigate this to some extent by manipulating the number of seats allocated to each party, or by allocating seats at a regional level. Moreover, BMV ensures that seats are only ever allocated to candidates in the place where they stand. However, it may be desirable to impose minimum thresholds on the number of votes a party must receive (at regional or national level) before they can be awarded seats. This is, of course, a common component of current PR systems worldwide.

In our work, we used the voting data from both the 2010 and 2015 General Elections. While our proposed allocations give reasonable results they do not allow us to pick up any changes in voting patterns that the introduction of a new system would produce. This is left for future research, where for example game theoretic approaches might address such interesting issues.