Abstract
The gradual relocation of part of the energy-intensive industries (EIIs) outside of Europe is one of the possible consequences of the combination of emission charges and higher electricity prices entailed by the EU-Emission Trading System (EU-ETS). The geographical distribution of cement plants is a relevant factor in relocation decisions because cement sector is characterized by high transportation costs. In order to mitigate this effect, EIIs have asked for CO\(_2\) allowance grandfathering and long-term power contracts whereby they would be supplied from dedicated power capacities at a lower price. We model this situation on a prototype cement international market calibrated on ETS regulated and unregulated countries, with a particular focus on the Italian market. The analysis is based on an oligopolistic partial equilibrium model with a detailed technological representation of the whole production process. The model is a Generalized Nash game that accounts for the interactions of cement companies. In particular, we investigate the role played by the transportation costs in the clinker/cement production relocation and evaluates the effectiveness of CO\(_2\) allowance grandfathering and of the application of long-term power contracts in mitigating this phenomenon. To this aim, we conduct empirical experiments taking into account different transportation costs and progressively higher CO\(_2\) allowance prices with and without long-term contracts. Our results show that the European and Italian cement markets are affected by the EU-ETS and react by importing clinker from unregulated regions. Both allowance grandfathering and long-term power contracts only partially mitigate this relocation phenomenon.











Similar content being viewed by others
Notes
The expression “carbon-leakage” refers to the relocation of economic activities and emissions, namely it corresponds to an increase of greenhouse gas emissions in third countries where industry would not be subject to comparable carbon constraints. In particular, the Intergovernmental Panel on Climate Change (IPCC) measures carbon leakage through a ratio that is defined as “emission increase from a specific sector outside the country (as a result of the policy affecting that sector in the country) over the emission reductions in the sector (again as a result of the environmental policy)”.
Because of the high level of international competitiveness, EU cement industry has not been able to pass through this electricity price increase, as well as that of the other manufacturing costs, in its end price paid by consumers.
The European Commission has issued a list of all sectors that are deemed to be subject to the risk of carbon leakage and cement sector is one of them. The sector included in this list will receive free CO\(_2\) allowance in the third phase. The first carbon leakage list was adopted by the European Commission at the end of 2009 and is applicable for the free allocation of allowances in 2013 and 2014. It has to be updated every 5 years. The Commission will determine the next list by the end of 2014, which will apply for the years 2015–2019.
See Oggioni and Smeers (2012) for more details on these long-term contracts.
See Cembureau (1999) for a complete list of alternative fuels.
These plants include integrated plants that produce both clinker and cement and a few cement mills that produce cement using clinker from other installations.
In our model, we select these companies because they cover about the 70 % of the Italian cement market. Note that, apart from Cal.Me, these are multinational industries that control several plants around the world. In fact, the cement sector is highly concentrated. It suffices to say that the multinational cement companies Holcim, Lafarge, Cemex, HeidelbergCement and Italcementi respectively cover the 58 % and the 30 % of EU and global market (see Cook 2011). Finally, note that Buzzi is included in the HeidelbergCement group.
This database is available online at http://www.wbcsdcement.org/GNR-2010/index.html.
The company’s websites are: http://www.buzziunicem.it (Buzzi), http://www.calme.it (Cal.Me), http://www.cementirholding.it (Cementir), http://www.colacem.it (Colacem), http://www.holcim.it (Holcim), http://www.italcementi.it (Italcementi). See also Oggioni et al. (2011) for additional information.
Small perturbations of this parameter preserving in elasticity of the demand do not significantly affect our results.
See documents available at http://ec.europa.eu/clima/policies/ets/cap/allocation/documentation_en.htm.
Imports from unregulated countries can be also interpreted as a relocation of clinker production outside Europe.
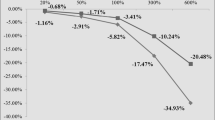
Clinker imports respectively cover the 36, 48 and 64 % respectively in the EU-ETS 30, EU-ETS 40 and EU-ETS 60 scenarios.
Under the Transport Base, these proportions are respectively 62 and 39 % in EU-ETS 30 and EU-ETS 40. These rise to 90 and 51 % in the respective cases of the Transport High.
See McKinsey & Company and Ecofys (2006).
The level of cement produced in the coastal Italian region and locally consumed under environmental regulation amounts to 58, 59 and 60 % a respectively in the EU-ETS 30 EU-ETS 40 and EU-ETS 60 cases. Considering the inland region, the levels of the Italian cement locally produced and consumed are 73, 72 and 75 % respectively in the previous EU-ETS cases.
The increases are on average equal to 26 and 17 % respectively in the coastal and in inland regions in the four EU-ETS cases. Without EU-ETS, these percentages are lower and equal to 24 and 15 % respectively in the coastal and inland areas. Note that this raise is higher in the coastal region, since the local consumption of Italian cement was already high in the Transport Base scenarios.
In the NO EU-ETS case, the quantity of European cement used to satisfy the local coastal consumption amounts to 50 %. With the application of the EU-ETS, this level respectively becomes 50, 53, 51 and 49 % in the EU-ETS 30 EU-ETS 40, EU-ETS 60 and EU-ETS 80 scenarios.
The increases computed with respect to the Transport Base scenarios are, on average, equal to 21 and 30 % respectively in the coastal and in inland regions. Note that these increases holds with and without EU-ETS.
The increase of transportation costs makes the cement coming in the Far East more economically convenient because the production costs in that region are globally lower than in the Mediterranean area.
This is equivalent to assume that power comes from nuclear power plants.
See Nagurney (1999) for a detailed presentation of VIs and their use in economic modeling.
References
Boston Consulting Group. (2008a). Assessment of the impact of the 2013–2020 ETS proposal on the European cement industry. Final project report. http://www.oficemen.com/show_doc.asp?id_doc=9.
Boston Consulting Group, (2008b). Assessment of the impact of the 2013-2020 ETS proposal on the European cement industry. Methodology and assumptions.
Boston Consulting Group. (2012). Key arguments justifying the European cement industry’s application for state aid to balance offshoring risk caused by the increase of electricity prices due to EU-ETS. http://ec.europa.eu/competition/consultations/2012_emissions_trading/cembureau2_en.
Cembureau. (1999). Best available techniques for cement industry. http://193.219.133.6/aaa/Tipk/tipk/4_kitiGPGB/40.
Cook, G. (2011). Investment, carbon pricing and leakage. In A cement sector perspective. Climate Strategies Discussion Paper. http://www.climatestrategies.org/component/reports/category/61/339.html.
Demailly, D., & Quirion, P. (2006). CO\(_2\) abatement, competitiveness and leakage in the European cement industry under the EU-ETS: Grandfathering versus output-based allocation. Climate Policy, 6, 93–113.
Demailly, D., & Quirion, P. (2008). Changing the allocation rules in the EU-ETS: Impact on competitiveness and economic efficiency. In Fondazione Eni Enrico Mattei 89-2008.
Droege, S. (2013). Carbon pricing and its future role for energy-intensive industries. Climate Strategies, Discussion Paper. http://www.climatestrategies.org/component/reports/category/61/367.html.
European Commission. (2010). Integrated pollution prevention and control (IPPC). In Reference document on best available techniques in the cement, lime and magnesium oxide manufacturing industries. http://eippcb.jrc.es/reference/cl.html.
European Commission. (2011). Decision 2011/278/EU on determining Union- wide rules for harmonised free emission allowances pursuant to Article 10a of Directive 2003/87/EC. Brussels: European Commission.
Facchinei, F., Fischer, A., & Piccialli, V. (2007). On generalized Nash games and variational inequalities. Operations Research Letters, 35, 159–164.
Facchinei, F., & Kanzow, C. (2007). Generalized Nash equilibrium problems. 4OR, 5, 173–210.
Facchinei, F., & Kanzow, C. (2010). Generalized Nash equilibrium problems. Annals of Operations Research, 5, 173–210.
Facchinei, F., & Pang, J. S. (2003). Finite-dimensional variational inequalities and complementarity problems (Vol. 1 and 2). New York: Springer.
Ferris, M. C., & Munson, T. S. (1998). Complementarity problems in GAMS and the PATH solver. Journal of Economic Dynamics and Control, 24, 2000.
Ferris, M. C., & Munson, T. S. (1999). Interfaces to PATH 3.0: Design, implementation and usage. Computational Optimization and Applications, 12, 207–227.
Ghemawat, P., & Thomas, C. (2008). Strategic interaction across countries and multinational agglomeration: An application to the cement industry. Management Science, 44, 1980–1996.
Harker, P. T., & Pang, J. S. (1990). Finite-dimensional variational inequality and nonlinear complementarity problems: A survey of theory, algorithms and applications. Mathematical Programming, 115, 153–188.
Hartman, P., & Stampacchia, G. (1966). On some non-linear elliptic differential-functional equations. Acta Mathematica, 115, 271–310.
Laing, T., Sato, M., Grubb, M., & Comberti, C. (2014). The effects and side-effects of the EU emissions trading scheme. WIREs Clim Change, 5(4), 509–519.
Linares, P., & Santamaria, A. (2012). The effects of carbon prices and anti-leakage policies on selected industrial sectors: An application to the cement, steel and oil refining industries in Spain. Climate Strategies Discussion Paper. http://www.climatestrategies.org/research/our-reports/category/61/363.html.
McKinsey & Company and Ecofys (2006) EU ETS review. Report on International Competitiveness. http://ec.europa.eu/clima/policies/ets/docs/report_int_competitiveness_20061222_en.
Meunier, G., & Ponssard, J. P. (2012). A sectoral approach balancing global efficiency and equity. Environmental and Resource Economics, 53, 522–533.
Meunier, G., & Ponssard, J. P. (2014). Capacity decisions with demand fluctuations and carbon leakage. Resource and Energy Economics, 36, 436–454.
Nagurney, A. (1999). Network Economics: A Variational Inequality Approach. Dordrecht, The Netherlands: Kluwer Academic Publishers.
Oggioni, G., Riccardi, R., & Toninelli, R. (2011). Eco-efficiency of the world cement industry: A data envelopment analysis. Energy Policy, 39, 2842–2854.
Oggioni, G., & Smeers, Y. (2012). Evaluating the application of different pricing regimes and low carbon investments in the European electricity market. Energy Economics, 34, 1356–1369.
Ortega, J. M., & Rheinboldt, W. C. (1970). Iterative solution of nonlinear equations in several variables. New York: Academic Press.
Point Carbon. (2010). Carbon 2010. http://www.pointcarbon.com/research/promo/research/.
Ponssard, J. P. (2009). Carbon leakage from the EU emission trading scheme. A comment on the cement sector. Climate Strategies Working Paper. http://www.ponssard.net/wp-content/uploads/2011/01/ponssard_feb_2009_formatted_v21.
Ponssard, J. P., & Walker, N. (2008). EU emissions trading and the cement sector: A spatial competition analysis. Clim Policy, 8, 467–493.
Reinaud, J. (2005). Industrial competitiveness under the European Union Emission Trading Scheme. IEA Information Paper.
Reinaud, J. (2008a). Issues behind competitiveness and carbon leakage focus on heavy industry. IEA Information Paper.
Reinaud, J. (2008b). Climate policy and carbon leakage-impacts of the European Emission Trading Scheme on aluminium. IEA Information Paper.
Reinaud, J. (2009). Trade, competitiveness and carbon leakage: Challenges and opportunities. In Energy, environment and development programme Paper 09-01.
Sandbag, (2011). Carbon fat cats 2011: The companies profiting from the EU Emissions Trading Scheme. Sandbag Climate Campaign: Report.
Sartor, O., Pallire, C., & Lecourt, S. (2014). Benchmark-based allocations in EU ETS Phase 3: An early assessment. Climate Policy, 14(4), 507–524.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Mathematical structure
Let X be a nonempty, closed and convex subset of the n-dimensional Euclidean space \(\mathbb R^n\) and \(F:X\rightarrow \mathbb R^n\) a continuous mapping. The variational inequality problem (VI for short) is the problem of finding a point \(x^*\in X\) such that
where we denote by \(F(x^*)^{\top }\) the transpose of \(F(x^{*})\).Footnote 26 The solution set of VI (18) is denoted by SOL(X, F).
Most existence results of solutions for VIs are proved by using various fixed point theorems. For instance, it is well known that, as a consequence of Brouwer fixed point theorem, VI (18) has a solution if X is compact and F is continuous.
Theorem 1
(Hartman and Stampacchia 1966) If X is a nonempty, compact and convex set and F is continuous on X, then VI (18) admits at least one solution.
In general, a VI can have more than one solution. Theorem 3 below recalls a condition under which VI (18) has a unique solution; this result needs a generalized monotonicity assumption.
Definition 1
Let X be a convex set in \({\mathbb {R}}^{n}\). A mapping \(F:X\subseteq {\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{n}\) is said to be
-
\(\mathrm {monotone}\) on X if \((F(x)-F(y))^\top (x-y)\geqslant 0\), \(\forall x,y\in X\);
-
\(\mathrm {strictly \ monotone}\) on X if \((F(x)-F(y))^\top (x-y)>0\), \(\forall x,y\in X\) and \(x\ne y\).
For a continuously differentiable mapping \(F:X\rightarrow \mathbb {R}^{n}\), we recall the following well-known monotonicity criteria, where \(\nabla F\) denotes the matrix that has as its i-th column the gradient of \(F_i\), \(\nabla F_i\).
Theorem 2
(Ortega and Rheinboldt 1970) Let X be an open convex set in \({\mathbb {R}}^n\) and let \(F:X\subseteq {\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{n}\) be continuously differentiable on X.
-
F is monotone on X if and only if \(\nabla F\) is positive semidefinite on X;
-
F is strictly monotone on X if \(\nabla F\) is positive definite on X.
Under assumptions of monotonicity of F and compactness of the set X, we can establish existence and uniqueness of the solutions of a VI.
Theorem 3
(Harker and Pang 1990) If F is strictly monotone, then VI (18) has at most one solution.
VIs are closely related to many problems of Nonlinear Analysis, such as complementarity, fixed point and optimization problems. A complementarity problem (CP) is problem (18) in the case where X is a cone. In particular, when \(X= {\mathbb {R}}_+^n\), the non-negative orthant of \({\mathbb {R}}^{n}\), the CP is the problem of finding a point \(x^{*}\) such that:
where \(F: {\mathbb {R}}_+^{n} \rightarrow {\mathbb {R}}^{n}\). We recall that condition (19) can be explicitly written as:
Let us now consider a Generalized Nash Equilibrium Problem (GNEP) with N players. Let \(x^{\nu }\in {\mathbb {R}}^{n_{\nu }}\), \(\nu = 1,\dots ,N\), denote the variables controlled by player \(\nu \) and \({\mathbf {x}}=\left( (x^1)^{\top },(x^{2})^{\top },\dots , (x^{N})^{\top }\right) ^{\top }\) be the vector of all decision variables (see Facchinei and Kanzow 2007 for a complete review on the topic). Let us also denote by \({\mathbf {x}}^{-\nu }\) the vector formed by all players’ decision variables except those of player \(\nu \). The problem of player \( \nu \in \{1,\dots ,N\}\), given the other players’ strategies, is to solve:
where \(f_{v}\) is the cost function of player \(\nu \) and \(X_{\nu }({\mathbf {x}}^{-\nu })\in {\mathbb {R}}^{n_{\nu }}\) is the set of strategies depending on the rival players’ strategies, \({{\mathbf {x}}}^{-\nu }\). For any \({{\mathbf {x}}}^{-\nu }\), the solution set of problem (21) is denoted by \({\mathcal {S}}_{\nu }({{\mathbf {x}}}^{-\nu })\). The GNEP can be defined as follows.
Definition 2
The GNEP is the problem of finding a vector \(\bar{\mathbf {x}}\) such that
The GNEP can be interpreted as the problem of finding a vector of equilibrium strategies for all players \( \nu = 1,\dots ,N\), where the feasible region of each player is defined by two sets of constraints: the set of constraints only depending on decision variables of player \(\nu \) and the set of common constraints. In electricity markets, for instance, common constraints arise in modeling transmission lines capacities. Equilibria of GNEPs, however, are extremely difficult to compute. A particular case is that of jointly convex common constraints. We recall that jointly convex common constraints mean that the (convex) feasible sets of all players still depend on the rivals’ strategies, but are the same for all players. More precisely, we assume that there is a common strategy space \({\mathbf {X}} \subseteq {\mathbb {R}}^n\), \(n = \sum _\nu n_\nu \) such that the feasible set of player \(\nu =1,\dots , N\) is given by
Theoretical results show that, under the assumption of jointly convex constraints, there exist equilibria of GNEPs that are also solutions to particular Variational Inequalities (VIs) and viceversa.
The following theorem (see Facchinei et al. 2007) highlights the relationship between the solution of a VI and the solutions of a GNEP. Recall that a function \(f: {\mathbb {R}}^{p} \rightarrow {\mathbb {R}}\) is called pseudo-convex on a set \(K \subseteq \mathbb R^p\) if there exists an open superset A of K such that f is continuously differentiable on A and, for all \(x,y \in A\),
Theorem 4
(Facchinei et al. 2007) Let us suppose that the GNEP satisfies the following assumptions for all \(\nu = 1,\dots ,N\):
-
i)
for every player \(\nu \in N\), \(f_{\nu }\) is continuously differentiable in \({\mathbf {x}}\);
-
ii)
for every player \(\nu \in N\), \(f_{\nu }\), the function \(f_{\nu }(\cdot , {\mathbf {x}}^{-\nu })\) is pseudo-convex in \(x^{\nu }\);
-
iii)
the feasible set of player \(\nu \) can be written as \(X_{\nu }({\mathbf {x}}^{-\nu })=\{x^{\nu }:(x^{\nu },{\mathbf {x}}^{-\nu })\in \mathbf {X}\}\), with \(\mathbf {X}\) closed and convex.
Then, every solution of the VI\(({\mathbf {X}}, {\mathbf {F}})\) is a solution of the GNEP, where \({\mathbf {F}}:{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{n}\) is defined as follows:
Theorem 4 states that a solution of a VI is also a solution of a GNEP. In this light, existence results for the solutions of a VI also ensure existence of equilibria in the GNEP. An existence result for a GNEP complying with the set-up of Theorem 4 is stated in the following result, which combines Theorems 1 and 4.
Corollary 1
Let assumptions i), ii), iii) of Theorem 4 hold and let \(\mathbf {F}\) as well be defined as in Theorem 4. Furthermore, suppose that the set \(\mathbf {X}\) is compact. Then a solution of VI\((\mathbf {X},\mathbf {F})\) exists and this is also a solution of the corresponding GNEP.
A tighter relation between the solution sets of VIs and GNEPs can be derived in the particular case where \(\mathbf {X}\) is defined as follows:
with \(n = \sum _{\nu = 1}^{N} n_\nu \), where \(n_\nu \) is the dimension of the decision variables of player \(\nu \), and \(g:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^m\) is such that \(g_i: {\mathbb {R}}^n\rightarrow {\mathbb {R}}\) is convex and continuously differentiable for all \(i=1,\dots ,m\).
Suppose also that \({\mathbf {x}}\) is a solution of the GNEP. Then the following classical Karush–Kuhn–Tucker (KKT) conditions are satisfied for each player \( \nu = 1,\dots ,N\):
where \(\lambda ^{\nu } \in {\mathbb {R}}^m\) is a vector of multipliers. The KKT conditions for VI\((\mathbf {X},\mathbf {F})\) are the following:
where \(\lambda \in {\mathbb {R}}^m\) is a vector of multipliers.
The following theorem, among the solutions of a GNEP, characterizes those that are also VI’s solutions.
Theorem 5
(Facchinei et al. 2007) Let us suppose that the GNEP satisfies assumptions i), ii) and iii) of Theorem 4 and the set \({\mathbf {X}}\) is given by (23). Vector \({\mathbf {x}}\) is a solution of VI\(({\mathbf {X}},{\mathbf {F}})\) at which the KKT conditions (25) hold if and only if \({\mathbf {x}}\) is a solution of the GNEP at which KKT conditions (24) hold with \(\lambda ^1=\dots =\lambda ^N=\lambda \).
Appendix 2: Notation: sets, parameters and variables of the model
In this appendix we list the sets, the parameters and the variables used in our models.
Sets
- J :
-
Set of cement companies operating in the market.
- I :
-
Set of zones in which the market is divided. We define \(I = I_{{\textit{ETS}}}\cup I_{{\textit{NETS}}}\), where \(I_{{\textit{ETS}}}\) includes all zones subject to the EU-ETS while \( I_{{\textit{NETS}}}\) indicates those zones without environmental regulation. Each zone \(i\in I\) can be further partitioned in \(\widehat{l}\) homogeneous regions that we indicate as \(i_1, i_2,\dots , i_{\widehat{l}}\). We denote \(Z_i=\{i_l: l\in L\}\), where \(L=\{1,\dots ,\widehat{l}\}\), for all \(i\in I\). For example \(l=1,2\) distinguish between coastal and inland regions in each zone \(i\in I\).
- W :
-
Set of technologies used for producing clinker.
- V :
-
Set of technologies used for producing cement.
- G :
-
Set of fuel employed in clinker production.
- \(N_{j,i_l}\) :
-
Set of plants of company \(j \in J\) located in the region \(i_l \in Z_l\), where \(i\in I\) and \(l\in L\).
- \(W_n\) :
-
Set of clinker technologies available in plant \(n \in N_{j,i_l}\).
- \(V_n\) :
-
Set of cement technologies available in plant \(n \in N_{j,i_l}\).
Parameters and variables
-
Clinker parameters
- \(t^k_{j,i_l,h_r}\) :
-
Clinker transportation cost sustained by company \(j \in J\) to move clinker from region \(i_l \in Z_l\) to region \(h_r \in Z_h\).
- \(p^{mk}_{i}\) :
-
Price of the stones (limestone, chalk, marl and shale) in zone \(i\in I\) used as raw material for producing clinker.
- \(\gamma ^k_{g,i,w}\) :
-
Proportion of fuel \(g\in G\) used in clinker production in zone \(i\in I\), with technology \(w\in W\) (ton/ton).
- \(p^f_{g,i}\) :
-
Price of fuel \(g \in G\) in zone i used in clinker production.
- \({\alpha _w}\) :
-
Electricity consumption per tons of clinker produced with technology \(w \in W\) (KWh/ton).
- \({Q}^k_{n,w}\) :
-
Capacity of the kiln of technology \(w \in W_n\) of plant \(n \in N_{j,i_l}\).
- \(p^k_i\) :
-
Price of clinker for each zone \(i\in I\) (euro/ton).
- \(\rho _{i}\) :
-
Clinker to cement ratio applied in zone \(i\in I\) (%).
- \(\sigma _{i}\) :
-
Raw material to clinker ratio applied in zone \(i\in I\) (%).
-
Cement related parameters
- \(t^c_{j,i_l,h_r}\) :
-
Cement transportation cost sustained by company \(j \in J\) to move cement from region \(i_l \in Z_l\) to region \(h_r \in Z_r\).
- \(p^{mc}_i\) :
-
Price of the material (gypsum, slag, limestone) used for producing cement in zone \(i\in I\).
- \({Q}^c_{n,v}\) :
-
Grinding mill capacity of technology \(v \in V_n\) of plant \(n \in N_{j,i_l}\).
- \({\beta _v}\) :
-
Electricity consumption per tons of cement produced with technology \(v \in V\) (KWh/ton).
-
Other parameters
- \({p^e_i}\) :
-
Average electricity price in zone \(i\in I\).
- \(p^{CO_2}\) :
-
Allowance price (€/ton CO\(_2\)).
- \({GA}_{n,w}\) :
-
Amount of grandfathered allowances for plant \(n \in N_{j,i_l}\) with technology \(w\in W_n\) (ton/year).
- \(\tau _{i,w}\) :
-
Average emission factor per ton of clinker produced depending on the zone \(i\in I\) and technology \(w \in W\).
Variables
-
Clinker variables
- \(q^k_{n,w}\) :
-
Clinker produced by plant \(n \in N_{j,i_l}\) with technology \(w \in W_n\) (ton/year).
- \(s^k{j,i_l,\bar{j},h_r}\) :
-
Clinker produced by company \(j\in J\) in region \(i_l\in Z_l\) and sold to company \(\bar{j}\in J, \bar{j}\ne j\), in region \(h_r \in Z_h\) (ton/year).
- \(b^k_{j,i_l,\bar{j},h_r}\) :
-
Clinker bought by company \(j\in J\) to satisfy demand in region \(i_l\in Z_l\) from company \(\bar{j}\in J, \bar{j}\ne j\), in region \(h_r \in Z_h\) (ton/year).
- \(u^k_{j,i_l}\) :
-
Clinker produced by company \(j\in J\) in region \(i_l\in Z_l\) and used in the same region (ton/year).
- \(m^k_{n}\) :
-
Raw material (limestone, chalk, marl and shale) used by plant \(n \in N_{j,i_l}\) to produce clinker (ton/year).
- \(e^k_{n}\) :
-
Electricity used by plant \(n \in N_{j,i_l}\) to produce clinker (KWh/year).
- \(f^k_{g,n,w}\) :
-
Fuel of type \(g \in G\) used by plant \(n \in N_{j,i_l}\) to produce clinker with technology \(w \in W_n\) (ton/year).
-
Cement variables
- \(q^c_{n,v}\) :
-
Cement produced by plant \(n \in N_{j,i_l}\) with technology \(v \in V_n\) (ton/year).
- \(s^c_{j,i_l,h_r}\) :
-
Cement produced by company \(j\in J\) in region \(i_l\in Z_l\) and sold in region \(h_r \in Z_h\) (ton/year).
- \(e^c_{n}\) :
-
Electricity used by plant \(n \in N_{j,i_l}\) to produce cement (KWh/year).
- \(m^c_{n}\) :
-
Material (gypsum, slag, limestone) used by plant \(n \in N_{j,i_l}\) to produce cement (ton/year).
Appendix 3: Complementarity version of the clinker and cement producer problem
-
Clinker complementarity conditions
$$\begin{aligned} 0\le & {} - \lambda s^k_{\widehat{j},i_l} + \sigma _i \cdot \lambda m^k_n + \alpha _w \cdot \lambda e^k_n + \gamma _{g,i,w} \cdot \lambda f_{g,n,w} \nonumber \\&+ \,\lambda Q^k_{n,w} + \tau _{i,w} \cdot p^{CO_2} \bot \ q^k_{n,w}\ge 0, \quad \forall \ \ i \in I_{{\textit{ETS}}}, \ i_l\in Z_i,\ n \in N_{\widehat{j},i_l}, w \in W_n \end{aligned}$$(26)$$\begin{aligned} 0\le & {} - \lambda s^k_{\widehat{j},i_l} + \sigma _i \cdot \lambda m^k_n + \alpha _w \cdot \lambda e^k_n + \gamma _{g,i,w} \cdot \lambda f_{g,n,w} \nonumber \\&+\, \lambda Q^k_{n,w} \bot \ q^k_{n,w}\ge 0, \quad \forall \ \ i \in I_{{\textit{NETS}}}, \ i_l\in Z_i,\ n \in N_{\widehat{j},i_l}, w \in W_n \end{aligned}$$(27)$$\begin{aligned} 0\le & {} -p^k_h{ +} \lambda sb^k_{\widehat{j},i_l,j,h_r}+\lambda s^k_{\widehat{j},i_l} \ \bot \ s^k_{\widehat{j},i_l,j,h_r}\ge 0, \forall i,h \in I, \ i_l\in Z_i, \ h_r\in Z_h, \ j\in J, \ j\ne \widehat{j}\nonumber \\ \end{aligned}$$(28)$$\begin{aligned} 0\le & {} { \lambda q^k_{i_l}} +\lambda s^k_{\widehat{j},i_l} - { \lambda b^k_{\widehat{j}}} \ \bot \ u^k_{\widehat{j},i_l}\ge 0,\qquad \forall \ \ i \in I, \ i_l\in Z_i \end{aligned}$$(29)$$\begin{aligned} 0\le & {} \lambda q^k_{i_l}+p^k_i+t^k_{\widehat{j},h_r,i_l} - \lambda bs^k_{j,h_r,\widehat{j},i_l}-\lambda b^k_{\widehat{j}}\ \bot \ b^k_{\widehat{j},i_l,j,h_r}\ge 0,\quad \nonumber \\&\forall \ i\in I,h\in I, \ i_l\in Z_i,\ h_r\in Z_h, \ j\in J, j\ne \widehat{j} \end{aligned}$$(30)$$\begin{aligned} 0\le & {} p^{mk}_i-\lambda m^k_{n}\ \bot \ m^k_{n}\ge 0,\quad \forall \ i \in I, \ i_l\in Z_i,\ n \in N_{\widehat{j},i_l} \end{aligned}$$(31)$$\begin{aligned} 0\le & {} p^e_i -\lambda e^k_{n} \ \bot \ e^k_{n}\ge 0,\quad \forall \ i \in I, \ i_l\in Z_i,\ n \in N_{\widehat{j},i_l} \end{aligned}$$(32)$$\begin{aligned} 0\le & {} p^f_{g,i}-\lambda f_{g,n,w}\ \bot \ f_{g,n,w}\ge 0,\quad \forall \ i\in I, \ i_l\in Z_i, \ n \in N_{\widehat{j},i_l},\ w\in W_n,\ g\in G \end{aligned}$$(33)$$\begin{aligned} 0\le & {} Q^k_{n,w} - q^k_{n,w} \ \bot \ \lambda Q^k_{n,w}\ge 0, \quad \forall \ i\in I,\ i_l\in Z_i, \ n \in N_{\widehat{j},i_l},\ w\in W_n \end{aligned}$$(34)
-
Cement complementarity conditions
$$\begin{aligned}&0\le -\lambda q^c_{\widehat{j},i_l}+\rho _i \cdot \lambda b^k_{\widehat{j}}+(1-\rho _i)\cdot \lambda m^c_{n}+\beta _v\cdot \lambda e^c_{n}\nonumber \\&\quad -0.8\cdot \lambda q^k_{i_l}+\lambda Q^c_{n,v}\ \bot \ q^c_{n,v} \ge 0,\quad \forall \ i\in I, \ i_l\in Z_i, \ n \in N_{\widehat{j},i_l}, \ v\in V_n \end{aligned}$$(35)$$\begin{aligned}&0\le p^m_i -\lambda m^k_{n}\ \bot \ m^k_{n}\ge 0,\quad \forall \ i\in I,\ i_l\in Z_i, \ n \in N_{\widehat{j},i_l} \end{aligned}$$(36)$$\begin{aligned}&0\le p^e_i -\lambda e^c_{n}\ \bot \ e^c_{n}\ge 0,\quad \forall \ i\in I,\ i_l\in Z_i, \ n \in N_{\widehat{j},i_l} \end{aligned}$$(37)$$\begin{aligned}&0\le -P_{h_r} { -} \frac{\partial P_{h_r}}{\partial s^c_{\widehat{j},i_l,h_r}}\cdot \displaystyle { \sum _{\begin{array}{c} d \in I,\ d_o\in Z_d,\\ h_p\in Z_h \end{array} }} s^c_{\widehat{j},d_o,h_p}+t^c_{\widehat{j},i_l,h_r} \nonumber \\&\quad +\,\lambda q^c_{\widehat{j},i_l}\bot \ { s^c_{\widehat{j},i_l,h_r}} \ge 0 \quad \forall \ i\in I,\ i_l\in Z_i, \ n \in N_{\widehat{j},i_l} \end{aligned}$$(38)$$\begin{aligned}&0 \le Q^c_{n,v} - q^c_{n,v} \ \bot \ \lambda Q^c_{n,v}\ge 0, \quad \forall \ i\in I,\ i_l\in Z_i, \ n \in N_{\widehat{j},i_l}, \ v\in V_n \end{aligned}$$(39)
Rights and permissions
About this article
Cite this article
Allevi, E., Oggioni, G., Riccardi, R. et al. An equilibrium model for the cement sector: EU-ETS analysis with power contracts. Ann Oper Res 255, 63–93 (2017). https://doi.org/10.1007/s10479-016-2200-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-016-2200-x
Keywords
- Cement sector competitiveness
- Complementarity modeling
- EU-ETS
- Generalized Nash game
- Long-term power contracts