Abstract
The environment in which airlines operate is uncertain for many reasons, for example due to the effects of weather, traffic or crew unavailability (due to delay or sickness). This work focuses on airline reserve crew scheduling under crew absence uncertainty and delay for an airline operating a single hub and spoke network. Reserve crew can be used to cover absent crew or delayed connecting crew. A fixed number of reserve crew are available for scheduling and each requires a daily standby duty start time. This work proposes a mixed integer programming approach to scheduling the airline’s reserve crew. A simulation of the airline’s operations with stochastic journey time and crew absence inputs (without reserve crew) is used to generate input disruption scenarios for the mixed integer programming simulation scenario model (MIPSSM) formulation. Each disruption scenario corresponds to a record of all of the disruptions that may occur on the day of operation which are solvable by using reserve crew. A set of disruption scenarios form the input of the MIPSSM formulation, which has the objective of finding the reserve crew schedule that minimises the overall level of disruption over the set of input scenarios. Additionally, modifications of the MIPSSM are explored, a heuristic solution approach and a reserve use policy derived from the MIPSSM are introduced. A heuristic based on the proposed MIPSSM outperforms a range of alternative approaches. The heuristic solution approach suggests that including the right disruption scenarios is as important as the quantity of disruption scenarios that are added to the MIPSSM. An investigation into what makes a good set of scenarios is also presented.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
To maximise profits, airlines need to maximise the utilisation of resources (crew and aircraft), resulting in flight schedules with little slack. This makes each resource a critical component of an airline’s network and if a component is missing all flights related to that component may be disrupted. Crew can be absent (e.g. ill) or be delayed on connecting flights. In such circumstances airlines may call on reserve crew. This work focusses on reserve crew scheduling, i.e. determining the appropriate times at which to allocate standby reserve crew duties. In this work the possible start times for reserve crew standby duties are discretised according to the scheduled departure times of the airline’s schedule. This approach is aimed at making reserve crew recovery actions available at times as close as possible to the scheduled departure times as to minimise reserve crew induced delays.
A method has been developed called the mixed integer programming simulation scenario model (MIPSSM) which will use information from repeat simulations of an airline network where reserve crew are not available. The simulation data is used to generate disruption scenarios which are used to form the constraints and coefficients of the MIPSSM formulation. The MIPSSM formulation is then solved to find the reserve crew schedule that would have minimised the level of delay and cancellation that would have occurred in the original simulations (used to derive the disruption scenarios).
The remainder of the paper is structured as follows. Section 2 gives an overview of the proposed MIPSSM approach. Section 3 outlines closely related work. Section 4 introduces the simulation used to generate disruption scenarios and how disruption scenarios are derived from the simulation. Section 5 presents the formulation of the MIPSSM and Sect. 6 gives several modifications and variants of the basic MIPSSM formulation including a scenario selection heuristic. Section 7 describes how a look up table reserve policy can be derived for a reserve crew schedule using an adapted version of the MIPSSM formulation. Section 8 introduces several alternative objective functions for the MIPSSM. Section 9 gives experimental results. Section 10 presents an investigation into what makes a good set of input scenarios for the MIPSSM formulation with respect to solution reliability and the quality of the resultant reserve crew schedule. Section 11 discusses the possible future work. Section 12 concludes the paper with a summary of the main findings.
This paper adds a new approach that complements the existing literature on approaches to increasing airline schedule robustness (see Sect. 3). This work focusses on the problem of reserve crew scheduling, and treats the reserve crew schedule as a means of augmenting the robustness of the airline’s crew schedule. Airline reserve crew scheduling is an important problem because of the dependencies that exist between the aircraft, crew and passenger layers of an airline’s overall schedule. Disruptions in one layer of the schedule can spread laterally to the other layers and can also be propagated (longitudinally) downstream to subsequent flights. So reserve crew can be strategically scheduled to minimise disruptions for which crew-related disruptions are the root cause.
This work proposes a scenario based approach for scheduling reserve crew that is an adaptation from robust optimisation, see Sect. 3, and so provides an example of such an approach applied within a different problem domain. As far as the authors are aware no previous work has used a scenario based approach for reserve crew scheduling. The proposed model is based on an airline operating a single hub airline network. The large domestic airline on whose data and practises this work is based have reserve crew stationed at their hub station who are on standby and are ready to replace disrupted crew. Disrupted crew include both absent and delayed crew. This work proposes an approach for assigning reserve crew to standby duties with the aim of minimising day of operation disruptions. The presented problem formulation is based on the case of a single crew and single fleet type. There are four reasons for doing this: (1) it simplifies the analysis of the results, allowing for a clear demonstration of how the approach can yield reserve crew schedules that minimise cancellations and delay disruptions; (2) the single crew and fleet type model still captures the main difficulty of this problem, that of modelling the uncertain demand for reserve crew; (3) the single crew and fleet type model is directly applicable to captain and first officer scheduling as these crew types are each normally qualified for a single fleet type and are usually scheduled separately (this is the case for the airline on whose operations this work is based); and (4) extending the model to a multiple crew and fleet type model is a relatively simple matter and the proposed solution approaches are directly applicable to the extended model. The implications of considering multiple fleets, crew ranks, and qualifications on the model and solution approach are discussed in more detail in Sect. 11.2.
The contributions of this paper are both practical and methodological. The practical contributions include: the introduction of a framework for solving a challenging real world scheduling problem whose only input requirement is a simulation of the airline’s operations; and experimental results that demonstrate that this approach has the potential to minimise day of operation delay and cancellation disruptions. The methodological contributions include: a specification of how to derive disruption scenarios from the airline’s simulator; and the introduction of a scenario selection heuristic which is shown to be capable of deriving higher quality reserve crew schedules using fewer input scenarios compared to the standard formulation.
2 Overview of the MIPSSM
This section describes the sequence of stages involved in the MIPSSM approach. Additionally a function that converts delays into an equivalent measure of cancellations is introduced, the purpose of which is to retain the simplicity of a single objective in the MIPSSM formulation.
2.1 Stages of the MIPSSM approach
Figure 1 illustrates the stages that are required to be performed sequentially in the proposed MIPSSM approach, from input data through to validation. Note that the input data and validation simulation stages are not part of the MIPSSM approach to reserve crew scheduling, but have been included in Fig. 1 to illustrate the full cycle of deriving and testing reserve crew schedule and policy combinations. The MIPSSM approach to reserve crew scheduling involves three main stages:
-
1.
A simulation stage is used to derive disruption scenarios. A disruption scenario corresponds to the set of disrupted flights in a single run of the airline simulation, where a single run corresponds to executing the airline’s schedule in the considered time horizon from start to finish once. A disrupted flight in the simulation results in a disruption added to the disruption scenario. For each disruption in a disruption scenario there is a corresponding record of all of the reserve crew start times (discretised to match the scheduled departure times) which, if scheduled, would allow the corresponding reserve crew to be used to remove completely, or reduce, the given disruption.
-
2.
A MIPSSM formulation is solved to find the best reserve crew schedule for the set of disruption scenarios generated in the first stage. In the MIPSSM formulation there are two types of variables: x the reserve crew schedule and y the reserve use variables. For each disruption scenario there is a corresponding subset of the reserve use variables. The reserve use decisions made for each disruption scenario have to be feasible with respect to the overall reserve schedule x (i.e. reserve crew can only be used if they are scheduled). The difficulty is finding a reserve schedule that allows disruptions in many scenarios to be covered in an efficient manner. Solving the MIPSSM formulation over a set of input disruption scenarios in an appropriate solver finds both the reserve crew schedule x and the reserve use decisions y that together minimise delay and cancellations over all of the input disruption scenarios.
-
3.
Lastly, a reserve policy is derived, corresponding to the reserve crew schedule found in the MIPSSM formulation stage, which defines the conditions on the day of operation under which reserve crew use is permitted. The policy takes the form of a look up table which specifies the minimum number of reserve crew that should be available at each departure time if reserve crew are to be permitted to be used to absorb crew-related delay affecting a given departure.
2.2 Cancellation measure of a delay
The goal of the MIPSSM approach is to schedule reserve crew to minimise delay and cancellation disruptions. To retain the simplicity of a single objective problem in the MIPSSM formulation, Eq. 1 converts delay into a measure of cancellation. The simulation cancels flights with a delay over the cancellation threshold so the maximum cancellation measure of a delay is 1. Table 1 defines the notation required for calculating delays and delay cancellation measures. \(td_{h}\) (Eq. 2) is the total delay of flight h, \(cd_{h}\) (Eq. 3) is the delay of flight h due to crew over and above delay due to the aircraft, i.e. the delay which could be absorbed by using reserve crew. Equation 4 gives the total delay that occurs when reserve crew with start time index l (\(\text {start time}=D_{l}\) as reserve start times are discretised according to scheduled departure times) are used to replace the delayed connecting crew of flight h. The cancellation measure associated with using reserve crew can still be calculated from Eq. 1 by replacing the numerator by Eq. 4.
Using the delay cancellation measure function means that the objective measures of using reserve crew teams to cover delayed connecting crew and using reserve crew to cover absent crew are both in the same units, that of cancellations. A decision maker choice is required for the delay exponent n of the cancellation measure function and provides a method of pinpointing a solution from a set of delay/cancellation trade off solutions. Choosing higher values for \(n>1\) corresponds to giving lower weight to delays below the cancellation threshold. In general using \(n>1\) is advisable, assuming that having two delays of half the cancellation threshold is considered a smaller disruption than an actual cancellation. In experiments it was found that smaller values of n reduce delays but increase cancellations, as n increases the average delay increases and the cancellation rate decreases. In the following, \(n=2\) is used. The particular choice of \(n=2\) permits a balanced demonstration of how this work accounts for delay and cancellation disruptions. Note however that any value of n could be used.
The disruption scenario generation stage collects information about the possible objective value (cancellation measures) of using reserve crew scheduled at different times for different disruptions in each disruption scenario.
2.3 Disruption scenarios
The proposed MIPSSM approach uses the concept of disruption scenarios. A disruption scenario corresponds to a set of crew-related disruptions that could occur during the implementation of an airline’s schedule. In the MIPSSM approach, disruption scenarios are collected from a simulation of an airline. The simulation has stochastic crew absence and journey time inputs instantiated from corresponding statistical distributions. For each disruption in a disruption scenario information must be maintained about the disruption size (in the form of a cancellation measure), the number of reserve crew required to cover the disruption, and the benefits of using reserves crew scheduled at different times to cover the disruption. The information about the benefit of using reserves scheduled at different possible times is stored in the form of sets of feasible reserve instances corresponding to each disruption in each disruption scenario (see Sect. 2.4)
2.4 Feasible reserve instances
In the simulation which generates disruption scenarios, information regarding the benefit of using reserve crew scheduled at different times to absorb a given disruption is collected. For each reserve start time that is feasible to absorb a given disruption, a feasible reserve instance is generated. A feasible reserve instance therefore corresponds to a combination of a reserve crew duty start time and a disruption that could be absorbed by using a reserve crew with such a duty start time. For each feasible reserve instance there is a cancellation measure which replaces the cancellation measure of the original disruption if the reserve is used (in the MIPSSM formulation) to cover the disruption. The use of feasible reserve instances means that the MIPSSM formulation only contains binary variables corresponding to feasible reserve crew which can, if scheduled, be used to cover disruptions. Reserve feasibility constraints are therefore not required as only feasible reserve recovery actions are included in the MIPSSM formulation.
Let b denote a given feasible reserve instance. For each feasible reserve instance there is:
-
1.
A corresponding cancellation measure (\(\textit{CM}\left( b\right) \)) which is calculated in the disruption scenario generation stage. This is the cancellation measure that applies in the MIPSSM formulation if reserve crew with the duty start time (corresponding to b) are used to cover the disruption (corresponding to b).
-
2.
An associated unique reserve use variable index (\(V\left( b\right) \)) which identifies the binary reserve use variable in the MIPSSM formulation associated with the feasible reserve instance.
-
3.
A unique (knock-on effect) reserve use variable index (\(U\left( b\right) \)) corresponding to feasible reserve instances which can absorb a root delay that subsequently propagates, hence reducing the secondary delay.
-
4.
A reserve delay (\(\textit{RD}\left( b\right) \)) caused by waiting for the given reserve crew to start their standby duty before they can be used for the disruption associated with the given feasible reserve instance.
Feasible reserve instances generated in the disruption scenario generation phase are each stored in two sets. In one set containing all of the feasible reserve instances which were generated for the same disruption and the same disruption scenario, and in a second set containing all of the feasible reserve instances generated with the same reserve start time and for the same disruption scenario. These sets are then used to form the constraints of the MIPSSM formulation (Sect. 5).
3 Related work
The MIPSSM approach has similarities to recoverable robustness as introduced by Liebchen et al. (2007). Recoverable robustness provides a framework for timetabling problems with the objective that the schedule must be feasible in each of a limited set of disruption scenarios given limited availability of recovery from disruptions. Their approach reduces to strict robustness (feasible in all outcomes without recovery actions) if the feature of limited available recovery is removed. The similarity between recoverable robustness and the MIPSSM approach lies in the idea of solving a scheduling problem over a limited number of realistic disruption scenarios, but differs because recoverable robustness assumes a fixed capacity for recovery exists whereas in this work the recovery action is what is being scheduled. The MIPSSM approach is influenced by stochastic programming, which optimises over a set of explicit independent possible outcomes as opposed to optimising over the expected outcome, which may not even correspond to a possible outcome.
There has been relatively little work on reserve crew scheduling in the past and none looks at exactly the same problem. Sohoni et al. (2006) present an airline reserve crew scheduling model that takes training days and bidline conflicts into account. Such conflicts arise when crew bid for rosters which overlap with recurring training and this leads to open time (flights without scheduled crew) which have to be covered with reserve crew. The work of Sohoni et al. primarily focusses on scheduling reserve crew in anticipation of reserve crew demand from scheduling conflicts due to reoccurring training, less attention is given to reserve demand due to day of operation disruption, which is the main focus of this work. The work of Boissy (2006) describes an absenteeism forecast model and a model for minimising the cost of reserve crew and missing crew. Boissy defines tension as the number of disruptions divided by the number of reserve crew, using more reserve crew decreases tension but increases the crew cost. Boissy’s model is used to find the optimal tension, which corresponds to the minimum cost of missing crew plus reserve crew cost. Boissy’s main focus is manpower planning whereas in this work the focus is on the scheduling of the available manpower. Dillon and Kontogiorgis (1999) present an approach for pilot reserve crew scheduling that generates reserve pairings which are then subject to crew bidding. They focus on quality of life considerations such as regularity. Their work helped in negotiations with pilot unions. The work of Dillon and Kontogiorgis refers to the specific case of US airlines, who have permanent reserve crew who are used to fill open or disrupted pairings. Open pairings are crew pairings that do not have crew assigned. Dillon and Kontogiorgis generate call out day pairings for reserve crew and focus on generating pairings with regularity and varying lengths. Generating varying length pairings allows for reserve crew who have different amounts of time off in a given month. In contrast to Dillon and Kontogiorgis, in this work reserve crew pairings are all regular as they start at the same time every day, and also have fixed lengths, since this is the way that KLM operate.
The work of Paelinck (2001) describes a practical approach which was implemented at KLM to optimise cabin crew reserve duties. The approach calculates daily demands for reserve crew and the expected number of reserve crew remaining each day, and uses a reserve block stacking approach. The aim is to always have standby reserve crew available. Paelinck (2001) also highlights some of the difficulties associated with the planning and scheduling of reserve crew, including how many should be scheduled, when and what is the best way to use them in response to disruptions.
As described in Sect. 1 a reserve crew schedule augments the robustness of an already existing crew schedule. Shebalov and Klabjan (2006) increase crew schedule robustness using the concept of move-up crews. Move-up crews refers to crews who can swap pairings in the event of delay (the available crew can adopt the delayed crew’s pairing). Their objective is to maximise the availability of move-up crews. Shebalov measures the robustness of schedules/quality of the scheduled move-up crews in computational experiments in terms of the number of deadheads (crew transported as passengers to the origin of their next flight leg), reserve crew used, number of uncovered flight legs and the cost of the crew schedule. The simulation used in the MIPSSM approach includes crew swap recovery actions, and therefore the MIPSSM approach takes the pre-existing robustness of the crew schedule into account. This means that if the input crew schedule for the MIPSSM was derived from an approach such as that of Shebalov and Klabjan, the MIPSSM would preserve the increased schedule robustness which was introduced by their approach and add extra schedule robustness. On a similar note, the approach of Ageeva and Clarke (2000) was to increase the availability of swap recovery actions by encouraging ground time overlaps, whilst Smith (2004) did the same for aircraft swap opportunities (using the concept of station purity).
Other work on increasing airline schedule robustness, which is complementary to that proposed in this work, has also been carried out. Sohoni et al. (2011) introduce stochastic programming models for modifying airline schedule departure times within allowable time windows, with the aim of increasing on-time performance and minimising the probability of passengers missing connections. Weide et al. (2010), Dunbar et al. (2012) and Duck et al. (2012) took the approach of performing crew pairing and aircraft routing in an integrated fashion, which helped to reduce disruptions resulting from dependencies between the crew and the aircraft schedules. These complementary approaches, including the MIPSSM, to increasing airline schedule robustness can all be applied during the applicable planning phases, the result of which will be even greater schedule robustness.
The MIPSSM approach uses simulation to obtain information about the most beneficial times to schedule standby reserve crew. Simulation has also been used to determine operational crew costs for an airline crew pairing problem. In particular, Rosenberger et al. (2002) use a simulation approach to replace planned pairing costs with operational costs. The reasoning behind such approaches is that minimising planned costs is an optimistic approach (i.e. assuming no disruptions leads to fragile schedules), whereas the operational cost based solution, despite costing more than the planned cost, will on average cost less after the recovery costs are added to the planned costs. In experiments they show that their approach minimises expected crew costs compared to state of the art approaches based on planned costs.
Abdelghany et al. (2004) introduce an approach for the crew recovery problem which considers crew swaps, reserve crew and dead heading as possible recovery actions. Their model takes as input the status of the airline operations at a given time in terms of the current crew schedule and any associated disruptions. Their objective is to recover as many disrupted crew trip-pairs (crew pairings) as possible, with the least deviation from the original schedule and with the minimum incurred cost. Their model is also able to anticipate future disruptions up to a day before they occur (due to minimum rest rules) and prevent these from occurring. In contrast to the work presented here, the work of Abdelghany et al. (2004) considers the use of reserve crew who have already been scheduled. Their underlying model considers disruption scenarios that are in progress, whereas as in this work many possible future disruption scenarios are generated in order to find a single reserve crew schedule that works well in all of them.
The work of Bayliss et al. (2012) introduced a probabilistic model of crew absence and reserve crew used to cover absence. The approach was based on the knowledge of the probabilities of crew absence for each flight in an airline’s schedule. The probabilistic model evaluated the effect a given reserve crew schedule has on the probabilities of cancellations due to crew absence. The solution space of reserve crew schedules was then searched to find the reserve crew schedule that minimised the probabilities of cancellations due to crew absence. It was found that constructive heuristics provided near optimal solutions when solving the model presented in Bayliss et al. (2012) whilst a hybrid dynamic programming and branch and bound heuristic approach was able to find the optimal solutions. In contrast to Bayliss et al. (2012) this work investigates the alternative approach of modelling reserve demand uncertainty using a scenario based approach rather than a probabilistic model.
4 Disruption scenario generation simulation
This section explains the disruption scenario generation stage of the MIPSSM approach. Section 4.1 gives details of the single hub airline simulation, which is used firstly for disruption scenario generation and then later reused for experimental validation of reserve crew schedules. Section 4.2 defines what is meant by a disruption scenario and how the information it stores is collected from the simulation. Table 2 defines the input airline schedule notation. Table 3 defines the notation used for disruption scenarios.
4.1 Simulation
The simulation of a single hub airline is used without reserve crew to generate a set of disruption scenarios which contain information on the possible benefit of using reserve crew scheduled at specified times to mitigate the the given disruption. These disruption scenarios form the input for the MIPSSM formulation (Sect. 5.1).
Simulation takes as input the airline’s scheduled flights and the crew and aircraft which are scheduled to each of those flights. The simulation’s stochastic inputs are journey times and crew absence, each of which have corresponding statistical distributions derived from real data. Crew and aircraft were scheduled using first in first out scheduling (see Sect. 9.1 for details of the test schedule instance).
The simulation has a dual purpose: disruption scenario generation and reserve crew schedule validation. For disruption scenario generation, no reserve crew are scheduled and none are therefore available for recovery (as the point of disruption scenario generation is to find information about when reserve crew are most needed). In contrast the validation simulation does include a reserve crew schedule and is used to compare the reserve crew schedules which were found using the MIPSSM against reserve crew schedules obtained using alternative approaches.
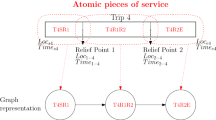
Figure 2 illustrates: how the simulation models the execution of an airline’s schedule; how crew absence uncertainty and journey time uncertainty are included in the simulation; the process of airline recovery and the points in the simulation at which information is yielded about disruptions that are solvable by using reserve crew. This is then used to derive the disruption scenarios. A single run of the simulation proceeds by considering each scheduled departure in departure time order. If a departure corresponds to the start of a crew pairing then the number of absent crew is instantiated from the cumulative statistical distribution. If crew are absent and reserve crew are not available (as is always the case in the disruption scenario generating simulation) then the flight has to be cancelled. At this point in the simulation, information on the possible benefit of scheduling reserve crew at different start times is collected (Sect. 4.2). If reserve crew are available (as may be the case in the validation simulation used in Sect. 9) they are considered for use in earliest start time order. If a departure is delayed by more than the delay threshold (\(\textit{DT}=15\) min) all combinations of single crew and aircraft swaps are considered in an attempt to recover from the delay. Swaps are only considered feasible if the swap can take place without invoking additional delay on either of the flights affected by the swap, however this can be relaxed easily to allow some additional delay of the affected flight if this reduces overall delay. The crew must be able to complete each other’s duties without violating maximum working hours and it must be possible to undo the swap in the overnight break (i.e. the crew must stay overnight at the same station).
In the disruption scenario generation simulation, if the delay is still above the delay threshold even after the consideration of swap recovery actions, information is collected on the possible benefit of scheduling reserve crew at different possible start times (Sect. 4.2). The validation simulation also considers reserve crew as a possible recovery action from delays. If the delay is still above the cancellation threshold (180 minutes) the flight is cancelled.
4.2 Simulation derived scenarios
A given disruption scenario i corresponds to a single run of the simulation. This section explains how simulation is used to derive the information for disruption scenarios.


In disruption scenario i, a disruption j corresponds to the j th crew disrupted flight for which reserve crew use could be a beneficial recovery action. Reserve crew use is beneficial when a flight either has a delay which is greater than the delay threshold (the minimum delay that is considered a delay worth recovering from), even after the consideration of swap recovery, or has to be cancelled due to crew absence. Such disrupted flights have a positive cancellation measure, where \(cm_{i,j}\) denotes the cancellation measure of disruption j in disruption scenario i.
In a given run of the simulation, when a disruption occurs that can be absorbed by using reserve crew, data is collected regarding all of the possible feasible reserve start times that, if scheduled, could be used to reduce the disruption. For each such beneficial reserve start time, feasible reserve instances are generated. A feasible reserve instance (Sect. 2.4) corresponds to a feasible reserve crew duty start time index which can be used to cover a given crew disrupted flight in a given scenario (i.e. reserve start time/disruption pair). For each disruption the number of feasible reserve instances which are generated for each feasible reserve start time index is equal to the number of reserve crew required to cover the given disruption, which is either the number of crew absent (for a crew absence disruption) or the size of the crew team assigned to flight h (\(crewSize_{h}\)) for a delay. Let \(F_{i,j}\) denote the set of feasible reserve instances corresponding to possible reserve start times that could, if scheduled, be used to solve or reduce disruption j of disruption scenario i.
For the specific case of delay disruptions it is also possible that reserve crew use can have the effect of reducing or preventing knock-on delays. For this purpose the set \(G_{i,j}\) is introduced which denotes the set of feasible reserve instances corresponding to the possible use of reserve crew which were originally used to absorb the root delay also being used to absorb the knock-on disruption. Note that crew-related delays occur when a flight has to wait for crew on a delayed connecting flight, so the reserve used for the root delay can only influence the delay of the following flight if other reserve crew are not used to absorb the delay of that following flight. Algorithms 1 and 2 outline the procedure of collecting information for the disruption scenarios from the single hub airline simulation.
Algorithm 1 is used in the disruption scenario generating simulation when a crew absence occurs, the algorithm considers all of the possible ways the absence disruption can be covered using reserve crew (reserve crew with different start time indices l) and generates \(N_{i,j}\) feasible reserve instances for each. The number of reserve crew required to cover a disruption equals the number of absent crew (line 6). The cancellation measure of the absence disruption is the number of hub departures in the disrupted crew pairing that would have to be cancelled if reserve crew were unavailable to cover the absent crew (line 7), with no delay contribution to the cancellation measure.
The algorithm then considers each possible reserve start time (line 8) used to cover absent crew at each hub departure in the disrupted crew pairing (line 9). If a reserve is feasible, \(N_{i,j}\) new feasible reserve instances are generated with unique reserve use variable indices and cancellation measures equal to the number of flights that have to be cancelled before crew absence is covered at the m th hub departure in the disrupted crew pairing plus a delay cancellation measure contribution from any delay caused by the reserve start time (lines 13–20). The newly generated feasible reserve use instances are stored in sets according to which disruption and scenario they are applicable to (line 17) and to which reserve start time index and scenario they are applicable to (line 18). These sets are useful later on when creating the constraints for feasible reserve use in the MIPSSM formulation.
Algorithm 2 is used in the disruption scenario generating simulation when a crew-related delay occurs. The algorithm stores the size of the disruption and then considers all of the possible reserve crew recovery actions and generates feasible reserve instances for each. Algorithm 2 differs from Algorithm 1 because of the type of disruption (delay rather than absence) and because of the possibility that, if they were used, feasible reserve instances generated for previous crew delay disruptions in the same simulation run could have reduced the current delay. If the current crew-related delay is a delay propagated from a previous crew-related delay, feasible reserve instances are generated corresponding to the reserve crew which could have been used to absorb the root crew-related delay and are being used to cover the knock-on delay also. These feasible reserve instances are stored in the set \(G_{i,j}\). The number of reserve crew required to cover the given disruption in Algorithm 2 is the number of crew in the delayed crew team (line 6). The cancellation measure of the delay disruption when reserve crew are not available to cover the delayed crew is computed on line 7. The algorithm then considers each possible reserve start time (line 8) which could be used to cover the delay. If the reserve start time is feasible (line 9) and can absorb the delay, then \(N_{i,j}\) (\(=crewSize_{k}\)) new feasible reserve instances are generated (line 11) with unique reserve use variable indices and cancellation measures as calculated on line 10.
Lines 21 to 33 of Algorithm 2 apply if feasible reserve instances generated for the previous flight prevent or reduce the delay propagated to the current flight. For such feasible reserve use instances (line 24) \(U\left( F_{i,o,l}\right) \) (line 29) stores a new unique reserve use variable index corresponding to the same reserve being used to absorb the delay of the following flight. The reason why an extra reserve variable index is generated for the same reserve used on a following flight is that it is possible that other reserve crew might instead be used to cover the knock-on delay if the reserves used for the root crew-related delay do not absorb all of the delay and some delay can still propagate. The set G stores feasible reserve instances corresponding to the feasible reserve instances which were generated for the root crew-related delay. Line 25 calculates the corresponding cancellation measures for these feasible reserve instances, which depend upon the amount of delay that would have propagated if the feasible reserve instance corresponding to the root crew delay was utilised. The MIPSSM has constraints that ensure that the beneficial knock-on effects can only apply if the reserve is actually used to absorb the root crew delay.
5 The MIPSSM’s mixed integer programming formulation (MIPSSM formulation)
This section explains the mixed integer linear programming formulation. Section 5.1 presents and explains the objective and constraints and Table 4 defines the notation used.
5.1 Mixed integer programming formulation (MIPSSM formulation)
A set of disruption scenarios is used to form the objective and constraints of the MIPSSM formulation. The MIPSSM formulation finds the reserve crew schedule (x) that minimises the total cancellation measure over all disruption scenarios which were added to the formulation. The reduced cancellation measures that replace the original cancellation measures, that occurred in the disruption scenario generating simulations, depend on which reserve use variables (y) are selected to cover each disruption.
s.t.
Objective 5 minimises the sum of all cancellation measures over all disruptions in all of the scenarios included in the model. Constraint 6 ensures that disruptions are only considered covered if the required number of reserve crew are used for the given disruption. Constraint 6 forces \(\delta _{i,j}\) to 1 when no reserve recovery can be applied to disruption j in scenario i and to 0 otherwise. Constraint 6 means that it is acceptable to cover a crew-delayed departure with a combination of reserve crew used now and reserve crew used to cover a preceding crew delay that propagated. This may be useful if some of the reserve crew which are used to cover the root delay are not feasible to cover the following flight. Constraint 7 ensures that no more than the total number of reserve crew available (TR) are scheduled. Constraint 8 ensures that in each disruption scenario the number of reserve crew used with the same start time index does not exceed the number of reserve crew which are scheduled to that start time index. Constraint 9 ensures that knock-on delays can only be absorbed by reserve crew if those reserve crew are actually used to cover the root delay. Constraints 10 to 12 ensure that the cancellation measure associated with a given disruption is the maximum of that associated with the recovery actions used for the given disruption. If no reserve crew are used for a given disruption, that disruption gets the cancellation measure \(cm_{ij}\) that occurred in the simulation run in which the disruption occurred. If reserve crew are used, the cancellation measure is that for the reserve crew used for that disruption that invokes the largest cancellation measure (as the flight can’t take off before all of the crew are present). Constraints 13 to 15 are the integrality constraints.
6 Variants and modifications of the MIPSSM formulation
This section firstly considers 2 alternative objective functions for the basic MIPSSM formulation given in Eqs. 5–15. Then a scenario selection heuristic is introduced which is designed to address the question of whether the types of scenarios or the number of scenarios included in the formulation has the greatest effect on solution quality.
6.1 Alternative objectives for the MIPSSM
6.1.1 MiniMax 1
The objective of minimising the sum of cancellation measures over all disruption scenarios included in the model (Objective 5) could be replaced with the alternative objective MiniMax1 of minimising the largest sum of cancellation measures for any scenario. This is a minimax objective function, discussed in Williams (2002), and can be implemented by replacing Objective 5 with Objective 16 and adding Constraint 17. This approach will have the effect of finding a reserve crew schedule that minimises the extent of the worst case scenario as opposed to minimising the average cancellation measure.

6.1.2 MiniMax 2
Instead of minimising the total cancellation measure of the disruption scenario with the largest cancellation measure, the same principle can be applied to individual scenarios with the alternative objective MiniMax2. I.e. find the reserve crew schedule that minimises the single largest disruption. To implement this approach replace Constraint set 17 with Constraint set 18.
In the results (Table 5) there is no performance measure which is directly relevant to the MiniMax2 formulation because in the reserve crew schedule validation simulation the worst single disruption is a cancellation and these will inevitably occur in each method. However in the MiniMax2 formulation the worst single disruption is leaving an absence disruption uncovered which would result in all flights on the absent crew’s line of flight being cancelled.
6.2 Scenario selection heuristic
The basic MIPSSM and the two alternative formulations MiniMax1 and MiniMax2 are solved over a given set of disruption scenarios in a linear programming solver (CPLEX in this case). Although CPLEX yields optimal solutions, the solutions are only optimal for the set of disruption scenarios considered in the model. This section introduces a scenario selection heuristic (SSH) to address the issue of the choice of scenarios which should be included in the MIPSSM formulation. The solution time increases sharply as the number of disruption scenarios increases, which provides another motivation for considering a scenario selection heuristic solution approach, which includes the right scenarios rather than ensuring that plenty of disruption scenarios are included in the model.
The following heuristic is based on adding one disruption scenario to the model at a time and stopping when a new acceptable disruption scenario cannot be found within the iteration limit (itLim) (line 3 of Algorithm 3), for which the sub-problem objective value (subObj) is larger than the objective contribution of the scenario already in the master problem with the largest objective contribution (\(\max _{j}(\textit{masterObj}_j)\)). The sub-problem objective value of a new scenario is calculated (line 8) from the MIPSSM formulation with the new scenario as the only input disruption scenario and with the incumbent reserve crew schedule (X) fixed. This heuristic is analogous to column generation in which the master problem and pricing problem are solved iteratively. In summary, this scenario selection approach focusses on finding a reserve schedule that can cope with a wide variety of difficult scenarios as opposed to a random set of scenarios representing the average outcome. This scenario selection heuristic can be expressed by Algorithm 3.
7 Optimal reserve use policy derivation
This section introduces an approach for deriving an optimal reserve use policy for a given reserve schedule, by solving the MIPSSM formulation for a fixed reserve schedule repeatedly, over a single disruption scenario, at a time and learning the circumstances in which reserve crew use is eventually beneficial in the long run. The policy is optimal only in the sense that it is learned from the optimal decisions for a given set of disruptions scenarios which are solved by the MIPSSM
The simulation (Sect. 4.1) which is used to test reserve schedules has a default policy of using reserve crew whenever this is immediately beneficial. The default policy also uses reserve crew in earliest start time order, so as to leave the largest amount of unused reserve crew capacity available for subsequent disruptions. The MIPSSM approach uses reserve crew in each disruption scenario in an optimal way based on full knowledge of future disruptions. Knowledge of future disruptions is not available in the simulation, if a scenario which was included in the MIPSSM formulation is repeated in the validation simulation, reserve crew might not necessarily be used in the same optimal way.
The reserve policy derived from the MIPSSM formulation is based on reserve use decisions in response to delayed crew, where a team of reserve crew could be constructed and used to absorb the delay. The policy consists of threshold minimum numbers of reserve crew remaining for each departure for which using reserve teams to absorb crew-related delay is deemed globally beneficial. The threshold values are calculated by repeatedly solving the reserve use variables of the MIPSSM for different disruption scenarios with the given reserve crew schedule fixed. The threshold value for a given flight is the average number of reserve crew remaining immediately before that flight if reserve crew were used in the way recommended by the MIPSSM formulation.
The default policy is used for reserve crew use in response to crew absence since the penalty for not replacing absent crew with reserve crew is cancellation. In general, using teams of reserve crew to cover delayed connecting crew is expensive as it solves a smaller disruption (a delay compared to a cancellation) using more reserve crew than are usually required to cover absent crew. However in certain circumstances using teams of reserve crew to cover delayed connecting crew can be globally beneficial. .
8 Alternative methods
8.1 Probabilistic reserve crew scheduling under uncertainty
The probabilistic approach (Prob) to reserve crew scheduling contains important extensions of the work by the same authors in Bayliss et al. (2012). This current work has extended the work in Bayliss et al. (2012) to account for different numbers of crew being absent from each crew pairing in an airline schedule. Moreover the constraint that reserve crew are only feasible for disruptions if their duty start time is no later than the scheduled departure time of the disrupted flight has been relaxed so that some reserve delay is permitted, just as in the MIPSSM. Reserve delays in the probabilistic approach are accounted for using the delay cancellation measure (Eq. 1).
8.2 Area under the graph
The area under the graph (Area) method is based on running a number of simulations and recording the cumulative demand for reserve crew with respect to time in the form of a bar chart (in terms of the cancellation measure that could be avoided if reserve crew were available). Reserve crew are then scheduled at equal area intervals under the reserve demand graph over the whole time horizon. The Area approach is based on a simulation without reserve crew to find reserve demand independent of the effects of a reserve crew schedule.
8.3 Uniform start rate
The uniform start rate method (USR) schedules reserve crew at equal time intervals.
8.4 Zeros
The Zeros method schedules all reserve crew to begin standby duties at the first departure of the first day.
9 Experimental results
The MIPSSM (Sect. 5.1), MiniMax1 and MiniMax2 (Sect. 6.1) and SSH (Sect. 6.2) approaches are tested and compared to one another. IBM CPLEX Optimization Studio version 12.5 with Concert technology is used as the MIP solver, on a desktop computer with a 2.79 GHz Core i7 processor and 6 Gb of RAM. These methods are also compared to the alternative methods for reserve crew scheduling (described in Sect. 8).
9.1 Experiment design
All reserve crew scheduling approaches described above are used to schedule reserve crew for a generated test instance, which is now described. The input airline schedule features fully detailed crew connections and aircraft routings. Journey time uncertainty is modelled by statistical distributions based on real data, crew absence uncertainty is modelled as each individual scheduled crew member having a 1 % chance of being absent and missing their entire crew pairing. All teams of crew consist of 4 individuals with identical rank (primarily aimed at cabin crew, but extending also to cockpit crew). The schedule is based on a 3 day single hub airline schedule with 243 flight legs a day with half of these being from the hub station and the other half back to the hub. The schedule uses 148 teams of crew and 37 aircraft (single fleet). The schedule was generated using a first in first out approach with stochastic parameters controlling the rate of crew aircraft changes (0.3) and the 60th percentile journey time from each destination’s cumulative journey time distribution. These parameters influence the likelihood of delay propagation and the occurrence of delayed connecting crew. The following section investigates the effect of the number of reserve crew available for scheduling for each solution approach.
9.2 Investigating the effect of varying the number of reserve crew available for scheduling
The results in Fig. 3 show the effect on the average cancellation measure of varying the number of reserve crew available for scheduling, using 20,000 repeat validation simulations for the reserve crew schedules from each solution approach. The MIPSSM based approaches are restricted to 50 input disruption scenarios and a maximum of 1 h to find a solution.
Figure 3 shows how the various reserve crew scheduling approaches compare for different numbers of reserve crew available for scheduling. The SSH, MIPSSM and Prob approaches obtain the lowest average cancellation measures of those tested for all numbers of available reserve crew. The Prob model gives a smooth curve of average cancellation measures, whereas MIPSSM and SSH have small fluctuations in average cancellation measure as the number of reserve crew available for scheduling changes. This fluctuation can in part be attributed to the limited number of disruption scenarios used as input for these methods. The MiniMax1 modification generally leads to higher average cancellation measures especially when between 9 and 12 reserve crew were available for scheduling. MiniMax2 gave the unexpected result that scheduling more reserve crew can lead to a higher average cancellation measure. This fluctuating behaviour of the MiniMax2 modification was also observed to a lesser extent in the other methods based on the MIPSSM (as well as the MIPSSM approach itself) and can be explained by the fact that the objective of the MiniMax2 modification is to suppress the single largest delay or cancellation disruption that can occur and is not to minimise the average cancellation measure. This fluctuation is due to the resultant schedules being designed for worst case disruptions as opposed to the average outcomes. The Area under the graph approach lead to average cancellation measures similar to those from the MiniMax2 modification but without the fluctuations. The USR approach lead to the highest average cancellation measures when 10 or fewer reserve crew are available for scheduling. For more than 10 reserve crew the zeros approach gave the highest cancellation measures.
The difference between the various solution approaches is clearest when there are around 10 to 12 reserve crew available for scheduling, which also appears to be the most sensible number of reserve crew to schedule (due to diminishing returns). In this range, Figure 3 shows that the best performing solution approach was the SSH. 10 to 12 reserve crew for the given problem instance is approximately proportionate to the number of reserve crew scheduled in reality.
Figure 4 shows the effect of using the MIPSSM derived reserve use policy described in Sect. 7 compared to the default policy of using reserve crew as demand occurs. Using the MIPSSM derived policy had the effect of reducing the average cancellation measure.
9.3 Other performance measures and solution reliability
Table 5 gives average performance measures when each method is applied to the same problem instance 20 times, for the MIPSSM approaches the simulation generated scenarios differ in each of the 20 repeats as they start with a different random seed. The results of Table 5 correspond to the case where 11 reserve crew are available for scheduling. The first column gives the methods which are being compared, the second column gives the average cancellation measures attained by each method in the validation simulations. The third column gives the average delay calculated over the flights which experienced positive delays. The fourth column gives the probability that a flight is delayed by more than 30 min. The fifth column gives the probability a flight is cancelled. The sixth column gives the average reserve utilisation rate. The last column gives the average time in minutes to derive the reserve schedule using each method.
The results show that on average the MIPSSM performs best on cancellation rate, however the MIPSSM is also the slowest method with average solution times of 28 min. The average cancellation measure can be interpreted as the number of cancellations expected in each of the simulations, but this also includes delays which have been converted to a cancellation measure using Eq. 1 of Sect. 2.2. On the whole, the SSH is a highly efficient approach with the lowest cancellation measure, a low average delay and a low solution time in comparison with the MIPSSM approach. The low solution time of the SSH in comparison to the that of the MIPSSM is a result of the termination criteria being satisfied before more than 10 disruption scenarios are added to the master problem. This result suggests that the SSH outperforms the MIPSSM approach because it is possible to find a better reserve crew schedule with fewer input disruption scenarios, provided that some effort is made to find such a set of scenarios. The Prob approach has the second lowest average cancellation measure, good average delay performance and a solution time much quicker than those of the MIPSSM based approaches.
The results in Table 5 suggest that there is merit in both the probabilistic and MIPSSM based approaches (SSH in particular) for scheduling airline reserve crew under uncertainty. Table 5 also includes performance measures when no reserve crew are scheduled at all as a point of reference. Contrary to expectation the probability of delay over 30 min is lower without reserve crew, as is the average delay, however this can be attributed to the high cancellation rate, since cancelled flights do not count as delays and also to delays introduced when waiting for reserve crew to cover for absent crew.
Figure 5 shows the spread of cancellation measures corresponding to each method over the 20 repetitions of each method, with each being tested in 20,000 repeat validation simulations. The percentile axis has an exponential scale (cubed) for clarity, as this increases the linearity of the data. Figure 5 also displays the 100th percentile (worst case) cancellation measure from each approach, and this is the most appropriate validation criteria for the MiniMax2 objective. The MiniMax2 objective does not have the lowest cancellation measure for the 100th percentile, so it appears that this objective does not achieve its goal. The reason for this is that MiniMax2 schedules reserve crew with respect to the worst case scenarios in a limited set of scenarios, so when a worst case scenario occurs in the validation simulation which is different from the worst case scenarios used to derive the reserve crew schedule, the reserve crew schedule performs worse than a reserve crew schedule aimed at the average case scenario.
Figure 5 demonstrates that for each given percentile the ordering of the methods supports the results given in Table 5 except for the zeros approach which has the lowest worst case cancellation measure. This result suggests that the worst scenario is, for a very large number of crew to be absent at the start of each day, which is precisely the situation the zeros approach can cope with. The MiniMax2 approach will only achieve it’s goal if such worst case scenarios happen to be in the limited sets of scenarios. The other methods have relatively high worst case cancellation measures because they are aimed at the average case scenario.
Table 5 and Fig. 5 show that the MiniMax1 and MiniMax2 approaches which were aimed at minimising the effects of the worst case scenarios do not appear to have been effective in achieving this goal when considering the relatively high probabilities of delay over 30 min (Table 5) and the 100th percentile (worst case) cancellation measures (Fig. 5) associated with these approaches. The possible explanation is that the best reserve crew schedule for one worst case is not the best reserve crew schedule for a different worst case scenario.
Each point on Fig. 6 represents a solution to the given method starting from a different random seed in the simulation used to generate the set of disruption scenarios over which the method is solved. Figure 6 shows that the MIPSSM based methods have a solution reliability issue. Figure 6 also shows that the MIPSSM based methods have the potential to give solutions of higher quality that the probabilistic method (Prob), but this depends on the selection of disruption scenarios which are used as input for the given MIPSSM based method. For this reason further research was performed to investigate the scenario selection mechanism.
10 The effect of scenario sets on reserve crew schedule quality
The basic MIPSSM formulation requires a set of input disruption scenarios. This section attempts to address the issue of solution reliability illustrated in Fig. 6, through careful selection of the scenarios added to the MIPSSM formulation of Sect. 5.1. Disruption scenarios were generated randomly in the previous sections. In the case of the SSH, scenarios are selected if the cancellation measure for the new scenario is worse than the cancellation measure in any of the already selected scenarios, with the incumbent reserve crew schedule. This section investigates what makes a good set of scenarios. To answer this question attributes of sets of scenarios are defined. These are defined by the pool of scenarios that scenarios in the set belongs to and the number of scenarios in the set. Three pools of scenarios are considered, and these are generated using the procedure outlined in Fig. 7 of Sect. 10.1. The presence or lack of correlations between the attributes of sets of scenarios and the resultant reserve crew schedule quality was investigated. Sect. 10.1 presents an investigation into the effect of the number of scenarios selected and the different types of pools from which they are selected of scenarios on the quality of reserve crew schedules derived from those sets of scenarios using the MIPSSM formulation.
10.1 Attributes of sets of scenarios
As previously mentioned, the attributes of a set of scenarios are defined as the number of scenarios and the pool from which the scenarios are selected. Each pool of scenarios has a defining criterion for accepting scenarios into the pool.
10.1.1 Pool A: 1000 random scenarios
Pool A consists of 1000 randomly generated scenarios.
10.1.2 Pool B: good individual scenarios
Figure 7 shows how the two pools of scenarios B and C are derived from pool A. To create pool B, the first step is to solve the MIPSSM formulation for each scenario in pool A on its own to obtain a reserve crew schedule corresponding to each scenario in pool A. Each reserve crew schedule corresponding to each scenario in pool A is then tested in the validation simulation to obtain an associated average cancellation measure. Pool B is then populated with the 100 scenarios from pool A which have the lowest associated average cancellation measures. Pool B represents scenarios, that when solved alone in the MIPSSM formulation, give good reserve crew schedules.
10.1.3 Pool C: good scenarios for sets
To create pool C, 200 sets of scenarios of various sizes are randomly sampled from pool A and solved in the MIPSSM formulation. The reserve crew schedules corresponding to each set of scenarios are tested in the validation simulation to obtain associated average cancellation measures. Pool C is then populated with the 100 scenarios from pool A with the lowest average cancellation measures, where the average cancellation measure is calculated from the cancellation measures corresponding to the sample sets of scenarios they are a member of. Pool C represents scenarios that improve the quality of reserve crew schedules when added to a set of scenarios to be solved in the MIPSSM formulation. Figure 7 outlines the process of populating pools B and C from pool A. Figure 7 also illustrates the process of deriving data points for Fig. 8, which is designed to show the quality and variance of the quality of reserve crew schedules derived from sets of scenarios selected from each pool of scenarios.
10.2 Testing pools of scenarios
A total of 200 sets of scenarios were each selected, without replacement, from each pool (A, B and C), where the number of scenarios selected for each set is distributed uniformly between 5 and 45. The results in Fig. 8 show the cancellation measures of the reserve schedules which were obtained by solving these scenarios selected from a given pool of scenarios. Each data point in Fig. 8 gives the number of scenarios in a set of scenarios used as input for the MIPSSM and the cancellation measure of the resultant reserve crew schedule, as derived from the validation simulation. The colour of the data point indicates which pool of scenarios the scenario set was selected from. The results displayed in Fig. 8 show that the number of scenarios in a set is weakly negatively correlated with the average cancellation measure associated with the reserve crew schedule derived from that set of scenarios for all pools. I.e. Increasing the number of scenarios will decrease cancellations/delays. Figure 8 also shows that the quality of reserve crew schedules derived from sets of scenarios selected from pools B and C is on average greater than reserve crew schedules derived from sets of scenarios from pool A. Furthermore the quality of reserve crew schedules corresponding to sets of scenarios derived from Pool B is much less sensitive to the number of scenarios in those sets. This is intuitive as scenario pool B consists of scenarios that give good solution quality when solved alone. This also suggests that scenarios that work well as the single input for MIPSSM do not necessarily lead to improved solutions when used together as a set of input scenarios for the MIPSSM. Figure 8 shows that the average cancellation measure of reserve crew schedules derived from sets of scenarios selected from pool C has the most convincing negative correlation (highest negative gradient and magnitude of correlation coefficient R) with the number of scenarios in those sets. This is also intuitive as pool C represents scenarios that improve reserve crew schedule when included in a set of scenarios.
The conclusion is that scenarios which are used as input for the MIPSSM can be divided according to whether they work best as the sole input scenario (pool B) or whether they are scenarios that complement a pre-existing set of scenarios (pool C). The difference in the gradients of the regression lines corresponding to pools B and C in Fig. 8 shows that pools B and C contain different scenarios. It is also interesting to note that the best result in Fig. 8 occurred for a set of scenarios derived from pool C that only contained 16 scenarios. Increasing the number of scenarios beyond around 15 leads to an improvement in solution reliability for sets selected from pools B and C, however the same does not occur for the random scenarios of pool A. This is a positive result as solution reliability is one of the MIPSSM’s biggest problems (Fig. 6).
To exploit these findings, one possible algorithm would involve finding the single scenario that leads to the highest solution quality. This could be a tractable approach since solution time is proportional to the number of scenarios in a set, with one scenario being solved very rapidly. Such a scenario can be said to have coincidental coverage. Another algorithm would search for scenarios that work well as part of a set, however such an algorithm may be less scalable than the first suggested algorithm. The reason being that the measure used to populate pool C involves solving lots of sets of scenarios and testing the resultant reserve crew schedules, which can be very time consuming.
11 Extensions and future work
Three potential extensions to this work are discussed in this section.
11.1 Multiple hub extension
The current work is based on a single hub model to reflect the airline whose data the case study is based on. This single hub model accounts only for disruptions that occur at the hub, whilst assuming that disruptions that occur at spoke stations are dealt with there. Therefore, to extend the current model to the case of multiple hubs, one option would be to solve the model separately from each hub’s perspective. However, if there are often frequent flights between hubs, a partially integrated multiple hub model may be more appropriate. Another alternative would be to model the schedules for the hubs as a single combined schedule. In this approach reserve crew could be scheduled in the same way as described in this work, provided that the additional spatial constraints for reserve crew use are respected.
11.2 Extension to a multiple fleet type, crew rank and qualification model
The current work applies to the case of a single fleet and a single variety of crew. Extension to the multiple fleet, crew rank and qualification type case gives rise to the possibility of different flights having different crewing requirements for each rank. Furthermore, not all reserve crew will be qualified to operate on all fleet types. The consideration of reserve crew ranks also introduces the possibility of reserve crew “flying below rank”.
The single crew and fleet type model presented in this work extends to the multiple fleet, crew rank and qualification type case with only a few minor modifications. The required modifications include an increase of the cardinality of the input and decision variables—namely for the rank (r) and qualification type (q) of reserve crew—and a few extra constraints to prevent reserve crew from “flying above rank”. In particular, the reserve crew schedule variable \(x_{l}\) becomes \(x_{l,q,r}\) to denote the number of reserve crew of qualification type q and rank r allocated to the duty start time index l. A similar change applies to the feasible reserve instance sets F, G and R, because feasible reserve instances will have specific ranks and qualifications. In the disruption scenario generation phase, feasible reserve instances will only need be generated for qualified reserve crew. Additional feasible reserve instances can also be generated for higher rank reserve crew to allow for the possibility of “flying below rank”. The possibility of “flying below rank” requires Constraint 6 to be modified to state that the total number of reserve crew used to cover a disruption equals the number of disrupted crew whilst no reserve crew “fly above rank”. This can be implemented with a nested set of constraints for each rank level, each of which stating that the number of reserve crew used at each rank level or lower must be greater than or equal to the number of disrupted crew of that rank level or lower.
The same solution methodologies apply to the extended model. The solution space of the extended model is slightly increased due to the increased cardinality of the variables compared to that of the single crew type model, namely because of the possibility of “flying below rank”.
11.3 Improved solution methodologies
One of the issues with the approaches to reserve crew scheduling based on the MIPSSM is that the number of scenarios has a big impact on the time required to solve the resultant MIPSSM formulation. Future work could develop specialised solution techniques other than solving the model directly in CPLEX. The possible alternatives include developing a hybrid approach where a meta-heuristic is used to search a subset of the variables, which are then fixed for an iteration of the MIPSSM. Another approach might involve further improvements of the SSH where scenarios are not only added but can also be removed. A further possible improvement might involve an iterative solution approach of the MIPSSM formulation where the reserve schedule variables (x) and the reserve use variables (y) are alternately held fixed, this would greatly reduce the number of variables in each iteration, the desired outcome is that the solution converges to the optimal solution of the full problem.
An additional potential area for future research is in the use of the MIPSSM formulation in an online context to aid recovery decisions. The solution time is small when considering a single disruption scenario with a fixed reserve crew schedule. This could be exploited to evaluate alternative reserve crew recovery decisions, by solving the MIPSSM for each of a large sample of possible future disruption scenarios for each alternative recovery decision. Such an approach would require an airline to have the facility to run simulations of future events based on the current schedule and expected departure and arrival times for all flights.
12 Conclusion
In conclusion, a simulation-based mixed integer programming approach to airline reserve crew scheduling has been introduced. The main idea is to schedule reserve crew using information from repeat simulations of an airline network where reserve crew are not available, and then scheduling reserve crew in a hindsight fashion in such a way that had they been available, the level of delay and cancellation that was related to disrupted crew would have been minimised. The MIPSSM formulation also took potential knock-on delays into account.
The SSH approach showed that the individual scenarios included in the model is at least as important as the number of scenarios, as this heuristic scenario selection approach yielded solutions of higher quality on average compared to the MIPSSM approach, with only a fraction of the input disruption scenarios. The Probabilistic model (Prob) represented an entirely different approach to the MIPSSM and gave comparable results, suggesting that both approaches have their own merits. In general it was found that the MIPSSM, SSH and Prob approaches gave results that were very similar on average, however the MIPSSM based approaches had lower solution reliability from one run to the next due to the stochastic nature of these approaches, but significantly outperformed the Prob approach in some cases. Further investigation of the effect of selecting scenarios from pools of scenarios with particular characteristics revealed the existence of scenarios that work well as the single scenario solved in the MIPSSM formulation to find a reserve crew schedule, such scenarios were said to have a high level of coincidental coverage. In contrast, evidence was also found for the existence of scenarios that work well as one of a set of scenarios from the same pool.
References
Abdelghany, A., Ekollu, G., Narasimhan, R., & Abdelghany, K. (2004). A proactive crew recovery decision support tool for commercial airlines during irregular operations. Annals of Operations Research, 127, 309–331.
Ageeva, Y.V., & Clarke, J.-P. (2000). Approaches to incorporating robustness into airline scheduling. Master’s thesis, MIT.
Bayliss, C., Maere, G. D., Atkin, J., & Paelinck, M. (2012). Probabilistic airline reserve crew scheduling model. In D. Delling & L. Liberti (Eds.), 12th workshop on algorithmic approaches for transportation modelling, optimization, and systems, openaccess series in informatics (OASIcs) (Vol. 25, pp. 132–143) Dagstuhl, Germany: Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik.
Boissy, A. (2006). Crew reserve sizing. In AGIFORS symposium.
Dillon, J. E., & Kontogiorgis, S. (1999). US airways optimises the scheduling of reserve flight crews. Interfaces, 29(5), 123.
Duck, V., Ionescu, L., Kliewer, N., & Suhl, L. (2012). Increasing stability of airline crew and aircraft schedules. Transportation Research, 20, 47–61.
Dunbar, M., Froyland, G., & Wu, C.-L. (2012). Robust airline scheduling planning: Minimizing propagated delay in an integrated routing and crewing framework. Transportation Science, 46(2), 204–216.
Liebchen, C., Lubbecke, M., Mohring, R. H., & Stiller, S. (2007). Recoverable robustness. Technical report.
Paelinck, M. (2001). KLM cabin crew reserve duty optimisation. In AGIFORS proceedings.
Rosenberger, J. M., Schaefer, A. J., Goldsman, D., Johnson, E. L., Kleywegt, A. J., & Nemhauser, G. L. (2002). A stochastic model of airline operations. Transportation Science, 36(4), 357–377.
Shebalov, S., & Klabjan, D. (2006). Robust airline crew pairing: Moveup crews. Transportation science, 40(3), 300–312.
Smith, B.C. (2004). Robust Fleet Assignment. Ph.D. thesis, Georgia Institute of Technology.
Sohoni, M., Lee, Y.-C., & Klabjan, D. (2011). Robust airline scheduling under block-time uncerainty. Journal of Air Transport Management, 45(4), 451–464.
Sohoni, M. G., Johnson, E. L., & Bailey, T. G. (2006). Operational airlines reserve crew scheduling. Journal of Scheduling, 9, 203–221.
Weide, O., Ryan, D., & Ehrgott, M. (2010). Iterative approach to robust aircraft routing and crew scheduling. Computers and Operations Research, 37, 833–844.
Williams, H. P. (2002). Model building in mathematical programming. New York: Wiley.
Acknowledgments
This work was made possible by funding from the EPSRC LANCS initiative (Grant ref EP/F033214/1). Additionally the authors would like to thank the administration and technical support teams at the University of Nottingham for their essential work which is important yet goes unnoticed. Thanks go also to the staff at KLM who provided schedule data and answered many question related to airlines scheduling and operations, particularly regarding reserve crew. We would also like to thank all three of the anonymous reviewers for their helpful feedback that has helped us to improve this article.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bayliss, C., De Maere, G., Atkin, J.A.D. et al. A simulation scenario based mixed integer programming approach to airline reserve crew scheduling under uncertainty. Ann Oper Res 252, 335–363 (2017). https://doi.org/10.1007/s10479-016-2174-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-016-2174-8