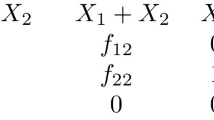Impact of equity and equality on stability and collusion in a decentralized network

Abstract

We develop a noncooperative game theoretic model to examine network performance and stability related implications of allocation mechanisms that endogenously balance equity vis-à-vis equality, and hence, the degree of collusion among the network firms in a decentralized setting. We obtain the structural results and bounds for our model parameters in this regard by focusing on two important factors: (i) synergy between the firms, and (ii) the number of network firms. Our contribution to the existing literature is threefold in showing that: (i) perfect equality among the network firms can be suboptimal, (ii) explicit cooperation among the firms is not always necessary for the efficient network performance, and (iii) the network firms do not completely collude, and yet, network stability can be enhanced. By particularly modeling a two-tier network, we exhibit our results in a decentralized setting and highlight the role of a coordinating agent in enhancing competitiveness of the network firms. We demonstrate that inefficiencies and instability of decentralization can be eliminated by incorporating an additional degree of freedom in the network formation game. Our model and the structural results are applicable to networks such as producers’ cooperatives, cartels, exclusive production facilities, industrial clusters, joint production and research facilities, etc., wherein the conflicts of equity–equality and degree of collusion are predominant.

Appendices

Appendix 1

In this appendix, we present proofs of the results described in the main body of the paper and also state additional results required in developing the proofs. The proofs of these additional results are presents in the following appendix.

Proof of Theorem 1

For expositional purpose, we split the proof of Theorem 1 into two parts. In the first part, we state Lemma 1. (Proof of the lemma is relegated to “Appendix 2”.) Using Lemma 1, we prove our results described in Theorem 1 in the second part.

Lemma 1

The best response functions for the network and independent firms are given by:

$$\begin{aligned} q_N^* \left( \theta , q_I\right)&= {\left\{ \begin{array}{ll} \dfrac{f_N \left( \theta , q_I\right) }{\left[ 2+\left( m-1 \right) \theta \right] \beta } &{}\quad \text {if} \, \, f_N \left( \theta , q_I\right) \ge 0 \\ 0 &{}\quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(24)

$$\begin{aligned} q_I^* \left( \theta , q_N\right)&= {\left\{ \begin{array}{ll} \dfrac{f_I \left( \theta , q_N\right) }{\left( n-m+1\right) \beta } &{} \text {if} \, \, f_I \left( \theta , q_N\right) \ge 0 \\ 0 &{}\quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(25)

$$\begin{aligned} \hbox {where } f_N \left( \theta , q_I\right)&= \psi \left[ \alpha - \beta \left( n-m\right) q_I \right] - \delta c \end{aligned}$$

(26)

$$\begin{aligned} f_I \left( \theta , q_N\right)&= \alpha - c - \beta m q_N \end{aligned}$$

(27)

Using the response functions provided in Lemma 1, we determine the equilibrium production levels for the firms in the market. Note that each network firm’s response function is linear and non-increasing in the quantity supplied by the independent firms, and vice versa. Therefore, the solution obtained by simultaneously solving the response functions is the unique pure-strategy Nash equilibrium such that the equilibrium profits for the competing firms are uniquely determined.

To prove Theorem 1, it is sufficient to show that the solution specified by (7)–(8) satisfies simultaneously the response functions (24)–(25) from Lemma 1.

From (6), we observe that $\psi$ is increasing in $\theta$. Define

$$\begin{aligned} k_N&= \psi \alpha + \left[ \left( n-m\right) \psi - \left( n-m+1\right) \delta \right] c \end{aligned}$$

(28)

$$\begin{aligned} k_I&= \alpha - \left[ \left( m-1\right) \theta + \left( 2-m \delta \right) \right] c \end{aligned}$$

(29)

Clearly, $k_N$ is linearly increasing in $\theta$. From (4) and (28), it is straightforward to note that $k_N\left( \theta \right) > 0$ for $\theta > \theta _{\min }$ and $k_N\left( \theta _{\min }\right) = 0$. Similarly, $k_I$ is linearly decreasing in $\theta$. From (5) and (29), we note that $k_I\left( \theta \right) < 0$ for $\theta > \theta _{\max }$ and $k_I\left( \theta _{\max }\right) = 0$. From (4)–(5), we also note that $\theta _{\max } > \theta _{\min }$ as $\theta _{\max } - \theta _{\min } = \dfrac{\left( \alpha -c\right) \left[ \alpha +\left( n-m\right) c+m \delta c \right] }{\left( m-1\right) \left[ \alpha +\left( n-m\right) c \right] } > 0$. Now, we complete the proof by considering the following three cases.

• Case 1   When $\theta \le \theta _{\min }$. Consider the solution $q_N^* = 0$ and $q_I^* = \left( \alpha - c\right) / \left( n-m+1\right) \beta$ as given in (7)–(8). From (27), we obtain $f_I = a - c \ge 0$ which satisfies (25). Similarly, from (26), we obtain $f_N = \psi \left[ \alpha - \beta \left( n-m\right) \left( \alpha - c \right) /\left( n-m+1\right) \beta \right] - \delta c = \left\{ \left[ \left( m-1\right) \theta + 1 \right] \left[ \alpha + \left( n-m\right) c \right] - \delta c \right\} / m \left( n-m+1\right) \le 0$ for $\theta \le \theta _{\min }$ which satisfies (24).

• Case 2   When $\theta _{\min } < \theta < \theta _{\max }$. From (28)–(29), consider the solution $q_N^* = k_N/ \left\{ \left[ ( n-m+2)+ ( m-1)\theta \right] \beta \right\}$ and $q_I^* = k_I/ \left\{ \left[ ( n-m+2)+ ( m-1)\theta \right] \beta \right\}$ as given in (7)–(8). Then, from (26) we obtain $f_N = \psi \lbrace \alpha - \beta ( n-m)k_N/ \lbrace \left[ ( n-m+2)+ ( m-1)\theta \right] \beta \rbrace \rbrace - \delta c = ( n-m+1)\beta k_I/ \lbrace [ ( n-m+2) + ( m-1)\theta ] \beta \rbrace$. Similarly, from (27) we obtain $f_I = \alpha - c - \beta m k_N/ \lbrace [ 2+( n-m)+ ( m-1)\theta ] \beta \rbrace = [ 2+( m-1)\theta ] \beta k_N/ \lbrace [ ( n-m+2) + ( m-1)\theta ] \beta \rbrace$. Clearly both $f_N$ and $f_I$ satisfy (24) and (25), and the rest follows.

• Case 3   When $\theta \ge \theta _{\max }$. Consider the solution $q_N^*=\left( \psi \alpha - \delta c\right) / \left[ 2+\left( m-1\right) \theta \right]$ and $q_I^*=0$ as given in (7)–(8). From (26), we note that $f_N = \psi \alpha - \delta c > 0$ as $f_N \left( \theta _{\max } \right) = \left( \alpha -c\right) \left( \alpha +\delta m c\right) / m c \ge 0$, which satisfies (24). Similarly, from (27), we obtain $f_I = \alpha - c - \beta m \left( \psi \alpha - \delta c\right) / \left[ 2+\left( m-1\right) \theta \right] = \left\{ \alpha - \left[ m\left( 1-\delta \right) +1\right] c + \left( m-1\right) \left( 1-\theta \right) c \right\} / \left[ 2+\left( m-1\right) \theta \right] \le 0$ which satisfies (25). $\square$

Proof of Theorem 2

For expositional purpose, we split the proof of Theorem 2 into two parts. In the first part, we state Lemmas 2 and 3. (Proofs of the lemmas are presented in “Appendix 2”.) In the second part, using Lemmas 2 and 3, we show our results described in Theorem 2.

In keeping with (9), to solve Problem ${\textit{SP}}$ we define Problem ${\textit{SP}}_1$ and ${ SP}_2$ as follows:

$$\begin{aligned} { SP}_1: \, \pi _1^*&= \max _{\begin{array}{c} \theta \ge \theta _{\max }, \\ 0 \le \theta \le 1 \end{array}} \, \pi ^*\left( \theta \right) \\ { SP}_2: \, \pi _2^*&= \max _{\begin{array}{c} \theta _{\min } \le \theta \le \theta _{\max }, \\ 0 \le \theta \le 1 \end{array}} \, \pi ^*\left( \theta \right) \end{aligned}$$

The optimal solution to Problem ${ SP}$ is given by $\pi ^* = \max \left\{ 0, \pi _1^*, \pi _2^* \right\}$. In this regard, we provide the optimal solutions to Problem ${{ SP}}_1$ and ${{ SP}}_2$ separately in Lemma 3 below. In order to facilitate the proof for Lemma 3, we completely characterize the profit function $\pi ^*\left( \theta \right)$ for Problem ${{ SP}}_1$ and ${{ SP}}_2$ in Lemma 2.

Lemma 2

Define

$$\begin{aligned}&\displaystyle \theta _3 = \dfrac{\alpha +\left( 3m-2 \right) \delta c}{\left( m-1 \right) \left( \alpha +\delta c \right) } \end{aligned}$$

(30)

$$\begin{aligned}&\displaystyle \theta _4 = \dfrac{\left[ 2 \left( n-m \right) +1 \right] \left[ \alpha + \left( n-m \right) c \right] - \left( n-m+1 \right) \left( n-4m+2 \right) \delta c}{\left( m-1 \right) \left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1+\delta \right) -1 \right] c \right\} } \end{aligned}$$

(31)

In Problem ${{ SP}}_1$, $\pi ^*\left( \theta \right)$ is strictly concave in $\theta$ for $\theta < \theta _3$, and it is strictly convex for $\theta > \theta _3$. Similarly, in Problem ${{ SP}}_2$, $\pi ^*\left( \theta \right)$ is strictly concave in $\theta$ for $\theta < \theta _4$, and it is strictly convex for $\theta > \theta _4$.

Lemma 3

The optimal solution to Problem ${{ SP}}_1$ is given by:

$$\begin{aligned} \theta ^*&= {\left\{ \begin{array}{ll} \theta _1^* &{} \quad \text {if } \delta \le \delta _1 \\ \theta _{\max } &{}\quad \text {if } \delta _1 < \delta \le \delta _3 \\ \emptyset &{}\quad \text {if } \delta _3 < \delta \le 1 \end{array}\right. } \end{aligned}$$

(32)

Here, $\theta ^* = \emptyset$ implies that Problem ${{ SP}}_1$ is infeasible. Similarly, the optimal solution to Problem ${{ SP}}_2$ is given by:

$$\begin{aligned} \theta ^*&= {\left\{ \begin{array}{ll} \theta _{\max } &{}\quad \text {if } m \le \bar{m} \text{ and } \delta \le \delta _3; \text { or if } m > \bar{m} \text{ and } \delta \le \delta _2 \\ 1 &{}\quad \text {if } m \le \bar{m} \text{ and } \delta _3 < \delta \le 1 \\ \theta _2^* &{}\quad \text {if } m > \bar{m} \text{ and } \delta _2 < \delta \le 1 \end{array}\right. } \end{aligned}$$

(33)

Recall that the optimal solution to Problem ${{ SP}}$ is given by $\pi ^* = \max \left\{ 0, \pi _1^*, \pi _2^* \right\}$, where $\pi _1^*$ and $\pi _2^*$ are obtained from Problem ${{ SP}}_1$ and ${{ SP}}_2$, respectively. From Lemma 3 we observe that $\pi _1^* \ge 0$ and $\pi _2^* \ge 0$. Therefore, to prove our results it is sufficient to show that $\delta _1 \le \delta _3 \le \delta _2 \le 1$ for $m \le \bar{m}$ and $\delta _1 \le \delta _2 \le \delta _3 \le 1$ for $m > \bar{m}$. Clearly, for $1 \le m \le n$, $\delta _2 - \delta _1 \ge 0$ and $\delta _2 \le 1$ as $\alpha > c$. Similarly, $\delta _3 - \delta _1 \ge 0$ and $\delta _3 \le 1$. Further, $\delta _ 2 - \delta _3 = \dfrac{\left( n-2m+1\right) \left( \alpha -c\right) }{\left( n-m+1\right) m c} \ge$ if $m \le \bar{m}$; the rest follows. $\square$

Proof of Proposition 1

To prove our results, in Table 2 we characterize the optimal solution to the coordinator’s problem in the cooperative setting.

Table 2 A complete characterization of the optimal solution in the centralized setting

From (12), it is direct to note that $\delta _1 \le \delta _2 < 1$ for $1 \le m \le n$ and $\alpha > c$. Using Tables 1 and 2, we observe that $\pi ^* = \left( \alpha -\delta c\right) ^2 / 4 \beta = \pi ^{c*}$ when $\delta \le \delta _1$ for $1 \le m \le n$. Similarly, $\pi ^* = \left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1- \delta \right) - 1 \right] c \right\} ^2 / 4 \left( n-m+1 \right) \beta = \pi ^{c*}$ when $\delta _2 < \delta \le 1$ for $m > \bar{m}$. Thereby, the first part of the proposition—efficient network—follows. To prove the second part—inefficient network—of the proposition, we show that $\pi ^* \le \pi ^{c*}$ when $\delta _1 < \delta \le \delta _2$ for $m > \bar{m}$, and when $\delta _1 < \delta \le 1$ for $m \le \bar{m}$.

Consider $m > \bar{m}$ and $\delta _1 < \delta \le \delta _2$. Note that $\pi ^* = \left( 1-\delta \right) \left( \alpha -c \right) c / \beta$ and $\pi ^{c*} = \left( \alpha -\delta c\right) ^2 / 4 \beta$. We obtain $\pi ^{c*} - \pi ^* = \left[ \alpha -\left( 2-\delta \right) c \right] ^2 / 4 \beta \ge 0$.

Consider $m \le \bar{m}$. In this scenario, we consider three different cases for $\delta$: (i) $\delta \in \left[ \delta _1, \delta _3 \right]$, (ii) $\delta \in \left( \delta _3, \delta _2 \right)$, and (iii) $\delta \in \left[ \delta _2, 1 \right]$. For ease of exposition, we present the proof in the order of Case (i), (iii) and (ii).

• Case (i) When $\delta \in \left[ \delta _1, \delta _3 \right]$. In this case, $\pi ^* = \left( 1-\delta \right) \left( \alpha -c \right) c / \beta$ and $\pi ^{c*} = \left( \alpha -\delta c\right) ^2 / 4 \beta$. We obtain $\pi ^{c*} - \pi ^* = \left[ \alpha -\left( 2-\delta \right) c \right] ^2 / 4 \beta \ge 0$.

• Case (iii) When $\delta \in \left[ \delta _2, 1 \right]$. In this case, $\pi ^* = \left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1- \delta \right) - 1 \right] c \right\} ^2 / \left( n+1\right) ^2 \beta$ and $\pi ^{c*} = \left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1- \delta \right) - 1 \right] c \right\} ^2 / 4 \left( n-m+1 \right) \beta$. We obtain

  $$\begin{aligned} \pi ^{c*} - \pi ^*= & {} \left( n-2m+1 \right) ^2 \left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1- \delta \right) - 1 \right] c \right\} ^2 /\nonumber \\&4 \left( n+1 \right) ^2 \left( n-m+1 \right) \beta \ge 0. \end{aligned}$$

• Case (ii) When $\delta \in \left( \delta _3, \delta _2 \right)$. In this case, $\pi ^* = \left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1- \delta \right) - 1 \right] c \right\} ^2 / \left( n+1\right) ^2 \beta$ and $\pi ^{c*} = \left( \alpha -\delta c\right) ^2 / 4 \beta$. From case (iii) above, we know that $\left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1- \delta \right) - 1 \right] c \right\} ^2 / 4 \left( n-m+1 \right) \beta \ge \lbrace \alpha + [ \left( n-m+1 \right) \left( 1- \delta \right) - 1 ] c \rbrace ^2 / \left( n+1\right) ^2 \beta$. From Case (i) above, it is known that $\left( \alpha -\delta c\right) ^2 / 4 \beta \ge \left( 1-\delta \right) \left( \alpha -c \right) c / \beta$. From our results presented in Theorem 2, it follows that $\left( 1-\delta \right) \left( \alpha -c \right) c / \beta \ge \left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1- \delta \right) - 1 \right] c \right\} ^2 / \left( n+1\right) ^2 \beta$ for $m \le \bar{m}$ and $\delta _3 < \delta \le 1$. Clearly, $\left( \alpha -\delta c\right) ^2 / 4 \beta \ge \left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1- \delta \right) - 1 \right] c \right\} ^2 / \left( n+1\right) ^2 \beta$ for $m \le \bar{m}$ and $\delta _3 < \delta \le 1$, and thereby, $\pi ^{c*} - \pi ^* \ge 0$ for for $m \le \bar{m}$ and $\delta _3 < \delta < \delta _2$.$\square$

Proof of Proposition 2

From Table 1, when $m > \bar{m}$, the condition for internal stability $\pi _N^*\left( m\right) \ge \pi _I^*\left( m-1\right)$ translates into $\delta \le \delta _{u2}$. Similarly, the condition for external stability $\pi _I^*\left( m\right) \ge \pi _N^*\left( m+1\right)$ translates into $\delta \ge \delta _{l2}$.

When $m \le \bar{m}$, $\pi _N^*\left( m\right) \ge \pi _I^*\left( m-1\right)$ requires $\left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1- \delta \right) - 1 \right] c \right\} ^2 / \left( n+1\right) ^2 \beta \ge \left\{ \alpha - \left[ \left( m-1 \right) \left( 1-\delta \right) + 1\right] c \right\} ^2/ \left( n+1 \right) ^2 \beta$, i.e., $n c \left( 1-\delta \right) \ge 0$ which clearly satisfies for $\delta \in \left[ 0, 1 \right]$. Similarly, $\pi _I^*\left( m\right) \ge \pi _N^*\left( m+1\right)$ requires

$$\begin{aligned}&\left\{ \alpha - \left[ m \left( 1-\delta \right) + 1\right] c \right\} ^2/ \left( n+1 \right) ^2 \beta \\&\quad \ge \left\{ \alpha + \left[ \left( n-m \right) \left( 1- \delta \right) - 1 \right] c \right\} ^2 / \left( n+1\right) ^2 \beta , \hbox {i.e}., - n c \left( 1-\delta \right) \ge 0 \end{aligned}$$

which clearly never satisfies for $\delta \in \left[ 0, 1 \right]$.$\square$

Proof of Corollary 1

The proof is straightforward from Proposition 2.$\square$

Proof of Proposition 3

The proof parallels that for Proposition 2, and hence, omitted.$\square$

Proof of Corollary 2

The proof is direct from Proposition 3, and hence, omitted.$\square$

Proof of Corollary 3

The proof is direct from the first part of Proposition 2, and hence, omitted.$\square$

Appendix 2

Proof of Lemma 1

First, we characterize the response functions for both network and independent firms for the generic system in which the optimal production quantities for no two network firms are identical, and the same is valid for the independent firms. In this case, the response functions for both network firms and independent firms are as follows:

$$\begin{aligned} q_i^* \left( \theta , q_{-i}\right)&= {\left\{ \begin{array}{ll} \dfrac{f_i \left( \theta , q_{-i}\right) }{2 \psi \beta } &{} \quad \, \, \, \text {if} \, \, f_i \left( \theta , q_{-i}\right) \ge 0 \\ 0 &{}\quad \, \, \, \text {otherwise} \end{array}\right. } \end{aligned}$$

(34)

$$\begin{aligned} q_{k}^* \left( \theta , q_{-k}\right)&= {\left\{ \begin{array}{ll} \dfrac{f_k \left( \theta , q_{-k}\right) }{2 \beta } &{}\quad \text {if} \, \, f_k \left( \theta , q_{-k}\right) \ge 0 \\ 0 &{}\quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(35)

$$\begin{aligned} \hbox {where, }\quad f_i \left( \theta , q_{-i}\right)&= \psi \left( \alpha - \beta \sum _{h \ne i} q_h - \beta \sum _{l=1}^{n-m} q_l \right) - \left( \dfrac{1-\theta }{m} \right) \beta \sum _{h \ne i} q_h - \delta c \end{aligned}$$

(36)

$$\begin{aligned} f_k \left( \theta , q_{-k}\right)&= \alpha - \beta \sum _{h=1}^{m} q_h - \beta \sum _{l \ne k} q_l - c \end{aligned}$$

(37)

The proof for (34)–(35) is as follows. Note that Problem $N_i$ is a convex program; the Kurush–Kuhn–Tucker (KKT) conditions are necessary and sufficient for optimality. Let $L_i$ be the Lagrangian for Problem $N_i$ and $q_i^*, \lambda _i^*$ be the optimal solution.

$$\begin{aligned} L_i \left( \theta , q_{-i} \right)&= \theta \left( \alpha - \beta \sum _{h = 1}^{m} q_h - \beta \sum _{l=1}^{n-m} q_l \right) q_i + \left( \dfrac{1-\theta }{m} \right) \sum _{j=1}^{m} \left( \alpha - \beta \sum _{h =1}^{m} q_h - \beta \sum _{l=1}^{n-m} q_l \right) \nonumber \\&\qquad q_j - \delta c q_i + \lambda _i q_i \end{aligned}$$

(38)

The KKT optimality conditions for Problem $N_i$ are as follows:

$$\begin{aligned}&\displaystyle q_i^* \left( \theta , q_{-i} \right) = \dfrac{\psi \left( \alpha - \beta \sum _{h \ne i} q_h - \beta \sum _{l=1}^{n-m} q_l \right) - \left( \dfrac{1-\theta }{m} \right) \beta \sum _{h \ne i} q_h - \delta c + \lambda _{i}^*}{2 \psi \beta }\nonumber \\&\displaystyle = \dfrac{f_i \left( \theta , q_{-i}\right) + \lambda _i^*}{2 \psi \beta } \end{aligned}$$

(39)

$$\begin{aligned}&\displaystyle q_i^* \lambda _{i}^* = 0 \end{aligned}$$

(40)

$$\begin{aligned}&\displaystyle q_i^*, \lambda _{i}^* \ge 0 \end{aligned}$$

(41)

Clearly, $q_i^*$ as defined in (34) together with $\lambda _{i}^* = \max \left\{ 0, -f_i \left( \theta , q_{-i}\right) \right\}$ satisfies KKT conditions (39)–(41) and the rest follows. Similarly, the response functions for the independent firms can be obtained.

Now, by the symmetry of the system, we substitute $q_i^* = q_N^*$, $i = 1,2, \ldots , m$, and $q_{k}^* = q_I^*$, $k = 1,2, \ldots , \left( n-m\right)$, in (34)–(35) and simplify to obtain (24)–(25).$\square$

Proof of Lemma 2

First, consider Problem ${{ SP}}_1$. From (9), we obtain

$$\begin{aligned} \pi ^*\left( \theta \right)&= \dfrac{\alpha + \left[ \left( m-2 \right) -\left( m-1\right) \theta \right] \delta c}{2+\left( m-1\right) \theta } \cdot \dfrac{m \left[ \psi \alpha - \delta c \right] }{\left[ 2+\left( m-1\right) \theta \right] \beta } \nonumber \\ \dfrac{d \pi ^*\left( \theta \right) }{d \theta }&= - \dfrac{\left( m-1 \right) ^2 \left( \alpha +m\delta c \right) \left[ \left( \alpha +\delta c \right) \theta - 2\delta c \right] }{\beta \left[ 2 + \left( m-1 \right) \theta \right] ^3} \end{aligned}$$

(42)

$$\begin{aligned} \dfrac{d^2 \pi ^*\left( \theta \right) }{d \theta ^2}&= \left\{ \dfrac{2 \left( m-1 \right) ^2 \left( \alpha +m\delta c \right) }{\beta \left[ 2 + \left( m-1 \right) \theta \right] ^4} \right\} \Bigg \{ \left( m-1 \right) \left( \alpha + \delta c \right) \theta - \left[ \alpha + \left( 3m-2 \right) \delta c \right] \Bigg \} \end{aligned}$$

(43)

Consider $\theta _3$ as given in (30). From (43), it is straightforward to note that $d^2 \pi ^*\left( \theta \right) / d \theta ^2 < 0$ for $\theta < \theta _3$, and hence, the function is strictly concave in $\theta$. Thereby, the first part of the lemma follows.

Now, consider Problem ${{ SP}}_2$. From (9), we obtain

$$\begin{aligned} \pi ^*\left( \theta \right) =&\dfrac{\alpha - \left\{ \left[ n-\left( m-1\right) \left( 2-\theta \right) \right] \delta -\left( n-m\right) \right\} c}{\left( n-m+2 \right) +\left( m-1\right) \theta } \cdot \nonumber \\&\quad \dfrac{m\left\{ \psi \alpha + \left[ \psi \left( n-m\right) - \delta \left( n-m+1\right) \right] c\right\} }{\left[ \left( n-m+2 \right) + \left( m-1\right) \theta \right] \beta } \nonumber \\ \dfrac{d \pi ^*\left( \theta \right) }{d \theta } =&\left\{ \dfrac{\left( m-1 \right) \left[ \alpha +m\delta c + \left( n-m \right) c \right] }{\beta \left[ \left( n-m+2 \right) + \left( m-1 \right) \theta \right] ^3 } \right\} \nonumber \\&\Bigg \{ \left( n-m \right) \left[ \alpha + \left( n-m \right) c \right] \nonumber \\&- \left( n-m+1 \right) \left( n-3m+2 \right) \delta c \nonumber \\&- \left( m-1 \right) \left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1+\delta \right) -1 \right] c \right\} \theta \Bigg \} \end{aligned}$$

(44)

$$\begin{aligned} \dfrac{d^2 \pi ^*\left( \theta \right) }{d \theta ^2} =&\left\{ \dfrac{2 \left( m-1 \right) ^2 \left[ \alpha +m\delta c + \left( n-m \right) c \right] }{\beta \left[ \left( n-m+2 \right) + \left( m-1 \right) \theta \right] ^4} \right\} \Bigg \{- \left[ 2 \left( n-m \right) +1 \right] \left[ \alpha + \left( n-m \right) c \right] \nonumber \\&+ \left( n-m+1 \right) \left( n-4m+2 \right) \delta c + \left( m-1 \right) \left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1+\delta \right) -1 \right] c \right\} \theta \Bigg \} \end{aligned}$$

(45)

Consider $\theta _4$ as given in (31). From (45), it is straightforward to note that $d^2 \pi ^*\left( \theta \right) / d \theta ^2 < 0$ for $\theta < \theta _4$, and hence, the function is strictly concave. Thereby, the second part of the lemma follows.$\square$

Proof of Lemma 3

Using Lemma 2, we prove our results in Lemma 3 below.

First, consider Problem ${{ SP}}_1$. In keeping with our results in Lemma 2 above, we show optimality of the solution by analyzing the problem over two disjoint regions for $\theta$, i.e., $\theta \le \theta _3$ and $\theta > \theta _3$. In particular, note that when $\theta _3 > 1$, Problem ${{ SP}}_1$ is a concave program. Thereby, for brevity of the proof without losing analytical insights, we show our results for the case wherein $\theta _3 \le 1$.

Consider the solution $\theta _1^*$ as given in (13). From (13) and (30), we note that $\theta _3 \ge \theta _1^*$ as $\theta _3 - \theta _1^* = \dfrac{\alpha + m \delta c}{\left( m-1 \right) \left( \alpha + \delta c \right) } \ge 0$. From (5) and (13) we observe that $\theta _1^* - \theta _{\max } = - \dfrac{\left( \alpha + m \delta c \right) \left( \alpha -2c + \delta c \right) }{\left( m-1 \right) \left( \alpha + \delta c \right) c} \ge 0$ if $\delta \le \delta _1$. Also, $1 - \theta _{\max } = \dfrac{\left( m+1 \right) c - \alpha - m \delta c}{\left( m-1 \right) c} \ge 0$ if $\delta \le \delta _3$. From (12), it is straightforward to note that $\delta _1 \le \delta _3 \le 1$. Now, consider the following three cases with respect to $\delta$.

• Case 1   $\delta \le \delta _1$: Clearly, $\theta _{\max } \le \theta _1^* \le \theta _3$. Consider the region $\theta _{\max } \le \theta \le \theta _3$. From Lemma 2, the function $\pi ^*\left( \theta \right)$ is strictly concave in $\theta$. The first order condition is necessary and sufficient to show optimality of the solution $\theta _1^*$. Clearly, the solution is feasible, i.e., $\theta _1^* \ge \theta _{\max }$ and $\theta _1^* \in \left[ 0,1\right]$, and it satisfies (42), and hence, the solution is indeed optimal to Problem ${{ SP}}_1$ over $\theta _{\max } \le \theta \le \theta _3$. Now, consider the region $\theta > \theta _3$. From Lemma 2, the function is strictly convex in $\theta$, and hence, the optimal solution exists at the extreme. Further, from (42) we obtain $\dfrac{d \pi ^*\left( \theta _3 \right) }{d \theta } = - \dfrac{\left( m-1 \right) \left( \alpha + \delta c \right) ^3}{27 m \beta \left( \alpha + m \delta c\right) } \le 0$, thereby the optimal solution over $\theta > \theta _3$ is $\theta _3$. Therefore, for the combined region, i.e., $\theta \ge \theta _{\max }$, when $\delta \le \delta _1$, the optimal solution to Problem ${{ SP}}_1$ is $\theta _1^*$.

• Case 2   $\delta _1 < \delta \le \delta _3$: In this case, $\theta _1^* < \theta _{\max } \le \theta _3$ or $\theta _1^* < \theta _3 \le \theta _{\max }$. Therefore, we consider two cases separately: (i) $\theta _{\max } \le \theta _3$, or (ii) $\theta _{\max } > \theta _3$.

  • Case (i)   $\theta _{\max } \le \theta _3$: In this case, consider the two regions $\theta _{\max } \le \theta < \theta _3$ and $\theta \ge \theta _3$ separately. From Case 1 above, it is straightforward to note that the optimal solution is $\theta _{\max }$ in each region.

  • Case (ii)   $\theta _{\max } > \theta _3$: For $\theta \ge \theta _{\max }$, the function $\pi ^*\left( \theta \right)$ is strictly convex in $\theta$, and hence, from Case 1 above, the optimal solution is $\theta _{\max }$. From the above two cases, the optimal solution to Problem ${{ SP}}_1$ when $\delta _1 < \delta \le \delta _3$ is $\theta _{\max }$.

• Case 3   $\delta _3 < \delta \le 1$: In this case, $\theta _{\max } > 1$, and hence, Problem ${{ SP}}_1$ is infeasible.

Now, consider Problem ${{ SP}}_2$. The proof parallels that for Problem ${{ SP}}_1$ above. Consider the solution $\theta _2^*$ as given in (14). From (4) and (14) we note that $\theta _2^* \ge \theta _{\min }$ as $\theta _2^* - \theta _{\min } = \dfrac{\left( n-m+1 \right) \left[ \alpha + m\delta c + \left( n-m \right) c \right] \left[ 2\alpha - c + \left( n-m \right) c \right] }{\left( m-1 \right) \left[ \alpha + \left( n-m \right) c \right] \left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1+\delta \right) -1 \right] c \right\} } \ge 0$. From (14) and (31), we note that $\theta _4 \ge \theta _2^*$ as $\theta _4 - \theta _2^* = \dfrac{\left( n-m+1 \right) \left[ \alpha + m \delta c + \left( n-m \right) c\right] }{\left( m-1 \right) \left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1+\delta \right) -1 \right] c \right\} } \ge 0$. From (5) and (14), we observe that $\theta _2^* - \theta _{\max } = \dfrac{\left[ \alpha + m \delta c + \left( n-m \right) c\right] \left[ -\alpha + \left( n-m+2 \right) c - \left( n-m+1 \right) \delta c\right] }{\left( m-1 \right) \left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1+\delta \right) -1 \right] c \right\} c} \ge 0$ if $\delta \le \delta _2$. We also note that $\theta _2^* \le 1$ if $m \ge \bar{m}$ as $\left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1-\delta \right) -1 \right] c \right\} \ge 0$ for $\delta \in \left[ 0,1\right]$.

In keeping with our results in Lemma 2 above, we show optimality of the solution by analyzing the problem over two disjoint regions for $\theta$, i.e., $\theta \le \theta _4$ and $\theta > \theta _4$. In particular, note that when $\theta _4 > 1$, Problem ${{ SP}}_2$ is a concave program. Thereby, for brevity of the proof without losing analytical insights, we show our results for the case wherein $\theta _4 \le 1$.

Consider the following two cases with respect to m.

• Case 1   $m \le \bar{m}$: We observe that $\delta _ 3 \le \delta _2$ as $\delta _ 2 - \delta _3 = \dfrac{\left( n-2m+1\right) \left( \alpha -c\right) }{\left( n-m+1\right) m c} \ge$ if $1 \le m \le \bar{m}$. Therefore, we obtain $\delta _ 3 \le \delta _2 \le 1$. Now consider the following three cases with respect to $\delta$.

  • Case (i)   $\delta \le \delta _3$: Clearly, $\theta _{\max } \le \theta _2^* \le \theta _4$. Problem ${{ SP}}_2$ is infeasible over the region $\theta > \theta _4$. Consider the region $\theta _{\max } \le \theta \le \theta _4$. From Lemma 2, for $\theta _{\min } \le \theta \le \theta _{\max }$, we know that the function $\pi ^*\left( \theta \right)$ is strictly concave in $\theta$ with $\theta _2^*$ satisfying the first order condition (44), and hence, it is straightforward to note that the optimal solution is $\theta _{\max }$.

  • Case (ii)   $\delta _3 < \delta \le \delta _2$: In this case, $\theta _{\max } > 1$, and hence, from Case i above it is straightforward to note that $\theta ^* = 1$.

  • Case (iii)   $\delta _2 < \delta \le 1$: In this case, $\theta _{\min } \le \theta _2^* \le \theta _{\max }$ and $\theta _2^* \ge 1$. Thereby, from Case i above, the optimal solution to Problem ${{ SP}}_2$ is $\theta ^* = 1$.

• Case 2   $m > \bar{m}$: From Case 1 above, we know that $\delta _ 2 \le \delta _3 \le 1$. Now consider the following three cases with respect to $\delta$.

  • Case (i)   $\delta \le \delta _2$: This case is similar to Case 1-i above; we conclude that the optimal solution to Problem ${{ SP}}_2$ is $\theta ^* = \theta _{\max }$.

  • Case (ii)   $\delta _2 < \delta \le \delta _3$: Consider the solution $\theta _2^*$ and the region $\theta _{\min } \le \theta \le \theta _4$. From Lemma 2, $\pi ^*\left( \theta \right)$ is strictly concave in $\theta$, thereby the first order condition is necessary and sufficient to show optimality of the solution $\theta _2^*$. Clearly, the solution is feasible, i.e., $\theta _{\min } \le \theta _2^* \le \theta _{\max }$ and $\theta _2^* \in \left[ 0,1\right]$, and it satisfies (44), and hence, the solution is indeed optimal to Problem ${{ SP}}_2$. Consider the region $\theta _4 < \theta \le \theta _{\max }$. The function $\pi ^*\left( \theta \right)$ is strictly convex and the optimal solution exists at the extreme. Further, from (9), we note that $\pi ^* \left( \theta _{\min } \right) = 0$ and $\pi ^* \left( \theta _{\max } \right) > 0$, and hence, it is straightforward to note that $\theta _{\max }$ is the optimal solution. Now, it is straightforward to note that the solution $\theta _2^*$ is optimal to Problem ${{ SP}}_2$ when $\delta _2 < \delta \le \delta _3$.

  • Case (iii)   $\delta _3 < \delta \le 1$: In this case, $\theta _{\max } > 1$, and hence, from Case ii above, it is straightforward to that the solution $\theta _2^*$ is optimal to Problem ${{ SP}}_2$.$\square$

Analytical results: Extensions

In what follows, we provide analytical details of our results presented in Section 8.

1.1 Implications of surplus sharing

A complete characterization of the unique pure-strategy Nash equilibrium of the firm’s problem under the surplus sharing mechanism is as shown in Theorem 3 below.

Theorem 3

Define

$$\begin{aligned} \theta _{\max }&= \dfrac{\alpha - \left( 2-\delta \right) c}{\left( m-1\right) \left( 1-\delta \right) c} \end{aligned}$$

(46)

The unique Nash equilibrium of the firm’s problem is given by:

$$\begin{aligned} q_N^* \left( \theta \right)&= {\left\{ \begin{array}{ll} \dfrac{\psi \left\{ \alpha + \left[ \left( n-m+1\right) \left( 1-\delta \right) -1 \right] c \right\} }{\left[ \left( n-m+2 \right) + \left( m-1\right) \theta \right] \beta } &{} \, \, \text {if } \theta < \theta _{\max } \\ \dfrac{\psi \left( \alpha - \delta c\right) }{\left[ 2+\left( m-1\right) \theta \right] \beta } &{} \, \, \text {otherwise } \end{array}\right. } \end{aligned}$$

(47)

$$\begin{aligned} q_I^* \left( \theta \right)&= {\left\{ \begin{array}{ll} \dfrac{\alpha - \left[ 2-\delta + \theta \left( m-1\right) \left( 1-\delta \right) \right] c}{\left[ \left( n-m+2 \right) + \left( m-1\right) \theta \right] \beta } &{} \quad \text {if } \theta < \theta _{\max } \\ 0 &{} \quad \text {otherwise } \end{array}\right. } \end{aligned}$$

(48)

Theorem 4

Define

$$\begin{aligned} \theta _2^*&= \dfrac{n-m}{m-1} \end{aligned}$$

(49)

A complete characterization of the optimal solution to the coordinator’s problem is given in Table 3.

Table 3 A Complete Characterization of the Optimal Solution to the Coordinator’s Problem under Surplus Sharing Mechanism

1.2 Convex costs

When the firms’ cost functions are increasing convex, the equilibrium supply quantities, given $\theta$ from the coordinator, for both network and independent firms are as shown below:

$$\begin{aligned} q_N^* \left( \theta \right)&= \dfrac{\alpha \psi \left( \beta + 2 c \right) }{\theta \beta \left( m-1 \right) \left( \beta +2 c \right) + \left( \beta +2 \delta c \right) \left[ \left( n-m+1 \right) \beta +2 c \right] + \beta \left( \beta +2 c \right) } \end{aligned}$$

(50)

$$\begin{aligned} q_I^* \left( \theta \right)&= \dfrac{\alpha \left( \beta + 2 \delta c \right) }{\theta \beta \left( m-1 \right) \left( \beta +2 c \right) + \left( \beta +2 \delta c \right) \left[ \left( n-m+1 \right) \beta +2 c \right] + \beta \left( \beta +2 c \right) } \end{aligned}$$

(51)

1.3 Competing coalition

When the non-network firms form a cartel (and their cost functions are increasing convex), the equilibrium supply quantities, given $\theta$ from the coordinator, for both network and independent firms are as shown below:

$$\begin{aligned} q_N^* \left( \theta \right)&= \dfrac{\alpha \psi \left[ \beta \left( n-m\right) + 2 c \right] }{\theta \beta \left( m-1 \right) \left[ \beta \left( n-m\right) +2 c \right] + \beta \left[ 3 \beta \left( n-m\right) + 4 c \right] + 4 \delta c \left[ \beta \left( n-m\right) + c \right] } \end{aligned}$$

(52)

$$\begin{aligned} q_I^* \left( \theta \right)&= \dfrac{\alpha \left( \beta + 2 \delta c \right) }{\theta \beta \left( m-1 \right) \left[ \beta \left( n-m\right) +2 c \right] + \beta \left[ 3 \beta \left( n-m\right) + 4 c \right] + 4 \delta c \left[ \beta \left( n-m\right) + c \right] } \end{aligned}$$

(53)

1.4 Asymmetric setting

For simplicity, let there be n firms in the network with a particular firm i, $i=1,2,3\ldots ,n$, having the aggregate cost equal to $\delta c_i q_i^2$. In this case, given $\theta$, equilibrium supply quantity for all firms (ensuring non-negativity) are as shown below:

$$\begin{aligned} q_{Ci}^* \left( \theta \right) =&\dfrac{\mathcal {A}_i}{\mathcal {B}} \end{aligned}$$

(54)

$$\begin{aligned} \text {where} \qquad \mathcal {A}_i =&\alpha \left[ 1+\left( n-1\right) \theta \right] \prod _{j \ne i} \left( \beta \theta + 2 \delta c_j \right) \end{aligned}$$

(55)

$$\begin{aligned} \mathcal {B} =&\left( n-1\right) b^n - \left( n-2\right) b^{n-1} \sum _{i} \mathcal {K}_i + \left( n-3\right) b^{n-2} \sum _{i, j>i} \mathcal {K}_i \mathcal {K}_j \nonumber \\&- \left( n-4\right) b^{n-3} \sum _{i, j>i, \mathcal {K}>j} \mathcal {K}_i \mathcal {K}_j \mathcal {K}_k + \cdots + \left( -1\right) ^{n-1} \prod _{i}^{n} \mathcal {K}_i \end{aligned}$$

(56)

$$\begin{aligned} \mathcal {K}_i =&2 \beta \left[ 1+\left( n-1\right) \theta \right] + n \delta c_i; \qquad i=1,2,\ldots ,n \end{aligned}$$

(57)

Additional results

In what follows, we provide additional results that we use in discussing our important findings presented in the paper.

Proposition 5

For $\theta > \theta _{\min }$, $q_N^*$ is increasing in $\theta$.

Table 4 A Complete Characterization of Nash Equilibrium of the Firm’s Problem

Proof of Proposition 5

In Table 4, we completely characterize the Nash equilibrium of the firm’s problem. Here, $q_N^*\left( \theta \right)$ and $q_I^*\left( \theta \right)$ are obtained by substituting (7)–(8) in (24)–(25), and the rest is straightforward.

From Table 4, we consider the following two cases.

Case 1.   : We have $\dfrac{d q_N^*}{d \theta } = \dfrac{\left( m-1 \right) \left( n-m+1 \right) \left[ \alpha + m \delta c + \left( n-m \right) c \right] }{\left[ \left( n-m+2\right) + \left( m-1\right) \theta \right] ^2 m \beta } \ge 0$.

Case 2.   $\theta \ge \theta _{\max }$: We have $\dfrac{d q_N^*}{d \theta } = \dfrac{\left( m-1 \right) \left( \alpha + m \delta c \right) }{\left[ 2 + \left( m-1\right) \theta \right] ^2 m \beta } \ge 0$. $\square$

Proposition 6

For $m > \bar{m}$ and $\delta _2 < \delta \le 1$, $\pi ^*$ is monotonically increasing in m. Similarly, $\pi _N^*$ is monotonically increasing in m for $m > \bar{\bar{m}}$.

Proof of Proposition 6

From Table 1, we get $\pi ^*\left( \delta \right) = \left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1- \delta \right) - 1 \right] c \right\} ^2 / 4 \left( n-m+1 \right) \beta$ and $\pi _N^*\left( \delta \right) = \dfrac{\left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1- \delta \right) - 1 \right] c \right\} ^2}{4m \left( n-m+1 \right) \beta }$. For ease of exposition, we assume that m is a continuous variable. As a result we obtain

$$\begin{aligned}&\dfrac{d \pi ^*\left( \delta \right) }{d m} = \dfrac{\left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1- \delta \right) - 1 \right] c \right\} \left\{ \alpha - c - \left( n-m+1 \right) \left( 1- \delta \right) c \right\} }{4 \left( n-m+1 \right) ^2 \beta } > 0\\&\quad \text { for } \delta > \delta _2 \\&\dfrac{d \pi _N^*\left( \delta \right) }{d m}\\&\quad = \dfrac{\left\{ \alpha + \left[ \left( n-m+1 \right) \left( 1- \delta \right) - 1 \right] c \right\} \left\{ m \left\{ \left( 2 \alpha -c \right) + \left[ n-\left( n+1 \right) \delta \right] c \right\} - \left( n+1 \right) \left\{ \alpha + \left[ n-\left( n+1 \right) \delta \right] c \right\} \right\} }{4 m^2 \left( n-m+1 \right) ^2 \beta } \\&\quad > 0 \text { for } m > \bar{\bar{m}} \end{aligned}$$

Clearly, the result is valid for discrete m.$\square$

Proposition 7

For $m \le \bar{m}$, if $\delta \le \delta _3$, the network is internally stable and externally unstable. Similarly, the network is internally stable and externally unstable when $\delta \le \delta _2$ for $m > \bar{m}$.

Proof of Proposition 7

First consider the case $m > \bar{m}$. From Table 1, for $\delta \le \delta _2$, $\pi _N^* \left( m \right) > 0$ and $\pi _I^* \left( m \right) = 0$. Further, $\delta _2$ is monotonically decreasing in m, and hence, $\pi _N^* \left( m+1 \right) > 0$ and $\pi _I^* \left( m-1 \right) = 0$. Clearly, the network is internally stable and externally unstable. Similarly, we can show our results for $m \le \bar{m}$.$\square$

Proposition 8

For given $\delta$, if $\lfloor \dfrac{\alpha -c}{\left( 1-\delta \right) c} \rfloor \le \bar{m}$, the network is internally stable and externally unstable when $m \in \left[ \lfloor \dfrac{\alpha -c}{\left( 1-\delta \right) c} \rfloor , \left( n+1 \right) - \lfloor \dfrac{\alpha -c}{\left( 1-\delta \right) c} \rfloor \right]$.

Proof of Proposition 8

For given $\delta$, when $\lfloor \dfrac{\alpha -c}{\left( 1-\delta \right) c} \rfloor \le \bar{m}$, we obtain $\lfloor \dfrac{\alpha -c}{\left( 1-\delta \right) c} \rfloor \le \bar{m} \le \left( n+1 \right) - \lfloor \dfrac{\alpha -c}{\left( 1-\delta \right) c} \rfloor$. We observe that $\delta \le \delta _3$ when $m \ge \lfloor \dfrac{\alpha -c}{\left( 1-\delta \right) c} \rfloor$ and $\delta \le \delta _2$ when $m \le \left( n+1 \right) - \lfloor \dfrac{\alpha -c}{\left( 1-\delta \right) c} \rfloor$. For $m \in \left[ \lfloor \dfrac{\alpha -c}{\left( 1-\delta \right) c} \rfloor , \left( n+1 \right) - \lfloor \dfrac{\alpha -c}{\left( 1-\delta \right) c} \rfloor \right]$, we obtain $\delta \le \delta _3$ and $\delta \le \delta _2$. We know that $\delta _2 \left( \delta _3\right)$ is monotonically decreasing (increasing) in m. Clearly, by Proposition 7, the network is internally stable and externally unstable.

When $\lfloor \dfrac{\alpha -c}{\left( 1-\delta \right) c} \rfloor > \bar{m}$, we obtain . Thus, $m \ge \lfloor \dfrac{\alpha -c}{\left( 1-\delta \right) c} \rfloor$ implies $m \ge \bar{m} > \left( n+1 \right) - \lfloor \dfrac{\alpha -c}{\left( 1-\delta \right) c} \rfloor$, and hence, $\delta \ge \delta _2$. Similarly, $m \le \left( n+1 \right) - \lfloor \dfrac{\alpha -c}{\left( 1-\delta \right) c} \rfloor$ implies $m \ge \bar{m} < \lfloor \dfrac{\alpha -c}{\left( 1-\delta \right) c} \rfloor$, and hence, $\delta > \delta _3$. Now, from Table 1, both network and independent firms compete. $\square$