Abstract
In this paper, we study a queueing system serving N customers with an unreliable server subject to disruptions even when idle. Times between server interruptions, service times, and times between customer arrivals are assumed to follow exponential distributions. The main contribution of the paper is to use general distributions for the length of server interruption periods/down times. Our numerical analysis reveals the importance of incorporating the down time distribution into the model, since their impact on customer service levels could be counterintuitive. For instance, while higher down time variability increases the mean queue length, for other service levels, can prove to be improving system performance. We also show how the process completion time approach from the literature can be extended to analyze the queueing system if the unreliable server fails only when it is serving a customer.
Similar content being viewed by others
References
Almasi, B. (1996). Response time for finite heterogeneous nonreliable queueing systems. Computers and Mathematics with Applications, 31(11), 55–59.
Almasi, B., & Sztrik, J. (1993). A queueing model for a non-homogeneous terminal system subject to BR992. Computers and Mathematics with Applications, 25(4), 105–111.
Almasi, B., & Sztrik, J. (1998a). A queueing model for a nonreliable multiterminal system with polling scheduling. Journal of Mathematical Sciences, 92(4), 3974–3981.
Almasi, B., & Sztrik, J. (1998b). The effects of service disciplines on the performance of a nonreliable terminal system. Journal of Mathematical Sciences, 92(4), 3982–3989.
Almasi, B., & Sztrik, J. (1999). Optimization problems on the performance of a nonreliable terminal system. Computers and Mathematics with Applications, 38(3), 13–21.
Almasi, B., & Sztrik, J. (2004). Reliability investigations of heterogeneous terminal systems using MOSEL. Journal of Mathematical Sciences, 123(1), 3795–3801.
Altıok, T. (1997). Performance analysis of manufacturing systems. New York, NY: Springer.
Atencia, I., Bouza, G., & Moreno, P. (2008). An \(M^{[X]}/G/1\) retrial queue with server breakdowns and constant rate of repeated attempts. Annals of Operations Research, 157(1), 225–243.
Avi-Itzhak, B., & Naor, P. (1963). Some queueing problems with the service station subject to breakdown. Operations Research, 11(3), 303–320.
Balcıog̃lu, B., Jagerman, D. L., & Altıok, T. (2007). Approximate mean waiting time in a \(GI/D/1\) queue with autocorrelated times to failures. IIE Transactions, 39, 985–996.
Chakravarthy, S. R., & Agarwal, A. (2003). Analysis of a machine repair problem with an unreliable server and phase type repairs and services. Naval Research Logistics, 50(5), 462–480.
Federgruen, A., & Green, L. (1986). Queueing systems with service interruptions. Operations Research, 34(5), 752–768.
Federgruen, A., & Green, L. (1988). Queueing systems with service interruptions II. Naval Research Logistics, 35, 345–358.
Fiems, D., Maertens, T., & Bruneel, H. (2008). Queueing systems with different types of server interruptions. European Journal of Operational Research, 188(3), 838–845.
Gaver, D. P. (1962). A waiting line with interrupted service, including priorities. Journal of the Royal Statistical Society, 24(1), 73–90.
Gupta, U. C., & Srinivasa Rao, T. S. S. (1996). Computing the steady state probabilities in \(\lambda (n)/G/1/K\) queue. Performance Evaluation, 24, 265–275.
Haque, L., & Armstrong, M. J. (2007). A survey of the machine interference problem. European Journal of Operational Research, 179(2), 469–482.
Katehakis, M. N., Smit, L. C. & Spieksma, F. M. (2015b). A comparative analysis of the successive lumping and the lattice path counting algorithms. Journal of Applied Probability (forthcoming).
Katehakis, M. N., Smit, L. C., & Spieksma, F. M. (2015a). DES and RES processes and their explicit solutions. Probability in the Engineering and Informational Sciences, 29, 191–217.
Ke, J.-C., & Wang, K.-H. (1999). Cost analysis of the \(M/M/R\) machine repair problem with balking, reneging, and server breakdowns. Journal of the Operational Research Society, 50(2–3), 275–282.
Lam, Y., Zhang, Y. L., & Liu, Q. (2006). A geometric process model for \(M/M/1\) queueing system with a repairable service station. European Journal of Operational Research, 168(1), 100–121.
Liang, W. K., Balcıog̃lu, B., & Svaluto, R. (2013). Scheduling policies for a repair shop problem. Annals of Operations Research, 211, 273–288.
Liu, B., & Cao, J. (1995). A machine service model with a service station consisting of r unreliable units. Microelectronics Reliability, 35(4), 683–690.
Mitrany, I. L., & Avi-Itzhak, B. (1968). A many server queue with service interruptions. Operations Research, 16(3), 628–638.
Neuts, M. F., & Lucantoni, D. M. (1979). A Markovian queue with \(N\) servers subject to breakdowns and repair. Management Science, 25(9), 849–861.
Sahba, P., Balcıog̃lu, B., & Banjevic, D. (2013). Analysis of the finite-source multi-class priority queue with an unreliable server and setup time. Naval Research Logistics, 60, 331–342.
Stecke, K. E., & Aronson, J. E. (1985). Review of operator/machine interference models. International Journal of Production Research, 23(1), 129–151.
Sztrik, J., & Gál, T. (1990). A recursive solution of a queueing model for a multi-terminal system subject to breakdowns. Performance Evaluation, 11(1), 1–7.
Tang, Y. H. (1997). A single-server \(M/G/1\) queueing system subject to breakdowns: Some reliability and queueing problems. Microelectronics Reliability, 37(2), 315–321.
Thiruvengadam, K. (1963). Queueing with breakdown. Operations Research, 11, 62–71.
Wang, K.-H. (1990). Profit analysis of the machine-repair problem with a single service station subject to breakdowns. Journal of the Operational Research Society, 41(12), 1153–1160.
Wang, K.-H. (1993). Cost analysis of the \(M/M/R\) machine-repair problem with mixed standby spares. Microelectronics Reliability, 33(9), 1293–1301.
Wang, J., Cao, J., & Li, Q. (2001). Reliability analysis of the retrial queue with server breakdowns and repairs. Queueing Systems, 38(4), 363–380.
Wang, K.-H., & Hsu, L. Y. (1995). Cost analysis of the machine-repair problem with \(R\) non-reliable service stations. Microelectronics Reliability, 35(6), 923–934.
Wang, K.-H., & Kuo, M.-Y. (1997). Profit analysis of the \(M/Ek/1\) machine repair problem with a non-reliable service station. Computers and Industrial Engineering, 32(3), 587–594.
White, H., & Christie, L. (1958). Queueing with preemptive priorities or with breakdown. Operations Research, 6(1), 79–95.
Acknowledgments
This work was supported in part by Natural Sciences and Engineering Research Council (NSERC) of Canada. The authors thank Dr. Elizabeth Thompson, for proofreading the manuscript. The authors thank the two anonymous referees and the editors for their invaluable suggestions to improve the manuscript.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Proofs
Proof of Theorem 1
If we divide both sides of Eq. (7) by \(e^{-{N\lambda y -\int _{0}^{y}\beta (x)dx}}P_{N,1}(0)\) and Eq. (8) by \(e^{-{i\lambda y -\int _{0}^{y}\beta (x)dx}}P_{N,1}(0)\), we get
which are first order differential equations. We solve Eqs. (23) and (24) using Eq. (21) as
Considering the definition given in Eq. (21), and employing Eqs. (5), (6) and (9), we obtain
For simplicity, we define
In order \({\mathcal {Q}}_i\) and \({\mathcal {B}}_i\) to be finite, we will show that \(Q_{i}(y)\) is bounded for all \(i=0,\ldots ,N\), which is proved in the following Lemma.
Lemma 1
\(\lim _{y\rightarrow \infty } Q_{i}(y)=Q_{i}(\infty )\) exists and is finite. We also have \(Q_{i}(y)\le Q_{i}(\infty )\).
Proof. Lemma 1
From Eq. (21), \(Q_{i}(y)\ge 0\) and from Eq. (26), we see that \(Q_{i}(y)\) is increasing in y. Let \(Q_{i}(\infty )=\lim _{y\rightarrow \infty } Q_{i}(y)\). Then, \(Q_{i}(y)\le Q_{i}(\infty ),\ 0\le i\le N-1\). If we take the limit as \(y\rightarrow \infty \) in Eq. (26),
Starting with \(Q_{N}(\infty )=1\) (due to Eq. 25) and using induction from the above equation, we see that \(Q_{i}(\infty )\) is finite for all \(i=0,\ldots ,N\). \(\square \)
Let \(\Phi _{i}(s)=\int _{0}^{\infty }Q_{i}(y)e^{-sy}dy\) be the LT of the function \(Q_{i}(y)\). In this case, the LT’s of \(Q_{N}(y)\) and \(Q_{i}(y)\) from Eqs. (25) and (26) will be
Starting from Eq. (30) and using the recursive formula in Eq. (31), we establish
Using
Eq. (32) can be rewritten as
Observe that \((l\lambda +s)^{-1}\) on the right hand side of Eq. (33) is the LT of \(e^{-l\lambda y}\). Using this, when we invert \(\Phi _{i}(s)\), we obtain
Substituting Eq. (34) in Eq. (29), we have Eq. (14) where
This leads to Eqs. (12) and (13). Together with Eq. (14) as defined in Eq. (29), Eq. (22) gives Eqs. (10) and (11).
We define \({\mathcal {D}}_i=i\lambda \int ^{\infty }_0(P_{i,1}(y)/P_{N,1}(0))dy\). Noting from Eq. (26) that \(dQ_{i}(y)=(i+1)\lambda Q_{i+1}(y)e^{-\lambda y}\), if we rewrite Eq. (29) as \({\mathcal {B}}_i=-\int ^{\infty }_0Q_{i}(y)e^{-i\lambda y}d\overline{F}(y)\), integration yields
Considering Eq. (21) for \({\mathcal {D}}_i\), the above given equation gives Eqs. (15) and (18). With Eq. (9) and the definitions given in Eqs. (21) and (22), we obtain Eq. (17). \(\square \)
Proof. Corollary 1
Substituting Eq. (21) in Eq. (34), we arrive at Eq. (19)
Proof of Theorem 2
By definition \(\sum ^N_{i=0}\overline{P}_i=\sum ^N_{i=0}(P_{i,0}+\int ^{\infty }_0P_{i,1}(y)dy)=1\), which by using Eq. (9), becomes \(\sum ^N_{i=0}(P_{i,0}(0)/\alpha +\int ^{\infty }_0P_{i,1}(y)dy)=1\). If we divide this equation by \(P_{N,1}(0)\), we have
where \(S_N(y)=\sum ^N_{i=0}P_{i,1}(y)/P_{N,1}(0)\).
Summing up Eqs. (7) and (8), we obtain the first order differential equation
that has a solution of \(S_N(y)=S_N(0)e^{-\int ^y_0{\beta (x)dx}}=S_N(0)\overline{F}(y)\). Substituting this in Eq. (36) and using the fact that \(E[D]=\int _0^{\infty }\overline{F}(y)dy\) gives us
Considering Eqs. (22) and (21), \(S_N(0)=\sum ^N_{i=0}{\mathcal {Q}}_i\); after substituting it in the equation given above, and using the boundary condition in Eq. (9) we obtain Eq. (20). \(\square \)
Appendix 2: The ODD 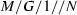 queue
queue
In this section, we summarize how results from the literature can be easily used in analyzing the  queue where unlike the model studied in this paper, the server can experience disruptions only if it has customers. We make the same assumptions and employ the same notations introduced in Sect. 2 for the underlying r.v.s with two differences. First, the actual service time of a job—in the absence of disruptions—is a general i.i.d. r.v. with the LT of \(\tilde{b}(s)\). Second, while \(\alpha \) still denotes the rate of the exponential times to interruption, the interruption process is halted when the server becomes idle until it becomes busy again. To handle this problem, one can use the process completion time (PCT) r.v. (Gaver 1962) that is the total time a customer spends on the server including its actual service time plus possible OFF periods it may experience. Let C denote the PCT r.v. the LT of which is given by (e.g., Altiok 1997, p. y94)
queue where unlike the model studied in this paper, the server can experience disruptions only if it has customers. We make the same assumptions and employ the same notations introduced in Sect. 2 for the underlying r.v.s with two differences. First, the actual service time of a job—in the absence of disruptions—is a general i.i.d. r.v. with the LT of \(\tilde{b}(s)\). Second, while \(\alpha \) still denotes the rate of the exponential times to interruption, the interruption process is halted when the server becomes idle until it becomes busy again. To handle this problem, one can use the process completion time (PCT) r.v. (Gaver 1962) that is the total time a customer spends on the server including its actual service time plus possible OFF periods it may experience. Let C denote the PCT r.v. the LT of which is given by (e.g., Altiok 1997, p. y94)
where \(\tilde{f}(s)\) is the LT of the OFF periods.
The PCT r.v., C, includes all the information of ON and OFF periods. We can use it as the service time r.v. in an  queue without interruptions analyzed by Gupta and Srinivasa Rao (1996), which will be referred to as the
queue without interruptions analyzed by Gupta and Srinivasa Rao (1996), which will be referred to as the  queue. Note that the
queue. Note that the  queue has the same \(\lambda \) and N as in the original ODD
queue has the same \(\lambda \) and N as in the original ODD  queue, and additionally uses \(\tilde{c}(s)\) from Eq. (37) as the LT of the service time. Using the algorithm by Gupta and Srinivasa Rao, one obtains \(P_i\) in the
queue, and additionally uses \(\tilde{c}(s)\) from Eq. (37) as the LT of the service time. Using the algorithm by Gupta and Srinivasa Rao, one obtains \(P_i\) in the  queue, which coincides with the probability of having i customers in the original ODD
queue, which coincides with the probability of having i customers in the original ODD  queue. With these probabilities, the expected system size and the probability of the server is idle in the ODD
queue. With these probabilities, the expected system size and the probability of the server is idle in the ODD  queue can be computed. The limitation of using the PCT approach is that we are unable to find the probability that the server is down or serving a customer, \(P_D\) and \(P_B\), respectively.
queue can be computed. The limitation of using the PCT approach is that we are unable to find the probability that the server is down or serving a customer, \(P_D\) and \(P_B\), respectively.
Rights and permissions
About this article
Cite this article
Sahba, P., Balcıog̃lu, B. & Banjevic, D. The impact of disruption characteristics on the performance of a server. Ann Oper Res 317, 239–252 (2022). https://doi.org/10.1007/s10479-015-2075-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-015-2075-2



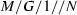 queue
queue