Decomposition algorithms for data placement problem based on Lagrangian relaxation and randomized rounding

Abstract

The data placement problem arises in the design and operation of Content Delivery Networks—computer systems used to efficiently distribute Internet traffic to the users by replicating data objects (media files, applications, database queries, etc.) and caching them at multiple locations in the network. This allows not only to reduce the processing load on the server hardware, but also helps eliminating transmission network congestion. Currently all major Internet content providers entrust their offered services to such systems. In this paper we formulate the data placement problem as quadratic binary programming problem, taking into account server processing time, storage capacity and communication bandwidth. Two decomposition-based solution approaches are proposed: the Lagrangian relaxation and randomized rounding. Computational experiments are conducted in order to evaluate and compare the performance of presented algorithms.

1 Introduction

In the last decade the locational analysis has received a special attention from the computer networking community, due to the widespread development of large scale Internet applications. The deployment of a number of application servers placed in different locations, providing replicated data to the users, has become a necessity for high-traffic Web sites. This allows not only to reduce the processing load on the server hardware, but also helps eliminating transmission network congestion and improves reliability. However, in order to benefit from Web sites’ content replication, the operator of server network needs to decide where to place the data, on behalf of content publishers, in order to serve the users’ demands with maximum performance. Unfortunately, the optimal placement of data objects and assignment of users to their respective best replicas can be identified to be an NP-hard problem.

In this paper we formulate a very general class of optimization problems arising from the planning of content delivery network or other similar large scale data delivery system in the Internet (e.g. video-on-demand). Our model incorporates all three resources that need to be taken into consideration in the context of computer systems: server processing time, storage capacity and communication bandwidth, and is essentially an extension of data placement problem devised in Baev et al. (2008). The problem is formulated in terms of quadratic binary programming, with both covering and packing constraints, and can be seen as a special case of generalized capacitated facility location (Hajiaghayi et al. 2003).

Two different decomposition-based approaches to solving the formulated problem are proposed. The first decomposition is based on Lagrangian relaxation, and leads to various heuristic algorithms, depending on particular subroutines used for solving smaller subproblems (which are still NP-hard, although have much simpler structure). The second decomposition is based on the linear programming relaxation and employs randomized rounding. Both decompositions involve solving generalized assignment problem, which for many years has been a central problem in many applications of operations research. However this problem does not admit constant factor approximations without violating capacity constraints. We compare the effectiveness of these decompositions in an experimental study.

The presented methods combine in a novel way several known techniques from the area of global optimization and approximation algorithms. Three important problems that are of independent interest constitute the basis of proposed solutions: subgradient ascent method, generalized assignment problem and knapsack problem.

2 Related work

Data placement problems have been studied extensively in the context of database management (Gavish and Suh 1992; Liu Sheng and Lee 1992; Pirkul 1986; Wolfson et al. 1997), organization of distributed file systems (Bokhari 1987; Laning and Leonard 1983), cooperative caching in networks (Korupolu et al. 1999), and more recently, content delivery networks and Web traffic (Bektas et al. 2007, 2008; Rodolakis et al. 2006; Sivasubramanian et al. 2004). Related problems of on-line data management were considered in the competitive analysis framework, e.g. Lund et al. (1999). Issues emerging from the decentralization typically concern the selfishness of involved servers (assuming that they belong to different owners, e.g. Internet Service Providers), and are considered with the use of algorithmic game theory (Chun et al. 2004; Khan and Ahmad 2009; Laoutaris et al. 2006). In contrast, in this paper we assume that all servers are under control of a single agent, and the goal is to design a mechanism allowing to optimize the system with minimal exchange of information between server nodes.

For somewhat less general model, the first constant-factor approximate algorithm based on rounding of LP relaxation was given in Baev and Rajaraman (2001), and subsequently improved in Baev et al. (2008). These formulations did not include the processing costs in objective function, as well as processing capacities in constraints, while methods presented in this paper seek to fill this gap.

Considered problem can be seen as a special variant of universal facility location problem (also known as generalized facility location problem) (Hajiaghayi et al. 2003; Mahdian and Pál 2003). Its uncapacitated variant can be approximated up to a constant factor using local search (Williamson and Shmoys 2011). In this paper we deal with two types of capacity constraints (concerning server processing and storage capacity). Capacitated facility location in the context of content delivery networks has been recently studied in Bateni and Hajiaghayi (2009).

3 Problem statement

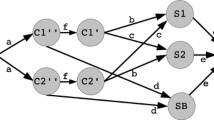
Let us consider the model of a wide area computer network, such as a group of autonomous systems (see e.g. Tanenbaum 2003, Chap. 5.6), as illustrated in Fig. 1. It is represented by undirected graph in which vertices stand for access routers of local area networks and the edges denote bidirectional communication links. Users of each local area network proclaim their demands to the Internet Service Providers (ISPs), that manage the routers. A numeric value of aggregated demand is assigned to each router. ISP is responsible for servicing the users in local area networks behind each router. To take full advantage of the system’s capabilities, ISP needs to decide from where to service the demand assigned to each router, i.e. to which network node to route the requests from local area networks.

Fig. 1

Overview of the network model in the data placement problem

Servicing all the demands from a single location (one node) would be highly inefficient, if possible at all. A single server, even if equipped with very efficient processors, may quickly fall under the burden of thousands concurrent requests. The system should be scalable with respect to the amount of traffic, which means that users’ waiting time should be almost unaffected by the amount of total demand. This is especially important for computation-intensive applications which need to perform a considerable amount of server-side processing in order to fulfill the requests. This fact is exploited by the coordinated network attacks, called distributed denial of service, which flood the server with streams of fake requests, making it inaccessible for other users (see Tanenbaum 2003, Chap. 8.6).

The second concern in centralized architectures is that a large group of users may be located too far from the server, behind congested links. As the architecture of Internet assumes that a data packet will be a subject to multiple queuing delays before it reaches the user, it is highly advisable to avoid long transmissions through backbone network, whenever possible. This is especially important for bandwidth-demanding applications, such as video streaming (Leighton 2009).

To alleviate these problems, each access router in the considered system is equipped with a cache server which can store copies of data objects. The cache memory is assumed to be connected to the router via very fast transmission bus, thus the location of access router is equivalent to the location of its cache server.

If a data object is stored inside a cache server, then it can be served directly to the users associated with that location (i.e. connected to the Internet through the considered access router). In such a case data do not travel through the backbone, so there is no transmission cost incurred (local area network transmission time is neglected). There is, however, the cost resulting from the requests processing delay on a cache server. This cost is proportional to the amount of demand that is processed by that cache.

If a data object is not stored in cache, then a data object can be accessed by a node from any remote cache server storing that object. In that case we call the non-caching node a client (of a remote cache server). Accessing remote data, however, incurs transmission cost (proportional to the network latency), and there is also a cost resulting from processing delay on the remote machine. Thus, each client perceives a performance loss proportional to the total processing load of the server to which is assigned.

In the computer systems design, there are three resources to allocate that determine the overall performance and utility of the system: processing time (CPU time), memory and communication bandwidth. From the system’s operator point of view, the problem of optimal design can be stated as follows: given users’ demands and limited resources, allocate the resources to the demands in such a way to minimize the total cost of service. Here, the cost is understood as the performance loss perceived by the user. This cost is also directly related to the real costs and profits achieved by the operator: the better performance is experienced by the users, the more they will be willing to pay for the service.

In the considered problem, we are given a set of client local area networks (LANs, henceforth called simply clients) and cache server locations. Each of them is located at a vertex of a connected graph G=(V,E), |V|=N. In general, each node may be occupied by both client LAN and cache server at the same time. A matrix of nonnegative distances between nodes D=[d _ij ] is given (d _ii =0 for all i). These distances are assumed to be proportional to the latency perceived by the receiver during transmission of unit of data. They reflect the transmission link throughputs, and neglect the signal propagation delay (which is negligible in case of transmitting large data objects). There are M data objects to be accessed by users through access router nodes. Each object p∈{1,…,M} has size s _p units, and is characterized by the access demand w _ip ≥0, which reflects the number of users’ requests the node i∈V issues in a unit of time for accessing data object p. This demand may be assumed to be proportional to the number of client machines inside ith LAN.

Two groups of decision variables are used. The first one is denoted as three dimensional binary matrix x=[x _ijp ], i,j=1,…,N, p=1,…,M. The variable x _ijp assumes value one if only if client node i is assigned to the server node j for accessing object p, and value zero otherwise. The second group of decision variables is denoted as binary matrix of data placement decisions z=[z _ip ], i=1,…,N, p=1,…,M. If data object p is placed inside cache server at node i then z _ip =1, and such a server is called active; otherwise z _ip =0. All copies of the same object are referred to as replica objects. The summary of notation is presented in Table 1.

Table 1 Summary of notation

There are three types of costs considered in the problem, and all of them can be expressed in the time units. Each of the costs is related to the service latency on a router and associated cache server (which translates to the performance experienced by the users). The total cost is the sum of costs carried by all access routers.

The first cost is equal to the time needed to transmit the requested data from a remote cache server to the access router of client LAN. If a data object is cached at node i, then this cost is equal to zero. Otherwise it is proportional to the link latency d _ij of transmitting a unit of data from the selected jth cache server. The quantity d _ij s _p is thus equal to the time needed to transmit pth object. Consequently, the total cost of serving ith client’s demand for accessing pth object is equal to d _ij w _ip s _p .

The second cost is equal to the time needed to process the requests on a cache server. Assuming that the jth server processes a unit of data in h _j units of time at average (e.g. h _j =0.001 means one thousand requests per second), then the total expected waiting time for a server to process the assigned demands is proportional to l _j =∑ _i,p x _ijp w _ip s _p . This quantity is also called the processing load on a server. The actual cost caused by the load depends on the type of processors and mechanisms used for serving the incoming requests. In general, the time elapsed before sending back a response to client is a function T _j (l _j ,h _j ), non-decreasing in both arguments.

Finally, the third cost is the price charged for installation and storage of data object in a cache server. The inclusion of this cost depends on the caching decision. The uncached data objects are located at the origin servers, which are not directly accessed by users. Thus at least one cache server has to store a copy of each data object. The origin servers are not included in the vertex set V. Instead, the installation (placement) cost of object p in the cache server j is represented by the value b _jp ; this cost is proportional to the distance from the source server to node j and to the installed object size. It also may depend on the object type, as well as the additional maintenance concerns, such as the required object update frequency. Value of b _jp can be seen as the sum of times needed to download the object from an origin server to a cache server plus the time needed to send updates.

Without the loss of generality, we may assume that each vertex i∈V represents both client LAN and cache server, and put w _ip =0 for node i that is server-only, b _jp =∞ for node j that is client-only.

The individual cost paid by a single access router (or cache server) at node i is defined as (1). This value represents the tradeoff between the installation and processing costs (resulting from accessing the cached objects by all routers assigned to it), and the transmission cost and remote server’s processing cost, in case of not using the cache.

$$ v_i (\mathbf{x}, \mathbf{z}) = \sum _{p=1}^M \Biggl(\,\sum_{j=1}^N d_{ij} w_{ip} s_p x_{ijp} + \sum _{j=1}^N x_{ijp} T_j \Biggl(\,\sum_{k=1}^N \sum _{q=1}^M x_{kjq} w_{kq} s_q, h_j\Biggr) + b_{ip} z_{ip} \Biggr). $$

(1)

In this paper we consider only the processing time given by linear function of total demand, that is T _j (l _j ,h _j )=h _j ∑ _i,p x _ijp w _ip s _p . This is the worst-case waiting time perceived by all the client routers assigned to j. The processing time, however, may depend differently on the number of requests, for example if multiple CPUs are used in parallel on a single node.

In order to characterize the best object placement z and the best assignment of clients to the objects x, we employ the utility theory, which is typically used in the context of a large scale computer network (Chiang et al. 2007; Kelly et al. 1998). It is assumed that the performance of the system is described by utility function $U(\mathbf{x}, \mathbf{z}) = \sum_{i=1}^{N} U_{i}(\mathbf{x}_{i}, \mathbf{z}_{i})$ being the sum of individual client utilities. Assuming that the profit of network operator is equal to the total utility, the goal is to maximize U. A general class of utility functions used in the performance evaluation of a computer network is U _i (t)=t ^1−α/(1−α), where α≠1 is a parameter allowing to implement different notions of fairness (this class of functions is sometimes called isoelastic). In this study we assume that each client LAN wishes to maximize the mean rate $v_{i}^{-1}(\mathbf{x}, \mathbf{z})$ computed as reciprocal of the delay time (1). Thus, putting the parameter α=2, the individual utility of a node is U _i (x,y)=−v _i (x,z). Maximization of such class of utility function leads to the allocation that is called minimum potential delay fair (Chiang et al. 2007). Since minimizing the negative value of sum of such utilities is equivalent to the maximization of total utility U, the problem can be stated as to minimize:

(2)

The objective function (2) is minimized subject to the following constraints:

(3)

(4)

(5)

(6)

(7)

Constraint (4) assures that each client has selected exactly one server for each data object. Constraint (5) guarantees that client i will access object p only if that object is available in cache server j. Constraint (6) imposes processing capacities for cache servers; any jth server can maintain no more than S _j simultaneous connections, expressed as a sum of connected users’ demand. These constraints together also assure that at least one server is available for every data object. Finally, constraint (7) imposes capacities for cache server storages; the total size of cached objects cannot exceed the storage capacity R _j .

It can be easily seen that the problem is NP-hard (for example, capacitated facility location reduces to this problem, Williamson and Shmoys 2011). As both decision variables are binary, this formulation is the case of unsplittable flows in the facility location terminology (Hale and Moberg 2003; Kao 2008). Whenever constraints (6)–(7) are included, we will call the problem capacitated. Ignoring these two constraints (i.e. putting S _j =∞, R _j =∞, which makes them redundant) results in the uncapacitated variant of the problem. This variant is much easier to analyze, since it allows for considering the placement of each data object p independently. An additional source of difficulties comes from the fact that the objective function is quadratic, due to the inclusion of server processing times. The variant of the problem when this factor is negligible (i.e. h _j =0 for all j) appears to be much easier to deal with in practice. Here we consider the full generality (i.e. h _j >0 for at least some j).

4 Linearization

Initially, let us linearize the quadratic problem (2)–(7). This allows to obtain an equivalent binary linear program at the price of including a set of new constraints. One particularly useful linearization technique, specifically designed for (mixed) binary quadratic problems, was given and analyzed in Adams et al. (2004). This linearization introduces N ² M new variables y _ijp , which substitute the quadratic terms as follows. First, the middle sum of the objective function is rewritten with the use of new variables y _ijp , defined as y _ijp =x _ijp g _ijp (x), where $g_{ijp}(\mathbf{x}) = h_{j} \sum_{k=1}^{N} \sum_{q=1}^{M} x_{kjq} w_{kq} s_{q}$. In addition, 3N ² M new constraints are included. This gives the following reformulation:

$$ \mbox{minimize } Q_L(\mathbf{x},\mathbf{y},\mathbf{z}) = \sum_{i=1}^N \sum _{j=1}^N \sum_{p=1}^M d_{ij} w_{ip} s_p x_{ijp} + \sum _{i=1}^N \sum_{j=1}^N \sum_{p=1}^M y_{ijp} + \sum _{j=1}^N \sum_{p=1}^M b_{jp} z_{jp} $$

(8)

subject to the constraints (3)–(7) and:

(9)

(10)

(11)

The sets of optimal solutions of (2)–(7) and (8)–(11) are the same. To see this, it is enough to show that y _ijp equals x _ijp h _j ∑ _k ∑ _q w _kq s _q x _kjq for all optimal x ^∗ in the original problem. Clearly, if for some i, j, p, $x_{ijp}^{*} = 0$, then from the constraint (9) we have 0≤y _ijp as all terms h _j w _kp s _q will be subtracted. Since the sum of y _ijp undergoes minimization, thus optimal y _ijp =0 (the upper bound in constraint (10) is nonnegative). Otherwise, if $x_{ijp}^{*}=1$, in the left-hand side of condition (9) the term (1−x _ijp ) becomes 0, and the value of y _ijp must be at least h _j ∑ _k ∑ _q w _kq s _q x _kjq , which is also the minimal value.

5 Decomposition based on Lagrangian relaxation

In this section a decomposition method is presented, which allows to construct efficient heuristics, capable of finding good solutions for the general case of data placement problem. We propose to relax the constraints (5) and (9), by introducing Lagrange multipliers λ _ijp ≥0, μ _ijp ≥0. The Lagrange function can be written as:

(12)

where $W = \sum_{k=1}^{N} \sum_{q=1}^{M} w_{kq} s_{q}$ and c _ijp =d _ij w _ip s _p .

Since the Lagrange function lower bounds the minimal value of original problem, the problem can be now stated as:

$$ \max_{\boldsymbol{\lambda} \geq0,\, \boldsymbol{\mu} \geq0} \min_{\mathbf{x}, \mathbf{y}, \mathbf{z}} L(\mathbf{x}, \mathbf{y}, \mathbf{z}; \boldsymbol {\lambda}, \boldsymbol{\mu}) $$

(13)

subject to constraints (3)–(4), (6)–(7), (10)–(11).

Given fixed values of Lagrange multipliers λ, μ, it is possible to decompose the problem of minimizing (12) into two independent subproblems.

The first subproblem is to minimize with respect to x and y the function:

(14)

subject to:

(15)

(16)

(17)

(18)

(19)

The second subproblem is to maximize with respect to z the function:

$$ \sum_{j=1}^N \sum _{p=1}^M z_{jp} \Biggl(\,\sum _{i=1}^N \lambda_{ijp} - b_{jp} \Biggr) $$

(20)

subject to:

(21)

(22)

The first subproblem (14)–(19) can be reduced to an instance of generalized assignment problem (GAP) in the variables x. Given a matrix of multipliers μ, let us eliminate the variables y by the following substitution:

$$y_{ijp} = \left \{ \begin{array}{@{}l@{\quad}l@{}} h_j \sum_{k=1}^N \sum_{q=1}^M w_{kq} s_q x_{kjq}, & \mbox{if } \mu_{ijp} > 1,\\[3pt] 0, & \mbox{otherwise}. \end{array} \right . $$

Let $Y^{\boldsymbol{\mu}}_{ijp}$ denote the indicator variable, which assumes value 1 if μ _ijp >1, and value 0 otherwise; also let $\bar {Y}^{\boldsymbol{\mu}}_{ijp} = 1- Y^{\boldsymbol{\mu}}_{ijp}$. The objective function (14) can be rewritten as:

(23)

and the set of constraints becomes (15)–(16) and (18).

The cost matrix of generalized assignment problem is composed of the coefficients π _ijp , and the remaining terms are constant (they do not depend on x). The generalized assignment problem is NP-hard and most of the known approximation results require violation of packing constraint and rely on LP relaxations. Since solving large instances of GAP may require a substantial computational effort, we use a fast greedy heuristic, given as Algorithm 1. The algorithm minimizes the function ∑ _i ∑ _j ∑ _p π _ijp x _ijp . The method simply assigns clients to a server as long as there is enough capacity, starting from the cheapest server and subsequently proceeding to the more expensive ones. The algorithm requires NM sorting operations of lists of N numbers.

Algorithm 1

Greedy algorithm for generalized assignment problem

The second subproblem (20)–(22) consists of N instances of knapsack problem, for each j=1,…,N. It is worth stressing that currently even very large instances of knapsack problem can be solved to optimality very quickly in practice (Kellerer et al. 2004). Let us recall Algorithm 2 which solves the following knapsack problem in pseudopolynomial time using dynamic programming (Williamson and Shmoys 2011):

$$ v_j^* = \max_{\mathbf{z}_j} \Biggl\{ \sum _{p=1}^M a_{jp} z_{jp}{:}\ \sum _{p=1}^M s_p z_{jp} \leq R_j,\ z_{jp} \in\{ 0, 1 \} \Biggr\}, $$

(24)

where $a_{jp} = \sum_{i=1}^{N} \lambda_{ijp} - b_{jp}$.

Algorithm 2

Dynamic programming algorithm for knapsack problem (24)

The value of Lagrange function (12) is no greater than the value of the optimal solution for any feasible (x,y,z). After solving both subproblems for fixed values of Lagrange multipliers, a maximization in (13) should be performed repeatedly with respect to the multipliers. As for fixed (x,y,z) this is a concave maximization problem, it is proposed to solve it using subgradient optimization method. The outline of a general subgradient scheme is given as Algorithm 3.

Algorithm 3

Subgradient method of solving Lagrangian relaxation

The presented general scheme allows for constructing a family of solution algorithms for the master problem (2)–(7), as it uses calls to external solution routines for GAP and knapsack problems. Depending on the algorithms used to solve them, different outcomes may be obtained (although the application of exact algorithms may result in a prohibitive running time). However, since the constraint (5) connecting both types of decision variables is relaxed, solving two above subproblems separately (i.e. minimizing with respect to x and z) may result in an infeasible solution of the master problem. This is why in Step 4 it may be required to modify the obtained solution to make it feasible, and this can also be performed in many different ways, e.g. by activating each inactive server that has connected clients.

6 Decomposition with randomized rounding

The second proposed method is also based on the decomposition with respect to decision variables x, z. First, the placement of objects z is determined in a way that guarantees preservation of constraint (7) with high probability. In order to obtain low placement cost, usually the technique of randomized rounding is applied (Raghavan and Tompson 1987). The rounding is executed based on the probability distribution obtained from a lower bound on the optimal solution, such as fractional solution $(\hat{\mathbf{x}}, \hat{\mathbf{z}})$, that $Q(\hat{\mathbf{x}}, \hat{\mathbf{z}}) \leq Q(\mathbf{x}^{*}, \mathbf{z}^{*})$. Such a bound can be computed in polynomial time by solving the linear programming relaxation of the original problem (if h _j >0 then a linearization step is required first).

Below we present the motivation of the rounding-based decomposition. Assume that we are able to compute a fractional solution $\hat{\mathbf{z}}$ that gives a lower bound on the optimal (binary) placement decisions z ^∗, i.e.

$$\sum_{j=1}^N \sum _{p=1}^M b_{jp} \hat{z}_{jp} \leq\sum_{j=1}^N \sum _{p=1}^M b_{jp} z_{jp}^*. $$

We can round up variable z _jp =1 with probability $\hat{z}_{jp}$ for all j, p, which results in a solution that has in expectation the same cost of placement as the linear relaxation. Unfortunately, this way we do not have any guarantee that at least one object of each type p will be selected, nor that server capacity constraint (7) will be preserved. To get rid of the first issue, we can construct a probability distribution $q_{p}(j) = \hat{z}_{jp} / \zeta_{p}$ for each object p, where $\zeta_{p} = \sum_{j} \hat{z}_{jp}$ is a normalization constant. Subsequently, for each object p we can select randomly m _p ∈ℕ servers according to this distribution, in a way which gives a bound on the value of placement decisions (here J _p is a discrete random variable distributed according to q _p (j)):

$$\sum_{p=1}^M m_p \mathbf{E} [ b_{J_p p} ] \leq m_0 \sum_{p=1}^M \sum_{j=1}^N b_{jp} \frac{\hat{z}_{jp}}{\zeta_p} \leq\frac{m_0}{\zeta_{0}} \sum_{p=1}^M \sum_{j=1}^N b_{jp} \hat{z}_{jp} \leq\frac {m_0}{\zeta_{0}} \sum_{p=1}^M \sum_{j=1}^N b_{jp} z_{jp}^* $$

where ζ ₀ is the minimum of ζ _p and m ₀ is the maximum of m _p . Observe that the sampling is done with replacement, so the actual cost is no greater than $M \sum_{p} \mathbf{E} [ b_{J_{p} p} ]$, as in case a server is selected twice, the cost is counted only once.

Unfortunately, the above method of approximating z does not guarantee that the constraint (7) will be preserved. The probability of constraint violation clearly depends on m _p . The probability that object p will be placed at the server j is the probability of at least one success in m _p Bernoulli trials with success probability q _p (j). Let us denote this probability by B(1,m _p ,q _p (j)).

Then the expected storage space used on the server j is, by the Chernoff bound (Raghavan and Tompson 1987) applied for β _jp =(1−m _p q _p (j))/(m _p q _p (j)):

$$\sum_{p=1}^M s_p B\bigl(1, m_p, q_p(j)\bigr) \leq\sum _{p=1}^M s_p \exp \biggl( - \frac{\beta_{jp}^2 m_p q_p(j)}{3} \biggr) $$

if 0<β _jp ≤1.

On the other hand, the more replicas of an object are created, potentially the lower is the cost of connection and processing (as determined by the variable x). In order to establish the best values of m ₁,…,m _M , we employ the reasoning from Lin and Vitter (1992). Let c _ijp =d _ij w _ip s _p , and given a fractional solution (x,y,z) of linearized problem (8), $C_{ip} = \sum_{j} (c_{ijp} \hat{x}_{ijp} + \hat {y}_{ijp})$. Define:

$$V_{ip} = \bigl\{ j{:}\ c_{ijp} + \hat{y}_{ijp} \leq(1+\epsilon) C_{ip} \bigr\} $$

and observe that if we can construct a binary solution z that

$$ \forall_i\ \forall_p \quad \sum _{j \in V_{ip}} z_{jp} \geq1 $$

(25)

and binary x satisfies (4)–(7), then the connection cost is bounded:

$$\sum_{i=1}^N \sum _{j=1}^N \sum_{p=1}^M ( c_{ijp} x_{ijp} + \hat {y}_{ijp} ) \leq(1+\epsilon) \sum_{i=1}^N \sum _{j=1}^N \sum_{p=1}^M ( c_{ijp} \hat{x}_{ijp} + \hat{y}_{ijp} ). $$

In Lin and Vitter (1992) it is proved that it is enough to sample m _p =⌈(1+1/ϵ)ζ _p log(M/δ)⌉ times in order to satisfy (25) with probability (1−δ), for any ϵ>0 and 0<δ<1.

The problem of determining m ₁,…,m _M can be stated as finding feasible solution to the problem:

Subsequently, it remains to determine x, which gives a routing of clients’ requests to particular replica objects. Let F _p ={j: z _jp =1} denote the set of servers that contain a replica of object p. The problem can be stated as generalized quadratic assignment problem. The problem is to minimize:

$$ \sum_{p=1}^M \sum _{i=1}^N \sum_{j \in F_p} d_{ij} w_{ip} s_p x_{ijp} + \sum _{p=1}^M \sum_{i=1}^N \sum_{j \in F_p} \sum_{k=1}^N \sum_{q=1}^M h_j w_{kq} x_{ijp} x_{kjq} $$

(26)

subject to:

(27)

(28)

(29)

7 Experimental results

Computational experiments were performed on randomly generated problem instances. Input data have been generated in a way to reflect the aspects of wide area networks (connection topology determined by distance matrix d _ij based on typical round trip times, distribution of users’ demands w _ip , object sizes s _p ). Each of N nodes in the network represents an access router that is connected to both cache server and client LAN. Moreover, only problem instances with nonempty solution sets were considered, i.e. there always existed an assignment of all objects to servers and all user-object pairs to servers.

The first considered algorithm, denoted Algorithm $\mathcal{A}$, implements the subgradient ascent scheme for Lagrangian relaxation. The first subproblem in the decomposition—generalized assignment problem—is solved either exactly by CPLEX branch and bound method (for smaller instances) or approximately with the use of greedy Algorithm 1 (if execution time for the exact algorithm exceeds given limit). The second subproblem is solved exactly with the use of dynamic programming Algorithm 2. For larger problem instances, the exact knapsack algorithm was replaced by fractional greedy knapsack approximation algorithm. If the obtained pair (x,z) is infeasible, then in Step 4 of the Lagrangian scheme the variable z is simply adjusted by setting z _ip =1 whenever corresponding x _ijp =1.

The second algorithm, denoted Algorithm $\mathcal{B}$, first solves the linear programming relaxation of linearized problem with the use of CPLEX solver, and then generates feasible solution z with the use of sampling method described in Sect. 6. Given binary z, the remaining GAP problem is solved with the use of greedy Algorithm 1, with all prices π _ijp =0 for corresponding z _jp =0.

Optimal solutions for selected problem instances were obtained using general purpose branch and bound method for integer programming, implemented in the CPLEX solver. Unfortunately, for larger data instances the time required to obtain an optimal solution was prohibitive. Their values are presented in the last columns of Tables 2 and 3, along with the values of solutions computed by Algorithms $\mathcal{A}$ and $\mathcal{B}$. The respective approximate running times are also given (the experiments were run on a Blade cluster with 8-core 2.4 GHz 64-bit AMD processors and 8 GB of RAM). Table 2 contains “easy” problem instances, i.e. when parameters h _j =0; in these instances the limited processing capabilities of servers are reflected only in the constraint set (6), and the latency resulting from multiple clients competing for the same server is neglected. Table 3 contains the “hard” instances, with parameter h _j drawn uniformly between 0.1–1.0, reflecting the full generality of the model. These instances required considerably more time to solve.

Table 2 Comparison of solutions computed by Algorithm $\mathcal{A}$ and Algorithm $\mathcal{B}$ for h _j =0, along with respective running times. The last column contains values of optimal solutions

Table 3 Comparison of solutions computed by Algorithm $\mathcal{A}$ and Algorithm $\mathcal{B}$ for h _j >0, along with respective running times. The last column contains values of optimal solutions

For the first set of instances, both heuristics behaved well in practice. With only a few exceptions, Algorithm $\mathcal{A}$ terminated with solutions up to 15 %–20 % worse than optimal. While the Lagrangian relaxation tends to give better assignments and the rounding algorithm tends to find better placements, values of solutions were comparable. For the second set of instances, the quality of obtained solutions was significantly worse, with rounding algorithm performing better on small networks. We also observed that the huge impact on the performance is due to the number of considered objects M, as the obtained solutions tend to get worse with large M even for smaller N.

The main advantage of the rounding algorithm was its speed. Its running time is practically equivalent to the time spent on solving LP relaxation. In contrast, the Lagrangian relaxation algorithm runs much slower, which results from the need for performing multiple iterations, each involving repeated calls to knapsack and GAP subroutines. However, in each iteration it provides increasingly tighter lower and upper bounds on the optimal solution, and a feasible solution corresponding to the upper bound. This allows to stop the execution at any time, and get an intermediary feasible solution.

The scalability of Lagrangian relaxation algorithm is better than the one of randomized rounding algorithm, especially for large M, since the latter generates a linear programming relaxation with very large number of variables and constraints. While Algorithm $\mathcal{B}$ usually generates better solutions for “hard” instances of moderate size, it fails to terminate in reasonable time for both “easy” and “hard” instances of larger size. In contrast, Algorithm $\mathcal{A}$ gives more flexibility, but due to the need of successively performing a number of expensive subgradient steps, it requires significant amount of time to terminate with good solution. Nevertheless, both algorithms can be used for network planning, when no real time constraints are imposed.

8 Conclusions and further work

In this paper we studied the problem of replicated data placement across network and assigning clients in a way to minimize the access latency and at the same time to avoid violation of servers’ capacities. Due to the complexity of the problem, obtaining optimal solutions requires considerable computational effort. Consequently heuristic methods, guided by the results from the theory of approximation algorithms, were proposed. Two decompositions of the problem were examined, leading to different solution approaches. The main advantage of these decomposition is the reduction of structural complexity of the original problem which allows for applying specialized algorithms for solving smaller subproblems.

One of the most interesting directions for future work is decentralized implementation of solution algorithms. Since the considered problem is motivated by the large scale distributed system design, it is natural that the relevant pieces of input data for the solution algorithms are spatially distributed. In such case there are two approaches for dealing with optimization of such system: in a (semi-)centralized way, or in a fully decentralized way. In the former approach, the input data needs to be gathered at one specifically distinguished network node that runs the actual optimization algorithm centrally. Then the result is propagated to the appropriate destination nodes. Variants of this approach include a hierarchical processing of small subproblems on selected nodes, followed by merging the final result. But either way, it relies on the system asymmetry, i.e. a subset of nodes needs to be distinguished. On the other hand, there are many arguments in favor of moving away from the centralized design. Computing locally as much as possible allows to reduce the communication between nodes. Since each node operates on a smaller amount of data (compared to the one central processor operating on whole problem data) the computational requirements are also lower. Moreover, the implementation of decentralized algorithms is usually symmetric, which means that all nodes execute roughly the same program code (on different data). This makes it easier to deploy and maintain such systems, making it possible to perform system reconfigurations (random attachments or detachments of nodes during the execution of algorithm). Additionally, decentralized implementations are naturally reliable, since it is easier to avoid single points of failure.

The study of fully decentralized optimization algorithms is a relatively new field of research. Its roots can be traced back to the works on distributed linear programming, see e.g. Elkin (2004), Papadimitriou and Yannakakis (1993). Although currently several methods for solving restricted classes of linear programming problems in decentralized environments were already developed (e.g. Mosk-Aoyama et al. 2010; Shental et al. 2008), their practical applications are still very limited.