An analytic framework to develop policies for testing, prevention, and treatment of two-stage contagious diseases

Abstract

In this paper we consider healthcare policy issues for trading off resources in testing, prevention, and cure of two-stage contagious diseases. An individual that has contracted the two-stage contagious disease will initially show no symptoms of the disease but is capable of spreading it. If the initial stages are not detected which could lead to complications eventually, then symptoms start appearing in the latter stage when it would be necessary to perform expensive treatment. Under a constrained budget situation, policymakers are faced with the decision of how to allocate budget for prevention (via vaccinations), subsidizing treatment, and examination to detect the presence of initial stages of the contagious disease. These decisions need to be performed in each period of a given time horizon. To aid this decision-making exercise, we formulate a stochastic dynamic optimal control problem with feedback which can be modeled as a Markov decision process (MDP). However, solving the MDP is computationally intractable due to the large state space as the embedded stochastic network cannot be decomposed. Hence we propose an asymptotically optimal solution based on a fluid model of the dynamics in the stochastic network. We heuristically fine-tune the asymptotically optimal solution for the non-asymptotic case, and test it extensively for several numerical cases. In particular we investigate the effect of budget, length of planning horizon, type of disease, population size, and ratio of costs on the policy for budget allocation.

1 Introduction

In this paper we consider spread and containment of contagious diseases. Although the description pertains to humans, the models can be suitably extended to other living beings as well. We state the problem in an abstract manner and do not concentrate on any specific disease, however we restrict our study to two-phase contagious diseases. These diseases are such that when a person contracts the disease, he or she does not show any symptoms in the initial phase but can spread the disease. This initial phase is called the latent stage. In the latter phase of the disease, symptoms may appear and the individual may need to be treated, typically using expensive treatments. The latter phase is usually referred to as the symptomatic stage. If an individual is healthy, shots (usually vaccines) can be administered so that he or she does not contract the contagious disease at least for a period of time. If an individual is in the initial phase of the disease, he or she can be treated inexpensively (as opposed to when the symptoms appear) and can be cautious about not spreading the disease. Notice that individuals that are healthy cannot be distinguished from those that are in the initial stages of the disease, unless tested. The spread of such contagious diseases can be contained by testing individuals, giving shots to healthy individuals and treatment to individuals known to have the disease. The objective of this paper is to devise an algorithm to optimally allocate financial resources for testing, vaccination, and treatment by evaluating their trade-offs across a finite planning horizon.

The main goal of this paper is to present an analytic framework that can be used for a wide range of two-phase contagious diseases. However, for the sake of clarity in exposition, we present a few examples. In particular, AIDS and cervical cancer can be modeled as two-stage contagious diseases where the first stage is contracting the virus and the second stage is getting AIDS or cervical cancer, respectively. Since cervical cancer has received a lot of attention in the media recently, there is a reasonable amount of data available for it and hence we use it for model illustration as well as numerical analysis in this paper. In that light, it is worthwhile to further describe cervical cancer briefly. The cause for almost all patients suffering from cervical cancer is Human Papilloma Virus (HPV) which can be controlled using vaccinations that lasts four years. When a healthy person contracts HPV, there are no symptoms until the person actually gets cancer, a process which may take many years (Cervical-Cancer 2006). Therefore the two-stages of cervical cancer can be thought of as: (a) having HPV but not cancer; (b) having cancer for which treatment is required (such as surgery, radiation therapy, and chemotherapy (Cervical-Cancer-Center 2006)). On the brighter side, treatments for cervical cancer are fairly successful (AICR 2006). However the cost of treatment is significantly higher than many other cancers, such as breast cancer, hence not all patients can afford the treatment (Wolstenholme and Whynes 1998).

Besides cervical cancer and AIDS, there are other examples of such two-stage contagious diseases such as small pox and measles that people and animals are typically vaccinated against. However, it is worthwhile noting that policies from a management standpoint in terms of the spread of these diseases mentioned above have been well established. Where there is a serious shortcoming is in being prepared against newly emerging disease outbreaks in which human beings are infected by agents (such as bacteria or viruses) that spread even before any symptoms are observed. These agents could have a long incubation period (i.e. the time between when an individual is infected to when symptoms appear). In addition, the disease could be communicable (i.e. the agent spreads to other individuals) even during the incubation period. Under these circumstances there is a need to perform quick what-if analysis with limited data to make policy decisions. The major concern is the impact in terms of large-scale testing, vaccination, and treatment that would overwhelm existing resources. We seek to develop a strategy that aims to allocate a constrained budget between testing, vaccination, and treatment subsidy across a finite time horizon.

We develop a methodology for budget allocation that would seek to optimize any objective specified by the policymaker given any Markovian disease spread model. Modeling and analyzing this problem deals with multi-dimensional decision variables under a stochastic-network environment. Thus, it difficult to analyze the system using dynamic programming. There are a relatively large number of states in this system and the transition rates are also dependent upon the state of the system. In essence, the budget allocation problem over a finite horizon is a complex stochastic dynamic program where the objective is to determine the optimal set of actions in each stage of the horizon which is a dynamic control problem with feedback. The contribution of this paper is in not only providing a tool for policymakers to effectively divide a given budget for a specific two-stage disease in healthcare, but also to develop a methodology to handle complex dynamic control problems effectively.

This paper is organized as follows. In Sect. 2 we present a review of the literature pertinent to the problem described above. Further, the problem is presented in detail, along with notations in Sect. 3. In Sect. 4 we characterize the system as a stochastic network under dynamic control with feedback and model it as a Markov decision process (MDP). However due to the curse of dimensionality the MDP is intractable. Therefore we develop an asymptotically optimal solution based on a fluid model of the dynamics to solve the MDP in Sect. 5. We present extensive numerical results to evaluate the model performance on a wide experimental design benchmarking on a cervical cancer case study in the United States in Sect. 6. Then in Sect. 7 we evaluate the impact of various factors to develop insights for policy and healthcare. Finally in Sect. 8 we present our findings and make concluding remarks.

2 Literature review

In this section we present a review of the literature by categorizing it into four phases: historical perspective, modeling, optimization, and recent trends including our main case study of HPV.

2.1 History perspective

Mathematical modeling of epidemic diseases has been an active area of research since the 1920s. A number of statistical models have been developed in order to be able to predict various factors, such as the spread rate of the disease, the number of infected people, mortality rate, etc. within a given time horizon. Early research was mainly devoted to developing deterministic models. This is mainly due to the fact that these models are simpler. Anderson and May (1991) studied various existing deterministic models, along with several applications based on real data. Stochastic epidemic models started to come around with the one proposed by McKendrick (1926). This work was a stochastic continuous time version of the deterministic model proposed by Kermack and McKendrick (1927). Reed and Frost introduced the chain-binomial model (Andersson and Britton 2000). Barlett (1949) studied the stochastic version of the Kermack-McKendrick model. Since then, a substantial amount of research has been done in this field. For example, Gabriel et al. (1990), Bailey (1975) and Anderson and May (1991) are excellent resources that have covered stochastic as well as deterministic models. These sources also discuss the statistical inference and a large number of applications to real data. Further, Daley and Ganni (1999) reviewed the existing stochastic and deterministic models and included statistical inference. Andersson and Britton (2000) provided a summary of stochastic models that are being used in the area. In addition, Diekmann and Heesterbeek (2000) focused on mathematical epidemiology of infectious diseases and used real data for illustrations.

2.2 Analytical models

The most common type of models used for infectious diseases are SIR (Susceptible-Infected-Removed) models, first proposed by Reed and Frost. A mixed population is the basic assumption in that mode there are some infectious individuals (I) and some susceptible individuals (S). During the infectious period, an infective person makes contact with a susceptible individual with a given probability. Different researchers use different methods to obtain this probability, e.g., the contact number as defined by Hethcote (2000). If a susceptible person has contact with the infectious person, he/she becomes infectious and is immediately able to infect other individuals. There is usually a distribution assigned to the duration of the infectious period. An individual is considered removed (R) when he/she becomes immune to the disease after his/her infectious period is over, and plays no further part in the spread of the disease. Newmann (2002) showed that a large class of SIR models of epidemic disease can be solved exactly on wide variety of networks.

2.3 Optimization

Most of the existing models found in the literature deal with obtaining the measures, such as the rate of transmission for the disease. To the best of our knowledge, not many researchers have used the models to optimize scenarios by changing the different probabilities and rates. Some researchers have suggested strategies to minimize the costs at different stages, for example, in developing vaccinations (Wu et al. 2005), or to minimize the cost of examinations (Wein and Zenios 1996). Li et al. (2004) proposed a vaccination program when the total population size is not constant.

2.4 Recent trends in epidemic diseases including HPV

There is extensive research on dynamics of infectious disease transmission. However, each particular disease has a unique behavior; therefore mathematical models can be different. For example, hepatitis B is transmitted shortly after exposure to the virus with severe symptoms (Goldstein et al. 2005). In the case of AIDS, since the virus infection till the time the symptoms appear takes, on average, ten years (Perelson and Nelson 1999). Therefore, a representative mathematical model should be based on the properties of a specific disease while incorporating basic assumption and avoiding unnecessary details. In that light it is worthwhile mentioning that our model in this paper for disease spread is simplistic, however powerful enough to be applicable in a much broader setting.

Probabilistic models (as opposed to statistical models are also focused on pertaining to two-stage contagious diseases. For example, Lipsitch et al. (2003) studied the dynamics of Severe Acute Respiratory Syndrome (SARS) transmission to estimate the infectiousness of SARS as well as possibility of outbreak epidemic after observing an infected case within the susceptible society. They used stochastic simulation to show the robustness of outcomes of the model, such as reproductive numbers.

Elbasha et al. (2007) developed a model to investigate the transmission dynamics of HPV. In their model, they considered a more sophisticated version of SIR model which included demographic and epidemiologic components. They also included seventeen age groups and three levels of sex activity to address the probability of becoming infected realistically. Wodarz and Nowak (2002) developed a mathematical model to study dynamic of HIV spread, its progression, evolution, and effects of different control mechanism. The authors used this mathematical model to target both individual treatment design and social virus control in long term. They used real data to show the effectiveness of their proposed model.

Another important aspect of studying disease control is to choose the most relevant (i.e. cost-efficient) set of actions (controls). Taira et al. (2004) studied the cost efficiency of HPV vaccinations in the United States. They showed that cost efficiency of the HPV vaccination is correlated with the duration of immunity and the vaccination age. Kim and Goldie (2008) studied the cost-efficiency of including boys in HPV vaccination. The results showed that the vaccination age plays an important role in the overall immunity of the society but including boys is not cost-efficient.

Garnett et al. (2006) studied the value of screening (examination) to control infectious diseases. They suggest that a combination of screening and vaccinating is beneficial in disease control. In Sect. 4, we leveraged upon the results of these works to restrict the set of possible actions. Gray et al. (2003) studied the dynamic of HIV transmission in Rakai, Uganda. They used a stochastic simulation model to observe the effect of vaccination and antiviral treatment. They showed that antiviral treatment can reduce the number of infected people, however the treatment alone cannot stop the epidemic since it will result in more infected people in future. They found vaccination to be more effective in controlling the virus transmission than the treatment. Therefore, combination of two may achieve a promising result.

3 Problem description

Consider a large population of individuals. At the beginning, we assume the individuals are in one of the following different states: u ¹: Healthy individuals (susceptible), u ²: Individuals having the disease (first stage) but are unaware of it, u ³: Individuals that are in the first stage of the disease and are conscious of that, and u ⁴: people in the second stage of the disease. Then, we consider a long time horizon (20 years for the cervical cancer and AIDS) and define each year as a period where a decision can be made regarding the number of vaccines, examinations and treatments to be administered. This decision is made at the beginning of the period based on the state of the system (i.e. all individuals taken together). In the beginning of each period, the policymaker must specify an objective that needs to be maximized subject to satisfying some constraints, of which the most important being the budget. The objective function is a function of number of people in different states of the system at different time periods. It also can take into account the number of total effective vaccinations, probability of an individual contracting the disease at the end of the time horizon.

In order to solve this control problem of deciding the number of vaccines, treatments, and testing in each period, it is critical to characterize the dynamics of the system using a stochastic network. We consider different states in the system, where apart from the aforementioned states, we also have states for people who died during the time horizon (u ⁵) and states for people in the different stages of vaccinations (for the cervical cancer case where vaccinations work for four years, v ¹, v ² and v ³ are the states denoting vaccinations done 1, 2 and 3 years ago respectively). In order to keep track of the system dynamics, we also account for the birth process, death process, vaccinations.

An important consideration is that states u ¹ and u ² are indistinguishable. For any policy, a certain number of vaccinations are going to be given to some infected people (these include individuals in u ¹ and u ²). An effective vaccination is the one where the individual getting the vaccination and hence would not contract the disease for the duration of the vaccination effectiveness period (4 years in case of cervical cancer). The vaccination could also be given to people who do not know that they have the disease (i.e. state u ²), but it would be ineffective since they are already infected. Similarly, examinations can be termed effective only if the person actually had the disease (i.e. state u ²), and was not a healthy individual in the susceptible state (i.e. state u ¹). However, while treating a patient in the second stage, the complete information about the state of the person exists. When a person gets treated, they can move to one of the three states: healthy and susceptible or return to first stage of disease.

Aside from the transitions based on our decisions, we also keep track of ‘natural’ flows in the system. Since we are considering a long time horizon, we need to keep track of the births and deaths. All newborns are assumed to go to the healthy state (although this could be easily modified in the model). Independent of the state an individual is in, there is a chance that the person dies of natural causes. These are also taken into consideration in the model.

The probability that a healthy individual gets the disease is dependent upon the number of individuals who actually have the disease, and their awareness level. The people in u ² are more likely to spread the disease as compared to the ones in u ³ and u ⁴. Hence, the probability a healthy individual gets the disease can be given by a function of number of individuals in these three different states. When an individual is in the first phase of the disease, the chance of that person getting to the second stage is dependent upon the person’s awareness level. If individuals know that they have the disease, they can take precautions (and treatments in some cases) to reduce the risk of going to the second stage. Hence, the probability of a person getting to the second stage of the disease is different depending on the person’s knowledge of their condition. In the next section we present a model for analysis and control of the system described above.

4 MDP model for dynamic control with feedback

The aforementioned system is analyzed using a Markov decision process where W _n is the state of the system at the n ^th period. Note that W _n is a vector of the number of individuals in various states and would be described in Sect. 4.2. The decision variable, i.e. action to take in the n ^th period is to determine how many vaccinations (denoted by x _n ), how many treatments (denoted by y _n ), and how many tests (denoted by z _n ) to administer during that period. Let X, Y and Z be T-dimensional vectors denoting the control action in T periods.

The objective is to optimize a function specified by the policymaker in terms of the expected value of the state of the system at the end of each period in the horizon (consisting of T periods): f(E[W ₁],E[W ₂],…,E[W _T ]) with the understanding that the expectation of a vector of random variables is the expected value of the individual elements of the vector. The optimization is subject to

$$c_n^x x_n + c_n^yy_n + c_n^z z_n \le R_n$$

where R _n , $c_{n}^{x}$, $c_{n}^{y}$ and $c_{n}^{z}$ are respectively the total budget, cost of vaccines, cost of treatment, and cost of testing in period n. While solving the problem the budget constraint is usually a binding constraint at which time we denote $c_{n}^{x} x_{n}/R_{n}$, $c_{n}^{y} y_{n}/R_{n}$ and $c_{n}^{z} z_{n}/R_{n}$ as the fraction of budget allocated for vaccines, treatment and testing in period n. By averaging over all n∈[1,T] we obtain the corresponding average values.

The main problem is to determine an optimal control A=(X,Y,Z) that optimizes the specified objective function subject to budget constraints. The optimal control is sequential with feedback, i.e. for n=0,1,2,…,T−1 the problem is to determine the action in the (n+1)^st period A _n+1 = (x _n+1,y _n+1,z _n+1) given W _n (and history which can be ignored if the stochastic process {W _n ,n≥0} is Markovian) for the overall objective across all periods.

4.1 Assumptions

It is critical to note that most of the assumptions are not necessary for the model to work, in fact it would be quite straightforward to change the stochastic network or the optimization problem accordingly. The reason they are described in detail is in order to appropriately interpret the numerical findings as well as to replicate the experiments by other researchers.

• The budget constraint cannot be violated in any period. In addition, any portion of the budget amount not used in a period cannot be transferred to other periods. The consequence of this assumption is that for most objective functions, the budget constraint is binding in every period.

• All treatments are successful, but a person who moves out of the second stage of disease may still end up in the first stage.

• All tests for presence of disease are perfect (no false positives or false negatives).

• Chronological order of events in each period is: vaccination, spread of disease, birth, going from stage one to two, test, treatment, death due to disease, and natural death.

• All newborns are healthy.

• A person in the first stage of the disease and knowing about it is less likely to spread it as compared to the person who does not know that he/she has the disease.

• The persons who know that they have the disease are less likely to get to the second stage as compared to the persons who do not know about their having the disease, since the former is better equipped with knowledge of how to avoid getting to the second stage.

• The only way a person can learn whether he/she is in the first stage of the disease is through examination.

• Only the people who are in the first stage of the disease can go to the second stage.

• All individuals behave rationally, i.e., they would not lose the opportunity to get tested, vaccinated or treated, whichever applies to them.

Thereby using the above assumptions, we now model the system using a Markov decision process.

4.2 Markov decision process

Since each person in the population under consideration within each period can be in one of eight possible states, we define the following notations. Let $U_{n}^{1}$ be the number of healthy persons that are not vaccinated in the n ^th period (corresponding to being in state u ¹). Similarly, define $U_{n}^{2}$, $U_{n}^{3}$, $U_{n}^{4}$, $U_{n}^{5}$ $V_{n}^{1}$, $V_{n}^{2}$ and $V_{n}^{3}$ respectively as the number of people in the n ^th period in stage-1 of the disease and are unaware of it, in stage-1 and are aware of it, in stage-2, dead due to disease, healthy and vaccinated in the previous period, healthy and vaccinated two periods ago, and healthy and vaccinated three periods ago (this model illustrates HPV-based cervical cancer where the number of periods for vaccination effectiveness is 4; however for other diseases the number would have to be suitably modified). Therefore the system state in the n ^th period for HPV-based cervical cancer disease (W _n ) is an 8-dimensional vector

$$W_n = \bigl(U_n^1, U_n^2,U_n^3, U_n^4,U_n^5, V_n^1,V_n^2, V_n^3\bigr).$$

By modeling W _n , we ensure the Markov property. Therefore in order to determine A _n+1, the action in the (n+1)^st stage, we only need W _n . In addition, to determine W _n+1 only W _n and A _n+1 would suffice. The transition probability function is given by:

where q _b (b) is the probability that there are b births (or new entrants), q _t (k;z _n+1,i ₁,i ₂) is the probability that k out of the z _n+1 tests were administered on the i ₂ individuals, q _v (ℓ;x _n+1,i ₁+i ₈) is the probability that ℓ of the x _n+1 vaccines were given to the i ₁+i ₈ healthy individuals, q _s (m;i ₁+i ₈−ℓ,i ₂−k) is the probability that out of the i ₁+i ₈−ℓ healthy individuals m get the disease, q _r (t ₂,t ₃;i ₂−k,i ₃+k) is the probability that t ₂ people get removed from having the disease out of the i ₂−k individuals who do not know that they have the disease, and t ₃ people get removed from having the disease from i ₃+k individuals who know that they have the disease, q _h (y _n+1−α ₂−α ₃,α ₂,α ₃;y _n+1,i ₄) is the probability that of the y _n+1 treatments, α ₂ people still have the disease in the first stage and do not know about it and α ₃ people know that they still have the disease but in the first stage, q _n (d _c ;i ₄) is the probability that d _c people die due to the disease among the i ₄ number of second stage carriers, q _d (⋅) is the probability of the number of deaths in each state given the number of people in the respective state, and q _c (j ₂,j ₃;i ₂,i ₃) is the probability that j ₂ people got the second stage of the disease among the i ₂ people who do not know they are in the first stage and j ₃ people got to the second stage of the disease from the i ₃ people that know they are in the first stage. It is possible to obtain formulae for the probabilities: q _b (b), q _t (k;z _n+1,i ₂), q _v (ℓ;x _n+1,i ₁+i ₇), q _s (m ₁,m ₂;i ₁+i ₇−ℓ,i ₃+k,i ₂−k), and q _c (j ₁,j ₂;i ₂,i ₃) in terms of the following parameters: p _v =a ₂ i ₂+a ₃ i ₃+a ₄ i ₄ which is the probability of getting the disease, p _c2 which is the probability of getting to the second stage of the disease when the person does not know he/she is in the first stage, p _c3 which is the probability of getting to the second stage of the disease when the person knows he/she is in the first stage, p _d−cancer which is the probability of death due to second stage, p _d−nat which is the probability of natural death, p _birth which is the probability of birth, p _r1 which is the probability of recovery from stage one for a person that does not know they are in stage one, p _r2 which is the probability of recovery from stage one for a person that knows they are in stage one, p _y2 which is the probability of being treated for second stage and move to first stage but not knowing, and p _y3 which is the probability of being treated for second stage and move to first stage while being aware.

Remark 1

Although it is possible to formulate the problem as an MDP, the difficulty is in solving it. Due to the curse of dimensionality, this MDP is indeed intractable. None of the standard techniques such as value iteration or policy iteration (see Puterman 1994) can be employed to obtain the optimal actions for any given state vector in a reasonable amount of time.

As a result we propose an asymptotically optimal solution based on a fluid model of the dynamics of the resultant stochastic network in the next section.

5 Asymptotically optimal solution and implementation

The problem studied in this research belongs to a class of control problems in stochastic networks that are difficult to solve. It is well documented (see Bauerle 2000) that such problems are mainly solved by converting them into their corresponding fluid optimization problem (i.e. the equivalent deterministic control). Although such a conversion appears to be an approximation, they are indeed asymptotically exact. In other words if we let the number of individuals in the various states be extremely large (more precisely let the number approaches infinity) then the optimal policy converges to the equivalent deterministic control problem. Therefore the policy is known as asymptotically optimal solution obtained by taking the fluid limit (also called fluid scaling).

It is worthwhile to explain the fluid model using a simplified example. Consider a population with N individuals of which a fraction α is given the vaccine (assume they are 100% effective). If p is the probability that each of the non-vaccinated individuals gets the disease during a year, then the fraction of individuals affected is according to a binomial distribution with mean (1−α)p and standard deviation $\sqrt{(1-\alpha)p(1-p)/N}$. As N→∞, this fraction converges to the deterministic quantity (1−α)p and the standard deviation converges to zero. When N is finite, the fluid model would predict that after a year the number of individuals affected by the disease is N(1−α)p.

One of the main benefits of fluid models is that they are easy to solve. However in this paper the deterministic optimal control problem is itself difficult to solve mainly because the resulting mathematical program is such that the objective function cannot be written as a closed-form algebraic expression of the decision variables. But the rationale behind using the asymptotically optimal policy in this paper is that the population is indeed large and we conjecture that the policy would be fairly accurate. However, we propose an adjustment to the policy to further improve the quality of the solution.

Before further describing the fluid model and its adjustment, we should introduce the notion of feedback control and control without feedback. Notice that the MDP formulation in Sect. 4.2, is a stochastic optimal control problem with feedback and the corresponding fluid model can be thought of as an optimal control problem without feedback (as there is no uncertainty in terms of the state of the system in the deterministic case). The feedback would not provide any new information in the decision-making process since the dynamics are deterministic. However, in the real system the feedback would be somewhat different than what is predicted and hence we need an algorithm to adjust based on the feedback. In summary, we consider a fluid model where the aim is to obtain a dynamic control without feedback. In other words, the set of control actions A=(X,Y,Z) can be set a priori and they depend only on the knowledge of the initial system state W ₀ (and other states W _n for n=1,2,…,T are known only probabilistically). A major portion of the approximate analysis description would revolve around this dynamic control problem without feedback. However toward the end of this section we describe how to extend this to the case of dynamic control with feedback as a sequential approximation (see Sect. 5.3).

Even for the optimal control without feedback, it is extremely difficult to write the objective function as a closed-form algebraic expression in terms of the decision variables, i.e. X, Y, and Z. However for a given set of X, Y, and Z values, it is possible (although not straightforward) to obtain the objective function. We take advantage of this observation to develop our approximate algorithm. In particular, we select a meta-heuristic to efficiently search through the space of all possible values of X, Y, and Z. One of the key requirements for the meta-heuristic is an engine that would evaluate the objective function for a given (X,Y,Z). This is depicted in Fig. 1. Our goal in this paper is to select an appropriate meta-heuristic and to develop alternative methodologies to evaluate the objective function (i.e. objective function evaluating engine) for a given set of X, Y and Z values. These tasks are addressed in the next two sub-sections (viz. 5.1 and 5.2) respectively.

Fig. 1

Meta-heuristic and objective function evaluation engine

5.1 Meta-heuristic selection: genetic algorithm

Genetic algorithm is one of the most applicable methodologies for analyzing large scale systems. Since the approach is well-studied in the literature and due to page limitations, we do not provide a description of the algorithm or the jargon used therein. The reader is encouraged to refer to articles such as Whitley (1994). In this specific implementation of genetic algorithm, we have a population of chromosomes, or solutions, consisting of values for our three T-dimensional decision variables: Number of vaccinations (X), number of treatments (Y), and number of examinations (Z). Each chromosome can be evaluated for its ‘fitness’ by computing the objective value using one of the techniques we describe (in Sect. 5.2).

In summary, we generate the population for each of the generations. Each chromosome is evaluated for its fitness and subsequent generations obtained from this generation. This process is repeated for a large, pre-specified number of generations. From the first generation, we store the best solution as the incumbent solution and at the end of the run, obtain it as the best solution, which is expected to be close to the optimal solution.

For this implementation, we used the following parameter values: population size is 100, number of generations is 1000, separation is 10, distance factor is 0.1, and number of periods is 20. Crossovers and mutations account for 90% of the chromosomes for the new generation. We pick the top one-fifth of the chromosomes for mutation.

5.2 Determining the objective function value

The crucial item required for the genetic algorithm in Sect. 5.1 is an engine for evaluating the objective function value for a given action (X,Y,Z) as described in Fig. 1. In order to evaluate the objective function value f(E[W ₁],E[W ₂],…,E[W _T ]) we need to obtain E[W ₁],E[W ₂],…,E[W _T ] values given the initial state W ₀ and action (X,Y,Z). Since the approximation does not use any feedback, it is possible to evaluate the objective function with just the initial state and action which is generated by the genetic algorithm. We describe three techniques to evaluate E[W ₁],E[W ₂],…,E[W _T ], namely, deterministic analysis (Sect. 5.2.1), individual Markov chains (Sect. 5.2.2), and simulation (Sect. 5.2.3). The three techniques would converge asymptotically as the number of individuals in each state approaches infinity for the first two and the number of replications besides the number of individuals approaches infinity for simulation. Therefore, although the techniques are indeed approximations, the conditions for the problem domain are conducive for asymptotic analysis as the population is large and simulation replications for large populations (due to central limit theorem and strong law of large numbers) are doable. However the main reason we present various techniques is for broader considerations (such as for different population numbers, other diseases, other types of stochastic networks, generic MDPs, etc.). In addition to the three techniques, we also present bounds (best case and worst case) for the objective function value in Sect. 5.2.4.

5.2.1 Deterministic analysis

The deterministic analysis is an approximation where the state of the system is known deterministically at the beginning of each period. In particular, given the state at the beginning of a period and the action during that period, the state of the system at the beginning of the next period is approximated as its expected value (rounded off to the nearest integer). As a result, the analysis is reduced to a deterministic dynamic programming problem. However we continue to use the genetic algorithm to generate candidate solutions and search through the solution space.

Mathematically, the deterministic analysis is explained as follows. The state of the system at the beginning of the (n+1)^st period, W _n+1, given W _n and the action during the n+1^st period A _n+1=(x _n+1,y _n+1,z _n+1) is approximated as

Therefore for a given action set (X,Y,Z) and initial state W ₀, we obtain E[W ₁]. To obtain E[W ₂] given W ₁ and the action during that period, we approximate by using E[W ₁] instead of all possible values of W ₁. In this manner we recursively obtain E[W ₂],E[W ₃],…,E[W _T ]. As an example, we can compute $E[U_{n+1}^{1} | W_{n} = (i_{1}, i_{2}, i_{3}, i_{4}, i_{5},\allowbreak i_{6}, i_{7}, i_{8}),A_{n+1} = (X_{n+1}, Y_{n+1}, Z_{n+1})]$ as

Thereby, using the deterministic approximation we evaluate the objective function f(E[W ₁],E[W ₂],…,E[W _T ]).

5.2.2 Individual Markov chains

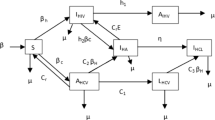
Instead of modeling the system for the entire population, we can also model the passage of each individual through the various possible states: u ¹, u ², u ³, u ⁴, u ⁵, v ¹, v ², and v ³. The state an individual is within a particular period can be modeled as a Markov chain with 8 elements (i.e. the 8 states mentioned earlier for the HPV-based cervical cancer in Sect. 4.2) in its state-space. The transition diagram is described in Fig. 2. Let P _n be the one-step transition probability matrix for the n ^th stage. Since it is straightforward to express P _n from the transition diagram, we do not explicitly present it here.

Fig. 2

Transition diagram for an individual

Note that the Markov chain is not time-homogeneous and that is why there is a subscript n in P _n . This is because some of the transition probabilities depend on the number of people that are present in each state and as this number changes from stage to stage, so does the transition probability matrix. We consider two approximations to estimate P _n given the action (X,Y,Z). The first approximation uses the initial number of individuals in each state across the horizon which can be computed easily and thereby P _n becomes independent of n. The second approximation uses the deterministic analysis in Sect. 5.2.1 to estimate the average number of individuals in each state in each stage.

Then using the P _n matrices and knowing the number of individuals in each state initially, one can obtain the average number of individuals in each state in every stage. For the first method we can just use $P_{1}^{20}$ and for the second method we need P ^∗=P ₁×P ₂×⋯×P ₂₀. Also, using the number of new individuals that enter the system at stages other than the first stage, they also can be included in the computation (by considering the right stages in the analysis). Thereby we obtain E[W ₁],E[W ₂],…,E[W _T ] which can be used in the objective function.

5.2.3 Simulations

We consider Monte Carlo simulation as another alternative to evaluate the objective function. In particular, using the initial state W ₀ and action (X,Y,Z), we generate sample realizations of W ₁,W ₂,…,W _T and statistically estimate the values of E[W ₁],E[W ₂],…,E[W _T ], and thereby obtain an estimate of the objective function f(E[W ₁],E[W ₂],…,E[W _T ]). The simulations also enable us to get estimates of Var[W ₁],Var[W ₂],…,Var[W _T ].

From an implementation standpoint, in order to obtain a small confidence interval with high level of confidence, we ran 1000 replications (i.e. sample realizations) of W ₁,W ₂,…,W _T . For that we needed a fast way to simulate the transitions as Bernoulli trials for each individual in the population are computationally tedious. Therefore, assuming that the number of people in each state is large (using Central Limit Theorem) we generate transitions by sampling from a Normal distribution (however, Poisson distribution would have also sufficed since in the limit the binomial distribution converges to Poisson). We use the Box-Muller formula for generating the samples as described in Banks et al. (2005).

5.2.4 Bounds

Note that it is not possible to distinguish between people in states u ¹ (healthy and no vaccination) and u ² (in first stage but do not know). Vaccinations and tests are provided to people in both states. For a given policy (X,Y,Z) we study the best possible scenario (vaccines are administered to people in u ¹ and tests to people in u ²) and the worst possible scenario (vaccines are administered to people in u ² and tests to people in u ¹). By comparing against the best-case and the worst-case scenarios, we can study the impact of having complete information and wrong information.

5.3 Incorporating feedback

So far we have assumed there is no feedback. The genetic algorithm together with the objective function evaluation engine will produce an action set (X,Y,Z) for a given initial state W ₀ and no other information (such as feedback). However, consistent with standard MDPs, it is possible to obtain W ₁,W ₂,…,W _T values by sampling the population at the end of each period. We propose an algorithm to incorporate the feedback that is obtained periodically over time.

In order to determine the action in the n+1^st period (i.e. A _n+1=(x _n+1,y _n+1,z _n+1)), given the state at the beginning of that period (i.e. W _n ), we solve the approximation without feedback for the remaining T−n periods and choose the prescribed action for the first of those periods, namely, A _n+1. Therefore at the beginning of each period the approximation without feedback is performed as though the current state is the initial state and the horizon is the number of periods that are remaining. We describe the algorithm using a flow chart in Fig. 3.

Fig. 3

Flow chart of the proposed algorithm

6 Numerical results: modeling perspective

We divide the numerical experiments into two categories. First we focus on the modeling aspects in this section and in Sect. 7 we evaluate the impact of various factors on healthcare and policy issues. We perform several numerical evaluations to (a) analyze the resulting control action between dimensions and across the horizon, (b) implement various objective functions, (c) compare the different engines for objective function evaluation, (d) study the effect of the main constraint by considering different budgets, (e) contrast the policies obtained by considering feedback against those that do not consider feedback, and (f) understand requirements in terms of computational time and effort for the various approximation schemes. In order to not clutter graphs and also to avoid being repetitive, we divide up the evaluations into categories and only present a subset of the results.

As an example of a two-stage contagious disease, we consider a case study of HPV-based cervical cancer. However, we would like to make a few disclaimers. It is crucial to notice that the objective is only to illustrate the type of policy decisions that are possible using this research study. In practice one would require excellent estimates of various quantities and a more appropriate disease spread model than what is considered in this example. Further, notice that we have tried to obtain as realistic estimates as possible for the numerical values for the parameters described in Sects. 3 and 4. Next we present the parameter values and describe the sources (if estimated) or a clarification regarding how they were obtained.

We consider the entire population in the United States with the understanding that it is purely for illustration purposes and not a suggestion for either the level at which policymaking must take place or the type of diseases this model can be applied to. We predominantly use HPV and cervical cancer statistics provided by Center for Disease Control and Prevention in years 2005 and 2006 (HPV-Associated-Cancer-Statistics 2006). Based on the U.S. Census Bureau data (US-Census-Bureau 2006), the population of the United State was 298,444,215 in 2006. Of that, 170,113,202, were female and about 65% of the female population was between the age of 12 and 60—most likely to be susceptible to HPV. As a result we approximate the initial susceptible population (i ₁) to be 100 million. Note that we exclude men from our model (AMCHP-Fact-Sheet 2006).

The number of people who have HPV, whether they are aware of it (i ₂) or not (i ₃) is estimated to be 18 million (HPV-Statistics 2006), i.e. i ₂+i ₃=18,000,000. For the purpose of our simulations we arbitrarily use i ₂=10,000,000 and i ₃=8,000,000 but assume only i ₂+i ₃ is known for our analysis. It is estimated (Cervical-Cancer-Statistics 2006) that about 25,000 HPV-associated cancers had occurred each year in the period between 1998 and 2003. As a result, the number of women with cervical cancer (i ₄) in 2006 would have been between 250,000 to 500,000 (CRI 2006). For our computations we use the overestimated value of 500,000. Further, it has been estimated that 6.2 million new HPV infections occur each year (HPV-Statistics 2006). Hence as an initial estimate for the probability of becoming infected by the virus p _v =6.2/(0.65×170113202)=0.056.

We allow p _v to change from one year to another based on the number of individuals during that year that have the disease. To capture the dynamics of the disease spread we define a linear model so that if i ₂, i ₃, and i ₄ are as described above during any year then there exists constants a ₂, a ₃, and a ₄ such that the probability of becoming infected by the virus for a susceptible individual is p _v =a ₂ i ₂+a ₃ i ₃+a ₄ i ₄. We arbitrarily choose a ₂=7×10⁻⁹ and a ₃=a ₄=7×10⁻¹². Next we describe other measures used in the transition probabilities from one year to another.

It is important to realize that cervical cancer was one of the most common causes of cancer-related fatalities for American women. Then, between 1955 and 1992, the cervical cancer mortality rate declined by 74% and continues to decline by nearly 4% each year (CRI 2006). On average, cervical cancer will lead to the death of 4,000 women in the USA and 12,000 new cases are diagnosed each year (Cervical-Cancer-Statistics 2006). We use this data to realistically measure the transition probabilities as: p _c2=0.00006, p _c3=0.00004 and the probability of dying from cervical cancer as p _d−cancer =0.03. We arbitrarily assume the recovery probabilities as p _r2=0.02, p _r3=0.04, p _y1=0.6, p _y2=0.3, p _y3=0.1. Note that the latter probabilities are relatively high, due to the high chance of recovering from HPV and success of surgical treatment of cervical cancer (Cervical-Cancer-Treatment 2006). We would like to particularly emphasize that we consider a wide range for the population of women with HPV to account for the inherent uncertainties in this number, mostly due to the declining rate of diagnosis of cervical cancer and the declining rate of cancer-related mortality.

Further, the birth (p _birth ) and natural death (p _d−nat ) probabilities in 2006 have been estimated to be 0.012 and 0.006 respectively, based on CDC statistics (Birth-Data 2006). Also, in terms of the costs, we assume that a single vaccination costs $90–$125 in 2006 (HPV-Vaccine 2006), a test costs between $40 and $50 (OBGYN 2006), and a cervical cancer treatment runs about $7,000 to $24,000 per woman (Cervical-Cancer-Treatment 2001). Using that we chose vaccination costs as c ^x=90, treatment cost as c ^y=8000, and testing cost as c ^z=40. Finally, we arbitrarily choose w ₀=0.25, w ₁=0.1, w ₂=−0.2, w ₃=0, w ₄=−0.5, w ₅=−8 as weight coefficients in the objective function—more details in Sect. 6.2.

We present the results of the numerical evaluations as follows: first we consider a static policy in Sect. 6.1, then we describe results for dynamic policy without feedback in Sect. 6.2, and finally we present results for dynamic policy with feedback in Sect. 6.3. While we describe the details of the above three categories later, we should point out here that the objective functions for the three categories are not chosen to be the same. This is done intentionally to clarify that our contribution is not in selecting an objective function, but if the policymaker provides an objective function of the format f(E[W ₁],E[W ₂],…,E[W _T ]) and other input data, then our tool will prescribe a policy (or control action) that should be taken.

6.1 Static policy evaluations

As described above, the first of the three categories that we consider is the static policy. Here we impose a constraint on the problem described in Sect. 3. We require that the control policy in each period be the same. The motivation for this comes from the fact that the policymaker may be inclined to announce publicly what control action he/she proposes (and many times it appears reasonable if the action is uniform in each year). It is important to note that this restriction implies that there is no feedback and the policy is made upfront. Although this is significantly different from what is described in Sect. 3, the reason it is presented before the other categories that are much closer is that our intention is to describe results in an order where the objective function value improves with the categories.

For this set of experiments we use the objective function $f(E[W_{1}], E[W_{2}], \ldots,\allowbreak E[W_{T}]) = (E[W_{T}] - E[W_{T}']) \cdot [w_{1} \; w_{2} \; w_{3} \; w_{4} \; w_{5} \; w_{0} \; w_{0} \; w_{0}]$ for T=20 years where w _i are given weights and $E[W_{T}']$ is the state of the system under the “do nothing” policy. The “do nothing” policy corresponds to giving zero vaccinations, zero treatments and zero testing (in other words zero budget). Essentially this objective is a weighted function of the improvement in each state between the do nothing policy and the static policy. The objective function translates to the following (for T=20)

$$\sum_{i=1}^5 w_i \bigl(E\bigl[U_T^i\bigr]-E\bigl[U_T^{'i}\bigr]\bigr) + \sum_{t=1}^Tw_0 E\bigl[V_t^1\bigr].$$

We first study the objective function obtained using the three methods: deterministic, individual Markov chains (using both P ²⁰ as well as the product of P _n values), and simulation as described in Sect. 5.2. In Table 1 we compare the objective function values for various budgets using the three methods (although there are four columns, the last two correspond to the same “method”). Note that these are indeed the optimum objective function values generated by the genetic algorithm. From the analysis it is evident that the objective value obtained using simulation is always close to the that using the deterministic approximation. The individual Markov chain methodology produces results are close to the simulation values (but not as close as the deterministic analysis). Although the simplest to implement and the fastest, the individual Markov chain model with the approximate P matrix which is raised to higher powers was not as close as the others. Note that similar results in terms of the performance of the simulation, deterministic analysis, and individual Markov chains were obtained for the dynamic policies both with or without feedback (these corresponding results are not presented in the results section for the dynamic policies).

Table 1 Objective function for static control for various budgets

Next we present the results for the bounds described in Sect. 5.2.4 in Fig. 4. In particular the bounds are obtained using the worst case and best case of administering of vaccines as well as tests. Clearly, significant benefits can be obtained with additional information and significant losses would be incurred if erroneous information is used. The results are similar for the dynamic policies as well and hence are not presented in that section.

Fig. 4

Objective function, best case and worst case versus budget

Finally, for the static policy where the control action is identical in every period, it is easy to tabulate the policy for various budget values. The results are presented in Table 2. In that table, note that X, Y, and Z respectively denote the number of vaccines, number of treatments and number of tests in every period for each budget value. It is encouraging from a fairness standpoint to note that the resulting policy implements the action over all three domains (and not just one, although such all-or-none policies are fairly common in other applications).

Table 2 Policies for static control for various budgets

6.2 Dynamic policy without feedback

The second of the three categories that we consider is the dynamic policy without feedback. Here we do not impose any constraints such as in the static policy. However we do not use feedback. Therefore this does not describe the final step of the approximation when using feedback. For this set of experiments (and those in the next section which deals with dynamic policy with feedback) we use the objective function $f(E[W_{1}], E[W_{2}], \ldots, E[W_{T}]) = \frac{1}{T}\sum_{n=1}^{T} (E[W_{n}] - E[W_{n}']) \cdot [w_{1} \; w_{2} \; w_{3} \; w_{4} \; w_{5} \; w_{0} \; w_{0} \; w_{0}]$ for T=20 years where w _i are given weights and $E[W_{T}']$ is the state of the system under the do nothing policy. This objective is a weighted function of the improvement in each state between the do nothing policy and the dynamic policy. In terms of the number of people in various stages, the objective function translates to:

$$\frac{1}{T} \sum_{t=1}^T \sum _{i=1}^5 w_i \bigl(E\bigl[U_t^i\bigr]-E\bigl[U_t^{'i}\bigr]\bigr) + \sum_{t=1}^Tw_0 E\bigl[V_t^1\bigr].$$

We first analyze the effect of dynamic policy on the action space over time. We arbitrarily pick a budget value of 1 Billion units for the analysis (with the understanding that for other budget values the results are more or less similar). In Table 3 we illustrate the vector of X, Y, and Z values for this dynamic policy without feedback. The policy is indeed dynamic and the results appear to be different at the extremes (than in the middle periods). This is due to the fact that the horizon is finite and the policy could be potentially different near the start and finish.

Table 3 Dynamic policy vectors for 1 billion budget

Next we compare the dynamic policy without feedback against the static policy. Although there is merit in announcing a “static” policy for vaccination, treatment, and tests, the dynamic policy possibly produces better results. For this purpose we compare the objective function for the dynamic policy against the static policy for various budget values as shown in Fig. 5. There is a significant improvement in the objective (higher value is better) when the static constraint is removed.

Fig. 5

Objective function for static versus dynamic policies for various budgets

Finally we compare the actions for the dynamic policy in each period against the static policy. Across different periods we plot the number of vaccinations (X), number of treatments (Y), and number of tests (Z) respectively in Figs. 6, 7 and 8. The figures present the policies for both static as well as dynamic policy without feedback.

Fig. 6

Number of vaccines in each period, static vs. dynamic policies

Fig. 7

Number of treatments in each period, static vs. dynamic policies

Fig. 8

Number of tests in each period, static vs. dynamic policies

6.3 Dynamic policy with feedback

The last of the three categories that we consider is the dynamic policy with feedback. This essentially is the complete approximation to the MDP described in Sect. 5. For this set of experiments we use the same objective function as in Sect. 6.2.

We first analyze the effect of dynamic policy with feedback on the objective function for various budgets. Table 4 contains the objective values (in 1000’s) for the static policy, dynamic policy without feedback and dynamic policy with feedback. The dynamic policy with feedback is indeed better than without feedback but not significantly. It can be concluded that the additional complexity due to obtaining the state information does not result in significantly stronger numerical results.

Table 4 Objective function for various policies for different budgets

Next we compare the control policy of the various policies. In particular, we plot the average number of vaccinations, average number of treatments and average number of tests in each period. This is done in Fig. 9. The control actions even after averaging are reasonably different for each policy.

Fig. 9

Comparing static, dynamic without feedback and dynamic with feedback policies

7 Numerical experiments: evaluating impact for policy and healthcare

In this section we design experiments to evaluate the performance of our model with respect to several factors including (a) comparing against existing HPV vaccination policy, (b) contrasting our model for HPV and HIV AIDS, (c) judging the impact of time horizon, (d) impact of cost ratios, and (e) population size. For these experiments we stick to the following modeling considerations: The objective function is $f(E[W_{1}], E[W_{2}], \ldots, E[W_{T}]) = \frac{1}{T}\sum_{n=1}^{T} (E[W_{n}] - E[W_{n}']) \cdot [w_{1} \; w_{2} \; w_{3} \; w_{4} \; w_{5} \; w_{0} \; w_{0} \; w_{0}]$; the budget is 5 million; objective function engine is chosen to be simulation; dynamic policy with feedback is used for all the results. In addition, all the HPV parameters are identical to that in Sect. 6, Table 5 describes the baseline case and the various factors that would be changed in each of the experiments. For example in Sect. 7.3 we will use all the baseline cases but try a horizon of 5 years besides 20 years to evaluate its impact on the policy.

Table 5 Scope of design of experiments

7.1 Impact of policy

The state of the literature suggests that seventy percent of eligible population be vaccinated (Garnett et al. 2006). A natural question to ask is: what if the budget required to vaccinate 70% of the eligible was available to allocate among examinations, vaccinations, and treatment subsidy? We seek to evaluate the effect on the objective function by comparing that for our model versus the state of the literature. It is crucial to notice that the choice of objective function will not affect the validity of the developed methodologies.

Figure 10 illustrates a comparison of the objective function where static policy refers to the state of the literature and dynamic policy refers to our proposed policy. There is over 30% improvement in the objective function by incorporating our proposed policy which is by all means extremely significant. Although we do not present the budget allocation, our results suggest a more balanced allocation for testing, vaccination and treatment subsidy as opposed to investing only in vaccination. Understandably for HPV although the testing is included for free in most health plans, this paper suggests providing financial incentives to go perform the examinations (which is more crucial than vaccinating most of the eligible population).

Fig. 10

Comparing the existing policy versus that proposed in this paper

7.2 Comparing HPV with HIV

Besides cervical cancer caused by HPV, another two-stage disease is AIDS caused by HIV. The question we seek to address is if the budget allocation for examinations, vaccinations, and treatment subsidy would be any different for the two diseases. It is critical to understand a few nuances with respect to HIV. First of all there is not a 100% effective vaccine against HIV (efficiency is 25–75% (Gray et al. 2003)). Secondly, although we have kept several model parameters similar (population, budget, etc.), there still are differences between HPV/Cervical-Cancer and HIV/AIDS. The main differences are: There is higher chance getting AIDS after having the HIV than getting cervical cancer after being infected by HPV; The most common treatment for cervical cancer is by surgery (more costly) which is a one-time action, however in the case of AIDS the treatment is over time and by using drugs (less costly); The HPV vaccine is effective for 4 years and after that it should be repeated, but for HIV the chance of immunity is low but it remains for longer time. Based on these conditions, we compare our budget allocation policies for HIV and HPV.

For HPV we used the same numerical values as stated in Sect. 6, however for HIV we use (source: AIDS-Vaccine-Initiative 2009): a ₂=5×10⁻¹⁰, a ₃=5×10⁻¹², a ₄=5×10⁻¹², p _c2=0.0005, p _c3=0.0003, p _y2=0.006, p _y3=0.005, i ₁=100000000, i ₂=10000000, i ₃=8000000, i ₄=500000, i ₅=0, c ^x=150, c ^y=2500, and c ^z=200. Also parameters that are identical to the HPV case are not reported above.

Figure 11 shows the average fraction of budget allocated for vaccination, examination, and treatment per year. The average is computed over the 20-year horizon for both cases of HIV and HPV. Based on the results in Fig. 11, we conclude that in the case of HPV the policy assigns more of the budget to vaccination, whereas for HIV more of the budget is assigned to treatment and testing. One reason is that the HIV vaccinations are not as effective and the other means of preventing the spread appear to be more effective. Because of space limitations we only show the baseline case of HPV for the remaining experiments emphasizing that the qualitative conclusions for the other factors are fairly similar for HIV ad HPV. The only interesting finding we would like to present is that the vaccination is more favored when the population is larger.

Fig. 11

Comparing the policies for HPV-Cervical cancer against HIV-AIDS

7.3 Impact of planning horizon

For policymakers a critical decision-making paradigm is the horizon to consider for the policies. In order to address that issue we consider two planning horizons and compare the policies for them: 20 years and 5 years. An interesting result from a modeling standpoint that is that as the planning horizon becomes shorter, the difference between having feedback and not having the feedback in dynamic policy becomes more significant (since in a long horizon we anticipate deviations from predicted states to average out). We evaluate by comparing the policy for 5 versus 20 years in Fig. 12 which shows the effect of length of planning horizon on the policy. Note that only the first five bars in the charts since that is the place the two policies can be compared.

Fig. 12

Comparing the effect of planning horizon of 20 versus 5 years on (a) testing, (b) treatment and (c) vaccinations

Our findings indicate the following: in the case of short horizon, treatment plays a more important role and in fact most of the budget goes into treatment. But when the horizon is longer vaccination becomes more important because it helps to reduce the overall cost in future. In other words, longer horizon emphasizes on the value of future, which is exactly the reason for vaccinating. We compare the graphs, in the first 5 periods the short horizon model assigns most of the money to treatment whereas in long term horizon a significant portion of the budget was allocated to vaccination in the first 5 periods.

7.4 Impact of cost ratio

As mentioned before the examination cost can be thought of an incentives for citizens to perform tests, it is worthwhile to see the effect on policy for various examination costs. We use the ratio of examination cost to the vaccination cost. As illustrated in Fig. 13, the ratio increases to 0.8 (meaning the cost of examination is close to vaccination cost), there are more vaccination. Since the basic reason of having examination is preventing the cost of vaccination when it is not efficient, if their costs are similar it is clear that vaccinations would be better.

Fig. 13

Evaluating the impact of the ratio of examination cost to vaccination cost

We observe in Fig. 13 that the effect of the ratio is not smooth. Instead of fixing the vaccination cost and just changing the examination cost (which would have resulted in a smooth curve), we emphasize that besides the ratio, the individual cost parameters are also crucial. Therefore the figure shows the effect on number of vaccination and examination as the cost ratio (exam/vaccine) increases. The reason that the number of examination does not converge to zero even when it costs more than vaccination is that examination has two other advantages in our model: the people who know they have the virus have a smaller chance of getting cancer (they can take better care) and also a better chance of recovering.

7.5 Impact of population

We also study the effect of population size on the policies. In particular, we study the impact of population size on how the budget is allocated among the three dimensions: testing, vaccination and treatment. From Fig. 14 it is apparent that when the population size is large, the budget is relatively evenly spread between testing, vaccination and treatment. However, when the population size is not as large (small is still over 50,000) it appears as if it would make more sense to spend more on treatment than either of the other two options. From a policymaking standpoint this is interesting if we consider small nations or small populations with little or no interactions with the rest of the world.

Fig. 14

Comparing the policies for large and small sized populations

8 Concluding remarks

In this paper we study policies for budget allocation to prevent and cure two-stage contagious diseases. The methodologies developed in this paper, are independent of the choice of objective functions and can be adapted to variety of real world policy making decisions. The decision-support tool would also need appropriate parameters as well as model for disease spread which would typically be provided by epidemiologists. Further, to make our recommendations, we formulate a Markov decision process (MDP) problem to obtain the optimal dynamic control with feedback. However since solving the MDP is computationally intractable, we use an asymptotic optimal policy based on a fluid model of the stochastic network dynamics. This results in dynamic policies without feedback that we iteratively solve for the feedback case as information rolls in. The paper uses a genetic algorithm which heuristically searches through the space of possible actions and evaluates the objective function value for each candidate action. One of the contributions is the development of methods to characterize the objective function value for a given action vector.

8.1 Implementation

Due to the large state and action space for the MDP, we implement meta-heuristic methods using genetic algorithm combined with an evaluating engine as shown in Fig. 1. The evaluating engine step in all cases takes less than a second in total for the entire computation. However, the genetic algorithm part depends on the policy. In our experiments the static policy took an average of 13 seconds using the deterministic methodology whereas 25 seconds on average with simulations. The dynamic policy without feedback was only fractionally slower. For that the deterministic version took 15 seconds and the simulation methodology took 27 seconds on average. However, the dynamic policy with feedback which only runs as a simulation took about 8300 seconds on average, although it could take up to a day in the worst case. Further, we ran several sensitivity analysis experiments and they indicate that the results are fairly robust. Among all the experiments we performed, the largest change in the objective function was 2%.

8.2 Key findings

We perform several numerical experiments which resulted in the following findings: the methodology to determine the action in each period can be implemented in a timely fashion; the resulting control policy is not easy to characterize—however for the static policy the prescribed solution spreads across the action space, for the dynamic policies the solutions look different near the boundaries as compared to the center of the horizon; the different engines for objective function evaluation namely simulation, individual Markov chains, and deterministic analysis produce reasonably close solutions; there was a noticeable difference in the policy as the budgets changed; as expected the static policy was inferior to dynamic; the dynamic policy without feedback was not significantly worse off compared to the case with feedback; the dynamic policy without feedback is not only just marginally worse than with feedback, it runs much faster (few seconds) than with feedback (few hours). It is important to realize that the results depend on the choice of objective function. Also, generally speaking the technique described in this paper is applicable to solve generic MDPs approximately especially when there is curse of dimensionality.

In addition, we also perform several experiments to demonstrate the potential impact of various factors in terms of healthcare policy decisions. In particular, by comparing against existing HPV vaccination policy of vaccinating 70% of eligible population, our policy seems to perform much better in improving the objective function. In essence it would be worthwhile using the budget for examinations (essentially incentives) and treatment. Further, to study how the policies differ between HIV-AIDS and HPV. Since HIV vaccination is not as effective, it is natural to devote more of the budget to examination and treatment as compared to HPV. We also find that since the impact of vaccinations cannot be realized in a short time-horizon, the decisions are significantly different for both HPV and HIV. In addition, for both HIV and HPV as the population size becomes small it is more effective to use a larger fraction of the budget for treatment (as opposed to the large population where the budget is spent more-or-less evenly between testing, vaccination and treatment). Returning to the HPV incentives for examinations, it appears that using a weak incentive would favor more examinations versus vaccinations and vice versa (contradicting human behavior) forces policymakers to consider this issue more closely.

8.3 Limitations

The goal of this study is to illustrate the potential of Operations Research methods (especially stochastic control) for solving problems in healthcare policies. However, it is crucial to realize that the claims made such as the ones in the previous section ought to be first validated using appropriate statistical methods. In particular, some of the findings in the previous paragraph come with a disclaimer that they are based on the objective function and disease spread model described in the paper. Thus while developing a decision-support tool, we recommend investigating a variety of objective functions, disease spread models, robustness analysis, sensitivity analysis, and model uncertainty.

There are other situations for which the model would perhaps have to be fine tuned significantly. For example, the budget for the entire planning horizon we assume is known deterministically. Further, we assume that the model parameters are known with a reasonable amount of certainty but that is not realistic considering the variability in model structure and scarce data. This is critical and would have to be considered while building a decision-support tool where the eventual solution should be checked for robustness with respect to perturbation of the model parameters. However, we should clarify that addressing this parameter uncertainty issue is beyond the scope of this study as our manuscript presents a probabilistic analysis (and not a statistical analysis). The data used in this paper is purely for illustrative purposes.

In particular, the disease spread model may have to be suitably modified when the spreading mechanism changes (this would not be as straightforward in general but the methodology would remain unchanged as long as the behavior is Markovian). From a modeling standpoint, the only major requirement in terms of the disease model is that it must satisfy the Markov property. In fact one could also include herd immunity which is gaining a lot of importance in large-scale vaccinations. Although we have not explicitly considered herd immunity, there is an implicit provision for that in our proposed framework. In particular, our model considers spread of disease as a function of the number of individuals who are not being vaccinated. This way, herd immunity can be incorporated into our proposed framework. However, considering the focus of this paper and space limitations, we feel herd immunity is best left as a limitation of our study.

In summary, our key finding is that the resource allocation problem considered in this paper be solved first to determine a rough estimate for the number of vaccinations, examinations and treatment subsidies. Using this coarse first cut via a simplistic model, one could use the extensive literature on disease spread to determine a strategy for implementation on individuals. In essence, this paper provides a tool for effective pro-active management of two-stage communicable diseases. However, the entire analysis is probabilistic, therefore a significant statistical analysis is required before building an appropriate decision-support tool.