Skip to main content
SpringerLink
Log in

Asymptotic behavior of solutions for a nonlinear differential equation with constant impulsive jumps

  • Published:
Acta Mathematica Hungarica Aims and scope Submit manuscript

Abstract

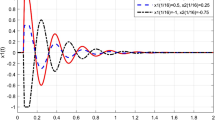
We investigate the asymptotic behavior of solutions to the nonlinear neutral delay differential equation (1.1) with constant impulsive jumps and forced term. By employing a new approach which is different from Lyapunov functionals and an effective technic for the constant impulsive jumps, new sufficient conditions are obtained to guarantee every non-oscillatory/oscillatory solution of the equation tends to zero as t→∞. Our results improve and generalize some known results in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. V. Anokhin, L. Berezansky and E. Braverman, Exponential stability of linear delay impulsive differential equations, J. Math. Anal. Appl., 193 (1995), 923–941.

    Article  MathSciNet  MATH  Google Scholar 

  2. T. A. Burton, Stability and Periodic Solutions of Ordinary and Functional Differential Equations, Academic Press (Orlando, Florida, 1985).

    MATH  Google Scholar 

  3. K. Guan and J. Shen, Asymptotic behavior of solutions of a first-order impulsive neutral differential equation in Euler form, Appl. Math. Lett., 24 (2011), 1218–1224.

    Article  MathSciNet  MATH  Google Scholar 

  4. L. Hatvani, Annulus arguments in the stability theory for functional differential equations, Differential and Integral Equations, 10 (1997), 975–1002.

    MathSciNet  MATH  Google Scholar 

  5. G. Ladas et al., Asymptotic behavior of solutions of retarded differential equations, Proc. Amer. Math. Soc., 88 (1983), 247–253.

    Article  MathSciNet  MATH  Google Scholar 

  6. V. Lakshmikantham, D. D. Bainov and P. S. Simeonov, Theory of Impulsive Differential Equations, World Scientific (Singapore, 1989).

    Book  MATH  Google Scholar 

  7. X. Liu and J. Shen, Asymptotic behavior of solutions of impulsive neutral differential equations, Appl. Math. Lett., 12 (1999), 51–58.

    Article  MathSciNet  MATH  Google Scholar 

  8. J. Shen and J. Li, Impulsive control for stability of Volterra functional differential equations, J. for Anal. and its Appl., 24 (2005), 721–734.

    MathSciNet  Google Scholar 

  9. J. Shen, Y. Liu and J. Li, Asymptotic behavior of solutions of nonlinear neutral differential equations with impulses, J. Math. Anal. Appl., 322 (2007), 179–189.

    Article  MathSciNet  Google Scholar 

  10. J. Shen, Z. Luo and X. Liu, Impulsive stabilization of functional differential equations via Lyapunov functionals, J. Math. Anal. Appl., 240 (1999), 1–15.

    Article  MathSciNet  MATH  Google Scholar 

  11. J. H. Shen and J. S. Yu, Asymptotic behavior of solutions of neutral differential equations with positive and negative coefficients, J. Math. Anal. Appl., 195 (1995), 517–526.

    Article  MathSciNet  MATH  Google Scholar 

  12. W. Gengping and J. Shen, Asymptotic behavior of solutions of nonlinear impulsive delay differential equations with positive and negative coefficients, Math. Computer Model., 44 (2006), 1089–1096.

    Article  MATH  Google Scholar 

  13. J. S. Yu and B. G. Zhang, Stability theorem of delay differential equations with impulses, J. Math. Anal. Appl., 199 (1996), 162–175.

    Article  MathSciNet  MATH  Google Scholar 

  14. B. Zhang, Asymptotic stability in functional differential equations by Lyapunov functionals, Tran. Amer. Math. Soc., 347 (1995), 1375–1382.

    MATH  Google Scholar 

  15. A. Zhao and J. Yan, Asymptotic behavior of solutions of impulsive delay differential equations, J. Math. Anal. Appl., 201 (1996), 943–954.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Hangzhou Normal University, Hangzhou, Zhejiang, 310036, China

    Fangfang Jiang & Jianhua Shen

Authors
  1. Fangfang Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jianhua Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jianhua Shen.

Additional information

Supported by the NNSF of China (No. 11171085), and the Zhejiang Provincial Natural Science Foundation (No. Y6090057).

Corresponding author.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jiang, F., Shen, J. Asymptotic behavior of solutions for a nonlinear differential equation with constant impulsive jumps. Acta Math Hung 138, 1–14 (2013). https://doi.org/10.1007/s10474-012-0282-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10474-012-0282-8

Key words and phrases

Mathematics Subject Classification

Search

Navigation