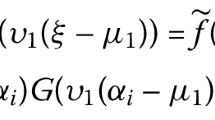1 Introduction

According to the order of derivative, differential equations can be classified into integer-order and fractional differential equations. Fractional differential equations are a generalization of arbitrary noninteger-order equations. Both of them are unified and widely used in mathematical modeling of practical applications in the real world. For more detail on the theory, see, for example, [1–3] and references therein. However, many dynamical systems possess an impulsive dynamical behavior due to abrupt changes at certain instants during the evolution process. The mathematical description of these phenomena leads to impulsive differential equations [4]. Indeed, they appeared as a more natural framework for mathematical modeling of many real-world phenomena often and occur in applied science and engineering [4–8], for example, in as physics, population dynamics, ecology systems, optimal control, industrial robotic, etc. The idea of impulsive differential equations has been a subject of interest not only among mathematicians, but also among physicists and engineers.

In recent years, the research on relevant issues of solutions are of main interest; see, for example, [9–13] on the existence of solutions for some (singular) fractional differential equations under different conditions and [6, 7, 14–23] on the asymptotic behavior of solutions for various kinds of impulsive differential equations. As is well known, there are two main methods for investigating the asymptotic properties of solutions. The first one is the Lyapunov method; see, for example, [14–19] and references therein. Wei and Shen [18] studied the following nonlinear impulsive neutral delay differential equation with positive and negative coefficients:

$$ \textstyle\begin{cases} [x(t)-c(t)x(t-\tau)]'+p(t)f(x(t-\delta))-q(t)f(x(t-\sigma))=0, \quad t\geq t_{0}>0, t\neq t_{k},\\ x(t_{k}^{+})=b_{k}x(t_{k})\\ \phantom{x(t_{k}^{+})=}+(1-b_{k})(\int_{t_{k}-\delta}^{t_{k}}p(s+\delta )f(x(s))\,ds-\int_{t_{k}-\sigma}^{t_{k}}q(s+\sigma)f(x(s))\,ds), \quad k\in \mathbb{Z}_{+}, \end{cases} $$
(1.1)

and obtained that every solution of (1.1) tends to a constant as \(t\to+\infty\) (i.e. asymptotic constancy). Similar impulsive perturbations were considered in [14] by studying the asymptotic constancy of an impulsive neutral differential equation of Euler form with unbounded delays,

$$ \textstyle\begin{cases} [x(t)-C(t)x(\alpha t)]'+\frac{P(t)}{t}x(\beta t)=0, \quad t\geq t_{0}>0, t\neq t_{k},\\ x(t_{k}^{+})=b_{k}x(t_{k})+(1-b_{k})\int_{\beta t_{k}}^{t_{k}}\frac{P(s/\beta )}{s}x(s)\,ds, \quad k\in\mathbb{Z}_{+}. \end{cases} $$
(1.2)

Note that the impulsive terms in (1.1)–(1.2) contain integral expressions, which implies that the impulsive jumps \(x(t_{k}^{+})-x(t_{k})\) not only depend on values of the state x at \(t_{k}\) but also depend on previous values of \(t_{k}\). As practice shows, the appearance of such impulsive perturbations leads to application of the Lyapunov method.

The other method is the technique of considering asymptotic properties of nonoscillatory and oscillatory solutions; see, for example, [20–23] and references therein. In [22], the authors studied the asymptotic behavior of the following linear impulsive neutral delay differential equation:

$$ \textstyle\begin{cases} [x(t)-px(t-\tau)]'+\sum_{i=1}^{n}q_{i}(t)f(x(t-\sigma_{i}))=h(t),\quad t\neq t_{k},\\ x(t_{k}^{+})-x(t_{k})=b_{k}x(t_{k}),\quad k\in\mathbb{Z}_{+}, \end{cases} $$
(1.3)

where \(q_{i}, h\in C^{0}([0,+\infty),\mathbb{R})\). Moreover, there are also several papers dedicated to this subject for some types of systems with constant impulsive jumps, i.e. \(x(t_{k}^{+})-x(t_{k})=\alpha_{k}\), and \(\alpha_{k}\) are constants. The constant impulse is a class of common impulsive perturbations appearing in many physical applications. However, the aforementioned two methods cannot be simply and directly applied to derive sufficient conditions such that every solution tends to a constant, and even to zero, as \(t\to+\infty\). In fact, the Lyapunov method can only be applied to deal with the specific impulse of the integral term, but the constant jumps \(\alpha_{k}\) lead to the failure of positive definiteness of Lyapunov function/functional.

In this paper, inspired by (1.1)–(1.3), we investigate the asymptotic behavior of solutions for a class of impulsive neutral differential equations with unbounded delays, positive and negative coefficients of Euler form, forced term, and constant impulsive jumps as follows

$$ \textstyle\begin{cases} [x(t)-C(t)g(x(\tau(t)))]'+ \frac{P(t)}{t}f(x(\alpha t))-\frac {Q(t)}{t}f(x(\beta t))=h(t),\quad t\geq t_{0}>0, t\neq t_{k},\\ x(t_{k}^{+})-x(t_{k})=\alpha_{k},\quad k\in{\mathbb{Z}_{+}}, \end{cases} $$
(1.4)

where \(P, Q, h\in \mathit{PC}([t_{0}, +\infty),\mathbb{R})\) satisfy \(P(t)>0\), \(Q(t)>0\), and \(\mathit{PC}(\cdot,\cdot)\) denotes a set of piecewise continuous functions. Hereinafter, to obtain the desired results, we introduce the function \(H(t)=\int_{t}^{+\infty}h(s)\,ds\) for \(t\in(t_{k},t_{k+1}]\) and \(H(t_{k})=\int_{t_{k}}^{+\infty}h(s)\,ds+\alpha_{k-1}^{+}\), \(k\in\mathbb {Z}_{+}\), which establishes a link between the constant impulsive jumps and the force term. We cannot simply and directly apply any one of the two methods mentioned. However, by constructing auxiliary functions and applying the technique of considering properties of nonoscillatory and oscillatory solutions we provide some new sufficient conditions to guarantee that every (non)oscillatory solution of (1.4) tends to zero as \(t\to+\infty\).

This paper is organized as follows. In Section 2, we present some preliminaries. In Section 3, we state and prove our main results. In Section 4, we give an example to illustrate the obtained results. Conclusion is outlined in Section 5.

2 Preliminaries

Consider the impulsive neutral differential equation with positive and negative coefficients of Euler form, unbounded delays, and constant impulsive jumps

$$ \textstyle\begin{cases} [x(t)-C(t)g(x(\tau(t)))]'+ \frac{P(t)}{t}f(x(\alpha t))-\frac {Q(t)}{t}f(x(\beta t))=h(t),\quad t\geq t_{0}>0, t\neq t_{k},\\ x(t_{k}^{+})-x(t_{k})=\alpha_{k},\quad k\in{\mathbb{Z}_{+}}, \end{cases} $$
(2.1)

where \(C\in C^{0}([t_{0}, +\infty),\mathbb{R})\), \(g, f\in C^{0}(\mathbb {R},\mathbb{R})\), \(P, Q, h\in \mathit{PC}([t_{0}, +\infty),\mathbb{R})\) with \(P(t)>0\) and \(Q(t)>0\); \(\tau(t)\) is increasing and satisfies \(\tau (t)\leq t\) and \(\lim_{t\to+\infty}\tau(t)=+\infty\), α and β are constants satisfying \(0<\alpha, \beta<1\), \(\{t_{k}\}\) denotes an impulsive time sequence satisfying \(t_{0}< t_{k}< t_{k+1}\uparrow+\infty\) as \(k\to+\infty\), \(\{\alpha_{k}\}\) is a constant impulsive perturbed sequence, \(\mathbb{R}\) denotes the set of real numbers, \(\mathbb{Z}_{+}\) denotes the set of positive integers, and \(\mathit{PC}([t_{0}, +\infty),\mathbb{R})\) denotes the set of functions \(\varphi: [t_{0}, +\infty)\to\mathbb{R}\) such that φ is continuous everywhere except at some points \(t_{k}, k\in\mathbb{Z}_{+}\), and the limits \(\varphi(t_{k}^{+})=\lim_{t\to t_{k}^{+}}\varphi(t)\), \(\varphi(t_{k}^{-})=\lim_{t\to t_{k}^{-}}\varphi(t)\) exist with \(\varphi(t_{k})=\varphi(t_{k}^{-})\).

In this paper, we assume the following hypotheses for (2.1).

\((H1)\) :

There exist \(M_{2}\geq M_{1}>0\) such that \(M_{1}\leq\frac {f(x)}{x}\leq M_{2}\) for \(x\neq0\).

\((H2)\) :

There exist \(0< N_{1}\leq N_{2}\leq1\) such that \(N_{1}\leq \frac{g(x)}{x}\leq N_{2}\) for \(x\neq0\).

\((H3)\) :

The integral \(\int_{t}^{+\infty}h(s)\,ds\) is convergent for \(t\geq t_{0}\).

\((H4)\) :

\(\tau(t_{k})\), \(k\in\mathbb{Z}_{+}\), are not impulsive points.

We associate with (2.1) the initial value condition

$$ x(t)=\varphi(t),\quad t\in[t_{0}-\gamma,t_{0}], $$
(2.2)

where \(\gamma=t_{0}-\min\{\inf_{t\geq t_{0}}\{t-\tau(t)\}, (1-\alpha)t_{0}, (1-\beta)t_{0}\}\).

It is easy to show the global existence and uniqueness of solutions of the initial value problem (2.1)–(2.2). In the following, we give two relevant definitions.

Definition 2.1

A function \(x(t)\) is called as a solution of (2.1)–(2.2) if

  1. (1)

    \(x(t)=\varphi(t)\) for \(t\in[t_{0}-\gamma,t_{0}]\), and \(x(t)\) is continuous for \(t\geq t_{0}\), \(t\neq t_{k}\), \(k\in\mathbb{Z}_{+}\);

  2. (2)

    \(x(t)-C(t)g(x(\tau(t)))\) is continuously differentiable for \(t\geq t_{0}\), \(t\neq t_{k}\), \(t\neq t_{k}/\alpha\), \(t\neq t_{k}/\beta\), \(k\in \mathbb{Z}_{+}\), and satisfies (2.1);

  3. (3)

    \(x(t_{k}^{+})\) and \(x(t_{k}^{-})\) exist with \(x(t_{k})=x(t_{k}^{-})\), \(k\in \mathbb{Z}_{+}\), and satisfy (2.1).

Definition 2.2

A solution \(x(t)\) is said to be eventually positive (negative) if it is positive (negative) for all sufficiently large t. It is called an oscillatory solution if it is neither eventually positive nor eventually negative. Otherwise, it is called as a nonoscillatory solution.

3 Main results

Theorem 3.1

Let \((H1)\)–\((H4)\) hold. Assume that \(\limsup_{t\to+\infty }|C(t)|=C<1\), \(\lim_{k\to+\infty}\alpha_{k}^{+}=0\), \(\frac{P(t/\alpha)}{t}-\frac{Q(t/\beta)}{t}\geq0\) for sufficiently large t,

$$ \int_{t_{0}}^{+\infty} \biggl[\frac{P(t/\alpha)}{t}- \frac{Q(t/\beta )}{t} \biggr]\,dt=+\infty, $$
(3.1)

and there exists a constant \(\lambda>0\) such that

$$ \int_{\alpha t}^{t}\frac{P(s/\alpha)}{s}\,ds\leq\lambda< \frac{1-CN_{2}}{M_{2}} $$
(3.2)

for t large enough, where \(\alpha_{k}^{+}=\max\{\alpha_{k}, 0\}\), \(k\in \mathbb{Z}_{+}\), and \(CN_{2}<1\). Then every nonoscillatory solution of (2.1) tends to zero as \(t\to+\infty\).

Proof

Choose sufficiently large \(t_{N}\) such that (3.2) holds for \(t\geq t_{N}\). Since \(\lim_{t\to+\infty}\tau(t)=+\infty\), there exists a positive integer m large enough such that \(\tau(t_{m})>t_{N}\), where m is the smallest subscript satisfying \(\tau(t_{m})>t_{N}\). Let \(x(t)\) be any nonoscillatory solution of (2.1) and assume that it is an eventually positive solution. The case where \(x(t)\) is eventually negative is symmetric. Now we let \(x(t)>0\) for \(t\geq t_{N}\) and set

$$\begin{aligned}[b] y(t)={}&x(t)-C(t)g\bigl(x\bigl(\tau(t)\bigr)\bigr)\\ &- \int_{\alpha t}^{t}\frac{P(s/\alpha )}{s}f\bigl(x(s)\bigr) \,ds+ \int_{\beta t}^{t}\frac{Q(s/\beta )}{s}f\bigl(x(s)\bigr) \,ds+H(t)-\alpha(t)\end{aligned} $$
(3.3)

for \(t\geq t_{M}\triangleq\max\{t_{m}, t_{N}/r\}\) and \(r=\min\{\alpha ,\beta\}\), where \(\alpha(t)\) and \(H(t)\) are of the form

$$ \alpha(t)=\left \{ \textstyle\begin{array}{l@{\quad}l}\alpha_{M^{t}}^{+},&t>t_{M+1},\\ 0,&t\in[t_{M},t_{M+1}], \end{array}\displaystyle \right . $$
(3.4)

where \(M^{t}\) denotes the largest subscript of impulsive points in \((t_{M}, t)\), and

$$ H(t)=\left \{ \textstyle\begin{array}{l@{\quad}l}\int_{t}^{+\infty}h(s)\,ds, &t\in(t_{k},t_{k+1}],\\ \int_{t}^{+\infty}h(s)\,ds+\alpha_{k-1}^{+}, &t=t_{k}, k\in\mathbb{Z}_{+}, \end{array}\displaystyle \right . $$
(3.5)

with \(\alpha_{0}=0\). When \(t>t_{M}\) and \(t\neq t_{k}\), it follows that \(\alpha'(t)=0\). Furthermore, for \(t>t_{M}\), \(t\neq t_{k}\), \(t\neq t_{k}/\alpha\), \(t\neq t_{k}/\beta\), and \(k\in \mathbb{Z}_{+}\), we have

$$ \begin{aligned}[b] y'(t)={}&\bigl[x(t)-C(t)g \bigl(x\bigl(\tau(t)\bigr)\bigr)\bigr]'-\frac{P(t/\alpha)}{t}f\bigl(x(t) \bigr)+\frac {P(t)}{t}f\bigl(x(\alpha t)\bigr)+\frac{Q(t/\beta)}{t}f\bigl(x(t) \bigr) \\ &-\frac{Q(t)}{t}f\bigl(x(\beta t)\bigr)-h(t)\\ ={}& \biggl[-\frac{P(t/\alpha )}{t}+ \frac{Q(t/\beta)}{t} \biggr]f\bigl(x(t)\bigr), \end{aligned} $$
(3.6)

whereas for \(t=t_{M+1}\), we have that \(y(t_{M+1}^{+})-y(t_{M+1})=\alpha _{M+1}-\alpha_{M}^{+}-\alpha_{M+1}^{+}\leq0\), and for \(t=t_{k}\), \(k=M+2, M+3,\ldots\) , it follows from (3.4)–(3.5) that

$$ y\bigl(t_{k}^{+} \bigr)-y(t_{k})=\alpha_{k}-\alpha_{k-1}^{+}- \alpha_{k}^{+}+\alpha _{k-1}^{+}\leq0. $$
(3.7)

Hence from (3.6)–(3.7) it follows that \(y(t)\) is nonincreasing on \([t_{M}, +\infty)\).

Let \(L=\lim_{t\to+\infty}y(t)\). We claim that \(L\in\mathbb{R}\). Otherwise \(L=-\infty\), and then \(x(t)\) is unbounded. If \(x(t)\) is bounded, then there exists a constant \(G>0\) such that

$$ y(t)\geq x(t)-CN_{2}x\bigl(\tau(t)\bigr)-G \int_{\alpha t }^{t }\frac{P(s/\alpha )}{s}\,ds+H(t)-\alpha(t). $$

As \(t\to+\infty\), by \((H3)\)–\((H4)\) and (3.2) we have that \(L>-\infty\), a contradiction, and so \(x(t)\) is unbounded. Due to \(L=-\infty\), we choose \(t^{*}\geq t_{M}\) (sufficiently large if necessary) such that \(y(t^{*})-H(t^{*})+\alpha(t^{*})<0\) and \(x(t^{*})=\max\{x(t): \min\{rt^{*}, \tau(t^{*})\}\leq t\leq t^{*}\}\). Furthermore, we have that

$$\begin{aligned} 0&>y\bigl(t^{*}\bigr)-H\bigl(t^{*}\bigr)+\alpha\bigl(t^{*}\bigr)> x\bigl(t^{*} \bigr)-CN_{2}x\bigl(\tau\bigl(t^{*}\bigr)\bigr)-M_{2} \int_{\alpha t^{*} }^{t^{*} }\frac{P(s/\alpha )}{s}x(s)\,ds \\ &> x\bigl(t^{*}\bigr) \biggl[1-CN_{2}-M_{2} \int_{\alpha t^{*} }^{t^{*} }\frac{P(s/\alpha )}{s}\,ds \biggr]>0.\end{aligned} $$

This is a contradiction, and so \(L\in\mathbb{R}\).

By integrating (3.6) from \(t_{M}\) to t we have that

$$ \begin{aligned}[b] \int_{t_{M}}^{t}\biggl[\frac{P(s/\alpha)}{s}- \frac{Q(s/\beta)}{s}\biggr]f\bigl(x(s)\bigr)\,ds ={}&{-} \int_{t_{M}}^{t}y'(s)\,ds \\ ={}&y(t_{M})-y(t)+\sum_{t_{M}< t_{k}\leq t}\bigl[y \bigl(t_{k}^{+}\bigr)-y(t_{k})\bigr] \\ < {}&y(t_{M})-L. \end{aligned} $$
(3.8)

Then \(\int_{t_{0}}^{+\infty}[\frac{P(s/\alpha)}{s}-\frac{Q(s/\beta )}{s}]f(x(s))\,ds<+\infty\), and it follows from (3.1) that \(f(x(t))\in L^{1}([t_{M},+\infty),\mathbb{R})\), and thus \(\liminf_{t\to+\infty}f(x(t))=0\). We next show that

$$ \liminf_{t\to+\infty}x(t)=0. $$
(3.9)

Choose a sequence \(\{S_{m}\}\) satisfying \(S_{m}\rightarrow+\infty\) as \(m\rightarrow+\infty\) such that \(\lim_{m\rightarrow+\infty }f(x(S_{m}))=0\). Then \(\liminf_{m\rightarrow+\infty}x(S_{m})=\xi=0\). In fact, if \(\xi>0\), then there exists a subsequence \(\{S_{m_{k}}\}\) such that \(x(S_{m_{k}})\geq\frac{\xi}{2}\) for k sufficiently large. Furthermore, \(f(x(S_{m_{k}}))\geq\frac{M_{1}\xi}{2}>0\) for k large enough, a contradiction. Hence (3.9) holds.

Now we show that the limit \(\lim_{t\to+\infty}x(t)\) exists and is finite. Set

$$ z(t)=y(t)+ \int_{\alpha t}^{t}\frac{P(s/\alpha)}{s}f\bigl(x(s)\bigr) \,ds- \int _{\beta t}^{t}\frac{Q(s/\beta)}{s}f\bigl(x(s)\bigr) \,ds-H(t)+\alpha(t). $$
(3.10)

By the preceding proofs we have that \(\lim_{t\to+\infty}z(t)=\mu \) exists and is finite, which, together with (3.4) and (3.10), means that

$$ \lim_{t\to+\infty}\bigl[x(t)-C(t)g\bigl(x\bigl(\tau(t) \bigr)\bigr)\bigr]=\mu. $$
(3.11)

Since \(0\leq \liminf_{t\to+\infty}|C(t)|\leq \limsup_{t\to +\infty}|C(t)|=C<1\), we have three possible cases.

Case I. If \(0<\liminf_{t\to+\infty}|C(t)|<\limsup_{t\to+\infty}|C(t)|=C<1\), then \(C(t)\) is eventually positive or eventually negative. Otherwise there exists a sequence \(\{\xi_{k}\}\) with \(\xi_{k}\to+\infty\) as \(k\to+\infty\) such that \(\lim_{k\to+\infty}C(\xi_{k})=0\), a contradiction. Hence we can find a sufficiently large T such that \(0<|C(t)|<1\) for \(t>T\).

Let \(\eta=\limsup_{t\to+\infty}x(t)\) and assume that there exist two sequences \(\{u_{n}\}\) and \(\{v_{n}\}\) satisfying \(u_{n}\to+\infty\) and \(v_{n}\to +\infty\) as \(n\to+\infty\) such that

$$ \lim_{t\to+\infty}x(u_{n})=0,\qquad\lim _{t\to+\infty}x(v_{n})=\eta. $$

It follows that there exists sufficiently large \(n_{0}\) such that \(\tau (u_{n})\geq t_{M}\) and \(\tau(v_{n})\geq t_{M}\) for all \(n\geq n_{0}\).

  1. (1)

    \(-1< C(t)<0\) for \(t>\max\{T, \tau(u_{n_{0}}), \tau (v_{n_{0}})\}\). We have that

    $$ \begin{gathered} \mu=\lim_{n\to+\infty}\bigl[x(u_{n})-C(u_{n})x \bigl(\tau(u_{n})\bigr)\bigr]\leq\lim_{n\to +\infty}x(u_{n})+ \limsup_{n\to+\infty}\bigl[-C(u_{n})x\bigl( \tau(u_{n})\bigr)\bigr]\leq C\eta, \\ \mu=\lim_{n\to+\infty}\bigl[x(v_{n})-C(v_{n})x \bigl(\tau(v_{n})\bigr)\bigr]\geq\lim_{n\to +\infty}x(v_{n})+ \liminf_{n\to+\infty}\bigl[-C(v_{n})x\bigl( \tau(v_{n})\bigr)\bigr]\geq\eta. \end{gathered} $$

Since \(\eta\geq0\) and \(0< C<1\), it follows that \(\eta=0\), and so \(\lim_{t\to+\infty}x(t)=0\).

  1. (2)

    \(0< C(t)<1\) for \(t>\max\{T, \tau(u_{n_{0}}), \tau(v_{n_{0}})\} \). We have that

    $$ \begin{gathered} 0=\lim_{n\rightarrow+\infty}x(u_{n})\geq \lim_{n\rightarrow+\infty }\bigl[x(u_{n})-C(u_{n})x\bigl( \tau(u_{n})\bigr)\bigr]+\liminf_{n\rightarrow\infty } \bigl[C(u_{n})x\bigl(\tau( u_{n})\bigr)\bigr]\geq\mu, \\ \eta=\lim_{n\rightarrow+\infty}x(v_{n})\leq\lim _{n\rightarrow \infty}\bigl[x(v_{n})-C(v_{n})x\bigl(\tau( v_{n}) \bigr)\bigr]+\limsup_{n\rightarrow\infty } \bigl[C(v_{n})x\bigl(\tau(v_{n} )\bigr)\bigr]\leq\mu+C\eta. \end{gathered} $$

Since \(0< C<1\) and \(\eta\geq0\), it follows that \(\eta=0\), and so \(\lim_{t\to+\infty}x(t)=0\).

Case II. If \(0=\liminf_{t\to+\infty}|C(t)|<\limsup_{t\to+\infty}|C(t)|=C\), then as in Case I, we get \(\lim_{t\to+\infty}x(t)=0\).

Case III. If \(\liminf_{t\to+\infty}|C(t)|=\limsup_{t\to+\infty}|C(t)|=C\), then the proof is as in Theorem 2.1 in [22] and so is omitted. The proof is complete. □

Theorem 3.2

Let \((H1)\)–\((H4)\) hold. Assume that \(\limsup_{t\to+\infty }|C(t)|=C<1\) satisfies \(CN_{2}<1/2\), \(\limsup_{k\to+\infty}|\alpha _{k}|=0\), and there exists a constant \(\lambda>0\) such that

$$ \limsup_{t\to+\infty}\bigl(I_{1}(t)+I_{2}(t) \bigr)\leq\lambda< \frac{1-2CN_{2}}{2M_{2}}, $$
(3.12)

where \(I_{1}(t)=\int_{\alpha t}^{t/\alpha}\frac{\Delta(s)}{s}\,ds\) with \(\Delta(t)=P(t/\alpha)-Q(t/\beta)>0\) for \(t\geq t_{0}\) and \(I_{2}(t)=\int_{\alpha t}^{\beta t}\frac{Q(s/\beta)}{s}\,ds\) with \(\alpha<\beta\). Then every oscillatory solution of (2.1) tends to zero as \(t\to+\infty\).

Proof

Let \(x(t)\) be any oscillatory solution of (2.1). We first show that \(x(t)\) is bounded. Otherwise \(x(t)\) is unbounded, and then there exists a positive integer N sufficiently large such that \(\lim_{t\to+\infty}\sup_{\tau(t_{N})\leq s\leq t}|x(s)|=+\infty\) and \(\sup_{\tau(t_{N})\leq s\leq t}|x(s)|=\sup_{t_{N}/\alpha\leq s\leq t}|x(s)|\) for \(t> t_{N}/\alpha\). Set

$$\begin{aligned}[b] y(t)={}&x(t)-C(t)g\bigl(x\bigl(\tau(t)\bigr)\bigr)\\&- \int_{\alpha t}^{t}\frac{\Delta (s)}{s}f\bigl(x(s)\bigr) \,ds- \int_{\alpha t}^{\beta t}\frac{Q(s/\beta )}{s}f\bigl(x(s)\bigr) \,ds+H(t)-\alpha(t),\end{aligned} $$
(3.13)

where \(H(t)\) is defined as in (3.5), and \(\alpha (t)\triangleq\alpha^{+}_{k^{t}}\) for \(t>t_{0}\), where \(k^{t}\) denotes the largest subscript of impulsive points in \((t_{0}, t)\). When \(t> t_{N}/\alpha\), we have that

$$ \begin{aligned}[b] \big|y(t)\big|\geq{}& \big|x(t)\big|-CN_{2}\big|x\bigl(\tau(t) \bigr)\big|-M_{2} \int_{\alpha t}^{t}\frac{\Delta (s)}{s}\big|x(s)\big| \,ds\\ &-M_{2} \int_{\alpha t}^{\beta t}\frac{Q(s/\beta )}{s}\big|x(s)\big|\,ds -\big|H(t)\big|-\big| \alpha(t)\big| \\ \geq{}&\big|x(t)\big|-\sup_{\tau(t_{N})\leq s\leq t}\big|x(s)\big|\bigl[CN_{2}+M_{2} \bigl(I_{1}(t)+I_{2}(t)\bigr)\bigr]-\big|H(t)\big|-\big|\alpha(t)\big|. \end{aligned} $$

Furthermore,

$$ \begin{aligned}[b] \sup_{t_{N}/\alpha\leq s\leq t}\big|y(s)\big|\geq{}& \sup_{t_{N}/\alpha\leq s\leq t}\big|x(s)\big|\bigl[1-CN_{2}-M_{2} \bigl(I_{1}(t)+I_{2}(t)\bigr)\bigr]\\ &-\sup_{t_{N}/\alpha\leq s\leq t}\big|H(s)\big|- \sup_{t_{N}/\alpha\leq s\leq t}\big|\alpha(s)\big|. \end{aligned} $$
(3.14)

It follows from (3.12) that \(1-CN_{2}-M_{2}\lambda>0\), and then \(\limsup_{t\to+\infty}|y(t)|=+\infty\) due to \((H3)\)–\((H4)\).

On the other hand, when \(t\neq t_{k}\), \(t\neq t_{k}/\alpha\), \(t\neq t_{k}/\beta \), we have that

$$ y'(t)=-\frac{\Delta(t)}{t}f \bigl(x(t)\bigr) $$
(3.15)

and \(y(t_{k}^{+})-y(t_{k})\leq0\) for \(t=t_{k}\), \(k\in\mathbb{Z}_{+}\). So \(y'(t)\) is oscillatory by \((H1)\). Furthermore, there exists a sufficiently large \(\xi\geq t_{N}/\alpha\) such that

$$ \big|y(\xi/\alpha)\big|=\sup_{t_{N}/\alpha\leq s\leq\xi/\alpha }\big|y(s)\big|,\qquad y'(\xi)=0. $$

Hence \(x(\xi)=0\). Integrating (3.15) from ξ to \(\xi /\alpha\), we have that

$$ \begin{aligned} [b]y(\xi/\alpha)\leq{}& y(\xi)- \int_{\xi}^{\xi/\alpha} \biggl[\frac {P(t/\alpha)}{t}- \frac{Q(t/\beta)}{t} \biggr]f\bigl(x(t)\bigr)\,dt \\ ={}&{ -}C(\xi)g\bigl(x\bigl(\tau(\xi)\bigr)\bigr)\\&- \int_{\alpha\xi}^{\xi/\alpha}\frac {\Delta(t)}{t}f\bigl(x(t)\bigr)\,dt- \int_{\alpha\xi}^{\beta\xi}\frac {Q(t/\beta)}{t}f\bigl(x(t)\bigr)\,dt +H(\xi)-\alpha(\xi). \end{aligned} $$
(3.16)

Furthermore,

$$ \big|y(\xi/\alpha)\big|\leq\sup_{\tau(t_{N})\leq s\leq\xi/\alpha }\big|x(s)\big| \bigl[CN_{2}+M_{2}\bigl(I_{1}(\xi)+I_{2}( \xi)\bigr)\bigr]+\big|H(\xi)\big|+\big|\alpha(\xi)\big|. $$
(3.17)

Together with (3.14) and (3.17), this gives

$$ \begin{gathered} \bigl[-1+2CN_{2}+2M_{2}\bigl(I_{1}( \xi)+I_{2}(\xi)\bigr)\bigr]\\\quad{}+\frac{|H(\xi)|+|\alpha(\xi)|}{ \sup_{\tau(t_{N})\leq s\leq\xi/\alpha}|x(s)|}+ \frac{\sup_{t_{N}/\alpha\leq s\leq\xi/\alpha}|H(s)|+\sup_{t_{N}/\alpha\leq s\leq\xi/\alpha}|\alpha(s)|}{\sup_{\tau(t_{N})\leq s\leq \xi/\alpha}|x(s)|}\geq0.\end{gathered} $$

Let \(\xi\to+\infty\) and note that \(\lim_{\xi\to+\infty}\sup_{\tau(t_{N})\leq s\leq\xi /\alpha}|x(s)|=+\infty\), so it follows from \((H3)\)–\((H4)\) and (3.12) that \([-1+2CN_{2}+2M_{2}\lambda]\geq0\). This is a contradiction, and thus \(x(t)\) is bounded.

Now we show that \(\mu=\limsup_{t\to+\infty}|x(t)|=0\). Similarly, we analyze the function \(y(t)\) of the form

$$ y(t)=x(t)-C(t)g\bigl(x\bigl(\tau(t)\bigr)\bigr)- \int_{\alpha t}^{t}\frac{\Delta (s)}{s}f\bigl(x(s)\bigr) \,ds- \int_{\alpha t}^{\beta t}\frac{Q(s/\beta )}{s}f\bigl(x(s)\bigr) \,ds+H(t)-\alpha(t). $$

Then \(y(t)\) is bounded, and for sufficiently large t, we have that

$$ \big|y(t)\big|\geq\big|x(t)\big|-CN_{2}\big|x\bigl(\tau(t) \bigr)\big|-M_{2}\sup_{t_{N}/\alpha\leq s\leq t}\big|x(s)\big|\bigl(I_{1}(t)+I_{2}(t) \bigr)-\big|H(t)\big|- \big|\alpha(t)\big|. $$

Hence from \((H3)\)–\((H4)\) we have that

$$ \beta=\limsup_{t\to+\infty}\big|y(t)\big| \geq\mu\Bigl[1-CN_{2}-M_{2}\limsup_{t\to+\infty} \bigl(I_{1}(t)+I_{2}(t)\bigr)\Bigr]. $$
(3.18)

On the other hand, for \(t\neq t_{k}\), \(t\neq t_{k}/\alpha\), \(t\neq t_{k}/\beta\), \(k\in\mathbb{Z}_{+}\), it follows that

$$ y'(t)= \biggl[- \frac{P(t/\alpha)}{t}+\frac{Q(t/\beta)}{t} \biggr]f\bigl(x(t)\bigr), $$
(3.19)

and \(y'(t)\) is oscillatory. Hence there exists a sequence \(\{\xi_{m}\}\) satisfying \(\lim_{m\to+\infty}\xi _{m}=+\infty\) such that

$$\lim_{m\to+\infty}\big|y(\xi_{m})\big|=\beta,\qquad y'(\xi_{m})=0, $$

and then \(x(\xi_{m})=0\) for \(m=1,2,3,\dots\).

Integrating (3.19) from \(\xi_{m}\) to \(\xi_{m}/\alpha\), with analysis similar to (3.16), we get

$$ \big|y(\xi_{m}/\alpha)\big|\leq\sup _{\tau(\xi_{m})\leq s\leq \xi_{m}/\alpha}\big|x(s)\big|\bigl[CN_{2}+M_{2} \bigl(I_{1}(\xi_{m})+I_{2}(\xi_{m}) \bigr)\bigr]+\big|H(\xi_{m})\big|+ \big|\alpha(\xi_{m})\big|. $$

Letting \(\xi_{m}\to+\infty\), by \((H3)\)–\((H4)\) it follows that

$$ \beta\leq\mu\Bigl[CN_{2}+M_{2}\limsup _{m\to+\infty}\bigl(I_{1}(\xi_{m})+I_{2}( \xi_{m})\bigr)\Bigr]. $$
(3.20)

Combining thus with (3.18) and (3.20), we get

$$ \mu\Bigl[1-CN_{2}-M_{2}\limsup_{t\to+\infty} \bigl(I_{1}(t)+I_{2}(t)\bigr)\Bigr]\leq\mu \Bigl[CN_{2}+M_{2}\limsup_{m\to+\infty} \bigl(I_{1}(\xi_{m})+I_{2}(\xi_{m}) \bigr)\Bigr]. $$
(3.21)

Hence \(\mu(-1+2CN_{2}+2M_{2}\lambda)\geq0\), which, together with (3.12) and \(\mu\geq0\), implies that \(\lim_{t\to+\infty }x(t)=0\). The proof is complete. □

4 Example

Consider the following impulsive neutral delay differential equation:

$$ \left \{ \textstyle\begin{array}{ll}[x(t)-\frac{1}{4}x(\frac{t}{e})\sin t]'+ \frac {1}{2t(\ln\frac{1}{2}t-1)}x(\frac{t}{2e})- \frac{1}{4t(\ln t-1)}x(\frac{t}{e})=\frac{1}{t^{2}}, \quad t\geq t_{0}=2e, t\neq t_{k}, \\ x(k^{+})-x(k)=(-1)^{k}k^{-1}, \quad k=1,2,3,\dots. \end{array}\displaystyle \right . $$
(4.1)

Obviously, \(f(x)=g(x)=x\), \(C(t)=\frac{1}{4}\sin t\), \(P(t)={\frac {1}{2(\ln\frac{1}{2}t-1)}}>0\), \(Q(t)={\frac{1}{4(\ln t-1)}}>0\) for \(t\geq2e\), \(\tau(t)=\frac{t}{e}\) satisfies \(\lim_{t\to+\infty }(1-1/e)t=+\infty\) and \(\tau(t)< t\), \(\alpha=\frac{1}{2e}< \beta =\frac{1}{e}\), \(h(t)=\frac{1}{t^{2}}\), \(\alpha_{k}=(-1)^{k}k^{-1}\). It is easy to verify that \((H1)\)–\((H4)\) hold. Moreover, \(\limsup_{t\to+\infty}|C(t)|=\frac{1}{4}, \liminf_{t\to+\infty}|C(t)|=0\), and \(\lim_{t\to+\infty}\alpha _{k}^{+}=\lim_{t\to+\infty}|\alpha_{k}|=0\). Choosing \(M_{1}=M_{2}=N_{1}=N_{2}=1\), we claim that every solution of (4.1) tends to zero as \(t\to +\infty\). In fact, it follows that, for \(t\geq2e\),

$$ \frac{\Delta(t)}{t}=\frac{P(t/\alpha)}{t}-\frac{Q(t/\beta )}{t}=\frac{1}{4t\ln t}>0. $$

On one hand, \(\int_{2e}^{+\infty}\frac{1}{4t\ln t}\,dt=+\infty\) and \(\int_{\frac{t}{2e}}^{t}\frac{dt}{2t\ln t}<\frac{1}{2}\ln2<\frac {1-CN_{2}}{M_{2}}\) for t sufficiently large. So by Theorem 3.1, every nonoscillatory solution of (4.1) tends to zero as \(t\to +\infty\).

On the other hand, by simple computations we have \(I_{1}(t)=\frac {1}{4}\ln\frac{\ln2et}{\ln\frac{t}{2e}}\) and \(I_{2}(t)=\frac {1}{4}\ln\frac{\ln\frac{t}{e}}{\ln\frac{t}{2e}}\). Furthermore, \(\limsup_{t\to+\infty}(I_{1}(t)+I_{2}(t))=0\). So by Theorem 3.2 every oscillatory solution of (4.1) tends to zero as \(t\to+\infty\). In conclusion, every solution of (4.1) tends to zero as \(t\to+\infty\).

5 Conclusion

In this paper, we have investigated asymptotic properties of solutions for an impulsive neutral differential equation with positive and negative coefficients, unbounded delays, forced term, and constant impulsive jumps. By constructing auxiliary functions, using analytical method and combining with the technique of considering asymptotic behaviors of nonoscillatory and oscillatory solutions, we have provided two criteria for tending to zero of every (non)oscillatory solution of the system as \(t\to+\infty\). Finally, as an application, we have given an example to illustrate the effectiveness of the obtained results.