1 Introduction

Operational-transconductance-amplifier (OTA) with active cascode-current-mirror load is an well-known topology often used in analog CMOS integrated circuits [1]. It is also used as a suitable differential-to-single-ended converter in analog signal processing using differential signals. In today’s highly scaled low-voltage CMOS systems and applications the low-voltage-cascode-current-mirror (LVCCM) [1,2,3] is often used instead of the regular cascode-current-mirror to overcome the voltage headroom constraint. It has found application in many commercial CMOS ICs as well [4]. The small-signal mid-band analysis of the OTA with active LVCCM is however not available in [1] or other classic texts such as [5,6,7,8]. In several recent articles [9,10,11,12] the 2nd author provided simplified small-signal analysis for a large number of various gain-stages which were not available before. Also, recently in [13] co-authored by the 2nd author, the accurate mid-band analysis of the differential-amplifier OTA with the standard current-mirror load was provided indicating superior accuracy compared to the gain equation provided in [1]. In addition, in [14] an accurate gain-expression for the non-ideal differential-amplifier OTA was also provided by the 2nd author with significantly higher accuracy than that available in [1]. In this article, an exact small-signal mid-band analysis of the OTA with LVCCM load is provided which is not available in any text-book, article or web-source. Results of circuit simulations using the 180-nm and 65-nm TSMC CMOS process technologies are provided to indicate the progressively higher accuracy of the derived exact gain-expression of the OTA with LVCCM load with technology scaling. This new exact gain-expression as well as a simplified form of this exact gain-expression performs better than the classical expression by providing a more accurate mid-band gain value and a further degree of freedom in tuning the gain of the OTA with LVCCM load, using an additional transconductance parameter. It thus provides more design insight in adjusting the mid-band gain of the OTA with LVCCM load, compared to the classical approximate expression available in open literature and textbooks. The simplified form of this new exact gain expression is also amenable to first order gain calculation in a simplified way while providing better design intuition using one additional design parameter as compared to the classical equation. Standard notations employed in [1, 5, 7, 8] have been used in the equations in this article for describing all the CMOS parameters in the small-signal modelling following the standard convention in analog CMOS circuit analysis. In addition, appropriate DC, AC and composite voltage/current signal symbols are employed. Also, it is to be clarified in this context, that, all voltages and currents in lower-case letters along with upper-case subscripts are quantities containing both a large-signal DC Bias (quiescent) value and a small-signal (AC) variation (perturbation) superimposed on it. All voltages/currents in uppercase letters along with uppercase subscripts are DC-bias quantities, and all voltages/currents in lowercase letters along with lowercase subscripts are just the AC perturbation quantities.

2 Exact analysis of the differential-amplifier (OTA) with low-voltage-cascode-current-mirror load

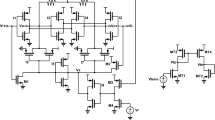
A CMOS OTA with low-voltage-cascode-current-mirror load [1] is shown in the Fig. 1 along-with the composite input and output signals and the DC-bias voltages. Next, Fig. 2 shows its AC-equivalent circuit with all the bias-voltages set at AC ground. For a fully matched input differential-pair the drain of M7 (d7) can be considered to be at AC-ground (Virtual ground) and hence the input differential-pair can be decoupled and decomposed into two half-circuit components near the AC ground. Figure 3 shows this decomposition of the input circuit for a matched input differential-pair. Here,

$$v_{d} = (v_{in1} - v_{in2} )$$
(1)
Fig. 1
figure 1

A standard CMOS OTA with active low-voltage-cascode-current-mirror load [1] showing composite signals at the inputs and the output

Full size image
Fig. 2
figure 2

AC equivalent circuit of the standard CMOS OTA with active low-voltage-cascode-current-mirror load showing small-signal inputs and output

Full size image
Fig. 3
figure 3

The decoupling and decomposition of the input circuit of the differential amplifier OTA with low-voltage-cascode-current-mirror load for a fully matched OTA

Full size image

Next, Fig. 4 presents the left-half-circuit of the AC-equivalent circuit of the OTA and the technique for determining the load impedance (RL) looking into the drain of M1 using a voltage source, vl that drives the current, il into the load of M1. Following on, Fig. 5 depicts the small-signal equivalent circuit for the load (RL) connected to the drain of M1 in the Fig. 4(b). In Fig. 6 the equivalent circuit of the Fig. 5 is simplified by realizing that vgs5,6 = vl and that vg3 and vb3 are at the ground potential. Next, Fig. 7 provides a further simplified form of the equivalent circuit in the Fig. 6 by merging the two current sources for M3 and removing the negative sign by inverting the direction of the combined current-source for M3. Finally, Fig. 8 provides the reduced and simplified form of the equivalent circuit for the load (RL) looking at the drain of M1 by converting the Norton sources to Thevenin’s sources. A simplified pictorial approach using successive simplification of small-signal equivalent circuits without sacrificing any mathematical details is thus demonstrated here in transforming from Fig. 5 through to Fig. 8 just by inspection. Only one simple source transformation from Norton source to thevenin’s source is employed in the Fig. 8 and no complicated circuit analysis or theorems is used. Then, from the Fig. 8,

$$v_{s3} = (i_{l} r_{05,6} - g_{m5,6} v_{l} r_{05,6} )$$
(2)
Fig. 4
figure 4

a Left-half circuit of the AC-equivalent circuit of the OTA in Fig. 3 b determining the load impedance (RL) looking into the load of M1

Full size image
Fig. 5
figure 5

Small-signal equivalent circuit for the load (RL) connected to the drain of M1 in the Fig. 4(b)

Full size image
Fig. 6
figure 6

Simplified form of the equivalent circuit in Fig. 5 by considering that vgs5,6 = vl and that vg3 and vb3 are at AC ground potential

Full size image
Fig. 7
figure 7

Further simplified form of the equivalent circuit in Fig. 6 by merging the current sources for M3 and inverting the arrow to account for the negative sign

Full size image
Fig. 8
figure 8

Reduced and simplified form of the equivalent circuit in Fig. 7 obtained by converting Norton sources to Thevenin’s sources

Full size image

So that,

$$(g_{m3,4} + g_{{m{\text{b}} 3,4}} )v_{s3} = (g_{m3,4} + g_{mb3,4} )(i_{l} r_{05,6} - g_{m5,6} v_{l} r_{05,6} )$$
(3)

Hence, KVL along the equivalent circuit in Fig. 8 produces,

$$v_{l} = (g_{m3,4} + g_{mb3,4} )(i_{l} r_{05,6} - g_{m5,6} v_{l} r_{05,6} )r_{03,4} + i_{l} r_{05,6} + i_{l} r_{03,4} - g_{m5,6} v_{l} r_{05,6}$$
(4)

From which, by changing sides,

$$\begin{gathered} v_{l} + g_{{{\text{m}} 5,6}} v_{l} r_{05,6} + (g_{m3,4} + g_{mb3,4} )g_{m5,6} v_{l} r_{05,6} r_{03,4} \hfill \\ \quad \quad = i_{l} (g_{m3,4} + g_{mb3,4} )r_{05,6} r_{03,4} + {\text{i}}_{l} r_{05,6} + i_{l} r_{03,4} \hfill \\ \end{gathered}$$
(5)

Or, the load resistance, RL looking at the drain of M1 is given by,

$$R_{L} = \frac{{v_{l} }}{{i_{l} }} = \frac{{(g_{m3,4} + g_{mb3,4} )r_{05,6} r_{03,4} + r_{05,6} + r_{03,4} }}{{1 + g_{m5,6} r_{05,6} + (g_{m3,4} + g_{mb3,4} )g_{m5,6} r_{05,6} r_{03,4} }}$$
(6)

Hence, the small-signal voltage at the drain of M1 (and also at the gates of M5 and M6) is given by,

$$v_{drainM1} = v_{g5,6} = - \frac{{v_{d} }}{2}g_{m1,2} (r_{01,2} //R_{L} )$$
(7)

Next, Fig. 9 shows the right-hand-side half-circuit of the AC-equivalent circuit in Fig. 3 where vg6 = vdrainM1. Following-on, Fig. 10 provides the Norton equivalent circuit model for the PMOS cascode upper input section (with input at the gate of M6) formed by M4 and M6 in the Fig. 9 inspecting at the output. This Norton model has an equivalent transconductance, GX and an equivalent output impedance, RX given by [9],

$$G_{{\text{X}}} = \frac{{g_{{\text{m5,6}}} r_{{\text{o5,6}}} \left\{ {(g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + 1} \right\}}}{{r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + r_{{\text{o3,4}}} }}$$
(8)
$$R_{{\text{X}}} = r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + r_{{\text{o3,4}}}$$
(9)
Fig. 9
figure 9

Right-hand-side half-circuit of the AC-equivalent circuit in the Fig. 3 where vg6 = vd1

Full size image
Fig. 10
figure 10

Norton equivalent circuit model for the PMOS cascode upper-section formed by M4 and M6 in Fig. 9 inspecting at the output

Full size image

Figure 11 shows the final reduced form of the small-signal equivalent circuit for the matched composite CMOS OTA with active low-voltage-cascode-current-mirror load. Next, using (7, 8 and 9) and Fig. 11,

$$v_{out} = \frac{{v_{d} }}{2}[G_{\text{X}} \{ g_{m1,2} (r_{01,2} //R_{L} )\} + g_{m1,2} ](r_{01,2} //R_{\text{X}} )$$
(10)
Fig. 11
figure 11

Reduced form of the final small-signal equivalent circuit for the matched composite CMOS OTA with active low-voltage-cascode-current-mirror load

Full size image

Since vg6 is negative, both the current-sources will accumulate and drop on the load to produce a positive output voltage. Next, expanding the terms, GX, RL and RX in (10) the exact differential voltage-gain (with vd being the input), \(A_{V\_exact}\) is given by (11) at the top of the next page.

$$\begin{gathered} A_{V\_exact} = \frac{1}{2}[\left( {\frac{{g_{{\text{m5,6}}} r_{{\text{o5,6}}} \left\{ {(g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + 1} \right\}}}{{r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + r_{{\text{o3,4}}} }}} \right) \times \left( {g_{m1,2} \times \{ \frac{{r_{01,2} \times \frac{{(g_{m3,4} + g_{mb3,4} )r_{05,6} r_{03,4} + r_{05,6} + r_{03,4} }}{{1 + g_{m5,6} r_{05,6} + (g_{m3,4} + g_{mb3,4} )g_{m5,6} r_{05,6} r_{03,4} }}}}{{r_{01,2} + \frac{{(g_{m3,4} + g_{mb3,4} )r_{05,6} r_{03,4} + r_{05,6} + r_{03,4} }}{{1 + g_{m5,6} r_{05,6} + (g_{m3,4} + g_{{{\text{mb}} 3,4}} )g_{m5,6} r_{05,6} r_{03,4} }}}}\} } \right) + g_{m1,2} ] \hfill \\ \quad \quad \quad \times [\frac{{r_{01,2} \times \{ r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + r_{{\text{o3,4}}} \} }}{{r_{01,2} + \{ r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + r_{{\text{o3,4}}} \} }}] \hfill \\ \end{gathered}$$
(11)

Next, employing approximations assuming long-channel devices (large device output impedances) in relation to technology, to the various constituent terms of the exact and accurate gain-expression in (11), a concise form of the gain-expression can be obtained, while progressing towards the classical gain-expression, as follows:

In the term, \(\frac{{g_{{\text{m5,6}}} r_{{\text{o5,6}}} \left\{ {(g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + 1} \right\}}}{{r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + r_{{\text{o3,4}}} }}\), for the denominator \([r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + r_{{\text{o3,4}}} ]\) it is assumed that \([r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} ] \gg r_{{\text{o3,4}}}\), so that the denominator can be simplified as just equal to \([r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} ]\) based on the cascode output impedance approximation for long channel devices[1]. Hence the term, \(\frac{{g_{{\text{m5,6}}} r_{{\text{o5,6}}} \left\{ {(g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + 1} \right\}}}{{r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + r_{{\text{o3,4}}} }} \approx g_{{\text{m5,6}}}\).

Similarly, in the term, \(\frac{{(g_{m3,4} + g_{mb3,4} )r_{05,6} r_{03,4} + r_{05,6} + r_{03,4} }}{{1 + g_{m5,6} r_{05,6} + (g_{m3,4} + g_{mb3,4} )g_{m5,6} r_{05,6} r_{03,4} }}\), the numerator \([(g_{m3,4} + g_{mb3,4} )r_{05,6} r_{03,4} + r_{05,6} + r_{03,4} ]\) can be approximated as just equal to, \([(g_{m3,4} + g_{mb3,4} )r_{05,6} r_{03,4} + r_{05,6} ]\), and for the denominator \([1 + g_{m5,6} r_{05,6} + (g_{m3,4} + g_{mb3,4} )g_{m5,6} r_{05,6} r_{03,4} ]\) it is assumed that, in general, for technology with large channel lengths, the approximation, \([g_{m5,6} r_{05,6} + (g_{m3,4} + g_{mb3,4} )g_{m5,6} r_{05,6} r_{03,4} ] \gg \;1\) holds, so that the denominator can be simplified as, \([g_{m5,6} r_{05,6} + (g_{m3,4} + g_{mb3,4} )g_{m5,6} r_{05,6} r_{03,4} ]\). Next taking \(g_{m5,6}\) common, the simplified denominator becomes, \(g_{m5,6} [r_{05,6} + (g_{m3,4} + g_{mb3,4} )r_{05,6} r_{03,4} ]\), thus rendering the term,

$$\frac{{(g_{m3,4} + g_{mb3,4} )r_{05,6} r_{03,4} + r_{05,6} + r_{03,4} }}{{1 + g_{m5,6} r_{05,6} + (g_{m3,4} + g_{mb3,4} )g_{m5,6} r_{05,6} r_{03,4} }} \approx \frac{1}{{g_{m5,6} }}$$

Consequently, the accurate and exact version of the gain-expression in (11) can be collapsed into the reduced and simplified form given by,

$$\begin{gathered} A_{V\_simplified} \approx \frac{1}{2}[g_{{\text{m5,6}}} \times \left( {g_{m1,2} \times \{ \frac{{r_{01,2} \times \frac{1}{{g_{m5,6} }}}}{{r_{01,2} + \frac{1}{{g_{m5,6} }}}}\} } \right) + g_{m1,2} ] \hfill \\ \quad \quad \quad \times [\frac{{r_{01,2} \times \{ r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + r_{{\text{o3,4}}} \} }}{{r_{01,2} + \{ r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + r_{{\text{o3,4}}} \} }}] \hfill \\ \end{gathered}$$
(12)

After further simplification of the term \(r_{01,2} + \frac{1}{{g_{m5,6} }}\) to just \(r_{01,2}\), assuming that, \(r_{01,2} \gg \frac{1}{{g_{m5,6} }}\) based on long channel device approximation [1] in relation to technology, the simple approximate form of the gain-expression is given by,

$$\begin{aligned} A_{V\_approx} \approx& \frac{1}{2}[g_{{\text{m5,6}}} \times \left( {g_{m1,2} \frac{1}{{g_{m5,6} }}} \right) + g_{m1,2} ] \hfill \\ \quad \quad \quad &\times \left[\frac{{r_{01,2} \times \{ r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + r_{{\text{o3,4}}} \} }}{{r_{01,2} + \{ r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + r_{{\text{o3,4}}} \} }}\right] \hfill \\ \end{aligned}$$
(13)

And hence, in the final approximate form, the mid-band gain-expression is given by,

$$\begin{gathered} A_{V\_approx} \approx g_{m1,2} \times \left[\frac{{r_{01,2} \times \{ r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + r_{{\text{o3,4}}} \} }}{{r_{01,2} + \{ r_{{\text{o5,6}}} + r_{{\text{o5,6}}} (g_{{\text{m3,4}}} + g_{{\text{mb3,4}}} )r_{{\text{o3,4}}} + r_{{\text{o3,4}}} \} }}\right] \hfill \\ \hfill \\ \end{gathered}$$
(14)

Which is the classical gain-expression similar to the approximate gain-expression for an OTA with standard cascode-current-mirror load. The difference in the accuracy between the gain expressions in (11 and 14) thus relates to process technology. Comparing (11 and 14) it is evident that employing the approximate gain expression of a standard cascode-current-mirror load is quite inaccurate compared to the exact form of the gain for the OTA with LVCCM load particularly for advanced technologies where the device output impedance reduces progressively compared to that for long channel devices. The gain-expression in (11) provides significantly more design insight by indicting that the gain is a product of a complex composite transconductance term (involving all the devices in the structure) with the output-impedance at the single-ended output, instead of being the product of just the transconductance of the differential input-pair devices with the output-impedance at the single-ended output. Based on (11) and from its reduced form in (12) a further degree of freedom in the design is available through the fine-tuning of the transconductance of the cascode mirror devices (M5, M6) which gets cancelled mid-way through the further simplification step in (13). This additional design parameter is thus missing in the simple approximate (classical) expression in (14). Hence the simplified expression in (12) provides better design intuition through the additional degree of freedom using one additional design parameter as compared to the classical equation. Also, as device output impedances becomes generally smaller with reduced channel lengths through process scaling, the exact gain-expression in (11) will yield a gain-value closer to the actual circuit-simulated value compared to the classical approximate expression in (14). In addition, the simplified gain-expression in (12) deduced from the exact expression in (11) provides an improvement over the classical method represented by the approximate expression in (14), due to the additional design insight and accuracy provided by the additional transconductance parameter, gm5,6 of (M5, M6) while still being amenable to the evaluation of the first order gain in a simplified way.

The calculated gain-error factors for the exact gain-expression in (11), and the approximate (classical) gain-expression in (14) with respect to the actual Cadence circuit simulated gain (\(A_{v\_actual}\)) can be given by,

$$G_{error\_exact} = \left[\frac{{A_{v\_exact} - A_{v\_actual} }}{{A_{v\_actual} }}\right]$$
(15)
$$G_{error\_approx} = \left[\frac{{A_{v\_approx} - A_{v\_actual} }}{{A_{v\_actual} }}\right]$$
(16)

The derivations provided in this paper also assists in finding the mirror pole [1], \(\omega_{{\text{PM}}}\) at the drain of M1 (mirror node) using the derived value of RL in (6) for the time-constant,\(\tau_{PM}\) at this node. It is thus approximately given by,

$$\omega_{{\text{PM}}} = \frac{1}{{\tau_{PM} }} \approx \frac{1}{{R_{L} C_{E} }}$$
(17)

where, CE is approximately the total capacitance at the mirror node, and, is given by,

$$C_{{\text{E}}} = \left( {C_{{{\text{GD}}\_{\text{M1}}}} + C_{{{\text{DB}}\_{\text{M1}}}} + C_{{{\text{DB}}\_{\text{M3}}}} + C_{{{\text{DG}}\_{\text{M3}}}} + C_{{{\text{GS}}\_{\text{M5}}}} + C_{{{\text{GS}}\_{\text{M6}}}} + C_{{{\text{GD}}\_{\text{M5}}}} + C_{{{\text{GD}}\_{\text{M6}}}} } \right)$$
(18)

Consequently, the derivations in this paper also helps in estimating the frequency response of the OTA with low-voltage cascode current mirror load.

3 Numerical analysis and circuit simulation results

The small-signal gain of the CMOS OTA with LVCCM load in the Fig. 1 was simulated through AC-analysis on Cadence Spectre. The gain was also numerically calculated on MATLAB using both (11 and 14). These results were then compared. Two sets of calculations and circuit simulations were performed employing the 180-nm and the 65-nm CMOS process technologies.

Simulation and calculation set I: A power-supply of 1.8 V and the 180-nm TSMC CMOS technology was employed for this set of calculations and simulations. The total bias-current through the tail device M7 was 19.2189 µA with 9.60943 µA in each half-circuit. The bias-voltages were, VB1 = 600 mV, VB2 = 900 mV, and the DC common-mode bias voltage at the two differential-inputs was 800 mV. The MOSFET device sizes and their respective threshold-voltages, transconductances, body transconductances, and output impedances were as follows:

For (M1, M2), (W/L) = 7 µm/0.6 µm, gm = 156.25µ-mho, gmb = 40.774 µ-mho, ro = 1.336 MΩ, and Vth = 575.76 mV. For (M3, M4), (W/L) = 2.7 µm/0.5 µm, gm = 74.71 µ-mho, gmb = 24.172 µ-mho, ro = 866.569 kΩ, and Vth = − 561.25 mV. For (M5, M6), (W/L) = 6.2 µm/0.5 µm, gm = 102.74 µ-mho, gmb = 35.13 µ-mho, ro = 213.33 kΩ, and Vth = − 516.69 mV. Finally, for M7, (W/L) = 5 µm/0.6 µm, gm = 225.619 µ-mho, gmb = 63.812 µ-mho, ro = 176.076 kΩ, and Vth = 515.51 mV.

Figure 12 shows the comparison of the actual Cadence Spectre simulated differential-gain (Av_actual) of the CMOS OTA with LVCCM load, with the MATLAB calculated estimates using the new exact gain-expression in (11) and the approximate (classical) expression for standard cascode-current-mirror load equivalence in (14), employing the 180-nm TSMC CMOS process technology. The actual AC-simulated mid-band gain (Av_actual) was 183.02 (= 45.25 dB), the calculated mid-band gain using (11) was 185.14 (= 45.35 dB), and the calculated mid-band gain using (14) was 195.66 (= 45.83 dB).

Fig. 12
figure 12

Comparison of the actual Cadence simulated differential-gain (Av_actual) of the CMOS OTA with LVCCM load, with the numerical estimates using the new exact gain-expression in (11) and the approximate (classical) gain-expression for standard cascode-current-mirror load equivalence in (14), employing the 180-nm TSMC CMOS process for the circuit in Fig. 1

Full size image

Simulation and calculation set II: A power-supply of 1 V and the 65-nm TSMC CMOS technology was employed for the 2nd set of calculations and simulations. The total bias-current through the tail device M7 was 67.03 µA with 33.51 µA in each half-circuit. The bias-voltages were, VB1 = 400 mV, VB2 = 550 mV, and the DC common-mode bias voltage at the two differential-inputs was 450 mV. The MOSFET device sizes and their respective threshold-voltages, transconductances, body transconductances, and output impedances were as follows:

For (M1, M2), (W/L) = 1 µm/0.1 µm, gm = 408.4µ-mho, gmb = 64.6 µ-mho, ro = 53 kΩ, and Vth = 422.7 mV. For (M3, M4), (W/L) = 11 µm/0.1 µm, gm = 564.4 µ-mho, gmb = 59.65 µ-mho, ro = 19.3 kΩ, and Vth = − 389.9 mV. For (M5, M6), (W/L) = 5 µm/0.1 µm, gm = 468.6 µ-mho, gmb = 55.9 µ-mho, ro = 20.91 kΩ, and Vth = − 367 mV. Finally, for M7, (W/L) = 3 µm/0.1 µm, gm = 867.2 µ-mho, gmb = 149.3 µ-mho, ro = 6.221 kΩ, and Vth = − 416.2 mV.

Figure 13 depicts the comparative plot of the actual Cadence simulated differential-gain (Av_actual) of the CMOS OTA with LVCCM load, along-with the MATLAB calculated estimate using the new exact gain-expression in (11) and the approximate (classical) gain-expression for standard cascode-current-mirror load equivalence in (14), employing the 65-nm TSMC CMOS process technology. The simulated mid-band gain (Av_actual) was 17.82 (= 25.02 dB), the mid-band gain using (11) was 18.22 (= 25.21 dB), and the gain using (14) was 20.25 (= 26.13 dB).

Fig. 13
figure 13

Comparison of the actual Cadence simulated differential-gain (Av_actual) of the CMOS OTA with LVCCM load, with the numerical estimate using the new exact gain-expression in (11) and the approximate (classical) gain-expression for standard cascode-current-mirror load equivalence in (14), employing the 65-nm CMOS process for the circuit in Fig. 1

Full size image

It is thus clearly evident that the plots for the exact mid-band gain-expression in (11) matches very closely (almost tracing) the simulated mid-band gain obtained through AC circuit-simulation. The mid-band gain obtained using the approximate (classical) gain-expression in (14) is quite inaccurate compared to the exact gain-expression in (11). Table 1 shows a comparison of the results for the two sets of simulations and calculations using the 180-nm and the 65-nm TSMC CMOS process technologies. As the output impedances of the devices becomes smaller (having smaller finite values) with technology scaling the classical mid-band gain-expression in (14) becomes more inaccurate compared to the exact mid-band gain-expression in (11). For the 180-nm CMOS process, employing (15) the gain-error compared to the actual Cadence Spectre circuit-simulated value (Av_actual) is only around 1.15% by using the exact mid-band gain-expression in (11). Whereas, the error by using the approximate (classical) gain-expression in (14) compared to the circuit-simulation (Av_actual) was 7%. For the 65-nm CMOS process, employing (15) the gain-error is around 2.24% by using the exact gain-expression in (11). On the other hand, the gain-error employing (16) by using the approximate (classical) gain-expression in (14) compared to the circuit-simulated mid-band gain (Av_actual) was as much as 12%. And, hence, the gain-error increases with technology scaling with the reduction in channel length.

Table 1 Comparisons of the new exact mid-band gain-expression with the approximate (classical) gain-expression for two different process technologies
Full size table

4 Conclusion

An exact small-signal mid-band gain-expression for the CMOS differential-amplifier OTA with low-voltage-cascode-current-mirror load has been deduced employing an innovative technique. This exact gain-expression indicates that the actual gain is only a fraction of the gain calculated by an approximate (classical) gain-expression using the standard cascode-current-mirror equivalence and the accuracy of the exact gain-expression increases significantly with reducing technology node. This new exact gain-expression thus provides a more accurate gain-estimate for today’s low-voltage deep nano-metric CMOS processes, and, has not been reported before. Both Cadence Spectre circuit simulations and numerical analysis using MATLAB is provided employing the 180-nm and 65-nm TSMC CMOS process technologies. The derived exact expression also provides new design insight in fine-tuning the gain of the OTA with LVCCM load using the transconductance gm5,6 of the cascode mirror devices (M5, M6) as can be seen from (11 and 12). The simplified expression in (12) deduced from the exact expression in (11) provides an improvement over the approximate (classical) method, due to the additional accuracy provided by this additional transconductance parameter, gm5,6 of (M5, M6) while still being amenable to first order gain analysis. This additional degree of design freedom in gain adjustment is lost through the approximation steps as can be seen from (13 and 14). Hence this paper provides an improved analysis and better design intuition on the topic of mid-band gain expression for the OTA with low-voltage cascode current mirror load.