ADC based on a fully differential current mode integrator

Abstract

The paper presents current mode Analog to Digital Converters (ADC) for a standard digital CMOS technology in a nm scale. It is shown that such converters composed of a fully differential current mode integrator make it possible to achieve a several-bit resolution necessary for pipeline processing. The proposed fully differential structure provides a 1-bit higher resolution in comparison to a non-balanced structure. The goal of the paper is obtained without voltage increasing above the standard 1.2 V supply. The pipelined ADC, composed of two 5-bits converters, consumes 1.5 mW of power and its Walden figure-of-merit equals 104.34 fJ/conv.

1 Introduction

Advanced standard digital CMOS technologies make it possible to realize an ADC with a resolution of several bits. With the use of these simpler converters a dozen or more bits can be achieved in pipeline processing.

Many realizations of ADC are based on a switched capacitor technique [1,2,3] which uses mainly operational amplifiers, not easy to implement in up-to-date CMOS technologies. Such voltage mode elements are often energy-expensive, [4], although they are used as components for example in SAR ADCs [5,6,7]. Hence, current mode circuits can be useful in analog to digital converters [8,9,10].

The paper proves that several bits are attainable in a converter composed of a current mode integrator. The additional advantage of an analog circuit operating in the current mode is a standard supply voltage, the same one which is used in the digital part of the network [19, 20]. A supply voltage exceeding the standard value may be necessary for voltage mode circuits, especially in case they are implemented in a standard digital CMOS nanometre technology, [11].

The paper is structured in the following way. Sections 2 and 3 briefly describe basic properties of algorithmic converters based on an integrator. A detailed analysis of a fully differential current mode integrator is presented in Sects. 4 and 5 contains a corresponding analysis for an ADC based on the integrator. The last section concludes the paper.

2 Algorithmic ADC

A commonly used algorithm for converting a decimal number into a binary form is based on a successive division of the number by 2. The binary number bits are obtained as remainders of the divisions. The sampled signal is on the decrease in the successive steps, which is the main disadvantage of such algorithm. For example the signal is 1024 times smaller providing that we want to obtain it as a number composed of 10 bits.

Modification of this algorithm consists of a multiplication of the sampled signal S by 2 and a subtraction of the reference signal R from the product. If the result obtained at the comparator (Comp) output is positive then $b=1$ and the residual signal $S_r =2S-R$ is delivered to the input of the multiplier ($\times$2) to calculate the next bit. If the signal at the comparator output is less than or equal to zero then $b=0$ and the signal $S_r =2S$ is delivered to the multiplier input. Implementation of such an algorithm is presented in Fig. 1, in which the sub-circuit composed of two transmission gates (TG) acts as a one-bit Digital to Analog Converter (DAC).

The number of clock periods necessary to process the signal in the converter in Fig. 1 is equal to the number of bits. The next sample of signal S can be transmitted via the TG input only after such time period. However, residual signal $S_r$ can be delivered not to the input of the same ADC but to the successive converter. This conversion is realized during a one clock period with a latency and is called pipeline processing.

It is easy to implement all operations of the algorithmic ADC in the current mode,[12].

ADC in Fig. 1 doubles the error in each operation step. To reduce the error, instead of one-bit converters, higher precision several-bit ADCs are used in pipeline processing. In this case the one-bit DAC and multiplication by 2 must also be replaced by a several-bit Multiplying Digital to Analog Converter (MDAC),[13].

Fig. 1

Hardware implementation of the algorithmic ADC

3 Converters based on an integrator

Fig. 2

ADC implementation with single integration

3.1 Single integration

The implementation of an ADC with single integration, composed of a comparator (Comp), an integrator (Integr), a transmission gate (TG) and an n-bit register (nBitRegist), is presented in Fig. 2. The digital signal of an $f_c$ frequency is delivered by a clock. The result of the integration of reference signal R is compared to sampled signal S. Integration time is proportional to S according to the following relation:

$$\begin{aligned} S=\frac{1}{\tau }\int _0^T Rdt=RT/\tau , \end{aligned}$$

(1)

where $\tau$ is a time constant of the integrator.

If Eq. (1) is met then the transmission gate is closed and the register shows the counted number of clock periods.

3.2 Double integration

Double integration is performed during two periods. The integration of the sampled signal S occurs during the first one $T_r \ge 2^n /f_c$, where n is the bit number and $f_c$ is the clock frequency. The second integration period of reference signal R is continued as long as the comparator recognizes equality of the following integrals:

$$\begin{aligned} \frac{1}{\tau }\int _0^{T_r} Sdt=\frac{1}{\tau }\int _0^T Rdt. \end{aligned}$$

(2)

Therefore we can write:

$$\begin{aligned} ST_r =RT, \;\;\;\;\;\;\;\; S=RT/T_r \end{aligned}$$

(3)

Let us note that $2^n /f_c$ is the minimal time necessary to achieve an n-bit precision and that in case of the double integration the result does not depend on the time constant $\tau$ of the integrator. Hence, an ADC with double integration is more precise than the one with single integration at the cost of speed.

4 Fully differential current mode integrator

Fig. 3

Continuous-time current mode integrator in a fully differential structure

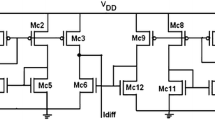
Drain currents in the saturation mode of nMOS and pMOS transistors presented in Fig. 3 can be described using a simple quadratic model, with

$$\begin{aligned} I_{Dn}=\frac{\beta _n}{2}(V_{GS}-V_{Tn})^2, \;\;\; I_{Dp}=\frac{\beta _p}{2}(V_{SG}+V_{Tp})^2, \end{aligned}$$

(4)

where $V_{GS}=V_{1,2}-V_{SS}$, $V_{SG}=V_{DD}-V_{1,2}$. We assume, without losing generality and for the simplification of calculations, that the supply voltages are symmetrical $V_{DD}=-V_{SS}=V_{s}$. The same applies to gate voltages $V_{1}=-V_{2}=V_g$. Hence, drain currents (4) have the following form

$$\begin{aligned} I_{Dn}=\frac{\beta _n}{2}(\pm V_{g}+V_{s}-V_{Tn})^2, \;\;\; I_{Dp}=\frac{\beta _p}{2}(V_{s}\mp V_{g}+V_{Tp})^2, \end{aligned}$$

(5)

where the upper signs are taken for transistors in the positive signal path (the top circuit part) and the lower signs for transistors in the negative signal path (the bottom circuit part) of the circuit in Fig. 3. If the supply is asymmetrical, $V_{DD}\ne |V_{SS}|$, then all voltages in the fully differential circuit are shifted by $V_{sh}=(V_{DD}+V_{SS})/2$.

All complementary transistor pairs used in this circuit feature properly sized channel dimensions so that $\beta _n =\beta _p$. For the fully differential structure we can assume all circuit elements in both positive and negative paths are the same. Hence,

$$\begin{aligned} \beta _{n1}= & {} \beta _{p1}=\beta _{n2}=\beta _{p2}=\beta _{i}, \nonumber \\ \beta _{n3}= & {} \beta _{p3}=\beta _{n4}=\beta _{p4}=\beta _{f}, \nonumber \\ \beta _{n5}= & {} \beta _{p5}=\beta _{n6}=\beta _{p6}=\beta _{o}. \end{aligned}$$

(6)

Similarly, the integrating capacitances

$$\begin{aligned} C_1 =C_2 =C. \end{aligned}$$

(7)

For the circuit in Fig. 3 we can write equations obtained using the Kirchhoff’s Current Law (KCL) in the following form

$$\begin{aligned} I^+_i +I_{f1}+I_{Dp1}= & {} I_{Dn1}+I_{C1}, \end{aligned}$$

(8)

$$\begin{aligned} I^-_i +I_{f2}+I_{Dp2}= & {} I_{Dn2}+I_{C2}, \end{aligned}$$

(9)

$$\begin{aligned} I_{Dp3}= & {} I_{Dn3}+I_{f2}, \end{aligned}$$

(10)

$$\begin{aligned} I_{Dp4}= & {} I_{Dn4}+I_{f1}, \end{aligned}$$

(11)

$$\begin{aligned} I_{Dp5}= & {} I_{Dn5}+I^+_o , \end{aligned}$$

(12)

$$\begin{aligned} I_{Dp6}= & {} I_{Dn6}+I^-_o , \end{aligned}$$

(13)

for nodes 1, 2, 3, 4, 5, 6, respectively. Pairs of Eqs. (8) and (9), (10) and (11), (12) and (13), after the subtraction of both sides, give the following result

$$\begin{aligned} I_i =I^+_i -I^-_i= & {} I_{Dn1}-I_{Dn2}+I_{Dp2}-I_{Dp1}\nonumber \\&+I_{C1}-I_{C2}+I_{f2}-I_{f1}, \end{aligned}$$

(14)

$$\begin{aligned} I_{f2}-I_{f1}= & {} I_{Dp3}-I_{Dp4}+I_{Dn4}-I_{Dn3}, \end{aligned}$$

(15)

$$\begin{aligned} I_o =I^+_o -I^-_o= & {} I_{Dp5}-I_{Dp6}+I_{Dn6}-I_{Dn5}. \end{aligned}$$

(16)

Using relations (5) and (6), component $I_{Dn1}-I_{Dn2}$ of Eq. (14) can be written in the following form

$$\begin{aligned} I_{Dn1}-I_{Dn2}= & {} \frac{\beta _i }{2}(V_{g}+V_{s}-V_{Tn})^2\nonumber \\&-\frac{\beta _i }{2}(-V_{g}+V_{s}-V_{Tn})^2\nonumber \\= & {} 2\beta _i (V_s -V_{Tn})V_{g}, \end{aligned}$$

(17)

while component $I_{Dp2}-I_{Dp1}$ in the following form

$$\begin{aligned} I_{Dp2}-I_{Dp1}= & {} \frac{\beta _i }{2}(V_{s}+V_{g}+V_{Tp})^2\nonumber \\&-\frac{\beta _i }{2}(V_{s}-V_{g}+V_{Tp})^2\nonumber \\= & {} 2\beta _i (V_s +V_{Tp})V_{g}. \end{aligned}$$

(18)

Similarly we can obtain components

$$\begin{aligned} I_{Dp3}-I_{Dp4}= & {} -2\beta _f (V_s +V_{Tp})V_{g}, \end{aligned}$$

(19)

$$\begin{aligned} I_{Dn4}-I_{Dn3}= & {} -2\beta _f (V_s -V_{Tn})V_{g}, \end{aligned}$$

(20)

$$\begin{aligned} I_{Dp5}-I_{Dp6}= & {} -2\beta _o (V_s +V_{Tp})V_{g}, \end{aligned}$$

(21)

$$\begin{aligned} I_{Dn6}-I_{Dn5}= & {} -2\beta _o (V_s -V_{Tn})V_{g}, \end{aligned}$$

(22)

of remaining Eqs. (15) and (16). Hence, equations (14), (15) and (16) can be written as

$$\begin{aligned} I_i= & {} 2\beta _i (2V_s -V_{Tn}+V_{Tp})V_g \nonumber \\&+2sCV_g +I_{f2}-I_{f1}, \end{aligned}$$

(23)

$$\begin{aligned} I_{f2}-I_{f1}= & {} -2\beta _f (2V_s -V_{Tn}+V_{Tp})V_g , \end{aligned}$$

(24)

$$\begin{aligned} I_o= & {} -2\beta _o (2V_s -V_{Tn}+V_{Tp})V_g , \end{aligned}$$

(25)

if currents $I_{C1}$, $I_{C2}$ are changed with $I_{C1}=sCV_{1}=sCV_g$ and $I_{C2}=sCV_{2}=-sCV_g$ for $C_1 =C_2 =C$. After a simple algebraic calculation we obtain a transfer function of the circuit in Fig. 3 in the form

$$\begin{aligned} H(s)=\frac{I_o (s)}{I_i (s)}=-\frac{\beta _o (2V_s -V_{Tn}+V_{Tp})}{sC+(\beta _i -\beta _f )(2V_s -V_{Tn}+V_{Tp})}. \end{aligned}$$

(26)

This transfer function can be written as

$$\begin{aligned} H(s)=-\frac{1}{s\tau +(a_i -a_f )}, \end{aligned}$$

(27)

where

$$\begin{aligned} \tau =\frac{C}{\beta _o (2V_s -V_{Tn}+V_{Tp})}, \end{aligned}$$

(28)

denotes a time constant and

$$\begin{aligned} a_i =\frac{\beta _i}{\beta _o}, \;\; a_f =\frac{\beta _f}{\beta _o}, \end{aligned}$$

(29)

denote attenuations of input and feedback stages. Providing that $a_i =a_f$, transfer function (27) describes an ideal integrator.

The integrator from Fig. 3, in which the pMOS transistors are used as current sources, [14], in a similar analysis provides a transfer function in the same form (27), but with a time constant of

$$\begin{aligned} \tau =\frac{C}{\beta _o (V_s -V_{Tn})}. \end{aligned}$$

(30)

This result denotes that the integrator composed of current sources needs a higher supply voltage $V_s$ to achieve the same operating speed.

5 ADC structure with double integration

Fig. 4

Implementation of a fully differential ADC with double integration

The fully differential integrator described in the previous section is used in the ADC presented in Fig. 4.

5.1 Basic cells of a double integration converter

Basic cells of the converter with double integration are as follows:

• a multiplexer Mux composed of transmission gates, which is keying the following voltage signals: sampled S, reference R and zero 0,

• a voltage-to-current converter VIC, [15],

• a current mode integrator Int, loaded with high resistance Lo (a complementary transistor pair in a diode connection),

• a several-stage (inverters) comparator Comp,

• a control unit ContrUnit, which collects signals of comparator outputs, controls multiplexer Mux and register BitReg, and closes/opens transmission gate TG for clock fc.

5.2 ADC operation

Operation of the fully differential ADC with double integration is as follows:

• 1. The processed signal S is integrated during a $T_r =2^n /f_c$ period, one of the comparators, in positive or negative paths, shows the sign of S which is recognized by ContrUnit,

• 2. During the first integration period ContrUnit prepares the register for counting (resets and if $S>0$ it assigns the value of 1 to the most significant bit),

• 3. In the beginning of the second integration period ContrUnit transmits (via Mux to VIC inputs) the reference signal of the opposite sign to the sampled signal sign (if $S>0$ then $-R$ to the non-inverting and R to inverting inputs, if $S<0$ then R to the non-inverting and $-R$ to inverting inputs are delivered) and via TG clock signal $f_c$ to BitReg,

• 4. The second integration period T lasts as long as ContrUnit detects a zero value at Comp output (the condition $S*T_r =R*T$ is met), then TG is closed and counting of the clock signal is finished.

• 5. For the remaining time $T_r -T$ContrUnit transmits the 0 value via Mux to both VIC differential inputs.

The last point provides the sampling time of signal S equal to $2T_r$. However, the first and the second of the above points denote that an (n+1)-bit precision of the ADC is achieved. Hence, the ADC in a fully differential structure is as fast as a converter with single integration.

5.3 Operation of a real ADC

In a real ADC operation it is necessary to take into account the latency of blocks used in the converter, especially the one of the comparator Comp. A total latency $T_{lat}$ can achieve several clock periods and to compensate it, the transmission gate TG should be open with a delay of $T_{lat}$. Because of the latency, a non-zero value is achieved at the integrator output and to reset it, instead of a 0, an appropriate pulse should be delivered to its input via Mux. The reset pulse is supplied just before the beginning of the first integration time. The reset time (pulse duration) is denoted by $T_{del}$. The reset pulse amplitude is normally equal to the supply voltage, however for the small input signal S it is lowered to $A_{low}$ value. The signal is recognized as small if the second integration time is smaller than $T_{low}$. All of the times $T_{lat}$, $T_{del}$, $T_{low}$ are given in clock periods. Both times $T_{lat}$ and $T_{del}$/$T_{low}$ lengthen the sampling time during appropriate clock periods.

5.4 Realization of a fully differential ADC

The analog part, especially integrator Int, comparator Comp and converter VIC, were designed for the 65 nm CMOS technology. The control unit ContrUnit was implemented in the VHDL-AMS language. Simulations were performed in the Mentor Graphics environment to obtain responses for chosen input waveforms, for example a rectangle waveform or a staircase signal.

The most important option in these simulations is the examination of the transfer characteristic. To achieve this goal the staircase input signal is going through a transient analysis. The step rise equals $A_{in}$ in a voltage range of $V_{min}=-0.6$ V to $V_{max}=0.6$ V which corresponds to the standard supply of the 65 nm CMOS technology. Hence, the number of sub-ranges in which the transient analysis is performed is $tr=(V_{max}-V_{min})/A_{in}$. To preserve static behavior of the transfer characteristic, its each point is obtained as a median of mode successive results of the transient analysis, which gives number of points equal to tr / mode. An example of such a characteristic for $A_{in}=2$ mV and $mode=13$ is shown in Fig. 5.

The operation algorithm of the ContrUnit makes it possible to run simulations for different reference values $A_{ref}$ and different latency $T_{lat}$. The characteristic in Fig. 5 was obtained for $A_{ref}=560$ mV, $A_{low}=200$ mV and $T_{lat}=T_{del}=T_{low}=2$. The obtained DNL and INL parameters are presented in Figs. 6 and 7, respectively. Other parameters obtained in simulations are as follows: $SNDR=27.307$ dB, which gives $ENOB=4.2438$ and $SNR=35.68$ dB at a 20 MHz frequency range.

Authors also performed a PVT analysis in order to evaluate the dispersion of both non-linearities. Maximum INL and DNL values were determined via simulations for each level of the dispersion. The analysis of the process variation was performed using technological files provided by the TSMC manufacturer. The results are shown in Fig. 8. The dispersions of DNL and INL in respect to the supply voltage were calculated in the range of 0.48–0.78 V ($-20\%/+30\%$ of VDD–VSS values) and are shown in Fig. 9. Similarly, an analysis of the circuit operating in the temperature range of $(-40/+120)\,{^{\circ }}\hbox {C}$ was performed. The result is presented in Fig. 10. The simulations prove that in most cases INL and DNL errors remain below the level of 1 LSB. Only for the case of voltage dispersion, the error reaches the level of 1.5 LSB and, as it was noted in paper [15], in some applications it might be necessary to use rectifiers for the supply of the current mode ADC.

Fig. 5

Transfer characteristic of the realized ADC

Fig. 6

DNL of the realized ADC

Fig. 7

INL of the realized ADC

The estimated power consumption of the digital part of the ADC equals $P_d =690~\upmu \hbox {W}$, and obtained from simulations for the analog part is equal to $P_a =59~\upmu \hbox {W}$. For the clock frequency $f_c =1.6$ GHz used in the simulations we obtain the sampling period equal to $F_s =40~\hbox {MS}/\hbox {s}$. Let us assume that 10 bit ADC ($ENOB=2*4.2438=8.49$) is composed of two converters presented in this paper. We have then $FoM=2(P_a +P_d )/(F_s 2^{ENOB})=104.34fJ/c-s$ (Walden), which is comparable to results reported in literature, [13, 16, 17]. Let us note that the power consumption as well as ENOB for a 10-bit ADC FoM calculation are twice as big as for the 5-bit one used two times in pipeline processing, as mentioned in Sect. 2. Table 1 presents the achieved results in comparison with the solutions presented in the above papers. Parameters like power consumption and FOM are better than in [16, 17] and similar to the ones presented in [13].

Fig. 8

DNL and INL dependence on process variation

Fig. 9

Dispersions of DNL and INL with respect to supply voltage

Fig. 10

Dispersions of DNL and INL with respect to temperature

Fig. 11

Layout of the realized ADC

Fig. 12

Transfer characteristic of the realized ADC obtained in post-layout simulations

The converter layout was designed in Mentor Graphics environment for TSMC 65 nm CMOS technology on a chip area $55.973~\upmu \hbox {m} \,\times \, 25.691~\upmu \hbox {m}$. This macro-cell, composed of cells denoted in Fig. 4, is presented in Fig. 11. The parasitic parameters of the circuit were extracted with the use of Calibre. The results of simulations are similar to the obtained previously, as it is shown in the example of the transfer characteristic in Fig. 12.

Table 1 Designed ADC performance comparison with other works

6 Conclusions

The ADC presented in the paper and composed of current mode cells can be implemented in a digital nm scale CMOS technology with a standard voltage supply. A modified version of the integrator makes it possible to achieve an increasing operating speed without raising voltage. The proposed fully differential structure provides a 1-bit higher resolution in comparison to a non-balanced structure. The elaborated operation algorithm of the control unit provides a latency compensation of analog cells, especially of the comparator. As a result, the high-resolution ADC implementable in a current standard digital 65 nm CMOS technology with 1.2 V supply and available for pipeline processing is obtained. The achieved result is in competition with the presented in the literature. The converter layout was designed and the post-layout simulations confirm the results based on the integrator schematic.