1 Introduction

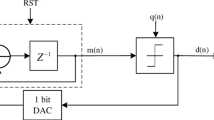
Using a digital \(\varSigma \varDelta\) modulator, number of data bits in a digital-to-analog converter (DAC) can be lowered and hence a less complex set of analog components can be utilized [15]. In fact, by employing oversampling and digital \(\varSigma \varDelta\) noise shaping, higher effective resolution can be achieved from a nominally lower-resolution DAC. A drawback, however, is the higher quantization noise which is spectrally shaped to out-of-band frequencies by the modulator. An oversampling DAC can be modified, as shown in Fig. 1, to an interpolating stage, digital \(\varSigma \varDelta\) modulator and a semi-digital finite-impulse response (FIR) filter. semi-digital FIR digital-to-analog converters (SDFIR DAC), used as filters and data converters, are implemented as switched-capacitor network or in current-steering architectures, and reported previously in [2, 4,5,6,7, 16, 21,22,23, 25]. In this configuration, N-bit base-band data is up-sampled and filtered through the interpolator and then applied to the digital \(\varSigma \varDelta\) modulator. The output of the \(\varSigma \varDelta\) modulator is an M-bit signal where M would typically be significantly smaller than N. The M-bit data is converted to analog signal through the SDFIR DAC and resulting analog signal is then filtered with analog reconstruction filter to remove aliasing images at integer multiples of sample frequency. The semi-digital FIR DAC architecture provides both analog filtering to suppress the spectrally-shaped quantization noise, as well as digital-to-analog conversion.

Fig. 1
figure 1

Oversampling \(\varSigma \varDelta\) semi-digital FIR DAC

Full size image

In this paper, we formulate the FIR optimization problem such that it considers the transfer characteristics of the \(\varSigma \varDelta\) modulator, the semi-digital FIR filter response, and the Sinc roll-off due to the DAC zero-order hold pulse amplitude modulation all together. The analog implementation parameters are also included in the optimization procedure. Through the optimization we can minimize the impact of typical analog imperfections (mismatch, noise, etc.) on the output signal. To systematically tackle the problem, we define different set of parameters and metrics to be used in the optimization problem of SDFIR filter; magnitude metrics, energy metrics and analog metrics (or hardware cost). In the formulated optimization problem, each of these metrics can be selected as objective function or constraint.

This paper is organized as follows. In Sect. 2, a short background on SDFIR DAC is given. Different metrics are defined and utilized in the optimization problem formulation. These metrics are described in detail in Sects. 3 and 4. Coefficients precision effect on SDFIR DAC optimization metrics is studied in Sect. 5. Analog metrics used in the optimization procedure is presented in detail in Sect. 6, and in Sect. 7, a set of optimization problems are outlined employing different optimization metrics. These use-cases are demonstrating how we can select the optimization metrics depending on the application. Finally, the remarks of this paper are concluded in Sect. 8.

2 Semi-digital FIR DAC

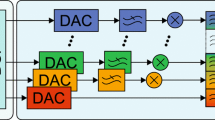
Although most of the published SDFIR DACs utilize single bit \(\varSigma \varDelta\) quantizer, in the general case, the number of bits at the output of the \(\varSigma \varDelta\) quantizer can be extended to more than one bit, and having a multi-bit semi-digital FIR filter where each tap of the filter is realized with a sub-DAC of M bits and weighted according to the FIR coefficients. Multi-bit and single-bit block diagram of SDFIR DACs are shown in Figs. 2 and 3, respectively, where \(X_{in}\) is the input digital data to the SDFIR DAC, and \(h_n\), (for \(n=0 \ldots N\)), is the FIR filter coefficients. In current steering architecture implementation of SDFIR DAC, the analog multipliers are realized by weighted current sources according to the corresponding FIR filter coefficient. The negative coefficients of FIR filter in a differential structure, is realized by swapping the output polarity. FIR filters, are causal, linear and time-invariant systems that can be uniquely described by their impulse response, and the transfer function can be derived as

$$\begin{aligned} H(z) =\frac{Y(z)}{X(z)}= \sum _{n=0}^N h_n z^{-n}, \end{aligned}$$
(1)

where X(z) is the input in the \(z-\)domain, \(h_n\) denotes the filter coefficients, and the output Y(z), will be directly proportional to the output current. In time domain, for a SDFIR DAC, we have \(y(nT) = I_{\text {out}}(nT)/I_u\), where \(I_u\) is the nominal current of a unit current source.

Fig. 2
figure 2

Multi-bit semi-digital FIR filter architecture

Full size image
Fig. 3
figure 3

Single-bit semi-digital FIR filter architecture

Full size image

2.1 Coefficients precision

The full-scale current at the output is derived from the output load and the voltage swing specification. For instance if the differential voltage swing of 400 mV peak-to-peak, over a 50 \(\varOmega\) termination load is required, the maximum full-scale current, \(I_{\text {max}}\), will be 4 mA. The maximum current scenario happens when all the taps are conducting, i.e.,

$$\begin{aligned} I_{\text {max}} = k~I_u \sum _{n=0}^{N-1} |h_n|, \end{aligned}$$
(2)

where \(h_n\) denotes the filter coefficients and k is the scaling factor and corresponds to the coefficients precision. The design method commonly adopted for SDFIR DAC, is to use a standard digital FIR filter design algorithms (e.g. Parks-McClellan algorithm [17]), and choose a practical numerical resolution for the FIR coefficients [2, 4, 9, 11, 22, 23, 26]. The design of linear-phase FIR filters with fractional coefficients are widely discussed in the literature [20, 24]. In this work, we are considering the coefficient precision into the formulation of the SDFIR DAC optimization problem together with the analog metrics and implementation restrictions. A SDFIR DAC design problem can be formulated to optimize the magnitude of the frequency response in different frequency segments. Or it can be formulated to optimize the total energy in particular segment of the frequency. For each approach, we define corresponding metrics (magnitude or energy) to be utilized, as objective or constraint, in the optimization problem formulation of a SDFIR DAC. Moreover, a set of analog metrics will be also defined to be included in the optimization problem.

3 Design for magnitude metrics

When designing for magnitude metrics, the \(\varSigma \varDelta\) modulator noise transfer function, and SDFIR filter response, and the Sinc roll-off frequency response of the DAC are cascaded to get the overall magnitude frequency response. Considering an Nth-order FIR filter with impulse response coefficients \(h_n\), the transfer function is as in (1). If the impulse response coefficients are either symmetric \(\left( h_n = h_{N-n}\right)\) or anti-symmetric \(\left( h_n = -h_{N-n}\right)\), the transfer function will exhibit linear-phase characteristics and the frequency response can be written as \(H\left( e^{j\omega T}\right) = e^{-j N \omega T/2} H_R(\omega T)\), where \(H_R(\omega T)\) is a real-valued linear function, called the zero-phase frequency response. As \(|H\left( e^{j\omega T}\right) | = |H_R(\omega T)|\), it is possible to consider only \(H_R(\omega T)\) in design of the filter. For symmetric cases, \(H_R(\omega T)\) for odd N, can be written as:

$$\begin{aligned} H_R(\omega T) = 2 \sum _{n=1}^{(N+1)/2} h{\left( \tfrac{N+1}{2}-n \right) } \cos \left( \omega T\left( n-\tfrac{1}{2}\right) \right) , \end{aligned}$$
(3)

and for even N:

$$\begin{aligned} H_R(\omega T) = h{\left( \tfrac{N}{2}\right) } + 2 \sum _{n=1}^{N/2} h \left( \tfrac{N}{2}-n\right) \cos \left( \omega T n\right) . \end{aligned}$$
(4)

Similar expressions exist for the anti-symmetric cases. To design a FIR filter, a desired function, \(D(\omega T)\), and an error weighting function, \(W(\omega T)\), are required. The absolute approximation error, \(\delta (\omega T)\), can then be written as

$$\begin{aligned} \delta (\omega T)= & {} |W(\omega T)\left[ H_R(\omega T) - D(\omega T) \right] | \nonumber \\= & {} |W(\omega T)| \left| H_R(\omega T) - D(\omega T) \right| . \end{aligned}$$
(5)

The FIR filter design problem is often formulated as minimizing \(\delta _{\infty } = \max ~\delta (\omega T)\), i.e., the minimax \(L_{\infty }\) (or Chebyshev error) [24].

3.1 SDFIR design considering \(\varSigma \varDelta\) modulator and Sinc roll-off response

The real-valued noise power transfer function of the \(\varSigma \varDelta\) modulator (NTF) can be extracted in the same way as for a FIR filter and it helps to calculate the magnitude metric in a closed form. However this is not necessary since the linear phase response of the \(\varSigma \varDelta\) modulator NTF is not of interest. Instead we can use the absolute value of the noise transfer function. This is specifically important when the \(\varSigma \varDelta\) modulator poles are not located in the origin. The total transfer function including the \(\varSigma \varDelta\) modulator and semi-digital FIR filter can be expressed as \(H_{ total }(\omega T) = H_R(\omega T)~|{\text {NTF}}(\omega T)|\). Finally, by considering anti-Sinc function in the SDFIR DAC response, we can write the total transfer function as:

$$\begin{aligned} H_{ total }(\omega T) = H_{R}(\omega T)~ |{\text {NTF}}(\omega T)|~ P(\omega T), \end{aligned}$$
(6)

where the Sinc function is defined as

$$\begin{aligned} P(\omega T) = \frac{\sin (\omega T /2 )}{\omega T / 2}. \end{aligned}$$
(7)

This cascaded transfer function can be utilized in (5) to form the magnitude metrics in designing the semi-digital DAC coefficients.

4 Design for energy metrics

If we design the FIR filter for total energy in particular frequency band, the square of the error function within the whole band of interest is integrated to get the energy [14]. Considering the absolute approximation error, \(\delta (\omega T)\), defined in (5), the energy metric can be defined in the frequency band of \(\varOmega\) as

$$\begin{aligned} E= \int \limits _{\omega T \in \varOmega } {\left| \delta (\omega T)\right| }^2 d \omega T. \end{aligned}$$
(8)

Let us assume an example of a type-I low-pass FIR filter, i.e., an even order filter with a symmetric impulse response. The desired function in this example, is one in the pass-band and zero in the stop-band. The energy function in the stop-band (\(\varOmega _S\)) simplifies to \(\int {\left| H_R(\omega T) \right| }^2 d \omega T\). By inserting the filter transfer function we get energy function E as

$$\begin{aligned} E= \int \limits _{\omega T \in \varOmega _S} \left[ h{\left( \tfrac{N}{2}\right) } + 2 \sum _{n=1}^{N/2} h{\left( \tfrac{N}{2}-n\right) } \cos (\omega T n) \right] ^2 d \omega T. \end{aligned}$$
(9)

By further expanding the equation, it yields

$$\begin{aligned} E=\,& {} h^2{\left( \tfrac{N}{2}\right) } I(0,0) + 4 h{\left( \tfrac{N}{2}\right) } \sum _{n=1}^{N/2} h{\left( \tfrac{N}{2}-n\right) } I(0,n) \nonumber \\&+ 4 \sum _{n=1}^{N/2} \sum _{m=1}^{N/2} h{\left( \tfrac{N}{2}-n\right) } h{\left( \tfrac{N}{2}-m\right) } I(m,n), \end{aligned}$$
(10)

where the integral function, I(m, n), is

$$\begin{aligned} I(m,n)=\int \limits _{\omega T \in \varOmega _S}{\cos (\omega T m) \cos (\omega T n)} d\omega T . \end{aligned}$$
(11)

The integral function can either be approximated numerically, or if possible, even expressed in a closed form.

4.1 Considering \({\varvec{\Sigma}}{\varvec{\Delta}}\) modulator NTF and Sinc roll-off response

The overall transfer function \(H_{ total }(\omega T)\) from (6), can be now plugged in (5) and (8) to give the energy metric

$$\begin{aligned} E = \int \limits _{\omega T \in \varOmega _S} {\left| H_{R}(\omega T)~{\text {NTF}}(\omega T)~ P(\omega T) \right| }^2 d \omega T . \end{aligned}$$
(12)

The energy in the band of interest can further be expanded and written as in (10), where the integral function, I(m, n), now becomes

$$\begin{aligned} I(m,n)= & {} \int \limits _{\omega T \in \varOmega _S} \cos (\omega T m) \cos (\omega T n) 2^{2L} \nonumber \\&\left( \sin ^{2L} { \frac{\omega T}{2} } \right) \frac{\sin ^2({\omega T/2}) }{( \omega T/2)^2 } d\omega T. \end{aligned}$$
(13)

The integral function above can be approximated numerically.

5 Coefficients precision consideration

The magnitude and energy metrics in the previous sections are reviewed in a general case of fractional coefficients with infinite precision. Although finite coefficient precision effect on FIR frequency response has been generally studied before in literature [3, 10, 12]. In this section we will look at particular cases of SDFIR DAC design and quantify the coefficient precision impact on the analog complication and SDFIR DAC frequency response. One approach to determine the coefficient precision is to truncate the coefficients to get the as close as possible to the wanted current value in the current sources implementation. One way to do this is to manually adjust sizing of each current source to get the current so that the total sum of the SDFIR coefficients be for instance 4 mA as in (2) and the ratio between the coefficients are also maintained get the frequency selective properties of the FIR filter. This approach is tedious if we the SDFIR filter order increases. There is also a limitation on the accuracy of the current source due to the minimum sizing of transistors allowed in each technology. That is in one point you have to truncate your coefficient and will introduce truncation error. Another SDFIR DAC approach which is more similar to standard general DAC design is to define a unit current source and then instantiate a number of this unit current sources for each tap. However the coefficients need to be integer to be able to instantiate integer number of the unit current sources. to make the coefficients integer, one would multiply the coefficients with a scaling factor k, and truncate to integer number. And there again the truncation error is introduced. The truncation error will degrade the accuracy of the FIR filter, for instance, the attenuation level in the stop-band. To achieve the required filtering specification from the designed SDFIR DAC, one has to over-design the FIR filter to be able to meet the requirement after introducing the coefficient truncation errors.

Another issue is the filter coefficient variation that imposes limits to the achievable stop-band attenuation [19]. This means that if there is a variation in the coefficients we cannot achieve an infinitely small output since the output is actually the sum of the coefficients. This problem becomes important in SDFIR DAC implementation since there will be mismatch among the current sources that implement the filter taps. We should consider this bound when designing the filter as the higher bound on the achievable attenuation level [18, 19]. The question is now how to determine the scaling factor, or in other words, what coefficient precision should we select.

We have suggested in this work to formulate the problem from the beginning such that we put constraint on the coefficient to be integer numbers. There of course we need to consider the scaling factor k, in our optimization problem and specify the coefficient precision as one of the optimization parameters basically. In this section we will review the scaling factor k effect on the magnitude and energy metrics. The \(H_R(\omega T)\), will be considered here is for simplification of the equations and the actual transfer function can be cascade of the SDFIR, \(\varSigma \varDelta\) modulator and the Sinc roll-off as we will see in Sect. 7.

5.1 Scaling factor in magnitude metrics

Assuming a type-I low-pass FIR filter with equal ripples, the desired pass-band (which was one before) is multiplied by scaling factor (k), and stop-band will be zero. The magnitude metric, i.e., the error function simplifies to

$$\begin{aligned} H_R(\omega T)\le & {} k (1+\delta _c(\omega T)) \qquad \omega T\in \varOmega _C \nonumber \\ H_R(\omega T)\ge & {} k (1-\delta _c(\omega T)) \qquad \omega T\in \varOmega _C \nonumber \\ H_R(\omega T)\le & {} k \delta _s(\omega T) \qquad \omega T\in \varOmega _S \nonumber \\ H_R(\omega T)\ge & {} - k \delta _s(\omega T) \qquad \omega T\in \varOmega _S, \end{aligned}$$
(14)

Now we introduce a fine-tuning variable pass-band gain, s. The k parameter is selected to give the approximate pass-band gain for the optimization, and s parameter is defined to find the optimum pass-band gain in the vicinity of the given pass-band gain (k). We let s be over an interval such that the overall gain sweeps between two consecutive k values. Hence the magnitude metric (14) simply multiplies with the variable s:

$$\begin{aligned} H_R(\omega T)\le & {} s k (1+\delta _c(\omega T)) \qquad \omega T\in \varOmega _C \nonumber \\ H_R(\omega T)\ge & {} s k (1-\delta _c(\omega T)) \qquad \omega T\in \varOmega _C \nonumber \\ H_R(\omega T)\le & {} s k \delta _s(\omega T) \qquad \omega T\in \varOmega _S \nonumber \\ H_R(\omega T)\ge & {} - s k \delta _s(\omega T) \qquad \omega T\in \varOmega _S . \end{aligned}$$
(15)

5.2 Scaling factor in energy metrics

Considering the same example, type-I low-pass FIR filter, the energy metrics becomes

$$\begin{aligned} E = \frac{1}{k^2} \int \limits _{\omega T \in \varOmega _S} {\left| H_R(\omega T) \right| }^2 d \omega T. \end{aligned}$$
(16)

The energy metric is either an optimization objective or a constraint that needs to be kept smaller than a parameter here introduced as \(\epsilon\) and the constraint will be

$$\begin{aligned} E=\frac{1}{k^2} \int \limits _{\omega T \in \varOmega _S} {\left| H_R(\omega T) \right| }^2 d \omega T \le \epsilon . \end{aligned}$$
(17)

In case of the energy metric being an optimization objective, the \(\epsilon\) must be minimized. In case of being a constraint, it needs to be guaranteed that \(\epsilon \le \epsilon _{\text {fix}}\). The scaling factor as defined previously is k. The variable s is again the fine-tuning gain. In either case, the optimization problem turns out to be non-convex when inserting the variable s, since it eventually appears as \(s^2\) in the optimization problem which employs the energy metric. For example, if the objective function is the energy, E, we have

$$\begin{aligned} E= \frac{1}{k^2} \int \limits _{\omega T \in \varOmega _i} {\left| H_R(\omega T) \right| }^2 d \omega T \le s^2 \epsilon , \end{aligned}$$
(18)

where \(\epsilon\) must be minimized. This is now a non-convex problem and cannot be solved.

5.3 Joint magnitude and energy metrics

To overcome the issue with non-convex optimization problem, we change the tuning variable \(s=s_{\text {fix}} + \alpha\), where \(s_{\text {fix}}\) is a fixed value and \(\alpha\) is a variable. \(s^2\) can now be estimated as

$$\begin{aligned} s^2 = (s_{\text {fix}} + \alpha )^2 \approx s_{\text {fix}}^2 + 2s_{\text {fix}}\alpha , \end{aligned}$$
(19)

since the variable \(\alpha\) is small compared to \(s_{\text {fix}}\) we neglect the \(\alpha ^2\) term. The energy metric in (18) becomes

$$\begin{aligned} E= \frac{1}{k^2} \int \limits _{\omega T \in \varOmega _i} {\left| H_R(\omega T) \right| }^2 d \omega T \le (s_{\text {fix}}^2 + 2s_{\text {fix}}\alpha ) \epsilon . \end{aligned}$$
(20)

This simple modification will now make the optimization problem a convex problem. However, it will actually also result in a small over-design (due to the \(\alpha ^2 = 0\) approximation) since the right hand side of (20) will become smaller and therefore we put more stringent constraint.

6 Design for analog metrics of SDFIR DAC

Once we have the coefficient values established in our SDFIR, through either rounding off or optimization, we still are prone to imperfections in the actual implementation. These imperfections, such as noise, mismatch, non-linearity, etc., will also cause errors in the filter response, normally decreasing the attenuation level in the stop-band. Mismatch among the elements within each DAC results in harmonic distortion in the semi-digital FIR reconstruction filter response while the mismatch between the FIR taps DACs only varies the transfer function of the filter, i.e., pass-band and stop-band ripples and frequency edges [11]. Therefore, we need to also consider typical analog design constraints in the optimization loop. In this section, we will overview some analog parameters and performances that could be included in the optimization loop - either as a constraint or as an objective value. With respect to the SDFIR, analog design essentially deals with the design of the filter’s sub-cells, i.e., designing a certain number of unit current sources, switches and delay elements. The number of sources per tap effectively equals the filter coefficients, \(h_i\). From an implementation point of view, the order of the filter is desired to be as low as possible to minimize the area and length of interconnect and bias distributions nets. The order also dictates the number of delay elements which in turn influences the power consumption. Moreover we want switching glitches to have minimum impact on performance [8]. Glitches are dependent on the signal and any skew between switching instants for different coefficients. With respect to glitches we focus on the filter response to be able to model the impact of glitches [8, 26], and to have a common reference for comparison between the different results. As a glitch model we count the number of taps/bits that toggle between two different switching instants. For a given FIR filter we have the impulse response

$$\begin{aligned} h(nT) = \sum _{i=0}^{N-1} h_i \delta ( (n-i)T ), \end{aligned}$$
(21)

we can thereby see that at the i to \(i+1\) transition in the impulse response, the total number of elements that switch is \(|h_i| + |h_{i+1}|\). For example, if all taps would be equal, \(h_0\), and we would apply an impulse, we would get the same value out, \(y(nT) = h_0\), but every clock cycle we would switch two current sources and the glitch would be proportional to \(2 h_0\). We aim for minimizing the sum of glitches

$$\begin{aligned} A_{\text {sum}} = \sum _{i=0}^{N-1} |h_i| + |h_{i+1}| = 2\sum _{i=0}^{N-1} |h_i|, \end{aligned}$$
(22)

which turns out that the sum of the glitches is proportional to the absolute sum of coefficients \(\varSigma h\), defined as \(\Sigma h = \sum_{i=0}^{N-1}\left| h_i \right|\). In terms of power consumption the output power delivered to the load is constant as we are fulfilling the required full-scale current or same output voltage swing requirements, regardless of filter design. The power dissipation in analog circuitry like the bias and switch drivers however depends on how many unit element current source we have in our SDFIR DAC and hence the total number unit elements should be minimized. The digital power consumption, however, will depend on the number of delay elements, i.e., the FIR filter length and the number of bits in the sub-DAC, M. Hence we have \(P_{ dig } = P_{ unit } M N\), where \(P_{ unit }\) is the power dissipation of each individual unit cell.

With respect to mismatch, we assume that the analog area is constant as a given design requirement. This means that we can formulate the expected mismatch in each coefficient as \(\sigma _i = \sqrt{h_i} \sigma _x\), where \(\sigma _x\) is the standard deviation of the error of one single current source. The relative error for each coefficient would then be \(\epsilon _i = \sigma _x / \sqrt{h_i}\). The mismatch error is therefore minimized by maximizing all filter coefficients. A cost function could be the sum over the absolute square values in the FIR filter, assuming uncorrelated errors between the coefficients.

$$\begin{aligned} \varSigma _x = \sum _{i=0}^{N-1} h_i^2 ( \sigma _x / \sqrt{h_i} )^2 = \sigma _x^2 \sum _{i=0}^{N-1} |h_i| . \end{aligned}$$
(23)

This equation is now quite similar to the requirement on the sum of all coefficients. Thus the absolute sum of the filter coefficients, \(\varSigma h\), turns out to be a good indicator of the analog cost of the SDFIR filter.

7 Optimization problem formulation

In the previous sections, different metrics were defined for designing SDFIR DAC: magnitude, energy and analog metrics. When designing the SDFIR DAC, any of these metrics can be used as optimization objective versus other metrics as constraint. There are different combinations and depends very much on the application. In this section we describe some optimization problem formulation examples utilizing the defined metrics for different practical cases. In all use cases, a single bit \(\varSigma \varDelta\) Modulator (\(M=1\)) is considered.

7.1 Analog metrics as objective function and magnitude metrics as constraint

A practical optimization problem can be defined as having a spectrum emission mask requirement as constraint and optimize the SDFIR DAC with respect to the analog cost which includes the total number of current sources and the filter order. Hence, we use the magnitude metrics in the pass-band and stop-band which was reviewed previously, as constraint. To illustrate the effect of optimization we choose a communication standard spectral emission mask. The emitted spectral power should fulfill a frequency mask as shown in Fig. 4, with offset to the center frequency. The SDFIR DAC can be optimized to give the attenuation level such that with minimum filter order and analog complexity, the emitted noise is below the mask. A second-order (\(L=2\)) \(\varSigma \varDelta\) modulator with \({\text {OSR}} = 128\) and \(f_s = 640~{\hbox {MHz}}\) is selected for this use case example. The optimization problem is formulated as minimizing the analog complexity or hardware cost, subject to the magnitude metrics, i.e., to fulfill the emission requirement,

$$\begin{aligned} {\text {Minimize}}\; &\varSigma h \nonumber \\ {\text {Subject}}\,{\text{to}}&\\&H_{R}(\omega T) P(\omega T) \le k (1+\delta _c) \qquad \omega T \in \varOmega _C\nonumber \\&H_{R}(\omega T) P(\omega T) \ge k (1-\delta _c) \qquad \omega T \in \varOmega _C\nonumber \\&H_R(\omega T) ~|{\text {NTF}}(e^{j \omega T})|~ P(\omega T) \le k \delta _s \qquad \omega T \in \varOmega _S\nonumber \\&H_R(\omega T) ~|{\text {NTF}}(e^{j \omega T})|~ P(\omega T) \ge - k \delta _s \qquad \omega T \in \varOmega _S,~ \nonumber \end{aligned}$$
(24)

where k is the fixed power-of-two [10], scaling factor as pass-band gain (\(k=2^{w}\)) and \(\delta _c\) and \(\delta _s\) denote the pass-band and stop-band ripples, which are selected to be 0.2 dB and 76 dB respectively. The optimization problem is initially solved with fractional coefficients to find the minimum possible filter order (\(N_{\text {min}}\)). The objective is to find the minimum hardware which is achieved by minimizing the scaling factor k as discussed before. The results of the integer optimization problem with different word-length (w) and N values in the vicinity of the minimum filter order, is shown in Table 1. \(N_{\text {min}}\) is found to be 16 in this case. We see from Table 1, that if we increase the filter order from \(N_{\text {min}}\), 16, to 20, the problem will be feasible even with smaller w which implies more hardware savings except the number of delay elements that we add due to an increased filter order. This is negligible comparing to the savings in the analog cost and the complexity. The optimum solution in this case is found with \(N = 20\) and \(w = 7\) and the resulting filter response is illustrated in Fig. 4. The absolute sum of the SDFIR unit elements in this case is \(\varSigma h=117\).

Table 1 Sum of coefficients (\(\varSigma h\))
Full size table
Fig. 4
figure 4

Optimization results from example 1 (based on model). Also shown are the \(\varSigma \varDelta\) modulator noise transfer function (NTF), spectral emission mask (SEM), semi-digital FIR filter (SDFIR) response, and DAC Sinc roll-off (PAM)

Full size image

7.2 Analog metrics as objective and magnitude metrics as constraint with variable coefficient precision

The filter coefficients are integer numbers, and the optimum result fulfilling the specification depends on scaling factor or pass-band gain. In Sect. 7.1, the pass-band gain was fixed. We reformulate the optimization problem here, such that we let the pass-band gain or the scaling factor vary using the fine-tuning parameter, which is a continuous variable “s” defined in Sect. 5.1. The s variable is defined in the interval of [0.7, 1.4]. The formulation of the problem is as follows

$$\begin{aligned} {\text {Minimize }}\; &\varSigma h \nonumber \\ {\text {Subject}}\,{\text{to}}&\\&H_{R}(\omega T) P(\omega T) \le s k (1+\delta _c) \qquad \omega T \in \varOmega _C\nonumber \\&H_{R}(\omega T) P(\omega T) \ge s k (1-\delta _c) \qquad \omega T \in \varOmega _C\nonumber \\&H_R(\omega T) ~|{\text {NTF}}(e^{j \omega T})|~ P(\omega T) \le s k \delta _s \qquad \omega T \in \varOmega _S\nonumber \\&H_R(\omega T) ~|{\text {NTF}}(e^{j \omega T})|~ P(\omega T) \ge -s k \delta _s \qquad \omega T \in \varOmega _S \nonumber \\&0.7 \le s \le 1.4. \nonumber \end{aligned}$$
(25)

With this optimization method and the same specification (\(L=2\), \({\text {OSR}}=128\), \(A_{\text {min}}=-76~{\hbox {dB}}\), \(A_{\text {max}}=0.2~{\hbox {dB}}\)), the optimization problem is solved for different filter orders and word lengths and the result is summarized and presented in Table 2. The table presents the absolute sum of the filter coefficients (\(\varSigma h\)), found by solving the optimization problems. As can be observed, by selecting a filter order of 18 and a word length of \(w=7\) bits, a minimum absolute sum of coefficients of \(B=91\) is obtained which is shown in Table 2. The true pass-band gain is achieved by multiplying k with the fine-tuning variable s. The total pass-band gain in the best case (\(N=18\), \(w = 7\), and \(s=0.7692\)) is 98.5. The SDFIR filter response model for the optimum case, together with NTF, SEM and output models, are illustrated in Fig. 5. The simulation results with a multi-tone signal is shown in Fig. 6. The spectra are averaged over 500 test runs to properly display the transfer functions and mimic long simulation runs.

Table 2 Sum of the coefficients (\(\varSigma h\)) for the variable pass-band gain problem in example 1
Full size table
Fig. 5
figure 5

\(\varSigma \varDelta\) modulator noise transfer function (NTF), spectral emission mask (SEM), semi-digital FIR filter (SDFIR), pulse amplitude modulation effect (PAM). Optimization result in example 1 with fine-tuning variable s, based on the model

Full size image
Fig. 6
figure 6

\(\varSigma \varDelta\) modulator noise transfer function (NTF), spectral emission mask (SEM), semi-digital FIR filter (SDFIR). Simulation results in example 1 with fine-tuning variable s

Full size image

7.3 Minimizing the energy metric

In this use-case we formulate the optimization problem to minimize the energy in the stop-band, i.e., the total integrated noise. This is of interest in some of the SDFIR DAC applications such as feedback DAC in ADCs [1, 13], or in frequency synthesizers and \(\varDelta \varSigma\) PLLs [27, 28]. Hence the problem can be formulated as

$$\begin{aligned} {\text {Minimize }}\,& E \nonumber \\ {\text {Subject}}\,{\text{to}}&\\&H_R(\omega T) P(\omega T)\le k (1+\delta _c) \qquad \omega T \in \varOmega _C \nonumber \\&H_R(\omega T) P(\omega T)\ge k (1-\delta _c) \qquad \omega T \in \varOmega _C , \nonumber \end{aligned}$$
(26)

where E represents the energy in the stop-band, i.e.,

$$\begin{aligned} E = \frac{1}{k^2} \int \limits _{\omega T \in \varOmega _S} {\left| H_R(\omega T) \right| }^2 \left| {\text {NTF}}(\omega T) \right| ^2 \left| P(\omega T)\right| ^2 d \omega T . \end{aligned}$$
(27)

The minimum achievable total noise in the stop-band depends on the filter order and scaling factor (pass-band gain values). Assuming a second-order \(\varSigma \varDelta\) modulator, 0.5-dB ripple in the pass-band and \({\text {OSR}} = 64\), the problem was solved with different N and k values. From Fig. 7 it can be observed that for each filter order, by increasing the word length (w) the total achievable noise energy in the stop-band is reduced. It saturates after specific values of k for each N which indicates that the word length effect is not the dominant limiting factor anymore. However we cannot arbitrary select the word length since the absolute sum of coefficients in SDFIR is directly proportional to the word length. Assuming that a noise energy less than 37 dB is required in the stop-band, from Fig. 7, we can select \(N=30\) and \(k=2^{8}\). The absolute sum of coefficients obtained for this optimization problem is 255. There is a trade-off between the noise energy in the stop-band achieved by the SDFIR and the order of the analog reconstruction filter.

Fig. 7
figure 7

Noise in the stop-band versus filter order N and word length

Full size image

7.4 Minimizing the analog metrics, with energy and magnitude metrics as constraints

Another way of formulating the optimization problem, is to constrain the total noise in the stop-band and the magnitude metrics in the pass-band, and target a cost function based on analog metrics, i.e., total sum of coefficients to minimize. The filter order and the pass-band gain can be selected from the plot in Fig. 7, depending on the allowed noise energy in the stop-band. The problem can be formulated as

$$\begin{aligned} \begin{aligned} {\text {Minimize }}\;&\varSigma h \\ {\text {Subject}}\,{\text{to}}&\\&H_R(\omega T) P(\omega T)\le k (1+\delta _c) \qquad \omega T \in \varOmega _C \\&H_R(\omega T) P(\omega T)\ge k (1-\delta _c) \qquad \omega T \in \varOmega _C \\&\frac{1}{k^2}\int \limits _{\omega T \in \varOmega _S} {\left| G(\omega T) \right| }^2 d \omega T \le E_{\text {fix}}, \end{aligned} \end{aligned}$$
(28)

where \(E_{\text {fix}}\), is the energy constraint and G is defined as

$$\begin{aligned} \left| G(\omega T)\right| ^2 = \left| H_R(\omega T) \right| ^2 ~ \left| {\text {NTF}}(\omega T) \right| ^2 ~ \left| P(\omega T)\right| ^2. \end{aligned}$$
(29)

This problem is now a quadrature-constraint quadratic problem (QCQP). It is solved for the given parameters and the filter response is illustrated in blue in Fig. 8. The total sum of elements is found to be 255 in this case as well.

Fig. 8
figure 8

Comparison of SDFIR filter response of the optimized scaling method and the original scaling (Sects. 7.4 and 7.5)

Full size image

7.5 Minimizing the analog metrics, with energy and magnitude constraints and variable coefficient precision

As discussed previously, we can let the optimization tool find the optimum coefficient precision (pass-band gain) such that the objective function (absolute sum of filter coefficients in this example) is minimized subject to energy constraint in the stop-band and magnitude constraint in the pass-band. Therefore we consider a fine-tuning pass-band gain as a variable (s) besides the fixed pass-band gain (k) and formulate the optimization problem as

$$\begin{aligned} \begin{aligned} {\text {Minimize }} \; &\varSigma h \\ {\text {Subject}}\,{\text{to}}&\\&H_R(\omega T) P(\omega T)\le sk (1+\delta _c) \qquad \omega T \in \varOmega _C \\&H_R(\omega T) P(\omega T)\ge sk (1-\delta _c) \qquad \omega T \in \varOmega _C \\&\frac{1}{k^2} \int \limits _{\omega T \in \varOmega _S} {\left| G(\omega T) \right| }^2 d \omega T \le s^2 E_{\text {fix}}, \end{aligned} \end{aligned}$$
(30)

where \(\left| G(\omega T)\right| ^2\) is defined in (29). This problem, as discussed in Sect. 5.3, becomes a non-convex problem and therefore we use the method described in that section to solve the problem. The optimization problem now becomes

$$\begin{aligned} \begin{aligned} {\text {Minimize }}\,&\varSigma h \\ {\text {Subject}}\,{\text{to}}&\\&H_R(\omega T) P(\omega T)\le sk (1+\delta _c) \qquad \omega T \in \varOmega _C \\&H_R(\omega T) P(\omega T)\ge sk (1-\delta _c) \qquad \omega T \in \varOmega _C \\&\frac{1}{k^2} \int \limits _{\omega T \in \varOmega _S} {\left| G(\omega T) \right| }^2 d \omega T \le (s_{\text {fix}}^2 + 2s_{\text {fix}}\alpha ) E_{\text {fix}} \\&s=s_{\text {fix}} + \alpha \\&-0.1 \le \alpha \le 0.1 . \end{aligned} \end{aligned}$$
(31)

By sweeping \(s_{\text {fix}}\) in the points (0.7, 0.8, 0.9, 1.0,1.1, 1.2, 1.3, 1.4) and keeping \(\alpha\) as a variable in the interval \([-0.1 ~ 0.1]\), we solved the problem with design parameters \(L=2\), \({\text {OSR}}=64\), \(N=30\), \(A_{\text {max}} = 0.5\) dB, pass-band gain \((k = 2^8)\). The optimization results are presented in Table 3. The filter response of the optimized scaling method and the original scaling is illustrated in Fig. 8. The point with \(s=0.7\) and \(\alpha =-0.011\) is the best point since it gives the minimum absolute sum of the SDFIR filter coefficients (\(B=176\)) while fulfilling the energy and magnitude constraints. Comparing this result to the results achieved without using a fine-tune scaling variable, we get more than 30% saving in hardware (\(\varSigma h\)). The resulting SDFIR is simulated with a multi-tone signal and the filter response together with input and output waveform for \(k = 2^8\), and \(s_{\text {fix}}=0.7\), are shown in Fig. 9. As shown in these examples by considering the \(\varSigma \varDelta\) modulator and the Sinc function, together with SDFIR filter response we can find the optimal SDFIR coefficient to avoid the over-design mentioned in [26]. Furthermore the analog cost can be employed as one of the optimization metrics as either objective function or the constraint.

Table 3 Optimization results with variable pass-band gain
Full size table
Fig. 9
figure 9

Signal at \(\varSigma \varDelta\) modulator output (SDM), semi-digital FIR filter response, and signal at the output of SDFIR (Sout)

Full size image

8 Conclusions

The optimization of semi-digital FIR DACs, considering different types of metrics and sigma-delta modulators is presented in this paper. Different optimization factors such as analog, magnitude metrics and energy metrics were discussed in detail and could be utilized when optimizing the SDFIR DAC design. A new method with introducing the variable pass-band gain in optimization procedure was proposed to avoid non-convex optimization problems. The results were presented in five different use-cases. It was shown that we can save up to 22% in the total number of unit elements of the SDFIR filter when targeting the analog metric as the optimization objective subject to magnitude constraint in the pass-band and stop-band. In another use-case the energy in the stop-band and magnitude ripples in the pass-band was constrained and the analog metrics (total number of current source unit elements) as the optimization objective. The optimization result showed about 30% reduction in the analog hardware cost comparing to the case without introducing the variable pass-band gain.