1 Introduction

With the advance of ultra low-power circuits, new applications in wireless sensor nodes capable of operating for years on a single battery have emerged. Nevertheless, certain applications require an even longer lifetime when it, for example, is impossible or at least impractical to change the battery once the sensor node has been deployed. For some of these applications, energy harvesting can be the solution. By harvesting energy from either an ambient power source, such as solar, vibrations, or temperature gradient, or from a supplied power source, such as RF or induction, the lifetime of the system is increased without the need of a higher-capacity battery. Many of these applications operate in an environment where vibrations are the only feasible energy source. Examples are medical implants, such as pacemakers, and structural health monitoring in, for example, roads, bridges, and houses. There the sensor is not exposed to the sun, and no substantial thermal gradient exists removing solar and temperature energy harvesting as viable options. It is also impractical to power them through RF or induction since such a power source is not available. However, vibration energy harvesting is feasible since, in for example medical implants, the patient moves, the lungs expand and collapse, and the heart beats or in structural health monitoring when a car passes, vibrations are coupled to the sensor.

Fig. 1
figure 1

Overview of a vibration energy harvesting system

Full size image

In recent years a significant amount of research has been done on vibration energy harvesting interfaces that extract the maximum possible power from a given transducer [1,2,3]. This has been achieved by utilizing high-performance rectifiers [4], novel impedance matching techniques [1, 5], high-efficiency DC–DC converters [6,7,8], and regulators [9]. Even though the required power for the applications described above is low (a few micro-watts) the available energy is also low, making the system design very challenging and only a few systems have been demonstrated [1, 8, 10,11,12].

In order to design a single wide-range converter devices that combine low threshold voltage, high drain-source breakdown voltage and good conductivity are required. Such combination is rarely possible. One architectural solution to achieve the same effect is to employ a bootstrapping technique, however this increases the complexity and could be power inefficient. Another solution is to let the wide-range be handled by different separate paths.

This paper presents a piezoelectric vibration energy harvesting system containing two efficient rectifiers and three reconfigurable switched-capacitor DC–DC converters—two step-up and one step-down. It extends a previous work [13] by the same authors, with full system description and measurements. The system targets medical implants and structural health monitoring applications. These two applications have similar specifications; they are excited with a low acceleration, low-frequency vibration, and require power in the micro-watt range. These applications also place tough requirements on the DC–DC converters which, in order to facilitate maximum power point tracking (MPPT), need to have a high power efficiency over a wide range of input voltages while providing a regulated output voltage.

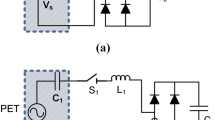
Figure 1 shows a simplified diagram of such a system. The piezoelectric harvester (PEH) is excited with acceleration from the environment which is converted into current due to the piezoelectric effect. The PEH can be modeled as a current source in parallel with a parasitic capacitance \(C_P\) and a damping resistance \(R_P\) [14]. This current is proportional to the input excitation acceleration and thus varies in direction over time, hence a rectifier is used to produce a DC voltage. In the targeted applications the average power consumption is low but when, for example, the sensor nodes communicate with a host the instantaneous power spikes. Therefore a storage capacitor is placed after the DC–DC converter so it can handle these high load current spikes without the need for a fast DC–DC control loop.

The paper is organized as follows Sect. 2 describes the architecture of the system and its operation followed by the design of the rectifier and DC–DC converters. Section 3 discusses the stability of the system while Sect. 4 presents the measurement results from a fabricated chip, and Sect. 5 concludes the paper.

2 System architecture and operation

Figure 1 shows the system architecture. The PEH is connected to one of the rectifiers at the time. To reduce voltage ripple, a smoothing capacitor is placed after the rectifier. The DC–DC converter takes charge from this smoothing capacitor and either steps-up or steps-down the voltage to regulate to the target voltage at the output. All DC–DC converters ratios are programmed externally and regulate the output voltage by controlling the switching frequency to achieve finer control of the output voltage and minimize the switching losses.

Since the system is designed to handle a large variety of input voltages the appropriate combination, for a specific input voltage, of a rectifier and DC–DC converter, has to be set externally.

The rectifiers contain a negative voltage converter (NVC) followed by an active diode driven by a self-biasing amplifier. This approach provides a low voltage drop over the rectifier and no static power consumption. For certain applications, this is essential since the excitation of the PEH can have a very low duty-cycle potentially causing an active interface to drain the energy storage.

2.1 Rectifier design

As mentioned previously the rectifier contains a negative voltage converter (NVC) [4] followed by a diode driven by a self-biased amplifier [15], shown in Fig. 2. As the PEH voltage (\(V_\mathrm{{PEH}}\)) increases, transistors \(M_2\) and \(M_3\) conduct more than \(M_1\) and \(M_4\) causing current from \(V_\mathrm{{PEH+}}\) to flow to \(V_\mathrm{{X}}\) thereby increasing the potential at \(V_\mathrm{{X}}\). When \(V_\mathrm{{X}}\) exceeds \(V_\mathrm{{Rect}}\) the adaptive body biasing changes the bulk connection of \(M_5\) to \(V_\mathrm{{X}}\). Then the self-biased amplifier lowers \(V_\mathrm{{G}}\) and turns on \(M_5\) to allow current to continue flowing into \(V_\mathrm{{Rect}}\). Figure 3 shows a transient simulation of the turn on and turn off behavior of the rectifier with the current path for the above example illustrated. As can be seen, the PEH voltage increases over the rectified voltage before the comparator triggers and starts to conduct. This is due to an intentional offset of the amplifier which reduces the risk of conduction in the reverse direction. However, this offset drops the efficiency since energy is dissipated when \(V_\mathrm{{PEH}}\) increases by \(\Delta V\) over \(V_\mathrm{{Rect}}\). Assuming the charging of the parasitic capacitor is lossless the energy dissipated is equal to,

$$E_\mathrm{{offset}} = \frac{C_P \left( \Delta V + V_\mathrm{{Rect}} \right) ^2 - C_P V_\mathrm{{Rect}}^2}{4}$$
(1)
$$= \frac{C_P}{4} \left( \Delta V^2 + 2 V_\mathrm{{Rect}} \Delta V \right)$$
(2)

which in simulations gives an efficiency drop around \(1\%\) due to the short duration compared to the long conduction period. However a small negative offset, causes the smoothing capacitor to discharge at the end of every half-cycle. The intentional offset will limit the lowest possible input voltage the rectifier can operate from but the increase in efficiency motivates it.

Fig. 2
figure 2

Rectifier circuit with a negative-voltage converter (NVC) followed by an active diode with adaptive body biasing

Full size image

During an inactive period, when the PEH voltage is low, \(V_\mathrm{{X}}\) will discharge back to the harvester through \(M_3\) and \(M_4\) and decrease in voltage. As this happens \(V_\mathrm{{G}}\) will start to approach \(V_\mathrm{{Rect}}\) and turn \(M_5\) off. When \(V_\mathrm{{X}}\) has dropped low enough \(M_6\) in the amplifier will stop conducting and the amplifier will turn off and only consume leakage current.

Shown in Fig. 2 is the rectifier. Two different rectifiers has been designed, using the same architecture, one supports higher input voltages up-to 5.5 V and the other one supports input voltage up-to 1.8 V. However, the low-voltage rectifier uses thinner gate-oxide transistors resulting in a lower threshold voltage and the minimum input voltage required for the circuit to function correctly is correspondingly lower. The difference in transistor sizes can be seen in Table 1.

Fig. 3
figure 3

Simulation of the rectifier showing the input voltages, active diode transistor gate voltage, and rectified voltage

Full size image
Table 1 Transistor sizes for the two different rectifiers
Full size table

2.2 Switched-capacitor DC–DC converter design

The following section describes the structure and function of the DC–DC converters and how the regulation is performed.

2.2.1 Converter structure

The proposed DC–DC converters are self-oscillating stacked time-interleaved switched-capacitor DC–DC converters. Since a wide input voltage range was essential for the targeted applications the presented chip contains three separate converters; two step-up converters and one step-down converter.

Each converter is built around a ring oscillator with nine stages which generate the desired timing/control signals. The nine stages are time-interleaved which reduces the output voltage ripple and thus relaxes the requirement on the output capacitor. In each of these stages, there are three levels of stacked voltage doublers followed by a delay circuit with logic level restoring buffers, Fig. 4. The authors of [16] proposed a self-oscillating voltage doubler, equivalent to one level in our proposed converter. Our proposed architecture extends this approach to a stacked structure to facilitate selectable voltage conversion ratios (VCRs) without having to cascade stages. While the two architectures in their core, the switched capacitor network, have the same power efficiency, the overhead of the control signal generation is lower for the stacked architecture.

Fig. 4
figure 4

Block diagram of the DC–DC converters with 3 levels and 9 stages

Full size image

The VCR in this architecture can be set to 1 : n, where \(n \in {1+1,..,N}\) and N is the number of levels, by shorting the driver and opening a switch in series with the flying capacitor. In this specific implementation the VCR can thus be set to be either 1:2, 1:3, or 1:4.

Fig. 5
figure 5

Simplified diagram of a single DC–DC converter stage diagram with two stacked voltage-doublers

Full size image

Figure 5 shows the schematic of a single converter stage where only three levels are shown for clarity. Each intermediate voltage rail is denoted as V\(_n\) where \(n \in {1,..,N}\) and N is the number of levels. In step-up operation, the input power source is connected to \(V_1\) and the output is taken at \(V_N\), while the opposite is true in step-down operation. As the control signal In\(_n\) is high during \(\phi _1\) the NMOS transistors turn on and charge \(C_\mathrm{{fly}}\) from either the preceding level or the input to, nominally, \(\mathrm{{V}}_\text {in}\). During \(\phi _2\), when the control signals are low, \(C_\mathrm{{fly}}\) are discharged to either the next level or the output and at the same time connected to a higher bottom plate voltage boosting the top plate voltage. The timing of this delay is illustrated in Fig. 6. As the capacitors top plate voltage goes high the delay cell is enabled and the control signal is delayed with a bleeding NMOS transistor, \(M_L\), which triggers a break-before-make latch to minimize the power consumption. The logic level of the output from the delay cell is then restored using two buffers capacitively coupled to the lower and higher levels to synchronize all control signals and restore the their edges.

Fig. 6
figure 6

Timing diagram from simulations showing the input levels control signals for the medium-voltage step-up DC–DC converter. The upper graph shows the delay between the input and output signal while the lower graph shows the delay from the delay cell followed by the logic restored delayed signal

Full size image

To achieve the best possible performance the flying capacitor sizes should be tapered with the largest capacitor for the lowest level. This is because the power from each level is constant but since the voltage increases for the higher levels the output current decreases. For an ideal SC DC–DC converter with constant output current, the output voltage can be expressed as

$$\begin{aligned} V_\mathrm{out} = \frac{V_\mathrm{{in}}}{m} - \frac{I_\mathrm{{load}}}{C_\mathrm{{fly}}\, f_\text {sw}} \end{aligned}$$
(3)

where m is the VCR, \(I_\mathrm{{load}}\) the output current, \(C_\mathrm{{fly}}\) the flying capacitor, and \(f_\mathrm{{sw}}\) the switching frequency. In order to keep the same \(\Delta V\), thus keeping the power efficiency the same for the different stages, the increase in \(I_\mathrm{{load}}\) should be compensated with an increase in \(C_\mathrm{{fly}}\) since \(f_\mathrm{{sw}}\) is the same for all levels. For example in a step-up converter based on this architecture the lowest level should have a flying capacitor of \(C_\mathrm{{fly}}\), the next level \(C_\mathrm{{fly}}/2\), etc.

However, in the design phase this fact was overlooked and all flying capacitor sizes for the DC–DC converters were designed to be the same.

Since the converters target different VCRs and input voltages the design parameters differs, shown in Table 2. The biggest difference is in the low-voltage step-up where both the flying capacitors and the drivers are bigger. This is to enable correct operation at low input voltages and low power levels.

Table 2 Component sizing that differ between the DC–DC converters
Full size table

2.2.2 Regulation

The proposed converters have, besides the selectable VCR, also a fine regulation which tunes the oscillation frequency to achieve the target output voltage. Looking at Eq. 3 we can see that when \(f_\mathrm{{sw}}\) increases the conduction loss decreases which increases the output voltage. The drawback is that the power efficiency drops when the output voltage is decreased in the same way as for a linear regulator.

In the proposed converter the output voltage is compared to a reference voltage and \(f_\mathrm{{sw}}\) is increased when the output voltage is lower than the reference voltage and decreased when the output voltage is higher.

Fig. 7
figure 7

Block diagram of the output voltage regulation; comparator and charge pump. \(\dagger\): Only in the low-voltage step-up converter

Full size image

Figure 7 shows this regulation loop. It is clocked by the lowest level control signal of the DC–DC converter, \(\mathrm{{Out}}_1\). For the low-voltage step-up converter, the regulator is supplied from the output enabling operation at very low input voltages, however this means that the regulator clock has to be level-shifted up. For the medium-voltage step-up converter and the step-down converter, the regulators \(\mathrm{{V}}_\text {DD}\) is taken from \(\mathrm{{V}}_1\) and thus no level-shifter is needed. Furthermore, the frequency is divided down to reduce the gain of the regulation loop. The resulting control signal is used to control a dynamic latch comparator which compares the reference voltage with the output voltage and directly controls a dynamic low-leakage charge pump [8]. The charge pump output voltage steps are proportional to \(V_{DD} C_{step}/C_{ctrl}\), and it has a very low energy dissipation per step. To enable low oscillation frequencies, transistors \(M_1\) and \(M_2\) isolate the control signal between the steps and reduce the voltage droop. Due to the non-linear nature of the comparator in the control loop, the system never settles and instead limit-cycles around the target control voltage.

Table 3 Step-up converter comparison table
Full size table

3 Stability

Due to the output voltage regulation loop of the DC–DC converter, its input power tends to be constant and independent on the harvester voltage. This means that the DC–DC converter presents a negative incremental impedance to the harvester, degrading the stability of the system as a whole. This effect has been well studied in the context of power distribution networks [17].

Consider Fig. 8, where the power from the harvester is plotted against the load impedance. When operating on the right side of the maximum power point (MPP) and the load is a constant input power DC–DC converter, a reduction of the mechanical excitation of the harvester will tend to move the operating point to the left. This will restore the available power. However, if the operating point is to the left of the MPP, any reduction of the harvester excitation will cause a runaway reduction of the available power shutting the system down.

Fig. 8
figure 8

Harvester power and voltage versus load impedance were the unstable and stable regions of the DC–DC converter output voltage regulation system is shown

Full size image

By only regulating the output voltage the system will become unstable for low harvester excitation. Therefore, in order to guarantee stability it is necessary to allow the power to drop when operating at harvester voltages lower than the one corresponding to the MPP.

4 Measurement results

Shown in Fig. 9 is a micrograph of the fabricated chip in 0.18 \(\upmu\)m CMOS measuring 3 mm\(^{2}\). In order to evaluate the system a custom prototype piezoelectric harvester was excited using a shaker table and used as the power source. The harvester is made of lead zirconate titanate (PZT), has a physical size of 17.5 \(\times\) 4.5 \(\times\) 0.3 mm, has a parasitic capacitance of 14 nF, and a resonance frequency of 42.3 Hz.

Fig. 9
figure 9

Chip micrograph with the DC–DC converters highlighted

Full size image

The rectifiers and DC/DC converters are separated on-chip and their configuration is set are done off-chip. In the DC/DC converters the ratio is also set externally by setting a register which controls the configuration switches.

4.1 Rectifiers

As shown in Figs. 10 and 11 the optimal load resistance is around 500 k\(\Omega\). The peak output power measured for an acceleration of 251 mg was 48.7 \(\upmu\)W but even from 28 mg the PEH with the rectifier can deliver several microwatts. The drop across the harvester varies with the load but is typically around 5–20 mV.

Fig. 10
figure 10

Rectifier output power versus load and acceleration

Full size image
Fig. 11
figure 11

Rectifier output voltage versus load and acceleration

Full size image

4.2 SC DC–DC converters

The configuration of the VCR and the voltage reference are generated off-chip. For the measurements, an output voltage that varies between \(\pm \,10\,\%\) around the target output voltage is considered acceptable. The target voltage and \(\pm \,10\,\%\) band are marked in the plots with a solid and dashed line respectively.

4.2.1 Low-voltage step-up converter

Figure 12 shows the measured power efficiency and the regulated output voltage of the low-voltage step-up converter for the different VCRs. The target voltage is 1.8 V with input voltages of: 1 V for a ratio of 1:2, 0.725 V for 1:3, and 0.475 V for 1:4.

For ratio 1:2 the output voltage exceeds the target voltage for output load power lower than 1 \(\upmu\)W, this is because the switching frequency cannot be reduced more. The opposite happens when the output power exceeds 150 \(\upmu\)W, the switching frequency cannot be increased more, and the output voltage drops.

For ratio 1:3 the power efficiency has a smaller lower limit load power compared to ratio 1:2 because the voltage across the delay cells are lower and therefore they leak less and can oscillate slower. However more current has to be extracted from the input compared to the 1:2 ratio and at higher load powers the maximum oscillation frequency is met earlier resulting in a decreased maximum load power of 100 \(\upmu\)W. The oscillation frequency is limited by the maximum conduction of the driver as well as the minimum delay of the delay stage.

Fig. 12
figure 12

Power efficiency and output voltage versus output power for the low voltage step-up converter. Input voltage is 1 v (ratio 1:2), 0.725 V (1:3), and 0.475 V (1:4) with a target voltage of 1.8 V

Full size image

For the 1:4 ratio the peak power efficiency while in regulation is 54% at a load power of 2.65 \(\upmu\)W. The efficiency is less for lower load powers since the drivers in each level operate close to the threshold voltage of 450 mV. As the load power increases above 3 \(\upmu\)W the output voltage quickly drops since the maximum oscillation frequency is met earlier due to the low overdrive of the transistors.

Table 4 Step-down converter comparison table
Full size table
Fig. 13
figure 13

Power efficiency and output voltage versus output power for the medium voltage step-up converter. Input voltage is 2 V (ratio 1:2), 1.45 V (1:3), and 0.95 V (1:4) with a target voltage of 3.3 V

Full size image

4.2.2 Medium-voltage step-up converter

The measurements for the medium voltage step-up converter are similar to the low voltage step-up converter. Here the target output voltage is 3.3 V with input voltages of: 2 V for a ratio of 1:2, 1.45 V for 1:3, and 0.95 V for 1:4. Shown in Fig. 13 is the output voltage and power efficiency for different load powers. As can be seen for ratio 1:2 the regulation starts operating at a load power of 2 \(\upmu\)W and continues operating up to 500 \(\upmu\)W while maintaining a power efficiency of more than 60%. Compared to the low voltage step-up converter the range is much wider due to the higher overdrive voltage on the converter drivers but has a higher lower limit due to additional parasitic capacitances and smaller flying capacitors.

For the 1:3 ratio the power efficiency stays above 40% between 1 and 200 \(\upmu\)W while supplying a regulated output voltage. When increasing the ratio to 1:4 the power efficiency is above 20% between load powers of 9 and 30 \(\upmu\)W while in regulation.

4.2.3 High-voltage step-down converter

Shown in Fig. 14 is the output voltage and power efficiency of the step-down converter. The target output voltage is set to 3.3 V for all ratios. For the 2:1 ratio the input voltage is 7.5 V, for 3:1—14 V, and for 4:1—18 V. Peak power efficiency for ratio 2:1 is 68.7% and is achieved for load power between 10 and 100 \(\upmu\)W. Since the voltage across each level is relatively high the leakage in the delay circuit sets a higher minimum limit on the oscillation frequency which causes the power efficiency to quickly drop for low output powers.

Fig. 14
figure 14

Power efficiency and output voltage versus output power for the step-down converter. Input voltage is 7.5 V (ratio 2:1), 14 V (3:1), and 18 V (4:1) with a target voltage of 3.3 V

Full size image

For ratio 3:1 the power efficiency is over 40% for load powers between 16 and 200 \(\upmu\)W. Lastly for ratio 4:1 the converter has a narrow load power band where it regulates, between 200 and 900 \(\upmu\)W. This is because the leakage through the delay circuit is high compared to what is controlled by the regulator loop and the oscillation frequency cannot be reduced enough.

4.2.4 Input voltage variations

As mentioned earlier the reason for having three different converters is to enable a wide input-voltage range. Seen in Fig. 15 is the output voltage and power efficiency for input voltages between 500 mV and 11 V with a target output voltage of 1.8 V and a 200 k\(\Omega\) load resulting in a load power of 16.2 \(\upmu\)W.

As can be seen, the regulated voltage level differs between the converters. This is due to different offset voltages of the comparators used in the regulation loop. Looking at the output voltage the converters maintain an output voltage of 1.8 V \(\pm \,10\%\) between 0.55 and 10 V if this offset is reduced.

The peak power efficiency is 80% with a power efficiency above 40% for all input voltages except between 2 and 4 and 5.2 to 5.8 V. For the medium voltage step-up converter and input voltages between 1–4 V, the desired output voltage is lower than the input voltage times the minimum ratio of two, this results in an efficiency curve of a linear regulator. For higher voltages, there is a drop in efficiency for the high voltage step-down converter around 5.2–5.8 V where the desired ratio is close to three, causing poor power efficiency for both ratios of 2:1 and of 3:1.

In one of the targeted applications, structural health monitoring, the input power is either low, during normal operation, or high, when, for example, a car passes by. The rectified voltage will follow this and be either high or low. Therefore the system has been designed for high power efficiency for voltages between 0.5 and 1.5 V, for low input power, and 4–10 V, when the input power is high.

Fig. 15
figure 15

Output voltage and power efficiency versus input voltage for all DC–DC converters. Target voltage is 1.8 V and the load is 200 k\(\Omega\)

Full size image

4.3 System

The following section presents the measurements of the whole system. For this particular harvester and the targeted output voltage, the 5 V rectifier followed by the medium-voltage step-up DC–DC converter with a target voltage of 1.9 V was used.

Shown in Fig. 16 is the output voltage and output power of the whole system for the different measurement points. It can be seen that for light loads and low accelerations the system is not regulating well. This is mainly due to the light load which makes the regulation more sensitive, an increase in the switching frequency will quickly increase the output voltage. For a heavier load the regulation is more damped and hence more stable.

With an increasing input acceleration the input voltage to the harvester increases. When it approached the breakdown voltage the measurements were stopped.

The flat output power comes from the fact that the output voltage is regulated to a fixed voltage and a fixed load is being used, this means that the maximum available power for these accelerations is higher than shown in Fig. 16.

Fig. 16
figure 16

System measurement with the medium voltage rectifier cascaded with the medium voltage boost DC–DC converter for various loads. The DC–DC converter has a target voltage of 1.9 V

Full size image

5 Conclusion

In this paper, we propose a fully-integrated piezoelectric energy harvesting system consisting of a rectifier with a low voltage drop, and a self-oscillating stacked time-interleaved switched capacitor DC–DC converter. The system contains two different rectifiers with a total input voltage range of 0.45–5.5 V, and three different DC–DC converters with a total input voltage range of 0.45–20 V. It has been demonstrated together with a piezoelectric transducer were the regulated output voltage is 1.9 V for input voltages between 0.5 and 11 V while maintaining high power efficiency for \(\upmu\)W power levels.

The proposed DC–DC converter architecture shows promise even though the selected flying capacitor ratios was not optimal. Shown in Table 3 is a comparison with state-of-the-art step-up converters with similar voltage ranges and output powers. The proposed step-up converters show a comparably wide voltage range and high power density. Table 4 shows a comparison with similar state-of-the-art step-down converters. The proposed step-down converter has a competitive peak power efficiency while supporting a much wider input voltage range. The power density is lower than the references which is mainly due to the low targeted output power levels.