1 Introduction

The practical problems in scientific and engineering fields are usually either continuous, discrete, constrained or unconstrained, which makes researchers pay more attention to the optimization techniques (Heidari et al. 2019). In the past decades, with the increasing nonlinear, nonconvex, multimodal, non-differential and even dynamic problems in industrial organizations (Gao et al. 2015), it is hard to meet the actual demands by traditional methods which are based on formal logics or mathematical optimization, such as conjugate gradient, fast steepest, sequential quadratic programming, quasi-Newton methods and so on (Wu 2016). Therefore, based on different motivations and steps, a large number of MHAs are proposed (Yang et al. 2020).

Compared to the conventional optimization solutions, MHAs can effectively solve many problems (especially the NP-complete problems) as competitive alternative solvers (Liu et al. 2019). In addition, the core operations of these methods do not rely on gradient information of the objective landscape or its mathematical traits (Dréo et al. 2006). Over the last forty years, motivated by the natural selection and biological evolution, many researchers have designed varieties of MHAs, such as HHO (Heidari et al. 2019), GA (Liu et al. 2021) SA (Abdel-Basset et al. 2021), PSO (Song et al. 2020), ABC (Gao et al. 2020), WOA (Mirjalili and Lewis 2016), JSO (Chou and Truong 2021), SMO (Dinesh et al. 2021), SMA (Chakraborty et al. 2023), SOS (Chakraborty et al. 2022), BOA (Sharma et al. 2022), NPO (Salih and Alsewari 2020), ACO (Wang et al. 2015), AFSA (Zhang et al. 2021) and so on. Besides, those techniques have been successfully implemented in various practical applications including engineering systems, large-scaled complex networks, health care management systems. With the further development of MHAs, most of them have shown a sensitivity of the parameter defined by users and tend to converge to local optimum in many cases. Moreover, they also suffer from the curse of dimensionality problem as it takes quadratic, cubic, or polynomial time with an increase in the number of parameters (Vinod and S. and Anand H. S. 2021). Finding a proper balance between exploration and exploitation is a challenging task in the development of any MHA due to the stochastic nature of the optimization process. Therefore, some new MHAs or MHAs improved on basis of original algorithms have become a hot topic increasingly.

MHAs have different classifications and can be classified into different groups, depending on the considered standard, such as population based, iterative based, stochastic, deterministic (Karaboga and Basturk 2007), etc. According to literature (Talbi 2009), there are two sorts of categorization: single-solution based and population based. Considering different sources of inspiration, nature-inspired MHAs are divided into three kinds: a) SI algorithms, b) Non-swarm intelligence algorithms, c) Physical and chemical algorithms (Bidar et al. 2018). MHAs proposed by mimicking biological or physical phenomena are grouped into three kinds: evolution-based, physics-based, and swarm-based methods (Mirjalili and Lewis 2016). Evolution-based methods are inspired by the laws of natural evolution, the most popular evolution-inspired technique is GA (Liu et al. 2021) that simulates the Darwinian evolution, other popular algorithms are ES (Beyer and Sendhoff 2017), GP (Suganuma et al. 2017), and BBO (Bidar et al. 2018). Physics-based methods imitate the physical rules in the universe. The most popular algorithms are SA (Abdel-Basset et al. 2021), BSA(Albashish et al. 2021), GLSA (Nama et al. 2022), BBBC (Ji et al. 2017), and CFO (Al-Marashdeh et al. 2018). The third group of nature-inspired methods includes swarm-based techniques that mimic the social behavior of groups of animals. The most popular algorithm is PSO (Song et al. 2020), ABC (Gao et al. 2020), ACO (Wang et al. 2015), AFSA (Zhang et al. 2021), and MFO (Sahoo et al. 2023), etc. Other metaheuristic methods inspired by human behaviors are also studied, such as TLBO (Hang et al. 2017; Venkatarao 2021), GSO (Chen et al. 2021; Abualigah 2021), LCA (Teimourzadeh and Mohammadi-Ivatloo 2020), CBO (Kumar et al. 2020; Farzam and Kaveh 2020).

The four categories of MHAs divided in this paper is as shown in Fig. 1. SI algorithms play an important role in MHAs. In addition to the algorithms mentioned above, many newly proposed SI algorithms are also gradually used in different fields. Motivated by the behavior of jellyfish in the ocean, Chou and Truong developed a novel metaheuristic method called JSO (Chou and Truong 2021). However, in the search space, the JSO converges prematurely with different dimensions and is prone to falling into local optimum during evolution, as well as decreasing population diversity (Cheng and Zhao 2020). Dhiman et al. proposed RSO which was inspired by the aggressive behavior of rats in many situations (Yong et al. 2020). ALO is a novel metaheuristic swarm-based approach introduced by Abualigah to emulate the hunting behavior of ant lions in nature life (Dhiman et al. 2020). As the number of iterations increases, the predator–prey radius of ALO decreases, and there is an unbalance between exploration and exploitation. It is easy to fall into a local optimum, affecting the convergence speed and accuracy (Abualigah et al. 2021). The main inspiration of SSA designed by Mirjalili et al. is the swarming behaviour of salps that is navigating and foraging in oceans (Guo et al. 2020). However, the SSA suffers from the same limitations the other MHAs, such as slow convergence since its exploitation ability is not ideal (Mirjalili et al. 2017). Based on the foraging behavior of spider monkeys, the SMO (Dinesh et al. 2021) was presented for numerical optimization, but SMO whereas can tend to prematurity easily. To overcome the inefficient exploration and exploitation resulted from the poor tuning of the control parameters, a novel parameter-free multi-swarm metaheuristic called NPO was put forward (Salih and Alsewari 2020). Nonetheless, the algorithm is even more complicated. Therefore, the various problems of MHAs need to be further developed and improved.

Fig. 1
figure 1

Classification and summarization of metaheuristic algorithms

Full size image

In this paper, the study is focused on HHO and its related variants with excellent convergence ability in SI algorithms. Due to the simple principle, free-special parameters and strong global search ability, HHO has been applied in the fields of image segmentation (Ibrahim et al. 2019), neural network training (Jia et al. 2020), motor control (Fan et al. 2020) and so on. Nevertheless, like other SI algorithms, when HHO faces the complex optimization problems, there are some defects such as slow convergence speed, low optimization precision and sometimes easy to fall into local optimum. According to the no free lunch theorem, it is impossible for a method to outperform all other algorithms on every problem (Saravanan et al. 2020). This fact motivates researchers to create the variants of HHO, which can be helpful to solve a set of standard benchmark functions, different engineering or multi-objective optimization problems. Exploration (diversification) and exploitation (intensification) are the two main phases of most MHAs. The exploration phase ensures that the algorithm explores the search space carefully while the exploitation phase seeks out around the best solutions and chooses the best candidates or places (Yang et al. 2020). The main differences among metaheuristics are how to balance the two processes (Wolpert and Macready 1997)-(Ahmadianfar et al. 2020). A mature SI algorithm should be able to make an excellent balance between the exploration and exploitation tendencies. Otherwise, the chance of being got into local optimum and immature convergence drawbacks increases (Heidari et al. 2019).

To improve the performance of the basic HHO, there are roughly two types of strategies: 1) the modification of the solution search equation and 2) the hybridization with other MHAs (Gao et al. 2015, 2020; Liu et al. 2019; Kaur et al. 2020)-(Song et al. Oct. 2020). It has been proven that these introduced variants can improve performance of the algorithm to some extent. According to literature (Heidari et al. 2019), based on the escaping energy E of the prey, the convergence process can transfer from exploration to exploitation, and operate among exploitative behaviors based on the E of the prey. With the increase of iteration times, the E of prey gradually decreases linearly to zero, it also marks the end of the optimization process. However, the main drawback lies in the value of E cannot be larger than 1 in the end of the iteration, which means that the global search ability is weak in this phase (Bao et al. 2019). Due to the linear attenuation of parameter E, its convergence rate is slow and it is easy to fall into the local optimum. Moreover, in terms of the actual escaping process of the prey, the reduction of energy cannot be linear. In order to improve the performance of HHO, avoid falling into local optimum and find suitable energy decay factors, a large number of experiments are carried out in this paper, and some nonlinear energy decay factors with better performance are obtained.

Based on the need of balancing exploration and exploration ability, EAHHO is proposed in the paper, since the energy of natural biological activities cannot be linearly decayed and adaptive adjustment strategy of key variables among MHAs is necessary for the stochastic optimization. After the establishment of the Markov chain model (Zhang et al. 2020), the convergence of EAHHO is proved. Furthermore, the Lyapunov principle (Brémaud 2013) is used to prove its stability. The proposed approach is applied to optimize a set of the benchmark functions. 13 HHO variants and some typical SI algorithms are used for comparison. The comparison results show that the proposed EAHHO method provides a very promising performance.

The major contributions of the paper are to enhance adaptive-convergence in HHO algorithm. First, this paper proposes a novel EAHHO algorithm with nonlinear energy decay factor E, which is designed by dynamically adjusting adaptive-convergence factor a based on the nonlinear characteristic of the energy decay of natural biological activities. Second, the convergence and stability of EAHHO are analyzed. The core of convergence analysis of EAHHO is to establish a Markov chain model for its updating process. By constructing an updating mechanism in three different situations: search phase, soft besiege phase and hard besiege phase, the transition probability matrix is built up to prove that the stability condition of reducible stochastic matrix can be satisfied. And then Lyapunov stability theory are used to prove its stability. Third, numerical simulation analysis of 14 HHOs and 15 other state-of-the-art algorithms are done on 48 test functions to verify the performance of the proposed EAHHO algorithm. Finally, the CEC competition test functions are used to further verify the performance of the algorithm, and the high dimensions and graph size Internet of Vehicles routing problem is solved by the proposed EAHHO.

The rest of this paper is organized as follows. Section 2 briefly introduces the original HHO. In Section 3, we compare with the research works on modified HHOs. Section 4 analyzes the convergence and stability of proposed algorithm. Section 5 demonstrates the simulation results and the comparison with other algorithms. Finally, the conclusion is drawn in Section 6.

2 Original HHO

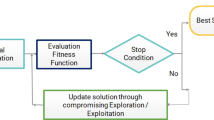
HHO (Heidari et al. 2019) proposed by Heidari et al. simulates the cooperative behavior and chasing style of Harris’ hawks in nature. Harris’ hawks can reveal a variety of chasing patterns based on the dynamic nature of scenarios and escaping patterns of the prey. HHO is mainly made up of three phases, including exploration, transition (from exploration to exploitation), and exploitation. The position of a Harris’ hawk represents a solution of the optimization problem, and different fitness function of the corresponding solution can be set. The number of Harris’ hawks equals the colony.

2.1 Exploration phase

At the beginning, an initial population P is produced randomly which consists of N solutions with D-dimensional vector. Harris’ hawks randomly inhabit somewhere and uses the following two strategies to find the prey. Random number q is used to select the strategy to be adopted.

$$\left\{\begin{array}{l}X(t+1)=\left\{\begin{array}{l}X_{rand}(t)-r_1\vert X_{rand}(t)-2r_2X(t)\vert,q\geq0.5\\X_{rabbit}(t)-X_m(t)-r_3(LB+r_4(UB-LB)),q<0.5\end{array}\right.\\X_m(t)=\frac1N\sum\limits_{i=1}^NX_i(t)\end{array}\right.$$
(1)

where \(X(t)\) is current position vector of hawks, \({X}_{m}\) is the average position of the current population of hawks.

2.2 Transition phase

HHO switches among different behaviors according to the amount of energy the prey escapes. At the same time, the escaping energy of the prey will continue to decrease during the escaping behavior. The escaping energy E can be expressed as:

$$\left\{\begin{array}{c}E={E}_{0}\times a\\ a=2(1-\frac{t}{T})\end{array}\right.$$
(2)

where \({E}_{0}\) is the initial state of energy which randomly changes inside the interval \((-\text{1,1})\) in each iteration process. \(a\) represents the nonlinear convergence factor. T is the maximum number of iterations, t is the current iteration number. At this stage, when \(0.5\le E<1\), the Harris’ hawks will initiate a soft besiege; when \(E<0.5\), they will initiate a hard besiege.

2.3 Exploitation phase

2.3.1 Soft besiege

When \(r\ge 0.5\) and \(|E|\ge 0.5\), this behavior is modeled by the following rules:

$$\left\{\begin{array}{l}X(t+1)=\Delta X(t)-E|J{X}_{rabbit}(t)-X(t)|\\ \Delta X(t)={X}_{rabbit}(t)-X(t)\end{array}\right.$$
(3)

where \(\Delta X(t)\) is the distance between the prey and the Harris’ hawk, J is a random number between 0 and 2.

2.3.2 Hard besiege

When \(r\ge 0.5\) and \(|E|\ge 0.5\), the current position is updated with the following rules:

$$X(t+1)={X}_{rabbit}(t)-E|\Delta X(t)|$$
(4)

2.3.3 Soft besiege with progressive rapid dives

When still \(|E|\ge 0.5\) but \(r<0.5\), a soft besiege is still constructed before the surprise pounce because the prey has enough energy to escape successfully. To perform the process of soft besiege, the Harris’ hawks can decide their next move based on the following rule:

$$\left\{\begin{array}{l}X(t+1)=\left\{\begin{array}{c}Y,F(Y)<F(X(t))\\Z,F(Z)<F(X(t))\end{array}\right.\\Y=X_{rabbit}(t)-E\vert JX_{rabbit}(t)-X(t)\vert\\Z=Y+S\times LF(D)\end{array}\right.$$
(5)

where S is a random vector by size \(1\times D\) and LF is the levy flight function.

2.3.4 Hard besiege with progressive rapid dives

When \(|E|<0.5\) but \(r<0.5\), the following rule is performed in hard besiege condition:

$$\left\{\begin{array}{l}X(t+1)=\left\{\begin{array}{c}Y,F(Y)<F(X(t))\\Z,F(Z)<F(X(t))\end{array}\right.\\Y=X_{rabbit}(t)-E\vert JX_{rabbit}(t)-X_m(t)\vert\\Z=Y+S\times LF(D)\end{array}\right.$$
(6)

The flow chart of HHO is shown in Fig. 2.

Fig. 2
figure 2

The flow chart of HHO

Full size image

3 The proposed EAHHO algorithm

In original HHO, escaping energy E is a key parameter which represents the linear properties. According to the updated characteristics of the HHO, E plays a decisive role in the transition from exploration to exploitation. If \(\left|E\right|\ge 1\), Harris’ hawks will adopt a global search strategy to find the prey. On the contrary, if \(\left|E\right|<1\), the local search strategy will be applied to hunt the prey. Furthermore, if \(\left|E\right|<0.5\), “Hard besiege” strategies will be applied; if \(0.5\le \left|E\right|<1\), “Soft besiege” schemes will be chosen by Harris’ hawks. If the attenuation factor of E cannot meet the needs, the variant of HHO algorithm will easily lead to poor convergence accuracy and fall into local extreme value, then our improvement will become meaningless. In HHO, E is used to simulate the gradually weaker strength of the prey during the escape, calculated by Eq. (2) for each Harris’ hawk per iteration.

During the predation process of the Harris’ Hawks, due to its cooperative behavior and tracking mode, the reduction of energy will not be linear. Inspired by the characteristics of the E, a lot of experiments are carried out according to its different attenuation modes, and finally 13 different energy attenuation modes with better performance are selected, which is further analyzed and compared among 23 benchmark functions. Subsequently, in order to verify the outstanding performance of EAHHO, complexity and volatility analysis is carried out. The curves and their mathematical formulas of different nonlinear convergence factors (a1-a14) are shown in Fig. 3 and Table 1, respectively Tables 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13.

Fig. 3
figure 3

Different strategies of nonlinear convergence factor

Full size image
Table 1 Mathematical Formulas Of Nonlinear Convergence Factor
Full size table
Table 2 [Please provide Table 2 caption]
Full size table
Table 3 Comparisons Of Complexity Between Hho And Eahho
Full size table
Table 4 The Common Control Parameters And Each Algorithm Specific Control Parameters For 16 Algorithms
Full size table
Table 5 Result comparisons among EAHHO and typical algorithms on 30-dimentional functions F1-F13
Full size table
Table 6 Result comparisons among EAHHO and typical algorithms on 50-dimentional functions F1-F13
Full size table
Table 7 Result comparisons among EAHHO and typical algorithms on 100-dimentional functions F1-F13
Full size table
Table 8 Result comparisons among EAHHO and typical algorithms on fixed-dimentional functions F14-F23
Full size table
Table 9 Result comparisons among EAHHO and SI algorithms on 30-dimensional Unimodal functions CEC 2005
Full size table
Table 10 Result comparisons among EAHHO and SI algorithms on 30-dimensional Basic and Expand functions CEC 2005
Full size table
Table 11 Result comparisons among EAHHO and SI algorithms on 30-dimensional Hybrid Composition functions CEC 2005
Full size table
Table 12 Result comparisons among EAHHO and typical algorithms on 30-dimentional functions
Full size table
Table 13 Results obtained over 50 runs by different IoV problem’s dimensions and variables of graph sizes
Full size table

3.1 Comparison among 14 HHOs with different E1

To verify the performance of the HHOs with 14 different nonlinear convergence factors, especially the proposed EAHHO with a2, numerical simulation analysis is presented. Numerical simulation analysis involves optimization precision analysis, volatility analysis of optimal results, and algorithm complexity analysis.

3.2 Numerical simulation analysis settings

Numerical simulation analysis is done on 23 benchmark functions in Appendix A Table 14, where involves different types of problems such as unimodal, multimodal and fixed-dimension multimodal distribution. 14 HHOs run 10 times independently and are stopped when the maximum number of 1000 function evaluations (FEs) is reached in each run.

3.3 Precision analysis

Figure 4 shows the convergence curves of 14 HHOs tested on 6 representative benchmark functions in Appendix A Table 14.

Fig. 4
figure 4

Convergence curves of 14 HHO algorithms on 23 test functions

Full size image

It can be clearly seen from Fig. 4 that EAHHO with a2 consistently outperforms the other 13 HHOs in most cases. In addition, although the convergence speed of EAHHO on F15 are not so fast at the beginning, the optimization process gradually accelerates after multiple iterations, and its convergence accuracy also outperforms the other 13 related HHOs. This can be explained that the attenuation characteristic of the convergence factor of EAHHO shows that the initial decay is very fast, and the period of exploration phase is relatively short, which leads to its convergence speed behaving slowly compared with others in the initial stage of the iteration. As the number of iterations increases, for the transition from exploration phase to the exploitation phase, the convergence factor decays slowly, and the exploitation phase has experienced enough time, which greatly optimizes the convergence accuracy.

3.4 Volatility analysis of optimal results

To evaluate the merits of the algorithm performance, one of the criteria is to search out the optimal value with desired precision. After 14 HHOs independently operate 10 times, we get the best value and calculate the standard deviations (SD) and means of 10 optimization results of 14 HHOs, respectively. Furthermore, the SD are used to reflect and compare the performance of 14 HHOs which are obtained after lots of experiments, and they are shown in Fig. 5 and Table 2. For clarity, the result of the excellent algorithm is marked in bold.

Fig. 5
figure 5

Standard deviations of optimization results of 14 HHO algorithms

Full size image

We can see from Table 2 that EAHHO improves the convergence accuracy in most cases, especially in terms of the Best on F1, F2, F3, F4, F7, F10, F14, F16, F17, F18 and F23. From Fig. 5 and Table 2, SD of EAHHO also have the smallest value in most benchmark functions, indicating that the fluctuation of the optimization results of EAHHO is the smallest in the most of situations, and this algorithm can guarantee higher accuracy.

3.5 Complexity analysis

The complexity of algorithms is another standard to measure the merits of algorithm. After the previous series of analysis and comparison, the energy attenuation curve of EAHHO is finally determined. Here, the time complexity of EAHHO and original HHO is mainly compared. The setting of convergence precision of functions can be seen in the CP column of the Table 3. Two algorithms independently operate 50 times, we also use 13 benchmark functions with D = 30, 50, or 100 and the maximum number of iterations (Iters) corresponds to 1000,2000,4000, respectively. Average optimization time (Avg_Time) and average iteration number (Avg_Iters) which these algorithms demand to achieve the predetermined convergence precision are shown in Table 3.

From Table 3, it is clear that the iteration number that EAHHO requires is obviously less than the requirements of HHO under the most of benchmark functions except Generalized Rosenbrock with D = 50,100, Step with D = 50, Quartic with D = 100 and Generalized Penalized with D = 30. Moreover, we can observe that EAHHO does not show a great advantage over HHO in some functions in terms of convergence time, this is because the time of each iteration of the two algorithms is different under different benchmark functions. Although the number of iterations of EAHHO is much less than that of HHO in the most of situation, the performance of its convergence time on some functions may not reflect this advantage. In conclusion, the result comparison of time complexity of HHO and EAHHO tested on the 13 functions again verify the effectiveness of EAHHO, EAHHO could make full use of the information of the neighborhood and perform an ideal balance between the exploration and the exploitation.

4 Convergence and stability analysis of EAHHO

4.1 Convergence analysis

The convergence is one of the important characteristics for intelligent algorithm, which shows that the algorithm can tend to a certain value after infinite iterations. The convergence ability of an algorithm can be analyzed and proved with the help of mathematical theory knowledge. The existing methods of convergence proof mainly include the convergence criterion of discrete martingale (Shahri et al. 2020), Banach compression mapping theorem (Kusuoka 2020), reducible random matrix stability theorem (Brieussel and Zheng 2021), convergence in probability (Mehta 2004) and some other theories. In addition to the above convergent proof methods, Markov chain theory is a common tool to analyze the convergence of SI algorithms. By proving the nonexistence of conditions for this Markov chain to be a stationary process, Ren et.al. confirmed from the transition probability that the PSO is not global convergent (Ning and Zhang 2013). Bansal et.al. presented the convergence analysis of ABC algorithm using theory of dynamical system (Ren et al. 2011). Ning et.al came to conclusion that artificial bee colony state sequence is a finite homogeneous of Markov chain and the state space of artificial bee colony is irreducible. Then it is proved that ABC ensures the global convergence as the algorithm meets two assumptions of the random search algorithm for the global convergence (Bansal et al. 2018a). Huang et.al proved that Each position state corresponds to a state of a finite Markov chain, then the stability condition of a reducible stochastic matrix can be satisfied (Huang et al. 2012). Finally, the global convergence of AFSA is proved. In this paper, the core of convergence analysis of EAHHO is to establish a Markov chain model for its updating process. By constructing an updating mechanism in three different situations: search phase, soft besiege phase, hard besiege phase, the transition probability matrix is constructed to prove that the stability condition of reducible stochastic matrix can be satisfied. In conclusion, EAHHO converges with probability 1.

4.2 Markov chain model of EAHHO

To explain Markov chain model of the EAHHO, some related mathematical descriptions and definitions are given as follow:

Definition 1

(State and State space of Harris’ hawk).

The state is made up of the position of a single Harris’ hawk, denoted as X, \(\text{x}\in \text{A}\), A is the feasible solution space. The collection of all possible states constitutes the state space, denoted as \(\text{X}=\left\{X|X\in A\right\}\)

Definition 2

(State and State space of Harris’ hawks).

The positions of all the Harris’ hawks constitute the state of Harris’ hawks in the group, denoted as \(s=({X}_{1},{X}_{2,}\cdots {X}_{SN})\), \({X}_{i}\) represents the state of the i-th Harris’ hawk. The set of all possible states of Harris’ hawks constitutes the state space of the Harris’ hawks, denoted as \(S=\left\{s=\left({X}_{1},{X}_{2,}\cdots {X}_{SN}\right)|{X}_{i}\in X,1\le i\le SN\right\}\)

Definition 3

(State transition).

For \(\forall {X}_{i}\in s, \forall {X}_{j}\in s\), the state of Harris’ hawk is transferred from Xi to Xj in one step in the iterative process of EAHHO, denoted as \({T}_{s}\left({X}_{i}\right)={X}_{j}\).

Definition 4

(State transition probability).

For \(\forall {s}_{i}\in S, \forall {s}_{j}\in S\), in the iterative process of EAHHO, the state of Harris’ hawks is transferred from si to sj in one step, denoted as \({T}_{s}\left({s}_{i}\right)={s}_{j}\). The transition probability can be expressed as: \(\text{p}\left({T}_{s}\left({s}_{i}\right)={s}_{j}\right)=\prod_{m=1}^{SN}p({T}_{s}\left({X}_{im}\right)={X}_{jm})\).

Theorem: In EAHHO, the state sequence \(\left\{{\varvec{S}}\left({\varvec{t}}\right):{\varvec{t}}>0\right\}\) is a finite homogeneous Markov chain

The search space of any optimization algorithm is finite, so the state space X of Harris’ hawks is finite. The state space of Harris’ hawks is also finite because \(s=\left({X}_{1},{X}_{2,}\cdots {X}_{SN}\right)\) is composed of SN Harris’ hawks, and SN is a finite positive integer.

From the definition 4, the state transition probability of the Harris’ hawks is determined by the transition probability of every Harris’ hawk in the state space. According to the updating formula of EAHHO in different situations, the state transition probability of any Harris’ hawk in the group is only related to the state \(\text{X}(\text{t}-1)\), the random state \({X}_{rand}(t-1)\), the state \({X}_{rabbit}\left(t-1\right)\) of the prey, the random factor r1、r2、r3、r4、r5、u、v, default constant β, maximum value UB and minimum value LB of the solution to the optimization problem, the average value \({\text{X}}_{m}(\text{t}-1)\) of states of all Harris’ hawks and the initial energy E0, so the state transition probability is only related to the state at t-1. It means that the state sequence of Harris’ hawks has Markov property. In addition, the state space is a finite set, so it constitutes a finite Markov chain. Moreover, the state transition probability is only related to the state at t-1, not time. Therefore, the state sequence \(\left\{s\left(t\right):t\ge 0\right\}\) is a finite homogeneous Markov chain.

4.3 State transition matrix of EAHHO

Definition 5

For square matrix \(\text{A}\in {R}^{n\times n}\):

  • \(\forall i,j\in \left\{\text{1,2},\cdots n\right\}\), if \({a}_{ij}\ge 0\), it is called a non-negative matrix.

  • \(\forall i,j\in \left\{\text{1,2},\cdots n\right\}\), if \({a}_{ij}>0\), it is called a totally positive matrix.

  • If A is a non-negative matrix and \(\sum_{j=1}^{n}{a}_{ij}=1\), it is called a random matrix.

  • If A is a random matrix and all rows are the same, it is called a stable matrix.

L emma

If \(P=\left[\begin{array}{cc}C& 0\\ D& E\end{array}\right]\) is a random matrix, where C is a m-dimensional full positive random square matrix, and each row of matrix D has at least one non-zero element. In conclusion, matrix P has a limit value and its convergence probability is 1.

EAHHO includes three phases: Search phase, Soft besiege phase, and Hard besiege phase.

  1. a.

    Search phase

    The probability matrix of search phase is \(\text{S}=({s}_{ij})\), where \({s}_{ij}\) is the probability of Harris’ hawk transferring from state i to state j, and its change in probability conforms to the total probability theorem:

    $$\sum_{j=1}^{L}{S}_{ij}=1$$
    (7)
  2. b.

    Soft besiege phase

    The soft besiege process is an updating strategy adopted under the condition of \(0.5\le E<1\). In each iteration, each Harris’ hawk will approach its prey in a certain way. The probability matrix of a soft besiege is \(H=({h}_{ij})\), where hij is the probability that Harris’ hawk transfers from state i to state j. The rate of information exchange between Harris’ Hawk and prey is \({\chi }_{j}\), so the probability matrix of the soft besiege process conforms to:

    $${h}_{ij}=\prod_{j=1}^{L}{\chi }_{j}$$
    (8)

    The probability \({\chi }_{j}\) is positive, H is a totally positive matrix.

  3. c.

    Hard besiege phase

    The probability matrix for the hard besiege process is \(U=({u}_{ij})\), \({u}_{ij}\) is the probability that the Harris’ hawk transfers from state i to state j, and its probability change conforms to the full probability formula.

    $$\sum_{i=1}^{L}{s}_{ij}=1$$
    (9)

    Matrix S is a non-negative random matrix, and each row has at least one positive element.

4.4 Proof of EAHHO convergence

The position of prey is optimal position. The Harris’ Hawk which is closest to the prey in this article is regarded as the position 1. The newly generated state transition probability matrix is recorded as \({S}^{*}\)(State transition probability matrix in the search phase), \({H}^{*}\)(State transition probability matrix in the soft besiege phase) and \({U}^{*}\)( State transition probability matrix in the hard besiege phase).

$$\left\{\begin{array}{l}{S}^{*}=diag(S,S,\cdots S)\\ {H}^{*}=diag(H,H,\cdots H)\\ {U}^{*}=diag(U,U,\cdots U)\end{array}\right.$$
(10)

Update of each position will record the optimal solution at the position that is closest to the prey. The location of optimal resource is from \({Z}_{1}=({X}_{Y1},{X}_{1},{X}_{2},\cdots ,{X}_{N})\) to \({Z}_{2}=({X}_{Y2},{X}_{1},{X}_{2},\cdots ,{X}_{N})\), and its state transition probability may be:

  1. a.

    XY1 is the position where Harris’ hawk is closest to the prey in the group and XY2 is the position satisfying \(f\left({X}_{Y1}\right)>f({X}_{Y2})\), its state transition probability \(\text{P}\left({Z}_{2}|{Z}_{1}\right)=1\).

  2. b.

    If the fitness function values corresponding to XY1 and XY2 are the same, the state transition probability is \(\text{P}\left({Z}_{2}|{Z}_{1}\right)=1\).

  3. c.

    Other cases: \(\text{P}\left({Z}_{2}|{Z}_{1}\right)=0\)

If all state is arranged in the order of the target value of the first variable from good to bad, the state transition probability matrix is shown below:

$$R=\left[\begin{array}{cccc}{R}_{11}& & & \\ {R}_{21}& {R}_{22}& & \\ \vdots & \vdots & \ddots & \\ {R}_{|D|1}& {R}_{|D|2}& \cdots & {R}_{|D|D}\end{array}\right]$$
(11)

Each column in \({R}_{ij}\) has at least one 1.

The state transition probability matrix of Markov chain in the whole iterative process is:

$${P}^{*}={S}^{*}{H}^{*}{U}^{*}R=\left[\begin{array}{cccc}SHU{R}_{11}& & & \\ SHU{R}_{21}& SHU{R}_{22}& & \\ \vdots & \vdots & \ddots & \\ SHU{R}_{|D|1}& SHU{R}_{|D|2}& \cdots & SHU{R}_{|D||D|}\end{array}\right]$$
(12)

Since the matrix S is non-negative and each row has at least one positive element, the matrix H is a fully positive matrix, the matrix SH is a fully positive matrix; At the same time, since the matrix U is a random matrix, the matrix SHU is a fully positive matrix. From the fact that there is at least one 1 in each column of \({R}_{11}\), it can be deduced that the matrix SHUR11 is a fully positive matrix.

The matrix P is partitioned in the manner of matrix block method according to the lemma:

$$C=[SHU{R}_{11}]$$
(13)
$$D=\left[\begin{array}{c}SHU{R}_{21}\\ SHU{R}_{31}\\ \vdots \\ SHU{R}_{|D|1}\end{array}\right]$$
(14)
$$E=\left[\begin{array}{ccc}SHU{R}_{22}& & \\ & \ddots & \\ SHU{R}_{|D|1}& & SHU{R}_{|D||D|}\end{array}\right]$$
(15)

Since matrix ECS is a fully positive matrix and the matrix R is a non-zero matrix and each column has at least 1, it can be deduced that each row in the matrix D has at least one non-zero element.

In conclusion, it can be seen from the above analysis that the block matrix C, D, E of the matrix P is consistent with the conditions of each block matrix in the lemma. Therefore, the probability that EAHHO cannot find out the ideal position is 0, in other words, EAHHO finally converges to the optimal value with probability 1.

4.5 Stability analysis

At present, the stability of intelligent algorithms is analyzed and proved by the theoretical knowledge of control system owing to the lack of mathematical theory. The methods mainly include Lyapunov Stability Theory (Gerwien et al. 2021), Routh-Hurwitz Criterion (Yousef et al. 2021), Z-transform (Djenina et al. 2020) and so on. Bansal et.al presented the stability analysis of ABC using von Neumann stability criterion for two-level finite difference scheme (Bansal et al. 2018b). Based on the Lyapunov technique, Rubio assured the error stability of the modified Levenberg–Marquardt algorithm (Rubio 2020). Stability analysis of PSO with inertia weight and constriction coefficient is carried out by von Neumann stability criterion (Gopal et al. 2020). Because the updating formula of EAHHO is too complex to obtain the characteristic equation, this paper uses Lyapunov stability theory to analyze the stability of EAHHO.

4.6 Equilibrium state

If \(f(\text{x})\) is objective function of EAHHO, then state equation can be shown as follows:

$$\dot{x}=f(x,t)$$
(16)

where f is continuous in time t and locally Lipschitz function in solution x.

For any time, the state \({x}_{e}\) that satisfies \(\dot{x}=f\left({x}_{e},t\right)=0\) is called an equilibrium state. δ and ε represent the radii of the two domains, respectively. For any given ε that is greater than 0 corresponds to \(\updelta \left(\upvarepsilon ,{t}_{0}\right)>0\),and \(\delta ,\varepsilon \in R\). Initial state x0 satisfies the condition of \(\Vert x-{x}_{e}\Vert \le \delta (\varepsilon ,{t}_{0})\). The solution x corresponding to any initial state \({x}_{0}\) satisfies as follows:

$$\| x-{x}_{e}\| \le \xi$$
(17)

In conclusion, the equilibrium state \({x}_{e}\) of the system is stable. If δ is independent of t0, then the \({x}_{e}\) is uniformly stable. If all state solutions starting from the initial state domain S(δ) do not exceed the state solution domain S(ε), it can be concluded that this system is stable.

Furthermore, \({x}_{max}\) is defined as the equilibrium point under Lyapunov Stability Theory, the proof is as follows.

if \(t\to \infty\), x will tend to the global optimal position \({x}_{\text{max}}\), shown as follows:

$$\underset{t\to \infty }{\text{lim}}\| x(t:{x}_{0},{t}_{0})-{x}_{e}\| =0$$
(18)

Translate state equation down by \({x}_{max}\) unit lengths, and then a new state equation can be obtained:

$$\dot{x}=f(x,t)-f({x}_{\text{max}})$$
(19)

And then the equilibrium state \({x}_{e}\) is satisfied for all t:

$${\dot{x}}_{e}=f({x}_{e},t)-f({x}_{\text{max}})=0$$
(20)

Hence, the EAHHO has an equilibrium point \({x}_{max}\), equilibrium state \({\dot{x}}_{e}=f({x}_{\text{max}},t)\).

4.7 Stability analysis based Lyapunov stability theory

It can be seen from the convergence of the algorithm that EAHHO eventually converges to the position of the prey that is the global optimal point. No matter where the initial state is, \(x(t:{x}_{0},{t}_{0})\) will eventually return to the global optimal point. Therefore, hypothesis \({x}_{max}\) is the equilibrium point of EAHHO in the Lyapunov sense.

A schematic diagram of optimal region is shown in Fig. 6. The \(f({x}_{max})\) and \(f({x}_{max2})\) represent the optimal value and the sub-optimal value of the objective function, respectively; \({D}_{max}\) is the optimal region with a range of [x1, x2]; x3 and x4 are the intersections of \(S(\upvarepsilon )\) and \(f(\text{x})\). The center of the circle of the \(S(\updelta )\) and the \(S(\upvarepsilon )\) is the global best point.

Fig. 6
figure 6

The schematic diagram of the optimal region

Full size image

The initial state \(x({t}_{0};{t}_{0};{x}_{0})\) is in the interval of\({D}_{max}\), that is, the area where the \(S(\updelta )\) intersects with the objective function \(f(\text{x})\) is included by \({D}_{max}\). The EAHHO will only approach the \({x}_{max}\), namely:

$$\left\{\begin{array}{l}\delta \le min(\| {x}_{\text{max}}-{x}_{1}\| ,\| {x}_{\text{max}}-{x}_{2}\| )\\ \delta \le min(f({x}_{\text{max}})-f({x}_{3}),f({x}_{\text{max}})-f({x}_{4}))\le \varepsilon \end{array}\right.$$
(21)

For any given ε, there always exists δ that satisfies Eq. (21), and \(\delta ,\varepsilon \in R\). It makes the motion starting from any initial state \({x}_{0}\) satisfy the inequality (22):

$$\| x(t;\;{x}_{0},{t}_{0})-{x}_{\text{max}}\| \le \delta \le \varepsilon$$
(22)

Hence, the solutions of the equations are all in \(S(\updelta )\), and the radius δ is independent of \({t}_{0}\). In summary, the equilibrium state \({x}_{max}\) of EAHHO is not only stable under the Lyapunov stability theory, but also the equilibrium state satisfies uniformly asymptotic stability.

5 Comparison with other state-of-the-art algorithms

To evaluate the performance of EAHHO, we use the former 13 benchmark functions with D = 30, 50, or 100 (Karaboga and Akay 2009)-(Wang and Dang 2007) and the latter 10 functions with Dim which is set according to the Appendix A Table 14.

To make a fair comparison among PSO (Kennedy and Eberhart 1995), AFSA (Li 2002), SSA (Mirjalili et al. 2017), SSA-PSO (Ibrahim et al. 2019), ABC (Karaboga and Basturk 2007), ALO (Mirjalili 2015a), DA (Mirjalili 2016a), GOA (Saremi et al. 2017), MFO (Mirjalili 2015b), MVO (Mirjalili et al. 2016), SCA (Mirjalili 2016b), WOA(Mirjalili and Lewis 2016), HHO (Heidari et al. 2019), GWO (Mirjalili et al. 2014), SSA-GWO (Wan et al. 2019) and EAHHO, these algorithms adopt the parameter settings as follows: the size of population is equal to 50 (Piotrowski et al. 2020), limit is set to be 200, and all algorithms run with same configuration of the system and with respect to same number of function evaluations. The common control parameters and Each algorithm specific control parameters for 16 algorithms are given in Table 4. Furthermore, all algorithms run 50 times independently and are stopped when the maximum number of 50,000, 100,000, and 200,000 function evaluations (FEs) in the cases of the former 13 benchmark functions is reached in each run. During the maximum number of 50,000 FEs in the condition of the latter 10 benchmark functions is got, those algorithms also run 50 times respectively and then end the optimization process. And the results are the Best (the optimal value of the objective function found by each algorithm), Mean (the mean value of the objective function found by each algorithm), STD (the standard deviation value of the objective function found by each algorithm) and Time (the average running time for a run taken by each algorithm) values of all the runs. Boldface in the tables represents the optimal results. The “NaN” means “Not a Number” returned by the test.

Some insightful conclusions can be drawn from Tables 5, 6, 7, 8. For the most part, EAHHO performs significantly better than the other algorithms. Particularly, for the low-dimensional (30 dimensions) functions in Table 4, the performance of EAHHO is much better than that of other SI algorithms on F1, F2, F3, F4, F7, F9, F10, F11. In the rest of performance of algorithm optimization, although the precision is not the best, the stability of EAHHO is better than other algorithms. For example, EAHHO has the smaller standard deviation on F1, F3, and F10. Analyzing the results of the mid-dimensional (50 dimensions) functions in Table 4, it is explicit that EAHHO significantly outperforms the other chosen algorithms in most functions. EAHHO exceeds other compared methods on F1, F2, F3, F9, F10 and F11, respectively. While EAHHO cannot perform the superiority on all the cases. For the remaining cases they perform the same, while EAHHO improves the robustness in performance on the most case. From the results of high-dimensional (100 dimensions) functions in Table 7, in the case that F1, F2, F3, F4, F9, F11 run, compared with other algorithms, EAHHO has a very superior performance.

Table 8 has compared with the performance that EAHHO and other chosen algorithms run in the fixed-dimensional benchmark functions, the EAHHO have advantage over others on the F1, F2, F3, F5, F7. In the remaining cases, EAHHO is similar to other algorithms under the optimization performance. To vividly describe the advantage of EAHHO, the convergence graphs of some test functions are plotted in Fig. 7.

Fig. 7
figure 7

Convergence curves of EAHHO and typical algorithms on representative test functions

Full size image

In conclusion, it can be seen from Tables 5, 6, 7, 8 and Fig. 7 that EAHHO has obvious superiority over the other contenders on almost all the cases. However, ABC almost occupies a relatively large advantage in the optimization time, but in terms of exploitation phase, EAHHO performs better than ABC in the accuracy of convergence. Escaping energy E plays a key role in the transition from exploration to exploitation.

6 Test on CEC 2005 benchmark functions

A set of 25 CEC 2005 benchmark functions are chosen to further test the performance of EAHHO. A brief introduction to these benchmark functions is specified in Appendix B Table 15. A more detailed discussion about them can be referred to Mirjalili et al. (2016). The results of algorithms with the maximum number of 30,000 FEs are shown in Table 8, 9, 10. It can be seen from Table 9, 10, 11 that EAHHO offers significantly better results than the competing SI algorithms in the most test functions. Specially, EAHHO significantly outperforms other typical algorithms on F41, F42, F43. For the remaining cases, although performance of EAHHO is not the best, it still has great advantages in the process of optimization, even, EAHHO improves the robustness.

7 Test on CEC 2017 benchmark functions

A set of 8 CEC 2017 benchmark functions are chosen to further test the performance of EAHHO. A brief introduction to these benchmark functions is specified in Appendix CTable 16. A more detailed discussion about them can be referred to Liang et al. (2013). The experimental results are shown in Table 12. Table 11 presents the comparison results among SSA, SSAPSO, ALO, GOA, WOA, HHO, GWO, SSA-GWO, NCHHO (Dehkordi et al. 2021), and EAHHO. In most cases, it can be observed that EAHHO outperforms the other 9 algorithms, especially, on F3, F4, F5, F7 and F8. The operation time of EAHHO is advantageous compared to HHO and NCHHO. This is because EAHHO could perform an ideal balance between the exploration and the exploitation.

8 Solving internet of vehicles routing problem

To further verify the effectiveness of the proposed EAHHO algorithm, an Internet of Vehicles routing problem (Mirjalili et al. 2014) is implemented. The objective of this problem is to maximize the probability of connectivity and link QoS of the available routes from source to destination as illustrated in Dehkordi et al. (2021). In Table 13, It is clear that EAHHO algorithm has strong optimization ability and can be used to solve such practical Internet of Vehicles routing problems. Although EAHHO is inferior to NCHHO in individual cases, EAHHO is outstanding in the overall view, and can calculate high dimensions and graph size of IoV routing problem. Especially compared with HHO algorithm, EAHHO nonlinear adaptive-convergence factor plays an important role.

9 Conclusion

In this paper, a novel harris’ hawks optimization algorithm with enhanced adaptive-convergence is proposed to overcome the drawback of slow convergence. The proposed EAHHO algorithm provides new break through and is new and useful to determine the speed of the process from exploration to exploitation and the balance between diversification and intensification of optimization. In addition, 13 HHO variants with different nonlinear convergence factors are designed to find a better energy decay factor so that the convergence speed and accuracy can achieve better results. To come up with the best among the 14 HHOs, a comparative study on 23 representative benchmark functions is carried out. Result comparisons show that EAHHO significantly surpasses other 13 HHO variants on the most of test functions, contributing to higher solution accuracy and stronger algorithm reliability. Moreover, constructed transition probability matrix Markov chain model prove that the stability condition of reducible stochastic matrix can be satisfied, consequently, the convergence of EAHHO is proved. The stability of EAHHO is also proved by Lyapunov principle because of its nonlinear characteristics. Finally, by comparing with 16 well-established algorithms on 56 test functions and solving Internet of Vehicles routing problem, EAHHO significantly surpasses other compared algorithms on the most cases, contributing to higher solution accuracy and stronger algorithm reliability. In this paper, constructed transition probability matrix Markov chain model prove that the stability condition of reducible stochastic matrix can be satisfied, consequently, the convergence of EAHHO is proved. The stability of EAHHO is also proved by Lyapunov principle because of its nonlinear characteristics.