1 Introduction

The idea of analyzing a complex network is the analysis of network performance from the perspective of structure, which has attracted a lot of attention in recent years (Sheng et al. 2020a). The theoretical principles of complex networks show that influential nodes strongly affect applications such as synchronizing, propagating and cascading (Zhao et al. 2023a; Yan et al. 2023). Therefore, addressing the problem of identifying influential nodes is of theoretical importance. At the same time, the efficient solution of this problem has outstanding value for applications such as rumor control, sickness spreading, online advertising, opinion monitoring, and viral marketing. Apart, the identification of influential nodes in complex networks is one of the main topics in the field of network information mining, and it is still an interesting and open topic (Rezaeipanah et al. 2020; Guo et al. 2022).

According to the information used from the network to calculate the centrality, these metrics are divided into three groups: local, semi-local, and global (Jannesari et al. 2023). Metrics such as degree (Freeman 2002), cluster coefficient (Serrano and Boguna 2006), PageRank (Brin and Page 1998), trust-PageRank (Sheng et al. 2020b), local neighbor contribution (Dai et al. 2019), and normalized local centrality (Zhao et al. 2018) use only local structural information of the network to calculate centrality and are categorized as local centrality metrics. Furthermore, metrics such as Betweenness (Freeman 1977), Closeness (Sabidussi 1966), Eigenvector (Bonacich 2007), and relative change of average shortest path (Lv et al. 2019) use information of holistic network to calculate centrality and are categorized as global centrality metrics.

Basically, local centrality metrics have low accuracy because they perform rankings with very limited information. However, the calculation of these metrics is simple and with low computational complexity, because they only consider the nearest neighbors (Cao et al. 2022, 2023; Wang et al. 2023). On the contrary, global centralities use data from all nodes in the network to calculate the influence of a node and obviously have a better performance than local centrality metrics. However, it is difficult to use these metrics for large-scale networks due to the numerous calculations (Kumar and Panda 2020). Also, global centrality metrics often identify the most active nodes instead of the most influential nodes due to ignoring the connections between neighbors and relying on the position of the nodes (Lv et al. 2019; Guo et al. 2023).

Due to the low accuracy of local centralities and the high complexity of global metrics, some mixed centrality metrics have recently been developed (Zhao et al. 2020). These metrics focus on combining both local and global structure and are known as semi-local centrality metrics. NCvoteRankcentrality (Kumar and Panda 2020), k-shell (Kitsak et al. 2010), k-shell decomposition (Sheng et al. 2020b), semi-local centrality (Chen et al. 2012), mixed degree decomposition (Zeng and Zhang 2013), and local structural centrality (Gao et al. 2014) are examples of semi-local centrality metrics (Nasiri et al. 2023).

Recently, researchers have sought to use competitive information with more efficient and stable features to more effectively identify influential nodes to simultaneously maintain high accuracy with relatively low complexity (Tang et al. 2023; Yue et al. 2023). Average Shortest Path (ASP) theory in complex networks is defined as the average length of all the shortest paths in the network (Huang et al. 2023; Zhao et al. 2023b). Recently, Lv et al. (2019) introduced Relative change of ASP (RASP) as a new centrality metric. RASP measures the change in ASP of a network after the removal of a node. Normally, removing a node leads to ignoring its links and thus the entire topology may be affected. Hence, the removal of an important node leads to more relative changes in the network structure and provides a higher RASP value. Since the shortest paths between all pairs of nodes are considered in ASP, RASP is categorized as a global centrality metric. RASP imposes high complexity for large-scale networks and may be impractical to measure. Zhang et al. (2023) apply RASP considering a subgraph of network with semi-local structure. Here, the nearest neighbors with fixed length are used as a subgraph to calculate RASP.

Although RASP configuration with semi-local structure provides a balance between complexity and accuracy, but extracting a subgraph from the network to calculate the important of each node is challenging. To address the above-mentioned challenges, we propose a new centrality metric using Local RASP (LRASP) considering the Extended Neighborhood Concept (ENC) (as LASPN). ENC can provide high performance for LRASP in dealing with the extraction of subgraphs from large-scale networks. Here, LRASP is combined into a weighted semi-local centrality to identify influential nodes. We investigate a range of weights to find the best performance. LASPN as the proposed semi-local centrality metric considers both topological position and semi-local structure simultaneously. Topological position refers to the connections associated with each pair of nodes considered using LRASP. Meanwhile, the semi-local structure is applied by simultaneously considering the importance of the node itself as well as the influence of the neighbors near the desired node. The semi-local structure in LASPN means that the importance of each node depends not only on the node itself but also on its nearest neighbors.

The main contribution of this paper is as follows:

  • LRASP is configured by considering the ENC to achieve high performance in dealing with the extraction of subgraphs from large-scale networks.

  • LRASP is linked as topological position with semi-local structure to develop an efficient semi-local centrality metric.

  • A weighted semi-local centrality based on LRASP is developed by considering different ranges of weights.

The rest of the paper is as follows: Centrality metrics and related works are summarized in Sect. 2. Section 3 provides details of LASPN as a proposed centrality metric. The evaluation of LASPN through simulation is given in Sect. 4. Finally, Sect. 5 concludes the paper.

2 Literature review

Consider an unweighted and undirected network as \(G=(V,E)\) where there are \(N=\left|V\right|\) nodes and \(M=\left|E\right|\) edges. The adjacency matrix associated with \(G\) is described by \(A=\left\{{a}_{u,v}\right\}\in {R}^{N,N}\), where \({a}_{u,v}=0\) and \({a}_{u,v}=1\) indicate the absence and presence of edges between \(u\) and \(v\), respectively (Cheng et al. 2023; Sun et al. 2023). Meanwhile, \(\Gamma (v)\) denotes the set of neighbors associated with node \(v\) and \({k}_{v}\) denotes the degree of node \(v\). \({k}_{v}\) is defined by the Eq. (1).

$${k}_{v}=\sum_{u\in V}{a}_{u,v}$$
(1)

Degree Centrality (DC) is a well-known metric in the local category that calculates the importance of nodes using only the degree of their neighbors (Freeman 2002). Thus, a node with a higher degree is more influential in the network than other nodes. Although DC is a simple and time-saving metric, it does not perform satisfactorily in most cases due to the use of limited local information. Another metric of local centrality is PageRank (PR), which interprets the ranking of nodes as the sorting of web pages (Brin and Page 1998). Trust-PageRank (TPR) is an extended version of the PR that applies the trust value of neighboring nodes during web page sorting (Sheng et al. 2020b).

Betweenness Centrality (BC) is a global metric that measures the frequency of nodes in all shortest paths (Freeman 1977). The influential nodes in BC include the nodes with the highest observations on the shortest paths. Closeness Centrality (CC) is another global metric that is defined for each node based on the reciprocal of the sum of geodesic distances to other nodes (Sabidussi 1966). Influential nodes from the perspective of CC include nodes with the lowest average distance to other network nodes. Eigenvector Centrality (EC) is another global metric that is defined based on the normalized eigenvector belonging to the largest eigenvalue (Bonacich 2007). EC is distinguished by the DC metric when some nodes with high/low degree are connected to many nodes with low/high degree. Another global metric is RASP, which is measured based on relative changes in ASP after removing a node (Lv et al. 2019). RASP includes the difference of ASP before and after removing a node from the network.

Due to the increasing development of complex networks, semi-local centralities have attracted more attention. K-Shell (KS) is one of the most well-known semi-local metrics that finds influential nodes in the core position of the topology (Kitsak et al. 2010). In KS, the nodes whose degree is 1 are removed and then the degree of the nodes is changed accordingly. This process is repeated until the degree of all nodes exceeds 1. After that, this strategy is applied to nodes with degree 2 and higher. Here, \(k\) refers to the degree of nodes to be removed. Finally, the remaining nodes are ranked based on degree. Mixed Degree Decomposition (MDD) is an extended version of KS that simultaneously considers exhausted degree and residual degree to calculate centrality (Zeng and Zhang 2013). Semi-local Centrality (SC) is a semi-local metric that considers the degree of first and second level neighbors to calculate influence (Chen et al. 2012). Local Structural Centrality (LSC) is another semi-local metric developed based on topological connections between neighbors (Gao et al. 2014). LSC simultaneously considers the number of neighbors and the number of nearest neighbors with fixed levels. In addition, LSC enforces topological connections between neighbors during ranking.

Liu et al. (2016) considered the influence of both nodes and edges to rank nodes. Here, Degree and Importance of Lines (DIL) is proposed as a semi-local centrality method. Hajarathaiah et al. (2022) developed Local RASP (LRASP) centrality metric to identify influential nodes. RASP is applied to the entire topology, while LRASP considers a subgraph with local structure. Zhang et al. (2023) measured the influence of a node based on three aspects: the importance of the node itself, the influence of the neighbors near the desired node, and importance of the LRASP metric (as INASP). The authors extract the induced subgraph used in LRASP with an innovative and time-saving technique. Shetty and Bhattacharjee (2022) proposed a Weighted Hybrid Centrality (WHC) to identify influential nodes in contact networks. WHC considers the importance of both nodes and edges to measure influence.

A summary of the reviewed centrality metrics along with their formula is given in Table 1.

Table 1 Details of centrality metrics
Full size table

3 Proposed centrality metric

The influence of a node in a complex network is determined not only by its own influence but also by the influence of its neighbors. Meanwhile, ASP theory can show the effectiveness of a node by considering the relative changes in the network structure after removing that node. Moreover, the insight in the literature summons the need to develop a semi-local weighted centrality metric. In this paper, we propose LASPN as a semi-local weighted centrality based on ASP theory, which considers several aspects of each node's information to identify influential nodes.

The proposed LASPN metric simultaneously combines three features to calculate influence: 1) the importance of the node itself, 2) the importance of the node's nearest neighbors, and 3) the RASP index. However, RASP was developed for the global network and seems impractical for large-scale networks. To address this challenge, LRASP is generalized as an extended version of RASP by considering a subgraph of the network with local structure (Zhang et al. 2022; Wu et al. 2024). LRASP extracts a local subgraph consisting of a fixed-length set of nearest neighbors of a node for the RASP configuration. Normally, extracting a local subgraph from the entire network for each node requires numerous calculations. LASPN solves this problem by considering the ENC in LRASP.

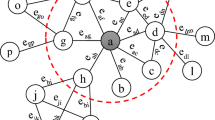
We extract a subgraph of \(G\) by considering the ENC for each node. This subgraph leads to a reduced complexity to calculate the influence for each node. After that, the extracted subgraph is weighted with a predefined weighting policy. Then, we calculate three features including “Local-Influence”, “Semi-Local-Influence”, and “LRASP-Influence” on the extracted subgraph. Finally, the combination of these factors is presented as the influence of a node in the network. Figure 1 shows an overview of the proposed centrality metric.

Fig. 1
figure 1

Overview of the proposed centrality metric

Full size image

3.1 Edge weight

Insights into the literature show that network edges are critical communication channels. However, the contribution of all edges is assumed to be the same in centrality metrics based on unweighted networks, where this is an unrealistic assumption of interactions between users. To prove the effectiveness of weighted edges in measuring influence, we define Reputation-Optimism (RO) index. “Reputation” indicates the popularity of a user in the network and “Optimism” indicates the higher following of other users. RO in an undirected network for an edge between nodes \(u\) and \(v\) is defined by Eq. (2).

$${RO}_{u,v}=\frac{2.{k}_{u}.{k}_{v}}{{k}_{u}+{k}_{v}}$$
(2)

Let \({w}_{u,v}\) be the weight of the edge associated with nodes \(u\) and \(v\), where \({w}_{u,v}={RO}_{u,v}\). In general, nodes \(u\) and \(v\) may be connected by one or more paths of fixed length. Here, the importance of paths between nodes is emphasized by applying a weight. The weight of an edge is the strength of that edge, and multiplying the weight of edges can provide reliability by considering the effect of path length. Hence, we define \({w}_{u,v}\) as the weight of a path between nodes \(u\) and \(v\), as shown in Eq. (3).

$${\widehat{w}}_{u,v}={\beta }^{\left|{Path}_{u,v}\right|}.\prod_{(x,y)\in {Path}_{u,v}}{w}_{x,y}$$
(3)

where \({Path}_{u,v}\) is the shortest available path between \(u\) and \(v\), \(\left|{Path}_{u,v}\right|\) is the length of the shortest path, and \(\beta\) is a damping factor less than 1. Yang et al. (2022), found the best value for \(\beta\) to be 0.5.

3.2 ENC based subgraph

LRASP can well make a compromise between complexity and accuracy, but there is still the challenge of extracting a subgraph for each node of the network. In LASPN, LRASP is applied based on ENC to maintain high efficiency for extracting subgraphs from large-scale networks. ENC technique can identify the nearest neighbors of a node with low complexity. ENC extracts a subgraph containing 1-hop, 2-hop, …, and \(L\)-hop neighbors as nodes with nearest neighbors, where \(L\) is the maximum hop for the nearest neighbor.

Although \({A}^{l}\) can provide the number of paths of length \(l\) with low complexity, but LRASP requires the paths themselves, which are not available (Cao et al. 2024). All paths between a pair of nodes can be calculated by methods such as Rubin, but they have high computational complexity (Rubin 1978). ENC consists of a distributed strategy for discovering paths with finite lengths and thus extracting a subgraph from the network. The process of extracting the subgraph associated with node \(v\) by ENC with maximum length \(L\) is as follows:

  1. 1.

    Node \(v\) broadcasts control packet ‘P1’ with fields \(SourceID=v\), \(NodeID=v\), and \(PathLength=L\) to the network. The packet broadcast process includes sending it to all neighbors.

  2. 2.

    Any neighbor node such as \(u\) that received the packet ‘P1’, updates its fields and rebroadcasts it in the network. This update contains \(SourceID=v\), \(NodeID=u\), and \(PathLength=L-1\). If \(PathLength=0\), then node \(u\) drops the packet and does not send it again.

  3. 3.

    Any neighbor node such as \(u\) that received the packet ‘P1’, generates the control packet ‘P2’ as a response. This packet contains the fields \(SourceID=u\), \(PathLength=L\) and, \(DestinationID={SourceID}_{P1}\), where \({SourceID}_{P1}\) refers to the \(SourceID\) field of the ‘P1’ packet. The control packet ‘P2’ is sent to all the neighbors of node \(u\).

  4. 4.

    Any node such as \(w\) that received the packet ‘P2’, updates its fields and resends it in the network. This update contains \(SourceID=u\), \(PathLength=L-1\), and \(DestinationID={SourceID}_{P1}\). If \(DestinationID=w\), then the node pointed to in the \(SourceID\) field (i.e., \(u\)) is stored in the nearest neighbor list of nodes \(w\). If \(PathLength=0\) or \(DestinationID=w\), then node \(w\) drops the packet and does not send it again.

Obviously, ENC creates for each node an \(L\)-level neighbor list containing the set of all nearest neighbors of maximum length \(L\). According to the nodes in the neighborhood list as well as the adjacency matrix, the local subgraph associated with each node of the network can be extracted. Let \(\widehat{G}(v)\) be a cut local subgraph of \(G\) for node \(v\)

3.3 LASPN centrality

Hajarathaiah et al. (2022) proposed a local version of RASP called LRASP. Although LRASP depends on local network structure and reduces complexity, it only considers topological connections to measure centrality and neglect’s semi-local structure information. Also, LRASP lacks a specific strategy for extracting local subgraphs from the entire network for each node. Zhang et al. (2023) proposed the INASP metric, which simultaneously considers LRASP and semi-local structure information to calculate centrality. Although INASP uses a distributed strategy to extract local subgraphs, but their solution is still inefficient. INASP needs to configure a dedicated neighborhood table for each node, which is often not available in complex networks.

This paper proposes the LASPN metric to identify the influential nodes in complex networks. LASPN simultaneously considers three features to measure influence: the importance of the node itself, the influence of the neighbors near the desired node, and the LRASP metric considering ENC. Accordingly, LASPN includes the following four definitions:

Definition 1.

Local-Influence: We represent the local influence of node \(v\) based on its degree in graph \(G\). Since the number of network nodes can affect the density, we divide the node degree by the total number of nodes. \({\varphi }_{Local}(v)\) is defined as the local influence of node \(v\) by Eq. (4).

$${\varphi }_{Local}\left(v\right)=\frac{{k}_{v}}{N}$$
(4)

Definition 2.

Semi-Local-Influence: Insight from the literature shows that the centrality of a node includes the importance of its neighbors. Basically, a node with more influential neighbors has a higher importance in the network topology. On the other hand, the distance between the node and its neighbors should not be ignored, because it is inversely proportional to the influence rate. Since considering all network nodes as neighbors imposes great complexity, we consider only fixed-length nearest neighbors for influence measurement. In this case, a semi-local structure is used instead of a global structure. Hitherward, 1-hop, 2-hop, …, and \(L\)-hop neighbors are considered as nearest neighbors. Furthermore, we apply the contribution of edges as a weight in the influence calculation, where it is a realistic assumption of interactions between users. \({\varphi }_{Semi\_Local}(v)\) is defined as the semi-local effect of node \(v\) by Eq. (5).

$${\varphi }_{Semi\_Local}\left(v\right)=\frac{1}{\left|{G}_{{N}_{L}(v)}\right|}.\sum_{l=1}^{L}\sum_{u\in {\Gamma }_{l}(v)}\sqrt{\frac{{\widehat{w}}_{u,v}.{k}_{v}}{{d}_{u,v}.({k}_{u}+{k}_{v})}}$$
(5)

where \(\left|{G}_{{N}_{L}(v)}\right|\) is the set of all neighbors up to level \(L\) of node \(v\) in network \(G\), and \({\Gamma }_{l}(v)\) is the set of all neighbors at level \(l\) of node \(v\). Also, \({\widehat{w}}_{u,v}\) is the weight of edges associated to nodes \(u\) and \(v\) via a reliable path, as discussed in subSect. 3.1.

Definition 3.

LRASP-Influence: In the analysis of complex networks, ASP includes the average length of the shortest path/distance for all pairs of nodes. Let \({d}_{u,v}\) be the shortest path between \(u\) and \(v\) available through an algorithm such as Dijkstra (Kermack and McKendrick 1927). Traditionally, the ASP for a graph \(G\) is defined by Eq. (6).

$$\begin{array}{c}ASP[G]=\frac{\sum_{u\ne v\in G}{d}_{u,v}}{N\left(N-1\right)}\end{array}$$
(6)

The RASP metric consists of the relative observable changes in the graph \(G\) after the removal of a node. In RASP, ASP value should be calculated for each node on the entire network. Hence, we use LRASP instead of RASP, which is configured with a local structure. Here, for each node a subgraph is extracted considering ENC and based on that LRASP is calculated. The details of subgraph extraction based on ENC are discussed in subSect. 3.2. Considering the subgraph \(\widehat{G}(v)\) instead of the graph \(G\) to calculate the centrality of node \(v\), the LRASP is defined by Eq. (7) after removing this node.

$$\Delta ASP\left[\widehat{G}(v)\right]=\frac{\left|ASP\left[\widehat{G}(v)\right]-ASP[{\widehat{G}}_{v}(v)]\right|}{ASP[\widehat{G}(v)]}$$
(7)

where \(\widehat{G}(v)\) is the extracted subgraph of \(G\) for node \(v\), and \(ASP[\widehat{G}(v)]\) represents the ASP value for the subgraph \(\widehat{G}(v)\). Also, \({\widehat{G}}_{{\varvec{v}}}(v)\) is the subgraph of \(\widehat{G}(v)\) after removing node \(v\). If no path between two nodes is available to calculate \(ASP[{\widehat{G}}_{{\varvec{v}}}(v)]\), the shortest path \({d}_{u,v}\) is equal to the diameter of the network before node \(v\) is removed (i.e., \(D=\underset{u\ne v\in \widehat{G}(v)}{{\text{max}}}{d}_{u,v}\)).

Since we cut a subgraph from the original network, subgraph resizing must also be considered in LRASP, which is clearly neglected in previous works. Let \(\Delta SZ\left[\widehat{G}(v)\right]\) be the size change of the extracted subgraph calculated by Eq. (8).

$$\Delta SZ\left[\widehat{G}(v)\right]=\frac{\left|SZ\left[\widehat{G}(v)\right]-SZ[{\widehat{G}}_{v}(v)]\right|}{SZ\left[\widehat{G}(v)\right]}$$
(8)

where \(SZ\left[\widehat{G}(v)\right]={N}_{\widehat{G}(v)}\times {E}_{\widehat{G}(v)}\) is the size of the topology associated with \(\widehat{G}(v)\), where \({N}_{\widehat{G}(v)}\) and \({E}_{\widehat{G}(v)}\) refer to the number of nodes and edges in \(\widehat{G}(v)\), respectively.

According to \(\Delta ASP\left[\widehat{G}(v)\right]\) and \(\Delta SZ\left[\widehat{G}(v)\right]\), we calculate \({\varphi }_{LRASP}\left(v\right)\) as LRASP-influence by Eq. (9).

$${\varphi }_{LRASP}\left(v\right)=\Delta SZ\left[\widehat{G}\left(v\right)\right].{\text{exp}}(\Delta ASP\left[\widehat{G}\left(v\right)\right]*{\psi }^{2L}\left[\widehat{G}\left(v\right)\right])$$
(9)

where \(\psi\) is a parameter to control the density of the extracted subgraph compared to the original graph, which is defined by Eq. (10). Since a local subgraph is cut based on a hop-count of the entire network, it is obvious that the size of the subgraph relative to the original graph has a significant impact on the LRASP value. Therefore, we include density during the LRASP calculation to reduce its impact on the LRASP metric as much as possible. According to this parameter, it can be shown that the neighborhood level \(L\) has a significant effect on the identification of influential nodes. Inspired by Hajarathaiah et al. (2022), we consider \(L\) to be the half-diameter of the network.

$$\psi \left[\widehat{G}\left(v\right)\right]=\frac{SZ\left[\widehat{G}(v)\right]}{SZ[G]}$$
(10)

where \(SZ[G]\) is the size of the topology associated with node \(G\).

Definition 4.

Total-Influence: The total influence of a node includes the combination of the previous three definitions. Accordingly, LASPN estimates the importance of nodes by combining three features: the importance of the node itself, the influence of the neighbors near the desired node, and the importance of LRASP metric. \(LASPN(v)\) indicates the importance of node \(v\) in terms of the LASPN metric, as defined by Eq. (11).

$$LASPN\left(v\right)=\xi .{\varphi }_{Local}\left(v\right)+\delta .{\varphi }_{Semi\_Local}\left(v\right)+\gamma .{\varphi }_{LRASP}\left(v\right)$$
(11)

where \(\xi\), \(\delta\), and \(\gamma\) are tunable parameters between 0 and 1 for local-influence, semi-local-influence, and LRASP-influence, respectively. here, we set the effect of all tunable parameters to be the same, where \(\xi +\delta +\gamma =1\).

3.4 Example of LASPN

To further clarify the computational procedure of the proposed LASPN metric, we describe a numerical example. An undirected and unweighted graph with 10 nodes and 13 edges is assumed as shown in Fig. 2. We give an example of calculating \(LASPN(v)\) for \(v=3\) at \(L=2\) and \({w}_{u,v}={RO}_{u,v}\). According to definition 1; \({\varphi }_{Local}\left(3\right)=0.5\), because \({k}_{v}=5\) and \(N=10\). According to definition 2; \({\varphi }_{Semi\_Local}\left(3\right)\) is calculated by the Eq. (12).

$${\varphi }_{Semi\_Local}\left(3\right)=\frac{1}{8}.\left({\left[{\left(\frac{2.16}{8}\right)}_{u=1}+{\left(\frac{2.16}{8}\right)}_{u=2}+{\left(\frac{1.89}{7}\right)}_{u=4}+{\left(\frac{2.36}{9}\right)}_{u=6}+{\left(\frac{2.16}{8}\right)}_{u=7}\right]}_{l=1}+{\left[{{\left(\frac{2.37}{14}\right)}_{u=5}+\left(\frac{2.72}{14}\right)}_{u=9}+{\left(\frac{1.87}{12}\right)}_{u=10}\right]}_{l=2}\right)=0.233$$
(12)

where \(\left|{G}_{{N}_{L}(v)}\right|=8\), \({\Gamma }_{1}\left(v\right)=\{\mathrm{1,2},\mathrm{4,6},7\}\), and \({\Gamma }_{2}\left(v\right)=\{\mathrm{5,9},10\}\).

Fig. 2
figure 2

A simple graph with 10 nodes and 13 edges

Full size image

Also, according to definition 3; \({\varphi }_{LRASP}\left(3\right)\) is calculated by Eqs. (13–15).

$$\Delta ASP\left(\widehat{G}(3)\right)=\frac{\left|1.9167-2.7143\right|}{1.9167}=0.4161$$
(13)

New….

$$\Delta SZ\left(\widehat{G}(3)\right)=\frac{\left|108-56\right|}{108}=0.4815$$
(14)
$${\varphi }_{LRASP}\left(3\right)=0.4815\times {\text{exp}}\left(0.4161\times {0.8308}^{4}\right)=0.587$$
(15)

where \(\widehat{G}(3)\) contains a subgraph of the original graph in which node 8 does not exist, because only this node is not in the first and second level neighborhood of node 3. Also, \({\widehat{G}}_{3}(3)\) contains a subgraph of the original graph without nodes 3 and 8. Here, \(ASP\left[\widehat{G}(3)\right]\) and \(ASP[{\widehat{G}}_{3}(3)\) are calculated by Eqs. (16) and (17), respectively. Besides, \(\psi \left[\widehat{G}\left(3\right)\right]\) is calculated as the density control rate associated with node 3 by Eq. (18).

$$\begin{array}{c}ASP\left[\widehat{G}(3)\right]=\frac{138}{9\times \left(9-1\right)}=1.9167\end{array}$$
(16)
$$\begin{array}{c}ASP[{\widehat{G}}_{3}(3)]=\frac{152}{8\times \left(8-1\right)}\end{array}=2.7143$$
(17)
$$\psi \left[\widehat{G}\left(3\right)\right]=\frac{108}{130}=0.8308$$
(18)

Finally, \(LASPN(3)\) is calculated by considering the tunable parameters including \(\xi =0.33\), \(\delta =0.33\) and \(\gamma =0.33\) according to Eq. (19). Table 2 shows the details of the LASPN metric results for all nodes in Fig. 2.

Table 2 LASPN metric results for all nodes in Fig. 2
Full size table
$$LASPN\left(3\right)=0.33\times 0.5+0.33\times 0.233+0.33\times 0.587=0.4356$$
(19)

4 Experimental results and analysis

This section includes implementation details and simulations as well as related results. Empirical experiments are conducted to verify the performance of the proposed centrality metric. We prove that the proposed metric performs better compared to classical centrality metrics as well as state-of-the-art metrics.

4.1 Testbed setup

We implemented the proposed centrality metric and other metrics used for comparison with the MATLAB R2021a simulator. All simulations are done on a Windows 10 machine with Intel® Core™ i5 Processor up to 3.5 GHz and 32 GB of RAM. The influence of all nodes in the network is calculated using any centrality metric, and then the rank of the nodes is determined according to the influence values. Finally, the \(TopK\) nodes with the largest ranking from each centrality method are considered as the most influential nodes. Inspired by Ullah et al. (2022), we set \(TopK\) to 10 in the simulations.

The proposed metric consists of three terms, and the impact coefficient of these terms in the final influence value is determined by \(\xi\), \(\delta\), and \(\gamma\). We set the impact coefficient of these terms to be the same according to Zhang et al. (2023). Therefore, \(\xi =\delta =\gamma =0.33\). The only tunable parameter of the proposed metric is \(L\). This parameter determines the maximum level of neighborhood and we analyze its effectiveness with different values. Meanwhile, we have made the source code of proposed metric available for real readers. The reader can download the source code of LASPN metrics from https://github.com/influentialnodes/LASPN.

4.2 Description of datasets

Simulations are performed to evaluate different centrality metrics on six complex real-world networks that are unweighted and undirected. These networks include Karate-Club, USAir97, Infect-Dub, Web-Polblogs, Bio-Dmela, and Ca-AstroPh. Selected complex networks are drawn from various fields and are available via https://networkrepository.com/networks.php. The topological properties of these networks are given in Table 3. Network parameters include number of nodes (\(N\)), number of edges (\(M\)), average degree (\({k}_{Avg}\)), maximum degree (\({k}_{max}\)), and average clustering coefficient (\(CC\)).

Table 3 Details of complex networks used for simulations
Full size table

In the Karate-Club network, the nodes are the karate clubs and the edges represent the connections between them. In the USAir97 network, nodes are US airports in 1997 and edges represent flights between them. The nodes in the Infect-Dub network are humans, and the edges represent the relationships between them. Nodes appear as web pages in the Web-Polblogs network, and edges refer to edges. Bio-Dmela network is introduced as a biological network. Also, the Ca-AstroPh network contains nodes in the roles of authors of articles, where edges indicate citations between articles and collaboration between authors.

4.3 Performance evaluation

The simulations were based on the Susceptible-Infected-Recovered (SIR) model (Kermack and McKendrick 1927) and comparisons were made based on Kendall's correlation coefficient (Shao et al. 2019; Huang et al. 2024). This model is used to analyze the diffusion process of influential nodes and to study the effectiveness of information diffusion in the network (Zhang et al. 2023). SIR is a well-known model for analyzing the spread process in complex networks that places individuals in one of the Susceptible (S), Infected (I), or Removed (R) categories. Considering an interaction between individual \(u\) and individual \(v\), the transmission process in the SIR model is defined by Eqs. (20) and (21). According to these definitions, individual \(v\) from group I interacts with individual \(u\) from group S with probability \(\lambda\) to become an individual from group I.

$$S\left(u\right)+I(v)\stackrel{\lambda }{\to }I\left(u\right)+I(v)$$
(20)
$$I(u)\stackrel{\mu }{\to }R(u)$$
(21)

where \(\lambda\) is the infection rate and \(\mu\) is the recovery rate.

Each centrality metric selects \(TopK\) nodes with the largest rank and these nodes are considered as initial infected nodes in SIR. According to the SIR model, each infected node can infect its neighbors with probability \(\lambda\) and can recover with probability \(\mu\). Let \(F(t)\) be the sum of nodes from categories I and R at time \(t\), as shown in Eq. (22). \(F(t)\) is a measure to evaluate the influence on the initial infected nodes, where \(t\) is considered as a step in the simulation.

$$F\left(t\right)=\frac{{N}_{I(t)}+{N}_{R(t)}}{N}$$
(22)

where \({N}_{I(t)}\) and \({N}_{R(t)}\) are the number of nodes from categories I and R, respectively.

Many researchers use Kendall's \(\tau\) coefficient to evaluate the correlation of ranking lists (Sheng et al. 2020a; Zhang et al. 2023). In Kendall's coefficient, each observation is considered as the rank of nodes in a centrality metric. Let \(A=\{{a}_{1},{a}_{2},\dots ,{a}_{i},\dots ,{a}_{N}\}\) and \(B=\{{b}_{1},{b}_{2},\dots ,{b}_{j},\dots ,{b}_{N}\}\) be two ranking lists containing nodes' influence scores. Let list \(A\) be generated by a centrality metric and list \(B\) by SIR model. Suppose \(\left({a}_{i},{b}_{i}\right)\) and \(\left({a}_{j},{b}_{j}\right)\) are pairs of common nodes from sets \(A\) and \(B\), respectively. According to Kendall's \(\tau\) coefficient, if \(\left({a}_{i}-{a}_{j}\right)\left({b}_{i}-{b}_{j}\right)>0\), then the influence score for these two pairs of nodes is concordant and otherwise they are discordant. Equation (23) defines Kendall's \(\tau\) coefficient.

$$\tau =\frac{{N}_{c}-{N}_{d}}{0.5N(N-1)}$$
(23)

where \({N}_{c}\) and \({N}_{d}\) are the number of concordant and discordant pairs, respectively. Also, \(\tau\) is a number in the range of -1 to 1, such that a higher value indicates similar behavior of the two ranking lists.

4.4 Benchmark metrics

In this paper, the correlation between LASPN as a proposed metric is evaluated with classical centrality metrics such as DC (Freeman 2002), BC (Freeman 1977), CC (Sabidussi 1966), KS (Garas et al. 2012), and SC (Chen et al. 2012). Also, we show that LASPN performs reasonably well compared to some state-of-the-art centrality metrics such as LSC (Gao et al. 2014), DIL (Liu et al. 2016), LRASP (Hajarathaiah et al. 2022), WHC (Shetty and Bhattacharjee 2022), and INASP (Zhang et al. 2023). Meanwhile, all the metrics are simulated with the same implementation setup so that the comparison results are fair.

4.5 Analysis of results

This section is related to the results of the simulations and the discussion about it. First, we analyze the parameters of the proposed metric. Then we show the correlation between LASPN and existing centrality metrics based on Kendall's coefficient. We prove that LASPN outperforms classical and state-of-the-art centrality metrics. We also analyze the computational complexity of LASPN.

4.5.1 Analysis of LASPN parameters

The only tunable parameter in LASPN is the neighborhood level (i.e., L). The neighborhood level exists in the semi-local-influence and LRASP-influence definitions of LASPN. The value of \(L\) plays an important role in identifying the influencing nodes for LRASP-influence, because \(L\) is applied as a hop-count to extract the local subgraph. According to Hajarathaiah et al. (2022), we consider the level \(L\) in LRASP-influence to be half the network diameter. However, the level \(L\) is unknown in the definition associated with semi-local-influence. Most semi-local centrality metrics are only based on first- and second-degree neighbors (Chen et al. 2012). However, \(L\) with higher neighborhood levels may contain valuable information to identify influential nodes. Hence, we analyze the value of \(L\) to calculate semi-local-influence with different values to evaluate the performance of LASPN.

Table 4 shows the results of this evaluation for different networks based on Kendall's \(\tau\) coefficient. These results are reported based on \(\mu =1\), \(\lambda =0.1\), and \({w}_{u,v}={RO}_{u,v}\). Each row shows the results for a complex network, while the last row is dedicated to average results. Here, better results are highlighted in bold. According to the average results, LASPN achieves the best performance with \(L=3\), and the results with \(L=2\) are also promising. Hence, other experiments are performed based on this level of neighborhood for LASPN.

Table 4 Evaluation of LASPN with different levels of neighborhood through \(L\) parameter
Full size table

The research society shows strong evidence of the significant impact of edges on centrality metrics (Kang et al. 2016). However, most centrality metrics consider the contribution of edges to be the same, which is an unrealistic assumption of interactions between users. To prove the effectiveness of weighted edges in influence estimation and also to find the best effectiveness for LASPN, we compare several different weight indexes. The proposed weights include connection strength, local and global characteristics along with the frequency of interactions between users. In addition to RO index, we consider Common Neighbors (CN) (Lorrain and White 1971), Jaccard Coefficient (JC) (Jaccard 1901), and FriendLink (FL) (Papadimitriou et al. 2012) as edge weights. These indexes are defined by Eqs. (24–26).

$${CN}_{u,v}=\left|\Gamma (u)\cap \Gamma (v)\right|$$
(24)
$${JC}_{u,v}=\frac{\left|\Gamma (u)\cap \Gamma (v)\right|}{\left|\Gamma (u)\cup \Gamma (v)\right|}$$
(25)
$${FL}_{u,v}=\sum_{l=1}^{L}{\beta }^{l}.\frac{\left|{Paths}_{u,v}^{<l>}\right|}{\prod_{k=2}^{l}(N-k)}$$
(26)

where \(\Gamma (u)\) is the list of neighbors of node \(u\), \(\left|{Paths}_{u,v}^{<l>}\right|\) is the number of available paths between \(u\) and \(v\) with length \(l\), \(\beta\) is a damping factor to reduce the effect of longer paths, and \(L\) is the maximum path length. When the adjacency matrix \(A\) reaches power \(l\), then the number of paths of length \(l\) will be available between each pair of nodes.

The results in Table 5 show that setting \({RO}_{u,v}\) as the edge weight provides the best performance for LASPN. These results are based on \(\mu =1\) and \(\lambda =0.1\), and report Kendall's \(\tau\) coefficient. Each row shows the results associated with a complex network, and the last row is the average results. Furthermore, we set \({w}_{u,v}\) to ‘1’, which represents the unweighted version of LASPN. The results prove that considering the edge weight has led to improved results in LASPN, where it is achieved in comparisons with all four weight indexes in all networks. In this table, better results are highlighted in bold. According to the average results, \({w}_{u,v}={RO}_{u,v}\) has the best performance for LASPN. Hence, other experiments are performed based on this edge weight for LASPN.

Table 5 Evaluation of LASPN with different adjusted indexes for edge weight
Full size table

4.5.2 Comparison based on Kendall's \({{\tau}}\) coefficient

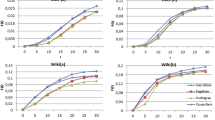
Kendall's \(\tau\) coefficient is a common criterion for comparing centrality metrics considering the SIR model. According to Ullah et al. (2022), in the simulations \(\mu\) is equal to 1 and \(\lambda\) is analyzed in the range of 0.01 to 0.1. Figure 3 shows the results related to Kendall's τ coefficient for the proposed metric (i.e., LASPN) and classical centrality metrics (i.e., DC, BC, CC, KS, and SC). The comparison between LASPN and state-of-the-art centrality methods such as LSC, DIL, LRASP, WHC and INASP is presented in Fig. 4. The results of these comparisons are presented for six complex networks including Karate-Club, USAir97, Infect-Dub, Web-Polblogs, Bio-Dmela, and Ca-AstroPh. Here, the results of all metrics are reported based on the average of more than 15 runs to be reliable.

Fig. 3
figure 3

Results of Kendall's \(\tau\) coefficient for LASPN and classical centrality metrics in different complex networks

Full size image
Fig. 4
figure 4

Results of Kendall's \(\tau\) coefficient for LASPN and state-of-the-art centrality metrics in different complex networks

Full size image

In this experiment, the relationship between influence measured by \(F(t)\) and other classical centrality metrics with different \(\lambda\) probabilities is reported. As a reminder, \(F(t)\) represents the sum of nodes from infected and removed categories at time \(t\). It is obvious that the value of \(F(t)\) will increase as \(t\) increases. In these figures, rank correlation as \(\tau\) represents Kendall's coefficient, which shows the correlation between cumulative infected nodes in a centrality metric and \(F(t)\). It is worth noting that a higher rank correlation for a centrality metric indicates a more positive correlation with the spreading ability of \(F(t)\).

The simulation results show that the proposed LASPN metric is not correlated with the existing centrality metrics and is more efficient in dealing with large-scale networks. LASPN has achieved lower complexity with higher accuracy due to the application of LRASP based on ENC. As illustrated, LASPN reports better results compared to all classical centrality metrics, where it is obtained with different values of \(\lambda\). Only SC as a classical semi-local metric has competitive results with LASPN. Considering the average results in all complex networks, LASPN is confirmed as an effective solution for identifying influential nodes due to considering the three features of the importance of the node itself, influence of the neighbors near the desired node, and also the importance of LRASP. On average, LASPN improved Kendall's \(\tau\) coefficient by 9.1%, 7.1%, 8.2%, 17.8%, and 3.7% compared to DC, BC, CC, KS, and SC, respectively.

4.5.3 Complexity analysis

The complexity of LASPN includes the time complexity for calculating local-influence, semi-local-influence and LRASP-influence. The time complexity for calculating local-influence is \(O(1)\), because it is only one mathematical operation. The time complexity for semi-local-influence calculation is \(O(3{N}_{v}.K+{E}_{v}.\mathit{log}{N}_{v})\), because it mainly considers three terms “weight calculation”, “ENC technique” and “finding the shortest path”. The weight calculation for a node is applied against all neighbors with maximum level \(L\). Therefore, the computational complexity for calculating the weight associated with node \(v\) is \(O\left({N}_{v}\right).O(K)\), where \({N}_{v}=\left|{N}_{L}\left(v\right)\right|\) is the set of all neighbors of node \(v\) up to level \(L\), and \(K\) is a constant complexity to calculate the weight between two nodes. The time complexity associated with the ENC technique is \(O\left({N}_{v}\right)\), since it only involves sending a control packet to all neighbors of node \(v\) up to level \(L\). The time complexity for finding the shortest path assuming the use of Dijkstra's algorithm is equal to \(O({N}_{v}+{E}_{v}.\mathit{log}{N}_{v})\). Meanwhile, the time complexity of LRASP-influence for a single node is \(O({N}_{v}^{L})\) because it only depends on \(L\) and ENC. Finally, the computational complexity for our proposed centrality metric (i.e., LASPN) is \(O(3{N}_{v}^{l}.K+{E}_{v}.\mathit{log}{N}_{v}+{N}_{v}^{L})\).

5 Conclusions

This paper proposed LASPN as a weighted semi-local centrality metric based on local ASP theory and extended neighborhood concept to identify influential nodes in complex networks. In addition to the importance of nodes, LASPN also considers the importance of edges in the ranking. By applying ASP theory semi-locally and extracting the subgraph associated with each node in a distributed manner, LASPN provides a reasonable compromise between complexity and accuracy. Meanwhile, LASPN uses some features based on topological position and semi-local structure to improve the performance of identifying influential nodes. LASPN has been evaluated by extensive experiments in comparison with classical and equivalent centrality metrics. Numerical simulations on six complex real-world networks demonstrate the acceptable performance of LASPN, where high accuracy is provided with low complexity. Considering network dynamics to calculate centrality metrics is clearly neglected in the existing literature. This can be applied as a future work on LASPN.