Gene selection for high dimensional biological datasets using hybrid island binary artificial bee colony with chaos game optimization

Abstract

Microarray technology, as applied to the fields of bioinformatics, biotechnology, and bioengineering, has made remarkable progress in both the treatment and prediction of many biological problems. However, this technology presents a critical challenge due to the size of the numerous genes present in the high-dimensional biological datasets associated with an experiment, which leads to a curse of dimensionality on biological data. Such high dimensionality of real biological data sets not only increases memory requirements and training costs, but also reduces the ability of learning algorithms to generalise. Consequently, multiple feature selection (FS) methods have been proposed by researchers to choose the most significant and precise subset of classified genes from gene expression datasets while maintaining high classification accuracy. In this research work, a novel binary method called iBABC-CGO based on the island model of the artificial bee colony algorithm, combined with the chaos game optimization algorithm and SVM classifier, is suggested for FS problems using gene expression data. Due to the binary nature of FS problems, two distinct transfer functions are employed for converting the continuous search space into a binary one, thus improving the efficiency of the exploration and exploitation phases. The suggested strategy is tested on a variety of biological datasets with different scales and compared to popular metaheuristic-based, filter-based, and hybrid FS methods. Experimental results supplemented with the statistical measures, box plots, Wilcoxon tests, Friedman tests, and radar plots demonstrate that compared to prior methods, the proposed iBABC-CGO exhibit competitive performance in terms of classification accuracy, selection of the most relevant subset of genes, data variability, and convergence rate. The suggested method is also proven to identify unique sets of informative, relevant genes successfully with the highest overall average accuracy in 15 tested biological datasets. Additionally, the biological interpretations of the selected genes by the proposed method are also provided in our research work.

1 Introduction

In the domains of bioinformatics and biotechnology, DNA microarray technology is regarded as a valuable asset. This technology’s breakthrough, combined with gene expression techniques, has revealed various mysteries about the biological characteristics of all live cells, enabling the examination and therapy of such endogenous genetic expression. However, conducting an experiment on hundreds of genes simultaneously (Yang et al. 2006), remains challenging work, not only because of the extensive number of genes but also because of the redundancy and irrelevance of some of them, which reduces and affects the performance of the microarray technology. As a result, the gene selection issue is being addressed using the Feature Selection (FS) technique (Dash and Liu 1997). By using gene expression data, the feature selection strategy can decrease the number of features, shorten calculation times, improve accuracy, and make data easier to understand.

The fundamental goal of FS process is the reduction of the number of features (NFs) by eliminating unnecessary ones. It could facilitate model inference and increase the classification model’s precision. Filter, wrapper, and embedding are the different feature selection techniques (Chandrashekar and Sahin 2014). Wrapper and embedded methods (Chen and Chen 2015; Lal et al. 2006; Yan et al. 2019; Erguzel et al. 2015) are based on classification techniques, and gene selection is a part of the training phase of the learning algorithms. In contrast, filter methods are based on ranking techniques to select genes that are ranked above the fixed threshold (Sánchez-Maroño et al. 2007). Due to the size of the solution space and the overall NFs count, Selecting the optimal subset of attributes is viewed as a hard combinatorial optimization problem (OP), with NP-completeness (Wang et al. 2007).

The search for the nearly ideal subset of characteristics is a crucial consideration while building an FS algorithm. The standard comprehensive approaches, such as breadth searches, depth searches, and others, are impractical for choosing the optimal subset of characteristics in large datasets. The production and evaluation of 2N subsets of a dataset with N features are required by wrapper-based methods like neural networks (Guyon and Elisseeff 2003), which is a computationally demanding task, especially when assessing subsets separately. FS is therefore thought of as an NP-hard optimization issue. Its primary purpose is to pick the fewest possible characteristics while maintaining the highest level of classification accuracy. To overcome this difficulty, FS is often built as a single-objective OP by merging these two goals using the weighted-sum approach, or as a multi-objective OP to discover compromise alternatives between the two competing goals (Xue et al. 2015). In the literature, two main objectives are frequently used: minimizing the NFs count and the classification error rate, which do not necessarily conflict with one another. For instance, in some subspaces, reducing the NFs count also reduces the classification error rate (CER) because redundant features are eliminated (Xue et al. 2012; Vieira et al. 2009; Al-Tashi et al. 2018). Due to this reason, we choose to use a single-objective strategy rather than a multi-objective one.

Furthermore, metaheuristic strategies are incorporated into feature selection since they are superior methodologies in many NP-hard issues. It can be explained by the fact that the search for the best subset in feature space is also an NP-hard problem (Yusta 2009). Additionally, compared to conventional optimization techniques, the wrapper approach based on meta-heuristic algorithms may adjust classifier parameters and choose the best feature subset, both of which can enhance classification outcomes (Huang 2009; Oliveira et al. 2010; Saha et al. 2009). Generally, metaheuristics are inspired by nature, biological and social behaviour, several approaches were proposed to handle the FS problem, such as Simulated Annealing (SA) (Meiri and Zahavi 2006), Genetic Algorithm (GA) (Oliveira et al. 2003), Ant Colony Optimization (ACO) (Chen et al. 2010; Liu et al. 2013), Differential Evolution (DE) (Hancer et al. 2018), Artificial Bee Colony (ABC) (Rao et al. 2019), Particle swarm optimization (PSO) (Wang et al. 2018), Crow Search Algorithm (CSA) (Al-Thanoon et al. 2021), Chaotic Binary Black Hole Algorithm (CBBHA) (Qasim et al. 2020), Tabu Search (TS) (Oduntan et al. 2008), etc. However, these mentioned approaches demand continuous adjustment of parameters and lack rapidity in execution time.

On the other hand, all metaheuristic algorithms must strike a balance between the exploitation and exploitation phases to prevent being caught in local optima or failing to converge (Del Ser et al. 2019). These issues have risen on by the MH algorithms’ unpredictable solution-seeking process. In this situation, it is necessary to combine concepts from many scientific disciplines. Hybridization, which combines the best features of several algorithms into a single improved technique, can result in an algorithm with higher performance and accuracy (Talbi 2002). The literature claims that hybrid algorithms outperformed single ones. However, as per the No Free Lunch (NFL) theorem, no strategy is better than all others in all feature selection tasks (Wolpert and Macready 1997). As a result, in order to better handle feature selection challenges, new algorithms must be developed or existing algorithms must be improved by modifying some of their variables. Consequently, we proposed a novel hybrid FS technique, named iABC-CGO, which is further adapted to the discrete FS problem by developing the binary variant iBABC-CGO.

The main aims and contributions of this research work are summarized as follows:

• (1) This paper proposes an enhanced binary version of an island-based model of artificial bee colonies (iBABC) combined with Chaos Game Optimization (CGO) to tackle the FS problem using gene expression data. The integration of CGO principles in the migration process aims to improve the convergence behaviour of iBABC and helps in escaping local optimum.

• (2) The performance of the suggested variants, iBABC-CGO-S and iBABC-CGO-V, is first verified by extensive testing on 15 challenging biological datasets. With the use of average accuracy values and the average number of selected features, performance comparisons have been done with a variety of current metaheuristics. Results reveal that the suggested strategy maintains performance accuracy despite controlling a large number of genes and yielding the most important subset of attributes.

• (3) The fitness of proposed iBABC-CGO variants for different biological data sets is further tested and analysed with the standard statistical measures, Wilcoxon tests, Friedman tests, Quade test, box plots, and radar plots. All of these tests and plots further demonstrate the superiority of the proposed method in terms of average accuracy over the compared metaheuristics for most of the datasets.

• (4) Finally, we also provided the biological interpretations of the genes, which are selected by the proposed iBABC-CGO method.

Accordingly, this paper is structured as follows: Section 2 provides insight into the established prior works of the FS problem using gene expression data, Section 3 explains the methodology of the island artificial bee colony (iABC) for global optimization metaheuristic, Section 4 details the proposed binary version of iABC-CGO named iBABC with the two versions iBABC-CGO-S and iBABC-CGO-V. Section 5 provides the experimental results based on several gene expression datasets, and Section 6 presents the biological interpretations of the selected genes by the proposed iBABC-CGO method. Section 7 provides insights into the pros and cons of the proposed approach. Finally, Section 8 presents the paper’s conclusion and future directions.

2 Related works

Metaheuristic techniques have emerged as powerful tools in the realm of optimization problems. They have provided fresh insights into various optimization challenges, including large-scale optimization functions, combinatorial optimization, and bioinformatics.

In large-scale optimization problems, the dimensionality of the solution space becomes prohibitively high. Traditional optimization techniques often struggle with such problems due to the sheer number of variables involved, leading to computational inefficiencies or even infeasibility. Metaheuristics, with their iterative and heuristic-based approach, offer a more scalable solution. They can handle a large number of variables and constraints more effectively, making them particularly well-suited for problems where the search space is vast and the optimal solution is difficult to locate.

Metaheuristics are strategies employed to solve optimization problems by targeting near-optimal solutions for specific problems. This search process can involve multiple agents who work together, applying mathematical equations or rules iteratively until a predefined criterion is met. This point of near-optimality is known as convergence (Yang et al. 2014).

Unlike exact methods that provide optimal solutions at the cost of high computational time, heuristic methods yield near-optimal solutions more quickly but are typically problem-specific. Metaheuristics, being a level above heuristics, have gained popularity due to their ability to deliver solutions with reasonable computational costs. Combining effective heuristics with established metaheuristics can produce high-quality solutions for a wide range of real-world problems.

In order to comprehend metaheuristics, it’s crucial to understand the foundational terms in metaheuristic computing, an approach that employs adaptive intelligent behavior. According to Wang (2010), these terms can be defined as follows:

• A heuristic is a problem-solving strategy based on trial-and-error.

• A metaheuristic is a higher-level heuristic used for problem-solving.

• Metaheuristic computing is adaptive computing that uses general heuristic rules to solve a variety of computational problems.

Wang (2010) provides a generalized mathematical representation of a metaheuristic as:

$$\begin{aligned} MH = (O, A, Rc, Ri, Ro) \end{aligned}$$

(1)

where:

• $O$ is a set of metaheuristic methodologies (metaheuristic, adaptive, automotive, trial-and-error, cognitive, etc.)

• $A$ is a set of generic algorithms (e.g., genetic algorithm, particle swarm optimization, evolutionary algorithm, ant colony optimization, etc.)

• $Rc = O \times A$ is a set of internal relations.

• $Ri \subseteq A \times A, A \wedge A$ is a set of input relations.

• $Ro \subseteq c \times C$ is a set of output relations.

Additional concepts such as neighborhood search, diversification, intensification, local and global minima, and escaping local minima are also important. Fundamental strategies in metaheuristics involve balancing exploration and exploitation, identifying promising neighbors, avoiding inefficient ones, and limiting searches to unpromising areas.

The exploration versus exploitation dichotomy, central to optimization methods, requires expanding the search to explore unvisited areas (exploration) and focusing on promising regions based on accumulated search experience for optimal utilization and convergence (exploitation) (Črepinšek et al. 2013).

Other key considerations in metaheuristics include local versus global search, single versus population-based algorithms, and hybrid methods. The choice between single-solution or population-based algorithms depends on whether the metaheuristic is more inclined towards exploitation or exploration. Ultimately, balancing exploration and exploitation is vital for both types of algorithms (Abualigah et al. 2022).

Bioinformatics is a multidisciplinary field that combines biology, computer science, and statistics to analyze and interpret biological data. With the advent of high-throughput technologies, bioinformaticians now deal with massive datasets that require efficient processing and analysis. Metaheuristic techniques have found applications in areas such as protein folding, sequence alignment, and phylogenetic tree reconstruction. They offer the ability to handle complex biological data, accommodate uncertainties, and provide solutions that are both computationally feasible and biologically meaningful.

Gene selection plays a crucial role in profiling and predicting different forms of abnormalities in the field of bioinformatics, particularly within the scope of optimization problems. Given the vast amount of gene expression data available, there is a need for a reliable and accurate approach to selecting the most pertinent genes. The feature selection approach serves this purpose by reducing the dimensionality and removing redundancy in gene expression data.

Gene expression data typically involves thousands of genes measured across various experimental conditions or time points. However, not all these genes are equally relevant for understanding or predicting biological processes or abnormalities. Many genes may exhibit similar expression patterns, leading to redundancy in the data, while others may be irrelevant to the specific condition under investigation. This high-dimensional and redundant data poses significant challenges for analysis, making gene selection an essential step.

Feature selection aims to identify a subset of the most informative genes that contribute significantly to the condition under study. This process involves three key steps: evaluation, search, and validation. In the evaluation step, each gene is assessed based on its relevance and contribution to the target condition. Statistical tests, information theory, or machine learning techniques are commonly used to assign scores or ranks to genes according to their importance.

In the search step, different algorithms, such as sequential forward selection, sequential backward elimination, or metaheuristic algorithms, are applied to identify the optimal subset of genes. These algorithms operate iteratively, adding or removing genes based on their scores, and aim to balance the trade-off between including informative genes and minimizing redundancy.

In the validation step, the selected subset of genes is tested on independent data to assess its performance in profiling or predicting the condition under investigation. Techniques like cross-validation or bootstrapping are used to ensure that the selected genes are robust and generalizable across different datasets.

The feature selection approach offers several advantages. By reducing the dimensionality of the data, it facilitates easier and more interpretable analysis. Eliminating redundancy leads to more robust and reliable results, as irrelevant or correlated genes are removed. Additionally, selecting a smaller subset of genes helps in reducing the cost and time associated with experimental validation.

Researchers have proposed a variety of techniques for applying Feature Selection (FS) to gene expression data. Lu et al. (2017) proposed a hybrid FS approach that integrates the mutual information maximization (MIM) and the adaptive genetic algorithm (AGA) to classify gene expression data. This method reduces the size of the original gene expression datasets and eliminates data redundancies. First, the authors used the MIM filter technique to identify relevant genes. Subsequently, they applied the AGA algorithm, coupled with the extreme learning machine (ELM) as a classifier.

In another study, Dhrif et al. (Dhrif et al. 2019) introduced an improved binary Particle Swarm Optimization (PSO) algorithm with a local search strategy (LS) for feature selection in gene expression data. This approach facilitates the selection of specific features by using the LS to guide the PSO search, thereby successfully reducing the overall number of features. Shukla et al. (2019) presented a hybrid wrapper model for gene selection that combines the gravitational search algorithm (GSA) and a teaching-learning-based optimization algorithm (TLBO). To apply the FS methodology, the authors converted the continuous search space into binary form.

Sharma and Rani (2019) employed a hybrid strategy for gene selection in cancer classification that integrates the Salp Swarm Algorithm (SSA) and a multi-objective spotted hyena optimizer. The authors initially used the filter method to obtain a reduced subset of significant genes. The most pertinent gene subset is then identified using the hybrid gene selection approach, applied to the pre-processed gene expression data. Masoudi et al. (2021) proposed a wrapper FS approach to select the optimal subset of genes based on a Genetic Algorithm (GA) and World Competitive Contests (WCC). This method was applied to 13 biological datasets with diverse features, including cancer diagnostics and drug discovery, and demonstrated better performance than many currently used solutions.

Ghosh et al. (2019) developed a modified version of the Memetic Algorithm (MA), called the Recursive MA (RMA), for gene selection in microarray data. The proposed method outperformed the original MA and GA-based FS algorithms on seven microarray datasets using SVM, KNN, and Multi-layer Perceptron (MLP) classifiers. Kabir et al. (2012) proposed a wrapper FS methodology that employed an enhanced Ant Colony Optimization (ACO) variant, termed ACOFS, as a search method. ACOFS showed remarkable results compared to popular FS approaches when tested on multiple biological datasets. For high-dimensional microarray data classification, authors in (Apolloni et al. 2016) developed two hybrid FS algorithms by combining a Binary Differential Evolution (BDE) algorithm with a rank-based filter methodology. These BDE-based FS algorithms were tested for robustness using SVM, KNN, Naive Bayes (NB), Decision Trees (C4.5), and six high-dimensional microarray datasets. It was observed that the proposed FS methods produced substantially equivalent classification results with more than a $95\%$ reduction in the initial number of features/genes. In a recent study (Shukla et al. 2020), various feature selection methods were investigated using gene expression data.

In the paper (Yaqoob et al. 2023), the authors address the challenge of dimensionality in high-dimensional biomedical data, which complicates the identification of significant genes in diseases like cancer. They explore new machine learning techniques for analyzing raw gene expression data, which is crucial for disease detection, sample classification, and early disease prediction. The paper introduces two dimensionality reduction methods, feature selection and feature extraction, and systematically compares several techniques for analyzing high-dimensional gene expression data. The authors present a review of popular nature-inspired algorithms, focusing on their underlying principles and applications in cancer classification and prediction. The paper also evaluates the pros and cons of using nature-inspired algorithms for biomedical data. This review offers guidance for researchers seeking the most effective algorithms for cancer classification and prediction in high-dimensional biomedical data analysis.

The article (Aziz 2022) addresses the challenge of designing an optimal framework for predicting cancer from high-dimensional and imbalanced microarray data, a common problem in bioinformatics and machine learning. The authors focus on the independent component analysis (ICA) feature extraction method for Naïve Bayes (NB) classification of microarray data. The ICA method effectively extracts independent components from datasets, satisfying the classification criteria of the NB classifier. The authors propose a novel hybrid method based on a nature-inspired metaheuristic algorithm to optimize the genes extracted using ICA. They employ the cuckoo search (CS) and artificial bee colony (ABC) algorithms to find the best subset of features, enhancing the performance of ICA for the NB classifier. According to their research, this is the first application of the CS-ABC approach with ICA to address the dimensionality reduction problem in high-dimensional microarray biomedical datasets. The CS algorithm improves the local search process of the ABC algorithm, and the hybrid CS-ABC method provides better optimal gene sets, improving the classification accuracy of the NB classifier. Experimental comparisons show that the CS-ABC approach with the ICA algorithm performs a deeper search in the iterative process, avoiding premature convergence and producing better results compared to previously published feature selection algorithms for the NB classifier.

The article (Chen et al. 2023) addresses the issue of high-dimensional genetic data in contemporary medicine and biology. The authors propose a new wrapper gene selection algorithm called the artificial bee bare-bone hunger games search (ABHGS), which integrates the hunger games search (HGS) with an artificial bee strategy and a Gaussian bare-bone structure. The performance of ABHGS is evaluated by comparing it with the original HGS and a single strategy embedded in HGS, as well as six classic algorithms and ten advanced algorithms using the CEC 2017 functions. Experimental results show that ABHGS outperforms the original HGS. In comparison to other algorithms, it improves classification accuracy and reduces the number of selected features, indicating its practical utility in spatial search and feature selection.

The work proposed by (Coleto-Alcudia and Vega-Rodríguez 2020), introduces a new hybrid method for gene selection in cancer research, aimed at classifying tissue samples into different classes (normal, tumor, tumor type, etc.) effectively with the fewest number of genes. The proposed approach comprises two steps: gene filtering and optimization. The first step employs the Analytic Hierarchy Process, using five ranking methods to select the most relevant genes and reduce the number of genes for consideration. In the second step, a multi-objective optimization approach is applied to achieve two objectives: minimize the number of selected genes and maximize classification accuracy. An Artificial Bee Colony based on Dominance (ABCD) algorithm is proposed for this purpose. The method is tested on eleven real cancer datasets, and results are compared with several multi-objective methods from the scientific literature. The approach achieves high classification accuracy with small subsets of genes. A biological analysis on the selected genes confirms their relevance, as they are closely linked to their respective cancer datasets.

The paper (Pashaei and Pashaei 2022) presents a new wrapper feature selection method based on the chimp optimization algorithm (ChOA) for the classification of high-dimensional biomedical data. Due to the presence of irrelevant or redundant features in biomedical data, classification methods struggle to accurately identify patterns without a feature selection algorithm. The ChOA is a newly introduced metaheuristic algorithm, and this work explores its potential for feature selection. Two binary variants of the ChOA are proposed, using transfer functions (S-shaped and V-shaped) or a crossover operator to convert the continuous version of ChOA to binary. The proposed methods are validated on five high-dimensional biomedical datasets, as well as datasets from life, text, and image domains. The performance of the proposed approaches is compared to six well-known wrapper-based feature selection methods (GA, PSO, BA, ACO, FA, FP) and two standard filter-based methods using three different classifiers. Experimental results show that the proposed methods effectively remove less significant features, improving classification accuracy, and outperforming other existing methods in terms of selected genes and classification accuracy in most cases.

The paper (Pashaei and Pashaei 2021) presents a new hybrid approach (DBH) for gene selection that combines the strengths of the binary dragonfly algorithm (BDF) and binary black hole algorithm (BBHA). The proposed approach aims to identify a small and stable set of discriminative genes without sacrificing classification accuracy. The approach first applies the minimum redundancy maximum relevancy (MRMR) filter method to reduce feature dimensionality and then uses the hybrid DBH algorithm to select a smaller set of significant genes. The method was evaluated on eight benchmark gene expression datasets and compared against the latest state-of-art techniques, showing a significant improvement in classification accuracy and the number of selected genes. Furthermore, the approach was tested on real RNA-Seq coronavirus-related gene expression data of asthmatic patients to select significant genes for improving the discriminative accuracy of angiotensin-converting enzyme 2 (ACE2), a coronavirus receptor and biomarker for classifying infected and uninfected patients. The results indicate that the MRMR-DBH approach is a promising framework for identifying new combinations of highly discriminative genes with high classification accuracy.

The paper (Pashaei 2022) addresses the challenge of microarray data classification in bioinformatics. The authors propose a new wrapper gene selection method called mutated binary Aquila Optimizer (MBAO) with a time-varying mirrored S-shaped (TVMS) transfer function. This hybrid approach employs the Minimum Redundancy Maximum Relevance (mRMR) filter to initially select top-ranked genes and then uses MBAO-TVMS to identify the most discriminative genes. TVMS is used to convert the continuous version of Aquila Optimizer (AO) to binary, and a mutation mechanism is added to the binary AO to enhance global search capabilities and avoid local optima. The method was tested on eleven benchmark microarray datasets and compared to other state-of-the-art methods. The results indicate that the proposed mRMR-MBAO approach outperforms the mRMR-BAO algorithm and other comparative gene selection methods in terms of classification accuracy and the number of selected genes on most of the medical datasets.

To tackle the challenges associated with analyzing gene expression data generated by DNA microarray technology, authors in (Alomari et al. 2021) propose a new hybrid filter-wrapper gene selection method combining robust Minimum Redundancy Maximum Relevancy (rMRMR) as a filter approach to select top-ranked genes, and a Modified Gray Wolf Optimizer (MGWO) as a wrapper approach to identify smaller, more informative gene sets. The MGWO incorporates new optimization operators inspired by the TRIZ-inventive solution, enhancing population diversity. The method is evaluated on nine well-known microarray datasets using a support vector machine (SVM) for classification. The impact of TRIZ optimization operators on MGWO’s convergence behavior is examined, and the results are compared to seven state-of-the-art gene selection methods. The proposed method achieves the best results on four datasets and performs remarkably well on the others. The experiments confirm the effectiveness of the method in searching the gene search space and identifying optimal gene combinations.

However, these methods still have several drawbacks, such as local optima stagnation, premature convergence, and onerous criteria and execution times (Abu Khurma et al. 2022; Agrawal et al. 2021; Abiodun et al. 2021). To mitigate these shortcomings, this paper introduces a new, enhanced wrapper algorithm based on the island model of the ABC metaheuristic. Over the years, numerous extensions and applications of the ABC algorithm have been proposed. For instance, the study in (Zorarpacı and Özel 2016) presented a hybrid approach that integrates differential evolution with the ABC method for feature selection. In (Garro et al. 2014), distance classifiers and the ABC method were employed to classify DNA microarrays. The study in (Alshamlan et al. 2019) introduced an ABC-based technique for accurate cancer microarray data classification, utilizing an SVM as a classifier. Various other hybridizations and expansions of the ABC algorithm have been proposed over time. Recently, (Awadallah et al. 2020) introduced the island model to the standard ABC algorithm for global optimization (denoted as iABC), achieving impressive success compared to its competitors.

Building upon these developments, the objective of this study is twofold. First, we propose a hybridized version of iABC, termed iABC-CGO, which incorporates Chaos Game optimization to tackle the standard ABC’s slow convergence problem, which arises from modifying only a single decision vector dimension. Subsequently, we introduce a binary variant of iABC-CGO, referred to as iBABC-CGO, designed to address the feature selection (FS) problem in the context of gene expression data. This hybrid approach aims to harness the strengths of both Chaos Game optimization and the island model of the ABC metaheuristic, potentially offering improved convergence rates and enhanced feature selection capabilities.

3 Preliminaries

3.1 Overview of island ABC (iABC) for optimization

ABC algorithm is a swarm-based metaheuristic motivated by how bees forage for food, where the location of the food source indicates potential ideal solutions and the quantity of nectar suggests the quality of the solution (Rao et al. 2019). ABC intrigued the authors of (Awadallah et al. 2020) due to its many benefits, and they suggested a new version of ABC paired with the island model for enhancing the convergence speed and diversity of solutions. However, the original ABC algorithm still struggles with three major deficiencies in the search behaviour, which are: (i) the search equation favours exploration over exploration (Zhu and Kwong 2010; (ii) numerous fitness evaluations (Mernik et al. 2015); and (iii) tendency to stuck in local optima due to premature convergence, especially while applying to complex optimization problems (Karaboga et al. 2014).

Therefore, the island model concept (Wu et al. 2019) has been introduced mainly to address the lack of heterogeneity from which most population-based algorithms suffer. The original algorithm is independently run, either synchronously or asynchronously, on each island. Therefore, a migration mechanism is used to shift certain individuals from one island to another in order to increase the algorithm’s effectiveness. This procedure might adhere to a number of strategies that guarantee the spatial exploration of newer areas of the search area (Tomassini 2006). The wide use of this technique can be explained by its balance between exploration and exploitation. Moreover, dividing individuals (potential solutions) into different islands reduces the computational time and increases the probability that weak solutions reach the best values (Whitley et al. 1997).

Several island-based metaheuristic studies were proposed such as island ACO (Mora et al. 2013), island bat algorithm (Al-Betar and Awadallah 2018), island GA (Corcoran and Wainwright 1994; Whitley et al. 1997; Palomo-Romero et al. 2017), island PSO (Abadlia et al. 2017), island harmony search algorithm (Al-Betar et al. 2015), and island crow search algorithm (Turgut et al. 2020). The proposed approaches succeeded in reducing the computational requirements and providing good results. However, choosing the adequate values of different parameters and adopting the suitable migration policy for the island-based technique greatly impact the final results as proved by many studies (Cantú-Paz et al. 1998; Fernandez et al. 2003; Skolicki and De Jong 2005; Tomassini 2006; Ruciński et al. 2010).

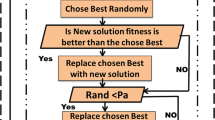
The island model requires at first two parameters: the quantity also referred to as the number of islands ($I_n$) and the size of islands ($I_s$). Then, the four key variables that determine the migration process between the islands are the migration rate, the migration frequency, the migration policy, and the migration topology. The migration rate ($R_m$) represents the number of solutions transferred between islands. The migration frequency ($F_m$) defines the periodic time for the exchange. The migration topology structures the path of exchanging solutions among islands. Several topologies were proposed in the literature and mainly categorized into two sets, one for static and the second for dynamic. Static topologies include ring, mesh, and star, where the structured paths are predefined and remain static during the migration process (da Silveira et al. 2019). Dynamic topologies, as the name implies, randomly define paths and changes in every migration process (Duarte et al. 2017). The migration policy determines which solutions are exchanged between islands. Researchers introduced different policies based on greed or random selection. The most used policies are the best-worst policy dealing with replacing the worst solutions of one island with the best solutions from the other(Kushida et al. 2013). The random policy consists of migrating solutions randomly(Araujo and Merelo 2011). Finally, the migration process with all its factors can be carried out in two ways: synchronously or asynchronously. In iABC algorithm, the artificial bee colony population is divided into islands, and solutions are enhanced separately and locally on each island. Once a certain number of iterations are over, a migration procedure based on random ring topology is applied to exchange solutions within islands. The flowchart of iABC is presented in Fig. 1 and detailed in (Awadallah et al. 2020).

Fig. 1

The flowchart of iABC algorithm

3.2 Overview of choas game optimization (CGO)

Chaos game optimization (CGO) (Talatahari and Azizi 2021), which incorporates both game theory and the mathematical idea of fractals, is a recent innovative optimization metaheuristic method. Fractals are built using a polygon form that begins with a random beginning point and an affine function. The iterative series of points produces the fractal shape by continually applying the chosen function to a new point. The CGO algorithm seeks to produce a Sierpinski Triangle based on characteristics of fractals in chaos theory. There are many solution candidates (X) in the CGO’s initial population. Each potential solution $(X_i)$, which comprises the decision variables (xi, j), offers a Sierpinski triangle as an eligible point in the search space. The following criteria are used to generate the eligible points:

$$\begin{aligned} x_{i}^{j}(0)=x_{i,min}^{j}+{\text {rand}} .\left( x_{i,max}^{j}-x_{i,min}^{j}\right) , \quad \left\{ \begin{array}{l} i=1,2, \ldots , n \\ j=1,2, \ldots , d \end{array}\right. \end{aligned}$$

(2)

The dimension of each solution is given by d, where n is the total number of candidates for eligible solutions. The beginning locations of the solutions are indicated by the variable $x_{i}^{j}(0)$. The maximum and minimum values of the $x_{i,max}^{j}$ and $x_{i,min}^{j}$ variables serve as the $j^{th}$ decision variable of the $i^{th}$ solution, while the rand variable denotes a random value in the range of [0, 1] .

For the initial search, a temporary Sierpinski triangle is created inside the search space for each potential solution depending on the locations of three vertices as follows:

• The Global Best (GB).

• The Mean Group $(MG_i)$.

• The $i^{th}$ solution candidate $(X_i)$.

Four different approaches are used to update positions. The first one mimics how the solution $X_i$ moves to GB and $MG_i$ using the following mathematical formulation:

$$\begin{aligned} \text{ Seed } _{i}^{1}=X_{i}+\alpha _{i} \times \left( \beta _{i} \times GB-\gamma _{i} \times MG_{i}\right) , \quad i=1,2, \ldots , n \end{aligned}$$

(3)

where $\alpha {i}$ denotes a factorial formed at random, $\beta {i}$ and $\gamma {i}$ denote a random number equal to 0 or 1, respectively. The following equation models how GB moves in relation to $X_i$ and $MG_i$:

$$\begin{aligned} \text{ Seed } _{i}^{2}=GB+\alpha _{i} \times \left( \beta _{i} \times X_{i}-\gamma _{i} \times MG_{i}\right) , \quad i=1,2, \ldots , n \end{aligned}$$

(4)

The tertiary technique shows how $MG_i$ moves in the direction of $X_i$ and GB. This technique is mathematically represented:

$$\begin{aligned} \text{ Seed } _{i}^{3}=MG_{i}+\alpha _{i} \times \left( \beta _{i} \times X_{i}-\gamma _{i} \times GB\right) , \quad i=1,2, \ldots , n \end{aligned}$$

(5)

The exploitation phase of the CGO optimization process is defined by the position update described by the first three approaches. The mutation for the exploration phase is shown in the fourth technique, which is mathematically represented as follows:

$$\begin{aligned} \text{ Seed } _{i}^{4}=X_{i}\left( x_{i}^{k}=x_{i}^{k}+R\right) , \quad k=[1,2, \ldots , d] \end{aligned}$$

(6)

where k is a randomly generated integer in the range of [1, d] and R is a uniformly distributed random (UDR) number in the range of [0, 1]. Four possible formulations for $\alpha _{I}$ are considered to adjust the global and local search rates of the CGO.

$$\begin{aligned} \alpha _{i}=\left\{ \begin{array}{l} \text{ Rand } \\ 2 \times \text{ Rand } \\ (\delta \times \text{ Rand } )+1 \\ (\varepsilon \times \text{ Rand } )+(\sim \varepsilon ) \end{array}\right. , \end{aligned}$$

(7)

The variables $\delta$ and $\varepsilon$ denote random numbers in the interval [0, 1], where Rand is a UDR number in the range of [0, 1]. Figure 2 shows the CGO algorithm’s flowchart.

Fig. 2

The flowchart of CGO algorithm

The CGO algorithm offers an efficient optimization technique using multigroup behaviour as a basis. Easy to implement and simple to understand is what best describes the CGO algorithm, where it performs well in many optimization problems (Talatahari and Azizi 2020; Ponmalar and Dhanakoti 2022; Ramadan et al. 2021). However, it converges early due to a talent imbalance between exploration and exploitation. In fact, excessive exploration wastes time and has a poor convergence rate, whereas high exploitation destroys variety and traps people in local optimums (Roshanzamir et al. 2020).

4 Proposed approach

FS can be formulated as a binary optimization problem since it deals with the binary decision of whether to select a feature or not. Consequently, to adapt the FS problem using gene expression data, a hybrid binary version of iABC algorithm with CGO algorithm is suggested in this work named iBABC-CGO. The proposed iBABC-CGO approach combines the swarm intelligence ABC metaheuristic, the island model concept, the chaos game optimization principles and the binary version to handle the large dimension of the gene expression data and the considerable number of irrelevant and redundant genes.

4.1 iABC-CGO

The island model offers one of the most useful techniques for partitioning the population into a number of sub-population. The searching activities of the metaheuristic algorithm are repeated synchronously or asynchronously on each island. In order to exchange migrants between islands, a migration mechanism must be implemented. This procedure allows the metaheuristic algorithm to rigorously explore the search space resulting in performance improvement of the final solution (Tomassini 2006). The algorithm can arrive at a global optimal solution due to the increased population diversity because of the exchange of individuals with diverse fitness values across islands (Tomassini 2006). Indeed, the count of islands in the model or the frequency of inter-island migrant transfers impacts the efficiency of the algorithm.

The migration policy, which specifies who will be relocated off the island and decides their location on the other island, influences the efficacy of the island model (Araujo and Merelo 2010; Ruciński et al. 2010). Numerous academics have examined the influence of the chosen migration topology on the algorithm efficiency (Cantú-Paz et al. 1998; Tomassini 2006; Ruciński et al. 2010; Fernandez et al. 2003). Therefore, we decide to introduce a new migration policy based on the principles of the CGO algorithm.

Indeed, the CGO method relies on the Sierpinski triangle, which consists of three positional vertices of the global Best, the mean group, and the $i^{th}$ solution candidate $(X_i)$. Since the CGO method is developed on the concept of sub-populations, the idea of replacing the traditional random ring topology with the CGO position update formulas emerged.

Therefore, the $R_{\textrm{m}} \times I_{\textrm{s}}$ solutions are to be exchanged among islands after a predefined number of iteration $F_{\textrm{m}}$. Those solutions are selected using the roulette wheel technique (Lipowski and Lipowska 2012).

The detailed proposed iABC-CGO algorithm is represented by the flowchart in Fig. 3.

Fig. 3

The flowchart of iABC-CGO

4.2 Binary version of iABC-CGO (iBABC-CGO)

In the continuous version of the proposed iABC-CGO algorithm, the bees change their position in a continuous search space. Therefore, a feature subset is encoded as a one-dimensional vector with the same length as the NFs count in the binary optimization, where limits on the search agents’ positions (the bees) are enforced in the order of 0, 1 values. Non-chosen features are set to 0, while those selected are set to 1.

Afterward, the conversion of the continuous optimization algorithm into a binary version is performed using transfer functions (TFs) which are an effective tool to perform this conversion (Mirjalili and Lewis 2013). In this work, two commonly used S-shaped and V-shaped TFs are chosen to develop the two binary versions of iABC, namely iBABC-CGO-S and iBABC-CGO-V. The probability of updating an element’s position in the TFs S and V in binary form to be 1 or 0 is given by Eq (7):

$$\begin{aligned} P(x_i^d(t))=TF(x_i^d(t)), \end{aligned}$$

(8)

where TF is the transfer function that can be Sigmoid for the S-shaped TF given in Eq. (8) or Hyperbolic tang for V-shaped TF defined in Eq. (9), and $x_i^d(t)$ presents the $i^{th}$ bee position in dimension $d^{th}$ at iteration t.

$$\begin{aligned}{} & {} TF(x_i^d(t))=\frac{1}{1+e^{-x_i^d(t)}} \end{aligned}$$

(9)

$$\begin{aligned}{} & {} TF(x_i^d(t))=|\tanh (x_i^d(t))| \end{aligned}$$

(10)

The probability value produced by Eq. (7) is then applied to Eq. (10) to generate the binary value for the S-shaped transfer function or Eq. (11) for the V-shaped TF in order to update the position vectors of bees.

$$\begin{aligned} x_i^d(t+1)= & {} \begin{Bmatrix} 0 \quad \text {if}\quad \text {rand} < P(x_i^d(t))\\ 1 \quad \text {if}\quad \text {rand} \ge P(x_i^d(t)) \end{Bmatrix} \end{aligned}$$

(11)

$$\begin{aligned} x_i^d(t+1)= & {} \begin{Bmatrix} x_i^d(t)^{-1} \quad \text {if}\quad \text {rand} < P(x_i^d(t))\\ x_i^d(t) \quad \quad \text {if}\quad \text {rand} \ge P(x_i^d(t)) \end{Bmatrix} \end{aligned}$$

(12)

with rand as a random vector in [0, 1].

The general steps of iBABC-CGO are presented in Algorithm 1 and followed by a flowchart as illustrated in Fig. 4 and detailed as follows:

• Step 1: Set iBABC-CGO algorithm’s parameters to initial values. These parameters are Solution number (SN), Maximum cycle number (MCN), limit, Island number ($I_n$), Island size ($I_s$), Migration frequency ($F_m$) and Migration rate ($R_m$).

• Step 2: Generate randomly the initial population. Each Bee (i.e. Solution) is spawned according to this formula: $X_i^j=r*(Ub_j-Ul_j)+Ul$, where r is a uniform random number between 0 and 1, and $Ub_j$ and $Lb_j$ are respectively the upper bound and the lower bound of the $j^{th}$ dimension.

• Step 3: Create a set of $I_n$ islands from the iBABC-CGO population.

• Step 4: The search process according to ABC principles. The four stages (Steps 4a–4d) of this procedure are as follows:

  • Step 4a: Send the employed bees using island based mechanism as per lines no. 19–31 in the pseudo-code (Algorithm 1). This stage involves doing a binary transformation in accordance with the function binary_transformation’s pseudo code.

  • Step 4b: Calculate the probability values as per line no. 32–36 (Algorithm 1). In this stage, a binary transformation is carried out in accordance with the function binary_transformation’s pseudo code.

  • Step 4c: Send the onlooker bee as per line no. 37–46 (Algorithm 1). In accordance with the pseudo-code of the function binary_transformation, a binary transformation is carried out in this phase.

  • Step 4d: Send the scout bee as per line no. 53–57 (Algorithm 1). During this step, a binary transformation is performed as per the pseudo-code of the function binary_transformation.

• Step 5: The migration procedure of the iBABC-CGO algorithm is in charge of transferring food supplies across islands, which starts when a certain number of iterations (Fm) are finished. This process is described in Algorithm 1 as shown in Lines 58–71.

• Step 6: Record the best solution in each island ($MG_t$).

• Step 7: Memorize the best solution (GB) of all islands.

• Step 8: Stop condition. Repeat steps 4, 5, 6, and 7 until the MCN is reached.

Fig. 4

The flowchart of iBABC-CGO algorithm

4.3 iBABC-CGO complexity

According to the original iABC, the time complexity is $\mathcal {O}(MCN \times I_s \times I_n \times d)$ by neglecting the compute time for calculating the objective function. However, for our proposed approach iBABC, the fitness assessment takes more time than other modules and we note it as ’fe’. In addition, the slight variation between the original iABC and the binary variant iBABC lies in the integration of the transfer function (TF) calculation. Overall, the complexity of iBABC is $\mathcal {O}(MCN \times I_s \times I_n \times d \times fe \times TF)$. The latter could be simplified by neglecting the part ${\textbf {TF}}$ since the function used in this study is simple and fast to calculate.

However, the migration method for iBABC-CGO is the main difference from that of iBABC. In this stage, the proposed approach uses the principles of the CGO algorithm by updating a randomly selected solution using roulette wheel selection. This update procedure concerns $R_m*I_s$ solutions on each island as same as the iBABC. The used migration mechanism in iBABC is the random ring topology which is based on replacing the worst solution of an island t with the best solution in the previous island $t-1$. Since the computational complexity of the newly proposed migration mechanism is slightly more time-consuming than the random ring topology, we decide to consider them equivalent. Therefore, the complexity of iBABC-CGO does not differ from the complexity of iBABC which is $\mathcal {O}(MCN \times I_s \times I_n \times d \times fe )$.

4.4 iBABC for feature selection using gene expression data

As previously stated, FS is a binary optimization problem that involves identifying and evaluating a subset of significant features while maintaining good accuracy. The best relevant subset of features is chosen based on two objectives: the lowest CER and the fewest features, as expressed in the objective function Eq. (12). At the core of the fitness function, each determined solution is evaluated with the KNN machine learning classifier.

$$\begin{aligned} \downarrow fitness=\alpha \gamma _R(D)+\ (1-\alpha )\frac{|R|}{|C|}, \end{aligned}$$

(13)

where $\gamma _R(D)$ denotes the CER of the classifier R with respect to the decision D as formulated in Eqs. (13) and (14), |R| defines the length of the selected feature subset, |C| shows the total features count, and $\alpha \in [0,1]$, $(1-\alpha )$ parameters defines the importance of the classification quality and the length of the subset as adopted from literature (Emary et al. 2016). During this study, we set the value of $\alpha$ to 0.1.

$$\begin{aligned}{} & {} \gamma _R(D)= 1- Acc \end{aligned}$$

(14)

$$\begin{aligned}{} & {} Acc = \frac{C_{\text{ num } }}{C_{\text{ num } }+I_{\text{ num } }} * 100 \%, \end{aligned}$$

(15)

where $C_{\text{ num } }$ and $I_{\text{ num } }$ denote the count of correctly and incorrectly classified labels, respectively.

5 Experimental results

The proposed approaches were implemented using MATLABR2020a and run on an Intel Core i7 machine, 2.6 GHz CPU and 16GB of RAM. Experiments were repeated 51 independent times to obtain statistically meaningful results. For evaluation purposes, the $k-$fold (Fushiki 2011) cross-validation method is used to evaluate the consistency of the generated results. The data is partitioned into K equivalent folds, with $K-1$ folds used for training the classifier during the optimization phase and the remaining fold used for testing and validating the classifier. Using different folds as a test set, the method runs K times. The standard form of this technique in wrapper feature selection algorithms is based on the KNN (k-nearest neighbor) classifier with $K=5$ (Friedman et al. 2001), which will be held during this study.

5.1 Datasets description and parameter settings

For evaluating the proposed iBABC-CGO, fifteen biological gene expression datasets are used for experiments detailed in Table 1. The studied datasets express different types of cancerous diseases and contain two different types: binary-class (BC) and multi-class (MC) datasets. For performance comparison, seven metaheuristic feature selection approaches are chosen, namely: original ABC (Rao et al. 2019), Island-based ABC (iABC) (Awadallah et al. 2020). In addition, four recent metaheuristics: Binary Atom Search Optimization (BASO) (Too and Rahim Abdullah 2020), Binary Equilibrium Optimizer (BEO) (Gao et al. 2020), and Binary Henry Gas Solubility Optimization (BHGSO) (Neggaz et al. 2020), are chosen. In the end, another state-of-the-art metaheuristic Binary Genetic Algorithm (BGA) (Babatunde et al. 2014) is selected. These selected comparative metaheuristics have performed well in the past in solving different OPs including the feature selection problem. Table 2 summarizes details of all the comparative studies and models examined during this study.The parameters of these methods for the feature selection problem are detailed in Table 3 and selected according to their original respective papers.

Table 1 Details of datasets with Class Distribution (CD)

Table 2 Key to comparative methods

Table 3 Algorithms parameter settings

5.2 Results for microarray datasets

Table 4 Percentage of average performance using KNN, SVM, and NB classifiers on 15 microarray datasets

Table 5 Classification accuracy using selected genes by filter-based gene selection methods with a fixed set of 50 selected genes

Table 6 Classification accuracy using selected genes by filter-based gene selection methods with a fixed set of 100 selected genes

Table 4 presents the average performance of three classifiers KNN, SVM, and NB across 15 microarray datasets. The performance is measured in terms of four metrics: Accuracy (Acc), Precision (Pr), Recall (Rc), and ROC (Roc). Across the datasets: The "Lymphoma" dataset shows an impressive performance with the KNN classifier, achieving perfection across all metrics. The "9-tumors" dataset appears challenging for all classifiers, though SVM manages to outperform the others slightly. The "Leukemia-1" dataset highlights the strength of the SVM classifier, with nearly perfect scores across the metrics. In the "Ovarian" dataset, while KNN and SVM offer competitive performances, the NB classifier shines with near-perfect results. For the "SRBCT" dataset, the SVM classifier emerges as the dominant one, showcasing an accuracy close to 95.12%. While each classifier exhibits strengths in specific datasets, SVM consistently demonstrates a robust performance across a broader range.

The presented Table 5, details the classification accuracy of three classifiers (KNN, SVM, and NB) when utilizing filter-based gene selection methods. Each classifier was tested with four different filters: mRMR, CMIM, Chi-square, and Relief-F. The experiment kept the number of selected genes constant at 50 for each filter. The data indicates that no single classifier or filter consistently outperforms others across all datasets; the optimal combination varies depending on the specific dataset. For instance, KNN achieves standout results with the CMIM filter on the "11-tumors" dataset and with mRMR for the "Lymphoma" dataset. For the majority of datasets, KNN’s performance is quite variable, but in several cases, it either matches or slightly surpasses the other classifiers.

On the other hand, SVM often shines when paired with the Chi-square filter, as seen in its exemplary performance on the "SRBCT" dataset. The variation in classifier performance emphasizes the importance of method selection tailored to individual datasets. NB achieves perfect scores on both the "Lymphoma" and "SRBCT" datasets when paired with the mRMR and Chi-square filters respectively. In several datasets like "Brain tumor 1", "DLBCL", and "Prostate tumor", NB outperforms both KNN and SVM, illustrating its potential strength when the underlying assumptions of the Naive Bayes classifier hold true for the data. As for the mRMR filter method, it shows consistently competitive performance across all three classifiers. Especially for NB, it offers the best results in a significant number of datasets. While the CMIM filter provides leading results in a few datasets (notably for KNN), its performance is not consistently top-tier across all datasets. On the other hand, Chi-square filter especially when paired with SVM and NB, produces some of the highest accuracy across multiple datasets. Relief-F results are mixed. While it yields the best performance in a few cases, it doesn’t consistently outperform the other filters. While SVM paired with the Chi-square filter method often yields strong results, it’s clear that no single combination of classifier and filter universally outperforms others across all datasets.

Table 6, displays the classification accuracy obtained from various combinations of classifiers and filter-based gene selection methods, using a consistent set of 100 selected genes. Three classifiers KNN, SVM, and NB are evaluated with four filter methods: mRMR, CMIM, Chi-square, and Relief-F. The results are presented for 15 datasets. A single glance reveals that the best-performing combination varies greatly across datasets, highlighting the non-uniform nature of optimal classifier and filter method pairing. For instance, in the "11-tumors" dataset, KNN combined with the CMIM filter shows a peak performance of 88.99%. Meanwhile, in the "SRBCT" dataset, both SVM and NB, when paired with the Chi-square filter, achieve a perfect accuracy of 100%. The fluctuations in performance underscore the dataset specific efficiency of each combination.

Fig. 5

Comparing the Mean Classification Accuracy of KNN, NB, and SVM Classifiers for Top 50 and Top 100 Genes Selected via Various Filter-Based Feature Selection Algorithms

Fig. 5, represents the classification accuracy achieved using a fixed set of genes 50 and 100 across various combinations of classifiers and filter-based gene selection methods. When comparing the two sets, it becomes evident that the number of selected genes and the dataset in use significantly influence the optimal choice of classifier and filter method. Across the two configurations, the KNN, SVM, and NB classifiers are evaluated using four filter methods: mRMR, CMIM, Chi-square, and Relief-F for 15 distinct datasets. Notably, for some datasets, an increase in the number of genes from 50 to 100 leads to noticeable changes in classification accuracy. For example, in the "11-tumors" dataset, when 100 genes are used, KNN combined with the CMIM filter achieves a peak performance of 88.99%. On the other hand, when using 50 genes, different combinations might exhibit optimal performance. The variability in results underscores the importance of selecting an appropriate number of genes, classifier, and filter method combinations, tailored to the specific characteristics of each dataset.

5.3 Evaluation of the proposed iBABC-CGO using different classifiers

Table 7 Statistical results of the proposed iBABC-CGO using different classifiers (KNN, SVM and NB)

In this part, we run a comprehensive series of simulations to identify the optimal classifier to pair with our Feature Selection (FS) algorithm. By conducting these rigorous simulations, we aim to ensure that the chosen classifier synergizes well with our FS approach, thus maximizing the overall effectiveness of the solution. This process not only underscores our commitment to a methodical research approach but also emphasizes our pursuit to ensure that each component of our solution - from the FS algorithm to the classifier - is optimized for peak performance. However, it is important to bear in mind that once the optimal subset has been determined, the performance of the iBABC-CGO on biomedical datasets is assessed using leave-one-out cross-validation (LOOCV).

Therefore, in an effort to find the best classifier for our proposed approach, Table 7, represents the performance results in terms of statistical metrics i.e. Best and mean values for various datasets using the proposed iBABC-CGO with different classifiers: KNN, SVM, and NB. When examining the KNN classifier, for datasets such as "11-tumors" and "9-tumors", the iBABC-CGO-V variant seems to have an edge in terms of both best and mean values. However, for other datasets like "Brain tumor 1", "Brain tumor 2", and "CNS", the iBABC-CGO-S version performs slightly better in terms of best values. In the case of SVM, the iBABC-CGO-S consistently outperforms the iBABC-CGO-V across all datasets for the best metric values, though for mean metric values, there’s a mixed performance between the two versions. For the Naive Bayes classifier, the iBABC-CGO-V version holds better best values for several datasets, including "Brain tumor 1" and "CNS". Interestingly, for the "Ovarian" dataset, the performance remains the same across all classifiers and versions, suggesting a consistent result for that particular dataset. It is clear from the statistical results that among KNN, SVM, and NB classifiers, the SVM classifier is the best classifier to be combined with the proposed iBABC-CGO-V variant.

Table 8 Average accuracy of the proposed iBABC-CGO using different classifiers (KNN, SVM and NB)

Table 8, presents the average accuracy of the proposed iBABC-CGO method using various classifiers: KNN, SVM, and NB. Upon a cursory examination, the SVM classifier with the iBABC-CGO-V version displays the highest accuracy for several datasets, achieving a perfect score of 100% on multiple occasions. Both the "Lymphoma" and "Ovarian" datasets achieved consistent 100% accuracy across all classifiers and versions, indicating that the model fits them perfectly. For datasets like "11-tumors" and "9-tumors", the KNN classifier using iBABC-CGO-S has higher accuracy compared to its iBABC-CGO-V counterpart. The Naive Bayes classifier, indicated as "NB", also exhibits competitive performance, especially with the iBABC-CGO-S version.

Table 9 Average selected features of the proposed iBABC-CGO using different classifiers (KNN, SVM and NB)

Table 9, showcases the average number of selected features for various datasets using the proposed iBABC-CGO method paired with different classifiers: KNN, SVM, and NB. A glance at the data reveals a distinct pattern. The SVM classifier with the iBABC-CGO-V version often tends to select a larger number of features compared to the iBABC-CGO-S variant, as seen in the "9-tumors" and "Breast" datasets. The minimal differences in feature selection numbers across classifiers for datasets like "Brain tumor 2", "DLBCL", and "Lymphoma" indicate a level of consistency in the importance of certain features across different classification methods. The "Lymphoma" dataset stands out with a consistent selection of 2 features across all classifiers and versions, suggesting that a minimal set of features is significant for classification in this particular dataset.

5.4 Statistical analysis compared to other NIOAs

In the remaining parts of the experiments, we have fixed the SVM classifier (since it provided the best results among other classifiers) to be used in combination with all the metaheuristics that are to be tested. The results for comparison are based on statistical tests in terms of Best, Mean and Standard deviation (Std) fitness values, which represent the minimum, average, and standard deviation, respectively of the 51 independent readings collected from every FS experiment. The results of these parameters are displayed in Table 10, which clearly indicate that the proposed iBABC-CGO-V approach produced minimum average fitness values by performing much better than the traditional ABC, iABC, iBABC-S, iBABC-V, and other binary metaheuristic approaches on 8 out of 15 datasets. In the rest of the datasets, the suggested iBABC-CGO-V also performs competitively well against the comparative algorithms, where only the iBABC-V algorithm shows better results. Results regarding the Average classification accuracy (CLACC) and the reduction of the selected number of features (SNFs) values are also shown in Tables 11 and 13 in the next sub-section.

Table 10 Comparison of iBABC-CGO versus other metaheuristic algorithms in terms of fitness values using SVM classifier

5.4.1 Analysis using average accuracy and number of selected features

To further investigate the efficacy of the suggested approach, a classification accuracy (CLACC) comparison is outlined in Table 11. The highest value of this metric is desired as it signifies the ability of the suggested approach to classify the features accurately. The introduced iBABC-CGO-V method attained the best classification accuracy on 43.5% datasets (i.e. 7 out of 15 datasets shown in boldface) as compared to the other tested FS approaches. Whereas, for the rest of the 9 datasets, the CLACC results of the suggested method are very competitive in comparison to the other metaheuristics. Moreover, the proposed iBABC-CGO-V variant also obtained the highest overall classification accuracy of all datasets as depicted in Fig. 6, which demonstrates the strength of the suggested approach in classifying selected features accurately.

Table 11 Comparison of iBABC-CGO versus other metaheuristic algorithms for average classification accuracy using SVM classifier

Table 12 Comparison of iBABC-CGO versus other metaheuristic algorithms in terms of Precision, Recall and ROC values using SVM classifier

Fig. 6

Average accuracy on 15 datasets

Fig. 7

Average number of features selected on 15 datasets

Table 13 presents the comparative results of the suggested method in terms of the average number of selected features (SNFs) with the other algorithms. The minimum value of this performance parameter is desired. As can be seen, the suggested approach provides better results in terms of the minimum SNFs for nearly 31% datasets (i.e. 5 out of 15 datasets) against the compared algorithms and for the rest of the datasets, the standard binary version iBABC-V performed better than all tested metaheuristics. It should be noted that except iBABC-CGO-V and iBABC-V, no other comparative algorithm performed well in providing good SNFs results. However, for all the minimum SNFs outcomes provided by the iBABC-V are not supported by good accuracy values, as it manages to provide good accuracy in only 18.7% datasets. Therefore, the overall findings confirm that the proposed iBABC-CGO-V method has the best ability to maintain an adequate exploration-exploitation ratio during the optimization search process, which resulted in providing good average CLACC and competitive average SNFs outcomes. Moreover, the proposed iBABC-CGO-S variant scored the minimum number of selected features overall all algorithms on the average of 15 datasets, as depicted in Fig. 7, which demonstrates the capacity of the suggested approach in reducing the number of selected features.

Table 13 Comparison of iBABC-CGO versus other optimization algorithms in terms of the average SNFs

Table 14 contains the Wilcoxon rank sum (WRS) test, a non-parametric statistical test to examine whether the suggested method’s outcomes are statistically distinguishable from those of other algorithms (Rey and Neuhäuser 2011). WRS test produces a p-value to compare the significance levels of the two methods. P-values below 0.05 imply the existence of a statistically significant difference at the 5% confidence level between iBABC-CGO and the other compared method.

The p-values in Table 14 indicate that the suggested iBABC-CGO-V technique produces significantly different outcomes than most existing algorithms on most gene expression datasets with 95% confidence level except for the binary iBABC-V. In order to further strengthen the evidence of the superiority of our suggested iBABC-CGO-V method over the compared algorithms, we conducted statistical tests such as the Friedman test (whose lower rank is desired), Friedman align test (higher rank is desirable) and Quade test (lower rank is considered best) on the average CLACC results to rank the performance of each FS algorithm. The collected outcomes as shown in Table 15, clearly indicate that the suggested iBABC-CGO-V obtained the best ranks among tested algorithms for all the tests followed by the iBABC-V approach.

Table 14 p-values of the Wilcoxon signed rank test of iBABC-CGO-V versus other metaheuristic (insignificant values with p$\ge$0.05 are highlighted in bold)

Table 15 Statistical results of the Friedman test, Friedman align test and Quade test

5.4.2 Box plot and radar plot analysis

The boxplot analysis is the best way to represent the data distribution characteristics of collected results and to find out data anomalies such as skewness and outliers. Boxplots show the data distributions in the form of different quartiles namely the lower (lowest point/edge of the whisker) and upper (highest point/edge of the whisker) quartiles, which represent the minimum and maximum values of the data distribution. The lower and higher quartiles are shown by the corners of the rectangles. A small boxplot rectangle represents strong data concordance. Figures 8 and 14 show the box plots generated from the results of different algorithms for different medical datasets. The boxplots of the proposed iBABC-CGO-V, for most datasets are very narrow as compared to other algorithm distributions. Indeed, the proposed iBABC-CGO-V method is superior to the other algorithms on the bulk of the investigated datasets.

Fig. 8

Boxplots analysis of algorithms across six datasets

Figure 9 presents the radar chart that ranks the algorithms based on their average best and average mean fitness results. Levels near the centre of the radar graph represent higher best fitness and average fitness values. Therefore, a resilient algorithm has a narrow area, which is the proposed iBABC-CGO-V approach at first, followed by the iBABC-V algorithm. The performance of the tested FS methods is compared in Tables 12, 13 and the radar plot in Fig. 9, from which it can be deduced that the suggested method is superior to the established methods.

Fig. 9

The radar plot curves of the proposed iBABC-CGO and the comparative algorithms obtained with 15 medical datasets

5.4.3 Convergence analysis

Additionally, Figs. 10 and 15 demonstrate that for practically all sixteen datasets, the convergence values of iBABC-CGO-V considerably increase after a few iterations. This tendency suggests that iBABC-CGO-V requires identifying only a few genes from high-dimensional data to improve classification performance. As can be seen from Figs. 10 and 15, iBABC-CGO-V obtained a better convergence rate followed by the iBABC-V algorithm.

Fig. 10

Convergence curves of algorithms on six datasets

5.5 Statistical analysis compared to other state-of-art approaches

In this section, we perform a rigorous comparison of the performance of the proposed method with other state-of-the-art approaches. The datasets cover a variety of biological conditions and reflect the diverse applications of these algorithms. Results showing accuracy percentages and their variability provide an overview of the robustness and consistency of each method. With these results, we aim to highlight not only a method’s accuracy, but also its reliability over multiple iterations.

Table 16 Evaluating the performance of the proposed method in comparison to existing approaches (Part1)

In the presented Table 16, various algorithms are compared for their performance on several datasets, with the iBABC algorithm standing out in particular. The iBABC-CGO-S variant demonstrates commendable accuracy, particularly when considering levels such as 90.75% for dataset 11 tumors and 91.01% for brain tumor 1. However, the iBABC-CGO-V variant stands out for its impressive performance, achieving 100% accuracy on datasets 11 tumors and brain tumor 1. While the iBABC algorithm shines in many scenarios, it’s pertinent to note that other methods also have their moments of excellence. For example, the BAOAC-SA algorithm achieved almost 97% on the 11-tumors and Brain tumor 1 datasets, while BChOA-C-KNN presented levels in excess of 95% in the datasets on which it was evaluated. However, even among these high-performance algorithms, the iBABC-CGO-V variant stands out for its unrivalled accuracy across multiple datasets. This analysis therefore underlines the superiority of the iBABC algorithm, particularly its CGO-V variant, while acknowledging the strengths of the other methods.

Table 17 Evaluating the performance of the proposed method in comparison to existing approaches (Part2)

In Table 17, which evaluates the performance of various algorithms on different datasets (namely CNS, Colon, DLBCL, Leukemia 1, and Lung Cancer), we can observe a continuation of the trend noted in the previous table. The iBABC algorithm remains competitive, with the iBABC-CGO-S variant achieving 100% accuracy on the DLBCL and Leukemia 1 datasets, and the iBABC-CGO-V variant also achieving the same 100% accuracy on these two datasets, but with slightly lower variability. However, it is essential to note that other algorithms also show good results. The rMRMR-MGWO algorithm, for example, achieves a remarkable 99.38% on the CNS dataset. The TLBOSA-SVM algorithm performs extraordinarily well, achieving a near-perfect 99.87% on the lung cancer dataset and 99.01% on the colon dataset. Another remarkable observation is the performance of CFC-FBBA, which boasts 100% accuracy on the DLBCL and Leukemia 1 datasets. On the other hand, algorithms such as BChOA-C-KNN and BChOA-KNN present impeccable results with 100% accuracy on the Leukemia 1 dataset. The IG-MBKH algorithm also deserves special mention, as it has consistently achieved results above 96% in all datasets on which it has been tested. While iBABC variants continue to achieve admirable results on different datasets, several algorithms show comparable performance in specific cases.

Table 18 Evaluating the performance of the proposed method in comparison to existing approaches (Part3)

Table 18, evaluates the performance of the algorithms on the Lymphoma, MLL, Ovary, Prostate Tumor and SRBCT datasets. Many algorithms in the hybrid category, such as IG-MBKH, rMRMR-MGWO and CFC-FBBA, show consistently high performance across multiple datasets, reaching 100% accuracy in several cases. For example, the IG-MBKH method achieves perfect scores for the MLL and Ovarian datasets. Interestingly, the performance of the iBABC algorithm remains excellent, with both its variants (iBABC-CGO-S and iBABC-CGO-V) achieving impressive results. Both variants consistently achieve 100% accuracy on datasets such as Lymphoma, Ovarian and SRBCT, with minor variations in variability. The TLBOSA-SVM algorithm achieves a remarkable 99.13% on the prostate tumor dataset, and the BCOOT-CSA and BAOAC-SA methods both stand out for their uniform 100% accuracy across multiple datasets with minimal variability. On the SRBCT dataset, numerous algorithms, including BChOA-C-KNN, IG-MBKH, rMRMR-MGWO, IDGA-F-SVM, BCO-KNN, iBABC-CGO-S and iBABC-CGO-V, all achieved perfect 100% accuracy, despite variations in the associated variability values. In the filter category, the NB-mRMR method continues to display the robust performance of previous data sets. Both variants (100 and 50) achieved 100% accuracy for the Lymphoma and SRBCT datasets, making it a consistent contender. This comparative table reaffirms the effectiveness of hybrid algorithms, particularly the iBABC variants.

Fig. 11

Accuracy results of the various state-of-the-art hybrid methods and proposed iBABC algorithms for different datasets

As also can be seen from Fig. 11, algorithms classified as hybrid methods frequently achieve high accuracy rates on a wide range of data sets. In the hybrid category, iBABC-CGO-S and iBABC-CGO-V variants consistently deliver first-rate performance. Their near-perfect or perfect accuracy scores on multiple datasets underline their robustness and efficiency. The NB-mRMR filter-based method also produces competitive accuracy rates. This shows that while hybrid methods can be powerful, well-optimized traditional methods can still be of great use. Beyond accuracy, the variability values provided with many algorithms give a better understanding of the situation. Algorithms with lower variability can be more consistent and therefore more reliable, particularly in critical applications such as medical diagnostics.

5.6 Overall assessment

Overall, the simulation results in the previous subsections demonstrate that iBABC-CGO-V is an effective wrapper-based feature selection method capable of solving a wide range of feature selection problems. Feature selection optimization differs from the continuous search space in which search agents can freely move. A thorough exploration is required to change the variable from 0 to 1 and vice versa. The algorithm must also avoid local optima, which occurs when the variables of a binary problem are changed infrequently compared to the number of iterations. The adaptive mechanism of the binary island ABC algorithm accelerates convergence. It also plays a crucial role in establishing an adequate exploitation-exploration balance, so that feature selection problems do not have many local solutions. This fundamentally distinguishes iBABC-CGO-V from the other algorithms in this study in terms of performance.

We have seen that the iBABC-CGO-V offers the highest accuracy and the fewest number of genes. Having said that, it is also important to note that iBABC-CGO-V demands more time to compute than the many other algorithms in this study. The suggested method uses the SVM classifier, and switching to a different classifier could result in longer execution times. As a result, attention should be taken when using a different classifier. We can conclude from the experimental analysis and comparisons that the V-shaped version of iBABC-CGO has the advantage of superior outcomes and high performance compared to other algorithms. The reasons for this high performance are attributed to the given factors; the island binary ABC provides the benefits of mobility, which can strike a better exploration-exploitation balance; the integration of the CGO algorithm further escapes local optima and improves convergence rate. These advantages allow for avoiding the local optimum and accelerating convergence to the global optimum. Besides, when the solution is in an unsatisfactory search space region, the binary transfer function based on the V shape causes it to move. This feature, therefore, suggests that the algorithm operates effectively for the gene selection problem.

6 The biological interpretations of the selected genes by the proposed iBABC-CGO method

In this section, we delve into the biological significance of the best subset of genes that have been identified using our proposed method. For each binary dataset, which includes Breast, CNS, Colon, DLBCL, Leukemia, Ovarian, and Prostate, the gene names and indices are shown in Table 19. Their specific biological relevance can be further consulted in Tables 20, 21, 22, 23, and 24.

It should be mentioned that the interpretation of genes from the prostate cancer and DLBCL datasets is not included, given the absence of specific gene names in these datasets.

To further comprehend the biological implications of the selected genes, we relied on two reputable online resources and comprehensive databases of human genes, namely GeneCards (https://www.genecards.org/), and the National Center for Biotechnology Information (NCBI) (https://pubmed.ncbi.nlm.nih.gov/). These two databases present searchable and comprehensive genetic analysis data that provides concise information on all known and predicted human genes in the genome, proteome, transcription, genetics and function. The insights gained from these platforms confirm that our method is capable of identifying cancer-relevant genes in each respective dataset.

Furthermore, to better visualize the expression patterns of genes across various tumor samples, we employed heat maps Figs. 12 and 13. These graphical representations facilitate a deeper understanding of the data distribution and highlight differential gene expression across samples. The process involves the grouping of genes that share similar expression profiles into clusters. What’s particularly noteworthy is that upon closer examination, a substantial proportion of these genes within these clusters exhibit a synchronized down-regulation in their expression levels. This coordinated down-regulation of gene expression suggests a strong likelihood of these genes being subject to shared regulatory mechanisms or being functionally linked. This result highlights not only the importance of understanding the collective behavior of genes, but also the potential importance of these co-regulated genes in specific biological processes or pathways.

Table 19 The best subset of selected genes from the gene selection method iBABC-CGO-V for binary datasets

Table 20 The best subset of selected genes for Breast Cancer Dataset

The comprehensive gene analysis for the 28 genes listed in the Table 20, was carried out to ascertain their potential relation with breast cancer. These genes were studied for their respective pathways and functional associations using authoritative genomic databases.

Our analysis indicates that several of these genes are implicated in key cellular processes, fundamental for maintaining cell integrity and function. Some genes are particularly noteworthy:

-MDM4: Known to inhibit the p53 tumor suppressor protein, its overexpression has been linked with various human cancers. Its potential role in breast cancer could be explored in the context of p53 pathway dysregulation.

-CD44: This cell-surface glycoprotein is involved in cell-cell interactions, cell adhesion, and migration. It’s implicated in many types of cancers, including breast cancer.

-CD69 Molecule: While CD69 is primarily known for its role in immune regulation, the association of this gene with diseases like Coccidioidomycosis and Eosinophilic Pneumonia suggests an inflammatory component that might be relevant in the tumor microenvironment of breast cancer.

-HIG1 Hypoxia Inducible Domain Family Member 2A: Hypoxia, or low oxygen levels, is a common feature in solid tumors like breast cancer. Genes associated with hypoxia can contribute to the survival and proliferation of tumor cells.

Based on their identified functions and associations, it is plausible that these genes can influence cellular activities such as adhesion, migration, differentiation, proliferation, and apoptosis processes that, when disrupted, can lead to tumorigenesis. Notably, the involvement of certain genes in pathways associated with cancer development makes them promising candidates as tumor-specific biomarkers.

Table 21 The best subset of selected genes for CNS Cancer Dataset

For the CNS Cancer Dataset presented in Table 21, a deep-dive was executed into a selection of genes to determine their potential significance in CNS cancer. Notable genes and their relevance include:

CDP-Diacylglycerol Synthase 2: It functions downstream of many G protein-coupled receptors and tyrosine kinases, which are crucial in various cellular signalling pathways. Any aberrations here can influence cell growth and proliferation, common in CNS cancers. It could be explored as a potential biomarker for signalling anomalies in CNS tumors.

Non-SMC Condensin II Complex Subunit D3: Its primary function in mitotic chromosome assembly suggests its importance in cell division. Malfunctions could lead to uncontrolled proliferation, a hallmark of cancer. Given its association with developmental diseases, this gene might be indicative of tumors with proliferative behavior.

Somatostatin: This hormone is involved in various physiological processes, including neurotransmission. Disruption in its expression might influence tumor growth, especially if CNS tumors show deregulation of neuroendocrine pathways.

Cyclin Dependent Kinase Inhibitor 3: Cyclin-dependent kinases play pivotal roles in cell cycle progression. Abnormalities in these pathways can lead to unchecked cell growth, typical of cancers. If overexpressed or silenced in CNS tumors, it may be a strong candidate biomarker for aggressive growth.

Apolipoprotein E: While its primary function relates to lipid metabolism, any genetic mutations might affect cell membrane structure or function, possibly aiding tumor cell survival or migration in CNS.

Histidine Rich Glycoprotein: Given its presence in plasma and platelets, any associations with vascular or angiogenesis-related changes in CNS tumors might make it a relevant biomarker.

Purine Rich Element Binding Protein A: DNA-binding proteins have regulatory functions. Disruptions can affect genes downstream, potentially driving tumorigenesis. It may be a marker for transcriptional anomalies in CNS tumors.

Solute Carrier Family 1 Member 1: Involved in neurotransmission, changes in its expression might relate to neurologically active tumors or those affecting neurotransmission in CNS cancer.

Bromodomain Containing 2: As a transcriptional regulator, its abnormal activity can lead to broad changes in gene expression profiles. If found to be consistently deregulated in CNS tumors, it may be a viable biomarker for diagnostic or prognostic purposes.

Several of these genes, based on their function and associated diseases, have clear implications in critical cellular processes and diseases. Some of these processes include cell growth, chromosome assembly, protein synthesis, neurotransmission, and DNA binding. Understanding these genes’ pathways and interactions can shed light on their role in CNS cancers.

Table 22 The best subset of selected genes for Colon Cancer Dataset

For the Colon Cancer Dataset, the implications of each gene presented in Table 22 and their potential as diagnostic or prognostic biomarkers are explored below:

-Thymosin Beta 10: Thymosins play key roles in cell migration, differentiation, and proliferation, processes that are crucial during tumorigenesis. Thymosin Beta 10 is implicated in actin monomer binding, suggesting a potential role in the cell’s cytoskeletal dynamics. Its association with thyroid gland cancer implies it might be involved in other malignancies as well.

-Dermatopontin: Extracellular matrix (ECM) proteins are fundamental in tissue architecture and integrity. Dysregulation of ECM components, like Dermatopontin, can influence cell-cell and cell-matrix interactions, potentially facilitating tumor growth, invasion, and metastasis in the colon.

-CEA Cell Adhesion Molecule 6: Carcinoembryonic antigen (CEA) family members, including CEACAM6, have been previously associated with various cancers. They play roles in cell adhesion, a fundamental process that when altered can contribute to the invasiveness of cancer cells and their potential to metastasize. Given its association with gastrointestinal carcinoma, CEACAM6 might serve as a diagnostic or prognostic biomarker in colon cancer.

As with any potential biomarkers, it is essential to validate their association with colon cancer in extensive clinical studies. This involves comparing their expression or mutation status in a broad range of colon cancer samples and correlating these findings with clinical outcomes.

Table 23 The best subset of selected genes for Leukemia Cancer Dataset

For the Leukemia Cancer Dataset, each gene’s potential implications in leukemia presenetd in Table 23 and their possible utility as diagnostic or prognostic biomarkers is depicted below:

-Eukaryotic Translation Initiation Factor 3 Subunit E: Translation initiation factors are vital for protein synthesis. Any aberrations in their function can lead to deregulated protein synthesis, which might contribute to malignant transformation and tumor progression. EIF3E’s association with breast cancer implies that its dysregulation might be important in other cancers as well.

-Natriuretic Peptide Receptor 3: Natriuretic peptides play roles in regulating blood volume, blood pressure, and certain metabolic processes. Changes in the function of their receptors, like NPR3, might lead to altered cellular responses, which could potentially influence the leukemic microenvironment or the behavior of leukemia cells.

Table 24 The best subset of selected genes for Ovarian Cancer Dataset

For the Ovarian Cancer Dataset, understanding the role of each gene and its implications in ovarian cancer presented in Table 24 can shed light on potential diagnostic or prognostic biomarkers.

-ADAM Metallopeptidase With Thrombospondin Type 1 Motif 18: ADAMTS family members are known for their roles in tissue remodeling and cell-matrix interactions. Given that cancer often involves tissue remodeling, changes in the expression of this gene may influence ovarian tumor growth, invasion, or metastasis. If ADAMTS18 is found to be consistently deregulated (either overexpressed or underexpressed) in ovarian tumors compared to normal tissue, it could serve as a potential biomarker for disease onset, progression, or even therapeutic targeting.

-APC Regulator Of WNT Signaling Pathway: The Wnt signaling pathway is pivotal in numerous cellular processes, including cell growth, differentiation, and migration. The APC protein acts as a tumor suppressor, and its dysfunction can lead to aberrant activation of the Wnt pathway, promoting tumorigenesis. Its role is well-established in colorectal cancers, but any changes in ovarian tumors could indicate similar pathway dysregulation.

-Collagen Triple Helix Repeat Containing 1: While primarily involved in vascular remodeling, the process is also crucial in tumor growth, as tumors require new blood vessels to support their rapid growth-a process called angiogenesis. Alterations in CTHRC1 might be linked to ovarian tumor vascularization or metastatic potential.

For effective clinical translation, it would be essential to study these genes in a larger cohort of ovarian cancer patients, assessing their expression or mutation status and correlating with clinical outcomes. This will determine their true potential as biomarkers for ovarian cancer diagnosis, prognosis, or therapeutic intervention.

Fig. 12

A heatmap representation of the gene expression patterns (Part 1)

Fig. 13

A heatmap representation of the gene expression patterns (Part 2)

7 Pros and Cons of the proposed method

This section describes the advantages and disadvantages of the suggested iBABC-CGO-V method. In addition, suggestions for improving this strategy are also highlighted. Numerous research works demonstrate that metaheuristic algorithms (MHs) are excellent optimization approaches, although they may have downsides such as premature convergence, an imbalanced exploration-exploitation ratio, and an inability to escape from the local optimal region. In order to create an efficient FS approach using an MH algorithm to improve classification performance, we researched contemporary algorithms and their features. The iABC is a relatively latest modified version of the ABC metaheuristic algorithm that has been shown in the literature to be effective at resolving practical optimization issues. It utilises the structured population mechanism by incorporating the island model for improving the exploration of the original ABC. Due to its straightforward approach and few parameters, the iABC is simple to implement. It demonstrated better performance on CEC 2015 functions in (Awadallah et al. 2020) when compared to a number of other MH methods.

However, besides its advantages, the iABC still struggles with slow convergence, lack of direct application to the discrete optimization problems, unbalanced exploration-exploitation ratio, and the possibility of getting trapped in local optima. Therefore, we integrated two mechanisms to the original iABC, which are highlighted as the following:

• We adapted the S and V transfer functions to convert the continuous version of the iABC to its equivalent binary version so that it fits the discrete FS problem. Besides the binary conversion, the transfer functions also reportedly help in improving exploration and exploitation abilities.

• CGO method is incorporated in the migration phase of the original iABC to further improve exploration, rate of convergence, and escape local optima.

These advantages of integration of binary transfer functions, CGO method, and use of SVM classifier in iBABC-CGO-V approach also come with certain disadvantages, which are listed along with their future proposed resolutions below:

• However, to select the minimum NFs for classifying features accurately, the proposed approach still requires more improvement as it provides second-best results. This may be due to the use of a weighted approach and manual adjustment of weights for the lowest classification error rate and the fewest features in the fitness calculation. This problem can be resolved by employing the multi-objective approach, which considers both objectives viz. classification error and selection of the fewest features simultaneously.

• iBABC-CGO-V requires more time to compute than many compared algorithms in this study due to the use and integration of binary transfer functions, the CGO method, and the use of an island approach. Careful use and integration with the other metaheuristic approach are the resolutions to reduce the compute time of the suggested approach. The convergence rate can be further enhanced by using chaotic maps or opposition-based learning methods in the initialization phase.

However, as per the NFL theory, no universally effective optimization algorithm exists for all optimization problems for all datasets. As a result, the authors conclude that the proposed iBABC-CGO-V, like the other MH methods, follows the same rule; nonetheless, it surpasses several other contemporary and well-known algorithms.

8 Conclusion

This paper presents a unique Hybrid island Binary Artificial Bee Colony with Chaos Game Optimization (iBABC-CGO) method as a wrapper-based technique for feature selection problem. This new approach merges the simplicity and flexibility of the ABC algorithm, the island concept that ensures diversity during the search process of solutions, the advantage of the CGO algorithm ensuring better exploration-exploitation ratio and escaping local optima, and a binary model to better address the discrete feature selection optimization problem using microarray data. In this work, the efficacy of the proposed technique was validated using 15 real-world high-dimensional datasets. According to our research, the suggested iBABC-CGO method beats the competing algorithms across most datasets. Furthermore, the iBABC-CGO successfully identified a subset of highly discriminative characteristics that effectively characterised the target ideas among competitors. Overall, in feature selection operations on 15 datasets, the iBABC-CGO frequently attains the best accuracy on most individual datasets and the highest overall average accuracy as well. The proposed method obtained the best results among tested metaheuristics in terms of highest classification accuracy, highest overall average accuracy, competitive number of selected features, and largest area under the ROC curves. At last, the biological interpretations of the selected genes by the proposed method are provided, which delve into the biological significance of the best subset of genes that have been identified by our method. Future research can utilize iBABC-CGO-V for various technical and clinical applications, including electromyography pattern recognition, optimized deep neural networks, and power quality. The performance of iBABC-CGO can also be improved by using several improved initialization procedures, the selection of an alternative classifier, and the use of a multi-objective approach for optimizing classification accuracy and the fewest number of features selected objectives simultaneously.

Additional simulations

See Figs. 14 and 15.

Fig. 14

Boxplots analysis of algorithms across 9 remaining datasets

Fig. 15

Convergence analysis of algorithms across 9 remaining datasets