Machine and deep learning for longitudinal biomedical data: a review of methods and applications

Abstract

Exploiting existing longitudinal data cohorts can bring enormous benefits to the medical field, as many diseases have a complex and multi-factorial time-course, and start to develop long before symptoms appear. With the increasing healthcare digitisation, the application of machine learning techniques for longitudinal biomedical data may enable the development of new tools for assisting clinicians in their day-to-day medical practice, such as for early diagnosis, risk prediction, treatment planning and prognosis estimation. However, due to the heterogeneity and complexity of time-varying data sets, the development of suitable machine learning models introduces major challenges for data scientists as well as for clinical researchers. This paper provides a comprehensive and critical review of recent developments and applications in machine learning for longitudinal biomedical data. Although the paper provides a discussion of clustering methods, its primary focus is on the prediction of static outcomes, defined as the value of the event of interest at a given instant in time, using longitudinal features, which has emerged as the most commonly employed approach in healthcare applications. First, the main approaches and algorithms for building longitudinal machine learning models are presented in detail, including their technical implementations, strengths and limitations. Subsequently, most recent biomedical and clinical applications are reviewed and discussed, showing promising results in a wide range of medical specialties. Lastly, we discuss current challenges and consider future directions in the field to enhance the development of machine learning tools from longitudinal biomedical data.

1 Introduction

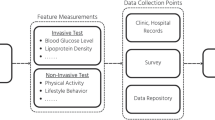
Longitudinal studies, also known as panel data studies, involve the analysis of repeated measures on the same subject over time. They complement cross-sectional or transverse studies, which focus on analysing a population at a given point in time, and play a prominent role in economic, social, and behavioural sciences, as well as in biological and agricultural sciences, among other disciplines. Healthcare is no exception, and it has long been recognised that tracking the temporal changes of individual-level biomarkers can provide key information to explore alterations and factors influencing health and disease trajectories (Sontag 1971). The biomedical field is associated with a wide range of repeated measurements and data, from medical history (e.g. disease status, medication, treatment response) to clinical data (medical images, lab results, genetic tests). Specifically, biomedical data is a term used to describe any data that can provide information about a person’s health status. These including data collected in the clinic and by healthcare professionals, physiological data captured by sensors, and behavioural data collected by smartphones and online media. Clearly, an adequate analysis of these types of data and disease trends can bring enormous benefits, including understanding of risk factors, early diagnosis and identification of at-risk individuals, and guidelines on available preventive strategies or treatments.

Researchers have developed and exploited different approaches for the analysis of longitudinal data. Historically, these mainly involve the use of statistical methods. A comprehensive review on such approaches for processing longitudinal data can be found at (Gibbons et al. 2010). Generalised Linear Mixed Models (GLMMs) introduced by Nelder and Wedderburn (1972) in 1972 are an early example of widely used approaches for modelling the response of a repeated outcome over time. These methods can achieve satisfactory results when the focus is on the analysis of the statistical associations between a small number of variables. However, when the goal is to make more advanced and complex clinical predictions, it is frequently advantageous to use many variables to capture the phenomenon in question and to model non-linear relationships. In this context, statistical methods such as GLMMs present some limitations, as the user has to specify a parametric form for the relationships between all the variables. Such relationships are typically not known a priori and, thus, high nonlinear relationships are not easily captured. On the other hand, machine learning (ML) techniques are ideally suited for modelling complex nonlinear relationships not known a priori (Ngufor et al. 2019), and to handle high-dimensional data (Du et al. 2015). This fact has led in recent years to a growing interest in the application of ML to clinical-risk prediction and modelling with longitudinal data (Bull et al. 2020).

Applications of ML outperforming traditional risk-scoring algorithms include early detection of suicide risk (Nguyen et al. 2016), long-term prediction of chronic heart disease development (Razavian et al. 2015; Pimentel et al. 2018), or short-term prediction of complications in intensive care units, where patients need to be constantly monitored (Meyer et al. 2018; Vellido et al. 2018). Moreover, many works have demonstrated that prediction accuracy improves with the inclusion of longitudinal big data and with an adequate implementation of the ML models (Konerman et al. 2015; Cui et al. 2018).

These initial results suggest that the development and at-scale adoption of enhanced ML methods for longitudinal studies could lead to a two-fold gain for healthcare. On the one hand, on an individual level, this could allow for earlier detection and, therefore, treatment of diseases. On the other hand, this could lower expenses through early intervention and prevention, which will reduce the number of hospitalisations and treatments.

1.1 Challenges remaining of ML on longitudinal data

For the reasons discussed above, ML is a thriving field for learning to perform clinical tasks from longitudinal data. However, compared to the application of ML methods to cross-sectional studies, longitudinal data represent some inherent challenges that make the problem non-trivial and worthy of discussion, among which we highlight:

• Repeated measures for an individual tend to be correlated with each other; not all ML algorithms are suitable for modelling such correlations, as they break the so-called ‘independent and identically distributed’ (“i.i.d”) assumption. Not taking these correlations into account may lead to biased results.

• There are often missing measurements or dropouts in longitudinal data cohorts, while the time intervals between one measurement and another are not necessarily evenly distributed. These facts hamper an off-the-shelf application of ML time-series algorithms built on the assumptions of complete samples.

• Longitudinal data trajectories may be highly complex and non-linear (e.g., large variations between individuals)—again breaking the i.i.d. assumption.

• The repeated measures can be subject to very different, and sometimes hard to estimate, uncertainties, which may also vary with time—from instrument inaccuracy to the specificity of the individual (e.g., different pain thresholds).

These issues make the development of ML models for longitudinal data challenging, and point to the need for different strategies and algorithms.

1.2 Scope of this review

Although a few application-specific reviews on longitudinal biomedical data exist, namely on clinical risk prediction (Bull et al. 2020), Alzheimer’s disease (Martí-Juan et al. 2020) and prediction in critical care units (Plate et al. 2019), there have been thus far no comprehensive reviews that cover the wide range of available ML methods, in particular on emerging deep learning algorithms and applications.

Hence, we carefully reviewed 117 articles¹ investigating ML implementations on longitudinal biomedical data with a two-fold objective: (i) to provide a detailed guide on available ML algorithms for longitudinal data, pointing out the strengths and the limitations of every method, in order to lower the barriers to entry for researchers from a variety of backgrounds; and (ii) to explore ML achievements in the biomedical field by describing practical use cases, so as to show how longitudinal ML applications can help improve healthcare delivery for the patients. These two goals are reflected in the organisation of the paper.

First, the technical Sect. 2 features introductions to the different ML concepts, followed by a more technical description of all algorithms. Section 3 covers key domains of application in the biomedical field, and reports the results achieved, promises and current limitations. Readers who are not interested in the technical details of longitudinal ML can skip directly to Sect. 3, which provides a detailed review of the applications of longitudinal ML in the biomedical field.

For the convenience of the reader, all abbreviations used throughout the paper are compiled in Appendix A.

2 Overview of machine learning methods for longitudinal data

The two main types of ML strategies used to build models from biomedical data are supervised and unsupervised learning. In this section, both will be described in detail, while a general overview of an ML pipeline with longitudinal data is shown in Fig. 1.

More precisely, firstly, we present suitable sources of longitudinal data. We then describe supervised and unsupervised ML techniques. Next, we discuss several strategies for handling missing values when building longitudinal ML models. Finally, recent developments emerging in the field are summarised.

Fig. 1

Overview of the pipeline of ML on longitudinal data. Given a defined observation window, which is the time period source of longitudinal variables, and, for a supervised learning problem, the time of prediction, which is the future period where the outcome of interest is recorded, there is a prior step to render longitudinal data in a suitable format for ML algorithms and define the relative tasks (see upper box). Subsequently, a classical ML pipeline is built. Precisely, it consists of data preparation (namely, removing duplicates, correcting errors, dealing with missing values, normalisation, data type conversions, etc.), choosing a model, training and evaluating the model, and hyperparameter tuning (an experimental process used to improve the accuracy of the model). The final step is typically the prediction or creation of subgroups, applied once the model is considered to be ready for practical applications

2.1 Sources of longitudinal data: existing cohorts

The development of a robust ML model depends primarily on the availability of a sufficient number of data. In the context of longitudinal analysis, this is challenging due to the large amount of information that needs to be collected over time; a task which can be time-consuming and expensive. Typically, longitudinal studies are observational, but they can also be interventional in order to evaluate direct impacts of treatment or preventive measures on disease. Typical interventional studies, also known as clinical trials, are commonly used to test the effectiveness and safety of treatments for patients. Randomized controlled trials (RCTs) are a type of interventional study that aim to reduce sources of bias by randomly assigning subjects to two or more groups and comparing their responses to different treatments. RCTs are widely considered the design of choice for evaluating health interventions. However, they are not feasible when random assignment could be unethical, unfeasible or potentially reduce the effectiveness of the intervention (Kunz et al. 2007; Jadad 1998). In these cases, non-randomized controlled trials (non-RCTs) are often used, in which the assignment to the group is not at random, but decided by participants themselves or the researchers, so that patients are typically allocated to treatments that are correctly considered most appropriate for their circumstances (McKee et al. 1999).

Generally, there are two main types of longitudinal studies, namely prospective or retrospective studies:

• 1. Prospective: These studies observe subjects over time to determine the incidence of a specific outcome after different exposures to a particular factor. They require the generation and collection of new data sets.

• 2. Retrospective: These studies look back in time to identify a cohort of individuals in a given time interval before the development of a specific disease or outcome, to establish the exposure status. They often use existing real world data such as electronic medical records.

Retrospective cohort studies are less expensive because the data sets are readily available. However, they come with several limitations, such as poor control over the data quality and the exposure factors (Euser et al. 2009). Typical retrospective studies use electronic health records (EHRs) to simulate prospective developments of predictive models and applications of different clinical scenarios. On the other hand, prospective studies are usually more time consuming and expensive, as the researchers have to collect new data sets over long periods of time. Prospective studies are generally more stable in terms of confounders and biases. This is due to the fact that retrospective studies use data measured in the past, often for a different purpose (e.g. patient care) (Euser et al. 2009), thus sources of bias related to missing or incorrect information using existing registers (information bias), or due to selection bias as individuals are selected after the outcome has occurred, are more frequent. It should be noted that both types of cohort studies, whether prospective or retrospective, are susceptible to issues of generalisability. Shifts in the distribution of ML training and validation data, bias due to underrepresented populations, and failure to capture data drifts can cause the predictive power of an algorithm to decrease in other populations or over time (Ramirez-Santana 2018; Sedgwick 2014). Therefore, when designing both prospective and retrospective cohort studies, researchers must always consider these limitations and reduce their impact on the generalisation of results. To reach this goal, it should be noted that proper preparation of a database to extract the useful knowledge it contains is necessary, as is the choice of data pre-processing methods (Ribeiro and Zárate 2016).

Tables 1, 2, 3 provide a set of longitudinal cohorts available. Specifically, Tables 1 and 2 cover all the cohorts found in this literature survey, whereas Table 3 depicts the cohorts used in the LongITools project,² a large-scale European project focused on determining the health and disease trajectories based on longitudinal exposome, biological and health data.

Table 1 Examples of longitudinal cohorts identified in this survey

Table 2 Examples of interventional cohorts found in this survey

Table 3 Example of longitudinal cohorts from the LongITools project (www.longitools.org)

2.2 Supervised learning

The term supervised learning refers to the ML task aimed at learning or inferring a function that maps an input to an output, based on input–output pairs. That is, it involves ML tasks where the goal is to learn a model for making predictions over a variable of interest. When the output is numerical (e.g., level of glucose in blood), this is known as a regression problem, and when the output is discrete or categorical (e.g., having a disease or not), this is a classification problem.

Formally, let us assume to have from past experience a set of labelled instances $\mathcal {D} = \{(\mathbf {x_i},y_i),i=1,...,N \}$, known as the training set, where $\mathbf {x_i} = (x_{i1},...,x_{in})$ is the instance vector (input), whose components are called features, and $y_i$ is the corresponding label (output). The pairs $(\mathbf {x_i},y_i) \in \mathcal {X}\times \mathcal {Y}$ are assumed to be realisations of random variables (X, Y) with values in $(\mathcal {X}\times \mathcal {Y})$, distributed according to some (unknown) probability measures P over $(\mathcal {X}\times \mathcal {Y})$. Moreover, the data points are often assumed to be drawn independently, and this pair of assumptions is called the “i.i.d. assumption”, an abbreviation for independent and identically distributed. Given this setting, the goal is to compute a classifier $f: \mathcal {X} \longrightarrow \mathcal {Y}$, so that for a new pair $(\textbf{x}^*,y^*)\sim P$ the output $y^*$ can be estimated as $f(\textbf{x}^*)$.

For classification there are two possible approaches, namely, (i) probabilistic (such as Logistic Regression (LR)), which would yield a probability distribution over the set of possible outcomes for each input sample, where the probabilities of every label are called prediction scores, and (ii) deterministic (such as Support Vector Machines (SVM)), which only returns the predicted value/label/outcome.

The following paragraphs formulate the notation and the problem specifically for longitudinal data.

2.2.1 Problem formulation for longitudinal data

Data input There are two types of input variables, namely (i) longitudinal features are variables which are sampled many times, i.e., their values are recorded at different time points in a defined time period, which is called observation window (such as laboratory values or questionnaire responses etc.), and (ii) static features (such as genetic or socio-demographics variables etc.). In the general case, the total number of observations is different over subjects (some patients may have more assessments).

Formally, given a subject $i \in \{1,...,N\}$, where N is the number of subjects under study, and an instant $t \in \{1,..., T_i\}$, with $T_i$ total number of follow-ups, let $\mathbf {x_{it}} = (x_{it1},...,x_{itn})$ be the vector of the n measures recorded, realisation of a random vector $X_{t}$. Then, by scrolling through the time index, let $\mathbf {x_i} = (\mathbf {x_{i1}},...,\mathbf {x_{i{T_i}}})$ be the ${T_i}\times n$ matrix of all the longitudinal variables recorded for the $i^{th}$ subject. In addition to this, $\{\mathbf {z_i}, i = 1,...,N\}$ represents the set of static features, with every $\mathbf {z_i}$ being a realisation of a random vector Z of dimension m.

Depending on the data and the modelling chosen, different custom processing methods might be required, such as data normalisation. It is also common to normalise the frequency of the follow-ups by discretising and aggregating the observations in defined intervals steps, for example, by taking their mean (Lipton et al. 2016).

Data output Regarding the outputs, there are two scenarios, namely:

• (i) static output: the goal is the prediction of a single outcome at a pre-determined time (e.g. diagnosis or risk prediction at one time point;

• (ii) longitudinal output: the goal is to predict multiple outcomes concerning different time points (e.g. disease progression over time).

On this basis, the prediction time for a static output is an instant (e.g. risk prediction of developing a disease at 1 year in the future) or an interval (e.g. risk prediction of developing a disease within 1 to 3 years in the future), while for a longitudinal outcome is a set of instants or intervals.

Regarding the modelling of the longitudinal output, some approaches are naturally designed to directly predict multiple outcomes by exploiting temporal correlation, while for others it is necessary to build several independent models with the respective outcome. In this review, we focus on the discussion of ML methods for the static output scenario, highlighting those that could be also directly applied for the longitudinal output scenario.

Objective With the set of data input–output introduced, the aim is to build a function f which given an example $(\mathbf {x_i},\mathbf {z_i},y_i)$ accurately estimates the output $y_i$ as $f(\mathbf {x_i},\mathbf {z_i})$.

To achieve the goal, one possible solution is expanding the features’ space and building a training set where all the repeated and static variables recorded for a subject is an instance stored in a single row. However, in some studies, different patients may have very different numbers of follow-ups, while many classifiers assume fixed length inputs. Thus, another straight solution allowing for a variable number of follow-ups is building a dataset where every row is the set of recorded measures at a particular instant. Hence, each subject $i{th}$ contributes with $T_i$ rows of fixed length n in the dataset. However, by means of this approach the i.i.d. assumption is violated, as instances of the same subject are correlated to each other and this could lead to bias in the results.

From these first attempts it can be deduced that the added temporal dimension increases the complexity of the data representation and there are possible ways to deal with it. Indeed, contrary to cross-sectional studies, an important preliminary step is to render the data in a suitable format and formulate the learning paradigm. Subsequently, an algorithm is used to learn the relationship between the input and output, which can be a classical ML technique or one adapted to allow exploiting the temporal information in the longitudinal data.

To summarise, two steps closely related with each other need to be decided:

• 1. Data formulation methodology, i.e. the process of constructing input–output data and formulating the objective. This could consist of a simple dataset construction, for example if variables are aggregated losing the time index. However, in certain cases it may involve the use of a specific paradigm, such as Multi-Task Learning, as will be shown (Caruana 1997).

• 2. The subsequent algorithm for estimating the classifier.

2.2.2 Supervised ML methodologies for longitudinal data

An overview of the main different methodologies is provided in Table 4 and are described in detail here. In addition, readers are advised to look at the FIgs. 2 and 3 to facilitate understanding.

2.2.2.1 Summary features (SF)

The simplest approach to handle longitudinal data is aggregating the repeated measures up to a certain instant into summary statistics and removing the time dimension, as shown in Fig. 2. Towards this aim, popular approaches include using the temporal temporal mean/mode/median (Nguyen et al. 2019; Ng et al. 2016; Makino et al. 2019; Zhao et al. 2019; Konerman et al. 2015; Mubeen et al. 2017; Bernardini et al. 2020; Simon et al. 2018; Du et al. 2015; Singh et al. 2015; Nadkarni et al. 2019; Ioannou et al. 2020), standard deviation or variance (Makino et al. 2019; Zhao et al. 2019; Lipton et al. 2016), variation (Ng et al. 2016; Koyner et al. 2018; Nguyen et al. 2019; Choi et al. 2016; Rodrigues and Silveira 2014; Nadkarni et al. 2019; Ioannou et al. 2020), rate of change (Mubeen et al. 2017; Danciu et al. 2020), minimum/maximum value of available measurements for each individual (Danciu et al. 2020; Konerman et al. 2019; Zhao et al. 2019; Razavian et al. 2016; Koyner et al. 2018; Konerman et al. 2015; Simon et al. 2018; Zheng et al. 2017; Nguyen et al. 2019; Mani et al. 2012; Lipton et al. 2016; Nadkarni et al. 2019; Ioannou et al. 2020), count (Simon et al. 2018; Ng et al. 2016; Walsh et al. 2018; Choi et al. 2017; An et al. 2018; Walsh et al. 2017; Zheng et al. 2017, 2020; Chen et al. 2019), last observation (Danciu et al. 2020; Koyner et al. 2018; Rahimian et al. 2018; Razavian et al. 2016) or binary variables: 1 if the feature is present in a given patient’s medical history and 0 otherwise (Barak-Corren et al. 2017; An et al. 2018; Singh et al. 2015; Rahimian et al. 2018; Razavian et al. 2016).

Formally, for every subject i, a feature vector is built aggregating with some vector-valued function $\textbf{g}$ the observations $\mathbf {x_i}$ and concatenating the static features $\mathbf {z_i}$. The function $\textbf{g}$ has k components: $\textbf{g}(\mathbf {x_i}) = (g_1(x_{i11},...,x_{iT_{i}1}),...,g_k(x_{i1n},...,x_{iT_{i}n}))$, where each component $g_i, i = 1,.., k$ is an aggregation function (such as mean, projection and so on) of the respective variable over time, and n is the number of different variables recorded at each time point. Then, one output is assigned to every subject, obtaining the final training set: $\mathcal {D} = \{(\textbf{g}(\mathbf {x_i}),\mathbf {z_i},y_i),i=1,...,N \}$.

By means of this approach, it is not necessary that each subject has the same numbers of follow-ups, and, thus, it is robust to missing values. Besides, summarising the measures can minimise the effect of measurement error, although its main advantage is the enormous simplicity. Nevertheless, this approach can result in loss of significant information, especially in the context of clinical data where the variability of some variables may show underlying trends. Indeed, Singh et al. (2015) called this approach “non-temporal”, as usually it does not model the sequential order of the data. Despite this limitation, models based on summary features can outperform models using only one instant (Wang et al. 2018) and they are typically used as a baseline model.

2.2.2.2 Longitudinal features (LF)

In an effort to better exploit/capture data information, an alternative to summary features is the use of longitudinal features. By means of this approach, the features’ space is expanded, by considering every variable’s observation as a feature and stack them horizontally, as depicted in Fig. 2. Specifically, every $\mathbf {x_i}$ is a row of the dataset for $i = 1,...,N$, i.e., the training set is $\mathcal {D} = \{(\mathbf {x_i},\mathbf {z_i},y_i),i=1,...,N \}$. Then, a supervised algorithm is used to build the classifier, that can be time-aware (sequential) or not (non-sequential), as detailed below.

• LF: Non-Sequential In the case of classifiers based on non-sequential LF, an input of fixed length is required. This means that every subject in the sample needs to have the same number of observations per interval time and the same number of follow-ups, i.e., $T_{i} = T$ $\forall$ i. Then, a non-sequential classifier is applied (i.e. the result is invariant by permuting the order of the features), such as SVM or LR. It is important to note that the introduction of a large set of correlated features could lead to overfitting (Singh et al. 2015), and so it could be necessary to apply dimensionality reduction (Simon et al. 2018; Lee et al. 2016; Zhang et al. 2012; Finkelstein and cheol Jeong 2017; Tang et al. 2020). Despite being very popular, Kim et al. (2017); Razavian et al. (2015); Nguyen et al. (2016); Du et al. (2015); Ardekani et al. (2017); Lipton et al. (2016); Tabarestani et al. (2019); Aghili et al. (2018); Zhao et al. (2017); Huang et al. (2016); Bhagwat et al. (2018); Zhao et al. (2019); Chen and DuBois Bowman (2011); Zhao et al. (2019); Singh et al. (2015); Tang et al. (2020), this approach treats all elements across all time steps in exactly the same way, rather than incorporating any explicit mechanism to capture temporal dynamics (the time index is discarded). Moreover, requiring the same number of follow-ups over subjects could be too restrictive for particular studies.

• LF: Sequential Alternatively, classifiers that take into account the sequential nature of features can be used. More precisely, in the case of such classifiers the learning technique is aware of the temporal relationship between dynamic features of consecutive time steps (the time index is preserved). This category includes recurrent models and other adapted classifiers, as detailed in Sect. 2.2.3. In general, the training dataset has the same form of the Non-Sequential approach, but for some models the hypothesis of $T_{i} = T$ $\forall$ i is not necessary, which turns out to be very convenient.

Fig. 2

Graphic representation of Summary Features and Longitudinal Features, which are the most popular approaches, (see Fig. 5). The notation is the same of data input–output introduced and n stands for the number of variables recorded at each time point

2.2.2.3 Stacked vertically (SV)

Another way of handling longitudinal measures is not considering the correlation between the repeated measures and building a dataset where every visit of each patient is a separate instance allowing different number of visits over subjects, see Fig. 3. Formally, the training set is $\mathcal {D} = \{( \mathbf {x_{it}},\mathbf {z_i},y_i),t = 1,...,T_i, i=1,...,N \}$. Features tracking the time component could be added (such as a cumulative feature or the respective visit’s number). Precisely, given an instant t and a vector-valued function $\textbf{g}(t,\mathbf {x_{it}}) = (g_0(t),g_1(x_{i11},...,x_{it1}),...,g_n(x_{i1n},...,x_{itn}))$, the training set is $\mathcal {D} = \{( \mathbf {x_{it}},\mathbf {z_i}, \textbf{g}(t,\mathbf {x_{it}}),y_i),t = 1,...,T_i, i=1,...,N \}$. With this approach, an output needs to be assigned to every instant. It can either be the same value repeated for all instances (Cui et al. 2018) or different in the case of longitudinal outputs (Bhat and Goldman-Mellor 2017).

Given the introduced training set, a ML algorithm is trained providing $T_i$ (number of follow-ups) estimations of the outcome for the subject i. Then, the final prediction can be obtained (i) by aggregating these estimations (e.g. by computing the majority vote (Bernardini et al. 2020; Zhang et al. 2012) or by averaging the prediction scores (Cui et al. 2018, 2019; Zhang et al. 2012)); or (ii) by only considering the prediction of a specific instant $f(\mathbf {x_{i{T_i}}},\textbf{g}(T_i,\mathbf {x_{i{T_i}}}),\mathbf {z_i})$ (typically chosen when a temporal feature is in the model).

This approach is robust to missing encounters, as every subject can have a different number of follow-ups. Despite this, it does not take into account the correlated structure of the data and it violates the i.i.d. hypothesis. This limitation can lead to worse performance, as most predictive models would have high variance. Moreover, it does not exploit the sequential information, because the time dependencies are disregarded. For this reason, it is not common and typically used as a baseline model in comparison to more sophisticated ones, except in Bhat and Goldman-Mellor (2017).

2.2.2.4 Multiple instance learning (MIL)

MIL is a non-standard supervised learning method that takes a set of labelled bags, each containing many instances as input training examples (Hernández-González et al. 2016). Note that, in contrast to traditional supervised learning, labels are assigned to a set of inputs (bags) rather than providing input/label pairs.

In applications of MIL to longitudinal data, the bags are typically defined as containing repeated observations of every subject and the associated output. Note that each bag is allowed to have a different size (i.e. different number of follow-ups per subject). Then, for a binary classification, a bag is labelled “negative” (0) if all the instances it contains are negative. On the other hand, a bag is “positive” (1), if at least one instance in the bag is positive.

This methodology is akin to the SV approach when the outcome is replicated and the results of each example are aggregated (see Fig. 3). In contrast to SV, in the current literature on MIL (Vanwinckelen et al. 2016), the loss function for classification is usually at the bag-level, while in SV it is at the level of the instance. Similar to SV, MIL is flexible in allowing for different numbers of follow-ups, but typically assumes that data instances inside a bag are i.i.d., so it does not model the sequential nature of the data. There are exceptions to overcome this limitation, such as the work of Zhang et al. (2011), which proposed two MIL algorithms allowing correlated instances. By means of their approach, they showed that the prediction performance can be significantly improved when the correlation structure is considered.

2.2.2.5 Multi-task learning (MTL)

This approach involves the generation of a separate model for each instant recorded, i.e. for each recorded follow-up, resulting in time-specific models as many as the number of follow-ups. Subsequently, the models are trained jointly. Formally, given $T = \max \limits _{i = 1,...,N} T_i$ the maximum number of follow-ups recorded in the population, a task for each instant 1, .., T is considered, with its respective training set: $\mathcal {D}_t = \{(\mathbf {x_{it}},\mathbf {z_i},y_i), i=1,...,N \}$, for $t = 1,...,T$, i.e., all observations at that time across all subjects. Then, the goal is to compute the classifiers $f_t$ for $t = 1,...,T$. Typically, the tasks are jointly estimated by using information contained in the training signals of other related tasks in order to increase performance. By means of this strategy, a temporal smoothness constraint can be enforced on the weights from adjacent time-windows.

This method is used to predict the label at a specific time in the future (static output scenario), similar to the application of SV. Also, as in SV, each model $f_t$ predicts a label, and all the predictions are aggregated by majority voting or otherwise (Wiens et al. 2016; Singh et al. 2015; Oh et al. 2018).

MTL is flexible, as it can handle a different number of follow-ups for different subjects, similarly to MIL and SV. As an advantage over SV, it takes into account the sequential nature of the data by means of the joint learning of separate classifiers for each time t. As a limitation, we note that it requires a sufficient number of observations at every instant for training of each model, $f_t$.

2.2.2.6 Mixed-effects ML (MEML)

The so-called mixed effects models are among the most used methods for the statistical modelling of longitudinal data. In their simplest form are “Linear mixed-effects models” (LMMs) (Laird and Ware 1982). LMMs assume that the repeated outcome of a specific subject, $y_i$, can be decomposed into three contributions: one associated to the population average, one incorporating specifics of that subject that separate him/her from the population average, and a residual contribution associated to unobserved factors. More precisely, one writes

$$\begin{aligned} y_i = \tilde{X}_i \beta + \tilde{Z_i} b_i + \epsilon _i \end{aligned}$$

(1)

where $\beta$ is the vector of population-average (or fixed) regression coefficients, while $b_i$ are the subject-specific regression coefficients realisation of a random variable, called the random effects. $\tilde{X_i}$ is the ${T_i} \times p$ matrix containing the p features considered fixed, i.e., not subject-specific, while $\tilde{Z_i}$ contains the q variables related to the subject-specific effects. We remark that in this framework the distinction is between random and fixed features, not dynamic and static. Indeed, both dynamic and static aspects can contribute to the random ($b_i$) and fixed ($\beta$) effects coefficients.

The introduction of random effects b allows to describe the intrinsic deviation of each subject from the average evolution in the population, while assuming a general form for the matrix makes it possible to account for the correlations within the measurements of the same subject.

A natural extension of LMMs are the so called “Generalised Linear Mixed Models” (GLMMs), introduced in Nelder and Wedderburn (1972) to allow categorical outcomes. Nevertheless, the relation between the response and the fixed-effects variables cannot assume an arbitrary form. In order to overcome this limitation, research over the last decade has focused on incorporating mixed effects into more flexible models, e.g. using ML to estimate the relation between the response fixed-effects features.

The basic idea of Mixed-Effects Machine Learning (MEML) with random effects is to rewrite the LMM response in the following form Ngufor et al. (2019):

$$\begin{aligned} y_i = f(\tilde{X_i}) + \tilde{Z_i} b_i + \epsilon _i \end{aligned}$$

(2)

where $b_i$ and $\epsilon _i$ are random variables, and f is an unknown function to be estimated through a ML algorithm. Different implementations of MEML follow from the different possible choices for ML algorithm, guided on their underlying strengths, the data available, and the objective of the project (Amiri et al. 2020).

Once the model for f has been trained, one obtains predictions for the response $y_i$ of new subjects i by inputting their features $\{ \tilde{X}_i, \tilde{Z}_i \}$ on the right-hand-side of Eq. (2). An obvious challenge here is the estimation of the subject-specific random-effects coefficients, $b_i$, for unobserved subjects. This limitation results in a limited use of mixed-effects models in prediction scenarios. Ngufor et al. (2019) set the random effects to zero and used only the population level function. Efforts to estimate the random-effects part for new subjects include the works of Finkelman et al. (2016) and Ni et al. (2018).

Fig. 3

Overview of different methodologies for preparing longitudinal data for classification. In all approaches, but Multiple Instance Learning, an outcome is assigned to every instant considered. It should be noted that MTL differs from the other approaches by generating multiple models, specifically one model per recorded instant, and then learning them jointly

2.2.3 Supervised ML algorithms

In this section, we will describe the most commonly used classifiers applied after the input and output have been adequately formulated by means of one of the methodologies detailed in Sect. 2.2.2. It should be noted that the majority of classifiers are non-temporal, i.e., they do not naturally account for the sequential structure of the data, but rather rely on the data preparation step to better exploit the temporal component of the data. Thus, in this review, we pay particular attention to temporal algorithms, such as recurrent models, that overcome this limitation.

2.2.3.1 Non-temporal

Common non-sequential classifiers are Logistic Regression (LR), Naïve Bayes (NB), Decision Tree (DT), Random Forest (RF), Support Vector Machines (SVM), Gradient Boosting Machines (GBM), and K-nearest neighbours (KNN). In addition, there exist also deep learning (DL) models, namely Artificial Neural Networks (ANN), which are able to capture complex nonlinear relationships between the response variable and its predictors. Common examples are Multi Layer Perceptron (MLP) and Convolutional Neural Networks (CNN). The interested readers can find an exhaustive review in Kotsiantis et al. (2007). These algorithms can be used with every data methodology.

2.2.3.2 Longitudinal features: recurrent models

Fig. 4

Overview of the recurrent networks architectures. In particular, many-to-one is used for a static outcome, such as diagnosis or risk prediction, while one-to-many and many-to-many for a longitudinal outcome. The many-to-many architecture (A) is typically used to make real-time predictions, while (B) is appropriate for the prediction of trajectories progression in the future. The notation for data input and output is the same as in Figs. 2 and 3 of the manuscript

Recurrent neural networks (RNN) (Rumelhart et al. 1986) are a class of feed-forward neural networks used with the LF methodology described in Sect. 2.2.2. They are naturally designed to model sequential data by using a transformation in the hidden-state depending not only on the current input but also on information from the past. In this sense, hidden states are used as the memory of the network such that the current state of the hidden layer depends on the previous time. There are two ways to model the additional static features: through replication at every time point and using the features as input to the recurrent cell (Thorsen-Meyer et al. 2020; Meyer et al. 2018), or by processing each feature separately and then concatenating all the features (Ioannou et al. 2020; Lee et al. 2019a, b).

An important property of RNNs derived by the recursive modelling is the ability of handling different inputs lengths, which is convenient in a longitudinal framework. RNNs are also very flexible because there are different types of architectures based on the number of inputs and outputs (see Fig. 4), namely (i) one-to-many, where given a single input multiple outputs are provided, (ii) many-to-one, multiple inputs are needed to provide one output, and (iii) many-to-many, where both the input and output are sequential. The majority of works analysed adopted a many-to-one setting, i.e., given historical data, predicting an outcome at a future instant point, or classifying the sequence. Several works leveraged the many-to-many architecture in order to model a longitudinal outcome and predict several time points simultaneously (Andreotti et al. 2020; Tabarestani et al. 2019; Ghazi et al. 2018; Kaji et al. 2019; Ashfaq et al. 2019).

One problem of standard RNNs is the gradient vanishing, due to the fact that the error is back-propagated through every time step, so it is a deep network. Two prominent variants designed to overcome this issue and to capture the effect of long-term dependencies are widely used: the long short-term memory (LSTM) unit (Hochreiter and Schmidhuber 1997), and the gated recurrent unit (GRU) (Cho et al. 2014). Indeed, from the study of the literature, it emerges that the most used method is LSTM, followed by GRU and standard RNN. There is little work using Bidirectional GRU (BRGU), which allows for learning not only from the past but also from the future inputs (Cui et al. 2018, 2019), and one using Echo State Networks (ESN) (Verplancke et al. 2010).

In general, RNNs are a popular state-of-art set of models to work with temporal data. The interested readers can find a complete review in Lipton et al. (2015). Due to the importance of RNNs in the field of longitudinal biomedical data, many adaptations have been produced:

• Recurrent models allowing irregular visits Typically, only the longitudinal features vectors $\mathbf {x_i} = (\mathbf {x_{i1}},...\mathbf {x_{i{T_i}}})$ are used to train a recurrent model. This means that the timing vector is discarded, losing important information. This choice is indirectly assuming that time points are evenly spaced. However, in real-world biomedical applications this assumption is not necessarily true as the frequency of visits could be irregular, depending on the patient’s needs. Thus, a recurrent architecture which takes irregular elapsed times into account is more appropriate for longitudinal data. For this reason, many works extended recurrent models in order to handle unevenly visits, such as in Wang et al. (2018); Aczon et al. (2017); Choi et al. (2016); Baytas et al. (2017), by giving as additional input to the architecture the time interval between two adjacent visits. In the real world, this interval can be set according to a user’s need, which means the future prediction time point can be customised as needed.

• Recurrent models with incorporated attention While RNNs are a strong tool in order to capture the temporal sequences, sometimes this comes with a lack of interpretability. In order to tackle this limitation, some researchers adapted the models incorporating a scheme called attention, which can identify variables driving predictions (Suo et al. 2017; Andreotti et al. 2020; Choi et al. 2016; Kaji et al. 2019). An attention vector learns weights corresponding to each feature in order to focus the next layer of the model on certain features. In this field, RETAIN (Choi et al. 2016) (“REverse Time AttentIoN model”) is considered one of the state-of-the-art models, incorporating attention in RNNs for predicting the future diagnoses. RETAIN is a two-level neural attention model for sequential data to interpret visit and variable level importance. This was achieved by Choi et al. (2016) using a factorised approach to calculate attention over both variables and time using embedded features rather than the immediate input features themselves.

2.2.3.3 Longitudinal Features: temporal convolutional neural networks (TCN)

The adaptation of CNN to sequential data is very recent (Lea et al. 2016) and it is based upon two principles: the network can take a sequence of any length and produces an output of the same length, and the convolution is causal, i.e. there is no leakage from the future into the past. The are few works using TCNs but the results are promising (Bai et al. 2018; Catling and Wolff 2020; Zhao et al. 2019):

2.2.3.4 Longitudinal Features: longitudinal support vector machines (LSVM)

Chen and DuBois Bowman (2011) proposed an extension of SVM classifiers for longitudinal high dimensional data, known as longitudinal support vector classifier (LSVC). LSVC extracts the features of each cross-sectional component as well as temporal trends between these components for the purpose of classification and prediction. Specifically, assuming that $T_i = T$ $(\forall i = 1,...,N)$ and that a single output $y_i$ is assigned to each subject, the objective function incorporates the decision hyperplane function parameters and the temporal trend parameters to determine an optimal way to combine the longitudinal data. Following this approach, Du et al. (2015) proposed longitudinal support vector regression (LSVR) model adapted to numerical outcomes. Their results (Chen and DuBois Bowman 2011; Du et al. 2015) showed that these algorithms leverage the additional longitudinal information, without requiring high computational cost.

2.2.4 Comparison between longitudinal supervised learning methods

The data formulation methodologies described in this review can be grouped according to their ability to exploit the dynamic nature of the data. SV does not exploit it, nor does MIL, although there are some exceptions such as the work of Zhang et al. (2011); SF strictly depends on the aggregation function, but usually it loses some temporal information, as the statistics typically used include metrics, such as mean and standard deviation, which summarise the trend but lose trajectory-specific information; LF depends on the subsequent classifier applied and whether it considers the temporal order and models the sequential nature of the features, as is the case with RNNs, or not; finally, MTL and MEML model the time correlations. A summary of the advantages and disadvantages of each method is provided in Table 4, but there is no absolute best method. The final choice strictly depends on the specific problem. Hence, it is recommended to always consider simple models against more sophisticated ones, as this will be illustrated in some of the applications listed in Sect. 3.

Fig. 5

Distribution of the presented supervised learning approaches for longitudinal data in the reviewed literature. The most commonly used approaches are summary features, followed by longitudinal features with a sequential classifier (precisely, recurrent neural networks) and longitudinal features with a non-sequential classifier

Table 4 Overview of the main methodologies for handling longitudinal data

Moreover, the present review reveals that SF, LF with RNNs, and LF with a standard non-dynamic supervised algorithms are the most common approaches. Regarding SF, this is due to the fact that aggregating the temporal measures typically outperforms one instance model. Instead, LF representation does not violate i.i.d. assumption and discard any information. However, as already noted, sometimes it could not be possible to apply LF because there is a large number of follow-ups or there are not enough data to use RNNs.

Finally, an important finding of the present review is the lack of algorithms exploiting the dynamic aspect of longitudinal datasets, with the exception of RNNs, LSVM and TCN. Indeed, most works model the data in such a way as to allow the use of non-sequential classifiers. This differs substantially from the statistical approach, which typically uses methods considering the temporal correlation. The latter can be adapted in scenarios where the ultimate goal is not the classification or prediction per se, but rather interpretation of the dependencies between a small number of variables. However, in the case of prediction, ML approaches have been proven to be more efficient than statistical techniques thanks to their ability to capture non-linear relationships between a large set of variables. This will be further discussed in detail in the next section.

2.2.5 Evaluation of longitudinal supervised learning models

To evaluate the performance of ML algorithms, it is common to split the data into three different subgroups, called the training set, validation set and testing set. The training set is used to build a first version of the classifier. The validation set is used to fine-tune the values of the hyperparameters such that the classifier generalises well to unseen instances beyond those used for training. Lastly, the testing set is used to assess and report the performance of the final model. These subsets need to be selected in such way that they follow the same distribution of the original sample, i.e., they share the demographic distributions, in order to represent a real world scenario and respect the i.i.d. assumption.

In the longitudinal framework, there are two main approaches for splitting the dataset: (i) “record-wise” split where each measurement or record is randomly split into training and test sets, allowing records from each subject to contribute to both the training and test sets; and (ii) “subject-wise” split where all the records of each subject are randomly assigned as a group to either the training set or to the test set. Special care should be put in (i), as using the same subjects both in the training and testing set could lead to an under-estimation of the prediction error due to the presence of “identity confounding” (Neto et al. 2019).

2.3 Unsupervised learning

Unsupervised learning is the ML task of drawing inferences and finding patterns from input data without the use of labelled outcomes. Practically speaking, in the longitudinal setting, such approaches are used for (i) selecting a convenient set of descriptive features (typically for dimensionality reduction) and (ii) for creating groups of patients with similar disease progression, without having prognostic labels. In the ML literature, the first case is known as unsupervised features learning or extraction, while the second as clustering. In the biomedical context, unsupervised learning is less common than supervised learning (only 16% of the works found in the survey use it).

2.3.1 Unsupervised feature learning

The main goal is to learn from unlabelled examples a useful feature representation that can then be used for other tasks, e.g. supervised learning. This replaces manual feature engineering and some examples include principal component analysis (PCA) (Wold et al. 1987), autoencoders (Rumelhart et al. 1985) and matrix factorisation (Srebro et al. 2004). A total of 8% of the reviewed papers in this review used unsupervised feature learning as a preliminary step to supervised or unsupervised learning, specifically using autoencoders architectures as described as follows.

2.3.1.1 Autoencoders

They are neural networks (NNs) typically used for dimensionality reduction of the data features. This is achieved by using the same data as input and output, and letting the hidden layers compress the data into a lower dimensional embedding. In this manner, the model automatically identifies patterns and dependencies in the data and learns compact and general representations. Every patient is then represented using these features and such deep representation can be applied to supervised learning (Suo et al. 2018; Lasko et al. 2013; Chu et al. 2020) or clustering (Suo et al. 2018; Baytas et al. 2017; Li et al. 2020; Gong et al. 2019). There are possible extensions, such as Denoising Autoencoders (DAEs), used in order to develop a model robust to data noise (Chu et al. 2020; Suo et al. 2018; Miotto et al. 2016), and Variational Autoencoders (VAEs) (de Jong et al. 2019). VAEs assume that the source data has an underlying probability distribution (such as Gaussian) and then attempt to find the parameters of the distribution.

2.3.2 Clustering

The task of clustering longitudinal data aims to group together subjects with “similar” progression over time. It is important to notice that there are different concepts of “similarity”: based on distance, resemblance or likelihood. Common algorithms for achieving the goal are K-means clustering, hierarchical clustering, growth mixture modelling and more sophisticated group-based trajectory models. The interested readers can find a review of these methods applied to longitudinal data in Den Teuling et al. (2021). As concerns the study analysed, the majority adopted the K-means algorithm, which is described below. Other common techniques include Fuzzy Clustering (Fang 2017), Multi Layer Clustering (Gamberger et al. 2017), Hierarchical clustering (Bhagwat et al. 2018), and collaborative learning (Lin et al. 2016) and group-based trajectory modelling (Kandola et al. 2020).

2.3.2.1 K-means

It is the most basic and popular clustering method, which groups unlabelled data into K clusters. Each data point belongs to the cluster with the closest mean, where closest is in the sense of a certain metric, usually the Euclidean distance. In the context of longitudinal studies, the input is the data in the longitudinal representation, i.e. for each subject we have the vector containing all observations. However, this metric calculates the distance as the average of all distances in each dimension (including time), risking that trajectories with similar global shape, but shifted in time, are allocated to different clusters. To avoid this, the options are two: features selection (typically with autoencoders (Baytas et al. 2017; Gong et al. 2019; Lasko et al. 2013; Li et al. 2020; Miotto et al. 2016) or factor analysis (Ilmarinen et al. 2017; Karpati et al. 2018)) or using an alternative metric. In this sense, Sun et al. (2016) proposed K-means based on the extended Frobenius norm (Efros) distance. In order to apply the K-means algorithm, the number of cluster needs to be specified a priori, as it is not learnt from the algorithm. Towards this aim, Ilmarinen et al. (2017) used a prior step, applying Ward hierarchical cluster, which automatically learns the number of clusters. Gong et al. (2019) defined the number of clusters by comparing the inertia, the sum of squared distances to the closest centroid for all observations; while Dai et al. (2020) used Calinski-index.

The popularity of K-means as a clustering approach is closely related to the fact that it is relatively simple to implement, scales to large datasets and guarantees convergence. However, there are several limitations: it is easy to fall into local extremum depending on the initialisation (it is recommended to run it several times and keep the best result); and it is sensitive to the initial chosen centres and the noise.

2.3.3 Evaluation of longitudinal unsupervised learning

Validating the results of a clustering algorithm is more challenging compared to supervised ML algorithms, as there are no existing ground truth labels. Popular approaches involve (i) “internal” evaluation (based on the data that was clustered itself), (ii) “external” evaluation, i.e., comparison with an existing “ground truth” classification, (iii) “manual”, i.e., evaluation by a human expert, and (iv) “indirect” evaluation, i.e., evaluation of the utility of the clustering in its intended application. Many different metrics have been proposed, such as Purity, class entropy, Rand Statistic, Jaccard Coefficient, Normalised Mutual Information (NMI) and so on. The interested readers find a complete review in Amigó et al. (2009).

2.4 Handling missing data in longitudinal machine learning

Longitudinal cohorts often contain missing values in the biomedical field, such as due to dropped out participants or unsuccessful measurements. This situation poses a major difficulty for modelling longitudinal data, since most ML models require complete data. One straight solution is to remove subjects or time points with missing data. However, this can result in a significant loss of amount of information and in the potential introduction of biases in the model. From a statistical point of view, there are three different mechanisms of missing data (Rubin 1976):

• Missing completely at random (MCAR): The probability of missing information is related neither to the specific value that is supposed to be obtained nor to other observed data. As an example, some subjects have missing laboratory values due to an improper processing. In this case, the missing data reduce the analysable population of the study and consequently, the statistical power, but do not introduce bias. They are probably rare in clinical studies.

• Missing at random (MAR): The probability of missing information depends on other observed data but is not related to the specific missing value that is expected to be obtained. As an example, the probability of completion of a survey on depression severity is related to subjects’ sex (fully observed) but not on the expected answers. Excluding the observations can lead to biased or unbiased results.

• Missing not at random (MNAR): The probability of missing information is related to the unobserved data, that is to events or factors which are not measured by the researcher. As an example, subjects with severe depression (unobserved) are more likely to refuse to complete the aforementioned survey.

Researchers must pay attention especially in the case of MAR and MNAR missing data. A correct modelling of missing data can improve the performance of a task (Rubin 1976), as the values of missing rates are usually correlated with the desired outcomes (Che et al. 2018). Despite the importance of handling missing data, 46% of the applications analysed in this review are not mentioning or addressing the problem. This implies different scenarios: (i) the dataset is already complete, which is unusual in the real world; (ii) the ML model chosen is robust, e.g. it uses summary features or approaches where each time point is processed separately; (iii) the missing values are discarded or handled without specifying.

It appears that it is common to pre-process the data by using methods such as data imputation and interpolation, by replacing missing values with means or other statistics, by applying regression models, or by using more sophisticated methods; 47% of the papers identified in this review used such pre-processing methods. For example, Lasko et al. (2013) first applied a Gaussian process then a warped function. Within the imputation methodology, it is possible to introduce indicator variables which indicate if the value is missing or not. This strategy is usually applied with recurrent models and the indicators are called in this case masking vectors. In total, 8% of the works use such indicators. As an example, Lipton et al. (2016) treated the irregular-visits problem as a missing-values problem, by considering temporally irregular data to be missing data and introducing as features some indicator variables. Comparing the choice of introducing masking vectors in a zero-imputation framework with other established methods, the authors found that this choice was the most effective.

It should be noted that combining the imputation methods with prediction models often results in a two-step process where imputation and prediction models are separated. Nevertheless, there is evidence that by doing so, the missing patterns are not effectively explored in the prediction model, thus leading to suboptimal analysis results (Che et al. 2018). This explains why 7% of the works analysed designed ad hoc models for handling missing values (Ghazi et al. 2018; Jie et al. 2016; Fang 2017; Lei et al. 2020; de Jong et al. 2019; Huang et al. 2016; Che et al. 2018). In this sense, the work by Che et al. (2018) is particularly significant, as the authors developed a novel recurrent architecture exploiting the missing patterns to improve the prediction results. Specifically, they applied masking and interval time (using a decay term) to the inputs of a GRU network, and jointly trained all model components using back-propagation. The authors showed that this method outperformed other imputation methods, such as the work of Lipton et al. (2016).

However, by introducing many parameters, the networks as well as the risk of overfitting increase. To prevent this, Ghazi et al. (2019, 2018) proposed a generalised method for training LSTM networks that handles missing values in both target and predictor variables without encoding the missing values. This was achieved by applying the batch gradient descent algorithm in combination with the loss function and its gradients normalised by the number of missing values in input and target. By means of this model, the results outperformed those obtained in Che et al. (2018); Lipton et al. (2016).

2.5 Recent developments

In recent years, research in the field of machine learning applied to longitudinal biomedical data has seen less use of techniques that do not model the sequential nature of the data, such as LF in Pang et al. (2021) and SF (Shuldiner et al. 2021), in favour of those that do it, for example by incorporating mixed effects (Mandel et al. 2021; Speiser 2021; Hu and Szymczak 2023; Capitaine et al. 2021) or with the use of recurrent neural networks (Men et al. 2021; Lei et al. 2022; Lee et al. 2022; Dixit et al. 2021; De Brouwer et al. 2021; Lu et al. 2021; Montolío et al. 2021). Furthermore, innovative models for sequential data such as transformers (Vaswani et al. 2017), typically used in the field of natural language processing to analyse texts, have started to be applied in the biomedical field on longitudinal data (Prakash et al. 2021; Nitski et al. 2021; Zeng et al. 2022; Chen and Hong 2023; Gupta et al. 2022; Lee et al. 2022). Specifically, a transformer is a deep learning model that adopts the attention mechanism, weighting the meaning of each part of the input data differently. Like RNNs, transformers are designed to process sequential input data, but unlike RNNs, transformers process the entire input at once, eliminating the recurrence mechanism. In particular, this is achieved through the use of positional coding, which provides the context of order to the non-recursive architecture. Overall, transformer architectures are less complex and accommodate parallelisation, resulting into faster overall computational (Vaswani et al. 2017), which explains the increasing number of studies exploiting this architecture.

3 Results of application domains

This section reviews in detail a wide range of application of longitudinal machine learning methods in a number of medical areas. Particular attention is paid to the field of chronic diseases (including both physical and mental disorders) due to the high potential of longitudinal ML for studying diseases that do not present a linear trend, but rather require repeated follow-ups in order to make long-term predictions. We also provide a detailed overview of applications in the field of emergency medicine, where there is a need for new data-driven tools to rapidly choose the right course of actions in emergency situations.

3.1 Cardiometabolic diseases (CMDs)

CMDs include cardiovascular diseases (CVDs), diabetes mellitus, and chronic renal failure (Sarafidis et al. 2006). These diseases are mainly caused by poor lifestyle, such as smoking, unhealthy diet, and inactivity, and they are closely linked to each other. Early signs of CMDs are manifested early in life as insulin resistance. Subsequently, CMDs progress to metabolic syndrome and pre-diabetes, and can finally result in type 2 diabetes mellitus (T2DM) and CVD (Guo et al. 2014). The socio-economic burden associated with CMDs and their comorbidities is extremely high. Indeed, CVDs alone account for one-third of all global deaths, and their economic cost only in Europe is currently estimated to be EUR 210 billion per year. Therefore, accurate, reliable and early identification of people at high risk of CMDs plays a crucial role in early intervention and improved patient management.

3.1.1 CVD Prediction

Several models have been proposed for prediction of CVD events, including the Framingham risk score (Wilson et al. 1998), American College of Cardiology/American Heart Association (ACC/AHA) Pooled Cohort Risk Equations (Goff et al. 2014), PROCAM (Assmann et al. 2002), SCORE (Conroy et al. 2003) and QRISK (Hippisley-Cox et al. 2007). These models are typically built using a combination of cross-sectional risk factors such as hypertension, diabetes, cholesterol, and smoking status. Despite the importance of these conventional models, the risk factors used explain only 50-75% of the variance in major adverse cardiovascular events (Kannel and Vasan 2009). Thus, significant efforts have focused on developing new risk models based on ML that can better exploit patient information. These models were proven extremely efficient in predicting CVD events and outperformed classical methods, especially when data from earlier time-points were included (see Table 5).

More precisely, using a sample of 109,490 individuals (9824 cases and 99 666 healthy controls), Zhao et al. (2019) demonstrated that a wide variety of ML models (LR, RF, GBM, CNN, LSTM) outperforms the conventional ACC/AHA model in the task of predicting 10-year CVD events, while the best ML performance was achieved when 7 years of longitudinal information was considered. ACC/AHA equations reached an average accuracy (AUC) of 0.732, ML models using summary EHR features attained 0.765$-$0.782, while by using Longitudinal Features all the ML models reached an AUC ranging from 0.781 to 0.790 with GBM and CNN achieving the highest (AUC=0.79). Similar results were obtained by Korsakov et al. (2019) when comparing longitudinal ML for predicting heart failure (HF) with SCORE, PROCAM, and Framingham equations. These findings suggest that the choice of modelling and data to feed the classifier play a crucial role in the achieved performance.

Apart from the choice of the modelling approach (ML versus conventional) and methodology (longitudinal versus summary), a significant number of studies focused on quantifying the amount of historical information needed to build accurate models. Specifically, in several works  (Choi et al. 2017; Ng et al. 2016; Chen et al. 2019), the authors conducted several experiments to predict HF using incremental EHR information. Towards this, they varied the observation and prediction windows, and analysed the respective performance achieved. As expected, the accuracy increased as the observation windows grew. Specifically, Ng et al. (2016) used LR and RF with summary features varying the observation window length from 30 days to 5 years. The prediction accuracy improved progressively from 0.66 to 0.79 as the observation window length increased up to 2 years. Nonetheless, longer observation windows (3, 4 and 5 years) had minimal impact on model performance (up to 0.80 AUC). This might imply that the target outcome could be weakly correlated with variables too distant in time or that there is a need for more advanced models to capture temporal connections further back in time. In this direction, Chen et al. (2019) used a RNN and compared its performance with two simpler models, a LR and a RF with summary features. The authors varied the observation window from 3 months up to 3 years, with a fixed prediction window of 1 year. Contrary to LR and RF, the accuracy obtained by means of the RNN grew steadily up to 3 years, achieving maximum AUC of 0.791 when data of all domains (demographics, vitals, diagnoses, medications, and social history) was used.

Despite the importance of these findings and the high performance achieved, it should be noted that the clinical use of complex models may be hampered by a lack of interpretability of the results. To tackle this limitation, efforts have been focusing on developing explainable ML tools. An example in this direction is the work by Choi et al. (2016), who incorporated an attention mechanism in the neural network architecture. More precisely, the authors, by using the RETAIN architecture 2.2.3.2,, emulated the clinicians’ behaviour, looking at the visits in reverse order and pointing out the most meaningful ones. In total, 3884 cases and 28 903 controls with 18 months of historical data were used. RETAIN achieved an AUC of 0.870, while a RNN of 0.871, outperforming LR and MLP with summary features. Overall, RETAIN had the predictive power of a RNN and additionally allowed for interpretation by highlighting influential past visits in the EHR along with the significant clinical variables within those visits for the diagnosis of hearth failure.

3.1.2 T2DM prediction

The identification of subjects at high risk of developing T2DM is usually done by labs tests, which is a costly and time-consuming process. Moreover, it enables solely the detection of people when specific indicators reach abnormal levels, while it would be preferred to identify people at risk before this stage (Pimentel et al. 2018). Traditional models for T2DM onset, such as ARIC (Kahn et al. 2009), San Antonio Heart Study (Stern et al. 2002), AUSDRISK (Chen et al. 2010), and FINDRISC (Lindström and Tuomilehto 2003), provide potential solutions for more accurate risk assessment. Nonetheless, these models require a time-consuming and costly screening step (Najafi et al. 2016).

With the advent of big data, tools for early prediction of T2DM with ML, exploiting the large sample of information presents in EHR, started to appear. In this direction, Razavian et al. (2015) considered the prediction of the onset of T2DM in a period of time between one and three years into the future by using a large sample of 6,97,502 individuals, of which 13,835 developed T2DM within the prediction window. Thanks to ML, the authors could handle 769 features, both static and longitudinal covering the entire life (discretised in 3 intervals) up to December 31, 2008. The AUC of predicting the onset of T2DM between 2010 and 2012 achieved by the longitudinal ML model was 0.78, while that achieved by classical models was limited to 0.74.

Despite the importance of the findings, one recurrent problem in such works is that the sample used is highly unbalanced, with a relatively low percentage of individuals developing T2DM. This could lead to models not able to identify the high-risk population. For example, Mani et al. (2012) developed a model capable of predicting diabetes one year before the actual diagnosis with an AUC of 0.80. However, the positive predicted value (PPV), or precision, was only 24% due to the high unbalanced nature of the dataset (only 10% of true positive cases after random undersampling of the control group). In an effort to overcome this problem, while avoiding using an undersampling technique as in Zheng et al. (2017), the Synthetic Minority Over-sampling Technique (SMOTE) (Chawla et al. 2002) was adopted in Nguyen et al. (2019); Pimentel et al. (2018). These authors used the same dataset and same settings, but different ML models, in order to predict diabetic patients by using data from one to three years before the onset of the disease. The results between the two studies differed significantly. In Pimentel et al. (2018), the performance of their RF model using SMOTE to increase the diabetic cohort by 150% and 300% remarkably improved AUC and sensitivity scores. On the contrary, in Nguyen et al. (2019) the DL models using SMOTE (150 and 300%) presented higher sensitivity (by 24.34 and 42.45%, respectively), but decreased AUC (by 0.6 and 1.89%, respectively) and specificity (6.02 and 19.59%, respectively) with respect to Pimentel et al. (2018). It should be noted that a prediction model for T2DM with good sensitivity could reduce the risk of unnecessary interventions for low risk patients. Thus, a model with slightly less accuracy in terms of AUC, but with significant gain in sensitivity, may be preferable to clinicians. It is also important to note that the SMOTE technique may distort the meaning of the probabilistic outputs in the models and systematically overestimate the probability for the minority class  (van den Goorbergh et al. 2022). To avoid such issues, it is always recommended to study the impact of imbalance corrections on discrimination performance. Moreover, it is worth noting that although the aforementioned papers evaluate the performance of ML models on unbalanced datasets, they primarily use AUC as the evaluation metric, which is known to be inappropriate if the data imbalance is severe (Davis and Goadrich 2006). A more holistic evaluation approach is recommended in these scenarios, considering other complementary metrics as well, such as area under Precision-Recall curve (Davis and Goadrich 2006) and Matthews’s correlation coefficient, which take into account both the true positive and false positive rates (Chicco and Jurman 2020; Luque et al. 2019).

3.1.3 Chronic kidney diseases (CKDs)

Individuals with T2DM are at higher risk of developing diabetic kidney disease (DKD) because elevated blood glucose can damage renal blood vessels over time. Generally, even though diabetes is considered the most common cause of Chronic Kidney Diseases (CKDs), other common risk factors include high-blood pressure, CVDs, smoking and obesity. Besides, people with CKD have an increased risk for CVDs mostly due to problems with the blood vessels. Specifically, CKD progression is associated with a deterioration in kidney function, and, in the worst case scenario, can lead to kidney failure (Levey and Coresh 2012). The early identification and targeted intervention of CKD is, therefore, of vital importance, because it can reduce the number of patients with more serious conditions.

Since kidney function is well-defined by the estimated glomerular filtration rate (eGFR), the progression of kidney disease can be predicted if the future eGFR can be accurately estimated. In this context, several studies (Singh et al. 2015; Zhao et al. 2019) focused on predicting the progression of CKD based on eGFR predicted values by relatively simple ML models.

Singh et al. (2015) varied the number of historical records used from 6 months up to 5 years, and demonstrated that multi-task learning outperformed summary and longitudinal features methodologies in every scenario in the task of predicting renal function deterioration quantified as loss of eGFR. Interestingly, with longitudinal features the accuracy initially improved, but eventually dipped as the number of years of temporal information increased over a limit. This is probably related to the greater possibility of overfitting as the number of features introduced in the model increases, as already discussed in Paragraph 2.2.2.2. In particular, the highest accuracy in predicting values of percentage drop of eGFR greater than 10% was achieved using 3 years of historical data (AUC = 0.69).

Zhao et al. (2019) treated the prediction of eGFR values as a regression problem followed by a classification into CKD stages. First, they predicted the eGFR values in the year 2015, 2016, and 2017, using data from 2011 to 2014 and a cohort of 1,20,495 EHR data. They obtained an average $R^2 = 0.95$ for the prediction of eGFR for all three years of interest. Subsequently, they classified the subjects into different CKD stages by using RF with 11 features. Among these features, four were temporal and corresponded to the values of eGFR from 2011 to 2014. They achieved a 88% macro-averaged recall and a 96% macro-averaged precision by averaging over the 3 years. Given the high performance of the model in terms of accuracy, precision and recall and the fact that it provides the most important features used to make the final classification, its potential to be translated into a clinical decision support tool is excellent.

Table 5 Selected studies in the domain of CMDs

3.2 Neurodegenerative diseases

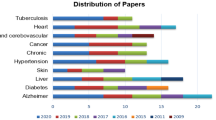
Neurodegenerative diseases are a heterogeneous group of illnesses characterised by the progressive deterioration of neurons. Although treatments can alleviate the symptoms, currently there is no available definitive therapy. The risk of being affected by neurodegenerative diseases increases with the age, but it has been proven that the disease development begins 10 to 20 years prior to the first clinical symptoms (Sheinerman and Umansky 2013). Furthermore, according to the World Alzheimer Report 2011, therapies are more likely to be effective when first applied during the early stages in order to slow down the progression. Given the incredible burdens that these diseases pose on healthcare, identifying high-risk subjects in order to implement a timely intervention is crucial. Therefore, a significant amount of research focused on prediction of Alzheimer disease (AD), Parkinson disease (PD), Huntington disease (HD), and amyotrophic lateral sclerosis (ALS), with AD being the most studied. This is in part thanks to the publicly available Alzheimer Disease Neuroimaging Initiative (ADNI) cohort (see Table 1). There are over 1800 publications based on ADNI data, and for the interested readers, there are several reviews of the works and results achieved (Weiner et al. 2013; Toga and Crawford 2015; Weiner et al. 2017; Martí-Juan et al. 2020).

In the next paragraphs, we summarise the main results on diagnosis and prediction of progression of AD and MCI; further details on the studies on neurodegenerative diseases identified in our survey are provided in Table 6.

3.2.1 Diagnosis of AD

Use of longitudinal data for an early diagnosis of AD is particularly interesting given the complexity of AD diagnosis and that it would enable early intervention.

In the context of ADNI data, which is a multi-modal heterogeneous longitudinal dataset, differentiation between Alzheimer’s Disease (AD), Mild Cognitive Impairment (MCI), and healthy control subjects (HC) is a challenging problem due to (i) high similarity between brain patterns, (ii) high portions of missing data from different modalities and time points, and (iii) inconsistent number of test intervals between different subjects.

To deal with this challenging task, Chen and DuBois Bowman (2011), used a LSVC model on 12 months data with two follow-ups and obtained an AUC of 0.78 for discriminating between HC and AD subjects. In a different approach, Cui et al. (2018, 2019) focused on magnetic resonance images (MRI) in order to develop a complete data-driven approach capable of jointly learning the spatial and the temporal dependencies using RNNs. More precisely, MLP and CNN were used in Cui et al. (2018) and Cui et al. (2019) respectively, to extract the spatial features from MRI images at every time point, for a maximum of 5 encounters in a period of 36 months. Then, both studies used BGRU to capture the temporal dependence, using a masking layer to account for sequences that had less than 5 time points. They achieved accuracies of 0.90 and 0.91, respectively. Moreover, they demonstrated that by increasing the number of time-points considered from 1 to 5, the accuracy steadily increases (from 0.87 to 0.90 with ML (Cui et al. 2018), from 0.88 to 0.91 with CNN (Cui et al. 2019)). Lastly, they showed that the performance of the proposed model is superior to that of a Stacked-Vertically MLP and a CNN by 3% in Cui et al. (2018) and 2.34% in Cui et al. (2019) respectively. This suggests that deep learning models are able to capture the progression of Alzheimer’s disease better.

In an effort to leverage multi-modal longitudinal data for AD diagnosis, Aghili et al. (2018) focused on integrating multi-source data, i.e. features from MRI and positron emission tomography (PET), cognitive tests, and genetic features. More precisely, the dataset used contained 1721 subjects scanned at 24 different time points over the course of 11 years. Data from each instant was represented by 47 features extracted from the different modalities. To handle missing values, the authors proposed three strategies: (i) direct replacement with zero values, (ii) using the values from the previous time step, and (iii) stacking the available intervals and then padding to the maximum size. Subsequently, they compared the performance of a MLP with Longitudinal Features, a LSTM and a GRU using the three proposed approaches for missing values. They demonstrated that for RNNs padding had the worst performance (AUC 0.9527 for AD vs. HC, 0.8468 for AD vs. MCI, 0.7585 for MCI vs. HC), while the best one was achieved by means of the replicate filling strategy for distinguishing between AD and HC (AUC=0.9586) and by zero filling for the other cases (0.8579 for AD vs. MCI, 0.7729 for MCI vs. HC). Moreover, LSTM and GRU models were superior to the MLP network in most of the cases, except for screening of HC vs. MCI, where MLP achieves the same accuracy as LSTM (0.7729). Distinguishing between MCI and AD subjects (AUC=0.8579) or MCI and HC (AUC=0.7536) is far more challenging than AD versus healthy. This led several research efforts to focus on MCI progression, as detailed in the next paragraph.

3.2.2 Prediction of MCI conversion

Several works based on the ADNI dataset focused on subjects affected by MCI in an effort to model the progression of neurodegeneration and make a distinction between stable (sMCI) and progressive (pMCI) patients, i.e., patients whose condition will worsen. Towards this aim, in Lee et al. (2016); Ardekani et al. (2017), the authors used the rate of change of new biomarkers (callosal atrophy and hippocampal volumetric integrity respectively) based on two measurements: at baseline and at one year follow-up. The sample consisted of 132 and 164 MCI subjects respectively. Despite differences in predictors and techniques, both works found a significant increase in classification accuracy for women (0.84 and 0.89 in female, 0.60 and 0.79 in male respectively). This suggests that the development of predictors is different dependent on sex, and, therefore, sex differences in brain atrophy should be taken into account. In contrast with these studies that were based on a 1-year follow-up, Mubeen et al. (2017) focused on modelling the progression of MCI patients based on MRI and cognitive biomarkers at baseline and at rough 6-month follow-up evaluation achieving an AUC of 0.80. They compared the performance of their model to that of using only baseline and cross-sectional data (AUC=0.72), demonstrating that even the use of a short longitudinal period of 6 months data significantly improves classification accuracy.

All aforementioned works were based on single modality MRI data with the features being extracted in a prior step. However, incorporating multi-modal data, both cross-sectional and longitudinal, is a far more challenging task. In Lee et al. (2019a, 2019b), developed a general model capable of integrating multi-source (cognitive score, neuroimaging data, CSF biomarker, demographic data) longitudinal and static data. Towards this, they developed a deep learning-based python package, called multimodal longitudinal data integration framework (MildInt), that provides a pre-constructed deep learning architecture for a classification task, consisting of two learning phases. First, a feature representation from each modality of data is learnt using a GRU architecture. Then, a classifier is trained for the final decision. Using ADNI, they demonstrated the superiority of their approach that permitted the integration of multi-source data at multiple time points compared to using single modality or static data.

Table 6 Selected studies using longitudinal ML (supervised or unsupervised) in the domain of neurodegenerative diseases

3.3 Other chronic diseases

More in general, the analysis of longitudinal data with ML is convenient for chronic diseases, such as CMDs and neurodegenerative diseases. These are defined broadly as conditions that last 1 year or more and require ongoing medical attention, or limit activities of daily living, or both. In this paragraph particular attention is paid to chronic respiratory diseases and chronic hepatitis C; further details on the studies on chronic diseases identified in our survey are provided in Table 7.

Table 7 Selected studies in the domain of other chronic diseases

3.3.1 Chronic respiratory diseases

Respiratory diseases are considered those complications that affect the lungs and airways, with the most common being asthma and chronic obstructive pulmonary disease (COPD). Among the most common causes are pollution and smoking. Currently, there is no definitive cure. Thus, as is the case with other chronic diseases, an early intervention could aid prevention of more serious situations. It is interesting that two of the three works found in this field are using telemonitoring data (Orchard et al. 2018; Finkelstein and cheol Jeong 2017), both showing that ML achieve better performance compared to classical models.

More precisely, in Orchard et al. (2018) the analysis leveraged a mean of 363 days of telemonitoring data from 135 patients from the Telescot COPD program (see Table 2) in order to predict the start of corticosteroid or the occurrence of hospitalisation 24 h ahead by using 15 days of observations. ML models with summary features approach were developed imputing missing values and were then compared to symptom-counting scores. The best ML models achieved AUCs of 0.74 and 0.765 when predicting the admission and corticosteroid decision respectively, outperforming the best symptoms-counting algorithm which achieved AUCs of 0.60 and 0.66 respectively for the same tasks. Thus, ML showed promise in achieving the goal of facilitating earlier interventions, although there is a need for larger datasets with which to develop more accurate algorithms.

In Ilmarinen et al. (2017), the authors used the cohort SAAS, described in Table 1, in order to construct phenotypes of adult-onset asthma by carrying out a cluster analysis with inclusion of variables from diagnosis to a 12-year follow-up visit. The study population consisted of 171 patients with new-onset asthma, and the analysis was carried out in three steps. First, factor analysis was performed to select input features. Then, Ward Hierarchical clustering was applied in order to find the optimum number of groups. Lastly, the K-means algorithm was used to create the clusters. The model identified five clusters: (i) low prevalence of rhinitis asthma, (ii) smoking asthma, (iii) female asthma with normal weight, (iv) obesity-related asthma, and (v) early-onset adult asthma. The model was then validated by carrying out K-means algorithm 10 times using a leave-one-out approach to ensure stability and repeatability. As the authors pointed out, the characterisation of a disease’s temporal phenotype using diagnostic data provides clinicians with a method of assessing the progress of the disease at an early stage, allowing to plan the most suitable treatment. Thus, these results have the potential to help clinicians better understand the prognosis of certain individuals and develop personalised therapy based on the phenotype.

3.3.2 Chronic hepatitis C (CHC)

CHC is a liver disease caused by the hepatitis C virus (HCV). It can cause serious health problems, including liver damage, cirrhosis, liver cancer (being its major cause), hepatocellular carcinoma (HCC), and even death. The WHO estimated that in 2016, approximately 399 000 people died from the consequences of CHC. Therefore, it is crucial to act promptly by administrating the correct therapy.

Konerman et al. (2015) aimed to develop a ML model to predict the stage of fibrosis progression and clinical outcomes (liver-related death, hepatic decompensation, hepatocellular carcinoma, liver transplant, or increase in Child-Turcotte-Pugh score) by incorporating longitudinal data. The dataset used consists of subjects from the Hepatitis C Antiviral Long-term Treatment Against Cirrhosis (HALT-C) randomised control trial, see Table 2. Only patients randomised to no treatment in the training set were considered, because drug therapy can have an effect on laboratory results, which in turn may impact their predictive value. In order to highlight the importance of taking into account longitudinal measures, the authors showed that LR, RF and GBM using summary features outperformed the models using only baseline data. In particular, for the task of predicting the next year fibrosis, the best models (RF and GBM with summary features) achieved an AUC of 0.86$-$0.88, which is substantially higher than prior studies (0.66). For the task of predicting clinical outcomes, the best accuracy was reached by using one year of observations’ data (0.84 with summary features RF).

Ioannou et al. (2020) focused on HCC, another common complication in patients with HCV, likely to occur post fibrosis or cirrhosis development. The authors built a model to identify high-risk patients by using 48 151 EHR patients with HCV-related cirrhosis and at least 3 years of follow-up after the diagnosis of cirrhosis. During the follow-up period 22.3% developed HCC. RNNs proved superior to LR using only baseline data and to LR based on summary features. More precisely, RNN achieved an AUC of 0.76, while cross-sectional LR achieved 0.69, and LR with summary features 0.68. The large difference in performance suggests that the used data exhibit high non-linearity and complex relationships, which are better captured by deep learning (RNNs).

3.4 Mental disorders

Mental disorders are a set of heterogeneous conditions that affect the behaviour, thinking, feeling and mood of a subject. Typical mental disorders include depression, bipolar disorder, schizophrenia and autism. Generally, the risk of suicide is markedly greater in people with a current or previous diagnosis of mental disorder than those without such a diagnosis (San Too et al. 2019). In this paragraph the focus is first placed on depression and then on the suicide issues; further details on the studies on mental disorders identified in our survey are provided in Table 8.

3.4.1 Patterns in depression trajectories

Depression is a complex and heterogeneous dynamic disease with early recognition and initiation of treatment being associated with a better outcome. However, choosing the right treatment is particularly complicated as the response varies a lot among people. In this context, being able to identify some underlying patterns of the disease could give the clinicians a quantitative understanding of the progression, which is clinically relevant for designing monitoring and treatment follow-up strategies.

Gong et al. (2019) and Lin et al. (2016) proposed approaches based on unsupervised learning to identify subgroups in the in depressed populations. Interestingly, although the methods were different, the results were in accordance, with both studies identifying five groups. Both works leveraged a common tool to monitor the level of depression, namely the Patient Health Questionnaire-9 (PHQ-9) (Kroenke et al. 2001). The PHQ-9 can be administered either by medical or trained personnel or can be self-administered, and consists of 9 multiple-choice questions referring to the previous two weeks. The authors conducted the study using person-level PHQ-9 observations included in EHR. Due to the sparsity of the data, the first step consisted in changing the longitudinal observations into continuous trajectories. More precisely, in Lin et al. (2016) the trajectory of PHQ-9 was fitted using splines, while in Gong et al. (2019), they used the Gaussian process regression proposed in Lasko et al. (2013) on both PHQ-8 (which is the questionnaire without item 9) and item 9 (which evaluates passive thoughts of death or self-injury within the last two weeks). Then, in Lin et al. (2016) the authors focused on 9306 individuals receiving ongoing treatment, with an average follow-up duration of 2.2 years. They applied three different algorithms, namely K-means with Euclidean distance, collaborative modelling (CM) and similarity-based collaborative modelling (SCM) on the coefficients of the splines, and identified five clusters: stable high, stable low, fluctuating moderate, an increasing, and a decreasing group. Statistical comparisons between the results of the three methods showed that they are not independent, but are similar. In Gong et al. (2019), the authors worked on a subset of the same sample, containing 610 patients with at least six PHQ-9 scores recorded during twenty consecutive two-week periods from the original sample. They used autoencoders to discover subtypes of depression patterns from the fitted depression trajectories, followed by an embedding in a two-dimensional space using t-Distributed Stochastic Neighbour Embedding (t-SNE) and finally K-means. By analysing the mean trajectories of average PHQ-8 and Item 9 by groups, using the clustering results they observed that three groups had a trend of decreasing PHQ-8 over time, one had a trend of PHQ-8 increasing first and then decreasing, and the last one had a trend of relative stability.

3.4.2 Suicide prevention

Death caused by suicide is a complex issue which causes pain worldwide to hundreds of thousands of people every year. According to the World Health Organization (WHO), in 2016 death by suicide represented the 1.4% of deaths worldwide, making suicide the 18th leading cause of death. Suicidal behaviour is strongly associated with mental disorders, especially with depression, substance use disorders and psychosis, however, anxiety and other disorders contribute as well. Other known risk factors are genetics, family history and socio-economic status, making it a heterogeneous and multifactorial issue. Although some risk factors have higher weights than others in statistical models (such as ANOVA and regression analysis) predicting suicide attempts, two meta-analyses (Franklin et al. 2017; Ribeiro et al. 2016) demonstrated that there is no known single risk factor or small set of risk factors being able to predict suicide more accurately than random guessing (AUCs = 0.50).

The failure of these approaches is probably related to the complex nature of suicidal behaviour, which consists of an evolving and multifactorial set of components that act together, but vary from one individual to another. Thus, ML based on longitudinal data has been proposed as an alternative that can model such complex relations and lead to increased accuracy. Nguyen et al. (2016) developed a ML model to predict suicide attempts at different time-points in the future (from 15 to 360 days). They based their study on 7 399 patients’ EHR data, who received at least one suicide risk assessment, but who did not attempt suicide. The results showed that RF, GBM, NN, sparse LR using 49 months of historical data outperformed clinicians who relied on an 18 point checklist of predefined risk factors with significant margin (AUC increased by 6% for 15-days horizon to 25% for 360-days horizon). Moreover, RF, GBM, NN outperformed LR and DT, suggesting that non-linear methods can exploit the data structure better in order to find patterns corresponding to the risk factors, achieving an AUC of almost 0.75 in the task of predicting the suicide risk one year in advance.

One limitation of the work of Nguyen et al. (2016) is that the sample is built out of patients with prior history of depression or other mental health conditions. However, for many suicide attempts, there are no prior records of psychiatric disorders. To overcome this limitation, Bhat and Goldman-Mellor (2017) used a broad heterogeneous subset of a young population (age 10–19) consisting of 5,22,056 patients records from California emergency Department. The authors developed a model that could compute an individualised risk of suicide attempt/fatality for all patients. Towards this, they used a NN with every visit stacked vertically, representing one record in the sample, including a feature which kept track of the time, employing the cumulative sum of diagnosis vectors. Since the model allowed each subject to have a different number of visits, they analysed the impact of using data from more than one visit by varying the test set from subjects who have at least one encounter to 5. As expected, the AUC steadily increased from 0.80 to 0.96 demonstrating that including repeated measures improves the performance. It should be noted that despite the fact that AUC and specificity were high, sensitivity of the model was lower (0.703). This is due to the high imbalance of the dataset with only 2.59% of cases corresponding to subjects with suicidal attempts. To tackle this recurrent problem in chronic disease modelling, Zheng et al. (2020) applied bootstrapping to a sub-cohort of subjects with mental illness to increase the disease incidence from 0.21 to 5%. Overall, ML models using temporal data from EHRs are able to identify high-risk individuals to attempt suicide better than classical models, and therefore, could easily be translated into routine medical care practice.

Table 8 Selected studies in the domain of mental disorders

3.5 Hospital emergency

In the context of hospital emergencies, ML algorithms can serve as a useful auxiliary tool for clinicians by making short-term, dynamic predictions. In particular, three broad categories in which the use of ML comes in handy, have been identified: monitoring patients in intensive care units (ICUs), minimising unplanned hospital readmission, and prevention of hospital acquired infections (HAIs). Details on the studies on hospital emergencies identified in our survey are summarised in Table 9.

3.5.1 ICU monitoring

Patients in ICUs suffer from serious health problems, requiring urgent care and constant monitoring to avoid further complications. This implies that the assessments of cardiovascular, respiratory and metabolic variables must be extremely frequent, if not continuous, to allow early identification of adverse trends and prompt therapeutic intervention. In order to better exploit this rich multi-source information, recent studies suggested the use of ML over classical scoring systems (Meyer et al. 2018; Vellido et al. 2018). The latter include SAPS (Le Gall et al. 1993), APACHE (Knaus et al. 1985), SOFA (Vincent et al. 1996), and qSOFA (Seymour et al. 2016) which are common for evaluating morbidities in the ICU. However, one challenge in developing models for ICU subjects is the nature of the data: episodes vary in length, stays range from a few hours to multiple months; observations are heterogeneous coming from sensor data, vital signs, laboratory test results, and subjective assessments; acquisition is irregular and plagued by missing values; long-term temporal dependencies complicate learning with many algorithms. Therefore, the majority of ML studies within the ICU framework are based on RNNs as they can leverage multiple variables and permit dynamic integration allowing to incorporate temporal trends of those variables.

The authors in Verplancke et al. (2010), as a proof of concept, adopted an echo-state network (ESN) for predicting the need for dialysis in the ICU. Using diuresis values and creatinine levels of the first three days after admission of 830 patients, they predicted the need for dialysis between day 5 and day 10 of ICU admission achieving an AUC of 0.82. Comparing the performance with SVM and NB algorithms they achieved 0.83 and 0.85 AUCs. However, SVM and NB required almost 5 h of computation time, while the ESN only 2 s.

Another important work in this field is that of Meyer et al. (2018) who developed three models to predict complications in postoperative cardiac surgery care, i.e., mortality, renal failure with a need for renal replacement therapy, and postoperative bleeding, in a real world setting. First, the authors used EHR data from a German tertiary care for training and testing and, then, externally validated their approaches on the MIMIC-III dataset, an openly available dataset developed by the MIT Lab.³ More precisely, they proposed a many-to-many GRU architecture, where measurements of dynamic clinical markers were collected at 30-min intervals and used as an input. The outcome was the probability of the occurrence of the corresponding complication after 24 h from the open-heart surgery. For the first dataset, they selected 9269 patients corresponding to 11,492 admissions. They achieved a high performance, particularly in comparison to the clinical reference tool: AUC of 0.87 vs. 0.58 for bleeding, 0.95 vs. 0.71 for mortality, 0.96 vs. 0.73 for renal failure. In addition to this, they analysed the trend of the model over time. As expected, the model’s accuracy increased with the addition of more time-points until reaching the highest value. This happened at different time-points depending on the type of complication, e.g., bleeding prediction required data from longer times (several hours) to achieve maximum performance, while mortality and renal failure could be predicted with high accuracy almost immediately after admission to the ICU. Predictions with RNNs were more accurate compared to those of humans for every time step considered. The external validation on the MIMIC dataset resulted in a lower performance: AUC of 0.75 vs. 0.66 for bleeding, 0.82 vs. 0.63 for mortality, 0.91 vs. 0.66 for renal failure.

3.5.2 Unplanned readmission emergency

Emergency hospital admissions are associated with significant costs to the medical system and put patients at risk of hospital-acquired infections and clinical errors (Felix et al. 2015). Given the avoidable nature of a large number of such admissions, there has been a growing research and policy interest in effective ways of averting them. Traditionally, approaches based on classical methods, such as linear predictors using static information, are adopted. Nonetheless, these methods tend to have a poor ability to predict re-admissions (Aramide et al. 2016; Kansagara et al. 2011). The failure suggests the presence of complex relationships and the importance of taking into account time varying variables.

Leveraging the richness of longitudinal data, ML has been proposed in an effort to obtain better insights and achieve more accurate predictions. In this direction, Rahimian et al. (2018) tested the hypothesis that the predictive ability of ML models is stronger than that of conventional models when outcomes in the more distant future are to be predicted, as they are able to better capture multiple known and unknown interactions. To this end, they used EHR data of 4.6 million of patients with at least 1 year of registration with a general practice. Conducting several experiments with different prediction windows (readmission occurring within 12, 36, 48, and 60 months), they compared GBM and RF with Cox proportional hazards (CPH), a well-known regression model commonly used in statistical medical research, using different sets of predictors. The first set consists of 43 variables from the established QAdmissions model. In the second set, 13 predictors such as comorbidities and the number of general practices in the year before baseline, were added. Lastly, for constructing the third set, they changed some predictors of the second configuration in order to hold more accurate temporal information, i.e. instead of binary variables for the occurrence of an event, they included the time since that event had happened. ML models outperformed CPH for every set of variables and every prediction window. Moreover, all three models achieved higher performance with the third set of variables. Interestingly, the accuracy of GBM increased over time, achieving an AUC of 0.86 for 60 months. These experiments confirm again that ML can outperform classical models. Besides, the fact that the best performance was always achieved using the third set of summarised variables indicates that the way of aggregating the observations impacts the final result in the same way the choice of variables affects the performance when summary features are used.

Similarly, in Ashfaq et al. (2019) also dealt with the problem of readmission using longitudinal ML. However, they focused on identifying congestive heart failure (CHF) high-risk patients with a potential 30-day readmission at the time of discharge, which commonly occurs in 1 out of 4 patients. Precisely, they built a model with human-derived features based on relevant medical literature and machine-derived contextual embeddings of the clinical codes. Furthermore, they modelled the sequential visits occurring within a time-frame of 6 months after the first admission to the hospital by means of a LSTM architecture in a cost-sensitive classification framework. The approach permitted to adequately deal with class imbalance. For the evaluation, they used two strategies for splitting the dataset into testing and training. First, splitting was preformed by applying a simple 70% (training) - 30% (testing) rule with no additional criteria, but ensuring that data of a subject is only used once, i.e. either for training or testing. According to the second strategy, splitting was based on time, i.e. data from 2012 to 2015 were used for training, while testing was performed on the complete set, i.e. from 2012 to 2016. An AUC of 0.77 and 0.83 was achieved respectively. Nonetheless, when using splitting on time, there exists the risk of data leakage and the results is less generalisable. Last, but not least, they showed that selectively offering an intervention to patients at high risk of readmission identified by their model, could lead to 22% of maximum possible annual cost savings. Overall, deployment of such a model in clinical practice would enable physicians to monitor patient risk scores and take the necessary actions on time to avoid unplanned admissions.

3.5.3 Hospital acquired infections (HAI)

Also known as nosocomial infections, HAIs are a subset of infectious diseases acquired 48 h after admission to the hospital. The impact of HAIs is not only seen at the individual patient level, but also at the community level, as they have been linked to multidrug-resistant infections. Identifying patients with risk factors for HAIs and multidrug-resistant infections is very important for the prevention and minimisation of these infections (Lobdell et al. 2012).

In this context, two works (Wiens et al. 2016; Oh et al. 2018) focus on Clostridium difficile infection (CDI), which usually affects people who have recently been treated with antibiotics and have low immune defences. The disease is often contracted in the hospital setting, is very contagious and is considered one of the most common HAIs. Both works aimed at providing daily predictions of the risk of CDI, as the risk is likely to change over the course of hospitalisation. Once the predicted risk exceeded a certain threshold, considered as dangerous, they stopped the predictions. Both works implemented a multi-task learning (MTL) approach, i.e., they modelled every day as a different task and they learnt the time-specific models jointly, by using L2-regularised LR, which has the advantage of being simple. The prediction of every day was then obtained by a cumulative moving average, in order to account for the information contained in the evolution of patient risk. In particular, Wiens et al. (2016) leveraged 50,000 EHR patients to obtain an AUC value of 0.81 in the held-out test set. Approximately half of these cases were correctly identified; cases could be identified at least one week in advance of their positive CDI diagnosis.

In addition to this, Wiens et al. compared the performance of this approach with the simple Stacked-Vertically features and with a model considering the different tasks, but learning these independently. Interestingly, the first two models performed almost identically on the test set, while the multi-task approach with an independent optimisation for each model had the worst performance (AUC = 0.80). This probably implies that the developed model failed to leverage the entire sample and relationships. Besides, when they divided the patients in the test set based on the length of the risk period, their approach performed better compared to the other two, which is preferable as they could lead to an early intervention.

Another common HAI is surgical site infection (SSI). SSI occurs up to 30 days after surgery in the part of the body where the surgery took place. It represents up to 30% of all hospital acquired infections and is associated with considerable morbidity and mortality. Thus, in Soguero-Ruiz et al. (2015), Soguero et al. used blood tests trajectories of 1005 subjects, routinely used in the clinic and pose minimal burden to the patients, to predict SSI risk both pre- and post-operatively (0.88 and 0.90 AUC respectively). By means of this approach, they demonstrated that there is the potential for real-time prediction and identification of patients at risk for developing SSI. Moreover, it was shown that non-linear classifiers performed consistently better than linear models.

Table 9 Selected studies in the domain of hospital-related emergencies

4 Discussion and conclusions

4.1 Current challenges and limitations

The analysis of longitudinal biomedical data using machine and deep learning presents undoubtedly great opportunities for medical care. Nonetheless, there are several challenges to tackle related to the nature of both biomedical and longitudinal data.

First, challenges are posed by the modelling of the problem as there are multiple decisions to take and compare: how to model the population (i.e., building a suitable dataset for training and testing), formulate the respective tasks to be solved, and select an appropriate algorithm. The best choice usually depends on the available data and it is not known a priori. Thus, several comparisons need to be performed. As an example, even if RNNs seem to be the ones achieving the best performance in many real world applications presented in this review, a sufficiently large sample is necessary for their application. Regarding the modelling stage, another decision to take is regarding the size of the observation window. Contrary to what one might have anticipated, including a longer time interval does not always lead to an increase in performance (see Sect. 3). This could be explained by the fact that the target outcome in the future could be weakly correlated with features too distant in time and by the risk of over-fitting due to the introduction of many variables (especially for non-sequential longitudinal methodology).

Missing values represent another challenge, being often present in longitudinal studies, which complicates the building of suitable ML models. Even though discarding these values is the simplest strategy for tackling the problem, it is usually not a good option as it can lead to a reduction in model performance. Alternatives for handling missing data require pre-processing techniques or ad hoc models, which increase the complexity of the problem.

Other challenges arise from the nature of longitudinal biomedical data. First, they can be extremely heterogeneous, with different types of data in the same study (images, text, or numerical values), each requiring its own processing technique. This motivated the investigations of models capable of handling multi-source and multi-modality data (Lee et al. 2019a). Moreover, due to the nature of particular diseases, often data cohorts are highly unbalanced as seen in Sect. 3. In such situation, models can have poor predictive performance for the minority class, which is yet often the most important class. Although a straightforward and common solution is to apply under-sampling, this is not an ideal option, as this means much of the existing data is not exploited. Other possible solutions include over-sampling, penalised models or data synthesis.

Last, ML models are often referred to as black-box models, as the processes between input and output variables are difficult to comprehend, especially for non-experts. The lack of natural explainability of ML models is even more pronounced in the case of longitudinal models as they are associated with increased complexity. There is a need to develop explainable ML method specifically for longitudinal biomedical data to ensure the clinicians can understand the ML-derived predictions and trust the recommendations in real world practice. However, it should be emphasized that even if explainability methods may not always be able to reassure the correctness of an individual decision, this should not necessarily prevent the beneficial use of ML in the healthcare. Instead, as suggested by Ghassemi et al. (2021), the use of high-performance ML models should be based primarily on their thorough internal and external validation.

Nonetheless, this is not currently the case with a significant amount of research on ML models being based on single center-studies, completely missing external validation. This fact along with other limitations of the study design (Kelly et al. 2019) hinder the adoption of ML models in the clinic. In particular, most of the studies did not consider important aspects such as: (i) external validation of the results based on independent data sources to avoid over-optimistic predictions; (ii) fairness analysis to prevent the derivation of biased models against underrepresented subgroups; (iii) usability of the model, ensuring practical implementation; (iv) effective results reports with intuitive explanations of model decisions; (v) the impact of possible data drifts on models degradation trough time. These issues limit the trustworthiness of the developed models, which partly explains why only 221 AI-based medical products have received FDA approval as of April 2023 Central (2023).

To bridge the gap between ML model development and deployment in the clinic, it is crucial to ensure that these models comply with current guidelines and recommendations (de Hond et al. 2022; Lekadir et al. 2021). Last but not least, for ML models to be adopted in clinical settings, their acceptance and trust must involve not only the healthcare community, but also patients and the entire population that will interact with the ML tools. Addressing these concerns is crucial for developing trustworthy ML models and promoting their safe and effective use in clinical practice (Asan et al. 2020; Banerjee et al. 2022).

4.2 Future perspectives

Despite the challenges, the enormous potential of exploiting longitudinal data with machine learning has been demonstrated in this survey through a comprehensive list of use case applications.

By comparing single instance-based models with those introducing repeated measures, several researchers have shown the improvement obtained by modelling historical information (see Sect. 3). This is in accordance with the way clinicians work; by analysing historical data in medical records they can understand better the patient’s trajectory and take more suitable clinical decisions.

In addition to this, several of the studies revealed that machine learning typically outperforms classical methods for prediction tasks, especially in the presence of big data and when using deep learning based methods. This can be explained by the fact that humans and classical algorithms may fail to capture all the non-linear relations between the factors that contribute to the development or progression of a disease. On the other hand, several machine learning models can autonomously capture highly complex relationships among variables, going far beyond traditional additive and linear models.

For these reasons, the number of studies based on ML for longitudinal biomedical data are expected to continue to grow. However, given the current challenges and limitations, we highlight two major directions for future research: (i) the construction of robust models, therefore well-generalisable and not affected by bias, and (ii) explainable machine learning for multifactorial longitudinal data.

Regarding the first, it is important to focus on building ad hoc models adapted to real world data, by addressing noisy and missing values, and by implementing solutions for the problem of class imbalance. More generally, it is necessary to conduct new longitudinal models in line with current guidelines and recommendations (de Hond et al. 2022). Regarding the second direction, researchers should develop explainable ML models for longitudinal data that enable clinicians to understand better the predicted health and disease trajectories (Arrieta et al. 2020; Adadi and Berrada 2018). In addition, for ML models to be implemented in clinics, their acceptance and trust must involve not only the healthcare community, but also patients and the entire population that will interact with the ML tools (Asan et al. 2020; Banerjee et al. 2022).

4.3 Conclusions

This article is intended as a unique resource to guide data scientists and clinical researchers working in the field of ML-focused longitudinal studies. The review comprises a detailed presentation and critical analysis of the available algorithms. Researchers can use these technical presentations to understand the whole workflow and the different options for building longitudinal ML models, and to determine the best ML implementation and strategy for their use case given the strengths and limitations of the different machine and deep learning algorithms. Furthermore, the paper lists in great detail a wide range of applications in medicine, such as in cardiology, neurology, mental health and emergency medicine. This shows great promise for future applications, and provides insights into approaches that can be pursued in other domains to design, develop and evaluate ML-driven clinical tools that can be used by clinicians to better assess and anticipate specific patient trajectories and outcomes. Building on the achievements reviewed in this paper, and with the increasing availability of large-scale longitudinal cohorts from real-world clinical registries, we except the field to continue to grow in the years to come, both technically (e.g., explainable longitudinal ML) and clinically to improve healthcare delivery and medicine outcomes in the age of personalised medicine.