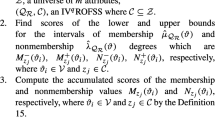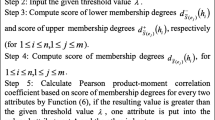Parameter reduction analysis under interval-valued m-polar fuzzy soft information

Abstract

This paper formalizes a novel model that is able to use both interval representations, parameterizations, partial memberships and multi-polarity. These are differing modalities of uncertain knowledge that are supported by many models in the literature. The new structure that embraces all these features simultaneously is called interval-valued multi-polar fuzzy soft set (IVmFSS, for short). An enhanced combination of interval-valued m-polar fuzzy (IVmF) sets and soft sets produces this model. As such, the theory of IVmFSSs constitutes both an interval-valued multipolar-fuzzy generalization of soft set theory; a multipolar generalization of interval-valued fuzzy soft set theory; and an interval-valued generalization of multi-polar fuzzy set theory. Some fundamental operations for IVmFSSs, including intersection, union, complement, “OR”, “AND”, are explored and investigated through examples. An algorithm is developed to solve decision-making problems having data in interval-valued m-polar fuzzy soft form. It is applied to two numerical examples. In addition, three parameter reduction approaches and their algorithmic formulation are proposed for IVmFSSs. They are respectively called parameter reduction based on optimal choice, rank based parameter reduction, and normal parameter reduction. Moreover, these outcomes are compared with existing interval-valued fuzzy methods; relatedly, a comparative analysis among reduction approaches is investigated. Two real case studies for the selection of best site for an airport construction and best rotavator are studied.

1 Introduction

Interval representations, parameterizations, partial memberships and multi-polarity are various modalities of uncertain knowledge. They have been combined in a myriad of forms in the literature (Akram et al. 2018; Alcantud et al. 2020b; Atanassov 1986; Chen et al. 2014; Jiang et al. 2010; Maji et al. 2001; Molodtsov 1999; Roy and Maji 2007; Yang et al. 2009; Zadeh 1965). The main purpose of this paper is the formalization of a model that takes all these features into account. We call it interval-valued multi-polar fuzzy soft set, also interval-valued m-polar fuzzy soft set or IVmFSS for short. Then we prove its versality with several theoretical and applied developments, inclusive of fundamental operations, parameter reductions, and applications to decision-making.

Soft set theory (Molodtsov 1999) was designed to overcome the lack of parameterization tools in traditional uncertainty theories, including probability theory (Varadhan 2001), fuzzy set theory (Zadeh 1965), intuitionistic fuzzy set theory (Atanassov 1986), and rough set theory (Pawlak 1982). However, the theory of soft sets is not a generalization of previous mathematical theories: the concept behind the production of soft sets is strikingly different from classical models for handling uncertainties. Real and potential applications of soft set theory have been reported in different domains such as game theory, decision-making, measurement theory, medical diagnosis, etc.

The inception of soft sets inspired numerous researchers who were attracted by this powerful idea, for example, for the purpose of studying its fundamentals, hybrid structures or its interactions with other disciplines. In this way basic properties of soft set theory were presented by Maji et al. (2003). Ali et al. (2009) argued that some features of soft sets discussed in (Maji et al. 2003) were not true in general. They thus produced some novel formal properties of soft sets and verified the applicability of De Morgan’s laws for soft sets.

Maji and Roy (2002) solved a decision-making problem based upon soft sets. In their analysis they realized that in a given problem whose structure pertains to soft set theory, there might exist one or more parameters that have no effect on the optimal decision. Such parameters may be safely removed from the dataset in order to reduce the simulation cost. Accordingly they took advantage of the idea of attribute reduction in rough set theory ( Pawlak 1982) in order to launch the investigation of parameter reduction in soft set theory. Several additional investigations on the reduction of parameters in soft sets have been reported. For instance, Chen et al. (2005) and Kong et al. (2008) launched parameterization and normal parameter reductions for soft sets, respectively, to overcome the deficiencies of decision-making applications in (Maji and Roy 2002). Ma et al. (2011) developed a novel efficient normal parameter reduction method in order to further improve (Chen et al. 2005; Maji and Roy 2002; Pawlak and Skowron 2007). Following their strategy, Ali Ali (2012) introduced an alternative approach for the reduction of parameters in soft sets. Now a practical distinction is in order. In normal parameter reduction approaches, the reduction set in a given problem can be reused when the expert needs to add some new parameters. However this is not the case of parameter reduction based on optimal choice, as it relies on the preservation of the the decision object. The application scope of parameter reduction based on optimal choice is wider than the former case, but this comes at the cost of a natural inconvenience: when new parameters are added to the set of parameters, an altogether new reduction process is needed, because the optimal object may have changed. In short, the reduction set cannot be reused in the case of parameter reduction based on optimal choice when new parameters are added to the required set of parameters. Clearly we find the same difficulty in rank based parameter reduction, for it keeps the ranking order of all objects.

Soft set theory developed beyond the original formulation soon. Roy and Maji Roy and Maji (2007) proposed a more general model, namely, fuzzy soft sets, which allows to model and solve a different sort of decision-making cases. Alcantud et al. (2017) presented an alternative approach to solve decision-making problems based on fuzzy soft sets. The idea of attributes reduction has also received considerable attention by many researchers in the analyses of fuzzy soft sets and its extensions. For example, Feng et al. (2010b) proposed the idea of parameter reduction of fuzzy soft sets based on concept of level soft sets. With the help of level soft sets in an intuitionistic fuzzy environment, Jiang et al. (2011) developed a reduction approach for the intuitionistic fuzzy soft set model that had been introduced by Maji et al. (2001), Maji et al. (2004). The combination of the soft set and interval-valued fuzzy set models (Deschrijver and Kerre 2003; Gorzalczany 1987) prompted Yang et al. (2009) to present interval-valued fuzzy soft sets (IVFSSs). Following their approach, Feng et al. (2010a) proposed an alternative way to solve decision-making problems with IVFSS data. And Ma et al. (2014) developed different parameter reduction techniques for IVFSSs. On another note, Kong et al. (2020) proposed three types of attribute reducts for multi-granulation information systems, and Akram et al. (2020) presented parameter reduction method of N-soft sets (Fatimah et al. 2018) and studied its applications to decision-making.

Most of the real world problems ranging from medical to social fields involve bipolar information: artificial vs. natural, profit vs. loss, et cetera, are normally two facets in different decision-making situations. For instance, an expert panel voted on December 10, 2020 in the United States to recommend that the F.D.A. (Food and Drug Administration) authorize a vaccine developed by the German company BioNTech and the American company Pfizer. Efficacy and fast-track approval are accompanied by potential safety issues and erosion of public trust. Although there were benefits and risks, the committee decided the former outweighed the later.¹ Based on this fact, in 1994, Zhang (1994) was the first who presented a formalization of the idea of bipolar fuzzy sets (YinYang bipolar fuzzy sets). They are a natural extension of fuzzy sets because in bipolar fuzzy sets, the membership value range is extended from [0, 1] to $[-1, 1]$. In other words, Yin and Yang represents the two opposite parts of a phenomenon. Yin is the negative part while Yang is the positive part. From inspection of the research of the past two decades, one can easily observe that there exist many applications of bipolar fuzzy sets (and its hybrid models with other uncertainty theories) in several domains, including artificial intelligence systems. For example, Ali et al. (2019) explored an alternative technique to solve decision-making problems based upon bipolar fuzzy soft sets and investigated certain reduction approaches for them. In addition, Ali et al. (2020) developed attribute reduction methods in bipolar fuzzy relation decision systems, and they also produced applications to decision-making.

But nowadays, scientists accept the fact that many real world problems contain or are affected by multipolar information. Therefore there is a need for innovative mathematical models in this domain. Motivated by this concern, Chen et al. (2014) introduced the concept of mF sets as an extension of bipolar fuzzy sets. In an mF set, the membership interval range of an alternative is extended to $[0, 1]^m$, which allows the practitioner to capture all the m distinct characteristics of an alternative. However in some multipolar situations, it is still not possible to represent the various membership degrees of an alternative by a precise number. That is, even at the level of mF sets, intervals may be more suitable than exact membership degrees. This issue has recently prompted Mahapatra et al. (2020) to introduce IVmF sets as an extension of mF sets. They discussed the applications of this model in graph theory as well.

At this point, the criticism was raised that there are many real-world decision-making problems involving IVmF information which cannot be solved due to the lack of a convenient parameterization tool. For instance, suppose the metro stations of China and we want to give membership degree on the basis of criteria as follows: the capacity of metro trains that can travel in the metro station in a month and the ticket fare of journey. No doubt, the above mentioned notions contain uncertainty because the number of visits on the metro station in a month may vary and the ticket fare is also not unique. Thus in both of these situations, a novel hybrid model is needed because IVmF sets (Mahapatra et al. 2020) are not useful to deal with these types of situations in the presence of different parameters.

Motivated by all these factors, the aim of this research article is to produce a framework to deal with IVmF soft information involving vagueness and imprecision in a parameterized setting. We introduce a novel hybrid model that combines the advantages of both IVmF sets (Mahapatra et al. 2020) and soft sets (Molodtsov 1999), and we call it IVmFSS. Actually, IVmFSS theory developed in this research article can be viewed both as a multipolar generalization of the IVFSS model (Yang et al. 2009), as an IVmF generalization of the soft set model (Molodtsov 1999), or as an interval-valued generalization of the mF soft set model ( Akram et al. 2018). The reason is that the IVmFSS model here proposed is based on all mF soft sets, IVmF sets, and IVFSSs. Further, three parameter reduction approaches for this novel hybrid model are presented along with their algorithms. Moreover, two real case studies (this is, an airport site selection and selection of rotavator) are explored. Finally, a comparison of the proposed model with some existing interval-valued fuzzy methods is discussed, and a comparative analysis among the reduction approaches is also provided.

For more useful notions not discussed in the article, the readers are suggested to refer to (Adeel et al. 2020; Akram 2019; Alcantud et al. 2020a; Ali and Akram 2020; Danjuma et al. 2017; Deng and Wang 2012; Jiang et al. 2010; Perveen et al. 2019; Zhan and Alcantud 2019; Zhang 2013; Kumar and Mohanraj 2017; Prasad 1996).

The structure of this research article is as follows. Section 2 first recalls some definitions like soft sets, mF sets, mF soft sets and IVmF sets. Then it presents the concept of IVmFSS and briefly discusses the basic operations in their context. Numerical examples help to understand all the new concepts. Section 3 studies the three parameter reduction approaches for the new hybrid model. Section 4 explores two real case studies of an airport site selection and rotavator selection and it contains a solution of these critical problems by the methodology of IVmFSSs and their parameter reduction techniques. Section 5 discusses a comparative analysis among the reduction approaches, and it also investigates a comparison of the proposed model with some existing interval-valued fuzzy methods. Finally in Sect. 6, we provide the conclusions and future research directions.

2 Interval-valued mF soft sets

This section firstly recalls some basic notions briefly, including soft set and IVmF sets which are very helpful in the remaining study of the paper. Secondly, IVmFSS model is presented with its basic properties and decision-making mechanism.

Definition 1

(Molodtsov 1999) Let U be an initial universal set and Z be a set of parameters related to the objects of the universe. Let $C\subseteq Z$ then a soft set $(\psi ,C)$ is defined as below:

$$\begin{aligned} (\psi ,C)=\{(c,\psi (c))~|~c\in C, \psi \in P(U)\}, \end{aligned}$$

where $\psi :C\rightarrow P(U)$ is a mapping where P(U) denotes the collection of all subsets of U.

Definition 2

(Chen et al. 2014) A function $A: U \rightarrow [0,1]^{m}$ is called an mF set (or a $[0,1]^{m}$-set ) and it is represented as (U, A) where $A=\left( p_{1} \circ A, p_{2} \circ A, \ldots p_{m}\right.$ o A ) and $p_{i} \circ A$ is the $i^{t h}$ part of A.

Definition 3

(Akram et al. 2018) Let U be an initial universe, Z a set of parameters and $C\subseteq Z$. Then, a pair $(\gamma , C)$ is said to be an mF soft set on U, which is given as below:

$$\begin{aligned} (\gamma , C)=\{(u, p_i\circ C_{\epsilon }(u)):u\in U ~ \text {and} ~\epsilon \in C\}. \end{aligned}$$

Let ${\tilde{M}}=\left[ M_{L}, M_{U}\right]$ be an interval number where $0 \le M_{L} \le M_{U} \le 1 .$ We denote the collection of all sub-intervals of the closed interval [0, 1] by D[0, 1] . If both the lower and the upper bound of an interval are same, that is, [M, M], then $M \in [0,1].$ For interval numbers ${\widetilde{M}}_{i}=\left[ M_{L_{i}}, M_{U_{i}}\right] \in D[0,1], i\in \{1,2, \ldots \}={\mathbb {N}}$ define $i n f {\widetilde{M}}_{i}=\left[ \wedge _{i \in {\mathbb {N}}} M_{L_{i}}, \wedge _{i \in {\mathbb {N}}} M_{U_{i}}\right]$ and $\sup {\widetilde{M}}_{i}=\left[ \vee _{i \in {\mathbb {N}}} M_{L_{i}}, \vee _{i \in {\mathbb {N}}} M_{U_{i}}\right]$. For three interval values ${\widetilde{M}},~{\widetilde{M}}_1,~{\widetilde{M}}_2$, we have

• 1. ${\widetilde{M}}_{1} \le {\widetilde{M}}_{2} \Leftrightarrow M_{L_{1}} \le M_{L_{2}}$ and $M_{U_{1}} \le M_{U_{2}}$.

• 2. ${\widetilde{M}}_{1}={\widetilde{M}}_{2} \Leftrightarrow M_{L_{1}}=M_{L_{2}}$ and $M_{U_{1}}=M_{U_{2}} .$

• 3. ${\widetilde{M}}_{1}<{\widetilde{M}}_{2} \Leftrightarrow {\widetilde{M}}_{1} \le {\widetilde{M}}_{2}$ and ${\widetilde{M}}_{1} \ne {\widetilde{M}}_{2}$.

• 4. $k {\tilde{M}}=\left[ k M_{L}, k M_{U}\right] ,$ where $0 \le k \le 1$

Definition 4

(Mahapatra et al. 2020) An IVmF set $\zeta$ in U is a function $\zeta : U \rightarrow D[0,1]^{m},$ which is defined as follows:

$$\begin{aligned} \zeta =\Big \{\big (a,\langle \left[ M_{L_{1}(a)}, M_{U_{1}(a)}\right] ,\left[ M_{L_{2}(a)}, M_{U_{2}(a)}\right] ,\left[ M_{L_{3}(a)}, M_{U_{3}(a)}\right] \ldots \left[ M_{L_{m}(a)}, M_{U_{m}(a)}\right] \rangle \big )~|~a\in U\Big \} \end{aligned}$$

where $M_{L_{i}(a)}$ and $M_{U_{i}(a)}$ are the lower and upper limits of the $i^{t h}$ interval of the element a.

Now we develop a novel MCDM model called IVmFSSs and investigate its fundamental properties with examples.

Definition 5

Let U be a nonempty universe and Z be a set of parameters. For any $C\subset Z$, a pair $(\eta , C)$ is called an interval valued mF soft set or IVmFSS of U which is given as follows:

$$\begin{aligned} (\eta ,C)=\{\langle c,\eta (c) ~|~c\in C\rangle \}, \end{aligned}$$

(1)

where $\eta (c)$ is an IVmF subset of U, for all $c\in C$. In other words,

$$\begin{aligned} \eta (c)=\Big \{\big (u,\langle \left[ M_{L_{1}(u)}, M_{U_{1}(u)}\right] ,\left[ M_{L_{2}(u)}, M_{U_{2}(u)}\right] ,\left[ M_{L_{3}(u)}, M_{U_{3}(u)}\right] \ldots \left[ M_{L_{m}(u)}, M_{U_{m}(u)}\right] \rangle \big )~|~u\in U\Big \}. \end{aligned}$$

Let $U=\{\textit{u}_1,\textit{u}_2,\cdots ,\textit{u}_n\}$ be a universe having ‘n’ objects, and $C=\{\textit{c}_1,\textit{c}_2,\cdots ,\textit{c}_r\}$ be a set of parameters. Then, the tabular arrangement of an IVmFSS $(\eta ,C)$ is given below (see Table 1).

Table 1 Tabular form of the IVmFSS $\eta ,C)$

Example 1

Let $U=\{u_1,u_2,\ldots ,u_5\}$ be a set of five hotels and $Z=\{c_1=\mathrm{material},c_2=\mathrm{location},c_3=\mathrm{beauty},c_4=\mathrm{price}\}$ be a universe of parameters and $C=\{c_1,c_3,c_4\}\subseteq Z$. These parameters are further characterized as follows.

• The parameter “Material” includes wooden, aluminum and concrete.

• The parameter “Location” includes centrality, neighborhood and commercial development.

• The parameter “Beauty” includes landscape, furniture and wall decorations.

• The parameter “Price” includes cheap, costly, very costly.

Then, the tabular representation of an IV3FSS $(\eta , C)$ is displayed in Table 2.

Table 2 Tabular form of the IV3FSS $(\eta ,C)$

From Table 1, one can easily see that the evaluations for every object regarding parameters are not clear unless the lower and upper bounds of these evaluations are provided. For instance, one cannot describe the exact membership value about wooden material used in the hotel $\textit{u}_1$ in the first pole of first cell of Table 2, that is, the least membership degree bound regarding wooden material is 0.6 and most membership degree bound is 0.8.

Definition 6

Let $(\eta , C)$ be an IVmFSS over a universe U and $\eta (c)$ be the IVmF set of parameter c, then a set of all IVmF sets in IVmFSS $(\eta , C)$ are called IVmF class of $(\eta , C)$, and is denoted by $Cl_{(\eta ,C)}$, then

$$\begin{aligned} Cl_{(\eta ,C)}=\{\eta (c)~|~c\in C\}. \end{aligned}$$

Example 2

Consider Example 1, then $Cl_{(\eta ,C)}=\{\eta (c_1),\eta (c_3),\eta (c_4)\}$, where

$$\begin{aligned} \eta (c_1)&=\big \{\big (u_1,\big \langle [0.6,0.8],[0.2,0.4],[0.5,0.7] \big \rangle \big ),\big (u_2,\big \langle [0.4,0.6],[0.7,0.9],[0.2,0.5]\big \rangle \big ),\\ {}&~~~~\big (u_3,\big \langle [0.7,0.9],[0.5,0.6],[0.3,0.8]\big \rangle \big ),\big (u_4,\big \langle [0.1,0.3],[0.9,1.0],[0.7,0.8]\big \rangle \big ),\\ {}&~~~~\big (u_5,\big \langle [0.5,0.7],[0.6,0.9],[0.2,0.4]\big \rangle \big )\big \},\\ \eta (c_3)&=\big \{\big (u_1,\big \langle [0.5,0.6],[0.7,0.8],[0.5,0.9]\big \rangle \big ),\big (u_2,\big \langle [0.5,0.7],[0.4,0.6],[0.1,0.4]\big \rangle \big ),\\ {}&~~~~\big (u_3,\big \langle [0.1,0.5],[0.3,0.7],[0.7,1.0]\big \rangle \big ),\big (u_4,\big \langle [0.2,0.4],[0.5,0.8],[0.4,0.8]\big \rangle \big ),\\ {}&~~~~\big (u_5,\big \langle [0.1,0.3],[0.7,0.9],[0.2,0.5]\big \rangle \big )\big \},\\ \eta (c_4)&=\big \{\big (u_1,\big \langle [0.7,0.9],[0.1,0.3],[0.8,1.0]\big \rangle \big ),\big (u_2,\big \langle [0.8,1.0],[0.6,0.8],[0.3,0.5]\big \rangle \big ),\\ {}&~~~~\big (u_3,\big \langle [0.5,0.8],[0.3,0.5],[0.4,0.6]\big \rangle \big ),\big (u_4,\big \langle [0.3,0.6],[0.1,0.4],[0.7,0.9]\big \rangle \big ),\\ {}&~~~~\big (u_5,\big \langle [0.4,0.7],[0.2,0.6],[0.6,0.8]\big \rangle \big )\big \}. \end{aligned}$$

Definition 7

Let U be a universal set, Z be a universe of parameters and $C_1,C_2 \subseteq Z$. For two IVmFSSs $(\eta _1,C_1)$ and $(\eta _2,C_2)$, we say that $(\eta _1,C_1)$ is called the IVmF soft subset of $(\eta _2,C_2)$ and is denoted by $(\eta _1,C_1)\Subset (\eta _2,C_2)$ if

• 1. $C_1 \subseteq C_2$,

• 2. $\eta _{1}(c)$ is an IVmF subset of $\eta _{2}(c),$ for all $c\in C_1$.

Here, IVmFSS $(\eta _2,C_2)$ is called an IVmF soft super-set of IVmFSS $(\eta _1,C_1)$.

Example 3

Consider Example 1, where $U=\{u_1,u_2,\ldots ,u_5\}$ is a set of five hotels. Let $C_1=\{c_2=\mathrm{location}, c_4=\mathrm{price}\}$ and $C_2=\{c_2=\mathrm{location}, c_3=\mathrm{beauty}, c_4=\mathrm{price}\}$ be two subsets of Z. Then, two IV3FSS $(\eta _1,C_1)$ and $(\eta _2,C_2)$ are given by Tables 3 and 4 , respectively.

Table 3 Tabular form of the IV3FSS $(\eta _1,C_1)$

Table 4 Tabular form of the IV3FSS $(\eta _2,C_2)$

Clearly, $C_1\subseteq C_2$ and for all $c\in C_1$, $\eta _1(c)$ is the IVmF subset of $\eta _2(c)$. Thus, $(\eta _1,C_1)\Subset (\eta _2,C_2)$.

Definition 8

Two IVmFSSs $(\eta _1,C_1)$ and $(\eta _2,C_2)$ over a universal set U are called equal IVmFSSs if

• 1. $(\eta _1,C_1)$ is an IVmF soft subset of $(\eta _2,C_2)$.

• 2. $(\eta _2,C_2)$ is an IVmF soft subset of $(\eta _1,C_1)$.

It is denoted by $(\eta _1,C_1)=(\eta _2,C_2)$.

Definition 9

The complement of an IVmFSS $(\eta ,C)$ over a nonempty universe U is represented by $(\eta ,C)^{\sim }=(\eta ^{\sim },\lnot C)$, which is given as

$$\begin{aligned} (\eta ,C)^{\sim }=(\eta ^{\sim },\lnot C)=\{\langle \lnot c,\eta ^{\sim }(\lnot c) ~|~\lnot c\in C\rangle \}, \end{aligned}$$

(2)

where $\eta ^{\sim }(\lnot c)$ is an IVmF set of U, $\forall ~c\in C$. In other words,

$$\begin{aligned} \eta ^{\sim }(\lnot c)&=\big \{u,\langle \left[ 1-M_{U_{1}(u)}, 1-M_{L_{1}(u)}\right] ,\left[ 1-M_{U_{2}(u)}, 1-M_{L_{2}(u)}\right] , \ldots ,\left[ 1-M_{U_{m}(u)}, 1-M_{L_{m}(u)}\right] \rangle \big \}, \end{aligned}$$

for all $\lnot c\in \lnot C$ and $u\in U$. Here $\lnot C$ represent the not set of parameters which holds opposite meaning corresponding to each parameter $c\in C$.

Example 4

Assume data in Example 1 again, where an IV3FSS is given in Table 2. Then, by Definition 9 its complement is computed in Table 5.

Table 5 Tabular form of the complement of IV3FSS $(\eta ,C)$

Definition 10

Let $(\eta _1,C_1)$ and $(\eta _2,C_2)$ be two IVmFSSs over a universal set U, then the operation “AND” among them is represented as $(\eta _1,C_1){\bar{\wedge }}(\eta _2,C_2)$ and is given by

$$\begin{aligned} (\eta _1,C_1){\bar{\wedge }}(\eta _2,C_2)=(\varPsi , C_1\times C_2), \end{aligned}$$

where $\varPsi (\sigma ,\lambda )=\eta _1(\sigma )\cap \eta _2(\lambda )$ for all $(\sigma ,\lambda )\in C_1\times C_2$.

Example 5

Let $U=\{u_1,u_2,\ldots ,u_5\}$ be a set of five flats and $C_1=\{c_1=\mathrm{convenient ~traffic}, c_3=\mathrm{modern ~repair}\},~C_2=\{c_1=\mathrm{convenient ~traffic}, c_2=\mathrm{in~ good~ repair}, c_3=\mathrm{modern ~repair}\}\subseteq Z$ be two sets of parameters. Then, two IV3FSSs $(\eta _1,C_1)$ and $(\eta _2,C_2)$ are respectively given by Tables 6 and 7 .

Table 6 Tabular form of the IV3FSS $(\eta _1,C_1)$

Table 7 Tabular form of the IV3FSS $(\eta _2,C_2)$

The result of “AND” operation of IV3FSSs $(\eta _1,C_1)$ and $(\eta _2,C_2)$ is displayed in Table 8.

Table 8 Tabular form of the “AND” between IV3FSSs $(\eta _1,C_1)$ and $(\eta _2,C_2)$

Definition 11

Let $(\eta _1,C_1)$ and $(\eta _2,C_2)$ be two IVmFSSs on a universal set U, then the operation “OR” among them is represented by $(\eta _1,C_1){\bar{\vee }}(\eta _2,C_2)$ and is given as

$$\begin{aligned} (\eta _1,C_1){\bar{\vee }}(\eta _2,C_2)=(\varLambda , C_1\times C_2), \end{aligned}$$

where $\varLambda (\sigma ,\lambda )=\eta _1(\sigma )\cap \eta _2(\lambda )$, $\forall ~(\sigma ,\lambda )\in C_1\times C_2$.

Example 6

Consider Example 5 again, where two IV3FSSs $(\eta _1,C_1)$ and $(\eta _2,C_2)$ are respectively given by Tables 6 and 7. The result of “OR” operation of IV3FSSs $(\eta _1,C_1)$ and $(\eta _2,C_2)$ is displayed in Table 8 (Table 9).

Table 9 Tabular form of the “OR” between IV3FSSs $(\eta _1,C_1)$ and $(\eta _2,C_2)$

We now investigate the DeMorgan’s laws for IVmFSSs.

Theorem 1

Let $(\eta _1,C_1)$ and $(\eta _2,C_2)$ be two IV m FSSs on a universal set U. Then,

• 1. $\big ((\eta _1,C_1)\barwedge (\eta _2,C_2)\big )^{\sim }=(\eta _1,C_1)^{\sim }{\bar{\vee }} (\eta _2,C_2)^{\sim }$,

• 2. $\big ((\eta _1,C_1){\bar{\vee }}(\eta _2,C_2)\big )^{\sim }=(\eta _1,C_1)^{\sim }{\bar{\wedge }} (\eta _2,C_2)^{\sim }$.

Proof

$$\begin{aligned} (\eta _1,C_1)^{\sim }{\bar{\vee }} (\eta _2,C_2)^{\sim }&=({\eta _1}^{\sim },\lnot C_1){\bar{\vee }} ({\eta _2}^{\sim },\lnot C_2),\\&=(\varLambda , \lnot C_1\times \lnot C_2), ~\mathrm{where}~\varLambda (\lnot \sigma ,\lnot \lambda )={\eta _1}^{\sim }(\sigma )\cup {\eta _2}^{\sim }(\lambda ),\\&=(\varLambda , \lnot (C_1\times C_2)), \end{aligned}$$

for all $(\sigma ,\lambda )\in C_1\times C_2$. Suppose that $(\eta _1,C_1)\barwedge (\eta _2,C_2)=(\varPsi , C_1\times C_2)$, then we obtain $\big ((\eta _1,C_1)\barwedge (\eta _2,C_2)\big )^{\sim }=(\varPsi , C_1\times C_2)^{\sim }=(\varPsi ^{\sim }, \lnot (C_1\times C_2))$. Now for all $(\sigma ,\lambda )\in C_1\times C_2$, we have

$$\begin{aligned} \varPsi ^{\sim }(\lnot \sigma ,\lnot \lambda )&=(\varPsi (\sigma ,\lambda ))^{\sim },\\&=(\eta _1(\sigma )\cap \eta _2 (\lambda ))^{\sim },\\&={\eta _1(\sigma )}^{\sim }\cup {\eta _2 (\lambda )}^{\sim },\\&={\eta _1}^{\sim }(\lnot \sigma )\cup {\eta _2}^{\sim } (\lnot \lambda ). \end{aligned}$$

From the above discussion, we get $\big ((\eta _1,C_1)\barwedge (\eta _2,C_2)\big )^{\sim }=(\eta _1,C_1)^{\sim }{\bar{\vee }} (\eta _2,C_2)^{\sim }$. Similarly, the other part can be easily followed by similar arguments. $\square$

Theorem 2

Let $(\eta _1,C_1)$, $(\eta _2,C_2)$ and $(\eta _3,C_3)$ be three IV m FSSs over a universal set U. Then,

• 1. $(\eta _1,C_1){\bar{\wedge }}\big ((\eta _2,C_2){\bar{\wedge }}(\eta _3,C_3)\big )=\big ((\eta _1,C_1){\bar{\wedge }}(\eta _2,C_2)\big ){\bar{\wedge }}(\eta _3,C_3),$

• 2. $(\eta _1,C_1){\bar{\vee }}\big ((\eta _2,C_2){\bar{\vee }}(\eta _3,C_3)\big )=\big ((\eta _1,C_1){\bar{\vee }}(\eta _2,C_2)\big ){\bar{\vee }}(\eta _3,C_3),$

• 3. $(\eta _1,C_1){\bar{\wedge }}\big ((\eta _2,C_2){\bar{\vee }}(\eta _3,C_3)\big )=\big ((\eta _1,C_1){\bar{\wedge }}(\eta _2,C_2)\big ){\bar{\vee }}\big ((\eta _1,C_1){\bar{\wedge }}(\eta _3,C_3)\big ),$

• 4. $(\eta _1,C_1){\bar{\vee }}\big ((\eta _2,C_2){\bar{\wedge }}(\eta _3,C_3)\big )=\big ((\eta _1,C_1){\bar{\vee }}(\eta _2,C_2)\big ){\bar{\wedge }}\big ((\eta _1,C_1){\bar{\vee }}(\eta _3,C_3)\big ).$

Proof

For all $\sigma \in C_1, \sigma _2\in C_2$ and $\sigma _3\in C_3$, we have $\eta _1(\sigma _1)\cap (\eta _2(\sigma _2)\cap \eta _3(\sigma _3))= (\eta _1(\sigma _1)\cap \eta _2(\sigma _2))\cap \eta _3(\sigma _3),$ by the properties of interval-valued fuzzy sets, from which we directly obtain that $(\eta _1,C_1)\bar{\wedge }\big ((\eta _2,C_2){\bar{\wedge }}(\eta _3,C_3)\big )=\big ((\eta _1,C_1)\bar{\wedge }(\eta _2,C_2)\big ){\bar{\wedge }}(\eta _3,C_3).$ Using similar arguments, it can be easily see that $(\eta _1,C_1)\bar{\vee }\big ((\eta _2,C_2){\bar{\vee }}(\eta _3,C_3)\big )=\big ((\eta _1,C_1)\bar{\vee }(\eta _2,C_2)\big ){\bar{\vee }}(\eta _3,C_3).$

For all $\sigma \in C_1, \sigma _2\in C_2$ and $\sigma _3\in C_3$, by the properties of interval-valued fuzzy sets, we get $\eta (\sigma _1)\cap (\eta _2(\sigma _2)\cup \eta (\sigma _3))=(\eta (\sigma _1)\cap \eta _2(\sigma _2))\cup (\eta (\sigma _1)\cap \eta (\sigma _3))$, from which we directly obtain that $(\eta _1,C_1){\bar{\wedge }}\big ((\eta _2,C_2){\bar{\vee }}(\eta _3,C_3)\big )=\big ((\eta _1,C_1){\bar{\wedge }}(\eta _2,C_2)\big ){\bar{\vee }}\big ((\eta _1,C_1){\bar{\wedge }}(\eta _3,C_3)\big )$. The remaining part (4) directly follow by similar arguments. $\square$

Definition 12

Let $U=\{\textit{u}_1,\textit{u}_2,\cdots ,\textit{u}_n\}$ be a universe, $Z=\{\textit{c}_1,\textit{c}_2,\cdots ,\textit{c}_r\}$ a universal set of parameters and $C\subseteq Z$. For an IVmFSS $(\eta , C)$, we define the scores for the lower and upper bounds of membership degree intervals are respectively represented by $b_{\textit{L}_j}^-(\textit{u}_i)$ and $b_{\textit{L}_j}^+(\textit{u}_i)$ and defined as follows:

$$\begin{aligned} b_{\textit{L}_j}^-(\textit{u}_i)&=\sum \limits _{s=1}^n (M_{L_j}(\textit{u}_i)-M_{L_j}(\textit{u}_s)),\end{aligned}$$

(3)

$$\begin{aligned} b_{\textit{U}_j}^+(\textit{u}_i)&=\sum \limits _{s=1}^n (M_{U_j}(\textit{u}_i)-M_{U_j}(\textit{u}_s)). \end{aligned}$$

(4)

for each $\textit{c}_j\in C,~(j=1,2,\cdots ,r)$.

Definition 13

Let $U=\{\textit{u}_1,\textit{u}_2,\cdots ,\textit{u}_n\}$ be a universe, $Z=\{\textit{c}_1,\textit{c}_2,\cdots ,\textit{c}_r\}$ a universal set of parameters and $C\subseteq Z$. For an IVmFSS $(\eta , C)$, the accumulated score of an object regarding an arbitrary parameter for all given poles is denoted by $(b_{\textit{c}_j}(\textit{u}_i))$, and is computed by

$$\begin{aligned} b_{\textit{c}_j}(\textit{u}_i)&=\sum \limits _{t=1}^m(b_{\textit{L}_j^t}^-(\textit{u}_i)+b_{\textit{U}_j^t}^+(\textit{u}_i)), \end{aligned}$$

(5)

where $b_{\textit{L}_j^t}^-(\textit{u}_i)$ and $b_{\textit{U}_j^t}^-(\textit{u}_i)$ are the scores of lower and upper bounds for the intervals of membership degrees and ‘m’ represents the number of poles.

Definition 14

Let $U=\{\textit{u}_1,\textit{u}_2,\cdots ,\textit{u}_n\}$ be an initial universal set, $Z=\{\textit{c}_1,\textit{c}_2,\cdots ,\textit{c}_r\}$ a universal set of parameters and $C\subseteq Z$. For an IVmFSS $(\eta , C)$, we define the final score $S_i$ for every element $\textit{u}_i$ of the universe which is given as

$$\begin{aligned} S_i=\sum \limits _{\textit{c}_j\in C} (b_{\textit{c}_j}(\textit{u}_i)). \end{aligned}$$

(6)

This novel proposed decision-making method under IVmFSS model is supported by an algorithm below (see Algorithm 1).

Example 7

Let $U=\{\textit{u}_1,\textit{u}_2,\textit{u}_3,\textit{u}_4,\textit{u}_5,\textit{u}_6\}$ be the set of six laptops, $Z=\{\textit{c}_1=\mathrm{costly},\textit{c}_2=\mathrm{beauty},\textit{c}_3=\mathrm{design},\textit{c}_4=\mathrm{technology},\textit{c}_5=\mathrm{material}\}$ a set of parameters and $C=\{\textit{c}_1,\textit{c}_2,\textit{c}_3\}\subseteq Z$. Then, an IVmFSS $(\eta ,C)$ is displayed in Table 10. We now apply Algorithm 1 to IVmFSS $(\eta ,C)$.

Table 10 Tabular representation of the IVmFSS $(\eta ,C)$

By using Equations (3) and (4), the scores of lower and upper bounds for every pole (interval) are given in Tables 11 and 12 . First cell of the Table 11 is computed as below.

$$\begin{aligned} b_{\textit{c}_1}^-(\textit{u}_1)&=\sum \limits _{s=1}^6 (M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_s)),\\&=(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_1))+(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_2))+(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_3))+\\ {}&~~~~(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_4))+(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_5))+(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_6)),\\&=(0.2-0.2)+(0.2-0.1)+(0.2-0.3)+(0.2-0.4)+(0.2-0.1)+(0.2-0.2),\\&=-0.1. \end{aligned}$$

Similarly, one can readily compute the remaining values, which are displayed in Table 11 and 12 .

Table 11 Scores of lower bounds for each pole of IV3FSS $(\eta ,C)$

Table 12 Scores of upper bounds for each pole of IV3FSS $(\eta ,C)$

From Definition 13, the tabular representation for the accumulated scores of membership values of IV3FSS $(\eta ,C)$ with respect to each parameter is displayed by Table 13.

Table 13 Accumulated score with respect to each parameter of membership degrees of IV3FSS $(\eta ,C)$

By Definition 14, the final score of every laptop $\textit{u}_i$ is displayed in Table 14. First entry of final score table is computed as:

$$\begin{aligned} S_1&=\sum \limits _{\textit{c}_j\in Z}(b_{\textit{c}_j}(\textit{u}_1))\\&=b_{\textit{c}_1}(\textit{u}_1)+b_{\textit{c}_2}(\textit{u}_1)+b_{\textit{c}_3}(\textit{u}_1),\\&=(-1.3)+(0.9)+(3.3) =2.9. \end{aligned}$$

Table 14 Final score table

From Table 14, the object having highest score is $S_4=6.3$. Thus, it can be used as decision object.

Example 8

Let $U=\{\textit{u}_1,\textit{u}_2,\textit{u}_3,\textit{u}_4\}$ be the set f four cars, $Z=\{\textit{c}_1=\mathrm{costly},\textit{c}_2=\mathrm{beauty},\textit{c}_3=\mathrm{design},\textit{c}_4=\mathrm{technology},\textit{c}_5=\mathrm{material}\}$ a set of parameters and $C=\{\textit{c}_1,\textit{c}_3\}\subseteq Z$. Then, an IV4FSS $(\eta ,C)$ is displayed in Table 15. We now apply Algorithm 1 to IV4FSS $(\eta ,C)$.

Table 15 Tabular representation of the IV4FSS $(\eta ,C)$

By using Equations (3) and (4), the scores of lower and upper bounds for every pole (interval) are given in Tables 16 and 17 . First cell of the Table 16 is computed as below.

$$\begin{aligned} b_{\textit{c}_1}^-(\textit{u}_1)&=\sum \limits _{s=1}^5 (M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_s)),\\&=(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_1))+(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_2))+(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_3))+\\ {}&~~~~(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_4))+(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_5)),\\&=(0.4-0.4)+(0.4-0.2)+(0.4-0.3)+(0.4-0.1)+(0.4-0.3),\\&=0.8. \end{aligned}$$

Similarly, one can readily compute the remaining values, which are displayed in Table 16 and 17 .

Table 16 Scores of lower bounds for each pole of IV4FSS $(\eta ,C)$

Table 17 Scores of upper bounds for each pole of IV4FSS $(\eta ,C)$

From Definition 13, the tabular representation for the accumulated scores of membership values of IV4FSS $(\eta ,C)$ with respect to each parameter is displayed by Table 18.

Table 18 Accumulated score with respect to each parameter of membership degrees of IV4FSS $(\eta ,C)$

By Definition 14, the final score of every car $\textit{u}_i$ is displayed in Table 19. First entry of final score table is computed as:

$$\begin{aligned} S_1&=\sum \limits _{\textit{c}_j\in Z}(b_{\textit{c}_j}(\textit{u}_1))\\&=b_{\textit{c}_1}(\textit{u}_1)+b_{\textit{c}_3}(\textit{u}_1),\\&=(3.6)+(0.5) =4.1. \end{aligned}$$

Table 19 Final score table

From the Table 19, the object having highest score is $\textit{u}_1$ because $S_1=4.1$. Thus, $\textit{u}_1$ can be selected as decision.

In the following, to find the optimal decision based on IVmF soft sets, we construct a flowchart diagram which describe the proposed mathematical method more precisely and feasibly.

Fig. 1

Flowchart of selecting the suitable option

By the analysis of above examples, one can easily see that developed decision-making method under IVmFSSs is useful and reliable. Although, decision-making hybrid methods involving soft sets as one of their component may contain some redundant parameters. To remove this drawback in the developed hybrid model, we now provide three parameter reductions approaches for IVmFSSs.

3 Parameter reductions of IVmFSSs

An approach to reduce the parameter set to acquire a minimal subset of parameter set that provides a decision similar to the whole set of parameter is called parameter reduction. In this section, we investigate three kinds of parameter reductions of IVmFSSs to handle different reduction situations.

• 1. Parameter reduction based on optimal choice

  We discuss the parameter reduction based on optimal choices and then give an algorithm for this parameter reduction approach, which is explained through an example.

Definition 15

Let $U=\{\textit{u}_1,\textit{u}_2,\cdots ,\textit{u}_n\}$ be a universe, $Z=\{\textit{c}_1,\textit{c}_2,\cdots ,\textit{c}_m\}$ a set of parameters and $C\subseteq Z$. For an IVmFSS $(\eta , C)$, we denote a subset ${O}_C\subseteq U$ as a set having optimal values of final score $S_i$. For any $A\subseteq C$, if $O_{C-A}=O_C$, then A is said to be dispensable in C, else, A is said to be indispensable in the favorable parameter set C. The set C of parameters is said to be independent if each $A\subset C$ is indispensable in C, otherwise, C is dependent. Any set $B\subset C$ is called a parameter reduction based on optimal choice (PR-OC, henceforth) of C if it satisfy the following axioms.

• 1. B is independent (it means $B\subset C$ which is minimal and keeps the decision unchanged).

• 2. $O_B=O_C$.

Using the Definition 15, we present an algorithm for PR-OC which remove the irrelevant parameters while preserving the decision invariant.

Example 9

Consider Example 7 where $C=\{\textit{c}_1,\textit{c}_2,\textit{c}_3\}\subseteq Z$. We apply Algorithm 2 to the IVmFSS $(\eta ,C)$. Using Table 20, we deduce that for $B^{'}=\{\textit{c}_2,\textit{c}_3\}$, we obtain $O_{C-B^{'}}=O_C$. Hence, one PR-OC of IVmFSS $(\eta ,C)$ is given by $C-B^{'}=\{\textit{c}_1\}$ which is displayed in Table 20.

Table 20 PR-OC

From Table 20, one can easily see that $u_4$ is the decision after reduction. Definitely, the subset $\{\textit{c}_1\}\subset C$ is smallest which preserves decision invariant.

• 2. Rank based parameter reduction

Nowadays, most of the practical problems are mainly solved to find the rank of all the alternatives under consideration. Since, the objects other than optimal choice are not considered in PR-OC technique. To tackle this issue, we define a novel parameter reduction which preserves the rank of all the objects and develop an algorithmic method which maintains the ranking order of all the objects after reduction.

Definition 16

Let $U=\{\textit{u}_1,\textit{u}_2,\cdots ,\textit{u}_n\}$ be a universe, $Z=\{\textit{c}_1,\textit{c}_2,\cdots ,\textit{c}_r\}$ a set of parameters and $P\subset Z$. For an IVmFSS $(\eta , Z)$, an indiscernibility relation is given as

$$\begin{aligned} IND(P)=\{(\textit{u}_i,\textit{u}_j)\in X\times X~|~S_P(\textit{u}_i)=S_P(\textit{u}_j)\}, \end{aligned}$$

where $S_P(\textit{u}_i)=\sum \limits _{\textit{c}_s\in P}M_{\textit{c}_s}(\textit{u}_i)$. For any IVmFSS $(\eta , Z)$ on $U=\{\textit{u}_1,\textit{u}_2,\cdots ,\textit{u}_n\}$, the decision partition is given by

$$\begin{aligned} D_Z=\{\{\textit{u}_1,\textit{u}_2,\cdots ,\textit{u}_i\}_{S_1},\{\textit{u}_{i+1},\cdots ,\textit{u}_j\}_{S_2},\cdots ,\{\textit{u}_k,\cdots ,\textit{u}_n\}_{S_z}\}, \end{aligned}$$

where for every sub-class $\{\textit{u}_a,\textit{u}_{a+1},\cdots ,\textit{u}_{a+b}\}_{S_i},~S_Z(\textit{u}_a)=S_Z(\textit{u}_{a+1})=\cdots =S_Z(\textit{u}_{a+b})=S_i,$ and $S_1\ge S_2\ge \cdots \ge S_r,$ it means there exist r sub-classes. Actually, in RB-PR elements of the universe are ranked regarding scores $S_i$, where $i\in \{1,2,\cdots ,n\}$.

Definition 17

Let $U=\{\textit{u}_1,\textit{u}_2,\cdots ,\textit{u}_n\}$ be a universe, $Z=\{\textit{c}_1,\textit{c}_2,\cdots ,\textit{c}_r\}$ a set of parameters and let $(\eta ,Z)$ be an IVmFSS. For every $C\subseteq Z$, if $D_{Z-C}=D_Z$, then C is called dispensable in Z, otherwise, C is indispensable in Z. The set Z of parameters is called independent if every $C\subset Z$ is indispensable in Z, otherwise, Z is dependent. A set $B\subset Z$ is called a rank based parameter reduction (RB-PR, in short) of Z if it satisfy the following two conditions.

• 1. B is independent (it means $B\subset Z$ is smallest which keeps the ranking order of all the objects invariant, including optimal decision object).

• 2. $D_B=D_Z$.

Using Definition 17, we now present an algorithm(see Algorithm 3) for the RB-PR method that reduces the set of parameters while preserving the original rank fation.

Example 10

Let $U=\{\textit{u}_1,\textit{u}_2,\textit{u}_3,\textit{u}_4,\textit{u}_5\}$ be the set of five houses, $Z=\{\textit{c}_1=\mathrm{costly},\textit{c}_2=\mathrm{beauty},\textit{c}_3=\mathrm{design},\textit{c}_4=\mathrm{location},\textit{c}_5=\mathrm{material}\}$ a set of parameters and $C=\{\textit{c}_3,\textit{c}_4,\textit{c}_5\}\subseteq Z$. Then, an IV3FSS $(\eta ,C)$ is displayed in Table 21. We now apply Algorithm 1 to IV3FSS $(\eta ,C)$.

Table 21 Tabular representation of the IV3FSS $(\eta ,C)$

By using Equations (3) and (4), the scores of lower and upper bounds for every pole (interval) are given in Tables 22 and 23 . First cell of the Table 22 is computed as below.

$$\begin{aligned} b_{\textit{c}_1}^-(\textit{u}_1)&=\sum \limits _{s=1}^5 (M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_s)),\\&=(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_1))+(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_2))+(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_3))+\\ {}&~~~~(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_4))+(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_5)),\\&=(0.5-0.5)+(0.5-0.2)+(0.5-0.4)+(0.5-0.6)+(0.5-0.3),\\&=0.5. \end{aligned}$$

Similarly, one can readily compute the remaining values, which are displayed in Table 22 and 23 .

Table 22 Scores of lower bounds for each pole of IV3FSS $(\eta ,C)$

Table 23 Scores of upper bounds for each pole of IV3FSS $(\eta ,C)$

From Definition 13, the tabular representation for the accumulated scores of membership values of IV3FSS $(\eta ,C)$ with respect to each parameter is displayed by Table 24.

Table 24 Accumulated score with respect to each parameter of membership degrees of IV3FSS $(\eta ,C)$

By Definition 14, the final score of every laptop $\textit{u}_i$ is displayed in Table 25. First entry of final score table is computed as:

$$\begin{aligned} S_1&=\sum \limits _{\textit{c}_j\in Z}(b_{\textit{c}_j}(\textit{u}_1))\\&=b_{\textit{c}_3}(\textit{u}_1)+b_{\textit{c}_4}(\textit{u}_1)+b_{\textit{c}_5}(\textit{u}_1),\\&=(-2.8)+(-4.3)+(2.9) =-4.2. \end{aligned}$$

Table 25 Final score table

From the Table 25, one can readily see that the object having highest score is $\textit{u}_4$ because $S_4=6.8$. Thus, $\textit{u}_4$ is the optimal decision object. Furthermore, using Table 25, it can readily computed that

$$\begin{aligned} D_C=\{\{\textit{u}_4\}_{6.8},\{\textit{u}_5\}_{0.8},\{\textit{u}_3\}_{0.3},\{\textit{u}_2\}_{-3.7},\{\textit{u}_2\}_{-4.2}\}. \end{aligned}$$

By applying Algorithm 3, we now compute a minimal subset of C which preserves the rank of all objects of the universe. Thus, for $B^{'}=\{\textit{c}_5\}$, we obtain $D_{C-B^{'}}=\{\{\textit{u}_4\}_{6.9},\{\textit{u}_5\}_{5.4},\{\textit{u}_3\}_{-2.1},\{\textit{u}_2\}_{-3.1},\{\textit{u}_2\}_{-7.1}\}$ with $D_{C-B^{'}}=D_C$. Notice that partition and rank of elements of the universe are same after reduction. Thus, $\{\textit{c}_3,\textit{c}_4\}$ is the only RB-PR of IV3FSS $(\eta ,C)$ as displayed by Table 26.

Table 26 RB-PR

Clearly, $\{\textit{c}_3,\textit{c}_4\}\subset C$ is the only minimal subset which keeps the ranking order of all objects invariant.

• 3. Normal parameter reduction

The reduction approaches discussed above may not be useful in different real situations. That’s why, we give another reduction approach called normal parameter reduction (NPR) for IVmFSSs, which handles the issue of added parameters. We propose the notion of NPR and provide its algorithmic approach, that is, how to remove redundant parameters using NPR method.

Definition 18

Let $U=\{\textit{u}_1,\textit{u}_2,\cdots ,\textit{u}_n\}$ be a universe of objects, $C\subset Z=\{\textit{c}_1,\textit{c}_2,\cdots ,\textit{c}_r\}$ a favorable set of parameters. For an IVmFSS $(\eta , C)$, B is said to be dispensable if we compute a set $B=\{\textit{c}_1,\textit{c}_2,\cdots ,\textit{c}_p\}\subset C$, which verify the expression given below.

$$\begin{aligned} \sum \limits _{\textit{c}_j\in B} b_{\textit{c}_j}(\textit{u}_1)=\sum \limits _{\textit{c}_j\in B} b_{\textit{c}_j}(\textit{u}_2)=\cdots =\sum \limits _{\textit{c}_j\in B} b_{\textit{c}_j}(\textit{u}_n). \end{aligned}$$

Otherwise, B is called indispensable. A set $N\subset C$ is said to be NPR of C, if it satisfy the conditions given as follows.

• 1. N is indispensable.

• 2. $\sum \limits _{\textit{z}_j\in C-N} b_{\textit{c}_j}(\textit{u}_1)=\sum \limits _{\textit{c}_j\in C-N} b_{\textit{c}_j}(\textit{u}_2)=\cdots =\sum \limits _{\textit{c}_j\in C-N} b_{\textit{c}_j}(\textit{u}_n).$

Using Definition 18, we develop the NPR algorithm as below:

Example 11

Let $U=\{\textit{u}_1,\textit{u}_2,\textit{u}_3,\textit{u}_4\}$ be the set of four houses, $Z=\{\textit{c}_1=\mathrm{costly},\textit{c}_2=\mathrm{beauty},\textit{c}_3=\mathrm{design},\textit{c}_4=\mathrm{location},\textit{c}_5=\mathrm{material}\}$ a set of parameters and $C=\{\textit{c}_1,\textit{c}_2,\textit{c}_5\}\subseteq Z$. Then, an IV3FSS $(\eta ,C)$ is displayed in Table 27. We now apply Algorithm 4 to IV3FSS $(\eta ,C)$.

Table 27 Tabular representation of the IV3FSS $(\eta ,C)$

By using Equations (3) and (4), the scores of lower and upper bounds for every pole (interval) are given in Tables 28 and 29 . First cell of the Table 28 is computed as below.

$$\begin{aligned} b_{\textit{c}_1}^-(\textit{u}_1)&=\sum \limits _{s=1}^5 (M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_s)),\\&=(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_1))+(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_2))+(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_3))+\\ {}&~~~~(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_4)),\\&=(0.4-0.4)+(0.4-0.6)+(0.4-0.5)+(0.4-0.7),\\&=-0.6. \end{aligned}$$

Similarly, one can readily compute the remaining values, which are displayed in Table 28 and 29 .

Table 28 Scores of lower bounds for each pole of IV3FSS $(\eta ,C)$

Table 29 Scores of upper bounds for each pole of IV3FSS $(\eta ,C)$

From the Definition 13, the tabular representation for the accumulated scores of membership values of IV3FSS $(\eta ,C)$ for each parameter is displayed by Table 30.

Table 30 Accumulated score with respect to each parameter of membership degrees of IV3FSS $(\eta ,C)$

By Definition 14, the final score of every house $\textit{u}_i$ is displayed in Table 31. First entry of final score table is computed as:

$$\begin{aligned} S_1&=\sum \limits _{\textit{c}_j\in Z}(b_{\textit{c}_j}(\textit{u}_1))\\&=b_{\textit{c}_1}(\textit{u}_1)+b_{\textit{c}_2}(\textit{u}_1)+b_{\textit{c}_5}(\textit{u}_1),\\&=(-1.2)+(1.5)+(1.2) =1.5. \end{aligned}$$

Table 31 Final score table

Clearly, objects $u_1$ and $u_4$ have maximum score that is 1.5. Thus, one from them can be chosen as optimal decision. By Table 31, one can easily observe that for $N=\{\textit{c}_1,\textit{c}_5\}$, we have

$$\begin{aligned} \sum \limits _{\textit{c}_j\in N} b_{\textit{c}_j}(\textit{u}_1)=\sum \limits _{\textit{c}_j\in B} b_{\textit{c}_j}(\textit{u}_2)=\cdots =\sum \limits _{\textit{c}_j\in B} b_{\textit{c}_j}(\textit{u}_4)=0. \end{aligned}$$

Thus, $C-\{\textit{c}_1,\textit{c}_5\}=\{c_2\}$ is the NPR of IVmFSS $(\eta ,C)$, which is given by Table 32.

Table 32 NPR

4 Application to MCDM

This section solves two real decision-making situations using the developed model and discusses the impact of the proposed parameter reduction approaches on them.

• 1. Case Study: Selection of a suitable site for an airport

Choosing an appropriate site for another airport, or assessing how suitably a current site can be extended to give another significant airport, is a complicated procedure. A proportion must be accomplished among air-transport and aeronautical needs and the effect of the airport on its current circumstance. For an aeronautical perspective, the fundamental necessity of an airport is its generally flat area of land adequately enormous to adapt the runways and different services and that this site is in a territory liberated from such obstacles to air route as tall buildings and mountains. For the perspective of air-transport requirements, airport sites should be adequately near to population centers that these are thought to be approached by users easily. However, environmental factors demand that the location should be too much long way from urban areas which will overcome the noise and other destructive impacts on the population to tolerable levels. Moreover, the natural beauty of different areas and other important assets should not be destroyed by the airport. The environmental and aeronautical, nearly necessarily clash, with the conflict getting more serious as the size of the envisaged airport increases for these two sets of requirements. The most unassuming airport facility with an aircraft parking, a building, and a single runway that serves at the same time as terminal, control tower, and administration area can quietly be constructed on a location as little as 75 acres since it needs just a flat, very much depleted area adequate to oblige a short runway and its encompassing safety strip. On the other hand, more modern and huge airport facilities need a large number of runways of huge length, huge terminal aircraft parking areas, and huge territories of land committed to landside access roads and parking. For this kind of airport, a base area of 3000 acres is probably going to be needed. A few significant airports, for example, King Abdul Aziz International Airport close to Jeddah, Saudi Arabia, Charles de Gaulle Airport close to Paris, and Dallas-Fort Worth International Airport in Texas are based on destinations well in overabundance of above mentioned figure. The site selecting procedure for a huge airport can take several months; in some essential circumstances, it has gone on for several years. The difficulty in the process is due to the involvement of several factors. First, evaluate the operational capabilities of the station, especially for weather conditions (such as fog, low visibility, ice, snow, and wind), as well as obstacles to air navigation nearby the airport, especially on the approach and take-off paths. The location of the facility relative to the air traffic control airspace is also practically significant. Furthermore, the capability of available land must be evaluated to adjust the expected configuration of runways and other facilities. The landing must be flat or very gentle, because the runway must be constructed based on the maximum allowable slope, which depends on the performance of the aircraft during landing and takeoff. Also consider the ground access of the airport. Evaluate the distance to population centers, regional highway infrastructure, public transportation facilities (like railways), and the distance to land available for parking. Also consider the nature of the terrain, rock and soil conditions, drainage needs and local land value to estimate development costs. In a site selection process, the effect of an airport development on the environment is very high. The effect of aircraft noise on the surrounding population is usually a very important environmental factor, but in different countries, the effect on the fauna and flora of the area must also be considered, the pollution of local groundwater by chemical runoff, the existence of endangered species or important culture sites, and even bad changes in land use. Several countries now demand environmental analysis of airport development projects, including changes in employment patterns, assessments of population migration, transportation plans and distortions in existing regional land use. Suppose that government of a country planned to construct a new airport on a most suitable site from twenty alternatives. This critical task is given to a team of experts of the field. Let $U=\{u_1,u_2,\ldots ,u_{20}\}$ be a set of twenty sites for the selection of most suitable site for an airport construction and $Z=\{c_1=\mathrm{size},c_2=\mathrm{cost},c_3=\mathrm{environmental ~consequences},c_4=\mathrm{ground ~acces}\}$ be a set of parameters from which $C=\{c_2,c_3, c_4\}\subseteq Z$ are favorable according to the team of experts. These parameters can be further classified as follows:

• The parameter “Size” includes medium, large, very large.

• The parameter “Cost” includes low, medium, high.

• The parameter “Environmental  Consequences” includes distortion of existing regional land use, changes in employment patterns, and evaluations of population relocation.

• The parameter “Ground Access” includes public transport facilities, the regional highway infrastructure, distance from population centers.

The report collected from the team of experts is in the form of an IV3FSS, which is displayed by Table 33.

Table 33 Tabular representation of the IV3FSS $(\eta ,C)$

By using Equations (3) and (4), the scores of lower and upper bounds for every pole (interval) are given in Tables 34 and 35 . First cell of the Table 34 is computed as below.

$$\begin{aligned} b_{\textit{c}_2}^-(\textit{u}_1)&=\sum \limits _{s=1}^5 (M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_s)),\\&=(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_1))+(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_2))+(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_3))+\ldots +\\ {}&~~~~(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_{19}))+(M_{L_1}(\textit{u}_1)-M_{L_1}(\textit{u}_{20})),\\&=(0.4-0.4)+(0.4-0.5)+(0.4-0.3)+\ldots +(0.4-0.5)+(0.4-0.2),\\&=0.3. \end{aligned}$$

Similarly, one can readily compute the remaining values, which are displayed in Table 34 and 35 .

Table 34 Scores of lower bounds for each pole of IV3FSS $(\eta ,C)$

Table 35 Scores of upper bounds for each pole of IV3FSS $(\eta ,C)$

From Definition 13, the tabular representation for the accumulated scores of membership degrees of IV3FSS $(\eta ,C)$ with respect to each parameter is displayed by Table 36.

Table 36 Accumulated score with respect to each parameter of membership degrees of IV3FSS $(\eta ,C)$

By Definition 14, the final score of every site $\textit{u}_i$ is displayed Table 37.

Table 37 Final score table

Clearly, from Table 37 the object having highest score is $\textit{u}_{15}$ because $S_{15}=20.4$. Thus, $\textit{u}_{15}$ is the most suitable site from all the available alternatives. From the Table 37, it can be readily compute that $B^{'}=\{c_2\}\subseteq C$ such that $C-B^{'}=\{c_3,c_4\}$ is the only PR-OC. Regrettably, there is no RB-PR in present situation.

Now we apply our decision-making Algorithm 1 under IVmFSSs, and the reduction Algorithms 2, 3 and 4 , to another situation from agriculture engineering.

• 2. Case Study: Selection of a suitable rotavator machine

In agricultural engineering, a rotavator is a useful machine for seedbed preparation. It is directly connected with a tractor to plow the soil by a set of blades that cuts, mixes, pulverizes and level the soil and makes the ground perfect before planting bulbs and seeds. Thus blades become very essential components in the rotavator. This is an effective agriculture equipment which replaces the disc harrow, cultivator and leveler because it works collectively of these three equipments. It is better than traditional agricultural rotary machines due to its rapid and efficient seedbed preparation. The rotavator is a very reliable source of transmission of the engine power of a tractor directly to the soil without any serious reduction in transmission power loss and wheel slip. Due to this fact, it saves a lot of time and reduces the cost of operation more than other classical tillage machines. In the manufacturing process of a rotavator, major errors can be reduced by the analysis of its components design. The design optimization of a rotavator machine is achieved by decreasing its cost and weight, and by enhancing a field efficiency to high weed removal performance. Soil conditions directly affect the types of blades selected in terms of power requirement of rotary cultivator. For example, clay soil consumes more power than loamy soil. Therefore, soil condition is also an important factor in the development of a suitable rotavator. Other main factors which affect the selection procedure of an appropriate rotavator are: size, cost, fuel consumption and material quality.

Nowadays, with the advancement in agriculture sector, agriculture engineers are trying to enhance the rotavator design and its material, with the goal of achieving maximum outputs in minimum time and with the lowest cost. Experts believe that there are different characteristics which should be considered in the selection of a rotavator, such as size, cost, fuel consumption, blades shape, material quality, soil condition etc.

Suppose that an agricultural university arranges an agriculture exhibition where engineers can present their innovative agricultural equipments. The university management also announces an award to the best rotavator model from the ten alternatives which are evaluated by a team of senior agriculture experts with respect to some favorable parameters. Let $U=\{u_1,u_2,\ldots ,u_{10}\}$ be a set of ten alternatives (rotavators) for the selection of most suitable option and $Z=\{c_1=\mathrm{size},c_2=\mathrm{material~quality},c_3=\mathrm{cost},c_4=\mathrm{soil~condition}\}$ be a set of parameters from which $C=\{c_1,c_2, c_4\}\subseteq Z$ are favorable according to the team of experts. These parameters can be further classified as follows:

• The parameter “Size” includes medium, large, very large.

• The parameter “Material Quality” includes low, medium, and high.

• The parameter “Cost” includes low, medium, high.

• The parameter “Soil Condition” includes slit soil, clay soil, loamy soil.

The report collected from the team of experts is in the form of an IV3FSS, which is displayed by Table 38.

Table 38 Tabular representation of the IV3FSS $(\eta ,C)$

By using Equations (3) and (4), the scores of lower and upper bounds for every pole (interval) are given in Tables 39 and 40 .

Table 39 Scores of lower bounds for each pole of IV3FSS $(\eta ,C)$

Table 40 Scores of upper bounds for each pole of IV3FSS $(\eta ,C)$

From Definition 13, the tabular representation for the accumulated scores of membership degrees of IV3FSS $(\eta ,C)$ with respect to each parameter is displayed by Table 41.

Table 41 Accumulated score with respect to each parameter of membership degrees of the IV3FSS $(\eta ,C)$

By Definition 14, the final score of every site $\textit{u}_i$ is displayed Table 42.

Table 42 Final score table

Clearly, from Table 42 the object having highest score is $\textit{u}_{1}$ because $S_{1}=7.1$. Thus, $\textit{u}_{1}$ is the most suitable rotavator from all the available alternatives. From Table 42, it can be readily computed that $B^{'}=\{c_1, c_2\}\subseteq C$ such that $C-B^{'}=\{c_4\}$ is the only PR-OC. Regrettably, there is no RB-PR and NPR in the present situation.

Figure 2 presents a flowchart to compute the parameter reductions of IVmFSSs.

Fig. 2

Flowchart of the suitable parameter reduction approach

5 Comparison

This section provides a detailed comparison among the reduction methods developed in Sect. 3, in terms of their respective reduction of computational speed and scope of application. It also gives a comparative discussion between the IVmF model developed in this paper and some existing models.

5.1 Comparison of reduction of computational speed and scope of application

Suppose that $\kappa$ represents the number of parameter reductions calculated in one or more data-sets. Basically, $\kappa$ denotes the application scope of the developed reduction approaches in different situations and described as computation speed in reduction techniques.

• PR-OC only preserves the maximum score value, that is, decision object. That is the reason why PR-OC is an easy and fast way to compute reduction set. For example, $\{\textit{c}_1\}$ is the PR-OC in Example 7, $\{\textit{c}_1\}$ is the PR-OC in Example 8, $\{\textit{c}_4\}$ is the PR-OC in Example 10, $\{\textit{c}_2\}$ is the PR-OC in Example 11. Hence, $\kappa =100\%$ because in all presented numerical examples we easily computed PR-OC.

• The RB-PR approach maintains the rank of all alternatives under consideration. Therefore, RB-PR is difficult as compared to PR-OC because this reduction method not only preserves rank of optimal decision object but also sub-optimal choices. For example, $\{\textit{c}_3,\textit{c}_4\}$ is the RB-PR in Example 10 and $\{\textit{c}_2\}$ is the RB-PR in Example 11, It can be easily see that we find no RB-PR in Examples 7 and 8 . Thus, $\kappa =2/4=50\%$.

• NPR preserves not only rank but also maintain final score values of objects. The computation of NPR in a given problem is difficult as compared to aforementioned reduction techniques. Clearly, $\{\textit{c}_2\}$ is the only NPR in Example 11. Unfortunately, we compute no NPR in Examples 7, 8 and 10 . Hence, $\kappa =1/4=25\%.$

As we know, in the case of NPR the reduction set can be reused if new parameter added in the set of parameters. Now we give an example to examine this issue.

Example 12

Let $\{\textit{c}_1^{'},\textit{c}_2^{'}\}$ be the set of parameters we wish to add in the IVmFSSs $(\eta ,C)$ in Example 11 where

$$\begin{aligned} \eta (\textit{c}_1^{'})&=\big \{\langle \textit{u}_1,[0.6, 0.8],[0.4, 0.5],[0.6, 0.7]\rangle , \langle \textit{u}_2,[0.3, 0.4],[0.2, 0.3],[0.5,0.7]\rangle , \langle \textit{u}_3,[0.8, 0.9],[0.2,0.3],[0.1, 0.4]\rangle ,\\&~~~~~~\langle \textit{u}_4,[0.5, 0.6],[0.9, 1.0],[0.4,0.5]\rangle \big \},\\ \eta (\textit{c}_2^{'})&=\big \{\langle \textit{u}_1,[0.5, 0.7],[0.3, 0.5],[0.8, 0.9]\rangle , \langle \textit{u}_2,[0.2, 0.4],[0.8, 0.9],[0.5, 0.7]\rangle , \langle \textit{u}_3,[0.3, 0.4],[0.2, 0.3],[0.5, 0.7]\rangle ,\\ {}&~~~~~~\langle \textit{u}_4,[0.3, 0.5],[0.7, 0.8],[0.6, 0.9]\rangle \big \}. \end{aligned}$$

For the parameters $\textit{c}_1^{'}$ and $\textit{c}_2^{'}$, the final scores of the lower and upper bounds of membership degrees are displayed in Table 43.

Table 43 Added parameters score

By combining Tables 31 (Final score table of IVmFSS $(\eta ,C)$) and Table 32 (NPR for the IVmFSS $(\eta ,C)$) with Table 43 (added parameters final score table). From Tables 44 and 45 , one can readily find the following partitions.

$$\begin{aligned} D_{C+\{\textit{c}_1^{'},\textit{c}_2^{'}\}}=\{\{\textit{u}_4\}_{6.3},\{\textit{u}_1\}_{4.7},\{\textit{u}_3\}_{-3.3},\{\textit{u}_2\}_{-7.7}\}, \end{aligned}$$

and

$$\begin{aligned} D_{\{{\textit{c}_2}\}+\{\textit{c}_1^{'},\textit{c}_2^{'}\}}=\{\{\textit{u}_4\}_{6.3},\{\textit{u}_1\}_{4.7},\{\textit{u}_3\}_{-3.3},\{\textit{u}_2\}_{-7.7}\}, \end{aligned}$$

respectively. Thus, the rankings are similar in both cases. Hence, re-usability of reduction set is maximum in NPR case.

Table 44 Final scores table after adding new parameters

Table 45 NPR

5.2 Discussion

In this section, we give a comparison of the developed model with certain existing hybrid models and also provide a comparative analysis of the proposed reduction approaches with some existing reduction methods.

• 1. IVmFSSs constitute a generalized structure of IVmF sets or mF soft sets because they are still a function from set of parameters to the set of IVmF subsets of universal set.

  • IVFSS is arising as a significant model and has been attracted by many researchers. When $m=1$, the developed model degenerates into IVFSS model (Yang et al. 2009). To check the validity of the proposed model, decision-making method presented by Yang et al. (2009) applied to the developed Application in Sect. 4 and the experimental results are displayed in Table 46. One can easily observe from the Table 46 and Fig. 3 that optimal and sub-optimal decision objects are different. Since, $\textit{u}_{15}$ is the optimal decision object by the proposed decision-making method, that is, IVmFSSs, Clearly, $\textit{u}_{19}$ is the optimal decision object by the IVFSS model (Yang et al. 2009). Similarly, it can be readily see from the Table 47 that the overall rankings are also different for the proposed IVmFSS model and IVFSS model (Yang et al. 2009). The reason behind these differences is that IVFSSs (Yang et al. 2009) only consider one pole (one membership value) with respect to parameters, that is, in this case for a particular parameter its all properties are not considered which may lead to wrong decision because all the parameters and their further characterizations (poles) are independent. That’s why, when we consider all possible further features of a particular parameter, the ranking of optimal and suboptimal choices changed or we can say more exact decision choices computed because in the case of IVmFSSs decision is made on the basis of all the possible information in a given decision-making problem. Thus, IVmFSS model is more generalized because it has strength to consider all possible properties of any parameter in a decision-making problem as compared to IVFSSs (Yang et al. 2009).

  • When only one parameter and some of its characteristics are considered in decision-making process of the IVmFSSs, it degenerates into IVmF set theory (Mahapatra et al. 2020). We now apply the decision-making method proposed by Mahapatra et al. (2020) to the developed application in Sect. 4 and the obtained results are given in Table 46 and displayed by Fig. 3. From the Table 46 and Fig. 3, it can be easily see that $\textit{u}_{15}$ and $\textit{u}_{9}$ are the optimal decision objects for the proposed IVmFSSs and IVmF sets (Mahapatra et al. 2020), respectively. The reason behind these differences is that in a given problem all the parameters are independent, that is, their membership values are not dependent to each other. Intuitively, if there exist more than one important parameters in a given problem then IVmF set model (Mahapatra et al. 2020) only consider one parameter which may lead to wrong decision because in this case some important parameters may be missed in the decision-making process. Therefore, IVmFSS model is an extension of IVmF set model with respect to parameters and provides more accurate results than IVmF sets (Mahapatra et al. 2020).

  • Chen et al. (2014) proved that 2-polar fuzzy sets and bipolar fuzzy sets (YinYang bipolar fuzzy sets) are cryptomorphic mathematical tools. According to this strong fact, interval-valued bipolar fuzzy soft set model and IV2FSS model are crypotomorphic mathematical notions. Thus, interval-valued bipolar fuzzy soft set model is a particular case of our proposed IVmFSS model, for $m=2$.

  • When the mF values are fixed, that is, not in the interval form, IVmFSS model degenerates into mF soft set model (Akram et al. 2018).

  Thus, our proposed model is a generalization of the IVFSS model (Yang et al. 2009), IVmF set model (Mahapatra et al. 2020) and mF soft set model (Akram et al. 2018).

• 2. PR-OC approach only preserves the decision object invariant after reduction (it means, the ranking order of sub-optimal object may be varied after reduction). Thus, the re-usability of reduction set is lower. RB-PR method removes redundant parameters by keeping the partition and ranking order of all elements under consideration. Thus, the re-usability of reduction set is higher than PR-OC. With similar arguments, it is clear that the re-usability of reduction set is highest in case of NPR method. A comparison between the optimal decision values obtained by proposed IVmFSS model and its PR-OC on the Application explored in Sect. 4 is displayed in Fig. 4. Moreover, reduction set is obtained by applying the parameter reduction techniques discussed in (Ma et al. 2014) for IVFSS and is compared with reduction set computed for IV3FSS in Application 1 (Sect. 4). For more clarification, the obtained results are displayed in Fig. 5.

Table 46 Comparison with different hybrid models in Application 1 (Sect. 4)

Table 47 Comparison between rankings of proposed IVmFSS model with existing hybrid models in Application 1 (Sect. 4)

Fig. 3

Comparison with existing hybrid models in Application 1 (Sect. 4)

Fig. 4

Comparison between proposed model and its PR-OC in Application 1 (Sect. 4)

Fig. 5

Comparison between PR-OC (IVmFSSs) and PR-OC (IVFSSs in Ma et al. 2014) in Application 1 (Sect. 4)

6 Conclusions and future directions

The theory of IVFSSs is arising as a helpful expansion of soft sets which is upheld by genuine data-sets. In this study, we have improved upon the hypothetical premise of this theory in directions that are validated by their impact on specific settings and their role in various theories. In this context, we have developed a novel hybrid model, namely, IVmFSSs. It produces a formal generalization of many existing models. It can be regarded as a multi-fuzzy extension of the IVFSS model. Alternatively, it can be considered as a IVmF extension of the soft set model (Molodtsov 1999). At one and the same time, it is an interval-valued extension of the mF soft set model (Akram et al. 2018). Some fundamental operations, including complement, union, intersection, “AND”, “OR” are studied on the IVmFSSs and investigated through examples. An algorithm is developed to handle decision-making situations having data in interval-valued multi-fuzzy soft form, which has been applied on two numerical examples. In addition, three parameter reduction approaches in algorithmic expression are proposed for IVmFSSs, namely, PR-OC, RB-PR and NPR. After that, two real case studies for the selection of best site for an airport construction and best rotavator are explored. Finally, the significance and rationale behind the new hybrid model and its parameter reduction methods are discussed, particularly through a comparative analysis with some existing approaches like IVFSSs ( Yang et al. 2009).

We may advance some lines of research whose examination should produce innovative contribution:

• Alternative methodologies from additional perspectives for parameter reduction are still possible, regardless of whether they are original or imported from external settings.

• Our overall research objectives can be exported to other relevant settings such as spherical fuzzy soft sets (Perveen et al. 2019).