Abstract
Nowadays, breast cancer is the leading cause of cancer death for women all over the world. Since the reason of breast cancer is unknown, early detection of the disease plays an important role in cancer control, saving lives and reducing costs. Among different modalities, automated 3-D breast ultrasound (3-D ABUS) is a new and effective imaging modality which has attracted a lot of interest as an adjunct to mammography for women with dense breasts. However, reading ABUS images is time consuming for radiologists and subtle abnormalities may be overlooked. Hence, computer aided detection (CADe) systems can be utilized as a second interpreter to assist radiologists to increase their screening speed and sensitivity. In this paper, a general architecture representing different CADe systems for ABUS images is introduced and the approaches for implementation of each block are categorized and reviewed. In addition, the limitations of these systems are discussed and their performance in terms of sensitivity and number of false positives per volume are compared.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Breast cancer has become a real concern in various countries especially in the west. According to statistics, breast cancer is the most common cancer as well as the leading cause of cancer death in women aged 20–59 years (Siegel et al. 2016). Nowadays, different imaging modalities are utilized for early detection of breast cancer (Tornai et al. 2007; Durá et al. 2006) among which mammography is the most common imaging tool (Sree et al. 2011). Although mammography is treated as a gold standard screening technique (Drukteinis et al. 2013), it has some limitations. For example, its sensitivity degrades for young women and women with dense breasts. Moreover, it is notable that mammography is not recommended for pregnant and/or lactating women as well as women with certain types of wastes and abscesses (Wilczek et al. 2016) due to exposure to X-ray (because it may increase the risk of incidence for high-risk women). Furthermore, mammography may result in too many false positives such that 65–85% of cases are wrongly undergone biopsy surgery (Pena-Reyes et al. 2002). These unnecessary surgeries are expensive and stressful for patients. Therefore, utilizing a complementary modality beside mammography may increase the screening performance.
Handheld ultrasound (HHUS) is a common adjunct to mammography but it has some limitations such as its operator dependency. In addition, simultaneous gathering and interpretation of images make radiologists exhausted and may increase the missing rate of cancers. Another disadvantage of HHUS is that it is not reproducible. Reproducibility is essential when radiologists aim to assess the changes of lesions in certain time intervals (Drukker et al. 2014). Some disadvantages of the most common breast imaging modalities are summarized in Table 1.
1.1 Automated breast ultrasound acquisition systems
Recently, automated 3-D breast ultrasound system (ABUS) as a novel modality was developed to overcome the drawbacks of the traditional 2-D ultrasound. It usually involves compression of a membrane on the breast. On top of the membrane, with one swipe of a wide linear or curved transducer, a number of transversal images are generated. Some ABUS systems support 3-D reconstruction by which coronal and sagittal planes are also available. The 3-D volumes can be stored in picture archiving and communication system (PACS) so that they can be used for temporal comparisons. Depending on the size of the breast, usually 3–5 image acquisitions on different positions of the breast are made to cover the whole breast volume. Contrary to 2-D ultrasound, it is possible to view spiculation patterns associated with malignancy on coronal planes. Since the imaging procedure is standard, it is possible to perform temporal analysis on prior and current exams. Additionally, it has been shown that using ABUS images leads to high reliability of detection (Wenkel et al. 2008) and for mammographically dense breasts it could improve cancer detection in asymptomatic women (Giuliano and Giuliano 2013).
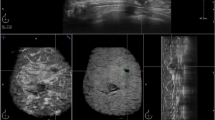
There are different automated 3-D breast ultrasound systems which are commercially in use. Most common systems include SonoCine ultrasound system, Somo-V automated 3-D breast ultrasound system, Invenia automated breast ultrasound, ACUSON S2000 automated breast volume scanner, Sonix Embrace automated breast ultrasound, SVARATM warm bath ultrasound breast imaging system and SOFIA 3D breast ultrasound system. These systems mainly differ in manually or automatically moving a 2-D transducer array across or around the breast with or without compression. Additionally, some systems further generate a 3-D volume in which the breast can be visualized in three orthogonal views (Tan 2014). An example set of 3-D ABUS images generated by Somo-V is depicted in Fig. 1. In addition to the aforementioned differences between ABUS systems, the width and frequency of the transducers also vary which result in different image resolutions. Moreover, the patient positioning for imaging is also different. Table 2 summarizes the main imaging properties of different ABUS systems.
2 Computer aided detection systems
The workload and cost of image acquisition using automated ultrasound systems are decreased compared to HHUS such that acquisition time for one exam for Siemens and U-System/GE is between 6 and 10 min, but the workload of radiologists is dramatically increased due to high number of slices (a volume may have 700 slices) as well as different views produced for each case. Therefore, screening process will be time consuming for radiologists and they may miss small and subtle lesions (Tan 2014). Hence, the computational capability of computers can be utilized as a second interpreter or concurrent reader to assist radiologists (van Zelst et al. 2018). If researchers successfully design a computerized system which automatically shows suspicious regions, then radiologists can focus on these regions and evaluate them more precisely. When image resolution and number of slices in each volume are increased it will be desirable to use computer aided systems to help radiologists in finding lesions. In this paper, a comprehensive study concentrating on computer aided mass detection (CADe) in ABUS volumes is presented. Most of CADe systems follow the general block diagram shown in Fig. 2 for finding masses.
Preprocessing is an essential step in medical image processing especially for ultrasonic images. Preprocessing in ABUS images is generally categorized into four sections: (1) despeckling (2) edge enhancement (3) gray level normalization (4) reduction of volume of interest (VOI).
The second block of the diagram determines the maximum sensitivity of a CADe system so that if a mass is missed in this step, it cannot be retrieved anymore. Therefore, this module is the most important component of the mass detection block diagram. For this reason, most of the CADe systems have been concentrated on this component and their main novelties have been emerged for this block. The most challenging issue of this component is related to mass shape, mass size and margins, because masses are very different in shape and size and they also have weak and unclear boundaries in ABUS images. Therefore, it is difficult to design a robust method for finding such variable structures. Moreover, any lesion detection method for ABUS images deals with a volumetric image (not a 2-D image) that makes the problem more challenging. The obtained regions from candidate regions extraction component contain some false positives which should be reduced. Most researchers use a classifier as an adaptive filter to learn patterns of false positives and true positives and then apply the classifier on test samples to discard false positives from candidate regions. Each classifier needs a feature vector corresponding to each sample in the training phase.
The third block in the CADe diagram is responsible for forming feature vectors regarding to candidates’ shape, texture and margins. Because of high dimensional space of features related to the 3-D candidate regions, feature selection methods are potential solutions to address the curse of dimensionality by excluding irrelevant and redundant features. After constructing feature vectors for the candidate regions, some of them are used for training and the rest for testing. Various testing strategies can be used for classifier performance evaluation among which cross validation is the most popular. To evaluate CADe systems, a FROC curve is generally used based on which several operating points are determined as the final outputs of the system.
3 Related works
In this section, the building blocks of a common CADe system including preprocessing, candidate regions extraction, false positive reduction, and CADe evaluation are described in details. For each building block, the state-of-the-art methods are investigated and their limitations are explained.
3.1 Preprocessing
Preprocessing is a major step for different medical image processing tasks. In mass detection for ABUS images, it directly affects the performance of the following building blocks such as candidate regions extraction as well as feature extraction for false positive reduction. In the following subsections, different preprocessing tasks including despeckling, edge enhancement, grey level normalization, and volume reduction are described.
3.1.1 Despeckling
The most important preprocessing of either 2-D or 3-D ultrasonic images is speckle noise reduction. Although speckle noise belongs to the category of multiplicative noises, some denoising methods which have been designed for additive noises can be utilized for ABUS images. To this end, a logarithm operator is applied to the noisy image (which is formed from a noise free image multiplied by a noise pattern). By applying logarithm on the image, multiplication operator (×) is transformed into addition operator (+) and hence additive noise removal methods can be used for multiplicative noise reduction. Despeckling methods are generally categorized into three classes: (1) spatial domain filters (2) wavelet domain filters and (3) compounding approaches (Cheng et al. 2010).
All despeckling methods used in 3-D ABUS images belong to the fist category (i.e. spatial domain filters) and other categories have not been tried. Spatial domain filters are divided into linear and nonlinear filters. Linear filters are not recommended for despeckling task since they blur edges too much without sensible noise attenuation. Nonlinear filters such as statistical filters have been applied as alternative despeckling approaches. Order statistical filters are proper for noises whose probability density functions have significant tails. Median filter is a special type of order statistical filters that preserves edge sharpness and has less blurring effect (Ikedo et al. 2007). In spite of edge preservation, median filter displaces edge positions and its despeckling effect is not good.
Another popular non-linear filter is anisotropic diffusion filter (ADF) which is an adaptive filter in which diffusion orientation and diffusion coefficient are controlled by an edge detector function (Chang et al. 2010). Noise reduction and edge enhancement simultaneously progress in ADF via solving a PDE equation. ADF was inherently developed for additive noise removal and not for multiplicative noises like speckle noise. Speckle Reducing Anisotropic Diffusion (SRAD) is particularly designed for despeckling (Yu and Acton 2002) but it is not applicable for CADe systems in ABUS images because a bounding box needs to be initialized whose variance corresponds to the noise variance. In fact, that bounding box must be placed in a region that is certainly a constant region in reality and its inhomogeneity is due to noise. The variance of the bounding box converges to zero during the evolution of SRAD. The key issue about SRAD is that it highly depends on the bounding box while the location of a constant region is unknown for the users. This crucial limitation makes SRAD inappropriate for despeckling of ABUS images in CADe systems (Kozegar et al. 2017).
Sigma filter is another filter that has been used for despeckling in ABUS images (Lo et al. 2014a; Moon et al. 2013). This filter derives a Gaussian distribution with mean µ and standard deviation σ from a neighborhood around a given central pixel. Subsequently, the number of neighbors (m) in the range [μ − 2σ, μ + 2σ] is calculated. If this number is greater than a predefined threshold (k) then the central pixel value is replaced by the average of those m neighbors. Otherwise, it is replaced by the average of all neighbors. Sigma filter’s performance highly depends on determining the value of k such that if k is considered large the sigma filter acts like a simple average filter and blurs the edges. On the other hand, if k is taken small then the denoising effect is not considerable.
Moon et al. used image clustering to remove speckle noise (Moon et al. 2014). They applied mean shift to each voxel separately to partition the input image. The main drawback of their method is the lack of a proper strategy to determine the number of clusters. If the number of clusters is taken low then adjacent regions with close intensities are merged and form a new region while they would be two different regions in reality. On the other hand, if the number of clusters is considered high, over-segmentation takes place.
Kozegar et al. (2017) used Optimized Bayesian Non-Local Mean (OBNLM) filter (Coupé et al. 2009) for despeckling and showed that it outperforms other state-of-the-art denoising methods such as Block Matching and 3-D filtering (BM3D) (Dabov et al. 2007), Bayes-Shrink (Chang et al. 2007), K-SVD (Elad and Aharon 2006) and Total Variation (Chang et al. 2007). OBNLM drastically removes speckle noise while it preserves edge sharpness. Table 3 summarizes pros and cons of despeckling methods of CADe systems for 3-D ABUS images.
3.1.2 Edge enhancement
Edge enhancement is another preprocessing operation which improves the performance of CADe systems. Only one method called stick filter (Awad J 2003) has been used to enhance lines in ABUS images (Chang et al. 2010; Lo et al. 2014a; Moon et al. 2014). Sticks are line segments with different orientations which are applied as templates to the image. This filter is implemented as follows: an Ns × Ns square is considered around a central pixel. 2Ns-2 lines with thickness of Ns pixels can be considered from the center of this square. Average values of all pixels on each line segment are calculated, and the maximum value is assigned to the central pixel. This filter only enhances lines and other non-linear features such as corners are not improved.
3.1.3 Grey level normalization
Grey level normalization is another important preprocessing which increases the robustness of CADe systems (Tan et al. 2013a) since databases usually include images which are acquired from different medical centers at different times. Obviously, different versions of devices with different settings may have been used to gather those images. Therefore, gray levels of tissues (like fat tissue, mass tissue, etc.) vary from patient to patient. Tan et al. used (1) for normalization:
where \( {\text{I}}_{\text{o}} \) is the original voxel intensity, \( {\text{I'}}_{97} \) is the 97th percentile and \( {\text{I'}}_{5} \) is the 5th percentile of intensity values of voxels, and \( {\text{I}}_{97} \) and \( {\text{I}}_{5} \) are constants representing reference values for the 97th percentile and the 5th percentile of intensity values, respectively. Tan et al. chose the percentiles empirically. These percentiles are used to avoid the influence of outliers on the normalization.
3.1.4 Volume reduction
Reduction of volume that is under processing by CADe system acts as another preprocessing which reduces false positives. Tan et al. excluded the top 6 mm slices to avoid responses of skin tissue and they also discarded tissues with more than 18 mm depth to minimize the presence of lung volume (Tan et al. 2013a). Kozegar et al. ignored the first seven and the last seven coronal slices because those slices are related to the skin and beyond the ribs wherein no masses would be emerged (Kozegar et al. 2017). Tan et al. proposed a novel method for detection of chest wall region to discard voxels which are placed beyond the ribs (Tan et al. 2013b). A sufficient reduction of volume of interest improves the performance of a CADe system in terms of speed and false positive rate.
3.2 Candidate regions extraction
Candidate regions extraction is the most important component of CADe systems and most novelties of CADe systems for ABUS images are related to this component. In this section, the proposed methods for this component are explained in details.
3.2.1 Toboggan watershed
Lo et al. (2014b) used a specific type of watershed called Toboggan Watershed for whole ABUS image segmentation. In toboggan based watershed, pixels slide to a local minimum. In this way, each pixel is connected to its minimum neighbor. This process is repeated for that minimum neighbor until a local minimum pixel is met. At last, all pixels which are connected to a common local minimum construct a catchment basin. The main problem of watershed based algorithms is over-segmentation. In (Lo et al. 2014b) a concept named minimum watershed depth was used to merge catchment basins to minimize over-segmentation. As indicated in Fig. 3, the minimum watershed depth is defined as the difference in height between a local minimum and the adjacent lowest point on watershed lines. Based on this method, two adjacent basins are merged if difference of their depth is smaller than a predefined threshold. In (Lo et al. 2014b) this threshold was set to 1/4 of the maximum watershed depth.
Watershed depth concept in toboggan based watershed (Lo et al. 2014b)
However, this method has some limitations. As mentioned above, all watershed algorithms suffer from over-segmentation problem. In spite of proposing the concept of watershed depth, the problem still remains when the algorithm encounters malignant tumors including hyper-echoic regions which result in separate catchment basins. This phenomenon degrades the performance of the CADe system since the shape of the segmented tumor, which inscribes those hyper-echoic regions, drastically deviates from the shape it should have. Moreover, these extracted hyper-echoic regions may increase the number of false positives of the detection system. It should be noted that the authors did not perform any sensitivity analysis on minimum watershed depth parameter while it seems that the performance of the proposed CADe system highly depends on this threshold.
3.2.2 Multi resolution blob detection
Moon et al. proposed a scale invariant blob detection algorithm based on the observation that tumors in ABUS images have blob-like structures with different sizes (Moon et al. 2013). In their method, blob like structures are enhanced based on eigenvalues of Hessian matrix which includes second derivatives along x, y and z directions. These derivatives are computed by convolving the original image with derivatives of a Gaussian kernel. The Hessian matrix is calculated as:
where σ controls the radius of blob-like structures which should be enhanced (i.e. greater values of σ lead to enhancement of bigger blob structures). In the proposed method, eigenvalues and eigenvectors are computed for each pixel. Subsequently, the likelihood of blob like structures (RB) and the magnitude of eigenvalues (M) are formulated as:
where λ1, λ2 and λ3 are the eigenvalues of the Hessian matrix in descending order. For blob structures, curvatures along all three perpendicular axes are almost equal and their magnitudes are high. Therefore, both RB and M are higher for object voxels compared to those of background voxels. Hence, they can be combined to discriminate objects and background. The combined formulation is as follows:
where \( \lambda_{p} \) indicates eigenvalue in position p. α and β denote the sensitivity parameters for RB and M, respectively, which control their contribution in (5). Therefore, a probability image is obtained in which a probability value is assigned to each voxel. Candidate regions can be extracted by thresholding the probability image. It should be noted that no thresholding value is mentioned by the authors in spite of its importance. The main advantage of this method is its invariance to scale because it considers different values of σ. On the other hand, the main drawback of this system returns to (3). The authors claim that the value of RB will be high for masses and this is a true proposition but the challenging issue is that the value of RB will be high for other structures such as vessels (i.e. lines) and circular fatty tissues (i.e. blobs which appear in only one slice) since denominator of the fraction in (3) is small for these structures. Therefore, these false structures will be extracted as candidate regions and hence degrade the performance of the mass detection system.
3.2.3 Using edges and intensity changes
Ikedo et al. introduced a new idea for mass detection in ABUS images (Ikedo et al. 2007). Based on their idea, the edge image obtained from a normal image consists of semi horizontal edges while edge image of an abnormal image contains semi vertical edges near the mass boundary. They found that the mass boundary either consists of two semi vertical edges or it is a combination of two semi vertical and one semi horizontal edges. In their method, semi horizontal edges in the posterior boundary were ignored due to posterior echo attenuation of some masses. Their proposed mass detection algorithm includes the following steps. At first, a 3-D edge image is obtained using Canny edge detector followed by a thinning algorithm (they called it EI). Afterwards, two types of edge images are constructed; one contains near vertical edges (n-VEI) and the other contains near horizontal edges (n-HEI). The first image (n-VEI) is obtained by subtracting EI from a translated version of EI along x axis and the second image is generated by subtracting n-VEI from EI. Then, several ROIs are extracted to determine if there are objects matching the above assumptions. In addition to this method, they used another candidate extraction algorithm separately and added its results to the previous candidate regions to increase the sensitivity of their CADe system. In this complementary method, intensity difference between consecutive slices is utilized for mass detection. This idea comes from the fact that radiologists interpret the whole 3-D image as a movie with consecutive frames. They actually pay attention to regions whose intensity differs from the previous or next slices.
Jeong et al. used another idea based on edge detection (Jeong et al. 2016). After applying median filtering and contrast enhancement to the original image, Canny edge detector is used to generate a binary image. Then, a 3-D Hough transform is performed to detect globular objects. Afterwards, to reduce false positives, they proposed to discard globular regions whose center intensity is greater than the mean intensity of the region. It should be noted that masses with posterior shadows would be challenging for this method since for those cases the shadow is connected to the mass and obviously the mass shape deviates from a globular shape.
All edge based methods suffer from a general problem in designing CADe systems for ABUS images. The problem is related to the low quality of the images as well as the complex tissue structure of breasts. Masses usually have weak edges in ABUS images which results in many discontinuous lines along border of masses. In addition, due to complexity of breast tissues many false edges emerge which degrade the performance of the CADe system.
3.2.4 Clustering
Clustering aims to categorize voxels such that samples in each cluster are similar to each other but differ from the samples in other clusters. All clustering approaches used for mass detection in ABUS images are classical algorithms.
Chang et al. proposed a method, for detection of masses and cysts in which gray levels of images are divided into 4 intervals: 0–26, 27–42, 43–71 and 72–255. Cysts belong to the first interval and masses appertain to the second and third intervals. The last interval is dedicated to the fibrous and glandular tissues as well as microcalcifications. After this categorization, the value of all voxels within a given cluster is replaced by the mean intensity of that cluster (Chang et al. 2010). The main drawback of this method is its low generalizability since it uses constant thresholds and is applicable only to cases which are obtained by constant time gain compensation (TGC) and dynamic range.
Drukker et al. used classical k-means clustering to detect mass candidate regions (Drukker et al. 2014). They studied women whose cancer was not detected in mammography screening and also women who belong to category 3 or 4 after BIRADS evaluation (i.e. women with heterogeneous dense breasts or very dense breasts) and they were referred for sonography scanning. According to their method, the whole volume of breast is divided into three clusters: a bright cluster indicating parenchyma, a dark cluster indicating nipple and a cluster of candidate regions. After clustering, they used an adaptive thresholding for 3-D segmentation in which a 2 × 2 × 2 cuboid is considered around the center of each region. The threshold value is the minimum intensity within the cuboid. After thresholding, the region that contains the center is regarded as a candidate region and other regions are excluded.
Fuzzy C-Means (FCM) is another classical clustering algorithm which usually results in better clusters than k-means. Lo et al. used FCM to cluster grey levels of ABUS images and assumed the number of clusters is 4 (Lo et al. 2014a). Pixels of the darkest cluster are selected and the others are removed. Afterwards, candidate regions are extracted using connected component labeling. Moon et al. used FCM clustering followed by a merging strategy to reduce the number of false positives (Moon et al. 2014). Based on their strategy, two adjacent regions are merged if the difference of their mean intensities is smaller than 4.
It is notable that the most challenging parameter in clustering approaches is the number of clusters. As mentioned above, some researchers considered three clusters and the others set it to four. Changing the number of clusters severely influences the results. Moreover, classical k-means and FCM are sensitive to the initialization of seed points. This sensitivity may affect the results after each run. Generally, clustering approaches for finding candidate regions are very trivial and researchers should try other state-of-the-art methods.
3.2.5 Supervised voxel detection
Tan et al. (2013a) trained five neural networks as voxel classifiers. For training this ensemble classifier, a set of labeled voxels is needed. In their dataset, the center positions of masses are known as ground truth. Since the average radius of masses was 9 mm, the authors decided to label all voxels within a ball with radius of 3.6 mm as mass voxels. On the other hand, voxels which were at least 18 mm far from the center were selected as normal samples. Then, seven important voxel features including depth, two types of contrast, two types of blobness and two types of spiculation were calculated for each sample voxel. After the training phase, when a 3-D test image is fed to the system, each classifier assigns one probability value to each voxel. The final probability for each voxel will be the mean probability of those five values. This value represents the voxel probability for being part of a mass. Therefore, a probability map is produced which is smoothed by a Gaussian kernel. Afterwards, a thresholding operation is performed on this probabilistic image and the resulting local maximas are given to the next module wherein an accurate 3-D segmentation is done using a dynamic programming method. In (Tan et al. 2015), Tan et al. used a relatively similar approach for detecting small tumors. They used Haar-like features beside the mentioned seven features to improve the detection rate of small tumors.
Ye et al. (2014) reused a topological texture based feature named Minkowski functional with gradient concentration filter for training a voxel classifier. The voxel classifier categorizes each voxel as mass or normal tissue. The authors applied the 2-D classification approach to sagittal, coronal and transversal views to generate 3-D mass candidates. Afterwards, a geodesic active contour (GAC) was used to produce more accurate candidate regions. They applied a directional search from the center of candidates to produce the edge map which GAC needs during its evolution process. It was demonstrated that the edge map production enables the algorithm to escape from local maxima.
3.2.6 Using iso-contours
Kozegar et al. introduced new findings for detection of masses in ABUS images (Kozegar et al. 2017). They showed that looking for dark circular regions to detect masses is not always effective because inside of masses is usually hyper-echoic and inhomogeneous. Based on their idea, although inside of some masses such as malignant masses are neither hypo-echoic nor homogenous, both of these properties increase near the mass boundary. Therefore, a contour called iso-contour (Wenger and Peters 2013) usually exists around masses in some consequent slices of the mass on which pixels have almost similar intensity values. Kozegar et al. quantized the original image and extracted all possible iso-contours. Then, many of false contours were discarded using domain specific knowledge to reduce false positives. In spite of high sensitivity of their method, it leads to many false positive regions.
Each of the described candidate region extraction methods has some limitations. Table 4 summarizes the limitations of different approaches.
3.3 False positive reduction
Many regions are wrongly considered as lesions in the candidate extraction module. The aim of this step is to reduce the number of false positives via supervised learning. For this purpose, a feature vector, which has high discriminability for normal and abnormal tissues, should be constructed for each candidate region. In the following three subsections, the features used for false positive reduction in ABUS images will be described. The fourth subsection explains the feature selection and classification methods.
3.3.1 Morphological features
Morphological features are generated based on shapes and margins of the objects. Some of them are extracted from projection of the objects on 2-D slices and the others are computed according to the whole 3-D region.
The most commonly used morphological feature is the volume of a detected region. This feature is useful for discarding very small regions representing noise as well as very big regions representing big fatty tissues and shadows (Kim et al. 2014).
Fatty tissues are generally seen as tinny and elongated regions in 3-D ABUS images. Therefore, to exclude fatty tissues, the ratio of the minor axis to the major axis can be used. Another important feature is region compactness which represents the circularity of a candidate. This feature has a value in the range [0, 1] and reaches to its maximum value for a circle (in 2-D) or a sphere (in 3-D).
Blobness is another feature which indicates how probable a given voxel is to be the center of a mass. After candidate extraction, the blobness value of voxels inside the region can be utilized for classification. For example, maximum, mean and standard deviation of those blobnesses can be considered as mass features.
The size of coronal region is another novel feature introduced in (Chang et al. 2010). A coronal image is generated by cross sectioning of sequential images in a given depth. Figure 4 illustrates an example of generating a coronal image from subsequent slices containing a mass. Generally, the coronal view of a mass is approximated by a dark ellipse. In addition, coronal area of a suspicious region is considerably large. Hence, a candidate can be excluded if the ratio of the area of an object to the area of coronal image is larger than a predefined threshold.
Formation of a coronal view from consequtive slices (Chang et al. 2010)
Lo et al. (2014a) used fitting ellipsoids to calculate morphological features such as the ratio of the minor axis to the major axis of the ellipsoid. Another feature is the angle between the major axis of the fitting ellipsoid and the x axis. They also used the overlapped area between the candidate region and the fitting ellipsoid as another feature.
3.3.2 Texture features
Texture features represent material properties of the objects such as roughness and homogeneity. First order moments belong to a type of features which are extracted from intensity histogram. Since masses look like dark regions, mean, standard deviation, skewness and kurtosis of the histogram can be used as first order moments. Lo et al. considered the contrast between a candidate region and its adjacent regions as a feature (Lo et al. 2014a). They defined the difference of intensity between these regions as:
where \( I_{Mean - adj} \) is the mean intensity of an adjacent region and \( N_{adj} \) is the number of adjacent regions.
Gray level co-occurrence matrix (GLCM) features are second order moments which have been frequently used for texture classification. After construction of GLCM matrices for different angles and displacements, various features such as energy, entropy, cluster shade, homogeneity and contrast can be extracted. For ABUS images, all these features are extracted from projection of regions onto 2-D slices. Therefore, they are useful for excluding false positives in 2-D slices and they can be somewhat extended to 3-D. Lo et al. (2014b) replaced features extracted from consequent slices by their average value. For example, they calculated energy feature for GLCM of each slice and the final energy feature was computed as the average of all energy values. Other features follow the same procedure.
Chang et al. (2010) introduced a new feature called non-persistence which has been inspired from background difference method in video processing. Calculation of this feature is as follows. Let ID be a frame including a mass. Based on ID, two sets of frames are defined: ID±p and \( I_{D}^{'} \); where ID±p represents consequent slices which may contain a mass. We assume the number of these frames is 2p + 1. To obtain the background image (IB), we skip all 2p + 1 frames and then the background image is calculated by averaging on \( I_{D}^{'} \). \( I_{D}^{'} \) includes frames which are b-a frames far from ID±p in forward direction or backward direction. Therefore, the intensity of each background pixel is computed as:
After generating the background image, the difference between ID and IB is calculated for each coordinate (x, y) within the candidate region and then a difference image is obtained. At last, average of difference values is regarded as non-persistence value.
In addition to the mentioned features, Tan et al. used coronal spiculation, gradient concentration, Haar, Gabor and GLCM features by considering different window sizes to detect small tumors (Tan et al. 2015). Based on their evaluation, using these features improves the sensitivity of CADe system for recognition of small masses whose radius is ranged between 1 and 5 mm.
3.3.3 Position based features
A simple and important feature to discard false positives is the depth where the candidate is appeared. In ultrasound images, features are changed once the depth is varied. Moreover, the likelihoods of emerging cancers for different depths are not the same. Depth feature can be used for discarding regions which are very close to skin as well as when they appear beyond the ribs.
The relative distance of candidates from specific reference structures such as nipple and chest wall have been used as features (Tan et al. 2013a; b). These reference structures usually produce dark regions which are wrongly regarded as masses. Tan et al. (2013a) used a 3-D circular Hough transform to detect nipple in the first slices of ABUS images. Moreover, they proposed a cylindrical model to detect ribs and chest wall (Tan et al. 2013b). Then, they proposed to use a negative distance for regions beyond the chest wall because those regions rarely contain a cancer. The minimum distance from the center of a candidate to the breast border can be used as another position based feature.
State-of-the-art methods usually use a combination of texture, morphological and positional features to reduce the number of false positives (Kozegar et al. 2017; Moon et al. 2013, 2014; Tan et al. 2013a, 2015). Table 5 summarizes these three types of features.
3.3.4 Feature selection and classification
To the best of our knowledge, all CADe systems for ABUS images have used stepwise backward/forward feature selection in which the classification error determines the merit of a feature set (Lo et al. 2014a; Moon et al. 2013; Kim et al. 2014). For a given feature set, if the classification error becomes smaller, that feature set leads to better results.
To reduce the number of false positive regions by classification, some authors defined their predefined rules as inductive bias. For example, if the mean intensity of a region is lower than a threshold then that region is discarded. In fact, they determined the threshold value by trial and error and not by considering distribution of samples in feature space. Such rules usually suffer from lack of generalizability due to constant thresholds. A better way is to use a classifier instead of constant rules. Most of the methods used in CADe systems for ABUS images have utilized traditional classifiers such as logistic regression, SVM, neural network and LDA. Some researchers have used ensemble of classifiers to improve the classification performance. Tan et al. (2013a) used an ensemble of 5 neural networks as their classifier. Kozegar et al. (2017) proposed an ensemble of four cascaded RUSBoosts (Seiffert et al. 2010). Each RUSBoost is trained on a different set of features. According to their cascading strategy, the imbalancity of training set is moderated using discarding false positives which are correctly classified by the previous classifier.
3.4 Deep learning based approaches
Defining discriminative features that well describe candidate regions directly affects the following classification step. Conventionally, domain specific features were formulated by experts according to their knowledge (Goceri and Songul 2018). However, the drawback of these hand-crafted features is the semantic gap between human and machine. Nowadays, deep learning has overcome this obstacle in a self-taught approach in which features are drawn in an unsupervised manner. These approaches are rapidly become state-of-the-art that usually outperform other competing methods (Goceri and Goceri 2017). A big advantage of deep learning approaches is that when the number of training images increases, the performance of the network improves.
Recently, various convolutional neural networks (CNNs) have been applied to common modalities such as mammography and 2-D sonography to detect abnormalities (Dhungel et al. 2015; Yap et al. 2017; Geras et al. 2017). However, few deep learning approaches have been designed for CADe systems in 3-D ABUS modality yet. To the best of our knowledge, only two methods have been developed for lesion detection in ABUS images. As the first attempt, Wang et al. (2018) utilized a 3-D U-Net basically introduced in (Ronneberger et al. 2015) as their backbone architecture and improved its performance by some modifications. Due to limited number of ABUS training samples as well as avoiding over-fitting issue, they used a pre-trained 3-D convolutional network (Tan et al. 2015) and fine-tuned the hyper-parameters of the network. Moreover, a densely deep supervision (DDS) mechanism was designed to capture the most discriminative features and to address the vanishing gradient issue. In addition, they employed Class-Balanced Cross Entropy (CBCE) loss to overcome the imbalancity problem of the dataset. The other contribution of the paper is concatenating and training a threshold map in the network to reduce the number of false positives. This layer adaptively refines the probability map for better detection. They showed the proposed 3-D U-Net outperforms other competing architectures such as 3-D SegNet (Badrinarayanan et al. 2017) and 3-D FCN (Long et al. 2017).
Chiang et al. designed a three stage method for tumor detection in ABUS (Chiang et al. 2019). In the first step, a fast sliding window detector is used to detect volumes of interest (VOIs). Each VOI is rescaled to 32 × 32 × 32. Afterwards, a 3-D CNN is applied to assign a tumor probability to each VOI. The architecture of the proposed 3-D CNN is similar to a simple VGG-Net with shallower depth. Finally, a prioritized aggregation scheme based on hierarchical clustering is proposed to merge overlapped VOIs with higher tumor probability.
3.5 CADe evaluation
Generally, free response operating characteristic curve is used for CADe evaluation and radiologists perform their analysis based on this curve. The horizontal and vertical axes indicate the average number of false positives per image (FPpI) and the system’s sensitivity, respectively. For constructing this curve, the most crucial variable of the algorithm (that is typically the classifier’s output) is thresholded to obtain different (sensitivity, FPpI) pairs. These pairs are connected to produce the whole FROC curve (Oliver et al. 2010). In literature, some operating points are reported to simplify the FROC curve for comparison. These operating points are qualitative points which depend on the radiologists’ points of view. Table 6 compares the operating points of different CADe systems. It is notable that all sensitivities are region based where all regions are treated independently because sometimes there are multiple cancers in one patient and detecting each of them is considered as a true positive.
4 Discussion
A number of existing computer-aided detection systems have been reviewed in this survey. The efficiency and effectiveness of these systems shall be investigated to answer the question that whether these systems can improve the performance of radiologists and meanwhile reduce the reading time which is essential for screening (Rella 2018). For example, van Zelst et al. (2017) showed that with an existing CADe system, the average area-under-the-curve (AUC) of the readers was significantly improved. Later in another reader study (van Zelst et al. 2018), it was found that CAD software for ABUS can decrease the screening time for dense breasts.
After investigating different CADe systems for ABUS images, it can be concluded that in spite of the necessity of noise reduction methods, they have been specially designed for additive noise and not for multiplicative noise such as speckle noise. In the future, it is expected that a 3-D despeckling method can be seamlessly applied to the whole breast region.
Most CADe systems have been concentrated on candidate regions extraction and their novelties are due to the improvements of this module because it determines the maximum sensitivity of the system such that if a lesion is missed in this step it is impossible to retrieve it later. Moreover, the accuracy of this module highly affects the performance of the next modules. For example, the morphological features would be useless if this module does not preserve the overall shape of the lesions. As another example, if the module results in too many false positives then their features dominate the feature space and bias the classifiers in favor of false positives. This phenomenon drastically degrades the sensitivity of CADe systems.
In feature extraction stage, researchers have usually adopted the feature extraction methods from 2-D ultrasonic images while we deal with 3-D regions in ABUS imaging. Especially in texture analysis, the CADe systems suffer from the lack of features representing texture in a 3-D fashion. Therefore, it is necessary to introduce features which preserve the spatial connection of voxels. For feature selection, to the best of our knowledge all methods have used the step wise backward method, which is a heuristic approach and would probably be trapped in local maximas, while state-of-the-art methods such as Minimum Redundancy Maximum Relevance (MRMR) (Hanchuan et al. 2005) have been frequently used in pattern recognition. As future works, the state of the art feature selection methods can be assessed to improve the accuracy of CADe systems.
Due to the high number of false positives which are extracted in the second module of CADe systems, single classifiers such as logistic, SVM and neural network are influenced by the dominated space of false positives. Hence, machine learning approaches are needed to overcome the problem of imbalanced datasets. One solution to this problem is using an ensemble of classifiers to improve the generalizability of classification. Another potential solution which has not been still utilized by researchers is sampling. To moderate the imbalancity of datasets, oversampling techniques can be used to increase the number of minor class samples or undersampling techniques can be utilized to decrease the number of major class samples.
Despite emerging various and very efficient deep learning models for object detection, few methods have been tried on ABUS images. Therefore, as a key solution, researchers are highly recommended to use deep learning to design CADe systems for cancer detection in 3-D ABUS images.
It is noteworthy that contrary to mammography and MRI, there is not yet any public dataset including ABUS images for evaluation and fair comparison of CADe systems. Each CADe system has been tested on a different dataset using a separate testing strategy and therefore the proposed CADe systems cannot be compared to each other statistically. Hence, gathering a dataset by medical centers and making it public for researchers can accelerate the evolution of CADe systems for ABUS images. The existence of such a dataset would motivate organizations to hold research challenges and events in the field of ABUS systems.
5 Conclusions
In this survey, we focused on 3-D automated breast ultrasound imaging modality which can lead to a revolution for early detection of breast cancer. In spite of the advantages of this modality, when image resolution and number of slices in each volume are increased, it will be inevitable to use computer aided systems to help radiologists in finding lesions. In this study, a common framework including four main components (preprocessing, candidate regions extraction, feature extraction and selection and classification) was depicted for all CADe systems for ABUS images. Moreover, state-of-the-art approaches for each component were surveyed and their novelties as well as their limitations were discussed. In addition, some ideas to address the challenges related to each component have been presented.
References
Awad J et al. (2003) Prostate’s boundary detection in transrectal ultrasound images using scanning technique. In: CCECE 2003—Canadian conference on electrical and computer engineering. Toward a Caring and Humane Technology (Cat. No.03CH37436), vol 2, pp 1199–1202
Badrinarayanan V, Kendall A, Cipolla R (2017) SegNet: a deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans Pattern Anal Mach Intel 39(12):2481–2495
Chang SG, Yu B, Vetterli M (2007) Adaptive wavelet thresholding for image denoising and compression. IEEE Trans Image Process 9:1532–1546
Chang R-F et al (2010) Rapid image stitching and computer-aided detection for multipass automated breast ultrasound. Med Phys 37(5):2063–2073
Cheng HD, Shan J, Ju W, Guo Y, Zhang L (2010) Automated breast cancer detection and classification using ultrasound images: a survey. Pattern Recognit 43(1):299–317
Chiang T, Huang Y, Chen R, Huang C, Chang R (2019) Tumor detection in automated breast ultrasound using 3-D CNN and prioritized candidate aggregation. IEEE Trans Med Imaging 38(1):240–249
Coupé P, Hellier P, Kervrann C, Barillot C (2009) Nonlocal means-based speckle filtering for ultrasound images. IEEE Trans Image Process 18(10):2221–2229
Dabov K, Foi A, Katkovnik V, Egiazarian K (2007) Image denoising by sparse 3D transform-domain collaborative filtering. IEEE Trans Image Process 16(8):1–16
Dhungel N, Carneiro G, Bradley AP (2015) Automated mass detection in mammograms using cascaded deep learning and random forests. In: International conference on digital image computing: techniques and applications (DICTA)
Drukker K, Sennett CA, Giger ML (2014) Computerized detection of breast cancer on automated breast ultrasound imaging of women with dense breasts. Med Phys 41(1):12901–12909
Drukteinis JS, Mooney BP, Flowers CI, Gatenby RA (2013) Beyond mammography: new frontiers in breast cancer screening. Am J Med 126(6):472–479
Durá E, Madhav P, Cutler SJ, Turkington TG, Tornai MP (2006) Initial comparison of registration and fusion of SPECT-CmT mammotomography images. In: Medical Imaging 2006: Image Processing, p 614438
Elad M, Aharon M (2006) Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans Image Process 15(12):3545–3736
Geras KJ, Wolfson S, Kim S, Moy L, Cho K (2017) High-resolution breast cancer screening with multiview deep convolutional neural networks, Mar 2017. Available at https://arxiv.org/abs/1703.07047
Giuliano V, Giuliano C (2013) Improved breast cancer detection in asymptomatic women using 3-D-automated breast ultrasound in mammographically dense breasts. Clin Imaging 37:480–486
Goceri E, Goceri N (2017) Deep learning in medical image analysis: recent advances and future trends. In: International conferences computer graphicscomputer Vision and Image Processing Visualization pp 300–304
Goceri E, Songul C (2018) Biomedical information technology : image based computer aided diagnosis systems. In: 7th international conference on advanced technologies
Hanchuan P, Fuhui L, Ding C (2005) Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans Pattern Anal Mach Intel 27(8):1226–1238
Ikedo Y et al (2007) Development of a fully automatic scheme for detection of masses in whole breast ultrasound images. Med Phys 34(11):4378–4388
Jeong J-W, Yu D, Lee S, Chang JM (2016) Automated detection algorithm of breast masses in three-dimensional ultrasound images. Healthc Inform Res 22(4):293
Kim JH et al (2014) Computer-aided detection system for masses in automated whole breast ultrasonography: development and evaluation of the effectiveness. Ultrasonography 33(April):105–115
Kozegar E, Soryani M, Behnam H, Salamati M, Tan T (2017) Breast cancer detection in automated 3D breast ultrasound using iso-contours and cascaded RUSBoosts. Ultrasonics 79:68–80
Lo C, Shen Y-W, Huang C-S, Chang R-F (2014a) Computer-aided multiview tumor detection for automated whole breast ultrasound. Ultrason Imaging 36(1):3–17
Lo CM et al (2014b) Multi-dimensional tumor detection in automated whole breast ultrasound using topographic watershed. IEEE Trans Med Imaging 33(7):1503–1511
Long J, Shelhamer E, Darrell T (2017) Fully convolutional networks for semantic segmentation. IEEE Trans Pattern Anal Mach Intel 39(4):640–651
Moon WK, Shen Y-W, Bae MS, Huang C-S, Chen J-H, Chang R-F (2013) Computer-aided tumor detection based on multi-scale blob detection algorithm in automated breast ultrasound images. IEEE Trans Med Imaging 32(7):1191–1200
Moon WK et al (2014) Tumor detection in automated breast ultrasound images using quantitative tissue clustering. Med Phys 41(4):042901
Oliver A et al (2010) A review of automatic mass detection and segmentation in mammographic images. Med Image Anal 14(2):87–110
Pena-Reyes CA, Sipper M, Prieto L (2002) Sensitive, specific, and interpretable: evolving a fuzzy mammographic-interpretation assessment tool. 2002 IEEE International Conference on Fuzzy Systems. FUZZ-IEEE’02. Proceedings, vol 2, pp 837–842
Rella R et al. (2018) Automated breast ultrasonography (ABUS) in the screening and diagnostic setting: indications and practical use. Acad Radiol 25(11):1457–1470
Ronneberger O, Fischer P, Brox T (2015) U-net: convolutional networks for biomedical image segmentation. In: International conference on medical image computing and computer-assisted intervention, pp 234–241
Seiffert C, Khoshgoftaar TM, Van Hulse J, Napolitano A (2010) RUSBoost: a hybrid approach to alleviating class imbalance. IEEE Trans Syst Man Cybern Part A Syst Humans 40(1):185–197
Siegel RL, Miller KD, Jemal A (2016) Cancer statistics. CA Cancer J Clin 66(1):7–30
Sree SV, Ng EY-K, Acharya RU, Faust O (2011) Breast imaging: a survey. World J Clin Oncol 2(4):171–178
Tan T (2014) Automated 3D breast ultrasound image analysis. Radboud University Nijmegen Medical Center, Nijmegen
Tan T, Platel B, Mus R, Tabar L, Mann RM, Karssemeijer N (2013a) Computer-aided detection of cancer in automated 3-D breast ultrasound. IEEE Trans Med Imaging 32(9):1698–1706
Tan T, Platel B, Mann RM, Huisman H, Karssemeijer N (2013b) Chest wall segmentation in automated 3D breast ultrasound scans. Med Image Anal 17(8):1273–1281
Tan T et al (2015) Computer-aided detection of breast cancers using Haar-like features in automated 3D breast ultrasound. Med Phys 42(4):1498–1504
Tornai M et al (2007) Initial hybrid SPECT-CT system for dedicated fully-3D breast imaging. J Nucl Med 48:45P
Tran D, Bourdev L, Fergus R, Torresani L, Paluri M (2015) Learning spatiotemporal features with 3D convolutional networks. In: ICCV, pp 4489–4497
van Zelst JCM et al (2017) Improved cancer detection in automated breast ultrasound by radiologists using computer aided detection. Eur J Radiol 89:54–59
van Zelst JCM et al (2018) Dedicated computer-aided detection software for automated 3D breast ultrasound; an efficient tool for the radiologist in supplemental screening of women with dense breasts. Eur Radiol 28(7):2996–3006
Wang N et al. (2018) Densely deep supervised network with threshold loss for cancer detection in automated breast ultrasound. In: Frangi AF, Fichtinger G, Schnabel JA, Alberola-López C, Davatzikos C (eds) Medical image computing and computer assisted intervention, vol LNCS 11073, Springer International Publishing, pp 641–648
Wenger R, Peters AK (2013) Marching cubes and variants. In: Carr H, Möller T, Alboul LS (eds) Isosurfaces: geometry, topology and algorithms, CRC Press, Boca Raton
Wenkel E et al (2008) Automated breast ultrasound: lesion detection and bi-rads classification-a pilot study. Fortschr Röntgenstr 180:804–808
Wilczek B, Wilczek HE, Rasouliyan L, Leifland K (2016) Adding 3D automated breast ultrasound to mammography screening in women with heterogeneously and extremely dense breasts: report from a hospital-based, high-volume, single-center breast cancer screening program. Eur J Radiol 85(9):1554–1563
Yap MH, Pons G, Mart J, Zwiggelaar R, Davison AK, Mart R (2017) Automated breast ultrasound lesions detection using convolutional neural networks. IEEE J Biomed Heal Inform 22(4):1218–1226
Ye C, Vaidya V, Zhao F (2014) Improved mass detection in 3D automated breast ultrasound using region based features and multi-view information. In: 36th annual international conference of the ieee engineering in medicine and biology society, pp 2865–2868
Yu Y, Acton ST (2002) Speckle reducing anisotropic diffusion. IEEE Trans Image Process 11(11):1260–1270
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kozegar, E., Soryani, M., Behnam, H. et al. Computer aided detection in automated 3-D breast ultrasound images: a survey. Artif Intell Rev 53, 1919–1941 (2020). https://doi.org/10.1007/s10462-019-09722-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10462-019-09722-7